1 Introduction

Thermal transfers are very important in many industrial areas. Several numerical and experimental methods have been developed to investigate enclosures with and without obstacle because these geometries have great engineering applications. Some applications are solar thermal receiver, cooling of electronic packages and heat exchangers.

Under certain circumstances, electronic components are packaged within sealed enclosures, while one or more of the walls are cooled. The main source of heat within the enclosures is electronic components and/or boards situated in various configurations. In this study, a complete numerical simulation is carried out to obtain the cooling performance of such electronic systems.

Over the past few decades, numerous theoretical, experimental and numerical efforts have been made to study the natural convection heat transfer. A numerical study was carried out by Refai and Yovanovich [2] to investigate the influence of discrete heat sources on natural convection heat transfer in a square enclosure filled with air. Nelson et al. [3] experimentally investigated the natural convection and thermal stratification in chilled-water storage systems. Oliveski et al. [4] analyzed numerically and experimentally the velocity and temperature fields at natural convection inside a storage tank. Tzong et al. [5] numerically simulate the laminar, steady, two-dimensional natural convection flows in a square enclosure with discrete heat sources on the left and bottom walls by using a finite-volume method. Nader Ben Cheikh et al. [6] numerically studied Natural convection of air in a two-dimensional, square enclosure with localized heating from below and cooled from above for a variety of thermal boundary conditions at the top and sidewalls. Localized heating is simulated by located a heat source on the bottom wall. Comparisons among the different thermal configurations considered are reported. Bazylak et al. [7] made a computational analysis of the heat transfer due to an array of heat sources on the bottom wall of a horizontal enclosure and reported the bifurcations in the Rayleigh–Bénard cell structures following the transition to convection dominated regime, reflecting the instabilities in the selected physical system.

Banerjee et al. [8] conducted simulation of natural convection in a horizontal, planar square cavity with two discrete heat sources. Baïri et al. [9] performed a numerical and experimental study to determine the thermal behavior in a cavity. By means of the finite volumes method and varying the difference of temperatures and the inclination angle of the cavity the dynamic and thermal aspects are examined for several configurations. Levoni et al. [10] investigated Buoyancy-induced flow regimes numerically for the basic case of a horizontal cylinder centered into a long co-axial square-sectioned cavity. In the frame of the 2D assumption; the threshold for the occurrence of time-dependent behaviour is explored. Wu et al. [11] experimentally investigated the laminar natural convection in an air-filled square cavity with a partition on the heated vertical wall. Sankar et al. [12] used an implicit finite difference method to analyze the heat transfer characteristics in a vertical annulus filled with a fluid-saturated porous medium.

Tahavvor et al. [13] used ANN to predict natural convection heat transfer and fluid flow from a column of cold horizontal circular cylinders having uniform surface temperature. D’Orazio et al. [14] experimentally studied Steady laminar free convection from a pair of vertical arrays of equally-spaced uniformly heated horizontal cylinders set in free air. Yousefi et al. [15] experimentally studied Steady laminar free convection from a pair of vertical arrays of equally-spaced uniformly heated horizontal cylinders set in free air. Yousefi et al. [16] experimentally studied the Natural convection heat transfer from the vertical array of five horizontal isothermal elliptic cylinders with vertical major axis which confined between two adiabatic walls. The effect of wall spacing and Rayleigh number on the heat transfer from the individual cylinder and the array were investigated.

For more than a decade, lattice Boltzmann method (LBM) has been demonstrated to be a very effective numerical tool, compared with traditional computational fluid dynamics for a broad variety of complex fluid flow phenomena. The continuous flow equation describes the macroscopic behavior of a microscopic world of particles [17] various authors have demonstrated the potential of the of the Lattice–Boltzmann technique considering numerical accuracy, numerical robustness, flexibility with respect to complex boundaries, computational efficiency, suitability for parallel computation, ease and robust handling of multiphase and others.

Jami et al. [18] numerically investigated the laminar natural convection heat transfer in an inclined enclosure. Numerical solutions are obtained by using the hybrid finite-difference lattice–Boltzmann method. Effects of partition inclination angle are studied. They also carried out a numerical investigation of laminar convective flows in a differentially heated, square enclosure with a heat-conducting cylinder [19]. Mezrhab et al. [20] analyzed the natural convection in a cavity by combined Lattice–Boltzmann finite difference method. The principle of lattice–Boltzmann techniques is recalled by authors and some of the difficulties to simulate convective flows are discussed. Natural convection in an open ended cavity was numerically investigated by Mohammad et al. [21]. The paper is intended to address the physics of flow and heat transfer in open end cavities and close end slots. They demonstrated that open boundary conditions used at the opening of the cavity is reliable.

A thermal lattice Boltzmann method based on the BGK model has been used by D’Orazio et al. [22] and Dixit and Babu [23] to simulate high natural convection in a square cavity. In [22] imposed heat flux at the wall is simulated, in [23] high Rayleigh numbers are obtained. They use the double populations approach to simulate hydrodynamic and thermal fields. Karimipour et al. [24] investigated the influence of natural convection in a micro channel. The traditional lattice Boltzmann method on a uniform grid has unreasonably high grid requirements at higher Rayleigh numbers which renders the method impractical. Therefore, the interpolation supplemented lattice Boltzmann method has been utilized. Kuznik et al. [25] used Boltzmann method with non-uniform mesh for the simulation of natural convection in a square cavity.

Most of the mentioned works investigated natural convection in cavities without a straight heated obstacle. The effect of systematic analysis of aspect ratio on the physics of flow and heat transfer is missing from the literature, which is worth being investigated. The LBM can be viewed as a minimal model for the Navier–Stokes equations instead of a full molecular dynamics approach. Indeed, fluid flow is mainly determined by the collective behavior of many molecules and not really by the detailed molecular interactions. Since the Boltzmann equation is kinetic-based, the physics associated with the molecular level interaction can be incorporated more easily in the LBE model. Hence, the LBE model can be fruitfully applied to micro-scale fluid flow problems. The kinetic nature of LBM introduces a number of advantages, such as linearity of the convection operator and the recovery of the NS equations in the nearly incompressible limit, thus avoiding solving difficult Poisson equations for the pressure. In other word, in the LBE method data communication is always local and the pressure is obtained through an equation of state. In addition, since LBM seeks the minimum set of velocities in phase space, only one or two speeds and a few moving directions are used in LBM, and the numerical solution of the kinetic equation is very simple. The another advantages of the LBM are including the parallel of algorithm, the simplicity of programming and implementation of boundary conditions, and the ability to incorporate microscopic interactions. Also, it is easy to search (by different CFD searching methods) in the computational domain in LBM.

This paper is organized as follows: In Sect. 2, a brief overview of the Lattice–Boltzmann model used in the present simulations is given, the density distribution function, f=f(x,c,t), is used to simulate the density and velocity fields and the internal energy density distribution function, g=g(x,c,t), is used to simulate the macroscopic temperature field. In Sect. 3, the obtained results are presented and validation of the LBM-code is done by comparing results against the published data. The results are depicted as streamlines and isotherm contours. The effect of the position and aspect ratio of heated plate (with constant temperature) on heat transfer and flow are addressed. Most of the mentioned works investigated the natural convection in cavities but investigation of natural convection in the presence of heated plate, considering the effects of the position by lattice–Boltzmann method, has not been studied before which will be addressed completely in the present work.

2 Lattice Boltzmann method

The lattice Boltzmann method provides a way to solve the partial differential equations by evolving variables on a set of lattices. LBM is a relatively new numerical scheme, the method was developed by Frisch et al. [26, 27], then in 1988 McNamara et al. [28], in 1989 Higuera [29] and in 1992 Chen et al. [30] extended the method. Higuera et al. [31] displayed that the lattice Boltzmann equation deriving from the Frisch–Hasslacher–Pomeau cellular automation, being free from microscopic fluctuations, provides a new appealing tool to simulate realistic incompressible hydrodynamics. Succi et al. [32] used the lattice Boltzmann equation (LBE) for the study of three-dimensional flows in complex geometries, Numerical results for low Reynolds number flows in a three-dimensional random medium are reported. In the Lattice–Boltzmann method, every node in the network is connected with its neighbor through a number of lattice velocities to be determined through the model chosen. More details can be found in [33]. Generally, there are three types of lattice Boltzmann models; multi-speed model [34] that uses the density distribution functions to simulate the density, velocity and temperature field, passive scalar approach [35] and double distribution function [36] that uses the internal energy density distribution function to simulate the macroscopic temperature field and for which the viscous heat dissipation and compression work done by the pressure can be incorporated.

Kinetic theory states that the evolution of the single-particle density distribution in a fluid system obeys the Boltzmann equation and the equation is discrete as [37]:

$$ f_{i}(\overrightarrow{x} + \overrightarrow{c}_{i}\Delta t,t + \Delta t) - f_{i}(\overrightarrow{x},t) = \varOmega_{i}(f). $$
(1)

Equation (1) consists of two parts; propagation (left-hand side), During the propagation step particles move to the nearest neighbors in the direction of its probable velocity, and collision (right hand side) which represent the collision of the particle distribution function.

There are a few versions of collision operator Ω i (f), the most well accepted version due to its simplicity and efficiency was the Bhatnagar–Gross–Crook (BGK) collision model [37]. The equation that represents this model is given by:

$$ \varOmega_{i}(f) = - \frac{f_{i} - f_{i}^{eq}}{\tau}. $$
(2)

In the above equation, \(f_{i}^{eq}\) is the equilibrium distribution function that has an appropriately prescribed functional dependence on the local hydrodynamic properties and τ is the time to reach equilibrium condition during collision process and is called relaxation time. By using the BGK approximation, the above equation become

$$\begin{aligned} &f_{i}(\overrightarrow{x} + \overrightarrow{c}_{i}\Delta t,t + \Delta t) \\ &\quad{}=f_{i}(\overrightarrow{x},t) - \frac{1}{\tau} \bigl[f_{i} - f_{i}^{eq}\bigr] + \Delta t F_{i}. \end{aligned}$$
(3)

In which ΔtF i is the external force. Luo [38] suggested that the force term can be introduced into the collision term as −3ρw i c i .F/c 2 which is similar to that adopted for lattice gas model [39]. The general form of the lattice velocity model is expressed as D n Q m where D represents spatial dimension and Q is the number of connections (lattice velocity) at every node. In this model, the velocity space is discretized in 9 distribution functions, which is the most popular model for the 2D case. Figure 1 shows the 9-velocities of the D2Q9 model.

Fig. 1
figure 1

Discrete velocity vectors for the D2Q9 model for 2D LBM

Full size image

The equilibrium distribution function of the nine-bit model is defined as:

$$\begin{aligned} f_{i}^{eq}(\overrightarrow{x},t) =& w_{i}\rho \biggl[1 + \frac{1}{c_{s}^{2}}(\overrightarrow{c}_{i}.\overrightarrow{u} ) \\ &{}+\frac{1}{2c_{s}^{4}}(\overrightarrow{c}_{i}.\overrightarrow{u} )^{2} - \frac{1}{2c_{s}^{2}}u^{2}\biggr]. \end{aligned}$$
(4)

The weighting factors, for D2Q9 are given as:

$$ \omega_{\alpha} = \left \{ \begin{array}{l@{\quad}l} \frac{4}{9} & \alpha = 1,\\ \frac{1}{9} & \alpha = 2 \sim 5,\\ \frac{1}{36} & \alpha = 6 \sim 9. \end{array} \right . $$
(5)

The streaming speed, c, is defined as:

$$ \begin{aligned} c_{x} = [0,1,0, - 1,0,1, - 1, - 1,1]; \\ c_{y} = [0,0,1,0, - 1,1,1, - 1, - 1]. \end{aligned} $$
(6)

The macroscopic quantities can be calculated from

$$\begin{aligned} &\rho = \sum_{i = 1}^{9} f_{i}, \end{aligned}$$
(7)
$$\begin{aligned} &\rho \overrightarrow{u} = \sum_{i = 1}^{9} \overrightarrow{c_{i}} f_{i}. \end{aligned}$$
(8)

Through the Chapman-Enskog procedure, the incompressible Navier–Stokes equations are derived from the incompressible LBM [40], and the relation between the relaxation time and viscosity is obtained as follows:

$$ \tau = 3\upsilon + 0.5. $$
(9)

Equation (9) indicates that the value of τ must be kept higher than 0.5 in order to avoid negative value of viscosity. It has been discussed in [36] that modified populations are used in order to eliminate the inconsistency for the definition of kinematic viscosity. Particularly, numerical instability may occur for the LBE if the viscosity is too small (or if τ is too close to 0.5).

The double population thermal LBM is presented and mathematically demonstrated in He et al. [36]. The main hypotheses of this model are:

  • The Bhatnagar, Gross and Krook approximation results that the collision operator is expressed as a single relaxation time to the local equilibrium.

  • The Knudsen number is assumed to be a small parameter.

  • The flow is incompressible.

The lattice Boltzmann equation of temperature field can be given by:

$$\begin{aligned} &g_{i}(\overrightarrow{x} + \overrightarrow{c}_{i}\Delta t,t + \Delta t) \\ &\quad{}=g_{i}(\overrightarrow{x},t) - \frac{1}{\tau_{h}} \bigl[g_{i} - g_{i}^{eq}\bigr]. \end{aligned}$$
(10)

\(g_{i}^{eq}\) is the equilibrium distribution function and can be expressed as:

$$ g_{i}^{eq}(\overrightarrow{x},t) = w_{i}T \biggl[1 + \frac{1}{c_{s}^{2}}(\overrightarrow{c}_{i}.\overrightarrow{u} )\biggr]. $$
(11)

c s is the dimensionless speed of sound. As the uniform grid (Δx=Δy=Δt) is used in the computational domain, it is equal to \(1/\sqrt{3}\).

τ h is single particle relaxation times for internal energy and related to the thermal diffusivity as Eq. (9):

$$ \tau_{h} = 3\alpha + 0.5. $$
(12)

Here, T is the macroscopic temperature and can be calculated by,

$$ T = \sum_{i = 1}^{9} g_{i}. $$
(13)

3 Boundary conditions in LBM

The distribution functions out of the domain are known from the streaming process. The unknown distribution functions are those toward the domain. The implementation of boundary conditions is very important for this simulation. As the fluid velocity at solid (non-moving) walls is set to zero, the simplest way to implement such boundary conditions in a LBM is “On-Node” bounceback [33]. In Fig. 2, the unknown distribution function, which needs to be determined, is shown as dotted lines for example for flow fields in the north boundary the following conditions is used:

$$ f_{4,n} = f_{2,n},\qquad f_{7,n} = f_{5,n}, \qquad f_{8,n} = f_{6,n}, $$
(14)

where n is the lattice on the boundary.

Fig. 2
figure 2

Domain boundaries and known (solid lines) and unknown (dotted lines) distribution functions

Full size image

For constant wall temperature, the unknown functions are obtained by using the following equation:

$$ g_{i} = \theta_{w}(w_{i} + w_{ - i}) - g_{ - i}. $$
(15)

In the above equation, “i” is the unknown direction and “−i” is the opposite direction in D2Q9 model. To impose constant temperature boundary conditions, the dimensionless temperature θ=0 refers to right and left walls. The unknown thermal distribution functions at the left wall, i.e. g 2, g 6, g 9, and at the right wall, i.e. g 4, g 7, g 8, should be determined. From the above equation at the left wall, the following conditions are used,

$$ g_{2} = - g_{4},\qquad g_{5} = - g_{7},\qquad g_{6} = - g_{8}. $$
(16)

Similarly, for the right wall we have,

$$ g_{4} = - g_{2},\qquad g_{7} = - g_{5}, \qquad g_{8} = - g_{6}. $$
(17)

To implement adiabatic boundary condition on the upper and lower cavity walls, we assume that the thermal distribution function gradient in the vertical direction to the wall is set to zero and this is somehow similar to the bounce back boundary condition [21]. Applying this treatment for adiabatic walls yields (for bottom adiabatic boundary):

$$ \begin{aligned} g_{3,n} = g_{3,n - 1}, \\ g_{6,n} = g_{6,n - 1}, \\ g_{7,n} = g_{7,n - 1}. \end{aligned} $$
(18)

n is the lattice on the boundary and n−1 denotes the lattice inside the cavity adjacent to the boundary.

4 Numerical method

In this paper, natural convection heat transfer in a square cavity induced by heated obstacle at constant temperature is studied numerically. Upper and lower walls of cavity are adiabatic; the two vertical walls of the cavity have constant temperature lower than obstacle temperature. The study is performed for different values of Grashof number from 103 to 105 for different aspect ratios and position of heated plate. Air is chosen as a working fluid (Pr=0.71) and the average Nusselt number is calculated as a measure of the heat transfer.

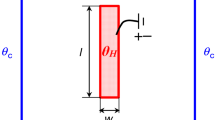
Geometry and boundary conditions are shown in Fig. 3. The non-dimensional parameters are:

$$\begin{aligned} &\Pr = \frac{\upsilon}{\alpha},\qquad \mathrm{Gr} = g\beta \Delta T \frac{H^{3}}{\upsilon^{2}}; \\ &\theta = \frac{T - T_{c}}{T_{h} - T_{c}}; \\ &A = \frac{h}{H},\qquad A_{1} = \frac{h_{1}}{H},\qquad A_{2} = \frac{h_{2}}{H}, \end{aligned}$$
(19)

where Gr is the Grashof number, Pr is Prandtl number and θ is the non-dimensional temperature. In this paper, for Gr=105, the values of τ and τ h are selected as 0.5195 and 0.5257, respectively. The non-dimensional parameter A is the aspect ratio of heated plate. A 1 is the distance of the plate to the parallel left wall for the vertical situation and the distance of the plate to the parallel upper wall for horizontal situation. A 2 is the distance of center of plate to the perpendicular upper wall for vertical situation and to the perpendicular left wall for second situation. The local and average Nusselt number on the left wall of cavity is defined as,

$$ \mathrm{Nu} = \frac{\partial \theta}{\partial Y}(Y = 0). $$
(20)
Fig. 3
figure 3

Horizontal and vertical positions of the obstacle inside a cavity

Full size image

Average Nusselt number is calculated by integrating Eq. (20) along the height of the cavity and dividing by number of lattices along the height. For each value of Grashof number, as well as the aspect ratio of obstacle, different grid sizes are employed to examine their effects on the results. We have also conducted a grid dependency study for each position case (Horizontal/Vertical position of obstacle). The results are assumed to be converged, when the average value of Nusselt number (on the left wall of the cavity) asymptotically approached a constant value. The relative error for calculation of the Nusselt number is less than 10−3 as a criterion of convergence. For all the simulations, the Mach number is set to be equal to 0.1 to make sure that the flow is fully in the incompressible regime. The Mach number is given as Ma=u/c s , where u is the characteristic velocity of the flow with order of magnitude of (gβΔTM)0.5 where M is the grid size in the vertical direction and c s is the speed of sound. This condition for Mach number gives right values for the kinematic viscosity and thermal diffusivity as presented in Sect. 2 of this paper. It is interesting to note that the accuracy of the present numerical method is 2nd order.

5 Results and discussion

5.1 Code validation

In order to ensure that the acquired results are correct, the present numerical results are compared with the available published results (see Kandaswamy et al. [41]). The results are shown for horizontal obstacle and also for vertical position of obstacle (in Table 1). The results were found to be similar to the published results of [41]. The grid size in the computational domain is also presented in Table 1. According to Eq. (19), the Prandtl number is 0.71 and study is performed for different Grashof numbers (from 103 to 105).

Table 1 Comparison of the numerical results of the present study with the benchmark solution of Lee et al. [24] (A=0.5, A 1=0.5)
Full size table

5.2 Obstacle located horizontally

When the heated obstacle is located horizontally, the results are obtained by changing the aspect ratio and position of the obstacle. Figure 4 shows the isotherm contours for A=0.5. The obstacle is located at the center of the cavity, i.e. A 1=0.5. The fluid motion inside the cavity is completely symmetric and the conduction heat transfer mechanism is dominant for the case of Gr=103.

Fig. 4
figure 4

Isotherm contours for A=0.5 and A 1=0.5, for Gr=103, 104, 105 (from up to down)

Full size image

When Gr. increases, the convection heat transfer mechanism becomes stronger and the fluid rotation over the obstacle is considerable (comparing to the one below the plate). When convection is the dominant mechanism of heat transport, the dimensionless temperature is shown on the isotherm counters.

Figure 5 shows isotherm contours for A=0.5 when obstacle is located in two different positions for Gr=105. When the position of obstacle is in A 1=0.8, the convection heat transfer mechanism is stronger than the case of A 1=0.2. If the hot obstacle is near the upper wall of the cavity, convection heat transfer is decreased and in reality there is no strong motion under the cavity. The straight isotherm contours under the obstacle introduce a weak convection heat transfer mechanism.

Fig. 5
figure 5

Isotherm contours for A=0.5, Gr=105; A 1=0.2 (up) and A 1=0.8 (down)

Full size image

Figure 6 shows isotherm contours by changing the aspect ratio of the obstacle in the case of Gr=105. When the aspect ratio of heated obstacle is increased, the flow pattern around the obstacle is changed; therefore the heat transfer is increased. It was observed that when A=0.2 the average Nusselt number on the left wall of the cavity is equal to 2.968. By increasing the aspect ratio to A=0.5, the average Nusselt number is about 1.3 times stronger than the previous case. Similarly, for A=0.8, the average Nusselt number is 1.9 times greater than the predicted value of Nusselt number for A=0.2.

Fig. 6
figure 6

Isotherm contours for A 1=0.5 and A 2=0.5

Full size image

Natural convection is caused by density differences in the fluid occurring due to temperature gradients. Typically, for free convection, the average Nusselt number is used to examine the rate of heat transfer. Nusselt number is the ratio of convective to conductive heat transfer and this is a dimensionless temperature gradient. Table 2 shows the average Nusselt number for horizontal position of obstacle at different values of Gr. The effects of position and dimension of the horizontal obstacle on the averaged Nusselt number is also presented in this table. It can be seen that heat transfer rate is increased by increasing the Gr. In other word, the convection mechanism of heat transfer becomes stronger by increasing the Gr. The average Nusselt number is also increased by increasing the aspect ratio (A) of obstacle. This increase in the Nusselt number can be related to the increasing of the surface of the obstacle. It is interesting to notice that there is an optimum vertical position (A 1) of obstacle in which the Nusselt number is maximized.

Table 2 Nusselt number for horizontal position of obstacle for different values of Gr, A 2=0.5
Full size table

5.3 Obstacle located vertically

Figure 7 shows the isotherm contours and for A=0.5 when the heated obstacle is located at the center of cavity, for different Grashof numbers from 103 to 105. For Gr=103, the conduction heat transfer mechanism is dominant and fluid motion is symmetric in the cavity. The isotherm contours show weak convection heat transfer inside the cavity. As Gr. Increases, convection heat transfer becomes stronger. For Gr =103 the average Nusselt number is equal to 1.738. By increasing the Grashof number, i.e. Gr=104, the calculated Nusselt number is about 1.46 times greater than the previous case. Increasing the average Nusselt number for Gr=105 is about 3 times of the case of Gr=103.

Fig. 7
figure 7

Isotherm contours for A 1=0.5, A 2=0.5 and A=0.5, for Gr=103, 104, 105 (from up to down)

Full size image

When the heated obstacle is located vertically, the results can be obtained by changing the position of the obstacle. Figure 8 shows the isotherm contours for A=0.5 and Gr=105. Because of the symmetric thermal boundary conditions, two position A 1=0.2 and A 1=0.8 are similar and we calculate the average Nusselt number only for the left wall.

Fig. 8
figure 8

Isotherm contours for A 1=0.2, A 2=0.5, Gr=105

Full size image

For A 1=0.8, the average Nusselt number on the left wall of cavity is equal to 4.452. When the space between left wall and obstacle is decreased, i.e. A 1=0.5, the average Nusselt number is about 1.15 times greater than the previous location (A 1=0.8). For A 1=0.2, the average Nusselt number is about 1.27 times more than the case of A 1=0.8.

Figure 9 shows the isotherms for different values of aspect ratio of heated plate. When heated obstacle aspect ratio increases, it means that the area of hot surface and also the temperature gradient increase; then convection mechanism is more effective than conduction and therefore heat transfer increases. For A=0.2 the average Nusselt number for the left wall is equal to 3.685. When the aspect ratio increases, for A=0.5, the average Nusselt number is about 1.38 times, and for A=0.8, 1.57 times greater than the case of A=0.2. For A=0.8, we can assume that there is two separate cavity with cold and hot walls.

Fig. 9
figure 9

Isotherm contours for A 1=0.5 and Gr=105; A=0.2 (up), A=0.8 (down)

Full size image

The Nusselt number is calculated for different aspect ratios of obstacle in the case of vertical position (see Table 3). When the aspect ratio increases, the density gradient increases and the buoyancy force becomes stronger, and therefore it causes to increase the rate of heat transfer. By increasing the parameter A 1, the space between the left wall and the obstacle is increased and therefore, the heat transfer rate to the left wall is increased. For comparison of the different position of obstacle (horizontally and vertically), we have calculated the average Nusselt number for both positions. The important term in the natural convection heat transfer is buoyancy force. When obstacle is located vertically, hot obstacle is in the direction of the gravity vector; and an upward near-wall motion will be induced. When hot obstacle located horizontally, the buoyancy force decreases and the rotation of fluid downward is prevented; thus we expected reduction in the rate of heat transfer. Comparison of the horizontal and vertical position of obstacle inside the cavity shows that heat transfer rate is higher for vertical situation than horizontal case.

Table 3 Nusselt number for vertical position of obstacle for different values of Gr, A 2=0.5
Full size table

5.4 Maximum rate of heat transfer

In order to obtain the optimum position of obstacle, for maximum rate of heat transfer, different position of the obstacle is checked and the average Nusselt number is plotted against A 1.

Figure 10 shows variation of the average Nusselt number by changing the position of the obstacle for both vertical and horizontal position for different Grashof Numbers. As indicated before, for horizontal position of obstacle, there is an optimum position for the obstacle which is in the interval of A 1=[0.5,0.7]. In this condition, both horizontal and vertical cases are studied for different values of parameter “A” (i.e. A=0.2 and A=0.8). As shown in Fig. 11, the same result is obtained. Figure 12 also shows the variation of the average Nusselt number for the case of vertical position for different values of parameter “A” (i.e. A=0.2 and A=0.8).

Fig. 10
figure 10

Variation of the average Nusselt number by changing the position of the obstacle for A=0.5 and A 2=0.5; horizontal case (up), vertical case (down)

Full size image
Fig. 11
figure 11

Variation of the average Nusselt number by changing the position of the obstacle for the horizontal position and A 2=0.5; A=0.2 (up), A=0.8 (down)

Full size image
Fig. 12
figure 12

Variation of the average Nusselt number by changing the position of the obstacle for the vertical position and A 2=0.5; A=0.2 (up), A=0.8 (down)

Full size image

By increasing the fluid velocity inside the channel, the convective heat transfer is augmented. In order to show the “increasing motion”, Fig. 13 shows the fluid LB-velocity on the vertical line passing through the centerline of the cavity for a horizontal obstacle and A=0.5. We can see that the fluid velocity (convective terms) increases by increasing the Grashof number. It can obviously augment the heat transfer rate in the cavity.

Fig. 13
figure 13

Fluid LB-velocity on the vertical line passing through the centerline of the cavity for a horizontal obstacle and A=0.5

Full size image

6 Conclusions

In this paper Natural convection heat transfer inside a square cavity in the presence of heated obstacle at constant temperature is investigated numerically for two different positions (vertically and horizontally). An existing two-dimensional Lattice Boltzmann method (LBM) was applied for the study. Following conclusions can be drawn:

  • Flow motion and rate of heat transfer in the cavity depend on the position of obstacle. For horizontal position of obstacle, there is an optimum position for the obstacle. When the obstacle located horizontally, the maximum rate of heat transfer occurs for a value of A 1 in the interval of [A 1=0.5,0.7].

  • As the aspect ratio of heated obstacle is increased, the heat transfer rate is increased. Increasing the parameter A has more effects on heat transfer than increasing A 1, for both horizontal and vertical cases. By increasing Gr number, heat transfer increases for both vertical and horizontal situations. By comparing the horizontal and vertical position of obstacle, it can be seen that heat transfer becomes more enhanced in the case of vertical situation than horizontal situation.

In future work intends to analyze cavities filled with obstacles of different geometries, curve and inclined obstacles, with Lattice Boltzmann model.