1 Introduction

Chatter, the high relative vibrations between the workpiece and tool during milling processes, lead to a poor quality of surface finished and undesirable wear of tool. These vibrations limit the material removal rate, and, consequently, result in low productivity. Reducing the levels of vibrations and stabilizing the milling process are of major concerns in the past decades. Tobias and Fishwick [1, 2] presented the stability charts, a diagram that associates the onset of chatter vibrations with certain machining parameters such as the spindle speed and chip load. Using this diagram, one can choose to perform the machining operation at optimal conditions. Following the Tobias and Fishwick’s celebrated works, considerable researches have been carried out on predicting the stability chart for the constant speed machining. Tlusty and Polacek [3] presented a frequency-domain approach based on transfer functions between the system displacements and cutting forces to determine the instability due to the regenerative effect. Minis and Yanushevsky [4] and Altintas and Budak [5] presented a frequency-domain approach based on transfer functions between the system displacements and cutting forces to determine the stable regions. Balachandran and Zhao [6] presented a unified mechanics based model with multiple degrees of freedom and numerical simulation were carried to investigate the stability of milling processes. Insperger and Stépán [7–9] improved the semi-discretization method to examine the stability of periodic solutions of delayed systems. Long and Balachandran [10] and Long et al. [11] predicted the stable cutting regions in the space of spindle speed and axial depth of cutting by semi-discretization method. In order to predict the stability boundaries related to chatter, one needs the information of frequency response function (FRF) or modal parameters of tool tip. Usually, high speed spindle is supported by the angular contact ball bearings. The stiffness of the ball bearing decreases as rotational speed increases. This consequently causes the decrease of the stiffness and the natural frequencies of the spindle with the increase of spindle speed due to the bearing softening. The stability lobe diagrams generated from stationary FRFs bring about inaccuracy for stability prediction of high speed milling. In recent years, some investigations related to the chatter stability including the speed dependent spindle dynamics have been carried out theoretically and experimentally. Shin [12] addressed the nonlinear behaviours of angular contact bearings at high speed based on Jones’s bearing model, and pointed out that the speed-varying characteristics of spindle bearings must be considered when predicting stability of high speed machining. Mavahhedy and Mosaddegh [13] predicated the chatter in high speed milling including gyroscopic effects of the rotating spindle and he found that gyroscopic effects lower the borders of stability lobes. Using Nyquist stability criterion, Cao [14], Gagnol et al. [15, 16] predicted the chatter stability lobes of high speed milling with the consideration of speed-varying spindle dynamics. Schmitz [17] measured the FRF of the rotating spindle and constructed the speed-dependent stability boundaries with the rotating tool FRF. Ertürk et al. [18] studied the tool point frequency response function by using an analytical model for spindle-tool assemblies. Rantatalo et al. [19] analyzed the machine tool spindle vibrations based on FEM and a contact-less dynamic spindle testing equipment. Results indicate the centrifugal force that acted on the bearing balls results in a softening of the bearing stiffness and this softening is shown to be more influential on the system dynamics than the gyroscopic moment of the rotor. In addition, in the former works with semi-discretization method to predict stability boundaries [7–10], only the first-order structural mode was considered. The second or higher order mode, however, may be dominantly on the stability of milling processes. Here, a speed dependent dynamic characteristics of spindle-workpiece model is constructed for a multiple mode milling system in two orthogonal directions. Semi-discretization method is used to determine the stability boundaries of high speed milling processes. The multiple mode effects of the spindle on the stability of the milling processes are also studied in the paper. The remainder of the paper is organized as follows. In the next section, the characteristics of ball bearing and then the effects on the frequency response functions are detailed. Following that, milling model with variable dynamic parameters and the stability analysis on the milling processes are presented in Sect. 3. Numerical results are presented and discussed in Sect. 4. Conclusions are given in the last section.

2 Speed-dependent dynamic characteristics of spindle

2.1 Variable bearing dynamic parameters

As shown in the Fig. 1a, when an angular contact ball bearing is in a point contact with a mating ball raceway in the static state, the contact angles between the ball and inner and outer raceways are identical. When the spindle starts rotating, the inner raceway contact angles increase and the outer raceway contact angles decrease due to the centrifugal force developed (Fig. 1b). This results in the stiffness of the ball bearing changes with respect to the rotational speed. To determine the rotational speed depended contact angles and stiffness of ball bearing, the ball bearing such as shown in Fig. 2 is investigated.

Fig. 1
figure 1

Angular contact ball bearing without/with rotation

Full size image
Fig. 2
figure 2

Ball bearing and angular position of ball

Full size image

When a bearing is installed, there is a preload along the radial direction or axial direction to increase the stiffness. When the spindle starts rotating, the additional loading such as centrifugal force and gyroscopic moment are applied. The ball loading at angle position ψ j is presented in Fig. 3. Considering the equilibrium of forces of the ball in the horizontal and vertical directions, one can obtain

$$ \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {Q_{ij} \sin \alpha_{ij} - Q_{oj} \sin \alpha_{oj} - \frac{{M_{gj} }}{{D_{b} }}(\lambda_{ij} \cos \alpha_{ij} - \lambda_{oj} \cos \alpha_{oj} ) = 0} \hfill \\ {Q_{ij} \cos \alpha_{ij} - Q_{oj} \cos \alpha_{oj} + \frac{{M_{gj} }}{{D_{b} }}(\lambda_{ij} \sin \alpha_{ij} - \lambda_{oj} \sin \alpha_{oj} ) + F_{cj} = 0} \hfill \\ \end{array} } \hfill & {j = 1,2, \ldots N} \hfill \\ \end{array} } \right. $$
(1)

where λ ij and λ oj are two constants for the raceway control. For the high speed bearing, the constants λ ij and λ oj equal to zero and two, respectively [20]. F cj and M gj are the centrifugal force and the gyroscopic moment at each ball, respectively, and can be written as

$$ \left\{ {\begin{array}{*{20}l} {F_{cj} = \frac{1}{2}d_{m} \omega^{2} \left( {\frac{{\omega_{m} }}{\omega }} \right)_{j}^{2} } \hfill \\ {M_{gj} = J\left( {\frac{{\omega_{b} }}{\omega }} \right)_{j} \left( {\frac{{\omega_{m} }}{\omega }} \right)_{j} \omega^{2} \sin \beta } \hfill \\ \end{array} } \right. $$
(2)

where J is the mass moment of inertia. Assuming pure rolling occurs only at the outer raceway, one can written the ball attitude angle for inner and outer raceways, β as

$$ \tan \beta = \frac{{\sin \alpha_{oj} }}{{\cos \alpha_{oj} + {\raise0.7ex\hbox{${D_{b} }$} \!\mathord{\left/ {\vphantom {{D_{b} } {d_{m} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${d_{m} }$}}}} $$
(3)
Fig. 3
figure 3

Ball loading at angle position ψ j

Full size image

In Eq. (2), (ω m /ω) j and (ω b /ω) j are the ratio of orbital speed and spindle speed and the ratio of angular speed of ball about its own axis and the spindle speed, respectively. For the outer-ring control, one has

$$ \left( {\frac{{\omega_{m} }}{\omega }} \right)_{j} = \frac{{1 - \left( {{{D_{b} } \mathord{\left/ {\vphantom {{D_{b} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right)\cos \alpha_{ij} }}{{1 + \cos (\alpha_{ij} - \alpha_{oj} )}} $$
(4)
$$ \left( {\frac{{\omega_{b} }}{\omega }} \right)_{j} = \frac{ - 1}{{\left( {\frac{{\cos \alpha_{oj} + \tan \beta \sin \alpha_{oj} }}{{1 + \left( {{{D_{b} } \mathord{\left/ {\vphantom {{D_{b} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right)\cos \alpha_{oj} }} + \frac{{\cos \alpha_{ij} + \tan \beta \sin \alpha_{ij} }}{{1 - \left( {{{D_{b} } \mathord{\left/ {\vphantom {{D_{b} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right)\cos \alpha_{ij} }}} \right)\left( {{{D_{b} } \mathord{\left/ {\vphantom {{D_{b} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right)\cos \beta }} $$
(5)

When the bearing starts rotating, the centrifugal force gyroscopic moment are applied to the bearing, the distance between the curvature center of the bearing rings changes in the x–y plane. Figure 4 shows new ball center as well as curvature centers.

Fig. 4
figure 4

Positions of ball center and raceway groove curvature centers at angular position ψ j

Full size image

Based on Jones’s theory, the relationship between the positions of ball center and raceway groove curvature centers could be obtained:

$$ \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\left[ {A_{1j} - \left( {r_{o} - 0.5D_{b} + \delta_{oj} } \right)\sin \alpha_{oj} } \right]^{2} - \left( {r_{i} - 0.5D_{b} + \delta_{ij} } \right)^{2} (1 - \cos^{2} \alpha_{ij} ) = 0} \hfill \\ {\left[ {A_{2j} - \left( {r_{i} - 0.5D_{b} + \delta_{ij} } \right)\cos \alpha_{ij} } \right]^{2} - \left( {r_{o} - 0.5D_{b} + \delta_{oj} } \right)^{2} (1 - \sin^{2} \alpha_{oj} ) = 0} \hfill \\ \end{array} } \hfill & {j = 1,2, \ldots N} \hfill \\ \end{array} } \right. $$
(6)

where δ ij and δ oj are the inner and outer normal contact deformations, respectively. r i and r o represent the inner and outer raceway groove curvature radii, respectively. α ij and α oj are the inner and outer raceway contact angles at ball location ψ j . \( \psi_{j} = \frac{2\pi }{N}(j - 1) \). A 1j and A 2j are the axial and radial distances between the loci of inner and outer raceway groove curvature centers at ball location ψ j . D b is the ball diameter, and N is the number of balls.

Suppose the displacements of bearing along the axial, radial and angular direction are δ a , δ r , and θ, respectively. By Fig. 4, one has

$$ \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {A_{1j} = BD_{b} \sin \alpha^{0} + \delta_{a} + \theta R_{i} \cos \psi_{j} } \hfill \\ {A_{2j} = BD_{b} \cos \alpha^{0} + \delta_{r} \cos \psi_{j} } \hfill \\ \end{array} } \hfill & {j = 1, \, 2, \ldots ,N} \hfill \\ \end{array} } \right. $$
(7)

where B = f i  + f o − 1. α 0 is the designed contact angle. f i and f o are the inner and outer ratios of radius of raceway curvature to ball diameter, respectively. R i is the radius to locus of raceway groove curvature centers.

To determine the relationship between the loading and deformation of ball, the Hertzian theory is used. The contact forces between the inner ring and the balls, and the outer ring and the balls are expressed by

$$ \left\{ \begin{aligned} Q_{ij} = K_{ij} \delta_{ij}^{1.5} \hfill \\ Q_{oj} = K_{oj} \delta_{oj}^{1.5} \hfill \\ \end{aligned} \right.\quad j = 1,2, \ldots ,N $$
(8)

where K ij and K oj are the load–deflection factor, and are the functions of contact angles α ij and α oj .

Considering the entire bearing, one can obtain the force and moment equilibrium equations as

$$ \left\{ {\begin{array}{*{20}l} {F_{a} - \sum\limits_{j = 1}^{N} {Q_{ij} \sin \alpha_{ij} = 0} } \hfill \\ {F_{r} - \sum\limits_{j = 1}^{N} {Q_{ij} \cos \alpha_{ij} \cos \psi_{j} = 0} } \hfill \\ {M - \sum\limits_{j = 1}^{N} {Q_{ij} \sin \alpha_{ij} R_{i} \cos \psi_{j} = 0} } \hfill \\ \end{array} } \right. $$
(9)

where F a and F r are the external force along the axial and radial directions, respectively. M is the external moment. The stiffness of ball bearing can be written as

$$ K = \frac{dF}{d\delta } $$
(10)

For a given F a , F r , and M, one can obtain the value of α ij , α oj , δ ij , δ oj , δ a , δ r and θ by solving Eqs. (1), (6), (8), and (9) through Newton–Raphson method.

To illustrate the analysis, an angular contact ball bearing which is used in high speed spindle is examined. The parameters of the ball bearing are presented in Table 1. In Fig. 5, the centrifugal force and the gyroscopic moment of ball are presented. By Fig. 5a, one can find that the centrifugal force of ball increases quickly with respect to the spindle speed. For different axial preload, the curve of centrifugal force are close each other. The centrifugal force of the ball with higher preload is little smaller than that of the ball with lower preload. Due to that, the inner raceway contact angle increases and the outer raceway contact angle decreases with respect to speed increase, as shown in Fig. 6. The gyroscopic moment presented in Fig. 5b has the opposite direction with different preload. One can find the increase of the gyroscopic moment of ball with lower preload is faster than that of the ball with higher preload with the increase of spindle speed. By observing Fig. 6, one can also find the variation of the contact angles with respect to speed will become smaller when the axial preload is larger.

Table 1 Parameters of angular contact ball bearing B7009C/P4
Full size table
Fig. 5
figure 5

Variations of centrifugal force and gyroscopic moment with respect to the spindle speed. a Centrifugal force, b gyroscopic moment

Full size image
Fig. 6
figure 6

Variations of contact angle with respect to the spindle speed

Full size image

In Fig. 7, the variations of radial stiffness of angular contact ball bearing with respect to speed and axial preload are presented. By this figure, one can say the radial stiffness increases as the axial preload increases with a given speed and decreases as the spindle speed increases with a given axial preload, besides the range of high speed with very low axial preload. In the case of small axial preload (lesser than 100 N), the radial stiffness decreases firstly with the increase of speed and then increases with the increase of speed in higher speed range.

Fig. 7
figure 7

Variations of radial stiffness of angular contact ball bearing with respect to spindle speed and axial preload

Full size image

2.2 Effects of speed on dynamical characteristics of spindle

The high speed spindles are most commonly supported by the ball bearing. The dynamic characteristics of spindle are functions of rotational speed. To investigate the effects of the spindle speed on the dynamic characteristics of spindle, a finite element model (FEM) [22] of spindle is used to calculate the natural frequency and mode shape of the shaft bearing system, such as shown in Fig. 8. In this figure, L1 and L2 are the length of the tool and shaft of spindle, respectively. For simplification, the connections among the tool, holder, and shaft are assumed as rigidity. The front bearing and the back bearing are indicated by two springs with variable stiffness with the change of the spindle speed. In this FEM model, the Euler beam element is used and only the lateral vibrations are considered. The gyroscopic effect of the shaft is ignored due to this effect doesn’t result into substantial changes on the natural frequency by comparing with the effects of the centrifugal force of bearing ball at the first several order modes [19]. For a system with p nodes, the displacements at discrete points along the structure are defined by vectors \( {\mathbf{x}}(t) = [x_{1} (t),x_{2} (t), \ldots ,x_{p} (t)]^{T} \) and \( {\mathbf{y}}(t) = [y_{1} (t),y_{2} (t), \ldots ,y_{p} (t)]^{T} \).

Fig. 8
figure 8

Model of spindle system

Full size image

By considering the speed-varying characteristics of spindle bearings, the governing equation of motion is of the following form

$$ \left[ \begin{aligned} {\mathbf{M}}_{{{\mathbf{xx}}}} \, {\mathbf{M}}_{{{\mathbf{xy}}}} \hfill \\ {\mathbf{M}}_{{{\mathbf{yx}}}} \, {\mathbf{M}}_{{{\mathbf{yy}}}} \hfill \\ \end{aligned} \right]\left[ \begin{aligned} {\ddot{\mathbf{{x}}}}(t) \hfill \\ {\ddot{\mathbf{y}}}(t) \hfill \\ \end{aligned} \right] + \left[ \begin{aligned} {\mathbf{C}}_{{{\mathbf{xx}}}} (\omega ) \, {\mathbf{C}}_{{{\mathbf{xy}}}} (\omega ) \hfill \\ {\mathbf{C}}_{{{\mathbf{yx}}}} (\omega ) \, {\mathbf{C}}_{{{\mathbf{yy}}}} (\omega ) \hfill \\ \end{aligned} \right]\left[ \begin{aligned} {\dot{\mathbf{x}}}(t) \hfill \\ {\dot{\mathbf{y}}}(t) \hfill \\ \end{aligned} \right] + \left[ \begin{aligned} {\mathbf{K}}_{{{\mathbf{xx}}}} (\omega ) { }{\mathbf{K}}_{{{\mathbf{xy}}}} (\omega )\hfill \\ {\mathbf{K}}_{{{\mathbf{yx}}}} (\omega ) { }{\mathbf{K}}_{{{\mathbf{yy}}}} (\omega )\hfill \\ \end{aligned} \right]\left[ \begin{aligned} {\mathbf{x}}(t) \hfill \\ {\mathbf{y}}(t) \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} {\mathbf{F}}_{{\mathbf{x}}} (t) \hfill \\ {\mathbf{F}}_{{\mathbf{y}}} (t) \hfill \\ \end{aligned} \right] $$
(11)

where \( {\mathbf{M}}_{{{\mathbf{x,y}}}} \), \( {\mathbf{C}}_{{{\mathbf{x,y}}}} (\omega ) \), and \( {\mathbf{K}}_{{{\mathbf{x,y}}}} (\omega ) \) represent the discrete system mass, damping, and stiffness matrices, respectively. \( {\mathbf{F}}_{{\mathbf{x}}} (t ) \) and \( {\mathbf{F}}_{y} (t ) \) are the cutting forces acted on the tool along x and y-directions, respectively. The system stiffness matrix consists of the shaft stiffness matrix and the bearing stiffness matrix

$$ \left\{ \begin{aligned} {\mathbf{K}}_{{{\mathbf{xx}}}} (\omega )= {\mathbf{K}}_{{{\mathbf{xs}}}} + {\mathbf{K}}_{{{\mathbf{xb}}}} (\omega ) \hfill \\ {\mathbf{K}}_{yy} (\omega )= {\mathbf{K}}_{{y{\mathbf{s}}}} + {\mathbf{K}}_{{y{\mathbf{b}}}} (\omega ) \hfill \\ \end{aligned} \right. $$
(12)

where the subscribe s represents the shaft and the subscribe b represents the bearing. \( {\mathbf{C}}_{{{\mathbf{x,y}}}} (\omega ) \) is proportional damping and can be written as

$$ \left[ \begin{aligned} {\mathbf{C}}_{{{\mathbf{xx}}}} (\omega ) \, {\mathbf{C}}_{{{\mathbf{xy}}}} (\omega ) \hfill \\ {\mathbf{C}}_{{{\mathbf{yx}}}} (\omega ) \, {\mathbf{C}}_{{{\mathbf{yy}}}} (\omega ) \hfill \\ \end{aligned} \right] = c_{1} \left[ \begin{aligned} {\mathbf{M}}_{{{\mathbf{xx}}}} \, {\mathbf{M}}_{{{\mathbf{xy}}}} \hfill \\ {\mathbf{M}}_{{{\mathbf{yx}}}} \, {\mathbf{M}}_{{{\mathbf{yy}}}} \hfill \\ \end{aligned} \right] + c_{2} \left[ \begin{aligned} {\mathbf{K}}_{{{\mathbf{xx}}}} (\omega ) { }{\mathbf{K}}_{{{\mathbf{xy}}}} (\omega )\hfill \\ {\mathbf{K}}_{{{\mathbf{yx}}}} (\omega ) { }{\mathbf{K}}_{{{\mathbf{yy}}}} (\omega )\hfill \\ \end{aligned} \right] $$
(13)

where c 1 = 2 × 10−5 and c 2 = 6 × 10−6 are constants which are selected to fit the tested frequency response curves by modal test at the static state. For the modal analysis, a homogenous equation of the motion for the finite element assembly used and can written as

$$ \left[ \begin{aligned} {\mathbf{M}}_{{{\mathbf{xx}}}} \, {\mathbf{M}}_{{{\mathbf{xy}}}} \hfill \\ {\mathbf{M}}_{{{\mathbf{yx}}}} \, {\mathbf{M}}_{{{\mathbf{yy}}}} \hfill \\ \end{aligned} \right]\left[ \begin{aligned} {\ddot{\mathbf{x}}}(t) \hfill \\ {\ddot{\mathbf{y}}}(t) \hfill \\ \end{aligned} \right] + \left[ \begin{aligned} {\mathbf{C}}_{{{\mathbf{xx}}}} (\omega ) \, {\mathbf{C}}_{{{\mathbf{xy}}}} (\omega ) \hfill \\ {\mathbf{C}}_{{{\mathbf{yx}}}} (\omega ) \, {\mathbf{C}}_{{{\mathbf{yy}}}} (\omega ) \hfill \\ \end{aligned} \right]\left[ \begin{aligned} {\dot{\mathbf{x}}}(t) \hfill \\ {\dot{\mathbf{y}}}(t) \hfill \\ \end{aligned} \right] + \left[ \begin{aligned} {\mathbf{K}}_{{{\mathbf{xx}}}} (\omega ) { }{\mathbf{K}}_{{{\mathbf{xy}}}} (\omega )\hfill \\ {\mathbf{K}}_{{{\mathbf{yx}}}} (\omega ) { }{\mathbf{K}}_{{{\mathbf{yy}}}} (\omega )\hfill \\ \end{aligned} \right]\left[ \begin{aligned} {\mathbf{x}}(t) \hfill \\ {\mathbf{y}}(t) \hfill \\ \end{aligned} \right] = {\mathbf{0}} $$
(14)

Solving Eq. (14), one can determine the dynamic characteristics of spindle with a given axial preload.

In Figs. 9, 10, and 11, the speed dependent dynamic characteristics of spindle which is supported by the examined angular contact ball bearing in Sect. 2.1 with F a  = 100 N are presented. As shown in Fig. 9, the first and the second-order natural frequencies decrease obviously as the increase of speed, however, the changes of the third-order and forth-order natural frequencies with respect to the increase of speed are small. Similar to the radial stiffness of bearing presented in Fig. 7, the first-order natural frequency of spindle decreases firstly with the increase of speed and then increases with the increase of speed in higher speed range. This is similar to the experimental results presented by Gradišek et al. [21]. Figures 10 and 11 show the change of the modal stiffness and modal mass of tool tip (the structural mode unit normalized at the tool tip) with respect to the speed. By this two figures, one can say that the speed has a considerable effect on the modal parameters of the first-order and second-order modes, especially on the modal parameters of the first-order mode. However, the effects of speed on the modal parameters of the third and fourth-order modes are less. This changes indicate that the decrease of the bearing stiffness with respect to the increase of speed has a considerable effect on the first and second-order modes (the rigid body modes of shaft, Fig. 12a, b), but has less effects on the remaining elastic modes.

Fig. 9
figure 9

Variations of natural frequencies with respect to spindle speed

Full size image
Fig. 10
figure 10

Variations of modal stiffness of tool tip with respect to spindle speed

Full size image
Fig. 11
figure 11

Variations of modal mass of tool tip with respect to spindle speed

Full size image
Fig. 12
figure 12

The first-four-order mode shapes

Full size image

3 Stability analysis of the milling processes

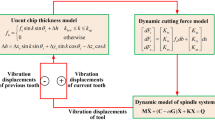
In this section, the dynamic model of the spindle presented in Sect. 2 is used for the analysis of stability of milling processes. The effects of speed dependent dynamic characteristics of spindle on the stability of system are investigated. The spindle tool set is considered to have two orthogonal degrees of freedom along the x-direction and y-direction, respectively, as shown in Fig. 13. The displacements along the x-direction and y-direction can be written in terms of modal coordinates as

$$ \left\{ \begin{aligned} {\mathbf{x}}(t) = {\mathbf{U}}_{{\mathbf{x}}} {\mathbf{q}}_{{\mathbf{x}}} (t) \hfill \\ {\mathbf{y}}(t) = {\mathbf{U}}_{{\mathbf{y}}} {\mathbf{q}}_{{\mathbf{y}}} (t) \hfill \\ \end{aligned} \right. $$
(15)

where \( {\mathbf{U}}_{{\mathbf{x}}} = [{\mathbf{\varphi }}_{x1} , \ldots ,{\mathbf{\varphi }}_{xr} ] \) and \( {\mathbf{U}}_{y} = [{\mathbf{\varphi }}_{y1} , \ldots ,{\mathbf{\varphi }}_{yr} ] \) are the structural mode shapes along the x-direction and y-direction, respectively. \( {\mathbf{q}}_{x} (t) = [q_{x1} (t), \ldots ,q_{xr} (t)]^{T} \) and \( {\mathbf{q}}_{y} (t) = [q_{y1} (t), \ldots ,q_{yr} (t)]^{T} \) represent the modal displacement vectors along x-direction and y-direction, respectively, and r is the number of mode to be considered. Considering the symmetry, one has \( {\mathbf{\varphi }}_{xi} = {\mathbf{\varphi }}_{yi} { (}i = 1,2,3, \ldots ,r) \). Ignoring the coupling effects of the x-direction and y-direction, the modal mass, damping, and stiffness matrices become

$$ \left\{ \begin{aligned} {\mathbf{M}}_{{\mathbf{q}}} (\omega ) & = \left[ \begin{aligned} {\mathbf{U}}_{{\mathbf{x}}}^{{\mathbf{T}}} {\mathbf{M}}_{{{\mathbf{xx}}}} {\mathbf{U}}_{{\mathbf{x}}} \hfill \\ {\mathbf{U}}_{{\mathbf{y}}}^{{\mathbf{T}}} {\mathbf{M}}_{{{\mathbf{yy}}}} {\mathbf{U}}_{{\mathbf{y}}} \hfill \\ \end{aligned} \right] \\ {\mathbf{C}}_{{\mathbf{q}}} (\omega ) & = \left[ \begin{aligned} {\mathbf{U}}_{{\mathbf{x}}}^{{\mathbf{T}}} {\mathbf{C}}_{{{\mathbf{xx}}}} (\omega ){\mathbf{U}}_{{\mathbf{x}}} \hfill \\ {\mathbf{U}}_{{\mathbf{y}}}^{{\mathbf{T}}} {\mathbf{C}}_{{{\mathbf{yy}}}} (\omega ){\mathbf{U}}_{{\mathbf{y}}} \hfill \\ \end{aligned} \right] \\ {\mathbf{K}}_{{\mathbf{q}}} (\omega ) & = \left[ \begin{aligned} {\mathbf{U}}_{{\mathbf{x}}}^{{\mathbf{T}}} {\mathbf{K}}_{{{\mathbf{xx}}}} (\omega ){\mathbf{U}}_{{\mathbf{x}}} \hfill \\ {\mathbf{U}}_{{\mathbf{y}}}^{{\mathbf{T}}} {\mathbf{K}}_{{{\mathbf{yy}}}} (\omega ){\mathbf{U}}_{{\mathbf{y}}} \hfill \\ \end{aligned} \right] \\ \end{aligned} \right. $$
(16)
Fig. 13
figure 13

Mechanical model of milling process

Full size image

The resulted governing equations of motion in the mode coordinates can be written as

$$ {\mathbf{M}}_{{\mathbf{q}}} (\omega ){\ddot{\mathbf{q}}}(t) + {\mathbf{C}}_{{\mathbf{q}}} (\omega ){\dot{\mathbf{q}}}(t) + {\mathbf{K}}_{{\mathbf{q}}} (\omega ){\mathbf{q}}(t) = {\mathbf{F}}_{{\mathbf{q}}} (t) $$
(17)

where \( {\mathbf{q}}(t) = \left[ {{\mathbf{q}}_{{\mathbf{x}}}^{T} (t) \, {\mathbf{q}}_{{\mathbf{y}}}^{T} (t)} \right]^{T} \) and \( {\mathbf{F}}_{{\mathbf{q}}} (t) = \left[ \begin{aligned} {\mathbf{U}}_{{\mathbf{x}}}^{{\mathbf{T}}} {\mathbf{F}}_{{\mathbf{x}}} (t) \hfill \\ {\mathbf{U}}_{{\mathbf{y}}}^{{\mathbf{T}}} {\mathbf{F}}_{{\mathbf{y}}} (t) \hfill \\ \end{aligned} \right] \).

3.1 Model of cutting force

Considering the cutting forces applied only on the tool tip, one has

$$ {\mathbf{F}}_{{\mathbf{x}}} (t) = [F_{x1} (t),0, \ldots ,0]^{T} ,\quad {\mathbf{F}}_{{\mathbf{y}}} (t) = [F_{y1} (t),0, \ldots ,0]^{T} $$
(18)

In the case of the structural modes have been unit normalized at the tool tip, the right-hand side of Eq. (17) becomes

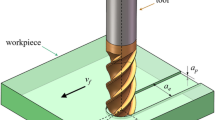
$$ {\mathbf{F}}_{{\mathbf{q}}} (t) = \left[ \begin{aligned} {\mathbf{U}}_{{\mathbf{x}}}^{{\mathbf{T}}} {\mathbf{F}}_{{\mathbf{x}}} (t) \hfill \\ {\mathbf{U}}_{{\mathbf{y}}}^{{\mathbf{T}}} {\mathbf{F}}_{{\mathbf{y}}} (t) \hfill \\ \end{aligned} \right] = [F_{x1} (t), \ldots ,F_{x1} (t),F_{y1} (t), \ldots ,F_{y1} (t)]^{T} $$
(19)

Similar to the cutting force model developed by Balachandran and Zhao [6] and Balachandran [23], in the cutting zone \( \theta_{s}^{{\prime }} < \theta (i,t,z) < \theta_{e}^{{\prime }} \), when the ith cutting tooth is in contact with workpiece, the corresponding cutting force components along the x-direction and the y-direction can be written as

$$ \left\{ {\begin{array}{*{20}c} {F_{x}^{i} (t)} \\ {F_{y}^{i} (t)} \\ \end{array} } \right\} = \int\limits_{{z_{1} (t,i)}}^{{z_{2} (t,i)}} {\left( {\left[ {\begin{array}{*{20}c} {\hat{k}_{11}^{i} (t,z)} & {\hat{k}_{12}^{i} (t,z)} \\ {\hat{k}_{21}^{i} (t,z)} & {\hat{k}_{22}^{i} (t,z)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A(t)} \\ {B(t)} \\ \end{array} } \right\}} \right)} dz $$
(20)

where

$$ \begin{aligned} A(t) & = q_{x} (t) - q_{x} (t - \tau ) + f\tau \\ B(t) & = q_{y} (t) - q_{y} (t - \tau ) \\ \end{aligned} $$
(21)

In Eq. (20), the time-periodic coefficient matrices are given by

$$ \left[ {\begin{array}{*{20}c} {\hat{k}_{11}^{i} (t,z)} & {\hat{k}_{12}^{i} (t,z)} \\ {\hat{k}_{21}^{i} (t,z)} & {\hat{k}_{22}^{i} (t,z)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \sin \theta (t,i,z)} & { - \cos \theta (t,i,z)} \\ { - \cos \theta (t,i,z)} & {\sin \theta (t,i,z)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {k_{1} k_{t} } \\ {k_{2} k_{t} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - \sin \theta (t,i,z)} & {\cos \theta (t,i,z)} \\ \end{array} } \right] $$
(22)

where

$$ \begin{aligned} k_{1} & = \frac{{k_{n} }}{\cos \eta } \\ k_{2} & = 1 + \tan \eta \left[ {\mu \left( {\cos \varphi_{n} - k_{n} \sin \varphi_{n} } \right)} \right] \\ \end{aligned} $$
(23)

When a cutting flute is outside the cutting zone or the dynamic uncut chip thickness associated with this flute is zero, there is loss of contact, then, the cutting force components associated with this flute are zero; that is,

$$ \left\{ {\begin{array}{*{20}c} {F_{x}^{i} (t)} \\ {F_{y}^{i} (t)} \\ \end{array} } \right\} = {\mathbf{0}} $$
(24)

Summing the cutting forces those act on the N cutting flutes, one can obtain the total cutting force acting on the tool; this takes the form

$$ \left\{ {\begin{array}{*{20}c} {F_{x1} (t)} \\ {F_{y1} (t)} \\ \end{array} } \right\} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{1} (t,i)}}^{{z_{2} (t,i)}} {\left[ {\begin{array}{*{20}c} {\hat{k}_{11}^{i} (t,z)} & {\hat{k}_{12}^{i} (t,z)} \\ {\hat{k}_{21}^{i} (t,z)} & {\hat{k}_{22}^{i} (t,z)} \\ \end{array} } \right]} } dz\quad \left\{ {\begin{array}{*{20}c} {A(t)} \\ {B(t)} \\ \end{array} } \right\} $$
(25)

Let

$$ {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (t) = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{1} (t,i)}}^{{z_{2} (t,i)}} {\left[ {\begin{array}{*{20}c} {\hat{k}_{11}^{i} (t,z)} & {\hat{k}_{12}^{i} (t,z)} \\ {\hat{k}_{21}^{i} (t,z)} & {\hat{k}_{22}^{i} (t,z)} \\ \end{array} } \right]} } dz $$
(26)

One has

$$ \begin{aligned} \left[ \begin{array}{c} F_{x1} (t) \hfill \\ F_{y1} (t) \hfill \\ \end{array} \right] &= {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (t)\left[ \begin{array}{c} x_{1} (t) - x_{1} (t - \tau ) \hfill \\ y_{1} (t) - y_{1} (t - \tau ) \hfill \\ \end{array} \right] + {\mathbf{f}}_{{\mathbf{0}}}^{{\mathbf{*}}} (t) \hfill \\ &= {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (t)\left[ \begin{array}{c} 1 \, \cdot \cdot \cdot 1 \, 0 \, \cdot \cdot \cdot 0 \hfill \\ 0 \, \cdot \cdot \cdot 0 \, 1 \, \cdot \cdot \cdot \, 1 \hfill \\ \end{array} \right]_{2 \times 2r} \left[ \begin{array}{c} {\mathbf{q}}_{{\mathbf{x}}} (t) - {\mathbf{q}}_{{\mathbf{x}}} (t - \tau ) \hfill \\ {\mathbf{q}}_{{\mathbf{y}}} (t) - {\mathbf{q}}_{{\mathbf{y}}} (t - \tau ) \hfill \\ \end{array} \right] + {\mathbf{f}}_{{\mathbf{0}}}^{{\mathbf{*}}} (t) \hfill \\ \end{aligned} $$
(27)

where τ is the time delay; \( {\mathbf{f}}_{{\mathbf{0}}}^{{\mathbf{*}}} (t) \) is the cutting force due to the feed effect and can be neglected on the stability analysis of the periodic motion [10].

Then the modal cutting forces \( {\mathbf{F}}_{{\mathbf{q}}} (t) \) can be expressed as

$$ {\mathbf{F}}_{{\mathbf{q}}} (t) = {\mathbf{k}}_{{\mathbf{c}}} (t)[{\mathbf{q}}(t) - {\mathbf{q}}(t - \tau )] $$
(28)

where

$$ {\mathbf{k}}_{{\mathbf{c}}} (t) = \left[ \begin{aligned} {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (1,1){ 0 } \cdots \, 0 \, {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (1,2){ 0 } \cdots \, 0 \hfill \\ \, \vdots \, \vdots \, \vdots \, \vdots \, \vdots \, \vdots \hfill \\ {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (1,1){ 0 } \cdots \, 0 \, {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (1,2){ 0 } \cdots \, 0 \hfill \\ {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (2,1){ 0 } \cdots \, 0 \, {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (2,2){ 0 } \cdots \, 0 \hfill \\ \, \vdots \, \vdots \, \vdots \, \vdots \, \vdots \, \vdots \hfill \\ {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (2,1){ 0 } \cdots \, 0 \, {\mathbf{k}}_{{\mathbf{c}}}^{{\mathbf{*}}} (2,2){ 0 } \cdots \, 0 \hfill \\ \end{aligned} \right]_{2r \times 2r} \left[ \begin{aligned} { 1 } \cdots \, 1{ 0 } \cdots \, 0 \hfill \\ \, \vdots \, \vdots \, \vdots \, \vdots \hfill \\ { 1 } \cdots \, 1{ 0 } \cdots \, 0 \hfill \\ { 0 } \cdots \, 0{ 1 } \cdots \, 1 \hfill \\ \, \vdots \, \vdots \, \vdots \, \vdots \hfill \\ { 0 } \cdots \, 0{ 1 } \cdots \, 1 \hfill \\ \end{aligned} \right]_{2r \times 2r} $$
(29)

3.2 Stability analysis

Substituting Eq. (28) into (17), one has

$$ {\mathbf{M}}_{q} (\omega ){\ddot{\mathbf{q}}}(t) + {\mathbf{C}}_{{\mathbf{q}}} (\omega ){\dot{\mathbf{q}}}(t) + {\mathbf{K}}_{{\mathbf{q}}} (\omega ){\mathbf{q}}(t) = {\mathbf{k}}_{{\mathbf{c}}} (t)[{\mathbf{q}}(t) - {\mathbf{q}}(t - \tau )] $$
(30)

Let \( {\mathbf{Q}}(t) = [{\mathbf{q}}^{T} (t) \, {\dot{\mathbf{q}}}^{T} (t)]^{T} \), Eq. (30) can be put in the state-space form

$$ {\dot{\mathbf{Q}}}(t) = {\mathbf{W}}_{{\mathbf{0}}} (t,\omega ){\mathbf{Q}}(t) + {\mathbf{W}}_{{\mathbf{1}}} (t,\omega ){\mathbf{Q}}(t - \tau ) $$
(31)

where \( {\mathbf{W}}_{{\mathbf{0}}} (t,\omega ) \) is the coefficient matrix associated with present states and \( {\mathbf{W}}_{1} (t,\omega ) \) are the coefficient matrix associated with delayed states. They are piecewise, periodic functions of time and given by

$$ {\mathbf{W}}_{{\mathbf{0}}} (t,\omega ) = \left[ {\begin{array}{cc} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{M}}_{q}^{ - 1} (\omega ){\mathbf{K}}_{q} (\omega ) + {\mathbf{M}}_{q}^{ - 1} (\omega ){\mathbf{k}}_{c} (t)} & { - {\mathbf{M}}_{q}^{ - 1} (\omega ){\mathbf{C}}_{q} (\omega )}\\ \end{array} } \right] $$
(32)
$$ {\mathbf{W}}_{{\mathbf{1}}} (t,\omega ) = \left[ {\begin{array}{*{20}l} {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ { - {\mathbf{M}}_{q}^{ - 1} (\omega ){\mathbf{k}}_{c} (t)} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right] $$
(33)

Equation (31) is a delay-differential system with time-periodic coefficients.

Next, the formulation of the semi-discretization method is presented. The time period T of the periodic orbit is first divided into n equal intervals with length Δt and the time interval Δt is chosen as

$$ \Delta t=\frac{T}{n}$$
(34)

For \( t \in [t_{j} ,t_{j + 1} ] \), the time-periodic coefficient matrices in Eq. (31) are approximated as

$$ {\mathbf{W}}_{j,0} (\omega ) \approx \frac{1}{\Delta t}\int\limits_{{t_{j} }}^{{t_{j + 1} }} {{\mathbf{W}}_{0} (t,\omega )dt} $$
(35)
$$ {\mathbf{W}}_{j,1} (\omega ) \approx \frac{1}{\Delta t}\int\limits_{{t_{j} }}^{{t_{j + 1} }} {{\mathbf{W}}_{1} (t,\omega )dt} $$
(36)

Then, over each time interval \( t \in \left[ {t_{j} ,t_{j + 1} } \right] \) for j = 0, 1, …, k − 1, Eq. (31) can be approximated as

$$ {\dot{\mathbf{Q}}}(t) = {\mathbf{W}}_{j,0} (\omega ){\mathbf{Q}}(t) + {\mathbf{W}}_{j,1} (\omega ){\mathbf{Q}}_{j - n} $$
(37)

Thus, the infinite-dimensional Eq. (31) has been replaced by a piecewise system of ordinary differential equations with constant coefficients in the time period \( t \in \left[ {t_{0} ,t_{0} + T} \right] \).

To proceed further, it is assumed that \( {\mathbf{W}}_{j,0} (\omega ) \) is invertible for all j. Then, writing Q(t j ) as Q j , the solution of Eq. (37) takes the form

$$ {\mathbf{Q}}(t) = e^{{{\mathbf{W}}_{j,0} (\omega ) \cdot (t - t_{j} )}} {\mathbf{Q}}_{j} + \left( {e^{{{\mathbf{W}}_{j,0} (\omega ) \cdot (t - t_{j} )}} - {\mathbf{I}}} \right){\mathbf{W}}_{j,0}^{ - 1} (\omega ){\mathbf{W}}_{j,1} (\omega ){\mathbf{Q}}_{j - n} $$
(38)

When t = t j + 1, Eq. (38) leads to

$$ {\mathbf{Q}}_{j + 1} = {\mathbf{M}}_{j,0} (\omega ){\mathbf{Q}}_{j} + {\mathbf{M}}_{j,1} (\omega ){\mathbf{Q}}_{j - n} $$
(39)

where the associated matrices are given by

$$ {\mathbf{M}}_{j,0} (\omega ) = e^{{{\mathbf{W}}_{j,0} (\omega ) \cdot\Delta t}} $$
(40)
$$ {\mathbf{M}}_{j,1} (\omega ) = \left( {e^{{{\mathbf{W}}_{j,0} (\omega ) \cdot \Delta t}} - {\mathbf{I}}} \right){\mathbf{W}}_{j,0}^{ - 1} (\omega ){\mathbf{W}}_{j,1} (\omega ) $$
(41)

The Eq. (39) can be used to construct the state vector

$$ {\mathbf{Y}}_{j} = ({\mathbf{Q}}_{j}^{T} ,{\mathbf{Q}}_{j - 1}^{T} , \ldots ,{\mathbf{Q}}_{j - n}^{T} )^{T} $$
(42)

and the linear discrete map

$$ {\mathbf{Y}}_{j + 1} = {\mathbf{B}}_{j} {\mathbf{Y}}_{j} $$
(43)

where, each B j matrix is given by

$$ {\mathbf{B}}_{j} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{j,0} (\omega )} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {M_{j,1} (\omega )} \\ {\mathbf{I}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{I}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{I}} & {\mathbf{0}} \\ \end{array} } \right] $$
(44)

For the Eq. (43), it follows that

$$ {\mathbf{Y}}_{k} = {\mathbf{B}}_{k - 1} \ldots {\mathbf{B}}_{1} {\mathbf{B}}_{0} {\mathbf{Y}}_{0} $$
(45)

From which the transition matrix can be identified as

$$ {\varvec{\Phi}} = {\mathbf{B}}_{k - 1} \ldots {\mathbf{B}}_{1} {\mathbf{B}}_{0} $$
(46)

This matrix Φ represents a finite-dimensional approximation of the “monodromy matrix” associated with the trivial solution Q(t) = 0 of (31). If the eigenvalues of this matrix are all within the unit circle, then the trivial fixed point of (31) is stable, and hence, the associated periodic orbit of (17) is stable.

4 Numerical results and discussions

In order to investigate the effect of dynamic modal parameters (DMP) on the stability, milling processes performed by the machine with the examined high speed spindle are to be studied. The workpiece is a cast iron. The machining parameters of milling processes are chosen as shown in Table 2 to illustrate the analysis. In the numerical analysis, the step number n = 40. The computational cost is about 110 s with a 2.8 GHz CPU to get a stability lobe diagram.

Table 2 Tool and machining parameters of milling system
Full size table

In Fig. 14a–d, the predicted stability lobes constructed for the first four dynamic modal parameters and static modal parameters (SMP) are presented. It is obviously that the minimum of the axial critical depth of cut (ADOC) obtained for the dynamic modal parameters is less than that obtained for the static modal parameters, and that the stability lobes obtained for the DMP shift to the low speed regions. By observing Fig. 14a, for the first-order mode, one can find there is remarkable difference between the stability lobes obtained by SMP and the stability lobes obtained by DMP, especially, in the high spindle speed regions. That is due to the first order modal stiffness of spindle decreases dramatically with the increase of the spindle speed. For example, one may choose 10,000 rpm as a stable and optimum operating speed, based on the stable lobes of SMP. However, the lobes of DMP indicate it isn’t a recommendable speed in term of stability. For the second-order mode, one can find the minimum of the ADOC obtained by the DMP is less than those obtained for the SMP, and that the stability lobes obtained for the DMP shift to the low speed range obviously. Due to effects on the third and the fourth-order modes are the less, the difference between the stability lobes obtained by the DMP and SMP is small, such as shown in Fig. 14c, d.

Fig. 14
figure 14

Stability lobes obtained for: a) the first mode, b) the second mode, c) the third mode, d) the fourth mode, e) the first four modes

Full size image

By comparing the stability lobes obtained for different modes with the static modal parameters in Fig. 14, one can find the stability lobes obtained for the first-order mode is far higher than those obtained for the second, third, and fourth-order mode in the case of system with static modal parameters. That is because the modal stiffness of first-order mode is far higher than the modal stiffness of the second, third, and fourth-order modes in the case of the spindle speed is zero (Fig. 10). With the increase of spindle speed, the modal stiffness of the first-order mode decreases dramatically and the others decrease less. In the case of the spindle speed up to 8000 rpm, the modal stiffness of the first-order mode closes to the modal stiffness of the others. The stability of the milling processes is determined by the first-order mode with the dynamic modal parameters. In Fig. 14e, the stability lobes obtained by the first-four-order modes of SMP and DMP are presented. By Fig. 14e, one can find the stability lobes obtained by the DMP are almost coinciding with the lobes obtained by the SMP in the low speed regions (less than 8000 rpm). This is because the dominant mode in term of stability is the fourth-order mode in the low speed regions. However, there is remarkable difference in the high spindle speed regions. That is due to the first order modal stiffness of spindle decreases dramatically with the increase of the spindle speed and the dominant mode in term of stability is the first-order mode in the high speed regions, such as shown in Fig. 10. In addition, one need to be notified is the loci of bifurcations are different between the system with SMP and the system with DMP.

In Fig. 15, from which one can find that as the number of modes considered increases, the stability boundaries decrease until the first-four-order modes are considered at the low rotational speed region (0–8000 rpm), so it will bring big errors if one predicts the stability boundaries only with the consideration of the first-order mode in such region. At the high speed region (above 8000 rpm), however, the variations with respect to the higher order modes are small and the first-order mode is dominant to determine the stability boundaries. These indicate both the effects of variable bearing stiffness and higher order modes cannot be ignored to predict the stability of the milling processes.

Fig. 15
figure 15

Stability lobes obtained for different modes included

Full size image

5 Conclusions

In this study, the speed dependent dynamic characteristics of high speed spindle with angular contact bearing have been presented through an analysis of bearing dynamics. Results show the stiffness and the natural frequencies of spindle decreases as spindle speed increases, especially for the first-order mode. The effects of variable dynamic characteristics with respect to the change of speed on the stability of milling processes are explored. By comparing the stability lobes obtained for different mode of the spindle-tool system, one can find higher order modes are dominant on the stability of milling processes in some cutting operation parameter space. To select a stable machining speed in high speed, the speed varying dynamic characteristics and higher order modes of a spindle should be considered properly.