Dynamic modeling and nonlinear vibration analysis of spindle system during ball end milling process

Abstract

In cutting process, the insufficiency in grasp of the tool vibration characteristics of spindle system seriously hinders the improvement of machining quality and efficiency. Thus, this paper develops a novel dynamic model of spindle system in ball end milling process considering the nonlinear contact behavior of bearings. For the sake of coupling with the motion differential equations of spindle shaft, a general analytical expression for the nonlinear contact force of matched angular contact ball bearings is proposed. Then, dynamic cutting force model during ball end milling is established with consideration of the influence of tool vibration on the uncut chip thickness. Furthermore, the effectiveness and feasibility of the proposed model is confirmed by some cutting tests. Finally, the effects of rotation speed, bearing preload, and cutting parameters on the tool end vibration response of spindle system are analyzed in detail. The investigations reveal that the main resonance frequency increases and the corresponding resonance amplitude decreases as bearing preload increases. The larger bearing preload can improve cutting stability and machining quality. It is also concluded that the change regarding axial depth of cut considerably affects the vibration behaviors of tool end. The proposed dynamic model can be applied to predict the vibration of spindle system during ball end milling, especially the tool vibration.

1 Introduction

The ball end milling technology is a very common subtractive manufacturing method for obtaining high-precision and complex curved parts in aerospace, automobile, and mold industries [1]. The spindle system is the core component of CNC (computer numerical control) milling machine tools, and its vibration behaviors have a severe impact on machining quality of parts and removal efficiency of surplus material [2]. During milling, generated cutting force is composed of the steady component caused by feed movement of tool or worktable system and the dynamic component considering regenerative effect [3]. As the spindle rotates, the steady component changes with time, causing the spindle system to produce forced vibration. While self-excited vibration of spindle system is caused by the cutting force part due to change regarding dynamic uncut chip thickness with consideration of the regeneration effect. The stronger forced and self-excited vibrations of spindle system are adverse in improving machining accuracy and productivity, and also reduce the reliability of the entire milling machine. However, there are few scientific reports on dynamic modeling and vibration analysis of spindle system in ball end milling process. The insufficiency in grasp of the tool vibration characteristics of spindle system during milling severely hinders the improvement of milling accuracy and the enhance of machining efficiency. Therefore, it has important engineering application value and theoretical significance for the investigation of vibration characteristics of spindle system during ball end milling process.

The dynamic modeling of spindle shaft is a decisive step in analyzing the vibration behavior of spindle system during ball end milling process. Over the past few decades, research scientists have done a lot of research on the modeling method of spindle. At early stages, machine tool spindle was modeled as a mass unit with five DOFs (degrees of freedom) including translational vibrations in three directions and titling vibrations about two radial directions [4]. This model was used by Alfares et all. [5, 6] to investigate the influence of the grinding force and the bearing preload on spindle system vibration. Karacay et al. [7] researched the ball passing vibration characteristics of bearing applying the five DOF model of spindle system. However, the accuracy of the above five DOF dynamic model and the conclusions drawn from the simulation results have not been experimentally verified. Zhang et al. [8,9,10] established a dynamic model of the aerostatic bearing spindle with five DOFs to study the effects of vibration response on the surface morphology and surface formation of machined parts. For the five DOF model of spindle system dynamics, the bending deformation of the shaft is not considered. In order to consider the flexibility of the shaft, Gao et al. [11] used lumped mass method to model spindle bearing system under unbalance force, and researched the nonlinear vibration behavior. Miao et al. [12] modeled the spindle system under unbalanced force accounting for bearing clearance, and considered the influence of bearing parameters on dynamics. In addition, some scholars developed the dynamic model of spindle system with application of finite element method to improve modeling accuracy. Cao et al. [13] modeled the dynamics of spindle system driven by the pulley, in which pulley was regarded as a rigid rotor and shaft dynamics was modeled on the basis of Timoshenko beam element theory. Accounting for the clearance between bearing outer ring and bearing housing, Cao et al. [14] used the rigid body elements to model rotor shaft to analyze vibration response and stability. The consistency between the measured and simulation results verified the effectiveness of the presented model. Xi et al. [15, 16] proposed a novel vibration model of spindle system dynamics. In dynamic model, the finite element method was adopted to model the dynamics of spindle shaft accounting for shear deformation, and the dynamic model of the bearing was formulated with bearing components having six DOFs. However, the cutting force in the simulation comes from experimental measurement, which wastes resources and time. And it is very difficult for measuring the cutting forces from all cutting conditions. From the above research review, it can be found that the dynamics of the spindle system during cutting process have received little attention.

In addition, angular contact ball bearings are very crucial components in spindle system, which have the advantages of low friction, high operation accuracy, higher support stiffness, and long operating life. The interface characteristics of ball bearings are the source of nonlinearity in the spindle system due to Hertz contact behaviors between balls and raceways [17]. An enormous amount of research has been done in the internal mechanics of bearings. Some researchers have addressed the connection between the restoring force of bearing and bearing vibration displacement to couple with the dynamic equations of rotor system. Xu et al. [18] concluded that the axial deformation of ball is an explicit expression with respect to the axial load of bearing by simplifying the relative deformation of ball. Wang et al. [19] calculated the contact force of rolling element under the coupling action of the deflection vibration and axial vibration of bearing inner ring. Some scholars have conducted extensive research on bearing stiffness. On the basis of the quasi-static model of bearing taking into account high-speed dynamic effect of balls, Noel et al. [20] provided the calculation technique for obtaining the expression for the bearing stiffness. The method was verified in dynamic analysis of spindle system of milling machine. Taking into account changes in the loaded ball number and the load distribution, Liu et al. [21] investigated the stiffness change of angular contact ball bearings. The simulation results showed that the changes in the loaded ball number and the load distribution have dramatic influence on bearing stiffness. By reviewing the above studies, it can be found that the above research objects were mainly concentrated on a single bearing. However, in order to provide higher axial, radial and moment load carrying capacity, matched bearings are extensively applied in rotor system. In some dynamic problems, matched ball bearings must be considered as a whole for analysis and research. But there are relatively few scientific research results on matched bearings. Applying Hertz contact theory, Gunduz et al. [22] derived the relationship between the displacement vector and load vector of double row ball bearings according to location relationship between bearing inner and outer rings. Xu et al. [23] formulated the five DOF model of duplex angular contact ball bearings considering misalignment of inner and outer rings for matched bearings of various ball arrangements. From the above literature review analysis, it can be found that there are few scientific reports on the restoring force of matched bearings.

Furthermore, there is a large amount of scientific research on ball end milling. Wojciechowski et al. [24] presented the cutting force prediction model during ball end milling with consideration of the influence of tool wear. The research demonstrated that tool wear influences greatly the prediction accuracy of cutting force. In the light of the mechanical cutting force model proposed by Lee et al. [25], Wojciechowski et al. [26] proposed the cutting force model during ball end milling progress considering varying feed rates and surface inclination of the machined workpiece. Besides, Wojciechowski et al. [27] integrated the manufacturing and assembly errors of spindle system and tool vibration as a result of cutting force to establish the displacement model of tool during machining. The displacement model of tool was used to formulate the surface roughness evaluation model of workpiece for cylindrical milling [28]. Wojciechowski et al. [29] researched the micro-milling forces and the quality evaluation of machining surface accounting for the tool inclination. The results revealed that the selection of the tool inclination and the feed per tooth have the significant influence on machining quality. Additionally, Wojciechowski et al. [30] researched the edge forces in ball end milling process considering the inclination of machining surface and the cutter abrasion during machining. It was conducted that the inclination of machining surface and the cutter abrasion during machining have the significant influence on the evaluation of the edge forces. From the above research review, it can be found that the instant cutting force model failed to consider the influence of tool vibration during machining. In fact, the vibration trajectory of the previous teeth of the tool can affect the chip thickness of the current tooth in ball end milling [31]. More importantly, the dynamic characteristics of spindle system, especially the nonlinear characteristics of bearings [16], have a dramatic effect on the vibration displacement of cutter. However, the above tool displacement evaluation did not consider the dynamic characteristics of spindle system. For the sake of avoiding chatter vibration during five-axis ball nose milling, a new method to automatically adjust the tool orientation is proposed by Chao et al. [1], considering tool-workpiece engagement, feed direction and machine kinematics. Sonawane et al. [32] formulated the chip geometry determination method considering the strain of deformed chip to improve evaluation accuracy of cutting force during milling. Wei et al. [33] made better cutting force model of elemental cutting edge and the uncut chip thickness model, in which the cutting edge curve for ball end mill was written as a novel expression with the elemental cutting edge’s axial position angle as parameter. The evaluation of the proportional cutting force coefficients is a very crucial step for accurate prediction of the cutting force of ball end mill. The proportional cutting force coefficients were assessed according to the average cutting force measured from the horizontal slot cutting [34, 35]. Among the representative methods, Lamikiz et al. [36] developed a calculated technique for obtaining the proportional cutting force coefficients, in which the shear cutting coefficients are polynomials related to the axial height of discrete cutting edge, while the edge cutting coefficients are constant. The experimental testing results showed that when the shear coefficients are a linear polynomial, the predicted cutting force has acceptable accuracy.

Through the above-mentioned literature review, there is little scientific research on the dynamics of spindle system in machining progress considering the nonlinear characteristics of bearing and dynamic uncut chip thickness. In addition, as far as we know, there are few scientific reports on the calculation method the nonlinear restoring force of bearing set. To make up for these deficiencies in related research field, it is necessary to conduct machining progress modeling and nonlinear vibration analysis of spindle system. The purpose of this paper is to develop an integrated dynamic model capable of simulating the vibration behavior of spindle system during ball end milling process, especially the tool vibration. The specific contributions of this paper are as follows: (1) develop a novel spindle dynamic model combined with the dynamic cutting force model; (2) propose a general analytical expression for the nonlinear contact restoring force of matched angular contact ball bearings to couple with the motion differential equations of spindle shaft, which is suitable for various bearing ball arrangements; (3) design and carry out some cutting experiments to confirm the effectiveness and feasibility of the proposed model; (4) numerically investigate the effects of rotation speed, bearing preload, as well as cutting parameters on dynamic response.

The rest content of this paper is structured as follows. Section 2 develops an integral dynamic model of spindle system in ball end milling process, proposes a general analytical expression for the nonlinear contact force of bearing set, establishes the dynamic cutting force model in ball end milling, and finally establishes the motion differential equations with 35 DOFs and time delays. In Sect. 3, the effectiveness and feasibility of the proposed model are confirmed by some experiments. In Sect. 4, the effects of rotation speed, bearing preload, and cutting parameters on dynamic response are numerically analyzed. Section 5 draws some conclusions and discusses the application of the proposed method.

2 Modeling of spindle dynamics during cutting

2.1 Equivalent dynamic model

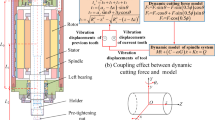
During ball end milling, the generated dynamic milling force can cause spindle system to vibrate, and the tool vibration may cause change in the dynamic uncut chip thickness, which in turn can cause dynamic change in cutting force. Figure 1 shows the coupling effect between dynamic cutting force and dynamic model in ball end milling process. Thence, an integral dynamic model combining the spindle system dynamic model and the dynamic cutting force model is proposed to investigate dynamic behavior in ball end milling process.

Fig. 1

Coupling effect between dynamic cutting force and dynamic model

The structure diagram of spindle system in the milling machine with three axes is shown in Fig. 2a. The main components of spindle system include ball end mill, tool holder, shaft, angular contact ball bearings, pulley and additional accessories. The shaft is supported by three bearing sets. The two angular contact ball bearings of the first and second bearing sets are arranged in tandem, but axial bearing direction of the first and second bearing sets are opposite. The two angular contact ball bearings of the third bearing set are arranged in back to back form.

Fig. 2

Spindle system. a Structure schematic diagram. b Equivalent dynamic model. c Five DOFs of lumped mass point

Some assumptions are made about the spindle system:

• 1. Balls in the bearing raceway are evenly spaced. The bearing is intact and there is no fault defect. Bearing lubrication and ball skidding have little effect on spindle dynamics.

• 2. The connections between the inner and outer rings of bearing and the corresponding parts are considered as rigid connection. The ball end mill is rigidly attached to tool holder, which is rigidly connected with spindle shaft.

• 3. Synchronous toothed pulley is simplified as rigid rotors fixed on the shaft. Besides, this study ignores the effects of other accessories on the vibration behaviors of spindle system.

The lumped mass method [37] is used to develop the equivalent dynamic model of spindle system during ball end milling, as illustrated in Fig. 2b. In Fig. 2b, O₁, O_b1, O₂, O_b2, O₃, O_b3, and O₄ are lumped mass points of the tool end, the first bearing set, the interval part between first and second bearing sets, the second bearing set, the interval part between second and third bearing sets, the third bearing set, and the pulley end, respectively; these lumped mass elements are connected by massless elastic shafts. EA₁, EA₂, EA₃, EA₄, EA₅, and EA₆ are the tension compression stiffness of cross section of massless elastic shafts; EI₁, EI₂, EI₃, EI₄, EI₅, and EI₆ are the bending stiffness of cross section of massless elastic shafts. Each lumped mass point has five DOFs including three translational displacements x, y, and z along X, Y, and Z directions and a pair of rotational displacements θ_x and θ_y around OX and OY directions, as displayed in Fig. 2c. During cutting process, the lumped mass point O₁ on the tool end is subjected to dynamic cutting forces in X, Y, and Z directions.

2.2 Analytical model of bearing set restoring force

2.2.1 Axial displacement of bearing inner ring under preload

In the spindle assembly, the spindle bearings should be preloaded to improve the support rigidity, avoid the collision between balls and raceways, and improve the machining accuracy. After angular contact ball bearing is preloaded, the contact angle increases, leading to changes in the internal mechanical properties of bearing. Therefore, when establishing the restoring force model of matched bearing set, the axial displacement of bearing inner ring under bearing preload must be analyzed theoretically first.

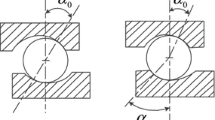
Regarding the jth ball of angular contact ball bearing, changes in the curvature centers of raceway grooves under preload are shown in Fig. 3. α₀ is initial contact angle between ball and raceway; B is comprehensive curvature coefficient, in which B = f_i + f_o − 1, f_i and f_o are curvature radius coefficients of inner and outer raceway grooves, respectively; D is ball diameter; α is contact angle after preload. o_ij and o_oj are curvature centers of inner and outer raceway grooves, respectively; o′_ij is curvature center of inner raceway groove after preload.

Fig. 3

Changes in curvature centers of raceway grooves under preload

The ball deformation along contact direction can be expressed by the variation in distance between the curvature centers of inner and outer raceway grooves. According to the geometric relationship, the ball deformation along normal direction under preload can be expressed as

$$\delta_{\mathrm N}=BD\left(\frac{\cos\;\alpha_0}{\cos\;\alpha}-1\right)$$

(1)

It is assumed that the contact mechanical behaviors between balls and raceways satisfy Hertz contact theory [38]. Such the normal contact force between ball and raceways can be calculated as

$$Q_{\mathrm N}=k_{\mathrm N}\delta_{\mathrm N}^{1.5}$$

(2)

where k_N is the total Hertz coefficient of ball in contact with raceways, which can be calculated as

$$k_{\mathrm N}=\left[\frac1{\left(1/k_i\right)^{1/1.5}+\left(1/k_o\right)^{1/1.5}}\right]^{1.5}$$

(3)

where k_i and k_o are the Hertz contact coefficient of ball in contact with inner and outer raceways, respectively, which can be calculated as follows

$$\left\{\begin{array}{c}k_{\mathrm i}=\frac{\sqrt{32}\left(\sum\rho_{\mathrm i}\right)^{-0.5}}{3\left(\delta_{\mathrm i}^\ast\right)^{1.5}}\left(\frac{1-\upsilon_{\mathrm b}^2}{E_{\mathrm b}}+\frac{1-\upsilon_{\mathrm i}^2}{E_{\mathrm i}}\right)^{-1}\\k_{\mathrm o}=\frac{\sqrt{32}\left(\sum\rho_\text{o}\right)^{-0.5}}{3\left(\delta_{\mathrm o}^\ast\right)^{1.5}}\left(\frac{1-\upsilon_{\mathrm b}^2}{E_{\mathrm b}}+\frac{1-\upsilon_{\mathrm o}^2}{E_{\mathrm o}}\right)^{-1}\end{array}\right.$$

(4)

where E_b, E_i, and E_o are elastic modulus of ball, inner ring and outer ring, respectively; v_b, v_i, and v_o are Poisson’s ratio of corresponding parts of bearing, respectively; ∑ρ_i and ∑ρ_o are contact curvature sum between ball and inner and outer raceway, respectively; $\delta_{i}^{*}$ and $\delta_{o}^{*}$ are inner and outer raceway constants dependent on the bearing geometrical parameters and material properties, respectively, and these two parameters are calculated according to the Ref. [38].

Because the resultant force of the contact forces of all balls is balanced with bearing axial preload, the force equilibrium equation of inner ring can be written as

$$\frac P{N_{\mathrm b}\sin\;\alpha}=k_{\mathrm N}\;B^{1.5\;}D^{1.5}{(\frac{\cos\;\alpha_0}{\cos\;\alpha}-1)}^{1.5}$$

(5)

where P is the bearing preload; N_b is the number of rolling elements.

Obviously, Eq. (5) is a nonlinear equation. The contact angle α between the ball and the raceway under preload can be iteratively calculated applying Newton–Raphson method. After solving the contact angle, the axial displacement of inner ring can be expressed as

$${\delta }_{a}=\frac{BD\;\mathrm{cos}\;{\alpha }_{0}}{\mathrm{cos}\;\alpha }\mathrm{sin}\;\alpha -BD\;\mathrm{sin}\;{\alpha }_{0}$$

(6)

2.2.2 Nonlinear restoring force of bearing set

In the research of this paper, matched angular contact ball bearings are used to support the spindle system of a three-axis vertical CNC milling machine. Matched angular contact ball bearings need to be regarded as a whole for the convenience of coupling with the motion differential equations of spindle shaft. Without loss of generality, this section presents a general calculation method of the nonlinear restoring force of matched angular contact ball bearings in back to back, face to face, and tandem arrangements, as shown in Fig. 4. This paper specifies matched angular contact bearings as bearing set. The dimensional parameters and material properties of the two bearings of bearing set are identical.

Fig. 4

Matched bearings arrangement. a Tandem. b Back to back. c Face to face

The bearing set coordinate system O_b-X_bY_bZ_b is established, in which origin O_b is the center of bearing set, O_bX_b and O_bY_b (this axis is not shown in Fig. 4) are the radial directions of the bearing set perpendicular to each other, and O_bZ_b is axial orientation of bearing set. The vibration displacements of inner ring of bearing set in relation to outer ring include three translational displacements and two rotational displacements. Three translational displacements are x_b, y_b, and z_b along O_bX_b, O_bY_b, and O_bZ_b, respectively. Two rotational displacements are θ_Xb, and θ_Yb around O_bX_b, and O_bY_b, respectively.

Regarding the jth ball of qth angular contact ball bearing of bearing set, the changes in the curvature centers of raceway grooves as a result of the external load are shown in Fig. 5, in which $o_{oq}^{j}$ is the curvature center of outer raceway groove; ${o}_{i}{}_{q}^{j}$and $o{^{\prime}}_{iq}^{j}$ are the unloaded and loaded curvature centers of inner raceway groove, respectively; α₀ and $\alpha_{q}^{j}$ are the unloaded and loaded contact angles between ball and raceway, respectively.

Fig. 5

Changes in the curvature centers of raceway grooves under the external load

The change values in inner raceway groove curvature center along axial and radial direction for the jth ball of qth angular contact ball bearing of bearing set can be expressed as

$$\left\{\begin{array}{l}\delta_{rq}^j=\text{(}x_{\mathrm b}+c_1e\theta_{Y_{\mathrm b}})\cos\;\varphi_q^j+\text{(}y_{\mathrm b}-c_1e\;\theta_{X_{\mathrm b}})\sin\;\varphi_q^j\\\delta_{zq}^j=z_{\mathrm b}\text{+}R_i\text{(}\theta_{X_{\mathrm b}}\sin\;\varphi_q^j-\theta_{Y_{\mathrm b}}\cos\;\varphi_q^j)\end{array}\right.$$

(7)

where e is axial distance between the ball center and the geometric center of bearing set; R_i is the track radius of inner raceway groove curvature center, given as follows

$$R_i=0.5d_{\mathrm m}+(f_{\mathrm i}-0.5)D\cos\;\alpha_0$$

(8)

where d_m is the pitch diameter of bearing set;

In Eq. (7), ${\varphi }_{q}^{j}$is the position angle of jth ball measured from O_bX_b, given as follows

$$\left\{\begin{array}{l}\varphi_q^j=\frac{2\pi}{N_{\mathrm b}}(j-1)-\omega_{\mathrm c}t,j=1,2,\cdots,N_{\mathrm b}\\\omega_{\mathrm c}=\frac\omega2(1-\frac{D\cos\;\alpha}{d_{\mathrm m}})\end{array}\right.$$

(9)

where ω is the angular speed of spindle shaft, in which the rotation direction of spindle system is opposite to Z axis positive orientation; t is the running time.

In Eq. (7), c₁ is a constant considering the position of angular contact bearing, given as follows:

$${c}_{1}=\left\{\begin{array}{l}-1 \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=1\\ 1 \, \, \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=2\end{array}\right.$$

(10)

where q is a constant related to the bearing position, q = 1 represents the bearing on the left side of bearing set, and q = 2 represents the bearing on the right side of bearing set.

Then, according to the geometric relationship of curvature centers of raceway grooves, the distance between curvature centers of inner raceway and outer raceway grooves in axial and radial direction can be expressed as

$$\left\{\begin{array}{l}{A}_{1q}^{j}=BD\sin\;{\alpha }_{0}+{\delta }_{aq}^{j}+{c}_{2}{\delta }_{zq}^{j}\\ {A}_{2q}^{j}=BD\cos\;{\alpha }_{0}+{\delta }_{ri}^{j}\end{array}\right.$$

(11)

where $\delta_{aq}^{j}$ is the axial displacement of qth bearing inner ring under preload; c₂ is a constant related to the ball arrangement and axial bearing direction of bearing, and the constant c₂ is given as follows.

For back to back arrangement,

$${c}_{2}=\left\{\begin{array}{l}1 \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=1\\ -1 \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=2\end{array}\right.$$

(12)

For face to face arrangement,

$${c}_{2}=\left\{\begin{array}{l}-1 \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=1\\ 1 \, \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=2\end{array}\right.$$

(13)

For tandem arrangement, when the axial bearing direction of bearing set is the positive direction of O_bZ_b axis,

$${c}_{2}=\left\{\begin{array}{l}1 \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=1\\ 1 \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, q=2\end{array}\right.$$

(14)

When the axial bearing direction of bearing set is the negative direction of O_bZ_b axis,

$$c_{2} = \left\{ \begin{gathered} - 1 \, \, \, \, \, \, \, \, \, \, {\text{ for }}q = 1 \hfill \\ - 1 \, \, \, \, \, \, \, \, \, \, {\text{ for }}q = 2 \, \hfill \\ \end{gathered} \right.$$

(15)

Based on the geometric relationship between curvature centers of raceway grooves, the distance between curvature centers of inner and outer raceway grooves and the loaded contact angle can be written as

$${A}_{q}^{j}=\sqrt{{\left({A}_{1q}^{j}\right)}^{2}+{\left({A}_{2q}^{j}\right)}^{2}}$$

(16)

$$\alpha_{q}^{j} = \arctan \left( {{{A_{1q}^{j} } \mathord{\left/ {\vphantom {{A_{1q}^{j} } {A_{2q}^{j} }}} \right. \kern-\nulldelimiterspace} {A_{2q}^{j} }}} \right)$$

(17)

Finally, the normal deformation of jth ball for qth angular contact ball bearing of bearing set under external load can be calculated as

$${\delta }_{q}^{j}=\left\{\begin{array}{l}{A}_{q}^{j}-{A}_{0} \, \, \, \, \, \, \, \, \, \, {A}_{q}^{j}-{A}_{0}\text{>}{0} \, \\ 0 \, \, \, \, \, \, \, \, \, \,\, \, \, \, \, \, \, \, \, \,\, \,\, \,\, \, {A}_{q}^{j}-{A}_{0}\le {0}\end{array}\right.$$

(18)

where A₀ is the initial distance between inner raceway groove curvature center and outer raceway groove curvature center.

If $A_{q}^{j}$ is greater than A₀, the jth ball can be deformed under external load, and vice versa. On the basis of Hertz contact theory, the normal contact force of jth ball for qth angular contact ball bearing of bearing set is written as

$$Q_q^j=k_{\mathrm N}\left(\delta_q^j\right)^{1.5}$$

(19)

Finally, the nonlinear restoring force acting on the center of the bearing set can be calculated as

$$\left\{\begin{array}{l}{F}_{{\text{b}}x}\\ {F}_{{\text{b}}y}\\ {F}_{{\text{b}}z}\\ {M}_{{\text{b}}x}\\ {M}_{{\text{b}}y}\end{array}\right\}=\sum_{q=1}^{2}\sum_{j=1}^{{N}_{b}}\left\{\begin{array}{l}{Q}_{q}^{j}\cos\;{\alpha }_{q}^{j}\cos\;{\varphi }_{q}^{j}\\ {Q}_{q}^{j}\cos\;{\alpha }_{q}^{j}\sin\;{\varphi }_{q}^{j}\\ {c}_{2}{Q}_{q}^{j}\sin\;{\alpha }_{q}^{j}-{c}_{2}P\\ {Q}_{q}^{j}({c}_{2}{R}_{i}\sin\;{\alpha }_{q}^{j}-{c}_{1}e\cos\;{\alpha }_{q}^{j})\sin\;{\varphi }_{q}^{j}\\ {Q}_{q}^{j}(-{c}_{2}{R}_{i}\sin\;{\alpha }_{q}^{j}+{c}_{1}e\cos\;{\alpha }_{q}^{j})\cos\;{\varphi }_{q}^{j}\end{array}\right\}$$

(20)

2.3 Dynamic milling force model

In this research, the ball end mill with constant lead is installed in the spindle system. Because the cutting conditions of all points on the cutting edge for ball end mill are different during cutting process, the dynamic cutting force in ball end milling should be predicted by using calculus idea. It is assumed that there are no geometric errors in spindle system in this paper.

The envelope schematic diagram of a ball end mill is shown in Fig. 6, in which O_c-X_cY_cZ_c is the cutter coordinate system, where O_c is the cutter tip, the Z_c axis positive direction is the axial upward direction of cutter, the X_c axis positive direction is the cutter feed direction, and the Y_c axis positive direction follows the right hand rule. In Fig. 6, R_c is the radius of ball end mill; α_c is the nominal helix angle; k is axial position angle of elemental cutting edge; ψ_j(t) is the plane projection angle between the jth cutting edge and Y_c axis; η_j is the plane projection angle of the line between cutting edge elemental point and cutter tip relative to the position of the jth cutting edge; θ_j is the plane projection position angle between Y_c axis and line between the elemental point on jth cutting edge and cutter tip.

Fig. 6

Envelope diagram of ball end mill. a Isometric view. b Top view. c Section A-A

Because the cutting edge helical curves of the ball end mill have a constant lead, the lag angle of the infinitesimal point of cutting edge can be written as the expression of the axial position angle k:

$$\eta \left(k\right)=\left(1-\mathrm{cos}\;k\right)\mathrm{tan}\;{\alpha }_{\text{c}}$$

(21)

The plane position angle ψ_j(t) of the jth cutting edge in ball end mill is written as

$${\psi }_{j}\left(t\right)={\psi }_{0}+\omega t+\left(j-1\right)2\pi /{N}_{c},j=\mathrm{1,2},\cdots ,{N}_{c}$$

(22)

where N_c is the flute number of ball end mill; ψ₀ is the reference position angle of the first flute; ω is the rotational angular velocity of cutter.

Then, according to three-dimensional position of envelope of ball end mill, the elemental point coordinates on the jth cutting edge is calculated as follows:

$$\left\{\begin{array}{l}{X}_{j}\left(t\right)={R}_{c}\sin\;k\sin\left({\psi }_{j}\left(t\right)-\eta \left(k\right)\right)\\ {Y}_{j}\left(t\right)={R}_{c}\sin\;k\cos\left({\psi }_{j}\left(t\right)-\eta \left(k\right)\right)\\ {Z}_{j}\left(t\right)={R}_{c}-{R}_{c}\cos\;k\end{array}\right.$$

(23)

From the expression of the cutting edge curve, the three coordinates of elemental edge point of jth cutting edge are the functions of parameter k. Then the length of the elemental edge can be calculated as

$$ds={R}_{c}\sqrt{1+{\mathrm{sin}}^{4}k\;{\mathrm{tan}}^{2}{\alpha }_{c}}dk$$

(24)

In this paper, the cutting force model of elemental cutting edge in Ref. [33] is applied:

$$\left[\begin{array}{c}d{F}_{\text{t}}\\ d{F}_{\text{r}}\\ d{F}_{\text{a}}\end{array}\right]=\left[\begin{array}{c}{K}_{\text{ts}}\\ {K}_{\text{rs}}\\ {K}_{\text{as}}\end{array}\right]{f}_{n}db+\left[\begin{array}{c}{K}_{\text{te}}\\ {K}_{\text{re}}\\ {K}_{\text{ae}}\end{array}\right]ds$$

(25)

where dF_t, dF_r, and dF_a are the tangential cutting force, radial cutting force and axial cutting force of elemental edge, respectively; K_ts, K_rs, and K_as are the shear cutting force coefficients; K_te, K_re, and K_ae are the edge cutting force coefficients; f_n is the elemental uncut chip thickness; db is elemental cutting chip width, db = R_cdk.

The uncut chip thickness of elemental cutting edge of jth tooth of ball end mill during cutting process can be written as follows

$$f_n=\left\{\begin{array}{lc}f_\text{c}\sin\;k\sin\theta_j+\Delta h&k_\text{low}\leq k\leq k_\text{up}\\0&\text{otherwise}\end{array}\right.$$

(26)

where f_c is the feed per tooth of cutter, f_c = f_s/(nN_c), in which n is the rotation speed of spindle system, f_s is the feed rate of spindle system; the term $f_{{\text{c}}} \sin k\sin \theta_{j}$ is the static thickness of elemental uncut chip related to the rigid body movement of cutter or workbench; Δh is the dynamic thickness of elemental uncut chip related to the vibration of the tool relative to the workpiece considering the regeneration effect; k_low and k_up are the minimum and maximum axial position angle of elemental cutting edge of jth tooth involved in the cutting, depending on the geometric parameters of cutter and the cutting amount.

It is assumed that the rigidity of the workpiece and workbench is large enough; the dynamic vibration displacements of the cutter in X_c, Y_c, and Z_c directions are follows

$$\left\{\begin{array}{l}\Delta {x}_{c}={x}_{c}\left(t\right)-{x}_{c}\left(t-{\tau }_{x}\right)\\ \Delta {y}_{c}={y}_{c}\left(t\right)-{y}_{c}\left(t-{\tau }_{y}\right)\\ \Delta {z}_{c}={z}_{c}\left(t\right)-{z}_{c}\left(t-{\tau }_{z}\right)\end{array}\right.$$

(27)

where x_c(t), y_c(t), and z_c(t) represent the vibration displacements of cutter at time t in X_c, Y_c, and Z_c directions, respectively; x_c(t-τ_x), y_c(t-τ_y), and z_c(t-τ_z) represent the vibration displacements of cutter at the time t-τ; τ_x, τ_y, and τ_z are tool tooth passing time in three directions, respectively.

Then, the dynamic thickness of elemental cutting chip [39] is written as

$$\Delta h=\Delta {x}_{\text{c}}\mathrm{sin}\;k\;\mathrm{sin}\;{\theta }_{j}+\Delta {y}_{\text{c}}\;\mathrm{sin}\;k\;\mathrm{cos}{\theta }_{j}-\Delta {z}_{\text{c}}\mathrm{cos}\;k$$

(28)

Through coordinate conversion, the projection of the differential cutting force in coordinate system O_c-X_cY_cZ_c in Fig. 6a can be written as follows

$$\left[\begin{array}{l}d{F}_{{\text{c}}x}^{j}\\ d{F}_{{\text{c}}y}^{j}\\ d{F}_{{\text{c}}z}^{j}\end{array}\right]=\left[\begin{array}{ccc}-\mathrm{cos}\;{\theta }_{j}& -\mathrm{sin}\;k\;\mathrm{sin}\;{\theta }_{j}& -\mathrm{cos}\;k\;\mathrm{sin}\;{\theta }_{j}\\ \mathrm{sin}\;{\theta }_{j}& -\mathrm{sin}\;k\;\mathrm{cos}\;{\theta }_{j}& -\mathrm{cos}\;k\;\mathrm{cos}{\;\theta }_{j}\\ 0& \mathrm{cos}\;k& -\mathrm{sin}\;k\;\end{array}\right]\left[\begin{array}{l}d{F}_{t}\\ d{F}_{r}\\ d{F}_{a}\end{array}\right]$$

(29)

where $dF_{{{\text{c}}x}}^{j}$, $dF_{{{\text{c}}y}}^{j}$, and $dF_{{{\text{c}}z}}^{j}$ are the projection of the elemental cutting forces in X_c, Y_c, and Z_c directions, respectively.

The cutting force for jth cutting edge in contact with workpiece can be obtained through integrating the cutting forces of elemental cutting edge along the jth cutter tooth in contact with workpiece. Then, the cutting forces during milling can be calculated by summing the cutting forces of all cutting teeth involved in cutting:

$$\left[\begin{array}{l}{F}_{{\text{c}}x}\\ {F}_{{\text{c}}y}\\ {F}_{{\text{c}}z}\end{array}\right]=\sum_{j}^{{N}_{\text{c}}}{\int }_{{k}_{\text{low}}}^{{k}_{\text{up}}}\left[\begin{array}{c}d{F}_{{\text{c}}x}^{j}\\ d{F}_{{\text{c}}y}^{j}\\ d{F}_{{\text{c}}z}^{j}\end{array}\right]dk$$

(30)

where F_cx, F_cy, and, F_cz are the cutting forces in X_c, Y_c, and Z_c directions, respectively.

2.4 Dynamic differential equations

The equivalent dynamic model of the spindle system with five lumped mass points and tool end subjected to dynamic cutting forces in three directions during milling process is shown in Fig. 2b. Each lumped mass point has five DOFs. According to the Lagrange equation, the 35 DOF motion control equations of the spindle system with three time delays can be written in matrix form as follows

$$\varvec{M}\ddot{\varvec{X}}+(\varvec{C}-\omega \varvec{G})\dot{\varvec{X}}+{\varvec{K}}\varvec{X}=\varvec{Q}$$

(31)

where M is the mass matrix of spindle system; K is the stiffness matrix of spindle system; C is the damping matrix of spindle system; G is the gyroscopic matrix of spindle system; X is the vibration displacement vector; Q is the external load vector, including bearing restoring forces and dynamic cutting forces. As the ball end mill rotates clockwise, the rotation direction of spindle system is opposite to the Z axis positive direction.

The mass matrix of the spindle system is calculated as

$$\varvec{M}=\left[\begin{array}{ccc}{\varvec{M}}_{x}& 0& 0\\ 0& {\varvec{M}}_{y}& 0\\ 0& 0& {\varvec{M}}_{z}\end{array}\right]$$

(32)

$$\begin{aligned}{\varvec{M}}_{x}={\varvec{M}}_{y}=\;&{\text{diag}}\left[{m}_{1},{I}_{{\text{d}}1},{m}_{{\text{b}}1},{I}_{{\text{db}}1},{m}_{2},{I}_{\text{d2}},{m}_{{\text{b}}2},{I}_{\text{db2}},\right. \\ & \left.{m}_{3},{I}_{\text{d3}},{m}_{{\text{b}}3},{I}_{\text{db3}},{m}_{4},{I}_{\text{d4}}\right]\end{aligned}$$

(33)

$${\varvec{M}}_{z}={\text{diag}}\left[{m}_{1},{m}_{{\text{b}}1},{m}_{2},{m}_{{\text{b}}2},{m}_{3},{m}_{{\text{b}}3},{m}_{4}\right]$$

(34)

where m₁, m_b1, m₂, m_b2, m₃, m_b3, and m₄ denote the mass of lumped mass points of the spindle system; I_d1, I_db1, I_d2, I_db2, I_d3, I_db3, and I_d4 denote moments of inertia of lumped mass points about radial direction.

The stiffness matrix of spindle shaft can be expressed as

$$\varvec{K}=\left[\begin{array}{ccc}{\varvec{K}}_{x}& 0& 0\\ 0& {\varvec{K}}_{y}& 0\\ 0& 0& {\varvec{K}}_{z}\end{array}\right]$$

(35)

where the calculation method of stiffness coefficients of K_x, K_y, and K_z is listed in the Appendix.

The gyroscopic matrix of the spindle system can be expressed as

$$\begin{aligned}\varvec{G}=\left[\begin{array}{ccc}0& -\varvec{J}& 0\\ {\varvec{J}}^{T}& 0& 0\\ 0& 0& 0\end{array}\right], \varvec{J}=\;&{\text{diag}}\left[0,{I}_{{\text{p}}1},0,{I}_{{\text{pb}}1},0,{I}_{\text{p2}},0,\right. \\ & \left.{I}_{\text{pb2}},0,{I}_{\text{p3}},0,{I}_{\text{pb3}},0,{I}_{\text{p4}}\right]\end{aligned}$$

(36)

where I_p1, I_pb1, I_p2, I_pb2, I_p3, I_pb3, and I_p4 are the moments of inertia of lumped mass rotors about axial direction.

The vibration displacement vector and external load vector can be written as

$$\begin{aligned}\varvec{X}=\;&\left[{x}_{1},{\theta }_{y1},{x}_{\text{b1}},{\theta }_{y{\text{b}}1},{x}_{2},{\theta }_{y2},{x}_{\text{b2}},{\theta }_{y{\text{b2}}},{x}_{3},\right. \\ & \left.{\theta }_{y3},{x}_{\text{b3}},{\theta }_{y{\text{b3}}},{x}_{4},{\theta }_{y4}, {y}_{1},{\theta }_{x{1}},{y}_{\text{b1}},{\theta }_{x{\text{b}}1},\right.\\&\left.{y}_{2},{\theta }_{x2},{y}_{\text{b2}},{\theta }_{x{\text{b2}}},{y}_{3},{\theta }_{x3},{y}_{\text{b3}},{\theta }_{x{\text{b3}}},{y}_{4},\right.\\& \left.{\theta }_{x4},{z}_{1},{z}_{\text{b1}},{z}_{2},{z}_{\text{b2}},{z}_{3},{z}_{\text{b3}},{z}_{4}\right]^{T}\end{aligned}$$

(37)

$$\begin{array}{c}\varvec{Q}=\left[{F}_{{\text{c}}x},0,-{F}_{{\text{b1}}x},-{M}_{{\text{b1}}y},\mathrm{0,0},-{F}_{{\text{b2}}x},-{M}_{{\text{b2}}y},\mathrm{0,0},-{F}_{{\text{b3}}x},-{M}_{{\text{b3}}y},\mathrm{0,0},\right.\\ {F}_{{\text{c}}y},0,-{F}_{{\text{b1}}y},-{M}_{{\text{b}}1x},\mathrm{0,0},-{F}_{{\text{b2}}y},-{M}_{{\text{b}}2x},\mathrm{0,0},-{F}_{{\text{b3}}y},-{M}_{{\text{b3}}x},\mathrm{0,0}\\ {\left.{F}_{{\text{c}}z},0,-{F}_{{\text{b1}}z},0,-{F}_{{\text{b2}}z},0,-{F}_{\text{b3z}},0\right]}^{T}\end{array}$$

(38)

where F_cx, F_cy, and F_cz are dynamic cutting forces in the three directions of tool end, coupled with the vibration displacement of the tool end; F_b1x, F_b1y, F_b1z, M_b1x, and M_b1y are nonlinear restoring forces and moments of first bearing set; F_b2x, F_b2y, F_b2z, M_b2x, and M_b2y are nonlinear restoring forces and moments of second bearing set; F_b3x, F_b3y, F_b3z, M_b3x, and M_b3y are nonlinear restoring forces and moments of third bearing set.

Because the main contribution of this research is to study the dynamics of spindle system in cutting process, the Rayleigh damping model [40] is applied to assess the damping matrix of spindle system, the damping matrix of spindle system can be expressed as

$$\varvec{C}=\alpha \varvec{M}+\beta \varvec{K}$$

(39)

$$\left\{\begin{array}{l}\alpha =\frac{4\pi\left({\xi }_{2}/{f}_{2}-{\xi }_{1}/{f}_{1}\right)}{\left(1/{f}_{2}^{2}-1/{f}_{1}^{2}\right)}\\ \beta =\frac{\left({\xi }_{2}{f}_{2}-{\xi }_{1}{f}_{1}\right)}{{{\pi}}\left({f}_{2}^{2}-{f}_{1}^{2}\right)}\end{array}\right.$$

(40)

where α and β are the proportionality coefficients; f₁ and f₂ are the first and second order natural frequencies of the spindle system, respectively; ξ₁ and ξ₂ are the corresponding damping ratios of the first and second order natural frequencies, respectively.

3 Validation of proposed model

A series of experiments are implemented on a milling machine to demonstrate the effectiveness of the developed dynamic model in ball end milling process. For the spindle system, the bearing model of the front and intermediate bearing set is 7014A5. The ball number of bearing 7014A5 is 18. The ball diameter of bearing 7014A5 is 10.40 mm. The bearing model of the rear bearing set is 7012A5. The ball number of bearing 7012A5 is 17. The ball diameter of bearing 7012A5 is 9.10 mm. The curvature radius coefficient of raceway groove for bearing 7014A5 and bearing 7012A5 is 0.525. The preloads of bearing 7014A5 and 7012A5 are 465 N and 350 N, respectively. The parameters of dynamic model are listed in Table 1. The type of tool holder installed on the spindle system is BT 40-ER32-100. The model of ball end mill installed on the spindle system is 1B230-1000-XA1630, the flute number N_c is 2, the radius of cutter R_c is 5 mm, and the nominal helix angle α_c is 30°. The radial rake angle of the tool is 10.5°, the axial rake angle is 1.5°, and the flank angle is 6°. The tool material is cemented carbide, and the tool coating is PVD AlCrN.

Table 1 The parameters of dynamic model of spindle system

3.1 Identification of modal parameters

In order to evaluate the damping ratios of the natural modes of spindle system, the modal hammering test is carried out, as shown in Fig. 7. The modal hammering test system mainly includes a force hammer, an acceleration sensor (PCB 352C04), a data acquisition system (DH5956), a charge amplifier (YE5852) and a computer. Since the spindle system is symmetrical about the rotation axis, the test is only performed in the X direction. The frequency response function is obtained by using the measured acceleration response and hammer force signal, as shown in Fig. 8. It can be evaluated from Fig. 8 that the first three natural frequencies are 450 Hz, 1000 Hz, and 1310 Hz, respectively. Based on half power bandwidth method [41], the damping ratios can be evaluated in accordance with the formula $\xi_{i} = \frac{{f_{ib} - f_{ia} }}{{2f_{i} }}$, in which f_i is the ith order natural frequency, f_ia and f_ib are the left and right frequency values corresponding to vibration amplitude ${{A_{i} } \mathord{\left/ {\vphantom {{A_{i} } {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}$, and A_i is the ith order natural vibration amplitude of the system. Finally, the damping ratios corresponding to the first three natural modes can be evaluated as 3.58%, 3.02%, and 2.09%, respectively.

Fig. 7

Hammering test bench

Fig. 8

a Hammer force signal, b acceleration signal, and c frequency response function

3.2 Evaluation of cutting force coefficients

When calculating dynamic cutting force of ball end milling, it is indispensable to evaluate the cutting force coefficients. The prediction ability of ball end milling force model largely is determined by the identification accuracy of cutting force coefficients. Since the geometric parameters of elemental cutting edge vary along helical curve for ball end mill, the shear cutting force coefficients are expressed as the linear functions of the axial position angle k, and the edge cutting force coefficients are expressed as the constants. According to the experimentally measured average cutting forces for horizontal groove cutting, the least squares linear regression method [33] is applied to determine cutting force coefficients. The cutting test bench is displayed in Fig. 9. The cutting force test equipment includes the force sensor (CL-YD-3210), the signal acquisition system (DH59596), the charge amplifiers (YE5852), and the computer. The processed workpiece is a piece of No. 45 steel with a length of 140 mm, a width of 140 mm and a thickness of 15 mm. During cutting test, the rotation speed of spindle system is 600 r/min. In order to reduce random errors, multiple horizontal groove cutting experiments are implemented. The experimental cutting parameters and average cutting forces are organized in Table 2. After calculation, the edge force coefficients are K_te = 8.65 N/mm, K_re = 5.53 N/mm, K_ae = − 1.20 N/mm; the shear force coefficients can be evaluated as

Fig. 9

Cutting force test bench

Table 2 The experimental cutting parameters and average cutting force

$$\left\{\begin{array}{l}{K}_{\text{ts}}=8354.14-5049.10k\\ {K}_{\text{rs}}=6474.96-4575.87k\\ {K}_{\text{as}}=-1651.66+2266.64k\end{array}\right.$$

(41)

3.3 Verification of the proposed model

Cutting tests at four different rotating speeds are implemented to evaluate the effectiveness of proposed dynamic model of spindle system in cutting process. During the experiment, the cutting way is horizontal groove cutting. In the simulation, the cutting parameters in the experiment case are applied to the developed dynamic model to obtain the simulated displacements. Then the simulated displacements are input to the cutting force model to obtain simulated dynamic cutting force. Regarding the dynamic cutting force, the comparison between the simulated results and the experimental results is shown in Fig. 10, which shows the basically agreement between the simulated and the experimentally measured results. It can be observed from the Fig. 10 that the time domain waveform of measured cutting force appears alternately with one big and one small, and some burrs appear on time domain waveform of measured cutting force. Because there are some manufacturing and installation errors of spindle tool system, the unbalanced force on the tool end may cause the tool to vibrate. The vibration frequency of the tool due to the unbalanced force is the rotation frequency of spindle. Therefore, tool vibration caused by unbalanced force can make the uncut chip thickness of two consecutive teeth different during cutting process. As a result of the difference in uncut chip thickness of two consecutive teeth for ball end milling process, the time domain waveform of measured cutting force will be presented in the form of one big and one small. Besides, the main reasons for these phenomena are as follows: (1) During the cutting process, the vibration of machine tool worktable system can affects the thickness of the undeformed chips, which further affects the size of the cutting force. (2) The random vibration and noise of the machine bed can cause burrs to appear on the time domain waveform of measured cutting force. (3) The surface unevenness of the machining workpiece and the manufacturing error of the tool will change the cutting thickness of the continuous teeth during the cutting process, which further causes the cutting force waveform to appear in the form of one large and one small. Therefore, the results demonstrate that the developed simulation model in ball end milling process is feasible and effective.

Fig. 10

Comparison of dynamic cutting force between simulation and experiment

4 Numerical simulation and parameter analysis

Since the motion control equations of the spindle system during milling are the nonlinear differential equations with time delays, it is difficult for solving the analytical solution of differential equations. Because the Newmark-β method is an unconditionally stable numerical integration method, the Newmark-β technique is applied to solve the developed motion control differential equations in this paper. The solution computer is configured with 8 GB RAM and AMD Ryzen 5 1400 Quad-Core Processor. In the following simulation analysis, ball end milling state is horizontal slotting.

4.1 Effects of spindle speed on vibration response

In engineering cases, the change in spindle speed has a major impact on the vibration response of spindle system during ball end milling process. For example, improper rotation speed may cause excessive vibration and chatter of tool. Excessive vibration or chatter may seriously reduce the surface quality of parts, accelerate tool wear, and even damage the spindle bearings. Bifurcation diagram is a significant tool for analyzing the vibration behaviors of spindle system. For the sake of studying the effects of rotation speed on the tool end vibration behavior of spindle system in cutting process, Fig. 11 depicts the bifurcation diagram and three-dimensional spectrum of the tool end vibration response in the feed direction with the change of rotational speed. In the simulation, the axial depth of cut a_p is 1.0 mm and the feed rate f_c is 0.03 mm. From Fig. 11, it can be observed that the tool end vibration response exhibits different behaviors at different rotation speeds. When rotation speed is in the range of 1.0 to 5.1 kr/min, the nonlinear manifestations of vibration response is mainly quasi periodic and chaotic. The nonlinear dynamics of spindle system mainly comes from two aspects in the cutting process. On the one hand, the nonlinearity comes from the restoring force of bearings due to Hertz contact action between ball and raceway. In addition, the dynamic cutting force model considers the tool end vibration displacements due to the regeneration effect. In this speed range of 1.0 to 5.1 kr/min, the frequency components of the vibration signals are mainly composed of f_T (passing frequency of cutting edge of ball end mill) and continuous spectrum close to 900 Hz, as shown in Fig. 11b. It can be found that when rotation speed is in the ranges of 5.8 to 5.9 kr/min, 7.3 to 7.6 kr/min, and 10.0 to 10.6 kr/min, the form of vibration response is the quasi-periodic motion. In addition, when rotation speed is in the ranges of 5.2 to 5.7 kr/min, 6.0 to 7.2 kr/min, 7.7 to 9.9 kr/min, and 10.7 to 12.0 kr/min, the tool end vibration response is stable period form, and the f_T and its frequency doubling appears in the corresponding position of the three-dimensional spectrum. In order to improve the machining quality, the reasonable spindle speed should be set before milling.

Fig. 11

Variation of tool end vibration response with the change of rotation speed. a Bifurcation diagram. b Three-dimensional spectrum

For the purpose of characterizing the tool end vibration response at different rotation speeds, Fig. 12 shows the displacement time domain diagram, frequency spectrum, phase and Poincaré diagram of vibration at five groups of rotation speeds 3.5 kr/min, 5.4 kr/min, 7.5 kr/min, 10.0 kr/min, and 11.3 kr/min. When the rotation speed is 3.5 kr/min, it can be found in Fig. 12(b1) and (c1) that the frequency components of vibration signal are mainly composed of f_T and 905.3 Hz, the phase trajectory is the winding closed curve band, and the nonlinear form of vibration is quasi-periodic. For the rotation speed 5.4 kr/min, the frequency components of vibration signal are mainly composed of f_T and 5f_T in Fig. 12(b2). In Fig. 12(c2), the Poincaré cross-section is an isolated point showing that vibration response is the stable single period motion. For the rotation speed 7.5 kr/min, the frequency components of vibration signal are mainly composed of f_T and 909.9 Hz in Fig. 12(b3). In Fig. 12(c3), the sampled points in Poincaré cross-section form a closed curve, indicating that the vibration is the quasi-periodic behavior. The tool end vibration response in feed direction is also the quasi-periodic motion when the rotation speed of spindle system is 10.0 kr/min. For the rotation speed 11.3 kr/min, the frequency components of the tool end vibration signal are f_T and 5f_T/2, and the two different points appear on in Poincaré diagram in Fig. 12(c5), indicating that the tool end vibration is the period-2 behavior. The results show that the tool end vibration response behaves different dynamic behaviors at different rotating speeds, and presents nonlinear behavior in certain rotation speed ranges due to the nonlinearity of bearing restoring force and dynamic cutting force.

Fig. 12

Tool end vibration responses at different speeds

4.2 Effects of bearing preload on vibration response

The premise of studying the effects of bearing preload on the vibration characteristics of spindle system is to analyze bearing preload influence on the contact behavior between balls and raceways. The changes in contact characteristic parameters inside the bearings of spindle system with bearing preload are evaluated in Fig. 13. With the increase of bearing preload, the contact angles of the bearing 7012A5 and 7014A5 increase in Fig. 13a, in which bearing 7012A5 has a larger change than bearing 7014A5 with greater bearing preload. The axial displacements of inner ring for the bearing 7012A5 and 7014A5 increase with the increase of bearing preload, but bearing 7012A5 changes more, showing that the axial stiffness of bearing 7012A5 is smaller than that of bearing 7014A5, as shown in Fig. 13b. As the bearing preload increases, the normal contact force increases approximately linearly in Fig. 13c.

Fig. 13

Change laws of spindle bearing contact parameters with preload. a Contact angle. b Axial displacement. c Normal contact force

For the purpose of studying the influence of bearing preload on vibration characteristics and cutting stability, the variation curves of tool end vibration amplitude with tooth passing frequency under three bearing preload grades 0.7P, 1P, and 2P are shown in Fig. 14. P = [465 N, 465 N, 350 N] is the preload of three bearing sets of the spindle system. In the numerical analysis, the axial depth of cut a_p is 0.5 mm, and the feed per tooth f_c is 0.03 mm. For the preload grade of the spindle bearing sets 0.7P, it can be observed that at multiple tooth passing frequencies, such as 186.7 Hz, 236.7 Hz, 326.7 Hz, 506.7 Hz, 1157.0 Hz, and 1777.0 Hz, the tool end vibration amplitude jumps. Besides, when the tooth passing frequency is in low-frequency scope, the tool end vibration amplitude changes chaotically. The main reason for these phenomena is that when the bearing preload becomes smaller, the support stiffness of the bearing decreases, and the contact nonlinearity between balls and raceways is more intense, resulting in the phase difference of the vibration of continuous tool teeth during the cutting process. The phase difference of the continuous teeth vibration can promote the appearance of chatter. It can be also found from Fig. 14 that there is a jumping discontinuity in the vibration amplitude near the resonance region close to 900 Hz when bearing preload grades are 0.7P and P, while there is no jumping phenomenon for bearing preload grade 2P. Under the bearing preload grades 0.7P and P, the main resonance region manifests softening nonlinearity. When the bearing preload grade becomes from P to 2P, the softening nonlinearity in the main resonance region disappears, which means that the greater the bearing preload, the weaker the nonlinearity of the spindle system. In addition, when the bearing preload level increases, the bearing support rigidity increases, which leads to an increase in the main resonance frequency and the reduction of corresponding resonance amplitude. This phenomenon also exists in the natural frequency near 450 Hz. Besides, when the tooth passing frequency is in the lower or higher frequency range, the tool end vibration amplitude becomes smaller, and the amplitude change with the tooth pass frequency becomes more stable with the increase of the bearing preload. It is worth noting that the super-harmonic resonances occur in the low frequency range, and the large bearing preload level can improve cutting stability.

Fig. 14

Variation curves of tool end vibration amplitude with tooth passing frequency under three different bearing preloads. a X direction. b Y direction

For in-depth analysis in change of tool end vibration response with bearing preload, the time domain diagram, frequency spectrum, phase and Poincaré diagram of vibration at the tooth pass frequencies 520.0 Hz and 856.7 Hz are shown in Fig. 15. For tooth passing frequency 520.0 Hz, as bearing preload increases, vibration amplitude decreases, and response changes from the quasi-periodic motion to the single period motion. For tooth passing frequency 856.7 Hz, the tool end vibration amplitude decreases as bearing preload decreases. Furthermore, when the bearing preload just starts to increase, the tool end vibration amplitude changes greatly, and when the bearing preload increases to a large extent, the tool end vibration amplitude changes less obviously.

Fig. 15

Change of tool end vibration response with bearing preload

4.3 Effects of cutting parameters on vibration response

4.3.1 Axial depth of cut

In order to study the effects of the axial depth of cut on vibration characteristics, Fig. 16 evaluates the variation of vibration amplitude in the tool end with axial depth of cut, in which the rotation speed of spindle system is 5.4 kr/min and feed rate f_c is 0.03 mm. It can be found that as the axial depth of cut increases, the tool end vibration amplitudes in X, Y, and Z directions show an increasing trend. As the axial depth of cut increases from 0.05 to 1.80 mm, the tool end vibration amplitudes change slowly, and the responses are always single period vibration, as shown in Fig. 17(a1), (a2), and (a3). In order to gain insight into vibration response, Fig. 18 shows time domain diagram, frequency spectrum, phase, and Poincaré diagram of dynamic response with the axial depth of cut a_p 1.5 mm. Tooth passing frequency and its multiplied frequency components appear on vibration signal frequency spectrum, and Poincaré section is a point, as shown in Fig. 18. When the axial depth of cut increases to 1.85 mm, the increase rate of the tool end vibration amplitude starts to become larger. At this time, the vibration response of the tool end changes from single period behavior to quasi-periodic behavior, as shown in Fig. 17(a1), (a2), and (a3). As the axial depth of cut continues to increase to 2.55 mm, the tool end vibration amplitude jumps strongly and the amplitude greatly increases in Fig. 16, in which the manifestation of vibration response is still the quasi-periodic behavior, as shown in Fig. 17(a1), (a2), and (a3). This indicates that the tool starts to chatter with a large vibration amplitude during ball end milling process when the axial depth of cut is 2.55 mm. More notably, it can be observed from Fig. 17(b1), (b2), and (b3) that the chatter frequency components appear in the frequency spectrum of the tool end vibration signal when the axial cutting depth is in the range of 2.55 to 5.00 mm. Figure 19 shows time domain diagram, frequency spectrum, phase and Poincaré diagram of vibration with axial depth of cut a_p 3.0 mm. It can be observed from Fig. 19 that the tool end vibration amplitudes increase with time until the large amplitude chatter during the cutting process, and large amplitude chatter is the quasi-periodic motion.

Fig. 16

Variation of vibration amplitude in tool end with axial depth of cut. a X direction. b Y direction. c Z direction

Fig. 17

Bifurcation and three-dimensional spectrum in tool end with axial depth of cut

Fig. 18

Tool end vibration response with axial depth of cut a_p 1.5 mm

Fig. 19

Tool end vibration response with axial depth of cut a_p 3.0 mm

4.3.2 Feed per tooth

The variation of vibration amplitude in tool end with the feed per tooth is evaluated in Fig. 20, in which the rotation speed of spindle system is 8.0 kr/min and the axial depth of cut a_p is 0.5 mm. Figure 21 shows the three-dimensional spectrum of the tool end vibration response with the feed per tooth as control parameter. When the feed per tooth just started to increase, the tool end vibration amplitudes in three directions decrease. Then as the feed per tooth increases, the tool end vibration amplitudes increase. Besides, it can be observed from Fig. 21 that the frequency components of vibration response of the tool end are always the tooth pass frequency and its frequency multiplication with the change of feed per tooth.

Fig. 20

Variation of vibration amplitude in tool end with feed per tooth. a X direction. b Y direction. c Z direction

Fig. 21

Three-dimensional spectrum of tool end vibration response with feed per tooth. a X direction. b Y direction. c Z direction

5 Conclusions

This paper presents a novel dynamic model of the spindle system during ball end milling progress with consideration of the nonlinear characteristics of spindle bearings. A general analytical expression for the nonlinear restoring force of matched angular contact ball bearings is proposed for three different ball arrangements. Then, the dynamic cutting force model in ball end milling is established considering the influence of the tool vibration on uncut chip thickness. Furthermore, the effectiveness of the proposed model is verified by experimental tests. Finally, the effects of some parameters on vibration behaviors are analyzed, and some conclusions are drawn:

• 1. In the cutting state, the tool end vibration response shows different behaviors at different speeds, such as single-periodic, doubling-periodic, quasi-periodic, and chaotic behaviors. In order to improve the machining quality, the reasonable spindle speed should be set during the ball end milling process.

• 2. The dynamic behavior of the tool end in cutting process exhibits rich nonlinear characteristics, including softening nonlinearities, jump phenomenon, and super-harmonic resonances. As bearing preload increases, the main resonance frequency of the spindle system increases and the corresponding amplitude decreases. In addition, the larger bearing preload can improve the cutting stability and machining quality.

• 3. In ball end milling process, the changes with respect to axial depth of cut and feed per tooth considerably affect the vibration behavior of the tool end. As the axial depth of cut increases, the vibration amplitude of the tool end shows an increasing trend. When the axial depth of cut increases to a certain extent, there will be tool chatter with a large vibration amplitude, and the large amplitude vibration is quasi-periodic motion.

The proposed dynamic model can be applied to predict the vibration behaviors of spindle system during ball end milling, especially the tool vibration. However, there some discrepancies between experimental and simulation results due to the vibration of worktable system and the geometric error of spindle system. Therefore, in order to heighten the predictive ability of the proposed model, the influence of the vibration of worktable system and the geometric error of spindle system on the dynamic cutting force should be considered in future research.

Appendix

The stiffness matrix of the spindle system is as follows

$$\varvec{K}_{x}=\left[\begin{array}{cccccccccccccc}{k}_{11}& {k}_{12}& {k}_{13}& {k}_{14}& & & & & & & & & & \\ {k}_{12}& {k}_{22}& {k}_{23}& {k}_{24}& & & & & & & & & & \\ {k}_{13}& {k}_{23}& {k}_{33}& {k}_{34}& {k}_{35}& {k}_{36}& & & & & & & & \\ {k}_{14}& {k}_{24}& {k}_{34}& {k}_{44}& {k}_{45}& {k}_{46}& & & & & 0& & & \\ & & {k}_{35}& {k}_{45}& {k}_{55}& {k}_{56}& {k}_{57}& {k}_{58}& & & & & & \\ & & {k}_{36}& {k}_{46}& {k}_{56}& {k}_{66}& {k}_{67}& {k}_{68}& & & & & & \\ & & & & {k}_{57}& {k}_{67}& {k}_{77}& {k}_{78}& {k}_{79}& {k}_{\mathrm{7,10}}& & & & \\ & & & & {k}_{58}& {k}_{68}& {k}_{78}& {k}_{88}& {k}_{89}& {k}_{\mathrm{8,10}}& & & & \\ & & & & & & {k}_{79}& {k}_{89}& {k}_{99}& {k}_{\mathrm{9,10}}& {k}_{\mathrm{9,11}}& {k}_{\mathrm{9,12}}& & \\ & & & & & & {k}_{\mathrm{7,10}}& {k}_{\mathrm{8,10}}& {k}_{\mathrm{9,10}}& {k}_{\mathrm{10,10}}& {k}_{\mathrm{10,11}}& {k}_{\mathrm{10,12}}& & \\ & & & 0& & & & & {k}_{\mathrm{9,11}}& {k}_{\mathrm{10,11}}& {k}_{\mathrm{11,11}}& {k}_{\mathrm{11,12}}& {k}_{\mathrm{11,13}}& {k}_{\mathrm{11,14}}\\ & & & & & & & & {k}_{\mathrm{9,12}}& {k}_{\mathrm{10,12}}& {k}_{\mathrm{11,12}}& {k}_{12,12}& {k}_{\mathrm{12,13}}& {k}_{\mathrm{12,14}}\\ & & & & & & & & & & {k}_{\mathrm{11,13}}& {k}_{\mathrm{12,13}}& {k}_{\mathrm{13,13}}& {k}_{\mathrm{13,14}}\\ & & & & & & & & & & {k}_{\mathrm{11,14}}& {k}_{\mathrm{12,14}}& {k}_{\mathrm{13,14}}& {k}_{\mathrm{14,14}}\end{array}\right]$$

(42)

$$\varvec{K}_{y}=\left[\begin{array}{cccccccccccccc}{k}_{11}& -{k}_{12}& {k}_{13}& -{k}_{14}& & & & & & & & & & \\ -{k}_{12}& {k}_{22}& -{k}_{23}& {k}_{24}& & & & & & & & & & \\ {k}_{13}& -{k}_{23}& {k}_{33}& -{k}_{34}& {k}_{35}& -{k}_{36}& & & & & & & & \\ -{k}_{14}& {k}_{24}& -{k}_{34}& {k}_{44}& -{k}_{45}& {k}_{46}& & & & & 0& & & \\ & & {k}_{35}& -{k}_{45}& {k}_{55}& -{k}_{56}& {k}_{57}& -{k}_{58}& & & & & & \\ & & -{k}_{36}& {k}_{46}& -{k}_{56}& {k}_{66}& -{k}_{67}& {k}_{68}& & & & & & \\ & & & & {k}_{57}& -{k}_{67}& {k}_{77}& -{k}_{78}& {k}_{79}& -{k}_{\mathrm{7,10}}& & & & \\ & & & & -{k}_{58}& {k}_{68}& -{k}_{78}& {k}_{88}& -{k}_{89}& {k}_{\mathrm{8,10}}& & & & \\ & & & & & & {k}_{79}& -{k}_{89}& {k}_{99}& -{k}_{\mathrm{9,10}}& {k}_{\mathrm{9,11}}& -{k}_{\mathrm{9,12}}& & \\ & & & & & & -{k}_{\mathrm{7,10}}& {k}_{\mathrm{8,10}}& -{k}_{\mathrm{9,10}}& {k}_{\mathrm{10,10}}& -{k}_{\mathrm{10,11}}& {k}_{\mathrm{10,12}}& & \\ & & & 0& & & & & {k}_{\mathrm{9,11}}& -{k}_{\mathrm{10,11}}& {k}_{\mathrm{11,11}}& -{k}_{\mathrm{11,12}}& {k}_{\mathrm{11,13}}& -{k}_{\mathrm{11,14}}\\ & & & & & & & & -{k}_{\mathrm{9,12}}& {k}_{\mathrm{10,12}}& -{k}_{\mathrm{11,12}}& {k}_{\mathrm{12,12}}& -{k}_{\mathrm{12,13}}& {k}_{\mathrm{12,14}}\\ & & & & & & & & & & {k}_{\mathrm{11,13}}& -{k}_{\mathrm{12,13}}& {k}_{\mathrm{13,13}}& -{k}_{\mathrm{13,14}}\\ & & & & & & & & & & -{k}_{\mathrm{11,14}}& {k}_{\mathrm{12,14}}& -{k}_{\mathrm{13,14}}& {k}_{\mathrm{14,14}}\end{array}\right]$$

(43)

$$\varvec{K}_{z}=\left[\begin{array}{ccccccc}{u}_{11}& {u}_{12}& & & & & \\ {u}_{12}& {u}_{22}& {u}_{23}& & & 0& \\ & {u}_{23}& {u}_{33}& {u}_{34}& & & \\ & & {u}_{34}& {u}_{44}& {u}_{45}& & \\ & & & {u}_{45}& {u}_{55}& {u}_{56}& \\ & 0& & & {u}_{56}& {u}_{66}& {u}_{67}\\ & & & & & {u}_{67}& {u}_{77}\end{array}\right]$$

(44)

The element of the stiffness matrix is calculated according to the method of flexibility influence coefficient in material mechanics, as follows

$$\left\{\begin{array}{l}{k}_{11}={b}_{11}\\ {k}_{12}={b}_{21}\\ {k}_{13}=-{b}_{11}\\ {k}_{14}={b}_{21}\end{array}\right.;\left\{\begin{array}{l}{k}_{22}={l}_{1}{b}_{21}-{b}_{31}\\ {k}_{23}=-{b}_{21}\\ {k}_{24}={b}_{31}\end{array}\right.;\left\{\begin{array}{l}{k}_{33}={b}_{11}+{b}_{12}\\ {k}_{34}=-{b}_{21}+{b}_{22}\\ {k}_{35}=-{b}_{12}\\ {k}_{36}={b}_{22}\end{array}\right.;\left\{\begin{array}{l}{k}_{44}={l}_{1}{b}_{21}-{b}_{31}+{l}_{2}{b}_{22}-{b}_{32}\\ {k}_{45}=-{b}_{22}\\ {k}_{46}={b}_{32}\end{array}\right.$$

(45)

$$\left\{\begin{array}{l}{k}_{55}={b}_{12}+{b}_{13}\\ {k}_{56}=-{b}_{22}+{b}_{23}\\ {k}_{57}=-{b}_{13}\\ {k}_{58}={b}_{23}\end{array}\right.;\left\{\begin{array}{l}{k}_{66}={l}_{2}{b}_{22}-{b}_{32}+{l}_{3}{b}_{23}-{b}_{33}\\ {k}_{67}=-{b}_{23}\\ {k}_{68}={b}_{33}\end{array}\right.;\left\{\begin{array}{l}{k}_{77}={b}_{13}+{b}_{14}\\ {k}_{78}=-{b}_{23}+{b}_{24}\\ {k}_{79}=-{b}_{14}\\ {k}_{\mathrm{7,10}}={b}_{24}\end{array}\right.;\left\{\begin{array}{l}{k}_{88}={l}_{3}{b}_{23}-{b}_{33}+{l}_{4}{b}_{24}-{b}_{34}\\ {k}_{89}=-{b}_{24}\\ {k}_{\mathrm{8,10}}={b}_{34}\end{array}\right.$$

(46)

$$\left\{\begin{array}{l}{k}_{99}={b}_{14}+{b}_{15}\\ {k}_{\mathrm{9,10}}=-{b}_{24}+{b}_{25}\\ {k}_{\mathrm{9,11}}=-{b}_{15}\\ {k}_{\mathrm{9,12}}={b}_{25}\end{array}\right.;\left\{\begin{array}{l}{k}_{\mathrm{10,10}}={l}_{4}{b}_{24}-{b}_{34}+{l}_{5}{b}_{25}-{b}_{35}\\ {k}_{\mathrm{10,11}}=-{b}_{25}\\ {k}_{\mathrm{10,12}}={b}_{35}\end{array}\right.;\left\{\begin{array}{l}{k}_{\mathrm{11,11}}={b}_{15}+{b}_{16}\\ {k}_{\mathrm{11,12}}=-{b}_{25}+{b}_{26}\\ {k}_{\mathrm{11,13}}=-{b}_{16}\\ {k}_{\mathrm{11,14}}={b}_{26}\end{array}\right.;\left\{\begin{array}{l}{k}_{\mathrm{12,12}}={l}_{5}{b}_{25}-{b}_{35}+{l}_{6}{b}_{26}-{b}_{36}\\ {k}_{\mathrm{12,13}}=-{b}_{26}\\ {k}_{\mathrm{12,14}}={b}_{36}\end{array}\right.$$

(47)

$$\left\{\begin{array}{c}{k}_{\mathrm{13,13}}={b}_{16}\\ {k}_{\mathrm{13,14}}=-{b}_{26}\\ {k}_{\mathrm{14,14}}={l}_{6}{b}_{26}-{b}_{36}\end{array}\right.$$

(48)

$$\left\{\begin{array}{c}{u}_{11}={d}_{1}\\ {u}_{12}=-{d}_{1}\\ {u}_{22}={d}_{1}+{d}_{2}\\ {u}_{23}=-{d}_{2}\end{array}\right.;\left\{\begin{array}{c}{u}_{33}={d}_{2}+{d}_{3}\\ {u}_{34}=-{d}_{3}\\ {u}_{44}={d}_{3}+{d}_{4}\\ {u}_{45}=-{d}_{4}\end{array}\right.;\left\{\begin{array}{c}{u}_{55}={d}_{4}+{d}_{5}\\ {u}_{56}=-{d}_{5}\\ {u}_{66}={d}_{5}+{d}_{6}\\ {u}_{67}=-{d}_{6}\\ {u}_{77}={d}_{6}\end{array}\right.$$

(49)

where

$${b}_{1i}=\frac{12E{I}_{i}}{{l}_{i}^{3}};{b}_{2i}=\frac{1}{2}{l}_{i}{b}_{1i};{b}_{3i}=\frac{1}{6}{l}_{i}^{2}{b}_{1i},{d}_{i}=\frac{E{A}_{i}}{{l}_{i}},\left(i=\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}\right)$$

(50)