1 Introduction

In milling processes, complex nonlinear dynamic behaviors are formed between the machine tool, the cutter, and the machined part, where regenerative chatter, belonging to the self-excited vibration, is one of the most common obstacles to high machining productivity and part quality [1, 2]. Many methods have been proposed during the recent decades to eliminate, or suppress the regenerative chatter, which can be classified into two categories, i.e., active suppression [3], and passive suppression [4]. The former usually utilizes auxiliary or additional instruments, such as computers, sensors, and actuators, to change the system characteristics; the latter usually utilizes certain methods, such as tool structure changes, damping energy absorption and milling parameter adjustment, to expand the stable area of stability lobe diagrams (SLDs) [5, 7]. It is worth mentioning that the milling parameter adjustment is widely used in CNC systems [8]. How to determine the appropriate milling parameters is attracting the attention of more and more researchers. So far, the semi-discretization method (SDM) [9], the full-discretization method (FDM) [10], the numerical integration method (NIM) [11], the frequency domain method [12], and the finite element analysis method [13] have been proposed to identify the stability boundaries in the parameter space of spindle speed and axial depth of cut. However, the effectiveness of these methods is limited by system variations.

The regenerative chatter is closely related to the cutting thickness changes which derives from improper phase differences between wavy surfaces left by adjacent teeth. There are two effective ways to extend the chatter suppression effect, i.e., variable pitch cutters (VPC) [14] and variable spindle speed (VSS) [7]. The variable pitch cutters can enlarge the axial depth of cut for certain target spindle speeds. The comparison between the VPC and the VSS turns out that continuously changing the spindle speed during machining is a more flexible way to the variation of system characteristics. The VSS technique can be divided into two types, i.e., sinusoidal VSS modulation and triangular VSS modulation [15], where the delay differential equation with varying time delay could be traced back to the 1970s. Sexton et al. [16] found out through experiments that any increase in either the amplitude or frequency of speed variation would significantly improve the stability and transient vibrations of the cutter. Zatarain et al. [17] simulated the effect of the sinusoidal VSS modulation and the triangular VSS modulation on the regenerative chatter suppression. It is found from the simulation results that the sinusoidal VSS modulation has a strong inhibition effect than the triangular VSS modulation. However, this work only analyzes the chatter suppression in the low-speed domain. Insperger et al. [18] investigated a single-degree-of-freedom (single-DOF) model of turning with sinusoidal VSS modulation and the corresponding delay-differential equation with time-varying delay. The time-varying cutting force makes it difficult to derive the mathematical analysis of VSS cutting processes. Seguy et al. [19] analyzed the effect of spindle speed variation in the high-speed domain for spindle speeds corresponding to the first flip (period doubling) and to the first Hopf lobes. Based on both numerical simulation and experiments using specific cutting operation parameters, they concluded that the sinusoidal VSS modulation is more effective than the triangular one for the same amplitude and frequency parameters, and for the same spindle dynamics the triangular VSS modulation allows larger modulation amplitude [20]. Taking the regenerative effect into account, Ding et al. [21] presented a semi-analytic method for stability analysis of milling with a VSS, where the spindle speed is periodically modulated around a nominal spindle speed. Subsequently, Niu et al. [22] proposed a variable-step numerical integration method with periodic spindle speed variation, where the results demonstrated that the modulation amplitude ratio is more influential than the modulation frequency ratio. Considering that machining instability control methods failed to provide detailed helix angle information matching the stability of milling cutters, Yang et al. [23] established a helix angle-based 2-DOF milling model with simultaneous tooth pitch and spindle speed variation to deal with the above problem. Long et al. [24] compared the stability behaviors of up-milling and down-milling with the VSSs. It is found that the up-milling with the VSS can provide better improvements compared to the down-milling with the VSS. To address heavy transient vibrations, Wang et al. [25] provided a transient vibration analysis method for predicting the transient behavior of VSS milling, which took external excitation of transient behaviors into account. Dong et al. [26] established a reconstructed semi-discretization method to analyze the milling stability with sinusoidal and triangular modulations. The results showed that compared with the SDM method, this work can improve the computation efficiency by three times while ensuring the prediction accuracy. Most of the existing methods can guarantee the prediction accuracy, but there is still much room for improvement in computation efficiency.

In this paper, the 3rd-order Newton-Cotes integration formula is adopted for the chatter suppression prediction and the parameter optimization in the VSS milling processes. It is utilized to approximate the solution of the time-varying delay term. The computation efficiency can be greatly improved while ensuring the prediction accuracy. Besides, the sinusoidal VSS modulation and triangular VSS modulation are analyzed in low-speed and high-speed domains in detail. This paper is organized as follows. In section 2, the dynamic model of VSS milling is first introduced. Next, the sinusoid spindle speed modulation and the triangular spindle speed modulation are respectively introduced in section 3. The 3rd-order Newton-Cotes stability analysis method is proposed in section 4. The simulation analysis and modulation parameter optimization are conducted in section 5. Finally, the conclusions are given in section 6.

2 Dynamic model of VSS milling

In the milling operations, a rotating tool removes material in the commanded feed direction. Fig. 1 shows a face milling operation with multiple flat-end cutters, where the spindle speed is denoted by Ω, the axial depth of cut is denoted by ap, the tool radial engagement is denoted by ae, and the immersion angle of the tool is denoted by φj. The dynamic model of the two-DOF face milling (see Fig. 1) considering the regenerative effect can be governed by a 2nd-order differential equation. By transforming the cutting forces into the orthogonal coordinate system and summing the cutting forces acting on all teeth, the dynamic model of the VSS milling system with two DOFs [22] can be expressed by

$$M\ddot{q}\left(t\right)+C\dot{q}\left(t\right)+Kq\left(t\right)={a}_{p}{K}_{C}\left(t\right)\left[q\left(t\right)-q\left(t-\tau \left(t\right)\right)\right]$$
(1)

where M is the mass matrix, C is the damping matrix, K is the stiffness matrix, KC(t) is the cutting force coefficient matrix, and \(\tau \left(t\right)\) is the time-variant delay of VSS milling. \(q\left(t\right)={\left[x\left(t\right),y\left(t\right)\right]}^{T}\) denotes the vibration displacement vector, and \(\dot{q}\left(t\right)\) and \(\ddot{q}\left(t\right)\) denote the 1st-order and 2nd-order derivatives of q(t) w.r.t t, respectively. Let x(t) be \(x\left(t\right)={\left[x\left(t\right),y\left(t\right),\dot{x}\left(t\right),\dot{y}\left(t\right)\right]}^{T}\), and then Eq. (1) can be expressed in a new form as follows:

$$\dot{x}\left(t\right)=Ax\left(t\right)+{a}_{p}B\left(t\right)x\left(t\right)-{a}_{p}B\left(t\right)x\left(t-\tau \left(t\right)\right)$$
(2)

where

$$A=\left[\begin{array}{cc}0& I\\ -{M}^{-1}K& -{M}^{-1}C\end{array}\right]$$
(3)
$$B\left(t\right)=\left[\begin{array}{cc}0& 0\\ -{M}^{-1}{K}_{C}\left(t\right)& 0\end{array}\right]$$
(4)
$${K}_{C}\left(t\right)=\left[\begin{array}{cc}{h}_{xx}\left(t\right)& {h}_{xy}\left(t\right)\\ {h}_{yx}\left(t\right)& {h}_{yy}\left(t\right)\end{array}\right]$$
(5)
$${h}_{xx}\left(t\right)=\sum_{j=1}^{N}g\left({\varphi }_{j}\left(t\right)\right){\text{sin}}\left({\varphi }_{j}\left(t\right)\right)\left[{K}_{t}{\text{cos}}\left({\varphi }_{j}\left(t\right)\right)+{K}_{n}{\text{sin}}\left({\varphi }_{j}\left(t\right)\right)\right]$$
(6)
$${h}_{xy}\left(t\right)=\sum_{j=1}^{N}g\left({\varphi }_{j}\left(t\right)\right){\text{cos}}\left({\varphi }_{j}\left(t\right)\right)\left[{K}_{t}{\text{cos}}\left({\varphi }_{j}\left(t\right)\right)+{K}_{n}{\text{sin}}\left({\varphi }_{j}\left(t\right)\right)\right]$$
(7)
$${h}_{yx}\left(t\right)=\sum_{j=1}^{N}g\left({\varphi }_{j}\left(t\right)\right){\text{sin}}\left({\varphi }_{j}\left(t\right)\right)\left[-{K}_{t}{\text{sin}}\left({\varphi }_{j}\left(t\right)\right)+{K}_{n}{\text{cos}}\left({\varphi }_{j}\left(t\right)\right)\right]$$
(8)
$${h}_{yy}\left(t\right)=\sum_{j=1}^{N}g\left({\varphi }_{j}\left(t\right)\right){\text{cos}}\left({\varphi }_{j}\left(t\right)\right)\left[-{K}_{t}{\text{sin}}\left({\varphi }_{j}\left(t\right)\right)+{K}_{n}{\text{cos}}\left({\varphi }_{j}\left(t\right)\right)\right]$$
(9)
$${\varphi }_{j}\left(t\right)=\frac{\pi }{30}{\int }_{0}^{t}\Omega \left(s\right){\text{d}}s+2\left(j-1\right)\frac{\pi }{N}$$
(10)

where N is the number of teeth.

Fig. 1
figure 1

Face milling cutting operation scheme

Full size image

3 Approximation of the delayed term

Sinusoidal and triangular spindle speed modulation schemes have been widely utilized for the chatter suppression. In this section, we focus on the sinusoidal and triangular spindle speed modulations, which will be discussed and analyzed below.

3.1 Sinusoidal spindle speed modulation

The sinusoidal spindle speed Ω(t) can be formulated as

$$\Omega \left(t\right)={\Omega }_{0}+{\Omega }_{A}{\text{sin}}\left(\omega t\right)$$
(11)

where Ω0 is the nominal spindle speed, ΩA is the spindle speed amplitude, and ω is the angular velocity. The modulation amplitude ratio RVA and the modulation frequency ratio RVF are introduced to quantify the periodic spindle speed variation as follows:

$$RVA=\frac{{\Omega }_{A}}{{\Omega }_{0}}$$
(12)
$$RVF=\frac{60}{{\Omega }_{0}T}$$
(13)

Substituting Eq. (12) and Eq. (13) into Eq. (11) yields

$$\Omega \left(t\right)={\Omega }_{0}\left[1+RVA\times {\text{sin}}\left(RVF{\Omega }_{0}\frac{\pi t}{30}\right)\right]$$
(14)

By combining Eq. (10) and Eq. (14), we obtain

$${\varphi }_{j}\left(t\right)=\frac{\pi }{30}{\Omega }_{0}t+\frac{RVA}{RVF}\left[1-{\text{cos}}\left(\omega t\right)\right]+2\left(j-1\right)\frac{\pi }{N}$$
(15)

\(\tau \left(t\right)\) is time-varying in the VSS milling operations, it can be implicitly expressed as

$${\int }_{t-\tau \left(t\right)}^{t}\frac{\Omega \left(s\right)}{60}{\text{d}}s=\frac{1}{N}$$
(16)

It is obvious that a closed form of \(\tau \left(t\right)\) cannot be solved by Eq. (16). Combining Eq. (14) and Eq. (16), we can obtain Eq. (17) as

$$\frac{1}{60}\left({\Omega }_{0}\tau \left(t\right)+\frac{{\Omega }_{A}}{{\omega }_{m}}{\text{cos}}\left({\omega }_{m}\left(t-\tau \left(t\right)\right)\right)-\frac{{\Omega }_{A}}{{\omega }_{m}}{\text{cos}}\left({\omega }_{m}t\right)\right)=\frac{1}{N}$$
(17)

From the sum difference product formula, Eq. (17) can be reformulated as

$$\tau \left(t\right)=\frac{60}{{\Omega }_{0}}\left(\frac{1}{N}-\frac{{\Omega }_{A}}{RVF{\Omega }_{0}\pi }{\text{sin}}\left({\omega }_{m}\left(t-\frac{\tau \left(t\right)}{2}\right)\right){\text{sin}}\left(\frac{{\omega }_{m}\tau \left(t\right)}{2}\right)\right)$$
(18)

3.2 Triangular spindle speed modulation

The triangular spindle speed modulation [27] can be expressed as:

$$\Omega \left(t\right)=\left\{\begin{array}{cc}{\Omega }_{0}\left(1+RVA\left(1-\frac{4}{T}{\text{mod}}\left(t,T\right)\right)\right)& 0\le {\text{mod}}\left(t,T\right)<\frac{T}{2}\\ {\Omega }_{0}\left(1+RVA\left(-3+\frac{4}{T}{\text{mod}}\left(t,T\right)\right)\right)& \frac{T}{2}\le {\text{mod}}\left(t,T\right)\le T\end{array}\right.$$
(19)

Substituting Eq. (18) into Eq. (19) leads to

$$\tau \left(t\right)=\left\{\begin{array}{cc}\frac{60}{N{\Omega }_{0}}\left(1-RVA\left(1-\frac{4}{T}{\text{mod}}\left(t,T\right)\right)\right)& 0\le {\text{mod}}\left(t,T\right)<T/2\\ \frac{60}{N{\Omega }_{0}}\left(1+RVA\left(3-\frac{4}{T}{\text{mod}}\left(t,T\right)\right)\right)& T/2\le {\text{mod}}\left(t,T\right)\le T\end{array}\right.$$
(20)

4 Newton-cotes stability analysis method

The dynamic model of the VSS milling system with two DOFs is expressed by Eq. (2), where B(t) is the periodic coefficient matrix, i.e., \(B\left(t\right)=B\left(t+T\right)\), and \(\tau \left(t\right)\) is the periodic delay term, i.e.,\(\tau \left(t\right)=\tau \left(t+T\right)\). The first step to construct the transition function is to divide the period T into n equal intervals, obtaining \({\left\{{t}_{i}\right\}}_{i=0}^{n}\in {\mathbb{R}}\). The average time delay \({\tau }_{i}\) in \(\left[{t}_{i},{t}_{i+1}\right]\) can be defined as

$$\begin{array}{cc}{\tau }_{i}=\frac{1}{{t}_{i+1}-{t}_{i}}{\int }_{{t}_{i}}^{{t}_{i+1}}\tau \left(t\right){\text{d}}t& i=\text{0,1},\cdots ,n\end{array}$$
(21)

The time series mi is computed from Eq. (21) as follows:

$${m}_{i}={\text{int}}\left(\frac{1}{2}+\frac{{\tau }_{i}}{{t}_{i+1}-{t}_{i}}\right)$$
(22)

where int() stands for the round function.

For the sinusoidal spindle speed modulation, substituting Eq. (18) into Eq. (22) gives mi as

$${m}_{i}={\text{int}}\left(\frac{1800RVA}{RVF{\Omega }_{0}^{2}N\pi {\left(\Delta t\right)}^{2}}\left({\text{cos}}\left(\frac{RVF{\Omega }_{0}\pi }{30}{t}_{i+1}\right)-{\text{cos}}\left(\frac{RVF{\Omega }_{0}\pi }{30}{t}_{i}\right)\right)+\frac{{\tau }_{0}}{\Delta t}+\frac{1}{2}\right)$$
(23)

where \(\Delta t={t}_{i+1}-{t}_{i}\).

For the triangular spindle speed modulation, mi can be deduced in the similar way.

By applying \(\left[{t}_{i},{t}_{i+1}\right]\) to Eq. (2), we can obtain

$${x}_{i+1}={e}^{A\Delta t}{x}_{i}+{a}_{p}{\int }_{{t}_{i}}^{{t}_{i+1}}{e}^{A\left({t}_{i+1}-\xi \right)}B\left(\xi \right)x\left(\xi \right){\text{d}}\xi -{a}_{p}{\int }_{{t}_{i}}^{{t}_{i+1}}{e}^{A\left({t}_{i+1}-\xi \right)}B\left(\xi \right)x\left(\xi -{\tau }_{i}\right){\text{d}}\xi$$
(24)

where \({x}_{i}=x\left({t}_{i}\right)\).

It should be noted that there are two integral terms. To solve the terms, the 3rd-order Newton-Cotes formula [28] is introduced as follows:

$${\int }_{a}^{b}f\left(\xi \right){\text{d}}\xi \approx \frac{b-a}{2}\left(f\left(a\right)+f\left(b\right)\right)$$
(25)

When the 3rd-order Newton-Cotes formula is applied to the first integral term, the first integral term can be approximately expressed as

$${a}_{p}{\int }_{{t}_{i}}^{{t}_{i+1}}{e}^{A\left({t}_{i+1}-\xi \right)}B\left(\xi \right)x\left(\xi \right){\text{d}}\xi \approx \frac{{a}_{p}\Delta t}{2}\left({e}^{A\Delta t}{B}_{i}+{B}_{i+1}\right)$$
(26)

where \({B}_{i}=B\left({t}_{i}\right)\).

The second integration term can be approximately expressed as

$${a}_{p}{\int }_{{t}_{i}}^{{t}_{i+1}}{e}^{A\left({t}_{i+1}-\xi \right)}B\left(\xi \right)x\left(\xi -{\tau }_{i}\right){\text{d}}\xi \approx {\sigma }_{i}\left({\alpha }_{i}{x}_{i-M}+{\beta }_{i}{x}_{i-M+1}\right)$$
(27)

where

$${\sigma }_{i}=\left(\left({e}^{A\Delta t}-1\right){B}_{i}+\left(-1+\left({e}^{A\Delta t}-1\right)\frac{1}{A\Delta t}\right)\left({B}_{i+1}-{B}_{i}\right)\right)\frac{1}{A}$$
(28)
$$B\left(t\right)\approx {B}_{i}+\left({B}_{i+1}-{B}_{i}\right)\frac{t-{t}_{i}}{\Delta t}$$
(29)
$$x\left(t-{\tau }_{i}\right)\approx {\alpha }_{i}{x}_{i-M}+{\beta }_{i}{x}_{i-M+1}$$
(30)

where \({\alpha }_{i}=\frac{1}{2}-{m}_{i}+\frac{{\tau }_{i}}{\Delta t}\) and \({\beta }_{i}=\frac{1}{2}+{m}_{i}-\frac{{\tau }_{i}}{\Delta t}\)

By substituting Eq. (26) and Eq. (27) into Eq. (24), the transition function is obtained by the following:

$$\left(I-\frac{\Delta t}{2}{B}_{i+1}\right){x}_{i+1}={e}^{A\Delta t}\left(1+\frac{\Delta t}{2}{B}_{i}\right){x}_{i}-{\sigma }_{i}\left({\alpha }_{i}{x}_{i-M}+{\beta }_{i}{x}_{i-M+1}\right)$$
(31)

where I is an identity matrix.

Based on the discrete map \({\text{col}}\left({x}_{i+1},{x}_{i},\cdots ,{x}_{i-M+1}\right)={C}_{i}{\text{col}}\left({x}_{i},{x}_{i-1},\cdots ,{x}_{i-M}\right)\), the transition function can be reformulated as

$$\Phi ={C}_{n-1}{C}_{n-2}{C}_{n-3}\cdots {C}_{1}{C}_{0}$$
(32)

where

$${C}_{i}=\left[\begin{array}{ccccc}{H}_{i+1}{e}^{A\Delta t}\left(1+\frac{\Delta t}{2}{B}_{i}\right)& 0& \cdots & -{\beta }_{i}{H}_{i+1}{\sigma }_{i}& -{\alpha }_{i}{H}_{i+1}{\sigma }_{i}\\ I& 0& \cdots & 0& 0\\ \vdots & \vdots & \ddots & 0& 0\\ 0& 0& \cdots & 0& 0\\ 0& 0& \cdots & I& 0\end{array}\right]$$
(33)
$${H}_{i+1}={\left(I-\frac{\Delta t}{2}{B}_{i+1}\right)}^{-1}$$
(34)

According to the Floquent theory [22], if all the moduli of the eigenvalues of \(\Phi\) are less than one, the milling system is stable; if any modulus of the eigenvalues of \(\Phi\) is more than one, the milling system is unstable. And \(\Phi\) only depends on the spindle speed rather than the axial depth of cut. This means that, when calculating \(\Phi\), it is not necessary to calculate the matrix exponential function repeatedly for different axial depths of cut for a given spindle speed. Take the semi-discretization method as an example. The matrix exponential function depends on both the spindle speed and the axial depth of cut, so the calculation amount is much larger than that of the method proposed in this paper. Given a \({N}_{s}\times {N}_{a}\) sized grid, where Ns denotes the number of the spindle speed, and Na denotes the number of the axis depth of cut, the semi-discretization method needs to compute the matrix exponential function \(n\times {N}_{s}\times {N}_{a}\) times to determine the stability boundary, while the method proposed in this paper only needs to compute the matrix exponential function \({N}_{s}\) times.

5 Simulation analysis

In this section, two milling examples with two DOFs are employed to verify the method proposed in this paper, the detailed parameters of which are listed in Table 1. To make the following discussion more concise, the method proposed in this paper is abbreviated as the NCM, and the axial depth of cut is abbreviated as the ADC. We compare the three algorithms, i.e., the SDM [9], the RSDM [26], and NCM, by two indexes that measure the computation efficiency and computation accuracy. The computation efficiency is measured by the time consumed for the stability boundary calculation. All algorithms in this paper are executed with MATLAB 2022b on a desktop computer [AMD Ryzen 5-5600H; CPU, 4.0GHz, 16GB].

Table 1 The benchmarked parameters
Full size table

5.1 Computation accuracy and efficiency

The stability lobe diagrams are obtained over a 200 × 100-sized grid in the parameter spaces of nominal spindle speed and axial depth of cut by using the SDM, the RSDM, and the proposed NCM, respectively. For fair comparisons, the discretization step size of the proposed NCM is kept the same with other methods in each comparison group. Since the approximation parameter is M = 44, the transition matrix is a matrix of 46 × 46. The three different modulation frequency ratios, i.e., RVF = 0.1, RVF = 0.2 and RVF = 0.5, are set while the modulation amplitude ratio is always equal to 1, i.e., RVA = 0.1.

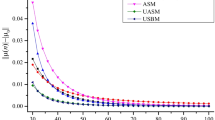
After applying each algorithm to predict the stability boundaries, the computation results for the Example I are schematically depicted in Fig. 2. Take RVA = 0.1 and RVF = 0.1 as an example. As observed from Fig. 2, although the three stability boundaries are nearly the same with each other when RVA = 0.1 and RVF = 0.1, there are obvious differences in the computation time. With the proposed NCM, the computation time is significantly decreased from 2178.56 to 691.41 s. Thanks to the 3rd-order Newton-Cotes integration formula, the computation time of the proposed NCM drops by over 60% than that of the SDM and the RSDM when RVF = 0.2 and RVF = 0.5. Through comparisons, the proposed NCM shows higher computation efficiency than the SDM and the RSDM.

Fig. 2
figure 2

Computational efficiency comparisons of the SDM, the RSDM, and the proposed NCM for Example I

Full size image
Fig. 3
figure 3

Computational efficiency comparisons of the SDM, the RSDM, and the proposed NCM for Example II

Full size image

Similarly, the benchmarked parameters of the Example II are adopted for further verification and analysis. The computation results are presented in Fig. 3. According to the comparisons with other methods, it is found that for the same RVA and RVF, the stability boundaries are nearly the same with each other, there are no obvious differences between the stability boundaries with the SDM, the RSDM and the proposed NCM. It can be observed that the computation time of the proposed NCM drops by over 80% than that of the SDM and the RSDM when RVF = 0.1, RVF = 0.2 and RVF = 0.5. Therefore, the proposed method is effective for improving the computation efficiency while ensuring the computation accuracy.

As shown in Fig. 4, six sets of cutting parameters, i.e., A(Ω= 3000 rpm, ap = 2.3 mm), B(Ω= 3000 rpm, ap = 2.8 mm), C(Ω= 5000 rpm, ap = 2.7 mm), D(Ω= 5000 rpm, ap = 3.2 mm), E(Ω= 7600 rpm, ap = 5.8 mm) and F(Ω= 7600 rpm, ap = 6.3 mm), are adopted to demonstrate the effectiveness of the proposed NCM for ensuring the computation accuracy. The circle ○ denotes the cutting parameters above the stability boundary. The square □ denotes the cutting parameters below the stability boundary. The numerical simulation analysis, which refers to Ref. [29], is carried out in the time domain. The analysis results are plotted in Fig. 5. It is noted that A, C and E in the stability region converge along time, while B, D and F in the unstable region diverge along time. According to Fig. 5, the stability lobe diagrams obtained with the proposed NCM shows the correctness of this work.

Fig. 4
figure 4

Stability lobe diagram obtained with the proposed NCM for computation accuracy verification

Full size image
Fig. 5
figure 5

Vibration displacements of (A), (B), (C), (D), (E) and (F) obtained with the proposed NCM for computation accuracy verification

Full size image

5.2 Milling stability boundaries

The stability lobe diagrams in Figs. 2 and 3 indicate that the introduction of SSV technique possibly enlarges the stability boundaries. It is concluded in Ref. [17] that the sinusoidal VSS modulation has a strong inhibition effect than the triangular VSS modulation. To further analyze the effect of VSS modulations on the stability boundaries, the stability boundaries in the low-speed domain and the high-speed domain are depicted in Figs. 6 and 7, respectively. The modulation amplitude ratio is set as 0.1, and the modulation frequency ratio is set as 0.5. The low-speed domain corresponds to the spindle interval from 2000 to 10000 rpm. The high-speed domain corresponds to the spindle interval from 14000 to 20000 rpm. It is shown from Fig. 6 that when the spindle speed changes from 2000 to 8160 rpm, the sinusoidal VSS modulation is better than the triangle VSS modulation, while the triangle VSS modulation becomes better than the triangular VSS modulation when the spindle speed changes from 8160 to 9120 rpm. The results also verify the previous conclusion. The sinusoidal VSS modulation has a strong inhibition effect than the triangular VSS modulation, but this case is limited to the low-speed domain. This alternation can also be observed in Fig. 7. It should be noted that the triangular VSS modulation has a strong inhibition effect than the sinusoidal VSS modulation in the high-speed domain.

Fig. 6
figure 6

Stability lobe diagrams in the low-speed domain obtained with the proposed NCM when RVA = 0.1 and RVF = 0.5

Full size image
Fig. 7
figure 7

Stability lobe diagrams in the high-speed domain obtained with the proposed NCM when RVA = 0.1 and RVF = 0.5

Full size image

5.3 Modulation parameter optimization

The VSS strategies can suppress the chatter to a greater extent. How to design the RVA and RVF is worth further study. Take Example II as an example. The 3D stability lobe diagrams are drawn with the proposed NCM in modulation spaces for Ω = 4900 rpm in Fig. 8 and Ω = 8000 rpm in Fig. 9, where the sinusoidal modulation and the triangular modulation are both considered. With spindle speed limit alim (denoted by the black surface), each stability lobe diagram can be divided into two parts, i.e., the feasible one and the infeasible one. The optimized parameters are selected from the feasible part. The maximum spindle acceleration amax cannot exceed the spindle speed limit, i.e., amax< alim, where alim is set as 400 rev/s2 in this work.

Fig. 8
figure 8

3D stability lobe diagrams of VSS milling with sinusoidal and triangular modulations when Ω = 4900 rpm

Full size image
Fig. 9
figure 9

3D stability lobe diagrams of VSS milling with sinusoidal and triangular modulations when Ω = 8000 rpm

Full size image

The maximum spindle acceleration amax [22] is introduced as

$${a}_{\text{max}}=\text{max}\left\{\frac{1}{60}\sum_{n=1}^{{n}_{u}}{A}_{n}n\omega \text{cos}\left(n\omega t+{\varphi }_{n}\right)\left|0\le t\le T\right.\right\}$$
(35)

For the sinusoidal modulation, combining Eq. (35) with Eq. (14), it yields

$${a}_{\text{max}}=\frac{2\pi \cdot {\Omega }_{0}^{2}\cdot RVA\cdot RVF}{3600}\le {a}_{\text{lim}}$$
(36)

For the triangular modulation, combining Eq. (35) with Eq. (19), it yields

$${a}_{\text{max}}=\frac{4\cdot {\Omega }_{0}^{2}\cdot RVA\cdot RVF}{3600}\le {a}_{\text{lim}}$$
(37)

The ADC limit of constant spindle speed milling is 1.4 mm for Ω = 4900 rpm and 2.5 mm for Ω = 8000 rpm, respectively. As shown in Figs. 8 and 9, four maximum ADC points, i.e., A, B, C and D, are chosen based on alim. As quantified in Table 2, the maximum ADC abbreviated as MADC reaches 3.6 mm and 3.4 mm for sinusoidal modulations and triangular modulation when Ω = 4900 rpm. And it reaches 3.8 mm and 4.3 mm when Ω = 8000 rpm. Although both modulation modes show some advantages, the feasible part spaces of triangular modulations are much broader than those of sinusoidal modulations. Thus, the triangular modulation provides a wider selection of the VSS parameters.

Table 2 Sinusoidal and triangular modulation optimization. “Irate” is the abbreviation of “Improvement rate”
Full size table

5.4 Chatter frequency analysis

It’s necessary to further alnalyze the chatter properties in the frequency domain. In this section, the VSS frequency and CSS frequency are calculated in an analytical way. For the VSS milling, the chatter frequency fv is introduced as [18]

$${f}_{\text{v}}=\pm \frac{{\omega }_{1}}{2}+j\frac{RVF\times \Omega \left(t\right)}{60}\left[{\text{Hz}}\right] \, j=\text{0,1},2,\cdots ,n$$
(38)

where \({\omega }_{1}\) denotes the positive imaginary part of the critical characteristic multiplier.

For the CSS milling, the chatter frequency fc is introduced as [27]

$${f}_{c}=\pm \frac{{\omega }_{1}}{{2}_{\pi }}+j\frac{N{\Omega }_{0}}{60}\left[{\text{Hz}}\right] \, j=\text{0,1},2,\cdots ,n$$
(39)

The modulation frequency fm is defined as

$${f}_{m}=j\frac{RVF\times {v}_{0}}{60}\left[{\text{Hz}}\right]\text{\hspace{1em}}j=\text{0,1},2,\cdots ,n$$
(40)

Take Example II as an example again. The spindle speed varies between 3000 and 6000 rpm. The ADC is set as 2.5 mm. According to Eqs. (38)–(40), the 17th-order modulation frequencies and chatter frequencies of the VSS milling and the CSS milling are obtained in Fig. 10. With the VSS milling strategy, the frequency band is reduced a lot. The CSS frequency exceeds 1500 Hz, while the VSS frequency does not exceed 900 Hz. When the chatter frequency curve covers the modulation frequency curve, the milling system tends to be stable. The VSS spectrum diagrams show that the spindle speed stability areas of the sinusoidal modulation are [3180 rpm, 3252 rpm], [3720 rpm, 4305 rpm], [4410 rpm, 5430 rpm], and [5550 rpm, 6000 rpm], and that the spindle speed stability areas of the triangular modulation are [3240 rpm, 3270 rpm], [3795 rpm, 3960 rpm], [4260 rpm, 4785 rpm], and [5340 rpm, 6000 rpm]. The CSS spectrum diagrams show that the spindle speed stability areas are [3105 rpm, 3135 rpm], [3210 rpm, 3585 rpm], [3585 rpm, 3690 rpm], [4290 rpm, 4500 rpm], [4680 rpm, 4695 rpm], and [5340 rpm, 5760 rpm]. The comparison results demonstrate that the VSS milling strategy can effectively suppress the chatter, and the sinusoidal modulation is superior to the triangular modulation in the low-speed domain.

Fig. 10
figure 10

Frequency spectrum diagrams of VSS milling and CSS milling

Full size image

6 Conclusions

This paper proposes a novel method for the stability analysis and parameter optimization of milling processes with variable spindle speed variation. Since the iterative calculation of the transition matrix only depends on the spindle speed, the proposed NCM shows higher computation efficiency than the SDM and the RSDM while ensuring the computation accuracy. In the low-speed domain, the sinusoidal VSS modulation has a strong inhibition effect than the triangular VSS modulation; in the high-speed domain, the triangular VSS modulation has a strong inhibition effect than the sinusoidal VSS modulation. It is found that the feasible part spaces of triangular modulations are much broader than those of sinusoidal modulations in the 3D stability lobe diagrams. Besides, the VSS modulation can effectively suppress the chatter, where the sinusoidal modulation is superior to the triangular modulation in the low-speed domain.