Dynamics of a clamped–clamped microbeam resonator considering fabrication imperfections

Abstract

We present an investigation into the static and dynamic behavior of an electrostatically actuated clamped–clamped polysilicon microbeam resonator accounting for its fabrication imperfections, which are commonly encountered in similar microstructures. These are mainly because of the initial deformation of the beam due to stress gradient and its flexible anchors. First, we show experimental data of the microbeam when driven electrically by varying the amplitude and frequency of the voltage loads. The results reveal several interesting nonlinear phenomena of jumps, hysteresis, and softening behaviors. Theoretical investigation is then conducted to model the microbeam, and hence, interpret the experimental data. We solve the Eigen value problem governing the natural frequencies analytically. We then utilize a Galerkin-based procedure to derive a reduced order model, which is then used to simulate both the static and dynamic responses. To achieve good matching between theory and experiment, we show that the exact profile of the deformed beam needs to be utilized in the reduced order model, as measured from the optical profiler, combined with a shooting technique simulation, which is capable of tracing the resonant frequency branches under very-low damping conditions.

1 Introduction

Clamped–clamped microbeams are used numerously in MEMS as solo components in devices or as spring components to support and add stiffness to other microstructures (Senturia 2001; Younis 2011; Tilmans and Legtenberg 1994; Ghayesh et al. 2013; Bhushana et al. 2014). They are commonly fabricated with unavoidable initial curvature due to stress gradients and other imperfections. For example, depositing material layers of different thermal expansion coefficients leads to thermal stress gradient among the layers that cause bimorph-like effect. The outcome of this is an initial curvature of the beam, which becomes in the shape of a shallow arch. Despite the fact that this initial curvature and initial deflection can be very small compared to the beam length; it has significant effect on its static and dynamic behavior. This is even more critical in the case of electrostatic excitation and capacitive detection, which have strong dependence on the gap separating the beam from the lower electrode.

Interest in the dynamic behavior of arches has started since the sixties (Humphreys 1966; Hsu et al. 1969). For example, Humphreys (1966) studied the dynamic snap-through of arch structures and defined the arch characteristics. Hsu et al. (1969) studied the stability of clamped–clamped arches due to time-wise step loads. At the Micro scale, arched and buckled beam structures have received significant attention due to their large stroke and snap-through behavior, which is promising for sensing and actuation applications. Sulfridge et al. (2004) presented a study that showed the different types of actuation that can be used in arch beams, such as electrostatic actuation, thermal actuation, piezoelectric actuation, and mechanical actuation. Xi and Shirong (2008) studied the stability of clamped–clamped arches due to mechanical and thermal actuation. Poon et al. (2002) used the Runge–Kutta method to study the response of a curved clamped–clamped beam excited by a sinusoidal signal, and found softening and hardening behaviors. Zhang et al. (2007) conducted some experimental and theoretical investigations of initially curved clamped–clamped beams when excited by a DC load and examined how this was affected by the level of curvature of the microbeams and the electrostatic load. Buchaillot et al. (2007) also conducted experimental and theoretical investigation of the dynamic of snap through motion for initially curved clamped–clamped beams when subjected to vibration.

Krylov et al. (2008, 2010, 2011) examined experimentally and theoretically the various scenarios of snap-through motion and pull-in instability in deliberately fabricated MEMS arches of deep capacitive gaps. They used the Galerkin procedure to solve for the dynamic response including geometric and electric nonlinearities. In Krylov and Dick (2010), they used the phase portrait method to understand the dynamics of an arch beam when actuated by a step voltage. They also studied the transient response and escape from one potential well to the other one. In Krylov et al. (2011) demonstrated the actuation of clamped–clamped arches using fringing effect of the electrostatic forces.

Das and Batra (2009) used finite and boundary element methods to study the transient analysis of arch beams, and showed that arch beams might face a softening effect before having a snap through motion. Sarı and Pakdemirli (2013) investigated the forced vibration response of curved microbeam due to the small AC loads using the perturbation method, the method of multiple scales. They examined effects of the nonlinear elastic foundation as well as the effect of curvature on the vibrations of the microbeams.

Ansari et al. (2014) investigated by means of an exact solution method and using modified coupled stress theory the postbuckling behavior of the functionally graded microbeams.

Younis et al. (2010) used the Galerkin procedure to discretize the equation of motion for the shallow arch. They studied both the dynamic and static responses for the micro arch, and also compared their results to experimental ones to validate their model. Ouakad and Younis (2010) studied the non-linear behavior of the shallow arch when actuated by both DC and AC load, used Galerkin to simulate the static response and to solve the Eigen value problem under DC load, and used the perturbation method of multiple scales to simulate the forced vibration under both AC and DC loads. Experimental investigation and reduced-order modeling of imperfect microbeams in the form of shallow arches have been presented in (Ruzziconi et al. 2013a, b). The effect of axial forces of MEMS arches has been investigated in (Alkharabsheh and Younis 2013a) whereas the influence of non-ideal boundary conditions on the dynamic response has been presented in (Alkharabsheh and Younis 2013b). The dynamical integrity of imperfect beams and arches have been investigated thoroughly in (Ruzziconi et al. 2013c, d). The use of dynamic-snap through of MEMS arches for filtering applications has been proposed in (Younis et al. 2010; Ouakad and Younis 2014).

While comparing the theoretical predictions to experimental data in (Ruzziconi et al. 2013a), large deviation was found at first, which was attributed to the uncertainty in the measured dimensions of the beam, particularly its thickness and initial curvature. The beam was assumed symmetrically curved up with a classical sinusoidal signal. In this work, we show that this classical assumption of the initial shape can lead to inaccurate predictions. Instead, we use the exact shape as acquired from the experiment in the reduced order model. This combined with the shooting technique should lead to more accurate results and better agreement with experiments.

2 The micro structure

The microstructure considered here is an imperfect polysilicon microbeam fabricated using surface micro machining procedure (Ruzziconi et al. 2013a). The beam is of a rectangular cross section forming one side of a capacitor, which can be approximated to act as a parallel plate capacitor. An SEM picture of the fabricated microbeam is shown in Fig. 1a. The lower electrode is placed underneath it a distance d with a gap filled with air. To acquire the beam’s dimensions and its exact shape, an optical interferometer profilometer is utilized. The profilometer reveals the topography of the beam by reflecting a light from a reference mirror that is then combined with a light reflected from the sample to produce interference fringes. The contrast of the fringes affects the focus of the image. The measured longitudinal profile of the beam is shown in Fig. 1b. From the figure, one can see that the microbeam is not straight, but has a configuration that is curled up a few microns at its midpoint. Figure 1c shows the 3D profile indicating clearly the curvature of the beam as a shallow arch.

Fig. 1

The microbeam under study: a an SEM picture, b the beam profile along its length showing, in microns, the length of the microbeam and the curled up configuration, c 3-D view of the beam profile

The experimental set-up used for testing the MEMS device is shown in Fig. 2. It consists of a micro system analyzer (MSA), under which the microchip is mounted horizontally inside a special vacuum chamber. The chamber is designed to fit directly underneath it. The chamber is equipped with a viewport window located on the top that is made of glass, which enables the laser to penetrate without any distortion. It has some ports placed in the lateral sides, which are for the pressure gauge and electrical connections. Also, the chamber is hooked up to a high vacuum pump. The AC and DC power sources are provided either by the MSA itself, which generates different type of signals that can be used to excite the microbeam, or by generating an electrical signal using the software LabVIEW. Then, this generated signal is passed through a data acquisition card, an amplifier, and a multimeter (to ensure the exact voltage) before reaching the micro-chip.

Fig. 2

Experimental set-up used for testing the device: the MSA analyzer (up right), the vacuum chamber (down right) and the monitor showing wire-bonded beams (left)

As clear from Fig. 1a and the screen picture in Fig. 2, one can see the actuation pads at the edges of the microbeam, which are used to connect the beam with the electrostatic force to excite it. The force is composed of a DC voltage load V _DC superimposed to an AC harmonic load of amplitude V _AC and frequency Ω.

Next, we excite the beam using a weak random signal, white noise, with a very small voltage load. This is to reveal its natural frequencies while staying in the linear regime, i.e., without the influence of the geometric or electrostatic nonlinearities. The results are shown in Fig. 3. Note that the first resonance frequency is near 148.32 kHz.

Fig. 3

First four measured natural frequencies when the beam is excited by white noise at V _DC  = 1 V and V _AC  = 1 V

After revealing the natural frequencies of the beam, we next examine the nonlinear response of the beam through frequency sweep tests. Toward this, we applied a signal from the LabVIEW program, and varied the voltages to get more controlled response around the main resonance. Next, we fixed the DC voltage at 0.7 V and varied the AC voltage. Figure 4a shows, as expected, that the first natural frequency of the beam is around 148 kHz. Then we fixed the DC load at 0.7 V and started increasing the AC load, such that we notice the softening behavior in our results, as shown in Fig. 4b through Fig. 4e. Notice that as the strength of the softening effect increases with the increase of the AC load, the difference in the response between the forward and backward sweep increases leading to considerable hysteresis regimes.

Fig. 4

Experimental measured frequency response curves at a V _AC  = 0.75 V, b V _AC  = 1 V, c V _AC  = 2 V, d V _AC  = 3 V, e V _AC  = 4 V. The forward and backward sweep are, respectively, in red stars and blue circles

3 Theoretical study

In this section, we investigate the response of the micromachined arch theoretically when actuated by both DC electrostatic load and AC harmonic loads. We use reduced order model ROM to solve the force vibration response due to the DC and AC load (Younis 2011). We use two modes of a straight beam in the ROM, two arch mode shapes, and then we compare the results among them. To account for the moving actuation pads of the microbeam, due to under itching, one can assume flexible anchors as in (Alkharabsheh and Younis 2013b). Another approach is to assume a new effective length of the beam (since effectively parts of the pads are moving with the beam as if they are part of it). This effective length of the beam can be chosen by matching the measured linear natural frequency of the beam to the experimental value. We also use a curve fitted function to represent the initial curvature of the beam, and compare the response by using a classical function from the literature.

3.1 Problem formulation

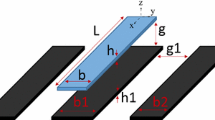
Consider a clamped–clamped micro arch as seen schematically in Fig. 5a. The expression governing the initial shape is taken typically as $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{o} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} ) = \frac{{b_{o} }}{2}[1 - \cos \left( {\frac{2\pi x}{L}} \right)]$, where b _o is the initial rise from the straight position. The micro-arch is actuated by an electrostatic force applied between the upper and the lower electrodes, and acts like a parallel plate capacitor. This electrostatic force is composed of a DC component V _DC superimposed to an AC harmonic load of amplitude V _AC and a frequency $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varOmega }$. The gap distance between the two electrodes is d, the length of the microbeam forming the upper electrode is L, and its width is b and thickness is h. We assume a shallow arch where $(d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{o} /dx)^{2} \ll 1$ (Dawe 1971), so the parallel plate assumption will be valid. Thus, the nonlinear equation of motion for the transverse deflection of the arch (Nayfeh 2000) is expressed as

$$\begin{gathered} EI\frac{{\partial^{4} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}^{4} }} + \rho A\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{2} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} }} = \left[{\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}^{2} }} + \frac{{d^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{o} }}{{d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}^{2} }}} \right]\times \left[{\frac{EA}{2L}\int_{0}^{L} {\left\{ {\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}} \right)^{2} + 2\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}\frac{{d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{o} }}{{d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}} \right)} \right\}} dx} \right] \hfill \\ - \frac{{\varepsilon b\left[ {V_{DC} + V_{AC} \cos (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varOmega } t)} \right]^{2} }}{{2(d + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{o} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} )^{2} }} \hfill \\ \end{gathered}$$

(1)

where E is the Young’s modulus; I is the moment of inertia, considering a rectangular cross section I = bh ³/12; ρ is the material density; A is the cross sectional area A = bh; $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$ is the viscous damping coefficient; and $\varepsilon$ is the dielectric constant of the gap medium (here is assumed air).

Fig. 5

a Electrically actuated clamped–clamped arch, b 3-D schematic for the arch

From Fig. 5 the boundary conditions of the clamped–clamped arch are clamped at the boundaries, that is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} (0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} ) = 0,\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} ) = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} (L,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} ) = 0,\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(L,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} ) = 0.$$

(2)

Next, we introduce nondimensional variables:

$$w = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}{d},w_{o} = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{o} }}{d},x = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}{L},t = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} }}{T}$$

(3)

where; $T = \sqrt {\frac{{\rho AL^{4} }}{EI}} .$

Next, we plug Eq. (3) into Eqs. (1) and (2), which yields the following nondimensional equation of motion and nondimensional boundary conditions:

$$\begin{gathered} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{\partial t} = \alpha_{1} \left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{d^{2} w_{o} }}{{dx^{2} }}} \right]\times\left[ {\int\limits_{0}^{1} {\left\{ {\left( {\frac{\partial w}{\partial x}} \right)^{2} + 2\left( {\frac{\partial w}{\partial x}\frac{{dw_{o} }}{dx}} \right)} \right\}dx} } \right] \hfill \\ - \frac{{\alpha_{2} \left[ {V_{DC} + V_{AC} \cos (\varOmega t)} \right]^{2} }}{{\left( {1 + w_{o} + w} \right)^{2} }} \hfill \\ \end{gathered}$$

(4)

$$w(0,t) = 0,\;\frac{\partial w}{\partial x}(0,t) = 0,\;w(1,t) = 0,\;\frac{\partial w}{\partial x}(1,t) = 0$$

(5)

where

$$w_{o} (x) = \frac{{b_{o} }}{2d}\left[ {1 - \cos (2\pi x)} \right]$$

(6)

and the nondimensional parameters are:

$$C = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} L^{4} }}{EIT};\alpha_{1} = 6\left( \frac{d}{h} \right)^{2} ;\alpha_{2} = \frac{{\varepsilon bL^{4} }}{{2EId^{3} }};\varOmega = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varOmega } }}{{\omega_{n} }};\omega_{n} = 1/T.$$

(7)

3.2 The Eigen value problem

We solve the Eigen value problem to get the natural frequencies and mode shapes at different initial rises. Thus, we solve the linearized undamped unforced equation of Eq. (4) (Nayfeh 2000), which can be written as

$$\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} w}}{{\partial t^{2} }} = \alpha_{1} \frac{{\partial^{2} w_{o} }}{{\partial x^{2} }}\int_{0}^{1} 2 \left( {\frac{\partial w}{\partial x}\frac{{dw_{o} }}{dx}} \right)dx$$

(8)

We plug Eq. (6) into Eq. (8) and use the separation of variables technique as

$$w\;(x,t) = \varPhi (x)e^{i\;\omega t}$$

(9)

where ω is the eigenvalue and Φ is the eigenfunction. Hence, we end up with:

$$\varPhi^{iv} - \omega^{2} \varPhi = 4\alpha_{1} \frac{{b_{o}^{2} }}{{d^{2} }}\pi^{3} \cos (2\pi x)\int_{0}^{1} {\sin (2\pi x)\varPhi^{\prime}}$$

(10)

Equation (10) has a solution consisting of two parts, the homogeneous part Φ _h (x) and the particular part Φ _p (x), that is

$$\varPhi (x) = \varPhi_{h} (x) + \varPhi_{p} (x).$$

(11)

The homogeneous part is the same as the mode shape of a straight beam:

$$\varPhi_{h} (x) = A\sin (\sqrt \omega x) + B\cos (\sqrt \omega x) + C\sinh (\sqrt \omega x) + D\cosh (\sqrt \omega x)$$

(12)

Next, we solve for the particular part by assuming

$$\varPhi_{p} (x) = c_{5} \cos (2\pi x)$$

(13)

Substituting Eq. (13) into Eq. (10) gives the constant c ₅

$$c_{5} = \frac{{4\alpha_{1} \frac{{b_{o}^{2} }}{{d^{2} }}\pi^{3} \int_{0}^{1} {\sin (2\pi x)\varPhi_{h}^{\prime } } (x)dx}}{{16\pi^{4} - \omega^{2} + 4\alpha_{1} \frac{{b_{o}^{2} }}{{d^{2} }}\pi^{4} }}$$

(14)

Thus, c ₅ is function of the unknowns A, B, C, and D. Accordingly, Eq. (11) can be written as

$$\begin{gathered} \varPhi (x) = A\sin (\sqrt \omega x) + B\cos (\sqrt \omega x) + C\sinh (\sqrt \omega x) + D\cosh (\sqrt \omega x) + \hfill \\ \frac{{4\alpha_{1} \frac{{b_{o}^{2} }}{{d^{2} }}\pi^{3} \int_{0}^{1} {\sin (2\pi x)\varPhi_{h}^{\prime } } (x)dx}}{{16\pi^{4} - \omega^{2} + 4\alpha_{1} \frac{{b_{o}^{2} }}{{d^{2} }}\pi^{4} }}\cos (2\pi x) \hfill \\ \end{gathered}$$

(15)

Equation (15) is subjected to the boundary conditions

$$\varPhi (0) = 0,\;\varPhi^{\prime}(0) = 0,\;\varPhi (1) = 0,\;\varPhi^{\prime}(1) = 0$$

(16)

To solve the Eigen value problem, we apply the boundary conditions Eq. (16). We end up with 4 algebraic equations in the following form:

$$\left[ {\begin{array}{*{20}c} {M_{11} } & {M_{12} } & {M_{13} } & {M_{14} } \\ {M_{21} } & {M_{22} } & {M_{23} } & {M_{24} } \\ {M_{31} } & {M_{32} } & {M_{33} } & {M_{34} } \\ {M_{41} } & {M_{42} } & {M_{43} } & {M_{44} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} A \\ B \\ C \\ D \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$

(17)

Each element in the M matrix is a function of the natural frequency ω. The determinant of this matrix will give the natural frequency (nondimensional). Then, we can get the values of the unknowns A, B, C and D, and calculate the unknown C ₅. Finally, we solve for the mode shape that is associated with each frequency.

3.3 Reduced order model

To get the response of the beam w(x, t) we use the Galerkin procedure to discretize the equation of the beam, Eq. (4), (Nayfeh et al. 1995; Younis et al. 2003). So the deflection of the arch is approximated as:

$$w(x,t) = \sum\limits_{i = 1}^{n} {\varPhi_{i} (x)u_{i} (t)}$$

(18)

where Φ _i (x) is the trial function that satisfies the boundary conditions of the arch, and u _i (t) is the modal coordinate.

For Φ _i (x), we can substitute any function that satisfies the boundary conditions, but most of the functions used in the literature are either the mode shapes of a straight beam (b _o = 0), or the exact mode shapes of the arch itself.

The mode shapes of a straight clamped–clamped beam from can be expressed as:

$$\varPhi_{i} (x) = \cosh (\sqrt {\omega_{i,non} } x) - \cos (\sqrt {\omega_{i,non} } x) - \sigma_{i} [\sinh (\sqrt {\omega_{i,non} } x) - \sin (\sqrt {\omega_{i,non} } x)]$$

(19)

where; σ ₁ = 0.982502, σ ₂ = 1.00078, σ ₃ = 0.999966, σ ₄ = 1; and ω _1,non  = 22.3733, ω _2,non  = 61.6728, ω _3,non  = 120.903, ω _4,non  = 199.859.

The exact mode shapes for the arch beam are obtained as discussed in Sect. 3.2. To solve Eq. (4) and derive the ROM., we follow the below procedure:

Multiply Eq. (4) by the denominator (1 + w _o  + w)², to avoid the computationally expensive spatial numerical integration in the course of the solution due to the electrostatic force term (Nayfeh et al. 2005). Hence, Eq. (4) becomes:

$$\begin{gathered} \left( {1 + w_{o} + w} \right)^{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{\partial t}} \right) = \hfill \\ \alpha_{1} \left( {1 + w_{o} + w} \right)^{2}\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{d^{2} w_{o} }}{{dx^{2} }}} \right]\times\left[ {\int\limits_{0}^{1} {\left\{ {\left( {\frac{\partial w}{\partial x}} \right)^{2} + 2\left( {\frac{\partial w}{\partial x}\frac{{dw_{o} }}{dx}} \right)} \right\}dx} } \right] - \alpha_{2} \left[ {V_{DC} + V_{AC} \cos (\varOmega t)} \right]^{2} . \hfill \\ \end{gathered}$$

(20)

Plug Eq. (18) into Eq. (20), which yields the following equation:

$$\begin{gathered} \left( {1 + w_{o} + \sum\limits_{i = 1}^{n} {\varPhi_{i}\left( x \right)u_{i} \left( t \right)} } \right)^{2}\times \left( {\sum\limits_{i = 1}^{n} {\varPhi_{i}^{\prime \prime \prime \prime }} \left( x \right)u_{i} \left( t \right) + \sum\limits_{i = 1}^{n} {\varPhi_{i} \left( x \right)\textit{\"{u}}_{i} \left( t \right)} + C\sum\limits_{i = 1}^{n} {\varPhi_{i} \left( x \right)\dot{u}_{i} \left( t \right)} } \right) = \hfill \\ \alpha_{1} \left( {1 + w_{o} + \sum\limits_{i = 1}^{n} {\varPhi_{i} \left( x \right)u_{i} \left( t \right)} } \right)^{2} \left[ {\sum\limits_{i = 1}^{n} {\varPhi_{i}^{\prime \prime } \left( x \right)u_{i} \left( t \right)} + \frac{{d^{2} w_{o} }}{{dx^{2} }}} \right]\times \hfill \\ \left[ {\int\limits_{0}^{1} {\left\{ {\left( {\sum\limits_{i = 1}^{n} {\varPhi_{i}^{\prime } \left( x \right)u_{i} \left( t \right)} } \right)^{2} + 2\left( {\sum\limits_{i = 1}^{n} {\varPhi_{i}^{\prime } \left( x \right)u_{i} \left( t \right)} + \frac{{dw_{o} }}{dx}} \right)} \right\}dx} } \right] \hfill \\ - \alpha_{2} \left[ {V_{DC} + V_{AC} \cos \left( {\varOmega t} \right)} \right]^{2} \hfill \\ \end{gathered}$$

(21)

• Multiply Eq. (21) by Φ _i (x) and integrate from 0 to 1, and we end up with a differential equation in terms of the modal coordinate u _i (t).

• We solve for u _i (t) and multiply it with Φ _i (x) to get the whole response w(x, t) from Eq. (18).

Next, we address the issue of how many modes should be used in the ROM and of which kind (of straight beam or of an arch). Toward this, we solve for the natural frequency of the microbeam arch for various values of initial rise and compare among the ROM results and the exact analytical solution. Figure 6 shows the results for the ROM when using one and two symmetric modes of a straight beam and also using one and two symmetric modes of the arch and compare the results to the analytical results of Sect. 3.2. We can note that using one or two arch modes or two straight modes should lead to good results. In this paper we use the first and the third mode of the arch as basis functions in the ROM to generate the frequency response curves in the following sections.

Fig. 6

Comparison between the exact solution of the eigenvalue problem of an arch and the results of the ROM when using straight beam mode shapes and the arch mode shapes for various values of initial rise of the arch. Shown also in the vertical straight line is the initial rise of the fabricated imperfect beam of the studied case

4 Comparison between theory and experiment

In this section, we attempt to match experimental data of the obtained frequency–response curves with results generated from long time integration of the modal equations of the ROM.

One should note that the arch of this study is connected from both sides with actuation pads that are flexible due to under etching (Alkharabsheh and Younis 2013b). Hence, it is noticed that part of the pads are moving when exciting the arch with the electrostatic force as if they are part of the arch. As discussed in (Alkharabsheh and Younis 2013b), these flexible pads or anchors reduce the stiffness of the arch considerably. One approach to deal with this is to assume soft springs at the boundaries of the arch. Another approach is to assume an effective length, which is longer than the measured length from the profilometer of Fig. 1. We follow here the second approach.

First, we solve the Eigen value problem for the theoretical natural frequency to match it with the experimental one. This yields a nondimensional first natural frequency of $\omega_{n}$ = 67.77 and the mode shape of Fig. 7. We convert this nondimensional frequency to the dimensional one as $\omega_{Hz} = \frac{{\omega_{n} }}{2\pi }\sqrt {EI/\rho AL^{4} }$. Substituting the numerical values of the arch with the length measured in Fig. 1 gives ω _Hz  = 288, 716 kHz, which is far from the experimental one (148.250 kHz). Using an effective length L _eff  = 1.395 original length matches the theoretical prediction with the experimental value.

Fig. 7

The first mode of the arch

To simulate the forced vibration using the ROM, we calculate the damping term, the quality factor Q based on Fig. 3 and obtain Q = 974. Using this value in the model, the effective length, and the other measured parameters of the each, we simulate the forced response for the electric loads of Fig. 4 by integrating the modal equations of the ROM over long period of time L–T I until reaching steady state. Figure 8 compares both the simulation and the experimental results. Figure 8 shows qualitative matching with the experiment, showing softening behavior, but not quantitative matching.

Fig. 8

The measured frequency response curve and the simulated one using long-time integration L–T I of the ROM, a V _AC  = 1 V, b V _AC  = 2 V, c V _AC  = 3 V, d V _AC  = 4 V, e V _AC  = 5 V

In order to improve the quantitative matching between theory and experiment, we implement next the exact profile of the arch in the ROM instead of the idealized shape, which traditionally used in such cases, of Eq. (6). Toward this we curve-fit the exact initial profile, which is shown in Figs. 9 as discretized points, into a fifth-order polynomial and obtain the new initial profile w _o (x) as

$$\begin{gathered} w_{o} (x) = - 0.0940438 \, + \, 3.94325 \, x \, + \, 40.1152 \, x^{2} \, + \, 15.9357 \, x^{3} - \, 254.592 \, x^{4} \, \hfill \\ + \, 280.601 \, x^{5} \, - \, 85.9134 \, x^{6} . \hfill \\ \end{gathered}$$

(22)

Fig. 9

Plot of the discretized points of the measured arch profile along its length

Fig. 10

The measured frequency response curve and the simulated one of an arch a V _AC  = 1 V, b V _AC  = 2 V, c V _AC  = 3 V, d V _AC  = 4 V, e V _AC  = 5 V, using the curve fitted function. The abbreviation L–T I C–F stands for (long-time integration using curve fitted function)

Figure 10 compares the experimental results to the simulation using long-time integration with Eq. (6) and the curve-fitted function of Eq. (22). Figure 10 shows improvement due to the use of Eq. (22); the upper curves become closer to the experimental ones. However, the agreement is mostly qualitative with the experiment and the discrepancy is still considerable.

Fig. 11

The measured frequency response curve and the simulated one of an arch using the shooting technique for a V _AC  = 1 V, b V _AC  = 2 V, c V _AC  = 3 V, d V _AC  = 4 V, and e V _AC  = 5 V

5 The shooting technique

In the previous simulations, we used long-time integration to solve the differential equations of the ROM. This technique depends on the basin of the attraction (Younis 2011). To capture a solution, the basin of attraction should be big and robust; otherwise, this technique will not capture a solution implying that no stable solution exists, which is not necessary true. In order to predict the entirety of the solutions, we need to use another numerical technique to solve the differential equations. One of the most robust techniques is the shooting technique, which can capture the periodic solution more accurately than long-time integration. In addition, it is capable of capturing both stable and unstable solutions, if needed, for bifurcation analysis. Following the procedure outlined in (Younis 2011), we show next results of the shooting technique using the classical shape of the initial curvature, Eq. (6), and then compare to the results obtained using the exact shape of Eq. (22). The results are depicted in Fig. 11.

Figure 11 shows much better match with the experiments using the shooting technique. The figures also show the difference between using the curve-fitted function to the classical one, and how the results were improved significantly by using the fitted one. This indicates the importance of accounting for the exact shape of the arch in the model.

It may also be noted that there is still a difference between the simulated results and the experimental ones; the upper simulated curves extend more than the experimental ones. This is expected since shooting keeps capturing periodic solutions even when their basin of attractions shrink too much to the extent that they cannot exist experimentally due to the presence of disturbance and noise. For more improvements in the theoretical predictions, analyzes of the basin of attraction of these upper curves needs to be conducted (Nayfeh et al. 1995).

6 Summary and conclusions

In this study we investigated the dynamic behavior of an imperfect microbeam (arch) theoretically and experimentally. We used several analytical techniques to match the theoretical results with the experimental measurements of the frequency–response curves of the arch. We found that using an effective length of the arch, to account for the flexible pads, the shooting technique, to capture most of the resonant curves especially near bifurcation points, and the exact shape of the arch, as captured through measurements, lead to improved matching with the experiments.