1 Introduction

With rapid developments in nanotechnology, nano structures have been the interest of many researchers over the past decade due to their several enhanced properties. Micro/Nanoelectromechanical Systems (M/NEMS) have become one of the most important components in constructing develop micro/nano-devices like actuators, switches, biosensors, nanowires, accelerometer, tweezers, ultra-thin films, etc. This is due to their low manufacturing cost, batch production, light weight, small size, durability, low energy consumption, potentials as sensitive and high frequency devices, and compatibility with integrated circuits [1–7].

Viscoelastic micro/nano systems exhibit both solid and liquid time-dependent behaviors together to some extent. Viscoelastic materials can present interesting properties such as high damping characteristics, low weight, high strength and excellent possibilities to absorb energy [8]. Such materials are widely used in some technologies, such as robots, artificial biological parts, aerospace, automotive and dampers [9]. Experimental observations showed that when the internal material length scale parameter is in the order of structural characteristic size such as thickness of beams, the size effect is urgent and vital in their static and dynamic behaviors of metals and polymers [10–13].

A typical beam-type M/NEMS are constructed from two conductive electrodes where on is movable and the other is fixed. When direct current voltage is applied across the two electrodes, the electrostatic force is generated and the movable electrode is actuated to deflect towards the substrate. The critical voltage and the corresponding maximum deflection which leads the beam to be unstable and pull-in onto the ground electrode, are known as the pull-in voltage and pull-in deflection, respectively [14]. Therefore, predicting the stable actuating range and the pull-in instability parameters are important issues for designing stable and safe M/NEMS. For example, pull-in instability should be avoided in micro/nano mechanical resonators and micro-mirrors in order to achieve stable operations and enhance device sensitivity [1, 15]. On the other hand, estimation of pull-in voltage is essential to control the switch on and off [16].

It is worth noting that as the dimensions of electromechanical systems reduce, NEMS present monograph characteristics, which differ greatly from their predecessor MEMS as the dispersion forces (Casimir and van der Waals attractions) appear in a significant contribution to the NEMS behavior [17, 18]. At micro-separations (typically larger than a few nanometers while smaller than a few micrometers), the attraction between two surfaces could be described by the Casimir interaction [19]. It represents attractive force between two flat parallel plates of solids that arises from quantum fluctuations in the ground state of the electromagnetic field. On the other hand, the van der Waals (vdW) force can significantly influence the NEMS performance if the initial gap between the two conductive electrodes is typically below several ten nanometers [19].

Several models are proposed in the literature to investigate the pull-in instability of electrically actuated M/NEMS devices. In this regard, the different nonclassical continuum theories are employed to investigate the mechanical performance of micro/nanostructures, in which material properties are highly affected by the dimensions and are size-dependent. These theories include some additional material constants besides two classical Lame’s constant for isotropic elastic material; the Eringen nonlocal elasticity theory which includes one additional material constant [20, 21], the classical strain gradient, the strain gradient, the classical couple stress and the modified couple stress theories of elasticity include five, three, two and one additional material constants, respectively [22–25].

Recently, the modified couple stress theory (MCST) developed by Yang et al. [24] has been successfully used to investigate mechanical behavior of microactuated beams as it overcomes the difficulties encountered in determining higher-order material constants by introducing only one additional material length scale parameter. Rahaeifard et al. [26] employed the MCST to study the size effect on the deflection and static pull-in voltage of silicon micro-cantilevers. Yin et al. [27] explored analytically the size effect of electrostatically actuated microbeams by using the MCST. Kong [28] presented approximate analytical solutions to the pull-in voltage and pull-in displacement of the electrostatically actuated microbeam based on the MCST using the Rayleigh–Ritz method. Baghani et al. [29] and Rokni et al. [30] analytically studied the response of electrostatically actuated microbeams and studied the effect of the applied voltage on the nonlinear size-dependent response of the microbeams. Static and dynamic pull-in instabilities of the functionally graded (FG) micro-beams subjected to a nonlinear electrostatic pressure and external heat source based on the MCST were studied by Zamanzadeh et al. [31]. Shaat and Mahmoud [32] investigated numerically and analytically the electrostatic behavior of microactuated cantilever beam including surface elasticity in the context of the MCST. Recently, this model was extended by Shaat and Abdelkefi [33] to study the effects of the material structure inhomogeneity of an electrostatically-actuated micro/nano Nc-Si cantilever beam on its pull-instability and sensitivity to bio-cells are investigated. Wang et al. [34] analyzed the effects of surface energy and material length scale parameter on the pull-in instability and free vibration of electrostatically actuated nanoplates considering the effect of Casimir force. Liang et al. [35] presented a nonlinear size-dependent model for the electrostatically actuated nanobeams incorporating Casimir force based on the strain gradient elasticity theory and Hamilton principle. The governing equations were solved numerically using the generalized differential quadrature (GDQ) method. Beni et al. [36] employed the modified strain gradient theory to study the size dependent pull-in instability of nano-bridges and nano-cantilevers, considering the effect of van der Waals intermolecular force. The Hamilton’s principle in conjunction with Euler–Bernoulli beam theory was applied for deriving the governing equation. Noghrehabadi and Eslami [37] investigated the size-dependent static behavior of clamped–clamped actuators in liquid electrolytes based on the MCST, where the effects of van der Waals force, midplane stretching and residual forces are included. The minimum total potential energy principle was used to derive the governing equation.

However, little attention has been paid for modeling the pull-in instability of the viscoelastic micro/nano devices with size effects. Bethe et al. [38] showed that for a thin silicon MEMS structure, the creep phenomenon of silicon became rather significant and consequently investigation of the viscoelastic effects in microbeams became necessary. The pull-in phenomenon of electrically actuated viscoelastic clamped–clamped microbeam based on the MCST was studied by Fu et al. [39], Fu and Zhang [40] and Zhang and Fu [41]. In these papers, the obtained governing equation was solved using Galerkin method and although the prescribed function in the space variable was chosen to satisfy the boundary conditions, it is not guaranteed to satisfy the governing equation. On the other hand, this approach is complicated if other sources of nonlinearity are added to the governing equation. Chen et al. [42] studied the buckling and dynamic stability of a simply supported piezoelectric viscoelastic nanobeam subjected to van der Waals forces based on the classical viscoelasticity theory.

This research study is the first attempt to analyze the nonlinear size-dependent pull-in instability of electromechanical viscoelastic micro/nanobeams including the simultaneous effects of material length scale parameter, intermolecular Casmir and vdW forces, electric forcing including fringing field, residual stress and mid-plane stretching geometric nonlinearity. To the author’s best knowledge, no previous studies which cover all these issues are available. The modified couple stress theory is employed to express the microstructure effect of viscoelastic microbeams in the context of linear viscoelastic theory. The nonlinear governing integro-differential equations and associated boundary conditions are formulated using the extended Hamilton principle and Bernoulli–Euler beam theory in conjunction with the standard solid model of viscoelasticity. Afterwards, a modified generalized differential-integral quadrature (GDIQ) method is developed to solve the obtained governing nonlinear equations. The developed model is verified for both elastic and viscoelastic benchmarks of microbeams. In the framework of viscoelastic theory, a detailed parametric study is performed to get an insight into the effects of intermolecular Casimir and vdW forces, relaxation time, durable modulus, material length scale parameter, initial gap and beam length on the size dependent pull-in response (instantaneous and durable pull-in voltages, pull-in time, pull-in deflection and creep deflection) of electrically actuated viscoelastic microbridges and microcantilevers.

2 Problem formulation

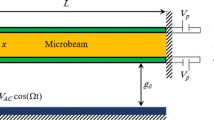
This section is intended to derive the equations of motion and associated boundary conditions of an electrically actuated viscoelastic microbeams given in Fig. 1. The beam is actuated by a distributed electrical, fringing field, Casimir and vdW forces between a flexible and a rigid stationary electrodes. The actuator is modeled by a long and thin beam with the length L, width b, uniform thickness h, and an initial gap d 0 between the beam and substrate. The x coordinate is taken along the length, z coordinate  is taken along the thickness, and the ycoordinate is taken along the width of the beam.

Fig. 1
figure 1

Schematic representation of electrically actuated. a micro-cantilever and b micro-bridge

Full size image

2.1 Modified couple stress theory in the framework of viscoelasticity

The modified couple stress theory (MCST) proposed by Yang et al. [24] for an elastic behavior will be extended to the case of viscoelastic behavior of microbeams in the framework of linear viscoelastic theory. The nonclassical viscoelastic constitutive equations can be obtained based on the classical Leaderman viscoelastic linear constitutive equations, Phan-Thien [43], and the modified couple stress theory, Yang et al. [24], as follows:

$$\sigma_{ij} \left( {x,t} \right) = \lambda \left( t \right)*\varepsilon_{mm} \left( {x,t} \right)\delta_{ij} + 2\mu \left( t \right)*\varepsilon_{ij} \left( {x,t} \right)$$
(1)
$$m_{ij} \left( {x,t} \right) = 2l^{2} \mu \left( t \right)*\chi_{ij} \left( {x,t} \right)$$
(2)

where \(\sigma_{ij} \left( {x,t} \right)\), \(\varepsilon_{ij} \left( {x,t} \right)\), \(m_{ij} \left( {x,t} \right)\) and \(\chi_{ij} \left( {x,t} \right)\) are the Cauchy force-stress tensor, the infinitesimal strain tensor, the deviatoric part of the couple-stress tensor and the symmetric curvature tensor, respectively, and δ ij is the Kronecker delta. The material length scale parameter l measures the effect of the couple-stress on viscoelastic behavior, Mindlin [22]. For simplicity, the length scale parameter is assumed to be time-independent. \(\lambda \left( t \right)\) and \(\mu \left( t \right)\) are the time-dependent Lame’s constants in classical viscoelastic theory. Note that throughout the paper, the summation convention and standard index notation are used, with the Latin indices from 1 to 3.

The components of the infinitesimal strain tensor and the symmetric curvature tensor are defined as follows, Yang et al. [24]:

$$\varepsilon_{ij} \left( {x,t} \right) = \frac{1}{2}\left[ {\left( {\nabla {\mathbf{u}}\left( {x,t} \right)} \right) + \left( {\nabla {\mathbf{u}}\left( {x,t} \right)} \right)^{T} } \right]$$
(3)
$$\chi_{ij} \left( {x,t} \right) = \frac{1}{2}\left[ {\left( {\nabla \theta \left( {x,t} \right)} \right) + \left( {\nabla \theta \left( {x,t} \right)} \right)^{T} } \right]$$
(4)

where \({\mathbf{u}}\left( {x,t} \right)\) and \(\theta \left( {x,t} \right)\) are the displacement and rotation vectors, respectively;

$$\theta_{i} \left( {x,t} \right) = \frac{1}{2}\left[ {\nabla \times {\mathbf{u}}\left( {x,t} \right)} \right]$$
(5)

The time-dependent viscoelastic Lame’s constants are given by, Phan-Thien [43]

$$\lambda \left( t \right) = \frac{\nu E\left( t \right)}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\quad {\text{and }}\, \mu \left( t \right) = \frac{E\left( t \right)}{{2\left( {1 + \nu } \right)}}$$
(6)

where E(t) is the relaxation function  and ν is the Poisson’s ratio, which assumed to be time-independent.

The Stieltjes’s convolution operation symbol ‘*’ appears in Eqs. (1) and (2) is defined as,

$${\mathbb{C}}\left( t \right) *{\mathbb{N}}\left( t \right) = {\mathbb{C}}_{0} {\mathbb{N}}\left( t \right) + \int_{0}^{t} {\frac{{d{\mathbb{C}}\left( {t - \xi } \right)}}{{d\left( {t - \xi } \right)}}{\mathbb{N}}\left( \xi \right) d\xi ,\quad {\mathbb{C}}_{0} \equiv {\mathbb{C}}\left( {t = 0} \right)}$$
(7)

Consequently, Eqs. (1) and (2) can be, respectively, rewritten as

$$\begin{aligned} \sigma_{ij} \left( {x,t} \right)& \equiv \sigma_{ij}^{e} \left( {x,t} \right) + \sigma_{ij}^{v} \left( {x,t} \right) \\ & = \left[ {\lambda_{0} \varepsilon_{kk} \left( {x,t} \right)\delta_{ij} + 2 \mu_{0} \varepsilon_{ij} \left( {x,t} \right)} \right] + \left[ {\int_{0}^{t} {\dot{\lambda }\left( {t - \xi } \right)\varepsilon_{kk} \left( {x,\xi } \right)\delta_{ij} d\xi + 2\int_{0}^{t} {\dot{\mu }\left( {t - \xi } \right)\varepsilon_{ij} \left( {x,\xi } \right) d\xi } } } \right] \\ \end{aligned}$$
(8)
$$m_{ij} \left( {x,t} \right) \equiv m_{ij}^{e} \left( {x,t} \right) + m_{ij}^{v} \left( {x,t} \right) = 2l^{2} \mu_{0} \chi_{ij} \left( {x,t} \right) + 2l^{2} \int_{0}^{t} {\dot{\mu }\left( {t - \xi } \right)\chi_{ij} \left( {x,\xi } \right) d\xi }$$
(9)

where λ 0 and μ 0 are the initial Lame’s constants; i.e. at t = 0. The superscripts ‘e’ and ‘v’ refer to the current instantaneous elastic and history due to viscoelastic behavior, respectively.

2.2 Kinematic and kinetic relations

Based on the Bernoulli–Euler beam hypothesis, the displacements \(\left( {u, v, w} \right)\) of an arbitrary point with coordinates \(\left( {x, y, z} \right)\) are given by,

$$\left\{ {\begin{array}{*{20}c} {u \left( {x,z,t} \right)} \\ {v\left( {x,z,t} \right)} \\ { w\left( {x,z,t} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {z\phi \left( {x,t} \right)} \\ 0 \\ {w\left( {x,t} \right)} \\ \end{array} } \right\},\quad \phi \left( {x,t} \right) = - w^{{\prime }} \left( {x,t} \right)$$
(10)

where \(\left( {\blacksquare } \right)^{{\prime }}\) denotes a derivative with respect to the spatial coordinate x, ϕ(x, t) is the rotation angle of the centroidal axis of the beam and \(w\left( {x,t} \right)\) is the uniform lateral deflection.

From Eqs. (7)–(10), the following non-zero components of strain tensor, rotation vector and symmetric curvature tensor are, respectively, given by

$$\varepsilon_{xx} \left( {x,t} \right) = - zw^{{{\prime \prime }}} \left( {x,t} \right)$$
(11)
$$\theta_{y} \left( {x,t} \right) = - w^{{\prime }} \left( {x,t} \right)$$
(12)
$$\chi_{xy} \left( {x,t} \right) = \chi_{yx} \left( {x,t} \right) = - \frac{1}{2}w^{{{\prime \prime }}} \left( {x,t} \right)$$
(13)

Substituting Eqs. (11) into (8) and Eqs. (13) into (9), the following nonzero components of classical force-stress and deviatoric part of the couple-stress tensors are obtained as

$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{e} \left( {x,t} \right)} \\ {\sigma_{yy}^{e} \left( {x,t} \right)} \\ {\sigma_{zz}^{e} \left( {x,t} \right)} \\ \end{array} } \right\} = - \left\{ {\begin{array}{*{20}c} \varGamma \\ {\varGamma \nu /\left( {1 - \nu } \right)} \\ {\varGamma \nu /\left( {1 - \nu } \right)} \\ \end{array} } \right\}E_{0} zw^{{{\prime \prime }}} \left( {x,t} \right)$$
(14a)
$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{v} \left( {x,t} \right)} \\ {\sigma_{yy}^{v} \left( {x,t} \right)} \\ {\sigma_{zz}^{v} \left( {x,t} \right)} \\ \end{array} } \right\} = - \left\{ {\begin{array}{*{20}c} \varGamma \\ {\varGamma \nu /\left( {1 - \nu } \right)} \\ {\varGamma \nu /\left( {1 - \nu } \right)} \\ \end{array} } \right\}\int_{0}^{t} {z\dot{E}\left( {t - s} \right)w^{{{\prime \prime }}} \left( {x,\xi } \right) d\xi }$$
(14b)

and

$$m_{xy}^{e} \left( {x,t} \right) = l^{2} \mu_{0} w^{{{\prime \prime }}} \left( {x,t} \right)$$
(15a)
$$m_{xy}^{v} \left( {x,t} \right) = \int_{0}^{t} {l^{2} \dot{\mu }\left( {t - s} \right)w^{{{\prime \prime }}} \left( {x,\xi } \right)d\xi }$$
(15b)

For wide beam (b ≥ 5 h), the effective Young’s modulus can be approximated by the plate modulus, Osterberg and Senturia [44], such that

$$\varGamma = \frac{1}{{\left( {1 - \nu^{2} } \right)}}\quad {\text{for }}b \ge 5h, \quad {\text{otherwise}}\quad \varGamma = 1$$
(16)

In the present study, the viscoelastic behavior is simulated using a single element of the standard linear solid model (generalized Maxwell viscoelastic model), in which the viscoelastic relaxation modulus E(t) is given by, Schapery [45]

$$E\left( t \right) = E_{1} + E_{2} e^{ - \psi t} \quad {\text{and}}\quad E_{0} \equiv E\left( {t = 0} \right) = E_{1} + E_{2}$$
(17)

where ψ is the reciprocal of the relaxation time, E 1 and E 2 are the durable and creep moduli of the material, respectively and E 0 refers to the instantaneous elastic Young’s modulus.

2.3 Variational formulation

For a viscoelastic continuum, the extended Hamilton principle is expressed as, Chen et al. [46]

$$\int_{{t_{i} }}^{{t_{f} }} {\left[ {\delta K - \delta \varPi^{e} + \left( {\delta W_{R} + \delta W_{S} + \delta W_{E} } \right) + \delta W^{v} } \right]dt = 0}$$
(18)

where \(\delta {\text{K}}\) and \(\delta \varPi^{e}\) are the variations of the kinetic energy and the total elastic strain energy due to bending incorporating the elastic part of microstructure effect, respectively. \(\delta {\text{W}}_{\text{R}}\), \(\delta {\text{W}}_{\text{S}}\), \(\delta {\text{W}}_{\text{E}}\) and \(\delta {\text{W}}^{v}\) are the virtual works due to residual stress, nonlinear mid-plane stretching, external stimuli forces and viscous dissipative forces including the dissipative part of microstructure effect, respectively. For the viscoelastic microbeam under consideration, these variations can be expressed as follows:

$$\delta K = \delta \frac{1}{2}\int_{0}^{L} {\int_{A} {\rho \dot{w}^{2} \left( {x,t} \right)dAdx = \int_{0}^{L} {\left( {\rho S\dot{w}\left( {x,t} \right)} \right)\delta wdx} } }$$
(19)
$$\delta \varPi^{e} = \delta \frac{1}{2}\int_{0}^{L} {\int_{A} {\left( {\sigma_{xx}^{e} \varepsilon_{xx} + 2 m_{xy}^{e} \chi_{xy} } \right)dAdx = \frac{1}{2}\left( {\varGamma IE_{0} + Sl^{2} \mu_{0} } \right)} } \delta \int_{0}^{L} {w^{\prime \prime 2} \left( {x,t} \right)d} x$$
(20)

where ρ is the mass density, \(S = bh\) and \(I = bh^{3} /12\) are is the cross-sectional area and the corresponding moment of inertia for the cross-section, respectively and L is the total length of the beam.

The virtual work due to residual stresses can be expressed as

$$\delta {\text{W}}_{\text{R}} = - \frac{1}{2}\sigma_{r} S \delta \int_{0}^{L} {w^{{{\prime }2}} \left( {x,t} \right)dx}$$
(21)

where the effective residual stress is given by \(\sigma_{r} = \left( {1 - \nu } \right)\sigma_{0}\), otherwise \(\sigma_{r} = \sigma_{0}\) for narrow beams (b < 5 h), where σ 0 is the initial biaxial residual stress in the beam, Osterberg and Senturia [44]. In this study, it is assumed that the cantilever microbeams are free from residual stresses and hence \(\delta {\text{W}}_{\text{R}}\) equals zero.

The virtual work attributed to the nonlinear stretching force in the case of an elastic microbeam with immovable ends can be written as, Nayfeh and Emam [47],

$$\delta {\text{W}}_{\text{S}}^{e} = - \frac{1}{8}\frac{{\varGamma SE_{0} }}{L}\delta \left[ {\int_{0}^{L} {} w^{{{\prime }2}} \left( {x,t} \right)dx} \right]^{2}$$
(22)

Exploiting Eqs. (7), (22) can be extended for a viscoelastic microbeam as follows:

$$\delta {\text{W}}_{\text{S}} = - \frac{\varGamma S}{2L}\left( {E_{0} \delta \int_{0}^{L} {w^{\prime2} \left( {x,t} \right)dx + \delta \int_{0}^{t} {\int_{0}^{L} {\dot{E}\left( {t - \xi } \right)w^{{{\prime }2}} \left( {x,\xi } \right) dxd\xi } } } } \right)$$
(23)

Note that the axial resultant force associated with the mid-plane stretching is not considered in the cantilever case and therefore the virtual work \(\delta {\text{W}}_{\text{S}}\) equals zero, this is due to that the cantilever beam possess a movable end.

Considering the distribution of external stimuli forces per unit length of the microbeam (f ext ), the virtual work by these external forces can be expressed as

$$\delta {\text{W}}_{\text{E}} = \int_{0}^{L} {f_{ext} \delta w\left( {x,t} \right)dx \equiv \int_{0}^{L} {\left[ {{\rm H}_{\text{elec}} \left( {x,t} \right) + {\rm H}_{\text{C}} \left( {x,t} \right) + {\rm H}_{\text{vdW}} \left( {x,t} \right)} \right]\delta w\left( {x,t} \right)dx} }$$
(24)

where f ext is the consists of the electrostatic Coulomb force unit length of the beam including the first order fringing field effect \({\rm H}_{\text{elec}}\) and the intermolecular Casimir and van der Waals (vdW) forces per unit length of the beam, \({\rm H}_{\text{C}}\) and \({\rm H}_{\text{vdW}}\), respectively. These forces can be written as the following, Huang et al. [48] and Gusso and Delben [49]:

$${\rm H}_{\text{elec}} \left( {x,t} \right) = \frac{{ \varepsilon_{0} bV^{2} }}{{2\left[ {d_{0} - w\left( {x,t} \right)} \right]^{2} }}\left( {1 + 0.65\frac{{d_{0} - w\left( {x,t} \right)}}{b}} \right)$$
(25)
$${\rm H}_{\text{C}} \left( {x,t} \right) = \frac{{\pi^{2} \bar{h}cb}}{{240\left[ {d_{0} - w\left( {x,t} \right)} \right]^{4} }}$$
(26)
$${\rm H}_{\text{vdW}} \left( {x,t} \right) = \frac{{{\text{A}}b}}{{6\pi \left[ {d_{0} - w\left( {x,t} \right)} \right]^{3} }}$$
(27)

where V is the applied voltage, d 0 is the initial is the initial gap between the movable part and the fixed ground plane, \(\varepsilon_{0} = 8.854 \times 10^{ - 12} {\text{C}}^{ 2} {\text{N}}^{ - 1} {\text{m}}^{ 2}\) is the permittivity of vacuum, \(\bar{h} = 1.0546 \times 10^{ - 34} J s\) is the reduced Planck’s constant divided by 2π, \(c = 2.998 \times 10^{8} \,{\text{m s}}^{ - 1}\) is the speed of light and \({\text{A}}\) is the Hamaker constant with values in the range \(\left[ {0.4, 4} \right] \times 10^{ - 19} {\text{J}}\), Batra et al. [50]. In the present analysis, all other external forces are assumed to be zero.

The virtual work due to the viscous dissipative forces including the dissipative part of couple-stress can be obtained as, Attia and Mahmoud [51]

$$\begin{aligned} \delta {\text{W}}^{v} & = - \delta \frac{1}{2}\int_{0}^{L} {\int {\int_{A} {\left( {\sigma_{xx}^{v} \varepsilon_{xx} + 2 m_{xy}^{v} \chi_{xy} } \right)dAdx} } } \\ & = \int_{0}^{L} {\int_{0}^{t} { - \left[ {\varGamma I\dot{E}\left( {t - \xi } \right) + Sl^{2} \dot{\mu }\left( {t - \xi } \right)} \right]w^{{{\prime \prime }}} \left( {x,\xi } \right)\delta w^{{{\prime \prime }}} \left( {x,\xi } \right)d\xi dx} } \\ \end{aligned}$$
(28)

Now, by substituting Eqs. (19)–(21), (23), (24) and (28) into the extended Hamilton’s principle (Eq. (18)), while invoking the condition of zero variation at times \(t = t_{0}\) and \(t = t_{f}\), the integro-differential equation of an electrically actuated viscoelastic microbeam based on the MCST in the framework of viscoelasticity can be derived as the following:

$$\begin{aligned} & \rho S\ddot{w}\left( t \right) + {\mathbb{E}}_{0} w^{{{\prime \prime \prime \prime }}} \left( t \right) + \mathop \int \limits_{0}^{t} {\dot{\mathbb{E}}}\left( {t - \xi } \right)w^{{{\prime \prime \prime \prime }}} \left( \xi \right)d\xi \\ & - \left[ {\sigma_{r} S + \frac{S\varGamma }{2L}E_{0} \mathop \int \limits_{0}^{L} w^{{{\prime }2}} \left( t \right)dx + \frac{S\varGamma }{2L}\mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{L} \dot{E}\left( {t - \xi } \right)w^{{{\prime }2}} \left( \xi \right)dxd\xi } \right]w^{{{\prime \prime }}} \left( t \right) - {\mathbb{H}}\left( t \right) = 0 \quad \forall x \in \left[ {0,L} \right] {\text{and}}\quad t \in \left[ {t_{i} ,t_{f} } \right] \\ \end{aligned}$$
(29)

in which

$${\mathbb{E}}_{0} = I\varGamma E_{0} + Sl^{2} \mu_{0},\quad {\mathbb{E}}\left( t \right) = I\varGamma E\left( t \right) + Sl^{2} \mu \left( t \right)$$
(30a,b)
$${\mathbb{H}}\left( t \right) = \frac{{\varepsilon_{0} bV^{2} }}{{2\left[ {d_{0} - w\left( t \right)} \right]^{2} }}\left( {1 + 0.65\frac{{d_{0} - w\left( t \right)}}{b}} \right) + \frac{{{\text{A}}b}}{{6\pi \left[ {d_{0} - w\left( t \right)} \right]^{3} }} + \frac{{\pi^{2} \bar{h}cb}}{{240\left[ {d_{0} - w\left( t \right)} \right]^{4} }}$$
(30c)

under the following boundary conditions:

$$\begin{aligned} & {\text{Either }}w = \tilde{w} \quad {\text{or}}\,\, {\mathbb{E}}_{0} w^{{{\prime \prime \prime }}} \left( t \right) + \int_{0}^{t} {{\dot{\mathbb{E}}}\left( {t - \xi } \right)w^{{{\prime \prime \prime }}} \left( \xi \right)d\xi } \\ & \quad - \left[ {\sigma_{r} S + \frac{S\varGamma }{2L}E_{0} \int_{0}^{L} {w^{{{\prime }2}} \left( t \right)dx + \frac{S\varGamma }{2L}\int_{0}^{t} {\int_{0}^{L} {\dot{E}\left( {t - \xi } \right)w^{{{\prime }2}} \left( \xi \right)dxd\xi } } } } \right]w^{{\prime }} \left( t \right) = 0\quad {\text{at}}\quad x = 0, L \\ \end{aligned}$$
(31a)
$${\text{Either}}\quad w^{{\prime }} = \tilde{w}^{{\prime }} \;{\text{or}}\;{\mathbb{E}}_{0} w^{{{\prime \prime }}} \left( t \right) + \int_{0}^{t} {{\dot{\mathbb{E}}}\left( {t - \xi } \right)w^{{{\prime \prime }}} \left( \xi \right)d\xi = 0 \quad {\text{at}}\quad x = 0, L}$$
(31b)

To transform the governing equation and associated boundary conditions into the nondimensional form, the following nondimensional variables are introduced as

$$w = \frac{{\hat{w}}}{{d_{0} }}, \quad x = \frac{{\hat{x}}}{L}, \quad {\text{and}}\quad t = \frac{{\hat{t}}}{T}$$
(32)

where T is a time scale and \(\left( {\widehat{{\blacksquare }}} \right)\) denotes a dimensional quantity and d 0 a reference value for the initial gap. For simplicity, we keep the same notations for variables having in mind they are in nondimensional form from now on. Substituting Eq. (32) into Eqs. (29) and (30) and considering no residual stress or axial stretching for microcantilever, the nondimensional governing equation of viscoelastic microbeam can be obtained as

$$\begin{aligned} & C_{0} \ddot{w}\left( t \right) + w^{{{\prime \prime \prime \prime }}} \left( t \right) - C_{1} \int_{0}^{t} {e^{{ - \bar{\psi }\left( {t - t_{0} } \right)}} w^{{{\prime \prime \prime \prime }}} \left( {t_{0} } \right)dt_{0} } \\ & \quad - \left[ {C_{\text{R}} + C_{\text{S}} \int_{0}^{1} {w^{{{\prime }2}} \left( t \right)dx - C_{\text{S}} \bar{\psi }\bar{E}_{2} \int_{0}^{1} {\int_{0}^{t} {e^{{ - \bar{\psi }\left( {t - t_{0} } \right)}} w^{{{\prime }2}} \left( {t_{0} } \right)dt_{0} dx} } } } \right]w^{{{\prime \prime }}} \left( t \right) - \frac{{C_{\text{E}} }}{{\left[ {1 - w\left( t \right)} \right]^{2} }} - \frac{{C_{\text{F}} }}{{\left[ {1 - w\left( t \right)} \right]}} \\ & \quad - \frac{{C_{\text{vdW}} }}{{\left[ {1 - w\left( t \right)} \right]^{3} }} - \frac{{C_{\text{C}} }}{{\left[ {1 - w\left( t \right)} \right]^{4} }} = 0\quad \forall x \in \left[ {0,1} \right]\, {\text{and}}\, t \in \left[ {t_{0} ,t_{f} } \right] \\ \end{aligned}$$
(33)

and the following boundary conditions:

(a) Microcantilever case (Clamped-Free):

$$w\left( {0,t} \right) = w^{{\prime }} \left( {0,t} \right) = 0,$$
(34a)
$$\begin{aligned} & - w^{{{\prime \prime \prime }}} \left( {1,t} \right) + C_{1} \left[ {\int_{0}^{t} {e^{{ - \bar{\psi }\left( {t - t_{0} } \right)}} w^{{{\prime \prime \prime }}} \left( {1,t_{0} } \right)dt_{0} } } \right]w^{{\prime }} \left( {1,t} \right) \\ & \quad = 0\quad {\text{and}}\quad w^{{{\prime \prime }}} \left( {1,t} \right) - C_{1} \int_{0}^{t} {e^{{ - \bar{\psi }\left( {t - t_{0} } \right)}} } w^{{{\prime \prime }}} \left( {1,t_{0} } \right)dt_{0} = 0 \\ \end{aligned}$$
(34b)

(b) Microbridge case (Clamped–Clamped):

$$w\left( {0,t} \right) = w^{{\prime }} \left( {0,t} \right) = 0,$$
(35a)
$$w\left( {1,t} \right) = w^{{\prime }} \left( {1,t} \right) = 0$$
(35b)

In above equations, the dimensionless parameters are given as follows:

$$\begin{aligned} \varGamma_{1} & = \varGamma I + \frac{{Sl^{2} }}{{2\left( {1 + \nu } \right)}},\quad C_{0} = \frac{I}{{\varGamma_{1} }},\quad C_{1} = \bar{\psi }\bar{E}_{2} ,\quad C_{\text{R}} = \frac{{L^{2} \sigma_{r} S}}{{E_{0} \varGamma_{1} }}, \quad C_{\text{S}} = \frac{\varGamma }{{\varGamma_{1} }}\frac{{Sd_{0}^{2} }}{2}, \\ C_{\text{E}} & = \frac{{I\bar{V}^{2} }}{{\varGamma_{1} }},\quad C_{\text{F}} = 0.65\frac{{d_{0} }}{b}C_{\text{e}} ,\quad C_{\text{vdW}} = \frac{{{\text{A}}bL^{4} }}{{6\pi d_{0}^{4} E_{0} \varGamma_{1} }}, \quad C_{\text{C}} = \frac{{\pi^{2} \bar{h}cbL^{4} }}{{240d_{0}^{5} E_{0} \varGamma_{1} }}, \\ \quad \bar{V} & = VL^{2} \sqrt {\frac{{\varepsilon_{0} b}}{{2d_{0}^{3} E_{0} I}}} ,\quad T = \frac{{L^{2} }}{h}\sqrt {\frac{12\rho }{{E_{0} }}} , \quad \bar{\psi } = \psi T\quad {\text{and}} \quad \bar{E}_{2} = \frac{{E_{2} }}{{E_{0} }} \\ \end{aligned}$$
(36)

The parameter is given by Eq. (16). Again, it should be noted that for the case of microcantilevers, the parameters of axial force due to residual stress and nonlinear stretching should be omitted from Eq. (33); i.e. \(C_{\text{R}} = C_{\text{S}} = 0\).

3 Solution procedure

Due to the high nonlinearity encountered in the governing equations and associated boundary conditions, analytical solutions for such integro-differential equations is cumbersome. Consequently, an approximate numerical solution is developed through a proposed generalized differential-integral quadrature (GDIQ) method, which is a combination of the well-known generalized differential quadrature (GDQ) method and a new developed generalized integral quadrature (GIQ) method. In this study, the GDQ method is employed to discretize the governing equation and associated boundary conditions in the space variable. Based on the fact that an indefinite integral of a function is its anti-derivative, a new generalized integral quadrature (GIQ) method is developed as the pseudo-inverse of GDQ method. The proposed GIQ method is applied to approximate the definite integrals included in the integro-differential equation (Eq. (33)). The proposed GDIQ discretization results in a system of ordinary differential equations that can be solved by Runge–Kutta method.

3.1 Generalized differential quadrature method

To render the article self-contained, the formulas of the GDQ method, Shu [52] is briefly introduced in this section. The shifted Chebyshev–Gauss–Lobatto grid points are used to generate grid points in x i direction

$$x_{i} = \frac{1}{2}\left\{ {1 - \cos \left( {\frac{i - 1}{N - 1}\pi } \right)} \right\},\quad i = 1, 2, \ldots ,N$$
(37)

By this method, m -th derivative of a function \(f\left( {x,t} \right)\) is discretized by series as follows:

$$\frac{{d^{m} }}{{dx^{m} }} = \mathop \sum \limits_{{j = 1}}^{N} a_{{ij}}^{{\left( m \right)}} \,f\left( {x_{j} ,t} \right)$$
(38)

The weighting coefficients a (m) ij for the m-th derivative are dependent on the distribution of grid points only and can be obtained from the recursive formula,

$$a_{ij}^{\left( m \right)} = m\left( {a_{ij}^{\left( 1 \right)} a_{ii}^{{\left( {m - 1} \right)}} - \frac{{a_{ij}^{{\left( {m - 1} \right)}} }}{{x_{i} - x_{j} }}} \right),\quad a_{ii}^{\left( m \right)} = - \mathop \sum \limits_{j = 1,j \ne i}^{N} a_{ij}^{\left( m \right)} , \quad i,j \in \left\{ {1, 2, \ldots ,N} \right\}$$
(39)

In matrix form, let the discrete values of f i  = f(x i ) at nodes \(i = 1, 2, \ldots ,N\), be given as a vector \(\varvec{f} = \left[ {f_{1} ,f_{2} , \cdots ,f_{n} } \right]^{T}\), then

$$\varvec{F}^{\left( m \right)} = {\mathbb{A}}^{\left( m \right)} \varvec{f} \equiv {\mathbb{A}}^{\left( 1 \right)} {\mathbb{A}}^{{\left( {m - 1} \right)}} \varvec{f}$$
(40)

In this work only homogeneous boundary conditions represented by Eqs. (34) and (35) are considered and hence its implementation is straight forward, see Shu [52].

3.2 Generalized integral quadrature method

Consider a differentiable function \(f\left( x \right)\) defined on the interval \(0 \le x \le 1\),

$$\frac{df}{dx} = F\left( x \right), \quad \int_{0}^{x} {F\left( x \right)dx = f\left( x \right) - f\left( 0 \right)}$$
(41a, b)

Using a pseudo-inverse algorithm such that the matrix \({\mathbb{B}}\) is pseudo-inverse of \({\mathbb{A}}^{\left( 1 \right)} ,\) one can rewrite Eq. (41a, b) as \(\varvec{f}^{\left( 1 \right)} = {\mathbb{B}}\varvec{F}^{\left( 1 \right)}\) and consequently the definite integral between two nodes x i and x j can be approximated as

$$\int_{{x_{i} }}^{{x_{j} }} {F\left( x \right)dx = f\left( {x_{j} } \right) - f\left( {x_{i} } \right) \cong \mathop \sum \limits_{k = 1}^{N} {\mathbb{R}}_{{\left[ {ij} \right]}} F_{k} ,\quad k = 1, 2, \ldots ,N}$$
(42)

Note that the row vector \({\mathbb{R}}_{{\left[ {ij} \right]}} = {\mathbb{B}}_{jk} - {\mathbb{B}}_{ik}\) is the difference between the \(j{\text{th}}\) and \(i{\text{th}}\) rows of \({\mathbb{B}}\). Thus, the integral \(\int_{0}^{1} {w^{{{\prime }2}} dx}\) included in Eq. (33) can be approximated using both GDQ and GIQ methods as follows:

$$\int_{0}^{1} {w^{{{\prime }2}} dx \cong {\mathbb{R}}_{{\left[ {1N} \right]}} \left( {\left( {{\mathbb{A}}^{\left( 1 \right)} w} \right)^{ \circ 2} } \right),\quad {\mathbb{R}}_{{\left[ {ij} \right]}} = {\mathbb{B}}_{jk} - {\mathbb{B}}_{ik} }$$
(43)

where the symbol \('\circ '\) denotes element by element operator. Note that matrix multiplication of the row \({\mathbb{R}}_{{\left[ {1N} \right]}}\) by the vector \(\left( {{\mathbb{A}}^{\left( 1 \right)} w} \right)^{ \circ 2}\) produces a scalar value approximating the definite integral.

3.3 GDIQ method for viscoelastic analysis

Following Attia and Mohamed [53], the following definitions are firstly introduced:

$$I_{1} = \mathop \int\limits_{0}^{t} e^{{ - \bar{\psi }\left( {t - t_{0} } \right)}} w^{{{\prime \prime \prime \prime }}} \left( {t_{0} } \right)dt_{0}$$
(44a)
$$I_{2} = \int_{0}^{1} {\int_{0}^{t} {e^{{ - \bar{\psi }\left( {t - t_{0} } \right)}} w^{{{\prime }2}} \left( {t_{0} } \right)dt_{0} dx} }$$
(44b)

Applying the Leibniz rule for differentiation under the integral sign, one can obtain

$$\dot{I}_{1} = w^{\prime\prime\prime\prime} \left( {x,t} \right) - \bar{\psi } I_{1} \quad {\text{and}}\quad \dot{I}_{2} = g\left( {x,t} \right) - \bar{\psi } I_{2}$$
(45a, b)

where

$$g\left( t \right) = \int_{0}^{1} {w^{{{\prime }2}} \left( t \right)dx}$$
(46)

Neglecting the inertia term for quasistatic analysis, then differentiation of Eq. (33) with respect to t in light of Eqs. (45a, b) yields to

$$\begin{aligned} & \dot{w}^{{{\prime \prime \prime \prime }}} \left( t \right) - C_{1} \dot{I}_{1} - \left[ {C_{\text{R}} + C_{\text{S}} \left\{ {g\left( t \right) - \bar{\psi }\bar{E}_{2} I_{2} } \right\}} \right]\dot{w}^{{{\prime \prime }}} - C_{\text{S}} \left\{ {\dot{g}\left( t \right) - \bar{\psi }\bar{E}_{2} \dot{I}_{2} } \right\}w^{{{\prime \prime }}} \\ & \quad = \left\{ {\frac{{2C_{\text{E}} }}{{\left[ {1 - w} \right]^{3} }} + \frac{{C_{\text{F}} }}{{\left[ {1 - w} \right]^{2} }} + \frac{{3C_{\text{vdW}} }}{{\left[ {1 - w} \right]^{4} }} + \frac{{4C_{\text{C}} }}{{\left[ {1 - w} \right]^{5} }}} \right\}\dot{w}\left( t \right)\quad \forall x \in \left[ {0,1} \right] \quad {\text{and}}\,\, t \in \left[ {t_{i} ,t_{f} } \right] \\ \end{aligned}$$
(47)

To this end, it is required to reduce Eq. (47) to a system of ODEs using GDQ and GIQ methods. GDIQ method is used to discretize the x-domain and approximate the partial derivatives with respect to x. At arbitrary time t, let \({\mathbf{w}} = \left[ {w_{1} ,w_{2} , \cdots w_{N} } \right]^{T}\) and \(\left\{ {{\dot{\mathbf{w}}}} \right\} = \left[ { {\dot{\mathbf{w}}}_{1} ,{\dot{\mathbf{w}}}_{2} , \ldots ,{\dot{\mathbf{w}}}_{N} } \right]^{T}\) be, respectively, the vectors of discrete values of deflection and velocity at the discrete points \(x_{1} ,x_{2} , \ldots ,x_{N}\) of the microbeam. Employing the GIQ method defined by Eq. (43) and using Eq. (46), \(\dot{g}\left( t \right)\) yields to a scalar value as follows

$$\dot{g}\left( t \right) = \int_{0}^{1} {2w^{{\prime }} \left( {x,t} \right)\dot{w}^{{\prime }} \left( {x,t} \right)dx = 2{\mathbb{R}}_{{\left[ {1N} \right]}} \left( {\left( {{\text{K}}_{1} {\mathbf{w}}} \right) \circ \left( {{\text{K}}_{1} {\dot{\mathbf{w}}}} \right)} \right)}$$
(48)

Consequently, \(\dot{g}\left( t \right)w^{{{\prime \prime }}}\) can be obtained using GDQ method as follows:

$${\text{K}}_{2} {\mathbf{w}}\dot{g}\left( t \right) = {\mathbb{S}}{\dot{\mathbf{w}}}, \quad {\mathbb{S}} = 2{\text{K}}_{2} {\mathbf{w}}{\mathbb{R}}_{{\left[ {1N} \right]}} {\mathbb{Q}}$$
(49a, b)

where \({\text{K}}_{l}\) denotes the coefficients matrix corresponding to the l-th derivatives modified by appropriate application of the boundary conditions. \({\mathbb{Q}}\) is an N-square matrix obtained from matrix \({\text{K}}_{1}\) by multiplying each element in its i-th row by the corresponding i-th element in vector \({\mathbf{w}}^{{\prime }} = {\text{K}}_{1} {\mathbf{w}}\). Finally, Eq. (47) can be rewritten

$${\mathbb{M}}{\dot{\mathbf{w}}} = \left( {{\mathbb{P}}{\mathbf{w}} - {\mathbb{C}}} \right)$$
(50)

where

$${\mathbb{M}} = {\text{K}}_{4} - \left[ {C_{\text{R}} + C_{\text{S}} \left\{ {g\left( t \right) - \bar{\psi }\bar{E}_{2} I_{2} } \right\}} \right]{\text{K}}_{2} - C_{\text{S}} {\mathbb{S}} - \left( {\frac{{2C_{\text{E}} }}{{\left[ {1 - \varvec{w}} \right]^{3} }} + \frac{{C_{\text{F}} }}{{\left[ {1 - \varvec{w}} \right]^{2} }} + \frac{{3C_{\text{vdW}} }}{{\left[ {1 - \varvec{w}} \right]^{4} }} + \frac{{4C_{\text{C}} }}{{\left[ {1 - \varvec{w}} \right]^{5} }}} \right)$$
(51a)
$${\mathbb{P}} = C_{1} {\text{K}}_{4} - \bar{\psi }\bar{E}_{2} C_{\text{S}} \left( {g - \bar{\psi } I_{2} } \right){\text{K}}_{2}$$
(51b)
$${\mathbb{C}} = \bar{\psi }C_{1} I_{1}$$
(51c)

It is important to refer to that Eqs. (45a, b) and (50) form the coupled system of ODEs obtained from Eq. (47) using GDIQ method. This system is solved using Runge–Kutta method. However, the initial conditions have to be computed first by substituting \(t = 0\) into Eq. (33),

$$w^{{{\prime \prime \prime \prime }}} - \left[ {C_{\text{R}} + C_{\text{S}} \int_{0}^{1} {w^{{{\prime }2}} dx} } \right]w^{{{\prime \prime }}} - \frac{{C_{\text{E}} }}{{\left[ {1 - w} \right]^{2} }} - \frac{{C_{\text{F}} }}{{\left[ {1 - w} \right]}} - \frac{{C_{\text{vdW}} }}{{\left[ {1 - w} \right]^{3} }} - \frac{{C_{\text{C}} }}{{\left[ {1 - w} \right]^{4} }} = 0 \quad \forall x \in \left[ {0,1} \right]$$
(52)

which can be solved using Newton’s iterative method to obtain \({\mathbf{w}}_{0}\).

4 Numerical results and discussion

In this section, the proposed model is verified by comparing the obtained results with those of available numerical and analytical methods in the literature. Also, a comprehensive parametric study is conducted to investigate the different viscoelastic material and geometrical parameters as well as the intermolecular forces on the quasistatic pull-in response of electrically actuated viscoelastic doubly-clamped microbridges and clamped-free microcantilevers in the framework of viscoelasticity.

4.1 Comparative study

Since, there is no available well-defined benchmarks to validate the present model for electrically actuated viscoelastic microbeams including the combined effects of length scale parameter, fringing field, residual stresses, mid-plane stretching and Casimir and vdW forces. Therefore, based on the quasi-elastic method proposed by Schapery [54], the current results of the nondimensional instantaneous and durable pull-in voltages (\(\bar{V}_{PI}\)) at times \(t = 0\) and \(\infty ,\) respectively, of a doubly-clamped microbridge viscoelastic microactuator are compared with those reported by Zhang and Fu [41], in which \(E_{0} = 169 \,{\text{GPa}}\), \(\bar{E}_{1} = 0.6,\) \(\nu = 0.22\), \(L = 150\,\upmu{\text{m}}\), \(b = 10\,\upmu{\text{m}}\), \(h = 2\,\upmu{\text{m}}\) and \(d_{0} = 1.2h\). For the purpose of comparison, the effects of the fringing field, residual stresses and Casimir and vdW forces are neglected; i.e. \(C_{\text{F}} = C_{\text{R}} = C_{\text{C}} = C_{\text{vdW}} = 0\), while the effect of mid-plane stretching is included. As shown in Fig. 2, it is found that the present results are in good agreement with those in the work of Zhang and Fu [41] for different values of nondimensional length scale parameter \(l/h\).

Fig. 2
figure 2

Nondimensional instantaneous and durable pull-in voltages of viscoelastic microbridge when \(C_{\text{F}} = C_{\text{R}} = C_{\text{C}} = C_{\text{vdW}} = 0\)

Full size image

Also, convergence of the present numerical method is verified as demonstrated in Table 1 which displays and compares the linear (without mid-plane stretching) and nonlinear (with mid-plane stretching) pull-in voltages of elastic microbridge of different lengths with varying total number of grid points N. As observed, the proposed numerical GDIQ method yields convergent results when N ≥ 21. Moreover, it is seen from Table 1 that the present results are in a good agreement with those obtained using numerical, analytical and experimental methods. Based on these results, all the following numerical results are obtained using N = 21.

Table 1 Convergence of the linear and nonlinear pull-in voltages (V) of an electrostatically actuated doubly–clamped elastic microbeam when \(C_{\text{C}} = C_{\text{vdW}} = 0\), \(E = 151 \,{\text{GPa}}\), \(\nu = 0.3\), \(L = 5{ \mu m}\), \(h = 1.5\,{\mu m}\), \(d_{0} = 1.18\,{\mu m}\), \(\sigma_{0} = 6/\left( {1 - \nu } \right) \,{\text{MPa}}\) and \(l = 0\)
Full size table

4.2 Parametric study

The developed model is used to investigate the nonlinear size-dependent quasistatic pull-in response of electrically actuated viscoelastic microbridges and microcantilevers based on the MCST. Combined effect of electrostatic actuation, fringing field, mid-plane stretching, residual stresses and Casimir and vdW forces are considered. Effect of mid-plane stretching, residual stresses, initial gap, beam length, Casimir force, vdW force, durable modulus, relaxation time, and material length scale parameter on the viscoelastic pull-in parameters; i.e. instantaneous and durable pull-in voltages, viscoelastic creep deflection, pull-in time and pull-in deflection, will be comprehensively studied in the next sections.

Material parameters of both doubly-clamped microbridge and clamped-free microcantilever are \(E_{0}\) = 77 GPa, \(\bar{E}_{1} = 0.6\), \(\bar{\psi }\) = 0.1, \(\nu\) = 0.33, \(l = 0.25h\) and the residual stress \(\sigma_{0}\) is taken 100 MPa for the case of doubly-clamped microbeam. Geometrical parameters are taken as \(L = 100 \,\upmu{\text{m}}\), \(b = 50 \,\upmu{\text{m}}\), \(h = 1 \,\upmu{\text{m}}\) and \(d_{0} = 0.08\,\upmu{\text{m}}\) for the microbridge and \(L = 300\,\upmu{\text{m}}\), \(b = 50\,\upmu{\text{m}}\), \(h = 1\,\upmu{\text{m}}\) and \(d_{0} = 0.15 \,\upmu{\text{m}}\) for the microcantilever. These material and geometrical parameters are hold constant except the parameter being studied, which is varied with larger or smaller value.

4.2.1 Effect of mid-plane stretching

It is worth noting that for the geometrical nonlinearity caused by mid-plane stretching to be significant, the beam ends must be immovable, Nayfeh and Mook [55]. Also, it is noticed from Eq. (36) that this source of nonlinearity is proportional to the square of the initial gap. The effect of mid-plane stretching on the instantaneous and durable pull-in voltages of the doubly-clamped microbridge for different initial gaps is presented in Fig. 3, using the quasi-elastic analysis. The results are obtained corresponding to both linear and nonlinear analyses based on the MCST for \(l/h = 0.25\) and ignoring the effects fringing field, residual stresses and intermolecular Casimir and vdW forces; i.e. \(C_{\text{F}} = C_{\text{R}} = C_{\text{vdW}} = C_{\text{C}} = 0\). According to these results, it is observed that as the initial gap increases, the instantaneous and durable pull-in voltages for both linear (without mid-plane stretching effect “\(C_{\text{S}}\) = 0”) and nonlinear (with mid-plane stretching effect “with \(C_{\text{S}}\)”) responses are significantly increased. Also, it is revealed that the nonlinear pull-in voltage is larger than that obtained from linear analysis and therefore ignoring nonlinearity due to mid-plane stretching leads to underestimation of both instantaneous and durable pull-in voltages especially at large initial gaps.

Fig. 3
figure 3

Linear and nonlinear instantaneous and durable pull-in voltages of viscoelastic microbridge at different initial gaps

Full size image

Creep of the linear and nonlinear nondimensional center deflection for different initial gaps and applied voltages is studied in Fig. 4. Here and throughout the paper, the solid line denote that the microactuator behaves stable when the applied voltage is lower than the durable one (\(V < V_{PI} \left( {t = \infty } \right))\), i.e. the microactuated beam will not collapse at any time instant. Both dash and dash-dot lines represent that the microactuator behaves in the durable region when \(V_{PI} \left( {t = \infty } \right) < V < V_{PI} (t = 0\)). Some selected numerical values for the nondimensional pull-in time (\(t_{PI}\)) and the corresponding nondimensional pull-in center deflection of microbridge (\(w_{PI}^{c}\)) are provided in Table 2. This Table and next tables throughout the paper can be recognized to three different regions according to the status of the microactuator response; namely stable, durable, and invisible regions. The stable region, where the beam will not collapse any time, is identified by nondimensional time elapsed by the microbeam to reach the steady-state response \(\left( {t_{ss} } \right)\) and corresponding nondimensional steady-state center deflection \(\left( {w_{ss}^{c} } \right)\), which appear with parentheses. The durable region reports the values of the nondimensional pull-in time (\(t_{PI} )\) and the corresponding nondimensional pull-in center deflection \(\left( {w_{PI}^{c} } \right)\) just before collapse. The third region presents the unstable or invisible one, which is filled by the symbol “–”, to indicate that no response exists. Noting that instantaneous pull-in (at no time) occurs in the transition between the durable and invisible regions (\(V > V_{PI} \left( {t = 0} \right))\), while the durable pull-in occurs between the durable and stable regions.

Fig. 4
figure 4

Creep of the nondimensional center deflection of viscoelastic microbridge with and without mid-plane stretching at different initial gaps

Full size image
Table 2 Linear and nonlinear nondimensional pull-in time and nondimensional pull-in center deflection of viscoelastic microbridge
Full size table

From the results presented in Fig. 4 and Table 2, it is noticed that the difference between linear and nonlinear responses of viscoelastic microbridge becomes more significant at large values of the initial gap. Also, at large initial gaps, including the nonlinear mid-plane stretching effect may drive the microbridge to behave in the durable region instead of the unstable one. It is also detected that for large initial gaps and applied voltages, the nondimensional pull-in time and nondimensional pull-in center deflection are underestimated while the nondimensional instantaneous center deflection (at \(t = 0\)) is overestimated when the mid-plane stretching effect is neglected, i.e. \(d_{0} = 1\,\upmu{\text{m}}\). If the microbridge behaves in the stable region for both linear and nonlinear analysis (\(d_{0} = 1\,\upmu{\text{m}}\) and \(V = 29 {\text{V}}\)), a remarkable decrease in the nondimensional steady-state time and nondimensional steady-state deflection is obtained when the mid-plane stretching is considered.

4.2.2 Effect of residual stresses

Depending on the fabrication sequences of the MEM actuators, the residual stresses can be tensile or compression, Kahn and Heuer [56]. Figure 5 illustrates the variation of the instantaneous and durable pull-in voltages of viscoelastic microbridge with the residual stress considering the fringing field effect when \(d = 0.15\,\upmu{\text{m}}\), \(l/h = 0.25\) and \(C_{\text{vdW}} = C_{\text{C}} = C_{\text{S}} = 0\). It is clear that increasing the residual stress from compressive towards tensile direction results in a significant increase in both instantaneous and durable pull-in voltages of the microbridge. Consequently the size of the stable region is increased, whilst the sizes of the durable and unstable regions are decreased. This is because that the tensile residual stress stiffens microbridges but conversely compressive residual stress softens them. Also, it is worth noting that varying the compressive residual stress has a more pronounced influence on the pull-in voltages rather than varying the tensile residual stress. As the residual stress is varied from −3.2 to −20 MPa, the instantaneous and durable pull-in voltages are decreased by 18.18 and 35.09% respectively. Changing the residual stress from 4 to 20.8 MPa shows a 13.22 and 20.61% increase in the instantaneous and durable pull-in voltages, respectively.

Fig. 5
figure 5

Instantaneous and durable pull-in voltages of viscoelastic microbridge for various residual stresses when \(C_{\text{vdW}} = C_{\text{C}} = C_{\text{S}} = 0\)

Full size image

Effect of the residual stress on the creep of the nondimensional center deflection of viscoelastic microbridge is shown in Fig. 6 and selected values of the nondimensional pull-in time and pull-in center deflection for various residual stresses are provided in Table 3. It is clear that as the tensile residual stress is increased, the nondimensional steady-state (durable) center deflection and time required to reach it are significantly decreased; this response is represented by the solid lines in Fig. 6 and the values appear with parentheses in Table 3. From the obtained results, it is noticed that compressive residual stress shows a distinct increase in the nondimensional instantaneous center deflection, while the nondimensional pull-in time and corresponding nondimensional pull-in center deflection are obviously decreased. In other words, compressive residual stress makes the microbridge state to be converted from the stable region to the durable or invisible one.

Fig. 6
figure 6

Creep of the nondimensional center deflection of viscoelastic microbridge at different residual stresses when \(C_{\text{vdW}} = C_{\text{C}} = C_{\text{S}} = 0\)

Full size image
Table 3 Effect of the residual stress on the nondimensional pull-in time and pull-in center deflection of microbridge when \(C_{\text{vdW}} = C_{\text{C}} = C_{\text{S}} = 0\)
Full size table

4.2.3 Effect of Casimir and vdW forces

Since the intermolecular forces are the spontaneous attractive forces between the flexible beam and the fixed substrate, the flexible beam will attach the fixed substrate even without an electrostatic attraction if the intermolecular Casimir and vdW forces reach certain critical values. It is clear from Eq. (36) that the Casimir and vdW parameters,\(C_{\text{C}}\) and \(C_{\text{vdW}}\) are inversely proportional to, respectively, the fourth and fifth power of the initial gap and both \(C_{\text{C}}\) and \(C_{\text{vdW}}\) are directly proportional to the fourth power of the beam length. Consequently, this section is intended to explore the effects of the intermolecular Casimir and vdW forces on the size-dependent pull-in stability by considering the following two case studies: (1) varying the initial gap d 0 while keeping other material and geometrical parameters as constants and (2) varying the beam length L while holding other material and geometrical parameters as constants. For both cases, the results are obtained for both viscoelastic microbridge and microcantilever with and without the effects of Casimir and vdW forces at \(l = 0.25h\) when the fringing field, mid-plane stretching and residual stress are neglected; i.e. \(C_{\text{F}} = C_{\text{S}} = C_{\text{R}} = 0\) .

Effect of the intermolecular Casimir and vdW forces on the instantaneous and durable pull-in voltages of viscoelastic microbridge and microcantilever is plotted in Fig. 7 for different values of the initial gap and Fig. 8 for various values of the beam length. As seen in Fig. 7, the instantaneous and durable pull-in voltages for both viscoelastic microbridge and microcantilever are decreased as the initial gap decreases. For a specific beam length, the difference between the critical initial gaps (\(d_{cr}\)) with and without considering intermolecular Casimir and vdW forces indicates the intermolecular forces significantly affect the value of the critical initial gap. Also, at small values of the initial gap \(\left( {d \le d_{cr} } \right)\), Casimir and vdW forces drive the microactuator to be collapsed at no time without applied voltage. It is evident in Fig. 8 that for both microbridge and microcantilever, increasing length of the microactuators results in a decrease in the instantaneous and durable pull-in voltages and consequently the region of stable response is decreased. For a constant initial gap, the maximum beam length such that the collapse will occur at no time at lengths just larger than it \(\left( {L \ge L_{D} } \right)\) in the absence of applied voltage, is known as the detachment length L D . It is clear that including the Casimir and vdW forces shows a remarkable decrease in the detachment length for both microbridge and microcantilever.

Fig. 7
figure 7

Effect of the intermolecular Casimir and vdW forces on the instantaneous and durable pull-in voltages at different initial gaps

Full size image
Fig. 8
figure 8

Effect of the intermolecular Casimir and vdW forces on the instantaneous and durable pull-in voltages at different lengths of the microbeam

Full size image

Moreover, it is detected that for viscoelastic microbridge and microcantilever, including the Casimir and vdW forces results in a noticeable decrease in the instantaneous and durable pull-in voltages. Also, it is observed that for large values of the initial gap or small values of the microactuator length, the pull-in voltage obtained with and without Casimir and vdW forces are identical. Comparing Fig. 7 with 8, it is found that the effect of decreasing the initial gap on the contribution of Casimir and vdW forces is more noticeable than that of increasing the microactuator length. Additionally, one can find that the effects of the initial gap and beam length are more pronounced for doubly-clamped microbridge.

Creep of the nondimensional pull-in center and tip deflections of the viscoelastic microbridge and microcantilever with and without the effect of Casimir and vdW forces is illustrated in Figs. 9–12. Figures 9 and 10 present the results for various initial gaps and Figs. 11 and 12 correspond to different values of beam length. Selected numerical values for the nondimensional pull-in time and crossponding nondimensional pull-in deflections with and without Casimir and vdW forces are provided in Tables 4 and 5 for various values of the initial gap and beam length, respectively.

Fig. 9
figure 9

Effect of Casimir and vdW forces on the creep of the nondimensional center deflection of viscoelastic microbridge at different initial gaps

Full size image
Fig. 10
figure 10

Effect of Casimir and vdW forces on the creep of the nondimensional tip deflection of viscoelastic microcantilever at different initial gaps

Full size image
Fig. 11
figure 11

Effect of Casimir and vdW forces on the creep of the nondimensional center deflection of viscoelastic microbridge at different microbeam lengths

Full size image
Fig. 12
figure 12

Effect of Casimir and vdW forces on the creep of the nondimensional tip deflection of viscoelastic microcantilever at different microbeam lengths

Full size image
Table 4 Effect of the Casimir and vdW forces on the nondimensional pull-in time and pull-in maximum deflection
Full size table
Table 5 Effect of the Casimir and vdW forces on the nondimensional pull-in time and pull-in maximum deflection
Full size table

According to the obtained results, for the same applied voltage, accounting for the intermolecular Casimir and vdW forces shows an increase in the nondimensional instantaneous deflection and a decrease in the nondimensional pull-in deflection, especially at small gap values or large lengths of the microactuator. This remark is for both viscoelastic microbridge and microcantilever.

At low applied voltages, the state of the beam lies in the stable region without and with the influence of Casimir or vdW forces (solid lines in Figs. 9–12 and values with parentheses in Tables 4 and 5) and both the viscoelastic instantaneous and durable (steady-state) deflections are significantly increased. However, the combined influence of Casimir and vdW forces may tend the microbeam to behave in the durable or invisible region instead of stable one and a remarkable increase in the instantaneous and pull-in deflections are detected. In the durable region, it is noted that the individual or combined effect of Casimir and vdW forces leads to a distinct decrease in the nondimensional pull-in time and nondimensional pull-in deflection. Consequently, ignoring the individual or combined effect of Casimir and vdW forces may lead to considerable errors in the estimation of the viscoelastic pull-in parameters.

Effects of the intermolecular Casimir and vdW forces on the pull-in are compared when investigating the pull-in instability parameters of viscoelastic microbridge and microcantilever, as shown in Tables 4 and 5. Interestingly, the contribution of Casimir and vdW forces depends on the type of boundary conditions of the microactuator besides the initial gap and microactuator length. For doubly-clamped microbridge, Casimir force has greater effect on the pull-in time pull-in maximum deflection than those of vdW force. In the case of clamped-free microactuator, the pull-in time, crossponding pull-in maximum deflection are highly influenced by vdW force rather than Casimir force. These contributions of Casimir and vdW forces are also detected to steady-state time and crossponding steady-state maximum deflection. However, the difference between effects of Casimir and vdW forces on the pull-in instability parameters increases as the initial gap decreases and length of the microactuator increase

4.2.4 Effect of the durable modulus

Since the residual stress, Casimir and vdW parameters, \(C_{\text{R}}\), \(C_{\text{C}}\) and \(C_{\text{vdW}}\), respectively, depend on the initial Young’s modulus \(E_{0}\). Investigating the effect of the durable modulus of elasticity \(\left( {E_{1} } \right)\) on the viscoelastic pull-in response is performed considering the simultaneous effect of microstructure, electric forcing including fringing field, mid-plane stretching, residual stress and Casimir and vdW forces. The geometrical and material parameters of the viscoelastic microbridge and microcantilever are taken as those stated in Sect. 4.2 except \(E_{1}\) is varied in the range from \(0.2E_{0}\) to \(0.75E_{0}\). Figure 13 illustrates the effect of nondimensional durable modulus \(\bar{E}_{1} = E_{1} /E_{0}\) on the instantaneous and durable pull-in voltages of viscoelastic microbridge and microcantilever. For both microbridge and microcantilever, it is noticed that there is no effect of \(\bar{E}_{1}\) on the instantaneous pull-in voltage and so the size of the invisible (unstable) region is unchanged by varying \(\bar{E}_{1}\). On the contrary, as \(\bar{E}_{1}\) increases, the durable pull-in voltage is significantly increased and therefore a noticeable increase and decrease in the stable and durable regions, respectively, are obtained.

Fig. 13
figure 13

Effect of the nondimensional durable modulus \(\bar{E}_{1}\) on the viscoelastic instantaneous and durable pull-in voltages

Full size image

Creep of the nondimensional center and tip deflections of microbridge and microcantilever is shown, respectively, in Figs. 14 and 15 for various values of \(\bar{E}_{1}\). Effect of \(\bar{E}_{1}\) on the nondimensional pull-in time and corresponding nondimensional maximum deflection is provided in Table 6. Again, it is noticeable that \(\bar{E}_{1}\) has no effect on the instantaneous deflection for all applied voltages. In the stable region (solid lines in Figs. 14 and 15 and values with parentheses in Table 6), the time required to attain the steady-state response (\(t_{ss}\)) and crossponding steady-state deflection (\(w_{ss}\)) are distinctly increased by decreasing \(\bar{E}_{1}\). Moreover, in the durable region, decreasing \(\bar{E}_{1}\) leads to a significant decrease in the pull-in time (\(t_{PI}\)), while the predicted pull-in deflection (\(w_{PI}\)) is negligibly changed. This is because of the decrease in the beam rigidity by decreasing \(\bar{E}_{1}\).

Fig. 14
figure 14

Effect of the nondimensional durable modulus \(\bar{E}_{1}\) on the creep of the nondimensional center deflection of viscoelastic microbridge

Full size image
Fig. 15
figure 15

Effect of the nondimensional durable modulus \(\bar{E}_{1}\) on the creep of the nondimensional tip deflection of viscoelastic microcantilever

Full size image
Table 6 Effect of the nondimensional durable modulus \(\bar{E}_{1}\) on the nondimensional pull-in time and pull-in maximum deflection
Full size table

4.2.5 Effect of the relaxation time

Effect of the nondimensional relaxation time \(\bar{\varPsi } = 1/\bar{\varPsi }\) on the creep response of maximum deflections of viscoelastic microbridge and microcantilever is plotted in Figs. 16 and 17, respectively, accounting for the combined influences of microstructure, electric forcing including fringing field, mid-plane stretching, residual stress and Casimir and vdW forces. All geometrical and material parameters of the beams are the same as those stated in Sect. 4.2 except \(\bar{\varPsi }\) is varied in the range from 0.05 to 100. The nondimensional pull-in time and corresponding maximum deflection are displayed in Table 7 for different values of the relaxation time. It is depicted that as the relaxation time tends to zero (\(\bar{\varPsi }\) tends to \(\infty\)), the predicted response is exactly identical with elastic one and the microbeam reaches its final response at almost no time (i.e. at \(\bar{\varPsi } = 0.01:\) \(t_{ss} = 0.121\) for microbridge at \(V = 1.25 {\text{V}}\) and \(t_{ss} = 0.198\) for microcantilever at \(V = 0.3 {\text{V}}\)). Also, the results show that there is no effect of the relaxation time on the instantaneous and final (steady-state or pull-in) deflection. In other words, both instantaneous and durable pull-in voltages are unaffected and consequently the microactuator response is unchanged from one region to another (stable, durable and unstable) by varying \(\bar{\varPsi }\).

Fig. 16
figure 16

Effect of the nondimensional relaxation time \(\bar{\varPsi }\) on the creep of the nondimensional center deflection of viscoelastic microbridge

Full size image
Fig. 17
figure 17

Effect of the nondimensional relaxation time \(\bar{\varPsi }\) on the creep of the nondimensional tip deflection of viscoelastic microcantilever

Full size image
Table 7 Effect of the nondimensional relaxation coefficient \(\bar{\varPsi }\) on the nondimensional pull-in time and pull-in maximum deflection
Full size table

The crucial role of the relaxation time is that it controls the time required to reach the final response of the microactuator; i.e. for a constant applied voltage, increasing the nondimensional relaxation time, the required time to attain the final response is increased. Interestingly, for the same applied voltage, the time required to reach the final response is almost directly proportional to the nondimensional relaxation time.

4.2.6 Effect of the length scale parameter (size effect)

To study the size effect induced by couple-stress, effect of the nondimensional material length scale parameter on the instantaneous and durable pull-in voltages, creep of the maximum deflection, pull-in time and pull-in deflection are investigated in the presence of the fringing field, mid-plane stretching, residual stress and Casimir and vdW forces. The viscoelastic material and geometrical parameters of microbridge and microcantilever are the same as those described in Sect. 4.2 except the nondimensional length scale parameter \(l/h\) is ranged from 0 to 1.

The instantaneous and durable pull-in voltages predicted by the present model (with size effect) are compared with the corresponding ones by the classical model (without size effect) as illustrated in Fig. 18. As could be seen in this figure, increasing the size scale \(l/h\) shows a significant increase in both instantaneous and durable pull-in voltages while the classical theory \(\left( {l = 0} \right)\) yields constant pull-in voltages. For large values of the size scale \(l/h\), a significant difference between pull-in voltage predicted by the MCST and classical beam theory is obtained. For small size scales \(l/h\), the results of MCST theory converge to those of classical theory. This behavior is attributed to that the microstructure effect (size effect) which presented by the material length scale parameter is modeled by an additional contribution on the rigidity of the microbeam.

Fig. 18
figure 18

Effect of the nondimensional material length scale parameter \(l/h\) on the viscoelastic instantaneous and durable pull-in voltages

Full size image

Figures 19 and 20 show, respectively, size dependency of the creep of the nondimensional center and tip deflections of microbridge and microcantilever by considering different \(l/h\). Table 8 gives some numerical values of the nondimensional pull-in time and crossponding nondimensional maximum deflection at various values of \(l/h\). According to these results, at a given applied voltage the nondimensional instantaneous deflection is distinctly decreased by increasing the size scale \(l/h\) due to the fact that increase of \(l/h\) increases the microbeam rigidity.

Fig. 19
figure 19

Effect of the nondimensional material length scale parameter \(l/h\) on the creep of the nondimensional center deflection of viscoelastic microbridge

Full size image
Fig. 20
figure 20

Effect of the nondimensional material length scale parameter \(l/h\) on the creep of the nondimensional tip deflection of viscoelastic microcantilever

Full size image
Table 8 Effect of the nondimensional material length scale parameter \(l/h\) on the nondimensional pull-in time and pull-in maximum deflection
Full size table

Also, it is worth noting that the viscoelastic pull-in response is size dependent. As the size scale \(l/h\) increases, the state of the microactuator may be changed from the unstable or durable region to the stable one. If the microbeam behaves in the stable region, increasing size scale \(l/h\), the time required to reach the steady-state response (\(t_{ss}\)) and crossponding steady-state maximum deflection (\(w_{ss}\)) are noticeably decreased and the creep rate of the maximum deflection is increased (at \(V = 1.3 {\text{V}}\) and \(V = 0.35 {\text{V}}\) for microbridge and microcantilever, respectively when \(l/h \ge 0.5\)). On the other hand, at large applied voltage (\(V = 1.5 {\text{V}}\) and \(V = 0.5 {\text{V}}\) for microbridge and microcantilever, respectively), the region of the microactuator is changed from unstable region to durable or stable one by increasing the size scale \(l/h\).

5 Conclusions

This paper investigates the size-dependent pull-in instability of nonlinear viscoelastic microcantilevers and microbridges subjected to the simultaneous effects of electrostatic actuation including fringing field, intermolecular Casimir and vdW forces, residual stress and mid-plane geometrical nonlinearity. Size effect is captured by employing the MCST in the context of linear viscoelasticity. The nonlinear integro-differential equation and boundary conditions of viscoelastic microactuators are established using the extended Hamilton principle in conjunction with Bernoulli–Euler beam theory. A modified generalized differential integral quadrature (GDIQ) method is developed for solving the governing equation together with boundary conditions. Both quasi-elastic and fully-viscoelastic solutions are obtained. The proposed model is verified against elastic and viscoelastic benchmarks and a very good agreement with previous published results is obtained. Effects of the various material and geometrical parameters on the size-dependent pull-in instability parameters of viscoelastic microbridge and microcantilever are discussed in detail in the framework of the MCST and linear viscoelastic theory. It can be concluded that:

  • The viscoelastic microbridge nonlinear model considering the mid-plane stretching effect gives smaller instantaneous and durable pull-in voltages than those of linear model. Also, accounting for the mid-plane stretching effect shows a distinct increase in the pull-in time and pull-in center deflection, while a significant decrease in the steady-state (durable) center defection and crossponding durable time is detected. Generally, the mid-plane stretching effect is increased as the initial gap increases.

  • Accounting for the tensile residual stress causes an increase in the instantaneous and durable pull-in voltages of the viscoelastic microbridge. Tensile residual stress shows a decrease in the durable center defection and durable time. On the other hand, compressive residual stress has opposite effects.

  • The neglect of intermolecular Casimir and/or vdW forces may result in an overestimation of pull-in parameters of viscoelastic microbridges and microcantilevers. Such overestimation becomes much crucially with decreasing the initial gap and increasing the microactuator length. The instantaneous maximum deflection is underestimated while the pull-in time and crossponding pull-in maximum deflection are overestimated when the intermolecular forces are ignored.

  • Comparing the influences of Casimir and vdW forces shows that, in the case of microbridge, Casimir force has the dominant influence on the parameters of pull-in instability, while vdW force becomes the dominant in the case of microcantilever.

  • Accounting for the intermolecular forces leads to an increase in the minimum critical gap and a decrease in the detachment length of the viscoelastic microactuators.

  • Without or with considering intermolecular forces, decreasing the initial gap or increasing the microactuator length shows a remarkable reduction in the instantaneous and durable pull-in voltages, pull-in time and pull-in maximum deflection while a significant increase in the steady-state time and crossponding maximum deflection is obtained.

  • Increasing the durable modulus of the microactuator shows increases in the durable pull-in voltage, steady-state time and crossponding maximum deflection, a distinct decrease in the pull-in time, a slight decrease in the pull-in maximum deflection and no effect on the instantaneous pull-in voltage and instantaneous deflection.

  • Sizes of stable, durable and unstable regions of the microactuator behavior are unaffected by varying the microactuator relaxation time. The time elapsed by the microactuator to attain the steady-state or pull-in response is almost linearly proportional to the relaxation time.

  • As the size scale parameter increases, the instantaneous and durable pull-in voltages are significantly increased. In the durable region, the pull-in time is obviously increased and the pull-in maximum deflection is slowly increased as the size scale parameter increases. Regardless the region of behavior, a pronounced decrease in the instantaneous deflection is detected by increasing the size effect.