Application of Bayesian Generative Adversarial Networks to Geological Facies Modeling

Abstract

Geological facies modeling is a key component in exploration and characterization of subsurface reservoirs. While traditional geostatistical approaches are still commonly used nowadays, deep learning is gaining a lot of attention within geoscientific community for generating subsurface models, as a result of recent advance of computing powers and increasing availability of training data sets. This work presents a deep learning approach for geological facies modeling based on generative adversarial networks (GANs) combined with training-image-based simulation. In a typical application of learned networks, all neural network parameters are fixed after training, and the uncertainty in the trained model cannot be analyzed. To address this problem, a Bayesian GANs (BGANs) approach is proposed to create facies models. In this approach, a probability distribution is assigned to the neural parameters of the BGANs. Only neural parameters of the generator in BGANs are assigned with a probability function, and the ones in the discriminator are treated as fixed. Random samples are then drawn from the posterior distribution of neural parameters to simulate subsurface facies models. The proposed approach is applied to the two different geological depositional scenarios, fluvial channels and carbonate mounds, and the generated models reasonably capture the variability of the training/testing data. Meanwhile, the model uncertainty of learned networks is readily accessible. To fully sample the spatial distribution in the training image set, a large collection of samples of network parameters is required to be drawn from the posterior distribution, thus significantly increasing computational cost.

1 Introduction

Modeling rock types, lithologies, or facies is a crucial step for the prediction and development of subsurface resources, such as groundwater and hydrocarbons, as well as for the storage potential of waste carbon dioxide in deep geological formations. The spatial distribution of facies and their connectivity affects fluid flow simulations (Laloy et al. 2018; Liu et al. 2019; Conjard and Grana 2021; Loe et al. 2021; Strebelle 2021). Therefore, accurate prediction of facies and quantification of their spatial distribution are required for precise flow simulations. Many geostatistical algorithms have been proposed for the generation of geological facies models (Mariethoz and Caers 2014; Pyrcz and Deutsch 2014; Grana et al. 2021) including variogram-based simulations (Chilès and Delfiner 1999), multiple-point statistics (Strebelle 2002), object-based methods (Michael et al. 2010), and process-based approaches mimicking depositional processes (Cojan et al. 2005).

In recent years, owing to the increasing availability of large data sets and constantly improving computing power, deep learning has drawn considerable interest among geoscientists to automate various modeling tasks, including inversion and classification problems. One of the most popular methods is generative adversarial networks (GANs) (Goodfellow et al. 2014), which can be trained to reproduce complex spatial patterns. For this reason, GANs have been applied to subsurface modeling to mimic spatial connectivity in porous rocks, especially in fractured rocks where the fracture network controls fluid flow (Dana et al. 2020; Ushijima-Mwesigwa et al. 2021), as well as in the depositional processes for the reconstruction of geological bodies (Dupont et al. 2018; Zhang et al. 2019; Azevedo et al. 2020). In the GANs framework, two network sub-models of generator and discriminator compete with each other in a game theory setting, such that new realistic images are stochastically simulated by the generator from the latent space distribution and are then judged by the discriminator as “real” or “fake” (Goodfellow et al. 2014). The goal of the generator is to generate images as realistic as possible, whereas the discriminator is aimed to distinguish those generated images from the real input. After an iterative training process, only the generator is used for the simulation. Several applications of GANs to geoscience problems have been presented in recent years. Mosser et al. (2017) apply GANs to reconstruct representative samples of porous media for the evaluation of variability in multiphase flow properties. Chan and Elsheikh (2019) investigate GANs for subsurface flow problems and generate multiple realizations of a binary variable representing channels. Tahmasebi et al. (2020) discuss the most recent advances of GANs and other machine learning algorithms in earth and environmental sciences. Progressive growing of GANs has been used for conditional simulation of facies realizations conditioned to global parameters and sparse pointwise hard data (Song et al. 2021a), as well as spatially distributed low-resolution soft data (Song et al. 2021b). Such trained GANs models have also been applied in many other geoscience research areas, including seismic inversion (Laloy et al. 2019; Mosser et al. 2020), reservoir modeling (Mosser et al. 2019; Zhong et al. 2021), and remote sensing (Cui et al. 2019; Rongier et al. 2020).

However, the aforementioned works on GANs only draw random samples from the target distribution of the training data, and do not include a rigorous analysis of the model uncertainty, as neural parameters are fixed after training, and thus the model uncertainty cannot be assessed. Uncertainty analysis is often required for decision making and risk reduction (Caers 2018). To obtain an uncertainty quantification in the context of geological modeling using GANs, the inversion and/or modeling problems can be probabilistically formulated. A probability distribution of the model parameters of interest is then defined, according to the classical Bayesian inference (Mosegaard and Tarantola 1995). By combining the prior information with the likelihood of measured data, the conditional posterior distribution of the model parameters is then derived, although analytical solutions are not always available for multimodal variables and non-linear problems. In some special cases, for example, when the forward model can be linearized, and the prior and model error are assumed to be Gaussian, then an analytical formulation of the posterior distribution can be derived with explicit expressions for means and covariance matrices, as discussed by Buland and Omre (2003), and Grana (2016). Otherwise, sampling algorithms such as Markov chain Monte Carlo (McMC) can be applied to draw random samples from the desired target distribution (Sambridge and Mosegaard 2002). The variational inference method can also be used to approximate those intractable posterior distributions as well, in which a Gaussian function is typically assumed for its simplicity (Blei et al. 2017).

Alternatively, a Bayesian interpretation of deep learning can be proposed to combine deep learning and probabilistic formulations (Ghahramani 2015). Rather than treating neural variables as fixed values, the estimation of model parameters in Bayesian networks amounts to the calculation of the posterior distribution of variables given observed or training data, assuming probability distribution of the neural parameters. According to this approach, the uncertainty analysis of the designed model is then built within the architecture of deep learning. The representation power of hierarchical networks is therefore leveraged to solve complex tasks, while the multimodal posterior distribution of model parameters can be inferred as well (Kendall et al. 2015). Many strategies have been developed to analyze uncertainty in the learned neural models. For example, Gal et al. (2017) propose the so-called concrete dropout approach, an extension of the Monte Carlo dropout strategy, requiring no hyper-parameter tuning of the associated dropout probabilities. Deep ensembles (Lakshminarayanan et al. 2017) is another approach for estimating model uncertainty by combining predictions from an ensemble of separately trained deep networks. A variational scheme is adopted by Feng et al. (2021a, b) to approximate the intractable posterior distribution of neural parameters, and the Bayesian learning is then formulated as an optimization process. McMC techniques have also been applied in Bayesian deep learning to draw samples from the space of parameters of interest. Saatchi and Wilson (2017) present Bayesian GANs (BGANs) to address the mode collapse problem in order to stabilize the training of GANs by allowing the network to learn parameter distribution over possible values. Metropolis–Hastings GANs (MH-GANs) are introduced by Turner et al. (2019) for sampling from the distribution implicitly defined by the network pair of discriminator and generator in GANs. In this research, a BGANs approach is proposed for the simulation of subsurface models, in which samples are drawn from the posterior distribution of the generator neural parameters, while the neural parameters in the discriminator are fixed. The trained generator with posterior samples can then be used to generate model realizations.

First the theory of BGANs is described; then the proposed method is applied to two case studies for different geological environments, namely channels and mounds. The simulated results are compared to traditional GANs where neural parameters are fixed without assigning any distribution.

2 Methodology

2.1 Traditional GANs

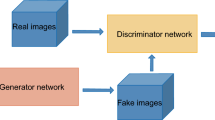
GANs represent a family of deep learning algorithm where the network architecture is made of two distinct components: a generator ($G$) and a discriminator ($D$) (Goodfellow et al. 2014), as schematically shown in Fig. 1. The generator and the discriminator are themselves deep neural networks with various architectures. The generator aims to generate realistic models from the random input or latent vector, which is a set of random samples drawn from a predefined distribution (Fig. 1). These models are then tested by the discriminator, which determines whether these models are consistent with the training data or a random model from the generator. This is equivalent to the approaches used in image recognition for the discrimination of real and fake images. By adopting this adversarial approach, the generator and discriminator can improve in their individual tasks incrementally. After the learning procedure, the target distribution of the models of interest is implicitly approximated (Goodfellow et al. 2014). In facies modeling (Fig. 1), the generator aims to learn the knowledge about the geological structures and distribution patterns, and the discriminator tries to distinguish fake images from real models in the training process (Song et al. 2021a). Generally, a large number of training data is required to train GANs, to include all the available geological information in the study area. In this application, the training data are composed of subsurface facies models that are generated using geostatistical methods (Fig. 1).

Fig. 1

Schematic high-level architecture of GANs model in which the generator and the discriminator are trained in a competitive formulation

The loss function $J\left(D,G\right)$ is an energy-like function and in GANs (Goodfellow et al. 2014) it is given by

$$ \mathop {\min }\limits_{G} \mathop {\max }\limits_{D} J\left( {D,G} \right) = \overbrace {{E_{x} \left[ {\log D\left( x \right)} \right]}}^{{{\mathcal{L}}_{1} :{\text{true}}\,{\text{given}}\,{\text{images}}}} + \overbrace {{E_{z} \left[ {\log \left( {1 - D\left( {G\left( z \right)} \right)} \right)} \right]}}^{{{\mathcal{L}}_{2} :{\text{generated}}\,{\text{fake}}\,{\text{images}}}}, $$

(1)

in which $D(x)$ outputs the probability of a sample $x$ being from the training data (the training image set); $G(z)$ represents the function performed by the generator to map the latent vector $z$ to the data space of interest with $z$ being sampled from a predefined distribution. As $G$ tries to learn the distribution of the training data, $D(G\left(z\right))$ is the probability that the image generated by $G$ is deemed "real", and therefore consistent with the training data. Hence, in Eq. (1), a two-player minimax game is played by $D$ and $G$, where $D$ aims to maximize ${\mathcal{L}}_{1}$ so that it can correctly classify real images as authentic, and $G$ aims to minimize ${\mathcal{L}}_{2}$ by increasing $D(G\left(z\right))$ such that $D$ fails to predict fake images (Goodfellow et al. 2014).

2.2 Bayesian GANs

The neural parameters in GANs are commonly fixed after training, and there is no information about the model uncertainty (Fig. 2a). Instead, a probability distribution over neural parameters can be introduced according to the Bayesian theory (Mosegaard and Sambridge 2002). In this context, BGANs can be regarded as a probabilistic model (Fig. 2b). The distributions of neural parameters of BGANs are learned from the training data, and the uncertainty in the learned model can be analyzed, extending the formulation of the traditional GANs to the Bayesian framework (Saatchi and Wilson 2017).

Fig. 2

a Transposed-convolutional process with fixed weight values in the kernel; b Bayesian networks with independent probability distribution assigned over neural parameters in the transposed-convolutional kernel

In Bayesian deep learning, the probability of new prediction $y$ is computed, given the unseen sample $z$ and training data $X$. A general probabilistic formulation for the network prediction is defined as

$$ p\left( {y{|}z,X} \right) = \int {p\left( {y{|}z,\theta } \right)p(\theta |X)} {\text{d}}\theta , $$

(2)

by integrating over all possible values of $\theta$ (Gal et al. 2017; Feng et al. 2021a), where $p(\theta |X)$ is the posterior distribution of neural parameter $\theta$ of interest, given $X$ (Fig. 3). Under the BGANs framework for the generation problems, $z$ is a set of samples drawn from the latent space distribution, and $y$ is a predicted sample from the distribution of the training data $X$, or more specifically $p\left(y|z,X\right)\sim p\left(X\right)$. Furthermore, BGANs can also be used for classification applications where only the discriminator is kept after training, with $z$ being the input features from unseen data.

Fig. 3

Schematic view for the posterior distribution of neural parameters $p(\theta |X)$, given the training data $X$. Each sample drawn from $p(\theta |X)$ could generate different plausible subsurface models in the generative applications by BGANs

In GANs, there are two parameter sets, ${\theta }_{\mathrm{g}}$ and ${\theta }_{\mathrm{d}}$, with pointwise estimates, corresponding to the generator and discriminator networks, respectively. In BGANs, these parameters are assigned with distribution functions and are predicted in the learning process. Let $p({\theta }_{\mathrm{g}}|X)$ and $p({\theta }_{\mathrm{d}}|X)$ denote the posterior distribution of generator and discriminator parameters, given the training data $X$, respectively. In practice, as proposed by Saatchi and Wilson (2017), the conditional posterior distribution of the neural parameters ${\theta }_{\mathrm{g}}$ and ${\theta }_{\mathrm{d}}$ can be iteratively sampled from the following distributions

$$ p\left( {\theta_{{\text{g}}} {|}Z,\theta_{{\text{d}}} } \right) \propto \mathop \prod \limits_{i = 1}^{{n_{{\text{g}}} }} D\left( {G\left( {z_{i} ;\theta_{{\text{g}}} } \right);\theta_{{\text{d}}} } \right) \times p_{0} \left( {\theta_{{\text{g}}} } \right), $$

(3)

$$ p\left( {\theta_{{\text{d}}} {|}Z,X,\theta_{{\text{g}}} } \right) \propto \mathop \prod \limits_{i = 1}^{{n_{{\text{d}}} }} D\left( {x_{i} ;\theta_{{\text{d}}} } \right) \times \mathop \prod \limits_{i = 1}^{{n_{{\text{g}}} }} \left( {1 - D\left( {G\left( {z_{i} ;\theta_{{\text{g}}} } \right);\theta_{{\text{d}}} } \right)} \right) \times p_{0} \left( {\theta_{{\text{d}}} } \right), $$

(4)

where ${p}_{0}\left({\theta }_{\mathrm{g}}\right)$ and ${p}_{0}\left({\theta }_{\mathrm{d}}\right)$ are the prior distributions of ${\theta }_{\mathrm{g}}$ and ${\theta }_{\mathrm{d}}$, respectively; ${n}_{\mathrm{g}}$ and ${n}_{\mathrm{d}}$ are the number of minibatches in the generator and discriminator; $X={\left\{{x}_{i}\right\}}_{1}^{{n}_{\mathrm{d}}}$ consists of the training data; ${z}_{i}$ is the ith latent vector drawn from a predefined distribution.

Equations (3) and (4) can be intuitively interpreted as Bayesian posterior distributions. In Eq. (3), the generator attempts to outperform the discriminator, and the product of the output probabilities of the discriminator is maximized, leading to increasing posterior probability $p\left({\theta }_{\mathrm{g}}|Z,{\theta }_{\mathrm{d}}\right)$ (Saatchi and Wilson 2017). A similar scenario can be observed for the discriminator in Eq. (4): when $D\left({x}_{i};{\theta }_{\mathrm{d}}\right)=1$, a true sample is correctly recognized by the discriminator, whereas if $D\left(G\left({z}_{i};{\theta }_{\mathrm{g}}\right);{\theta }_{\mathrm{d}}\right)=0$, the discriminator successfully catches the generator.

In addition, the update of GANs is implicitly conditioned on a set of latent samples from random noise $Z$, for the generation of model realizations (Goodfellow et al. 2014; Saatchi and Wilson 2017). In BGANs, the random noise $Z$ can be further marginalized from the posterior updates of generator and discriminator, using Monte Carlo integration as follows

$$ p\left( {\theta_{{\text{g}}} {|}\theta_{{\text{d}}} } \right) = \int {p\left( {\theta_{{\text{g}}} ,Z{|}\theta_{{\text{d}}} } \right)} {\text{d}}Z = \int {p\left( {\theta_{{\text{g}}} {|}Z,\theta_{{\text{d}}} } \right)p\left( {Z{|}\theta_{{\text{d}}} } \right)} {\text{d}}Z \approx \frac{1}{{J_{{\text{g}}} }}\mathop \sum \limits_{j = 1}^{{J_{{\text{g}}} }} p\left( {\theta_{{\text{g}}} {|}z_{j} ,\theta_{{\text{d}}} } \right), $$

(5)

where $p\left(Z|{\theta }_{\mathrm{d}}\right)={p}_{Z}(z)$, since random samples are not dependent on the discriminator, and ${z}_{j}\sim {p}_{Z}(z)$, by performing random sampling from the predefined marginal distribution of the latent vector, typically standard normal distribution $\mathcal{N}(\mathrm{0,1})$ (Saatchi and Wilson 2017; You et al. 2018). The Monte Carlo method in Eq. (5) is used to approximate the expectation of random variable $p\left({\theta }_{\mathrm{g}}|Z,{\theta }_{\mathrm{d}}\right)$, with respect to a given density function of $p\left(Z|{\theta }_{\mathrm{d}}\right)$. According to the same approach

$$ p\left( {\theta_{{\text{d}}} {|}\theta_{{\text{g}}} } \right) \approx \frac{1}{{J_{{\text{d}}} }}\mathop \sum \limits_{j = 1}^{{J_{{\text{d}}} }} p\left( {\theta_{{\text{d}}} {|}z_{j} ,X,\theta_{{\text{g}}} } \right). $$

(6)

In Eqs. (5) and (6), ${J}_{\mathrm{g}}$ and ${J}_{\mathrm{d}}$ are the number of noise samples in the integration process. Each sample in the Monte Carlo sum contributes to the estimate of the marginal posterior realizations. If uniform priors are assumed for ${\theta }_{\mathrm{g}}$ and ${\theta }_{\mathrm{d}}$, the proposed approach in Eqs. (3) and (4) then reduces to the classical GANs described by Goodfellow et al. (2014). By sampling from the distribution in Eq. (5), the posterior distribution of generator neural parameters is approximated, and a collection of multimodal generators is acquired. All these generators can simulate plausible models that are consistent with the training data. Similar to GANs, the loss function in Eq. (1) is used in BGANs as well, since the posterior neural parameters of ${\theta }_{\mathrm{g}}$ and ${\theta }_{\mathrm{d}}$ have the same role as those in GANs. Equation (2) is the general formulation of the trained BGANs for the model simulation. The posterior distribution of neural parameters $p(\theta |X)$ is derived explicitly in Eqs. (3)–(5). For classification problems, Eq. (6) can be used, but this application is beyond the scope of the current work.

In practical applications, the training data set and latent samples are split into small subsets of equal size (minibatches) over which the error gradient is calculated, and model parameters are updated iteratively [Eqs. (3) and (4)] (Sra et al. 2011). In the context of Bayesian training, the Hamiltonian Monte Carlo method, or more specifically, its stochastic gradient approach for the efficiency of big data computation, namely stochastic gradient Hamiltonian Monte Carlo (SGHMC), is used for sampling and generating realizations of neural parameters from marginalized posterior distributions. SGHMC is closely related to the momentum-based stochastic gradient descent (SGD) that is often used for training GANs. The parameter settings of SGD with momentum can also be used in SGHMC as shown by Chen et al. (2014).

2.3 Network Structures

The design of network architecture is critical for a successful application of deep learning. As shown in Radford et al. (2015), deep convolutional GANs, a direct extension of GANs, provide a suitable network architecture for generating facies models in this study. Figure 4 shows the architecture of the GANs with transposed-convolutional (Deconv) and convolutional (Conv) layers in both the generator and discriminator. The same padding is used in the transposed-convolutional and convolutional layers, and the stride is equal to 2 for shifting the filters over the input volume. Each layer is followed by the rectified linear unit (ReLU) activation, and the output layers in the generator and discriminator apply the hyperbolic tangent (tanh) and sigmoid functions, respectively. The same network structure is used in the proposed BGANs as well. All other hyper-parameters such as learning rate and training epochs are kept the same for GANs and BGANs. However, in BGANs, only the generator neural parameters are assigned with a probability distribution, while the neural parameters in the discriminator are treated as point estimates. The prior distribution of the neural parameters is assumed to be Gaussian with zero mean and unit variance.

Fig. 4

Network architecture for the generator (a) and discriminator (b). The neural parameters of ${\theta }_{\mathrm{g}}$ and ${\theta }_{\mathrm{d}}$ are composed of weights and biases in the transposed-convolutional and convolutional filters, respectively

3 Application

In this section, the results of two case studies are presented, for the generation of facies realizations under different geological environments, namely channels and mounds. A comparison between BGANs and GANs is also presented using statistical criteria, spatial distribution plots and quality assessment metrics described in the Appendix.

3.1 Channel Model

The first application refers to a geological environment with a meandering channel system where the dynamic behavior of fluid flow strongly depends on the channel connectivity and shape. The SNESIM multiple-point statistics method is adopted to generate a set of 1,000 binary-facies models (channel sand and non-channel shale) from a conceptual model (Strebelle 2002; Hansen et al. 2018). These facies models are used in the following as training data. Furthermore, 1,000 additional models are generated by SNESIM as well, which are statistically similar to the training image set and are regarded as the testing data. These testing models are not used for training the neural parameters and are only used for a comparison of the generated images by trained networks. Figure 5 shows a subset of training and testing facies models.

Fig. 5

Subset of the training (a) and testing (b) data of dimension 80 $\times$ 80 cells. The white color represents the channel sand, and the background black is the non-channel shale

Figure 6 shows a subset of facies models generated by the trained BGANs (Fig. 3), in which five samples are drawn from the posterior distribution of neural parameters [Eqs. (3) and (5)], as represented by ${\theta }_{\mathrm{g}}^{i}$ ($i=1,\dots ,5$). For each posterior sample of BGANs, 1,000 latent vectors are randomly drawn from a standard normal distribution and are used as inputs for the simulation. By sampling different parameters of the generator, BGANs aim to explore different values of the distribution inferred from the training data, including configurations of parameters associated to higher-order statistics that describe the length, width, stacking and azimuthal direction of channels. For example, in Fig. 6, each posterior sample in BGANs is able to generate channels that have a similar azimuthal direction, given random input vectors.

Fig. 6

Subset of channel models generated by BGANs. Random vectors drawn from a standard Gaussian distribution (${z}_{i}, i=1,\dots ,5$) are used as inputs for the simulation

Unlike BGANs, five classical GANs are trained independently, where the neural weights are initialized differently according to a standard normal distribution $\mathcal{N}(\mathrm{0,1})$, based on the same training data (Fig. 5a). The trained generator in GANs is used to generate realizations of the channel models (Fig. 7), based on 1,000 randomly sampled latent vectors. However, the neural parameters in GANs are fixed as point estimates after training, and the model uncertainty of learned networks is not accessible. The generated channel models by each trained GANs are quite similar with each other (Fig. 7), for example, there is no difference in the azimuthal direction as seen in Fig. 6. It is noted that the input latent vectors are different for each simulation by GANs and BGANs, as they are randomly sampled from a standard normal distribution.

Fig. 7

Subset of channel models generated by GANs that have been trained independently with different sets of parameters (${\theta }_{\mathrm{g}i},i=1,\dots ,5$)

The univariate distributions of neural parameters in BGANs are displayed in Fig. 8. Specifically, the histograms in Fig. 8a–e show the weights $(w)$ of the second transpose layer of the Bayesian generator (Deconv_2 in Fig. 4a) in terms of five chart features. The uncertainty of the weight values in the five samples drawn from the posterior distribution strongly reduces (Fig. 8a–e), compared to the prior Gaussian model (Fig. 8f). Instead of showing the posterior samples for each neural weight, the five sets of samples for all the weights at the transpose layer are displayed individually, for the uncertainty analysis in the trained network system.

Fig. 8

Histograms of neural weights at the transpose layer of BGANs for five samples drawn from the posterior distribution (a–e), and the Gaussian prior of the neural weights (f)

Figure 9 shows the MDS plot with pairwise Euclidean distances (Appendix), in which the testing data set (Fig. 5b) and generated models (1,000 for each posterior sample) by trained generator in BGANs are plotted in the reduced-dimensional space for a similarity assessment. The results indicate a good similarity between the testing and generated data sets, as the transformed data points are scattered within the same region of the MDS space (Zhang et al. 2021). However, the models generated by the posterior samples of trained networks cannot fully cover the MDS space of the testing data, because only a fraction of the full variability of the training data is explored by each sample of the posterior distribution of generator parameters in BGANs.

Fig. 9

MDS plot of the testing data and channel models generated by five different posterior samples from the BGANs

Figure 10a shows the MDS plot of the ensemble simulation by BGANs, in which 200 generated models are randomly selected from each of the five sets of 1,000 models by BGANs and then merged together to make a new set of 1,000 realizations. The results (Fig. 10a) are generally consistent with the MDS plot obtained from one of the trained GANs; however, the latter one with neural parameters as point estimates shows a better variability with a wider coverage in the reduced data space (Fig. 10b).

Fig. 10

MDS plot of the ensemble simulation by the five samples of BGANs (a) and generated models by one of the trained GANs (b)

The binary facies proportions for channel and non-channel are shown in Fig. 11. The generated models by GANs and BGANs can successfully reproduce the facies histogram of the testing data. Figure 12 shows the semi-variogram, and the two-point relation in the testing data is reproduced by the trained networks as well, although these metrics are generally considered not enough to guarantee a pattern reproduction.

Fig. 11

Binary facies (channel and non-channel) proportion of testing data, GANs (${\theta }_{\mathrm{g}3}$), BGANs (${\theta }_{\mathrm{g}}^{3}$) and ensemble realizations (${\theta }_{\mathrm{g}}^{\mathrm{e}}$)

Fig. 12

Semi-variogram of testing data, GANs (${\theta }_{\mathrm{g}3}$), BGANs (${\theta }_{\mathrm{g}}^{3}$) and ensemble realizations (${\theta }_{\mathrm{g}}^{\mathrm{e}}$)

The SSIM metrics (Appendix) are computed between each pair of generated models, and then averaged to obtain a scalar index (black circles in Fig. 13), for a quantitative evaluation of the variability. SSIM values between each pair of testing data sets are also calculated to benchmark the performance of trained networks. The mean SSIM value for testing facies models (TD in Fig. 13) is around 0.2, which indicates that facies models in the testing data are different from each other. Generally, the mean SSIM values by BGANs are larger than that of testing data (Fig. 13a), suggesting that the generated models by each posterior sample from BGANs are less variable. The mean SSIM values of GANs are smaller than that of BGANs (Fig. 13), as the former one tends to cover better than BGANs in the MDS space (Fig. 10). However, some of the SSIM values are quite high, for example, the maximum values shown as top gray caps in Fig. 13, since a random pair from the facies models could be similar to each other.

Fig. 13

Range of SSIM values between each pair of generated models by (a) BGANs and (b) GANs. Gray caps are the maximum and minimum values of SSIM, and black caps represent the 95th and fifth percentile of SSIM range. Black circles are the mean SSIM values. SSIM between each pair from the testing data (TD) is also calculated for comparison

3.2 Mounds Model

The second example of the application by BGANs represents a geological scenario with mounds in subsurface reservoirs. Figure 14a shows a subset of the 1,000 models of dimension 80 $\times$ 100 cells, which are simulated by using SNESIM (Strebelle 2002; Hansen et al. 2018). The model assumes two facies: carbonate mounds (the reservoir facies) in white and background rocks in black (Zhang et al. 2021). This image set is used as training data for learning the network parameters. A subset of 1,000 testing images is displayed in Fig. 14b, which have similar statistics as the training data.

Fig. 14

Subset of the training (a) and testing (b) data of dimension 80 $\times$ 100 cells. White represents the carbonate mounds and black is the background facies

A subset of the facies realizations generated by BGANs is shown in Fig. 15. Different sets of realizations by each neural posterior sample reproduce various features of the training data. For instance, the first two sets (${\theta }_{\mathrm{g}}^{1}$ and ${\theta }_{\mathrm{g}}^{2}$) replicate the main geobodies in the upper part, whereas the last two sets (${\theta }_{\mathrm{g}}^{4}$ and ${\theta }_{\mathrm{g}}^{5}$) replicate the geobodies in the lower part of the interval. For comparison, Fig. 16 shows the facies models generated by GANs, for five independently trained sets of neural parameters. These facies models are used for the analysis of MDS plots, SSIM metrics and other statistics, compared to the testing data displayed in Fig. 14b, for an assessment of the generalization ability of the trained networks.

Fig. 15

Subset of mounds models generated by BGANs. Random vectors drawn from a standard Gaussian distribution, such as ${z}_{i}, i=1,\dots ,5$, are used as inputs for the simulation

Fig. 16

Subset of mounds models generated by GANs with different sets of parameters (${\theta }_{\mathrm{g}i},i=1,\dots ,5$) that are trained independently

The distribution of neural biases ($b$) at the second deconvolutional layer in BGANs is shown in Fig. 17, which has a similar feature as observed in Fig. 8. The values of posterior samples are highly compacted, centering around zero. The reason for this might be the fact that only five samples are drawn, making them not representative enough for the full posterior distribution, and only binary facies models are considered in this research.

Fig. 17

Distribution of neural biases in BGANs for five samples drawn from the posterior distribution (a–e), and the Gaussian prior of the neural biases (f)

The MDS plot of BGANs (Fig. 18) shows that the transformed data points of generated models cannot fully cover the full range of the testing data in the reduced-dimensional space, and only part of the diverse patterns in the training set is learned by each sample of the posterior distribution.

Fig. 18

MDS plot of the testing data and mounds models generated by five different posterior samples from the BGANs

Figure 19a shows the MDS plot of the ensemble realizations obtained with BGANs, whereas Fig. 19b shows the MDS plot obtained with GANs. In this case, the GANs models show a larger variability with wider coverage in the reduced space.

Fig. 19

MDS plot of the ensemble simulation by the five samples of BGANs (a) and generated models by one of the trained GANs (b)

Moreover, the facies histograms of testing data and generated models are shown in Fig. 20, from which it can be seen that the proportion values in the testing data have been correctly represented by the realizations of GANs and BGANs. The semi-variogram also shows that the two-point statistics in the testing data is well captured by the generated models (Fig. 21).

Fig. 20

Binary facies (carbonate and non-carbonate) proportion of testing data, GANs (${\theta }_{\mathrm{g}3}$), BGANs (${\theta }_{\mathrm{g}}^{3}$) and ensemble realizations (${\theta }_{\mathrm{g}}^{\mathrm{e}}$)

Fig. 21

Semi-variogram of testing data and different generated models

Figure 22 displays the mean SSIM values between each pair of simulated models by BGANs and GANs, respectively, which confirms the results discussed in Fig. 19, showing smaller mean values for GANs. It is also suggested that there is a less variability within the generated models by each posterior sample of BGANs, as larger mean SSIM values are observed, compared to that of testing data (Fig. 22a).

Fig. 22

Range of SSIM values between each pair of generated models by a BGANs and b GANs. The symbols used have the same meaning with the ones shown in Fig. 13

4 Discussion

It is worth reminding that the goal of this work is not to propose an alternative approach to SNESIM or other traditional geostatistical algorithms. The main purpose of this paper specifically is focused on testing and validating a systematic Bayesian framework for GANs to assess uncertainty of the trained model parameters, for example, the generator weights. SNESIM is used just as a convenient way to generate a plausible training/testing set. Any other methods could also have been used in its place. In actual applications there is no need to use GANs if a variogram-based geostatistical algorithm or a SNESIM-based approach is deemed to be sufficient. However, when they are not sufficient, then as shown in the literatures (e.g., Zhang et al. 2019, and others), GANs provide an alternative solution. Moreover, the proposed BGANs can be regarded as a fully Bayesian method to address the analysis of the model uncertainty by allowing the network to learn the probability distribution of the network parameters, as opposed to obtaining one generator and one discriminator with fixed estimates in GANs. The posterior distribution of the neural parameters in BGANs can be highly multimodal, with each posterior sample corresponding to different generators.

In this proposed work, BGANs and GANs share the same network architecture shown in Fig. 4. The training cost of BGANs is more computationally demanding than that of GANs, as the former one requires stochastic sampling. The GPU (graphics processing unit) in Google Colab (Bisong 2019) provides a free cloud computing platform for machine learning, and it is used in this application to run the network models that are built using TensorFlow, an open-source package in Python. For each application, the computational time is approximately 5 h for BGANs and 1 h for GANs with 6,000 epochs, a batch size of 100 and a learning rate of 0.01. After training, generating 1,000 model realizations takes about 30 s.

One of the limitations in the proposed approach is that the full sampling of the spatial distribution of the patterns in the training data requires an extremely large set of posterior network parameter samples, which would significantly increase the computational cost and demand more internal memory in GPU. Indeed, the MDS plots for a subset of five samples show that the distribution in the testing data has not been fully recovered by BGANs especially in the mounds model (Figs. 18 and 19). The generated models by each posterior sample can then be combined together to represent the full variability of the training data theoretically. Due to the limitation of computing memory in GPU, only a few samples are drawn from the posterior distribution. A large collection of posterior samples could be obtained when a graphics card is available with more storage capacity. Moreover, other cloud computing platforms such as Microsoft Azure or Amazon EC2 might also be used to train the neural networks, and they are still under investigation.

Compared to other approximate methods such as variational inference, a full posterior distribution of the neural parameters with many local optima can be explored by Monte Carlo sampling with explicit representation. Instead, variational inference is limited by the intractable posterior that must be approximated using Gaussian distributions, which limits the analysis of the uncertainty to only one of the posterior modes. Moreover, the Kullback–Leibler divergence used in variational approaches generally provides an overly compact expression of the unimodal distribution, which is caused by the biases from the distribution-wise asymmetric calculation (Gal et al. 2017; Saatchi and Wilson 2017). Alternative to the HMC sampling algorithm implemented in this study, rejection sampling could also be applied for sampling the posterior distribution. The rejection sampler requires an evaluation of the posterior distribution and an estimation of normalization constant that should be larger than or equal to the maximum posterior probability, when the uniform distribution is adopted as the proposal distribution (Hansen 2020). In practice, the rejection sampler is rarely used, since it is more applicable for low-dimensional problems where few model parameters are to be determined (Tarantola 2005; Hansen 2020). In total, there are about 4 million trainable parameters in the generator of GANs, and about 20 million trainable parameters in BGANs with five samples drawn from the posterior distribution. Furthermore, it is not trivial to choose the normalization constant as its value greatly influence the sampling efficiency or the acceptance ratio. For example, if the constant is chosen to be too large, the acceptance ratio becomes too small, leading to less efficient sampling; while it is set too low, the rejection algorithm is not sampling the desired posterior distribution (Hansen 2020).

The model parameter uncertainty is analyzed for the trained models, in which probability distributions are assigned to the neural parameters. After training, the posterior samples of the generator parameters can be used to evaluate the uncertainty in the trained model (Figs. 8 and 17). On the other hand, the variability of the generated facies models is discussed for the geological patterns within the facies models, and it is evaluated on the MDS plot (Figs. 10 and 19), as the projected points in the reduced space should be sparsely distributed, rather than centering to a small cluster, when there is a diverse pattern in the facies models.

To further demonstrate its feasibility and effectiveness, the proposed BGANs approach can be extended for the simulation of three-dimensional and multi-facies models where process- or object-based methods are needed to build the training facies data, but the computational cost of these applications is generally prohibitive. In particular, three-dimensional modeling by BGANs is computationally extremely demanding, as the number of trainable neural parameters significantly increases, since three-dimensional network filters have to be used to account for the dimension expansion in the training data. Additionally, the network structure should also be modified for the multi-facies modeling, for example, the softmax function is to be implemented in the generator output layer to normalize and map input vectors into probability distributions over potential classes.

The proposed BGANs approach can also be used for conditional sampling in interpolation, classification, and inverse problem settings, using direct observations at the well locations or indirect measurements such as seismic data. In these cases, the network systems could be post-processed such that the unconditional training is first performed, then latent vectors associated with models consistent with observed data are searched and retained using optimization or Markov chain Monte Carlo sampling (e.g., Nesvold and Mukerji 2019). The conditioning ability can also be implemented by introducing an extra loss function to account for the dissimilarity between the input conditioning data and output facies models from the trained network (Song et al. 2021a). Either of these approaches to conditioning can be incorporated in BGANs theoretically, and will be a focus of the future research.

In this study, the training process of BGANs is supervised, which means that the generator is forced to learn the spatial distributions and geological patterns from the training data. After training, the learned generator reproduces realistic facies models with random inputs being drawn from a Gaussian distribution. BGANs could also be used in a semi-supervised approach as well for classification problems where a large amount of unlabeled data is utilized to train the networks, and the neural parameters of discriminator could be assigned with probability functions for the uncertainty analysis of the learned model.

5 Conclusion

This research discusses the capability of deep learning to simulate subsurface models based on training data. In this context, BGANs are used to generate geological facies models, in which the neural parameters are assigned with probability distribution, rather than deterministic values as in classic GANs. A sequence of random samples is drawn using SGHMC to approximate the target posterior distribution. The expected values of the target distribution can be estimated from the Monte Carlo samples. The samples are realizations of the posterior distribution of the network parameters and can be used to assess the variability of the results. In this research, BGANs and GANs are applied using a training data set obtained by traditional geostatistical methods and compared to the geostatistical testing realizations for validation purposes. In practical applications, outcrop data or conceptual models can be used to build the training data set for BGANs.

Appendix: Quality Evaluation Metrics

To assess the variability and similarity between the generated and testing data, the technique of multidimensional scaling (MDS) is used to reduce the high-dimensional problem to a low-dimensional data space while preserving similarity measure for comparison (Cox and Cox 2008). The MDS-transformed data points are unitless and can be plotted in the common Cartesian space. The main steps in the classical MDS algorithm are summarized as follows: (i) setup of the squared proximity matrix with Euclidean distance and double centering; (ii) determination of the first largest eigenvalues and corresponding eigenvectors of the double-centered matrix; (iii) calculation of the object coordinates in the new space (Cox and Cox 2008). The variability and similarity can be evaluated in the reduced dimension for the two model sets. For example, the projected data points can be sparsely distributed across the Cartesian space when diverse patterns exist in the original data or distributed in small clusters for multimodal distributions of patterns. The similarity of the data sets can be quantified by the range of these two clusters, and it should become indistinguishable when the two data sets are similar (Zhang et al. 2021).

For a quantitative measure of the variability within the generated models, the perception-based structural similarity index (SSIM) is introduced, on the basis of the definition given by Wang et al. (2004) and Sun (2018)

$$\mathrm{SSIM}\left(y,{y}^{*}\right)= \frac{(2{\mu }_{y}{\mu }_{{y}^{*}}+{c}_{1})(2{\sigma }_{y{y}^{*}}+{c}_{2})}{({\mu }_{y}^{2}+{\mu }_{{y}^{*}}^{2}+{c}_{1})({\sigma }_{y}^{2}+{\sigma }_{{y}^{*}}^{2}+{c}_{2})},$$

(A1)

where $y$ and ${y}^{*}$ represent two random images from the generated models, respectively; $\mu$ is the mean and ${\sigma }^{2}$ is the variance; ${c}_{1}$ and ${c}_{2}$ are constant values to stabilize the denominator, and are taking the values of ${0.01}^{2}$ and ${0.03}^{2}$, respectively, for the gray images. The value range of SSIM is between −1 and 1, where 1 means that the two images are identical, and −1 is reached when the two images are completely different (Sun 2018). In image recognition, SSIM quantifies image degradation as structural information change where pixels that are spatially close with each other should have strong inter-dependencies. The perceptual phenomena, including the masking terms of luminance and contrast, are also accounted for in the SSIM to ensure that image distortions are detected as well (Wang et al. 2004). In general, compared to the mean squared error, SSIM is more indicative of perceived dissimilarity/similarity in the models.