Simulation of Intrinsic Random Fields of Order $k$ with Gaussian Generalized Increments by Gibbs Sampling

Abstract

This work pertains to the simulation of an intrinsic random field of order $k$ with a given generalized covariance function and multivariate Gaussian generalized increments. An iterative algorithm based on the Gibbs sampler is proposed to simulate such a random field at a finite set of locations, resulting in a sequence of random vectors that converges in distribution to a random vector with the desired distribution. The algorithm is tested on synthetic case studies to experimentally assess its rate of convergence, showing that few iterations are sufficient for convergence to take place. The sequence of random vectors also proves to be strongly mixing, allowing the generation of as many independent realizations as desired with a single run of the algorithm. Another interesting property of this algorithm is its versatility, insofar as it can be adapted to construct realizations conditioned to pre-existing data and can be used for any number and configuration of the target locations and any generalized covariance model.

1 Introduction

Intrinsic random fields of order $k$ (for short, IRF-$k)$, that is, random fields whose generalized increments of order $k$ are second-order stationary, are used to model regionalized variables that exhibit long-range dependency and/or spatially varying mean values. Examples of such variables are the temperature, pressure, porosity and permeability in geothermal reservoirs (Chilès and Gable 1984; Suárez Arriaga and Samaniego 1998), the porosity, fluid saturation and geological boundaries in oil reservoirs (Haas and Jousselin 1976; Delfiner and Chilès 1977; Dimitrakopoulos 1990; Bruno and Raspa 1993), the hydraulic head, conductivity, resistivity, transmissivity and total discharge in aquifer systems (Kitanidis 1983, 1999; Dong et al. 1990; Shim et al. 2004), the seafloor depth and the terrain elevation (David et al. 1986; Keitt 2000), metal grades and layout of ore domains in mineral deposits (Capello et al. 1987; David 1988; Costa and Dimitrakopoulos 1998; Séguret and Celhay 2013), crop properties (Aggelopoulou et al. 2010), soil properties (McBratney et al. 1991; Chiasson and Soulié 1997; Buttafuoco and Castrignano 2005; De Benedetto et al. 2012) and soil contaminants (Christakos and Thesing 1993). Other applications include the modeling of non-stationary time series (Hamilton 1994), as well as automatic mapping or contouring (Dubrule 1983; Marcotte and David 1988).

Intrinsic random field of order $k$ can be used not only for the prediction of regionalized variables, but also for quantifying spatial uncertainty via stochastic simulation. A review of the most widely used algorithms for simulating an IRF-$k$ can be found in Chilès and Delfiner (2012) and references therein. Most of these algorithms, however, suffer from practical limitations. For instance, sequential simulation produces inaccurate results unless a unique neighborhood is used to determine the successive conditional distributions (Emery 2008; Chilès and Delfiner 2012), which restricts its use to small-scale problems. The same practical restriction applies to the covariance matrix decomposition (Davis 1987a; Alabert 1987), which can be used only when the number of points targeted for simulation is not too large (say, less than a few thousands). With the Poisson dilution approach (Mandelbrot 1975; Chilès and Delfiner 2012), the reproduction of the spatial correlation structure is approximate, except for a few specific models. As for the discrete spectral and circulant-embedding approaches (Dietrich and Newsam 1993; Stein 2002; Chilès and Delfiner 2012), they are restricted to the simulation of random fields over regular grids, which is problematical in the presence of conditioning data at scattered locations, as the procedure used to construct conditional realizations (kriging of residuals) requires knowing these realizations at the data locations (Chilès and Delfiner 2012). Finally, the turning bands approach (Dimitrakopoulos 1990; Yin 1996; Emery and Lantuéjoul 2008) only allows simulating intrinsic random fields of order $k$ with specific spatial correlation structures (power, spline or polynomial generalized covariances).

The aim of this paper is to present an iterative simulation algorithm that avoids these restrictions (Sect. 3), to assess its rates of convergence and mixing in a few synthetic case studies (Sect. 4) and to extend this algorithm to the problem of conditional simulation (Sect. 5). Beforehand (Sect. 2), an overview of the IRF-$k$ theory is given. The reader is referred to Matheron (1973) and Chilès and Delfiner (2012) for a detailed exposition of this theory.

2 Concepts and Notation

2.1 Basic Drift Functions and Generalized Increments

The theory of IRF-$k$ has been introduced to model regionalized variables with mean values that smoothly vary in space and can be approximated by linear combinations of known basic drift functions $\{f^\ell :\ell = 0,\ldots ,L\}$. The first basic function (with index 0) is constant in space, while the remaining $L$ functions are monomials in the coordinates. To represent a polynomial drift of degree $k$ in the $d$-dimensional space, one needs to consider $1+L=\frac{(d+k)!}{k!d!}$ basic functions (the list of such functions depends on the degree $k$ and on the space dimension $d)$.

A generalized increment of order $k$ can be defined as a set of weights and locations, say $\lambda = \{\lambda _{i},\mathbf{x}_{i}\}_{i\in I}$, such that, for any basic drift function $f^\ell$, one has

$$\begin{aligned} \sum \limits _{i\in I} {\lambda _i f^\ell ({\mathbf {x}}_i)} =0. \end{aligned}$$

(1)

The minimal number of terms in a generalized increment (cardinal of $I)$ depends on both the space dimension ($d)$ and the order of the increment $(k)$. In general, the weights $\{\lambda _{i}: i \in I\}$ depend on the spatial pattern of the locations $\{\mathbf{x}_{i}: i \in I\}$ and several sets of weights fulfilling Eq. (1) can be defined for a given set of locations (Chilès and Delfiner 2012). In the following, the set of generalized increments of order $k$ will be denoted by $\Lambda _{k}$.

2.2 Intrinsic Random Fields of Order $k$ and Representations

First definition An IRF-$k$ can be defined as a random field $Y=\{Y(\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$ whose generalized increments of order $k$ have zero mean and are second-order stationary, that is, a random field such that, for any $\mathbf{h}, \mathbf{h}^{\prime }\in {\mathbb {R}}^{d}$, $\lambda = \{ \lambda _{i},\mathbf{x}_{i}\}_{i\in I}$ and $\lambda ^{\prime }=\{\lambda _{j}^{\prime },\mathbf{x}_{j}^{\prime }\}_{j \in J} \in \Lambda _{k}$, one has (Chilès and Delfiner 2012)

$$\begin{aligned} \left\{ \begin{array}{l} E\left\{ \sum \limits _{i\in I} {\lambda _i Y({\mathbf {x}}_i+{\mathbf {h}})}\right\} =0 \\ \hbox {cov} \left\{ \sum \limits _{i\in I} {\lambda _i Y(\mathbf {x}_i +\mathbf {h})},\sum \limits _{j\in J} {{\lambda }_j^{\prime } Y({\mathbf {x}}_j^{\prime }+{\mathbf {h}^{\prime }})}\right\} \hbox { exists and only depends on } \mathbf {h}-\mathbf {h}^{\prime }. \end{array}\right. \end{aligned}$$

(2)

If $Y^{\prime }$ is another random field that differs from $Y$ by a polynomial of degree less than or equal to $k$, then

$$\begin{aligned} \sum \limits _{i\in I} {\lambda _i {Y}^{\prime }(\mathbf {x}_i)} =\sum \limits _{i\in I} {\lambda _i Y(\mathbf {x}_i)}. \end{aligned}$$

(3)

This identity holds because generalized increments of order $k$ filter out the polynomials of degree less than or equal to $k$, as per Eq. (1), thus $Y$ and $Y^{\prime }$ are indistinguishable if one only considers generalized increments of order $k$.

Second definition Based on the previous statements, one can extend the definition of an IRF-$k$ to an equivalence class of random fields that differ by a (deterministic or random) polynomial of degree less than or equal to $k$ and from which one member of the class (a representation) is an IRF-$k$ in the sense of the first definition [Eq. (2)]. This simplifies to define an IRF-$k$ as a linear mapping $\mathsf{Y }$ of the class of generalized increments of order $k$ into a Hilbert space of zero mean and finite variance random variables, such that

$$\begin{aligned} \forall \lambda \in \Lambda _k,\quad \mathsf{Y }(\lambda )=\sum \limits _{i\in I} {\lambda _i Y({\mathbf{x}}_i)} \end{aligned}$$

(4)

is a second-order stationary random field. To avoid confusion, the first definition will be modified as follows (Matheron 1973; Chilès and Delfiner 2012)

• $\{\mathsf{Y }(\lambda ):\lambda \in \Lambda _{k}\}$ is an IRF-$k$; this abstract random field, defined on $\Lambda _{k}$, corresponds to an equivalence class of random fields defined on ${\mathbb {R}}^{d}$ that generate the same generalized increments of order $k$;

• $\{Y(\mathbf{x}): \mathbf{x}\in {\mathbb {R}}^{d}\}$, as a particular member of the equivalence class, is a representation of the IRF-$k$.

2.3 Generalized Covariance Functions

For any IRF-$k$, there exists a generalized covariance function, hereafter denoted as $K(\mathbf{h})$ and defined up to an even polynomial of degree less than or equal to $2k$, such that the covariance between any two generalized increments of order $k$, say $\lambda = \{ \lambda _{i},\mathbf{x}_{i}\}_{i \in I}$ and $\lambda ^{\prime }=\{\lambda _{j}^{\prime },\mathbf{x}_{j}^{\prime }\}_{j \in J}$, can be expressed as (Chilès and Delfiner 2012)

$$\begin{aligned} \hbox {cov}\{\mathsf{Y }(\lambda ),\mathsf{Y }({\lambda }^{\prime })\} =\hbox {cov}\left\{ \sum \limits _{i\in I} {\lambda _i Y({\mathbf {x}}_i)},\sum \limits _{j\in J} {{\lambda }^{\prime }_j Y(\mathbf{x}^{\prime }_j)}\right\} =\sum \limits _{i\in I} {\sum \limits _{j\in J} {\lambda _i {\lambda }^{\prime }_j K({\mathbf {x}}_i-\mathbf{x}^{\prime }_j)}}.\nonumber \\ \end{aligned}$$

(5)

Therefore, one can calculate the covariance between two generalized increments of order $k$ as if there were a stationary covariance function, but by substituting the generalized covariance for this hypothetical stationary covariance function. Common models of generalized covariance functions include all ordinary covariance functions, as well as the power and spline models (Emery and Lantuéjoul 2008), respectively, defined as

• Power of exponent $\theta :K(\mathbf {h})=(-1)^{p+1}\vert {\mathbf {h}}\vert ^\theta$ for $p \in \{0,\ldots ,k\}$ and $\theta \in \,]2p,2p+2[$;

• Spline of exponent $2k:K({\mathbf {h}})=(-1)^{k+1}\vert {\mathbf {h}}\vert ^{2k}\ln (\vert {\mathbf {h}}\vert )$.

2.4 Intrinsic Kriging

Let $Y=\{Y (\mathbf{x}): \mathbf{x}\in {\mathbb {R}}^{d}\}$ be a representation of an IRF-$k$ with generalized covariance $K(\mathbf{h})$ and $\{\mathbf{x}_{1},\ldots ,\mathbf{x}_{p}\}$ a set of locations at which $Y$ is known. The intrinsic kriging predictor at location $\mathbf{x}_{0}$ is

$$\begin{aligned} Y^{*} ({\mathbf {x}}_0 )=\sum \limits _{\alpha =1}^p {\lambda _{\alpha } ({\mathbf {x}}_0)Y({\mathbf {x}}_{\alpha })}, \end{aligned}$$

(6)

where the weights $\{\lambda _{\alpha }(\mathbf{x}_{0}):\alpha =1,\ldots ,p\}$ are subject to the constraint that the prediction error is a generalized increment of order $k$, with zero expectation and minimum variance. They are found by solving a system of linear equations similar to that of universal kriging, except that the ordinary covariance or the variogram is replaced by the generalized covariance (Chilès and Delfiner 2012). One property of intrinsic kriging is that the prediction error is not correlated with any generalized increment of the data.

To ensure that the coefficient matrix of the kriging equations is nonsingular, the basic drift functions must be linearly independent at the data locations, that is

$$\begin{aligned} \sum \limits _{\ell } {c_{\ell } f^{\ell } ({\mathbf {x}}_{\alpha })}=0 \quad \forall \alpha =1,\ldots ,p \hbox { if and only if } c_{\ell } =0\ \forall \ell =0,\ldots ,L. \end{aligned}$$

(7)

2.5 Distribution of Generalized Increments

Hereafter, only the case of an IRF-$k$ with multivariate Gaussian generalized increments, for which the finite-dimensional distributions of the generalized increments are characterized by the generalized covariance function, will be considered. Examples of such random fields are the well-known fractional Brownian motions (one-dimensional) or surfaces (two-dimensional) with Hurst exponent $H\in \, ]0,1[,$ which correspond to IRF-0 with Gaussian increments and generalized covariance function $K(\mathbf{h})=-\omega \vert \mathbf{h}\vert ^{2H}$ with $\omega >0$ (Chilès and Delfiner 2012).

3 Non-conditional Simulation by Gibbs Sampling

3.1 Case of a Gaussian Random Vector

Let us consider a Gaussian random vector Y with $n$ components, zero mean and variance–covariance matrix C. In the following, it is assumed that C is strictly positive definite, that is, its eigenvalues are positive (if C has a zero eigenvalue, one or more components of Y are linear combinations of the other components and should be removed to obtain a strictly positive definite variance–covariance matrix). Numerous algorithms are currently available for generating realizations of Y, the most popular ones being the decomposition of the covariance matrix, sequential Gaussian and iterative algorithms based on Markov chains (Ripley 1987; Gentle 2009; Chilès and Delfiner 2012, and references therein). For the first two algorithms (matrix decomposition and sequential), some approximations are needed when the size of the vector to simulate is large, which become critical when these algorithms are applied to the simulation of non-stationary random fields (Emery 2008, 2010; Emery and Peláez 2011).

In view of a further generalization to the simulation of an IRF-$k$ with Gaussian generalized increments, let us consider the following iterative algorithm proposed by Lantuéjoul and Desassis (2012), based on an idea by Galli and Gao (2001).

Algorithm 1 (Gibbs Sampler for Gaussian Random Vectors)

• (1) Initialize the simulation by an arbitrary vector $\mathbf{Y}^{(0)}$.

• (2) For $j=1,2,\ldots ,J$:

  • (a) Split the set $\{1,\ldots ,n\}$ into two disjoint subsets, the first one (hereafter denoted by $S_{1}(j))$ containing $n-p$ indices and the second one (denoted by $S_{2}(j))$ containing the remaining $p$ indices. Any strategy can be used to select the indices belonging to $S_{2}(j)$, provided that every element of $\{1,\ldots ,n\}$ is selected as many times as desired for sufficiently large $J$.

  • (b) Split the current vector $\mathbf{Y}^{(j-1)}$ into two sub-vectors, namely ${\mathbf {Y}}_{S_1(j)}^{(j-1)}$ and ${\mathbf {Y}}_{S_2 (j)}^{(j-1)}$, with $n-p$ and $p$ components, respectively. Likewise, split the vector to simulate Y into two sub-vectors ${\mathbf {Y}}_{S_1(j)}$ and ${\mathbf {Y}}_{S_2(j)}$.

  • (c) Define ${\mathbf {C}}_{12}^{(j)}$ as the covariance matrix between ${\mathbf {Y}}_{S_1 (j)}$ and ${\mathbf {Y}}_{S_2 (j)}$, and ${\mathbf {C}}_{22}^{(j)}$ as the variance–covariance matrix of ${\mathbf {Y}}_{S_2 (j)}$. Note that ${\mathbf {C}}_{12}^{(j)}$ and ${\mathbf {C}}_{22}^{(j)}$ are sub-matrices of C (variance–covariance matrix of Y) and do not depend on the particular distribution of current vector $\mathbf{Y}^{(j-1)}$. Like C, ${\mathbf {C}}_{22}^{(j)}$ is strictly positive definite.

  • (d) Find out a symmetric square root $\mathbf{A}^{(j)}$ of ${\mathbf {C}}_{22}^{(j)}$ (this can be principal square root of ${\mathbf {C}}_{22}^{(j)}$ or its Cholesky factor, see Golub and Van Loan 1996), such that

    $$\begin{aligned} {\mathbf {C}}_{22}^{(j)}={\mathbf {A}}^{(j)}({\mathbf {A}}^{(j)})^\mathrm{T}. \end{aligned}$$

    (8)

  • (e) Define $\mathbf{Y}^{(j)}$ by putting

    $$\begin{aligned} \left\{ {\begin{array}{l} {\mathbf {Y}}_{S_2 (j)}^{(j)} ={\mathbf {A}}^{(j)}{\mathbf {V}}^{(j)} \\ {\mathbf {Y}}_{S_1 (j)}^{(j)} ={\mathbf {Y}}_{S_1 (j)}^{(j-1)} +[{\mathbf {Y}}_{S_1 (j)}^{(j)}]^{*}-[{\mathbf {Y}}_{S_1 (j)}^{(j-1)}]^{*}, \end{array}} \right. \end{aligned}$$

    (9)

    where $\mathbf{V}^{(j)}$ is a standard Gaussian random vector independent of $\mathbf{Y}^{(j - 1)}$ and with $p$ independent components, $[{\mathbf {Y}}_{S_1 (j)}^{(j-1)} ]^{*} ={\mathbf {C}}_{12}^{(j)} ({\mathbf {C}}_{22}^{(j)})^{-1}{\mathbf {Y}}_{S_2 (j)}^{(j-1)}$ is the simple kriging predictor of ${\mathbf {Y}}_{S_1 (j)}$ from ${\mathbf {Y}}_{S_2 (j)}^{(j-1)}$, and $[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{*}={\mathbf {C}}_{12}^{(j)} ({\mathbf {C}}_{22}^{(j)})^{-1}{\mathbf {Y}}_{S_2 (j)}^{(j)}$ is the simple kriging predictor of ${\mathbf {Y}}_{S_1 (j)}$ from ${\mathbf {Y}}_{S_2 (j)}^{(j)}$.

• (3) Return $\mathbf{Y}^{(J)}$.

The way to obtain ${\mathbf {Y}}_{S_2 (j)}^{(j)}$ at step (2e) is nothing but the covariance matrix decomposition algorithm (Davis 1987a; Alabert 1987). This algorithm is straightforward for simulating a vector of small size (here, a sub-vector with $p$ components), but may not be applicable to directly simulate the complete vector Y if its number $n$ of components is larger than a few thousands. In contrast, the proposed Gibbs sampler is able to simulate Y irrespective of its size.

It can be shown that the sequence $\{\mathbf{Y}^{(j)}: j \in {\mathbb {N}}\}$ converges in distribution to a Gaussian random vector with zero mean and variance–covariance matrix C (Lantuéjoul and Desassis 2012). Based on experimental observations, these authors suggest using a vector of zeros at the initialization stage $(\mathbf{Y}^{(0)}=\mathbf{0}),$ as this yields a faster convergence than, for example, using a random vector $\mathbf{Y}^{(0)}$ with independent components (in such a case, as the initial state is unstructured, one usually has to increase the number $J$ of iterations to obtain a final random vector $\mathbf{Y}^{(J)}$ with the desired variance–covariance matrix). For an experimental analysis of the rate of convergence, the reader is referred to Arroyo et al. (2012).

3.2 Case of an IRF-$k$ with Gaussian Generalized Increments

Consider now the problem of simulating an IRF-$k$, $\{{\mathsf {Y}}(\lambda ): \lambda \in \Lambda _{k}\}$, with generalized covariance function $K(\mathbf{h})$ and multivariate Gaussian generalized increments, at a finite set of locations $\mathbf{X}=\{\mathbf{x}_{1},\ldots ,\mathbf{x}_{n}\}$. Since this IRF-$k$ is determined up to a polynomial of degree $k$, the problem actually consists in simulating one specific representation $\{Y(\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$, that is, simulating the random vector $\mathbf{Y} = Y(\mathbf{X}) = (Y(\mathbf{x}_{1}),\ldots ,Y(\mathbf{x}_{n}))^\mathrm{T}$.

To specify the representation to be simulated, consider a set of locations $\mathbf{U}=\{\mathbf{u}_{0},\ldots ,\mathbf{u}_{L}\}$ such that the basic drift functions $\{f^{\ell } : \ell = 0,\ldots ,L\}$ are linearly independent [Eq. (7)], and consider the representation that vanishes at these locations, that is, $Y(\mathbf{U}) = \mathbf{0}.$ The set U can be chosen freely and does not need to be a subset of X or to intersect X; it is just used to identify the representation of the IRF-$k$ that will be simulated. Any other representation can be obtained by adding a polynomial of the coordinates.

The chosen representation $\{Y(\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$ is a so-called internal representation (Matheron 1973; Chilès and Delfiner 2012) and actually possesses a covariance function. Indeed, since $Y(\mathbf{U})=\mathbf{0},$ one has

$$\begin{aligned} Y({\mathbf {x}})=Y({\mathbf {x}})-Y^{*} ({\mathbf {x}}), \end{aligned}$$

(10)

where $Y^{*} ({\mathbf {x}})=\sum \nolimits _{\alpha =0}^L {\lambda _{\alpha } ({\mathbf {x}})Y({\mathbf {u}}_{\alpha })}=0$ is the intrinsic kriging predictor of $Y(\mathbf{x})$ from $Y(\mathbf{U})$ [Eq. (6)]. Thus, as an intrinsic kriging error, $Y(\mathbf{x})$ is a generalized increment: its distribution is Gaussian and has a finite variance. Moreover, any pair $(Y(\mathbf{x}),Y(\mathbf{x}^{\prime }))$ has a bivariate Gaussian distribution and a finite covariance and, more generally, any linear combination of the components of $\{Y(\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$ is Gaussian, which implies that $\{Y (\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$ is a Gaussian random field and Y is a Gaussian random vector.

To simulate Y, one could, therefore, think of applying Algorithm 1. However, $\{Y(\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$ is not stationary, so that the calculation and storage of the variance–covariance matrix of Y may be time- and/or memory-consuming when Y has many components. To avoid these drawbacks, a generalization of Algorithm 1 is proposed next.

Algorithm 2 (Gibbs Sampler for IRF- k with Gaussian Generalized Increments)

• (1) Initialize the simulation by an arbitrary vector, for example, a vector of zeros: $\mathbf{Y}^{(0)}=\mathbf{0}$.

• (2) For $j=1,2,\ldots ,J$:

  • (a) Split the set $\{1,\ldots ,n\}$ into two subsets $S_{1}(j)$ and $S_{2}(j)$ containing $n-p$ and $p$ indices, respectively (the same selection strategy as for Algorithm 1 can be used).

  • (b) Split the set of locations X into two subsets $\mathbf{X}_{S_1(j)}$ and $\mathbf{X}_{S_2(j)}$ containing $n-p$ and $p$ locations, respectively.

  • (c) Define as ${\mathbf {Y}}_{S_1(j)}$ and ${\mathbf {Y}}_{S_2(j)}$ the sub-vectors associated with $\mathbf{X}_{S_1(j)}$ and $\mathbf{X}_{S_2(j)}$, and as ${\mathbf {Y}}_3$ the sub-vector associated with $\mathbf{U}:{\mathbf {Y}}_{S_1(j)}=Y(\mathbf{X}_{S_1(j)}),{\mathbf {Y}}_{S_2(j)}=Y(\mathbf{X}_{S_2 (j)})$ and $\mathbf{Y}_{3}=Y(\mathbf{U})=\mathbf{0}.$

  • (d) Calculate the variance–covariance matrix ${\mathbf {C}}_{22}^{(j)}$ of the intrinsic kriging errors, when kriging ${\mathbf {Y}}_{S_2 (j)}$ from $\mathbf{Y}_{3}$. Since it is the variance–covariance matrix of a real-valued vector, ${\mathbf {C}}_{22}^{(j)}$ is symmetric positive semi-definite and has a symmetric square root $\mathbf{A}^{(j)}$ such that (Golub and Van Loan 1996)

    $$\begin{aligned} {\mathbf {C}}_{22}^{(j)} ={\mathbf {A}}^{(j)}({\mathbf {A}}^{(j)})^\mathrm{T}. \end{aligned}$$

    (11)

  • (e) Define ${\mathbf {Y}}_{S_2 (j)}^{(j)}$ by putting

    $$\begin{aligned} {\mathbf {Y}}_{S_2 (j)}^{(j)} =[{\mathbf {Y}}_{S_2 (j)}]^{*} +{\mathbf {A}}^{(j)}{\mathbf {V}}^{(j)}, \end{aligned}$$

    (12)

    where $[{\mathbf {Y}}_{S_2 (j)}]^{*}$ is the intrinsic kriging predictor of ${\mathbf {Y}}_{S_2 (j)}$ from $\mathbf{Y}_{3}$ (in the present case, it is a vector of zeros, since $\mathbf{Y}_{3}=\mathbf{0}),$ and $\mathbf{V}^{(j)}$ is a standard Gaussian random vector with $p$ independent components, independent of $\mathbf{Y}^{(j-1)}$.

  • (f) Define ${\mathbf {Y}}_{S_1 (j)}^{(j)}$ by putting

    $$\begin{aligned} {\mathbf {Y}}_{S_1 (j)}^{(j)} ={\mathbf {Y}}_{S_1 (j)}^{(j-1)} +[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}-[{\mathbf {Y}}_{S_1 (j)}^{(j-1)} ]^{**}, \end{aligned}$$

    (13)

    where $[{\mathbf {Y}}_{S_1 (j)}^{(j-1)} ]^{**}$ is the intrinsic kriging predictor of ${\mathbf {Y}}_{S_1 (j)}$ from $({\mathbf {Y}}_{S_2 (j)}^{(j-1)},{\mathbf {Y}}_3)$, $[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}$ is the intrinsic kriging predictor of ${\mathbf {Y}}_{S_1 (j)}$ from $({\mathbf {Y}}_{S_2 (j)}^{(j)},{\mathbf {Y}}_3)$.

  • (3) Return Y $^{(J)}$.

It can be shown (Appendix) that the sequence of random vectors $\{\mathbf{Y}^{(j)}: j \in {\mathbb {N}}\}$ converges in distribution to $\mathbf{Y}=Y(\mathbf{X}),$ that is, the joint distribution of $\mathbf{Y}^{(j)}$ converges pointwise to a multivariate Gaussian distribution with the same mean and variance–covariance matrix as Y, as $j$ tends to infinity (recall that Y is a Gaussian random vector, as the representation to simulate is a Gaussian random field). This property is stronger than just the convergence in distribution of the generalized increments generated from the simulated random vector $\mathbf{Y}^{(j)}$.

3.3 Rate of Convergence

The components of the vector $\mathbf{Y}^{(j)}$ obtained at steps (2e) and (2f) of Algorithm 2 are linear combinations of vectors $\mathbf{V}^{(j)}$ and $\mathbf{Y}^{(j - 1)}$, which in turn is a combination of vectors $\mathbf{V}^{(j - 1)}$ and $\mathbf{Y}^{(j - 2)}$, and so on. Given that $\mathbf{Y}^{(0)}=\mathbf{0},$ it is seen that the components of $\mathbf{Y}^{(j)}$ are linear combinations of the independent Gaussian random vectors $\mathbf{V}^{(1)},\ldots ,\mathbf{V}^{(j)}$. Therefore, at each iteration $j=1,\ldots ,J$, the simulated vector $\mathbf{Y}^{(j)}$ is a Gaussian random vector. In particular, its generalized increments are multivariate Gaussian, that is, $\mathbf{Y}^{(j)}$ is a representation of an IRF-$k$ with multivariate Gaussian increments.

However, because Algorithm 2 is stopped after finitely many iterations, the variance–covariance matrix of $\mathbf{Y}^{(J)}$ may not match that of Y (the match is only asymptotical, as $J$ tends to infinity). For want of theoretical results that allow quantifying the mismatch for a given total number of iterations $J$, the analysis of a few synthetic case studies will be held in the next section to gain an insight into the rate of convergence of the proposed Gibbs sampler.

4 Numerical Experiments

4.1 Description

In the following subsections, X is a set of $n=4{,}225$ locations forming a two-dimensional regular grid with $65\times 65$ nodes, origin $(1,1)$ and mesh $1\times 1.$ Algorithm 2 will be applied to simulate a representation of an IRF-$k$ on this grid, that is, $\mathbf{Y}=Y(\mathbf{X}),$ such that $Y(\mathbf{U})=\mathbf{0},$ where U is a set of $1+L$ locations that do not belong to the grid. It is of interest to experimentally assess the rates of convergence and mixing of the algorithm, as explained hereafter.

Convergence Let C be the variance–covariance matrix of the Gaussian random vector Y to simulate, which is equal to the variance–covariance matrix of the errors made when kriging $Y(\mathbf{X})$ from $Y(\mathbf{U}),$ and let $\mathbf{C}^{(j)}$ be the variance–covariance matrix of $\mathbf{Y}^{(j)}$ (Gaussian random vector obtained at iteration $j$ of Algorithm 2). The sequence of Gaussian random vectors $\{\mathbf{Y}^{(j)}: j \in {\mathbb {N}}\}$ converges in distribution to Y if the following index tends to zero as $j$ increases (Emery and Peláez 2011)

$$\begin{aligned} \eta _j =\frac{\Vert {\mathbf {C}}^{(j)}-{\mathbf {C}}\Vert }{\Vert {\mathbf {C}}\Vert }, \end{aligned}$$

(14)

where $\Vert \cdot \Vert$ stands for the Frobenius norm.

Mixing Assume that Algorithm 2 has converged at iteration $j$, that is, $\mathbf{Y}^{(j)}$ is a Gaussian random vector with the same variance–covariance matrix as Y, and let $\mathbf{C}^{(j,j+q)}$ denote the covariance matrix between $\mathbf{Y}^{(j)}$ and the Gaussian random vector $\mathbf{Y}^{(j+q)}$ obtained after $q$ additional iterations of the algorithm. Strong mixing (Bradley 2005) occurs when the two Gaussian random vectors $\mathbf{Y}^{(j)}$ and $\mathbf{Y}^{(j+q)}$ are asymptotically independent, that is, when $\mathbf{C}^{(j,j+q)}$ tends to the null matrix as $q$ increases or, equivalently, when the following index tends to zero as $q$ increases (Arroyo et al. 2012)

$$\begin{aligned} \nu _q =\frac{\Vert {\mathbf {C}}^{(j,j+q)}\Vert }{\Vert {\mathbf {C}}\Vert }. \end{aligned}$$

(15)

When $\eta _{j}\approx 0$ and $\nu _{q}\approx 0$, the successive vectors $\mathbf{Y}^{(j)},\mathbf{Y}^{(j+q)},\mathbf{Y}^{(j+2q)}\ldots$ can be viewed as independent realizations of the random vector Y. Therefore, with a single run of the chain $\{\mathbf{Y}^{(j)}: j \in {\mathbb {N}}\}$, one can generate as many independent realizations of Y as desired. If the chain is not mixing, or if the rate of convergence of $\nu _{q}$ to zero is slower than that of $\eta _{j}$, an alternative to obtain several independent realizations of Y is to run the chain several times, using different seeds for the generation of random numbers.

In the following, it is of interest to assess the rates of convergence of $\eta _{j}$ and $\nu _{q}$, as $j$ and $q$ increase. Computing both indices requires computing matrices $\mathbf{C}, \mathbf{C}^{(j)}$ and $\mathbf{C}^{(j,j+q)}$, which can be done when knowing the generalized covariance function $K(\mathbf{h})$ of the underlying IRF-$k$, similarly to what is presented in Arroyo et al. (2012) for stationary random fields. The experiments will be sensitized to the size $(p)$ of sub-vector $\mathbf{Y}_{2}$, the strategy to select its components, the visiting sequence and the generalized covariance function.

4.2 Sensitivity to Blocking Strategy

The blocking strategy refers to the way to select the $p$ indices of $\{1,\ldots , n\}$ at step (2a) of Algorithm 2. In the following, the case when $p=100$ components is considered and three strategies are compared: (i) a random blocking, for which the indices are randomly selected; (ii) a rectangular blocking, for which the indices are associated with adjacent positions of the grid, forming a rectangle of $20\times 5$ locations; and (iii) a square blocking, by considering a set of $10\times 10$ adjacent locations. In all the cases, the generalized covariance function is an isotropic power model of exponent 1.5 (corresponding to an IRF-0) and U is restricted to a single point with coordinate (32.55, 32.55). Figure 1 shows the evolution of $\eta _{j}$ and $\nu _{q}$ as a function of $j$ and $q$, respectively, and Table 1 gives their values for $j=q=500.$ Although convergence and mixing take place in every case (indices $\eta _{j}$ and $\nu _{q}$ always quickly tend to zero), one clearly observes faster rates of convergence and mixing when using the rectangular and square blockings, in comparison with the random blocking, the square blocking yielding slightly faster rates than the rectangular blocking.

Fig. 1

Standardized Frobenius norms of a, $\mathbf{C}^{(j)}-\mathbf{C}$ and b, $\mathbf{C}^{(j,j+q)}$ for three blocking strategies

Table 1 Standardized Frobenius norms of $\mathbf{C}^{(j)}-\mathbf{C}$ and $\mathbf{C}^{(j,j+q)}$ for three blocking strategies and $j=q=500$

4.3 Sensitivity to Updating Strategy

Consider a rectangular or square blocking strategy, each block being identified by the grid node located at the bottom-left corner. The updating strategy refers to the way these grid nodes are visited, also known as visiting sequence. In the following, three strategies are considered: random sweep, deterministic updating and random permutation (Galli and Gao 2001), using the same generalized covariance model as in the previous subsection and a square blocking with $p=100.$ It is seen (Fig. 2; Table 2) that the rate of convergence and mixing is slightly faster with the random permutation strategy compared to the random sweep strategy, and much faster compared to the deterministic updating.

Fig. 2

Standardized Frobenius norms of a, $\mathbf{C}^{(j)}-\mathbf{C}$ and b, $\mathbf{C}^{(j,j+q)}$, for three updating strategies

Table 2 Standardized Frobenius norms of $\mathbf{C}^{(j)}-\mathbf{C}$ and $\mathbf{C}^{(j,j+q)}$ for three updating strategies and $j=q=500$

4.4 Sensitivity to Block Size

The following experiments consider a square blocking and random permutation strategy, but varying block sizes: $p=1, 25, 100$ or 400. To get a fair comparison of the rates of convergence, the indices $\eta _{j}$ and $\nu _{q}$ are now plotted as a function of the CPU time in seconds. It is seen (Fig. 3; Table 3) that convergence is the fastest with large blocks $(p=400)$ and the slowest with $p=1.$

Fig. 3

Standardized Frobenius norms of a, $\mathbf{C}^{(j)}-\mathbf{C}$ and b, $\mathbf{C}^{(j,j+q)}$, for four block sizes

Table 3 CPU times to construct 100 realizations and standardized Frobenius norms of $\mathbf{C}^{(j)}-\mathbf{C}$ and $\mathbf{C}^{(j,j+q)}$ for four block sizes and $j=q=500$

4.5 Sensitivity to the Generalized Covariance Model

In this subsection, four isotropic covariance models are considered: power of exponent 0.5, power of exponent 1.5, power of exponent 3 and spline of exponent 2. The first two models correspond to an IRF-0 and use only one point with coordinates (32.55, 32.55) to constrain the realizations. In contrast, the last two models correspond to an IRF-1 and use a set of three points $\mathbf{U}=\{(0, 0), (32.55, 0), (66, 66)\}$ to constrain the realizations. Here, the rates of convergence and mixing turn out to be comparable for all covariance models (Fig. 4; Table 4).

Fig. 4

Standardized Frobenius norms of a, $\mathbf{C}^{(j)}-\mathbf{C}$ and b, $\mathbf{C}^{(j,j+q)}$, for four generalized covariance models

Table 4 Standardized Frobenius norms of $\mathbf{C}^{(j)}-\mathbf{C}$ and $\mathbf{C}^{(j,j+q)}$ for four generalized covariance models and $j=q=500$

5 Conditional Simulation

5.1 Simulation Algorithm

Consider now the case when some data on the IRF-$k$ are available, so that it is of interest to simulate $\mathbf{Y}=Y(\mathbf{X})$ conditionally to $Y(\mathbf{U}^{\prime })=\mathbf{y}$ for a given set of locations $\mathbf{U}^{\prime }$. This can be solved straightforwardly by substituting $\mathbf{U}^{\prime }$ for U and $\mathbf{Y}_{3}=\mathbf{y}$ for $\mathbf{Y}_{3}=\mathbf{0}$ at step (2) of Algorithm 2. If the number of locations in $\mathbf{U}^{\prime }$ is less than $1+L$, or if the basic functions $\{f^{\ell }:\ell = 0,\ldots ,L\}$ are not linearly independent at these locations [(Eq. (7)], one should complete $\mathbf{U}^{\prime }$ with extra locations where the simulated values are constrained to be zero.

5.2 Experiments

To illustrate this variant of Algorithm 2 for conditional simulation, consider the case of an IRF-$k$ with $k=0$ or $k=1$ on a regular grid G with $200\times 200$ nodes, with 15 scattered data at fixed positions as conditioning data. For practical implementation, square blocks of $p=100$ components and a random permutation strategy are used, and the algorithm is stopped after $J=40{,}000$ iterations.

Each experiment consists of the following steps:

• 1. Construct a set of conditioning data $\mathbf{Y}_{3}$. To this end:

  • (a) Among the 15 data locations, select $1+L$ locations and set the associated data values to zero.

  • (b) Calculate the kriging prediction and the variance–covariance matrix of intrinsic kriging errors at the remaining $14-L$ data locations.

  • (c) Simulate the values at these locations using the square root decomposition of the previous variance–covariance matrix.

• 2. Use $\mathbf{Y}_{3}$ in Algorithm 2 to construct a conditional realization over grid G.

• 3. Repeat the process with other realizations of $\mathbf{Y}_{3}$ at step (1). Therefore, only the positions of the conditioning data are the same in all the realizations, whereas the conditioning data values vary from one realization to another.

5.2.1 Example 1: Simulation of a Fractional Brownian Surface

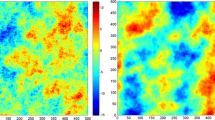
Consider the simulation of fractional Brownian surfaces with Hurst exponents 0.25 and 0.75, corresponding to representations of IRF-0 with multivariate Gaussian increments and generalized covariance function $K(\mathbf{h})=-0.01\vert \mathbf{h}\vert ^{0.5}$ and $-0.01\vert \mathbf{h}\vert ^{1.5}$, respectively. Here, the proposed simulation algorithm is validated by examining the experimental variograms of a set of 100 realizations: on average, these experimental variograms match the prior variogram model, as expected (Fig. 5a, b, corresponding to the power generalized covariance of exponents 0.5 and 1.5, respectively). Realizations in which the 15 conditioning data are set to zero (for illustrative purposes) are shown in Fig. 6a, b.

Fig. 5

Experimental generalized variograms of 100 realizations of an IRF-$k$ (green dashed lines), average of experimental generalized variograms (blue stars) and theoretical generalized variograms (solid black lines)

Fig. 6

Realizations of IRF-$k$ with a, b, c power generalized covariance of exponent 0.5, 1.5 and 3, and d spline generalized covariance of exponent 2. The conditioning data are set to zero and their positions are indicated with circles

5.2.2 Example 2: Simulation of an IRF-1

In this case, the validation relies on the generalized variogram of order 1, which is defined as (Chilès and Delfiner 2012)

$$\begin{aligned} \Gamma ({\mathbf {h}})=\frac{1}{6}E\{[Y({\mathbf {x}} +2{\mathbf {h}})-2Y({\mathbf {x}}+{\mathbf {h}})+Y({\mathbf {x}})]^2\}. \end{aligned}$$

(16)

This generalized variogram can be expressed as a function of the generalized covariance (Chilès and Delfiner 2012)

$$\begin{aligned} \Gamma ({\mathbf {h}})=K({\mathbf {0}})-\frac{4}{3}K({\mathbf {h}})+\frac{1}{3}K(2{\mathbf {h}}). \end{aligned}$$

(17)

Experimentally, $\Gamma ({\mathbf {h}})$ can be estimated for each realization $\{y(\mathbf{x}): \mathbf{x} \in {\mathsf {G}}\}$ by replacing the expectation in Eq. (16) by an average of the form

$$\begin{aligned} {\hat{\Gamma }}({\mathbf {h}})=\frac{1}{6}\frac{\sum \limits _{{\mathbf {x}}\in {\mathsf {G}}\cap {\mathsf {G}}_{-{\mathbf {h}}} \cap {\mathsf {G}}_{-2{\mathbf {h}}}} {[y({\mathbf {x}}+2{\mathbf {h}})-2y({\mathbf {x}}+{\mathbf {h}})+y({\mathbf {x}})]^2} }{\hbox {card}\{{\mathsf {G}}\cap {\mathsf {G}}_{-{\mathbf {h}}} \cap {\mathsf {G}}_{-2{\mathbf {h}}} \}}, \end{aligned}$$

(18)

where ${\mathsf {G}}_{-\mathbf{h}}$ and ${\mathsf {G}}_{-2\mathbf{h}}$ stand for the grid ${\mathsf {G}}$ shifted by vector $-\mathbf{h}$ and $-2\mathbf{h},$ respectively. In the following, two generalized covariance models are considered: a power model of exponent 3 (Fig. 5c) and a spline model of exponent 2 (Fig. 5d). In these figures, it is seen that, on average over the realizations, the experimental generalized variograms [Eq. (18)] match the theoretical generalized variogram, as given by Eq. (17). Examples of realizations in which the 15 conditioning data are set to zero are depicted in Fig. 6c, d.

5.3 Discussion

Apart from generating realizations that reproduce the desired spatial correlation structure, the proposed Gibbs sampling algorithm (Algorithm 2) stands out for its versatility: (i) it is applicable to any type of generalized covariance function, not only power models; (ii) it can be used for simulation conditional to scattered data, as shown in the previous subsections; and (iii) because of its iterative nature, it can be adapted to incorporate complex conditioning constraints, such as interval constraints, using annealing procedures or restricting the transition matrix of the algorithm (Emery et al. 2014). As a drawback, it is not directly applicable in the presence of too many conditioning data: kriging cannot be performed exactly if sub-vector $\mathbf{Y}_{3}$ is large and, when it is performed within a moving neighborhood, the sequence of simulated vectors may not converge in distribution any more (Emery et al. 2014). However, in such a case, a two-step approach can be used: first, simulate the random field at the data and target locations via Algorithm 2 (non-conditional simulation), then perform kriging of the residuals to convert the simulation into a conditional one (here, a moving neighborhood can be used as an approximation, without propagating errors, insofar as the conditioning process is not iterative).

6 Conclusions

The Gibbs sampler presented in Algorithm 2 offers a convenient solution to simulate an IRF-$k$ at a finite set of locations, for the following reasons: (i) it produces realizations with multivariate Gaussian generalized increments; (ii) it can be extended to conditional simulation problems, when pre-existing data (hard data or interval constraints) need to be reproduced; and (iii) it is applicable for any number and configuration of the locations targeted for simulation and for any generalized covariance model.

Because the algorithm is stopped after finitely many iterations, the variance–covariance matrix of the simulated vector may differ from the desired one. However, numerical experiments held on specific case studies suggest that the difference is imperceptible after few iterations, as the norm $\eta _{j}$ [Eq. (14)] quickly tends to zero when $j$ increases (especially if one uses a square or a rectangular blocking with large blocks and a random permutation strategy). If several realizations are needed, one can restart the algorithm with another seed for generating random numbers or, based on the mixing property, consider the successive random vectors $\mathbf{Y}^{(j)},\mathbf{Y}^{(j+q)},\mathbf{Y}^{(j+2q)}$ for some $j$ and $q$ such that $\eta _{j}$ and $\nu _{q}$ [Eqs. (14) and (15)] are close to zero.

Appendix: Convergence of Algorithm 2

The sequence of successive random vectors $\{\mathbf{Y}^{(j)}:j\in {\mathbb {N}}\}$ obtained with Algorithm 2 forms a homogeneous Markov chain. According to Tierney (1994) and Lantuéjoul (2002), this chain converges in distribution if and only if the following three properties are satisfied: (i) aperiodicity, (ii) irreducibility and (iii) existence of an invariant distribution for the transition matrix of the chain.

The first property (aperiodicity) holds because the chain can loop at one state (Lantuéjoul 2002), that is, one can have $\mathbf{Y}^{(j)}=\mathbf{Y}^{(j - 1)}$. Indeed, it suffices to have ${\mathbf {Y}}_{S_2 (j)}^{(j)} ={\mathbf {Y}}_{S_2 (j)}^{(j-1)}$ at step (2e), which is possible because the vector $\mathbf{V}^{(j)}$ defined at this step can take any value in ${\mathbb {R}}^{p}$.

The second property (irreducibility) implies that it is possible to go from each state to every other state in one or more iterations. To establish this property, let us assume that the chain is in a given state at iteration $j$, say $\mathbf{Y}^{(j)}=\mathbf{y}.$ At iteration $j+1,$ it is easy to see that ${\mathbf {Y}}_{S_2(j+1)}^{(j+1)}$ can take any value in ${\mathbb {R}}^{p}$, with an appropriate choice of $\mathbf{V}^{(j+1)}$ [Eq. (12)], while the value of ${\mathbf {Y}}_{S_1 (j+1)}^{(j+1)}$ will linearly depend on ${\mathbf {Y}}_{S_2 (j+1)}^{(j+1)}$, $\mathbf{y}_{S_2 (j+1)}$ and $\mathbf{y}_{S_1(j+1)}$ [Eq. (13)]. Similarly, at iteration $j+2,$ the value of ${\mathbf {Y}}_{S_1 (j+2)\cap S_2 (j+1)}^{(j+2)}$ will linearly depend on ${\mathbf {Y}}_{S_2 (j+2)}^{(j+2)},{\mathbf {Y}}_{S_2 (j+2)}^{(j+1)}$ and ${\mathbf {Y}}_{S_1 (j+2)\cap S_2 (j+1)}^{(j+1)}$; since this last vector (of size $m_{j+2} \le p)$ is a sub-vector of ${\mathbf {Y}}_{S_2 (j+1)}^{(j+1)}$, it can take any value in ${\mathbb {R}}^{m_{j+2}}.$ Adding the fact that ${\mathbf {Y}}_{S_2 (j+2)}^{(j+2)}$ can take any value in ${\mathbb {R}}^{p}$, the augmented vector ${\mathbf {Y}}_{S_2 (j+1)\cup S_2 (j+2)}^{(j+2)}$ can take any value in ${\mathbb {R}}^{p+m_{j+2} }$. Through recursive reasoning, at iteration $j+h$, it is seen that the vector ${\mathbf {Y}}_{S(j,h)}^{(j+h)}$, with $S(j,h)=\bigcup \nolimits _{i=1}^h {S_2 (j+i)}$, can take any value in ${\mathbb {R}}^{\mathrm{card}(S(j,h))}$. As the selection strategy is such that every element of $\{1,\ldots ,n\}$ will belong to $S_{2}(j+i)$ for some positive integer $i$, one finally has $S(j,h) = \{1,\ldots ,n\}$ for sufficiently large $h$, meaning that every state of ${\mathbb {R}}^{n}$ can be reached by the chain in a finite number of iterations.

As for the third property (existence of an invariant distribution), let $\{Y(\mathbf{x}): \mathbf{x} \in {\mathbb {R}}^{d}\}$ be a representation of an IRF-$k$ with generalized covariance function $K(\mathbf{h})$ and multivariate Gaussian generalized increments, such that $Y(\mathbf{U})=\mathbf{0}.$ Further assume that, for some $j \ge 1,$ $\mathbf{Y}^{(j-1)}$ has the same distribution as $Y(\mathbf{X}),$ that is, $({\mathbf {Y}}_{S_1 (j)}^{(j-1)},{\mathbf {Y}}_{S_2 (j)}^{(j-1)} )\mathop =\limits ^{\mathsf {d}} ({\mathbf {Y}}_{S_1 (j)} ,{\mathbf {Y}}_{S_2 (j)} )$, where ${\mathbf {Y}}_{S_1 (j)}$ and ${\mathbf {Y}}_{S_2 (j)}$ stand for $Y(\mathbf{X}_{S_1 (j)} )$ and $Y(\mathbf{X}_{S_2 (j)} )$, respectively. Then,

• ${\mathbf {Y}}_{S_2 (j)}$ can be written as the sum of two terms: (i) its intrinsic kriging $[{\mathbf {Y}}_{S_2 (j)}]^{*}$ from $Y(\mathbf{U})$ and (ii) the associated kriging error ${\mathbf {Y}}_{S_2 (j)} -[{\mathbf {Y}}_{S_2 (j)} ]^{*}$. As $Y(\mathbf{U})=\mathbf{0},$ the former is a vector of zeros, while the latter is a zero-mean Gaussian random vector with variance–covariance matrix ${\mathbf {C}}_{22}^{(j)}$. Because $\mathbf{A}^{(j)}$ is a symmetric square root of ${\mathbf {C}}_{22}^{(j)}$, the vector ${\mathbf {A}}^{(j)}{\mathbf {V}}^{(j)}$ defined in Eq. (12) is also Gaussian with zero mean and variance–covariance matrix ${\mathbf {C}}_{22}^{(j)}$ (Davis 1987b), that is, ${\mathbf {A}}^{(j)}{\mathbf {V}}^{(j)}\mathop =\limits ^{\mathsf {d}} {\mathbf {Y}}_{S_2 (j)} -[{\mathbf {Y}}_{S_2 (j)} ]^{*}$. Hence, ${\mathbf {Y}}_{S_2 (j)}^{(j)} \mathop =\limits ^{\mathsf {d}} {\mathbf {Y}}_{S_2(j)}$.

• Likewise, ${\mathbf {Y}}_{S_1 (j)}$ is the sum of two terms: (i) its intrinsic kriging $[{\mathbf {Y}}_{S_1 (j)} ]^{**}$ from ${\mathbf {Y}}_{S_2 (j)}$ and $Y(\mathbf{U}),$ and (ii) the associated kriging error, $\varvec{\upvarepsilon }_{S_1 (j)} ={\mathbf {Y}}_{S_1 (j)} -[{\mathbf {Y}}_{S_1 (j)} ]^{**}$. On the one hand, these two terms have the same distributions as the kriging predictor $[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}$ and kriging error ${\varvec{\upvarepsilon }}_{S_1 (j)}^{(j-1)} ={\mathbf {Y}}_{S_1 (j)}^{(j-1)} -[{\mathbf {Y}}_{S_1 (j)}^{(j-1)} ]^{**}$ defined in Eq. (13), respectively, insofar as ${\mathbf {Y}}_{S_2 (j)} \mathop =\limits ^{\mathsf {d}} {\mathbf {Y}}_{S_2 (j)}^{(j)}$ and $({\mathbf {Y}}_{S_1 (j)},{\mathbf {Y}}_{S_2 (j)} )\mathop =\limits ^{{\mathsf {d}}} ({\mathbf {Y}}_{S_1 (j)}^{(j-1)},{\mathbf {Y}}_{S_2 (j)}^{(j-1)})$. On the other hand, because $\mathbf{V}^{(j)}$ is independent of $\mathbf{Y}^{(j-1)}$, $[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}$ and ${\varvec{\upvarepsilon }}_{S_1 (j)}^{(j-1)}$ are independent. The same happens for $[{\mathbf {Y}}_{S_1 (j)} ]^{**}$ and ${\varvec{\upvarepsilon }}_{S_1 (j)}$: the latter is independent of any generalized increment of ${\mathbf {Y}}_{S_2 (j)}$, thus it is independent of ${\mathbf {Y}}_{S_2 (j)}$ itself [recall that the components of ${\mathbf {Y}}_{S_2 (j)}$ are already generalized increments (Eq. (10))] and, as a consequence, independent of $[{\mathbf {Y}}_{S_1 (j)} ]^{**}$. In summary, one has

  $$\begin{aligned} \left\{ {\begin{array}{l} {\mathbf {Y}}_{S_1 (j)} =[{\mathbf {Y}}_{S_1 (j)} ]^{**}+{\varvec{\upvarepsilon }}_{S_1 (j)} \\ {\mathbf {Y}}_{S_1 (j)}^{(j)} =[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}+{\varvec{\upvarepsilon }}_{S_1 (j)}^{(j-1)} \end{array}}\right. \end{aligned}$$

  (19)

  with $[{\mathbf {Y}}_{S_1 (j)} ]^{**}\mathop =\limits ^{\mathsf {d}}[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}$, ${\varvec{\upvarepsilon }}_{S_1 (j)} \mathop =\limits ^{\mathsf {d}} {\varvec{\upvarepsilon }}_{S_1 (j)}^{(j-1)}$, $[{\mathbf {Y}}_{S_1 (j)} ]^{**}$ independent of ${\varvec{\upvarepsilon }}_{S_1 (j)}$, and $[{\mathbf {Y}}_{S_1 (j)}^{(j)} ]^{**}$ independent of ${\varvec{\upvarepsilon }}_{S_1 (j)}^{(j-1)}$. It follows that ${\mathbf {Y}}_{S_1 (j)}$ and ${\mathbf {Y}}_{S_1 (j)}^{(j)}$ are equally distributed, that is, ${\mathbf {Y}}_{S_1 (j)} \mathop =\limits ^{\mathsf {d}}{\mathbf {Y}}_{S_1 (j)}^{(j)}$.

Therefore, it has been shown that, if ${\mathbf {Y}}^{(j-1)}\mathop =\limits ^{\mathsf {d}} Y(\mathbf{X})$, then ${\mathbf {Y}}^{(j)}\mathop =\limits ^{\mathsf {d}} Y(\mathbf{X})$. The distribution of the chosen representation of the IRF-$k$ (the representation vanishing at U) is invariant for the transition matrix of the chain. This completes the proof for the convergence of Algorithm 2, given that the three necessary properties (aperiodicity, irreducibility and existence of an invariant distribution) have been established: the sequence of random vectors $\{\mathbf{Y}^{(j)}: j \in {\mathbb {N}}\}$ converges in distribution to $\mathbf{Y}=Y(\mathbf{X}).$