Simulating Large Gaussian Random Vectors Subject to Inequality Constraints by Gibbs Sampling

Abstract

The Gibbs sampler is an iterative algorithm used to simulate Gaussian random vectors subject to inequality constraints. This algorithm relies on the fact that the distribution of a vector component conditioned by the other components is Gaussian, the mean and variance of which are obtained by solving a kriging system. If the number of components is large, kriging is usually applied with a moving search neighborhood, but this practice can make the simulated vector not reproduce the target correlation matrix. To avoid these problems, variations of the Gibbs sampler are presented. The conditioning to inequality constraints on the vector components can be achieved by simulated annealing or by restricting the transition matrix of the iterative algorithm. Numerical experiments indicate that both approaches provide realizations that reproduce the correlation matrix of the Gaussian random vector, but some conditioning constraints may not be satisfied when using simulated annealing. On the contrary, the restriction of the transition matrix manages to satisfy all the constraints, although at the cost of a large number of iterations.

1 Introduction

The simulation of Gaussian random vectors subject to inequality constraints arises in the analysis of spatial data, when all or part of the data values are interval constraints rather than single numbers. In a mineral resources evaluation, this situation occurs when the depth of a geological horizon is greater than the depth at which drilling has been stopped, when a measured grade is smaller than a detection limit, or when working with soft data defined by lower and upper bounds (Journel 1986). Interval constraints are also encountered when simulating continuous variables represented by chi-square random fields, as well as indicators and categorical variables represented by truncated Gaussian or plurigaussian random fields (Matheron et al. 1987; Le Loc’h et al. 1994; Bárdossy 2006; Emery 2005, 2007a, 2007b; Armstrong et al. 2011). For instance, let d be a positive integer and consider an indicator variable obtained by truncating a stationary Gaussian random field $Y = \{Y(\mathbf{x}): \mathbf{x} \in \mathbb {R}^{d}\}$ at a given threshold $y \in \mathbb {R}$. The following procedure can be used to simulate the indicator (Lantuéjoul 2002):

• (1) Simulate Y at the data locations, conditioned by the indicator data.

• (2) Simulate Y at the target locations of $\mathbb {R}^{d}$, conditioned by the Y-vector obtained in step (1).

• (3) Truncate the simulated Gaussian random field to obtain a realization of the indicator.

Any multivariate Gaussian simulation algorithm can be considered in step (2). Regarding step (1), one can use an iterative algorithm known as the Gibbs sampler. This algorithm is currently widely used to simulate Gaussian random vectors subject to constraints and relies on the fact that the value of Y at a given data location, conditioned by the values at the other data locations, has a Gaussian distribution whose mean and variance can be calculated by solving a kriging system (Geweke 1991; Freulon and de Fouquet 1993; Freulon 1994; Wilhelm and Manjunath 2011). In practice, when the data are numerous, kriging is performed with a moving search neighborhood rather than with a unique search neighborhood, which may make the simulated vector not follow the desired distribution. These problems are investigated in the following sections, by considering first the case of nonconditional simulation (Sect. 2), then the case of conditional simulation (Sect. 3).

2 Nonconditional Simulation

In this section, it is of interest to simulate a Gaussian random field with zero mean, unit variance, and known spatial correlation structure at a set of n locations x ₁,…,x _n of $\mathbb {R}^{d}$. Put another way, one wants to simulate a Gaussian random vector Y=(Y ₁,…,Y _n )^T with zero mean and variance-covariance matrix C=[C _ij ] _i,j=1,…,n having unit diagonal entries

$$ \forall i \in \{ 1,\ldots,n\},\quad C_{ii} = 1. $$

(1)

2.1 Using a Unique Search Neighborhood

Y can be simulated iteratively by Gibbs sampling: At each iteration, one of the vector components is selected and updated according to its distribution conditional to the other components. Specifically, the algorithm is as follows.

Algorithm 1

(Traditional Gibbs Sampler, Unique Search Neighborhood)

• (1) Initialize the simulation by an arbitrary vector of size n, for example, Y ⁽⁰⁾=(0,…,0)^T.

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}. Any selection strategy can be considered (regular selection, pure random selection, etc.), provided that all the indices in {1,…,n} are selected infinitely often as K tends to infinity (Amit and Grenander 1991; Roberts and Sahu 1997; Levine and Casella 2006). This condition will be assumed to be satisfied in all the algorithms presented in this work.

  • (b) Set Y ^(k)=Y ^(k−1), except for the ith component that is replaced by

    $$ Y_{i}^{(k)} = \sum_{j \ne i} \lambda_{j,i}Y_{j}^{(k - 1)} + \sigma_{i}U^{(k)}, $$

    (2)

    where λ _j,i is the simple kriging weight assigned to Y _j when estimating Y _i , $\sigma_{i}^{2}$ is the associated simple kriging variance and U ^(k) is a standard Gaussian random variable independent of $\{ Y_{j}^{(k - 1)}:j \ne i\}$.

• (3) Return Y ^(K).

The sequence of simulated vectors $\{\mathbf{Y}^{(k)}: k \in \mathbb {N}\}$ forms a Markov chain whose state space is $\mathbb {R}^{n}$. The chain is aperiodic and irreducible, that is, any state can be reached from any other state by a finite number of steps. Furthermore, the target Gaussian distribution is invariant for the transition matrix of the chain, that is, if Y ^(k−1) is a Gaussian random vector with zero mean and variance-covariance matrix C, then so is Y ^(k). Altogether, these three properties (irreducibility, aperiodicity, and existence of an invariant distribution) imply that the chain converges in distribution to a Gaussian random vector with zero mean and variance-covariance matrix C (Tierney 1994; Roberts 1996; Lantuéjoul 2002). In practice, the chain is stopped after a finite number K of iterations, resulting in a random vector Y ^(K) whose distribution may differ from the target distribution, although the difference (measured by the total variation distance between distributions) becomes negligible if K is large enough. Several practical criteria to determine how large K must be have been proposed in the literature (Lantuéjoul 2002; Emery 2007a, 2008; Armstrong et al. 2011).

2.2 Using a Moving Search Neighborhood

If n is greater than a few thousands, calculating the kriging weights and kriging variances becomes computationally prohibitive. To circumvent this issue, one option is to apply kriging with a moving search neighborhood and to modify the algorithm as follows (Freulon and de Fouquet 1993).

Algorithm 2

(Traditional Gibbs Sampler, Moving Search Neighborhood)

• (1) Initialize the simulation by an arbitrary vector of size n, for example, Y ⁽⁰⁾=(0,…,0)^T.

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}.

  • (b) Find the subset J of indices such that {x _j :j∈J} belong to a neighborhood centered on x _i with given characteristics (maximum distance to x _i along each direction, splitting into angular sectors, maximum number of locations within each sector, etc.).

  • (c) Set Y ^(k)=Y ^(k−1), except for the ith component that is replaced by

    $$ Y_{i}^{(k)} = \sum_{j \ne i} \tilde{ \lambda}_{j,i}Y_{j}^{(k - 1)} + \tilde{ \sigma}_{i}U^{(k)}, $$

    (3)

    where $\tilde{\lambda}_{j,i}$ and $\tilde{\sigma}_{i}^{2}$ are the simple kriging weights and simple kriging variance obtained when estimating Y _i from {Y _j :j∈J,j≠i}, and U ^(k) is a standard Gaussian random variable independent of $\{ Y_{j}^{(k - 1)}:j \ne i\}$. In Eq. (3), the convention $\tilde{\lambda}_{j,i} = 0$ has been used for j∉J.

• (3) Return Y ^(K).

As in Algorithm 1, the sequence of simulated vectors $\{\mathbf{Y}^{(k)}: k \in \mathbb {N}\}$ forms a irreducible and aperiodic Markov chain whose state space is $\mathbb {R}^{n}$. Whether or not this chain converges in distribution depends on whether or not there exists a distribution that is invariant for the transition matrix of the chain (Tierney 1994; Lantuéjoul 2002). To find out this invariant distribution, first note that at each iteration the random vector Y ^(k) is a zero-mean Gaussian random vector. Hence, if it exists, the invariant distribution should be Gaussian with zero mean. Let $\tilde{\mathbf{C}} = [\tilde{C}_{ij}]_{i,j = 1,\ldots,n}$ be its variance-covariance matrix. Then, if Y ^(k−1) is a Gaussian random vector with zero mean and variance-covariance matrix $\tilde{\mathbf{C}}$, so is Y ^(k). Using Eq. (3), this implies the following identities

$$\begin{aligned} \forall i \in \{ 1,\ldots,n\},\ \forall \ell \in \{ 1,\ldots,n\} - \{ i\},\quad \tilde{C}_{i\ell} =& {\mathop{\mathrm{cov}}} \bigl\{ Y_{i}^{(k)},Y_{\ell}^{(k)} \bigr\} \\ =& \sum_{j \ne i} \tilde{\lambda}_{j,i}{ \mathop{\mathrm{cov}}} \bigl\{ Y_{j}^{(k - 1)},Y_{\ell}^{(k - 1)} \bigr\} \\ =& \sum_{j \ne i} \tilde{\lambda}_{j,i} \tilde{C}_{j\ell}, \end{aligned}$$

(4)

and

$$\begin{aligned} \forall i \in \{ 1,\ldots,n\},\quad \tilde{C}_{ii} =& {\mathop{ \mathrm{cov}}} \bigl\{ Y_{i}^{(k)},Y_{i}^{(k)} \bigr\} \\ =& \sum_{j \ne i} \sum_{\ell \ne i} \tilde{\lambda}_{j,i}\tilde{\lambda}_{\ell,i}{\mathop{ \mathrm{cov}}} \bigl\{ Y_{j}^{(k - 1)},Y_{\ell}^{(k - 1)} \bigr\} + \tilde{\sigma}_{i}^{2}{\mathop{\operatorname{var}}} \bigl\{ U^{(k)}\bigr\} \\ =& \sum_{j \ne i} \sum_{\ell \ne i} \tilde{\lambda}_{j,i}\tilde{\lambda}_{\ell,i}\tilde{C}_{j\ell} + \tilde{\sigma}_{i}^{2}. \end{aligned}$$

(5)

Using Eq. (4), Eq. (5) becomes

$$ \forall i \in \{ 1,\ldots,n\},\quad\tilde{C}_{ii} = \sum _{\ell \ne i} \tilde{\lambda}_{\ell,i}\tilde{C}_{i\ell} + \tilde{\sigma}_{i}^{2}. $$

(6)

Equations (4) and (6) can be rewritten in matrix form

$$ \tilde{\mathbf{B}}\tilde{\mathbf{C}} = \mathbf{I}, $$

(7)

with I the identity matrix of size n×n and

$$ \tilde{\mathbf{B}} = \left ( \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \frac{1}{\tilde{\sigma}_{1}^{2}} & \frac{ - \tilde{\lambda}_{2,1}}{\tilde{\sigma}_{1}^{2}} & \cdots & \frac{ - \tilde{\lambda}_{n - 1,1}}{\tilde{\sigma}_{1}^{2}} & \frac{ - \tilde{\lambda}_{n,1}}{\tilde{\sigma}_{1}^{2}} \\ \frac{ - \tilde{\lambda}_{1,2}}{\tilde{\sigma}_{2}^{2}} & \frac{1}{\tilde{\sigma}_{2}^{2}} & & \frac{ - \tilde{\lambda}_{n - 1,2}}{\tilde{\sigma}_{2}^{2}} & \frac{ - \tilde{\lambda}_{n,2}}{\tilde{\sigma}_{2}^{2}} \\ \vdots & & \ddots & & \vdots \\ \frac{ - \tilde{\lambda}_{1,n - 1}}{\tilde{\sigma}_{n - 1}^{2}} & \frac{ - \tilde{\lambda}_{2,n - 1}}{\tilde{\sigma}_{n - 1}^{2}} & & \frac{1}{\tilde{\sigma}_{n - 1}^{2}} & \frac{ - \tilde{\lambda}_{n,n - 1}}{\tilde{\sigma}_{n - 1}^{2}} \\ \frac{ - \tilde{\lambda}_{1,n}}{\tilde{\sigma}_{n}^{2}} & \frac{ - \tilde{\lambda}_{2,n}}{\tilde{\sigma}_{n}^{2}} & \cdots & \frac{ - \tilde{\lambda}_{n - 1,n}}{\tilde{\sigma}_{n}^{2}} & \frac{1}{\tilde{\sigma}_{n}^{2}} \end{array} \right ). $$

(8)

Accordingly, if it exists, the Gaussian distribution with zero mean and variance-covariance matrix $\tilde{\mathbf{C}} = \tilde{\mathbf{B}}^{ - 1}$ is invariant for the transition matrix and, therefore, is the limit distribution of the chain. In the case of a unique search neighborhood (Algorithm 1), it is known (Dubrule 1983) that $\tilde{\mathbf{B}}$ is the inverse of C, thus the chain converges in distribution to a Gaussian random vector with zero mean and variance-covariance matrix C. However, in the case of a moving search neighborhood (Algorithm 2), the chain may not converge in distribution because $\tilde{\mathbf{C}}$ may not be a valid variance-covariance matrix, that is, a symmetric positive semidefinite matrix. The conditions for the existence of a limit distribution are:

• (1) $\tilde{\mathbf{B}}$ is a symmetric matrix, that is,

  $$ \forall i,j \in \{ 1,\ldots,n\},\quad \tilde{\lambda}_{j,i}\tilde{ \sigma}_{j}^{2} = \tilde{\lambda}_{i,j}\tilde{ \sigma}_{i}^{2}. $$

  (9)

• (2) The eigenvalues of $\tilde{\mathbf{B}}$ are nonnegative.

2.3 Numerical Experiments

To study the effect of a moving search neighborhood, numerical experiments have been conducted with the following parameters:

• The simulated random vector Y is a realization of a stationary Gaussian random field with an isotropic spherical covariance (Case 1) or an isotropic cubic covariance (Case 2), in both cases with a range of 15 units, over a regular two-dimensional grid with 50×50 nodes and a mesh of 1×1.

• The grid nodes are visited according to a random permutation strategy (Galli and Gao 2001) and the Gibbs sampler is stopped after 2,500,000 iterations, which corresponds to 1,000 permutations.

• The moving search neighborhood used for calculating the kriging weights and kriging variances is a disc centered at the target node. Three disc radii are considered (5, 15, and 25 units), for which the number of grid nodes found in the neighborhood can reach 80, 708, and 1960, respectively.

Figures 1 and 2 present the map of the final realization and a plot of the minimum and maximum simulated values as a function of the iteration number. When using a moving search neighborhood of 5 or 25 units, the apparent spatial variations agree with the covariance models (continuous variations for the spherical covariance, smooth variations for the cubic covariance), while the minimum and maximum simulated values fluctuate in a range that is consistent with what is expected from a standard Gaussian random field. However, things go wrong with a moving search neighborhood of 15 units: The map shows exaggeratedly smooth spatial variations or artifacts (Figs. 1(b) and 2(b)), and the range of the extreme simulated values becomes excessively large when the number of iterations increases (Figs. 1(e) and 2(e)). To explain these results, it is interesting to have a look at the matrix $\tilde{\mathbf{B}}$ defined in Eq. (8). Table 1 summarizes some properties of this matrix (minimum real eigenvalue, number of complex nonreal eigenvalues, maximum imaginary part of the complex eigenvalues, Frobenius norm of $\tilde{\mathbf{B}} - \tilde{\mathbf{B}}^{T}$ relative to the Frobenius norm of $\tilde{\mathbf{B}}$) in each case. These properties allow checking whether or not $\tilde{\mathbf{B}}$ satisfies the conditions for the existence of a limit distribution and, if not, how distant is this matrix from a symmetric positive semidefinite matrix. Not surprisingly, the case with a moving search neighborhood of radius 15 is the one for which $\tilde{\mathbf{B}}$ is far from being symmetric (higher relative Frobenius norm of $\tilde{\mathbf{B}} - \tilde{\mathbf{B}}^{T}$, larger number of nonreal eigenvalues) and has negative real eigenvalues with larger absolute values. Note that the requirement for a symmetric matrix (Eq. (9)) are never satisfied, thus, in all the cases, the sequences of simulated vectors do not converge in distribution. Accordingly, even with the moving search neighborhoods of radius 5 or 25, the observed spatial variations or the range of simulated values may not agree with the target distribution if the algorithm is stopped after more iterations.

Fig. 1

(a), (b), (c), maps of realizations obtained after 2,500,000 iterations by using three moving search neighborhoods; (d), (e), (f), minimum and maximum simulated values as a function of the iteration number (Case 1: isotropic spherical model)

Fig. 2

(a), (b), (c), maps of realizations obtained after 2,500,000 iterations by using three moving search neighborhoods; (d), (e), (f), minimum and maximum simulated values as a function of the iteration number (Case 2: isotropic cubic model)

Table 1 Properties of matrix $\tilde{\mathbf{B}}$ for each covariance model and moving search neighborhood

2.4 An Alternative for a Unique Search Neighborhood

To avoid using a moving search neighborhood, an alternative has been proposed by Galli and Gao (2001) and further examined by Lantuéjoul and Desassis (2012) and Arroyo et al. (2012). Let B=C ⁻¹ and X=BY (equivalently, Y=CX). Instead of simulating Y, the idea is to simulate X, which is a Gaussian random vector with zero mean and variance-covariance matrix B, and to set Y=CX once the simulation of X is completed. As the determination of kriging weights and kriging variances relies on the inverse of the variance-covariance matrix (i.e., B ⁻¹=C), it is no longer necessary to invert C, so that a unique search neighborhood can be considered. The algorithm is therefore as follows.

Algorithm 3

(Gibbs Sampler on X, Unique Search Neighborhood)

• (1) Initialize the simulation by an arbitrary vector of size n, for example, X ⁽⁰⁾=(0,…,0)^T.

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}.

  • (b) Set X ^(k)=X ^(k−1), except for the ith component that is replaced by

    $$ X_{i}^{(k)} = \sum_{j \ne i} \varpi_{j,i}X_{j}^{(k - 1)} + s_{i}V^{(k)}, $$

    (10)

    where ϖ _j,i is the simple kriging weight assigned to X _j when estimating X _i , $s_{i}^{2}$ is the associated simple kriging variance and V ^(k) is a standard Gaussian random variable independent of $\{ X_{j}^{(k - 1)}:j \ne i\}$. Letting C _ij be the entry of C at row i and column j, then (Dubrule 1983)

    $$\begin{aligned} s_{i}^{2} =& \frac{1}{C_{ii}}, \end{aligned}$$

    (11)
    $$\begin{aligned} \varpi_{j,i} =& - \frac{C_{ij}}{C_{ii}}. \end{aligned}$$

    (12)

    Let Y ^(k)=CX ^(k). Recalling that C _ii =1 (Eq. (1)), Eq. (10) can be rewritten as

    $$ X_{i}^{(k)} = X_{i}^{(k - 1)} - Y_{i}^{(k - 1)} + V^{(k)}. $$

    (13)

• (3) Return Y ^(K)=CX ^(K).

To speed up calculations, one can rewrite Algorithm 3 to directly simulate Y.

Algorithm 4

(Gibbs Sampler on Y, Unique Search Neighborhood)

• (1) Initialize the simulation by an arbitrary vector of size n, for example, Y ⁽⁰⁾=(0,…,0)^T.

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}.

  • (b) Set Y ^(k)=Y ^(k−1)+δ C _i , where C _i is the ith column of C, $\delta = - Y_{i}^{(k - 1)} + V^{(k)}$ and V ^(k) is a standard Gaussian random variable independent of Y ^(k−1).

• (3) Return Y ^(K).

This algorithm has been recently proposed by Lantuéjoul and Desassis (2012) and Arroyo et al. (2012). Using different approaches, these authors also established a variant in which several indices are selected in step 2(a).

3 Simulation Conditioned to Inequality Constraints

In the scope of truncated Gaussian and plurigaussian simulation, it is necessary to simulate the Gaussian random vector Y subject to inequality constraints on its components

$$ \forall i \in \{ 1,\ldots,n\},\quad a_{i} < Y_{i} < b_{i}, $$

(14)

where the bounds a ₁,…,a _n ,b ₁,…,b _n are real numbers or infinite. Two approaches (simulated annealing and restriction of the transition matrix) will be explored.

3.1 Simulated Annealing

Simulated annealing is an iterative procedure that can be used to simulate random vectors subject to complex conditioning constraints (Lantuéjoul 2002; Chilès and Delfiner 2012). The algorithm relies on three components: (i) a Markov chain that has the nonconditional distribution (here, a Gaussian with zero mean and variance-covariance matrix C) as its limit distribution, (ii) an objective function O(.) that measures the discrepancy between the simulated vector and the conditioning constraints, and (iii) a cooling schedule that defines a temperature t _k at the kth iteration of the algorithm. For instance, the objective function can be defined as follows

$$ O(\mathbf{Y}) = \sum_{i = 1}^{n} \bigl(\max \{ a_{i} - Y_{i},0\} + \max \{ Y_{i} - b_{i},0\} \bigr), $$

(15)

so that O(Y)≥0, with the equality O(Y)=0 if all the conditioning constraints are satisfied. As for the temperature, one example is to consider a cooling schedule of the form

$$ \forall k > 0,\quad t_{k} = t_{0}\alpha^{k}, $$

(16)

with given values of t ₀ in ]0,+∞[ and α in ]0,1[.

To avoid convergence problems due to a moving search neighborhood, the Markov chain considered for the simulated annealing procedure will be the Gibbs sampler proposed in Sect. 2.4 (Algorithm 4).

Algorithm 5

(Gibbs Sampler Combined with Simulated Annealing)

• (1) Initialize the simulation by an arbitrary vector Y ⁽⁰⁾ of size n, for example, a vector of zeros or a nonconditional realization of Y.

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}.

  • (b) Set Y′=Y ^(k−1)+δ C _i , where C _i is the ith column of C, $\delta = - Y_{i}^{(k - 1)} + V^{(k)}$ and V ^(k) is a standard Gaussian random variable independent of Y ^(k−1).

  • (c) Simulate a random variable U uniformly distributed in [0,1].

  • (d) Calculate the current temperature t _k , according to the chosen cooling schedule.

  • (e) If $U < \exp \{ \frac{O(\mathbf{Y}^{(k - 1)}) - O(\mathbf{Y}\boldsymbol{'})}{t_{k}}\}$, set Y ^(k)=Y′. Otherwise, set Y ^(k)=Y ^(k−1).

• (3) Return Y ^(K).

One issue with the above algorithm is that the rate of convergence to the target conditional distribution may be slow, depending on the chosen initial state and cooling schedule. If the algorithm is stopped after a finite number (K) of iterations, one obtains a random vector Y ^(K) that may not satisfy all the conditioning constraints (Eq. (14)). An illustration of this situation will be presented at Sect. 3.3.

3.2 Restriction of the Transition Matrix

The idea of restricting the transition matrix of the Gibbs sampler has been proposed by several authors (Geweke 1991; Freulon and de Fouquet 1993; Kotecha and Djuric 1999; Wilhelm and Manjunath 2011), who modified Algorithm 1 to forbid any transition to a state that does not satisfy the conditioning constraints (Eq. (14)). In practice, when the number n of vector components is large, a unique search neighborhood is impractical and a moving search neighborhood is used instead (Freulon and de Fouquet 1993), but as seen in Sect. 2.2, this is likely to make the sequence of simulated vectors not converge in distribution. To avoid such problems, rather than Algorithm 1, one can consider Algorithm 3 and restrict its transition matrix, as explained next.

Algorithm 6

(Gibbs Sampler on X, with Restriction of the Transition Matrix)

• (1) Initialize the simulation by a vector X ⁽⁰⁾ that satisfies the conditioning constraints. This requires finding a solution to the following system of linear inequalities

  $$ \forall i \in \{ 1,\ldots,n\},\quad a_{i} < \sum _{j = 1}^{n} C_{ij}X_{j} < b_{i}. $$

  (17)

  The set of solutions of the above system is an open convex region of $\mathbb {R}^{n}$, delimited by the hyperplanes defined by the equations $\sum_{j = 1}^{n} C_{ij}X_{j} = a_{i}$ and $\sum_{j = 1}^{n} C_{\ell j}X_{j} = b_{\ell}$ for all the indices i and ℓ such that a _i and b _ℓ are finite.

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}.

  • (b) Set X ^(k)=X ^(k−1), except for the ith component that is replaced by

    $$ X_{i}^{(k)} = \sum_{j \ne i} \varpi_{j,i}X_{j}^{(k - 1)} + V^{(k)}, $$

    (18)

    where ϖ _j,i is the simple kriging weight assigned to X _j when estimating X _i and V ^(k) is a standard Gaussian random variable independent of $\{ X_{j}^{(k - 1)}:j \ne i\}$ satisfying the constraints in Eq. (17). V ^(k) has a truncated Gaussian distribution whose range of values is an open interval bounded by (Eqs. (17)–(18))

    $$ \max_{p \in \{ 1,\ldots,n\}: C_{pi} \ne 0} \biggl\{ \min \biggl( \frac{a_{p} - \beta_{pi}}{C_{pi}}, \frac{b_{p} - \beta_{pi}}{C_{pi}} \biggr) \biggr\} $$

    (19)

    and

    $$ \min_{p \in \{ 1,\ldots,n\}: C_{pi} \ne 0} \biggl\{ \max \biggl( \frac{a_{p} - \beta_{pi}}{C_{pi}}, \frac{b_{p} - \beta_{pi}}{C_{pi}} \biggr) \biggr\} , $$

    (20)

    with $\beta_{pi} = \sum_{j \ne i} (C_{pj} + C_{pi}\varpi_{j,i})X_{j}^{(k - 1)}$.

  • (c) Set Y ^(k)=CX ^(k).

• (3) Return Y ^(K).

The sequence of simulated vectors $\{\mathbf{X}^{(k)}: k \in \mathbb {N}\}$ forms a Markov chain that is aperiodic and irreducible: Irrespective of the current state, any point of the convex open region solution of Eq. (17) can be reached in a finite number of iterations. Furthermore, let X=BY be a Gaussian random vector with zero mean and variance-covariance matrix B=C ⁻¹, and assume that X ^(k−1) is a random vector with the distribution of X conditioned by the inequality constraints in Eq. (17). Because the transition matrix in step (2) is identical to the transition matrix of Algorithm 3, except for the restrictions Eqs. (19) and (20) that make X ^(k) satisfy Eq. (17), the distribution of X ^(k) is the same as that of X ^(k−1), that is, this distribution is invariant for the transition matrix. Hence, the conditions for convergence (irreducibility, aperiodicity, and existence of an invariant distribution) are satisfied (Lantuéjoul 2002): The chain $\{\mathbf{X}^{(k)}: k \in \mathbb {N}\}$ converges in distribution to a Gaussian random vector with zero mean and variance-covariance matrix B conditioned by the constraints of Eq. (17). Equivalently, the chain $\{\mathbf{Y}^{(k)}: k \in \mathbb {N}\}$ converges in distribution to a Gaussian random vector with zero mean and variance-covariance matrix C conditioned by the constraints of Eq. (14). In practice, the main difficulty of Algorithm 6 is the initialization step, for which one may need to solve a large system of linear inequalities. To avoid this difficulty, it is convenient to rewrite this algorithm to directly simulate Y, as proposed next.

Algorithm 7

(Gibbs Sampler on Y, with Restriction of the Transition Matrix)

• (1) Initialize the simulation by a vector Y ⁽⁰⁾ that satisfies the conditioning the constraints of Eq. (14).

• (2) For k=1,2,…,K:

  • (a) Select an index i∈{1,…,n}.

  • (b) Set Y ^(k)=Y ^(k−1)+δ C _i , where C _i is the ith column of C, $\delta = - Y_{i}^{(k - 1)} + V^{(k)}$ and V ^(k) is a truncated Gaussian random variable independent of Y ^(k−1), such that the conditioning constraints of Eq. (14) are satisfied. The bounds for V ^(k) are

    $$ \max_{j \in \{ 1,\ldots,n\}:C_{ij} \ne 0} \biggl\{ \min \biggl( \frac{a_{j} - \gamma_{ij}}{C_{ij}}, \frac{b_{j} - \gamma_{ij}}{C_{ij}} \biggr) \biggr\} $$

    (21)

    and

    $$ \min_{j \in \{ 1,\ldots,n\}:C_{ij} \ne 0} \biggl\{ \max \biggl( \frac{a_{j} - \gamma_{ij}}{C_{ij}}, \frac{b_{j} - \gamma_{ij}}{C_{ij}} \biggr) \biggr\} , $$

    (22)

    with $\gamma_{ij} = Y_{j}^{(k - 1)} - C_{ij}Y_{i}^{(k - 1)}$.

• (3) Return Y ^(K).

As this algorithm is formally equivalent to Algorithm 6, the chain $\{\mathbf{Y}^{(k)}: k \in \mathbb {N}\}$ converges in distribution to a Gaussian random vector with zero mean and variance-covariance matrix C conditioned by the constraints of Eq. (14).

3.3 Numerical Experiments

We consider the two cases presented in Sect. 2.3 (simulation of a Gaussian random field with an isotropic spherical or cubic covariance model on a 50×50 grid) and now focus on simulation under inequality constraints. For the sake of simplicity, these constraints will be of the form

$$ \forall i \in \{1,\ldots, n\},\quad Y_{i} < 0\quad \mbox{or}\quad Y_{i} > 0. $$

(23)

Two simulation algorithms are used: simulated annealing (Algorithm 5) and restriction of the transition matrix (Algorithm 7). In simulated annealing, the initial state Y ⁽⁰⁾ is a nonconditional realization of Y obtained by Algorithm 4. The objective function and the cooling schedule presented in Eqs. (15) and (16) have been used, with an initial temperature t ₀=10,000 and a cooling parameter α=0.999999. For the restriction of the transition matrix approach, one option to define the initial state is to simulate each vector component Y _i via an acceptance-rejection method, by drawing a standard Gaussian random variable as many times as necessary until the simulated value satisfies the conditioning constraint (Eq. (23)). However, since the vector components are simulated independently one from another, this leads to an initial state with no spatial structure and a considerable number K of iterations are necessary to get a final random vector with the desired correlation matrix. To obtain a spatially structured initial state, another option is to run Algorithm 2 with a restriction of the transition matrix, that is, the distribution of U ^(k) in Eq. (3) is conditioned to the constraints given in Eq. (23). This option has been chosen in the experiments shown below, using a search radius of 5 units and a total of 2,500,000 iterations. For each covariance model (spherical and cubic), the experiment consists of the following steps:

• (1) Construct a nonconditional simulation of Y. This step has been achieved by using the algorithm proposed by Arroyo et al. (2012), a variant of Algorithm 4 in which several vector components (in the present case, four components associated with adjacent grid nodes) are selected at each iteration, instead of a single component.

• (2) Using the realization of step (1), define the conditioning constraints, depending on the signs of the simulated values (Eq. (23)).

• (3) Use these constraints to construct a conditional simulation of Y, using Algorithm 5 (simulated annealing) or Algorithm 7 (restriction of the transition matrix).

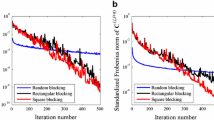
The overall procedure (steps 1–3) is repeated 50 times, with different seeds for random number generation each time. To ensure that the distribution of the simulated vector is close to the target conditional distribution, a large number of iterations (K=25,000,000) has been chosen for step (2) of Algorithms 5 and 7. This can be checked by comparing the experimental covariance of the conditional realizations with the prior covariance model: on average, the experimental covariance practically matches the prior model (Fig. 3). Reducing the number of iterations (for instance, to K=5,000,000) significantly decreases the computation time but may lead to a mismatch in the covariance reproduction, as illustrated in Fig. 4 for the restriction of the transition matrix algorithm applied to the simulation of a random vector with a cubic covariance. Examples of nonconditional and conditional realizations are presented in Fig. 5 for the restriction of the transition matrix (Algorithm 7), corroborating that the conditional realizations satisfy the interval constraints and have the same spatial correlation structure as the nonconditional realizations. A similar figure can be obtained for simulated annealing (Algorithm 5), except that some conditioning data are not satisfied as the algorithm is stopped before the objective function could reach a zero value (Fig. 6; Table 2). The number of conditioning data that are not satisfied could be decreased further at the cost of an increase of the number of iterations and of the associated computation time. From this viewpoint, the restriction of the transition matrix approach is preferable to simulated annealing.

Fig. 3

Prior covariance models (solid lines), experimental covariances (dashed lines) and average experimental covariances (stars) for conditional realizations obtained via simulated annealing (a), (b) and restriction of transition matrix (c), (d) with K=25,000,000 iterations

Fig. 4

Prior covariance model (solid line), experimental covariances (dashed lines) and average experimental covariances (stars) for conditional realizations obtained via restriction of transition matrix with K=5,000,000 iterations

Fig. 5

(a), (b), nonconditional realizations of Gaussian random fields; (c), (d), conditioning constraints (positive values in red, negative values in blue); (e), (f), examples of conditional realizations (restriction of transition matrix algorithm). Subfigures (a), (c), (e) correspond to spherical covariance model, and (b), (d), (f) to cubic covariance model

Fig. 6

Evolution of objective function with number of iterations for spherical (a) and cubic (b) covariance models (first realization)

Table 2 Number of conditioning constraints that are not satisfied after 25,000,000 iterations (statistics over 50 realizations)

4 Conclusions

The Gibbs sampler is an iterative algorithm that allows constructing a sequence of random vectors converging in distribution to a Gaussian random vector with zero mean and given variance-covariance matrix. However, convergence may no longer take place if a moving search neighborhood is used in the iteration stage. To avoid such problems, an alternative version of the algorithm has been presented, consisting of simulating a Gaussian random vector with the inverse covariance matrix. This new version can easily be performed with a unique search neighborhood. Furthermore, it lends itself to the simulation of a random vector conditioned to inequality constraints, by incorporating either a simulated annealing procedure or a restriction of the transition matrix in the iterative algorithm. In practice, simulated annealing only manages to approximately satisfy the conditioning constraints, whereas the restriction of the transition matrix can exactly satisfy these constraints. In both cases, a large number of iterations may be needed to accurately reproduce the target correlation matrix (for indication, the numerical experiments realized in this work have considered a number of iterations equal to ten thousand times the number of conditioning constraints). The number of iterations should be increased if the number of conditioning constraints increases or if these constraints are very restrictive (for example, if they consist of narrow intervals).