Spectral simulation of vector random fields with stationary Gaussian increments in d-dimensional Euclidean spaces

Abstract

This paper addresses the problem of simulating multivariate random fields with stationary Gaussian increments in a d-dimensional Euclidean space. To this end, one considers a spectral turning-bands algorithm, in which the simulated field is a mixture of basic random fields made of weighted cosine waves associated with random frequencies and random phases. The weights depend on the spectral density of the direct and cross variogram matrices of the desired random field for the specified frequencies. The algorithm is applied to synthetic examples corresponding to different spatial correlation models. The properties of these models and of the algorithm are discussed, highlighting its computational efficiency, accuracy and versatility.

1 Introduction

Random fields are extensively used in the earth and environmental sciences for spatial prediction and uncertainty quantification. To ease the inference of the spatial correlation structure, an assumption of stationarity is often made, by considering that the finite-dimensional distributions of the random field of interest are invariant under a translation in space (strict stationarity) or that the expectation and covariance function exist and are invariant under a translation in space (second-order stationarity) (Chilès and Delfiner 2012). However, these assumptions are sometimes questionable, in particular, in the presence of spatial trends, long-range dependence and persistence characteristics.

To cope with this situation, intrinsic random fields, i.e., random fields with second-order stationary increments, can be considered. A well-known example of such fields is the fractional Brownian surface, which has the property of repeating itself at all spatial scales (self-similarity). This model has been used in landscape modeling (Mandelbrot 1982; Palmer 1992; Arakawa and Krotkov 1994), seafloor topography (Malinverno 1995), geophysics (Jensen et al. 1991; Turcotte 1986, 1997), geology (Herzfeld 1993), hydrology (Chi et al. 1973; Molz et al. 2004), soil sciences (Comegna et al. 2013), environmental sciences (Ott 1981), image analysis (Peitgen and Saupe 1988; Chen et al. 1989; Huang and Turcotte 1989), telecommunication (Willinger et al. 1995), biology (Collins and De Luca 1994), ecology (Pozdnyakov et al. 2014), econometrics (Smith 1994; Asmussen and Taksar 1997) and social sciences (Romanow 1984), among other disciplines. Currently, a few exact algorithms exist for simulating a fractional Brownian surface, in particular the Cholesky factorization (Asmussen 1998; Michna 1999), circulant embedding approaches and discrete spectral representations (Beran 1994; Stein 2002; Danudirdjo and Hirose 2011). Approximate algorithms have also been designed, such as midpoint displacement approaches (Fournier et al. 1982; Voss 1985; Peitgen and Saupe 1988), wavelet representations (Combes et al. 1989; Flandrin 1989, 1992; Walker 1997; Dale and Mah 1998; Pipiras 2005; Albeverio et al. 2012), turning bands (Emery and Lantuéjoul 2008) and iterative algorithms based on Markov chains (Arroyo and Emery 2015). The reader is referred to Coeurjolly (2000), Chilès and Delfiner (2012) and references therein for details. Although most of these algorithms can be extended to the simulation of intrinsic random fields, they are applicable only for simulating at a limited number of locations or at evenly-spaced locations in $\mathbb {R}^d$. Two notable exceptions are the Gibbs sampler by Arroyo and Emery (2015) and the spectral turning-bands algorithm by Emery and Lantuéjoul (2008), which can approximately simulate intrinsic random fields at any set of locations in $\mathbb {R}^d$, irrespective of their spatial configuration.

The mathematical setting of the intrinsic random field theory is the following (Chilès and Delfiner 2012). A random field defined in a d-dimensional Euclidean space, say $Y=\{Y(\mathbf {x}):\mathbf {x}\in \mathbb {R}^d\}$, is an intrinsic random field without drift if the following conditions are satisfied:

• (1) Expectation of increments:

  $\forall \mathbf {x}, \mathbf {x}^{\prime} \in \mathbb {R}^{d},\mathbb {E}\left\{ Y(\mathbf {x}^{\prime}) - Y(\mathbf {x})\right\} = 0$.

• (2) Variance of increments:

  $\forall \mathbf {x}, \mathbf {x}^{\prime} \in \mathbb {R}^{d},\mathbb {E}\left\{ \left[ Y(\mathbf {x}^{\prime}) - Y(\mathbf {x})\right] ^{2}\right\} = 2 \gamma (\mathbf {\mathbf {x}^{\prime} - \mathbf {x}})$, where $\gamma$ is known as the variogram.

It can be shown (Appendix 1) that the covariance between any two increments exists and is invariant under a translation of the locations supporting these increments, therefore the intrinsic random field has second-order stationary increments. Since adding a constant to the random field does not change the above properties, a particular representation of the random field is often considered by setting $Y(\mathbf {0}) = 0$. Under this additional constraint, the previous two conditions are equivalent to expressing the expectation and covariance function of the intrinsic random field as follows (Appendix 1):

• (1′) Expectation: $\forall \mathbf {x}\in \mathbb {R}^{d},\mathbb {E}\left\{ Y(\mathbf {x})\right\} = 0$.

• (2′) Covariance function:

  $\forall \mathbf {x}, \mathbf {x}^{\prime} \in \mathbb {R}^{d},\mathbb {E}\left\{ Y(\mathbf {x}^{\prime})\cdot Y(\mathbf {x})\right\} = \gamma (\mathbf {x}^{\prime}) + \gamma (\mathbf {x}) - \gamma (\mathbf {x}^{\prime}-\mathbf {x})$.

For the purpose of simulation, one has to specify the finite-dimensional distributions of the intrinsic random field, not only its expectation and covariance function. In the following, we will consider the case of Gaussian random fields, i.e., random fields whose finite-dimensional distributions are multivariate Gaussian (multinormal). In such a case, the distribution of the increments is fully characterized by their first two moments (expectation and covariance function), so that the second-order stationarity of the increments is actually equivalent to their strict stationarity.

One can generalize the definition of an intrinsic Gaussian random field without drift to the multivariate case, by considering a vector random field $\mathbf {Y}=\{\mathbf {Y}(\mathbf {x}):\mathbf {x}\in \mathbb {R}^d\}$ with P components, such that:

• (1) $\mathbf {Y}(\mathbf {0}) = \mathbf {0}$.

• (2) Expectation: $\forall \mathbf {x}\in \mathbb {R}^{d},\mathbb {E}\left\{ \mathbf {Y}(\mathbf {x})\right\} = \mathbf {0}$.

• (3) Covariance of increments:

  $$\begin{aligned} \forall \mathbf {x}, \mathbf {x}+\mathbf {h} \in \mathbb {R}^{d}, \frac{1}{2}\mathbb {E}\left\{ \left[ \mathbf {Y}(\mathbf {x}+\mathbf {h})-\mathbf {Y}(\mathbf {x})\right] \left[ \mathbf {Y}(\mathbf {x}+\mathbf {h})-\mathbf {Y}(\mathbf {x})\right] ^T\right\} = \Upsilon (\mathbf {h}) \end{aligned}$$

  (1)

  where T indicates vector transposition and $\Upsilon (\mathbf {h})$ is the $P \times P$ matrix of direct (diagonal terms) and cross (off-diagonal terms) variograms of the vector random field for a given separation vector $\mathbf {h}$.

• (4) The finite-dimensional distributions of $\mathbf {Y}$ are multivariate Gaussian.

To our knowledge, there is no available algorithm for simulating such a vector random field for any number and configuration of the target locations in $\mathbb {R}^d$, a problem that will be addressed in the next sections. The outline is the following: Sect. 2 introduces a spectral simulation algorithm for generating multivariate intrinsic Gaussian random fields, while Sect. 3 shows applications of this algorithm to synthetic examples. Discussions and conclusions are presented in Sect. 4 and proofs are reported in Appendices.

2 Methodology

To simulate $\mathbf {Y}$, let us consider a vector random field $\mathbf {Y}_S$ defined as follows:

$$\begin{aligned} \forall \mathbf {x}\in \mathbb {R}^{d},\mathbf {Y}_S(\mathbf {x}) = \sum _{p=1}^{P}\varvec{\alpha }_p(\mathbf {U}_{p})\left[ \cos (2\pi \langle \mathbf {x}, \mathbf {U}_{p}\rangle +\phi _{p})-\cos (\phi _{p})\right] , \end{aligned}$$

(2)

where $\langle ,\rangle$ represents the inner product in $\mathbb {R}^d$, $\{\mathbf {U}_{p}: p = 1,\ldots , P\}$ are mutually independent vectors (frequencies) with probability density $g: \mathbb {R}^d \rightarrow \mathbb {R}_+$, $\{\phi _{p}: p = 1,\ldots ,P\}$ are mutually independent scalars (phases) uniformly distributed over the interval $\left[ 0, 2\pi \right)$, and $\{\varvec{\alpha }_p: p = 1,\ldots , P\}$ are deterministic vector-valued mappings with P real-valued components.

The vector random field $\mathbf {Y}_S$ so simulated clearly fulfills the first two properties of an intrinsic Gaussian random field:

• (1) $\mathbf {Y}_S(\mathbf {0}) = \mathbf {0}$.

• (2) $\forall \mathbf {x}\in \mathbb {R}^{d},\mathbb {E}\left\{ \mathbf {Y}_S(\mathbf {x})\right\} = \mathbf {0}$.

To characterize the spatial correlation structure of $\mathbf {Y}_S$, let us calculate its matrix of direct and cross variograms:

$$\begin{aligned} \displaystyle {\frac{1}{2}\mathbb {E}\left\{ \left[ \mathbf {Y}_S(\mathbf {x}+\mathbf {h})-\mathbf {Y}_S(\mathbf {x})\right] \left[ \mathbf {Y}_S(\mathbf {x}+\mathbf {h})-\mathbf {Y}_S(\mathbf {x})\right] ^T\right\} } \end{aligned}$$

$$\begin{aligned}=\, & {} 2\,\mathbb {E}\left\{ \left[ \sum _{p=1}^P\alpha _p(\mathbf {U}_p)\sin \left( \pi \langle 2\mathbf {x}+\mathbf {h}, \mathbf {U}_{p}\rangle +\phi _{p}\right) \sin \left( \pi \langle \mathbf {h}, \mathbf {U}_{p}\rangle \right) \right] \right. \\&\times \left. \left[ \sum _{q=1}^P\alpha _q(\mathbf {U}_q)\sin \left( \pi \langle 2\mathbf {x}+\mathbf {h}, \mathbf {U}_{q}\rangle +\phi _{q}\right) \sin \left( \pi \langle \mathbf {h}, \mathbf {U}_{q}\rangle \right) \right] ^T\right\} \\= \, & {} 2\,\mathbb {E}\left\{ \sum _{p=1}^P\sum _{q=1}^P\alpha _p(\mathbf {U}_p)\alpha _q^T(\mathbf {U}_q)\sin \left( \pi \langle \mathbf {h}, \mathbf {U}_{p}\rangle \right) \sin \left( \pi \langle \mathbf {h}, \mathbf {U}_{q}\rangle \right) \right. \\&\times \left. \sin \left( \pi \langle 2\mathbf {x}+\mathbf {h}, \mathbf {U}_{p}\rangle +\phi _{p}\right) \sin \left( \pi \langle 2\mathbf {x}+\mathbf {h}, \mathbf {U}_{q}\rangle +\phi _{q}\right) \right\} . \end{aligned}$$

Accounting for the fact that $\{\phi _{p}: p = 1,\ldots ,P\}$ are independent and uniformly distributed in $[0,2\pi )$, the only terms that do not vanish are found when $p = q$. The previous equation then simplifies into

$$\begin{aligned} \displaystyle {\frac{1}{2}\mathbb {E}\left\{ \left[ \mathbf {Y}_S(\mathbf {x}+\mathbf {h})-\mathbf {Y}_S(\mathbf {x})\right] \left[ \mathbf {Y}_S(\mathbf {x}+\mathbf {h})-\mathbf {Y}_S(\mathbf {x})\right] ^T\right\} } \end{aligned}$$

$$\begin{aligned}= \,& {} 2\,\mathbb {E}\left\{ \sum _{p=1}^P\alpha _p(\mathbf {U}_p)\alpha _p^T(\mathbf {U}_p)\sin ^2\left( \pi \langle \mathbf {h}, \mathbf {U}_{p}\rangle \right) \sin ^2\left( \pi \langle 2\mathbf {x}+\mathbf {h},\mathbf {U}_{p}\rangle +\phi _{p}\right) \right\} \\= & {} \sum _{p=1}^P\mathbb {E}\left\{ \alpha _p(\mathbf {U}_p)\alpha _p^T(\mathbf {U}_p)\right\} \sin ^2\left( \pi \langle \mathbf {h}, \mathbf {U}_{p}\rangle \right) \\= & {} \int _{\mathbb {R}^d}\sum _{p=1}^P\alpha _p(\mathbf {u})\alpha _p^T(\mathbf {u})\frac{1-\cos \left( 2\pi \langle \mathbf {h}, \mathbf {u}\rangle \right) }{2}g(\mathbf {u})\,\mathrm{d}\mathbf {u}. \end{aligned}$$

It is seen that these direct and cross variograms only depend on the separation vector $\mathbf {h}$, which indicates that the simulated vector random field $\mathbf {Y}_S$ has second-order stationary increments. Let us denote by $\Upsilon _S(\mathbf {h})$ its $P\times P$ matrix of direct and cross variograms. It comes:

$$\begin{aligned} \Upsilon _S(\mathbf {h}) = \int _{\mathbb {R}^d}\mathbf {A}(\mathbf {u})\mathbf {A}^T(\mathbf {u})\frac{1-\cos \left( 2\pi \langle \mathbf {h}, \mathbf {u}\rangle \right) }{2}g(\mathbf {u})\,\mathrm{d}\mathbf {u}, \end{aligned}$$

(3)

where $\mathbf {A}(\mathbf {u})$ is the $P\times P$ matrix whose p-th column is $\alpha _p(\mathbf {u})$.

Compare this expression with the spectral representation of a variogram (Chilès and Delfiner 2012):

$$\begin{aligned} \gamma (\mathbf {h})= & {} \int _{\mathbb {R}^d}\frac{1-\cos \left( 2\pi \langle \mathbf {h}, \mathbf {u}\rangle \right) }{4\pi ^2\Vert \mathbf {u}\Vert ^2}\chi (\mathrm{d}\mathbf {u}), \end{aligned}$$

where $\chi$ is a positive symmetric measure with no atom at the origin and satisfying

$$\begin{aligned} \int _{\mathbb {R}^d}\frac{\chi (\mathrm{d}\mathbf {u})}{1+4\pi ^2\Vert \mathbf {u}\Vert ^2}<\infty . \end{aligned}$$

If $\chi (\mathrm{d}\mathbf {u})$ is absolutely continuous, then the previous representation can be rewritten as:

$$\begin{aligned} \gamma (\mathbf {h})= & {} \int _{\mathbb {R}^d}\left[ 1-\cos \left( 2\pi \langle \mathbf {h}, \mathbf {u}\rangle \right) \right] f(\mathbf {u})\mathrm{d}\mathbf {u}, \end{aligned}$$

with $f(\mathbf {u}) \mathrm{d}\mathbf {u} = \displaystyle {\frac{\chi (\mathrm{d}\mathbf {u})}{4\pi ^2\Vert \mathbf {u}\Vert ^2}}$. Henceforth, f will be referred to as the spectral density of the variogram $\gamma (\mathbf {h})$. In the multivariate context, this spectral density becomes a $P \times P$ matrix $\mathbf {f}: \mathbb {R}^d \rightarrow H^+_P$, associated with the matrix $\Upsilon (\mathbf {h})$ of direct and cross variograms, where $H^+_P$ denotes the set of Hermitian positive semi-definite matrices of size $P\times P$ (Chilès and Delfiner 2012).

For the simulated vector random field $\mathbf {Y}_S$ to have direct and cross variograms associated with a given spectral density matrix $\mathbf {f}$, the following must be satisfied:

$$\begin{aligned} \frac{\mathbf {A}(\mathbf {u})\mathbf {A}^T(\mathbf {u})}{2}g(\mathbf {u})=\mathbf {f}(\mathbf {u}) \end{aligned}$$

or, equivalently,

$$\begin{aligned} \mathbf {A}(\mathbf {u})\mathbf {A}^T(\mathbf {u}) = \dfrac{2\mathbf {f}(\mathbf {u})}{g(\mathbf {u})}. \end{aligned}$$

(4)

The only necessary condition to find a real-valued matrix $\mathbf {A}(\mathbf {u})$ fulfilling the above equation is that $\mathbf {f}(\mathbf {u})$ is a real-valued symmetric positive semi-definite matrix for every $\mathbf {u} \in \mathbb {R}^{d}$ and that the support of g contains the support of $\mathbf {f}$ (so that the right-hand side member of Eq. (4) is defined for any $\mathbf {u}$ in $\mathbb {R}^d$ and is a real-valued symmetric positive-semi-definite matrix). In such a case, $\mathbf {A}(\mathbf {u})$ can be taken as a square root matrix of $\dfrac{2\mathbf {f}(\mathbf {u})}{g(\mathbf {u})}$. The only restriction to define the direct and cross variograms is to meet the positive semi-definiteness condition for the spectral density matrix $\mathbf {f}(\mathbf {u})$ for all $\mathbf {u} \in \mathbb {R}^d$.

Finally, to obtain a vector random field with multivariate Gaussian finite-dimensional distributions, one can add and properly scale many independent basic random fields defined as in Eq. (2):

$$\begin{aligned} \forall \mathbf {x}\in \mathbb {R}^{d},\mathbf {Y}_S(\mathbf {x})= & {} \frac{1}{\sqrt{L}}\sum _{l=1}^L\sum _{p=1}^{P}\varvec{\alpha }_p(\mathbf {U}_{l,p})\left[ \cos (2\pi \langle \mathbf {x}, \mathbf {U}_{l,p}\rangle +\phi _{l,p})-\cos (\phi _{l,p})\right] , \end{aligned}$$

(5)

with $L \in \mathbb {N}^{*}$. If L is large, the finite-dimensional distributions of $\mathbf {Y}_S$ are approximately multinormal, by virtue of the multivariate central limit theorem, while its expectation and its spatial correlation structure (direct and cross variograms) remain the same as that of the random field defined in Eq. (2).

Accordingly, the first three properties introduced in Sect. 1 to define an intrinsic vector Gaussian random field are exactly reproduced, while the fourth property is only approximate as the simulated random field is not perfectly Gaussian. To determine whether or not the approximation is acceptable, one approach is to compare the distribution of a linear combination of $\mathbf {Y}_S$ at specific locations with the distribution that would be obtained if $\mathbf {Y}_S$ were perfectly Gaussian; an upper bound of the Kolmogorov distance between both distributions can be obtained by using the Berry-Esséen theorem (Lantuéjoul 1994; Emery and Lantuéjoul 2008). Another approach is to check the fluctuations of regional statistics calculated over a set of realizations, by means of hypothesis testing (Emery 2008).

In summary, the steps for simulating a P-variate intrinsic Gaussian random field at a given set of target locations in $\mathbb {R}^d$ are the following:

• 1. Identify the spectral density matrix $\mathbf {f}: \mathbb {R}^d \rightarrow H^+_P$ associated with the direct and cross variograms of the target random field.

• 2. Choose a probability density $g: \mathbb {R}^d \rightarrow \mathbb {R}_{+}$ with support containing the support of $\mathbf {f}$.

• 3. Choose a large integer L.

• 4. For $p=1,\ldots ,P$ and $l=1,\ldots ,L$:

  • (a) Generate a random phase $\phi _{l,p}$ uniformly distributed on $[0,2\pi )$.

  • (b) Generate a random vector $\mathbf {U}_{l,p}$ with density g.

  • (c) Calculate the square root of matrix $\dfrac{2\mathbf {f}(\mathbf {U}_{l,p})}{g(\mathbf {U}_{l,p})}$.

  • (d) Identify $\alpha _p(\mathbf {U}_{l,p})$ as the p-th column of the square root matrix calculated at step (c).

• 5. Calculate the simulated random field $\mathbf {Y}_S$ at all target locations as per Eq. (5).

3 Examples

The proposed algorithm is now tested to simulate intrinsic random fields on a regular two-dimensional grid ($d=2$) with $500\times 500$ nodes and a unit mesh. The simulation is performed by adding $L = 500$ basic random fields in Eq. (5). The probability density g is chosen as the following function (depending on two positive scalar parameters a and $\nu$) with support equal to $\mathbb {R}^d$:

$$\begin{aligned} g(\mathbf {u},a,\nu )=\frac{(2\pi a)^{d}\Gamma \left( \nu +\frac{{d}}{2}\right) }{\Gamma (\nu )\pi ^{{d}/2}}\frac{1}{(1+(2\pi a)^2\,\Vert \mathbf {u}\Vert \,^2)^{\nu +{d}/2}}, \end{aligned}$$

(6)

which is nothing else than the spectral density of an isotropic Matérn variogram with unit sill, scale parameter a and shape parameter $\nu$ (Lantuéjoul 2002):

$$\begin{aligned} \mathrm {M}(\mathbf {h},a,\nu )=1-\frac{2^{1-\nu }}{\Gamma (\nu )}\left( \frac{\,\Vert \mathbf {h}\Vert \,}{a}\right) ^{\nu }K_{\nu }\left( \frac{\,\Vert \mathbf {h}\Vert \,}{a}\right) . \end{aligned}$$

(7)

According to Emery and Lantuéjoul (2006), a random vector in $\mathbb {R}^d$ with probability density g can be simulated by scaling a standard Gaussian random vector by the square root of an independent standard gamma random variable with shape parameter $\nu$. In the following examples, which differ by the expression assumed for the cross variograms of the simulated random fields, we will consider the specific values $a = 30$ and $\nu = 0.25$, although the algorithm is applicable with any other choice for these parameters.

3.1 Example 1: Intrinsic vector random field with power variograms

In this subsection, let us consider the case when all the direct and cross variograms are of the form $\mathbf {h}\longrightarrow \Vert \frac{\mathbf {h}}{b}\Vert ^{\theta }$, where $b > 0$ and $\theta \in (0, 2)$. The spectral density of such a power variogram is (Chilès and Delfiner 2012):

$$\begin{aligned} \forall \mathbf {u} \in \mathbb {R}^d, f(\mathbf {u},b,\theta ) = \frac{b^d\theta \Gamma \left( \frac{\theta +d}{2}\right) }{2\Gamma \left( 1-\frac{\theta }{2}\right) \pi ^{\theta +d/2}\Vert b\mathbf {u}\Vert ^{\theta +d}}. \end{aligned}$$

(8)

Consider a bivariate random field ($P=2$) with a matrix of direct and cross variograms of the form:

$$\begin{aligned} \forall \mathbf {h} \in \mathbb {R}^d, \Upsilon (\mathbf {h}) = \left( \begin{array}{rr} \Vert \mathbf {h}\Vert ^{\theta _1} &{} \rho \,\Vert \mathbf {h}\Vert ^{\theta _{12}} \\ \rho \,\Vert \mathbf {h}\Vert ^{\theta _{12}} &{} \Vert \mathbf {h}\Vert ^{\theta _2} \end{array} \right) , \end{aligned}$$

(9)

with $\theta _1 \in (0,2)$, $\theta _2 \in (0,2)$, $\theta _{12} \in (0,2)$ and $\rho \in \mathbb {R}$.

The corresponding spectral density matrix for a given frequency vector $\mathbf {u} \in \mathbb {R}^d$ is:

$$\begin{aligned} \mathbf {f}(\mathbf {u}) = \left( \begin{array}{ll} f(\mathbf {u},1,\theta _1) &{} \rho \,f(\mathbf {u},1,\theta _{12}) \\ \rho \,f(\mathbf {u},1,\theta _{12}) &{} f(\mathbf {u},1,\theta _2) \end{array} \right). \end{aligned}$$

(10)

This matrix is real-valued and symmetric. It is positive semi-definite for any $\mathbf {u}$ in $\mathbb {R}^d$ if and only if the following conditions hold (proof in Appendix 2):

• 1. $\theta _{12}=\displaystyle {\frac{\theta _1+\theta _2}{2}}$

• 2. $|\rho |\le \displaystyle {\frac{2\Gamma \left( 1-\frac{\theta _1+\theta _2}{4}\right) }{(\theta _1+\theta _2)\Gamma \left( \frac{\theta _1+\theta _2}{4}+\frac{d}{2}\right) }\sqrt{\frac{\theta _1\theta _2\Gamma \left( \frac{\theta _1+d}{2}\right) \Gamma \left( \frac{\theta _2+d}{2}\right) }{\Gamma \left( 1-\frac{\theta _1}{2}\right) \Gamma \left( 1-\frac{\theta _2}{2}\right) }}}.$

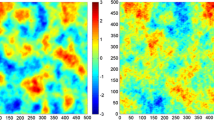
As an example, Fig. 1 shows the map of one realization obtained by running the proposed algorithm with $\theta _1=0.5, \theta _2=1.5, \theta _{12}=1.0$ and $\rho =0.5$. Figure 2 compares the experimental direct and cross variograms of one hundred realizations (calculated along the abscissa axis) with the theoretical power variograms. The average experimental variograms almost perfectly match the theoretical ones, which corroborates that the simulated random field reproduces the desired spatial correlation structure.

Fig. 1

Realizations of a bivariate intrinsic random field with power variograms (first component on the left and second component on the right), with $\theta _1=0.5, \theta _2=1.5, \theta _{12}=1$ and $\rho =0.5$

Fig. 2

Experimental variograms for 100 realizations (green dashed lines), average of experimental variograms (blue stars) and theoretical models (black solid lines). From left to right and top to bottom: direct variograms for first component, direct variograms for second component, and cross-variograms

3.2 Example 2: Intrinsic vector random field with power-Matérn variograms

In this subsection, one is interested in simulating a bivariate intrinsic random field whose direct variograms are power variograms with scale parameters $b_{1} > 0$ and $b_{2} > 0$ and exponents $\theta _{1}$ and $\theta _{2}$ in (0, 2), respectively, and whose cross variogram is a Matérn variogram with sill $\rho$ in $\mathbb {R}$, scale parameter $a_{12}>0$ and shape parameter $\nu _{12}>0$:

$$\begin{aligned} \forall \mathbf {h} \in \mathbb {R}^d, \Upsilon (\mathbf {h}) = \left( \begin{array}{ll} \Vert \frac{\mathbf {h}}{b_1}\Vert ^{\theta _1} &{} \rho \,\mathrm {M}(\mathbf {h},a_{12},\nu _{12}) \\ \rho \,\mathrm {M}(\mathbf {h},a_{12},\nu _{12}) &{} \Vert \frac{\mathbf {h}}{b_2}\Vert ^{\theta _2} \end{array} \right) . \end{aligned}$$

(11)

The corresponding spectral density matrix for a given frequency vector $\mathbf {u} \in \mathbb {R}^d$ is:

$$\begin{aligned} \mathbf {f}(\mathbf {u}) = \left( \begin{array}{ll} f(\mathbf {u},b_1,\theta _{1}) &{} \rho \,g(\mathbf {u},a_{12},\nu _{12}) \\ \rho \,g(\mathbf {u},a_{12},\nu _{12}) &{} f(\mathbf {u},b_2,\theta _{2}) \end{array} \right) . \end{aligned}$$

(12)

Again, this matrix is real-valued and symmetric. It is positive semi-definite for any $\mathbf {u}$ in $\mathbb {R}^d$ if and only if the following conditions hold (proof in Appendix 3):

• 1. $\displaystyle {\nu _{12}\ge \frac{\theta _1+\theta _2}{4}}$ 

• 2. $|\rho |\le \rho _{\max }$ (Eq. (17) in Appendix 3).

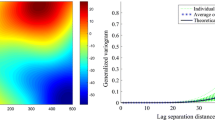
As an example, Fig. 3 shows the map of one realization for $\theta _1=0.5, \theta _2=1.5, b_1 = 10, b_2=20, a_{12}=10, \nu _{12} = 1$ and $\rho =0.4$, while Fig. 4 compares the experimental direct and cross variograms of one hundred realizations (calculated along the abscissa axis) with the theoretical power and Matérn variogram models. As for the first example, the match between the average experimental variograms and the theoretical variogram models is almost perfect.

Fig. 3

Realizations of a bivariate intrinsic random field (first component on the left and second component on the right) with power-Matérn variograms, with $\theta _1=0.5, \theta _2=1.5, b_1=10, b_2=20, a_{12} = 10, \nu _{12}=1$ and $\rho =0.4$

Fig. 4

Experimental variograms for 100 realizations (green dashed lines), average of experimental variograms (blue stars) and theoretical models (black solid lines). From left to right and top to bottom: direct variograms for first component, direct variograms for second component, and cross-variograms

4 Discussion and conclusions

Some comments about the presented algorithm are worth being made. At a given location $\mathbf {x}$, the simulated random field $\mathbf {Y}_S$ (Eq. (5)) is calculated by projecting $\mathbf {x}$ onto a set of frequency vectors $\{\mathbf {U}_{l,p}: l = 1, \ldots , L; p = 1,\ldots , P\}$, which makes the proposed algorithm a particular case of the turning bands method (Matheron 1973). Even more, since the basic random field defined in Eq. (2) is a weighted sum of cosine waves with weights $(\varvec{\alpha }_{p}(\mathbf {U}_{l,p}))$ that depend on the spectral density of the target direct and cross variograms, the proposal can be classified as a spectral turning-bands algorithm. Such an algorithm generalizes previous approaches for simulating stationary Gaussian vector random fields (Shinozuka 1971; Mantoglou 1987; Emery et al. 2016) or for simulating univariate random fields with stationary Gaussian increments (Emery and Lantuéjoul 2008).

Interestingly, the frequency vectors $\{\mathbf {U}_{l,p}: l = 1, \ldots , L;\,\,p = 1,\ldots , P\}$ turn out to be generated with a probability density g that can be chosen by the user, instead of the spectral density f of the variogram associated with a specific component of the desired intrinsic vector random field (Eq. 8), which is not a genuine probability density function (f is non-integrable in $\mathbb {R}^d$). Some solutions based on the spectral density f were proposed in the past decades, but they are approximate since they require truncating f at low frequencies (Chilès 1995). Also note that the algorithm proposed in this paper is intrinsically different from other spectral approaches based on discrete Fourier transforms, which rely on periodizations and/or circulant embeddings and allow simulating the desired random field only at evenly-spaced locations in $\mathbb {R}^d$. Here, the simulation can be performed for any number and any configuration of the target locations. Apart from this versatility, the proposed spectral turning-bands algorithm appears to be faster than existing algorithms, with a computational cost to generate a simulated field directly proportional to the number of target locations (see Emery et al. 2016 for an analysis of the necessary floating point operations), and is not demanding in terms of memory storage requirements.

The presented examples also show models for bivariate intrinsic random fields with different spatial correlation models. In particular, in the second example (power-Matérn model), each component of the simulated random field has a power variogram, therefore self-similar. However, the bivariate random field is no longer self-similar when one considers its two components jointly, because the cross variogram is not self-similar. In contrast, in the first example (power-power model), the direct and cross variograms are self-similar and so is the simulated bivariate random field (Herzfeld 1993); this random field is an approximation of a bivariate fractional Brownian surface (Amblard et al. 2013) that would be obtained if the number L of basic random fields were infinitely large, in which case the increments would have multivariate Gaussian distributions. Although this example is quite restrictive, insofar as the exponent associated with the cross-structure must be the average of the exponents associated with the direct structures, it is of interest because it could allow generating a long-range dependent field (with exponent greater than 1.0) cross-correlated with a low-range dependent field (with exponent less than 1.0). The procedure to find the conditions for admissible models, based on analyzing the positive semi-definiteness of the spectral density matrices, can easily be extended to identify cross variogram models other than the power or Matérn and to more components $(P > 2)$.

In conclusion, we designed a continuous spectral algorithm that simulates vector random fields with the spatial correlation structure of a desired multivariate intrinsic random field, its only approximation being the fact that the finite-dimensional distributions of the simulated random field are not exactly multivariate Gaussian because the number L of basic random fields that are summed in Eq. (5) is finite. The algorithm excels by its versatility, fastness and low computational cost.

Appendices

Appendix 1: Covariance and variogram

Consider a scalar intrinsic random field $Y=\{Y(\mathbf {x}):\mathbf {x}\in \mathbb {R}^d\}$ and denote by $\gamma (\mathbf {h})$ its variogram for the separation vector $\mathbf {h}$. For given locations $\mathbf {x}$, $\mathbf {x}'$ and $\mathbf {x}_0$, let us express the covariance between the two increments $Y(\mathbf {x}) - Y(\mathbf {x}_0)$ and $Y(\mathbf {x}') - Y(\mathbf {x}_0)$ in terms of the variogram:

$$\begin{aligned} C(\mathbf {x}, \mathbf {x}', \mathbf {x}_0):=\,\,& {} \mathrm {cov}\left\{ Y(\mathbf {x})-Y(\mathbf {x}_0),\, Y(\mathbf {x}')-Y(\mathbf {x}_0)\right\} \\= \,\,& {} \mathrm {cov}\left\{ Y(\mathbf {x})-Y(\mathbf {x}'),\, Y(\mathbf {x}')-Y(\mathbf {x})\right\} + \mathrm {cov}\left\{ Y(\mathbf {x}')-Y(\mathbf {x}_0),\, Y(\mathbf {x}')-Y(\mathbf {x}_0)\right\} \\&- \mathrm {cov}\left\{ Y(\mathbf {x}')-Y(\mathbf {x}_0),\, Y(\mathbf {x})-Y(\mathbf {x}_0)\right\} + \mathrm {cov}\left\{ Y(\mathbf {x})-Y(\mathbf {x}_0),\, Y(\mathbf {x})-Y(\mathbf {x}_0)\right\} \\= & {} -2 \gamma (\mathbf {x}-\mathbf {x}') + 2\gamma (\mathbf {x}' - \mathbf {x}_0) - C(\mathbf {x}, \mathbf {x}',\mathbf {x}_0) + 2\gamma (\mathbf {x}- \mathbf {x}_0). \end{aligned}$$

Accordingly:

$$\begin{aligned} C(\mathbf {x}, \mathbf {x}^{\prime}, \mathbf {x}_0) = \gamma (\mathbf {x}- \mathbf {x}_0) + \gamma (\mathbf {x}^{\prime} - \mathbf {x}_0) - \gamma (\mathbf {x}-\mathbf {x}^{\prime}). \end{aligned}$$

Note that this covariance is unchanged by shifting the locations $\mathbf {x}$, $\mathbf {x}'$ and $\mathbf {x}_0$ by a given vector $\mathbf {h}$, i.e., $C(\mathbf {x}, \mathbf {x}^{\prime}, \mathbf {x}_0) = C(\mathbf {x}+\mathbf {h}, \mathbf {x}^{\prime}+\mathbf {h}, \mathbf {x}_0+\mathbf {h})$, showing that the intrinsic random field has second-order stationary increments. Furthermore, by taking $\mathbf {x}_0 = \mathbf {0}$ and considering that $Y(\mathbf {0}) = 0$, it ensues:

$$\begin{aligned} \mathrm {cov}\left\{ Y(\mathbf {x}),\, Y(\mathbf {x}^{\prime})\right\} = \gamma (\mathbf {x}) + \gamma (\mathbf {x}^{\prime}) - \gamma (\mathbf {x}-\mathbf {x}^{\prime}), \end{aligned}$$

which shows that the knowledge of the variogram is equivalent to that of the covariance function of the random field.

Appendix 2: Existence conditions for Example 1

The spectral density matrix $\mathbf {f}(\mathbf {u})$ defined in Eq. (10) is Hermitian because it is a real symmetric matrix. To check that it is positive semi-definite, one therefore only needs to verify that its determinant is non-negative (Horn and Johnson 1985), that is:

$$\begin{aligned} f(\mathbf {u},1,\theta _1)\cdot f(\mathbf {u},1,\theta _2) \ge \rho ^2f^2(\mathbf {u},1,\theta _{12}), \end{aligned}$$

that is:

$$\begin{aligned} \frac{\theta _1\Gamma \left( \frac{\theta _1+d}{2}\right) }{2\Gamma \left( 1-\frac{\theta _1}{2}\right) \pi ^{\theta _1}\Vert \mathbf {u}\Vert ^{\theta _1}}\cdot \frac{\theta _2\Gamma \left( \frac{\theta _2+d}{2}\right) }{2\Gamma \left( 1-\frac{\theta _2}{2}\right) \pi ^{\theta _2}\Vert \mathbf {u}\Vert ^{\theta _2}} \ge \rho ^2\frac{\theta _{12}^2\Gamma ^2\left( \frac{\theta _{12}+d}{2}\right) }{4\Gamma ^2\left( 1-\frac{\theta _{12}}{2}\right) \pi ^{2\theta _{12}}\Vert \mathbf {u}\Vert ^{2\theta _{12}}}. \end{aligned}$$

(13)

From this inequality to hold, one first needs to verify the following:

$$\begin{aligned} \frac{1}{\Vert \mathbf {u}\Vert ^{\theta _1+\theta _2}}\ge \frac{1}{\Vert \mathbf {u}\Vert ^{2\theta _{12}}}. \end{aligned}$$

(14)

If $2\theta _{12}<\theta _1+\theta _2$, inequality (14) is not satisfied for $\Vert \mathbf {u}\Vert >1$, whereas if $2\theta _{12}>\theta _1+\theta _2$, inequality (14) is not satisfied for $\Vert \mathbf {u}\Vert <1$. Therefore, one must have

$$\begin{aligned} \theta _{12}=\frac{\theta _1+\theta _2}{2}, \end{aligned}$$

in which case Eq. (14) obviously holds $\forall \mathbf {u}\in \mathbb {R}^d$. Under this condition, one obtains from Eq. (13):

$$\begin{aligned} \rho ^2\le & {} \frac{4\theta _1\theta _2}{(\theta _1+\theta _2)^2}\frac{\Gamma \left( \frac{\theta _1+d}{2}\right) \Gamma \left( \frac{\theta _2+d}{2}\right) \Gamma ^2\left( 1-\frac{\theta _1+\theta _2}{4}\right) }{\Gamma \left( 1-\frac{\theta _1}{2}\right) \Gamma \left( 1-\frac{\theta _2}{2}\right) \Gamma ^2\left( \frac{\theta _1+\theta _2}{4}+\frac{d}{2}\right) }. \end{aligned}$$

Appendix 3: Existence conditions for Example 2

The spectral density matrix $\mathbf {f}(\mathbf {u})$ defined in Eq. (12) is Hermitian positive semi-definite if its determinant is non-negative, i.e.:

$$\begin{aligned} f(\mathbf {u},b_1,\theta _1)\cdot f(\mathbf {u},b_2,\theta _2) \ge \rho ^2g^2(\mathbf {u},a_{12},\nu _{12}), \end{aligned}$$

that is:

$$\begin{aligned} \varphi (\Vert \mathbf {u}\Vert ):=\frac{(2\pi a_{12})^{2d}\Vert \mathbf {u}\Vert ^{\theta _1+\theta _2+2d}}{\left( 1+(2\pi a_{12})^2\Vert \mathbf {u}\Vert ^2\right) ^{2\nu _{12}+d}}\le \frac{\omega }{\rho ^2}, \end{aligned}$$

(15)

with

$$\begin{aligned} \omega =\frac{\theta _1\theta _2\Gamma \left( \frac{\theta _1+d}{2}\right) \Gamma \left( \frac{\theta _2+d}{2}\right) \Gamma ^2(\nu _{12})}{4\pi ^{\theta _1+\theta _2}b_1^{\theta _1}b_2^{\theta _2}\Gamma \left( 1-\frac{\theta _1}{2}\right) \Gamma \left( 1-\frac{\theta _2}{2}\right) \Gamma ^2\left( \nu _{12}+\frac{d}{2}\right) }. \end{aligned}$$

The mapping $\varphi :\mathbb {R}_+\rightarrow \mathbb {R}$ is unbounded if $\theta _1+\theta _2>4\nu _{12}$, in which case inequality (15) cannot be satisfied. In the converse $(\theta _1+\theta _2\le 4\nu _{12})$, the maximum of $\varphi$ is found to be

$$\begin{aligned} \varphi _{\max }=\frac{(\theta _1+\theta _2+2d)^{(\theta _1+\theta _2)/2+d}}{(4\nu _{12}+2d)^{2\nu _{12}+d}}\times \frac{(4\nu _{12}-\theta _1-\theta _2)^{2\nu _{12}-(\theta _1+\theta _2)/2}}{(2\pi a_{12})^{\theta _1+\theta _2}}. \end{aligned}$$

 

Therefore, for the spectral density matrix $\mathbf {f}(\mathbf {u})$ to be positive semi-definite for all $\mathbf {u}\in \mathbb {R}^d$, the following necessary and sufficient conditions must be fulfilled:

$$\begin{aligned} \theta _1+\theta _2\le 4\nu _{12} \end{aligned}$$

(16)

and

$$\begin{aligned} |\rho |\le \rho _{\max } = \sqrt{\displaystyle {\frac{\omega }{\varphi _{\max }}}}. \end{aligned}$$

(17)

In the particular case when $\theta _1+\theta _2=4\nu _{12}$, then $\varphi _{\max }=(2\pi a_{12})^{-(\theta _1+\theta _2)}$, and the limit value for $|\rho|$ is given by

$$\begin{aligned} |\rho |\le \frac{\Gamma \left( \frac{\theta _1+\theta _2}{4}\right) }{2\Gamma \left( \frac{\theta _1+\theta _2}{4}+\frac{d}{2}\right) }\sqrt{\left( \frac{2a_{12}}{b_1}\right) ^{\theta _1}\left( \frac{2a_{12}}{b_2}\right) ^{\theta _2}\frac{\theta _1\theta _2\Gamma \left( \frac{\theta _1+d}{2}\right) \Gamma \left( \frac{\theta _2+d}{2}\right) }{\Gamma \left( 1-\frac{\theta _1}{2}\right) \Gamma \left( 1-\frac{\theta _2}{2}\right) }}. \end{aligned}$$