Influence of the Time of Increase in Contact Pressure in the Course of Braking on the Temperature of a Pad–Disc Tribosystem

We obtain exact solutions of the thermal problems of friction for a pad–disc tribosystem with regard for the time profiles of specific friction power corresponding to the exponential and linear increase in pressure during braking. We study the influence of time of attainment of the nominal value of contact pressure on temperature in the contact zone of a cermet pad with a cast-iron disc. It is shown that the maximal temperature linearly decreases as the time of attainment of the nominal value of contact pressure increases. At the same time, the time of attainment of this temperature increases.

The time dependences of the friction power are required for the evaluation of the temperature of disc brakes [1]. The analytic [2, 3], numerical-analytic [4], and numerical [5] methods were proposed for the investigation of transient temperature fields in friction elements for the a priori specified time profiles of specific friction power. The influence of this factor on the temperatures and temperature stresses of pad–disc tribosystems was studied for the case of rational mode of braking [6, 7].

The time profile of specific friction power is determined by the variations of pressure in the zone of contact between a pad and a disc and by the velocity determined from the solution of the corresponding initial-value problem for the equation of motion. In general, the level of pressure exponentially increases in the course of braking [8]. The solutions of the one-dimensional thermal problems of friction were obtained in quadratures with regard for the indicated increase in pressure for two half spaces [9, 10] and for a layer and a half space [11, 12].

The aim of the present work is to obtain engineering formulas for the determination of the influence of the time of increase in pressure on the maximal temperature in the course of single braking. For this purpose, we use approximations of the actual time profile of friction power with the help of power functions.

Statement of the Problem

We describe the behaviors of contact pressure p, velocity V, specific power q, and the work of friction w as functions of time t in the course of a single braking in the form [8]

$$ p(t)={p}_0{p}^{\ast }(t),\kern1em {p}^{\ast }(t)=1-{e}^{-t/{t}_i},\kern1em 0\le t\le {t}_s, $$

(1)

$$ V(t)={V}_0{V}^{\ast }(t),\kern1em {V}^{\ast }(t)=1-\frac{t}{t_s^0}+\frac{p^{\ast }(t){t}_i}{t_s^0},\kern1em {t}_s^0=\frac{W_0}{f{p}_0{A}_a{V}_0},\kern1em 0\le t\le {t}_s, $$

(2)

$$ q(t)={q}_0{q}^{\ast }(t),\kern1em {q}_0=f{p}_0{V}_0,\kern1em {q}^{\ast }(t)={p}^{\ast }(t)\left[1-\frac{t}{t_s^0}+\frac{p^{\ast }(t){t}_i}{t_s^0}\right],\kern1em 0\le t\le {t}_s, $$

(3)

$$ w(t)={w}_0{w}^{\ast }(t),\kern1em {w}_0={q}_0{t}_s^0,\kern1em 0\le t\le {t}_s, $$

(4)

$$ {w}^{\ast }(t)=\underset{0}{\overset{t}{\int }}{q}^{\ast }(s) ds=\frac{\left(1-0.5t/{t}_s^0\right)t}{t_s^0}-\frac{p^{\ast }(t)\left(1-t/{t}_s^0\right){t}_i}{t_s^0}-0.5{\left[\frac{p^{\ast }(t){t}_i}{t_s^0}\right]}^2, $$

(5)

where t_s is the time of stop, t_i > 0 is a parameter characterizing the rate of increase in contact pressure from zero to the nominal value p₀, f is the friction coefficient, A_a is the area of nominal zone of the pad–disc contact, and V₀ and W₀ are the initial velocity and kinetic energy, respectively.

For the time of stop t = t_s, it follows from relation (2) that

$$ {t}_i{p}^{\ast}\left({t}_s\right)={t}_s-{t}_s^0, $$

(6)

and the condition ${\left.d{q}^{\ast }/ dt\right|}_{t={t}_{\mathrm{max}}}=0$ gives the following formula for the time t_max of attainment by the function q^*(t) (3) its maximal value ${q}_{\mathrm{max}}^{\ast }$:

$$ \left({t}_s^0-{t}_{\mathrm{max}}\right){e}^{-{t}_{\mathrm{max}}/{t}_i}-\left(1-2{e}^{-{t}_{\mathrm{max}}/{t}_i}\right){t}_i{p}^{\ast}\left({t}_{\mathrm{max}}\right)=0. $$

(7)

Solving the nonlinear equations (6) and (7) by the bisection method [13], we arrive at the relations

$$ {t}_s={t}_s^0+0.99{t}_i,\kern1em {t}_{\mathrm{max}}=0.783\sqrt{t_i{t}_s^0},\kern1em 0\le {t}_i\le 0.3{t}_s^0. $$

(8)

As t_i → 0, it follows from relations (1)–(6) that

$$ p(t)={p}_0,\kern1em V(t)={V}_0\left(1-t\right),\kern1em q(t)={q}_0\left(1-t\right),\kern1em \mathrm{and}\kern1em w(t)={w}_0\left(1-0.5t/{t}_s^0\right)t/{t}_s^0,\kern1em 0\le t\le {t}_s^0. $$

Hence, the parameter ${t}_s^0$ (2) is the time of stop in the course of braking with constant deceleration.

Further, we expand the function p^*(t) (1) in power series and restrict ourselves to the first two terms in this expansion. As a result, we obtain

$$ {p}^{\ast }(t)=\frac{t}{t_i}H\left({t}_i-t\right)+H\left(t-{t}_i\right),\kern1em 0\le t\le {t}_s, $$

(9)

where H(⋅) is the Heaviside unit function. If the contact pressure (9) linearly increases, then we can write the time profiles of velocity V^*, specific power q^*, and the work of friction w^* (2)–(5) as follows [14]:

$$ {V}^{\ast }(t)=1-{V}_i^{\ast }(t)H\left({t}_i-t\right)-\left[{V}_i^{\ast}\left({t}_i\right)+{V}_s^{\ast }(t)\right]H\left(t-{t}_i\right),\kern1em 0\le t\le {t}_s, $$

(10)

$$ {V}_i^{\ast }(t)=\frac{0.5{t}^2}{t_s^0{t}_i},\kern1em {V}_s^{\ast }(t)=\frac{t-{t}_i}{t_s^0} $$

(11)

$$ {q}^{\ast }(t)={q}_i^{\ast }(t)H\left({t}_i-t\right)+{q}_s^{\ast }(t)H\left({t}_i-t\right),\kern1em 0\le t\le {t}_s, $$

(12)

$$ {q}_i^{\ast }(t)=\frac{\left[1-0.5{t}^2/\left({t}_s^0{t}_i\right)\right]t}{t_i},\kern1em {q}_s^{\ast }(t)=1-\frac{t-0.5{t}_i}{t_s^0}, $$

(13)

$$ {w}^{\ast }(t)={w}_i^{\ast }(t)H\left({t}_i-t\right)-\left[{w}_i^{\ast}\left({t}_i\right)+{w}_s^{\ast }(t)\right]H\left(t-{t}_i\right),\kern1em 0\le t\le {t}_s $$

(14)

$$ {w}_i^{\ast }(t)=\frac{0.5\left[1-0.25{t}^2/\left({t}_s^0{t}_i\right)\right]{t}^2}{t_s^0{t}_i},\kern1em {w}_s^{\ast }(t)=\frac{\left(1-0.5t/{t}_s^0\right)\left(t-{t}_i\right)}{t_s^0}. $$

(15)

Substituting relations (10) and (11) in condition V^*(t_s) = 0, we determine the braking time:

$$ {t}_s={t}_s^0+0.5{t}_i. $$

(16)

It was also proposed to approximate the time profile of specific power q^* (3) and the work of friction w^* (4), (5) in the form [1]

$$ q(t)={q}_0{q}^{\ast }(t),\kern1em {q}^{\ast }(t)=0.5\left(\upalpha +1\right)\left(\upalpha +2\right)\frac{t_s^0}{t_s}{\left(\frac{t}{t_s}\right)}^{\upalpha}\left(1-\frac{t}{t_s}\right),\kern1em 0\le t\le {t}_s, $$

(17)

$$ w(t)={w}_0{w}^{\ast }(t),\kern1em {w}^{\ast }(t)=0.5{\left(\frac{t}{t_s}\right)}^{\upalpha +1}\left[\left(\upalpha +1\right)\left(1-\frac{t}{t_s}\right)+1\right],\kern1em 0\le t\le {t}_s, $$

(18)

$$ \upalpha =\frac{t_{\mathrm{max}}}{t_s-{t}_{\mathrm{max}}},\kern1em 0\le \upalpha \le 1, $$

(19)

where the parameters t_s and t_max can be found from relations (8).

It follows from expressions (4) and (5), (14) and (15), (18) and (19) that the total work of friction w(t_s) does not depend on the parameter t_i and is equal to 0.5w₀. This means that the amounts of friction heat generated by the specific friction powers (3), (12), (13) and (17), (19) on the surface of the pad–disc contact are identical and, hence, we can compare the corresponding values of temperature. To find these values, we consider a one-dimensional model of friction heating of a pad–disc tribosystem. In the case of perfect thermal friction contact, we find the temperature fields T_l(z, t) in these elements from the solution of the boundary-value problem of heat conduction for two semiinfinite bodies z ≥ 0 (l = 1, pad) and z ≤ 0 (l = 2, disc) [9, 10]:

$$ \frac{\partial^2{T}_1^{\ast}\left(\upzeta, \uptau \right)}{\partial {\upzeta}^2}=\frac{\partial {T}_1^{\ast}\left(\upzeta, \uptau \right)}{\mathrm{\partial \uptau }}\kern1em \upzeta >0,\kern1em 0<\uptau \le {\uptau}_s, $$

(20)

$$ \frac{\partial^2{T}_2^{\ast}\left(\upzeta, \uptau \right)}{\partial {\upzeta}^2}=\frac{1}{k^{\ast }}\frac{\partial {T}_2^{\ast}\left(\upzeta, \uptau \right)}{\mathrm{\partial \uptau }}\kern1em \upzeta <0,\kern1em 0<\uptau \le {\uptau}_s, $$

(21)

$$ {K}^{\ast}\frac{\partial {T}_2^{\ast}\left(\upzeta, \uptau \right)}{\mathrm{\partial \upzeta }}{\left|{}_{\upzeta =0}-\frac{\partial {T}_1^{\ast}\left(\upzeta, \uptau \right)}{\mathrm{\partial \upzeta }}\right|}_{\upzeta =0}={q}^{\ast}\left(\uptau \right),\kern1em 0<\uptau \le {\uptau}_s, $$

(22)

$$ {T}_1^{\ast}\left(0,\uptau \right)={T}_2^{\ast}\left(0,\uptau \right)\equiv {T}^{\ast}\left(\uptau \right),\kern1em 0<\uptau \le {\uptau}_s, $$

(23)

$$ {T}_l^{\ast}\left(\upzeta, \uptau \right)\to 0,\kern1em \mid \upzeta \mid \to \infty, \kern1em 0<\uptau \le {\uptau}_s,\kern1em l=1,2, $$

(24)

$$ {T}_l^{\ast}\left(\upzeta, 0\right)=0,\kern1em \mid \upzeta \mid <\infty, \kern1em l=1,2, $$

(25)

$$ {\displaystyle \begin{array}{c}\upzeta =\frac{z}{a},\kern1em \uptau =\frac{k_1t}{a^2},\kern1em {\uptau}_i=\frac{k_1{t}_i}{a^2},\kern1em {\uptau}_s^0=\frac{k_1{t}_s^0}{a^2},\kern1em {\uptau}_s=\frac{k_1{t}_s}{a^2},\kern1em {K}^{\ast }=\frac{K_2}{K_1},\kern1em {k}^{\ast }=\frac{k_2}{k_1},\\ {}{T}_a=\frac{q_0a}{K_1},\kern1em {T}_l^{\ast }=\frac{T_l-{T}_0}{T_a},\end{array}}\kern1em $$

(26)

where q^*(τ) is the time profile of specific friction power, T_a is the initial temperature, K_l and k_l are the heat-conduction coefficient and thermal diffusivity, respectively, and $a=\max \left\{{a}_l\right\},{a}_l=\sqrt{3{k}_l{t}_s^0}$, are the effective depth of heat penetration into the pad and the disc [1].

Solution of the Problem

Bu using the Duhamel formula, we represent the solution of the boundary-value problem of heat conduction (20)–(26) on the contact surface ζ = 0 in the form [6]

$$ {T}^{\ast}\left(\uptau \right)=\frac{\upgamma}{\sqrt{\uppi}}\underset{0}{\overset{\uptau}{\int }}\frac{q^{\ast }(s)}{\sqrt{\uptau -s}} ds,\kern1em \upgamma =\frac{\sqrt{k^{\ast }}}{\sqrt{k^{\ast }}+{K}^{\ast }},\kern1em 0\le \uptau \le {\uptau}_s. $$

(27)

Substituting function q^*(τ) (3) in the integrand in relation (27), we obtain

$$ {T}^{\ast}\left(\uptau \right)=\frac{\upgamma}{\uptau_s^0}\left[\left({\uptau}_s^0+{\uptau}_i\right){I}_{0,0}\left(\uptau \right)-{I}_{1,0}\left(\uptau \right)-\left({\uptau}_s^0+2{\uptau}_i\right){I}_{0,1}\left(\uptau \right)+{I}_{1,1}\left(\uptau \right)+{\uptau}_i{I}_{0,2}\left(\uptau \right)\right],\kern1em 0\le \uptau \le {\uptau}_s, $$

(28)

$$ {I}_{n,m}\left(\uptau \right)=\frac{1}{\sqrt{\uppi}}\underset{0}{\overset{\uptau}{\int }}\frac{s^n{e}^{- ms/{\uptau}_i}}{\sqrt{\uptau -s}} ds,\kern1em n=0,1;\kern1em m=0,1,2. $$

(29)

Setting $x=\sqrt{\tau -s}$, we represent integrals (29) for m = 0 in the following form:

$$ {I}_{n,0}\left(\uptau \right)=\frac{2}{\sqrt{\uppi}}\underset{0}{\overset{\sqrt{\uptau}}{\int }}{\left(\uptau -{x}^2\right)}^n dx,\kern1em n=0,1. $$

(30)

By using the formula [15]

$$ \underset{0}{\overset{a}{\int }}{\left({a}^{\upmu}-{x}^{\upmu}\right)}^{\mathrm{v}-1} dx={\upmu}^{-1}{a}^{\upmu \left(\mathrm{v}-1\right)+1}B\left(v;{\upmu}^{-1}\right),\kern1em a,\upmu, v>0, $$

(31)

for $a=\sqrt{\uptau},\upmu =2$, and ν = n + 1, we find

$$ {I}_{n,0}\left(\uptau \right)=B\left(n+1;0.5\right){\uptau}^n\sqrt{\frac{\uptau}{\uppi}},\kern1em n=0,1,2,\dots, $$

(32)

where B(ν; μ⁻¹) is the beta function [16].

Taking into account the values B(1; 0.5) = 2 and B(2; 0.5) = 4/3 and relation (32), we obtain

$$ {I}_{0,0}\left(\uptau \right)=2\sqrt{\frac{\uptau}{\uppi}},\kern1em {I}_{1,0}\left(\uptau \right)=\frac{4}{3}\uptau \sqrt{\frac{\uptau}{\uppi}}. $$

(33)

If m ≠ 0, then, in view of $x=\sqrt{\uptau -s}$, we reduce integrals (29) to the form

$$ {I}_{0,m}\left(\uptau \right)=\sqrt{\uptau}F\sqrt{\frac{m\uptau}{\uptau_i}},\kern1em m=1,2,\kern1em {I}_{1,1}\left(\uptau \right)=\left(\uptau +0.5{\uptau}_i\right)\sqrt{\uptau}F\sqrt{\frac{\uptau}{\uptau_i}}-{\uptau}_i\frac{\sqrt{\uptau}}{\uppi}, $$

(34)

where the Dawson integral

$$ F(x)=\frac{2}{\sqrt{\uppi}}\frac{e^{-{x}^2}}{x}\underset{0}{\overset{x}{\int }}{e}^{s^2} ds $$

is calculated as follows [17]:

$$ F(x)=\frac{2}{\sqrt{\uppi}}\sum \limits_{n=0}^{\infty }{\left(-1\right)}^n\frac{{\left(2{x}^2\right)}^n}{\left(2n+1\right)!!},\kern1em 0\le x\le 3,\kern1em F(x)=\frac{2}{\sqrt{\uppi}}\sum \limits_{n=0}^{\infty}\frac{\left(2n-1\right)!!}{{\left(2{x}^2\right)}^{n+1}},\kern1em x>3. $$

Substituting the values of the integrals I_n,m(τ) (33), (34) in relations (28), we find

$$ {T}^{\ast}\left(\uptau \right)=\upgamma \sqrt{\uptau}\left[\left(1+\frac{\uptau_i}{{2\uptau}_s^0}-\frac{2\uptau}{{3\uptau}_s^0}\right)\frac{2}{\sqrt{\uppi}}-\left(1-\frac{\uptau}{\uptau_s^0}+\frac{{3\uptau}_i}{{2\uptau}_s^0}\right)F\left(\sqrt{\frac{\uptau}{\uptau_i}}\right)+\frac{\uptau_i}{\uptau_s^0}F\left(\sqrt{\frac{2\uptau}{\uptau_i}}\right)\right],\kern1em 0\le \uptau \le {\uptau}_s. $$

(35)

In the limiting case as τ_i → 0, solution (35) yields the well-known Fazekas formula for the temperature of the surface of pad–disc contact in the course of braking with constant deceleration [18]:

$$ {T}^{\ast}\left(\uptau \right)=2\upgamma \sqrt{\frac{\uptau}{\uppi}}\left(1-\frac{2\uptau}{{3\uptau}_s^0}\right),\kern1em 0\le \uptau \le {\uptau}_s. $$

(36)

Substituting function q^∗(τ) (12), (13) in relations (27), we obtain

$$ {T}^{\ast}\left(\uptau \right)=\upgamma \left\{{T}_i^{\ast}\left(\uptau \right)H\left({\uptau}_i-\uptau \right)+\left[{T}_i^{\ast}\left({\uptau}_i\right)-{T}_s^{\ast}\left({\uptau}_i\right)+{T}_s^{\ast}\left(\uptau \right)\right]H\left(\uptau -{\uptau}_i\right)\right\},\kern1em 0\le \uptau \le {\uptau}_s, $$

(37)

$$ {T}_i^{\ast}\left(\uptau \right)=\frac{I_{1,0}\left(\uptau \right)-0.5{I}_{3,0}\left(\uptau \right)/\left({\uptau}_s^0{\uptau}_i\right)}{\uptau_i},\kern1em {T}_s^{\ast}\left(\uptau \right)=\left(1+\frac{0.5{\uptau}_i}{\uptau_s^0}\right){I}_{0,0}\left(\uptau \right)-\frac{I_{1,0}\left(\uptau \right)}{\uptau_s^0}, $$

(38)

where, in view of the value B(4; 0, 5) = 32/35 and expression (32), we find

$$ {I}_{3,0}\left(\uptau \right)=\frac{32}{35}{\uptau}^3\sqrt{\frac{\uptau}{\uppi}}. $$

(39)

Substituting the integrals I_n,0(τ), n = 0,1 (33) and I_3,0(τ) (39) in relations (38), we get

$$ {T}_i^{\ast}\left(\uptau \right)=\frac{4\uptau}{\uptau_i}\sqrt{\frac{\uptau}{\uppi}}\left(\frac{1}{3}-\frac{{4\uptau}^2}{35{\uptau}_s^0{\uptau}_i}\right),\kern1em {T}_s^{\ast}\left(\uptau \right)=2\sqrt{\frac{\uptau}{\uppi}}\left(1+\frac{\uptau_i}{2{\uptau}_s^0}-\frac{2\uptau}{{3\uptau}_s^0}\right), $$

(40)

$$ {T}_i^{\ast}\left({\uptau}_i\right)-{T}_s^{\ast}\left({\uptau}_i\right)=-\frac{2}{3}\sqrt{\frac{\uptau_i}{\uppi}}\left(1+\frac{13{\uptau}_i}{70{\uptau}_s^0}\right). $$

(41)

Knowing functions ${T}_{i,s}^{\ast}\left(\uptau \right)$ (40) and (41), we can find, by using relation (37), the dimensionless temperature of the surface of pad–disc contact. Passing to the limit as τ_i → 0 and using expressions (37), (40), and (41), we arrive at the Fazekas solution (36).

Substituting function q^*(τ) (17) in relation (27), we find

$$ {T}^{\ast}\left(\uptau \right)=0.5\upgamma \left(\upalpha +1\right)\left(\upalpha +2\right)\frac{\uptau_s^0}{\uptau_s}\left[{I}_{\upalpha}\left(\uptau \right)-{I}_{\upalpha +1}\left(\uptau \right)\right],\kern1em 0\le \uptau \le {\uptau}_s, $$

(42)

$$ {I}_{\upalpha}\left(\uptau \right)=\frac{1}{\sqrt{\uppi}}\underset{0}{\overset{\uptau}{\int }}{\left(\frac{s}{\uptau_s}\right)}^{\upalpha}\frac{ds}{\sqrt{\uptau -s}}, $$

(43)

where the parameter 0 ≤ α ≤ 1 can be found from relations (8) and (19). With the help of the substitution x = $\sqrt{\uptau -s}$, we first rewrite integral (43) in the form

$$ {I}_{\upalpha}\left(\uptau \right)=\frac{2}{\sqrt{\uppi}}\underset{0}{\overset{\sqrt{\uptau}}{\int }}{\left(\uptau -{x}^2\right)}^{\upalpha} dx. $$

Taking a = $\sqrt{\uptau}$, μ = 2, and ν = α + 1 in relation (31), we find

$$ {I}_{\upalpha}\left(\uptau \right)=B\left(\upalpha +1;0.5\right){\left(\frac{\uptau}{\uptau_s}\right)}^{\upalpha}\sqrt{\frac{\uptau}{\uppi}}. $$

(44)

By using the dependences [16]

$$ B\left(\upalpha +1;0.5\right)=\sqrt{\uppi}\frac{\varGamma \left(\upalpha +1\right)}{\varGamma \left(\upalpha +1.5\right)},\kern1em B\left(\upalpha +2;0.5\right)=\frac{\left(\upalpha +1\right)B\left(\upalpha +1;0.5\right)}{\upalpha +1.5} $$

and substituting the functions I_α (τ) and I_α+1(τ) (44) in relation (42), we get

$$ {T}^{\ast}\left(\uptau \right)=0.5\upgamma \left(\upalpha +1\right)\left(\upalpha +2\right)\sqrt{\uptau}\frac{\varGamma \left(\upalpha +1\right){\uptau}_s^0}{\varGamma \left(\upalpha +1.5\right){\uptau}_s}{\left(\frac{\uptau}{\uptau_s}\right)}^{\upalpha}\left[1-\frac{\left(\upalpha +1\right)\uptau}{\left(\upalpha +1.5\right){\uptau}_s}\right],\kern1em 0\le \uptau \le {\uptau}_s, $$

(45)

where Γ(α) is the gamma-function [16]. For the linear decrease in velocity during braking, we have α = 0, ${\uptau}_s={\uptau}_s^0$. Then, with regard for the values Γ(1) = 1 and Γ(1.5) = 0.5$\sqrt{\uppi}$, we obtain the Fazekas solution (36) from relation (45).

Numerical Results

We performed calculations for a metal-ceramic (FMK-11) pad,

$$ {K}_1=34.3\mathrm{W}\cdot {\mathrm{m}}^{-1}\cdot {\mathrm{K}}^{-1},\kern1em {k}_1=15.2\cdot {10}^{-6}{\mathrm{m}}^2\cdot {\sec}^{-1}, $$

and cast-iron (ChNMKh) disc,

$$ {K}_2=51\mathrm{W}\cdot {\mathrm{m}}^{-1}\cdot {\mathrm{K}}^{-1},\kern1em {k}_2=14\cdot {10}^{-6}{\mathrm{m}}^2\cdot {\sec}^{-1} $$

(see [8]). For this friction pair, the coefficient of distribution of heat flows is equal to γ = 0.608, and the effective depth of heat penetration is $a={a}_1\sqrt{3{k}_1{t}_s^0}$. Thus, by using relations (26), we find the Fourier numbers τ = 0.33t^*, ${\uptau}_i=0.33{t}_i^{\ast }$, ${\uptau}_s^0=0.33$, and ${\uptau}_s=0.33{t}_s^{\ast }$, where ${t}^{\ast }=t/{t}_s^0,{t}_i^{\ast }={t}_i/{t}_s^0,\mathrm{and}\;{t}_s^{\ast }={t}_s/{t}_s^0$.

The duration of braking increases with the time of attainment of the nominal value of contact pressure and velocity nonlinearly decreases only in the initial stage of braking, where 0 ≤ t^* ≤ 0.3 (Fig. 1).

Fig. 1.

Evolutions of the dimensionless pressure p^* (solid curves) and velocity V^* (dashed curves) for some values of the parameter ${t}_i^{\ast }$.

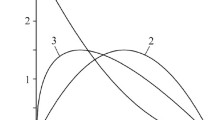
Knowing the dependences of contact pressure p^* and velocity V^* on the time of braking, we constructed plots for the product of these quantities, i.e., for the specific friction power q^* (Fig. 2). The presented time profiles of dimensionless specific friction power q^* have two branches. The ascending branch corresponds to the increase in contact pressure and, hence, in the friction force during braking. In this time interval, the increase in the friction force runs ahead of the decrease in velocity and, after certain time, the specific friction power reaches its maximal value. The descending branch of time profile of the friction power is caused by the rapid decrease in the braking speed with simultaneous insignificant growth of pressure. The work of friction, i.e., the area of the domain under the curve of specific friction power, is independent of the time of increase in contact pressure and, as shown above, is identical for both exact (3) and approximate (12), (13), and (17) representations of q^*. For a fixed value of the parameter t_i, the braking time t_s determined from relation (8) exceeds the braking time found from (16).

Fig. 2.

Evolutions of the dimensionless specific friction power q^* (a) and temperature T^* (b) for two values of the parameter ${t}_i^{\ast }$. The solid curves were plotted according to relations (3) and (35), the dashed lines were plotted by using (12), (13), and (37), and the dashed-dotted curves were plotted according to (17) and (45).

The evolutions of the dimensionless temperatures T^* corresponding to the time profiles of specific friction power q^* from Fig. 2а are illustrated in Fig. 2b. In the initial period of braking, the lower the time of attainment of the nominal value of contact pressure, the higher the rate of growth of temperature. In this stage, the highest temperature was found from solution (45) obtained by using the Chichinadze approximation (17).

At the same time, the lowest temperature was obtained by using the exact solution (35) with exponential increase in the contact pressure (1). In the last case, the temperature increases in the course of braking for the longest time and attains its maximal values. On the attainment of the maximum temperature, the process of cooling of the contact surface begins and goes until the complete stop.

In the course of braking with constant deceleration (τ_i = 0), the maximal value of dimensionless temperature ${T}_{\mathrm{max}}^{\ast }$ = 0.187 is attained at the time τ_max = 0.17 and is identical for the exact (35) and approximate (37) and (45) solutions (Fig. 3). As the parameter τi increases, the maximal temperature of the surface of pad–disc contact decreases, and the time of its attainment linearly increases. We determined the smallest (largest) drop of the maximal temperature for the exponential (1) [linear (9)] growth of contact pressure. For time τ_i = 0.1, the values of dimensionless maximal temperature ${T}_{\mathrm{max}}^{\ast }$ and time of its attainment τ_max determined from relations (35), (37), and (45), constitute 0.175, 0.154, and 0.164 and 0.28, 0.19, and 0.22, respectively.

Fig. 3.

Dependences of the dimensionless maximal temperature ${T}_{\mathrm{max}}^{\ast }$ (1) and the time of its attainment τ_max (2) on the parameter τ_i. The solid curves correspond to the results obtained by relation (35), the dashed curves correspond to formula (37), and the dashed-dotted curves correspond to (45).

Conclusions

We obtain computational formulas for the investigation of the influence of the time of attainment of the nominal value of pressure on the temperature of the surface of pad–disc contact. We consider the time profile of specific friction power with exponential growth of pressure during braking and two its approximations: linear and power proposed by Chichinadze. We obtain the exact solutions of the corresponding one-dimensional thermal problems of friction. It was shown that the maximal temperature and duration of braking are linear functions of the time of attainment of the nominal value of contact pressure. The temperatures found by using the approximate formulas are lower than the temperature determined for the exponential increase in pressure. The longer the time of attainment of the nominal value of pressure, the greater the differences between these temperatures.