The available mathematical models of friction heating in the process of operation of braking systems are based on the solutions of the corresponding thermal problems of friction, i.e., one-dimensional boundary-value problems of heat conduction with two specific boundary conditions on the surface of pad–disk contact [1, 2]. The first of these conditions is connected with the experimental results on the purity of treatment of the contact surfaces: their roughness and the presence of oxide films or wear products, etc. [3, 4]. If the working surfaces of friction elements are sufficiently smooth, then the temperatures of the pad and the disk on the contact surface are assumed to be equal. The second boundary condition expresses the equality of the sum of intensities of the heat fluxes directed along the normal to the contact surface into each element of the friction couple to the specific power of friction, i.e., the product of tangential stresses by the sliding velocity [5]. Hence, the changes in the friction power in the process of braking (time dependence) may exert a significant influence on the temperature of the friction elements of brakes.

The major part of analytic solutions of the thermal problems of friction in the course of braking were obtained for a linear decrease in the friction power with time [6,7,8]. This means that the friction force in the nominal domain of pad–disk contact is constant and the contact pressure reaches its nominal value with the onset of braking instantaneously. However, as follows from the experimental results, the time dependence of the friction power may substantially differ from linear function depending on the character of changes in the friction coefficient and contact pressure as functions of the braking time [9, 10]. The list of experimental dependences used to describe the variations of the specific power of friction in the case of one-time braking can be found in [11]. Among these dependences, it is necessary to distinguish the functions vanishing on approaching the stopping time. Braking with this type of time dependence of the friction power is regarded as rational.

The aim of the present work is to construct exact solutions of the one-dimensional thermal problem of friction for three chosen time dependences of the specific power of friction and to analyze, by using these solutions, the time-and-space distributions of temperature in the friction elements in the case of one-time braking.

Statement of the Problem

We represent the dependences of the specific power of friction as functions of time t in the process of braking up to the stopping time t s in the following form:

$$ {q}^{(i)}(t)={q}_0^{(i)}{q}^{(1)\ast }(t),\kern1em 0\le t\le {t}_s,\kern1em i=1,2,3. $$
(1)

In what follows, we consider braking processes for which the total work of braking is identical and equal to w s for each function q (i)(t) (1):

$$ \underset{0}{\overset{t_s}{\int }}{q}^{(i)}(t) dt={w}_s,\kern1em i=1,2,3. $$
(2)

Condition (2) is satisfied by assuming that

$$ {q}_0^{(i)}\equiv {q}_0={w}_s/{t}_s $$

in relation (1) and taking the dimensionless functions q (i)*(t), i = 1, 2, 3, in the form [11]

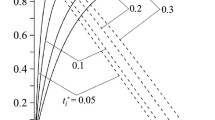
$$ {q}^{(1)\ast }(t)=3{\left(1-\frac{t}{t_s}\right)}^2,\kern1em {q}^{(2)}(t)=6\left(\frac{t}{t_s}\right)\left(1-\frac{t}{t_s}\right),\kern1em {q}^{(3)\ast }(t)=\sqrt{\frac{t}{t_s}}\left(1-\sqrt{\frac{t}{t_s}}\right). $$
(3)

For the first analyzed braking process, the specific friction power decreases according to a parabolic law from the maximal value \( {q}_{\mathrm{max}}^{(1)\ast }=3 \) at the initial time t = 0 to zero at the stopping time (Fig. 1, i = 1). It is known that even in the case of instantaneous growth of pressure in the braking system, the load applied to the

Fig. 1.
figure 1

Time dependences of the dimensionless specific power of friction q (i)∗(t), i = 1, 2, 3.

Full size image

contact surface and, hence, the friction force gradually increase as functions of the braking time prior to the decrease in the velocity [12]. Therefore, the specific friction power grows from the onset of braking up to the attainment of the maximal values

$$ {q}_{\mathrm{max}}^{(2)\ast }={q}_{\mathrm{max}}^{(3)\ast }=1.5 $$

at the times t = 0.5t s (i = 2) and t = 0.25t s (i = 3) (Fig. 1, i = 2, 3). After this, the decrease in the braking velocity begins to leave behind the process of growth of the friction force and the specific friction power vanishes at the stopping time.

The mathematical formulation of the thermal problem of friction in the course of braking for a pad–disk tribosystem is based on the following main assumptions: the free surfaces are adiabatic and the heat generated on the contact surface propagates into each element along the normal to this surface [13]. Therefore, the problem of finding temperature fields in the pad and in the disk is reduced to the construction of the solution of the onedimensional boundary-value problem of heat conduction for two semiinfinite bodies z ≥ 0 and z ≤ 0. In what follows, we denote all quantities for each of these bodies by subscripts 1 and 2, respectively. Hence, we get

$$ \frac{\partial^2{T}_1^{(i)\ast}\left(\upzeta, \uptau \right)}{\partial {\upzeta}^2}=\frac{\partial {T}_1^{(i)\ast}\left(\upzeta, \uptau \right)}{\partial \uptau},\kern1em \upzeta >0,\kern1em 0<\uptau \le {\uptau}_s,\kern1em i=1,2,3, $$
(4)
$$ \frac{\partial^2{T}_2^{(i)\ast}\left(\upzeta, \uptau \right)}{\partial {\upzeta}^2}=\frac{1}{k^{\ast }}\frac{\partial {T}_2^{(i)\ast}\left(\upzeta, \uptau \right)}{\partial \uptau},\kern1em \upzeta <0,\kern1em 0<\uptau \le {\uptau}_s, $$
(5)
$$ {K}^{\ast}\frac{\partial {T}_2^{(i)\ast}\left(\upzeta, \uptau \right)}{\partial \upzeta}{\left|{}_{\upzeta ={0}^{-}}-\frac{\partial {T}_1^{(i)\ast}\left(\upzeta, \uptau \right)}{\partial \upzeta}\right|}_{\upzeta ={0}^{+}}={q}^{(i)\ast}\left(\uptau \right),\kern1em 0<\uptau \le {\uptau}_s, $$
(6)
$$ {T}_1^{(i)\ast}\left({0}^{+},\uptau \right)={T}_2^{(i)\ast}\left({0}^{-},\uptau \right),\kern1em 0<\uptau \le {\uptau}_s, $$
(7)
$$ {T}_k^{(i)\ast}\left(\upzeta, \uptau \right)\to 0,\kern1em \left|\upzeta \right|\to \infty, \kern1em 0<\uptau \le {\uptau}_s,\kern1em k=1,2, $$
(8)
$$ {T}_k^{(i)\ast}\left(\upzeta, 0\right)=0,\kern1em -\infty <\upzeta <\infty, \kern1em k=1,2, $$
(9)

where

$$ {\displaystyle \begin{array}{c}\upzeta =\frac{z}{a1},\kern1em \uptau =\frac{k_1t}{a_1^2},\kern1em {\uptau}_s=\frac{k_1{t}_s}{a_1^2},\\ {}{K}^{\ast }=\frac{K_2}{K_1},\kern1em {k}^{\ast }=\frac{k_2}{k_1},\\ {}{T}_a=\frac{q_0{a}_1}{K_1},\kern1em {T}_k^{(i)\ast }=\frac{T_k^{(i)}-{T}_0}{T_a},\end{array}} $$
(10)

\( {T}_k^{(i)} \) are the temperatures of the first (k = 1) and second (k = 2) bodies corresponding to the time dependences of the specific density of friction power q (i)∗(τ), i = 1, 2, 3, K and k are the thermal conductivity and diffusivity,

respectively, and

$$ {a}_1=\sqrt{3{k}_1{t}_s} $$

is the effective depth of penetration of heat into the first body [12].

Solution of the Problem

We seek the dimensionless temperature fields \( {T}_k^{(i)\ast}\left(\upzeta, \uptau \right),\kern1em k=1,2,\kern1em i=1,2,3 \) by using the Duhamel formula [14]:

$$ {T}_k^{(i)\ast}\left(\upzeta, \uptau \right)=\underset{0}{\overset{\uptau}{\int }}{q}^{(i)\ast }(s)\frac{\partial }{\partial \uptau}{T}_k^{(0)\ast}\left(\upzeta, \uptau -s\right) ds,\kern1em 0\le \uptau \le {\uptau}_s, $$
(11)

where the solution of boundary-value problem (4)–(10) with the function q (0)∗(τ) = 1 in the boundary condition (6) has the form

$$ {T}_k^{(0)\ast}\left(\upzeta, \uptau \right)=2\sqrt{\uptau}{\left(1+\upvarepsilon \right)}^{-1}{F}_k\left(\upzeta, \uptau \right),\kern1em 0\le \uptau \le {\uptau}_s,\kern1em k=1,2, $$
(12)
$$ {F}_k\left(\upzeta, \uptau \right)=\frac{e^{-{Z}_k^2\left(\upzeta, \uptau \right)}}{\sqrt{\uppi}}-{Z}_k\left(\upzeta, \uptau \right){E}_k\left(\upzeta, \uptau \right),\kern1em {E}_k\left(\upzeta, \uptau \right)=1-\operatorname{erf}\kern0.5em {Z}_k\left(\upzeta, \uptau \right), $$
(13)
$$ {Z}_1\left(\upzeta, \uptau \right)=\frac{0.5\upzeta}{\sqrt{\uptau}},\kern1em \upzeta \ge 0,\kern1em {Z}_2\left(\upzeta, \uptau \right)=-\frac{0.5\upzeta}{\sqrt{k^{\ast}\uptau}},\kern1em \upzeta \le 0,\kern1em \upvarepsilon =\frac{K^{\ast }}{\sqrt{k^{\ast }}}, $$
(14)

and erf x is the error function [15]. It follows from relations (12)–(14) that

$$ \frac{\partial {T}_k^{(0)\ast}\left(\upzeta, \uptau -s\right)}{\partial \uptau}=\frac{{\left(1+\upvarepsilon \right)}^{-1}{e}^{-{Z}_k^2\left(\upzeta, \uptau -s\right)}}{\sqrt{\uppi \left(\uptau -s\right)}}. $$
(15)

Substituting the functions q (i)∗(τ), i = 1, 2, 3 (3), and the partial derivative (15) under the integral sign in relation (11), we obtain

$$ {T}_k^{(1)\ast}\left(\upzeta, \uptau \right)=3{\left(1+\upvarepsilon \right)}^{-1}\left[{I}_k^{(0)}\left(\upzeta, \uptau \right)-2{I}_k^{(1)}\left(\upzeta, \uptau \right)+{I}_k^{(2)}\left(\upzeta, \uptau \right)+{I}_k^{(2)}\left(\upzeta, \uptau \right)\right], $$
(16)
$$ {T}_k^{(2)\ast}\left(\upzeta, \uptau \right)=6{\left(1+\upvarepsilon \right)}^{-1}\left[{I}_k^{(1)}\left(\upzeta, \uptau \right)-{I}_k^{(2)}\left(\upzeta, \uptau \right)\right], $$
(17)
$$ {T}_k^{(3)\ast}\left(\upzeta, \uptau \right)=6{\left(1+\upvarepsilon \right)}^{-1}\left[{I}_k^{(0.5)}\left(\upzeta, \uptau \right)-{I}_k^{(1)}\left(\upzeta, \uptau \right)\right], $$
(18)
$$ {I}_k^{\left(\upalpha \right)}\left(\upzeta, \uptau \right)=\frac{1}{\sqrt{\uppi}}\underset{0}{\overset{\uptau}{\int }}\frac{e^{-{Z}_k^2\left(\upzeta, \uptau -s\right)}}{\sqrt{\uptau -s}}{\left(\frac{s}{\uptau_s}\right)}^{\upalpha} ds,\kern1em k=1,2,\kern1em \upalpha =0;0,5;1;2. $$
(19)

Integrals (19) were calculated with the help of the substitution

$$ x=1/\sqrt{\uptau -s} $$

and the formula [16]

$$ \underset{u}{\overset{\infty }{\int }}{x}^{-1}{\left(x-u\right)}^{\mathrm{v}}{e}^{-\upmu \mathrm{x}} dx={u}^{\mathrm{v}}\varGamma \left(v+1\right)\varGamma \left(-v;u\upmu \right), $$

where Γ(ν) is the gamma function, Γ(ν, x) is the incomplete gamma function [15], ν = n − 0.5, n = 0.1, u = 1/τ , and \( \upmu ={Z}_k^2\left(\upzeta, \uptau \right)\uptau . \) By using the values

$$ \varGamma (0.5)=\sqrt{\uppi},\kern1em \varGamma (1.5)=0.5\sqrt{\uppi},\kern1em \varGamma \left[0.5;{Z}_k^2\left(\upzeta, \uptau \right)\right]=\sqrt{\uppi}{E}_k\left(\upzeta, \uptau \right), $$

and

$$ \varGamma \left[-0.5;{Z}_k^2\left(\upzeta, \uptau \right)\right]=2\sqrt{\uppi}\frac{F_k\left(\upzeta, \uptau \right)}{Z_k\left(\upzeta, \uptau \right)}, $$

we find

$$ {I}_k^{(0)}\left(\upzeta, \uptau \right)=2\sqrt{\uptau}\kern0.5em {F}_k\left(\upzeta, \uptau \right),{I}_k^{\left(0,5\right)}\left(\upzeta, \uptau \right)=0.5\sqrt{{\uppi \uptau}_s}{\uptau}^{\ast}\left[{E}_k\left(\upzeta, \uptau \right)-2{Z}_k\left(\upzeta, \uptau \right){F}_k\left(\upzeta, \uptau \right)\right], $$
(20)
$$ {I}_k^{(1)}\left(\upzeta, \uptau \right)=2\sqrt{\uptau}{\uptau}^{\ast}\frac{2\left[1+{Z}_k^2\left(\upzeta, \uptau \right)\right]{F}_k\left(\upzeta, \uptau \right)-{Z}_k\left(\upzeta, \uptau \right){E}_k\left(\upzeta, \uptau \right)}{3}, $$
(21)
$$ {I}_k^{(2)}\left(\upzeta, \uptau \right)=2\sqrt{\uptau}{\uptau}^{\ast 2}\frac{\left[8+18{Z}_k^2\left(\upzeta, \uptau \right)+4{Z}_k^4\left(\upzeta, \uptau \right)\right]{F}_k\left(\upzeta, \uptau \right)-{Z}_k\left(\upzeta, \uptau \right)\left[7+2{Z}_k^2\left(\upzeta, \uptau \right)\right]{E}_k\left(\upzeta, \uptau \right)}{15}. $$
(22)

Knowing the functions \( {I}_k^{\left(\upalpha \right)}\left(\upzeta, \uptau \right) \) (20)–(22) and using relations (16)–(18), we determine the dimensionless temperature fields \( {T}_k^{(i)\ast}\left(\upzeta, \uptau \right) \) corresponding to the time dependences of the specific friction power q (i)∗(τ), i = 1, 2, 3 (3) in each element (k = 1, 2 ) of the friction couple:

$$ {\displaystyle \begin{array}{c}{T}_k^{(1)\ast}\left(\upzeta, \uptau \right)=\frac{2\sqrt{\uptau}}{\left(1+\upvarepsilon \right)}\left\{\left\{3-4\left(\frac{\uptau}{\uptau_s}\right)\left[1+{Z}_k^2\left(\upzeta, \uptau \right)\right]+\frac{1}{5}{\left(\frac{\uptau}{\uptau_s}\right)}^2\left[8+18{Z}_k^2\left(\upzeta, \uptau \right)+4{Z}_k^4\left(\upzeta, \uptau \right)\right]\right\}{F}_k\left(\upzeta, \uptau \right)\right.\\ {}+\left(\frac{\uptau}{\uptau_s}\right)\left.\left\{2{Z}_k\left(\upzeta, \uptau \right)-\frac{1}{5}\left(\frac{\uptau}{\uptau_s}\right){Z}_k\left(\upzeta, \uptau \right)\left[7+2{Z}_k^2\left(\upzeta, \uptau \right)\right]\right\}{E}_k\left(\upzeta, \uptau \right)\right\},\kern1em 0\le \uptau \le {\uptau}_s;\end{array}} $$
(23)
$$ {\displaystyle \begin{array}{c}{T}_k^{(2)\ast}\left(\upzeta, \uptau \right)=\frac{4\sqrt{\uptau}}{\left(1+\upvarepsilon \right)}\left(\frac{\uptau}{\uptau_s}\right)\left\{\left\{2\left[1+{Z}_k^2\left(\upzeta, \uptau \right)\right]-\frac{1}{5}\left(\frac{\uptau}{\uptau_s}\right)\left[8+18{Z}_k^2\left(\upzeta, \uptau \right)+4{Z}_k^4\left(\upzeta, \uptau \right)\right]\right\}\right.{F}_k\left(\upzeta, \uptau \right)\\ {}\left.-\left\{{Z}_k\left(\upzeta, \uptau \right)-\frac{1}{5}\left(\frac{\uptau}{\uptau_s}\right){Z}_k\left(\upzeta, \uptau \right)\left[7+2{Z}_k^2\left(\upzeta, \uptau \right)\right]\right\}{E}_k\left(\upzeta, \uptau \right)\right\},\kern1em 0\le \uptau \le {\uptau}_s;\end{array}} $$
(24)
$$ {\displaystyle \begin{array}{l}{T}_k^{(3)\ast}\left(\upzeta, \uptau \right)=\frac{1}{\left(1+\upvarepsilon \right)}\left(\frac{\uptau}{\uptau_s}\right)\left\{\left[3\sqrt{{\uppi \uptau}_s}+4\sqrt{\uptau}{Z}_k\left(\upzeta, \uptau \right)\right]{E}_k\left(\upzeta, \uptau \right)\right.\\ {}\kern4em -2\left.\left\{3\sqrt{{\uppi \uptau}_s}{Z}_k\left(\upzeta, \uptau \right)+4\sqrt{\uptau}\left[1+{Z}_k^2\left(\upzeta, \uptau \right)\right]\right\}{F}_k\left(\upzeta, \uptau \right)\right\},\kern1em 0\le \uptau \le {\uptau}_s,\end{array}} $$
(25)

where the functions F k (ζ, τ), E k (ζ, τ), and Z k (ζ, τ) are given by relations (13) and (14).

Numerical Results

The numerical analysis was performed according to relations (16)–(18) and (23)–(25). The role of dimensionless input parameters of the problem was played by the space variable ζ and the Fourier numbers τ and τs (10). The first element of the friction couple ζ ≥ 0 (disk) was made of ChNMKh cast iron (K 1 = 51Wm–1K–1, k 1 = 14 ·10–6m2 sec–1), while the second element ζ ≤ 0 (pad) was made of the friction material (FM-16L retinax with K 2 = 0.65Wm–1K–1 and k 2 = 4 ·10–7m2 sec–1) [9]. For this friction couple, by using formula (14), we determine the coefficient of relative thermal activity ε = 0.075.

The evolution of the dimensionless temperature

$$ {T}_k^{(i)\ast}\left(\upzeta, \uptau \right),\kern1em k=1,2;\kern1em i=1,2,3 $$

in the process of braking is depicted in Fig. 2. The highest temperature is attained on the contact surface ζ = 0. The time dependence of temperature on this surface is typical of the process of one-time braking, namely, the temperature increases with the onset of braking and reaches a certain maximal value with subsequent cooling up to the stopping time. The maximal values of dimensionless temperature

Fig. 2.
figure 2

Time dependences of the dimensionless temperature \( {T}_k^{(i)\ast}\left(\upzeta, \uptau \right): \) i = 1 (a); i = 2 (b); i = 3 (c) in the disk (solid curves; k = 1) and in the pad (dashed curves; k = 2) at different distances from the contact surface.

Full size image
$$ {T}_{\mathrm{max}}^{(i)\ast}\equiv {T}_k^{(i)\ast}\left(0,{\uptau}_{\mathrm{max}}^{(i)}\right) $$

and the time of their attainment \( {\uptau}_{\mathrm{max}}^{(i)} \) are equal to 1.12 and 0.32 for i = 1 (Fig. 2а), 1.09 and 0.75 for i = 2 (Fig. 2b), and 1.02 and 0.62 for i = 3, respectively (Fig. 2c). The dimensionless temperatures on the contact surface at the stopping time are equal to \( {T}_k^{(i)\ast}\left(0,{\uptau}_s\right) \) = 0, 63, 0.84, and 0.75 for i = 1, 2, and 3, respectively. Since retinax conducts heat much worse than cast iron, the temperature of the pad decreases much faster than the disk temperature with the distance from the contact surface. In this case, we observe the delay effect: as the distance from the friction surface increases, the time of attainment of the maximal temperature approaches the stopping moment. The monotone growth of the disk temperature from the onset of braking up to the stopping starts at the effective depth z = a 1 (ζ = 1), while the pad temperature monotonically increases even for z = − 0.2a 1 (ζ = – 0.2).

Conclusions

The results of our investigations demonstrate that the distributions of temperature in the friction elements of brakes (pad, disk) strongly depend on the time dependences of the specific friction power. This feature is especially pronounced for the contact surface with the maximal temperature. It was also discovered that there exists a direct dependence between the time of attainment of the maximal friction power \( {q}_{\mathrm{max}}^{(i)\ast } \) and temperature \( {T}_{\mathrm{max}}^{(i)\ast }, \) i = 1, 2, 3. Indeed, the time of attainment of the maximum temperature \( {T}_{\mathrm{max}}^{(i)\ast } \) increases with the time of attainment of \( {q}_{\mathrm{max}}^{(i)\ast } \). At the same time, the influence of the quantity \( {q}_{\mathrm{max}}^{(i)\ast } \) on the value of \( {T}_{\mathrm{max}}^{(i)\ast } \) is insignificant: for \( {q}_{\mathrm{max}}^{(1)\ast } \) = 3, we obtain \( {T}_{\mathrm{max}}^{(1)\ast } \) = 1.12 and, for \( {q}_{\mathrm{max}}^{(2)\ast } \) = \( {q}_{\mathrm{max}}^{(3)\ast } \) = 1.5, we get \( {T}_{\mathrm{max}}^{(2)\ast } \) = 1.09 and \( {T}_{\mathrm{max}}^{(3)\ast } \) = 1.02. The process of cooling of the contact surface after reaching the temperature maximum also strongly depends on the evolution of specific friction power. Indeed, the temperatures at the stopping time are equal to 56.2% , 77%, and 73.5% of the maximal temperatures \( {T}_{\mathrm{max}}^{(i)\ast }, \) i = 1, 2, 3.

The established exact solutions of the thermal problems of friction enable one to obtain formulas for the evaluation of an important tribological parameter, namely, the coefficient of distribution of thermal fluxes heating the disk and the pad in the course of braking for a given time dependence of the friction power.