Determination of the Maximal Temperature of a Pad–Disk Tribosystem during One-Time Braking

We propose a computational scheme for the evaluation of the maximal temperature of a pad–disk tribosystem in the course of one-time braking with regard for the time of increase in pressure up to its nominal level, the temperature dependence of the characteristics of materials, and the roughness of the friction surfaces. We perform calculations for a three-disk brake made of Termar-ADF carbon composite. For the case of exponential or linear increase in contact pressure in the course of braking, we analyze the influence of thermal sensitivity of the material on the evolution of the mean temperature in the nominal contact zone, flash temperature, and the maximal temperature of friction surfaces.

Introduction

The analyses of the thermal conditions of braking systems are usually performed for the maximal temperature [1, 2]. A procedure aimed at the evaluation of the maximal temperature based on the solution of the system of equations of the thermal dynamics of friction (TDF) was proposed in [3, 4]. This system of equations includes the experimental temperature dependences of the mechanical and thermal properties of materials, the regularities of changes in contact pressure during braking, the initial-value problem for the equation of motion, the thermal problem of friction for finding the average temperature in the nominal contact zone of the pad with the disk, the relations for the determination of flash temperature, and the hypothesis of summation of these two temperatures [5, 6]. Analytic methods for the evaluation of the average temperature of contact zone based on the solutions of one-dimensional boundary-value problems of heat conduction with regard for friction heat generation were proposed in [7,8,9]. In particular, some engineering formulas were obtained [10, 11] for the investigation of the influence of duration of the increase in contact pressure and, hence, of the time dependence of specific friction power, on the temperature of friction couples.

The aim of the present work is to adapt these equations to the system of TDF equations for a pad–disk tribosystem and investigate, on the basis of these equations, the influence of temperature dependence of the mechanical and thermal properties of the Termar-ADF frictional material on the evolution of the maximal temperature during one-time braking.

System of TDF Equations

In the case of intense braking, the volume temperature of the elements of friction couples often exceeds 400°С. In this case, the thermal and mechanical characteristics of materials undergo changes that can be as large as even 30–40% of their initial values [12]. We approximate the experimental temperature dependences of these characteristics by the following formulas [1]:

$$ {\displaystyle \begin{array}{c}{K}_l(T)={K}_{l,0}{K}_l^{\ast }(T),\kern1em {c}_l(T)={c}_{l,0}{c}_l^{\ast }(T),\\ {}{\uprho}_l(T)={\uprho}_{l,0}{\uprho}_l^{\ast }(T),\kern1em {HB}_l(T)={HB}_{l,0}{HB}_l^{\ast }(T),\end{array}} $$

(1)

$$ {K}_{l,0}\equiv {K}_l\left({T}_0\right),\kern1em {c}_{l,0}\equiv {c}_l\left({T}_0\right),\kern1em {\uprho}_{l,0}\equiv {\uprho}_l\left({T}_0\right),\kern1em {HB}_{l,0}\equiv {HB}_l\left({T}_0\right), $$

(2)

$$ {K}_l^{\ast }(T)={K}_{l,1}+\frac{K_{l,2}}{{\left[{K}_{l,3}\left(T-{K}_{l,4}\right)\right]}^2+1}+\frac{K_{l,5}}{{\left[{K}_{l,6}\left(T-{K}_{l,7}\right)\right]}^2+1}, $$

(3)

$$ {c}_l^{\ast }(T)={c}_{l,1}+\frac{c_{l,2}}{{\left[{c}_{l,3}\left(T-{c}_{l,4}\right)\right]}^2+1}+\frac{c_{l,5}}{{\left[{c}_{l,6}\left(T-{c}_{l,7}\right)\right]}^2+1}, $$

(4)

$$ {\uprho}_l^{\ast }(T)={\uprho}_{l,1}+\frac{\uprho_{l,2}}{{\left[{\uprho}_{l,3}\left(T-{\uprho}_{l,4}\right)\right]}^2+1}+\frac{\uprho_{l,5}}{{\left[{\uprho}_{l,6}\left(T-{\uprho}_{l,7}\right)\right]}^2+1}, $$

(5)

$$ {HB}_l^{\ast }(T)={HB}_{l,1}+\frac{HB_{l,2}}{{\left[{HB}_{l,3}\left(T-{HB}_{l,4}\right)\right]}^2+1}+\frac{HB_{l,5}}{{\left[{HB}_{l,6}\left(T-{HB}_{l,7}\right)\right]}^2+1}, $$

(6)

where T is temperature; T₀ is the initial temperature; K_l is the heat-conduction coefficient; c_l is the specific heat; ρ_l is density; HB_l is the Brinell hardness, and K_l,i, c_l,i, ρ_l,i, and HB_l,i, i = 1, 2,…, 7, are the approximation coefficients for the materials of the pad (l = 1) and disk (l = 2), respectively.

The time dependences of the contact pressure p, velocity V, and specific work of friction w in the course of braking are described by the formulas [11]

$$ p(t)={p}_0{p}^{\ast }(t),\kern1em {p}^{\ast }(t)=1-{e}^{-t/{t}_i},\kern1em 0\le t\le {t}_s, $$

(7)

$$ {\displaystyle \begin{array}{c}V(t)={V}_0{V}^{\ast }(t),\kern1em {V}^{\ast }(t)=1-\frac{t}{t_s^0}+{p}^{\ast }(t)\frac{t_i}{t_s^0},\kern1em {t}_s^0=\frac{W_0}{q_0{A}_a},\kern1em {q}_0={fp}_0{V}_0,\\ {}w(t)={w}_0{w}^{\ast }(t),\kern1em {w}_0={q}_0{t}_s^0,\end{array}} $$

(8)

$$ {w}^{\ast }(t)=\left(1-\frac{0.5t}{t_s^0}\right)\frac{t}{t_s^0}-{p}^{\ast }(t)\left(1-\frac{t}{t_s^0}\right)\frac{t_i}{t_s^0}-0.5{\left[{p}^{\ast }(t)\frac{t_i}{t_s^0}\right]}^2, $$

(9)

where A_a is the area of the nominal contact zone of the pad with the disk; f is the friction coefficient; V₀ and W₀ are the initial velocity and kinetic energy of the tribosystem, respectively; t_i is a parameter characterizing the time of increase in pressure up to its nominal level p₀, and t_s is the time of shutdown determined from the equation V(t_s) = 0. If $0\le {t}_i\le 0.3{t}_s^0$, then t_s = ${t}_s^0$ + 0.99t_i.

Under the conditions of linear increase in contact pressure, the time dependences of p^∗, V^∗, and w^∗ in (7)–(9) have the form [13]

$$ {p}^{\ast }(t)=\frac{t}{t_i}H\left({t}_i-t\right)+H\left(t-{t}_i\right), $$

(10)

$$ {V}^{\ast }(t)=1-{V}_i^{\ast }(t)H\left({t}_i-t\right)-\left[{V}_i^{\ast}\left({t}_i\right)+{V}_s^{\ast }(t)\right]H\left(t-{t}_i\right), $$

(11)

$$ {V}_i^{\ast }(t)=\frac{t^2}{2{t}_s^0{t}_i},\kern1em {V}_s^{\ast }(t)=\frac{t-{t}_i}{t_s^0}, $$

(12)

$$ {w}^{\ast }(t)={w}_i^{\ast }(t)H\left({t}_i-t\right)-\left[{w}_i^{\ast}\left({t}_i\right)+{w}_s^{\ast }(t)\right]H\left(t-{t}_i\right), $$

(13)

$$ {w}_i^{\ast }(t)=0.5\left[1-\frac{0.25{t}^2}{t_s^0{t}_i}\right]\frac{t^2}{t_s^0{t}_i},\kern1em {w}_s^{\ast }(t)=\left(1-\frac{0.5t}{t_s^0}\right)\frac{t-{t}_i}{t_s^0}, $$

(14)

where H(·) is the unit Heaviside function, and t_s = ${t}_s^0$ + 0.5t_i. Note that the complete works of friction under the conditions of exponential and linear increase in pressure are identical and equal to w(t_s) = 0.5w₀.

We seek the maximal temperature of the friction surface in the form

$$ {T}_{\mathrm{max}}(t)={T}_m(t)+{T}_f(t),\kern1em 0\le t\le {t}_s, $$

(15)

where T_m is the mean temperature of the nominal contact zone and T_f is the temperature of the actual contact zone (flash temperature).

For the exponential increase in contact pressure (7), we find [11]

$$ {T}_m(t)=\upgamma {T}_{m,0}{T}_m^{\ast }(t)+{T}_0,\kern1em 0\le t\le {t}_s, $$

(16)

$$ {T}_m^{\ast }(t)=\sqrt{\frac{t}{t_s^0}}\left[\left(1+\frac{t_i}{2{t}_s^0}-\frac{2t}{3{t}_s^0}\right)\frac{2}{\sqrt{\uppi}}-\left(1-\frac{t}{t_s^0}+\frac{3{t}_i}{2{t}_s^0}\right)F\left(\sqrt{\frac{t}{t_i}}\right)+\frac{t_i}{t_s^0}F\left(\sqrt{\frac{2t}{t_i}}\right)\right], $$

(17)

$$ {\displaystyle \begin{array}{c}F(x)=\frac{2}{\sqrt{\uppi}}\sum \limits_{n=0}^{\infty }{\left(-1\right)}^n\frac{{\left(2{x}^2\right)}^n}{\left(2n+1\right)!!},\kern1em 0\le x\le 3,\\ {}F(x)=\frac{2}{\sqrt{\uppi}}\sum \limits_{n=0}^{\infty}\frac{\left(2n-1\right)!!}{{\left(2{x}^2\right)}^{n+1}},\kern1em x>3,\end{array}} $$

(18)

$$ \upgamma =\frac{\sqrt{k^{\ast }}}{\sqrt{k^{\ast }}+\sqrt{k^{\ast }}},\kern1em {T}_{m,0}=\frac{q_0a}{K_{1,0}},\kern1em {K}^{\ast }=\frac{K_{2,0}}{K_{1,0}},\kern1em {k}^{\ast }=\frac{k_{2,0}}{k_{1,0}}, $$

(19)

$$ {k}_{l,0}=\frac{K_{l,0}}{\uprho_{l,0}{c}_{l,0}},\kern1em a=\max \left\{{a}_l\right\},\kern1em {a}_l=\sqrt{k_{l,0}{t}_s^0},\kern1em l=1,2. $$

(20)

If the level of pressure linearly increases in the course of braking (10), then the time dependence of the mean temperature in relation (16) is determined as follows [13]:

$$ {T}_m^{\ast }(t)={T}_i^{\ast }(t)H\left({t}_i-t\right)+\left[{T}_i^{\ast}\left({t}_i\right){T}_s^{\ast}\left({t}_i\right)+{T}_s^{\ast }(t)\right]H\left(t-{t}_i\right),\kern1em 0\le t\le {t}_s, $$

(21)

$$ {T}_i^{\ast }(t)=\frac{4t}{t_i}\sqrt{\frac{t}{\uppi {t}_s^0}}\left(\frac{1}{3}-\frac{4{t}^2}{35{t}_s^0{t}_i}\right),\kern1em {T}_s^{\ast }(t)=2\sqrt{\frac{t}{\uppi {t}_s^0}}\left(1+\frac{t_i}{2{t}_s^0}-\frac{2t}{3{t}_s^0}\right). $$

(22)

The results of our investigations demonstrate that the values of mean temperature of the friction surface obtained with and without taking into account the thermal sensitivity of materials differ by at most 10% [1]. At the same time, the procedure of evaluation of T_m with temperature-dependent mechanical and thermal properties (1)–(6) is quite complicated because it is based on the solution of nonlinear heat-conduction equations. Therefore, we determine the mean temperature according to relations (16)–(22) in which the constants K_l,0, c_l,0, and ρ_l,0 corresponding to the initial temperature T₀ are replaced with the corresponding parameters K_l,Θ, c_l,Θ, and ρ_l,Θ given by relations (1)–(6) for the volume temperatures of the pad and the disk averaged over the duration of braking:

$$ {\displaystyle \begin{array}{c}{\Theta}_l={T}_0+{\upvartheta}_{l,0}{\upvartheta}^{\ast },\\ {}{\upvartheta}_{l,0}=\frac{\upalpha_l{\uppsi}_l{W}_0}{G_l{c}_{l,0}},\kern1em {\upvartheta}^{\ast }=\frac{2}{t_s}\underset{0}{\overset{t_s}{\int }}{w}^{\ast }(t) dt,\kern1em l=1,2,\end{array}} $$

(23)

where G_l are the masses of effective heat-absorbing elements; α₁ = 1− γ and α₂ = γ are the coefficients of distribution of heat fluxes, and ψ_l are the coefficients taking into account the decrease in temperature caused by heat conduction beyond the friction zone. In view of relations (7)–(9), it follows from formula (23) that

$$ {\displaystyle \begin{array}{l}{\upvartheta}^{\ast }=\frac{2{t}_i^2}{t_s{t}_s^0}\left[1-\frac{t_i}{4{t}_s^0}+\left(\frac{t_s}{t_s^0}-1\right){e}^{-{t}_s/{t}_i}+\frac{t_i}{4{t}_s^0}{e}^{-2{t}_s/{t}_i}\right]\\ {}\kern8.25em -\frac{t_i}{t_s^0}\left(2-\frac{t_s}{t_s^0}+\frac{t_s}{t_s^0}\right)+\frac{t_s}{t_s^0}\left(1-\frac{t_s}{3{t}_s^0}\right).\end{array}} $$

(24)

For the linear increase in contact pressure (10)–(14), it follows from (23) that

$$ {\upvartheta}^{\ast}\frac{t_i^2}{3{t}_s{t}_s^0}\left(1+\frac{t_i}{10{t}_s^0}\right)-\frac{t_i}{t_s^0}\left(1-\frac{t_s}{2{t}_s^0}+\frac{t_i}{4{t}_s^0}\right)+\frac{t_s}{t_s^0}\left(1-\frac{t_s}{3{t}_s^0}\right). $$

(25)

The flash temperature is computed as follows:

$$ {T}_f(t)=\frac{\left(1+\sqrt{2}\right) fp(t)V(t){A}_a{d}_r(t)}{\sqrt{2}{A}_r(t)\left[4{K}_{2,m}(t)+\sqrt{\uppi V(t){d}_r(t){K}_{1,m}(t){c}_{1,m}(t){\uprho}_{1,m}(t)}\right]},\kern1em 0\le t\le {t}_s, $$

(26)

$$ {A}_r(t)=\frac{p(t){A}_a}{HB_m(t)},\kern1em {d}_r(t)={\left(\frac{8{r}_{av}{h}_{\mathrm{max}}}{v}\right)}^{1/2}{\left\{\frac{p_c(t)}{HB_m(t){b}_0}\right\}}^{1/(2v)}, $$

(27)

$$ {p}_c(t)=\frac{p(t){A}_a}{A_c(t)},\kern1em {A}_c(t)={A}_a{\left[\frac{p(t){b}_0^{v-1}}{HB_m(t)}\right]}^{1/\left(v+1\right)}, $$

(28)

$$ {K}_{l,m}(t)\equiv {K}_l\left[{T}_m(t)\right],\kern1em {c}_{l,m}(t)\equiv {c}_l\left[{T}_m(t)\right],\kern1em {\uprho}_{l,m}(t)\equiv {\uprho}_l\left[{T}_m(t)\right], $$

(29)

$$ {HB}_m(t)\equiv \min \left[{HB}_{1,m}(t),{HB}_{2,m}(t)\right],\kern1em {HB}_{l,m}(t)\equiv {HB}_l\left[{T}_m(t)\right],\kern1em l=1,2, $$

(30)

where ν, b₀, r_av, and h_max are the parameters of the reference curve for the harder element of the friction couple. Relations (26)–(30) are obtained under the assumption of plastic mechanism of deformation of microasperities on the contact surfaces [14] typical of the operation of high-loaded brakes.

Numerical Results

Our calculations were carried out for a braking system formed by three identical disks made of the Termar-ADF carbon composite. The input parameters were as follows [15]:

$$ {\displaystyle \begin{array}{c}{p}_0=0.602\ \mathrm{MPa},\kern0.5em {V}_0=23.8\ \mathrm{m}\cdot {\sec}^{-1},\kern0.49em {W}_0=103.54\ \mathrm{kJ},\kern0.49em {T}_0=20{}^{\circ}\mathrm{C},\kern0.49em f=0.27,\kern0.49em {t}_i=0.5\;\sec, \\ {}v=1.5,\kern0.49em {b}_0=2.5,\kern0.49em {r}_{av}=6.3\cdot {10}^{-4}\ \mathrm{m},\kern0.49em {h}_{\mathrm{m}\mathrm{ax}}=2.2\cdot {10}^{-6}\mathrm{m},\kern0.5em \upgamma =0.5,\kern0.49em {\uppsi}_l=0.92,\kern0.49em {A}_a=22.1\cdot {10}^{-4}\ {\mathrm{m}}^2,\\ {}{K}_{l,0}=21\ \mathrm{W}\cdot {\mathrm{m}}^{-1}\cdot {\mathrm{K}}^{-1},\kern0.49em {c}_{l,0}=728.5\ \mathrm{J}\cdot {\mathrm{kg}}^{-1}\cdot {\mathrm{K}}^{-1},\kern0.49em {\uprho}_{l,0}=1800\ \mathrm{kg}\cdot {\mathrm{m}}^{-3},\kern0.5em \mathrm{and}\kern0.5em H{B}_{l,0}=90.2\ \mathrm{MPa},\kern0.49em l=1.2.\end{array}} $$

For, these parameters, by using relations (8), (9), and (20), we obtain

$$ {t}_s^0=12.12\sec, \kern1em {q}_0=3.87\kern0.5em \mathrm{MW}\cdot {\mathrm{m}}^{-2},\kern1em {w}_0=46.87\kern0.5em \mathrm{MJ}\cdot {\mathrm{m}}^{-2},\kern1em {a}_l=a=0.014\mathrm{m}, $$

and

$$ {G}_l=3{A}_aa{\uprho}_{l,0}=0.167\mathrm{kg},\kern1em l=1.2. $$

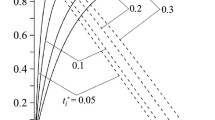
For the exponential increase in contact pressure (7), the braking time is t_s = 12.61sec and the volume temperature (23), (24) of the tribosystem constitutes Θ_l ≅ 566°C, l = 1.2. If the level of pressure linearly increases (10), then t_s = 12.37 sec and relations (23) and (25) give Θ_l ≅ 576°C, l = 1.2. By using the values of the coefficients K_l,i, c_l,i, and HB_l,i, i = 1, 2,…, 7, l = 1.2 [16], we plotted the functions ${K}_l^{\ast }(T)$, ${c}_l^{\ast }(T)$, and ${HB}_l^{\ast }(T)$ (3)–(6) for the Termar-ADF friction material (Fig. 1). The density of this material does not change as temperature increases [${\uprho}_l^{\ast }(T)$ = 1].

Fig. 1.

Dependences of the dimensionless thermal conductivity ${K}_l^{\ast }$ (1), specific heat ${c}_l^{\ast }$ (2), and Brinell hardness ${HB}_l^{\ast }$ (3) of the Termar-ADF material on temperature Т.

For the determined volume temperatures, it follows from Fig. 1 and relations (1), (2) that

$$ {K}_{l,\Theta}=16.75\kern0.5em \mathrm{W}\cdot {\mathrm{m}}^{-1}\cdot {}^{\circ}{\mathrm{C}}^{-1}\kern1em \mathrm{and}\kern1em {c}_{l,\Theta}=1723.5\kern0.5em \mathrm{J}\cdot {\mathrm{kg}}^{-1}\cdot {}^{\circ}{\mathrm{C}}^{-1},\kern1em l=1.2 $$

for the exponential increase in contact pressure and

$$ {K}_{l,\Theta}=16.64\kern0.5em \mathrm{W}\cdot {\mathrm{m}}^{-1}\cdot {}^{\circ}{\mathrm{C}}^{-1}\kern1em \mathrm{and}\kern1em {c}_{l,\Theta}=1730\kern0.5em \mathrm{J}\cdot {\mathrm{kg}}^{-1}\cdot {}^{\circ}{\mathrm{C}}^{-1},\kern1em l=1.2 $$

for the linear increase in pressure.

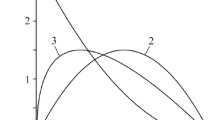
The mean temperature of friction surface T_m (16)–(20) under the conditions of braking with exponentially increasing contact pressure is higher than the temperature given by relations (16), (21), and (22) for the linear increase in pressure up to its nominal value (Fig. 2a). The values of T_m found for the thermal characteristics at the volume temperature Θ_l (23)–(25) are higher than the values computed for the characteristics at the initial temperature T₀. Thus, the maximal values of T_m are equal to 814.4 and 653.6°C (an increment of 19.75%) for the exponential growth and to 722.9 and 576.9°C (an increment of 20.2%) for the linear growth of pressure, respectively.

Fig. 2.

Evolutions of the average temperature T_m (a), flash temperature T_f (b), and maximal temperature T_max (c) during braking with exponential (1) or linear (2) increase in contact pressure. The solid lines were obtained with regard for the thermal sensitivity of materials; the dashed lines correspond to the constant thermal properties of materials.

The computational relations (26)–(30) for the flash temperature T_f contain the heat-conduction coefficient, heat capacity, and hardness of the friction material regarded as functions of the mean temperature T_m and, hence, its evolution exerts a decisive influence on the time dependence of T_f (Fig. 2b). For the analyzed friction material, the flash temperatures T_f are much lower than the corresponding values of T_m. The highest value (67°C) of flash temperature is observed for the exponential increase in pressure if we take into account the thermal sensitivity of the material. The maximal value of the mean temperature of friction surface is attained for about a half of the duration of braking (see Fig. 2a), whereas the highest flash temperature, according to the chosen mechanism of plastic deformation of roughnesses of the working surfaces is detected in the initial period of braking, when these surfaces are relatively cold. The maximal temperature of tribosystem T_max (15) is obtained as the sum of the mean temperature of the friction surface and the flash temperature T_f. Its evolution is mainly determined by the time dependence of T_m. For the exponential increase in pressure, the highest values of T_max are, respectively, 872 and 703.6°C (an increment of 19.3%) with and without taking into account the thermal sensitivity of the Termar-ADF composite. In the case of linearly increasing pressure, these values constitute, respectively, 776.95 and 622.93°C (an increment of 19.82%).

Conclusions

We propose a system of equations of the thermal dynamics of friction for the evaluation of the maximal temperatures of the friction elements of brakes. This system includes the temperature dependences of thermal and mechanical properties of the materials, the solution of the initial-value problem for the equation of motion with a friction force variable in the course of braking, and the relations for the mean temperature of the nominal contact zone of the pad with the disk, the volume temperature of these elements, and the temperature of the actual contact zone (flash temperature). We find the maximal temperature of the friction surface as the sum of the mean and flash temperatures. We performed numerical analyses for the case of a three-disk brake whose friction elements were made of the Termar-ADF carbon composite. The maximal temperature during braking with exponentially increasing contact pressure is higher than for the linear growth of pressure up to its nominal value. The difference between the temperatures determined with and without taking into account the thermal sensitivity of the material constitutes ∼ 20%, which confirms the importance of taking into account the temperature dependence of thermal characteristics of the Termar-ADF material in computing the thermal conditions in high-loaded multiple-disk brakes.

The present work was performed within the framework of Grant No. 2017/27/B/ST8/01249 of the National Scientific Center of the Republic of Poland.