Nonlinear Finite Element Bending Analysis of Composite Shell Panels

Abstract

This paper deals with the geometric nonlinear bending response of laminated composite shell panels subjected to transverse loading. The eight-noded degenerated shell element with five degrees of freedom per node is adopted in the present analysis to model the composite shell panels. The Green-Lagrange strain displacement relationship is adopted to formulate the matrices. The total Lagrangian approach is taken in the formulation. The arc-length method of solution is adopted in tracing the equilibrium path. The results by this method are compared with the available results and the conclusions are made.

1 Introduction

The composite shell panels are extensively used in many modern engineering structures in aerospace, hydrospace, automobile, missile, petrochemical and building industries. This is primarily because of high stiffness-to-weight, high strength-to-weight and lower machining and maintenance cost of the composite structures. These composite structures can also be designed very effectively by managing the volume of fibers, orientation of the fibers, volume of matrix etc. according to the requirement. During the service life the composite shell panels are subjected to heavy transverse load. At higher load the defection of the panels become large compared to its thickness. At this stage the linear solutions to this problem is not accurate. So a nonlinear analysis is preferred to trace the complete load-deflection curve. In many cases the laminated composite shell panels becomes unstable at some amount of transverse load. These structures may experience snap-through or snap-back instability during bending. So a proper solution scheme is necessary to define the whole equilibrium path or the load-deformation path. The Newton-Raphson method of solving the nonlinear equilibrium equation will not work if any instability arises in the structure at any point of time or any point of loading. Both the load-control and displacement-control fail in the snap-back type of instability. In this situation the arc-length method is one of the best option to be used in solving the nonlinear equation to trace the equilibrium path.

The nonlinear bending analysis of the shell panels has been carried out by many investigators. Sabir and Lock [9] had used the strain-based finite element method to carry out a large deflection analysis of isotropic cylindrical shells. To solve the nonlinear equations Riks [8] proposed a new solution procedure to overcome the limit points. Crisfield [3] modified the Riks’s approach and made it suitable for use in the finite element. This arc length method [3] was applied in conjunction with the Newton-Raphson method in both standard and modified forms. It is a path following technique where both load and displacement are independent parameters.

This method [3] can handle snap-through and snap-back type of instability during bending. Chang and Sawamiphakdi [2] had performed the large deformation analysis of laminated shells using finite element method. They had adopted a degenerated three-dimensional isoparametric element in the analysis. The nonlinear geometric element stiffness matrices were made on the basis of updated Lagrangian description. Sabir and Djoudi [10] presented the results of geometrically nonlinear bending behavior of shallow shells. Kim and Voyiadjis [5] studied the nonlinear bending behavior of moderately thick plates and shells using an eight-noded shell element with six degrees of freedom per node. It was limited to geometric imperfections that reduce the buckling capacity. Sze et al. [11] had analyzed the popular benchmark shell problems with geometric nonlinearity. They have solved eight benchmark shell problems by ABAQUS finite element software taking the effect of geometric nonlinearity and plotted the load-deflection curves. Kundu and Sinha [6] had presented the post-buckling analysis of transversely loaded laminated composite shells by finite element method.

In the present investigation, the nonlinear bending analysis of laminated composite cylindrical panels is carried out. The eight-noded degenerated shell element with five degrees of freedom per node is adopted in the present analysis to model the cylindrical panels. The Green-Lagrange strain displacement relationship is adopted and the total Lagrangian approach is taken in the formulation of the matrices. The material behavior is assumed to be linear and elastic. The nonlinear equilibrium equations are solved by Crisfield [3] arc-length method, explained by Fafard and Massicotte [4] and the results are reported.

2 Formulation

The cylindrical panels are modeled with Ahmad et al.’s [1] degenerated shell element with Green-Lagrange strain displacement relationship and laminated composite material properties. The element contains five degree of freedom per node, θ _z is neglected. Shear correction factor of 5/6 is adopted in the stress-strain relationship for transverse shear stresses. The formulation of the shell element is presented below.

3 Shell Element

The formulation of the present shell element is based on the basic concept of Ahmad et al.’s [1] shell element, where the three-dimensional solid element used to model the shell is degenerated with the help of certain extractions obtained from the consideration that the dimension across the shell thickness is sufficiently small compared to other dimensions. The detail derivation of this element for isotropic case and with linear strain displacement is available in the literature [1, 7, 13].

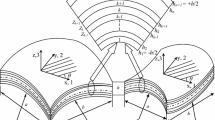
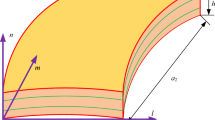
The element has a quadrilateral shape having eight nodes as shown in Fig. 1a where the external top and bottom surfaces of the element are curved with linear variation across the shell thickness. Figure 1b shows the global Cartesian and local co-ordinate system at any node i. The geometry of the element can be nicely represented by the natural coordinate system (ξ, η and ζ) where the curvilinear coordinates (ξ-η) are in the shell mid-surface while ζ is linear coordinate in the thickness direction. According to the isoparametric formulation, these coordinates (ξ, η and ζ) will vary from −1 to +1 on the respective faces of the element. The relationship (Eq. 1) between the global Cartesian coordinates (x, y and z) at any point of the shell element with the curvilinear coordinates holds good. This is the geometry of an element, which is described by the coordinates of a set of points taken at the top and bottom surfaces, where the line joining a pair of points (i _top and i _bottom ) is along the thickness direction i.e., normal to the mid-surface at the ith node point. The line joining the top and bottom points is the normal vector (V _3i ) at the nodal point i.

$$ \left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} = \mathop \sum \limits_{i = 1}^{8} N_{i} \left( {\xi ,\eta } \right) \frac{1 + \zeta }{ 2} \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}_{top} + \mathop \sum \limits_{i = 1}^{8} N_{i} \left( {\xi ,\eta } \right) \frac{1 - \zeta }{ 2} \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}_{bottom} $$

(1)

where N _i are the quadratic serendipity shape functions in (ξ-η) plane of the two-dimensional element.

Fig. 1

a Eight-noded quadrilateral degenerated shell element in curvilinear co-ordinates. b Global Cartesian co-ordinate (x, y and z) and local co-ordinate system at any node i

Equation 1 may be rewritten in terms of mid-surface nodal coordinates with the help of unit nodal vectors (v _3i ) along the thickness direction as,

$$ \left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} = \mathop \sum \limits_{i = 1}^{8} N_{i} \left( {\xi ,\eta } \right) \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\} + \mathop \sum \limits_{i = 1}^{8} N_{i} \left( {\xi ,\eta } \right) \frac{{\zeta \times h_{i} }}{ 2} \left\{ {\begin{array}{*{20}c} {l_{3i} } \\ {m_{3i} } \\ {n_{3i} } \\ \end{array} } \right\} $$

(2)

where, l _3i , m _3i and n _3i are direction cosines of the nodal vector (V _3i ), i.e. components of unit nodal vectors (v _3i ), v _3i is the unit vector along (V _3i ) direction, h _i is the thickness at node i.

Two orthogonal tangential vectors V _2i and V _1i are formed at the node i which are normal to V _3i vector. The two tangential vectors V _2i and V _1i not necessarily follow ξ and η directions. The unit vectors along V _2i and V _1i directions are v _2i and v _1i . The local co-ordinates x′, y′ and z′ are directed along V ₁, V ₂ and V ₃ directions respectively. The directions cosines of x′, y′ and z′ and V ₁, V ₂ and V ₃ are same as the components of unit vectors v ₁, v ₂ and v ₃. The displacement u, v and w are along the global coordinates x, y and z directions. Similarly the local displacement components u′, v′ and w′ are along the local coordinates x′, y′ and z′ directions. The rotations of the mid surface normal θ _x and θ _y are taken about the local coordinates y′ and x′ or v ₂ and v ₁ directions respectively.

The displacement field (Eq. 3) of a point within the element can be defined with the help of three mid surface nodal translational displacement (u _i , v _i and w _i ) along the global Cartesian co-ordinates directions and two rotational components θ _xi and θ _yi about the local coordinates y′ and x′ directions.

$$ \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \mathop \sum \limits_{i = 1}^{8} N_{i} \left( {\xi ,\eta } \right) \left\{ {\begin{array}{*{20}c} {u_{i} } \\ {v_{i} } \\ {w_{i} } \\ \end{array} } \right\} - \mathop \sum \limits_{i = 1}^{8} N_{i} \left( {\xi ,\eta } \right) \frac{{\zeta \times h_{i} }}{ 2} \left[ {\begin{array}{*{20}c} {l_{1i} } & {l_{2i} } \\ {m_{1i} } & {m_{2i} } \\ {n_{1i} } & {n_{2i} } \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\theta_{xi} } \\ {\theta_{yi} } \\ \end{array} } \right\} = \left[ {N_{D} } \right] \left\{ d \right\} $$

(3)

where, l _1i , m _1i and n _1i are direction cosines of the nodal vector (V _1i ), i.e. components of v _1i , l _2i , m _2i and n _2i are direction cosines of the nodal vector (V _2i ), i.e. components of v _2i , and {d} is nodal displacement vector,

$$ \left\{ d \right\} = [u_{1} v_{1} w_{1} \theta_{x1} \theta_{y1} u_{2} v_{2} \ldots \theta_{x8} \theta_{y8} ]^{T} . $$

(4)

The strain displacement relationship with Green-Lagrange strain of the element in local co-ordinate system (x′-y′-z′) can be expressed as,

$$ \left\{ {\user2{\varepsilon }^{'} } \right\} = \left\{ {\begin{array}{*{20}c} {\user2{\varepsilon }_{{\user2{x}^{'} }} } \\ {\user2{\varepsilon }_{{\user2{y}^{'} }} } \\ {\user2{\gamma }_{{\user2{x}^{'} \user2{y}^{'} }} } \\ {\user2{\gamma }_{{\user2{y}^{'} \user2{z}^{'} }} } \\ {\user2{\gamma }_{{\user2{x}^{'} \user2{z}^{'} }} } \\ \end{array} } \right\}~ = ~\left\{ {\begin{array}{*{20}c} {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{x}^{'} }}} \\ {\frac{{\partial \user2{v}^{'} }}{{\partial \user2{y}^{'} }}} \\ {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{y}^{'} }} + \frac{{\partial \user2{v}^{'} }}{{\partial \user2{x}^{'} }}} \\ {\frac{{\partial \user2{v}^{'} }}{{\partial \user2{z}^{'} }} + \frac{{\partial \user2{w}^{'} }}{{\partial \user2{y}^{'} }}} \\ {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{z}^{'} }} + \frac{{\partial \user2{w}^{'} }}{{\partial \user2{x}^{'} }}} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {~\frac{1}{2}\left( {\left( {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{x}^{'} }}} \right)^{2} + ~\left( {\frac{{\partial \user2{v}^{'} }}{{\partial \user2{x}^{'} }}} \right)^{2} + \left( {\frac{{\partial \user2{w}^{'} }}{{\partial \user2{x}^{'} }}} \right)^{2} } \right)} \\ {~\frac{1}{2}\left( {\left( {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{y}^{'} }}} \right)^{2} + ~\left( {\frac{{\partial \user2{v}^{'} }}{{\partial \user2{y}^{'} }}} \right)^{2} + \left( {\frac{{\partial \user2{w}^{'} }}{{\partial \user2{y}^{'} }}} \right)^{2} } \right)} \\ {~\left( {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{x}^{'} }} \times \frac{{\partial \user2{u}^{'} }}{{\partial \user2{y}^{'} }} + ~\frac{{\partial \user2{v}^{'} }}{{\partial \user2{x}^{'} }} \times \frac{{\partial \user2{v}^{'} }}{{\partial \user2{y}^{'} }} + ~\frac{{\partial \user2{w}^{'} }}{{\partial \user2{x}^{'} }} \times \frac{{\partial \user2{w}^{'} }}{{\partial \user2{y}^{'} }}} \right)} \\ {~\left( {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{y}^{'} }} \times \frac{{\partial \user2{u}^{'} }}{{\partial \user2{z}^{'} }} + ~\frac{{\partial \user2{v}^{'} }}{{\partial \user2{y}^{'} }} \times \frac{{\partial \user2{v}^{'} }}{{\partial \user2{z}^{'} }} + ~\frac{{\partial \user2{w}^{'} }}{{\partial \user2{y}^{'} }} \times \frac{{\partial \user2{w}^{'} }}{{\partial \user2{z}^{'} }}} \right)} \\ {\left( {\frac{{\partial \user2{u}^{'} }}{{\partial \user2{x}^{'} }} \times \frac{{\partial \user2{u}^{'} }}{{\partial \user2{z}^{'} }} + ~\frac{{\partial \user2{v}^{'} }}{{\partial \user2{x}^{'} }} \times \frac{{\partial \user2{v}^{'} }}{{\partial \user2{z}^{'} }} + ~\frac{{\partial \user2{w}^{'} }}{{\partial \user2{x}^{'} }} \times \frac{{\partial \user2{w}^{'} }}{{\partial \user2{z}^{'} }}} \right)} \\ \end{array} } \right\} $$

(5)

$$ \left\{ {\varepsilon^{\prime } } \right\} = \left\{ {\varepsilon_{0}^{\prime } } \right\} + \left\{ {\varepsilon_{nl}^{\prime } } \right\} $$

(6)

After performing number of operations using Eqs. (2) and (3) we can write,

$$ \left\{ {\varepsilon^{\prime } } \right\} = \left[ {B_{0}^{\prime } } \right] \left\{ d \right\} + \frac{1}{2} \left[ {B_{nl}^{\prime } } \right] \left\{ d \right\} $$

(7)

$$ \left\{ {\varepsilon^{\prime } } \right\} = \left[ {B_{0}^{\prime } } \right] \left\{ d \right\} + \frac{1}{2} \left[ A \right] \left[ {B_{G}^{\prime } } \right] \left\{ d \right\} $$

(8)

where, $\left[ {B_{0}^{\prime } } \right]$ and $\left[ {B_{nl}^{\prime } } \right]$ are strain-displacement matrices with respect to linear and nonlinear strain components respectively in local co-ordinate system(x′-y′-z′). The normal strain $\varepsilon_{{{\text{z}}^{\prime } }}$ along $z^{\prime }$ direction is neglected.

Knowing, the stress-strain relationship of the laminated composite material in each layer in its material axis system (1–2–3), the stress-strain relationship in the local co-ordinate systems(x′-y′-z′) can be found out by simple transformation. Here material axis 3 is directed along z′ direction. The material axes 1–2 lie in x′-y′ plane but it can be oriented at some angle θ. After transformation the stress-strain relationship in the local co-ordinate systems can be written as,

$$ \left\{ {\sigma^{\prime } } \right\} = \left[ {D^{\prime } } \right] \left\{ {\varepsilon^{\prime } } \right\} $$

(9)

After finding $\left[ {B_{0}^{\prime } } \right]$, $\left[ {B_{nl}^{\prime } } \right]$ and $\left[ {D^{\prime } } \right]$ matrices the secant stiffness matrix can be expressed as,

$$ \left[ k \right]_{S} \,= \int {\left[ {B_{0}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right]\left[ {B_{0}^{\prime } } \right] dV} + \frac{1}{2}\int {\left[ {B_{0}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right]\left[ {B_{nl}^{\prime } } \right]dV} + \int {\left[ {B_{nl}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right]\left[ {B_{0}^{\prime } } \right]dV} + \frac{1}{2}\int {\left[ {B_{nl}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right]\left[ {B_{nl}^{\prime } } \right]dV} $$

(10)

This secant stiffness matrix is not symmetric. To efficiently use the storage scheme which is used in linear analysis, this non symmetric scant stiffness matrix can be made symmetric [12] as,

$$ \begin{aligned} \left[ k \right]_{S} & = \int {\left[ {B_{0}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right]\left[ {B_{0}^{\prime } } \right] dV} + \frac{1}{2}\int {\left[ {B_{0}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{nl}^{\prime } } \right] dV} + \frac{1}{2} \int {\left[ {B_{nl}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{0}^{\prime } } \right] dV} \\ & \quad + \frac{1}{3} \int {\left[ {B_{nl}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{nl}^{\prime } } \right] dV} + \frac{1}{2} \int {\left[ {B_{G}^{\prime } } \right]^{T} \left[ \tau \right] \left[ {B_{G}^{\prime } } \right] dV} + \frac{1}{3} \int {\left[ {B_{G}^{\prime } } \right]^{T} \left[ {\tau_{nl} } \right] \left[ {B_{G}^{\prime } } \right] dV} \\ \end{aligned} $$

(11)

where, $\left[ {D^{\prime } } \right]$ matrix is stress-strain matrix in local co-ordinate system, and $\left[ \tau \right]$ and $\left[ {\tau_{nl} } \right]$ are stress matrix in local co-ordinate system for linear and nonlinear parts of the strain respectively.

The tangent stiffness matrix, which is used in the nonlinear solution of the equilibrium equation can be written as,

$$ \begin{aligned} \left[ k \right]_{T} & = \int {\left[ {B_{0}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{0}^{\prime } } \right] dV} + \int {\left[ {B_{0}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{nl}^{\prime } } \right] dV} + \int {\left[ {B_{nl}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{0}^{\prime } } \right] dV} \\ & \quad + \int {\left[ {B_{nl}^{\prime } } \right]^{T} \left[ {D^{\prime } } \right] \left[ {B_{nl}^{\prime } } \right] dV} + \int {\left[ {B_{G}^{\prime } } \right]^{T} \left[ {\tau + \tau_{nl} } \right] \left[ {B_{G}^{\prime } } \right] dV} \\ \end{aligned} $$

(12)

The secant and tangent stiffness matrices of all elements of the laminated composite cylindrical panel is calculated and assembled properly to form the global secant and tangent stiffness matrices of the structure. The load vector is calculated. The nonlinear equilibrium equations are solved by Crisfield arc-length method as explained by Fafard and Massicotte [4]. The tolerance is defined with respect to the displacement criterion.

4 Results and Discussions

The validation of the formulation is tested first by taking different examples, which are solved by earlier investigators. A hinged cylindrical panel subjected to concentrated load with isotropic and laminated composite material properties is taken for this purpose.

4.1 Hinged Isotropic Cylindrical Panel Subjected to Concentrated Load

A hinged isotropic cylindrical panel (Fig. 2) is considered for the validation of the results. The straight edges are hinged and the curved edges are free. The curved edge length is 508 mm and the angle θ is 0.1 radian. The projection of the curved edge length is 507.153 mm, but for analysis we can take it as 508 mm. The concentrated load P is applied at the center of the panel. The Young’s modulus (E) is taken as 3,105 N/mm² and the Poisson’s ratio (ν) is 0.3.

Fig. 2

Hinged cylindrical panel subjected to point load

The whole panel is modeled with 8 × 8 mesh for the analysis. The load deflection curve of the present analysis is presented in Fig. 3, along with the finite element results of Sabir and Lock [9], Crisfield [3] and Sze et al. [11]. The cylindrical panel is showing a snap-through type of instability during the bending process. It can be observed that the present results are matching well with the results of Sabir and Lock [9], Crisfield [3] and Sze et al. [11] up to the limit point. The present solution scheme is unable to trace the curve beyond the limit point. It needs little modification in the computer programming, which is being carried out.

Fig. 3

Load-deflection curve for the isotropic hinged cylindrical panel subjected to point load

4.2 Hinged Laminated Composite Cylindrical Panel Subjected to Concentrated Load

The same cylindrical panel with same geometry and loading is taken again to validate the present formulation with the composite material properties. The panel consist of three layer with equal thickness of lamina with 90/0/90 lamination scheme. The numbering of layers starts from the bottom to the top of the panel. The layer with 0° lamination means the fibers are aligned in the longitudinal direction (i.e. towards y-direction). The whole panel is modeled with 8 × 8 mesh for the analysis in this case also. The material properties considered are, E ₁ = 3,300 N/mm², E ₂ = 1,100 N/mm², G ₁₂ = G ₁₃ = G ₂₃ = 660 N/mm² and ν₁₂ = 0.25. The panel is subjected to a concentrated load at the center. The equilibrium path is plotted in Fig. 4 along with the finite element result of Sze et al. [11]. In this case also the present results are matching well up to the limit point with the results of Sze et al. [11].

Fig. 4

Load-deflection curve for the laminated composite hinged cylindrical panel (90/0/90) subjected to point load

5 Summary

The findings of the present investigation can be summarized as,

• 1. The formulation and geometrically nonlinear analysis of laminated composite shell panel with Green-Lagrange strain displacement relationship in total Lagrangian co-ordinate is presented. A computer program with Fortran 90 is developed to implement the formulation and the results are obtained.

• 2. The deflection results are matching well with the previous results up to the limit point both in isotropic and composite cases.