1 Introduction

The high specific strength/stiffness and better energy absorption properties of the laminated composite structures have made them favourable for the lightweight and high-performance engineering applications. In addition, the layered structure properties can also be tailor-made by changing the parameters like ply-angle to meet the specific functional requirements. Owing to their wide range of applications, the laminated composite structures (flat/curved) have appealed the attention of many researchers involved in structural design from the industries such as aviation, marine, nuclear, aerospace and shipbuilding for the past few decades [1]. However, it is also true that these structures are subjected to large deformation under the complex loading conditions throughout their operational life. As a result of this, the nonlinearity in geometry is induced, and the original geometries of the structure as well as the final responses of the structural component deviate from the expected line. Hence, an accurate knowledge of the deformation behaviour and the induced stresses in the laminated structures under higher load is extremely essential for the analysis and subsequent design of the final finished product. In this regard, many researchers have already put forward numerous attempts in the past to study the linear and the geometrically nonlinear static behaviour of the laminated flat and curved panel by using various existing [2, 3] and refined theories [4, 5]. We also note the widespread implementation of the finite element method (FEM) for the numerical analysis of the mechanical (free vibration, transient, buckling and post-buckling) responses of the laminated composite structures using various shear deformation plate/shell theories and nonlinear kinematic models [6]. However, besides involving complexities in the formulation and greater computational effort, the higher-order shear deformation theory (HOSDT) is mostly preferred over other available mid-plane kinematics [7–13]. This is because it assumes more realistic shear stress distribution through the panel thickness and eliminates the necessity of the shear correction factors. A brief literature survey on the available numerical, analytical and experimental investigations has been presented in the following lines to outline the prime objective of the present research.

Two displacement-based four-noded quadrilateral elements were developed by Zhang and Kim [14] for the analysis of the geometrical nonlinear bending behaviour of the laminated composite plate. The formulation is based on the first-order shear deformation theory (FOSDT) and von-Karman nonlinearity. Arciniega and Reddy [15] provided a simple tensor-based displacement FE model based on the FOSDT kinematics for the nonlinear deformation analysis of the shell structure. Kishore et al. [16] reported the nonlinear static behaviour of the laminated smart composite plate embedded with magnetostrictive layers using the third-order shear deformation theory (TSDT) and von-Karman type of geometrical nonlinearity. Similarly, the effect of random system properties on the transverse nonlinear central deflection of laminated composite spherical shell panel under the combined hygro-thermo-mechanical loading was investigated by Lal et al. [17]. In this analysis, the formulation is based on the HOSDT mid-plane kinematics and von-Karman nonlinearity. In subsequent year, the thermo-elastic stability responses of thin-walled multilayered plate and shell structures are analysed by Sabik and Kreja [18] using the FOSDT mid-plane kinematics. The static response of doubly curved laminated composite shell panels is examined theoretically by Viola et al. [19] via HOSDT mid-plane kinematics. Further, Green–Lagrange geometrical nonlinearity is employed first time by Naidu and Sinha [20] to study the large deformation bending characteristic of the laminated composite shell panel under hygrothermal environment using the FOSDT kinematic model. In the recent past, the significance of Green–Lagrange geometrical nonlinearity on the laminated curved structural responses like the thermal post-buckling [21] and the nonlinear free vibration [22] under the combined loading conditions has been reported by Panda and his co-authors for shallow shell structures.

In continuation to the aforementioned numerical/analytical studies, many experimental investigations on the mechanical behaviour of fibre-reinforced composite structures are also available in open literature. Paepegem and Degrieck [23] reported the bending fatigue performance of the woven glass/epoxy composite panel using the numerical and the experimental methods. Further, the practical importance of the geometrically nonlinear higher-order theories for the analysis of sandwich beam structures has been demonstrated by Sokolinsky et al. [24] by comparing the results with four-point bend test. Similarly, the flexural behaviour of S-2 glass and T700s carbon fibre-reinforced hybrid composites has been investigated by Dong and Devies [25]. Awad et al. [26] examined the behaviour of laminated glass fibre-reinforced polymer (GFRP) composite sandwich beams for different spans and cross sections. The combined influences of the in-plane load and the moment on the bending responses of the symmetric cross-ply laminated composite cantilever rectangular plate are investigated by Zhang et al. [27]. Correspondingly, the bending fatigue behaviour of the E-glass/epoxy composite structures has been examined by Koricho et al. [28] under the different levels of cyclic loading. Reddy et al. [29] described the ballistic performance of the E-glass/phenolic composite and claimed a nonlinear relationship between the energy absorption and the laminate thickness. The preceding literature survey reveals that a large number of numerical analysis have already been completed on the linear and geometrically nonlinear transverse deformations of the laminated composite structures. It is also clearly understood that most of the nonlinear studies are focused on the flat panel geometries and based on the FOSDT/HOSDT type of mid-plane kinematics in conjunction with von-Karman nonlinear strain instead of Green–Lagrange type of geometrical nonlinearity. We also note that no experimental validation of the nonlinear bending behaviour of the laminated composite flat/curved panel using the HOSDT mid-plane kinematics and Green–Lagrange nonlinearity has been reported in open literature.

In order to bridge the gap, the present work is mainly focused on the computation of linear and nonlinear bending responses of the glass/epoxy laminated composite flat/curved panel using three different shear deformation theories in the framework of the HOSDT/FOSDT kinematics and Green–Lagrange nonlinearity. The practical importance of the proposed geometrically nonlinear higher-order theories has been revealed first time by comparing the numerical responses with experimental (three-point bend test) and simulation (ANSYS) results. It is also worth mentioning that the present mathematical models have included all the nonlinear higher-order terms in the formulation to achieve the indispensable generality. The desired governing equations are obtained by minimizing the total potential energy expressions, and the desired results are computed numerically using Picard’s iterative method or popularly known as the direct iterative method. Further, a simulation model is developed in ANSYS environment using ANSYS parametric design language (APDL) code. It is also vital to mention that the mechanical properties of the laminated glass/epoxy panel are evaluated experimentally using simple tension test and utilized for the present numerical analysis. In order to demonstrate the efficacy of the present nonlinear model, the numerical results are compared with those available published literature and subsequent experimental results of the flat panel case only. Finally, the applicability of the proposed HOSDT models for the static analysis of the doubly curved shell panel has been explored by solving numerous examples for different parameters (the side-to-thickness ratios, the curvature ratios, the constraint conditions and the aspect ratios) and discussed in detail.

Fig. 1
figure 1

Laminated composite shallow doubly curved shell panel

Full size image

2 Theoretical modelling

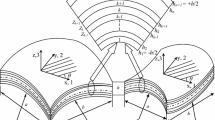
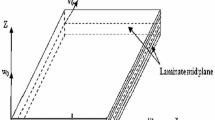
In this present analysis, a generalized doubly curved laminated composite shallow shell panel of uniform thickness ‘h’ is considered, and the details are shown in Fig. 1. The principal radii of curvatures along x- and y-directions of the shallow (twisting radius of curvature \(R_{xy}=\infty )\) shell panel are defined as \(R_{x}\) and \(R_{y}\), respectively. The two-dimensional projection of the shell panel is a rectangle with length, ‘a’, and breadth, ‘b’, along the x- and the y-directions, respectively. In this present investigation, the mathematical models of the laminated composite panel have been developed using two higher-order theories (Model-I and Model-II) as well as subsequent simulation model using the FOSDT (Model-III) kinematics, and the details are provided in the following subsections.

2.1 Displacement models

2.1.1 Model-I

Firstly, the laminated shell panel model is developed using HOSDT type of mid-plane kinematics as same as in [16] where the displacement functions are assumed to be varying cubically and linearly for the in-plane and transverse directions and conceded in the following form:

$$\begin{aligned} \left. {{\begin{array}{l} {u^{\left( k \right) }\left( {x,y,z} \right) } \\ {v^{^{\left( k \right) }}\left( {x,y,z} \right) } \\ {w^{^{\left( k \right) }}\left( {x,y,z} \right) } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {u_0 \left( {x,y} \right) } \\ {v_0 \left( {x,y} \right) } \\ {w_0 \left( {x,y} \right) } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{c} {\theta _x \left( {x,y} \right) } \\ {\theta _y \left( {x,y} \right) } \\ {\theta _z \left( {x,y} \right) } \\ \end{array} }} \right\} +z^{2}\left\{ {{\begin{array}{c} {\phi _x \left( {x,y} \right) } \\ {\phi _y \left( {x,y} \right) } \\ \end{array} }} \right\} +z^{3}\left\{ {{\begin{array}{c} {\lambda _x \left( {x,y} \right) } \\ {\lambda _y \left( {x,y} \right) } \\ \end{array} }} \right\} \end{aligned}$$
(1)

2.1.2 Model-II

Further, another kinematic model is assumed as in [3] considering the displacement variable through the thickness, \(w^{{\left( k \right) }}\left( {x,y,z} \right) \) to be inextensible or constant and expressed as:

$$\begin{aligned} \left. {{\begin{array}{l} {u^{\left( k \right) }\left( {x,y,z} \right) } \\ {v^{^{\left( k \right) }}\left( {x,y,z} \right) } \\ {w^{^{\left( k \right) }}\left( {x,y,z} \right) } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {u_0 \left( {x,y} \right) } \\ {v_0 \left( {x,y} \right) } \\ {w_0 \left( {x,y} \right) } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{c} {\theta _x \left( {x,y} \right) } \\ {\theta _y \left( {x,y} \right) } \\ \end{array} }} \right\} +z^{2}\left\{ {{\begin{array}{c} {\phi _x \left( {x,y} \right) } \\ {\phi _y \left( {x,y} \right) } \\ \end{array} }} \right\} +z^{3}\left\{ {{\begin{array}{c} {\lambda _x \left( {x,y} \right) } \\ {\lambda _y \left( {x,y} \right) } \\ \end{array} }} \right\} \end{aligned}$$
(2)

Here in Model-II, it is evident that only linear transverse normal strain \([\left( {\varepsilon _{zz} } \right) _\mathrm{l} ]\) is zero but not the total strain, i.e., \(\varepsilon _{zz} \ne 0\), whereas in Model-1 neither of the linear nor the total transverse strain is zero, i.e., \(\left( {\varepsilon _{zz} } \right) _\mathrm{l} \ne 0\).

2.1.3 Model-III

Now, the third model is derived using the FOSDT kinematic model as in [30], where both the in-plane and the out-of-plane kinematics are considered to be varying linearly. For this model, six degrees of freedom (DOF) per node have been considered and expressed as:

$$\begin{aligned} \left. {{\begin{array}{l} {u^{\left( k \right) }\left( {x,y,z} \right) } \\ {v^{^{\left( k \right) }}\left( {x,y,z} \right) } \\ {w^{^{\left( k \right) }}\left( {x,y,z} \right) } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {u_0 \left( {x,y} \right) } \\ {v_0 \left( {x,y} \right) } \\ {w_0 \left( {x,y} \right) } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{c} {\theta _x \left( {x,y} \right) } \\ {\theta _y \left( {x,y} \right) } \\ {\theta _z \left( {x,y} \right) } \\ \end{array} }} \right\} \end{aligned}$$
(3)

where \(u^{(k)}\), \(v^{(k)}\) and \(w^{(k)}\) are the displacements on any \(k{\mathrm{th}}\) layer along the longitudinal and transverse directions, i.e., x-, y-, and z-axes, respectively, as shown in Fig. 1. In addition, the displacements on the mid-plane are represented as \(u_{0}\), \(v_{0}\) and \(w_{0}\) along their corresponding direction as discussed previously. Similarly, \(\theta _x \) and \(\theta _y \) are the rotations of normal to the mid-plane, i.e., \(z = 0\), about y- and x-axes, respectively. Subsequently, \(\theta _z \) is the transverse normal extensional term through the thickness direction as seen in Model-I and III. Further, few more functions \((\phi _{x }, \phi _y, \lambda _x \) and \(\lambda _y )\), as presented in both the developed HOSDT models, correspond to the higher-order terms in Taylor’s series expansion and help in maintain the original transverse deformation modes.

2.2 Strain–displacement relations

The geometrical nonlinearity is incorporated for any general material continuum through the strain–displacement relations, and in the current model it is introduced through Green–Lagrange strain and expressed as in [31]:

$$\begin{aligned} \left\{ {{\begin{array}{c} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\varepsilon _{zz} } \\ {\varepsilon _{yz} } \\ {\varepsilon _{xz} } \\ {\varepsilon _{xy} } \\ \end{array} }} \right\} =\left\{ {\begin{array}{c} u_{,x} \\ v_{,y} \\ w_{,z} \\ v_{,z} +w_{,y} \\ u_{,z} +w_{,x} \\ u_{,y} +v_{,x} \\ \end{array}} \right\} +\frac{1}{2}\left[ {\begin{array}{c} \left( u{,_x } \right) ^{2}+\left( {v_{,x} } \right) ^{2}+\left( {w_{,x} } \right) ^{2} \\ \left( {u_{,y} } \right) ^{2}+\left( {v_{,y} } \right) ^{2}+\left( {w_{,y} } \right) ^{2} \\ \left( {u_{,z} } \right) ^{2}+\left( {v_{,z} } \right) ^{2}+\left( {w_{,z} } \right) ^{2} \\ 2\left\{ {\left( {u_{,z} } \right) \left( {u_{,y} } \right) +\left( {v_{,z} } \right) \left( {v_{,y} } \right) +\left( {w_{,z} } \right) \left( {w_{,y} } \right) } \right\} \\ 2\left\{ {\left( {u_{,z} } \right) \left( {u_{,x} } \right) +\left( {v_{,z} } \right) \left( {v_{,x} } \right) +\left( {w_{,z} } \right) \left( {w_{,x} } \right) } \right\} \\ 2\left\{ {\left( {u_{,x} } \right) \left( {u_{,y} } \right) +\left( {v_{,x} } \right) \left( {v_{,y} } \right) +\left( {w_{,x} } \right) \left( {w_{,y} } \right) } \right\} \\ \end{array}} \right] \end{aligned}$$
(4)

The total strain vector \(\left\{ \varepsilon \right\} \) can be expressed as the summation of the linear \(\left\{ {\varepsilon _\mathrm{l} } \right\} \)and the nonlinear \(\left\{ {\varepsilon _{\mathrm{nl}} } \right\} \) strain vectors and given by:

$$\begin{aligned} \left\{ \varepsilon \right\} =\left\{ {\varepsilon _\mathrm{l} } \right\} +\left\{ {\varepsilon _{\mathrm{nl}} } \right\} \end{aligned}$$
(5)

Now, substituting the Model-I in Eq. (4), we obtain the expression for the total strain as the function of transverse thickness coordinate as below:

$$\begin{aligned} \left\{ {\varepsilon _\mathrm{l} } \right\} +\left\{ {\varepsilon _{\mathrm{nl}} } \right\}= & {} \left\{ {{\begin{array}{c} {\varepsilon _1 ^{\mathrm{l}_0 }} \\ {\varepsilon _2 ^{\mathrm{l}_0 }} \\ {\varepsilon _3 ^{\mathrm{l}_0 }} \\ {\varepsilon _4 ^{\mathrm{l}_0 }} \\ {\varepsilon _5 ^{\mathrm{l}_0 }} \\ {\varepsilon _6 ^{\mathrm{l}_0 }} \\ \end{array} }} \right\} +\frac{1}{2}\left\{ {{\begin{array}{c} {\varepsilon _1 ^{\mathrm{nl}_0 }} \\ {\varepsilon _2 ^{\mathrm{nl}_0 }} \\ {\varepsilon _3 ^{\mathrm{nl}_0 }} \\ {2\varepsilon _4 ^{\mathrm{nl}_0 }} \\ {2\varepsilon _5 ^{\mathrm{nl}_0 }} \\ {2\varepsilon _6 ^{\mathrm{nl}_0 }} \\ \end{array} }} \right\} +z\left[ {\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{l}_1 }} \\ {k_2 ^{\mathrm{l}_1 }} \\ 0 \\ {k_4 ^{\mathrm{l}_1 }} \\ {\begin{array}{l} k_5 ^{\mathrm{l}_1 } \\ k_6 ^{\mathrm{l}_1 } \\ \end{array}} \\ \end{array} }} \right\} +\frac{1}{2}\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{nl}_1 }} \\ {k_2 ^{\mathrm{nl}_1 }} \\ {k_3 ^{\mathrm{nl}_1 }} \\ {2k_4 ^{\mathrm{nl}_1 }} \\ {\begin{array}{l} 2k_5 ^{\mathrm{nl}_1 } \\ 2k_6 ^{\mathrm{nl}_1 } \\ \end{array}} \\ \end{array} }} \right\} } \right] +z^{2}\left[ {\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{l}_2 }} \\ {k_2 ^{\mathrm{l}_2 }} \\ 0 \\ {k_4 ^{\mathrm{l}_2 }} \\ {\begin{array}{l} k_5 ^{\mathrm{l}_2 } \\ k_6 ^{\mathrm{l}_2 } \\ \end{array}} \\ \end{array} }} \right\} +\frac{1}{2}\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{nl}_2 }} \\ {k_2 ^{\mathrm{nl}_2 }} \\ {k_3 ^{\mathrm{nl}_2 }} \\ {2k_4 ^{\mathrm{nl}_2 }} \\ {\begin{array}{l} 2k_5 ^{\mathrm{nl}_2 } \\ 2k_6 ^{\mathrm{nl}_2 } \\ \end{array}} \\ \end{array} }} \right\} } \right] \nonumber \\&+\, z^{3}\left[ {\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{l}_3 }} \\ {k_2 ^{\mathrm{l}_3 }} \\ 0 \\ {k_4 ^{\mathrm{l}_3 }} \\ {\begin{array}{l} k_5 ^{\mathrm{l}_3 } \\ k_6 ^{\mathrm{l}_3 } \\ \end{array}} \\ \end{array} }} \right\} +\frac{1}{2}\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{nl}_3 }} \\ {k_2 ^{\mathrm{nl}_3 }} \\ {k_3 ^{\mathrm{nl}_3 }} \\ {2k_4 ^{\mathrm{nl}_3 }} \\ {\begin{array}{l} 2k_5 ^{\mathrm{nl}_3 } \\ 2k_6 ^{\mathrm{nl}_3 } \\ \end{array}} \\ \end{array} }} \right\} } \right] +z^{4}\frac{1}{2}\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{nl}_4 }} \\ {k_2 ^{\mathrm{nl}_4 }} \\ {k_3 ^{\mathrm{nl}_4 }} \\ {k_4 ^{\mathrm{nl}_4 }} \\ {\begin{array}{l} k_5 ^{\mathrm{nl}_4 } \\ k_6 ^{\mathrm{nl}_4 } \\ \end{array}} \\ \end{array} }} \right\} +z^{5}\frac{1}{2}\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{nl}_5 }} \\ {k_2 ^{\mathrm{nl}_5 }} \\ {k_3 ^{\mathrm{nl}_5 }} \\ {2k_4 ^{\mathrm{nl}_5 }} \\ {\begin{array}{l} 2k_5 ^{\mathrm{nl}_5 } \\ 2k_6 ^{\mathrm{nl}_5 } \\ \end{array}} \\ \end{array} }} \right\} +z^{6}\frac{1}{2}\left\{ {{\begin{array}{c} {k_1 ^{\mathrm{nl}_6 }} \\ {k_2 ^{\mathrm{nl}_6 }} \\ 0 \\ {\begin{array}{l} 0 \\ 0 \\ \end{array}} \\ {\begin{array}{l} 2k_6 ^{\mathrm{nl}_6 } \\ \end{array}} \\ \end{array} }} \right\} \end{aligned}$$
(6)

Now, rearranging the above strain–displacement relation in the matrix form as below:

$$\begin{aligned} \left\{ {\varepsilon _\mathrm{l} } \right\} +\left\{ {\varepsilon _{\mathrm{nl}} } \right\} =\left[ {T^{\mathrm{l}}} \right] \left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} +\frac{1}{2}\left[ {T^{\mathrm{nl}}} \right] \left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} \end{aligned}$$
(7)

where \(\left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} \), \(\left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} \), \(\left[ {T^{\mathrm{l}}} \right] \) and \(\left[ {T^{\mathrm{nl}}} \right] \) are the mid-plane linear and nonlinear strain and thickness coordinate matrices, respectively.

$$\begin{aligned} \left\{ {\bar{\varepsilon }_\mathrm{l} } \right\}= & {} \left\{ {\varepsilon _1^{\mathrm{l}_0 }\varepsilon _2 ^{\mathrm{l}_0 }\varepsilon _3 ^{\mathrm{l}_0 }\varepsilon _4 ^{\mathrm{l}_0}\varepsilon _5 ^{\mathrm{l}_0 }\varepsilon _6 ^{\mathrm{l}_0 }k_1 ^{\mathrm{l}_1 }k_2 ^{\mathrm{l}_1 }k_4^{\mathrm{l}_1 }k_5 ^{\mathrm{l}_1 }k_6 ^{\mathrm{l}_1 }k_1 ^{\mathrm{l}_2 }k_2 ^{\mathrm{l}_2 }k_4 ^{\mathrm{l}_2 }k_5^{\mathrm{l}_2 }k_6 ^{\mathrm{l}_2 }k_1 ^{\mathrm{l}_3 }k_2 ^{\mathrm{l}_3 }k_4 ^{\mathrm{l}_3 }k_5 ^{\mathrm{l}_3 }k_6^{\mathrm{l}_3 }} \right\} ^{T} \text { and }\\ \left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\}= & {} \left\{ {{\begin{array}{ccccccccccccccccccc} {\varepsilon _1 ^{\mathrm{nl}_0 }}&{} {\varepsilon _2 ^{\mathrm{nl}_0 }}&{} {\varepsilon _3^{\mathrm{nl}_0 }}&{} {\varepsilon _4 ^{\mathrm{nl}_0 }}&{} {\varepsilon _5^{\mathrm{nl}_0 }}&{} {\varepsilon _6 ^{\mathrm{nl}_0 }}&{} {k_1 ^{\mathrm{nl}_1 }}&{} {k_2 ^{\mathrm{nl}_1 }}&{} {k_3^{\mathrm{nl}_1 }}&{} {k_4 ^{\mathrm{nl}_1 }}&{} {k_5 ^{\mathrm{nl}_1 }}&{} {k_6 ^{\mathrm{nl}_1 }}&{} {k_1^{\mathrm{nl}_2 }}&{} {k_2 ^{\mathrm{nl}_2 }}&{} {k_3 ^{\mathrm{nl}_2 }}&{} {k_4 ^{\mathrm{nl}_2 }}&{} {k_5^{\mathrm{nl}_2 }}&{} {k_6 ^{nl_2 }}&{} {k_1 ^{\mathrm{nl}_3 }} \\ {k_2 ^{\mathrm{nl}_3 }}&{} {k_3 ^{\mathrm{nl}_3 }}&{} {k_4 ^{\mathrm{nl}_3 }}&{} {k_5 ^{\mathrm{nl}_3 }}&{} {k_6^{\mathrm{nl}_3 }}&{} {k_1 ^{\mathrm{nl}_4 }}&{} {k_2 ^{\mathrm{nl}_4 }}&{} {k_3 ^{\mathrm{nl}_4 }}&{} {k_4^{\mathrm{nl}_4 }}&{} {k_5 ^{\mathrm{nl}_4 }}&{} {k_6 ^{\mathrm{nl}_4 }}&{} {k_1 ^{\mathrm{nl}_5 }}&{} {k_2^{\mathrm{nl}_5 }}&{} {k_4 ^{\mathrm{nl}_5 }}&{} {k_5 ^{\mathrm{nl}_5 }}&{} {k_6 ^{\mathrm{nl}_5 }}&{} {k_1^{\mathrm{nl}_6 }}&{} {k_2 ^{\mathrm{nl}_6 }}&{} {k_6 ^{\mathrm{nl}_6 }} \\ \end{array} }} \right\} . \end{aligned}$$

The terms containing superscripts ‘\(\mathrm{l}_{0}\)’, ‘\(\mathrm{l}_{1}\)’, ‘\(\mathrm{l}_{2}-\mathrm{l}_{3}\)’ in \(\left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} \) and ‘\({\mathrm{nl}}_{0}\)’, ‘\(\mathrm{nl}_{1}\)’, ‘\(\mathrm{nl}_{2}-_{6}\)’ in \(\left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} \) are the membrane, curvature and higher-order strain terms, respectively. The strains for the Model-2 and the Model-3 can be obtained in the similar way, and the details can be seen in [22] and [30], respectively.

Again, the mid-plane strain vectors are expressed in the following form:

$$\begin{aligned} \left. {\begin{array}{l} \left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} =\left[ {B_\mathrm{l} } \right] \left\{ {\delta ^{{*}}} \right\} \\ \left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} =1\big /2\left[ {B_{\mathrm{nl}} } \right] \left\{ {\delta ^{{*}}} \right\} \\ \end{array}} \right\} \end{aligned}$$
(8)

or,

$$\begin{aligned} \left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} =1/2\left[ {B_{\mathrm{nl}} } \right] \left\{ {\delta ^{{*}}} \right\} = 1/2 \left[ A \right] \left[ G \right] \left\{ {\delta ^{{*}}} \right\} \end{aligned}$$

where \(\left[ {B_\mathrm{l} } \right] \) and \(\left[ {B_{\mathrm{nl}} } \right] \) are linear and nonlinear strain–displacement matrices, and \(\left\{ \delta \right\} \) is the corresponding displacement field vector. In addition, the details of [A] and [G] matrices can be seen in [22].

The stress–strain relationship for the laminated shell panel can be expressed as in [31]:

$$\begin{aligned} \left\{ \sigma \right\} =\left[ {\overline{Q}} \right] \left\{ \varepsilon \right\} \end{aligned}$$
(9)

where \(\left\{ \sigma \right\} \), \(\left[ {\overline{Q}} \right] \) and \(\left\{ \varepsilon \right\} \) are the stress vector, transformed reduced stiffness matrix and the strain vectors, respectively.

2.3 Governing equation of equilibrium

The static equilibrium equation of any structural element under the influence of external mechanical load can be expressed by minimizing the total potential energy. Thus, the governing equation can be conceded in the following form.

$$\begin{aligned} \partial \prod =0 \quad \mathrm{or}\quad \prod = U_{{\mathrm{total}}} -W_{{\mathrm{external}}} \end{aligned}$$
(10)

where \(\prod \) represents the total potential energy that can be obtained as the difference between the total strain energy \((U_{{\mathrm{total}}} )\) and the external work done \((W_{{\mathrm{external}}} )\).

Now, the total strain energy of the curved shell panel can be obtained using the general expression:

$$\begin{aligned} U_{{\mathrm{total}}} =1/2\int \limits _V {\left\{ \varepsilon \right\} ^{T}\left\{ \sigma \right\} \mathrm{d}V} \end{aligned}$$
(11)

Also, Eq. (11) can be rewritten by substituting the necessary strain and the stress tensors from Eqs. (7) and (9) and represented as:

$$\begin{aligned} U_{{\mathrm{total}}} =\frac{1}{2}\int \limits _A {\left( {\left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} ^{T}\left[ {D_\mathrm{l} } \right] \left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} +\left\{ {\bar{\varepsilon }_\mathrm{l} } \right\} ^{T}\left[ {D_{\mathrm{nl}1} } \right] \left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} +\left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} ^{T}\left[ {D_{\mathrm{nl}2} } \right] \left\{ {\bar{\varepsilon }_\mathrm{l}} \right\} +\left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} ^{T}\left[ {D_{\mathrm{nl}3} } \right] \left\{ {\bar{\varepsilon }_{\mathrm{nl}} } \right\} } \right) } \mathrm{d}A \end{aligned}$$
(12)

where

$$\begin{aligned} \left[ {D_\mathrm{l} } \right]= & {} \int \limits _{-h/2}^{+h/2} {\left[ {T^{\mathrm{l}}} \right] ^{T}} \left[ {\bar{Q}} \right] \left[ {T^{\mathrm{l}}} \right] \mathrm{d}z, \quad \left[ {D_{\mathrm{nl}1} } \right] =\int \limits _{-h/2}^{+h/2} {\left[ {T^{\mathrm{l}}} \right] ^{T}} \left[ {\bar{Q}} \right] \left[ {T^{\mathrm{nl}}} \right] \mathrm{d}z,\\ \left[ {D_{\mathrm{nl}2} } \right]= & {} \int \limits _{-h/2}^{+h/2} {\left[ {T^{\mathrm{nl}}} \right] ^{T}} \left[ {\bar{Q}} \right] \left[ {T^{\mathrm{l}}} \right] \mathrm{d}z \quad \text {and} \quad \left[ {D_{\mathrm{nl}3} } \right] =\int \limits _{-h/2}^{+h/2} {\left[ {T^{\mathrm{nl}}} \right] ^{T}} \left[ {\bar{Q}} \right] \left[ {T^{\mathrm{nl}}} \right] \mathrm{d}z. \end{aligned}$$

Now, the total work done under the external mechanical load (q) can be expressed as:

$$\begin{aligned} W_{{\mathrm{external}}} =\iint {\left\{ {\delta \left( {x,y} \right) } \right\} ^{T}q\left( {x,y} \right) } \mathrm{d}x\mathrm{d}y \end{aligned}$$
(13)

where q and \(\delta \) are the global load and displacement vectors, respectively.

3 Finite element model

In order to solve the present nonlinear deflection problem numerically, the developed HOSDT models are discretized using the displacement-based FE formulation steps. For the discretization purpose, a nine-nodded isoparametric Lagrangian quadrilateral element with ten \((\left\{ \begin{array}{c} {\delta ^{{*}}_i }\end{array} \right\} =\left\{ \begin{array}{cccccccccc} u_{0_i }&v_{0_i }&w_{0_i}&\theta _{x_i }&\theta _{y_i }&\theta _{zi}&\phi _{xi}&\phi _{yi}&\lambda _{xi}&\lambda _{yi} \end{array} \right\} ^{T})\) degrees of freedom per node and nine \((\left\{ {\delta ^{{*}}_i } \right\} =\left\{ \begin{array}{ccccccccc} u_{0_i }&v_{0_i }&w_{0_i}&\theta _{x_i }&\theta _{y_i }&\phi _{xi}&\phi _{yi}&\lambda _{xi}&\lambda _{xi} \end{array} \right\} ^{T})\) degrees of freedom per node is utilized for Model-I and Model-II, respectively. The displacement vector \(\left\{ {\delta _e } \right\} \) and the element geometry are represented by following relations using the FEM steps as in [32]:

$$\begin{aligned} \left\{ {\delta _e } \right\} =\sum _{i=1}^\mathrm{Ne} {\left[ {S_i } \right] } \left\{ {\delta ^{{*}}} \right\} _i\quad x=\sum _{i=1}^\mathrm{Ne} {\left[ {S_i } \right] } x_i \quad y=\sum _{i=1}^\mathrm{Ne} {\left[ {S_i } \right] } y_i \end{aligned}$$
(14)

where \([S_{i}]\) is the shape function for any \(i{\mathrm{th}}\) node, \(\left\{ {\delta ^{{*}}} \right\} _i \) is the displacement vector for the \(i{\mathrm{th}}\) node and Ne is the number of nodes per element. The polynomial functions utilized for the nodal approximation are as same as in [32].

The total strain energy \((U_{{\mathrm{total}}})\) and the work done \((W_{{\mathrm{external}}})\) expressions from Eqs. (12) and (13) are substituted in Eq. (10) and applying FE approximations as in Eq. (14), the final form of the static equilibrium equation is expressed as

$$\begin{aligned} \left[ K \right] \left\{ \delta \right\} =\{q\} \quad \hbox {or}\quad \left[ {K_\mathrm{l} +K_{\mathrm{nl}} } \right] \left\{ \delta \right\} =\left\{ q \right\} \end{aligned}$$
(15)

where [K] is the system stiffness matrix which comprises of the linear \([K_{l}]\) and the nonlinear \([(K_{\mathrm{nl}})]\) stiffness matrices. The nonlinear stiffness matrices are linearly and quadratic functions of the state-space variables. Similarly, \(\left\{ \delta \right\} \) is the global displacement vector and is obtained by assembling each elements considered for any particular analysis.

Fig. 2
figure 2

Solution steps for the nonlinear bending responses

Full size image

Equation (15) is now solved to compute the desired nonlinear bending responses using the direct iterative method, and the solution steps are explained in the flowchart in Fig. 2 as in [31]:

Fig. 3
figure 3

a, b Experimental set-up of three-point bend test and c specimens of four-layer angle-ply and cross-ply laminated glass/epoxy composite

Full size image
Fig. 4
figure 4

a Experimental set-up for tensile test and b specimens of four-layer angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) and cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated glass/epoxy composite plate

Full size image

4 Experimental procedure

As previously mentioned, the nonlinear flexural strength of the laminated structure computed experimentally for the comparison purpose and to show the relevance of presently developed HOSDT nonlinear model. In this regard, the central deflection values of glass/epoxy composite specimens are obtained via the three-point bend test. For the experimental purpose, the wrapped glass/epoxy composite plates (four-layer angle-ply \([(\pm 45^{\circ })_{\mathrm{s}}]\) and cross-ply \([(0^{\circ }/90^{\circ })_\mathrm{{s}}])\) are procured from Axzact Consultancy (P) Ltd., Bhubaneswar, Odisha, India. The plates are fabricated using glass fibre (300 gsm), LAPOX (L-12) matrix and K-6 hardener. Now, the bending analysis has been carried out using the universal testing machine (UTM)-INSTRON 5967 with environmental chamber and low capacity load cell (30 kN) available at National Institute of Technology (NIT) Rourkela, Odisha, India. The details regarding the bending three-point experimental set-up and the deformed test specimens for angle-ply and cross-ply plates are presented in Fig. 3a–c. For experimentation purpose, the specimen dimensions are prepared in accordance with ASTM standard D790 [33]. Also, the elastic properties of the laminated glass/epoxy composite specimens are obtained through the uniaxial tensile test via UTM-INSTRON 1195 at NIT Rourkela, Odisha, India. The detailed experimental set-up and the fractured samples are provided in Fig. 4a, b, respectively. In order to check the repeatability of the material properties and avoid further misperceptions, the test has been conducted for three different sets prepared from each type of plates, i.e., the cross-ply and angle-ply. The composite specimens from each plate are prepared for the tensile test as per ASTM standard D 3039/D 3039M [34]. The longitudinal and transverse Young’s modulus i.e., \(E_\mathrm{l} \) and \(E_\mathrm{t} \) are evaluated for each specimen (length 200 mm and width 25 mm) and averaged to obtain the final value. In addition, the modulus is also obtained for another sets of sample prepared at an inclined plane, i.e., \(E_{45} \) (angle of inclination \(45^{\circ }\) to the longitudinal direction), and the values are utilized for the calculation of the shear modulus. The properties of the laminated composite plate are obtained using the uniaxial tensile test through UTM by setting the loading rate as 1 mm/min to maintain the quasi-static type of load. It is important to mention that necessary Poisson’s ratio for the present study is taken 0.25 as same as in [3]. Now, the shear modulus of the individual specimens has been computed using the following formula given in [35]:

$$\begin{aligned} \left( {G_{lt} =1\Bigg /{\frac{4}{E_{45} }-\frac{1}{E_{l} }-\frac{1}{E_t }-\frac{2\upsilon _{12} }{E_{l} }}} \right) \end{aligned}$$
(16)

In addition, the flexural stress–strain diagrams of the three-point bend test for each specimens [\((\pm 45^{\circ })_\mathrm{{s}}\) and \((0^{\circ }/90^{\circ })_\mathrm{{s}}\)] are provided in Fig. 5a, b. Finally, the dimensions, lay-up schemes of each specimen of glass/epoxy plate and their corresponding experimental properties utilized for the present analysis are presented in Table 1.

Fig. 5
figure 5

Experimental stress–strain curve of laminated composite specimen of a four-layer angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) and b cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) plate

Full size image

5 Numerical results and discussion

The nonlinear static deflections of the laminated composite single/doubly curved panels are computed numerically using a customized homemade computer FE code developed in MATLAB environment with the help of present HOSDT mathematical models (Model-I and Model-II). Also, the results are computed using a simulation model developed in ANSYS by means of APDL code (Model-III). Further, the validity and the efficacy of the proposed models are examined by comparing the responses with those available numerical and experimental results in the published literature. The deflections of the laminated plate are found additionally through the experimentation (three-point bend test) and compared with the present numerical responses computed using the Model-I, Model-II and Model-III to evident the degree of accuracy. The variation of nonlinear bending responses due to various geometrical parameters such as the side-to-thickness ratio (a / h), shell panel curvature (R / a), aspect ratios (a / b) and different end constraint conditions are investigated using the developed nonlinear mathematical models of different mid-plane kinematics. For the present computation, different constraint conditions are utilized to avoid rigid body motion and provided in Table 2, where S, C and H represent the simply support, clamped and hinged type of end conditions, respectively. The nondimensionalized deflections and the mechanical load parameter are expressed using the formulae \(\overline{W} =\frac{w_\mathrm{c} }{h}\) and \(Q=\frac{qa^{4}}{E_2 h^{4}}\), respectively, where \(w_\mathrm{c} \) is the central deflection and q is the applied load.

Table 1 Experimental composite material properties
Full size table
Table 2 Different sets of end conditions employed in this present analysis
Full size table
Fig. 6
figure 6

Convergence behaviour of the nondimensional a linear and b, c nonlinear central deflection of simply supported four-layer symmetric cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) and angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) curved panels (\(R/a=20\) except flat panel and \(a/h=40\)) of different geometries

Full size image

5.1 Convergence and comparison study

As a very first step, the convergence behaviour of the linear and nonlinear deflection values of the laminated composite panels of different geometries (spherical, cylindrical, elliptical, hyperboloid and flat) has been tested. In each case, the responses are computed using both the developed FE models (Model-I and Model-II) for different mesh refinement and presented in Fig. 6a–c. For the computation purpose, simply supported laminated panels with \(a/h=40\) and \(R/a=20\) (except flat) under uniformly distributed load (UDL) parameter as \(Q =100\) are considered. The glass/epoxy composite material properties (as provided in Table 1) are considered in the present example. It is clearly observed that the present models are showing good convergence rate with mesh refinement. Subsequently, a (\(6 \times 6\)) mesh is utilized to compute the deflection responses throughout the study.

Table 3 Composite material properties considered for numerical parametric study
Full size table
Table 4 Linear central deflection (mm) of clamped four-layer symmetric cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) square plate subjected to UDL
Full size table

Now, the developed numerical models (Model-I and Model-II) are extended further to compute the linear central deflections of the square symmetric cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated flat composite panels under five mechanical UDLs (q) using the material properties similar to Zhang and Kim [14] (M1 in Table 3). The present nondimensional linear central deflections are compared with the published analytical [4] and numerical [14] values and presented in Table 4. It can clearly be observed that both the higher-order models are showing good agreement with the references.

Another example has been solved using the presently developed HOSDT (Model-I and Model-II) to examine the nonlinear bending behaviour of the laminated composite flat panel. The responses are computed for the square simply supported cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated panel under five different mechanical UDLs (\(Q = 50, 100, 150, 200\) and 250) by considering the geometrical parameter and material properties (M1) same as to the reference [14] and presented in Fig. 7. The nonlinear results obtained using both the higher-order models (Model-I and Model-II) are showing good agreement with the available sources [14] and [9]. It is also interesting to note that the differences between the present and reference are higher in few cases for the Model-I. This is because of the fact that the present model is developed based on the HOSDT kinematics and Green–Lagrange nonlinearity instead of the FOSDT/HOSDT kinematics with von-Karman nonlinearity as in the references. In addition to that, the displacement through the thickness for the Model-I is taken as the linear variation instead of constant as in the Model-II. It can also be noted that the Model-I is showing the higher values for the linear/nonlinear deflections in comparison with the Model-II, because of the more flexibility or lower stiffness.

Fig. 7
figure 7

Comparison study of the nondimensional nonlinear central deflection of a simply supported cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated composite flat panel \((a/h=40)\)

Full size image
Fig. 8
figure 8

Comparison study of the experimental and numerical linear central deflections of four-layer angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) and cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated composite flat panel subjected to point load

Full size image
Table 5 Comparison study of experimental and numerical nonlinear central deflection of four-layer (a) angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) and (b) cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated composite plate
Full size table

Further, the linear and nonlinear responses are computed using the numerical and the simulation models, i.e., Model-I, Model-II and Model-III, by considering the experimentally obtained material properties and compared with present experimental results. The transverse central deflection values of the laminated composite panels of two different laminations (cross-ply and angle-ply) are obtained experimentally via three-point bend test under point load using the INSTRON 5967 at NIT Rourkela, Odisha, India. The comparison of results for the linear bending responses are shown in Fig. 8, and the nonlinear responses of four-layer angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) and cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated composite plate are presented in Table 5a, b, respectively. It is clear from the comparison study that the results computed using all three models are showing good agreement with linear experimental results as in Fig. 8. It is worth noting that the present higher-order element in Model-I is better for computing the linear responses in cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) as compared to the angle-ply \((\pm 45^{\circ })_\mathrm{{s}}\) case. However, it is clearly observed from Table 5a, b that Model-I is more efficient to solve the nonlinear bending responses of the laminated composite panels for both the laminations specifically, corresponding to higher loading rates, i.e., when the geometrical nonlinearity is severe. It is also useful to mention that the Model-III (FOSDT) is incapable of solving the nonlinear bending responses of the laminated composite panels for both the laminations at higher load as evident from Table 5a, b. Thus, it is clear from the comparison study that the present higher-order nonlinear models with Green–Lagrange nonlinearity are most appropriate for the nonlinear bending analysis of laminated structures. It is also understood that the simulation model developed in ANSYS in the framework of the FOSDT type kinematics is unable to solve the nonlinear bending responses under higher load cases.

5.2 Parametric study

The convergence and the comparison study indicate that the present higher-order models (Model-I and Model-II) are capable of computing the linear and nonlinear bending responses accurately. Hence, the study is further extended to analyse the influence of different geometries, geometrical parameters and support conditions on the nonlinear static behaviour of the laminated composite flat/curved panels under different mechanical UDLs and discussed in detail. The glass/epoxy composite material properties (M2 as in Table 3), the simply supported (SSSS) end conditions and the square symmetric cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminations are considered throughout the investigation, if not stated otherwise.

Table 6 Variation of nonlinear bending responses of simply supported square cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) single/doubly curved panels \((R/a=20)\) for different thickness ratios using Model-2
Full size table

5.2.1 Variation of nonlinear bending responses with thickness ratio

It is true that the thickness ratio (a / h) plays an important role in determining the flexural strength of any structure or structural component, and it is more pronounced in the case of the laminated structures due to their flexibility. The influence of thickness ratio on the nonlinear bending behaviour is examined in this example and presented in Table 6. For the computational purpose, the square symmetric cross-ply laminated composite panel is analysed using two proposed models (Model-I and Model-II) for two thickness ratios (\(a/h = 40\) and 100) and five UDL load parameters (\(Q = 50, 100, 150, 200\) and 250). It is interesting to note that the nonlinear central deflections are higher and lower for hyperboloid and ellipsoid shell panel, respectively, for both the models.

Table 7 Variation of nonlinear bending responses of simply supported square cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) single/doubly curved panels \((a/h=40)\) for different curvature ratios using Model-2
Full size table
Table 8 Variation of nonlinear bending responses of simply supported cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) single/doubly curved panels (\(a/h=40\) and \(R/a=20\)) for different aspect ratios using Model-1
Full size table
Table 9 Influence of end conditions and panel geometries on the nonlinear central deflection values of square cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) panels (\(a/h=40\) and \(R/a=20\)) using Model-1
Full size table
Fig. 9
figure 9

Deformed shape of simply supported four-layer cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) flat/curved panels (\(a/h=20\), \(a/b=1\) and \(R/a=10\)) using Model-1 and Model-2 a, b cylindrical; c, d hyperboloid; e, f spherical, g, h flat; i, j ellipsoid

Full size image

5.2.2 Variation of nonlinear bending responses with curvature ratio

In general, the curvature ratio (R / a) defines the type of shell, i.e., deep/shallow, and it is well known that the stretching energy is high for the shell panel as compared to the bending energy. In this example, the effect of two curvature ratios (\(R/a = 20\) and 100) and the shell geometries (cylindrical/hyperboloid/elliptical/spherical/flat) on the nonlinear bending responses of laminated composite panel \((a/h = 40)\) is investigated under four UDL (\(Q= 50\), 100, 150 and 200) parameters using Model-I and Model-II and presented in Table 7. It can be observed that the nonlinearity is more pronounced for the higher values of the curvature ratio for any particular geometry. It is also seen that the hyperboloid shell panels have higher stretching energy as compared to all the other geometries due to the unequal (positive and negative) curvature.

5.2.3 Variation of nonlinear bending responses with aspect ratio

The aspect ratio (a / b) plays a significant role in determining the stiffness and stability characteristic of laminated composite curved panel structural element. In order to examine the effect of different aspect ratios (\(a/b= 0.5, 1\) and 1.5) on the nonlinear flexural behaviour of simply supported laminated composite shell panel this example is solved using the Model-I. The responses are computed using the geometrical parameters as \(a/h=40\) and \(R/a=20\) under the mechanical UDL (\(Q= 50, 100, 150\) and 200) and presented in Table 8. It is clear that the flat rectangular panel (\(a/b= 0.5\) and \(R/a=\infty )\) and square ellipsoid shell panels are showing the highest and lowest deflection values, respectively. The results also indicate that the doubly curved (unequal curvature) shell panels have higher stretching energy as compared to the bending energy.

5.2.4 Variation of nonlinear bending responses with support condition and panel geometries

It is well known that the flexibility of any structural component greatly depends on the type of constraint conditions. In this example, the effect of three different support conditions (SSSS, HHHH and CCCC) on the nonlinear bending behaviour of laminated composite shell panel (\(a/h=40\), \(a/b=1\) and \(R/a=20\)) is analysed using the Model-I. The responses are computed using four load parameters (\(Q = 50, 100, 150\) and 200) and given in Table 9. It is clearly observed from the computed responses that the results are following the expected line, i.e., the responses are highest for the simply supported (SSSS) case, lowest in clamped (CCCC) type of end conditions, whereas the values lie in between these two for all sides hinged (HHHH) case.

5.2.5 Variation of nonlinear bending responses with laminated shell geometry

Figure 9a–j shows the deformation behaviour of five different geometries (spherical, cylindrical, ellipsoid, hyperboloid and flat panel) of simply supported symmetric cross-ply \((0^{\circ }/90^{\circ })_\mathrm{{s}}\) laminated panels under load parameter, \(Q = 100\) using both the higher-order models (Model-I and Model-II). For the computational purpose, the geometrical parameter is taken as \(a/h=20\), \(a/b=1\) and \(R/a=10\). It is clearly observed that the deformation behaviour is increasing in the ascending order of ellipsoid, spherical, cylindrical, hyperboloid and flat panel. It is also interesting to note that the Model-I is showing higher deformation values than the Model-II, irrespective of the type of shell geometry. This may be attributed to the higher flexibility of Model-I in comparison with Model-II.

6 Summary and conclusions

In this article, the nonlinear transverse bending responses of the layered glass/epoxy composite curved panel of different geometries have been analysed using two different HOSDT mid-plane kinematics, i.e., ten DOF (Model-I) and nine DOF (Model-II), in conjunction with Green–Lagrange type of strain–displacement relations. The presently developed mathematical models included all the linear and the nonlinear strain terms to achieve the full geometrical nonlinearity as well as the generality. The equilibrium equation of the mechanically loaded layered structure is obtained via minimizing the total potential energy expression and discretized through the suitable isoparametric FE steps. Further, the nonlinear transverse deflection values are worked out using the direct iterative method. The stability and the validity of the proposed higher-order models have been determined through the proper convergence and comparison studies by solving the variety of numerical examples. Also, the results are verified with the simulation model (ANSYS) developed using APDL code (Model-III) as well as experimental values. The inevitability of the present approach has been recognized by comparing the results with those available published analytical and numerical results. Additionally, the static responses of the layered composite plate are also obtained experimentally with the help of three-point bend test and utilized for the comparison purpose. Based on the comparison study, it is understood that the presently developed HOSDT kinematic model together with the nonlinear higher-order terms has a crucial role in the evaluation of the bending strength of the laminated structure, especially when the degree of nonlinearity is significant. It is also concluded that various geometrical parameters such as the side-to-thickness ratio, the aspect ratio, the curvature ratios and the end conditions have the significant influence on the nonlinear deflection behaviour of the single/doubly curved shell panels.