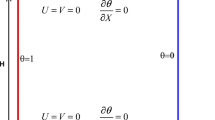Introduction

Generally, heat transfer is common in many applications from chemical reactions [1, 2] to energy storage [3] or energy production [4, 5], especially renewable energy sources [6]. The heat transfer at high temperatures happens in industrial [7, 8] as well as research applications [9, 10] from fossil sources [11] to solar collectors [12]. At high temperatures, to achieve higher heat transfer rates to avoid hot-spot and over-burning phenomena [13, 14], using porous materials is suggested which increases the overall thermal conductivity of the working fluid [15, 16]. Because of a high change in the temperature of working fluid/medium in these cases, the change in the thermal conductivity may be considerable. Hence, temperature-dependent thermal conductivity should be adopted [17, 18]. The present study aims at analytically investigating the heat transfer at high temperatures by considering the above-mentioned cases.

Analytical study of heat transfer which proposes a definite equation for the Nusselt number is the first aim of the researchers. But, because of the complexity of the real problems, it is not available for any cases very easily. Hence, many researchers tried to study the heat and fluid flow in porous media analytically in possible cases. Nield and Kuznetsov [19], for the first time, modeled the radiation heat transfer inside a porous material with a temperature-dependent thermal conductivity and proposed a closed-form solution for the forced convection inside a porous-filled channel. As mentioned, obtaining a closed-form solution for the convection–radiation heat transfer is not very easy [20] and Nield and Kuznetsov [19] only obtained the closed-form Nusselt number for two limiting cases of the clear fluid flow (i.e., s = 0, wherein s is the porous medium shape parameter) and for the slug flow (i.e., s → ∞). Later, Dehghan et al. [21] developed their study for a wide range of porous materials raging form clear fluid flow to the slug flow for the porous-filled channels using the Rosseland approximation method to model the radiation heat transfer in porous media. As mentioned, however, a theoretical study obtains more unproductive results, but theoretical dealing with such complicated problems is not very easy. Hence, numerical modeling of such problems is more common within the literature. Sheikholeslami et al. [22] numerically studied the natural convection heat transfer inside a fully nanofluid-filled porous media in the presence of a magnetic field and the radiation heat transfer modeled by the Rosseland approximation method. They found that the magnetic field has negative effects on heat transfer. Anirudh and Dhinakaran [23] numerically simulated the natural convection–radiation heat transfer in a flat-plate solar collector filled with porous media. They showed that there are many unknowns in the physical phenomenon and further experimental studies are required. Habib et al. [24] performed a pore-scale analysis on the dynamic response of forced convection in porous medium. It was concluded that the linearity of forced response is kept at smaller values of Reynolds number.

The heat transfer inside a tube is a classic and basic phenomenon that widely occurs in practical applications like solar collectors. Many studies have been done on this subject in the case of relatively low-temperature applications wherein the radiation heat transfer is not very dominant. At high temperatures, the radiation heat transfer cannot be ignored and plays a key role in the heat transfer, but performing experimental studies especially to find out what would happen inside the porous medium is not as easy as the low-temperature ones. Hence, to have a better look inside the problem, an analytical study may fill this gap. According to the above-mentioned literature study, no closed-form solution has been presented for the case of forced convection within a porous-filled tube with a temperature-dependent thermal conductivity and the present study aims at filling this gap. A linear profile is considered for the thermal conductivity variation with respect to temperature. Perturbation techniques are used to find closed-form Nusselt numbers, and then parametric studies are presented to discover the response of the heat transfer rate to the governing parameters.

2. Mathematical modeling

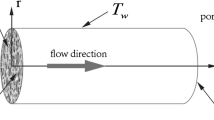
As shown in Fig. 1, the most general governing equation describing the conservation of momentum for the Darcy–Brinkman–Forchheimer is [26]

$$\mu_{{{\text{eff}}}} \left( {\frac{{{\text{d}}^{2} u*}}{{{\text{d}}r*^{2} }} + \frac{1}{r*}\frac{{{\text{d}}u*}}{{{\text{d}}r*}}} \right) - \frac{\mu }{K}u* - \frac{{C_{\text{F}} \rho u*^{2} }}{\sqrt K } + G = 0.$$
(1)
Fig. 1
figure 1

Schematic diagram of the saturated porous tube [25]

Full size image

The parameters used in the equations are introduced in the nomenclature. The porous medium assumed to be homogeneous and isentropic. The energy conservation equation for the porous medium is

$$\frac{\partial }{\partial x*}\left( {\rho C_{\text{p}} u*T} \right) = \frac{1}{r*}\frac{\partial }{\partial r*}\left( {r*k_{{}} \frac{\partial T}{{\partial r*}}} \right).$$
(2)

The effective thermal conductivity is

$$k = \left( {1 - \phi } \right)k_{\text{s}} + \phi k_{\text{f}} .$$
(3)

Because the thermal conductivity (k) is a function of temperature (T), it cannot be brought out form the differential operator. The boundary conditions of Eqs. (1) and (2) are

$$\left| {\frac{{\text{d}}u*}{{{\text{d}}u*}}} \right|_{r* - 0} = 0,u*(r* = R) = 0,$$
(4)
$$\begin{array}{*{20}l} {\frac{\partial T}{{\partial r*}} = {0 }} & {{\text{at}}} & {r* = 0} \\ {T = T_{{\text{w}}} } & {{\text{at}}} & { \, r* = R} \\ \end{array}.$$
(5)

Since a constant heat flux is imposed on the wall, the wall temperature (Tw) is not constant and varies along the flow direction.

Analysis and solution

To perform a general analysis, the governing equations, as well as the boundary conditions, should be converted to the dimensionless forms. The momentum equation becomes

$$M\left( {\frac{{{\text{d}}^{2} u}}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}u}}{{{\text{d}}r}}} \right) - \frac{u}{Da} - \frac{{MFu^{2} }}{{\sqrt {Da} }} + 1 = 0.$$
(6)
$$\left. {\frac{{\text{d}}u}{{{\text{d}}r}}} \right|_{r - 0} = 0,\quad u(r = 1) = 0,$$
(7)
$$r = \frac{r*}{R},\quad u = \frac{\mu u*}{{GR^{2} }},$$
(8)
$$M = \frac{{\mu_{{{\text{eff}}}} }}{\mu },\quad Da = \frac{K}{{R^{2} }},\quad F = \frac{{C_{F} \rho GR^{3} }}{{\mu \mu_{{{\text{eff}}}} }}.$$
(9)

The dimensionless momentum equation and the corresponding boundary conditions now are

$$\frac{{{\text{d}}^{2} u}}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}u}}{{{\text{d}}r}} - s^{2} u - Fsu^{2} + \frac{1}{M} = 0,$$
(10)
$$\left. {\frac{{\text{d}}u}{{{\text{d}}r}}} \right|_{{\text{r}} - 0} = 0, \quad u(r = 1) = 0.$$
(11)

s is called the porous medium shape parameter:

$$s = \frac{1}{{\sqrt {DaM} }},\sqrt {\frac{\phi }{Da}}.$$
(12)

The normalized velocity (\(\hat{u}\)) and the mean velocity (U*) are

$$\hat{u} = \frac{u*}{{U*}},$$
(13)
$$U* = \frac{2}{{R^{2} }}\int\limits_{0}^{R} {u*r*{\text{d}}r*}.$$
(14)

The above momentum equation with the corresponding boundary conditions was solved by considering two cases: large (s >  > 1) and small (s <  < 1) s values, respectively, by Hooman and Gurgenci [27] using straightforward expansion method and Dehghan et al. [25] using the matched asymptotic expansions method:

$$\hat{u} = 2(1 - r^{2} ) + \frac{{sF}}{{144{\text{M}}}}[2r^{6} - 9r^{4} + 9r^{2} - 2] + O(s^{2} );\quad s\, < \,1,$$
(15)
$$\hat{u} = \frac{{1 - \exp \{ s(r - 1)\} }}{{1 - 2\left( {s^{ - 1} + s^{ - 2} } \right)}} + O(s^{ - 3} );\quad s > {1}.$$
(16)

To solve the energy equation, the following parameters are introduced:

$$\theta = \frac{{T - T_{\text{w}} }}{{T_{\text{m}} - T_{\text{w}} }},$$
(17)
$$T_{{\text{m}}} = \frac{1}{{R^{2} U*}}\int_{0}^{R} {u*Tr*{\text{d}}r*}.$$
(18)

As mentioned, a linear dependency for the thermal conductivity on temperature is considered:

$$k = k_{\text{w}} \left( {1 + \varepsilon \frac{{T - T_{\text{w}} }}{{T_{\text{m}} - T_{\text{w}} }}} \right) = (1 + \varepsilon \theta ),$$
(19)

where kw is the thermal conductivity at Tw and \(\varepsilon\) is the linear dependency multiplier. The Nu is defined as

$$Nu = \frac{{2Rq^{\prime\prime}}}{{k_{0} \left( {T_{{\text{w}}} - T_{\text{m}} } \right)}}.$$
(20)

Equation (2) is rewritten as follows:

$$\rho _{{\text{f}}} C_{\text{p}} u*\frac{\partial }{{\partial x*}}\left( T \right) = \frac{\partial }{{\partial r*}}\left( {k_{{\text{w}}} (1 + \varepsilon \frac{{T - T_{{\text{w}}} }}{{T_{{\text{m}}} - T_{{\text{w}}} }})r*\frac{{\partial T}}{{\partial r*}}} \right).$$
(21)

The energy balance gives [18]

$$\frac{{\partial T}}{{\partial x*}} = \frac{{2q_{{\text{w}}}^{{\prime \prime }} }}{{\rho c_{{\text{p}}} RU*}}.$$
(22)

Now the dimensionless energy equation as well as the boundary conditions yields

$$\left( {1 + \varepsilon \theta } \right)\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} + \frac{{\left( {1 + \varepsilon \theta } \right)}}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + \varepsilon \left( {\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right)^{2} + \hat{u}Nu = 0,$$
(23)
$$\left. {\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right|_{{r = 0}} = 0,\;\theta \left( 1 \right) = 0.$$
(24)

To find the temperature field, an expansion according to the below is considered (for the case of s <  < 1):

$$\theta = \theta_{0} + s\theta_{1} + O\left( {s^{2} } \right).$$
(25)

One can find that

$$\begin{aligned} \theta = & Nu\left\{ {\frac{{r^{4} - 4r^{2} + 3}}{8} - \frac{Fs}{{4608M}}\left( {r^{8} - 8r^{6} + 18r^{4} - 16r^{2} + 5} \right)} \right\} \\ + & \,\frac{{\varepsilon Nu^{2} }}{128}\left( { - r^{8} + 8r^{6} - 22r^{4} + 24r^{2} - 9} \right) + O\left( {s^{2} } \right) \\ \end{aligned}.$$
(26)

By using the compatibility condition (\(\int_{0}^{1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} \theta r\text{d}r = 0.5}\)), one can show

$$Nu\left( {\frac{{11}}{{48}} - \frac{{29Fs}}{{34560{\text{M}}}}} \right) - \varepsilon Nu^{2} \frac{{59}}{{1920}} = 1.$$
(27)

Equation (27) is a singular algebraic perturbation equation which yields

$$Nu = \frac{{48}}{{11}}\left( {1 + \frac{{29Fs}}{{{\text{7920M}}}} + 0.58\varepsilon } \right) + O\left( {s^{2} } \right);\quad s < 1.$$
(28)

For the case of \(s \ge 1\), by adopting an expansion in the form of Eq. (29), one can show that dimensionless temperature would be according to Eq. (30):

$$\theta = \theta_{0} + s^{ - 1} \theta_{1} + s^{ - 2} \theta_{2} + O\left( {s^{ - 3} } \right),$$
(29)
$$\theta = \frac{Nu}{{4\left( {1 - \frac{2}{s} + \frac{2}{{s^{2} }}} \right)}}\left( {1 - r^{2} + \frac{{4e^{{\text{s}}({\text{r}} - 1)} }}{{s^{2} }} - \frac{4}{{s^{2} }}} \right) + \frac{{\varepsilon Nu^{2} }}{{32\left( {1 - \frac{2}{s} + \frac{2}{{s^{2} }}} \right)}}\left( { - r^{4} + 2r^{2} - 1} \right),$$
(30)

where the compatibility condition yields

$$\frac{Nu}{{8\left( {1 - \frac{2}{s} + \frac{2}{{s^{2} }}} \right)^{2} }}\left( {1 - \frac{24}{{s^{2} }} - \frac{{4e^{ - {\text{s}}} }}{{s^{2} }}} \right) - \frac{{\varepsilon Nu^{2} }}{{96\left( {1 - \frac{2}{s} + \frac{2}{{s^{2} }}} \right)^{3} }}\left( {1 - \frac{72}{{s^{2} }} - \frac{{54e^{ - {\text{s}}} }}{{s^{2} }} + \frac{{12e^{ - 2{\text{s}}} }}{{s^{2} }}} \right) = 1,$$
(31)

and finally, the Nu is obtained:

$$Nu = 8\left( {1 - \frac{4}{s} + \frac{9}{{s^{2} }} + \frac{{4e^{ - s} }}{{s^{2} }} + 0.66\varepsilon } \right) + O\left( {s^{ - 3} } \right);\quad s > 1.$$
(32)

The source of temperature-dependent thermal conductivity

The temperature-dependent thermal conductivity arises from at least two sources: (1) because of high-temperature variations which lead to having different thermal conductivities at different temperatures and hence a temperature-dependent thermal conductivity becomes important [17], and (2) from the radiation heat transfer within porous materials seen at high temperatures. The thermal conductivity of any material varies with temperature and, to describe this variation, the simplest model is a linear profile, which has been used in the present study. For the second case, the Rosseland approximation can be used for modeling the radiation wherein the porous medium is optically thick [19, 21]:

$$q_{r} = - \frac{{4\sigma n^{2} }}{{3\beta }}\frac{{{\text{d}}T^{4} }}{{{\text{d}}r^{*} }}.$$
(33)

One can rewrite the above equation as follows using the Taylor series (\(T^{4} = 4T_{0}^{3} T - 3T_{0}^{4}\)):

$$q_{\text{r}} = - k_{\text{r}} \frac{{{\text{d}}T}}{{{\text{d}}r^{*} }} = - \frac{{16\sigma n^{2} T_{0}^{3} }}{{3\beta }}\frac{{{\text{d}}T}}{{{\text{d}}r^{*} }} .$$
(34)

Here the molecular conductivity (kc) should be summed up with the radiative thermal conductivity (kr) to obtain the total or effective conductivity:

$$k = k_{\text{c}} + k_{\text{r}}.$$
(35)

Validation

First, the Nusselt number is translated at limiting values, i.e., for s = 0 and s → \(\infty\) which, respectively, show the clear fluid flow and the slug flow (or the Darcy regime). For s = 0, one can easily show that \({\text{Nu}} = \frac{48}{{11}}\left( {1 + 0.58\varepsilon } \right).\) The Nusselt number for the clear fluid flow (s = 0) and for the constant thermal conductivity (ε = 0) is Nu = 48/11≅4.36 [28] which is completely in agreement with the present study. For the slug flow, the present Nusselt number is \(Nu = 8\left( {1 + 0.66\varepsilon } \right)\) which shows that for a constant thermal conductivity the Nusselt number would be 8, in agreement with the Ref.[28]. For the ranges between these two limiting cases, Fig. 2 is plotted. It shows that the present Nusselt number is completely in agreement with that of Ref.[27].

Fig. 2
figure 2

Effects of thermal conductivity variation on the bulk mean Nusselt number

Full size image

Results and discussion

The Nusselt number versus a wide range of porous medium shape parameter (s) is shown in Fig. 2 for different values of linear dependency multiplier (ε) of thermal conductivity. The porous medium shape parameter (s) is a dimensionless parameter showing how much the porous medium affects the fluid flow. Very small s values represent the clear fluid flow corresponding to a parabolic velocity profile, while very large values of s represent the Darcy regime or the slug flow wherein the velocity profile is almost uniform in any cross section of the tube. For any ε value, the Nusselt number starts from a minimum value corresponding to s = 0 (the clear fluid flow) and increases by increasing the porous medium shape parameter to a maximum seen in the slug flow regime when s\(\hspace{0.17em}\to \infty\). The results show that the maximum sensitivity of the Nusselt number to the porous medium shape parameter is seen for the range of 10 < s < 100 wherein the maximum change in the velocity profile from the parabolic-shaped one to the flat one occurs, especially in the near-wall region which directly influences the convection heat transfer phenomena.

Meanwhile, it can be found that the Nusselt number is more sensitive to the linear dependency multiplier (ε) of thermal conductivity in the slug flow regime rather than the clear flow regime. In other words, by increasing the porous medium shape parameter, the sensitivity of the Nusselt number to the thermal conductivity enhancement originating from the temperature-dependent nature increases. This matter together with the fact that the thermal conductivity of a medium with a higher s value is higher than the counterpart one with a lower s value (for the combination of a low conductive fluid with a higher conductive solid substrate of a porous material) reveals that the heat transfer rate augmented much more for the case of slug flow than that of the cleat fluid flow with respect to the temperature-dependent nature of thermal conductivity. As mentioned earlier, the radiation heat transfer inside a porous material can be modeled using the Rosseland approximation method which yields a temperature-dependent thermal conductivity called the radiative conductivity (kr). Hence, the radiation heat transfer for a medium with higher s values increases the overall heat transfer more effectively compared to media with lower s values. According to Eqs. (28) and (32), analytical results revealed that the Nusselt number shows a linear dependence on the linear dependency multiplier (ε) of thermal conductivity with the factor of 0.58 for the case of clear fluid flow and 0.66 for the case of slug flow. This trend is seen in Fig. 3.

Fig.3
figure 3

Effects of porous media shape parameter on the Nusselt number

Full size image

Figure 4 illustrates the effects of the non-linear drag force (called the Forchheimer term, shown by F) on the Nusselt number. As expected, the non-linear drag has negligible direct effects on the Nusselt number. The non-linear drag only increases the pressure drop without any considerable change in the velocity profile. Hence, it has no direct effect on the Nusselt number. The physical interpretations confirm the analytical solutions obtained in Eqs. (28) and (32).

Fig. 4
figure 4

Effects of Forchheimer number (F) on the Nusselt number

Full size image

To find out the dominant parameters on the temperature field and to study their effects, Fig. 5 is potted. Because of a higher Nusselt number seen in Fig. 2 for higher porous medium shape parameter (s) and since the Nusselt number is the slope of the dimensionless temperature profile at the tube wall (i.e., r = 1), a temperature profile with a higher magnitude of the slope at r = 1 shows a higher dimensionless temperature value at the centerline. Hence, the centerline value of the dimensionless temperature profile is higher for the higher porous medium shape parameter. By increasing the temperature-dependency multiplier of the thermal conductivity (i.e., ε), the dimensionless temperature profile becomes more uniform which translates to a higher magnitude of the dimensionless temperature profile’s slope at r = 1 and as well a higher heat transfer rate and a higher Nusselt number is resulted, which are well consistent to the results obtained in Fig. 2.

Fig. 5
figure 5

Effects of porous medium shape parameter (s) on the dimensionless temperature profile: a constant conductivity (ε = 0); and b variable conductivity (ε = 0.2)

Full size image

To investigate this trend in more detail, Fig. 6 is plotted. It can be seen that the dimensionless temperature profile is more sensitive to the temperature-dependency multiplier of the thermal conductivity (i.e., ε) at the higher s value according to what was seen for the Nusselt number in Fig. 2. In other words, at higher porous medium shape parameters, wherein a denser (low porosity) porous medium is placed inside the tube, the role of temperature-dependent thermal conductivity or the radiation heat transfer (the two source of the temperature-dependent thermal conductivity) would be more important than the case of clear fluid flow or high porous materials which translates to low s values.

Fig. 6
figure 6

Effects of variable thermal conductivity assumption on the dimensionless temperature profile: a s = 0.01; and b s = 100

Full size image

Conclusions

The forced convection heat transfer inside a porous-filled tube under the constant heat flux thermal boundary condition has been studied analytically assuming a temperature-dependent thermal conductivity. The Darcy–Brinkman–Forchheimer equation has been used to model the flow within porous media. The energy equation has been solved by the perturbation techniques and closed-form Nusselt number relations have been obtained. The source of linear valuation of the thermal conductivity has been discussed and the parametric studies have shown that the Nusselt number increases linearly with a linear increase in the thermal conductivity. In addition, it has been found that the Nusselt number enhancement arising from the thermal conductivity increment is higher for higher porous medium shape parameters. In other words, the slug flow shows more enhancement in the heat transfer with respect to the thermal conductivity increment compared to the similar clear fluid flow case. This point proves the use of porous materials at high temperatures more than the previous findings which were founded on the enhanced thermal conductivity characteristic.