Numerical Investigation of Thermally Developing Non-Darcy Forced Convection in a Porous Circular Duct with Asymmetric Entrance Temperature Under LTNE Condition

Abstract

This paper numerically investigates the heat transfer performance of thermally developing non-Darcy forced convection in a fluid-saturated porous medium tube under asymmetric entrance temperature boundary conditions. The Brinkman flow model and the local thermal non-equilibrium (LTNE) model are employed to establish the mathematical model of the studied problem to predict the forced convective heat transfer. Then, the mathematical model is numerically solved using COMSOL Multiphysics. Consequently, the fluid velocity field, the solid temperature field, the fluid temperature field and the Nusselt number are obtained. Moreover, the dependences of the Nusselt number on some key parameters are analyzed in detail. The results show that the distribution characteristics of the Nusselt number are strongly dependent on the form of the entrance temperature function. Meanwhile, it is found that the Nusselt number increases first and then tends to approach an asymptotic value with the increase in the Darcy number and the Biot number. The Nusselt number monotonously increases with increasing the Péclet number. On the contrary, the Nusselt number decreases first and then tends to be an asymptotic value owing to the increase in the thermal conductivity ratio and the viscosity ratio. This study is of benefit to provide in-depth insights into the non-Darcy forced convective heat transfer in porous tubes with asymmetric inlet temperature under LTNE condition.

1 Introduction

Analytical study on forced convection in a porous medium tube or plate under LTNE condition is of significance in the field of heat transfer enhancement (e.g., Nield et al. 2003; Nield et al. 2017; Qu et al. 2012; Wang et al. 2017; Zhong et al. 2018; Li et al. 2018). As for porous plates, heat transfer analysis under the Darcy flow has been investigated extensively. For example, Yang and Vafai (2011) derived analytically the fluid and solid temperature distributions for five typical boundary conditions at the porous–fluid interface under LTNE condition and analyzed the influences of the parameters on the Nusselt number. Compared with the Darcy linear flow model, the Brinkman flow model (Brinkman 1946; Vafai and Tien 1982; Nithiarasu et al. 1997) can satisfy the no-slip condition at the interface between the porous medium flow region and the pure fluid flow region and account for the transitional flow between the boundaries. Therefore, it has been widely applied in the fields of flow, heat and mass transfer in porous media. For instance, Nield and Kuznetsov (2002) studied the effect of forced convection on heat transfer performance in a parallel-plate channel filled with a saturated porous medium under the Brinkman flow with constant wall temperature. In their article, the expression of the local Nusselt number was obtained, and the influences of the relevant parameters on the Nusselt number were analyzed. Besides, a number of scholars have studied the heat transfer of porous plate under the Brinkman flow with different boundary conditions. For example, Kuznetsov and Nield (2006) studied the temperature distribution and the Nusselt number distribution in porous tubes and plates under disturbed flow conditions and concluded that the increase in dimensionless frequency would lead to the change in the Nusselt number distribution in amplitude and phase. Hooman and Haji-sheikh (2007) analyzed the thermally developing Brinkman forced convection in a rectangular porous duct with isoflux walls. Xu et al. (2011b) numerically simulated the heat transfer performance of a sandwich plate filled with porous metal foams under the Brinkman flow with uniform heat flux boundary under LTNE condition. Cekmer et al. (2011) performed an analytical investigation of steady and fully developed forced convective heat transfer in a parallel-plate channel with asymmetric uniform heat flux boundary conditions under the Brinkman flow. Li and Hu (2019) studied the forced convective heat transfer in a channel partially filled by porous media located at two inner walls with a constant flux prescribed at the channel walls under LTNE condition and obtained the analytic solutions of velocity, fluid and solid temperatures and the Nusselt number. Besides, a number of researchers consider the effect of rarefied fluids on heat transfer. For instance, Buonomo et al. (2016) examined the heat transfer characteristics of fully developed forced convection in parallel-plate microchannels filled by porous media saturated with rarefied gases at high temperatures. An exact solution was derived for the Brinkman flow model with uniform heat flux at the microchannel walls. Seetharamu et al. (2017) conducted the analysis of forced convection heat transfer with internal heat generation in a microchannel filled by a porous medium saturated with a rarefied gas. The Brinkman flow model was applied to describe the fluid transport. Both the fluid and solid temperature distributions were obtained. Buonomo et al. (2018) numerically analyzed thermally developing forced convection in microchannels or channels in rarefied gas filled by porous media in slip flow regime under the Brinkman flow with uniform heat flux under LTNE condition.

Likewise, concerning porous media tubes or rings, there have been many studies on heat transfer characteristics under the Brinkman flow. For example, Xu et al. (2011a) obtained an analytical solution for fully developed forced convection in a tube partially filled by open-cell metal foam with uniform heat-flux boundary under the Brinkman flow. Wang et al. (2015) carried out a theoretical study on heat transfer characteristics of forced convective gaseous flow through a micro-annulus filled with a porous material under the Brinkman flow. Xu and Gong (2018) numerically studied the fully developed forced convection in a tube partially filled with composite metal foams. The LTNE model and the Brinkman flow model were employed to predict fluid and thermal transport.

In the previous work (Li et al. 2019), we investigated the forced convective heat transfer performance of porous media circular tube under LTNE condition with asymmetric inlet temperature. The exact solution of the Nusselt number was derived, and the influences of different inlet boundary conditions and related parameters on heat transfer performance were analyzed. Note that the above work is based on the Darcy flow model. In view of this point, the purpose of this study is to investigate the forced convection in a porous circular tube under LTNE condition in the framework of Brinkman flow model instead of Darcy flow model. The numerical solutions of fluid velocity profile, fluid and solid temperatures, and the Nusselt number are obtained by using FEA software, and the relevant parametric studies are carried out.

2 Mathematical Model

2.1 Governing Equations

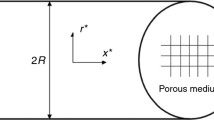
The schematic of thermally developing forced convection heat transfer problem in a porous circular tube is shown in Fig. 1. Herein, $T_{w}$ is a constant temperature prescribed on the impermeable wall of the porous tube, while $T_{\text{in}}$ is the fluid temperature at the entrance of the pipe. For simplicity, we make the following assumptions: (1) Porous medium is fluid-saturated, homogenous and isotropic, and the low-conductivity fluid flows from the inlet to the outlet. (2) Natural convection, diffusion and radiative heat transfer are ignored. (3) Longitudinal heat conduction is neglected. (4) Forced convection is steady and thermally developing but hydrodynamically developed.

Fig. 1

Schematic diagram of a circular pipe filled with porous media

Note that the Brinkman flow model is used to establish the momentum equation, and the two-temperature field equations reflecting the LTNE phenomenon are employed to describe the heat transfer problem.

Based on the above assumptions, the Brinkman momentum equation (Pangrle et al. 1991) and the two energy equations (Li et al. 2019) in three-dimensional cylindrical coordinates can be expressed as

$$\mu_{\text{eff}} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u}}{{\partial \varphi^{2} }}} \right) - \frac{\mu }{K}u - \frac{{{\text{d}}p}}{{{\text{d}}z}} = 0$$

(1)

$$k_{{s,{\text{eff}}}} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{s} }}{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{s} }}{{\partial \varphi^{2} }}} \right) + h(T_{f} - T_{s} ) = 0$$

(2)

$$k_{{f,{\text{eff}}}} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{f} }}{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{f} }}{{\partial \varphi^{2} }}} \right) - h(T_{f} - T_{s} ) = \rho c_{p} u\frac{{\partial T_{f} }}{\partial z}$$

(3)

where $r$, $\varphi$ and $z$ represent the radial, circumferential and longitudinal coordinates, respectively. $\frac{{{\text{d}}p}}{{{\text{d}}z}}$ denotes a constant pressure gradient. $T_{f}$ and $T_{s}$ mean the intrinsic phase average fluid and solid temperatures, respectively. $\mu_{\text{eff}}$, $\mu$, $u$, $\rho$ and $c_{p}$ represent the effective dynamic viscosity, actual dynamic viscosity, volume-averaged velocity, density and specific heat of the fluid, respectively. $K$ is the permeability of porous media, $h$ refers to the specific solid–liquid interface heat transfer coefficient, and $k_{{s,{\text{eff}}}}$ and $k_{{f,{\text{eff}}}}$ represent the effective thermal conductivities of solid and fluid phases, respectively, which are usually from the following expressions:

$$k_{{s , {\text{eff}}}} = (1 - \phi )k_{s} ,\quad k_{{f,{\text{eff}}}} = \phi k_{f}$$

(4)

where $\phi$ means the porosity of porous media and $k_{s}$ and $k_{f}$ represent the thermal conductivities of solids and fluids, respectively.

2.2 Boundary Conditions

The no-slip velocity boundary condition and the first-type thermal boundary condition on the circular duct wall are illustrated in Fig. 1. That is,

$$\left. u \right|_{{r = r_{0} }} = 0$$

(5)

$$\left. {T_{s} } \right|_{{r = r_{0} }} = \left. {T_{f} } \right|_{{r = r_{0} }} = T_{w}$$

(6)

where $r_{0}$ is the radius of the circular duct.

As stated by Li et al. (2018), in most cases, the fluid temperature at the entrance of the porous tube is uniform. However, there are also some instances where the inlet temperature or heat flux is non-uniform. Therefore, in this study, we discuss the general case of non-uniform inlet fluid temperature. That is, the entrance temperature is assumed to be an arbitrary function with respect to the radial coordinate and the circumferential coordinate. So we have

$$\left. {T_{f} } \right|_{z = 0} = T_{\text{in}} , \, T_{\text{in}} = f(r,\varphi )$$

(7)

where $f(r,\varphi )$ is a well-defined arbitrary function and applies to both uniform and non-uniform temperature distributions.

2.3 Dimensionless Mathematical Model

In order to normalize the mathematical model, the following non-dimensional variables are introduced:

$$\begin{aligned} & R = \frac{r}{{r_{0} }},Z = \frac{z}{{r_{0} }},U = \frac{\mu u}{{r_{0}^{2} ( - {\text{d}}p/{\text{d}}z)}},\theta_{s} = \frac{{T_{s} - T_{w} }}{{T_{0} - T_{w} }},\theta_{f} = \frac{{T_{f} - T_{w} }}{{T_{0} - T_{w} }} \\ & {\text{Bi}} = \frac{{hr_{0}^{2} }}{{k_{{s , {\text{eff}}}} }},{\text{Pe}} = \frac{{\rho c_{p} ( - {\text{d}}p/{\text{d}}z)r_{0}^{3} }}{{\mu k_{{s,{\text{eff}}}} }},\kappa = \frac{{k_{{f,{\text{eff}}}} }}{{k_{{s,{\text{eff}}}} }},M = \frac{{\mu_{\text{eff}} }}{\mu },{\text{Da}} = \frac{K}{{r_{0}^{2} }} \\ \end{aligned}$$

(8)

where $U$ denotes the dimensionless volume-averaged velocity of the fluid, $\theta_{s}$ and $\theta_{f}$ represent the dimensionless intrinsic phase average solid and fluid temperatures, respectively, and $T_{0}$ denotes the reference temperature. Bi is the Biot number, Pe is the Péclet number, $\kappa$ refers to the ratio of the effective thermal conductivity of fluid to that of solid, and $M$ is the ratio of fluid effective dynamic viscosity to actual dynamic viscosity.

With the definitions of dimensionless variables in Eq. (8), the non-dimensional governing equations and boundary conditions can be rewritten as follows:

$$M\left( {\frac{{\partial^{2} U}}{{\partial R^{2} }} + \frac{1}{R}\frac{\partial U}{\partial R} + \frac{1}{{R^{2} }}\frac{{\partial^{2} U}}{{\partial \varphi^{2} }}} \right) - \frac{1}{\text{Da}}U + 1 = 0$$

(9)

$$\frac{{\partial^{2} \theta_{s} }}{{\partial R^{2} }} + \frac{1}{R}\frac{{\partial \theta_{s} }}{\partial R} + \frac{1}{{R^{2} }}\frac{{\partial^{2} \theta_{s} }}{{\partial \varphi^{2} }} + {\text{Bi}}(\theta_{f} - \theta_{s} ) = 0$$

(10)

$$\kappa \left( {\frac{{\partial^{2} \theta_{f} }}{{\partial R^{2} }} + \frac{1}{R}\frac{{\partial \theta_{f} }}{\partial R} + \frac{1}{{R^{2} }}\frac{{\partial^{2} \theta_{f} }}{{\partial \varphi^{2} }}} \right) - {\text{Bi}}(\theta_{f} - \theta_{s} ) = {\text{Pe}}U\frac{{\partial \theta_{f} }}{\partial Z}$$

(11)

$$\left. U \right|_{R = 1} = 0$$

(12)

$$\left. {\theta_{s} } \right|_{R = 1} = \left. {\theta_{f} } \right|_{R = 1} = 0$$

(13)

$$\left. {\theta_{f} } \right|_{Z = 0} = f(R,\varphi ).$$

(14)

The governing equations (Eqs. 9–11) and boundary conditions (Eqs. 12–14) compose the non-dimensional mathematical model of the problem under consideration. In Sect. 3, we manage to solve this model numerically.

3 Numerical Method

3.1 Numerical Solutions by COMSOL Multiphysics

Considering the difficulty in deriving the analytical solution of the above mathematical model (viz. Eqs. 9–14), we employ the FEA software COMSOL Multiphysics to solve the mathematical model and obtain its FE solutions. It is worth mentioning that partial differential equations (PDEs) module in COMSOL Multiphysics is highly suitable for solving numerically the boundary value problems of user-defined PDEs.

Note that the governing equations (Eqs. 9–11) are in the framework of cylindrical coordinates. To date, they cannot be directly input into the PDEs module due to the limitation of the coordinate system in the software. Alternatively, we convert Eqs. (9)–(11) to the forms of Cartesian coordinate system as follows:

$$M\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) - \frac{1}{\text{Da}}U + 1 = 0$$

(15)

$$\frac{{\partial^{2} \theta_{s} }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta_{s} }}{{\partial Y^{2} }} + {\text{Bi}}(\theta_{f} - \theta_{s} ) = 0$$

(16)

$$\kappa \left( {\frac{{\partial^{2} \theta_{f} }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta_{f} }}{{\partial Y^{2} }}} \right) - {\text{Bi}}(\theta_{f} - \theta_{s} ) = {\text{Pe}}U\frac{{\partial \theta_{f} }}{\partial Z}.$$

(17)

Now, Eqs. (15)–(17) can be imported into the PDEs module. Also note that the coefficients matrix corresponding to Eqs. (15)–(17) has to conform to the required input form of the PDEs module. That is, all the second-order partial derivatives are placed into the corresponding differential operator, while the rest terms can be placed into the non-homogeneous source term (viz. $f$ term in the RHS).

While Eqs. (15)–(17) are input into the PDEs module, we establish the geometry model of the studied problem on the basis of Fig. 1 and impose the corresponding boundary conditions represented by Eqs. (12)–(14). After that, we mesh the geometry model and conduct the FE solving and obtain the numerical solutions of the unknown variables $U$, $\theta_{s}$ and $\theta_{f}$. Then, based on the above numerical solutions, we try to attain the Nusselt number in the next subsection.

3.2 Nusselt Number Calculation

3.2.1 Analytical Formula for the Nusselt Number

For the forced convective heat transfer problem within a circular duct under LTNE condition, Zhao et al. (2006) proposed the analytical expression for the average Nusselt number at the wall. That is,

$${\text{Nu}} = \frac{{2r_{0} h_{w} }}{{k_{{f,{\text{eff}}}} }} = \frac{{2r_{0} q_{w} }}{{k_{{f,{\text{eff}}}} (T_{w} - T_{f,b} )}}$$

(18)

where $q_{w}$ is the heat flux at the wall, $q_{w} = k_{{f,{\text{eff}}}} (\partial T_{f} /\partial r) + k_{{s,{\text{eff}}}} (\partial T_{s} /\partial r)$, and $T_{f,b}$ is the bulk mean fluid temperature and is defined by

$$T_{f,b} = \frac{1}{{\pi r_{0}^{2} }}\int_{0}^{{r_{0} }} {\int_{0}^{2\pi } {T_{f} r{\text{d}}\varphi {\text{d}}r} }.$$

(19)

Inserting Eq. (19) into Eq. (18) and implementing non-dimensionalization yield

$${\text{Nu}} = \frac{{2\pi \left. {\left( {\kappa \frac{{\partial \theta_{f} }}{\partial R} + \frac{{\partial \theta_{s} }}{\partial R}} \right)} \right|_{R = 1} }}{{ - \kappa \int_{0}^{1} {\int_{0}^{2\pi } {\theta_{f} R{\text{d}}\varphi {\text{d}}R} } }}.$$

(20)

Clearly, Eq. (20) is applicable to the studied problem in this work. Thereby, we employ Eq. (20) and the numerical $\theta_{s}$ and $\theta_{f}$ obtained in Sect. 3.2.2 to calculate the Nusselt number with the aid of COMSOL Multiphysics.

3.2.2 Numerical Solution of Nu

In COMSOL Multiphysics, we import and set the Nusselt number as a user-defined variable expressed by Eq. (20). Here, we elaborate on the calculation procedure of the Nusselt number Eq. (20). First, the denominator of Eq. (20) is the integral of fluid temperature $\theta_{f}$ on the cross section of the model, which can be realized by using the integral operator (intop) in the software. Second, the numerator part is the partial derivatives of solid temperature and liquid temperature with regard to the radial coordinate at the wall. As mentioned before, the partial derivatives in the cylindrical coordinate need to be converted into those in the rectangular coordinate. According to the chain rule, we have

$$\frac{{\partial \theta_{f} }}{\partial R} = \frac{{\partial \theta_{f} }}{\partial x}\cos \varphi + \frac{{\partial \theta_{f} }}{\partial y}\sin \varphi.$$

(21)

Thus, the Nusselt number can be entered into the software in the following form:

$${\text{Nu}} = \frac{{2\pi \left. {\left( {\kappa \left( {\frac{{\partial \theta_{f} }}{\partial x}\cos \varphi + \frac{{\partial \theta_{f} }}{\partial y}\sin \varphi } \right) + \frac{{\partial \theta_{s} }}{\partial x}\cos \varphi + \frac{{\partial \theta_{s} }}{\partial y}\sin \varphi } \right)} \right|_{R = 1} }}{{ - \kappa \cdot {\text{intop}}(\theta_{f} )}}.$$

(22)

It can be seen from Eq. (20) that the data set shall be defined at $R = 1$. After the mesh refinement, COMSOL built-in steady-state solver is used to calculate the Nusselt number.

4 Results and Discussion

4.1 Nusselt Number

4.1.1 Solutions of $U$, $\theta_{s}$ and $\theta_{f}$

In this paper, $U$, $\theta_{s}$, $\theta_{f}$ and Nu are obtained by COMSOL Multiphysics. It can be seen from Fig. 2a that $U$ decreases gradually with increasing $R$. As shown in Fig. 2b, the double temperatures decrease first and then increase with the increase in $\varphi$, but the fluid dimensionless temperature is always greater than the solid dimensionless temperature. Figure 2c displays the changes in $\theta_{s}$ and $\theta_{f}$ with $Z$. It can be seen that the two-temperature decreases rapidly and tends to 0 with the increase in $Z$.

Fig. 2

Dimensionless velocity and two-temperature changes with the variations of coordinates. a $U$ versus $R$. b $\theta_{S}$ and $\theta_{f}$ versus $\varphi$. c $\theta_{S}$ and $\theta_{f}$ versus $Z$

4.1.2 Comparison with the Case of the Darcy Flow

To our knowledge, there have been no available experimental data and analytical solutions for the studied problem. For simplicity, we degenerate the Brinkman flow into the Darcy flow. In the case of the Darcy flow, the change in the Nusselt number with the Biot number is taken as an example to verify the consistency between the numerical results in this paper and the analytical solution of the Nusselt number in Li et al. (2019). It is clear from Fig. 3 that the two curves have a good consistency. Meanwhile, the numerical solutions of the two temperatures for the Darcy flow are compared with the analytical solutions by Li et al. (2018), which also has a good consistency. Therefore, the correctness of the numerical results in this work can be verified indirectly.

Fig. 3

Nu versus Bi

Besides, we also investigate the accuracy of the numerical solution. Table 1 represents the relationship between the relative error of the Nusselt number at the location ($R = 1$, $\varphi = \frac{\pi }{2}$, $Z = 5$) and the grid number. It can be seen from Table 1 that the absolute value of the relative error decreases with increasing the grid number. In our simulation, the grid number is taken as 17,892 and the relative error is around 0.15%.

Table 1 Relative error of the Nusselt number versus the grid number

4.1.3 Nusselt Number Distribution Characteristics

As mentioned earlier, the Nusselt number is typically used for heat transfer analysis.

Here, the boundary conditions are defined as $f(R,\varphi ) = 0.5(1 + R\cos \varphi )$, where $M$, Pe, Bi, $\kappa$ and Da are taken as 0.1, 50, 100, 0.033988 and 1, respectively.

Figure 4a illustrates the change in the Nusselt number with the variations of coordinates. We find that the Nusselt number decreases rapidly when $Z$ is less than 5 and then tends to the asymptotic value. This implies that the intensity of convection heat transfer is strongest at the entrance and then decreases rapidly. This is because the intensity of convective heat transfer depends on the transfer of dimensionless temperature. In addition, it is clear from Fig. 4b that the Nusselt number first decreases and then increases with the variation of $\varphi$, which is determined by the inlet condition $f(R,\varphi ) = 0.5(1 + R\cos \varphi )$. Therefore, the intensity of convective heat transfer on the wall is closely related to the inlet.

Fig. 4

Change in the Nusselt number with the variations of the coordinates. a Nu versus $Z$. b Nu versus $\varphi$

The above results describe the variation characteristics of Nusselt number with the coordinates $Z$ and $\varphi$ when the related parameters are given and fixed. Next, we concentrate on the influences of the pertinent parameters on the Nusselt number.

4.2 Parametric Studies

4.2.1 Effect of $f(R,\varphi )$

As shown in Fig. 5a, when the symmetric entrance boundary condition is $f(R,\varphi ) = 1$ or $f(R,\varphi ) = R$, the Nusselt number of the wall surface is constant and does not change with $\varphi$. Then, we adopt the asymmetric inlet boundary conditions. That is, three different functions are chosen, which are $f(R,\varphi ) = 0.5(1 + R\sin \varphi )$, $f(R,\varphi ) = 0.5(1 + R\cos \varphi )$ and $f(R,\varphi ) = 0.5(1 + R(\cos \varphi + \sin \varphi ))$. In the situation of asymmetric entrance boundary conditions, we can see from Fig. 5a that the Nusselt number is a periodic function and its distribution is similar to that of the inlet boundary condition. This indicates that the intensity of convective heat transfer strongly relies on the inlet boundary condition. Meanwhile, as depicted in Fig. 5b, whether the inlet boundary condition is uniform or non-uniform, the Nusselt number is large at the inlet and then decreases rapidly with $Z$. And when $Z$ continues to increase, the Nusselt number tends to be an asymptotic value. The similar dependences of the Nusselt number on $f(R,\varphi )$ and $Z$ are also reported by Li et al. (2019) (see Fig. 3 therein).

Fig. 5

Change in the Nusselt number under different forms of $f(R,\varphi )$. a Nu versus $\varphi$. b Nu versus $Z$

4.2.2 Effect of Bi

It is observed from Fig. 6 that Nu increases and eventually reaches the asymptotic value as Bi increases. This is because the heat exchange rate between the fluid and the solid gradually becomes faster with the increase in Bi. Additionally, the LTNE model reduces to the LTE model as Bi approaches infinity. Besides, when the Brinkman flow degenerates to the Darcy flow, the numerical solution of Nu in this work is the same as the analytical solution (see Eq. (16) therein) reported by Li et al. (2019). Also note that Nu of Brinkman flow is smaller than that of Darcy flow as illustrated in Fig. 6. This is ascribed to the fact that the Brinkman flow takes shear energy dissipation into account, leading to lower flow velocity and weakening convective heat transfer.

Fig. 6

Nu versus Bi

4.2.3 Effect of Pe

It is obvious from Fig. 7 that Nu gradually increases with increasing Pe. The larger the Pe, the stronger the convection. This strengthens the degree of heat exchange. Therefore, it is applicable to enhance the heat transfer performance by increasing Pe.

Fig. 7

Nu versus Pe

4.2.4 Effect of $\kappa$

It can be found from Fig. 8 that Nu gradually decreases with $\kappa$. Herein, we give the following explanation. As $\kappa$ increases, the effective thermal conductivity of solid compared with that of liquid becomes smaller, the heat conduction inside the solid becomes weak, and the temperatures of solid and liquid significantly decrease. Therefore, the heat transfer can be increased by reducing $\kappa$.

Fig. 8

Nu versus $\kappa$

4.2.5 Effect of $M$

We can see from Fig. 9 that Nu decreases with the increase in $M$. Note that $M$ characterizes the magnitude of the viscosity. The larger the $M$, the greater the viscosity of the fluid, which leads to the lower velocity of the fluid. When $M$ tends to be 1, the fluid velocity becomes extremely slow. Thus, the forced convection is very weak and the heat transfer is almost achieved by the heat conduction. Thereby, Nu exhibits the above trend with $M$. In other words, in order to obtain a better heat exchange efficiency, $M$ shall be reduced.

Fig. 9

Nu versus $M$

4.2.6 Effect of Da

Figure 10 shows the dependence of Nu on Da. We can see that, as Da increases, Nu first increases and finally remains invariant. Remember that Da represents the permeability of porous media. That is, the larger the Da, the stronger the penetration ability of the fluid. In other words, as Da increases, the liquid permeates much faster in porous media. This results in much stronger convection. Therefore, the heat exchange becomes faster and Nu increases.

Fig. 10

Nu versus Da

5 Conclusions

In this paper, numerical investigation of forced convective heat transfer in a porous medium pipe with asymmetric inlet temperature under the Brinkman flow and LTNE conditions is carried out by using COMSOL Multiphysics. The major conclusions can be summarized as follows:

• (1) Nu decreases rapidly first and then tends to approach an asymptotic value with increasing $Z$. The variation of Nu with $\varphi$ is strongly determined by the form of the inlet temperature function.

• (2) As Bi and Da increase, Nu increases first and then tends to be an asymptotic value.

• (3) Nu increases monotonically with the increase in Pe.

• (4) As $\kappa$ and $M$ increase, Nu gradually decreases and then tends to be an asymptotic value.

• (5) The influences of $\kappa$, Pe and Bi on Nu are great, while the effects of Da and $M$ on Nu are relatively minor.

In this study, the heat transfer performance of a porous duct under non-uniform entrance temperature boundary condition is investigated. In engineering practices, however, besides the above case, there are other non-uniform or asymmetrical cases, for example, the case of heat flux at the inlet being non-uniform and the situation that the wall temperature or heat flux is asymmetric. Thereby, the latter asymmetrical situations will be considered in the near future.