Introduction

Today, the heat transfer rate enhancement is one of the most important primary goals in energy management [1, 2]. One of the methods to enhance the heat transfer rate is to decrease the hydraulic diameter of the flow passage, which has led to the introduction of microchannel heat sinks [3]. Up to now, microchannel heat sinks (MCHS) are the only applicable method for high heat flux removal in microscales [4]. Along with using decreased flow passages which result in a higher heat transfer rate per unit area, other novel passive and active methods have been proposed to achieve a higher heat transfer rate, namely the implementation of porous inserts within flow passages [5,6,7], using bulk heat generations/absorptions [8], modifying the flow passage configuration [9], and enhancing the working fluid’s thermal properties by adding nanoparticles with high thermal conductivities (i.e., using nanofluids) [10, 11].

Because of a relatively high-temperature variation along a small length, thermal properties of the working fluid flowing through MCHSs change considerably. Toh et al. [12] considered the effects of temperature-dependent properties in MCHSs for the first time. Later, Herwing and Mahulikar [13], Husain and Kim [14], Li et al. [15], Liu et al. [16, 17], Mirzaei and Dehghan [18], and Lee et al. [19] developed the assumption of a working fluid with variable thermal properties. Herwing and Mahulikar [13] revealed that assuming constant properties for the working fluid would lead only to approximations of reality. Husain and Kim [14] performed an optimization study based on a temperature-dependent fluid property approach. They discussed the width of channels and the thickness of the solid substrate. Liu et al. [16] obtained that effects of viscosity variation due to temperature gradients are higher than those of thermal conductivity. For the first time and for a nanofluid convecting in a MCHS, Mirzaei and Dehghan [18] considered the effects of temperature-dependent properties on the flow and heat transfer rate characteristics in terms of the Poiseuille and Nusselt numbers. They found that effects of temperature-dependent properties for a nanofluid are more important than those for a pure fluid due to the temperature-induced Brownian motion of nanoparticles [20,21,22]. Furthermore, they [18] showed that the Reynolds number along a typical MCHS may change up to 50% due to the property (especially viscosity) variation.

In addition to the variation of the working fluid’s molecular thermal conductivity with temperature, the effective thermal conductivity may be temperature dependent due to the radiation heat transfer modeling as an effective diffusion process (the Rosseland approximation method) [23]. In this case, the effective thermal conductivity includes two terms: the molecular thermal conductivity and a radiative thermal conductivity. Dehghan et al. [24, 25] investigated the effects of the radiative temperature-dependent thermal conductivity on the forced convection heat transfer inside macro- and microchannels filled with porous materials in both no-slip and slip flow regimes. Using a perturbation solution, Dehghan et al. [26] analytically solved the nonlinear convection heat transfer problem of a porous material with temperature-dependent thermal conductivity. They found that the Nusselt number linearly increases with a linear increase in the thermal conductivity with respect to temperature.

As mentioned earlier, another method to increase the heat transfer rate is to use converging flow passages. Hung et al. [27] found that a tapered channel shows a better performance considering thermal resistance and temperature distribution uniformity compared to conventional single-layered and double-layered microchannels. Hung and Yan [28] found that the thermal resistance is sensitive to variations in the channel number, channel width ratio, or width-tapered ratio but less sensitive to the height-tapered ratio. Dehghan et al. [29] revealed that a width-tapered channel shows the same heat transfer rate while the pumping power can be reduced up to 75% for their considered configuration. All these studies used pure water as the working fluid with constant properties. Recently, the case of heat transfer enhancement obtained by nanofluid flow through width-tapered micropassages was investigated using constant property assumption [30]. Compared to the straight channels, it was seen that the heat transfer rate shows more increase for nanofluid flow in width-tapered channels [30].

On the other hand, nanofluids have widely been investigated as an effective passive enhancement technique of forced convection heat transfer according to the above-mentioned literature survey. However, as the sensitivity of the working fluid to temperature is increased by the presence of nanoparticles, there are few studies investigating how much would be wrong the hydrodynamics and thermal characteristics of the flow in the case of assuming constant property approach compared to the real phenomena with spatial property gradients arising from spatial temperature gradients. To find the answer, an applied case study is considered in the present study wherein the temperature gradient would be high because of high heat flux. The present study aims at investigating the enhancement achieved by convecting Al2O3–water nanofluid through rectangular microchannels with different width-tapered configurations using the finite volume method (FVM). The effects of temperature-dependent thermophysical properties of the working nanofluid are analyzed based on the KKL model. 3D conjugate heat transfer and fluid flow are considered to obtain the convection heat transfer coefficient in the laminar flow regime.

Problem definition and mathematical modeling

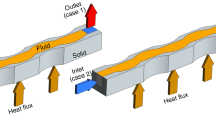
Figure 1 and Tables 1 and 2 present the schematic diagram of the problem, the dimensions of the considered microchannel heat sink, and the nanoparticle properties. Assumptions of the present study are listed below:

Fig. 1
figure 1

Schematic diagram of the problem: a isometric view of MCHS and b top view of a channel [29]

Full size image
Table 1 Dimensions of microchannel (μm)
Full size table
Table 2 Al2O3 nanoparticle properties
Full size table

  • The flow is incompressible.

  • According to the symmetry, only one half of the channel shown in the right side of Fig. 1 is considered.

  • The microchannel is made of aluminum with the thermal conductivity of 202 W m−1 K−1.

  • A maximum pressure value is adopted as the constraint of the problem. The maximum pressure value of the MCHS loop occurs at the entrance of the channel.

  • The inlet width of the flow passage is fixed for all simulations (Wi = 200 μm), while the outlet width (Wo) is assumed to be 200, 150, 100, and 75 μm.

Each case study has two identifying parameters: the outlet width, Wo, and the inlet pressure, Pi. Changing one of the two identifying parameters (Wo and Pi) gives a new case.

Governing equations

Continuity, momentum, and energy equations for the fluid part are as follows:

$$\begin{aligned} & \nabla \cdot (\rho_{\text{eff}} \vec{V}) = 0 \\ & \vec{V} \cdot \nabla (\rho_{\text{eff}} \vec{V}) = - \nabla p + \nabla \cdot (\mu_{\text{eff}} \nabla \vec{V}) \\ & \vec{V} \cdot \nabla ((\rho c_{\text{p}} )_{\text{eff}} T_{\text{f}} ) = (\vec{V} \cdot \nabla )p + \nabla \cdot (k_{\text{eff}} \nabla T_{\text{f}} ) \\ \end{aligned}$$
(1)

Energy balance in the solid part is:

$$\nabla \cdot (k_{\text{s}} \nabla T_{\text{s}} ) = 0$$
(2)

Subscripts f and s represent the “fluid” and “solid” parts, respectively. \(\vec{V}\) is the velocity vector, p is the pressure, \(\mu\) is the fluid viscosity, \(\rho\) is the fluid density, cp is the specific heat of the working fluid, k is the thermal conductivity, and T is the temperature.

Nanofluid properties

The problem is solved using two different approaches: constant properties and real-time (temperature-dependent) properties. In the constant property approach, the inlet properties of the fluid are used as definite values in simulations, while in the variable property approach, the variation of the working fluid’s properties with temperature is considered. Subsequently, Eqs. (3)–(7) along with Tables 3 and 4 are used to consider the temperature dependency of the working fluid’s properties. Density and specific heat coefficient of the nanofluid can be calculated by Eqs. (3–4):

Table 3 Thermophysical properties of water [15]
Full size table
Table 4 Coefficients of Eq. (6) [21]
Full size table
$$\rho_{\text{eff}} = \left( {1 - \phi } \right)\rho_{\text{bf}} + \phi \rho_{\text{p}}$$
(3)
$$(\rho C_{\text{p}} )_{\text{eff}} = \left( {1 - \phi } \right)(\rho C_{\text{p}} )_{\text{bf}} + \phi (\rho C_{\text{p}} )_{\text{p}}$$
(4)

To determine the effective thermal conductivity and viscosity, Koo–Kleinstreuer–Li (KKL) introduced by Li [21] and Li and Kleinstreuer [22] model is used. The KKL model is capable of predicting the variations of thermal conductivity and viscosity with respect to the temperature, particle diameter, the volume fraction of nanoparticles, and material properties of the first (i.e., the base fluid) and the second (i.e., nanoparticles) phases [31]. In this model, the thermal conductivity of nanofluid is composed of two parts: a static (conventional) part and a dynamic one originating from the Brownian motion of particles [21]:

$$\begin{aligned} k_{\text{eff}} & = k_{\text{static}} + k_{\text{Brownian}} \\ \frac{{k_{\text{static}} }}{{k_{\text{bf}} }} & = 1 + \frac{{3\left( {\frac{{k_{\text{p}} }}{{k_{\text{bf}} }} - 1} \right)\phi }}{{\left( {\frac{{k_{\text{p}} }}{{k_{\text{bf}} }} + 2} \right) - \left( {\frac{{k_{\text{p}} }}{{k_{\text{bf}} }} - 1} \right)\phi }} \\ k_{\text{Brownian}} & = 5 \times 10^{4} \phi \rho_{\text{bf}} C_{{{\text{p}},{\text{bf}}}} \sqrt {\frac{{\kappa_{\text{bf}} T}}{{\rho_{\text{p}} d_{\text{p}} }}} g^{\prime } (T,\phi ,d_{\text{p}} ) \\ \end{aligned}$$
(5)

where \(g^{\prime } (T,\phi ,d_{\text{p}} )\) is [21]:

$$\begin{aligned} g^{\prime } (T,\phi ,d_{\text{p}} ) & = [a_{1} + a_{2} \cdot \ln (d_{\text{p}} ) + a_{3} \cdot \ln (\phi ) + a_{4} \cdot \ln (\phi ) \cdot \ln (d_{\text{p}} ) + a_{5} \cdot \ln (d_{\text{p}} )^{2} ] \\ & \quad \times \ln (T) + a_{6} + a_{7} \cdot \ln (d_{\text{p}} ) + a_{8} \cdot \ln (\phi ) + a_{9} \cdot \ln (\phi ) \cdot \ln (d_{\text{p}} ) + a_{10} \cdot \ln (d_{\text{p}} )^{2} \\ \end{aligned}$$
(6)

a1–a10 are listed in Table 4.

Similar to the effective thermal conductivity, the effective viscosity is introduced as follows [21]:

$$\mu_{\text{eff}} = \mu_{\text{static}} + \mu_{\text{Brownian}} = \frac{{\mu_{\text{bf}} }}{{(1 - \phi )^{2.5} }} + \frac{{k_{\text{Brownian}} }}{{k_{\text{bf}} }} \times \frac{{\mu_{\text{bf}} }}{{\Pr_{\text{bf}} }}$$
(7)

It should be noted that both the static and Brownian parts of the effective thermal conductivity (Eq. 5) and effective viscosity (Eq. 7) are temperature dependent. The temperature dependency of static parts is listed in Table 3.

Boundary conditions

A constant heat flux equal to 100 W cm−2 is imposed to the bottom surface of the MCHS. The upper side is insulated. The left and right sides are symmetrical planes. The working fluid of 293 K with uniform velocity distribution enters at the inlet. A constant gauge pressure of 50 Pa is assumed at the exit. No-slip and no-jump, respectively, for the velocity and temperature of the working fluid are assumed at fluid–solid interfaces:

$$\begin{array}{*{20}l} {\vec{V} = 0} \hfill \\ {T_{\text{f}} = T_{\text{s}} } \hfill \\ { - k_{\text{f}} \frac{{\partial T_{\text{f}} }}{\partial n} = - k_{\text{s}} \frac{{\partial T_{\text{s}} }}{\partial n}} \hfill \\ \end{array} @\,{\text{walls}}$$
(8)

Solution method and mesh sizing

The present study is an extension of the study of Refs. [19, 29], and hence, the solution method and mesh sizing are the same. Finite volume method (FVM) using FLUENT software over a non-uniform structured mesh [32, 33] of hexahedron type [29] with an increase factor of 1.01 in the axial direction was used.

Results and discussion

Figure 2 compares the Nusselt number of the present study and that of Refs. [18, 19] obtaining by variable (temperature-dependent) properties for the straight channel (Wo = 200 μm). A good agreement between the data sets is observed. In addition, it is seen that the Nusselt number decreases along the channel because of the thermal boundary layer growth. Moreover, the Nusselt number follows a unique trend for different inlet pressures since it is a dimensionless number [34, 35]. Moreover, the Nusselt number shows a gradual decrease and asymptotically reaches the value of 6.075, which is the fully developed Nusselt number for a rectangular channel with the aspect ratio of 0.2 [36].

Fig. 2
figure 2

Nusselt number of Al2O3–water nanofluid flowing through a MCHS with straight flow passages (WO = 200 µm) with different inlet pressures (Pi) obtained by the variable property approach compared to those of Mirzaei and Dehghan [18] and Lee et al. [19]

Full size image

Using the real-time (temperature-dependent) property approach, Fig. 3 is provided to investigate the role of nanoparticles (Al2O3) of 4% Vol. added to the base fluid (pure water) for two different configurations: a straight channel (Wo = 200 μm) and a converging flow passage (Wo = 100 μm). Figure 3a shows that the convection heat transfer coefficient (h) of the KKL nanofluid (Al2O3–water of 4% Vol.) is higher than that of the pure base fluid (water). The enhancement of the convection heat transfer coefficient obtained by the KKL nanofluid compared to the pure water at the outlet is about 8000 W m−2 K−1 (33%) for the converging flow passage in comparison with about 2000 W m−2 K−1 (19%) for the straight channel. This matter confirms the implementation of nanofluid in converging flow passage to obtain more enhancements by nanoparticle addition. It is worth mentioning that the curvature of the convection heat transfer coefficient for the case of the converging channel shows a balance between the reduction in the heat transfer rate because of the tendency to increase in the thermal boundary layer thickness in the flow direction and the enhancement of the heat transfer rate because of increasing the average velocity in the flow direction arising from the passage convergence [29].

Fig. 3
figure 3

KKL nanofluid (NF) versus pure water (PW): a convection heat transfer coefficient, h, b the bulk mean temperature, Tb, and c the bottom-side wall temperature, Tw

Full size image

As seen in Fig. 3b, a converging flow passage results in higher bulk mean temperature (Tb) and hence a higher thermal conductivity value which leads to a higher heat transfer rate. More importantly, a higher bulk mean temperature translates to a lower viscosity, which results in a higher axial velocity. These two simultaneous effects enhance the heat transfer rate. Meanwhile, Fig. 3c reveals that the bottom-side wall temperature (Tw) of the flow passage for the KKL nanofluid is lower than that of pure water due to a higher heat transfer ability of the KKL nanofluid. Furthermore, it is seen that the wall temperature and the bulk mean temperature increase semi-linearly along the flow direction. The deviation from a linear increase arises from the temperature-dependent properties of the working fluid and the thermally developing nature of the flow [34, 35].

To investigate the errors associated with the temperature dependency of thermophysical properties of both nanofluid and pure base fluid, predictions obtained according to the simulations using the variable (temperature-dependent) property approach are compared with those of constant property approach in Figs. 4–7 for two different configurations: converging (Wo = 100 μm) and straight (Wo= 200 μm) flow passages. In Figs. 4–7, the working fluid is the KKL nanofluid (Al2O3–water of 4% Vol.).

Fig. 4
figure 4

Reynolds number (Re) of the variable property approach compared to the constant property approach: aWO = 100 and bWO = 200

Full size image

The Reynolds number of the variable property approach is compared with that of the constant property approach in Fig. 4. For the constant property approach, it is seen that the Reynolds number remains almost unchanged along the flow direction. This behavior is evident in the straight passage. For the converging flow passage, the product of the velocity and the hydraulic diameter remain almost constant at each section. Consequently, the Reynolds number almost remains unchanged. However, for the variable (temperature-dependent) property approach, the Reynolds number increases along the flow direction due to the reduction in viscosity. In addition, the predicted inlet Reynolds number for a similar situation (two fixed pressures at the inlet and outlet) is different for two approaches. The constant property approach predicts the inlet and outlet Reynolds numbers (or the inlet and outlet mean velocities), respectively, 31% and 64% off for the straight flow passage, while these errors for the converging flow passage are 55% and 141%, respectively. Such a high error level (up to 141%) cannot be ignored even for firsthand engineering estimations. Hence, one can conclude that assuming the property variation with respect to temperature is crucial for predictions of numerical simulations as well as correlations for microchannels.

It is seen that the area-weighted average pressure along the flow direction is almost the same for the variable (temperature-dependent) property and constant approaches in Fig. 5. This occurs since the pressure at the two ends is pre-defined (where the inlet pressure is 2000 Pa and the outlet one is 50 Pa). Meanwhile, it is seen that the absolute value of the pressure profile’s slope (i.e., \(- \partial P/\partial z\)) increases along the flow direction due to the flow acceleration along the converging flow passage (Fig. 5a). In addition, except a small region at the entrance, the pressure linearly decreases along the flow direction for the straight channel according to what was predicted by the hydrodynamically developed flow model (Fig. 5b) [37].

Fig. 5
figure 5

Axial pressure (P) of the variable property approach compared to the constant property approach: aWO = 100 and bWO = 200

Full size image

Figure 6 compares the required pumping power (Eq. 9) prediction for a single channel obtained by variable (temperature-dependent) and constant thermophysical property approaches for different outlet widths (Wo) in the dimensionless form (i.e., the convergence factor, Wi/Wo).

Fig. 6
figure 6

Pumping power required for a single channel

Full size image
$${\text{Pumping}}\,{\text{Power}} = \dot{Q} \times \left( {P_{\text{i}} - P_{\text{o}} } \right)$$
(9)

where \(\dot{Q}\) is the volumetric flow rate. Since the total pressure drop along the channel is the same for all configurations (Pi–Po = 2000 ± 10–50 = 1950 ± 10 Pa), the constant property approach gives lower pumping powers due to the lower velocity prediction compared to the variable property approach according to the above discussion presented for Fig. 4. In addition, it is seen that the pumping power decreases with an increase in the convergence factor of the channel (Wi/Wo). It reveals that using a suitable convergence factor (Wi/Wo) along with an appropriate flow rate yields a thermally enhanced microchannel with less energy consumption to convect out a pre-defined heat flux. Meanwhile, it should be noted that an increase in the convergence factor augments the bulk mean temperature as well as the wall temperature. However, a higher bulk mean temperature corresponds to the situation of more enhanced thermophysical properties (a higher thermal conductivity and a lower shear viscosity), but the wall temperature should be controlled not to pass the safe limit.

Figure 7 shows that the convection heat transfer coefficient (h) predicted by the constant property approach is lower than that of the variable (temperature-dependent) property one. It was expected since the effective thermal conductivity increases with the temperature, which yields higher heat transfer ability. Simultaneously, the viscosity decreases by an increase in temperature, and hence, the nanofluid’s velocity increases. These two simultaneous effects enhance the heat transfer rate. Since the temperature variation for the converging flow passage is higher than that of the straight one, the difference between the predicted h of these two approaches is higher in Fig. 7a compared to Fig. 7b. The difference between the predicted h of these two approaches at the exit is 30% and 19% for Fig. 7a, b, respectively, which is noticeable. To summarize the errors associated with the temperature dependency of nanofluids found in the present study, Fig. 8 is plotted for the case of converging MCHS (Wo = 100 µm).

Fig. 7
figure 7

Convection heat transfer coefficient (h) of the variable property approach compared to the constant property approach: aWO = 100 µm and bWO = 200 µm

Full size image
Fig. 8
figure 8

Errors associated with the temperature dependency of nanofluids in the converging MCHS (WO = 100 µm)

Full size image

Conclusions

The 3D conjugate heat transfer, as well as the flow, of a KKL nanofluid (Al2O3–water of 4% Vol.) through rectangular microchannel heat sinks with both straight and converging flow passages was numerically studied using FVM. Two approaches including the variable (temperature-dependent) property and constant property were adopted for the numerical simulations to find how much off-design would be resulted only due to the variation of the thermophysical properties and how much sensitive are the numerical predictions to the assumptions. It was shown that the constant property approach gives relatively rough results (up to 140%, 31%, and 33% errors, respectively, for Re number, convection heat transfer coefficient, and the required pumping power). In addition, the results revealed that the nanofluid compared to the pure base fluid (here pure water) obtains more enhanced heat transfer rates for a converging flow passage than a straight one. The study found that the temperature dependency of the working fluid’s thermophysical properties should be considered to obtain more realistic simulation results concerning the convection through microchannel heat sinks, especially for converging flow passages due to high-temperature gradients and for nanofluids with temperature-induced property gradients. Finally, the heat transfer rate and the pumping power are predicted higher and lower, respectively, compared to the real values if one adopts the constant property assumption, and hence, the microheat exchanger would be over-designed and might work under off-design and less-efficient conditions.