Introduction

The investigation of boundary layer flow and heat transfer by a stretching surface is essential in engineering and industrial technology. Examples of such flows are in aerodynamics, metallurgy, fluid movies in precipitation process, hot rolling, wire drawing, manufactured filaments and so on. In all these situations, the feature of final item relies upon the friction factor and heat transfer rate. It is frequently supposed in these flows that the surface is linearly stretched, i.e. the velocity of the surface is linearly and directly proportional to the distance from the fixed point. But in real-world, it is not necessary for the stretching sheet to be linear as contended by Gupta and Gupta (1997). For instance, Emmanuel and Khan (2006) considered an exponentially stretching surface. Exponentially stretching surface has more extensive applications for example, in the situation of softening and hardening of copper wires. Khan and Sanjayanand (2005) analytically investigated the flow and heat transfer properties past an exponentially stretching sheet. Nadeem and Lee (2012) wonderfully clarified the characteristics of nanofluid over an exponentially stretching surface.

Majority of the fluids are not good conductors of heat because of their lower thermal conductivity. By using the ordinary heat transfer fluids, cooling rate cannot be enhanced. To adapt up to this issue and to improve heat conductivity or other heat properties of these liquids, a recently created strategy is utilized which includes expansion of nano-sized particles of very good conductors of heat, for example titanium, iron and aluminum to the liquids (Choi 2009). Choi (1995) first introduced the term “nanofluid”. Choi et al. (2001) demonstrated that the thermal conductivity of typical liquids can be multiplied by adding nanoparticles to base liquids that likewise fuse other thermal properties. Nanoparticles along with their little volume fraction, stability and remarkable useful applications in optical, biomedical and electronic fields have opened new horizons of research. Recently many scholars have discussed the nanoparticle phenomena in different geometries with pertinent physical properties of fluid, see refs. (Sheikholeslami and Zeeshan 2017; Sheikholeslami and Sadoughi 2018; Sheikholeslami and Shehzad 2018; Hussain et al. 2018; Sheikholeslami et al. 2018a, b, 2019a, b; Sheikholeslami 2018, 2019a, b, c; Sheikholeslami and Seyednezhad 2018).

The recent improvements of carbon nanotubes (CNTs) have reformed the new field of nanotechnology and made extraordinary commitments to both fundamental science and designing. Since hybrid nanofluids are recent development in heat generation fluids, only a few studies have been carried out on their fusion. Lately, some numerical investigations (Nasrin and Alim 2014; Nimmagadda and Venkatasubbaiah 2015; Hayat and Nadeem 2017) were carried out on hybrid nanofluid as a new concept in technology. The measurement of viscosity and thermal conductivity of the Al2O3–Cu/H2O hybrid nanofluid has been conducted by Suresh et al. (2011). They concluded that all the parameters were enhanced with solid volume fraction of nanoparticles. Moghadassi et al. (2015) examined the impact of Al2O3–H2O which was nanofluid and hybrid which comprised Al2O3–Cu/H2O. He depicted that the Al2O3–Cu/H2O (hybrid nanofluid) possess a greater coefficient of heat transfer convention. Sarkar et al. (2015) brought to our knowledge the recent studies in the field of hybrid nanofluids. Tayebi and Chamkha (2016) examined the heat transfer phenomenon inside an annulus with Cu–Al2O3/H2O numerically. The influence of Lorentz force with Hybrid nanofluid has been studied by Devi and Devi (2016).

Magneto-hydrodynamic (MHD) manages the flow of conducting liquids. The uses of MHD spread an extensive variety of physical regions for example, MHD generators and pumps, modern metallurgy, sanitization of unrefined petroleum, optimal design warming, geophysics, plasma material science and liquid beads showers (Sheikholeslami et al. 2018a, b, 2019a, b; Hatami et al. 2014; Sheikholeslami and Ganji 2017; Sheikholeslami and Rokni 2017; Sheikholeslami and Zia 2016; Ellahi et al. 2018; Zeeshan et al. 2018; Fetecau et al. 2018; Hassan et al. 2018; Hussain et al. 2018; Majeed et al. 2018; Alamri et al. 2019). So, our objective here is to improve the properties of single particle nanofluids by introducing hybrid nanofluids which provide great enhancement in thermal properties by considering different aspects.

Momentum and temperature description

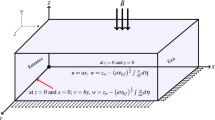
We propose the 3D, steady, rotating flow of an electrically conducting hybrid nanofluid over an exponentially stretching surface. The flow coincides with the plane \(z = 0\) (see Fig. 1). A uniform magnetic field is applied perpendicular to the surface to see its maximum effects. As carbon nanotubes have high thermal conductivity, we consider nanoparticles of SWCNT and MWCNT and water as a base fluid. First of all, MWCNT (\(\phi_{1}\)) of 0.1 volume fraction is dispersed into the water to constitute MWCNT-Water nanofluid. Further, nanoparticles of SWCNT (\(\phi_{2}\)) are scattered into the MWCNT-Water nanofluid to acquire our required hybrid nanofluid. The rotation of the fluid is about z-axis so that the angular velocity of the fluid is constant. Now the transport equations are

$$\nabla .\vec{V} = 0,$$
(1)
$$\rho_{\text{hnf}} \frac{{{\text{d}}\vec{V}}}{{{\text{d}}t}} + \vec{\varOmega } \times \vec{V} = - \nabla p + \left( {\mu_{\text{hnf}} } \right)\nabla^{2} \vec{V} + \vec{j} \times \vec{B},$$
(2)
$$\frac{{{\text{d}}T}}{{{\text{d}}t}} = \alpha_{\text{hnf}} \nabla^{2} T.$$
(3)

where \(\alpha_{\text{hnf}}\) is thermal diffusivity of hybrid nanofluid, \(\mu_{\text{hnf}}\) is hybrid nanofluid’s dynamic viscosity, \(\rho_{\text{hnf}}\) is the density of hybrid nanofluid, \(k_{\text{hnf}}\) is the thermal conductivity of hybrid nanofluid, \(\left( {\rho C_{p} } \right)_{\text{hnf}}\) is the heat capacity of hybrid nanofluid and \(\phi\) is the nanoparticle’s volume fraction which is defined as follows:

$$\left. \begin{aligned} &\alpha_{\text{hnf}} = \frac{{k_{\text{hnf}} }}{{(\rho c_{p} )_{\text{hnf}} }}, \;\mu_{\text{hnf}} = \frac{{\mu_{f} }}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}, \\ &\rho_{\text{hnf}} = \left[ {\left( {1 - \phi_{2} } \right)\left\{ {\left( {1 - \phi_{1} } \right)\rho_{\text{f}} + \phi_{1} \rho_{{{\text{s}}_{1} }} } \right\} + \phi_{2} \rho_{{{\text{s}}_{2} }} } \right], \\ & \left( {\rho C_{p} } \right)_{\text{hnf}} = \left[ {\left( {1 - \phi_{2} } \right)\left\{ {\left( {1 - \phi_{1} } \right)\left( {\rho C_{p} } \right)_{f} + \phi_{1} \left( {\rho C_{p} } \right)_{{{\text{s}}_{1} }} } \right\} + \phi_{2} (\rho C_{p} )_{{{\text{s}}_{2} }} } \right], \\ & \frac{{k_{\text{hnf}} }}{{k_{\text{nf}} }} = \frac{{\left( {k_{{{\text{s}}_{2} }} + 2k_{\text{nf}} } \right) - 2\phi_{2} \left( {k_{\text{nf}} - k_{{{\text{s}}_{2} }} } \right)}}{{\left( {k_{{{\text{s}}_{2} }} + 2k_{\text{nf}} } \right) + \phi_{2} \left( {k_{\text{nf}} - k_{{{\text{s}}_{2} }} } \right)}}, \frac{{k_{\text{nf}} }}{{k_{f} }} = \frac{{\left( {k_{{{\text{s}}_{1} }} + 2k_{f} } \right) - 2\phi_{1} \left( {k_{f} - k_{{{\text{s}}_{1} }} } \right)}}{{\left( {k_{{{\text{s}}_{1} }} + 2k_{f} } \right) + \phi_{1} \left( {k_{f} - k_{{{\text{s}}_{1} }} } \right)}}, \\ & \nu_{\text{hnf}} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}, \varOmega = \varOmega_{0} e^{{\frac{x + y}{L}}} . \\ \end{aligned} \right\}$$
(4)
Fig. 1
figure 1

Schematic diagram of the model

Full size image

After applying boundary layer approximation, we are left with the following equations (Hayat and Nadeem 2018; Hayat et al. 2018):

Continuity equation

$$\left[ {\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}} \right] = 0,$$
(5)

Momentum equations

$$\left[ {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} - 2\varOmega v} \right] = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{{\sigma B_{0}^{2} u}}{{\rho_{\text{hnf}} }},$$
(6)
$$\left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} + 2\varOmega u} \right] = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\frac{{\partial^{2} v}}{{\partial z^{2} }} - \frac{{\sigma B_{0}^{2} v}}{{\rho_{\text{hnf}} }}.$$
(7)

Energy equation

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = \alpha_{\text{hnf}} \left( {\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right)$$
(8)

Boundary conditions

$$\left. {\begin{array}{*{20}l} {u = u_{w} ,\;v = v_{w} ,\; - k_{\text{hnf}} \frac{\partial T}{\partial z} = h_{f} \left( {T_{w} - T} \right), {\text{at}}\;z = 0,} \\ {u \to 0,\;v \to 0,\;T \to T_{{ _{\infty } }} ,\;{\text{as}} \; {z}\to \infty .} \\ \end{array} } \right\}$$
(9)

Stretching velocities at surface and temperature at the wall are defined as follows:

$$u_{w} = u_{0} e^{{\frac{x + y}{L}}} ,v_{w} = v_{0} e^{{\frac{x + y}{L}}} ,T_{w} = T_{\infty } + T_{0} e^{{\frac{{A\left( {x + y} \right)}}{2L}}}$$
(10)

Using suitable similarity transformations given below,

$$\left. {\begin{array}{*{20}l} {u = u_{0} e^{{\frac{x + y}{L}}} p'\left( \eta \right),v = u_{0} e^{{\frac{x + y}{L}}} q'\left( \eta \right),w = - \left( {\frac{{\nu u_{0} }}{2L}} \right)^{{\frac{1}{2}}} e^{{\frac{x + y}{2L}}} \left\{ {p + \eta p' + q + \eta q'} \right\},} \hfill \\ {T = T_{\infty } + T_{0} e^{{\frac{{A\left( {x + y} \right)}}{2L}}} f\left( \eta \right),\eta = \left( {\frac{{u_{0} }}{2\nu L}} \right)^{{\frac{1}{2}}} e^{{\frac{x + y}{2L}}} z.} \hfill \\ \end{array} } \right\}$$
(11)

After applying the above similarity transformations on Eqs. (5–9), the continuity equation is identically satisfied while momentum and energy equations take the following form:

$$\frac{{\rho_{f} }}{{\rho_{\text{hnf}} }}\left( {A_{1} \left( \phi \right)} \right)p''' + p''\left( {p + q} \right) - 2p'\left( {p' + q'} \right) + 4\gamma g' - 2M\frac{{\rho_{f} }}{{\rho_{\text{hnf}} }}p' = 0,$$
(12)
$$\frac{{\rho_{f} }}{{\rho_{\text{hnf}} }}\left( {A_{1} \left( \phi \right)} \right)q''' + q''\left( {p + q} \right) - 2q'\left( {p' + q'} \right) - 4\gamma p' - 2M\frac{{\rho_{\text{f}} }}{{\rho_{\text{hnf}} }}q' = 0,$$
(13)
$$\frac{1}{\Pr }\frac{{\left( {k_{\text{hnf}} /k_{f} } \right)f''}}{{\left[ {\left( {1 - \phi_{2} } \right)\left\{ {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho C_{p} } \right)_{{s_{1} }} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right\} + \phi_{2} \frac{{(\rho C_{p} )_{{s_{2} }} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right]}} - A\left( {p^{\prime} + q^{\prime}} \right)f + \left( {p + q} \right)f^{\prime} = 0$$
(14)

The associated boundary conditions are

$$\left. {\begin{array}{*{20}l} {p\left( 0 \right) = 0,p'\left( 0 \right) = 1,q\left( 0 \right) = 0,} \hfill \\ {q^{\prime}\left( 0 \right) = \alpha ,f^{\prime}\left( 0 \right) = - {\text{Nc}}\left( {\frac{{k_{f} }}{{k_{\text{hnf}} }}} \right)\left( {1 - f\left( 0 \right)} \right), {\text{as}} \;\eta \to 0,} \hfill \\ {p^{\prime} \to 0,q^{\prime} \to 0,f \to 0, \;{\text{as }} \eta \to \infty .} \hfill \\ \end{array} } \right\}$$
(15)

where \(\gamma ,M,\alpha ,{\text{Nc}}\) and Pr signify rotation parameter, Hartmann number, stretching ratio parameter, convective parameter and Prandtl number, respectively, and they are defined as follows:

$$\left. {\begin{array}{*{20}r} \hfill {\gamma = \frac{{\varOmega_{0} L}}{{u_{0} }}, A_{1} \left( \phi \right) = \frac{{\mu_{\text{hnf}} }}{{\mu_{f} }} = \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}, \alpha = \frac{{v_{0} }}{{u_{0} }},} \\ \hfill {M = \frac{{\sigma B_{0}^{2} L}}{{\rho_{f} u_{0} }}e^{{ - \left( {\frac{x + y}{L}} \right)}} ,{\text{Nc}} = \frac{{h_{f} }}{{k_{f} }}\sqrt {\frac{{2\nu_{f} L}}{{u_{0} }}} e^{{ - \left( {\frac{x + y}{2L}} \right)}} ,\Pr = \frac{{(\mu C_{p} )_{f} }}{{k_{f} }}.} \\ \end{array} } \right\}$$
(16)

Further, the skin friction coefficients and Nusselt number can be defined as (Rao et al. 2015):

$$C_{\text{fx}} = \frac{{\tau_{\text{wx}} }}{{\frac{1}{2}\rho_{f} u_{w}^{2} }},C_{\text{fy}} = \frac{{\tau_{\text{wy}} }}{{\frac{1}{2}\rho_{f} u_{w}^{2} }},{\text{Nu}}_{x} = \frac{{xQ_{w} }}{{k_{f} \left( {T_{w} - T_{\infty } } \right)}},$$
(17)

where \(\tau_{\text{wx}} ,\tau_{\text{wy}}\) and \(Q_{\text{w}}\) are shear stresses at the surface along two lateral directions and heat flux at the surface, defined as follows:

$$\left. {\tau_{\text{wx}} = \mu_{\text{hnf}} \left( {\frac{\partial u}{\partial z}} \right)_{z = 0} , \tau_{\text{wy}} = \mu_{\text{hnf}} \left( {\frac{\partial v}{\partial z}} \right)_{z = 0} , Q_{w} = - k_{\text{hnf}} \left( {\frac{\partial T}{\partial z}} \right)_{z = 0} .} \right\}$$
(18)

The non-dimensional form after simplification is

$$\left. {\begin{array}{*{20}ll} {\frac{1}{\sqrt 2 }C_{\text{fx}} \left( {\text{Re}_{x} } \right)^{{\frac{1}{2}}} = A_{1}^{ - 1} p^{\prime\prime}\left( 0 \right), \frac{1}{\sqrt 2 }C_{\text{fy}} \left( {\text{Re}_{y} } \right)^{{\frac{1}{2}}} = A_{1}^{ - 1} q^{\prime\prime}\left( 0 \right), } \\ {\sqrt 2 \frac{L}{x}{\text{Nu}}_{x} \text{Re}^{{ - \frac{1}{2}}} = - \frac{{k_{\text{hnf}} }}{{k_{f} }}f'\left( 0 \right).} \\ \end{array} } \right\}$$
(19)

Numerical scheme

The coupled non-linear ordinary differential Eqs. (12–14) along with boundary conditions (15) are first converted into first order and are then solved numerically using BVP-4C technique (Shampine et al. 2000, 2003; Nadeem et al. 2019). The implicit MATLAB library bvp4c for boundary value problem executes 3-stage Lobatto IIIA formula. Due to their great stability properties, Lobatto IIIA method has been assumed for boundary value problems (BVP). The procedure of this technique is as follows:

$$p = y_{1} , p^{'} = y_{2} , p^{''} = y_{3} , q = y_{4} , q^{'} = y_{5} , q^{''} = y_{6} , f = y_{7} , f' = y_{8} ,$$
(20)
$$\left. \begin{aligned} & y_{3}^{'} = \frac{{\mu_{f} }}{{\mu_{\text{hnf}} }}\frac{{\rho_{\text{hnf}} }}{{\rho_{f} }}\left( {2y_{2} \left( {y_{2} + y_{5} } \right) - y_{3} \left( {y_{1} + y_{4} } \right) - 4\gamma y_{5} } \right) + 2\frac{{\mu_{f} }}{{\mu_{\text{hnf}} }}My_{2} , \\ & y_{6}^{'} = \frac{{\mu_{f} }}{{\mu_{\text{hnf}} }}\frac{{\rho_{\text{hnf}} }}{{\rho_{f} }}\left( {2y_{5} \left( {y_{2} + y_{5} } \right) - y_{6} \left( {y_{1} + y_{4} } \right) - 4\gamma y_{2} } \right) + 2\frac{{\mu_{f} }}{{\mu_{\text{hnf}} }}My_{5} , \\ & y_{8}^{'} = \left( {\frac{{k_{f} }}{{k_{\text{hnf}} }}} \right)\frac{{(\rho C_{p} )_{\text{hnf}} }}{{(\rho C_{p} )_{f} }}\Pr A\left( {y_{1} + y_{4} } \right)y_{7} - \left( {y_{2} + y_{5} } \right)y_{8} , \hfill \\ \end{aligned} \right\}$$
(21)

with boundary conditions

$$\left. {\begin{array}{*{20}ll} {y_{1} \left( 0 \right) = 0, y_{2} \left( 0 \right) = 1, y_{4} \left( 0 \right) = 0, y_{5} \left( 0 \right) = \alpha ,} \\ {y_{8} \left( 0 \right) = - {\text{Nc}}\frac{{k_{f} }}{{k_{\text{hnf}} }}\left( {1 - y_{7} \left( 0 \right)} \right), y_{2} \left( {10} \right) = 0,} \\ {y_{5} \left( {10} \right) = 0, y_{7} \left( {10} \right) = 0.} \\ \end{array} } \right\}$$
(22)

Now the above system is reduced to first-order ordinary differential equations and then this method is repeated until the criterion of \(10^{ - 6}\) is achieved. The solutions represent main characteristics of the problem which is analyzed graphically and in tabular form.

Graphical outcomes

See Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.

Fig. 2
figure 2

Impact of \(\phi_{2}\) on \(p'\left( \eta \right)\)

Full size image
Fig. 3
figure 3

Impact of \(\phi_{2}\) on \(q^{\prime}\left( \eta \right)\)

Full size image
Fig. 4
figure 4

Impact of \(\phi_{2}\) on \(f\left( \eta \right)\)

Full size image
Fig. 5
figure 5

Impact of \(\alpha\) on \(q^{\prime}\left( \eta \right)\)

Full size image
Fig. 6
figure 6

Impact of \(\phi_{2}\) on \(f\left( \eta \right)\)

Full size image
Fig. 7
figure 7

Impact of A on \(f\left( \eta \right)\)

Full size image
Fig. 8
figure 8

Impact of \(\alpha\) on \(f\left( \eta \right)\)

Full size image
Fig. 9
figure 9

Impact of Nc on \(f\left( \eta \right)\)

Full size image
Fig. 10
figure 10

Effect of \(\phi_{2}\) on \(f\left( \eta \right)\)

Full size image
Fig. 11
figure 11

Impact of skin friction along x axis with M and \(\gamma\)

Full size image
Fig. 12
figure 12

Impact of skin friction along y axis with M and \(\gamma\)

Full size image
Fig. 13
figure 13

Impact of local Nusselt number with M and \(\gamma\)

Full size image
Fig. 14
figure 14

Impact of skin friction along x axis with \(\alpha\) and \(\phi_{2}\)

Full size image
Fig. 15
figure 15

Impact of skin friction along y axis with \(\alpha\) and \(\phi_{2}\)

Full size image
Fig. 16
figure 16

Impact of local Nusselt number with \(\alpha\) and \(\phi_{2}\)

Full size image
Fig. 17
figure 17

Impact of local Nusselt number with \({\text{Nc}}\) and \(\phi_{2}\)

Full size image
Fig. 18
figure 18

Impact of local Nusselt number with \(A\) and \(\phi_{2}\)

Full size image

Results and discussion

We have examined in this section the velocity distribution in two lateral directions (\(p '\left( \eta \right)\), \(q '\left( \eta \right)\)) and temperature distribution \(f\left( \eta \right)\) for different pertinent parameters such as nanoparticle volume fraction \(\phi_{2}\), Hartmann number M, rotation parameter \(\gamma\), stretching ratio \(\alpha\), temperature exponent A and convective parameter \({\text{Nc}}\). The impact of \(\phi_{2}\) and Hartmann number \(M\) on velocities (\(p '\left( \eta \right)\), \(q '\left( \eta \right)\)) and temperature distribution \(f\left( \eta \right)\) is portrayed in Figs. 2, 3, 4. It is observed that velocity and temperature distribution increases for increasing values of \(\phi_{2}\). The reason behind that is, as \(\phi_{2}\) increases, the thermal conductivity of both nanofluid SWCNT-Water and hybrid nanofluid SWCNT-MWCNT/Water amplifies and that is why velocity and temperature profile increases. But \(M\) has the opposite impact on momentum and temperature profiles. The increasing value of Hartmann number \(M\) decreases the liquid velocity in both directions but enhances the temperature profile \(f\left( \eta \right)\). Physically, magnetic field is used to control the flow behavior. It creates Lorentz force which is the resistive force and restricts the motion of the fluid. That is why liquid velocity decreases.

Figure 5 elucidates the effects of stretching ratio \(\alpha\) on y component of velocity profile \(q '\left( \eta \right)\). Here one can observe that fluid velocity enhances with stretching ratio \(\alpha\). The impact of \(\phi_{2}\) on temperature profile \(f\left( \eta \right)\) is explored in Fig. 6. From this figure it is evident that temperature profile \(f\left( \eta \right)\) rises for any under consideration value of \(A\) with the elevation in nanoparticle volume fraction \(\phi_{2}\). Figure 7 demonstrates the behavior of temperature exponent \(A\) on temperature profile \(f\left( \eta \right)\). Here one can observe that temperature exponent \(A\) is the decreasing function of temperature profile \(f\left( \eta \right)\) for both nanofluid SWCNT-Water and hybrid nanofluid SWCNT-MWCNT/Water.

Figures 8 and 9 are sketched to depict the variation of \(\alpha\) and Nc on temperature profile \(f\left( \eta \right)\). An elevation in stretching ratio \(\alpha\) reduces the temperature as observed through Fig. 8. From Fig. 9, it is illustrated that there is a remarkable raise in temperature for both nanofluid SWCNT-Water and hybrid nanofluid SWCNT-MWCNT/Water with the elevation in convective parameter Nc. But from figure it is obvious that nanofluid SWCNT-Water has a lower temperature as compared to hybrid nanofluid SWCNT-MWCNT/Water. Physically, as \({\text{Nc}}\) enhances, the lower surface of the stretching sheet gets heated by the hot fluid which leads to convective heat transfer. Hence the temperature distribution increases. Figure 10 demonstrates the impact of nanoparticle volume fraction \(\phi_{2}\) and convective parameter \({\text{Nc}}\) on temperature profile \(f\left( \eta \right)\). Larger values of convective parameter \({\text{Nc}}\) with the raise in nanoparticle volume fraction \(\phi_{2}\) correspond to higher temperature profile \(f\left( \eta \right)\). Now we examine the behavior of various physical parameters for both nanofluid SWCNT-Water and hybrid nanofluid SWCNT-MWCNT/Water on skin friction coefficients (\(C_{\text{fx}}\), \(C_{\text{fy}}\)) and local Nusselt number \({\text{Nu}}_{x}\) through Figs. 11, 12, 13, 14, 15, 16, 17, 18. The nature of \(M\) and \(\gamma\) on \(C_{\text{fx}}\) is displayed in Fig. 11. It is observed that as we enhance the Hartmann number \(M\), the skin friction amplifies but it decreases with rotation parameter \(\gamma\). The enhancement in skin friction is due to the increase in Lorentz force which resists the motion of the fluid. As a result, the viscosity of the fluid increases and that is why \(C_{\text{fx}}\) increases. Figure 12 elucidates the effect of \(M\) and \(\gamma\) on y component of skin friction. Here we observe that skin friction along y direction increases with both \(M\) and \(\gamma\). Figure 13 portrays the nature of Hartmann number \(M\) and rotation parameter \(\gamma\) on the local Nusselt number. From figure it is clear that the rate of heat transfer decreases with both Hartmann number \(M\) and rotation parameter \(\gamma\). Here we observe that even in the presence of Hartmann number and rotation parameter, the rate of heat transfer of hybrid nanofluid SWCNT-MWCNT/Water is higher than simple nanofluid SWCNT-Water.

Figures 14, 15 and 16 describe the behavior of stretching ratio \(\alpha\) and \(\phi_{2}\) on skin friction coefficients along two lateral directions (\(C_{\text{fx}}\), \(C_{\text{fy}}\)) and the local Nusselt number \({\text{Nu}}_{x}\). Here, \(C_{\text{fx}}\) decreases with the \(\alpha\), but \(C_{\text{fy}}\) and rate of heat transfer enhance with \(\alpha\). In each figure, the friction factor and heat transfer rate increase with carbon nanotubes’ volume fraction \(\phi_{2}\). This is due to the reason that thermal conductivity of hybrid nanofluid SWCNT-MWCNT/Water intensifies with the increase in carbon nanotube volume fraction \(\phi_{2}\). As seen in Fig. 17, there is magnificent increase in the rate of heat transfer with the rise in even small values of convective parameter Nc. Figure 18 shows the variation of \(\phi_{2}\) and temperature exponent A on the rate of heat transfer. Here one can observe that the rate of heat transfer amplifies with temperature exponent A and \(\phi_{2}\). The thermo-physical properties of carbon nanotubes and base fluid are illustrated in Table 1. The effects of pertinent physical parameters such as Hartmann number \(\left( M \right),\) stretching ratio (\(\alpha\)), rotation parameter (\(\gamma\)), temperature exponent \(\left( A \right),\) convective parameter \(\left( {\text{Nc}} \right)\) and nanoparticle volume fraction (\(\phi_{2}\)) on skin friction coefficients (\(C_{\text{fx}}\), \(C_{\text{fy}}\)) and the local Nusselt number \({\text{Nu}}_{x}\) are presented in Table 2 where Table 3 represent the comparison table shows a good agreement which previous published data.

Table 1 Thermophysical properties of carbon nanotubes and base fluid
Full size table
Table 2 Impact of Hartmann number \(\left( M \right)\), stretching ratio parameter (\(\alpha\)), rotation parameter \((\gamma\)), temperature exponent \(\left( A \right),\) convective parameter \(\left( {\text{Nc}} \right)\) and nanoparticle volume fraction \(\left( {\phi_{2} } \right)\) on skin friction coefficient and local Nusselt number
Full size table
Table 3 Comparison of \(- p''\left( 0 \right)\) for various values of stretching parameter \(\alpha\) when \(\gamma = \phi_{1} = \phi_{2} = 0\)
Full size table

Key points

To examine the three-dimensional magneto hydrodynamic flow of hybrid nanofluid in the presence of CNTs along an exponentially stretching surface, a numerical analysis is executed. Impact of relevant physical parameters on two lateral velocities, temperature distribution, friction factor as well as on the rate of heat transfer are discussed in comprehensive form. The conclusion of present research is listed as follows:

  • Addition of \(\phi_{2}\) escalates the velocity, temperature, friction factor and heat transfer rate.

  • The flow of hybrid nanofluid plays a noteworthy part in heat transfer in the presence of magnetic field.

  • The rate of heat transfer increases with stretching ratio parameter, convective parameter and temperature exponent.

  • Hartmann number increases the friction factor but decreases the rate of heat transfer.

  • The temperature along with thermal boundary layer thickness escalates by adding solid volume fraction.

  • Enhancing the temperature exponent decreases the temperature profile.

  • It is noted that hybrid nanofluid gives significant heat transfer performance as compared to simple nanofluid.