Introduction

Heat transfer forms the origin of many industrial processes that are present in our daily life. The magnification of these exchanges and the improvement of the efficiency have become currently problematic in the industrial world, which turn out to be more conscious to the progressive collapse of energy resources. Confronted to these energy and environmental tasks, the technological challenge lies in the development of new processes for better energy controlling. Therefore, new optimization strategies must be studied. One of these strategies consists in improving the thermal properties of the heat transfer of the fluids used in thermal systems, in particular in heat exchangers. Significant progress in chemistry made it possible at the end of the 1990s to synthesize nanometric-sized particles, which, dispersed in a liquid carrier, constitute nanofluids [1,2,3,4]. Their synthesis comes upon the need to boost the thermal properties of fluids by inserting a solid phase with very high thermal conductivity such as metallic or metal oxide nanoparticles [5,6,7]. Heat transfer fluids can be gases, organic fluids, liquid metals, or water. Heat transfer fluids have been developed and used in a huge variety of applications. They are chosen according to the quantities required and their physicochemical properties, their thermal conductivity, their anticorrosive properties, their cost and their impact on the environment. Water is one of the most used because of its economy, its high thermal capacity and its high thermal conductivity.

Nanofluids are relatively a novel category of fluids which consist of a basic fluid with particles of nanometric size (1–100 nm), in suspension. Endowed with particular and interesting physicochemical properties, such as their high conductivity, nanofluids have an efficient thermal conductivity higher than that of base liquids [8,9,10]. Numerous researches have been conducted on the hydrothermal features of MHD, a phenomenon which is caused by the impact of magnetic fields on electrically conductive fluids [11, 12]. Mehryanet al. [13] have studied unsteady MHD natural convection inside an enclosure employing numerical simulation. Cavity is divided by an elastic film. The outcomes show that the variation in the Hartmann number affected the shape of the film and the heat transfer. Bahrami et al. [14] investigated numerically heat transfer enhancement inside an eccentric porous cylinder with an inner moving wall. They concluded that the insertion of porous supports with higher Darcy numbers improves heat transfer and its effect is very considerable for high Rayleigh numbers. Another research, Rashad et al. [15] studied the effectiveness of MHD convection in an enclosure. They reported that the Nusselt number declines with the Lorentz forces. Anjali et al. [16] investigated the magnetoconvection over a porous stretchable sheet. They observed that the thermal performance of the hybrid nanofluid is greater than the conventional nanofluid with magnetic field environment. Afrand et al. [17] analyzed experimentally the impacts of volume fraction on heat transfer. With different volume fractions (0.0375–1.2%), stable and homogeneous suspensions have been prepared and viscosity measurements were reported as temperatures between 25 and 50 °C. Aman et al. [18] presented exact solutions for the investigation of improved various parameters of Casson fluid (alumina and copper nanoparticles). Ghalambaz et al. [19] have studied the conjugate free convection Ag–MgO in a porous enclosure using LTE analysis. The outputs show that the hybrid nanoparticles decline the heat transfer rate and flow strength. Mehryan et al. [20] studied the natural convection hybrid nanofluid within a porous cavity under magnetic field based on two-equation energy model. Mohebbi et al. [21] investigated the natural convection within a permeable enclosure for solar power plants.

Many researchers have recently reported a more interesting contribution on this subject using different numerical methods [33,34,35,36,37,38,39]. The main objective of these numerical studies is to find a solution to the problems encountered in industrial and thermal systems.

To the authors’ best knowledge, from the previous recent literature review in this field no available paper at all deals with the entropy production due to MHD convection in an enclosure with a sinusoidal bottom and vertical wall which filled with hybrid nanofluid and porous media.

Problem description

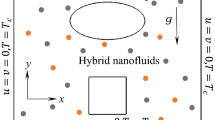
A schematic representation of free convection hybrid nanofluid flow in porous enclosure has been investigated in the present work (Fig. 1). The enclosure is heated sinusoidally from the bottom and right vertical wall where the top is adiabatic. The hybrid nanofluid flow considering laminar, incompressible and the external magnetic field is applied.

Fig. 1
figure 1

The geometry Mesh distribution for the physical model

Full size image

Governing equations

The steady MHD convection hybrid nanofluid flow in a square enclosure is analyzed here. To modeless a porous medium, the Brinkman [22] model is used. Heat equations and Navier–Stokes are expressed in Cartesian coordinates for the problem by considering the above assumptions that can be expressed in the non-dimensional model as follows:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(1)
$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \Pr \left( {\left. {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right)} \right. - \frac{\Pr }{\text{Da}}U + {\text{Ha}}^{2} \Pr U$$
(2)
$$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + \Pr \left( {\left. {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right)} \right. - \frac{\Pr }{\text{Da}}V + \Pr {\text{Ra}}\theta + {\text{Ha}}^{2} \Pr V$$
(3)
$$\left( {\left. {\frac{{\partial^{2} \theta_{{}} }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta_{{}} }}{{\partial Y^{2} }}} \right)} \right. = U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial V}$$
(4)

Entropy

Entropy production due to friction

$$S_{\uppsi} = \phi_{1} \left[ {\left[ {U^{2} + V^{2} } \right] + {\text{Da}} \times \left[ {2\left[ {\left( {\frac{\partial U}{\partial X}} \right)^{2} + \left( {\frac{\partial V}{\partial Y}} \right)^{2} } \right] + \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)^{2} } \right]} \right]$$
(5)

Thermal gradients:

$$S_{\uptheta} = \left[ {\left( {\frac{\partial \theta }{\partial X}} \right)^{2} + \left( {\frac{\partial \theta }{\partial Y}} \right)^{2} } \right]$$
(6)

Diffusion

$$S_{\text{c}} = \phi_{2} \left[ {\left( {\frac{\partial C}{\partial X}} \right)^{2} + \left( {\frac{\partial C}{\partial Y}} \right)^{2} } \right] + \phi_{3} \left[ {\left( {\frac{\partial \theta }{\partial X}} \right)\left( {\frac{\partial C}{\partial X}} \right) + \left( {\frac{\partial \theta }{\partial Y}} \right)\left( {\frac{\partial C}{\partial Y}} \right)} \right]$$
(7)

Magnetic field

$$S_{\text{M}} = \phi_{1} \times {\text{Ha}}^{2} \times \left[ {U\sin \varphi - V\cos \varphi } \right]$$
(8)
$$S_{\text{T}} = S_{\psi } + S_{\theta } + S_{\text{C}} + S_{\text{M}}$$
(9)

Using the following change of variables,

$$X = \frac{x}{L},\quad Y = \frac{y}{L},\quad U = \frac{u \cdot L}{\alpha },\quad V = \frac{v \cdot L}{\alpha },\quad P = \frac{{pL^{2} }}{{\rho \alpha^{2} }},\quad \theta = \frac{{T - T_{0} }}{{T_{i} - T_{0} }},\quad {\text{Ra}} = \frac{{\beta g\Delta TL^{3} }}{\alpha v},\quad {\text{Da}} = \frac{K}{{L^{2} }},\quad \Pr = \frac{v}{\alpha }$$
(10)

With the boundary conditions:

$$\begin{aligned} u(x,0) & = u(x,L) = u(0,y) = u(L,y) = 0 \\ V(X,0) & = V(X,1) = V(0,Y) = V(1,Y) = 0 \\ \theta (X,0) & = 1,\quad {\text{or}},\quad \theta (X,0) = \sin (\pi X),\frac{\partial \theta }{\partial Y}(X,1) = 0 \\ \theta (0,Y) & = 1\theta (0,Y) = \sin (\pi Y),\theta (1,Y) = 0 \\ \end{aligned}$$
(11)

Thermophysical properties of Al2O3–Cu/water are presented in Table 1. Those properties are expressed as

Table 1 Thermophysical properties of (Cu–Al2O3/water (50/50) [29]
Full size table

The diffusion coefficient is given by [24]:

$$\sigma_{\text{hnf}} = \left( {1 - \varphi } \right)\sigma_{\text{f}} + \varphi \sigma_{\text{np}}$$
(12)

The density of nanofluid is given by [23]:

$$\rho_{\text{hnf}} = \left( {1 - \varphi } \right)\rho_{\text{f}} + \varphi \rho_{\text{np}}$$
(13)

The thermal expansion coefficient [23]:

$$\left( {\rho \beta } \right)_{\text{hnf}} = \left( {1 - \varphi } \right)\left( {\rho \beta } \right)_{\text{f}} + \varphi \left( {\rho \beta } \right)_{\text{np}}$$
(14)

The specific heat capacity can be determined according to Pak and Cho [25]:

$$\left( {\rho c_{\text{p}} } \right)_{\text{hnf}} = \left( {1 - \varphi } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi \left( {\rho c_{\text{p}} } \right)_{\text{np}}$$
(15)
$$\alpha_{\text{hnf}} = \frac{{k_{\text{hnf}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{hnf}} }}$$
(16)

Thermal conductivity is defined as (Wasp model) [26]:

$$k_{\text{hnf}} = \frac{{k_{\text{np}} + \left( {n - 1} \right)k_{\text{f}} - \left( {n - 1} \right)\left( {k_{\text{f}} - k_{\text{np}} } \right)\varphi }}{{k_{\text{np}} + \left( {n - 1} \right)k_{\text{f}} + \left( {k_{\text{f}} - k_{\text{np}} } \right)\varphi }}k_{\text{f}}$$
(17)

The effective dynamic viscosity based on the Brinkman mode is considered as [27]

$$\mu_{\text{hnf}} = \frac{{\mu_{\text{f}} }}{{\left( {1 - \varphi } \right)^{2.5} }}$$
(18)

For nanoparticles Al2O3 and Cu, the properties are obtained [28]:

$$\varphi = \varphi {\text{Al}}_{2} O_{3} + \varphi {\text{Cu}}$$
(19)
$$\rho_{\text{np}} = \frac{{\varphi {\text{Al}}_{2} {\text{O}}_{3} (\rho ){\text{Al}}_{2} {\text{O}}_{3} + \varphi {\text{Cu}}(\rho ){\text{Cu}}}}{\varphi }$$
(20)
$$(c_{\text{p}} )_{\text{np}} = \frac{{\varphi {\text{Al}}_{2} {\text{O}}_{3} (c_{\text{p}} ){\text{Al}}_{2} {\text{O}}_{3} + \varphi {\text{Cu}}(c_{\text{p}} ){\text{Cu}}}}{\varphi }$$
(21)
$$\beta_{\text{np}} = \frac{{\varphi {\text{Al}}_{2} {\text{O}}_{3} \beta {\text{Al}}_{2} {\text{O}}_{3} + \varphi {\text{Cu}}\beta {\text{Cu}}}}{\varphi }$$
(22)
$$k_{\text{np}} = \frac{{\varphi {\text{Al}}_{2} {\text{O}}_{3} k{\text{Al}}_{2} {\text{O}}_{3} + \varphi {\text{Cu}}k{\text{Cu}}}}{\varphi }$$
(23)
$$\sigma_{\text{np}} = \frac{{\varphi {\text{Al}}_{2} {\text{O}}_{3} \sigma {\text{Al}}_{2} {\text{O}}_{3} + \varphi {\text{Cu}}\sigma {\text{Cu}}}}{\varphi }$$
(24)

The local and average Nusselt numbers calculation is very interesting. They are calculated by Roy [30]:

$${\text{Nu}}_{\text{local}} = \left\{ \begin{array}{ll} \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}\frac{\partial T}{\partial x}&\quad {\text{vertical walls}} \hfill \\ \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}\frac{\partial T}{\partial y}&\quad {\text{horizontal walls}} \hfill \\ \end{array} \right.$$
(25)
$${\text{Nu}}_{\text{average}} = \frac{1}{L}\int\limits_{0}^{L} {{\text{Nu}}_{\text{local}} {\text{d}}L} .$$
(26)

Validation and grid independency analysis

Grid analysis

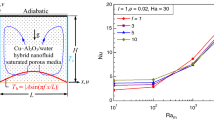
In this paper, Galerkin finite element procedure with penalty parameter is utilized to solve the nonlinear coupled PDEs for flow and temperature distributions. This method consists of converting nonlinear differential equations into a system of integral equations. Uniform quadratic grids were employed in the discretization of the field’s solution. To emphasize the grid independency of current solution, a mesh examining method was performed. Nusselt number is obtained for Al2O3–Cu/water (φ = 0.04) with Ra = 106. The aforementioned elements to develop an understanding of the grid finesse are shown in Table 2, and a grid size of 176 × 176 should be chosen.

Table 2 Comparison of Nuavg for different meshes
Full size table

Validation

The Galerkin finite element method was used for discretizing the Navier–Stokes equations. The computational domain is discretized into quadratic elements as shown in Fig. 1b. The verification of the present code is performed by comparing numerically Khanfer [31] and experimentally Krane and Jesee [32]. They investigated air flow in a cavity. The dimensionless temperature profile is plotted in Fig. 2 showing the very good agreement with a maximum deviation not exceeding 2%. According to Fig. 3, the present results exhibited negligible difference with numerical solutions of Roy [30].

Fig. 2
figure 2

Comparison of dimensionless temperature between the current research with numerical solution of Khanafer et al. [31] and experimental findings of Krane and Jesse [32]

Full size image
Fig. 3
figure 3

Comparison between current data and other studies for the temperature Roy [30]

Full size image

Results and discussion

This part clarifies the numerical outcomes for the stream function and isotherms lines for various parameters. The impact of control characteristics such as the Ha (0–80), Ra (103–106), Da (10−5 ≤ Da ≤ 10−2), nanoparticle concentration (0 ≤ φ ≤ 0.04) and porosity ratio (0.1 ≤ ε ≤ 0.9). The values of the Nuloc and Nuavg are also computed for several values of Ra, Ha, Da, ε and φ.

Stream functions and isotherms

Figures 4–6 show stream function and isotherms for various parameters with non-uniform heating of a bottom and vertical walls. As expected, the structures of tiny static fluid region are related to the corners of heated vertical wall for the non-uniform heating status. Moreover, for Ra = 105 and, due to the current non-uniform heating, the impacts of Ha on the isotherms profile are also exhibited in these figures. It is noted that the isotherms subject to estimation variations under Ha boost from 0 to 100 as Ra enhances. At high Ha, the conduction transfer mechanism is more obvious. Also, it is seen that the thermal performance becomes stronger with the enhancement of the Ra while it detracts with the rise in Ha. Due to the Ra increase, the flow cell becomes stronger. For Ra = 106 and higher Hartmann numbers, the isotherms remain constant which is an indication of convection predominance. The comparison of thermal gradient and total entropy generation for several Ra is shown in Fig. 7. The isentropic lines show an enhance behavior with enhancing values of various employing parameters except at Ha.

Fig. 4
figure 4

Isotherm and streamlines for various Ra at Ha = 0 ε = 0.4, φ = 0.04

Full size image
Fig. 5
figure 5

Isotherm and streamlines for different Ha at Ra = 106 ε = 0.4, φ = 0.04

Full size image
Fig. 6
figure 6

Isotherm and streamlines for different Da at Ra = 106 ε = 0.4, φ = 0.04

Full size image
Fig. 7
figure 7

Thermal gradient and total entropy generation for various Ha at Ra = 106, ε = 0.4, φ = 0.04

Full size image

Nusselt number

Figures 8 and 9 display the impact of Ra, Da, Ha and the porosity ratio at the heated horizontal (X) and vertical walls (Y). For the status of great values of Ra, the thermal performance is very high in both walls. Physically, this kind of conduct is due to the greater values of flow rate in the core of the enclosure. Moreover, for Ra = 106 heated walls, the convective regime boosts from the rims across the position with its high value at the position. But for weaker Rayleigh number, (Ra = 103), the main mechanism is conduction; for this reason there is not much difference for low Ra. As Da grows, the medium permeability rises and the convective heat transfer rate boosts.

Fig. 8
figure 8

Nusselt number variation along vertical wall

Full size image
Fig. 9
figure 9

Average Nusselt number variation along horizontal wall

Full size image

So, the transfer rate and the absolute values of the flow boost with the rise in Da. As the magnetic strength rises, the Lorentz aspect generates and these strengths decline the velocity of the hybrid nanofluid. Also, the heat transfer declines with the growth in the Ha. It is also appeared that the effect of the hybrid nanoparticles and porosity on the hydrothermal behavior is similar to that of the Rayleigh number.

Entropy generation

Figure 9 shows the variations of stream function max values, thermal gradient, total entropy generation and average Bejan number for diverse values of Ra and Ha. As we know, Bejan number points out the significance of fluid friction irreversibility and entropy generation due to the transfer heat. It is noticed from Fig. 9 that Beavg boosts with the decline in the values of Ha, but reduces with the boost in Ra. It is also seen that both the total entropy generation and thermal gradients are increased almost linearly with boosted of Ra and declined Ha numbers (Fig. 10).

Fig. 10
figure 10

Variations of a thermal gradient, b total entropy generation, c stream function max, d Beavg for different Ra

Full size image

Conclusions

In this paper, the numerical investigation of non-uniform heating of the bottom wall and one vertical wall on entropy production during heat transfer convection within a cavity in the presence of magnetic fields was done. The impacts of porosity ratio, nanoparticle concentration and Hartmann and Darcy numbers have been examined. The key findings and conclusions from the current work are as follows:

  • the thermal performance increases with the augmentation of Ra, ε, φ and Da and reduces with the enhancement of Ha.

  • For the situation of non-uniform heating, the transfer heat is lower at the rims of the heated sides and it reached its maximum value at the center of both heated sides. Also, the sinusoidal kind of changes in transfer heat is noted for non-uniform heating at Ra = 105

  • The entropy production boosts with growing Rayleigh number, while it declines with Ha

  • The influence of permeability of porous medium on entropy production due to transfer heat and fluid friction irreversibility is shown by the local designs of Sth and SGen. Due to lower permeability of porous medium at smaller Da, the heat transfer irreversibility is revealed to predominate the total entropy production in the enclosure.