1 Introduction

Numerous problems in science and engineering, optimization theory, nonlinear analysis, equilibrium theory and differential equations, lead to the study of variational inequality problem (VIP) in the sense of Stampacchia et al. in [19, 25]. This problem has been intensively investigated and developed after appearing in the mono graphic book [15, 26]. Let E be a real Banach space with norm \(\Vert \cdot \Vert\) and represent the dual of E by \(E^*\) with \(\langle x^*,x\rangle\) signifying the value of \(x^*\in E^*\) at \(x\in E.\) Suppose C is nonempty, closed with \(C\subset E\) and \({\mathcal {A}} : C\rightarrow E^*\) is a nonlinear mapping. The VIP is defined as finding \(u\in C\) such that

$$\begin{aligned} \langle {\mathcal {A}} u, v - u\rangle \ge 0 \ \ \forall v\in C. \end{aligned}$$
(1.1)

We shall denote by \(Sol(C,{\mathcal {A}}),\) the solution set of VIP (1.1).

The projected gradient method [18] is known to solve VIP (1.1) when \({\mathcal {A}}\) is strongly monotone and Lipschitz continuous. This method fails to converge to any solution of VIP (1.1) when \({\mathcal {A}}\) is monotone. The Extragradient Method (EGM) [27] was introduced to solve VIP (1.1) when \({\mathcal {A}}\) is continuous and Lipschitz continuous:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = P_C(x_n - \rho {\mathcal {A}} x_n),\\ x_{n+1} = P_C(x_n - \rho {\mathcal {A}} y_n), \ \ n\ge 0, \end{array}\right. } \end{aligned}$$
(1.2)

where \(P_C\) is the projection onto C. The weak convergence of EGM (1.2) is achieved when \(\rho \in (0,1/L),\) with L being the Lipschitz constant of \({\mathcal {A}}\) (see, [5,6,7,8, 10,11,12, 14, 21, 24, 33, 36, 40,41,42,43]). The major weakness in EGM (1.2) is that it involves two projection onto C per iteration and this requires solving a minimization problem twice per iteration during implementation, which can slow down the iterations. This motivated Tseng [37] to propose the following method;

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = P_C(x_n - \rho {\mathcal {A}}x_n),\\ x_{n+1} = y_n - \rho ({\mathcal {A}}y_n - {\mathcal {A}}x_n), \ \ n\ge 0 \end{array}\right. } \end{aligned}$$
(1.3)

which requires only one computation of \(P_C\) per iteration. The weak convergence of (1.3) was obtained in Hilbert spaces when either the step size \(\rho \in (0,1/L)\) or generated by a line search procedure. The requirement that the step size \(\rho\) in EGM (1.2) and (1.3) dependent on Lipschitz constant of the cost function is inefficient since the Lipschitz constant are difficult to estimate in most of the applications, and when they do, they are often too small and this in turn slows down the convergence of EGM (1.2) and (1.3).

It is very interesting to also study VIP in Banach spaces because several physical models and applications can be formulated as VIPs in real Banach spaces which are not Hilbert.

Recently, Jolaoso et al. [22] presented modified Bregman subgradient algorithms with line search technique for solving VIP with a pseudo-monotone operator without necessarily satisfying the Lipschitz condition. They introduced the following two algorithms:

figure a
figure b

Under suitable conditions of the given parameters, Jolaoso et al. [22] established the weak and strong convergence of Algorithm 1.1 and 1.2 respectively in reflexive Banach spaces. See also the recent paper by Reich et al. [31].

Following this direction, motivated and inspired by the presented results, we introduce a single projection method with self adaptive step size for solving the VIP (1.1) in a reflexive Banach space. The proposed algorithm uses variable step size from step to step which are updated over each iteration by a cheap computation. This step size allows the algorithm to work more easily without knowing previously the Lipschitz constant of operator \({\mathcal {A}}.\) Unlike [22], we do not use any linesearch in our algorithm (a linesearch means that at each outer-iteration we use an inner-loop until some finite stopping criterion is satisfied, and this can be time consuming). We provide an application and some numerical experiment to illustrate the performance and efficiency of our proposed method.

2 Preliminaries

In this section, we give some definitions and preliminary results which will be used in our convergence analysis. Let C be a nonempty, closed and convex subset of a real Banach space E with the norm \(\Vert \cdot \Vert\) and dual space \(E^*.\) We denote the weak and strong convergence of a sequence \(\{x_n\}\subset E\) to a point \(x^*\in E\) by \(x_n\rightharpoonup x^*\) and \(x_n \rightarrow x^*\) respectively.

Let \(f:E\rightarrow (-\infty , +\infty ]\) be a function satisfying the following:

  1. (i)

    \(\text{ int } (\text{dom }f) \subset E\) is a uniformly convex set;

  2. (ii)

    f is continuously differentiable on \(\text{ int }(\text{dom }f);\)

  3. (iii)

    f is strongly convex with strongly convexty constant \(\varrho >0,\) i.e.

    $$\begin{aligned} f(x)\ge f(y) - \langle \nabla f(y), x -y\rangle + \frac{\varrho }{2}\Vert x - y\Vert ^2, \ \ \ \forall x\in \text{dom } \ \ \text{ and } \ \ y\in \text{ int }(\text{dom }f). \end{aligned}$$

The subdifferential set of f at a point x denoted by \(\partial f\) is defined by

$$\begin{aligned} \partial f(x):= \{x^*\in E^*: f(x) - f(y) \le \langle y - x, x^*\rangle , \ \ y \in E\}, \end{aligned}$$

Every element \(x^* \in \partial f(x)\) is called a subgradient of f at x. Since f is continuously differentiable, then \(\partial f(x) = \{\nabla f(x)\},\) which is the gradient of f at x. The Fénchel conjugate of f is the convex functional \(f^*: E^* \rightarrow (-\infty , +\infty ]\) defined by \(f^*(x^*) = \sup \{\langle x^*,x\rangle - f(x): x \in E\}.\) Let E be a reflexive Banach space, the function f is said to be Legendre if and only if f satisfy the following conditions:

  1. (R1)

    \(\text{ int }(\text{dom }f) \ne \emptyset\) and \(\partial f\) is single-valued on its domain;

  2. (R2)

    \(\text{ int }(\text{dom } f) \ne \emptyset\) and \(\partial f^*\) is single-valued on its domain.

It is worth mentioning that the Bregman distance is not a metric in the usual sense because it does not satisfy the symmetric and triangular inequality properties. However, It posses the following interesting property called the three point identity: for \(x\in \text{dom } f\) and \(y,z \in \text{ int }(\text{dom }f),\) we have Let \(f: E \rightarrow {\mathbb {R}}\) be strictly convex and Gâteaux differentiable function. The Bregman distance \(\phi _f : \text{dom }f \times \text{ int }(\text{dom }f) \rightarrow {\mathbb {R}}\) with respect to f is defined by

$$\begin{aligned}&\phi _f(x,y)= f(x) - f(y) - \langle x -y, \nabla f(y)\rangle , \ \ \ \ \forall \ x\in \text{dom }f, \ y\in \text{ int }(\text{dom }f). \nonumber \\&\phi _f(x,y) + \phi _f(y,z) - \phi _f(x,z) \le \langle \nabla f(z) - \nabla f(y), x -y\rangle . \end{aligned}$$
(2.1)

The Bregman function has been widely used by many authors for solving many optimization problems in the literature (see [30] and the references therein).

Remark 2.1

Practical important examples of the Bregman distance function can be found in [3]. If \(f(x) =\frac{1}{2}\Vert x\Vert ,\) we have \(\phi _f(x,y) = \frac{1}{2}\Vert x -y\Vert ^2\) which is the Euclidean norm distance. Also, if \(f(x) = - \sum _{j=1}^{m}x_j\log (x_j)\) which is Shannon’s entropy for non-negative orthant \({\mathbb {R}}_{++}^m:=\{x\in {\mathbb {R}}^m:x_j>0\},\) we obtain the Kullback-Leibler cross entropy defined by

$$\begin{aligned} \phi _f(x,y) = \sum _{j=1}^{m}\left( x_j\log \left( \frac{x_j}{y_j}\right) - 1\right) + \sum _{j=1}^{m}y_i. \end{aligned}$$
(2.2)

Also, if f is \(\varrho\)-strongly convex, then

$$\begin{aligned} \phi _f(x,y) \ge \frac{\varrho }{2}\Vert x -y\Vert ^2, \ \ \forall x\in \text{dom }f, \ y\in \text{ int }(\text{dom }f). \end{aligned}$$
(2.3)

Definition 2.2

The Bregman projection (see e.g. [32]) with respect to f of \(x\in \text{ int }(\text{dom }f)\) onto a nonempty closed convex set \(C \subset \text{ int }(\text{dom }f)\) is the unique vector \(Proj_C^f(x) \in C\) satisfying

$$\begin{aligned} Proj_C^f(x):= \inf \{\phi _f(x,y): x\in C\}. \end{aligned}$$

The Bregman projection is characterized by the inequality

$$\begin{aligned} z = Proj_C^f(x) \Longleftrightarrow \langle \nabla f(x) - \nabla f(z), y -z\rangle \le 0, \ \ \forall y\in C. \end{aligned}$$
(2.4)

Also

$$\begin{aligned} \phi _f(y,Proj_C^f(x)) + \phi _f(Proj_C^f(x),x) \le \phi _f(y,x), \ \ \ \ \forall y\in C, \ x\in \text{ int }(\text{dom }f). \end{aligned}$$
(2.5)

Following [1, 13], we define the function \(V_f: E\times E \rightarrow [0,\infty )\) associated with f by

$$\begin{aligned} V_f(x,y) = f(x) - \langle x,y\rangle + f^*(y), \ \ \forall x,y \in E \end{aligned}$$
(2.6)

\(V_f\) is non-negative and \(V_f(x,y) = \phi _f(x,\nabla f(y))\) for all \(x,y\in E.\) Moreover, by the subdifferential inequality, it is easy to see that

$$\begin{aligned} V_f(x,y) + \langle z, \nabla f^*(y) - x\rangle \le V_f(x, z+y) \end{aligned}$$
(2.7)

for all \(x,y,z\in E.\) In addition, If \(f: E\rightarrow {\mathbb {R}} \cup \{+\infty \}\) is proper lower semicontinous, then \(f^*: E\rightarrow {\mathbb {R}} \cup \{+\infty \}\) is proper weak lower lower semicontinuous and convex. Hence, \(V_f\) is convex in second variable, i.e.,

$$\begin{aligned} \phi _f\left( z,\nabla f^*\left( \sum _{i=1}^{N}t_i\nabla f(x_i)\right) \right) \le \sum _{i=1}^{N}t_i\phi _f(z,x_i), \end{aligned}$$
(2.8)

where \(\{x_i\} \subset E\) and \(\{t_i\} \subset (0,1)\) with \(\sum _{i=1}^{N}t_i = 1.\)

Definition 2.3

Let \(f : E \rightarrow {\mathbb {R}} \cup \{+\infty \}\) be a G\({\hat{a}}\)teaux differentiable function. The function \(\phi _f : \text{dom }f \times \text{ int }(\text{dom }f) \rightarrow [0, +\infty )\) defined by

$$\begin{aligned} \phi _f(y,x) := f(y) - f(x) - \langle \nabla f(x) , y - x\rangle \end{aligned}$$
(2.9)

is the Bregman distance with respect to f. The Bregman distance does not satisfy the well-known properties of a metric, but it has the following important properties (see [28]): For any \(w,x,y,z \in E,\)

  1. (i)

    three point identity:

    $$\begin{aligned} \phi _f(y,z) + \phi _f(z,x) - \phi _f(y,x) = \langle \nabla f(z) - \nabla f(x), z - y\rangle ; \end{aligned}$$
    (2.10)
  2. (ii)

    four point identity: for

    $$\begin{aligned} \phi _f(z,w) + \phi _f(y,x) - \phi _f(z,x) - \phi _f(y,w) = \langle \nabla f(x) - \nabla f(w), z -y\rangle . \end{aligned}$$
    (2.11)

Definition 2.4

[28, 29] The Minty Variational Inequality Problem (MVIP) is defined as finding a point \({\bar{x}} \in C\) such that

$$\begin{aligned} \langle {\mathcal {A}} y, y -{\bar{x}}\rangle \ge 0, \ \ \forall y \in C. \end{aligned}$$
(2.12)

We denote by \(M(C,{\mathcal {A}}),\) the set of solution of (2). Some existence results for the MVIP has been presented in [28]. Also, the assumption that \(M(C,{\mathcal {A}}) \ne \emptyset\) has already been used for solving \(VI(C,{\mathcal {A}})\) in finite dimensional spaces (see e.g [36]). It is not difficult to prove that pseudomonotonicity implies property \(M(C,{\mathcal {A}}) \ne \emptyset ,\) but the converse is not true. Indeed, let \({\mathcal {A}}: {\mathbb {R}} \rightarrow {\mathbb {R}}\) be defined by \({\mathcal {A}}(x) = \cos x\) with \(C=[0,\frac{\pi }{2}].\) We have that \(VI(C,{\mathcal {A}}) = \{0,\frac{\pi }{2}\}\) and \(M(C,{\mathcal {A}}) = \{0\}.\) But if we take \(x=0\) and \(y=\frac{\pi }{2}\) in the definition of pseudomonotone (Assumption 3.1, (A1)), we see that \({\mathcal {A}}\) is not pseudomonotone.

Lemma 2.5

[29] Consider the VIP (1.1). If the mapping \(h:[0,1] \rightarrow E^*\) defined as \(h(t) = {\mathcal {A}}(tx + (1-t)y)\) is continuous for all \(x,y\in C\) (i.e. h is hemicontinuous), then \(M(C,{\mathcal {A}}) \subset VI(C,{\mathcal {A}}).\) Moreover, if \({\mathcal {A}}\) is pseudomonotone then \(VI(C,{\mathcal {A}})\) is closed, convex and \(VI(C,{\mathcal {A}}) = M(C,{\mathcal {A}}).\)

Lemma 2.6

[39] Let \(\{a_n\}\) be a sequence of nonnegative real numbers satisfying the following relation:

$$\begin{aligned} a_{n+1} \le (1-\alpha _n)a_n + \alpha _n\sigma _n + \gamma _n, \ \ n\ge 1. \end{aligned}$$

where (i) \(\{\alpha _n\} \subset [0,1],\) \(\sum \alpha _n = \infty ;\) (ii) \(\limsup \sigma _n \le 0;\) (iii) \(\gamma _n \ge 0;\) \((n\ge 1)\) \(\sum \gamma _n < \infty .\)

Then \(a_n \rightarrow 0,\) as \(n\rightarrow \infty .\)

3 Main result

In this section, we give concise statement of our algorithm, discuss some of its elementary properties and its convergence analysis. In the sequel, we assume that the following hold.

Assumption 3.1

Let C be a nonempty closed convex subset of a real reflexive Banach space E. The operator \({\mathcal {A}} : C \rightarrow E^*\) satisfies the following:

  1. (A1)

    \({\mathcal {A}}\) is pseudomonotone on C,  i.e, for all \(x,y \in E,\) \(\langle {\mathcal {A}}x, y-z \rangle \ge 0\) implies \(\langle {\mathcal {A}}y, y - x\rangle \ge 0;\)

  2. (A2)

    \({\mathcal {A}}\) is L-Lipschitz continuous, i.e. there exists \(L>0\) such that \(\Vert {\mathcal {A}}x - {\mathcal {A}}y\Vert \le L\Vert x -y\Vert ,\) for all \(x,y\in C.\) However, the information of L need not to be known;

  3. (A3)

    \({\mathcal {A}}\) is weakly sequentially continuous, i.e. for any \(\{x_n\} \subset E,\) we have \(x_n \rightharpoonup x\) implies \({\mathcal {A}}x_n \rightharpoonup {\mathcal {A}}x;\)

  4. (A4)

    \(Sol(C,{\mathcal {A}}) \ne \emptyset ;\)

  5. (A5)

    In addition, the function \(f: E \rightarrow [-\infty ,+\infty ]\) is proper, uniformly Fréchet differentiable on bounded subsets of E,  strongly convex with constant \(\varrho >0,\) strongly coercive and Legendre.

We now present our algorithm as follows.

figure c

Remark 3.3

   

  1. (1)

    The stepsize \(\rho _n\) in Algorithm 3.2 varies from step to step. This stepsize is updated at each iteration by a cheap computation. This stepsize rule allows Algorithm 3.2 to be implemented more easily where firstly the Lipschitz constant of \({\mathcal {A}}\) must not be the input parameter of the algorithm, i.e., this constant is not necessary to be known, and secondly the stepsize is found without any line-search which can be time-consuming.

  2. (2)

    The VIP is studied in a reflexive real Banach space which is more general than 2-uniformly convex real Banach space and real Hilbert space. This extends all the results in [9, 17, 33,34,35, 38] to mention but a few.

Lemma 3.4

Assume that \({\mathcal {A}}\) is Lipschitz continuous on E. Then the sequence generated by (3.3) is nonincreasing and

$$\begin{aligned} \lim _{n\rightarrow \infty } \rho _n = \rho \ge \min \left\{ \rho _0, \frac{\delta }{L}\right\} . \end{aligned}$$

Proof

It is easy to prove this Lemma, hence we omit it. \(\square\)

If at some iteration we have \(x_n = y_n\) or \({\mathcal {A}}y_n = 0\) then Algorithm 3.2 terminates and \(y_n \in Sol(C,{\mathcal {A}}).\) From now on, we assume that \(x_n\ne y_n\) and \({\mathcal {A}}y_n \ne 0\) for all n so that the algorithm does not terminate finitely.

Lemma 3.5

Let \(\{x_n\},\) \(\{y_n\}\) and \(\{z_n\}\) be defined Algorithm 3.2, then for every \(x^*\in Sol(C,{\mathcal {A}})\) the following inequalities holds for all \(n\ge 1.\)

$$\begin{aligned} \phi _f(x^*,z_n) \le \phi _f(x^*,x_n) - \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(z_n,y_n) - \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(y_n,x_n). \end{aligned}$$

Proof

Let \(x^*\in Sol(C,{\mathcal {A}}),\) then

$$\begin{aligned}&\phi _f(x^*, z_n) \nonumber \\&\quad = \phi _f(x^*, \nabla f^*(\nabla f(y_n) - \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n))\nonumber \\&\quad = f(x^*) - \langle x^* - z_n, \nabla f(y_n) - \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle - f(z_n)\nonumber \\&\quad = f(x^*) + \langle z_n - x^*, \nabla f(y_n)\rangle + \langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle - f(z_n)\nonumber \\&\quad = f(x^*) - \langle x^* - y_n, \nabla f(y_n)\rangle - f(y_n) + \langle x^* - y_n, \nabla f(y_n)\rangle + f(y_n) \nonumber \\&\qquad + \langle z_n - x^*, \nabla f(y_n)\rangle \nonumber \\&\qquad + \;\; \langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle - f(z_n)\nonumber \\&\quad = \phi _f(x^*,y_n) + \langle z_n - y_n, \nabla f(y_n)\rangle + f(y_n) - f(z_n) + \langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle \nonumber \\&\quad = \phi _f(x^*,y_n) - \phi _f(z_n,y_n) + \langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle \end{aligned}$$
(3.5)

Note that from (2.11), we get

$$\begin{aligned} \phi _f(x^*,y_n) - \phi _f(z_n,y_n)= & {}\, \phi _f(x^*,x_n) - \phi _f(z_n,x_n) + \langle \nabla f(x_n) - \nabla f(y_n), x^* - z_n \rangle . \end{aligned}$$
(3.6)

Hence from (3.5) and (3.6), we have

$$\begin{aligned} \phi _f(x^*,z_n)= & {}\, \phi _f(x^*,x_n) - \phi _f(z_n,x_n) + \langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle \nonumber \\&+ \langle \nabla f(x_n) - \nabla f(y_n), x^* - z_n\rangle . \end{aligned}$$
(3.7)

Also from (2.10), we have

$$\begin{aligned} \phi _f(z_n,x_n)= &\, {} \phi _f(z_n,y_n) + \phi _f(y_n,x_n) - \langle \nabla f(x_n) - \nabla f(y_n), z_n - y_n\rangle . \end{aligned}$$
(3.8)

Substituting (3.8) into (3.7), we obtain

$$\begin{aligned} \phi _f(x^*, z_n)= & {}\, \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n) + \langle \nabla f(x_n) - \nabla f(y_n), z_n - y_n\rangle \nonumber \\&+ \;\;\langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle + \langle \nabla f(x_n) - \nabla f(y_n),x^* - z_n\rangle \nonumber \\= & {}\, \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n) + \langle \nabla f(x_n) - \nabla f(y_n), x^* - y_n\rangle \nonumber \\&+ \;\; \langle x^* - z_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle \nonumber \\= & {}\, \phi _f(z^*, x_n) - \phi _f(z_n, y_n) - \phi _f(y_n,x_n) + \langle \nabla f(x_n) - \nabla f(y_n), x^* - y_n\rangle \nonumber \\&+ \;\; \langle z_n - y_n + y_n - z, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\nonumber \\= & {}\, \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n) + \langle \nabla f(x_n) - \nabla f(y_n), x^* - y_n\rangle \nonumber \\&+ \;\; -\langle z_n - y_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle - \langle y_n - x^*, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle \nonumber \\= & {}\, \phi _f(x^*,x_n) - \phi _f(z_n, y_n) - \phi _f(y_n,x_n) - \langle z_n - y_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle \nonumber \\&-\;\; \langle y_n - x^*,\rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n) - (\nabla f(y_n) - \nabla f(x_n))\rangle . \end{aligned}$$
(3.9)

Since \(y_n = Proj_C^f(\nabla f^*(\nabla f(x_n) - \rho _n{\mathcal {A}}x_n)),\) it follows from (2.4) that

$$\begin{aligned} \langle \nabla f(x_n) - \rho _n{\mathcal {A}}x_n - \nabla f(y_n), x^* - y_n\rangle \le 0. \end{aligned}$$
(3.10)

Also, since \(x^*\in Sol(C,{\mathcal {A}})\) then \(\langle {\mathcal {A}}x^*, y_n - x^*\rangle \ge 0.\) From the pseudomonotononicity of \({\mathcal {A}},\) we obtain

$$\begin{aligned} \langle {\mathcal {A}} y_n, y_n - x^*\rangle \ge 0. \end{aligned}$$
(3.11)

Combining (3.10) and (3.11), we get

$$\begin{aligned} \langle \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n) - (\nabla f(y_n) - \nabla f(x_n)), y_n - x^*\rangle \ge 0. \end{aligned}$$
(3.12)

Hence from (3.9), we obtain

$$\begin{aligned} \phi _f (x^*,z_n) \le \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \langle z_n - y_n, \rho _n({\mathcal {A}}y_n - {\mathcal {A}}x_n)\rangle . \end{aligned}$$
(3.13)

Now using (3.3) and Cauchy-Schwatz inequality, we have

$$\begin{aligned} \phi _f(x^*,z_n)\le & {} \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n) + \langle y_n - z_n, \rho _n({\mathcal {A}} y_n - {\mathcal {A}}x_n)\rangle \\\le & {} \phi _f(x^*, x_n) - \phi _f(z_n, y_n) - \phi _f(y_n,x_n) + \frac{\rho _n}{\rho _{n+1}}\rho _{n+1}\Vert y_n - z_n\Vert \Vert {\mathcal {A}}y_n - {\mathcal {A}}x_n\Vert \\\le & {} \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n) + \frac{\rho _n}{\rho _{n+1}}\delta \Vert y_n - z_n\Vert \Vert y_n - x_n\Vert \\\le & {} \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n)\\&+\;\; \frac{\rho _n}{\rho _{n+1}}\times \frac{\delta }{2}(\Vert z_n - y_n\Vert ^2 + \Vert y_n - x_n\Vert ^2). \end{aligned}$$

Then from (2.3), we obtain

$$\begin{aligned} \phi _f(x^*, z_n)\le & {}\, \phi _f(x^*,x_n) - \phi _f(z_n,y_n) - \phi _f(y_n,x_n)\nonumber \\&+ \;\; \frac{\rho _n}{\rho _{n+1}} \times \frac{\delta }{\varrho }(\phi _f(z_n,y_n) + \phi _f(y_n,x_n))\nonumber \\= & {}\, \phi _f(x^*,x_n) - \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(z_n,y_n) - \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(y_n,x_n). \end{aligned}$$
(3.14)

\(\square\)

Lemma 3.6

The sequence \(\{x_n\}\) generated by Algorithm 3.2, is bounded.

Proof

Note that since \(\delta \in (0,\varrho )\) and \(\varrho >0,\) we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) = 1 -\frac{\delta }{\varrho } >0. \end{aligned}$$

Then, there exists \(N>0\) such that

$$\begin{aligned} 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho } >0 \ \ \forall n\ge N. \end{aligned}$$

Thus, it from (3.14) that

$$\begin{aligned} \phi _f(x^*, z_n) \le \phi _f(x^*,x_n). \end{aligned}$$
(3.15)

Furthermore, from (3.4) and (3.15), we have

$$\begin{aligned} \phi _f(x^*,x_{n+1})= & {}\, \phi _f\left( x^*, \nabla f^*(\delta _n\nabla f(x_n) + (1-\delta _n)(\alpha _n\nabla f(u) + (1-\alpha _n)\nabla f(z_n))\right) \nonumber \\\le & {} \delta _n\phi _f(x^*,x_n) + (1-\delta _n)\phi _f(x^*, \alpha _n\nabla f(u) + (1-\alpha _n)\nabla fz_n)\nonumber \\\le & {} \delta _n\phi _f(x^*,x_n) + (1-\delta _n)[\alpha _n\phi _f(x^*,u) + (1-\alpha _n)\phi _f(x^*,z_n)]\nonumber \\\le & {} \delta _n\phi _f(x^*,x_n) + (1-\delta _n)[\alpha _n\phi _f(x^*,u) + (1-\alpha _n)\phi _f(x^*,x_n)]\nonumber \\= & {}\, \alpha _n(1-\delta _n)\phi _f(x^*,u) + (1-\alpha _n(1-\delta _n))\phi _f(x^*,x_n)\nonumber \\\le & {} \max \{\phi _f(x^*,u), \phi _f(x^*,x_n)\}\nonumber \\&\vdots&\nonumber \\\le & {} \max \{\phi _f(x^*,u), \phi _f(x^*,x_n)\}. \end{aligned}$$
(3.16)

This implies that \(\{\phi _f(x^*,x_n)\}\) is bounded. Hence, \(\{x_n\}\) is bounded. Consequently, we see that \(\{\nabla f(x_n)\},\) \(\{y_n\}\) and \(\{z_n\}\) are bounded. \(\square\)

Lemma 3.7

The sequence \(\{x_n\}\) generated by Algorithm 3.2 satisfies the following estimates:

  1. (i)

    \({\mathcal {S}}_{n+1} \le (1-\alpha _n(1-\delta _n)){\mathcal {S}}_n + \alpha _n(1-\delta _n) d_n,\)

  2. (ii)

    \(-1 \le \limsup _{n\rightarrow \infty }d_n < +\infty ,\)

where \({\mathcal {S}}_n = \phi _f(x^*,x_n)\) and \(d_n = \langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle\) for any \(x^*\in Sol(C,{\mathcal {A}}).\)

Proof

Now, let \(v_n = \nabla f^*\left[ \alpha _n(1-\delta _n)\nabla f(u) + (1-\alpha _n(1-\delta _n))\nabla f(u_n)\right] ,\) \(n\ge 1\) where

$$\begin{aligned}&u_n \nonumber \\&\quad = \nabla f^*\left[ \frac{\delta _n}{1-\alpha _n(1-\delta _n)}\nabla f(x_n) + \frac{(1-\alpha _n)(1-\delta _n)}{1-\alpha _n(1-\delta _n)}\nabla f(z_n)\right] , \ n\ge 1 \nonumber \\&\phi _f(x^*,x_{n+1}) \nonumber \\&\quad \le \phi _f(x^*, \nabla f^*(\alpha _n(1-\delta _n)\nabla f(u) + \delta _n\nabla f(x_n) + (1-\alpha _n)(1-\alpha _n)J_{E_1}^p(z_n))\nonumber \\&\quad =\phi _f(x^*, \nabla f^*(\alpha _n(1-\delta _n)\nabla f(u) + (1-\alpha _n)(1-\delta _n))\nabla f(u_n))\nonumber \\&\quad \le V_f(x^*,\alpha _n(1-\delta _n)\nabla f(u) + (1-\alpha _n(1-\delta _n))\nabla f(u_n))\nonumber \\&\quad \le V_f(x^*, \alpha _n(1-\delta _n)\nabla f(u)) + (1-\alpha _n(1-\delta _n))\nabla f(u_n) \nonumber \\&\qquad - \alpha _n(1-\delta _n)(\nabla f(u) - \nabla f(x^*))\nonumber \\&\qquad - \langle \nabla f^*(\alpha _n(1-\beta _n)\nabla f(u)) + (1-\alpha _n(1-\delta _n))\nabla f(u_n)) - x^*, \nonumber \\&\qquad -\alpha _n(1-\delta _n)(\nabla f(u) - \nabla f(x^*))\rangle \nonumber \\&\quad = \phi _f\left[ x^*, \nabla f^*(\alpha _n(1-\delta _n)\nabla f(x^*) + (1-\alpha _n(1-\delta _n))\nabla f(u_n))\right] \nonumber \\&\qquad + \alpha _n(1-\delta _n)\langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle \nonumber \\&\quad \le \alpha _n(1-\delta _n)\phi _f(x^*,x^*) + (1-\alpha _n(1-\delta _n))\phi _f(x^*,u_n)\nonumber \\&\qquad + \alpha _n(1-\delta _n)\langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle \nonumber \\&\quad =(1-\alpha _n(1-\delta _n))\phi _f(x^*,u_n)\nonumber \\&\qquad + \alpha _n(1-\beta _n)\langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle \nonumber \\&\quad \le (1-\alpha _n(1-\delta _n))\phi _f(x^*,x_n) + \alpha _n(1-\delta _n)\langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle . \end{aligned}$$
(3.17)

This established (i).

Next we show (ii). Since \(\{v_n\}\) is bounded, then we have

$$\begin{aligned} \sup _{n \ge 0} d_n\le \sup \Big (||v_n - x^*||||\nabla f(u) - \nabla f(x^*)||\Big ) < \infty . \end{aligned}$$

This implies that \(\limsup _{n \rightarrow \infty }d_n < \infty\). Next, we show that \(\limsup _{n \rightarrow \infty }d_n \ge -1.\) Assume the contrary, i.e. \(\limsup _{n \rightarrow \infty }d_n < -1\). Then there exists \(n_0 \in {\mathbb {N}}\) such that \(d_n < -1\), for all \(n \ge n_0\). Then for all \(n \ge n_0\), we get from (i) that

$$\begin{aligned} {\mathcal {S}}_{n+1}\le & {} (1-\alpha _n(1-\delta _n)){\mathcal {S}}_n + \alpha _n(1-\delta _n) d_n\\< & {} (1-\alpha _n(1-\delta _n)){\mathcal {S}}_n - \alpha _n(1-\delta _n)\\= & {}\, {\mathcal {S}}_n - \alpha _n(1-\delta _n)({\mathcal {S}}_n +1) \le {\mathcal {S}}_n - \alpha _n(1-\delta _n). \end{aligned}$$

Taking \(\limsup\) of the last inequality, we have

$$\begin{aligned} \limsup _{n \rightarrow \infty }{\mathcal {S}}_{n} \le {\mathcal {S}}_{n_0} - \lim _{n\rightarrow \infty }\sum _{i = n_0}^n \alpha _i = - \infty . \end{aligned}$$

This contradicts the fact that \(\{{\mathcal {S}}_n\}\) is a non-negative real sequence. Therefore \(\limsup _{n \rightarrow \infty }d_n \ge -1\). \(\square\)

We now present our main convergence result.

Theorem 3.8

Assume Conditions \((A1) - (A5)\) and suppose \(\{\alpha _n\},\) and \(\{\delta _n\}\) are sequences in (0, 1) and satisfy the following conditions:

  1. (i)

    \(\lim _{n\rightarrow \infty }\alpha _n = 0,\) and \(\sum _{n=1}^{\infty }\alpha _n = \infty ;\)

  2. (ii)

    \(0<\liminf _{n\rightarrow \infty } \delta _n \le \limsup _{n\rightarrow \infty } \delta _n <1.\)

Then the sequence \(\{x_n\}\) generated by Algorithm 3.2 converges strongly to an element in \(Sol(C,{\mathcal {A}}).\)

Proof

Let \(x^* \in Sol(C,{\mathcal {A}})\) and \({\mathcal {S}}_n = \phi _f(x^*,x_n).\) we divide the proof into two cases.

Case 1: Suppose that there exists \(n_0 \in {\mathbb {N}}\) such that \(\{{\mathcal {S}}_n\}_{n=n_0}^\infty\) is non-increasing. Then \(\{{\mathcal {S}}_n\}_{n=1}^\infty\) converges and

$$\begin{aligned} \lim _{n\rightarrow \infty } ({\mathcal {S}}_n - {\mathcal {S}}_{n+1}) = 0. \end{aligned}$$
(3.18)

Thus, from Lemma 3.5 we have.

$$\begin{aligned} \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(z_n,y_n) + \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(y_n,x_n)\le & {} \phi _f(x^*,x_n) - \phi _f(x^*,z_n). \end{aligned}$$
(3.19)

Also, from (3.16), we get

$$\begin{aligned}&\phi _f(x^*,x_n) - \phi _f(x^*,z_n) \nonumber \\&\quad \le \frac{\alpha _n(1-\delta _n)}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,u) + \frac{(1-\alpha _n(1-\delta _n))}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,x_n)\nonumber \\&\qquad - \;\; \frac{1}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,x_{n+1})\nonumber \\&\quad = \frac{\alpha _n(1-\delta _n)}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,u) - \frac{\alpha _n(1-\delta _n)}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,x_n)\nonumber \\&\qquad + \;\; \frac{1}{(1-\alpha _n)(1-\delta _n)}[\phi _f(x^*,x_n) - \phi _f(x^*,x_{n+1})]\nonumber \\&\quad \le \frac{\alpha _n(1-\delta _n)}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,u) + \frac{1}{(1-\alpha _n)(1-\delta _n)}[\phi _f(x^*,x_n) - \phi _f(x^*,x_{n+1})] \end{aligned}$$
(3.20)

From (3.19) and (3.20), we get

$$\begin{aligned}&\left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(z_n,y_n) + \left( 1- \frac{\rho _n\delta }{\rho _{n+1}\varrho }\right) \phi _f(y_n,x_n) \nonumber \\&\quad \le \phi _f(x^*,x_n) - \phi _f(x^*,z_n)\nonumber \\&\quad \le \frac{\alpha _n(1-\delta _n)}{(1-\alpha _n)(1-\delta _n)}\phi _f(x^*,u)\nonumber \\&\qquad + \;\; \frac{1}{(1-\alpha _n)(1-\delta _n)}[\phi _f(x^*,x_n) - \phi _f(x^*,x_{n+1})] \end{aligned}$$
(3.21)

Passing limit as \(n\rightarrow \infty\) in (3.21), since \(\underset{n\rightarrow \infty }{\lim }\phi _f(x^*,x_n)\) exists and \(\frac{\rho _n}{\rho _{n+1}} \rightarrow 1,\) we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \left( 1- \frac{\delta }{\varrho }\right) \phi _f(z_n,y_n) = 0. \end{aligned}$$

Also, since \(\delta \in (0,\varrho ),\) then

$$\begin{aligned} \lim _{n\rightarrow \infty } \phi _f(y_n,z_n) = 0. \end{aligned}$$

Thus

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert y_n - z_n\Vert = 0. \end{aligned}$$
(3.22)

Similarly from, (3.21), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } \left( 1- \frac{\delta }{\varrho }\right) \phi _f(y_n,x_n) = 0. \end{aligned}$$

Then

$$\begin{aligned} \lim _{n\rightarrow \infty }\phi _f(y_n,x_n) =0 \ \ \ \Rightarrow \ \ \lim _{n\rightarrow \infty }\Vert y_n - x_n\Vert = 0. \end{aligned}$$
(3.23)

Combining (3.22) and (3.23), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert z_n - x_n\Vert =0. \end{aligned}$$
(3.24)

Since \(\{x_n\}\) is bounded, there exists a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\) such that \(x_{n_k} \rightharpoonup z.\) We now show that \(z\in Sol(C,{\mathcal {A}}).\)

Since \(y_{n_k} = Proj_C^f(\nabla f^*(\nabla f(x_{n_k}) - \rho _{n_k}{\mathcal {A}}x_{n_k})),\) from (2.4), we have

$$\begin{aligned} \langle \nabla f(x_{n_k}) - \rho _{n_k}{\mathcal {A}}x_{n_k} - \nabla f(y_{n_k}), x -y_{n_k}\rangle \le 0 \ \ \forall x\in C. \end{aligned}$$

Hence

$$\begin{aligned} \langle \nabla f(x_{n_k}) - \nabla f(y_{n_k}), x - y_{n_k}\rangle\le & {} \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, x - y_{n_k} \rangle \\= &\, {} \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, x_{n_k} - y_{n_k}\rangle + \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, x - x_{n_k}\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \langle \nabla f(x_{n_k}) - \nabla f(y_{n_k}), x - y_{n_k}\rangle + \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, y_{n_k} - x_{n_k}\rangle \le \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, x - x_{n_k}\rangle . \end{aligned}$$
(3.25)

Since \(\Vert x_{n_k} - y_{n_k}\Vert \rightarrow 0\) and f is strongly coercive, then

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert \nabla f(x_{n_k}) - \nabla f(y_{n_k})\Vert = 0. \end{aligned}$$
(3.26)

Next, fix \(x\in C,\) it follows from (3.25) and (3.26) and the fact that \(\liminf _{k\rightarrow \infty }\rho _{n_k} >0,\) then

$$\begin{aligned} 0\le \liminf _{k\rightarrow \infty } \langle {\mathcal {A}} x_{n_k}, x - x_{n_k}\rangle \ \ \forall \ x\in C. \end{aligned}$$
(3.27)

Let \(\{\epsilon _k\}\) be a sequence of decreasing non-negative numbers such that \(\epsilon _k \rightarrow 0\) as \(k\rightarrow \infty .\) For each \(\epsilon _k,\) we denote by \(N_k\) the smallest positive integer such that

$$\begin{aligned} \langle {\mathcal {A}}x_{n_k}, x - x_{n_k}\rangle + \epsilon _k \ge 0 \ \ \forall \ k\ge N_k, \end{aligned}$$

where the existence of \(N_k\) follows from (3.27). Since \(\{\epsilon _k\}\) is decreasing, then \(\{N_k\}\) is increasing. Also, for some \(t_{N_k} \in C\) assume \(\langle {\mathcal {A}}x_{N_k},t_{N_k}\rangle = 1,\) for each k. Therefore,

$$\begin{aligned} \langle {\mathcal {A}}x_{N_k}, x + \epsilon _kt_{N_k} - x_{N_k}\rangle \ge 0. \end{aligned}$$

Since \({\mathcal {A}}\) is pseudomonotone, then we have from (3.27) that

$$\begin{aligned} \langle A(x + \epsilon _kt_{N_k}), x + \epsilon _kt_{N_k} - x_{N_k}\rangle \ge 0. \end{aligned}$$
(3.28)

Since \(\{x_{n_k}\}\) converges weakly to z as \(k\rightarrow \infty\) and \({\mathcal {A}}\) is weakly sequentially continuous, we have that \(\{{\mathcal {A}}\}\) converges weakly to \({\mathcal {A}}z.\) Suppose \({\mathcal {A}}z \ne 0\) (otherwise, \(z\in Sol(C,{\mathcal {A}}\)). Then by the sequentially weakly lower semicontinuous of the norm, we get

$$\begin{aligned} 0 < \Vert {\mathcal {A}}z\Vert = \liminf _{k\rightarrow \infty }\\{\mathcal {A}}x_{n_k}\Vert . \end{aligned}$$

Since \(\{x_{N_k}\} \subset \{x_{n_k}\}\) and \(\epsilon _k \rightarrow 0,\) we get

$$\begin{aligned} 0\le & {} \limsup _{k\rightarrow \infty }\Vert \epsilon _kt_{N_k}\Vert = \limsup _{k\rightarrow \infty }\left( \frac{\epsilon _k}{\Vert {\mathcal {A}}x_{n_k}}\Vert \right) \\\le & {} \frac{\limsup _{k\rightarrow \infty }\epsilon _k}{\liminf _{k\rightarrow \infty }\Vert {\mathcal {A}}x_{n_k}} \le \frac{0}{\Vert {\mathcal {A}}z\Vert }= 0, \end{aligned}$$

and this means \(\lim _{k\rightarrow \infty }\Vert \epsilon _kt_{N_k}\Vert = 0.\) Passing the limit \(k\rightarrow \infty\) in (3.28), we get

$$\begin{aligned} \langle {\mathcal {A}}x, x - z\rangle \ge 0. \end{aligned}$$

Therefore, from Lemma 2.5, we have \(z\in Sol(C,{\mathcal {A}}).\) Furthermore, from the definition of \(u_n\) and \(v_n,\) we get

$$\begin{aligned} \phi _f(u_n,x_n)= & {} \frac{\delta _n}{1-\alpha _n(1-\delta _n)}\phi _f(x_n,x_n) + \frac{(1-\alpha _n)(1-\delta _n)}{1-\alpha _n(1-\delta _n)}\phi _f(z_n,x_n)\\= & {} \frac{(1-\alpha _n)(1-\delta _n)}{1-\alpha _n(1-\delta _n)}\phi _f(z_n,x_n) \rightarrow 0, \ \ \text{ as } \ \ n\rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \phi _f(v_n,u_n)= &\, {} \alpha _n(1-\delta _n)\phi _f(u,u_n) + (1-\alpha _n(1-\delta _n))\phi _f(u_n,u_n)\\= &\, {} \alpha _n(1-\delta _n)\phi _f(u,u_n) \rightarrow 0, \ \ \text{ as } \ \ n\rightarrow \infty . \end{aligned}$$

Thus,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert u_n - x_n\Vert = 0 = \lim _{n\rightarrow \infty }\Vert v_n - u_n\Vert . \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_n - x_n\Vert =0. \end{aligned}$$

Since \(x_{n_k}\rightharpoonup z\) and \(\lim _{n\rightarrow \infty }\Vert v_n - x_n\Vert =0\) we have that \(v_{n_k} \rightharpoonup z.\) Hence from (2.4), we obtain that

$$\begin{aligned} \limsup _{n \rightarrow \infty } \langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle= & {} \lim _{k\rightarrow \infty }\langle v_{n_k} - x^*, \nabla f(u) - \nabla f(x^*)\rangle \\= & {}\, \langle z - x^*, \nabla f(u) - \nabla f(x^*)\rangle \le 0. \end{aligned}$$

Hence

$$\begin{aligned} \limsup _{n \rightarrow \infty } d_n = \limsup _{n \rightarrow \infty } \langle v_n - x^*, \nabla f(u) - \nabla f(x^*)\rangle \le 0. \end{aligned}$$
(3.29)

Using Lemma 2.6 and Lemma 3.7(i), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {S}}_n = \lim _{n\rightarrow \infty }\phi _f(x^*,x_n) = 0. \end{aligned}$$

This implies that \(\Vert x_n - x^*\Vert \rightarrow 0\) as \(n\rightarrow \infty .\) Therefore \(\{x_n\}\) converges strongly to \(x^*.\)

Case 2. Assume that \(\{{\mathcal {S}}_n\}_{n=1}^\infty\) is not a monotonically decreasing sequences. Set \(\Gamma _n := {\mathcal {S}}_n, \ \forall n\ge 1\) and let \(\tau : {\mathbb {N}} \rightarrow {\mathbb {N}}\) be a mapping for all \(n\ge n_0\) (for some \(n_0\) large enough) by

$$\begin{aligned} \tau (n) := \max \{k\in {\mathbb {N}}: k \le n, \ \Gamma _k \le \Gamma _{k+1}\}. \end{aligned}$$

Clearly, \(\tau\) is a nondecreasing sequence such that \(\tau (n) \rightarrow \infty\) as \(n\rightarrow \infty\) and

$$\begin{aligned} 0 \le \Gamma _{\tau (n)} \le \Gamma _{\tau (n)+1}, \ \ \forall n\ge n_0 \end{aligned}$$

Following a similar argument as in Case 1 we immediately conclude that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_{\tau (n)} - x_{\tau (n)}\Vert =0 \ \ \text{ and } \ \ \ \lim _{n\rightarrow \infty }\Vert x_{\tau (n)} - y_{\tau (n)}\Vert = 0. \end{aligned}$$

Also from (3.29), we get that

$$\begin{aligned} \limsup _{n \rightarrow \infty }d_{\tau (n)} = \limsup _{n\rightarrow \infty }\langle v_{\tau (n)} - x^*, \nabla f(u) - \nabla f(x^*)\rangle \le 0. \end{aligned}$$

From (3.17) we have that

$$\begin{aligned} {\mathcal {S}}_{\tau (n)} \le d_{\tau (n)} \end{aligned}$$

which implies

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {S}}_{\tau (n)}=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {S}}_{\tau (n)+1} =0. \end{aligned}$$

Therefore, for \(n\ge n_0,\) it is easy to see that \(\Gamma _{\tau (n)} \le \Gamma _{\tau (n)+1}\) if \(n \ne \tau (n)\) (that is, \(\tau (n) < n\)), because \(\Gamma _j \ge \Gamma _{j+1}\) for \(\tau (n)+1 \le j \le n.\) As a consequence, we obtain for all \(n\ge n_0\)

$$\begin{aligned} 0 \le \Gamma _{n} \le \max \{\Gamma _{\tau (n)},\Gamma _{\tau (n)+1}\} = \Gamma _{\tau (n)+1}. \end{aligned}$$

Hence, \(\lim _{n\rightarrow \infty } \Gamma _{n} = 0.\) This implies that \(\lim _{n\rightarrow \infty } \phi _f(x^*, x_n) = 0,\) thus \(\Vert x_n - x^*\Vert \rightarrow 0\) as \(n \rightarrow \infty .\) Therefore, \(\{x_n\}\) converges strongly to \(x^*.\) This completes the proof. \(\square\)

Remark 3.9

If the operator is monotone and Lipschitz continuous, then we do not need it to be sequentially weakly continuous. This is because the sequential weakly continuity assumption was only used after (3.25). From the definition of \(y_n,\) we have

$$\begin{aligned} \langle \nabla f(x_{n_k}) - \rho _{n_k}{\mathcal {A}}x_{n_k} - \nabla f(y_{n_k}, x -y_{n_k})\rangle \le 0, \ \ \forall x \in C. \end{aligned}$$

Thus from the monotonicity of \({\mathcal {A}}\),

$$\begin{aligned} 0\le & {} \langle \nabla f(y_{n_k}) - \nabla f(x_{n_k}), x - y_{n_k}\rangle + \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, x - y_{n_k}\rangle \\= &\, {} \langle \nabla f(y_{n_k}) - \nabla f(x_{n_k}), x -y_{n_k}\rangle + \rho _{n_k}\langle {\mathcal {A}}x_{n_k}, z -x_{n_k}\rangle + \rho _{n_k}\langle {\mathcal {A}} x_{n_k}, x_{n_k} - y_{n_k}\rangle \\\le & {} \langle \nabla f(y_{n_k}) - \nabla f(x_{n_k}), x -y_{n_k}\rangle + \rho _{n_k} \langle {\mathcal {A}}x, x -x_{n_k}\rangle + \rho _{n_k}\langle {\mathcal {A}} x_{n_k}, x_{n_k} - y_{n_k}\rangle . \end{aligned}$$

Since \(\nabla f\) is weakly - weakly continuous, passing to the limit in the last inequality as \(k\rightarrow \infty\) and using relation (3.23), we obtain \(\langle {\mathcal {A}} x, x - z\rangle \ge 0 \ \ \forall z\in C.\) Thus, from Lemma 2.5 we get that \(z\in Sol(C,{\mathcal {A}}).\) Hence the conclusion of Theorem 3.8 still hold.

4 Application

4.1 Application to computing dynamic user equilibria

In this section, we apply Algorithm 3.2 to compute dynamic user equilibria (see [16]). Let \({\mathcal {P}}\) be set of paths in the network. \({\mathbb {W}}\) be set of O-D pairs in the network, \(Q_{ij}\) be fixed O-D demand between \((i,j)\in {\mathbb {W}},\) \({\mathcal {P}}_{ij}\) be subset of paths that connect O-D (i, j),  t be continuous time parameter in a fixed time horizon \([t_0,t_1],\) \(h_p(t)\) be depature rate along path p at time t,  h(t) be complete vector of departure rates \(h(t) = (h_p(t) : p \in {\mathcal {P}}),\) \(\Psi _p(t,h)\) be travel cost along path p with departure time t,  under departure profile h,  \(v_{ij}(h)\) be minimum travel cost between O-D pair (i, j) for all paths and departure times.

Assume that \(h_p(\cdot ) \in L^2_{+}[t_0,t_1]\) and \(h(\cdot ) \in (L^2_{+}[t_0,t_1])^{|{\mathcal {P}}|}.\) Define the effective delay operator \(\Psi : (L^2_{+}[t_0,t_1])^{|{\mathcal {P}}|} \rightarrow (L^2_{+}[t_0,t_1])^{|{\mathcal {P}}|}\) as follows:

$$\begin{aligned} h(\cdot ) = \{h_p(\cdot ), p\in {\mathcal {P}}\}\mapsto \Psi (h) = \{\Psi _p(\cdot ,h), p\in {\mathcal {P}}\}. \end{aligned}$$

The travel demand satisfaction constraint satisfies

$$\begin{aligned} Q_{ij} = \sum _{p\in {\mathcal {P}}_{ij}}\int _{t_0}^{t_1}h_p(t)dt, \ \ \forall \ (i,j) \in {\mathbb {W}}. \end{aligned}$$

Then, the set of feasible path departures vector can be expressed as

$$\begin{aligned} \Lambda = \{h\ge 0: \sum _{p\in {\mathcal {P}}_{ij}}\int _{t_0}^{t_1}h_p(t)dt, \ \ \forall \ (i,j) \in {\mathbb {W}}\} \subset (L^2_{+}[t_0,t_1])^{|{\mathcal {P}}|}. \end{aligned}$$

Recall that a vector of departures \(h^*\in \Lambda\) is a dynamic user equilibrium with simultaneous route and departure time choice if

$$\begin{aligned} h^*_p(y) > 0, \ p\in {\mathcal {P}}_{ij} \Rightarrow \Psi _p(t,h^*) = v_{ij}(h^*), \ \ \text{ for } \text{ almost } \text{ every } \ t\in [t_0,t_1]. \end{aligned}$$
(4.1)

Note that (4.1) is equivalent to the following variational inequality ([16]):

$$\begin{aligned} \langle \Psi (h^*), h - h^*\rangle \ge 0, \ \ \ \forall \ h\in \Lambda . \end{aligned}$$
(4.2)

Based on Algorithm 3.2, we have the following algorithm.

figure d

If the delay operator \(\Psi\) is Lipschitz continuous and pseudomonotone, then we can apply Algorithm 4.1 to compute dynamic user equilibria.

5 Numerical examples

In this section, we consider some examples to illustrate the convergence of the proposed algorithm and compare it with other algorithms. We also compare the convergence of Algorithm 3.2 for various examples of the Bregman distance.

Example 5.1

Let \(E= \ell _2({\mathbb {R}})\) where \(\ell _2({\mathbb {R}}) = \{x=(x_1,x_2,x_3,...,), \ x_i \in {\mathbb {R}}: \sum _{i=1}^{\infty }\}\) with norm \(\Vert x\Vert _{\ell _2} = \left( \sum _{i=1}^{\infty }|x_i|^2\right) ^{\frac{1}{2}}\) and inner product \(\langle x,y\rangle = \sum _{i=1}^{\infty }x_iy_i,\) for all \(x =(x_1,x_2,x_3,...),\) \(y=(y_1,y_2,y_3,...) \in E.\) Let \(C = \{x= (x_1,x_2,x_3,...) \in \ell _2 : \Vert x\Vert \le 1\}\) and \({\mathcal {A}} : \ell _2 \rightarrow \ell _2\) be defined by

$$\begin{aligned} {\mathcal {A}}(x_1,x_2,x_3,...) = (x_1\exp (-x_1^2),0,0,...). \end{aligned}$$

It was shown in Example 2.1 of [4] that \({\mathcal {A}}\) is pseudomonotone, Lipschitz continuous and sequentially weakly continuous but not monotone in \(\ell _2({\mathbb {R}}).\)

We now list some known Bregman distances. These distances are listed in the following forms:

  1. (i)

    The function \(f^{IS}(x) = -\sum _{i=1}^{m}\log x_i\) and the Itakura-Saito distance

    $$\begin{aligned} \phi _f^{IS}(x,y) = \sum _{i=1}^{m}\left( \frac{x_i}{y_i} - \log \left( \frac{x_i}{y_i}\right) - 1\right) . \end{aligned}$$
  2. (ii)

    The function \(f^{KL}(x) = \sum _{i=1}^{m}x_i\log x_i\) and the Kullback-Leibler distance

    $$\begin{aligned} \phi _f^{KL}(x,y) = \sum _{i=1}^{m}\left( x_i\log \left( \frac{x_i}{y_i}\right) + y_i - x_i\right) . \end{aligned}$$
  3. (iii)

    The function \(f^{SE}(x) = \frac{1}{2}\Vert x\Vert ^2\) and the squared Euclidean distance

    $$\begin{aligned} \phi _f^{SE}(x,y) = \frac{1}{2}\Vert x -y\Vert ^2. \end{aligned}$$

The values \(\nabla f(x)\) and \(\nabla f^*(x) = (\nabla f)^{-1}(x)\) are computed explicitly. More precisely,

  1. (i)

    \(\nabla f^{IS}(x) = -(1/x_1,...,1/x_m)^T\) and \((\nabla f^{IS})^{-1}(x) = -(1/x_1,...,1/x_m)^T.\)

  2. (ii)

    \(\nabla f^{KL}(x) = (1+\log (x_1),...,1+\log (x_m))^T\) and

    $$\begin{aligned} (\nabla f^{KL})^{-1}(x) = (\exp (x_1-1),...,\exp (x_m - 1))^T. \end{aligned}$$
  3. (iii)

    \(\nabla f^{SE}(x) = x\) and \((\nabla f^{SE})^{-1}(x) = x.\)

The feasibility set of our problem VIP is of the form,

$$\begin{aligned} C =\{x =(x_1,x_2,...,x_m)^T \in {\mathbb {R}}^m: \Vert x\Vert \le 1 \ \ \text{ and } \ \ x_i \ge a>0, \ \ i=1,2,...,m\}, \end{aligned}$$

where \(a<1/\sqrt{m}\) (which ensures that \(C\ne \emptyset\)). For the experiment in Algorithm 3.2, we choose \(\alpha _n = \frac{1}{n+1},\) \(\delta _n = \frac{2n}{5n+4},\) \(u=\mu =0.5\) and \(\rho =3.5.\)

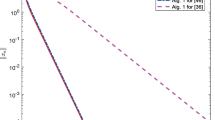
Let \(E_n = \Vert x_{n+1} - x_n\Vert ^2 < 10^{-4},\) we consider this example for various types of Bregman distance with \(m=10,20,50,80.\) The results of this experiment are reported in Fig. 1.

Fig. 1
figure 1

Example  5.1. Top left: \(m=10,\) Top right: \(m=20\), Bottom left: \(m=50,\) Bottom right: \(m=80\)

Full size image

Example 5.2

The following example was first considered in [20],

$$\begin{aligned} \min g(x)&= \dfrac{x^TPx+a^Tx+a_0}{b^Tx+b_0}\\ \text {subject to}~~ \,x \in X&=\{x\in {\mathbb {R}}^5: b^Tx+b_0 > 0 \}, \nonumber \end{aligned}$$

where

$$\begin{aligned} P= \begin{pmatrix} 5 &{} -1 &{} 2 &{} 0\\ -1 &{} 5&{} -1 &{} 3\\ 2 &{} -1 &{} 3 &{} 0 \\ 0 &{} 0 &{} 0&{} 1 \nonumber \end{pmatrix}, ~~ a= \begin{pmatrix} 1 \\ -2\\ -2\\ 1 \nonumber \end{pmatrix}~~b= \begin{pmatrix} 2\\ 1\\ 1\\ 0 \nonumber \end{pmatrix}, ~~a_0=-2,~~ b_0=4. \nonumber \end{aligned}$$

Since P is symmetric and positive definite, g is pseudoconvex on X. We minimize g on \(K=\{x \in {\mathbb {R}}^4: 1 \le x_i \le 3 \} \subset X.\)

It is easy to see that

$$\begin{aligned} F(x)=\nabla g(x)=\dfrac{(b^T x+b_0)(2Px+a)-b(x^T Px +a^T x+a_0)}{(b^T x +b_0)^2}. \end{aligned}$$
(5.1)

The following choices of parameters are made: \(\alpha _{n}=\frac{1}{n+1},\) \(\delta _n=\frac{2n}{5n+7},\) \(\rho =3.5\) and \(u =\mu =0.5.\)

We terminate the iterations at \(E_n=\Vert x_{n+1}-x_n\Vert ^2 \le \epsilon\) with \(\epsilon = 10^{-4}.\) The results are presented in Fig. 2 for various initial values of \(x_1.\)

Case 1::

\(x_1=(-10, -10, -10, -10)';\)

Case 2::

\(x_1=(1, 2, 3, 4)';\)

Case 3::

\(x_1=(4, 4, 4, 4)';\)

Case 4:

\(x_1=(5, 0, 0, 10)'.\)

We compare the performance of our Algorithm 3.2 with Algorithm 1.2. For algorithm 1.2, we let \(l=0.001\) and \(\gamma =0.002.\)

Fig. 2
figure 2

Performance of Algorithm 3.2 compared with Algorithm 1.2

Full size image