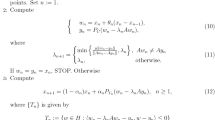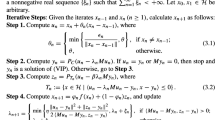1 Introduction

Suppose C is a nonempty, closed and convex subset of a real Hilbert space H and \(A:C\rightarrow H\) is a continuous operator. Consider the variational inequality problem (VI(A, C), for short): find \(x\in C\) such that

$$\begin{aligned} \langle Ax, y-x\rangle \ge 0 \quad \; \forall y \in C. \end{aligned}$$
(1)

Several real-world problems from mechanics, economics, engineering and so on, can be recast into VI(A, C)(1) (see, for example, [1, 2, 12, 14, 17,18,19, 23, 24]). We assume, throughout this paper, that S denotes the set of solutions of VI(A, C)(1).

One of the projection methods for solving VI(A, C) (1) is the subgradient extragradient method introduced in [6] by Censor et al.: \(x_1\in H\),

$$\begin{aligned} \left\{ \begin{array}{llll} &{} y_n = P_C(x_n-\lambda _n Ax_n),\\ &{} T_n:=\{w \in H:\langle x_n-\lambda _n Ax_n-y_n,w-y_n\rangle \le 0\},\\ &{} x_{n+1}=P_{T_n}(x_n-\lambda _n Ay_n), ~~n \ge 1, \end{array} \right. \end{aligned}$$
(2)

where \(0< \inf _{n\ge 1}\lambda _n \le \sup _{n\ge 1}\lambda _n < \frac{1}{L}.\) Censor et al. [6] proved that the sequence \(\{x_n\}\) generated by (2) converges weakly to a solution of VI(A, C)(1) (see also [5] for strong convergence results). The subgradient extragradient method (2) has shown numerically to improve the extragradient method of Korpelevich [20] when computing projection onto the feasible set C is computationally expensive (i.e., method (2) minimizes the number of projections onto C per iteration in the extragradient method) and has been studied by several authors when A is either monotone or pseudo-monotone in Hilbert spaces.

In [35], Yang et al. studied a modification of the subgradient extragradient method (2) with the following self-adaptive step-size procedure: Given \(\lambda _1>0, \; x_1 \in H\) and \(\mu \in (0,1)\),

$$\begin{aligned} \left\{ \begin{array}{llll} &{} y_n = P_C(x_n-\lambda _n Ax_n),\\ &{} T_n:=\{w \in H:\langle x_n-\lambda _n Ax_n-y_n,w-y_n\rangle \le 0\},\\ &{} x_{n+1}=P_{T_n}(x_n-\lambda _n Ay_n), \end{array} \right. \end{aligned}$$
(3)

where \(\{\lambda _n\}\) is given by

$$\begin{aligned} \lambda _{n+1}= \left\{ \begin{array}{llll} &{} \min \Big \{\frac{\mu (\Vert x_n-y_n\Vert ^2+\Vert x_{n+1}-y_n\Vert ^2)}{2\langle Ax_n-Ay_n,x_{n+1}-y_n\rangle },\lambda _n \Big \}, &{}\quad \langle Ax_n-Ay_n,x_{n+1}-y_n\rangle > 0\\ &{} \lambda _n, &{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$
(4)

and showed that the sequence \(\{x_n\}\) generated by (3) converges weakly to a solution of VI(A, C) (1).

Furthermore, Fan et al. in [13] studied the subgradient extragradient method (2) with a single inertial extrapolation step:

$$\begin{aligned} \left\{ \begin{array}{llll} &{} w_n= x_n+\theta _n(x_n-x_{n-1}),\\ &{} y_n=P_C(w_n-\lambda _n Aw_n),\\ &{} T_n:=\{w \in H:\langle w_n-\lambda _n Aw_n-y_n,w-y_n\rangle \le 0\},\\ &{} x_{n+1}=(1-\alpha _n)w_n+\alpha _nP_{T_n}(w_n-\lambda _n Ay_n), \end{array} \right. \end{aligned}$$
(5)

where \(0\le \theta _n\le \theta _{n+1}<1\), \(\lambda _n\rightarrow 0\) as \(n\rightarrow \infty \), \(\sum _{n=1}^{\infty } \lambda _n=\infty \),

$$\begin{aligned} \delta >\frac{4\theta [\theta (1+\theta )+\sigma ]}{1-\theta ^2} \end{aligned}$$

and

$$\begin{aligned} 0<\alpha \le \alpha _n\le \frac{\delta -4\theta [\theta (1+\theta )+\frac{1}{4}\theta \delta +\sigma ]}{4\delta [\theta (1+\theta )+\frac{1}{4}\theta \delta +\sigma ]}. \end{aligned}$$

Fan et al. [13] gave weak convergence result of method (5). Similar recent results on solving VI(A, C)(1) using versions of method (5) are found in [31], where \(0\le \theta _n\le \theta _{n+1}\le \frac{1}{10}\), \(\lambda _n\rightarrow 0\) as \(n\rightarrow \infty \) and \(\sum _{n=1}^{\infty } \lambda _n=\infty \); in [32] where \(0\le \theta _n\le \theta _{n+1}\le \frac{1}{4}\), \(0<\alpha \le \alpha _n\le \frac{1}{2}\) and \(\{\lambda _n\}\) is generated by a self-adaptive procedure; in [34] where \(0\le \theta _n\le \theta \le \frac{-2{\bar{\theta }}-1+\sqrt{8{\bar{\theta }}+1}}{2(1-{\bar{\theta }})}, {\bar{\theta }}:=\frac{1-\mu _0}{2}, 0<\mu<\mu _0<1\) and in [30] where \(\alpha _n=1\) and \(\theta _n\) is chosen as

$$\begin{aligned} \theta _n= \left\{ \begin{array}{llll} &{} \min \Big \{\frac{1}{n^2\Vert x_n-x_{n-1}\Vert ^2},\theta \Big \}, &{}\quad x_n\ne x_{n-1},\\ &{} \theta , &{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

and \(\theta >0\). It is observed in all the versions of inertial subgradient extragradient method mentioned above, the inertial term \(\theta _n\) in the single inertial extrapolation step is chosen such that \(0\le \theta _n \le \theta <1\).

Recently, Shehu et al. [27] proposed a relaxed version of inertial subgradient extragradient method to solve VI(A, C)(1):

$$\begin{aligned} \left\{ \begin{array}{llll} &{} w_n=x_n+\theta _n(x_n-x_{n-1}),\\ &{} y_n=P_C(w_n-\lambda _n Aw_n),\\ &{} T_n:=\{w \in H:\langle w_n-\lambda _n Aw_n-y_n,w-y_n\rangle \le 0\},\\ &{} x_{n+1}=(1-\alpha _n)x_n+\alpha _n P_{T_n}(w_n-\lambda _n Ay_n), \end{array} \right. \end{aligned}$$
(6)

where \( 0\le \theta _n\le 1\) and \( 0<\alpha _n<\frac{1}{2}\). Shehu et al. [27] obtained weak and strong convergence results giving the numerical advantage of the relaxed choice of inertia \(\theta _n \in [0,1]\) in (6) but no linear convergence result was given.

Quite recently, Chang et al. [7] introduced the following inertial subgradient extragradient algorithm with adaptive step sizes to solve VI(A, C)(1): \(x_1=x_0 \in H, y_1=P_C(x_1-\lambda _1 Ax_1)\),

$$\begin{aligned} \left\{ \begin{array}{llll} &{} z_{n+1}= x_n+\delta (x_n-x_{n-1}),\\ &{} y_{n+1}=P_C(z_{n+1}-\lambda _n Ay_n),\\ &{} T_n:=\{w \in H:\langle z_{n+1}-\lambda _n Ay_n-y_{n+1},w-y_{n+1}\rangle \le 0\},\\ &{} x_{n+1}=P_{T_n}(z_{n+1}-\lambda _n Ay_{n+1}), \end{array} \right. \end{aligned}$$
(7)

with the following conditions satisfied:

$$\begin{aligned} \left\{ \begin{array}{llll} &{} 0\le \delta<\frac{5-\sqrt{13}}{6},\\ &{} 0<\alpha< \frac{1}{1+\sqrt{2}+\delta },\\ &{} \delta (1+\delta )(1+\alpha )-\phi (\alpha )\Big (\delta ^2-\frac{\delta }{2} \Big )<\frac{(\phi (\alpha )-\delta \alpha )\phi (\alpha )(1-2\delta )}{2\phi (\alpha )-\delta \alpha -2\phi (\alpha )\delta },\\ &{}\phi (\alpha ):=1-(1+\sqrt{2})\alpha . \end{array} \right. \end{aligned}$$
(8)

Weak convergence of the sequence \(\{x_n\}\) generated by (7) was presented alongside some numerical results. However, neither strong nor linear convergence results for (7) was given by Chang et al. [7]. Another drawback of the method in [7] is that the inertia \(\delta \) is quite restrictive and chosen in \([0,\frac{1}{4})\) and moreover, the conditions imposed in (8) seem stringent on the iterative parameters. Some further recent results on inertial subgradient extragradient method are found in [8,9,10,11, 16].

Our aim in this paper is to further improve the inertial subgradient extragradient method to solve VI(A, C)(1). Specifically, in the present paper we study the inertial subgradient extragradient method and improve on the results in [7, 13, 27, 30,31,32, 34, 35] in the following ways:

  • We proposed inertial subgradient extragradient method with double inertial extrapolation steps and relaxation parameter. The method considered in Shehu et al. [27] becomes a special case and so also are the inertial subgradient extragradient methods studied in [6, 7, 13, 30,31,32, 34, 35]. One of the inertial factors in our double inertial extrapolation steps is allowed to be equal to 1 and the other inertial factor can be chosen as close as possible to 1 (see our proposed Algorithm 1 below) which is an improvement over the methods in [7, 13, 31, 32, 34] where the only single inertial extrapolation step is studied and the inertia is bounded away from 1.

  • We obtain weak, strong and linear convergence of our proposed method, respectively. Weak and strong convergence results are given for inertial subgradient extragradient method with double inertial extrapolation steps and relaxation parameter with self-adaptive step size. In the special case when the constant step size is considered alongside the known Lipschitz constant and modulus of strong pseudo-monotonicity of the cost operator, we show that linear rate of convergence is achieved. This is an improvement over the results in [6, 7, 13, 27, 31, 32, 34, 35] where no linear rate of convergence is obtained for inertial subgradient extragradient method.

  • We give numerical computations of our proposed method and compare it with the methods in [7, 13, 27, 30, 34, 35]. Our preliminary computational results show that our proposed method is efficient and converges faster (in terms of CPU time and number of iterations) than the inertial subgradient extragradient methods in [7, 13, 27, 30, 34, 35].

Our paper is organized as follows: We present some definitions and lemmas in Sect. 2. In Sect. 3, we introduce our proposed method. Weak convergence analysis of our proposed method is given in Sect. 4 and strong convergence analysis is given in Sect. 5. Furthermore, linear convergence is obtained in Sect. 6. We present numerical implementations in Sect. 7 and give some concluding remarks in Sect. 8.

2 Preliminaries

This section gives some definitions and lemmas that would be needed in our convergence analysis of this paper.

Definition 2.1

A mapping \( A: H \rightarrow H \) is called

  1. (a)

    \(\eta \)-strongly monotone on H if there exists a constant \(\eta > 0\) such that \(\langle Ax-Ay,x-y\rangle \ge \eta \Vert x-y\Vert ^2\) for all \(x,y \in H\);

  2. (b)

    monotone on H if \( \langle Ax - Ay, x-y \rangle \ge 0 \) for all \( x, y \in H\);

  3. (c)

    \(\delta \)-strongly pseudo-monotone on H if there exists \(\delta >0\) such that \(\langle Ay,x-y\rangle \ge 0 \Rightarrow \langle Ax,x-y\rangle \ge \delta \Vert x-y\Vert ^2, ~~x, y\in H\);

  4. (d)

    pseudo-monotone on H if, for all \(x,y \in H\), \(\langle Ax,y-x\rangle \ge 0 \Rightarrow \langle Ay,y-x\rangle \ge 0\);

  5. (e)

    L-Lipschitz continuous on H if there exists a constant \( L > 0 \) such that \( \Vert Ax - Ay \Vert \le L \Vert x-y \Vert \) for all \( x, y \in H\).

  6. (f)

    sequentially weakly continuous if for each sequence \(\{x_n\}\) we have: \(\{x_n\}\) converges weakly to x implies \(\{Ax_n\}\) converges weakly to Ax.

Remark 2.2

Observe that (a) implies (b), (a) implies (c), (c) implies (d), and (b) implies (d) in the above definitions. If A is \(\eta \)-strongly pseudo-monotone and continuous mapping on finite-dimensional subspaces, it has been shown (see, e.g., [36, Theorem 4.8]) that VI(A, C) (1) has unique solution.

Definition 2.3

The mapping \(P_C : H \rightarrow C\) which assigns to each point \(u \in H\) the unique point \(w \in C\) such that

$$\begin{aligned} \Vert u - w\Vert \le \Vert u-y\Vert ~~\forall y \in C \end{aligned}$$

is called the metric projection of H onto C.

The metric projection \(P_C\) satisfies (see, for example, [3])

$$\begin{aligned} \langle x-y, P_C x-P_C y \rangle \ge \Vert P_C x-P_C y\Vert ^2~~\forall x, y \in H. \end{aligned}$$
(9)

Furthermore, \(P_C x\) is characterized by the properties

$$\begin{aligned} P_Cx \in C \quad \text {and} \quad \langle x-P_C x, P_C x-y \rangle \ge 0~~\forall y \in C. \end{aligned}$$
(10)

This characterization implies that

$$\begin{aligned} \Vert x-y\Vert ^2\ge \Vert x-P_Cx\Vert ^2+\Vert y-P_Cx\Vert ^2~~\forall x \in H, \; \forall y \in C. \end{aligned}$$
(11)

Lemma 2.4

The following statements hold in H:

  1. (i)

    \( \Vert x+y\Vert ^2=\Vert x\Vert ^2+2\langle x,y\rangle +\Vert y\Vert ^2 \) for all \( x, y \in H \);

  2. (ii)

    \(\Vert x+y\Vert ^2 \le \Vert x\Vert ^2+2 \langle y,x+y\rangle \) for all \( x, y \in H \);

  3. (iii)

    \( \Vert \alpha x+\beta y\Vert ^2=\alpha (\alpha +\beta )\Vert x\Vert ^2+\beta (\alpha +\beta )\Vert y\Vert ^2-\alpha \beta \Vert x-y\Vert ^2 \quad \forall x, y \in H, \; \alpha , \beta \in \mathbb {R}\).

Lemma 2.5

(Maingé [21]) Let \(\{\varphi _{n}\}, \{\delta _{n}\}\) and \(\{\theta _{n}\}\) be sequences in \([0,+\infty )\) such that

$$\begin{aligned} \varphi _{n+1}\le \varphi _{n}+\theta _{n}(\varphi _{n}-\varphi _{n-1})+\delta _{n} ~~\forall n\ge 1,~\sum _{n=1}^{+\infty }\delta _{n}<+\infty , \end{aligned}$$

and there exists a real number \(\theta \) with \(0 \le \theta _{n}\le \theta <1\) for all \(n \in \mathbb {N}.\) Then the following assertions hold true:

  1. (i)

    \(\sum _{n=1}^{+\infty }[\varphi _{n}-\varphi _{n-1}]_{+}<+\infty ,\) where \([t]_{+}:=\max \{t,0\};\)

  2. (ii)

    there exists \(\varphi ^{*}\in [0,+\infty )\) such that \(\lim _{n\rightarrow \infty }\varphi _{n}=\varphi ^{*}.\)

Lemma 2.6

(Opial [25]) Let C be a nonempty subset of H and let \(\{ x_n\}\) be a sequence in H such that the following two conditions hold:

  1. (i)

    for any \(x\in C\), \(\lim _{n\rightarrow \infty }\Vert x_n-x\Vert \) exists;

  2. (ii)

    every sequential weak cluster point of \(\{ x_n\}\) is in C.

Then \(\{ x_n\}\) converges weakly to a point in C.

3 Proposed Method

In this section we introduce and discuss our projection-type method.

Assumption 3.1

  Suppose that the following assumptions are satisfied:

  1. (a)

    The feasible set C is a nonempty, closed, and convex subset of H.

  2. (b)

    \( A: H \rightarrow H \) is pseudo-monotone, L-Lipschitz continuous and A satisfies the following condition: whenever \(\{x_n\}\subset H\) and \(x_n \rightharpoonup v^*,\) one has \(\Vert Av^*\Vert \le \liminf \limits _{n\rightarrow \infty }\Vert Ax_n\Vert \).

  3. (c)

    The solution set S of VI(A, C) (1) is nonempty.

  4. (d)

    \( 0\le \theta _n \le \theta _{n+1}\le 1\).

  5. (e)

    \( 0\le \delta < \min \Big \{\frac{\epsilon -\sqrt{2\epsilon }}{\epsilon },\theta _1\Big \},~~ \epsilon \in (2,\infty )\).

  6. (f)

    \( 0<\alpha \le \alpha _n\le \alpha _{n+1}<\frac{1}{1+\epsilon },~~ \epsilon \in (2,\infty )\).

Remark 3.2

The condition " whenever \(\{x_n\}\subset H\) and \(x_n \rightharpoonup v^*,\) one has \(\Vert Av^*\Vert \le \liminf \limits _{n\rightarrow \infty }\Vert Ax_n\Vert \)." in Assumption 3.1(b) is strictly weaker than the sequentially weakly continuous assumption in [7, 13, 30,31,32,33,34,35]. For example, take \(A(v) = v\Vert v\Vert ~\forall v\in C\). Then A satisfies our assumption but not sequentially weakly continuous.

We propose our subgradient extragradient method with double inertial extrapolation step and self-adaptive step sizes.

figure a

Remark 3.3

Observe that if \(x_n=w_n=y_n\), then (12) implies the equality \(x_n=P_C(x_n-\lambda _n Ax_n)\) and so \(x_n \in S\).

Remark 3.4

Note that by (13), \(\lambda _{n+1} \le \lambda _n ~~\forall n \ge 1\) and there exists \(\lambda >0\) such that \(\underset{n\rightarrow \infty }{\lim }\lambda _n=\lambda \ge \min \left\{ \frac{\mu }{L}, \lambda _1\right\} \).

Remark 3.5

  1. (a)

    In our Algorithm 1, the inertia \(\theta _n=1\) is allowed. This is not the case for the methods in [7, 13, 31, 32, 34, 35] where \(\theta _n<1\). Observe also in our proposed Algorithm 1 that as \(\epsilon \) increases, so is \(\delta \) approaching 1 since \(\lim _{\epsilon \rightarrow \infty } \frac{\epsilon -\sqrt{2\epsilon }}{\epsilon }=1\). Furthermore, as \(\epsilon \) increases, \(\alpha _n\) reduces. Conversely, as \(\epsilon \) approaches 2, \(\delta \) approaches zero and \(\alpha _n\) approaches \(\frac{1}{3}\).

  2. (b)

    In the inertial subgradient extragradient methods proposed in [7, 32, 34], many stringent conditions are imposed on the inertial factor. For example, in [7], \(\delta \) is assumed to satisfy seemingly strong condition (8) above; in [32] that \(0\le \theta _n\le \theta \le \frac{1}{4}\) and \(\{\theta _n\}\) was assumed to satisfy the condition \(0\le \theta _n\le \theta \le \frac{-2{\bar{\theta }}-1+\sqrt{8{\bar{\theta }}+1}}{2(1-{\bar{\theta }})}, {\bar{\theta }}:=\frac{1-\mu _0}{2}, 0<\mu<\mu _0<1\) in [34]. Our Assumption 3.1(d)–(f) are easier to implement than the conditions in [7, 32, 34].

  3. (c)

    In the paper [13], it was assumed that \(0\le \theta _n\le \theta <1\) with

    $$\begin{aligned} \delta >\frac{4\theta [\theta (1+\theta )+\sigma ]}{1-\theta ^2} \end{aligned}$$

    and

    $$\begin{aligned} 0<\alpha \le \alpha _n\le \frac{\delta -4\theta [\theta (1+\theta )+\frac{1}{4}\theta \delta +\sigma ]}{4\delta [\theta (1+\theta )+\frac{1}{4}\theta \delta +\sigma ]}. \end{aligned}$$

    In the result of this paper, these strong assumptions are dispensed with and replaced with a more relaxed and seemingly easier conditions in Assumption 3.1 (d)-(f).

  4. (d)

    A self-adaptive step size rule is incorporated in Algorithm 1. It is more efficient than the step size rule in the methods of [13, 31], where it is assumed that \(\lambda _n\rightarrow 0\) as \(n\rightarrow \infty \) and that \(\sum _{n=1}^{\infty } \lambda _n = \infty \). Furthermore, our adaptive step size rule does not require the knowledge of the Lipschitz constant of A as an input parameter. Also, Algorithm 1 does not require any line search.\(\Diamond \)

4 Convergence Analysis

In this section we show that under Assumption 3.1, the sequence \( \{ x_n \} \) generated by Algorithm 1 converges weakly to a point in S.

For the rest of this paper, we define

$$\begin{aligned} u_n:=P_{T_n}(w_n-\lambda _n Ay_n) ~~\forall n\ge 1. \end{aligned}$$

First we prove the following lemma for \(\{x_n\}\) generated by Algorithm 1.

Lemma 4.1

Suppose that \( \{ x_n \} \) is generated by Algorithm 1 and Assumption 3.1 holds. Then \( \{ x_n \} \) is bounded.

Proof

Choose a point \(x^* \in S\). Then \(\langle Ax^*,y_n-x^*\rangle \ge 0\) and since A is pseudo-monotone, we have \(\langle Ay_n,y_n-x^*\rangle \ge 0\). Hence \(\langle Ay_n,y_n-x^*+u_n-u_n\rangle \ge 0\) and thus

$$\begin{aligned} \langle Ay_n,x^*-u_n\rangle \le \langle Ay_n,y_n-u_n\rangle . \end{aligned}$$
(15)

From the definition of \(T_n\) we have \(\langle w_n-\lambda _n Aw_n-y_n,u_n-y_n\rangle \le 0.\) Therefore

$$\begin{aligned}&\langle w_n-\lambda _n Ay_n-y_n,u_n-y_n\rangle \nonumber \\&\quad = \langle w_n-\lambda _n Aw_n-y_n,u_n-y_n\rangle +\lambda _n\langle Aw_n-Ay_n,u_n-y_n\rangle \nonumber \\&\quad \le \lambda _n\langle Aw_n-Ay_n,u_n-y_n\rangle . \end{aligned}$$
(16)

Using (11) and (15), we now obtain

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-\lambda _n Ay_n-x^*\Vert ^2-\Vert w_n-\lambda _n Ay_n-u_n\Vert ^2\nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n\Vert ^2+2\lambda _n \langle Ay_n,x^*-u_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n\Vert ^2+2\lambda _n \langle Ay_n,y_n-u_n\rangle \nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n+y_n-y_n\Vert ^2+2\lambda _n \langle Ay_n,y_n-u_n\rangle \nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2\nonumber \\&\quad +\, 2 \langle w_n-\lambda _nAy_n-y_n,u_n-y_n\rangle . \end{aligned}$$
(17)

Next, using (16) and (17), we see that

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2\nonumber \\&\quad +\, 2 \langle w_n-\lambda _nAy_n-y_n,u_n-y_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2\nonumber \\&\quad +\, 2\lambda _n \langle Aw_n-Ay_n,u_n-y_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2\nonumber \\&\quad +\, 2\lambda _n \Vert Aw_n-Ay_n\Vert \Vert u_n-y_n\Vert \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2\nonumber \\&\quad +\, \frac{2\lambda _n \mu }{\lambda _{n+1}} \Vert w_n-y_n\Vert \Vert u_n-y_n\Vert \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2\nonumber \\&\quad +\, \frac{\lambda _n \mu }{\lambda _{n+1}} \Big (\Vert w_n-y_n\Vert ^2+\Vert u_n-y_n\Vert ^2\Big )\nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Big (1-\frac{\lambda _n \mu }{\lambda _{n+1}}\Big )\Vert w_n-y_n\Vert ^2 \nonumber \\&\quad -\, \Big (1-\frac{\lambda _n \mu }{\lambda _{n+1}}\Big )\Vert u_n-y_n\Vert ^2. \end{aligned}$$
(18)

Since \(\underset{n \rightarrow \infty }{\lim }\Big (1-\frac{\lambda _n \mu }{\lambda _{n+1}}\Big )=1-\mu >0\), there exists a natural number \(N\ge 1\) such that

$$\begin{aligned} \Vert u_n - x^*\Vert \le \Vert w_n - x^*\Vert \; ~~\forall n \ge N. \end{aligned}$$
(19)

Now, from Algorithm 1, we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2= & {} \Vert (1-\alpha _n)(z_n-x^*)+\alpha _n(u_n-x^*)\Vert ^{2}\nonumber \\= & {} (1-\alpha _n) \Vert z_n-x^*\Vert ^2+\alpha _n\Vert u_n-x^*\Vert ^2\nonumber \\&\quad -\, \alpha _n(1-\alpha _n)\Vert z_n-u_n\Vert ^2\nonumber \\\le & {} (1-\alpha _n) \Vert z_n-x^*\Vert ^2+\alpha _n\Vert w_n-x^*\Vert ^2\nonumber \\&\quad -\, \alpha _n(1-\alpha _n)\Vert z_n-u_n\Vert ^2, \forall n\ge N. \end{aligned}$$
(20)

From \( x_{n+1}=(1-\alpha _n)z_n+\alpha _nu_n \) we have

$$\begin{aligned} \Vert u_n-z_n\Vert =\frac{1}{\alpha _n}\Vert x_{n+1}-z_n\Vert ,~~ \forall n\ge 1. \end{aligned}$$
(21)

Combining (21) with (20) gives

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} (1-\alpha _n) \Vert z_n-x^*\Vert ^2+\alpha _n\Vert w_n-x^*\Vert ^2\nonumber \\&\quad -\, \frac{(1-\alpha _n)}{\alpha _n}\Vert x_{n+1}-z_n\Vert ^2, \forall n\ge N. \end{aligned}$$
(22)

Also, by Lemma 2.4 (iii), we have

$$\begin{aligned} \Vert w_n-x^*\Vert ^{2}= & {} \Vert x_n + \theta _n(x_n-x_{n-1})-x^*\Vert ^{2}\nonumber \\= & {} \Vert (1+\theta _n)(x_n-x^*)-\theta _n(x_{n-1}-x^*)\Vert ^{2}\nonumber \\= & {} (1+\theta _n)\Vert x_n-x^*\Vert ^{2}-\theta _n\Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \theta _n(1+\theta _n)\Vert x_n-x_{n-1}\Vert ^{2}, \forall n\ge 1. \end{aligned}$$
(23)

Applying Lemma 2.4 (iii) again, we have

$$\begin{aligned} \Vert z_n-x^*\Vert ^{2}= & {} \Vert x_n + \delta (x_n-x_{n-1})-x^*\Vert ^{2}\nonumber \\= & {} \Vert (1+\delta )(x_n-x^*)-\delta (x_{n-1}-x^*)\Vert ^{2}\nonumber \\= & {} (1+\delta )\Vert x_n-x^*\Vert ^{2}-\delta \Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \delta (1+\delta )\Vert x_n-x_{n-1}\Vert ^{2}, \forall n\ge 1. \end{aligned}$$
(24)

Also,

$$\begin{aligned} \Vert x_{n+1}-z_n\Vert ^2= & {} \Vert x_{n+1}-(x_n+\delta (x_n-x_{n-1}))\Vert ^2 \nonumber \\= & {} \Vert (x_{n+1}-x_n)-\delta (x_n-x_{n-1})\Vert ^2\nonumber \\= & {} \Vert x_{n+1}-x_n\Vert ^2+\delta ^2\Vert x_n-x_{n-1}\Vert ^2-2\delta \langle x_{n+1}-x_n,x_n-x_{n-1}\rangle \nonumber \\\ge & {} \Vert x_{n+1}-x_n\Vert ^2+\delta ^2\Vert x_n-x_{n-1}\Vert ^2-2\delta \Vert x_{n+1}-x_n\Vert \Vert x_n-x_{n-1}\Vert \nonumber \\\ge & {} (1-\delta )\Vert x_{n+1}-x_n\Vert ^2+(\delta ^2-\delta )\Vert x_n-x_{n-1}\Vert ^2. \end{aligned}$$
(25)

Substituting (23), (24) and (25) into (22), we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} (1-\alpha _n)\Big [(1+\delta )\Vert x_n-x^*\Vert ^2-\delta \Vert x_{n-1}-x^*\Vert ^2 \nonumber \\&\quad +\, \delta (1+\delta )\Vert x_n-x_{n-1}\Vert ^2\Big ]+\alpha _n\Big [(1+\theta _n)\Vert x_n-x^*\Vert ^2 \nonumber \\&\quad -\, \theta _n\Vert x_{n-1}-x^*\Vert ^2+\theta _n(1+\theta _n)\Vert x_n-x_{n-1}\Vert ^2\Big ]\nonumber \\&\quad -\, \frac{(1-\alpha _n)}{\alpha _n}\Big [(1-\delta )\Vert x_{n+1}-x_n\Vert ^2+(\delta ^2-\delta )\Vert x_n-x_{n-1}\Vert ^2\Big ]\nonumber \\= & {} (1-\alpha _n)(1+\delta )\Vert x_n-x^*\Vert ^2-\delta (1-\alpha _n)\Vert x_{n-1}-x^*\Vert ^2 \nonumber \\&\quad +\, (1-\alpha _n)\delta (1+\delta )\Vert x_n-x_{n-1}\Vert ^2 +\alpha _n(1+\theta _n)\Vert x_n-x^*\Vert ^2 \nonumber \\&\quad -\, \alpha _n\theta _n\Vert x_{n-1}-x^*\Vert ^2+\alpha _n\theta _n(1+\theta _n)\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&\quad -\, \frac{(1-\alpha _n)(1-\delta )}{\alpha _n}\Vert x_{n+1}-x_n\Vert ^2 - \frac{(1-\alpha _n)(\delta ^2-\delta )}{\alpha _n}\Vert x_n-x_{n-1}\Vert ^2 \nonumber \\= & {} \Big ((1-\alpha _n)(1+\delta )+\alpha _n(1+\theta _n)\Big )\Vert x_n-x^*\Vert ^2\nonumber \\&\quad -\, \Big (\delta (1-\alpha _n)+\alpha _n\theta _n\Big )\Vert x_{n-1}-x^*\Vert ^2\nonumber \\&\quad +\, \Big [(1-\alpha _n)\delta (1+\delta )+\alpha _n\theta _n(1+\theta _n)- \frac{(1-\alpha _n)(\delta ^2-\delta )}{\alpha _n} \Big ]\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&\quad -\, \frac{(1-\alpha _n)(1-\delta )}{\alpha _n}\Vert x_{n+1}-x_n\Vert ^2\nonumber \\= & {} \Big (1+\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_n-x^*\Vert ^2-\Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^2\nonumber \\&\quad -\, \rho _n\Vert x_{n+1}-x_n\Vert ^2+\sigma _n\Vert x_n-x_{n-1}\Vert ^2, \end{aligned}$$
(26)

where

$$\begin{aligned} \rho _n:=\frac{(1-\alpha _n)(1-\delta )}{\alpha _n} \end{aligned}$$

and

$$\begin{aligned} \sigma _n:=(1-\alpha _n)\delta (1+\delta )+\alpha _n\theta _n(1+\theta _n)- \frac{(1-\alpha _n)(\delta ^2-\delta )}{\alpha _n}. \end{aligned}$$

Define

$$\begin{aligned} \Gamma _n:=\Vert x_n-x^*\Vert ^{2}-\Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^{2}+ \sigma _n\Vert x_n-x_{n-1}\Vert ^{2}, ~~n\ge 1. \end{aligned}$$

Then

$$\begin{aligned} \Gamma _{n+1}-\Gamma _{n}= & {} \Vert x_{n+1}-x^*\Vert ^{2}-\Big (\alpha _{n+1}\theta _{n+1}+\delta (1-\alpha _{n+1})\Big )\Vert x_n-x^*\Vert ^{2}\nonumber \\&\quad +\, \sigma _{n+1}\Vert x_{n+1}-x_{n}\Vert ^2-\Vert x_n-x^*\Vert ^2+\Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \sigma _n\Vert x_n-x_{n-1}\Vert ^{2}\nonumber \\\le & {} \Big (\alpha _n\theta _n+\delta (1-\alpha _n)-\alpha _{n+1}\theta _{n+1}-\delta (1-\alpha _{n+1})\Big )\Vert x_n-x^*\Vert ^{2}\nonumber \\&\quad -\, \rho _n\Vert x_{n+1}-x_{n}\Vert ^2+\sigma _{n+1}\Vert x_{n+1}-x_{n}\Vert ^{2}\nonumber \\= & {} \Big ((\theta _n-\delta )\alpha _n-(\theta _{n+1}-\delta )\alpha _{n+1} \Big )\Vert x_n-x^*\Vert ^{2}\nonumber \\&\quad -\, \rho _n\Vert x_{n+1}-x_{n}\Vert ^2+\sigma _{n+1}\Vert x_{n+1}-x_{n}\Vert ^{2}. \end{aligned}$$
(27)

Since \(\theta _n \le \theta _{n+1}, \alpha _n \le \alpha _{n+1}\) and \(0\le \delta \le \theta _1 \le \theta _n, \forall n \ge 1\), we have that \(\theta _n-\delta \ge 0\) and \(\theta _{n+1}-\delta \ge 0\) so that \(\theta _n-\delta \le \theta _{n+1}-\delta \) and \((\theta _n-\delta )\alpha _n \le (\theta _{n+1}-\delta )\alpha _{n+1}\) for all \(n \ge 1.\) Hence,

$$\begin{aligned} (\theta _n-\delta )\alpha _n-(\theta _{n+1}-\delta )\alpha _{n+1} \le 0. \end{aligned}$$
(28)

Then from (27), we have

$$\begin{aligned} \Gamma _{n+1}-\Gamma _{n}\le & {} -\rho _n\Vert x_{n+1}-x_{n}\Vert ^2+\sigma _{n+1}\Vert x_{n+1}-x_{n}\Vert ^{2}\nonumber \\= & {} -(\rho _n-\sigma _{n+1})\Vert x_{n+1}-x_{n}\Vert ^2. \end{aligned}$$
(29)

By Conditions (e) and (f) of Assumption 3.1, we have

$$\begin{aligned} \rho _n-\sigma _{n+1}= & {} \frac{(1-\alpha _n)(1-\delta )}{\alpha _n}-(1-\alpha _{n+1})\delta (1+\delta )-\alpha _{n+1}\theta _{n+1}(1+\theta _{n+1})\nonumber \\&\quad +\, \frac{(1-\alpha _{n+1})(\delta ^2-\delta )}{\alpha _{n+1}}\nonumber \\\ge & {} \epsilon (1-\delta ) +\epsilon (\delta ^2-\delta )- (1-\alpha _{n+1})\delta (1+\delta )-2\alpha _{n+1}\nonumber \\> & {} \epsilon (1-\delta ) +\epsilon (\delta ^2-\delta )- 2(1-\alpha _{n+1})-2\alpha _{n+1}\nonumber \\= & {} \epsilon (1-\delta ) +\epsilon (\delta ^2-\delta )- 2\nonumber \\= & {} \epsilon \delta ^2-2\epsilon \delta +\epsilon -2. \end{aligned}$$
(30)

Since \(\delta <\frac{\epsilon -\sqrt{2\epsilon }}{\epsilon }\), we have that \(\epsilon \delta ^2-2\epsilon \delta +\epsilon -2>0\). Therefore, from (29) and (30), we have

$$\begin{aligned} \Gamma _{n+1}-\Gamma _{n} \le -\beta \Vert x_{n+1}-x_{n}\Vert ^{2}, \end{aligned}$$
(31)

where \(\beta :=\epsilon \delta ^2-2\epsilon \delta +\epsilon -2>0\). Hence, \(\{\Gamma _n\}\) is non-increasing. Furthermore,

$$\begin{aligned} \Gamma _{n}= & {} \Vert x_{n}-x^*\Vert ^{2}-\Big (\alpha _{n}\theta _{n}+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^{2}+\sigma _n\Vert x_{n}-x_{n-1}\Vert ^{2}\nonumber \\\ge & {} \Vert x_{n}-x^*\Vert ^{2}-(\alpha _{n}\theta _{n}+\delta (1-\alpha _n))\Vert x_{n-1}-x^*\Vert ^{2}. \end{aligned}$$
(32)

So,

$$\begin{aligned} \Vert x_{n}-x^*\Vert ^{2}\le & {} \Big (\alpha _{n}\theta _{n}+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^{2}+\Gamma _{n}\nonumber \\\le & {} \Big (\alpha _{n}+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^{2}+\Gamma _n\nonumber \\\le & {} \Big (\frac{1}{1+\epsilon }+\delta (1-\alpha )\Big )\Vert x_{n-1}-x^*\Vert ^{2}+\Gamma _n\nonumber \\= & {} \gamma \Vert x_{n-1}-x^*\Vert ^{2}+\Gamma _n\nonumber \\\le & {} \gamma \Vert x_{n-1}-x^*\Vert ^{2}+\Gamma _1\nonumber \\&\vdots \nonumber \\\le & {} \gamma ^{n}\Vert x_{0}-x^*\Vert ^{2}+(1+\gamma +\cdots + \gamma ^{n-1})\Gamma _{1}\nonumber \\\le & {} \gamma ^{n}\Vert x_{0}-x^*\Vert ^{2}+\frac{\Gamma _{1}}{1-\gamma }, \end{aligned}$$
(33)

where \(\gamma := \frac{1}{1+\epsilon }+\delta (1-\alpha ) \in (0,1)\) since \(\delta<\frac{\epsilon -\sqrt{2\epsilon }}{\epsilon }<\frac{\epsilon }{(1+\epsilon )(1-\alpha )}, \alpha \in (0,1)\) by the choice of \(\delta \). Hence, \(\{\Vert x_{n}-x^*\Vert \}\) is bounded and so is \(\{x_n\}\). Also,

$$\begin{aligned} -\gamma \Vert x_{n-1}-x^*\Vert ^2\le & {} \Vert x_n-x^*\Vert ^2 -\gamma \Vert x_{n-1}-x^*\Vert ^2\nonumber \\\le & {} \Gamma _n \le \Gamma _1. \end{aligned}$$

Now,

$$\begin{aligned} \Gamma _{n+1}= & {} \Vert x_{n+1}-x^*\Vert ^{2}-\Big (\alpha _{n+1}\theta _{n+1}+\delta (1-\alpha _{n+1})\Big )\Vert x_{n}-x^*\Vert ^{2}\nonumber \\&\quad +\, \sigma _{n+1}\Vert x_{n+1}-x_{n}\Vert ^{2}\nonumber \\\ge & {} -\Big (\alpha _{n+1}\theta _{n+1}+\delta (1-\alpha _{n+1})\Big )\Vert x_{n}-x^*\Vert ^{2}. \end{aligned}$$
(34)

Using (33) and (34), we have

$$\begin{aligned} -\Gamma _{n+1}\le & {} \Big (\alpha _{n+1}\theta _{n+1}+\delta (1-\alpha _{n+1})\Big )\Vert x_{n}-x^*\Vert ^{2}\nonumber \\\le & {} \gamma \Vert x_{n}-x^*\Vert ^{2}\nonumber \\\le & {} \gamma ^{n+1}\Vert x_0-x^*\Vert ^{2}+\frac{\gamma \Gamma _{1}}{1-\gamma }. \end{aligned}$$
(35)

By (31) and (35), we get

$$\begin{aligned} \beta \sum _{k=1}^{n}\Vert x_{k+1}-x_{k}\Vert ^{2}\le & {} \Gamma _{1}-\Gamma _{n+1}\nonumber \\\le & {} \gamma ^{n+1}\Vert x_0-x^*\Vert ^{2}+\frac{\Gamma _{1}}{1-\gamma }. \end{aligned}$$
(36)

Therefore,

$$\begin{aligned} \sum _{n=1}^{\infty }\Vert x_{n+1}-x_{n}\Vert ^{2}\le \frac{\Gamma _{1}}{\beta (1-\gamma )} <+\infty . \end{aligned}$$
(37)

This implies that \(\underset{n\rightarrow \infty }{\lim }\Vert x_{n+1}-x_{n}\Vert =0.\) From (26) we get

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} \Big (1+\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_n-x^*\Vert ^2-\Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^2\nonumber \\&\quad -\, \rho _n\Vert x_{n+1}-x_n\Vert ^2+\sigma _n\Vert x_n-x_{n-1}\Vert ^2\nonumber \\\le & {} \Vert x_n-x^*\Vert ^2+(\alpha _n+\delta (1-\alpha _n))(\Vert x_n-x^*\Vert ^2-\Vert x_{n-1}-x^*\Vert ^2)\nonumber \\&\quad +\, \sigma _n \Vert x_n-x_{n-1}\Vert ^2\nonumber \\\le & {} \Vert x_n-x^*\Vert ^2+(\alpha _n+\delta (1-\alpha _n))(\Vert x_n-x^*\Vert ^2-\Vert x_{n-1}-x^*\Vert ^2)\nonumber \\&\quad +\, \Big [(1-\alpha )\delta (1+\delta )+\frac{2}{1+\epsilon }\nonumber \\&\quad +\, \frac{(1-\alpha )}{\alpha }(\delta -\delta ^2) \Big ]\Vert x_n-x_{n-1}\Vert ^2, \end{aligned}$$
(38)

where

$$\begin{aligned} \sigma _n \le (1-\alpha )\delta (1+\delta )+\frac{2}{1+\epsilon }+\frac{(1-\alpha )}{\alpha }(\delta -\delta ^2), \forall n \ge 1. \end{aligned}$$

Note also that

$$\begin{aligned} \alpha _n +\delta (1-\alpha _n)< \frac{1}{1+\epsilon }+\delta (1-\alpha )<1 \end{aligned}$$

since \(\delta <\frac{\epsilon }{(1+\epsilon )(1-\alpha )}\) because \(\delta<\frac{\epsilon -\sqrt{2\epsilon }}{\epsilon }< \frac{\epsilon }{(1+\epsilon )(1-\alpha )}\) for \(\alpha \in (0,1)\) and \(\epsilon \in (2,\infty )\). Invoking Lemma 2.5 in (38) (and noting (37)), we get

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }\Vert x_n-x^*\Vert \ \ \mathrm{exists. } \end{aligned}$$

Therefore, \( \{ x_n \} \) is bounded. \(\square \)

Theorem 4.2

Let the sequence \( \{ x_n \} \) be generated by Algorithm 1. If Assumption 3.1 holds, then it converges weakly to a point in S.

Proof

From \(\underset{n\rightarrow \infty }{\lim }\Vert x_{n+1}-x_{n}\Vert =0\), we have

$$\begin{aligned} \Vert x_{n+1}-z_n\Vert \le&\ \Vert x_{n+1}-x_n\Vert + \Vert x_{n}-z_n\Vert \\ =&\ \Vert x_{n+1}-x_n\Vert + \delta \Vert x_{n}-x_{n-1}\Vert \, \rightarrow 0,\ n\rightarrow \infty . \end{aligned}$$

Also,

$$\begin{aligned} \Vert x_{n+1}-w_n\Vert\le & {} \Vert x_{n+1}-x_n\Vert +\Vert x_n-w_n\Vert \\\le & {} \Vert x_{n+1}-x_n\Vert +\Vert x_{n}-x_{n-1}\Vert \rightarrow 0, n\rightarrow \infty . \end{aligned}$$

Now,

$$\begin{aligned} \Vert x_{n+1}-z_n\Vert =\alpha _n\Vert z_n-u_n\Vert \ge \ \alpha \Vert z_n-u_n\Vert , \end{aligned}$$

which means that

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }\Vert z_n-u_n\Vert =0. \end{aligned}$$
(39)

Furthermore,

$$\begin{aligned} \Vert w_n-z_n\Vert= & {} \Vert x_n+\delta (x_n-x_{n-1})-x_n-\theta _n(x_n-x_{n-1})\Vert \nonumber \\\le & {} \delta \Vert x_{n-1}-x_n\Vert +\theta _n\Vert x_{n}-x_{n-1}\Vert \nonumber \\\le & {} \delta \Vert x_{n-1}-x_n\Vert +\Vert x_{n}-x_{n-1}\Vert \rightarrow 0, n\rightarrow \infty , \end{aligned}$$
(40)

Now, from Algorithm 1 we have

$$\begin{aligned} \Vert u_n-z_n\Vert= & {} \frac{1}{\alpha _n}\Vert x_{n+1}-z_n\Vert \nonumber \\\le & {} \frac{1}{\alpha }\Vert x_{n+1}-z_n\Vert \rightarrow 0, n\rightarrow \infty , \end{aligned}$$
(41)

and similarly,

$$\begin{aligned} \Vert w_n-u_n\Vert \le \Vert w_n-z_n\Vert +\Vert u_n-z_n\Vert \rightarrow 0, n \rightarrow \infty . \end{aligned}$$

From (18), we have for some \(M>0\),

$$\begin{aligned} \Big (1-\frac{\lambda _n \mu }{\lambda _{n+1}}\Big )\Vert w_n-y_n\Vert ^2\le & {} \Vert w_n-x^*\Vert ^2-\Vert u_n-x^*\Vert ^2\nonumber \\= & {} \Big (\Vert w_n-x^*\Vert +\Vert u_n-x^*\Vert \Big )\Big (\Vert w_n-x^*\Vert -\Vert u_n-x^*\Vert \Big )\nonumber \\\le & {} M\Vert w_n-u_n\Vert \rightarrow 0, n \rightarrow \infty . \end{aligned}$$
(42)

By (42) (and noting that \(\lim _{n\rightarrow \infty } \lambda _n=\lambda \)), we see that \(\lim _{n\rightarrow \infty }\Vert w_n-y_n\Vert =0\). Also

$$\begin{aligned} \Vert x_n-z_n \Vert \le \Vert x_n-x_{n+1}\Vert +\Vert x_{n+1}-z_n \Vert \rightarrow 0, n \rightarrow \infty \end{aligned}$$
(43)

and

$$\begin{aligned} \Vert x_n-w_n \Vert \le \Vert x_n-x_{n+1}\Vert +\Vert x_{n+1}-w_n \Vert \rightarrow 0, n \rightarrow \infty . \end{aligned}$$
(44)

By Lemma 4.1, \(\{x_n\}\) is bounded. Hence, let \(v^*\) be a weak cluster point of \(\{x_n\}.\) Then, we can choose a subsequence of \(\{x_n\},\) denoted by \(\{x_{n_k}\}\) such that \(x_{n_k}\rightharpoonup v^*\in H.\) Since \(\lim _{n\rightarrow \infty } \Vert x_n-w_n\Vert =0\), we have that \(w_{n_k}\rightharpoonup v^*\in H.\) Therefore, we obtain from (42) that \(\lim _{k\rightarrow \infty } \Vert w_{n_k}-y_{n_k}\Vert =0\). Now using Lemma [29, Lemma 3.7], we have that \(v^* \in S\). Since \(\lim _{n\rightarrow \infty }\Vert x_n-x^*\Vert \) exists for any \(x^* \in S\) and every sequential weak cluster point of \(\{x_n\}\) is in S, the two assumptions of Lemma 2.6 are verified. Therefore, \(\{x_{n}\}\) converges weakly to a point in S. \(\square \)

Remark 4.3

All the results in this section can still be obtained for the case where A is a pseudo-monotone operator, L-Lipschitz continuous on bounded subsets of H and the functional \(g(x):=\Vert Ax\Vert , x \in H\) is weakly lower semi-continuous on H.

5 Strong Convergence

In this section, we give strong convergence result of our proposed Algorithm 1 when the operator A in VI(A, C) (1) is strongly pseudo-monotone and Lipschitz continuous on H. The strong convergence result is obtained without the prior knowledge of both the modulus of strong pseudo-monotonicity and the Lipschitz constant of the cost operator A.

Theorem 5.1

Suppose Assumption 3.1(a), (e) and (f) hold. Let the sequence \( \{ x_n \} \) be generated by Algorithm 1. If A is strongly pseudo-monotone and Lipschitz continuous on H, then \( \{ x_n \} \) converges strongly to the unique solution \(x^*\) of VI(A, C) (1).

Proof

Observe that the strong pseudo-monotonicity of A implies that VI(A, C) (1) has a unique solution. Let us denote this unique solution by \(x^*\). Hence, \(\langle Ax^*,y_n-x^*\rangle \ge 0\). By the strong pseudo-monotonicity of A, we have \(\langle Ay_n,y_n-x^*\rangle \ge \eta \Vert y_n-x^* \Vert ^2\), where \(\eta \) is some positive constant. Thus,

$$\begin{aligned} \langle Ay_n,y_n-u_n+u_n-x^*\rangle \ge \eta \Vert y_n-x^* \Vert ^2. \end{aligned}$$

and

$$\begin{aligned} \langle Ay_n,x^*-u_n\rangle \le \langle Ay_n,y_n-u_n\rangle -\eta \Vert y_n-x^* \Vert ^2. \end{aligned}$$
(45)

Using (11) and (53), we get

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-\lambda _nAy_n-x^*\Vert ^2- \Vert w_n-\lambda _nAy_n-u_n\Vert ^2\nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n\Vert ^2+ 2 \lambda _n \langle Ay_n, x^*-u_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n\Vert ^2+ 2 \lambda _n \langle Ay_n, y_n-u_n\rangle \nonumber \\&\quad -\, 2\lambda _n\eta \Vert y_n-x^* \Vert ^2\nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n+y_n-y_n-u_n\Vert ^2+ 2 \lambda _n \langle Ay_n, y_n-u_n\rangle \nonumber \\&\quad -\, 2\lambda _n\eta \Vert y_n-x^* \Vert ^2\nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2-2\lambda _n\eta \Vert y_n-x^* \Vert ^2\nonumber \\&\quad +\, 2 \langle w_n-\lambda _nAy_n-y_n, u_n-y_n\rangle . \end{aligned}$$
(46)

Using (16), we also have

$$\begin{aligned} \langle w_n-\lambda _n Ay_n-y_n,u_n-y_n\rangle \le \lambda _n\langle Aw_n-Ay_n,u_n-y_n\rangle . \end{aligned}$$

By (46), we get

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2-2\lambda _n\eta \Vert y_n-x^* \Vert ^2\nonumber \\&\quad +\, 2 \langle w_n-\lambda _nAy_n-y_n, u_n-y_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2-2\lambda _n\eta \Vert y_n-x^* \Vert ^2\nonumber \\&\quad +\, 2 \lambda _n\langle Aw_n-Ay_n,u_n-y_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2-2\lambda _n\eta \Vert y_n-x^* \Vert ^2\nonumber \\&\quad +\, \frac{\lambda _n \mu }{\lambda _{n+1}}\Vert w_n-y_n\Vert ^2+\frac{\lambda _n \mu }{\lambda _{n+1}}\Vert u_n-y_n\Vert ^2, \end{aligned}$$
(47)

where

$$\begin{aligned} 2\langle Aw_n-Ay_n,u_n-y_n\rangle\le & {} 2\Vert Aw_n-Ay_n\Vert \Vert u_n-y_n\Vert \\\le & {} \frac{2\mu }{\lambda _{n+1}}\Vert w_n-y_n\Vert \Vert u_n-y_n\Vert \\\le & {} \frac{\mu }{\lambda _{n+1}}\Vert w_n-y_n\Vert ^2+\frac{\mu }{\lambda _{n+1}}\Vert u_n-y_n\Vert ^2. \end{aligned}$$

Since \(\lim _{n\rightarrow \infty } \lambda _n=\lambda \) and the sequence \(\{\lambda _n\}\) is monotonically decreasing, we have \( \lambda _n \ge \lambda \; \; \forall n\ge 1\). Let \(\rho \) be a fixed number in the interval \((\mu ,1)\). Since \(\lim _{n\rightarrow \infty }\frac{\lambda _n \mu }{\lambda _{n+1}}=\mu <\rho \), there exists a natural number N such that \(\frac{\lambda _n \mu }{\lambda _{n+1}}< \rho \; \; \forall n \ge N\). So, \(\forall n \ge N\), we have

$$\begin{aligned} \lambda _n \ge \lambda , \; \; \frac{\lambda _n \mu }{\lambda _{n+1}}<\rho . \end{aligned}$$
(48)

Plugging (48) in (47), we have \(\forall n \ge N\),

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-x^*\Vert ^2-(1-\rho )\Vert w_n-y_n\Vert ^2-(1-\rho )\Vert y_n-u_n\Vert ^2-2\lambda \eta \Vert y_n-x^* \Vert ^2\nonumber \\= & {} \Vert (1+\theta _n)(x_n-x^*)-\theta _n(x_{n-1}-x^*)\Vert ^{2}-(1-\rho )\Vert w_n-y_n\Vert ^2\nonumber \\&\quad -\, (1-\rho )\Vert y_n-u_n\Vert ^2-2\lambda \eta \Vert y_n-x^* \Vert ^2\nonumber \\= & {} (1+\theta _n)\Vert x_n-x^*\Vert ^{2}-\theta _n\Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \theta _n(1+\theta _n)\Vert x_n-x_{n-1}\Vert ^{2}-(1-\rho )\Vert w_n-y_n\Vert ^2\nonumber \\&\quad -\, (1-\rho )\Vert y_n-u_n\Vert ^2-2\lambda \eta \Vert y_n-x^* \Vert ^2. \end{aligned}$$
(49)

Repeating similar arguments from (20) to (26), we obtain

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} \Big (1+\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_n-x^*\Vert ^2-\Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big )\Vert x_{n-1}-x^*\Vert ^2\nonumber \\&\quad -\, \rho _n\Vert x_{n+1}-x_n\Vert ^2+\sigma _n\Vert x_n-x_{n-1}\Vert ^2+2\alpha _n\lambda \eta \Vert y_n-x^* \Vert ^2, \forall n \ge N.\nonumber \\ \end{aligned}$$
(50)

Therefore,

$$\begin{aligned} 2\alpha \lambda \eta \Vert y_n-x^* \Vert ^2\le & {} \Vert x_n-x^*\Vert ^2-\Vert x_{n+1}-x^* \Vert ^2\nonumber \\&\quad +\, \Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big ) \Big (\Vert x_n-x^*\Vert ^2-\Vert x_{n-1}-x^* \Vert ^2 \Big )\nonumber \\&\quad +\, \sigma _n\Vert x_n-x_{n-1}\Vert ^2\nonumber \\\le & {} \Vert x_n-x^*\Vert ^2-\Vert x_{n+1}-x^* \Vert ^2\nonumber \\&\quad +\, \Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big ) \Big (\Vert x_n-x^*\Vert ^2-\Vert x_{n-1}-x^* \Vert ^2 \Big )\nonumber \\&\quad +\, M^*\Vert x_n-x_{n-1}\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} M^*:=(1-\alpha )\delta (1+\delta )+\frac{2}{1+\epsilon }- \frac{(1-\alpha )(\delta ^2-\delta )}{\alpha }. \end{aligned}$$

Hence

$$\begin{aligned} 2\alpha \lambda \eta \sum _{k=N}^{n} \Vert y_k-x^* \Vert ^2\le & {} \Vert x_N-x^*\Vert ^2-\Vert x_{n+1}-x^* \Vert ^2\nonumber \\&\quad +\, \Big (\alpha _n\theta _n+\delta (1-\alpha _n)\Big ) \Vert x_n-x^*\Vert ^2\nonumber \\&\quad -\, \Big (\alpha _{N-1}\theta _{N-1}+\delta (1-\alpha _{N-1})\Big )\Vert x_{N-1}-x^* \Vert ^2\nonumber \\&\quad +\, M^*\sum _{k=N}^{n} \Vert x_k-x_{k-1}\Vert ^2. \end{aligned}$$

Since the sequence \(\{x_n\}\) is bounded and \(\sum _{k=N}^{\infty } \Vert x_k-x_{k-1}\Vert ^2<\infty \) by (37), we have that \(\sum _{k=N}^{\infty } \Vert y_k-x^* \Vert ^2<\infty \). Hence \(\underset{n\rightarrow \infty }{\lim }\Vert y_n-x^* \Vert =0\). Consequently, we get

$$\begin{aligned} \Vert x_n-x^* \Vert \le \Vert x_n-w_n \Vert +\Vert w_n-y_n \Vert +\Vert y_n-x^* \Vert \rightarrow 0, n \rightarrow \infty . \end{aligned}$$

This concludes the proof. \(\square \)

Remark 5.2

Theorem 5.1 is obtained for the sequence \(\{x_n\}\) generated by Algorithm 1, which is a subgradient extragradient method with double inertial extrapolation steps without a priori knowledge of the modulus of strong pseudo-monotonicity and the Lipschitz constant of A. As far as we know, our result is one of the few available strong convergence results for solving VI(A, C) (1) with a combination of subgradient extragradient method and double inertial extrapolation steps. The benefits of adding double inertial extrapolation step as against single inertial extrapolation step are discussed in the numerical illustrations given in Sect. 7. \(\Diamond \)

6 Linear Convergence

In this section, we give linear rate of convergence of sequence \( \{ x_n \} \) generated by our proposed Algorithm 1 to the unique solution \(x^*\) of VI(A, C)(1) under the following assumptions:

Assumption 6.1

  1. (a)

    The feasible set C is a nonempty, closed, and convex subset of H.

  2. (b)

    \( A: H \rightarrow H \) is \(\eta \) strongly pseudo-monotone and L-Lipschitz continuous.

  3. (c)

    Choose the constant step size \(\lambda \in \Big (0, \frac{1}{L}\Big )\) such that \(\tau :=1-\frac{1}{2}\min \{1-\lambda L, 2\lambda \eta \} \in (\frac{1}{2},1)\).

  4. (d)

    Take \(\delta =0\) and choose \( \theta _n=\theta \in [0,1]\) such that \(0\le \theta <\frac{1-\tau }{\tau }\).

  5. (e)

    \( \alpha _n=\alpha \in (0,\frac{1}{3})\).

Under Assumption 6.1, our proposed Algorithm 1 reduces to the following Algorithm.

figure b

Using Assumption 6.1, we now give the linear convergence of Algorithm 2 below.

Theorem 6.2

Suppose that Assumption 6.1 is fulfilled. Then \( \{x_n\}_{n=1}^\infty \) generated by Algorithm 2 converges linearly to the unique point in S.

Proof

Let \(x^* \in S\) be the unique solution of VI(A, C) (1). Since A is \(\eta \)-strongly pseudo-monotone, we have that

$$\begin{aligned} \langle Ay_n,y_n-x^*\rangle \ge \eta \Vert y_n-x^* \Vert ^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \langle Ay_n,u_n-x^*\rangle= & {} \langle Ay_n,u_n-y_n\rangle + \langle Ay_n,y_n-x^*\rangle \\\ge & {} \eta \Vert y_n-x^*\Vert ^2+\langle Ay_n,y_n-x^*\rangle . \end{aligned}$$

Hence,

$$\begin{aligned} -2\lambda \langle Ay_n,u_n-x^*\rangle\le & {} -2\lambda \eta \Vert y_n-x^* \Vert ^2\nonumber \\&-2\lambda \langle Ay_n,u_n-y_n\rangle . \end{aligned}$$
(53)

By (11) and (53), we have

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-\lambda Ay_n-x^*\Vert ^2-\Vert w_n-\lambda Ay_n-u_n\Vert ^2\nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n\Vert ^2-2\lambda \langle Ay_n,u_n-x^* \rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n\Vert ^2-2\lambda \eta \Vert y_n-x^* \Vert ^2\nonumber \\&\quad -\, 2\lambda \langle Ay_n,u_n-y_n\rangle \nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-u_n+y_n-y_n\Vert ^2-2\lambda \eta \Vert y_n-x^* \Vert ^2\nonumber \\&\quad -\, 2\lambda \langle Ay_n,u_n-y_n\rangle \nonumber \\= & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2 \nonumber \\&\quad -\, 2\lambda \eta \Vert y_n-x^* \Vert ^2+2\langle w_n-\lambda Ay_n-y_n,u_n-y_n\rangle . \end{aligned}$$
(54)

Note that from the definition of \(T_n\), we get

$$\begin{aligned} \langle w_n-\lambda Aw_n-y_n,u_n-y_n\rangle \le 0 \end{aligned}$$

and thus

$$\begin{aligned} \langle w_n-\lambda Ay_n-y_n,u_n-y_n\rangle \le \lambda \langle Aw_n-Ay_n,u_n-y_n\rangle . \end{aligned}$$
(55)

Hence,

$$\begin{aligned} \Vert u_n-x^*\Vert ^2\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2 \nonumber \\&\quad -\, 2\lambda \eta \Vert y_n-x^* \Vert ^2+2\langle w_n-\lambda Ay_n-y_n,u_n-y_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_n-u_n\Vert ^2 \nonumber \\&\quad -\, 2\lambda \eta \Vert y_n-x^* \Vert ^2+2\lambda \langle Aw_n-Ay_n,u_n-y_n\rangle \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-(1-\lambda L)\Vert w_n-y_n\Vert ^2-(1-\lambda L)\Vert y_n-u_n\Vert ^2 \nonumber \\&\quad -\, 2\lambda \eta \Vert y_n-x^* \Vert ^2\nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-(1-\lambda L)\Vert w_n-y_n\Vert ^2-2\lambda \eta \Vert y_n-x^* \Vert ^2 \nonumber \\\le & {} \Vert w_n-x^*\Vert ^2-\frac{1}{2}\min \{1-\lambda L,2\lambda \eta \}\Vert w_n-x^* \Vert ^2 \nonumber \\= & {} \Big (1-\frac{1}{2}\min \{1-\lambda L,2\lambda \eta \}\Big )\Vert w_n-x^* \Vert ^2. \end{aligned}$$
(56)

From Algorithm 2, we get

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2= & {} \Vert (1-\alpha )(x_n-x^*)+\alpha (u_n-x^*)\Vert ^{2}\nonumber \\= & {} (1-\alpha ) \Vert x_n-x^*\Vert ^2+\alpha \Vert u_n-x^*\Vert ^2\nonumber \\&\quad -\, \alpha (1-\alpha )\Vert x_n-u_n\Vert ^2\nonumber \\\le & {} (1-\alpha ) \Vert x_n-x^*\Vert ^2+\alpha \tau \Vert w_n-x^*\Vert ^2\nonumber \\&\quad -\, \frac{(1-\alpha )}{\alpha }\Vert x_{n+1}-x_n\Vert ^2\nonumber \\\le & {} (1-\alpha ) \Vert x_n-x^*\Vert ^2+\alpha \tau \Big [(1+\theta )\Vert x_n-x^*\Vert ^{2}\nonumber \\&\quad -\, \theta \Vert x_{n-1}-x^*\Vert ^{2}+\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^{2}\Big ]\nonumber \\&\quad -\, \frac{(1-\alpha )}{\alpha }\Vert x_{n+1}-x_n\Vert ^2\nonumber \\= & {} (1-\alpha (1-\tau (1+\theta )))\Vert x_n-x^*\Vert ^2-\theta \alpha \tau \Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \theta (1+\theta )\alpha \tau \Vert x_n-x_{n-1}\Vert ^{2}-\frac{(1-\alpha )}{\alpha }\Vert x_{n+1}-x_n\Vert ^2. \end{aligned}$$
(57)

This implies that

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2+\frac{(1-\alpha )}{\alpha }\Vert x_{n+1}-x_n\Vert ^2\le & {} (1-\alpha (1-\tau (1+\theta )))\Vert x_n-x^*\Vert ^2\nonumber \\&\quad -\, \theta \alpha \tau \Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \theta (1+\theta )\alpha \tau \Vert x_n-x_{n-1}\Vert ^{2}. \end{aligned}$$
(58)

Since \(0<\alpha < \frac{1}{2}\), we have from (58) that

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2+\Vert x_{n+1}-x_n\Vert ^2\le & {} (1-\alpha (1-\tau (1+\theta )))\Vert x_n-x^*\Vert ^2\nonumber \\&\quad -\, \theta \alpha \tau \Vert x_{n-1}-x^*\Vert ^{2}\nonumber \\&\quad +\, \theta (1+\theta )\alpha \tau \Vert x_n-x_{n-1}\Vert ^{2}\nonumber \\\le & {} (1-\alpha (1-\tau (1+\theta )))\Vert x^k-x^*\Vert ^2\nonumber \\&\quad +\, \theta (1+\theta )\alpha \tau \Vert x^k-x^{k-1}\Vert ^{2}\nonumber \\= & {} (1-\alpha (1-\beta ^2(1+\theta )))\Big [\Vert x_n-x^*\Vert ^2\nonumber \\&\quad +\, \frac{\theta (1+\theta )\alpha \tau }{(1-\alpha (1-\tau (1+\theta )))}\Vert x_n-x_{n-1}\Vert ^{2} \Big ] \nonumber \\\le & {} (1-\alpha (1-\tau (1+\theta )))(\Vert x_n-x^*\Vert ^2\nonumber \\&\quad +\, \Vert x_n-x_{n-1}\Vert ^{2}), \end{aligned}$$
(59)

where the last inequality follows from the fact that \(\frac{\theta (1+\theta )\alpha \tau }{(1-\alpha (1-\tau (1+\theta )))}<1\).

Now, define \(a_n:=\Vert x_n-x^*\Vert ^2+\Vert x_n-x_{n-1}\Vert ^{2}\). Then we obtain from (59) that

$$\begin{aligned} a_{n+1} \le (1-\alpha (1-\tau (1+\theta )))a_n. \end{aligned}$$
(60)

By induction, we obtain

$$\begin{aligned} a_{n+1}\le (1-\alpha (1-\tau (1+\theta )))^na_1. \end{aligned}$$
(61)

Therefore, by the definition of \(a_n\), we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le (1-\alpha (1-\tau (1+\theta )))^na_1, n\ge 1. \end{aligned}$$

Hence, we obtain our desired conclusion. \(\square \)

Remark 6.3

  1. (a)

    If we choose the step size \(\lambda \) in Algorithm 2 such that \(\lambda \in \Big (\frac{1}{2\eta +L}, \frac{1}{L}\Big )\), then \(\tau =1-\frac{1}{2}\min \{1-\lambda L, 2\lambda \eta \}=1-\frac{1-\lambda L}{2} \in (\frac{1}{2},1)\). Thus Assumption 6.1(c) is fulfilled with this choice of \(\lambda \).

  2. (b)

    As \(\tau \) in Assumption 6.1(c) approaches \(\frac{1}{2}\), so is \(\theta \) in Algorithm 2 approaches 1 by Assumption 6.1(d).

7 Numerical Examples

In this section we present many computational experiments and compare the method we proposed in Sect. 3 with some existing methods which are available in the literature. All the codes were written in MATLAB R2019a and ran on a PC Desktop Intel(R) Core(TM) i7-6600U CPU @ 2.60GHz 2.81 GHz, RAM 16.00 GB.

In all these examples, we present numerical comparisons of our proposed Algorithm 1 with the methods in [7, 13, 27, 30, 34, 35]. In all the numerical implementations, we choose \(\delta \in \Big [0,\min \Big \{\frac{\epsilon -\sqrt{2\epsilon }}{\epsilon },\theta _1\Big \}\Big ),~~ \epsilon \in (2,\infty )\), \(\theta _n\in [0,1]\) and \(\alpha _n \in \Big (0,\frac{1}{1+\epsilon }\Big ),~~ \epsilon \in (2,\infty )\) in our Algorithm 1 for the numerical comparisons with the methods in [7, 13, 27, 30, 34, 35].

For convenience, [7, Algorithm 3.1] is denoted by “Chang Alg.”, [13, Algorithm 3.1] is denoted by “Fan Alg.”, [27, Algorithm 1] is denoted by “Shehu Alg.”, [30, Algorithm 3.1] is denoted by “Thong Alg.”, [34, (2) Theorem 3.1] is denoted by “Yang Alg.”, and [35, Algorithm 2] is denoted by “Yang2 Alg.” in this section.

Example 7.1

We define \(A: \mathbb {R}^m \rightarrow \mathbb {R}^m\) by

$$\begin{aligned} Ax = \left( e^{-x^TQx} + \beta \right) (Px + q), \end{aligned}$$

where Q is a positive definite matrix (i.e, \(x^TQx \ge \theta \Vert x\Vert ^2 \ \forall x\in \mathbb {R}^m\)), P is a positive semi-definite matrix, \(q\in \mathbb {R}^m\) and \(\beta > 0.\) It can be seen that A is differentiable and by the Mean Value Theorem A is Lipschitz continuous. It is also shown in [4, Example 2.1] that A is pseudo-monotone but not monotone.

Take \(C:=\{x\in \mathbb {R}^m | Bx \le b\},\) where B is a matrix of size \(l^*\times m\) and \(b\in \mathbb {R}^{l^*}_+\) with \(l^* = 10.\) Let us take \(x_0 = (1,1,...,1)^T\) and \(x_1\) is generated randomly in \(\mathbb {R}^m\). In this example, we use the stopping criterion \(\Vert w_n-y_n\Vert <10^{-5}\) with different dimensions m.

Table 1 Methods parameters for Example 7.1
Full size table
Table 2 Example 7.1 comparison for different values of m
Full size table
Table 3 Methods parameters for Example 7.2
Full size table
Table 4 Example 7.2 comparison for different k and m
Full size table
Table 5 Methods parameters for Example 7.3
Full size table
Table 6 Example 7.3 comparison for different cases
Full size table

Example 7.2

This example is taken from [15] and has been considered by many authors for numerical experiments (see, for example, [22, 26, 28]). The operator A is defined by \( Ax:= Mx+q \), where \( M= BB^T+ S + D \), with \( B, S, D \in {\mathbb {R}}^{m \times m} \) randomly generated matrices such that S is skew-symmetric (hence the operator does not arise from an optimization problem), D is a positive definite diagonal matrix (hence the variational inequality has a unique solution) and \( q = 0 \). The feasible set C is described by the linear inequality constraints \( B x \le b \) for some random matrix \(B \in {\mathbb {R}}^{k \times m} \) and a random vector \( b \in {\mathbb {R}}^k \) with nonnegative entries. Hence the zero vector is feasible and therefore the unique solution of the corresponding variational inequality. These projections are computed using the MATLAB solver fmincon. Hence, for this class of problems, the evaluation of A is relatively inexpensive, whereas projections are costly. We present the corresponding numerical results (number of iterations and CPU times in seconds) using different dimensions m and different numbers of inequality constraints k.

We choose the stopping criterion as \(\Vert e_n\Vert _2:=\Vert x_n\Vert \le \epsilon \), where \(\epsilon = 0.001.\) The sizes \(k =20, 30\) and \(m = 10, 20\). The matrices B, S, D and the vector b are generated randomly.

Fig. 1
figure 1

Example 7.1: \(m=100\)

Full size image
Fig. 2
figure 2

Example 7.1: \(m =120\)

Full size image
Fig. 3
figure 3

Example 7.2: \((m,k)=(10,20)\)

Full size image
Fig. 4
figure 4

Example 7.2: \((m,k)=(20,20)\)

Full size image
Fig. 5
figure 5

Example 7.2: \((m,k)=(10,30)\)

Full size image
Fig. 6
figure 6

Example 7.2: \((m,k)=(20,30)\)

Full size image

Next, we give some examples in an infinite dimensional Hilbert space.

Example 7.3

Let \(H:=L^2([0,1])\) with norm and inner product given by \(\Vert x\Vert :=\Big ( \int _{0}^{1}x(t)^2dt\Big )^{\frac{1}{2}}\) and \(\langle x,y \rangle :=\int _{0}^{1}x(t)y(t)dt,~~x,y \in H\), respectively. We define the feasible set C by: \(C:=\{x \in L^2([0,1]):\int _{0}^{1}tx(t)dt= 2\}\). Define \(A:L^2([0,1])\rightarrow L^2([0,1])\) by

$$\begin{aligned} Ax(t):=\max \{x(t),0\},~~x \in L^2([0,1]), \; \; t \in [0,1]. \end{aligned}$$

Then A is monotone and Lipschitz with \(L=1\). Observe that \(S\ne \emptyset \) since \(0 \in S\) and that

$$\begin{aligned} P_C(x)(t):=x(t)-\frac{\int _{0}^{1}tx(t)dt-2}{\int _{0}^{1}t^{2}dt}t, ~~t \in [0,1]. \end{aligned}$$

We set the stopping criterion to be \(e_n:=\Vert x_{n+1}-x_n\Vert <\epsilon \), where \(\epsilon = 10^{-4}\) and consider four different cases as follows:

Case I \(\displaystyle x_0 = \frac{1}{13}\left[ 97t^2 + 4t \right] \) and \(\displaystyle x_1 = \frac{1}{250}\left[ t^2 - e^{-7t} \right] \)

Case II \(\displaystyle x_0 = \frac{1}{13}\left[ 97t^2 + 4t \right] \) and \(\displaystyle x_1 = \frac{1}{100}\left[ \sin (3t) + \cos (10t) \right] \)

Case III \(\displaystyle x_0 = \frac{1}{250}\left[ t^2 - e^{-7t} \right] \) and \(\displaystyle x_1 = \frac{1}{100}\left[ \sin (3t) + \cos (10t) \right] \)

Case IV \(\displaystyle x_0 = \frac{1}{100}\left[ \sin (3t) + \cos (10t) \right] \) and \(\displaystyle x_1 = \frac{1}{13}\left[ 97t^2 + 4t \right] \)

Fig. 7
figure 7

Example 7.3: Case I

Full size image
Fig. 8
figure 8

Example 7.3: Case II

Full size image
Fig. 9
figure 9

Example 7.3: Case III

Full size image
Fig. 10
figure 10

Example 7.3: Case IV

Full size image

The following remarks on the numerical implementations given above are in order.

Remark 7.4

  1. (1).

    The numerical results from the above Examples (both finite and infinite dimension) show that our proposed Algorithm 1 is considerably fast, easy to implement and very efficient (Table 1).

  2. (2).

    For the given Examples, our proposed Algorithm 1, which is a subgradient extragradient method with double inertial extrapolation steps, outperforms several existing subgradient extragradient methods with single inertial extrapolation step studied in [7, 13, 27, 30, 34, 35]. This is evident from Tables 2, 3, 4, 5 and 6 and Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 with respect to speed and number of iterations.

8 Conclusion

We have proposed an inertial version of the subgradient extragradient method of Censor et al. [6] with the possibility \(\theta _n=1\) for the inertial factor and self-adaptive step sizes. Thus, in contrast with the methods considered so far, our proposed method extends the choices of the inertial factor to \(\theta _n=1\). We obtain weak convergence of our method in real Hilbert spaces under simpler conditions than previously assumed for other inertial subgradient extragradient methods. We also present a strong convergence result for the case where the cost function is strongly monotone with adaptive step sizes. In all our results the Lipschitz constant (or its estimate) of the cost function is not needed during implementations. Preliminary numerical experiments show that our methods are efficient and promising. One of the goals of our future projects is to estimate the rate of convergence for Algorithm 1.