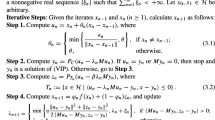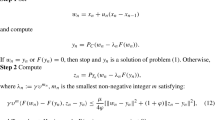1 Introduction

In this paper, we consider the classical variational inequality problem (VI) of Fichera [15, 16] and Stampacchia [37] (see also Kinderlehrer and Stampacchia [21]) in real Hilbert spaces. The (VI) is formulated as follows:

$$\begin{aligned} \text {Find a point }\ x^*\in C\ \text { such that }\ \langle Ax^*,x-x^*\rangle \ge 0 \ \text { for all }\ x\in C, \end{aligned}$$

where C is a nonempty closed convex subset in a real Hilbert space H,  \(A: H\rightarrow H\) is a single-valued mapping, \(\langle \cdot ,\cdot \rangle \) and \(\Vert \cdot \Vert \) are the inner product and the norm in H, respectively. Let us denote VI(C, A) by the solution set of the problem (VI).

In the last years, the techniques for the variational inequality problem have been applied to a variety of diverse areas, such as, operations research, nonlinear equations, and network equilibrium problems, see, for instance, [2, 3, 5, 14, 21, 24,25,26,27,28] and the extensive list of references therein.

Many authors have proposed and analyzed several methods for solving the problem (VI). One of the most popular methods is the extragradient method introduced by Korpelevich [23] which was called the extragradient method:

$$\begin{aligned} x_0\in C,\ \ y_n=P_C(x_n-\lambda Ax_n),\ \ x_{n+1}=P_C(x_n-\lambda Ay_n), \end{aligned}$$

where the mapping \(A:C\rightarrow H\) is monotone and L-Lipschitz continuous, \(\lambda \in \big (0,\dfrac{1}{L}\big )\). The algorithm converges to an element of VI(C, A) provided that VI(C, A) is nonempty.

In recent years, the extragradient method has been received great attention by many authors in various ways (see, for example, [6, 9,10,11,12, 19, 29, 30, 36, 39, 43] and the references therein).

Censor et al. [10, 11] proposed the subgradient extragradient method:

$$\begin{aligned} x_0\in H, y_n=P_C(x_n-\lambda Ax_n),\ \ x_{n+1}=P_{T_n}(x_n-\lambda Ay_n), \end{aligned}$$
(1)

where \(T_n=\{x\in H | \langle x_n -\lambda Ax_n-y_n,x-y_n\rangle \le 0\}\), the mapping \(A:H\rightarrow H\) is monotone and L-Lipschitz continuous, \(\lambda \in \big (0,\dfrac{1}{L}\big )\). This method replaces two projections onto C by one projection onto C and one onto a half-space. Since the projection onto the half-space \(T_n\) can be explicitly calculated, the subgradient extragradient requires only one projection per iteration. For this, recently, the subgradient extragradient method [10, 11] has been received great attention by many authors, they improved and extended it in various ways to obtain the weak and strong convergence of this method (see [8, 12, 22, 34, 35, 38, 39, 41, 42] and the references therein).

Inspired by the results in [10, 11], Kraikaew and Saejung [22] introduced the Halpern subgradient extragradient method for solving monotone variational inequalities as follows:

$$\begin{aligned} x_0\in H,\ \ y_n=P_C(x_n-\lambda Ax_n),\ \ x_{n+1}=\gamma _nx_0+(1-\gamma _n)P_{T_n}(x_n-\lambda Ay_n), \end{aligned}$$
(2)

where \(T_n=\{x\in H: \langle x_n-\lambda Ax_n-y_n,x-y_n\rangle \le 0\}\), the mapping \(A:H\rightarrow H\) is monotone and L-Lipschitz continuous and \(\lambda \in (0,\frac{1}{L})\), \(\{\gamma _n\}\subset (0,1)\), \(\lim _{n\rightarrow \infty } \gamma _n=0\), \(\sum _{n=1}^\infty \gamma _n =+\infty \), and they proved that the sequence \(\{x_n\}\) is generated by (2) converges strongly to a point \(x^*\), where \(x^*=P_{\mathrm{VI}(C,A)}x_0.\)

It is worth pointing out that the main shortcoming of algorithms (1) and (2) is that it requires to know the Lipschitz constant or at least to know some estimation of it. Very recently, in [42], motivated and inspired by the algorithms in [10, 11], they introduced a modified subgradient extragradient method for solving monotone variational inequalities with a new step size. It is worth pointing out that the convergence analysis of the algorithm in [42] doesn’t require either the prior knowledge of the Lipschitz constant of the variational inequality mapping or any additional evaluation of \(P_C\).

The pseudomonotone mappings in the sense of Karamardian were introduced in [20] as a generalization of the monotone mappings. The notion of the pseudomonotone mapping has found many applications in variational inequalities and economics.

It is a known fact that, in [12], Censor et al. showed that the subgradient extragradient method can be successfully applied for solving the pseudomonotone variational inequality in a finite dimensional Euclidean space. Since, in infinite dimensional spaces, the norm convergence is often more desirable, a natural question raises as follows:

How to design and extend the result of Censor et al. in [12] such that strong convergence is obtained in infinite dimensional Hilbert spaces?

To answer this question, in this paper, we develop a new version of the subgradient extragradient method with the technique of choosing stepsizes in [42] for finding an element of the set of solutions of a pseudomonotone and Lipschitz-continuous variational inequality problem in Hilbert spaces and prove that the sequence generated by the proposed algorithm converges strongly to a solution of the pseudomonotone variational inequality.

This paper is organized as follows: In Sect. 2, we recall some definitions and preliminary results for further use. In Sect. 3, we deal with analyzing the convergence of the proposed algorithm. Finally, in Sect. 4, we give several numerical experiments to illustrate the convergence of the proposed algorithm and compare it with previously known algorithms.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. The weak convergence of \(\{x_n\}\) to x is denoted by \(x_{n}\rightharpoonup x\) as \(n\rightarrow \infty \), while the strong convergence of \(\{x_n\}\) to x is written as \(x_n\rightarrow x\) as \(n\rightarrow \infty .\) For each \(x,y,z\in H\), we have

$$\begin{aligned} \Vert x+y\Vert ^2\le \Vert x\Vert ^2+2\langle y,x+y\rangle . \end{aligned}$$
(3)
$$\begin{aligned} \Vert \alpha x+\beta y+\gamma z\Vert ^2&= \alpha \Vert x\Vert ^2 + \beta \Vert y\Vert ^2 \nonumber \\&\quad +\gamma \Vert z\Vert ^2- \alpha \beta \Vert x-y\Vert ^2 - \alpha \gamma \Vert x-z\Vert ^2 - \beta \gamma \Vert y-z\Vert ^2 \end{aligned}$$
(4)

for all \(\alpha , \beta , \gamma \in [0; 1]\) with \(\alpha + \beta + \gamma = 1.\)

Definition 2.1

Let \(T:H\rightarrow H\) be a mapping. Then we have the following:

  1. (1)

    T is called L-Lipschitz continuous with \(L>0\) if

    $$\begin{aligned} \Vert Tx-Ty\Vert \le L \Vert x-y\Vert , \, \, \, \forall x,y \in H. \end{aligned}$$
  2. (2)

    T is called monotone if

    $$\begin{aligned} \langle Tx-Ty,x-y \rangle \ge 0, \, \, \, \forall x,y \in H. \end{aligned}$$
  3. (3)

    T is called pseudomonotone if

    $$\begin{aligned} \langle Tx,y-x \rangle \ge 0\,\, \Longrightarrow \,\, \langle Ty,y-x \rangle \ge 0, \, \, \, \forall x,y \in H. \end{aligned}$$
  4. (4)

    T is called sequentially weakly continuous if, for each sequence \(\{x_n\}\) in H with \(x_{n}\rightharpoonup x\) as \(n\rightarrow \infty \), \(Tx_n \rightharpoonup Tx\).

It is easy to see that every monotone operator T is pseudomonotone, but the converse is not true.

Now, we present an academic example of the variational inequality problem in an infinite dimensional space, where the cost function A is pseudomonotone, L-Lipschitz continuous and sequentially weakly continuous on C, but A fails to be a monotone mapping on H.

Example 1

Consider a Hilbert space defined as follows:

$$\begin{aligned} H=l_2:=\left\{ u=(u_1,u_2,\ldots ,u_i,\ldots ) : \sum _{i=1}^\infty |u_i|^2<+\infty \right\} \end{aligned}$$

equipped with the inner product and the induced norm on H:

$$\begin{aligned} \langle u,v\rangle =\sum _{i=1}^\infty u_i v_i,\quad \Vert u\Vert =\sqrt{\langle u,u\rangle } \end{aligned}$$

for any \(u=(u_1,u_2,\ldots ,u_i,\ldots ), v=(v_1,v_2,\ldots ,v_i,\ldots )\in H\), respectively. Let \(\alpha ,\beta \in {\mathbb {R}}\) such that \(\beta>\alpha>\dfrac{\beta }{2}>2\) and consider the set and the mapping:

$$\begin{aligned} C=\Big \{u=(u_1,u_2,\ldots ,u_i,\ldots )\in H: |u_i|\le \dfrac{1}{i}, \, \forall i\ge 1\Big \},\quad Au=(\beta -\Vert u\Vert )u. \end{aligned}$$

Then it is easy to see that \(VI(C,A)\ne \emptyset \) since \(0\in VI(C,A)\). Moreover, let

$$\begin{aligned} C_\alpha :=\{u\in H: \Vert u\Vert \le \alpha \}. \end{aligned}$$

It is known that A is pseudomonotone, \((\beta +2\alpha )\)-Lipschitz continuous on \(C_\alpha \) and A fails to be a monotone mapping on H (see [18, Example 4.1]).

Now, we show that \(C\subset C_\alpha \). Indeed, let \(u=(u_1,u_2,\ldots ,u_i,\ldots )\in C\). Then we have

$$\begin{aligned} \Vert u\Vert ^2=\sum _{i=1}^\infty |u_i|^2\le \sum _{i=1}^\infty \dfrac{1}{i^2}=1+ \sum _{i=2}^\infty \dfrac{1}{i^2}\le 1+ \sum _{i=2}^\infty \dfrac{1}{i^2-1}=1+\dfrac{3}{4}=\dfrac{7}{4}, \end{aligned}$$

which implies that \(\Vert u\Vert \le \alpha \), that is, \(u\in C_\alpha \) and so \(C\subset C_\alpha \).

Further, since \(C\subset C_\alpha \), it follows that A is pseudomonotone and \(\beta +2\alpha \)-Lipschitz continuous on C. On the other hand, since C is compact and A is continuous on H, A is sequentially weakly continuous on C.

Remark 2.1

(1) It should be noted here that the mapping A is not sequentially weakly continuous on \(C_\alpha \) since \(C_\alpha \) is not compact on H.

(2) An example on noncompact sets can be found in [4, Example 2.1], where the mapping A is pseudomonotone, Lipschitz continuous and sequentially weakly continuous.

For all point \(x\in H\), there exists a unique nearest point in C, denoted by \(P_Cx\), such that

$$\begin{aligned} \Vert x-P_Cx\Vert \le \Vert x-y\Vert , \,\,\, \forall y\in C. \end{aligned}$$

Then \(P_C\) is called the metric projection of H onto C. It is known that \(P_C\) is nonexpansive.

Lemma 2.1

([17]) Let C be a nonempty closed convex subset of a real Hilbert space H. Then, for any \(x\in H\) and \(z\in C\),

$$\begin{aligned} z=P_Cx\,\,\Longleftrightarrow \,\, \langle x-z,z-y\rangle \ge 0, \,\, \, \forall y\in C. \end{aligned}$$

Lemma 2.2

([7]) For any \(x\in H\) and \(v\in H\) with \(v\ne 0\), let \(T=\left\{ z\in H: \left\langle v, z-x\right\rangle \le 0\right\} \). Then, for all \(u\in H\), the projection \(P_T(u)\) is defined by

$$\begin{aligned} P_T(u)=u-\max \left\{ 0,\frac{\left\langle v, u-x\right\rangle }{||v||^2}\right\} v. \end{aligned}$$

In particular, if \(u\notin T\), then we have

$$\begin{aligned} P_T(u)=u-\frac{\left\langle v, u-x\right\rangle }{||v||^2}v. \end{aligned}$$

Lemma 2.2 gives us an explicit formula of the projection of any point onto a half-space. For more some properties of the metric projection, the interested reader can refer to Sect. 3 in [17] and Chapter 4 in [7].

The following lemmas are useful for the convergence of our proposed method:

Lemma 2.3

([13, Lemma 2.1]) Consider the solution set VI(C, A) of the problem (VI), where C is a nonempty closed convex subset of a real Hilbert space H and \(A : C \rightarrow H\) is pseudomonotone and continuous. Then \(x^*\in VI(C, A)\) if and only if

$$\begin{aligned} \langle Ax, x - x^*\rangle \ge 0, \,\,\, \forall x \in C. \end{aligned}$$

Lemma 2.4

( [33]) Let \(\{a_n\}\) be a sequence of nonnegative real numbers, \(\{\gamma _n\}\) be a sequence of real numbers in (0, 1) with \(\sum _{n=1}^\infty \gamma _n=\infty \) and \(\{b_n\}\) be a sequence of real numbers. Assume that

$$\begin{aligned} a_{n+1}\le (1-\gamma _n)a_n+\gamma _n b_n,\, \, \, \forall n\ge 1. \end{aligned}$$

If \(\limsup _{k\rightarrow \infty } b_{n_k} \le 0\) for every subsequence \(\{a_{n_k}\}\) of \(\{a_n\}\) satisfying

$$\begin{aligned} \liminf _{k\rightarrow \infty }(a_{n_k+1}-a_{n_k})\ge 0, \end{aligned}$$

then \(\lim _{n\rightarrow \infty }{a_n} = 0\).

3 Main results

In this section, we introduce a modified subgradient extragradient algorithm for solving the pseudomonotone variational inequality problem. Under mild assumptions, the sequence generated by the proposed method converges strongly to \(x^*\in VI(C,A)\), where

$$\begin{aligned} \Vert x^*\Vert =\min \{\Vert z\Vert : z\in VI(C,A)\}. \end{aligned}$$

First, the following conditions are assumed for the convergence of the method:

Condition 1

The feasible set C is a nonempty closed convex subset of a real Hilbert space H.

Condition 2

The mapping \(A:H\rightarrow H\) is L-Lipschitz continuous, pseudomonotone on H and the mapping \(A:H\rightarrow H\) satisfies the following condition

$$\begin{aligned} \text { whenever } \{x_n\} \subset C, x_n \rightharpoonup z, \text { one has } \Vert Az\Vert \le \liminf _{n\rightarrow \infty }\Vert Ax_n\Vert . \end{aligned}$$
(5)

Condition 3

The solution set of the problem (VI) is nonempty, that is, \(VI(C,A)\ne \emptyset \).

Condition 4

Assume that \(\{\gamma _n\}\) and \(\{\beta _n\}\) are two real sequences in (0, 1) such that \(\{\beta _n\}\subset (a,1-\gamma _n)\) for some \(a>0\) and

$$\begin{aligned} \lim _{n\rightarrow \infty }\gamma _n=0,\quad \sum _{n=1}^\infty \gamma _n=\infty . \end{aligned}$$

Now, we present our algorithm.

figure a

Remark 3.2

It is easy to show that condition (5) is weaker than the sequential weak continuity of the mapping A (see [1, 32]), which is frequently assumed in recent works on pseudomonotone variational inequality problems, (see, [40]). Indeed, if A is sequentially weakly continuous, then due to the weak lower semicontinuity of the norm, condition (5) is fulfilled. Conversely, let \(Ax = \Vert x|| x\) and suppose that \( x_n \rightharpoonup x.\) Due to the weak lower continuiuty of the norm, one has \(\Vert x\Vert \le \liminf _{n\rightarrow \infty } \Vert x_n\Vert ,\) hence,

$$\begin{aligned} \Vert Ax\Vert = \Vert x\Vert ^2 \le (\liminf _{n\rightarrow \infty }\Vert x_n\Vert )^2 \le \liminf _{n\rightarrow \infty }\Vert x_n\Vert ^2 = \liminf _{n\rightarrow \infty }\Vert Ax_n\Vert , \end{aligned}$$

Thus, condition (5) is satisfied. However, A is not sequentially weakly continuous. Indeed, let \(x_n = e_n + e_1,\) where \(\{e_n\}\) is an orthonormal system in H. Then \(x_n \rightharpoonup e_1.\) For \(n >1,\) \(Ax_n = \sqrt{2}(e_n + e_1) \rightharpoonup \sqrt{2}e_1 \ne A(e_1) = e_1.\)

Lemma 3.5

([42]) Assume that Conditions 1–3 hold. Then the sequence \(\{\lambda _n\}\) generated by (6) is a non-increasing sequence and

$$\begin{aligned} \lim _{n\rightarrow \infty } \lambda _n=\lambda \ge \min \Big \{\lambda _0,\dfrac{\mu }{L}\Big \}. \end{aligned}$$

The following lemmas are quite helpful to analyze the convergence of algorithm:

Lemma 3.6

Assume that Conditions 1–3 hold. Let \(\{w_n\}\) be a sequence generated by Algorithm 3.1 Then we have

$$\begin{aligned} \Vert w_{n}-x^*\Vert ^2\le \Vert x_n-x^*\Vert ^2 -\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-x_n\Vert ^2- \Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert w_{n}-y_n\Vert ^2\nonumber \\ \end{aligned}$$
(7)

for all \(x^*\in VI(C,A)\).

Proof

First, it is easy to see that, by the definition of \(\{\lambda _n\}\),

$$\begin{aligned} 2\langle Ax_n-Ay_n, w_n-y_n\rangle \le \dfrac{\mu }{\lambda _{n+1}}\Vert x_n-y_n\Vert ^2+\dfrac{\mu }{\lambda _{n+1}}\Vert w_n-y_n\Vert ^2,\,\,\, \forall n\ge 1. \end{aligned}$$
(8)

Indeed, if \(\langle Ax_n-Ay_n, w_n-y_n\rangle <0\), then the inequality (8) holds. Otherwise, from (6), we have

$$\begin{aligned} \lambda _{n+1}=\min \left\{ \mu \dfrac{\Vert x_n-y_n\Vert ^2+\Vert w_n-y_n\Vert ^2}{2 \langle Ax_n-Ay_n, w_n-y_n\rangle },\lambda _n\right\} \le \mu \dfrac{\Vert x_n-y_n\Vert ^2+\Vert w_n-y_n\Vert ^2}{2\langle Ax_n-Ay_n, w_n-y_n\rangle }. \end{aligned}$$

This implies that

$$\begin{aligned} 2\langle Ax_n-Ay_n, w_n-y_n\rangle \le \dfrac{\mu }{\lambda _{n+1}}\Vert x_n-y_n\Vert ^2+\dfrac{\mu }{\lambda _{n+1}}\Vert w_n-y_n\Vert ^2. \end{aligned}$$

Therefore, the inequality (8) holds. Now, using the inequality (8) and \(x^*\in VI(C,A)\subset C\subset T_n\), we prove that the inequality (7) holds. Indeed, we have

$$\begin{aligned} \Vert w_{n}-x^*\Vert ^2&=\Vert P_{T_n}(x_n-\lambda _n Ay_n)-P_{T_n}x^*\Vert ^2\le \langle w_n-x^*,x_n-\lambda _n Ay_n-x^*\rangle \\&=\dfrac{1}{2}\Vert w_n-x^*\Vert ^2+\dfrac{1}{2}\Vert x_n-\lambda _n Ay_n-x^*\Vert ^2-\dfrac{1}{2}\Vert w_n-x_n+\lambda _n Ay_n\Vert ^2\\&=\dfrac{1}{2}\Vert w_n-x^*\Vert ^2+\dfrac{1}{2}\Vert x_n-x^*\Vert ^2+\dfrac{1}{2}\lambda ^2_n \Vert Ay_n\Vert ^2- \langle x_n-x^*,\lambda _n Ay_n \rangle \\&\quad - \dfrac{1}{2}\Vert w_n-x_n\Vert ^2-\dfrac{1}{2}\lambda ^2_n \Vert Ay_n\Vert ^2-\langle w_n-x_n, \lambda _n Ay_n\rangle \\&=\dfrac{1}{2}\Vert w_n-x^*\Vert ^2+\dfrac{1}{2}\Vert x_n-x^*\Vert ^2 -\dfrac{1}{2}\Vert w_n-x_n\Vert ^2-\langle w_n-x^*, \lambda _n Ay_n\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \Vert w_n-x^*\Vert ^2\le \Vert x_n-x^*\Vert ^2 -\Vert w_{n}-x_n\Vert ^2-2\langle w_n-x^*, \lambda _n Ay_n\rangle . \end{aligned}$$
(9)

Since \(x^*\) is the solution of the problem (VI), we have \(\langle Ax^*,x-x^*\rangle \ge 0\) for all \(x\in C\). By the pseudomontonicity of A on C, we have \(\langle Ax,x-x^*\rangle \ge 0\) for all \(x\in C\). Taking \(x:=y_n\in C\), we get

$$\begin{aligned} \langle Ay_n,x^*-y_n\rangle \le 0. \end{aligned}$$

Thus we have

$$\begin{aligned} \langle Ay_n,x^*-w_n\rangle =&\langle Ay_n,x^*-y_{n}\rangle +\langle Ay_n,y_n-w_n\rangle \le \langle Ay_n,y_n-w_n\rangle . \end{aligned}$$
(10)

From (9) and (10), it follows that

$$\begin{aligned} \Vert w_n-x^*\Vert ^2&\le \Vert x_n-x^*\Vert ^2-\Vert w_n-x_n\Vert ^2+2\lambda _n\langle Ay_n,y_n-w_n\rangle \nonumber \\&=\Vert x_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_{n}-x_n\Vert ^2\nonumber \\&\quad -2\langle w_n-y_n,y_{n}-x_n \rangle +2\lambda _n\langle Ay_n,y_n-w_n\rangle \nonumber \\&= \Vert x_n-x^*\Vert ^2-\Vert w_n-y_n\Vert ^2-\Vert y_{n}-x_n\Vert ^2 +2\langle x_n-\lambda _n Ay_n-y_n,w_n-y_n\rangle . \end{aligned}$$
(11)

Since \(y_n=P_{T_n}(x_n-\lambda _n Ax_n)\) and \(w_n\in T_n\), we have

$$\begin{aligned} 2\langle x_n&-\lambda _n Ay_n-y_n,w_n-y_n\rangle \nonumber \\&=2\langle x_n-\lambda _n Ax_n-y_n,w_n-y_n\rangle +2\lambda _n \langle Ax_n-Ay_n,w_n-y_n\rangle \nonumber \\&\le 2\lambda _n \langle Ax_n-Ay_n,w_n-y_n\rangle , \end{aligned}$$
(12)

which, together with (8), implies that

$$\begin{aligned} 2\langle x_n-\lambda _n Ay_n-y_n,w_n-y_n\rangle \le \mu \dfrac{\lambda _n}{\lambda _{n+1}} \Vert x_n-y_n\Vert ^2+ \mu \dfrac{\lambda }{\lambda _{n+1}}\Vert w_n-y_n\Vert ^2 \end{aligned}$$

From (11) and (12), we get

$$\begin{aligned} \Vert w_n-x^*\Vert ^2\le&\Vert x_n-x^*\Vert ^2-\Big (1- \mu \dfrac{\lambda _n}{\lambda _{n+1}} \Big )\Vert y_{n}-x_n\Vert ^2- \Big (1- \mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert w_n-y_n\Vert ^2. \end{aligned}$$

This completes the proof. \(\square \)

Remark 3.3

Unlike the proof in [42], our Lemma 3.6 is proved when A is pseudomonotone instead of the fact that A is monotone.

We adapt the technique developed in [40] to obtain the following result.

Lemma 3.7

Assume that Conditions 1–3 hold and \(\{x_n\}\) is a sequence generated by Algorithm 3.1. If there exists a subsequence \(\{x_{n_k}\}\) convergent weakly to \(z\in H\) and

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0, \end{aligned}$$

then \(z\in VI(C,A).\)

Proof

We have

$$\begin{aligned} \langle x_{n_k}-\lambda _{n_k} Ax_{n_k}-y_{n_k},x-y_{n_k}\rangle \le 0, \, \,\, \forall x\in C. \end{aligned}$$

or, equivalently,

$$\begin{aligned} \dfrac{1}{\lambda _{n_k}}\langle x_{n_k}-y_{n_k},x-y_{n_k}\rangle \le \langle Ax_{n_k},x-y_{n_k}\rangle , \, \,\, \forall x\in C. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \dfrac{1}{\lambda _{n_k}}\langle x_{n_k}-y_{n_k},x-y_{n_k}\rangle +\langle Ax_{n_k},y_{n_k}-x_{n_k}\rangle \le \langle Ax_{n_k},x-x_{n_k}\rangle , \, \,\, \forall x\in C. \end{aligned}$$
(13)

Since \(\{x_{n_k}\}\) is weakly convergent, \(\{x_{n_k}\}\) is bounded. Then, by the Lipschitz continuity of A, \(\{Ax_{n_k}\}\) is bounded. Since \(\Vert x_{n_k}-y_{n_k}\Vert \rightarrow 0\), \(\{y_{n_k}\}\) is also bounded and, according to Lemma 3.5, we have

$$\begin{aligned} \lambda _{n_k}\ge \min \left\{ \lambda _0,\dfrac{\mu }{L}\right\} . \end{aligned}$$

Passing (13) to limit as \(k\rightarrow \infty \), we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax_{n_k},x-x_{n_k}\rangle \ge 0,\, \,\, \forall x\in C. \end{aligned}$$
(14)

Moreover, we have

$$\begin{aligned} \langle Ay_{n_k},x-y_{n_k}\rangle =\langle Ay_{n_k}- Ax_{n_k},x-x_{n_k}\rangle +\langle Ax_{n_k},x-x_{n_k}\rangle +\langle Ay_{n_k},x_{n_k}-y_{n_k}\rangle .\nonumber \\ \end{aligned}$$
(15)

Since \(\lim _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0\) and A is L-Lipschitz continuous on H, we get

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert Ax_{n_k}-Ay_{n_k}\Vert =0, \end{aligned}$$

which, together with (14) and (15), implies that

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ay_{n_k},x-y_{n_k}\rangle \ge 0,\,\,\, \forall x\in C. \end{aligned}$$

Next, we show that \(z\in VI(C,A).\) We choose a sequence \(\{\epsilon _k\}\) of positive numbers such that \(\{\epsilon _k\}\) is decreasing and convergent to 0. For each \(k\ge 1\), we denote by \(n_{N_k}\) the smallest positive integer such that

$$\begin{aligned} \langle Ay_{n_j},x-y_{n_j}\rangle +\epsilon _k \ge 0, \,\,\, \forall j\ge n_{N_k}. \end{aligned}$$
(16)

Since \(\{ \epsilon _k\}\) is decreasing, it is easy to see that the sequence \(\{n_{N_k}\}\) is increasing. Furthermore, for each \(k\ge 1\), since \(\{y_{n_{N_k}}\}\subset C\), we have \(Ay_{n_{N_k}}\ne 0\) and, setting

$$\begin{aligned} v_{n_{N_k}} = \dfrac{Ay_{n_{N_k}}}{\Vert Ay_{n_{N_k}}\Vert ^2 }, \end{aligned}$$

we have \(\langle Ay_{n_{N_k}}, v_{n_{N_k}}\rangle = 1\) for each \(k\ge 1\). Now, it follows from (16) that, for each \(k\ge 1\),

$$\begin{aligned} \langle Ay_{n_{N_k}}, x+\epsilon _k v_{n_{N_k}}-y_{n_{N_k}}\rangle \ge 0. \end{aligned}$$

Since A is pseudomonotone on H, we get

$$\begin{aligned} \langle A(x+\epsilon _k v_{n_{N_k}}), x+\epsilon _k v_{n_{N_k}}-y_{n_{N_k}}\rangle \ge 0. \end{aligned}$$

This implies that

$$\begin{aligned} \langle Ax, x-y_{n_{N_k}}\rangle \ge \langle Ax-A(x+\epsilon _k v_{n_{N_k}}), x+\epsilon _k v_{n_{N_k}}-y_{n_{N_k}} \rangle -\epsilon _k \langle Ax, v_{n_{N_k}}\rangle . \end{aligned}$$
(17)

Now, we show that \(\lim _{k\rightarrow \infty }\epsilon _k v_{n_{N_k}}=0\). Indeed, since \(x_{n_k}\rightharpoonup z\) and \(\lim _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0,\) we obtain \(y_{N_k}\rightharpoonup z \text { as } k \rightarrow \infty \). Since \(\{y_n\} \subset C\), we have \(z\in C\). We can suppose that \(Az \ne 0\) (otherwise, z is a solution). Since the mapping A satisfies the condition (5), we obtain

$$\begin{aligned} 0 < \Vert Az\Vert \le \liminf _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert . \end{aligned}$$

Since \(\{y_{n_{N_k}}\}\subset \{y_{n_k}\}\) and \(\epsilon _k \rightarrow 0\) as \(k \rightarrow \infty \), we obtain

$$\begin{aligned} 0 \le \limsup _{k\rightarrow \infty } \Vert \epsilon _k v_{n_{N_k}} \Vert = \limsup _{k\rightarrow \infty } \Big (\dfrac{\epsilon _k}{\Vert Ay_{n_k}\Vert }\Big )\le \dfrac{\limsup _{k\rightarrow \infty }\epsilon _k }{\liminf _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert }=0, \end{aligned}$$

which implies that \(\lim _{k\rightarrow \infty } \epsilon _k v_{n_{N_k}} = 0.\) Now, letting \(k\rightarrow \infty \), the right hand side of (17) tends to zero since A is Lipschitz continuous, \(\{x_{n_{N_k}}\}, \{v_{n_{N_k}}\}\) are bounded and \(\lim _{k\rightarrow \infty }\epsilon _k v_{n_{N_k}}=0\). Thus we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax,x-y_{n_{N_k}}\rangle \ge 0. \end{aligned}$$

Hence, for all \(x\in C\), we have

$$\begin{aligned} \langle Ax, x-z\rangle =\lim _{k\rightarrow \infty } \langle Ax, x-y_{n_{N_k}}\rangle =\liminf _{k\rightarrow \infty } \langle Ax, x-y_{n_{N_k}}\rangle \ge 0. \end{aligned}$$

Therefore, by Lemma 2.3, \(z\in VI(C,A)\). This completes the proof. \(\square \)

Remark 3.4

When A is monotone, it is not necessary to impose the sequential weak continuity of A, see [8].

Theorem 3.1

Assume that Conditions 1–4 hold. Then the sequence \(\{x_n\}\) generated by Algorithm 3.1 converges strongly to \(x^*\in VI(C,A)\), where

$$\begin{aligned} \Vert x^*\Vert =\min \{ \Vert z\Vert : z\in VI(C,A)\}. \end{aligned}$$

Proof

Since \(\lim _{n\rightarrow \infty }\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )=1-\mu >0\), there exists \(n_0\in {\mathbb {N}}\) such that

$$\begin{aligned} 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}>0, \,\,\,\forall n\ge n_0. \end{aligned}$$
(18)

Combining (7) and (18), we get

$$\begin{aligned} \Vert w_n-x^*\Vert \le \Vert x_n-x^*\Vert , \, \,\, \forall n\ge n_0. \end{aligned}$$
(19)

Claim 1. The sequence \(\{x_n\}\) is bounded. It follows from (19) that

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert&=\Vert (1-\gamma _n-\beta _n)x_n+\beta _n w_n- x^*\Vert \\&=\Vert (1-\gamma _n-\beta _n)(x_n-x^*)+\beta _n(w_n-x^*)-\gamma _n x^*\Vert \\&\le \Vert (1-\gamma _n-\beta _n)(x_n-x^*)+\beta _n(w_n-x^*)\Vert +\gamma _n \Vert x^*\Vert \\&\le (1-\gamma _n-\beta _n)\Vert x_n-x^*\Vert +\beta _n\Vert w_n-x^*\Vert +\gamma _n \Vert x^*\Vert \\&\le (1-\gamma _n-\beta _n)\Vert x_n-x^*\Vert +\beta _n\Vert x_n-x^*\Vert +\gamma _n \Vert x^*\Vert \ \ \forall n\ge n_0 \\&= (1-\gamma _n) \Vert x_n-x^*\Vert +\gamma _n\Vert x^*\Vert \ \ \forall n\ge n_0 \\&\le \max \{\Vert x_n-x^*\Vert ,\Vert x^*\Vert \}|\ \ \forall n\ge n_0 \\&\le \max \{\Vert x_{n_0}-x^*\Vert ,\Vert x^*\Vert \}. \end{aligned}$$

That is, the sequence \(\{x_n\}\) is bounded and \(\{w_n\}\) is also. Claim 2. Note that

$$\begin{aligned}&a\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert x_n-y_n\Vert ^2\\&\quad +a\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-w_n\Vert ^2\\&\quad \le \Vert x_n-x^*\Vert ^2-\Vert x_{n+1}-x^*\Vert ^2 +\gamma _n \Vert x^*\Vert ^2. \end{aligned}$$

Indeed, using (4), we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2&=\Vert (1-\gamma _n-\beta _n)x_n+\beta _n w_n- x^*\Vert ^2\nonumber \\&=\Vert (1-\gamma _n-\beta _n)(x_n-x^*)+\beta _n (w_n- x^*)+\gamma _n (-x^*)\Vert ^2\nonumber \\&=(1-\gamma _n-\beta _n)\Vert x_n-x^*\Vert ^2+\beta _n \Vert w_n- x^*\Vert ^2\nonumber \\&\quad +\gamma _n \Vert x^*\Vert ^2-\beta _n (1-\gamma _n-\beta _n)\Vert x_n-w_n\Vert ^2\nonumber \\&\quad -\gamma _n(1-\gamma _n-\beta _n) \Vert x_n\Vert ^2-\gamma _n \beta _n \Vert w_n\Vert ^2\nonumber \\&\le (1-\gamma _n-\beta _n)\Vert x_n-x^*\Vert ^2+\beta _n \Vert w_n- x^*\Vert ^2+\gamma _n \Vert x^*\Vert ^2. \end{aligned}$$
(20)

It follows from (7) and (20) that

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2&\le (1-\gamma _n-\beta _n)\Vert x_n-x^*\Vert ^2+\beta _n \Vert x_n- x^*\Vert ^2\\&\quad -\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert x_n-y_n\Vert ^2\\&\quad -\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-w_n\Vert ^2 +\gamma _n \Vert x^*\Vert ^2\\&=(1-\gamma _n)\Vert x_n-x^*\Vert ^2-\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert x_n-y_n\Vert ^2\\&\quad -\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-w_n\Vert ^2+\gamma _n \Vert x^*\Vert ^2\\&\le \Vert x_n-x^*\Vert ^2-\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert x_n-y_n\Vert ^2\\&\quad -\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-w_n\Vert ^2+\gamma _n \Vert x^*\Vert ^2. \end{aligned}$$

Thus we get

$$\begin{aligned}&\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert x_n-y_n\Vert ^2\\&\quad +\beta _n\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-w_n\Vert ^2\\&\quad \le \Vert x_n-x^*\Vert ^2-\Vert x_{n+1}-x^*\Vert ^2 +\gamma _n \Vert x^*\Vert ^2. \end{aligned}$$

Moreover, since \(\beta _n\ge a\) for all \(n\ge 1\), we obtain

$$\begin{aligned}&a\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert x_n-y_n\Vert ^2\\&\quad +a\Big (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\Big )\Vert y_n-w_n\Vert ^2\\&\quad \le \Vert x_n-x^*\Vert ^2-\Vert x_{n+1}-x^*\Vert ^2 +\gamma _n \Vert x^*\Vert ^2. \end{aligned}$$

Claim 3. Note that

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2&\le (1-\gamma _n)\Vert x_n-x^*\Vert ^2+\gamma _n[2\beta _n\Vert x_n-w_n\Vert \Vert x_{n+1}-x^*\Vert \\&\quad +2\langle x^*,x^*-x_{n+1}\rangle ],\,\,\, \forall n\ge n_0. \end{aligned}$$

Indeed, setting \(t_n=(1-\beta _n)x_n+\beta _n w_n\) for each \(n\ge 1\), we have

$$\begin{aligned} \Vert t_n-x^*\Vert&=\Vert (1-\beta _n)(x_n-x^*)+\beta _n(w_n-x^*)\Vert \nonumber \\&\le (1-\beta _n)\Vert x_n-x^*\Vert +\beta _n\Vert w_n-x^*\Vert \nonumber \\&\le (1-\beta _n)\Vert x_n-x^*\Vert +\beta _n\Vert x_n-x^*\Vert =\Vert x_n-x^*\Vert ,\,\,\, \forall n\ge n_0, \end{aligned}$$
(21)

and

$$\begin{aligned} \Vert t_n-x_n\Vert =\beta _n \Vert x_n-w_n\Vert . \end{aligned}$$
(22)

Using (21) and (22), we get

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2&=\Vert (1-\gamma _n-\beta _n)x_n+\beta _n w_n-x^*\Vert ^2\nonumber \\&=\Vert (1-\beta _n)x_n+\beta _n w_n-\gamma _n x_n-x^*\Vert ^2\nonumber \\&=\Vert (1-\gamma _n)(t_n-x^*)-\gamma _n(x_n-t_n)-\gamma _n x^*\Vert ^2. \end{aligned}$$
(23)

Now, using the inequality (3), we get

$$\begin{aligned}&\Vert (1-\gamma _n)(t_n-x^*)-\gamma _n(x_n-t_n)-\gamma _n x^*\Vert ^2\nonumber \\&\quad \le (1-\gamma _n)^2\Vert t_n-x^*\Vert ^2 -2\langle \gamma _n(x_n-t_n)+\gamma _n x^*,x_{n+1}-x^*\rangle . \end{aligned}$$
(24)

Combining (23) and (24), we obtain

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2&\le (1-\gamma _n)^2\Vert t_n-x^*\Vert ^2 \\&\quad +2 \gamma _n\langle x_n-t_n,x^*-x_{n+1}\rangle +2\gamma _n \langle x^*,x^*-x_{n+1}\rangle \\&\le (1-\gamma _n)\Vert t_n-x^*\Vert ^2 + 2\gamma _n \Vert x_n-t_n\Vert \Vert x_{n+1}-x^*\Vert \\&\quad +2\gamma _n \langle x^*,x^*-x_{n+1}\rangle \\&\le (1-\gamma _n)\Vert x_n-x^*\Vert ^2 + \gamma _n [2\beta _n\Vert x_n-w_n\Vert \Vert x_{n+1}-x^*\Vert \\&\quad +2 \langle x^*,x^*-x_{n+1}\rangle ],\,\,\, \forall n\ge n_0. \end{aligned}$$

Claim 4. \(\{\Vert x_n-x^*\Vert ^2\}\) converges to zero. Indeed, for each \(n\ge 0\), set

$$\begin{aligned} a_n:=\Vert x_n-x^*\Vert ^2 \ \ \text { and }\ \ \ b_n:=2\beta _n\Vert x_n-w_n\Vert \Vert x_{n+1}-x^*\Vert +2 \langle x^*,x^*-x_{n+1}\rangle . \end{aligned}$$

Then, Claim 3 can be rewritten as follows:

$$\begin{aligned} a_{n+1}\le (1-\gamma _n)a_n+\gamma _n b_n. \end{aligned}$$

By Lemma 2.4, it is sufficient to show that \(\limsup _{k\rightarrow \infty }b_{n_k}\le 0\) for every subsequence \(\{a_{n_k}\}\) of \(\{a_n\}\) satisfying

$$\begin{aligned} \liminf _{k\rightarrow \infty }(a_{n_k+1}-a_{n_k})\ge 0. \end{aligned}$$

This is equivalently to that we need to show \(\limsup _{k\rightarrow \infty }\langle x^*, x^*-x_{n_k+1}\rangle \le 0\) and \(\limsup _{k\rightarrow \infty }\Vert x_{n_k}-w_{n_k}\Vert \le 0\) for every subsequence \(\{\Vert x_{n_k}-x^*\Vert \}\) of \(\{\Vert x_n-x^*\Vert \}\) satisfying

$$\begin{aligned} \liminf _{k\rightarrow \infty }(\Vert x_{n_k+1}-x^*\Vert -\Vert x_{n_k}-x^*\Vert )\ge 0. \end{aligned}$$

Suppose that \(\{\Vert x_{n_k}-x^*\Vert \}\) is a subsequence of \(\{\Vert x_n-x^*\Vert \}\) such that

$$\begin{aligned} \liminf _{k\rightarrow \infty }(\Vert x_{n_k+1}-x^*\Vert -\Vert x_{n_k}-x^*\Vert )\ge 0. \end{aligned}$$

Then, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty }&(\Vert x_{n_k+1}-x^*\Vert ^2-\Vert x_{n_k}-x^*\Vert ^2)\\&=\liminf _{k\rightarrow \infty }[(\Vert x_{n_k+1}-x^*\Vert -\Vert x_{n_k}-x^*\Vert )(\Vert x_{n_k+1}-x^*\Vert +\Vert x_{n_k}-x^*\Vert )]\\&\ge 0. \end{aligned}$$

By Claim 2, we obtain

$$\begin{aligned}&\limsup _{k\rightarrow \infty }\Big [a\Big (1-\mu \dfrac{\lambda _{n_k}}{\lambda _{{n_k}+1}}\Big )\Vert x_{n_k}-y_{n_k}\Vert ^2 +a\Big (1-\mu \dfrac{\lambda _{n_k}}{\lambda _{{n_k}+1}}\Big )\Vert y_{n_k}-w_{n_k}\Vert ^2\Big ]\\&\quad \le \limsup _{k\rightarrow \infty }[\Vert x_{n_k}-x^*\Vert ^2-\Vert x_{{n_k}+1}-x^*\Vert ^2 +\gamma _{n_k} \Vert x^*\Vert ^2]\\&\quad \le \limsup _{k\rightarrow \infty }[ \Vert x_{n_k}-x^*\Vert ^2-\Vert x_{n_k+1}-x^*\Vert ^2]+\limsup _{k\rightarrow \infty }\gamma _{n_k} \Vert x^*\Vert ^2\\&\quad =- \liminf _{k\rightarrow \infty }[ \Vert x_{n_k+1}-x^*\Vert ^2-\Vert x_{_{n_k}}-x^*\Vert ^2]\\&\quad \le 0. \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0,\quad \lim _{k\rightarrow \infty }\Vert y_{n_k}-w_{n_k}\Vert =0. \end{aligned}$$

Thus we have

$$\begin{aligned} \Vert x_{n_k}-w_{n_k}\Vert \le \Vert x_{n_k}-y_{n_k}\Vert +\Vert y_{n_k}-w_{n_k}\Vert \rightarrow 0\quad \ \text { as }\ k\rightarrow \infty . \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \Vert x_{{n_k}+1}-x_{n_k}\Vert \le \gamma _{n_k} \Vert x_{n_k}\Vert +\beta _{n_k}\Vert x_{n_k}-w_{n_k}\Vert \rightarrow 0 \ \quad \text{ as } \ k\rightarrow \infty . \end{aligned}$$
(25)

Since the sequence \(\{x_{n_k}\}\) is bounded, it follows that there exists a subsequence \(\{x_{n_{k_j}}\}\) of \(\{x_{n_k}\}\), which converges weakly to some \(z\in H\), such that

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x^*,x^*-x_{n_k}\rangle =\lim _{j\rightarrow \infty }\langle x^*,x^*-x_{n_{k_j}}\rangle =\langle x^*,x^*-z\rangle . \end{aligned}$$
(26)

From \( \lim _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0\) and Lemma 3.7, we have \(z\in VI(C,A)\) and, from (26) and the definition of \(x^*=P_{VI(C,A)} 0\), we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x^*,x^*-x_{n_k}\rangle =\langle x^*,x^*-z\rangle \le 0. \end{aligned}$$
(27)

Combining (25) and (27), we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x^*,x^*-x_{n_k+1}\rangle \le \limsup _{k\rightarrow \infty }\langle x^*,x^*-x_{n_k}\rangle =\langle x^*,x^*-z\rangle \le 0. \end{aligned}$$
(28)

Hence it follows from (28), \(\lim _{k\rightarrow \infty }\Vert x_{n_k}-w_{n_k}\Vert =0\), Claim 3 and Lemma 2.4 that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n-x^*\Vert =0. \end{aligned}$$

This completes the proof. \(\square \)

Remark 3.5

Our result generalizes some related results in the literature and hence might be applied to a wider class of nonlinear mappings. For example, in the next section, we presented the advantages of our method compared with the recent results [22, Theorem 3.1], [34, Theorem 3.3], [41, Theorem 3.1] and [42, Theorem 3.7] as follows:

  1. (1)

    In Theorem 3.1, we replaced the monotonicity by the pseudomonotonicity and sequentially weakly continuity of A.

  2. (2)

    We also obtained the strong convergence without using the viscosity technique.

4 Numerical illustrations

In this section, we present numerical experiments relative to the problem (VI). The first example, we compare Algorithm 3.1 with Algorithm 2 of Yang et al. in [42]. The second example, we illustrate the convergence of Algorithms 3.1 and compare them with three well-known algorithms including Algorithm 2 of Yang et al. in [42], Algorithm 1 of Censor et al. in [10] and Algorithm 3.1 of Kraikaew et al. in [22]. All the numerical experiments are performed on a HP laptop with Intel(R) Core(TM)i5-6200U CPU 2.3GHz with 4 GB RAM. All the programs are written in Matlab2015a.

Problem 1

The first problem is the Example 2.1 in [4]. Assume that \(A:{\mathbb {R}}^m \rightarrow {\mathbb {R}}^m\) is defined by

$$\begin{aligned} Ax=(e^{-x^TQx}+\beta )(Px+q) \end{aligned}$$

where Q is a positive definite matrix, P is a positive semidefinite matrix, \(q \in {\mathbb {R}}^m\) and \(\beta >0\). Observe that A is differentiable and there exists \(M > 0\) such that \(\Vert \nabla Ax\Vert \le M \), \(x \in {\mathbb {R}}^m\). Therefore, by the Mean Value Theorem A is Lipschitz continuous. Also, A is pseudo-monotone but not monotone.

Table 1 Numerical results obtained by other algorithms
Full size table
Table 2 Numerical results of all algorithms with different \(x_0\)
Full size table

Let \(C:=\{x \in {\mathbb {R}}^m|Bx \le b\}\), where B is a matrix of size \(l \times m\) and \(b \in {\mathbb {R}}^l_{+}\) with \(l=10\).

For all tests, we take \(\beta =0.01\), \(P= R^TR, Q= U^TU\) with all entries of matrices \( R, U \in {\mathbb {R}}^{m \times m}\) and vector \(q \in {\mathbb {R}}^m\) are generated randomly from a normal distribution with mean zero and unit variance. B is a random matrix and random vector \(b \in {\mathbb {R}}^l\) with non-negative entries. The starting points are \(x_0=(1,1,\ldots ,1) \in {\mathbb {R}}^m\) and \(\lambda _0=0.5\) for Algorithms. To terminate Algorithms, we use the condition \(\Vert x_{n}-y_n\Vert \le \epsilon \) with \(\epsilon =10^{-3}\) . We choose \(\gamma _n=\frac{1}{(n+3)}\) and \(\mu =0.05\) for all algorithms and \(\beta _n=\frac{1}{10}(1-\gamma _n)\) for Algorithm 3.1. The numerical results are described in Table 1

Problem 2

Let \(H=L^{2}([0,1]) \) with the norm \(\Vert \cdot \Vert \) and the inner product \(\langle x,y\rangle \) defined by

$$\begin{aligned} \Vert x\Vert =(\int _{0}^{1}|x(t)|^{2}dt)^{\frac{1}{2}},\,\,\,\, \langle x,y\rangle =\int _{0}^{1}x(t)y(t)dt,\,\,\,\forall x, y\in H, \end{aligned}$$

respectively. The operator \(A:H\rightarrow H\) is defined by

$$\begin{aligned} Ax(t)=\max \{0,x(t)\},\,\,\, \forall x\in H,\, t\in [0,1]. \end{aligned}$$

It can be easily verified that A is 1-Lipschitz-continuous and monotone. The feasible set \(C:=\{x \in H:\Vert x\Vert \le 1\}\) be the unit ball. Observe that \(0\in VI(C,A)\) and so \(VI(C,A)\ne \emptyset .\) For all tests, we take \(\lambda =\lambda _0=0.5\) for all algorithms. We choose \(\gamma _n=\frac{1}{(n+3)}, \mu =0.05\) for Algorithm 2 of Yang et al. Algorithms 3.1 and \(\gamma _n=\frac{1}{(n+3)}\) for Algorithm 3.1 of Kraikaew et al. \(\beta _n=\frac{1}{10}(1-\gamma _n)\) for Algorithms 3.1. To terminate Algorithms, we use the condition \(\Vert x_{n}-0\Vert \le \epsilon \) with \(\epsilon =10^{-4}\) or iterations \(\ge \) 500. The numerical results are described in Table 2.

5 Conclusions

We proposed a new modified subgradient extragradient method for solving the pseudomonotone variational inequality problem in real Hilbert spaces. To obtain the strong convergence theorem, we combined by the subgradient extragradient method and the Mann type method [31]. The advantages of the proposed algorithm don’t need any requirement of additional projections and the knowledge of the Lipschitz constant of the mapping. Further, we gave several numerical experiments to illustrate the performance of the proposed algorithm with the known algorithms.