Convergence of Relaxed Inertial Subgradient Extragradient Methods for Quasimonotone Variational Inequality Problems

Abstract

In this paper, we present two new relaxed inertial subgradient extragradient methods for solving variational inequality problems in a real Hilbert space. We establish the convergence of the sequence generated by these methods when the cost operator is quasimonotone and Lipschitz continuous, and when it is Lipschitz continuous without any form of monotonicity. The methods combine both the inertial and relaxation techniques in order to achieve high convergence speed, and the techniques used are quite different from the ones in most papers for solving variational inequality problems. Furthermore, we present some experimental results to illustrate the profits gained from the relaxed inertial steps.

1 Introduction

Let ${\mathcal {C}}$ be a nonempty closed and convex subset of a real Hilbert space ${\mathcal {H}}$ with inner product $\langle \cdot ~, \cdot \rangle$, and associated norm $||\cdot ||$. Let $A:{\mathcal {H}}\rightarrow {\mathcal {H}}$ be a continuous mapping. The Variational Inequality Problem (VIP) is formulated as:

$$\begin{aligned} \hbox {Find} ~x\in {\mathcal {C}} ~\hbox {such that}~ \langle Ax,y-x\rangle \ge 0,~\forall y\in {\mathcal {C}}. \end{aligned}$$

(1.1)

The VIP is a fundamental problem in optimization and known to have numerous applications in diverse fields (see, for example [16, 17, 19, 20, 24, 26, 27] and the references therein). Its theory provides a simple, natural and unified framework for a general treatment of unrelated problems. The VIP was first considered for the purpose of modeling problems in mechanics by Stampacchia [41] (also independently by Fichera [16]).

One of the simplest methods for solving VIP (1.1) is the following gradient-projection method:

$$\begin{aligned} x_{n+1}=P_{\mathcal {C}}(x_n-\lambda Ax_n), n\ge 1. \end{aligned}$$

(1.2)

This method converges strongly to a unique solution of the VIP (1.1) if A is $\eta$-strongly monotone and L-Lipschitz continuous, with $\lambda \in \left( 0,\frac{2\eta }{L^2}\right) .$ However, if A is monotone and Lipschitz continuous, the gradient-projection method may fail to converge. For instance, take $C={\mathbb {R}}^2$ and A to be a rotation with $\frac{\pi }{2}$ angle. Then, A is monotone and Lipschitz continuous with (0, 0) being the unique solution of (1.1). But the sequence $\{x_n\}$ generated by (1.2) satisfies $||x_{n+1}||>||x_n||,~\forall n$. Thus, the gradient-projection method does not always work for monotone and Lipschitz continuous operators.

In [28], Korpelevich proposed a method in finite dimensional spaces which converges to a solution of the VIP (1.1) when the operator is monotone and Lipchitz continuous. This method which is known as the extragradient method is given as:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1\in {\mathcal {C}},\\ y_n=P_{{\mathcal {C}}}(x_n-\lambda _n Ax_n)\\ x_{n+1}=P_{{\mathcal {C}}}(x_n-\lambda _n Ay_n), n\ge 1, \end{array}\right. } \end{aligned}$$

(1.3)

where $\lambda _n\in \left( 0,\frac{1}{L}\right) .$ Since the introduction of the extragradient method, many authors have studied it in infinite dimensional spaces when A is monotone (see [5, 9, 19]) and when A is pseudomonotone (see [36, 48]).

However, the major drawback of this method is that it requires two projections onto the feasible set ${\mathcal {C}}$ per iteration, which can be costly if ${\mathcal {C}}$ has complex structure. In this case, $P_{{\mathcal {C}}}$ may not have a closed form formula, and a minimization problem has to be solved twice per iteration in implementing (1.3). Hence, the efficiency of the method may be affected.

To overcome this setback, Censor et al. [12] introduced the following subgradient extragradient method: $x_1\in {\mathcal {H}},$

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_{{\mathcal {C}}}(x_n-\lambda _n Ax_n)\\ T_n:= \{w\in {\mathcal {H}}:\langle x_n-\lambda _n Ax_n-y_n, w-y_n\rangle \le 0\},\\ x_{n+1}=P_{T_n}(x_n-\lambda _n Ay_n), n\ge 1. \end{array}\right. } \end{aligned}$$

(1.4)

They proved that $\{x_n\}$ generated by (1.4) converges weakly to a solution of problem (1.1) when A is monotone and Lipschitz continuous.

Unlike (1.3), Algorithm (1.4) requires only one projection onto ${\mathcal {C}}$ per iteration since the second projection is onto a half space $T_n$, which has an explicit formula. Hence, subgradient extragradient methods are less computationally expensive than extragradient methods. This method has also been considered by many authors for solving the VIP (1.1) in infinite dimensional spaces, when A is monotone [1, 10, 11, 25, 30] and when A is pseudomonotone [45, 51].

In recent years, algorithms with fast convergence rate have been of great interest. To accelerate the convergence of iterative methods for solving (1.1) and other related optimization problems, there exist different modifications of such iterative methods. In this paper, we consider the two very important modifications, namely; inertial and relaxation techniques. The inertial technique is based upon a discrete analogue of a second order dissipative dynamical system and is known for its efficiency in improving the convergence rate of iterative methods. The method was first considered by Polyak [38] for solving the smooth convex minimization problems. It was later made very popular by Nesterov’s acceleration gradient method [35], and was further developed by Beck and Teboulle in the case of structured convex minimization problem [6]. Since then, many authors have employed the use of inertial techniques for improving the convergence of their iterative methods (see for example [14, 15, 18, 21, 31, 32, 34, 37,38,39,40, 46, 47] and the references therein). On the other hand, the relaxation technique has proven to be an essential ingredient in the resolution of optimization problems due to the improved convergence rate that it contribute to iterative schemes. Moreover, both inertial and relaxation techniques naturally come from an explicit discretization of a dynamical system in time (see, for example [4, 49]).

Some authors have considered incorporating these two techniques into known methods in order to achieve high convergence speed of the resulting methods (see, [3, 4]). Also, in [23], the influence of inertial and relaxation techniques on the numerical performance of iterative schemes was studied.

Given the importance of these two techniques (inertial and relaxation) for solving optimization problems, our aim in this paper is to incorporate the inertial and relaxation techniques into Algorithm (1.4), when A is not necessarily pseudomonotone. That is, we design two new relaxed inertial subgradient extragradient methods, and prove that they converge weakly to a solution of VIP (1.1) when the operator A is quasimonotone and Lipschitz continuous, and when it is Lipschitz continuous without any form of monotonicity. The techniques employed in this paper are quite different from the ones used in most papers (see for example [14, 15, 22, 31, 32, 34, 37,38,39,40, 44, 46, 47]). Moreover, the assumptions on the inertial and relaxation factors in this paper, are weaker than those in many papers for solving VIPs. Finally, we provide some numerical implementations of our methods and compare them with other methods, in order to show the profits gained from the inertial and relaxation techniques.

The rest of the paper is organized as follows: Sect. 2 contains basic definitions and results needed in subsequent sections. In Sect. 3, we present and discuss the proposed methods. The convergence analysis of these methods are investigated in Sect. 4. In Sect. 5, we perform some numerical analysis of our methods in comparison with other methods in the literature. We then conclude in Sect. 6.

2 Preliminaries

In this section, we recall some concepts and results needed in subsequent sections. Henceforth, we denote the weak convergence of $\{x_n\}$ to a point $x^*$ by $x_n\rightharpoonup x^*$.

Let ${\mathcal {H}}$ be a real Hilbert space and $A:{\mathcal {H}}\rightarrow {\mathcal {H}}$ be a mapping. Then, A is said to be

• (i) $L-$Lipschitz continuous, if there exists $L>0$ such that

  $$\begin{aligned} \Vert Ax-Ay\Vert \le L\Vert x-y\Vert ,~ \forall x,y\in {\mathcal {H}}, \end{aligned}$$

• (ii) L-strongly monotone, if there exists $L>0$ such that

  $$\begin{aligned} \langle Ax-Ay,x-y\rangle \ge L\Vert x-y\Vert ^2,~ \forall x,y \in {\mathcal {H}}, \end{aligned}$$

• (iii) Monotone, if

  $$\begin{aligned}\big <Ax-Ay,x-y\big >\ge 0,~ \forall x,y \in {\mathcal {H}}, \end{aligned}$$

• (iv) Pseudomonotone, if

  $$\begin{aligned} \langle Ay, x-y \rangle \ge 0 \implies ~\langle Ax,x-y \rangle \ge 0,~\forall x,y \in {\mathcal {H}}, \end{aligned}$$

• (v) Quasimonotone, if

  $$\begin{aligned} \langle Ay,x-y\rangle >0 \implies \langle Ax, x-y\rangle \ge 0, ~\forall x,y\in {\mathcal {H}}, \end{aligned}$$

• (vi) Sequentially weakly-strongly continuous, if for every sequence $\{x_n\}$ that converges weakly to a point x, the sequence $\{Ax_n\}$ converges strongly to Ax, 

• (vii) Sequentially weakly continuous, if for every sequence $\{x_n\}$ that converges weakly to a point x, the sequence $\{Ax_n\}$ converges weakly to Ax.

Clearly, $(ii)\implies (iii)\implies (iv)\implies (v).$ But the converses are not always true.

Let $VI({\mathcal {C}}, A)$ be the solution set of problem (1.1) and $\Gamma$ be the solution set of the following problem:

$$\begin{aligned} \hbox {Find} ~x\in {\mathcal {C}} ~\hbox {such that}~ \langle Ay,y-x\rangle \ge 0,~\forall y\in {\mathcal {C}}. \end{aligned}$$

(2.1)

Then, $\Gamma$ is a closed and convex subset of ${\mathcal {C}}$, and since ${\mathcal {C}}$ is convex and A is continuous, we have the following relation

$$\begin{aligned} \Gamma \subseteq VI({\mathcal {C}}, A). \end{aligned}$$

(2.2)

Lemma 2.1

[50] Let ${\mathcal {C}}$ be a nonempty closed and convex subset of ${\mathcal {H}}$. If either

• (1) A is pseudomonotone on ${\mathcal {C}}$ and $VI({\mathcal {C}},A)\ne \emptyset ,$

• (ii) A is the gradient of G,  where G is a differential quasiconvex function on an open set ${\mathcal {K}}\supset {\mathcal {C}}$ and attains its global minimum on ${\mathcal {C}},$

• (iii) A is quasimonotone on $\mathcal {C,}\, \, A\, \, \ne 0$ on ${\mathcal {C}}$ and ${\mathcal {C}}$ is bounded,

• (iv) A is quasimonotone on ${\mathcal {C}},\, \,$A$\, \,\ne 0$ on ${\mathcal {C}}$ and there exists a positive number r such that, for every $x\in {\mathcal {C}}$ with $\Vert x\Vert \ge r,$ there exists $y\in {\mathcal {C}}$ such that $\Vert y\Vert \le r$ and $\langle Ax,y-x\rangle \le 0,$

• (v) A is quasimonotone on ${\mathcal {C}}, \text {int}\, \, {\mathcal {C}}$ is nonempty and there exists $x^*\in VI({\mathcal {C}},A)$ such that $Ax^*\ne 0.$

Then, $\Gamma$ is nonempty.

Recall that for a nonempty closed and convex subset ${\mathcal {C}}$ of ${\mathcal {H}}$, the metric projection denoted by $P_{\mathcal {C}}$ (see [43]), is a map defined on ${\mathcal {H}}$ onto ${\mathcal {C}}$ which assigns to each $x\in {\mathcal {H}}$, the unique point in ${\mathcal {C}}$, denoted by $P_{\mathcal {C}} x$ such that

$$\begin{aligned} ||x-P_{\mathcal {C}}x||=\inf \{||x-y||:~y\in {\mathcal {C}}\}. \end{aligned}$$

It is well known that $P_{\mathcal {C}}$ is characterized by the inequality

$$\begin{aligned} \langle x-P_{\mathcal {C}}x, y-P_{\mathcal {C}} x\rangle \le 0,~~\forall y\in {\mathcal {C}}. \end{aligned}$$

(2.3)

Following Attouch and Cabot [3, pages 5, 10], we note that if $x_{n+1}=x_n+\theta _n (x_n-x_{n-1})$, then for all $n\ge 1$, we have that

$$\begin{aligned} x_{n+1}-x_n=\left( \prod _{j=1}^n\theta _j\right) (x_1-x_0), \end{aligned}$$

which implies that

$$\begin{aligned} x_n=x_1+\left( \sum _{j=1}^{n-1}\prod _{j=1}^l\theta _j\right) (x_1-x_0). \end{aligned}$$

Thus, $\{x_n\}$ converges if and only if $x_1=x_0$ or if $\sum \limits _{l=1}^{\infty }\prod \limits _{j=1}^l\theta _j <\infty .$

Therefore, we assume henceforth that

$$\begin{aligned} \sum \limits _{l=i}^{\infty }\left( \prod \limits _{j=i}^l \theta _j\right) <\infty ~~\forall i\ge 1. \end{aligned}$$

(2.4)

Hence, we can define the sequence $\{t_i\}$ in ${\mathbb {R}}$ by

$$\begin{aligned} t_i:=\sum \limits _{l=i-1}^{\infty }\left( \prod \limits _{j=i}^l \theta _j\right) =1+\sum \limits _{l=i}^{\infty }\left( \prod \limits _{j=i}^l \theta _j\right) , \end{aligned}$$

(2.5)

with the convention $\prod \limits _{j=i}^{i-1} \theta _j=1~\forall i\ge 1.$

Remark 2.2

(See also [3]).

Assumption (2.4) ensures that the sequence $\{t_i\}$ given by (2.5) is well-defined, and

$$\begin{aligned} t_i=1+\theta _i t_{i+1},~\forall i\ge 1. \end{aligned}$$

(2.6)

The following proposition provides a criterion for ensuring assumption (2.4).

Proposition 2.3

[3, Proposition 3.1] Let $\{\theta _n\}$ be a sequence such that $\theta _n\in [0,1)$ for every $n\ge 1.$ Assume that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\left( \frac{1}{1-\theta _{n+1}}-\frac{1}{1-\theta _n}\right) =c, \end{aligned}$$

for some $c\in [0,1).$ Then,

• (i) Assumption (2.4) holds, and $t_{n+1}\sim \frac{1}{(1-c)(1-\theta _n)}$ as $n\rightarrow \infty ,$

• (ii) The equivalence $1-\theta _n \sim 1-\theta _{n+1}$ holds true as $n\rightarrow \infty .$ Hence, $t_{n+1}\sim t_{n+2}$ as $n\rightarrow \infty .$

Remark 2.4

Using Proposition 2.3, we can see that $\theta _n=1-\frac{{\bar{\theta }}}{n},$ ${\bar{\theta }}>1$, is a typical example of a sequence satisfying assumption (2.4).

Indeed, we have that

$$\begin{aligned} \lim _{n\rightarrow \infty }\left( \frac{1}{1-\theta _{n+1}}-\frac{1}{1-\theta _n}\right) =\lim _{n\rightarrow \infty }\left( \frac{1}{{\bar{\theta }}}(n+1)-\frac{1}{{\bar{\theta }}}n\right) =\frac{1}{{\bar{\theta }}}\in [0, 1), \end{aligned}$$

which satisfies the assumption of Proposition 2.3. Hence by Proposition 2.3(i), assumption (2.4) holds.

It is worthy of note that the example $\theta _n=1-\frac{{\bar{\theta }}}{n},$ ${\bar{\theta }}>1$, falls within the setting of Nesterov’s extrapolation methods. In fact, many practical choices for $\theta _n$ satisfy assumption (2.4) (for instance, see [3, 6, 13, 35]).

The corresponding finite sum expression for $\{t_i\}$ is defined for $i, n\ge 1$, by

$$\begin{aligned} t_{i, n}:={\left\{ \begin{array}{ll} \sum \limits _{l=i-1}^{n-1}\left( \prod \limits _{j=i}^l \theta _j\right) =1+\sum \limits _{l=i}^{n-1}\left( \prod \limits _{j=i}^l \theta _j\right) , &{} i\le n,\\ 0, &{} \hbox {otherwise}. \end{array}\right. } \end{aligned}$$

(2.7)

In the same manner, we have that $\{t_{i, n}\}$ is well-defined and

$$\begin{aligned} t_{i, n}=1+\theta _i t_{i+1, n} ~\forall i\ge 1,~n\ge i+1. \end{aligned}$$

(2.8)

The sequences $\{t_{i}\}$ and $\{t_{i, n}\}$ are very crucial to our convergence analysis. In fact, their effect can be seen in the following lemma which also plays a crucial role in establishing our convergence results.

Lemma 2.5

[3, page 42, Lemma B.1] Let $\{a_n\},\{\theta _n\}$ and $\{b_n\}$ be sequences of real numbers satisfying

$$\begin{aligned} a_{n+1}\le \theta _na_n+b_n ~~~\hbox {for every} ~~n\ge 1. \end{aligned}$$

Assume that $\theta _n\ge 0$ for every $n\ge 1.$

• (a) For every $n\ge 1,$ we have

  $$\begin{aligned} \sum \limits _{i=1}^{n}a_i\le t_{1,n}a_1+\sum _{i=1}^{n-1}t_{{i+1},n}b_i, \end{aligned}$$

  where the double sequence $\{t_{i,n}\}$ is defined by (2.7).

• (b) Under (2.4), assume that the sequence $\{t_i\}$ defined by (2.5) satisfies $\sum \limits _{i=1}^{\infty }t_{i+1}[b_i]_+<\infty .$ Then, the series $\sum \limits _{i\ge 1}[a_i]_+$ is convergent, and

  $$\begin{aligned} \sum \limits _{i=1}^{\infty }[a_i]_+\le t_1[a_1]_++\sum _{i=1}^{\infty }t_{i+1}[b_i]_+~, \end{aligned}$$

  where $[t]_+:=\max \{t,0\}$ for any $t\in {\mathbb {R}}$.

Lemma 2.6

[3, page 7, Lemma 2.1] Let $\{x_n\}$ be a sequence in ${\mathcal {H}}$ and $\{\theta _n\}$ be a sequence of real numbers. Given $z\in {\mathcal {H}}$, define the sequence $\{\Gamma _n\}$ by $\Gamma _n:=\frac{1}{2}\Vert x_n-z\Vert ^2.$ Then

$$\begin{aligned} \Gamma _{n+1}-\Gamma _{n}-\theta _n(\Gamma _{n}-\Gamma _{n-1})= & {} \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\langle x_{n+1}-w_n, w_{n}-z\rangle \nonumber \\&+\frac{1}{2}\Vert x_{n+1}-w_n\Vert ^2, \end{aligned}$$

(2.9)

where $w_n=x_n+\theta _n(x_n-x_{n-1})$.

The following lemmas are well-known.

Lemma 2.7

Let $\{x_n\}$ be any sequence in ${\mathcal {H}}$ such that $x_n\rightharpoonup x$. Then,

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\Vert x_n-x\Vert <\liminf \limits _{n\rightarrow \infty }\Vert x_n-y\Vert , \forall y\ne x. \end{aligned}$$

Lemma 2.8

Let $x,y\in {\mathcal {H}}$. Then,

$$\begin{aligned} 2\langle x,y\rangle =\Vert x\Vert ^{2}+\Vert y\Vert ^{2}-\Vert x-y\Vert ^{2}=\Vert x+y\Vert ^{2}-\Vert x\Vert ^{2}-\Vert y\Vert ^{2}. \end{aligned}$$

3 Proposed Methods

In this section, we present our methods and discuss their features. We begin with the following assumptions under which we obtain our convergence results.

Assumption 3.1

Conditions on the inertial and relaxation factors:

Suppose that $\theta _n\in [0,1)$ and $\rho _n\in (0, 1]$ for all $n\ge 1$ such that $\liminf \limits _{n\rightarrow \infty } \rho _n>0$. Assume that there exists $\epsilon \in (0,1)$ such that for n large enough,

$$\begin{aligned} {\left\{ \begin{array}{ll} 2(1-\epsilon )\frac{1-\rho _n}{2\rho _n}(1-\theta _{n-1})\ge \theta _nt_{n+1}\Big (1+\theta _n+2\Big [\frac{1-\rho _n}{2\rho _n}(1-\theta _n)-\frac{1-\rho _{n-1}}{2\rho _{n-1}}(1-\theta _{n-1})\Big ]_+\Big ), &{} \text{ if }~\rho _n\in (0, 1),\\ \\ (1-\epsilon )(1-\theta _{n-1})\ge \theta _nt_{n+1}\Big (1+\theta _n+\Big [\theta _{n-1}-\theta _n\Big ]_+\Big ), &{} \text{ if }~\rho _n= 1. \end{array}\right. } \end{aligned}$$

(3.1)

Assumption 3.2

We further make the following assumptions:

• (a) $\Gamma \ne \emptyset ,$

• (b) A is Lipschitz-continuous on ${\mathcal {H}}$ with constant $L>0,$

• (c) A is sequentially weakly continuous on ${\mathcal {C}}$,

• (d) A is quasimonotone on ${\mathcal {H}},$

• (e) The set $\{z\in {\mathcal {C}}:Az=0\}\setminus \Gamma$ is a finite set.

We now present the proposed methods of this paper.

When the Lipschitz constant L is known, we present the following method for solving the VIP (1.1).

In situations where the Lipschitz constant L is not known, we present the following method with adaptive stepsize for solving the VIP (1.1).

Remark 3.5

In a special case when $\rho _n=1,~\forall n\ge 1$, we have that $x_{n+1}=z_n$. Thus, Algorithms 3.3 and 3.4 reduce to the inertial version of the subgradient extragradient method of Censor et al. [10,11,12]. In such case, we have the following simple criteria which guarantee Assumption 3.1, as well as assumption (2.4).

We give the following remarks on the difference between our proposed Algorithms 3.3 and 3.4 and [29, Algorithm 3.3] below.

Remark 3.6

The method considered in [29, Algorithm 3.3] is a subgradient extragradient method without an inertial extrapolation step and without relation parameter. Our proposed Algorithms 3.3 and 3.4 are combinations of subgradient extragradient method, inertial exttrapolation step and relaxation parameter. It can also be easily seen that [29, Algorithm 3.3] is a special case of our proposed Algorithm 3.4 when $\theta _n=0$ and $\rho _n=1$ in Algorithm 3.4. As pointed out in the Introduction, the aim of adding inertial extrapolation step and relaxation parameter to [29, Algorithm 3.3] (as seen in our proposed Algorithms 3.3 and 3.4) is to increase the speed of convergence of [29, Algorithm 3.3] in terms of reduction in the number of required iterations and CPU time. Consequently, we have given the numerical comparisons in terms of number of iterations and CPU time of our proposed Algorithms 3.3, 3.4 and [29, Algorithm 3.3] (kindly see Tables 3, 4, 5 and Figs. 3, 4, 5 in Section 5). This is one of the novelties of this paper.

Proposition 3.7

Assume that $\{\theta _n\}$ is a nondecreasing sequence that satisfies $\theta _n\in [0,1)~ \forall n\ge 1$ with $\lim \limits _{n \rightarrow \infty }\theta _n=\theta$ such that the following condition holds:

$$\begin{aligned} 1-3\theta >0. \end{aligned}$$

(3.3)

Then, Assumptions (2.4) and 3.1 hold.

Proof

Observe that $\theta _n\le \theta , ~~ \forall n\ge 1.$ Thus, we have that assumption (2.4) is satisfied and $t_n\le \frac{1}{1-\theta }, ~\forall n\ge 1$ (see [3]). Now, observe that $1-3\theta >0$ implies that $(1-\theta )>\frac{\theta (1+\theta )}{1-\theta }.$ This further implies that there exists $\epsilon \in (0,1)$ such that

$$\begin{aligned} (1-\epsilon )(1-\theta )\ge \frac{\theta (1+\theta )}{1-\theta }. \end{aligned}$$

(3.4)

Since $\theta _n \le \theta , ~ \forall n\ge 1,$ we obtain from (3.4) that

$$\begin{aligned} (1-\epsilon )(1-\theta _{n-1})\ge \frac{\theta (1+\theta )}{1-\theta }\ge \theta _nt_{n+1}(1+\theta _n), \end{aligned}$$

(3.5)

for some $\epsilon \in (0,1).$

Since $\theta _{n-1}\le \theta _n, ~ \forall n\ge 1,$ we obtain that

$$\begin{aligned} \theta _nt_{n+1}(1+\theta _n)=\theta _nt_{n+1}(1+\theta _n+[\theta _{n-1}-\theta _n]_+). \end{aligned}$$

Combining this with (3.5), we get that Assumption 3.1 is satisfied. $\square$

Proposition 3.8

Suppose that $\theta _n \in [0,1),~\forall n\ge 1$ and there exists $c\in [0,\frac{1}{2})$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\left( \frac{1}{1-\theta _{n+1}}-\frac{1}{1-\theta _n}\right) =c \end{aligned}$$

(3.6)

and

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }(1-\theta _n)^2>\limsup \limits _{n\rightarrow \infty }\frac{\theta _n(1+\theta _n)}{1-2c}. \end{aligned}$$

(3.7)

Then, Assumptions (2.4) and 3.1 hold.

Proof

It follows from Proposition 2.3(i) that Assumption (2.4) holds.

Now, from (3.7), we obtain that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }(1-\theta _{n-1})^2>\limsup \limits _{n\rightarrow \infty }\frac{\theta _n(1+\theta _n)}{1-2c}. \end{aligned}$$

(3.8)

Thus, there exists $\epsilon \in (0,1)$ sufficiently small enough such that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }(1-\theta _{n-1})^2>\limsup \limits _{n\rightarrow \infty }\frac{\theta _n(1+\theta _n)}{1-2c-\epsilon (1-c)}>\limsup \limits _{n \rightarrow \infty }\frac{\theta _n(1+\theta _n)}{1-2c}. \end{aligned}$$

(3.9)

This implies that

$$\begin{aligned} (1+o(1))\theta _n(1+\theta _n)&\le [1-2c-\epsilon (1-c)+o(1)](1-\theta _{n-1})^2\\&=[(1-\epsilon )(1-c)-(2c-c+o(1))](1-\theta _{n-1})^2\\&\le [(1-\epsilon )(1-c)-\theta _n(c+o(1))](1-\theta _{n-1})^2, \end{aligned}$$

which implies that

$$\begin{aligned} (1-\epsilon )(1-c)(1-\theta _{n-1})^2&\ge (1+o(1))\theta _n\left( 1+\theta _n+(1-\theta _{n-1})^2+o\left( (1-\theta _{n-1})^2\right) \right) . \end{aligned}$$

(3.10)

Now, observe from (3.6) that

$$\begin{aligned} \theta _{n-1}-\theta _n+c(1-\theta _{n-1})(1-\theta _n)=o\left( (1-\theta _{n-1})(1-\theta _n)\right) , \end{aligned}$$

which implies from Proposition 2.3(ii) that

$$\begin{aligned} \theta _{n-1}-\theta _n&=-c(1-\theta _{n-1})(1-\theta _n)+o\left( (1-\theta _{n-1})(1-\theta _n)\right) \\&=-c(1-\theta _{n-1})^2+o(1-\theta _{n-1})^2~~ \text {as~~}~~ n\rightarrow \infty . \end{aligned}$$

This implies that

$$\begin{aligned} |\theta _{n-1}-\theta _n|&=|-c(1-\theta _{n-1})^2+o(1-\theta _{n-1})^2|\nonumber \\&\le c(1-\theta _{n-1})^2+o(1-\theta _{n-1})^2 ~~ \text {as~~}~~ n\rightarrow \infty . \end{aligned}$$

(3.11)

Combining (3.10) and (3.11), we obtain that

$$\begin{aligned} (1-\epsilon )(1-c)(1-\theta _{n-1})^2&\ge \left( 1+o(1)\right) \theta _n\left( 1+\theta _n+[\theta _{n-1}-\theta _n]_+\right) . \end{aligned}$$

(3.12)

By Proposition 2.3, we have that $t_{n+1}\sim t_n \sim \frac{1}{(1-c)(1-\theta _{n-1})}$ as $n\rightarrow \infty .$ Hence, (3.12) is equivalent to

$$\begin{aligned} (1-\epsilon )(1-c)(1-\theta _{n-1})^2&\ge \frac{\theta _n}{(1-c)(1-\theta _{n-1})}t_{n+1}\left( 1+\theta _n+[\theta _{n-1}-\theta _n]_+\right) , \end{aligned}$$

which further implies Assumption 3.1. $\square$

When $\rho _n\ne 1$, then we have the following proposition which provides some criteria for ensuring Assumption 3.1, as well as Assumption (2.4).

Proposition 3.9

(See for example, [3, Proposition 3.3])

Suppose that $\theta _n \in [0,1)$ and $\rho _n\in (0, 1)$ for all $n\ge 1$. Assume that there exist $c\in [0, 1)$ and ${\bar{c}}\in [c, 1)$ such that

$$\begin{aligned}&\lim _{n\rightarrow \infty }\left( \frac{1}{1-\theta _{n+1}}-\frac{1}{1-\theta _n}\right) =c, \\&\lim _{n\rightarrow \infty }\frac{\gamma _{n+1}-\gamma _n}{\gamma _n(1-\theta _{n})}={\bar{c}} \end{aligned}$$

and

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\gamma _n(1-\theta _n)^2>\limsup \limits _{n\rightarrow \infty }\frac{\theta _n(1+\theta _n)}{1-{\bar{c}}}, \end{aligned}$$

where $\gamma _n=\frac{1-\rho _n}{2\rho _n}$. Then, Assumptions (2.4) and 3.1 hold.

Remark 3.10

It is worthy of note that many practical choices for the inertial and relaxation factors $\theta _n$ and $\rho _n$, respectively, satisfy Assumption 3.1. In fact, similar conditions as in Propositions 3.7–3.9 have already been used in the literature to ensure the convergence of inertial and relaxation methods (see [31, 46, 47] and the references therein). Thus, Assumption 3.1, as well as assumption (2.4) are much more weaker than the assumptions in those papers.

Moreover, we shall give in Sect. 5, some typical examples of $\theta _n$ and $\rho _n$ which satisfy the conditions in Propositions 3.7–3.9 (therefore, satisfying assumption (2.4) and Assumption 3.1). Then, we check the sensitivity of both $\theta _n$ and $\rho _n$ in order to find numerically, the optimum choice of these parameters with respect to the convergence speed of our proposed methods.

4 Convergence Analysis

Lemma 4.1

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumption 3.2(a)-(b) hold. Then,

$$\begin{aligned}&\Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\\&\le \frac{1}{2}(\theta _n{+}\theta _n^2)\Vert x_n{-}x_{n-1}\Vert ^2{-}\gamma _n\Vert x_{n{+}1}{-}w_n\Vert ^2{-}\frac{\rho _n}{2}\left( 1{-}\lambda L\right) \left[ ||w_n{-}y_n||^2{+}||z_n{-}y_n||^2\right] , \end{aligned}$$

where $\gamma _n:=\frac{1-\rho _n}{2\rho _n}$ and $\Gamma _n:=\frac{1}{2}\Vert x_n-z\Vert ^2,~\forall z\in \Gamma .$

Proof

Let $z\in \Gamma .$ Since $x_{n+1}-w_n=\rho _n (z_n -w_n),$ we obtain

$$\begin{aligned} \langle x_{n+1}-w_n, \, \, w_n-z\rangle&=\rho _n\langle z_n-w_n, \, \,w_n-z_n \rangle +\rho _n\langle z_n-w_n, \, \, z_n-z\rangle \nonumber \\&=-\rho _n\Vert z_n-w_n\Vert ^2+\rho _n\langle z_n-w_n,\, \, z_n-z\rangle \nonumber \\&{=}{-}\rho _n^{{-}1}\Vert x_{n{+}1}{-}w_n\Vert ^2{+}\rho _n\langle z_n{-}w_n{+}\lambda Ay_n, \,z_n-z\rangle {-}\lambda \rho _n\langle Ay_n, \,z_n{-}z\rangle \nonumber \\&\le -\rho _n^{-1}\Vert x_{n+1}-w_n\Vert ^2+\lambda \rho _n\langle Ay_n,\, \,z-z_n\rangle , \end{aligned}$$

(4.1)

where the last inequality follows from $z\in \Gamma \subseteq T_n$ and the characteristic property of $P_{T_n}$ (see (2.3)).

Now, using (4.1) in Lemma 2.6, we obtain

$$\begin{aligned}&\Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\nonumber \\&\quad \le \frac{1}{2}(\theta _n{+}\theta _n^2)\Vert x_n{-}x_{n-1}\Vert ^2{-}\rho _n^{-1}\Vert x_{n+1}{-}w_n\Vert ^2{+}\lambda \rho _n\langle Ay_n,\, \,z-z_n\rangle +\frac{1}{2}\Vert x_{n+1}-w_n\Vert ^2\nonumber \\&\quad =\frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2-\frac{1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2\nonumber \\&\qquad +\lambda \rho _n\langle Ay_n,\, \,z-z_n\rangle \nonumber \\&\quad =\frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2+\lambda \rho _n\langle Ay_n, \, \,z-z_n\rangle \nonumber \\&\qquad -\frac{1}{2\rho _n}\cdot \rho _n^2\Vert w_n-z_n\Vert ^2\nonumber \\&\quad = \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2+\lambda \rho _n\langle Ay_n, \, \,z-z_n\rangle \nonumber \\&\quad -\frac{\rho _n}{2}\Vert w_n-y_n\Vert ^2-\frac{\rho _n}{2}\Vert y_n-z_n\Vert ^2-\rho _n\langle w_n-y_n,\, \,y_n-z_n\rangle , \end{aligned}$$

(4.2)

where the last equality follows from Lemma 2.8.

Since $y_n\subset {\mathcal {C}}$ and $z\in \Gamma ,$ we get from (2.1) that $\langle Ay_n,\, \,y_n-z\rangle \ge 0, \forall n\ge 1.$ That is $\langle Ay_n,\, \,y_n-z_n+z_n-z\rangle \ge 0, \forall n \ge 1.$ This implies that

$$\begin{aligned} \lambda \langle Ay_n,\, \,z-z_n\rangle -\langle w_n-y_n,\, \,y_n-z_n\rangle&\le \lambda \langle Ay_n,\, \,y_n-z_n\rangle -\langle w_n-y_n, \, \, y_n-z_n\rangle \nonumber \\&=\langle \lambda Ay_n-w_n+y_n, \, \,y_n-z_n\rangle . \end{aligned}$$

(4.3)

Substituting (4.3) into (4.2), we obtain that

$$\begin{aligned}&\Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\nonumber \\&\quad \le \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2 \nonumber \\&\qquad -\frac{\rho _n}{2}\left( \Vert w_n-y_n\Vert ^2+\Vert y_n-z_n\Vert ^2\right) +\rho _n\langle \lambda Ay_n-w_n+y_n, \, \, y_n-z_n \rangle \nonumber \\&\quad =\frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2-\frac{\rho _n}{2}\left( \Vert w_n-y_n\Vert ^2+\Vert y_n-z_n\Vert ^2\right) \nonumber \\&\qquad +\rho _n\langle w_n-\lambda Aw_n-y_n,\, \, z_n-y_n \rangle +\lambda \rho _n\langle Aw_n-Ay_n, \, \,z_n-y_n \rangle \nonumber \\&\quad \le \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2-\frac{\rho _n}{2}\left( \Vert w_n-y_n\Vert ^2+\Vert y_n-z_n\Vert ^2\right) \nonumber \\&\quad +\lambda \rho _n\langle Aw_n-Ay_n, \, \,z_n-y_n \rangle , \end{aligned}$$

(4.4)

where the last inequality follows from the definition of $T_n$.

Now, from the Lipschitz continuity of A, we obtain

$$\begin{aligned} \langle Aw_n-Ay_n, z_n-y_n\rangle\le & {} L||w_n-y_n||||z_n-y_n||\nonumber \\= & {} \frac{L}{2}\left[ ||w_n-y_n||^2+||z_n-y_n||^2-\left( ||w_n-y_n||-||z_n-y_n||\right) ^2\right] \nonumber \\\le & {} \frac{L}{2}\left( ||w_n-y_n||^2+||z_n-y_n||^2\right) . \end{aligned}$$

(4.5)

Substituting (4.5) into (4.4), we obtain the desired conclusion. $\square$

Lemma 4.2

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumption (2.4) and Assumption 3.2(a)-(b) hold. Then, the following inequality holds:

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n}\Big [\left( 2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)\right) \Vert x_i-x_{i-1}\Vert ^2+2\gamma _i(1-\theta _i)\\&\Big (\Vert x_{i+1}-x_i\Vert ^2-\Vert x_i-x_{i-1}\Vert ^2\Big )\Big ]\le 2t_1|\Gamma _1-\Gamma _0|+2\Gamma _0, \end{aligned}$$

where $t_{i, n}$ is as defined in (2.7).

Proof

By Lemma 2.8, we obtain

$$\begin{aligned} \Vert x_{n+1}-w_n\Vert ^2= & {} \Vert x_{n+1}-x_n-(x_n-x_{n-1})+(1-\theta _n)(x_n-x_{n-1})\Vert ^2\nonumber \\= & {} \Vert x_{n+1}-2x_n+x_{n-1}\Vert ^2+(1-\theta _n)^2\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&+2(1-\theta _n)\langle x_{n+1}-2x_n+x_{n-1}, x_n-x_{n-1}\rangle \nonumber \\= & {} \Vert x_{n+1}-2x_n+x_{n-1}\Vert ^2+(1-\theta _n)^2\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&+(1-\theta _n)\left[ \Vert x_{n+1}-x_{n}\Vert ^2- \Vert x_{n}-x_{n-1}\Vert ^2-\Vert x_{n+1}-2x_{n}+x_{n-1}\Vert ^2\right] \nonumber \\= & {} \theta _n \Vert x_{n+1}-2x_n+x_{n-1}\Vert ^2+(1-\theta _n)^2\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&+(1-\theta _n)\left[ \Vert x_{n+1}-x_{n}\Vert ^2- \Vert x_{n}-x_{n-1}\Vert ^2\right] \nonumber \\\ge & {} (1-\theta _n)^2\Vert x_n-x_{n-1}\Vert ^2+(1-\theta _n)\left[ \Vert x_{n+1}-x_{n}\Vert ^2- \Vert x_{n}-x_{n-1}\Vert ^2\right] .\nonumber \\ \end{aligned}$$

(4.6)

Using (4.6) in Lemma 4.1, and noting that $1-\lambda L> 0$, we obtain

$$\begin{aligned} \Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})&\le \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2-\gamma _n(1-\theta _n)^2\Vert x_n-x_{n-1}\Vert ^2\\&\quad -\gamma _n(1-\theta _n)\Big [\Vert x_{n+1}-x_n\Vert ^2-\Vert x_n-x_{n-1}\Vert ^2\Big ]\\&=\Big [\frac{1}{2}(\theta _n+\theta _n^2)-\gamma _n(1-\theta _n)^2\Big ]\Vert x_n-x_{n-1}\Vert ^2\\&\quad -\gamma _n(1-\theta _n)\Big [\Vert x_{n+1}-x_n\Vert ^2-\Vert x_n-x_{n-1}\Vert ^2\Big ]. \end{aligned}$$

This together with Lemma 2.5(a) imply that

$$\begin{aligned} \Gamma _n-\Gamma _0&=\sum _{i=1}^{n}(\Gamma _i-\Gamma _{i-1})\\&\le t_{1,n}(\Gamma _1-\Gamma _0)\\&\quad +\sum _{i=1}^{n-1} t_{i+1,n}\Big [\Big (\frac{1}{2}(\theta _i+\theta _i^2)-\gamma _i(1-\theta _i)^2\Big )\\&\quad \Vert x_i-x_{i-1}\Vert ^2-\gamma _i(1-\theta _i)\Big (\Vert x_{i+1}-x_i\Vert ^2-\Vert x_i-x_{i-1}\Vert ^2\Big )\Big ]. \end{aligned}$$

Noting that $t_{1,n}\le t_1,$ we obtain

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n}\Big [\left( 2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)\right) \Vert x_i-x_{i-1}\Vert ^2+2\gamma _i(1-\theta _i)\\&\quad \Big (\Vert x_{i+1}-x_i\Vert ^2-\Vert x_i-x_{i-1}\Vert ^2\Big )\Big ]\\&\quad \le 2t_{1,n}(\Gamma _1-\Gamma _0)+2(\Gamma _0-\Gamma _n)\\&\quad \le 2t_1|\Gamma _1-\Gamma _0|+2\Gamma _0-2\Gamma _n. \end{aligned}$$

Using $\Gamma _n=\frac{1}{2}\Vert x_n-z\Vert ^2\ge 0,~\forall n\ge 1$ in the above inequality, we obtain the desired conclusion $\square$

Lemma 4.3

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumptions (2.4) and 3.2(a)-(b) hold. Then, the following inequality holds:

$$\begin{aligned}&\sum _{i=1}^{n-1}2\gamma _{i-1}(1-\theta _{i-1})-\theta _it_{i+1}\Big (1+\theta _i+2\Big [\gamma _i(1-\theta _i)-\gamma _{i-1}(1-\theta _{i-1})\Big ]_+\Big )\Vert x_i-x_{i-1}\Vert ^2\\&\quad \le 2\Big [t_1|\Gamma _1-\Gamma _0|+\Gamma _0+t_1\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2\Big ]. \end{aligned}$$

Proof

Observe that

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n}\cdot 2\gamma _i(1-\theta _i)\Big [\Vert x_{i+1}-x_i\Vert ^2-\Vert x_i-x_{i-1}\Vert ^2\Big ]\nonumber \\&\quad =2\sum _{i=1}^{n-1}\Big (t_{i,n}\gamma _{i-1}(1-\theta _{i-1})-t_{i+1,n}\gamma _i(1-\theta _i)\Big )\Vert x_i-x_{i-1}\Vert ^2\nonumber \\&\qquad +2t_{1,n}\gamma _{n-1}(1-\theta _{n-1})\Vert x_n-x_{n-1}\Vert ^2-2t_{1,n}\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2\nonumber \\&\quad \ge 2\sum _{i=1}^{n-1}\Big (t_{i,n}\gamma _{i-1}(1-\theta _{i-1})-t_{i+1,n}\gamma _i(1-\theta _i)\Big )\Vert x_i-x_{i-1}\Vert ^2\nonumber \\&\qquad -2t_{1,n}\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2\nonumber \\&\quad \ge 2\sum _{i=1}^{n-1}\Big (t_{i,n}\gamma _{i-1}(1-\theta _{i-1})-t_{i+1,n}\gamma _i(1-\theta _i)\Big )\Vert x_i-x_{i-1}\Vert ^2\nonumber \\&\qquad -2t_1\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2, \end{aligned}$$

(4.7)

where the last inequality follows from $t_{1,n}\le t_1.$

Now, using (4.7) in Lemma 4.2, we obtain that

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n}\big (2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)\big )\Vert x_i-x_{i-1}\Vert ^2\\&\qquad +2\sum _{i=1}^{n-1}\big (t_{i,n}\gamma _{i-1}(1-\theta _{i-1})-t_{i+1,n}\gamma _i(1-\theta _i)\big )\Vert x_i-x_{i-1}\Vert ^2\\&\quad \le 2t_1|\Gamma _1-\Gamma _0|+2\Gamma _0+2t_1\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2. \end{aligned}$$

That is

$$\begin{aligned}&\sum _{i=1}^{n-1}\big [t_{i+1,n}(2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)-2\gamma _i(1-\theta _i))+2t_{i,n}\gamma _{i-1}(1-\theta _{i-1})\big ]\Vert x_i-x_{i-1}\Vert ^2\nonumber \\&\quad \le 2\Big [t_1|\Gamma _1-\Gamma _0|+\Gamma _0+t_1\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2\Big ]. \end{aligned}$$

(4.8)

Now, recall from (2.8) that $t_{i,n}=1+\theta _it_{i+1,n}$ for all $i\ge 1$ and $n\ge i+1.$ Hence, we have

$$\begin{aligned} 2t_{i,n}\gamma _{i-1}(1-\theta _{i-1})=2\Big [\gamma _{i-1}(1-\theta _{i-1})+\theta _it_{i+1,n}\gamma _{i-1}(1-\theta _{i-1})\Big ]. \end{aligned}$$

This implies that

$$\begin{aligned}&t_{i+1,n}\Big [2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)-2\gamma _i(1-\theta _i)\Big ]+2t_{i,n}\gamma _{i-1}(1-\theta _{i-1})\nonumber \\&\quad =t_{i+1,n}\big [2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)-2\gamma _i(1-\theta _i)+2\theta _i\gamma _{i-1}(1-\theta _{i-1})\big ]\nonumber \\&\qquad +2\gamma _{i-1}(1-\theta _{i-1})\nonumber \\&\quad =2\gamma _{i-1}(1-\theta _{i-1})+t_{i+1,n}\Big (-2\gamma _i\theta _i(1-\theta _i)-(\theta _i+\theta _i^2)+2\theta _i\gamma _{i-1}(1-\theta _{i-1})\Big )\nonumber \\&\quad =2\gamma _{i-1}(1-\theta _{i-1})-\theta _it_{i+1,n}\Big (2\gamma _i(1-\theta _i)+1+\theta _i-2\gamma _{i-1}(1-\theta _{i-1})\Big )\nonumber \\&\quad \ge 2\gamma _{i-1}(1-\theta _{i-1})-\theta _it_{i+1,n}\Big (1+\theta _i+2\Big [\gamma _i(1-\theta _i)-\gamma _{i-1}(1-\theta _{i-1})\Big ]_+\Big )\nonumber \\&\quad \ge 2\gamma _{i-1}(1-\theta _{i-1})-\theta _it_{i+1}\Big (1+\theta _i+2\big [\gamma _i(1-\theta _i)-\gamma _{i-1}(1-\theta _{i-1})\big ]_+\Big ), \end{aligned}$$

(4.9)

where the last inequality follows from $t_{i+1,n}\le t_{i+1}.$

Now, using (4.9) in (4.8), we obtain that the desired conclusion. $\square$

Lemma 4.4

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumptions (2.4), 3.1 and 3.2(a)-(b) hold. Then,

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\theta _nt_{n+1} \Vert x_n-x_{n-1}\Vert ^2<\infty . \end{aligned}$$

Proof

Without loss of generality, we may assume that inequality (3.1) holds true for all $n\ge 1.$ That is,

$$\begin{aligned} {\left\{ \begin{array}{ll} 2\epsilon \gamma _{n-1}(1-\theta _{n-1})\le 2\gamma _{n-1}(1-\theta _{n-1})-\theta _nt_{n+1}\Big (1+\theta _n+2\Big [\gamma _n(1-\theta _n)-\gamma _{n-1}(1-\theta _{n-1})\Big ]_+\Big ), &{} \hbox {if}~\rho _n\in (0, 1),\\ \epsilon (1-\theta _{n-1})\le (1-\theta _{n-1})-\theta _nt_{n+1}\Big (1+\theta _n+\Big [\theta _{n-1}-\theta _n\Big ]_+\Big ), &{} \hbox {if}~\rho _n= 1, \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.10)

where $\gamma _n=\frac{1-\rho _n}{2\rho _n}$, for all $n\ge 1$.

At this point, we divide our proof into two cases.

Case 1: Suppose that $\rho _n\in (0, 1),~\forall n\ge 1$. Then, using (4.10) in Lemma 4.3, we obtain

$$\begin{aligned} \sum _{i=1}^{n-1}\epsilon \gamma _{i-1}(1-\theta _{i-1})\Vert x_i-x_{i-1}\Vert ^2&\le t_1|\Gamma _1-\Gamma _0|+\Gamma _0+t_1\gamma _0(1-\theta _0)\Vert x_1-x_0\Vert ^2. \end{aligned}$$

(4.11)

Now, taking limit as $n\rightarrow \infty$ in (4.11), we obtain that

$$\begin{aligned} \sum _{i=1}^{\infty }\gamma _{i-1}(1-\theta _{i-1})\Vert x_i-x_{i-1}\Vert ^2<\infty . \end{aligned}$$

(4.12)

Again, from (4.10), we obtain that

$$\begin{aligned} \frac{1}{2}\theta _nt_{n+1}&\le \gamma _{n-1}(1-\theta _{n-1})-\frac{1}{2}\theta _n t_{n+1}\Big (\theta _n+2\Big [\gamma _n(1-\theta _n)-\gamma _{n-1}(1-\theta _{n-1})\big ]_+\Big )\nonumber \\&\qquad -\epsilon \gamma _{n-1}(1-\theta _{n-1})\nonumber \\&\le \gamma _{n-1}(1-\theta _{n-1}). \end{aligned}$$

(4.13)

Using (4.13) in (4.12), we obtain

$$\begin{aligned} \sum _{i=1}^{\infty }\theta _it_{i+1}\Vert x_i-x_{i-1}\Vert ^2<\infty . \end{aligned}$$

Case 2: Suppose that $\rho _n=1,~\forall n\ge 1$. Then, $x_{n+1}=z_n$ and $\gamma _n=0,~\forall n\ge 1$.

Setting $x=w_n-y_n$ and $y=x_{n+1}-y_n$ in Lemma 2.8, and using its result in Lemma 4.1, we obtain

$$\begin{aligned} \Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\le & {} \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&-\frac{1}{2}\left[ ||w_n-y_n+x_{n+1}-y_n||^2+||w_n-x_{n+1}||^2\right] \nonumber \\\le & {} \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2-\frac{1}{2}||w_n-x_{n+1}||^2. \end{aligned}$$

(4.14)

Now, using (4.6) in (4.14), and repeating the same line of proof as in Lemma 4.2, we get

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i{+}1,n}\Big [\left( (1{-}\theta _i)^2{-}(\theta _i{+}\theta _i^2)\right) \Vert x_i{-}x_{i{-}1}\Vert ^2{+}(1{-}\theta _i)\Big (\Vert x_{i{+}1}-x_i\Vert ^2-\Vert x_i{-}x_{i-1}\Vert ^2\Big )\Big ]\nonumber \\&\quad \le 2t_1|\Gamma _1-\Gamma _0|+2\Gamma _0. \end{aligned}$$

(4.15)

Similar to (4.7), we have

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n}(1-\theta _i)\Big [\Vert x_{i+1}-x_i\Vert ^2-\Vert x_i-x_{i-1}\Vert ^2\Big ]\nonumber \\&\quad \ge \sum _{i=1}^{n-1}\Big (t_{i,n}(1-\theta _{i-1})-t_{i+1,n}(1-\theta _i)\Big )\Vert x_i-x_{i-1}\Vert ^2-t_1(1-\theta _0)\Vert x_1-x_0\Vert ^2. \end{aligned}$$

(4.16)

Also, using (4.16) in (4.15), and repeating the same line of proof as in Lemma 4.3, we get

$$\begin{aligned} \sum _{i=1}^{n-1}(1-\theta _{i-1})-\theta _it_{i+1}\Big (1+\theta _i+\Big [\theta _{i-1}-\theta _i\Big ]_+\Big )\Vert x_i-x_{i-1}\Vert ^2\nonumber \\ \le 2t_1|\Gamma _1-\Gamma _0|+2\Gamma _0+t_1(1-\theta _0)\Vert x_1-x_0\Vert ^2. \end{aligned}$$

(4.17)

Using (4.10) in (4.17), and repeating the same line of proof as in Case 1, we obtain

$$\begin{aligned} \sum _{i=1}^{\infty }\theta _it_{i+1}\Vert x_i-x_{i-1}\Vert ^2<\infty , \end{aligned}$$

which yields the desired conclusion. $\square$

Lemma 4.5

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumption (2.4), Assumptions 3.1 and 3.2(a)-(b) hold. Then,

• (a) $\lim \limits _{n\rightarrow \infty }\Vert x_n-z\Vert$ exists for all $z\in \Gamma$, and consequently, $\{x_n\}$ is bounded.

• (b) $\lim \limits _{n\rightarrow \infty }\left[ \Vert w_n-y_n\Vert ^2+||z_n-y_n||^2\right] =0,$

• (c) $\lim \limits _{n\rightarrow \infty }\Vert x_n-w_n\Vert =0.$

Proof

• (a) From Lemma 4.1, we obtain

  $$\begin{aligned} \Gamma _{n+1}-\Gamma _n&\le \theta _n\Big (\Gamma _n-\Gamma _{n-1}\Big )+\frac{1}{2}\Big (\theta _n+\theta _n^2\Big )\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&\quad -\frac{\rho _n}{2}\left( 1-\lambda L\right) \left[ ||w_n-y_n||^2+||z_n-y_n||^2\right] \nonumber \\&\le \theta _n\Big (\Gamma _n-\Gamma _{n-1}\Big )+\theta _n\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&\quad -\frac{\rho _n}{2}\left( 1-\lambda L\right) \left[ ||w_n-y_n||^2+||z_n-y_n||^2\right] \end{aligned}$$

  (4.18)
  $$\begin{aligned}&\le \theta _n\Big (\Gamma _n-\Gamma _{n-1}\Big )+\theta _n\Vert x_n-x_{n-1}\Vert ^2, \end{aligned}$$

  (4.19)

  where the second inequality follows from $\theta _n^2\le \theta _n$ and the third inequality follows from $1-\lambda L>0$.

  Now, applying Lemmas 2.5(b) and 4.4 in (4.19), we obtain that $\sum \limits _{n=1}^{\infty }\Big [\Gamma _n-\Gamma _{n-1}\Big ]_+<\infty .$ Since $\Gamma _n=\frac{1}{2}\Vert x_n-z\Vert ^2,$ we get that $\lim \limits _{n\rightarrow \infty }\Vert x_n-z\Vert ^2$ exists. Hence, $\{x_n\}$ is bounded.

• (b) By applying Lemma 2.5(a) in (4.18), we obtain that

  $$\begin{aligned} \Gamma _n-\Gamma _0&=\sum _{i=1}^{n}\big (\Gamma _i-\Gamma _{i-1}\big )\\&\le t_{1,n}\Big (\Gamma _1-\Gamma _0\Big )+\sum _{i=1}^{n-1}t_{i+1,n}\Big [\theta _i\Vert x_i-x_{i-1}\Vert ^2\\&\quad -\frac{\rho _i}{2}\left( 1-\lambda L\right) \left[ ||w_i-y_i||^2+||z_i-y_i||^2\right] \Big ]\\&\le t_1\big (\Gamma _1-\Gamma _0\big )+\sum _{i=1}^{n-1}t_{i+1}\theta _i\Vert x_i-x_{i-1}\Vert ^2-\sum _{i=1}^{n-1}t_{i+1,n}\\&\quad \frac{\rho _i}{2}\left( 1-\lambda L\right) \left[ ||w_i-y_i||^2+||z_i-y_i||^2\right] \Big ], \end{aligned}$$

  which implies that

  $$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n}\frac{\rho _i}{2}\left( 1-\lambda L\right) \left[ ||w_i-y_i||^2+||z_i-y_i||^2\right] \Big ]\\&\quad \le \Gamma _0-\Gamma _n+t_1(\Gamma _1-\Gamma _0)+\sum _{i=1}^{n-1}t_{i+1}\theta _i\Vert x_i-x_{i-1}\Vert ^2\\&\quad \le \Gamma _0+t_1|\Gamma _1-\Gamma _0|+\sum _{i=1}^{n-1}t_{i+1}\theta _i\Vert x_i-x_{i-1}\Vert ^2\\&\quad < \infty , \end{aligned}$$

  where the last inequality follows from Lemma 4.4.

  Since $t_{i+1,n}=0$ for $i\ge n,$ letting n tend to $\infty ,$ the monotone convergence theorem then implies that

  $$\begin{aligned} \sum _{i=1}^{\infty }t_{i+1}\frac{\rho _i}{2}\left( 1-\lambda L\right) \left[ ||w_i-y_i||^2+||z_i-y_i||^2\right] \Big ]<\infty . \end{aligned}$$

  (4.20)

  Since $\liminf \limits _{n\rightarrow \infty }\rho _n>0,$ there exists $M>0$ such that $\rho _n\ge M$ for n large enough. Now, replacing i with n in (4.20) and noting that $t_n\ge 1, \forall n\ge 1,$ we obtain from (4.20) that $\sum \limits _{n=1}^{\infty }\frac{M}{2}\left( 1-\lambda L\right) \left[ ||w_n-y_n||^2+||z_n-y_n||^2\right] <\infty ,$ which further gives that $\lim \limits _{n\rightarrow \infty }\left[ ||w_n-y_n||^2+||z_n-y_n||^2\right] =0.$

• (c) Since $w_n=x_n+\theta _n(x_n-x_{n-1}),$ we obtain from Lemma 4.4 that

  $$\begin{aligned} \sum _{n=1}^{\infty }t_{n+1}\Vert w_n-x_n\Vert ^2\le \sum _{n=1}^{\infty }\theta _nt_{n+1}\Vert x_n-x_{n-1}\Vert ^2<\infty . \end{aligned}$$

  Noting that $t_n\ge 1, \forall n\ge 1,$ we conclude immediately that $\lim \limits _{n\rightarrow \infty }\Vert w_n-x_n\Vert =0.$

$\square$

Lemma 4.6

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumption (2.4), Assumptions 3.1 and 3.2(a)-(d) hold. If $x^*$ is one of the weak cluster points of $\{x_n\},$ then we have at least one of the following: $x^*\in \Gamma$ or $Ax^*=0.$

Proof

By Lemma 4.5(a), we can choose a subsequence of $\{x_n\}$ denoted by $\{x_{n_k}\}$ such that $x_{n_k}\rightharpoonup x^*\in {\mathcal {H}}.$ Also, from Lemma 4.5(b),(c), we obtain that $\lim \limits _{n\rightarrow \infty }\Vert y_n-x_n\Vert =0.$ Hence, we can choose a subsequence $\{y_{n_k}\}$ of $\{y_n\}$ such that $y_{n_k}\rightharpoonup x^*.$ Note that $x^*\in {\mathcal {C}}$ since $\{y_{n_k}\}\subset {\mathcal {C}}.$

We now consider two possible cases.

Case 1: Suppose that $\limsup \limits _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert =0.$ Then,$\lim \limits _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert =\liminf \limits _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert =0.$ Also, by the sequentially weakly continuity of A on ${\mathcal {C}},$ we obtain that $Ay_{n_k}\rightharpoonup Ax^*.$ Thus, by the weakly lower semicontinuity of $\Vert \cdot \Vert ,$ we have that

$$\begin{aligned} 0<\Vert Ax^*\Vert \le \liminf \limits _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert =0, \end{aligned}$$

(4.21)

which implies that $Ax^*=0.$

Case 2: Suppose that $\limsup \limits _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert >0.$ Then, without loss of generality, we can choose a subsequence of $\{Ay_{n_k}\}$ still denoted by $\{Ay_{n_k}\}$ such that $\lim \limits _{k \rightarrow \infty }\Vert Ay_{n_k}\Vert = M>0.$ Also by the characteristics property of $P_{{\mathcal {C}}},$ we obtain for all $x\in {\mathcal {C}}$ that

$$\begin{aligned} \langle w_{n_k}-\lambda Aw_{n_k}-y_{n_k},\, \,x-y_{n_k}\rangle \le 0. \end{aligned}$$

This implies that

$$\begin{aligned} \frac{1}{\lambda }\langle w_{n_k}-y_{n_k},x-y_{n_k}\rangle +\langle Aw_{n_k},\, \,y_{n_k}-w_{n_k}\rangle \le \langle A{w_{n_k}}, x-w_{n_k}\rangle . \end{aligned}$$

(4.22)

Thus, we obtain from Lemma 4.5(b) that

$$\begin{aligned} 0\le \liminf \limits _{k\rightarrow \infty }\langle Aw_{n_k},x-w_{n_k}\rangle&\le \limsup \limits _{k\rightarrow \infty }\langle Aw_{n_k}, x-w_{n_k}\rangle <\infty ,~\forall x\in {\mathcal {C}}. \end{aligned}$$

(4.23)

Now, note that

$$\begin{aligned} \langle Ay_{n_k},x-y_{n_k}\rangle =\langle Ay_{n_k}-Aw_{n_k},x-w_{n_k}\rangle +\langle Aw_{n_k},x-w_{n_k}\rangle +\langle Ay_{n_k},w_{n_k}-y_{n_k}\rangle . \end{aligned}$$

(4.24)

Moreover, since A is Lipschitz continuous on ${\mathcal {H}},$ we obtain from Lemma 4.5(b) that $\lim \limits _{k\rightarrow \infty }\Vert Aw_{n_k}-Ay_{n_k}\Vert =0.$ Hence, we obtain from Lemmas 4.5(b), (4.23) and (4.24) that

$$\begin{aligned} 0\le \liminf \limits _{k\rightarrow \infty }\langle Ay_{n_k}, x-y_{n_k}\rangle \le \limsup \limits _{k\rightarrow \infty }\langle Ay_{n_k},x-y_{n_k}\rangle <\infty ,~\forall x\in {\mathcal {C}}. \end{aligned}$$

(4.25)

Based on (4.25), we consider two cases under Case 2, as follows:

Case A: Suppose that $\limsup \limits _{k\rightarrow \infty }\langle Ay_{n_k}, x-y_{n_k}\rangle >0, \forall x\in {\mathcal {C}}.$ Then, we can choose a subsequence of $\{y_{n_k}\}$ denoted by $\{y_{n_{k_j}}\}$ such that $\lim \limits _{j\rightarrow \infty }\langle Ay_{n_{k_j}}, x-y_{n_{k_j}} \rangle >0$. Thus, there exists $j_0\ge 1$ such that $\langle Ay_{n_{k_j}},x-y_{n_{k_j}}\rangle >0, \forall j\ge j_0,$ which by the quasimonotonicity of A on ${\mathcal {H}},$ implies $\langle Ax,x-y_{n_{k_j}}\rangle \ge 0, \forall x\in {\mathcal {C}}, j\ge j_0.$ Thus, letting $j\rightarrow \infty ,$ we obtain that $\langle Ax, x-x^*\rangle \ge 0, \forall x\in {\mathcal {C}}.$ Hence, $x^*\in \Gamma .$

Case B: Suppose that $\limsup \limits _{k\rightarrow \infty } \langle Ay_{n_k},x-y_{n_k}\rangle =0, \forall x\in {\mathcal {C}}.$ Then, by (4.25), we obtain that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\langle Ay_{n_k}, x-y_{n_k}\rangle =0, \forall x\in {\mathcal {C}}, \end{aligned}$$

(4.26)

which implies that

$$\begin{aligned} \langle Ay_{n_k},x-y_{n_k}\rangle +|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}>0, \forall x\in {\mathcal {C}}. \end{aligned}$$

(4.27)

Also, since $\lim \limits _{k\rightarrow \infty }\Vert Ay_{n_k}\Vert =M>0,$ there exists $k_0\ge 1$ such that $\Vert Ay_{n_k}\Vert >\frac{M}{2}, \forall k\ge k_0.$ Therefore, we can set $q_{n_k}=\frac{Ay_{n_k}}{\Vert Ay_{n_k}\Vert ^2}, \forall k\ge k_0.$ Thus, $\langle Ay_{n_k}, q_{n_k}\rangle =1, \forall k\ge k_0.$ Hence, by (4.27), we obtain

$$\begin{aligned} \Big \langle Ay_{n_k}, x+q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}-y_{n_k}\Big ]\Big \rangle >0, \end{aligned}$$

which by the quasimonotonicity of A on ${\mathcal {H}},$ implies

$$\begin{aligned} \Big \langle A\Big (x+q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\Big ]\Big ), x+q_{n_k}\big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\big ]-y_{n_k}\Big \rangle \ge 0. \end{aligned}$$

This further implies that

$$\begin{aligned}&\langle Ax, x+q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\Big ]-y_{n_k}\rangle \nonumber \\&\ge \langle Ax, A(x{+}q_{n_k}\big [|\langle Ay_{n_k},x{-}y_{n_k}\rangle |{+}\frac{1}{k{+}1}\big ]), x{+}q_{n_k}\big [|\langle Ay_{n_k},x{-}y_{n_k}\rangle |{+}\frac{1}{k{+}1}\big ]{-}y_{n_k}\rangle \nonumber \\&\ge {-}\Vert Ax{-}A(x{+}q_{n_k}\Big [|\langle Ay_{n_k},x{-}y_{n_k}\rangle |{+}\frac{1}{k{+}1}\Big ])\Vert \cdot \Vert x{+}q_{n_k}\Big [|\langle Ay_{n_k},x{-}y_{n_k}\rangle |+\frac{1}{k+1}\Big ]\nonumber \\&\quad -y_{n_k}\Vert \nonumber \\&\ge -L\Vert q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\Big ]\Vert \cdot \Vert x+q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\Big ]-y_{n_k}\Vert \nonumber \\&=\frac{-L}{\Vert Ay_{n_k}\Vert }\Big (|\langle Ay_{n_k}, x-y_{n_k}\rangle |+\frac{1}{k+1}\Big )\cdot \Vert x+q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\Big ]-y_{n_k}\Vert \nonumber \\&\ge \frac{-2L}{M}\Big (|\langle Ay_{n_k}, x-y_{n_k}\rangle |+\frac{1}{k+1}\Big )M_1, \end{aligned}$$

(4.28)

for some $M_1>0,$ where the existence of $M_1$ follows from the boundedness of $\{x+q_{n_k}\Big [|\langle Ay_{n_k},x-y_{n_k}\rangle |+\frac{1}{k+1}\Big ]-y_{n_k}\}.$ Note from (4.26) that $\lim \limits _{k \rightarrow \infty }\Big (|\langle Ay_{n_k}, x-y_{n_k}\rangle |+\frac{1}{k+1}\Big )=0.$ Hence, letting $k\rightarrow \infty$ in (4.28), we get that $\langle Ax, x-x^*\rangle \ge 0, \forall x\in {\mathcal {C}}.$ Therefore, $x^*\in \Gamma .$ $\square$

Lemma 4.7

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that Assumption (2.4), Assumption 3.1 and 3.2(a)-(d) hold. Then $\{x_n\}$ has at most one weak cluster point in $\Gamma .$

Proof

Suppose on the contrary that $\{x_n\}$ has at least two weak cluster points in $\Gamma .$ Let $x^*\in \Gamma$ and ${\bar{x}}\in \Gamma$ be any two weak cluster points of $\{x_n\}$ such that $x^*\ne {\bar{x}}.$ Also, let $\{x_{n_j}\}$ be a subsequence of $\{x_n\}$ such that $x_{n_j}\rightharpoonup {\bar{x}}, \text {as}\, \,j\rightarrow \infty .$ Then, by Lemmas 4.5(a) and 2.7, we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert x_n-{\bar{x}}\Vert&=\lim \limits _{j\rightarrow \infty }\Vert x_{n_j}-{\bar{x}}\Vert \\&=\liminf \limits _{j\rightarrow \infty }\Vert x_{n_j}-{\bar{x}}\Vert \\&<\liminf _{j\rightarrow \infty }\Vert x_{n_j}-x^*\Vert \\&=\lim \limits _{n\rightarrow \infty }\Vert x_n-x^*\Vert \\&=\liminf \limits _{k\rightarrow \infty }\Vert x_{n_k}-x^*\Vert \\&<\liminf \limits _{k\rightarrow \infty }\Vert x_{n_k}-{\bar{x}}\Vert =\lim \limits _{n\rightarrow \infty }\Vert x_n-{\bar{x}}\Vert , \end{aligned}$$

which is a contradiction. Therefore, $\{x_n\}$ has at most one weak cluster point in $\Gamma .$ $\square$

Using similar line of arguments as in [29, Lemma 3.5], we obtain the following weak convergence result.

Theorem 4.8

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that assumption (2.4), Assumptions 3.1 and 3.2(a)-(e) hold. Then $\{x_n\}$ converges weakly to an element of $VI({\mathcal {C}}, A).$

Proof

By Assumption 3.2(e), $\{x\in {\mathcal {C}}:Ax=0\}\setminus \Gamma$ is a finite set. Hence, by Lemma 4.6 and Lemma 4.7, we have that $\{x_n\}$ has finite weak cluster points in $VI({\mathcal {C}}, A).$ Let $x^1,x^2,\cdots ,x^m$ be the weak cluster points of $\{x_n\}$, and let $\{x^i_{n_k}\}$ be a subsequence of $\{x_n\}$ such that $x^i_{n_k}\rightharpoonup x^i,$ as $k\rightarrow \infty .$ Then, we obtain

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Big \langle x^i_{n_k}, x^i-x^j\Big \rangle =\Big \langle x^i, x^i-x^j\Big \rangle , \forall j\ne i. \end{aligned}$$

(4.29)

Now, for $j\ne i,$ set $q=\beta ^{-1}(x^i-x^j),$ where $\beta =\Vert x^i-x^j\Vert .$ Then,

$$\begin{aligned} \langle x^i,q\rangle&=\beta ^{-1}\langle x^i, x^i-x^j\rangle \nonumber \\&=\beta ^{-1}\Big (\Vert x^i\Vert ^2-\langle x^i, x^j\rangle \Big )\nonumber \\&=\beta ^{-1}\Big [\Vert x^i\Vert ^2-\frac{1}{2}\Vert x^i\Vert ^2-\frac{1}{2}\Vert x^j\Vert ^2+\frac{1}{2}\Vert x^i-x^j\Vert ^2\Big ]\nonumber \\&=\frac{1}{2\beta }\Big (\Vert x^i\Vert ^2-\Vert x^j\Vert ^2\Big )+\frac{1}{2}\beta \nonumber \\&>\frac{1}{2\beta }\Big (\Vert x^i\Vert ^2-\Vert x^j\Vert ^2\Big )+\frac{1}{4}\beta . \end{aligned}$$

(4.30)

For sufficiently large k,  we obtain from (4.29) and (4.30) that

$$\begin{aligned} x^i_{n_k}\in \Big \{x:\langle x, q\rangle >\frac{1}{2\beta }\Big (\Vert x^i\Vert ^2-\Vert x^j\Vert ^2\Big )+\frac{1}{4}\beta \Big \}. \end{aligned}$$

(4.31)

Hence, there exists $N_1>N$ ($N\in {\mathbb {N}}$) such that

$$\begin{aligned} x^i_{n_k}\in B^i:=\bigcap ^m_{j=1, j\ne i}\Big \{x:\Big \langle x, \frac{x^i-x^j}{\Vert x^i-x^j\Vert }\Big \rangle >\frac{1}{2\Vert x^i-x^j\Vert }\Big (\Vert x^i\Vert ^2-\Vert x^j\Vert ^2\Big )+\epsilon _0\Big \}, \forall n\ge N_1, \end{aligned}$$

(4.32)

where

$$\begin{aligned} \epsilon _0=\text {min}\Big \{\frac{1}{4}\Vert x^i-x^j\Vert :i,j=1,2,\cdots ,m, i\ne j\Big \}. \end{aligned}$$

Now, from Lemma 4.5(b), we obtain that $\lim \limits _{n\rightarrow \infty }\Vert z_{n}-w_n\Vert =0.$ Since $x_{n+1}-w_n=\rho _n(z_n-w_n)$ and $\{\rho _n\}$ is bounded, we obtain that $\lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-w_n\Vert =0.$ This together with Lemma 4.5(c), imply that $\lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0.$ Hence, there exists $N_2>N_1>N$ such that $\Vert x_{n+1}-x_n\Vert <\epsilon _0, \forall n\ge N_2.$

Claim: $\{x_n\}$ has only one weak cluster point in $VI({\mathcal {C}},A).$

Suppose on the contrary that $\{x_n\}$ has more than one weak cluster points in $VI({\mathcal {C}}, A).$ Then, there exists $N_3\ge N_2>N_1>N$ such that $x_{N_3}\in B^i$ and $x_{N_3+1}\in B^j,$ where

$$\begin{aligned}&B^j:=\bigcap ^m_{i=1, i\ne j}\Big \{x:\Big \langle -x, \frac{x^j-x^i}{\Vert x^j-x^i\Vert }\Big \rangle <\frac{1}{2\Vert x^j-x^i\Vert }\Big (\Vert x^i\Vert ^2-\Vert x^j\Vert ^2\Big )-\epsilon _0\Big \},\nonumber \\&\quad i,j\in \{1,2,\cdots ,m\}\, \,\text {and}\, \,m \ge 2. \end{aligned}$$

(4.33)

In particular, we have

$$\begin{aligned} \Vert x_{N_3+1}-x_{N_3}\Vert <\epsilon _0. \end{aligned}$$

(4.34)

Since $x_{N_3}\in B^i$ and $x_{N_3+1}\in B^j,$ we obtain that

$$\begin{aligned} \Big \langle x_{N_3},\frac{x^i-x^j}{\Vert x^i-x^j\Vert }\Big \rangle >\frac{1}{2\Vert x^i-x^j\Vert }\Big (\Vert x^i\Vert ^2-\Vert x^j\Vert ^2\Big )+\epsilon _0 \end{aligned}$$

(4.35)

and

$$\begin{aligned} \Big \langle -x_{N_3+1},\frac{x^i-x^j}{\Vert x^j-x^i\Vert }\Big \rangle >\frac{1}{2\Vert x^i-x^j\Vert }\Big (\Vert x^j\Vert ^2-\Vert x^i\Vert ^2\Big )+\epsilon _0. \end{aligned}$$

(4.36)

Adding (4.35) and (4.36), and using (4.34), we obtain

$$\begin{aligned} 2\epsilon _0<\Big \langle x_{N_3}-x_{N_3+1},\frac{x_i-x^j}{\Vert x^i-x^j\Vert }\Big \rangle \le \Vert x_{N_3+1}-x_{N_3}\Vert < \epsilon _0, \end{aligned}$$

(4.37)

which is not possible. Hence, our claim holds. That is, $\{x_n\}$ has only one weak cluster point in $VI({\mathcal {C}},A).$ Therefore, we conclude that $\{x_n\}$ converges weakly to an element of $VI({\mathcal {C}},A).$ $\square$

Remark 4.9

• (i) The conclusion of Theorem 4.8 still hold even if $\lambda \in (0, \frac{1}{L})$ in Algorithm 3.3 is replaced with a variable stepsize $\lambda _n$ such that $0<\inf _{n\ge 1}\lambda _n\le \sup _{n\ge 1} \lambda _n <\frac{1}{L}.$ However, choosing this variable stepsize still requires the knowledge of the Lipschitz constant L.

• (ii) When the Lipschitz constant is not known, we refer to Algorithm 3.4, where the choice of $\lambda _n$ does not depend on its knowledge. Note from the stepsize $\lambda _n$ in (3.2), that $\lim \limits _{n\rightarrow \infty }\lambda _n=\lambda$ and $\lambda \in [\min \{\frac{\mu }{L}, \lambda _1\}, \lambda _1+d]$, where $d=\sum _{n=1}^\infty d_n$ (see also [29, Lemma 3.1]).

• (iii) When $d_n=0$, then the stepsize $\lambda _n$ generated by Algorithm 3.4 is similar to that in [52]. We recall that the stepsize in [52] is monotone non-increasing, thus, their methods may depend on the choice of the initial stepsize $\lambda _1$. However, the stepsize given in (3.2) is non-monotonic and hence, the dependence on the initial stepsize $\lambda _1$ is reduced.

In the light of the above remark, we analyze the convergence of Algorithm 3.4 in what follows.

Lemma 4.10

Let $\{x_n\}$ be a sequence generated by Algorithm 3.4 such that Assumption 3.2(a)-(b) hold. Then,

$$\begin{aligned}&\Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\\&\quad \le \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2-\gamma _n\Vert x_{n+1}-w_n\Vert ^2-\frac{\rho _n}{2}\left( 1-\lambda _n \frac{\mu }{\lambda _{n+1}}\right) \\&\quad \left[ ||w_n-y_n||^2+||z_n-y_n||^2\right] , \end{aligned}$$

where $\gamma _n:=\frac{1-\rho _n}{2\rho _n}$ and $\Gamma _n:=\frac{1}{2}\Vert x_n-z\Vert ^2,~\forall z\in \Gamma .$

Proof

By following the same line of proof used in obtaining (4.4), we have

$$\begin{aligned}&\Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\nonumber \\&\quad \le \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2+\frac{\rho _n-1}{2\rho _n}\Vert x_{n+1}-w_n\Vert ^2-\frac{\rho _n}{2}\left( \Vert w_n-y_n\Vert ^2+\Vert y_n-z_n\Vert ^2\right) \nonumber \\&\qquad +\lambda _n\rho _n\langle Aw_n-Ay_n, \, \,z_n-y_n \rangle . \end{aligned}$$

(4.38)

If $\langle Aw_n-Ay_n, z_n-y_n\rangle \le 0$, then we obtain the conclusion of Lemma 4.10 immediately from (4.38).

In the case that $\langle Aw_n-Ay_n, z_n-y_n\rangle > 0$, we obtain from (3.2) that

$$\begin{aligned} \langle Aw_n-Ay_n, z_n-y_n\rangle \le \frac{\mu }{2\lambda _{n+1}}\Big (\Vert w_n-y_n\Vert ^2+\Vert z_n-y_n\Vert ^2\Big ). \end{aligned}$$

(4.39)

Substituting (4.39) into (4.38), we obtain the desired conclusion. $\square$

Lemma 4.11

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 such that assumption (2.4) and Assumption 3.2(a)-(b) hold. Then, the following inequality holds:

$$\begin{aligned}&\sum _{i=1}^{n-1}t_{i+1,n} \Big [\left( 2\gamma _i(1-\theta _i)^2-(\theta _i+\theta _i^2)\right) \Vert x_i-x_{i-1}\Vert ^2+2\gamma _i(1-\theta _i)\\&\quad \Big (\Vert x_{i+1}-x_i\Vert ^2-\Vert x_i-x_{i-1}\Vert ^2\Big )\Big ]\le 2t_1|\Gamma _1-\Gamma _0|+2\Gamma _0, \end{aligned}$$

where $t_{i, n}$ is as defined in (2.7).

Proof

By following the same line of proof used in obtaining (4.6), we have

$$\begin{aligned} \Vert x_{n+1}-w_n\Vert ^2\ge & {} (1-\theta _n)^2\Vert x_n-x_{n-1}\Vert ^2+(1-\theta _n)\nonumber \\&\left[ \Vert x_{n+1}-x_{n}\Vert ^2- \Vert x_{n}-x_{n-1}\Vert ^2\right] . \end{aligned}$$

(4.40)

Also, by Remark 4.9(ii), we obtain that $\lim _{n\rightarrow \infty } \lambda _n \frac{\mu }{\lambda _{n+1}}=\mu \in (0, 1)$. Thus, there exists $n_0\ge 1$ such that $\forall n\ge n_0$, $0<\lambda _n \frac{\mu }{\lambda _{n+1}}<1$. Hence, we get from Lemmas 4.10 and (4.40) that

$$\begin{aligned} \Gamma _{n+1}-\Gamma _n-\theta _n(\Gamma _n-\Gamma _{n-1})\le & {} \frac{1}{2}(\theta _n+\theta _n^2)\Vert x_n-x_{n-1}\Vert ^2-\gamma _n\Vert x_{n+1}-w_n\Vert ^2\\\le & {} \Big [\frac{1}{2}(\theta _n+\theta _n^2)-\gamma _n(1-\theta _n)^2\Big ]\Vert x_n-x_{n-1}\Vert ^2\\&-\gamma _n(1-\theta _n)\Big [\Vert x_{n+1}-x_n\Vert ^2-\Vert x_n-x_{n-1}\Vert ^2\Big ], ~\forall n\ge n_0. \end{aligned}$$

The remaining part of the proof is the same as the proof of Lemma 4.2. $\square$

In similar manner, we have that Lemmas 4.3 to 4.7 hold for Algorithm 3.4. Thus, we have the following theorem whose proof is the same as the proof of Theorem 4.8.

Theorem 4.12

Let $\{x_n\}$ be a sequence generated by Algorithm 3.4 such that Assumption (2.4), Assumptions 3.1 and 3.2(a)-(e) hold. Then $\{x_n\}$ converges weakly to an element of $VI({\mathcal {C}}, A).$

Remark 4.13

From our analyses, one can see that Assumption 3.1 is mainly used to guarantee the summation:

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\theta _nt_{n+1} \Vert x_n-x_{n-1}\Vert ^2<\infty \end{aligned}$$

(4.41)

obtained in Lemma 4.4. Thus, if we assume that (4.41) directly, then we do not need Assumption 3.1 for the convergence of our methods.

In the case where $\rho _n=1,~\forall n\ge 1$, our methods correspond to the inertial subgradient extragradient methods. Note that if $\theta _n \in [0, \theta ]$ for every $n\ge 1,$ where $\theta \in [0,1),$ then $t_n\le \frac{1}{(1-\theta )}~~~\forall n\ge 1.$ Under these settings, (4.41) is guaranteed by the condition

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\theta _n\Vert x_n-x_{n-1}\Vert ^2 <\infty . \end{aligned}$$

(4.42)

Thus, instead of Assumption 3.1, we may assume directly that $\theta _n \in [0, \theta ],~ \forall n\ge 1$ and that condition (4.42) holds. Recall that this condition has been used by numerous authors to ensure convergence of inertial methods (see, for example, [2, 15, 31, 32, 34] and the references therein).

Remark 4.14

Note that we did not make use of Assumption 3.2(c)-(e) in the proof of Lemmas 4.1–4.5. Suppose that ${\mathcal {H}}$ is a finite dimensional Hilbert space, then under Assumption 3.2(a)-(b), we get from Lemma 4.5(a) that there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $\{x_{n_k}\}$ converges to some point $x^*$. By Lemma 4.5(b)(c), we get

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert w_{n_k}-y_{n_k}\Vert =0 \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert w_{n_k}-x_{n_k}\Vert =0. \end{aligned}$$

Thus, by the definition of $y_n$ and the continuity of A, we have

$$\begin{aligned} x^*=\lim _{k\rightarrow \infty } x_{n_k}=\lim _{k\rightarrow \infty } y_{n_k}=\lim _{k\rightarrow \infty } P_C(w_{n_k}-\lambda Aw_{n_k})=P_C(x^*-\lambda A x^*), \end{aligned}$$

which implies that $x^*\in VI({\mathcal {C}}, A)$.

Now, replacing z by $x^*$ in Lemma 4.5(a), we obtain that $\lim \limits _{n\rightarrow \infty }\Vert x_{n}-x^*\Vert ^{2}$ exists. Since $x^*$ is a cluster point of $\{x_n\}$, we obtain that $\{x_n\}$ converges to $x^*$.

In summary, in a finite dimensional Hilbert space, our methods require that $\Gamma \ne \emptyset$ and the operator A only needs to be Lipschitz continuous without any form of monotonicity.

To achieve this (convergence without any form of monotonicity) in infinite dimensional Hilbert space, we replace Assumption 3.2(d)-(e) with the following:

• (d)* If $x_n\rightharpoonup x^*$ and $\limsup \limits _{n\rightarrow \infty }\langle Ax_n, x_n\rangle \le \langle Ax^*, {\bar{x}}\rangle$, then $\lim \limits _{n\rightarrow \infty }\langle A x_n, x_n\rangle =\langle A x^*, x^*\rangle$.

• (e)* The set $VI({\mathcal {C}}, A)\setminus \Gamma$ is a finite set.

In fact, we have the following theorem.

Theorem 4.15

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 (or Algorithm 3.4) such that Assumptions (2.4), 3.1 and 3.2(a)-(c) and conditions (d)*-(e)* hold. Then $\{x_n\}$ converges weakly to an element of $VI({\mathcal {C}}, A).$

Proof

First notice that Assumption 3.2(d) was used only after (4.25) in order to establish the conclusion of Lemma 4.6.

But from (4.25), we have that

$$\begin{aligned} 0\le \liminf \limits _{k\rightarrow \infty }\langle Ay_{n_k}, x-y_{n_k}\rangle ,~\forall x\in {\mathcal {C}}. \end{aligned}$$

Now, let $\{c_k\}$ be a sequence of positive numbers such that $\lim \limits _{k\rightarrow \infty } c_k=0$ and $\langle Ay_{n_k}, x-y_{n_k}\rangle +c_k> 0,~\forall k\ge 0, x\in {\mathcal {C}}.$ Then,

$$\begin{aligned} \langle Ay_{n_k}, x\rangle +c_k> \langle Ay_{n_k}, y_{n_k}\rangle ,~\forall k\ge 0, x\in {\mathcal {C}}. \end{aligned}$$

(4.43)

Note that $y_{n_k}\rightharpoonup x^*$ and $x^*\in {\mathcal {C}}$. Thus, we have in particular,

$$\begin{aligned} \langle Ay_{n_k}, x^*\rangle +c_k> \langle Ay_{n_k}, y_{n_k}\rangle ,~\forall k\ge 0. \end{aligned}$$

(4.44)

Taking limit as $k\rightarrow \infty$ in (4.44), and using the sequentially weakly continuity of A, we obtain that

$$\begin{aligned} \langle Ax^*, x^*\rangle \ge \limsup \limits _{k\rightarrow \infty }\langle Ay_{n_k}, y_{n_k}\rangle , \end{aligned}$$

which by condition (d)* and (4.43) implies that

$$\begin{aligned} \langle Ax^*, x^*\rangle= & {} \lim _{k\rightarrow \infty }\langle Ay_{n_k}, y_{n_k}\rangle \\= & {} \liminf _{k\rightarrow \infty }\langle Ay_{n_k}, y_{n_k}\rangle \\\le & {} \lim _{k\rightarrow \infty }\left( \langle Ay_{n_k}, x\rangle +c_k\right) =\langle A x^*, x\rangle . \end{aligned}$$

This further implies that $x^*\in VI({\mathcal {C}}, A)$.

Now, using condition (e)* and following similar line of proof as in Lemma 4.7 and Theorem 4.15, we get that $\{x_n\}$ converges weakly to $x^*$. $\square$

Remark 4.16

• (i) If $x_n\rightharpoonup x^*$ and A is sequentially weakly-strongly continuous, then A satisfies condition (d)*.

• (ii) In the numerical experiments, we do not need to consider condition (e) (or (e)*). First note that whenever $||y_n-w_n||<\epsilon$, Algorithms 3.3 and 3.4 terminate in a finite step of the iterations (and $y_n$ is the solution of the VIP (1.1)). But from Lemma 4.5(b), $\lim \limits _{n\rightarrow \infty }||y_n-w_n||=0$ and condition (e) (or (e)*) was not used in establishing it.

We now give some remarks regarding the contributions and novelties of this paper.

Remark 4.17

• (1) If we set the inertial factor $\theta _n=0$ and relaxation factor $\rho _n=1$, then our Algorithm 3.4 reduces to [29, Algorithm 3.3]. Note that these parameters (factors) play vital role in improving the convergence rate of iterative methods. In fact, their influence with regards to the numerical performance of iterative schemes was discussed in [23]. Moreover, the benefits gained from incorporating the steps of these two parameters in our algorithms, are further verified in Sect. 5. Thus, bearing in mind the importance of these two parameters in iterative algorithms, we can see that our methods significantly improve the methods in [29].

• (2) In the study of inertial methods for solving VIPs (even for monotone mappings), the inertia parameter is usually restricted in $[0, \frac{1}{3})$ and/or required to be nondecreasing with an upper bound (see, for example, [2, 31, 46, 47]). In many cases, to ensure convergence, authors usually require the inertial parameter to depend on the knowledge of the Lipschitz constant of the cost operator which sometimes is very difficult to estimate in practice (see, for instance, [8]). Another condition usually imposed on the inertial parameter in the literature, is condition (4.42), which rely on the sequence $\{x_n\}$. One of the novelties of this paper is that we derived a general condition (Assumption 3.1) which is weaker than the above conditions used in the literature for ensuring the convergence of inertial methods for VIPs. As a result, we developed a different technique to ensure the convergence of our proposed Algorithms 3.3 and 3.4.

• (3) In addition to (2) above, bearing in mind the Nestrov’s accelerated scheme ( [35]), another novelty of this paper, is that the assumptions on the inertial and relaxation parameters in Algorithms 3.3 and 3.4 allow the case where inertial factor $\theta _n$ converges to the limit very close to 1 (see Remark 2.4 and the choices in Experiment 1 of Sect. 5), which is very crucial in the study of inertial methods. This is actually where the relaxation effect and the parameter $\rho _n$ come into play, as crucial ingredients of our methods. Thus, the novelty of this paper is not only in improving the convergence speed of the methods in [29] but to also provide weaker conditions on the inertial parameter in methods for solving VIPs and offer a different but unified technique in proving their convergence. Furthermore, we employed condition (Assumption 3.1) where joint adjustments of the inertial and relaxation parameters play crucial role (for instance, see Experiment 1). Indeed, this is a new perspective in the study of inertial methods for VIPs. Moreover, our study offers many possibilities for future research in this direction; like how to modify Assumption 3.1 so that inertial factor $\theta _n$ is allowed to converge to 1.

• (4) The method of proof of our proposed Algorithms 3.3 and 3.4 is different from the method of proof of [29, Algorithm 3.3]. For example, we use different arguments to show that the sequence $\{x_n\}$ is bounded in Lemma 4.5 (different from the arguments used in [29, Lemma 3.2]). We also use different arguments in Lemmas 4.1, 4.2, 4.3, and 4.4.

5 Numerical Experiments

In this section, we give some numerical examples to show the implementation of our proposed methods (Algorithms 3.3 and 3.4). We also compare our new methods with Algorithms 3.1 and 3.3 in [29], and Algorithm 2.1 in [50].

The codes are written in Matlab 2016 (b) and performed on a personal computer with an Intel(R) Core(TM) i5-2600 CPU at 2.30GHz and 8.00 Gb-RAM. In Tables 1, 2, 3, 4, 5, “Iter.” means the number of iterations while “CPU” means the CPU time in seconds.

In our computations, we define $\hbox {TOL}_n:=||y_n-w_n||$ for Algorithms 3.3 and 3.3. While for Algorithms 3.1 and 3.3 in [29], we define $\hbox {TOL}_n:=\Vert y_n-x_n\Vert /\hbox {min}\{\lambda _n,1\}$ and for Algorithm 2.1 in [50], we define $\hbox {TOL}_n:=\Vert x_n-z_n\Vert =\Vert x_n-P_{\mathcal {C}}(x_n-Ax_n)\Vert$ (as done in [29] and [50], respectively). Then, we use the stopping criterion $\hbox {TOL}_n<\varepsilon$ for the iterative processes, where $\varepsilon$ is the predetermined error. These choices of stopping criterion for these methods are the best to be able to terminate the algorithms based on the examples we consider. As done in [29], we take $\varepsilon =10^{-6}$ for all Algorithms.

We choose $\mu =0.5,~ d_n=\frac{100}{(n+1)^{1.1}}$ and $\lambda _1=1$ for Algorithm 3.4 and Algorithms 3.1 and 3.3 in [29]; $\lambda =\frac{1}{2L}$ for Algorithm 3.3; $\gamma =0.4$ and $\sigma =0.99$ for Algorithm 2.1 in [50]. These choices are the same as in [29, 50] and are optimal values for these parameters.

Example 5.1

Let ${\mathcal {C}}=[-1,1]$ and

$$\begin{aligned} Ax = \left\{ \begin{array}{ll} 2x-1,&{}~~ x>1, \\ x^2,&{}~~x\in [-1,1],\\ -2x-1, &{}~~ x<-1. \end{array} \right. \end{aligned}$$

Then, A is quasimonotone and 2-Lipschitz continuous. Also, $\Gamma =\{-1\}$ and $VI({\mathcal {C}},A)=\{-1,0\}.$

Example 5.2

Let ${\mathcal {C}}=\{x\in {\mathbb {R}}^2:x_1^2+x_2^2\le 1,\, \, 0\le x_1\}$ and $A(x_1,x_2)=(-x_1e^{x_2},x_2).$ Then, A may not be quasimonotone. We can also check that $(1,0)\in \Gamma$ and $VI({\mathcal {C}},A)=\{(1,0),(0,0)\}$ (see [29, Section 4]), which by Remark 4.14 satisfy our assumptions. This example was also tested in [29].

Example 5.3

We next consider the following problem which was also considered in [29, 33, 42].

Let ${\mathcal {C}}=[0,1]^m$ and $Ax=(f_1x,f_2x,\cdots ,f_mx),$

where $f_ix=x_{i-1}^2+x_i^2+x_{i-1}x_i+x_ix_{i+1}-2x_{i-1}+4x_i+x_{i+1}-1,\, \,i=1,2,\cdots ,m,$

$x_0=x_{m+1}=0.$

We test these examples under the following experiments.

Experiment 1

In this first experiment, we check the behavior of our methods by fixing the inertial parameter and varying the relaxation parameter. We do this in order to check the effects of the relaxation parameter on our methods.

For Example 1: We take $\theta _n=\frac{3n+1}{10n+5}$ with $\rho _n=1$ (which by Proposition 3.7, satisfies Assumptions (2.4) and 3.1), and $\theta _n=\frac{19}{20}-\frac{1}{(n+1)^\frac{1}{2}}$ with $\rho _n\in \{\frac{1}{20}+\frac{1}{(n+1)^2},~\frac{1}{20}+\frac{2}{(n+1)^3}, ~\frac{1}{20}+\frac{3}{(n+1)^4},\frac{1}{20}+\frac{5}{(n+1)^4}\}$ (which also satisfies Assumptions (2.4) and 3.1 by Proposition 3.9).

Also, we take $x_1=1$ and $x_0=0.5$ for this example. Since the Lipshitz constant is known for this example, we use Algorithms 3.3 and 3.4 for the experiment and obtain the numerical results listed in Table 1 and Fig. 1. From the table and graph, we can see that $\rho _n=1$ performs better than other choices made for Algorithms 3.3 and 3.4.

For Example 2 and Example 3: We take $\theta _n=\frac{9.9}{10}-\frac{1}{n+1}$ with $\rho _n=1$ (which by Proposition 3.8 (see also Remark 2.4), satisfies Assumption (2.4) and 3.1), and $\theta _n=\frac{9}{10}-\frac{1}{(n+1)^\frac{1}{3}}$ with $\rho _n\in \{\frac{1}{10}+\frac{1}{n+1},~\frac{1}{11}+\frac{1}{n+1}, ~\frac{1}{12}+\frac{1}{n+1},\frac{1}{13}+\frac{1}{n+1}\}$. Also, we take $x_1=(0.1, 0.5)$ and $x_0=(0.2, 0.1)$ for Example 2 while for Example 3, we choose $x_1$ and $x_0$ randomly with $m=50$. For these examples, we use Algorithm 3.4 for the experiment and obtain the numerical results listed in Table 2 and Fig. 2. From the table and graph, we can see that the $\rho _n=\frac{1}{11}+\frac{1}{n+1}$ performs better than other choices made for Example 2 while $\rho _n=\frac{1}{10}+\frac{1}{n+1}$ performs better for Example 3, which validates the benefits sometimes brought by the relaxation parameter.

Experiment 2

In this experiment, we compare our methods with Algorithms 3.1 and 3.3 in [29], and Algorithm 2.1 in [50]. Here, we randomly choose the $\theta _n$ and $\rho _n$ from Experiment 1, and then, consider the following cases for the starting points in each example.

For Example 1: Case I: $x_1=0.2$, $x_0=0.1$ and Case II: $x_1=0.6$, $x_0=0.2$.

For Example 2: Case I: $x_1=(1, 0.5)$, $x_0=(0.2, 0.1)$ and Case II: $x_1=(0.1, 0.2)$, $x_0=(0.3, 0.5)$.

For Example 3: Case I: $m=100$ and Case II: $m=150$ ($x_1$ and $x_0$ are randomly taken).

We use Algorithms 3.1 and 3.4 for the comparison in Example 1 while we use only Algorithm 3.4 for the comparison in Example 2 and Example 3. The numerical results are given in Tables 3, 4, 5 and Figs. 3, 4, 5. The results show that our methods perform better than Algorithms 3.1 and 3.3 in [29], and Algorithm 2.1 in [50].

Table 1 Numerical results for Example 1 (Experiment 1)

Fig. 1

The behavior of Algorithms 3.3 and 3.4 for Example 1 (Experiment 1)

Table 2 Numerical results for Algorithm 3.4 (Experiment 1)

Fig. 2

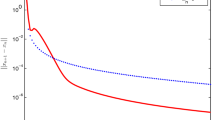
The behavior of Algorithm 3.4 for Examples 2 and 3 (Experiment 1)

Table 3 Numerical results for Example 1 (Experiment 2)

Fig. 3

The behavior of $\hbox {TOL}_n$ for Example 1 (Experiment 2): Left: Case I; Right: Case II

Table 4 Numerical results for Example 2 (Experiment 2)

Fig. 4

The behavior of $\hbox {TOL}_n$ for Example 2 (Experiment 2): Left: Case I; Right: Case II

Table 5 Numerical results for Example 3 (Experiment 2)

Fig. 5

The behavior of $\hbox {TOL}_n$ for Example 3 (Experiment 2): Left: Case I; Right: Case II

Remark 5.4

From Tables 3, 4, 5 and Figs. 3, 4, 5, one can see that our proposed Algorithms 3.3 and 3.4 are more efficient than [29, Algorithm 3.3] and outperform [29, Algorithm 3.3] in terms of number of iterations and CPU time based on our test problems due to the presence of inertial extrapolation step in Algorithms 3.3 and 3.4.

6 Conclusion

We propose and study two new subgradient extragradient methods with relaxed inertial steps for solving the variational inequality problems in real Hilbert spaces when the cost operator is not necessarily pseudomonotone. The first method is proposed when the Lipschitz constant of the cost operator is known while the second method which involves adaptive stepsize strategy, is proposed when the Lipschitz constant of the operator is not available. The techniques employed in this paper are quite different from the ones used in most papers, and the assumptions on the inertial and relaxation factors, are weaker than those in many papers for solving variational inequality problems. The benefits brought from the relaxation are further verified in Experiment 1, and as seen in Experiment 2, our methods performs better when compared with other methods for solving the non-pseudomonotone variational inequality problems.