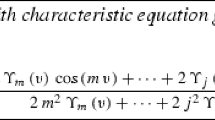1 Introduction

We consider in this paper numerical approximation of the following Klein–Gordon–Schrödinger (KGS) equations,

$$\begin{aligned} \left\{ \begin{aligned}&\mathrm {i} \partial _{t} \psi +\Delta \psi +\phi \psi +\mathrm {i} \nu \psi =0, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon ^{2} \partial _{tt} \phi +\gamma \varepsilon \partial _{t} \phi -\Delta \phi +\phi -|\psi |^{2}=0, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\psi ({\mathbf {x}}, 0)=\psi ^{(0)}({\mathbf {x}}), \quad \phi ({\mathbf {x}}, 0)=\phi ^{(0)}({\mathbf {x}}), \quad \partial _{t} \phi ({\mathbf {x}}, 0)=\phi ^{(1)}({\mathbf {x}}), \quad {\mathbf {x}} \in \Omega , \end{aligned} \right. \end{aligned}$$
(1.1)

where \(\Omega \) is a bounded domain in \({\mathbb {R}}^{d}\; (d=1,2,3)\), and \(\psi \) and \(\phi \) are prescribed with either homogeneous Dirichlet or periodic boundary conditions. In the absence of the interaction terms, the first equation of (1.1) is a Schrödinger equation, and the second one is a Klein–Gordon equation.

The KGS equations (1.1) describe the dynamic of the interaction of scalar nucleons interacting with neutral scalar mesons through Yukawa interaction. In the above, the complex-valued unknown function \(\psi =\psi ({\mathbf {x}}, t)\) represents a scalar nucleon field, the real-valued unknown function \(\phi =\phi ({\mathbf {x}}, t)\) represents a scalar meson field, \(\varepsilon >0\) is a parameter inversely proportional to the speed of light, and \(\gamma \) and \(\nu \) are two nonnegative parameters. In fact, when \(\varepsilon =1, \gamma =0\) and \(\nu =0\), it reduces to the standard KGS equations. The system (1.1) is dispersive with \(\nu =\gamma =0\), and dissipative when \(\nu >0\) and/or \(\gamma >0\).

The KGS equations have been extensively studied in the literature. We refer to [13,14,15,16,17,18,19, 28] (resp. [5, 6, 27]) and the references therein for the mathematical analysis of the conservative (i.e. \(\nu =\gamma =0\)) KGS equations (resp. the dissipative KGS equations).

The standard KGS equations have also been extensively studied numerically. For examples, Xiang [36] constructed a conservative spectral scheme for the periodic initial-value problem and provided its error analysis; Zhang [38] developed a conservative difference scheme in one dimension; Kong et al. [23, 24] and Hong et al. [21] considered multi-symplectic schemes; Hong et al. [20] compared the classical conservative properties of five difference schemes and investigated their numerical behaviors; Liang [26] constructed three linearly implicit Fourier pseudospectral algorithms; Chen et al. [8] developed a conservative and linearly implicit finite difference scheme with second order temporal accuracy and eighth order spatial accuracy by means of the Richardson extrapolation method; Li et al. [25] proposed a conservative linearized Galerkin finite element method; Wang [34] proposed a conservative high-order compact finite difference scheme for the KGS equation with Dirichlet boundary condition; Yang [37] developed methods involving a Crank–Nicholson time discretization for the Schrödinger equation part, a Crank–Nicholson leap frog method in time for the Klein–Gordon equation part, and local discontinuous Galerkin methods in space. For the KGS equations in the “nonrelativistic” regime, we refer to [2, 4]. For some recent work on the fractional KGS equations, we refer to [7, 12, 30, 35].

Numerical methods and sumilations for the KGS equations with damping mechanism (1.1) has received less attention. Bao and Yang [3] constructed efficient and accurate schemes with the time-splitting Fourier spectral technique for the Schrödinger-type operator, the Fourier pseudo-spectral method for the Klein–Gordon part, and the adoption of solving the ordinary differential equations (ODEs) in phase space analytically. Their numerical methods possess some nice discrete properties, e.g., time reversible, time transverse invariant, and it is shown through a formal Von Neumann analysis that the numerical solutions remain bounded but without proof for discrete energy dissipation. Ji and Zhang [22] developed a decoupled time-stepping method, based on the finite difference approximation in time and Fourier pseudo-spectral discretization in space, and the scheme is proved to preserve/dissipate the discrete wave energy for \(\nu \ge 0\) and dissipate the energy when \(\nu =0\) and \(\gamma \ge 0\). However, a nonlinear system needs to be solved in each time step. Thus, it is of great interests to develop an efficient, accurate numerical scheme that can preserve the conservation/dissipation properties of wave energy and Hamiltonian at the discrete level. The main difficulty is to avoid solving complicated nonlinear systems at each time step while preserving the conservation/dissipation properties.

The aim of this paper is to construct a class of efficient and accurate schemes for the KGS equations (1.1) based on the original SAV approach [31] and the SAV approach with Lagrange multipliers [9, 10]. These approaches were proposed for dissipative gradient flows, and recently they have been successfully applied to dispersive equations such as nonlinear Schrödinger and Zakharov equations [1, 11, 29, 32]. However, there are new challenges in application of these approaches to KGS equations (1.1). First, the Hamiltonian of KGS equations involves a non-quadratic term which is not necessarily bounded from below so the original SAV approach can not be directly applied. Second, the original SAV approach is designed to dissipate a modified total energy or Hamiltonian, but does not have a mechanism to preserve the wave energy. We employ a SAV approach with Lagrange multipliers to preserve the wave energy as well as to preserve/dissipate the original Hamiltonian. Combined with a Crank–Nicolson/Leap-Frog scheme in time, the proposed schemes enjoy the following distinct advantages:

  • The schemes are second-order accurate in time and can be combined with any Galerkin-type spatial discretization;

  • At each time step, they require solving only a sequence of linear decoupled systems with constant coefficients, and in the case of the schemes with Lagrange multipliers, an additional nonlinear algebraic system which can be solved with a negligible computational cost.

We carry out a series of numerical simulation to validate these schemes and to compare them under conservative and dissipative regimes.

The rest of paper is organized as follows. In Sect. 2, we reformulate the KGS equations with SAV, develop a SAV scheme based on Crank–Nicolson-leap-frog, and prove that it preserves/dissipates a modified Hamiltonian. In Sect. 3, we construct two schemes using the Lagrange multiplier approach and show that Scheme LM1 preserve the wave energy, as well as preserve/dissipate the original Hamiltonian, while Scheme LM2 preserves the Hamiltonian and wave energy in a slightly different form. In Sect. 4, we present various numerical simulations to compare and validate the proposed schemes for KGS equations, and apply our new approach to simulate soliton-soliton collisions in 1D with/without damping terms, as well as dynamics of a 2D problems in KGS equations. Some concluding remarks are presented in Sect. 5.

2 KGS System and Its SAV Reformulation

Throughout the paper, we shall use \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert \) to denote the inner product and norm in \(L^2(\Omega )\), respectively, and we denote norms in \(H^s(\Omega )\) by \(\Vert \cdot \Vert _s\).

For the sake of clarity, we first rewrite the KGS equations (1.1) as follows. Let \(\psi ({\mathbf {x}}, t)=p({\mathbf {x}}, t)+\mathrm {i} q({\mathbf {x}}, t)\), where both \(p({\mathbf {x}}, t)\) and \(q({\mathbf {x}}, t)\) are real-valued functions, and introduce a new variable \(u({\mathbf {x}}, t)=\varepsilon \partial _{t} \phi ({\mathbf {x}}, t)\) to reformulate (1.1) as a first-order-in-time differential system. Then the problem (1.1) becomes

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t} q+\nu q=\Delta p+\phi p, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\partial _{t} p+\nu p=-(\Delta q+\phi q), \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon \partial _{t} u=\Delta \phi -\phi +\left( p^{2}+q^{2}\right) -\gamma u, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon \partial _{t} \phi =u, \quad {\mathbf {x}} \in \Omega , \quad t>0. \end{aligned} \right. \end{aligned}$$
(2.1)

Similarly, p, q, u and \(\phi \) are prescribed with either homogeneous Dirichlet or periodic boundary conditions. We denote the unknowns of the above system by \({\mathbf {v}}=(p, q, u,\phi )^T\).

Theorem 2.1

The system (2.1) with homogeneous Dirichlet or periodic boundary conditions satisfies the following conservation laws:

$$\begin{aligned} \frac{d }{dt}(\Vert p\Vert ^2+\Vert q\Vert ^2)=-2\nu (\Vert p\Vert ^2+\Vert q\Vert ^2), \end{aligned}$$
(2.2)

where \(\Vert p\Vert ^2+\Vert q\Vert ^2\) is the wave energy, and

$$\begin{aligned} \frac{{d} H}{{d} t}=-\frac{\gamma }{\varepsilon } \Vert u\Vert ^2 -2\nu (\Vert \nabla p\Vert ^2+\Vert \nabla q\Vert ^2)+2\nu (\phi ,|p|^2+|q|^2), \end{aligned}$$
(2.3)

where \(H(t;{\mathbf {v}})\) is the Hamiltonian defined by

$$\begin{aligned} \begin{aligned} H(t;{\mathbf {v}})&=\{ \Vert \nabla p\Vert ^2+\Vert \nabla q\Vert ^2+\frac{1}{2} (\Vert \nabla \phi \Vert ^2+\Vert u\Vert ^2+\Vert \phi \Vert ^2)\} -(\phi ,|p|^2+|q|^2). \end{aligned} \end{aligned}$$
(2.4)

Proof

Taking the inner products of the first two equations in (2.1) with 2q and 2p respectively, and summing up the results, we obtain immediately (2.2).

Taking the inner products of the first two equations in (2.1) with \(-2( \partial _{t} p+\nu p)\) and \(2 (\partial _{t} q+\nu q)\) respectively, and summing up the results, we obtain

$$\begin{aligned}&\frac{d}{dt} \{\Vert \nabla p\Vert ^2+\Vert \nabla q\Vert ^2\}-(\phi ,\partial _t (|p|^2+|q|^2))\nonumber \\&\quad = -2\nu (\Vert \nabla p\Vert ^2+\Vert \nabla q\Vert ^2)+2\nu (\phi ,|p|^2+|q|^2). \end{aligned}$$
(2.5)

On the other hand, taking the inner products of the first two equations in (2.1) with \(u / \varepsilon \) and \(-\left( \Delta \phi -\phi +\left( p^{2}+q^{2}\right) \right) / \varepsilon \) respectively, and summing up the results, we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \{\Vert \nabla \phi \Vert ^2+\Vert u\Vert ^2+\Vert \phi \Vert ^2\}- (\partial _t\phi , |p|^2+|q|^2)=-\frac{\gamma }{\varepsilon }\Vert u\Vert ^2. \end{aligned}$$
(2.6)

Summing up the above two relations, we obtain (2.3). \(\square \)

Remark 2.1

We observe from the above that

  • When \(\nu = 0\), we have

    $$\begin{aligned} \frac{d}{dt} D(t;p,q)=0,\quad t \ge 0, \end{aligned}$$
    (2.7)

    where \(D(t;p,q):=\Vert p({\mathbf {x}}, t)\Vert ^{2}+ \Vert q({\mathbf {x}}, t)\Vert ^2\), and

    $$\begin{aligned} \frac{d}{dt} H(t;{\mathbf {v}})=-\frac{\gamma }{\varepsilon }\Vert u\Vert ^2, \quad t \ge 0. \end{aligned}$$
    (2.8)

  • When \(\nu > 0\), we derive from (2.2) that the wave energy decays exponentially, more precisely

    $$\begin{aligned} D(t;p,q):=\mathrm {e}^{-2 \nu t} D(0;p,q), \quad t \ge 0, \end{aligned}$$
    (2.9)

    but the Hamiltonian \(H(t;{\mathbf {v}})\) is not necessarily decreasing. However, it can be shown (cf. [14, 33]) that the Hamiltonian is bounded.

Since the Hamiltonian in the continuous case is not monotonically decreasing when \(\nu >0\), one can not expect to construct schemes which dissipate the Hamiltonian when \(\nu >0\). Therefore, we shall restrict ourselves to the case with \(\nu =0\), and concentrate on constructing numerical schemes which can preserve the conservation or dissipation properties (2.7) and (2.8). Note that all the schemes constructed below can be directly extended to deal with the case \(\nu >0\) by treating the linear term \(\nu p\) and \(\nu q\) in (2.1) implicitly.

2.1 The SAV Reformulation

When \(\nu =0\), one can see that (2.1) can be cast as a gradient system so one can in principle apply the original SAV approach introduced in [31], which also requires a suitable splitting of the Hamiltonian \(H(t;{\mathbf {v}})=H_0(t;{\mathbf {v}})+H_1(t;{\mathbf {v}})\) such that (i) \(\frac{\delta H_0}{\delta {\mathbf {v}}}\) is linear and positive definite; and (ii) \(H_1(t;{\mathbf {v}})\) is bounded from below.

While the non quadratic term \((\phi ,|p|^2+|q|^2)\) in the Hamiltonian is not bounded from below for arbitrary functions \((\phi ,p,q)\), it can be shown (cf. [14, 33]) that there exists \(C_0>0\) such that \(|(\phi ,|p|^2+|q|^2)|<C_0\) if \((\phi ,p,q)\) is a solution of (2.1). Hence, we split \( H(t;{\mathbf {v}})\) as follows:

$$\begin{aligned} \begin{aligned} H(t;{\mathbf {v}})&= \{ \Vert \nabla p\Vert ^2+\Vert \nabla q\Vert ^2+\frac{1}{2} (\Vert \nabla \phi \Vert ^2+\Vert u\Vert ^2+\Vert \phi \Vert ^2)-C_0\} + \{C_0 -(\phi ,|p|^2+|q|^2)\}\\&:=H_0(t;{\mathbf {v}})+H_1(t;{\mathbf {v}}). \end{aligned}\nonumber \\ \end{aligned}$$
(2.10)

Since \(H_1(t,{\mathbf {v}})>0\), we can define a SAV \(R(t)=\sqrt{H_{1}(t)}:=\sqrt{H_1(t,{\mathbf {v}})}\), and expand (2.1) as

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t} q=\Delta p+\frac{R(t)}{\sqrt{H_{1}(t)}} \phi p, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\partial _{t} p=-\left( \Delta q+\frac{R(t)}{\sqrt{H_{1}(t)}} \phi q\right) , \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon \partial _{t} u=\Delta \phi -\phi +\frac{R(t)}{\sqrt{H_{1}(t)}}\left( p^{2}+q^{2}\right) -\gamma u, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon \partial _{t} \phi =u, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&R_{t}=-\frac{1}{2 \sqrt{H_{1}(t)}}\left[ \left( 2 pp_{t}+2 qq_{t}, \phi \right) +\left( p^{2}+q^{2}, \phi _{t}\right) \right] . \end{aligned} \right. \end{aligned}$$
(2.11)

With \(R(0)=\sqrt{H_{1}(0)}\), it is clear that the above system is equivalent to (2.1) with \(R(t)=\sqrt{H_{1}(t)}.\)

2.2 Time Discretizations Using the SAV Approach

We construct a semi-discrete scheme based on Crank–Nicolson-leap-frog scheme using the SAV approach for the system (2.11).

Scheme SAV:

Initialization: Given \(q^{0}, p^{0}, u^{0}, \phi ^{0}\), determine \(q^{1}, p^{1}, u^{1}, \phi ^{1}\) by

$$\begin{aligned}&\frac{q^{1}-q^{0}}{2\delta t}= \frac{\Delta p^{1}+\Delta p^{0}}{2}+\frac{R^{1}+R^{0}}{ 2\sqrt{H_{1}^{0}}} \phi ^{0} p^{0}, \end{aligned}$$
(2.1)
$$\begin{aligned}&\frac{p^{1}-p^{0}}{2\delta t}=-\left( \frac{\Delta q^{1}+\Delta q^{0}}{2}+\frac{R^{1}+R^{0}}{ 2\sqrt{H_{1}^{0}}} \phi ^{0} q^{0}\right) ,\end{aligned}$$
(2.2)
$$\begin{aligned}&\quad \varepsilon \frac{u^{1}-u^{0}}{2\delta t}= \frac{\Delta \phi ^{1}+\Delta \phi ^{0}}{2}-\frac{\phi ^{1}+\phi ^{0}}{2}+\frac{R^{1}+R^{0}}{ 2\sqrt{H_{1}^{0}}}\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}\right) -\gamma \frac{u^{1}+u^{0}}{2}, \end{aligned}$$
(2.3)
$$\begin{aligned}&\varepsilon \frac{\phi ^{1}-\phi ^{0}}{2\delta t}=\frac{u^{1}+u^{0}}{2}, \end{aligned}$$
(2.4)
$$\begin{aligned}&\frac{R^{1}-R^{0}}{2\delta t} =-\frac{1}{2 \sqrt{H_{1}^{0}}}\left[ \left( 2 p^{0} \frac{p^{1}-p^{0}}{2\delta t}+2 q^{0} \frac{q^{1}-q^{0}}{2\delta t}, \phi ^{0} \right) + \left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2},\frac{\phi ^{1}-\phi ^{0}}{2\delta t}\right) \right] .\nonumber \\ \end{aligned}$$
(2.5)

Then, for \(n=1,2,\ldots \), we solve \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) from the following second-order Crank–Nicolson-leap-frog scheme:

$$\begin{aligned} \frac{q^{n+1}-q^{n-1}}{2\delta t}= & {} \frac{\Delta p^{n+1}+\Delta p^{n-1}}{2}+\frac{R^{n+1}+R^{n-1}}{ 2\sqrt{H_{1}^{n}}} \phi ^{n} p^{n}, \end{aligned}$$
(2.6)
$$\begin{aligned} \frac{p^{n+1}-p^{n-1}}{2\delta t}= & {} -\left( \frac{\Delta q^{n+1}+\Delta q^{n-1}}{2}+\frac{R^{n+1}+R^{n-1}}{ 2\sqrt{H_{1}^{n}}} \phi ^{n} q^{n}\right) , \end{aligned}$$
(2.7)
$$\begin{aligned} \varepsilon \frac{u^{n+1}-u^{n-1}}{2\delta t}= & {} \frac{\Delta \phi ^{n+1}+\Delta \phi ^{n-1}}{2}-\frac{\phi ^{n+1}+\phi ^{n-1}}{2}+\frac{R^{n+1}+R^{n-1}}{ 2\sqrt{H_{1}^{n}}}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}\right) \nonumber \\&-\gamma \frac{u^{n+1}+u^{n-1}}{2}, \end{aligned}$$
(2.8)
$$\begin{aligned} \varepsilon \frac{\phi ^{n+1}-\phi ^{n-1}}{2\delta t}= & {} \frac{u^{n+1}+u^{n-1}}{2}, \end{aligned}$$
(2.9)
$$\begin{aligned} \frac{R^{n+1}-R^{n-1}}{2\delta t}= & {} -\frac{1}{2 \sqrt{H_{1}^{n}}}\left[ \left( 2 p^{n} \frac{p^{n+1}-p^{n-1}}{2\delta t}+2 q^{n} \frac{q^{n+1}-q^{n-1}}{2\delta t}, \phi ^{n} \right) \right. \nonumber \\&\left. + \left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2},\frac{\phi ^{n+1}-\phi ^{n-1}}{2\delta t}\right) \right] . \end{aligned}$$
(2.10)

Note that the initialization step is of first-order but the local truncation error is of second-order. So the combined scheme is still of second-order.

Theorem 2.2

Let \(H_1^n=C_0-(\phi ^{n},|p^{n}|^2+|q^{n}|^2)\). There exists \(C_0>0\) such that if \(H_{1}^{n}>0\), we have \(H_{1}^{n+1}>0\) for all \(n\ge 0\).

The scheme (2.6)–(2.10) satisfies discrete energy laws:

$$\begin{aligned} H_{SAV}^{1}-H_{SAV}^{0}=-\delta t \frac{\gamma }{ 2\varepsilon }\left\| u^{1}+u^{0}\right\| ^{2}, \end{aligned}$$
(2.11)

and

$$\begin{aligned} H_{SAV}^{n+1}-H_{SAV}^{n-1}=-\delta t \frac{\gamma }{ 2\varepsilon }\left\| u^{n+1}+u^{n-1}\right\| ^{2}, \quad \forall n\ge 1, \end{aligned}$$
(2.12)

where

$$\begin{aligned} \begin{aligned} H_{SAV}^{n+1}&=\frac{1}{2}\left( \left\| \phi ^{n+1}\right\| ^{2} +\left\| u^{n+1}\right\| ^{2}+\left\| \nabla \phi ^{n+1}\right\| ^{2}\right) \\&\quad +\left( \left\| \nabla p^{n+1}\right\| ^{2}+ \left\| \nabla q^{n+1}\right\| ^{2}\right) + \left| R^{n+1}\right| ^{2}, \quad \forall n\ge 0. \end{aligned} \end{aligned}$$
(2.13)

Proof

Taking the inner products of the equations in (2.1)–(2.4) with \(-2 \frac{p^{1}-p^{0}}{2\delta t}\), \(2 \frac{q^{1}-q^{0}}{2\delta t}\), \(\frac{u^{1}+u^{0}}{2\varepsilon }\) and \(-\left( \frac{\Delta \phi ^{1}+\Delta \phi ^{0}}{2}-\frac{\phi ^{1}+\phi ^{0}}{2}+\frac{R^{1}+R^{0}}{ 2\sqrt{H_{1}^{0}}}\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}\right) \right) / \varepsilon \), respectively, and multiplying (2.5) by \(R^{1}+R^{0}\), summing up the results, we obtain (2.11).

Assuming \(H_{1}^{n}>0\), then (2.6)–(2.10) is well defined. Taking inner product of (2.6)–(2.9) with \(-2 \frac{p^{n+1}-p^{n-1}}{2\delta t}\), \(2 \frac{q^{n+1}-q^{n-1}}{2\delta t}\), \(\frac{u^{n+1}+u^{n-1}}{2\varepsilon }\) and \(-\Big (\frac{\Delta \phi ^{n+1}+\Delta \phi ^{n-1}}{2} -\frac{\phi ^{n+1}+\phi ^{n-1}}{2}+\frac{R^{n+1}+R^{n-1}}{ 2\sqrt{H_{1}^{n}}}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}\right) \Big )/ \varepsilon \), respectively, and multiplying (2.10) by \(R^{n+1}+R^{n-1}\), summing up the results, we obtain (2.12).

It remains to show \(H_{1}^{n+1}>0\).

From (2.12), we derive in particular that

$$\begin{aligned} \left\| p^{n+1}\right\| ^{2} +\left\| q^{n+1}\right\| ^{2} \le C_1 H_{SAV}^{n+1} \le C_1 H(0,{\mathbf {v}}):=C_2. \end{aligned}$$
(2.14)

On the other hand, we derive from the Sobolev inequality

$$\begin{aligned} \Vert f\Vert _{L^4}\le C\Vert f\Vert ^{1/4}\Vert \nabla f\Vert ^{3/4}\quad \forall f\in H_0^1(\Omega ) \;\text { or }\; H^1_p(\Omega ), \end{aligned}$$
(2.15)

and the Hölder inequality that

$$\begin{aligned} \begin{aligned} |(\phi ,|p|^2)|&\le C\Vert \phi \Vert _{L^4} \Vert p\Vert _{L^4}\Vert p\Vert \\&\le C \Vert \phi \Vert ^{1/4} \Vert \nabla \phi \Vert ^{3/4}\Vert p\Vert ^{5/4} \Vert \nabla p\Vert ^{3/4}\\&\le \frac{1}{8} (\Vert \phi \Vert ^2+\Vert \nabla \phi \Vert ^2+\Vert \nabla p\Vert ^2)+C_3\Vert p\Vert ^{10}. \end{aligned} \end{aligned}$$
(2.16)

Similarly we have

$$\begin{aligned} |(\phi ,|q|^2)|\le \frac{1}{8} (\Vert \phi \Vert ^2+\Vert \nabla \phi \Vert ^2+\Vert \nabla q\Vert ^2)+C_3\Vert q\Vert ^{10}. \end{aligned}$$
(2.17)

Therefore, we derive from the above and (2.14) that

$$\begin{aligned} |(\phi ^{n+1},|p^{n+1}|^2+|q^{n+1}|^2)|\le & {} H_{SAV}^{n+1} +C_3(\Vert p^{n+1}\Vert ^{10} +\Vert q^{n+1}\Vert ^{10})\nonumber \\\le & {} H(0,{\mathbf {v}})+2C_3C_2^5. \end{aligned}$$
(2.18)

Hence, setting \(C_0=H(0,{\mathbf {v}})+2C_3C_2^5+1\), we have \(H_{1}^{n+1}\ge 1\). \(\square \)

The scheme (2.6)–(2.10) can be efficiently implemented as follows.

Setting

$$\begin{aligned} \left\{ \begin{aligned}&q^{n+1}=q_{1}^{n+1}+R^{n+1}q_{2}^{n+1}, \\&p^{n+1}=p_{1}^{n+1}+R^{n+1}p_{2}^{n+1}, \\&u^{n+1}=u_{1}^{n+1}+R^{n+1}u_{2}^{n+1}, \\&\phi ^{n+1}=\phi _{1}^{n+1}+R^{n+1}\phi _{2}^{n+1}, \end{aligned} \right. \end{aligned}$$
(2.19)

in (2.6)–(2.9), and collecting all terms without or with \(R^{n+1}\), we obtain the following decoupled systems:

$$\begin{aligned} A {\mathbf {v}}_{1}^{n+1}={\mathbf {g}}_{1}^{n}, \end{aligned}$$
(2.20)
$$\begin{aligned} A {\mathbf {v}}_{2}^{n+1}={\mathbf {g}}_{2}^{n}, \end{aligned}$$
(2.21)

where

$$\begin{aligned} A=\left[ \begin{array}{cccc}{\frac{1}{2 \delta t}} &{} {-\frac{1}{2} \Delta } &{} {{\mathbf {0}}} &{} {{\mathbf {0}}} \\ {\frac{1}{2} \Delta } &{} {\frac{1}{2 \delta t}} &{} {{\mathbf {0}}} &{} {{\mathbf {0}}} \\ {{\mathbf {0}}} &{} {{\mathbf {0}}} &{} {\frac{\varepsilon }{2 \delta t}+\frac{\gamma }{2}} &{} {\frac{1}{2}-\frac{1}{2} \Delta } \\ {{\mathbf {0}}} &{} {{\mathbf {0}}} &{} {-\frac{1}{2} I} &{} {\frac{\varepsilon }{2 \delta t}}\end{array}\right] , \end{aligned}$$
(2.22)
$$\begin{aligned} {\mathbf {v}}_{1}^{n+1}=\left[ \begin{array}{l}{q_{1}^{n+1}} \\ {p_{1}^{n+1}} \\ {u_{1}^{n+1}} \\ {\phi _{1}^{n+1}}\end{array}\right] , \quad {\mathbf {v}}_{2}^{n+1}=\left[ \begin{array}{l}{q_{2}^{n+1}} \\ {p_{2}^{n+1}} \\ {u_{2}^{n+1}} \\ {\phi _{2}^{n+1}}\end{array}\right] , \end{aligned}$$
$$\begin{aligned} {\mathbf {g}}_{1}^{n}=\left[ \begin{array}{c}{\frac{1}{2\delta t} q^{n-1}+\frac{1}{2}\Delta p^{n-1}+\frac{R^{n-1}}{2 \sqrt{H_{1}^{n}}}\phi ^n p^n}\\ {\frac{1}{2 \delta t} p^{n-1}-\frac{1}{2} \Delta q^{n-1}-\frac{R^{n-1}}{2 \sqrt{H_{1}^{n}}}\phi ^n q^n}\\ {\left( \frac{\varepsilon }{2 \delta t}-\frac{\gamma }{2}\right) u^{n-1}+\left( \frac{1}{2}\Delta -\frac{1}{2}\right) \phi ^{n-1}+\frac{R^{n-1}}{2 \sqrt{H_{1}^{n}}}((p^n)^2+ (q^n)^2)}\\ {\frac{\varepsilon }{2 \delta t} \phi ^{n-1}+\frac{1}{2} u^{n-1}}\end{array}\right] , \quad {\mathbf {g}}_{2}^{n}=\left[ \begin{array}{c}{\frac{\phi ^{n}p^{n}}{2\sqrt{H_1^n}}} \\ {-\frac{\phi ^{n}q^{n}}{2\sqrt{H_1^n}}} \\ { \frac{\left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}}{2\sqrt{H_1^n}}} \\ {0}\end{array}\right] .\nonumber \\ \end{aligned}$$
(2.23)

After solving \({\mathbf {v}}_{1}^{n+1}\) and \({\mathbf {v}}_{2}^{n+1}\) from (2.20) and (2.21), we plug (2.19) into equation (2.10) to obtain the following linear algebraic equation for \(R^{n+1}\):

$$\begin{aligned}&\left( 1+\frac{1}{2\sqrt{H_1^n}}(2p^n p_2^{n+1}+2q^n q_2^{n+1}, \phi ^n)+((p^n)^2+(q^n)^2, \phi _2^{n+1})\right) R^{n+1}\nonumber \\&\quad =R^{n-1}-\frac{1}{2\sqrt{H_1^n}} \left[ 2(p^n\phi ^n, p_1^{n+1}-p^{n-1})+2(q^n\phi ^{n}, q_1^{n+1}-q^{n-1})+((p^n)^2+(q^n)^2, \phi _1^{n+1}-\phi ^{n-1})\right] ,\nonumber \\ \end{aligned}$$
(2.24)

from which \(R^{n+1}\) can be obtained explicitly.

To summarize, Scheme SAV (2.6)–(2.10) can be implemented as follows:

  1. 1.

    Compute right-hand term \({\mathbf {g}}_1^{n}\) and \({\mathbf {g}}_2^{n}\) by (2.23);

  2. 2.

    Solve for \(q_{i}^{n+1}, p_{i}^{n+1}, u_{i}^{n+1}, \phi _{i}^{n+1}, i=1, 2\) from (2.20)–(2.21);

  3. 3.

    Find \(R^{n+1}\) by solving (2.24);

  4. 4.

    Update \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) by (2.19).

The first step (2.1)–(2.5) can be implemented similarly.

Scheme SAV enjoys the following advantages:

  • It is second-order accurate, conserves the modified Hamiltonian when \(\gamma =0\), and is unconditionally energy stable when \(\gamma >0\);

  • It only requires solving decoupled, linear systems with constant coefficients at each time step.

3 SAV Approach with Lagrange Multipliers

The Scheme SAV conserves/dissipates a modified Hamiltonian, not the original Hamiltonian, and it does not preserve the wave energy. Below, we adopt the Lagrange multiplier approach [9, 10] to construct efficient schemes which can conserve/dissipate the original Hamiltonian as well as conserve the wave energy.

3.1 The First Lagrange Multiplier Approach

We introduce two Lagrange multipliers \(\eta \left( t\right) \), \(\lambda \left( t\right) \) to reformulate the KGS equations (2.1) as

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t} q=\Delta p+\eta \left( t\right) \phi p +\lambda \left( t\right) p, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\partial _{t} p=-\left( \Delta q+\eta \left( t\right) \phi q +\lambda \left( t\right) q \right) , \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon \partial _{t} u=\Delta \phi - \phi +\eta \left( t\right) \left( p^{2}+q^{2}\right) -\gamma u, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&\varepsilon \partial _{t} \phi =u, \quad {\mathbf {x}} \in \Omega , \quad t>0, \\&-\frac{{d}}{{d}t}\left( p^{2}+q^{2}, \phi \right) =- \eta \left( t\right) \left[ \left( 2 pp_{t}+2 qq_{t}, \phi \right) +\left( p^{2}+q^{2}, \phi _{t}\right) \right] \\&-\lambda (t)\left[ \left( 2p, p_{t}\right) +\left( 2q, q_{t}\right) \right] ,\\&\frac{{d}}{{d}t}\left( p^{2}+q^{2}, 1\right) =0, \end{aligned} \right. \end{aligned}$$
(3.1)

with \(\eta (0)=1\) and \(\lambda (0)=0\). Comparing with the original KGS equations (2.1), we find that the exact solutions for \(\eta (t)\) and \(\lambda (t)\) are \(\eta (t)\equiv 1\) and \(\lambda (t)\equiv 0\). In the above \(\lambda (t)\) is introduced to enforce the conservation of the wave energy, while \(\eta (t)\) is introduced to enforce the rate of change of \((\phi , |p|^2+|q)^2)\), which is nonlinear part of the Hamiltonian. Note that we added an extra zero term \(-\lambda \int _{\Omega }2pp_{t}+2qq_{t}\mathrm {d} {\mathbf {x}}\) at the end of the second last equation. This term is essential in the design of unconditionally energy stable schemes below.

Scheme LM1:

Initialization: Given \(q^{0}, p^{0}, u^{0}, \phi ^{0}\), determine \(q^{1}, p^{1}, u^{1}, \phi ^{1}\) by

$$\begin{aligned}&\frac{q^{1}-q^{0}}{2 \delta t}= \frac{\Delta p^{1}+\Delta p^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2} \phi ^{0} p^{0} +\frac{\lambda ^{1}+\lambda ^{0}}{2}p^{0}, \end{aligned}$$
(3.2)
$$\begin{aligned}&\frac{p^{1}-p^{0}}{2 \delta t}= -\left( \frac{\Delta q^{1}+\Delta q^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2} \phi ^{0} q^{0} + \frac{\lambda ^{1}+\lambda ^{0}}{2}q^{0}\right) , \end{aligned}$$
(3.3)
$$\begin{aligned}&\varepsilon \frac{u^{1}-u^{0}}{2 \delta t}=\frac{\Delta \phi ^{1}+\Delta \phi ^{0}}{2}-\frac{\phi ^{1}+\phi ^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2}\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}\right) -\gamma \frac{u^{1}+u^{0}}{2}, \end{aligned}$$
(3.4)
$$\begin{aligned}&\varepsilon \frac{\phi ^{1}-\phi ^{0}}{2 \delta t}=\frac{u^{1}+u^{0}}{2}, \end{aligned}$$
(3.5)
$$\begin{aligned}&-\frac{\left( \left( p^{1}\right) ^{2}+\left( q^{1}\right) ^{2}, \phi ^{1}\right) -\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, \phi ^{0}\right) }{2 \delta t}\nonumber \\&\quad = -\frac{\eta ^{1}+\eta ^{0}}{2}\left[ \left( 2p^{0} \frac{p^{1}-p^{0}}{2 \delta t}+ 2q^{0} \frac{q^{1}-q^{0}}{2 \delta t}, \phi ^{0}\right) +\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, \frac{\phi ^{1}-\phi ^{0}}{2\delta t}\right) \right] \nonumber \\&\qquad -\frac{\lambda ^{1}+\lambda ^{0}}{2} \left[ \left( 2p^{0}, \frac{p^{1}-p^{0}}{2 \delta t}\right) + \left( 2q^{0}, \frac{q^{1}-q^{0}}{2 \delta t} \right) \right] , \end{aligned}$$
(3.6)
$$\begin{aligned}&\left( \left( p^{1}\right) ^{2}+\left( q^{1}\right) ^{2}, 1\right) = \left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, 1\right) , \end{aligned}$$
(3.7)

Then, for \(n=1,2,\ldots \), we solve \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) as follows:

$$\begin{aligned}&\frac{q^{n+1}-q^{n-1}}{2 \delta t}= \frac{\Delta p^{n+1}+\Delta p^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2} \phi ^{n} p^{n} +\frac{\lambda ^{n+1}+\lambda ^{n-1}}{2}p^{n}, \end{aligned}$$
(3.8)
$$\begin{aligned}&\frac{p^{n+1}-p^{n-1}}{2 \delta t}= -\left( \frac{\Delta q^{n+1}+\Delta q^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2} \phi ^{n} q^{n} + \frac{\lambda ^{n+1}+\lambda ^{n-1}}{2}q^{n}\right) , \end{aligned}$$
(3.9)
$$\begin{aligned}&\varepsilon \frac{u^{n+1}-u^{n-1}}{2 \delta t}=\frac{\Delta \phi ^{n+1}+\Delta \phi ^{n-1}}{2}-\frac{\phi ^{n+1}+\phi ^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2}\left( \left( p^{ n}\right) ^{2}+\left( q^{n}\right) ^{2}\right) \nonumber \\&\quad \quad \quad \quad \quad \qquad \quad \quad -\gamma \frac{u^{n+1}+u^{n-1}}{2} , \end{aligned}$$
(3.10)
$$\begin{aligned}&\varepsilon \frac{\phi ^{n+1}-\phi ^{n-1}}{2 \delta t}=\frac{u^{n+1}+u^{n-1}}{2}, \end{aligned}$$
(3.11)
$$\begin{aligned}&-\frac{\left( \left( p^{n+1}\right) ^{2}+\left( q^{n+1}\right) ^{2}, \phi ^{n+1}\right) -\left( \left( p^{n-1}\right) ^{2}+\left( q^{n-1}\right) ^{2}, \phi ^{n-1}\right) }{2 \delta t} = -\frac{\eta ^{n+1}+\eta ^{n-1}}{2}\nonumber \\&\quad \left[ \left( 2p^{n} \frac{p^{n+1}-p^{n-1}}{2 \delta t}+ 2q^{n} \frac{q^{n+1}-q^{n-1}}{2 \delta t}, \phi ^{n}\right) +\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}, \frac{\phi ^{n+1}-\phi ^{n-1}}{2\delta t}\right) \right] \nonumber \\&\quad -\frac{\lambda ^{n+1}+\lambda ^{n-1}}{2} \left[ \left( 2p^{n}, \frac{p^{n+1}-p^{n-1}}{2 \delta t}\right) + \left( 2q^{n}, \frac{q^{n+1}-q^{n-1}}{2 \delta t} \right) \right] , \end{aligned}$$
(3.12)
$$\begin{aligned}&\left( \left( p^{n+1}\right) ^{2}+\left( q^{n+1}\right) ^{2}, 1\right) = \left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, 1\right) , \end{aligned}$$
(3.13)

Theorem 3.1

The scheme (3.8)–(3.13) preserves the wave energy, and conserves/dissipates the original Hamiltonian in the sense that

$$\begin{aligned} H^{1}-H^{0}=-\delta t \frac{\gamma }{ 2\varepsilon }\left\| u^{1}+u^{0}\right\| ^{2}, \end{aligned}$$
(3.14)

and

$$\begin{aligned} H^{n+1}-H^{n-1}=-\delta t \frac{\gamma }{ 2\varepsilon }\left\| u^{n+1}+u^{n}\right\| ^{2},\quad \forall n\ge 1, \end{aligned}$$
(3.15)

where

$$\begin{aligned} \begin{aligned} H^{n+1}&=\frac{1}{2}\left( \left\| \phi ^{n+1}\right\| ^{2} +\left\| u^{n+1}\right\| ^{2}+\left\| \nabla \phi ^{n+1}\right\| ^{2}\right) \\&\quad +\left( \left\| \nabla p^{n+1}\right\| ^{2}+ \left\| \nabla q^{n+1}\right\| ^{2}\right) -\left( \left( p^{n+1}\right) ^{2}+\left( q^{n+1}\right) ^{2}, \phi ^{n+1}\right) ,\quad \forall n\ge 0. \end{aligned} \end{aligned}$$
(3.16)

Proof

Taking the inner products of the equations in (3.2)–(3.5) with \(-2 \frac{p^{1}-p^{0}}{2\delta t}\), \(2 \frac{q^{1}-q^{0}}{2\delta t}\), \(\frac{u^{1}+u^{0}}{2\varepsilon }\) and \(-\left( \frac{\Delta \phi ^{1}+\Delta \phi ^{0}}{2}-\frac{\phi ^{1}+\phi ^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2}\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}\right) \right) / \varepsilon \), respectively, summing up the results, we obtain (3.14).

Taking inner product of (3.8)–(3.11) with \(-2 \frac{p^{n+1}-p^{n-1}}{2\delta t}\), \(2 \frac{q^{n+1}-q^{n-1}}{2\delta t}\), \(\frac{u^{n+1}+u^{n-1}}{2 \varepsilon }\) and

\(-\left( \Delta \frac{\phi ^{n+1}+\phi ^{n-1}}{2}-\frac{\phi ^{n+1}+\phi ^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}\right) \right) /\varepsilon \), respectively, we obtain (3.15). \(\square \)

Scheme LM1 can be efficiently implemented similarly as Scheme SAV. More precisely, setting

$$\begin{aligned} \left\{ \begin{aligned}&p^{n+1}=p_{1}^{n+1}+\eta ^{n+1}p_{2}^{n+1}+\lambda ^{n+1}p_{3}^{n+1}, \\&q^{n+1}=q_{1}^{n+1}+\eta ^{n+1}q_{2}^{n+1}+\lambda ^{n+1}q_{3}^{n+1}, \\&\phi ^{n+1}=\phi _{1}^{n+1}+\eta ^{n+1}\phi _{2}^{n+1}+\lambda ^{n+1}\phi _{3}^{n+1}, \\&u^{n+1}=u_{1}^{n+1}+\eta ^{n+1}u_{2}^{n+1}+\lambda ^{n+1}u_{3}^{n+1}, \end{aligned} \right. \end{aligned}$$
(3.17)

in (3.8)–(3.11), we find that

$$\begin{aligned}&A {\mathbf {v}}_1^{n+1}={\mathbf {g}}_1^{n}, \end{aligned}$$
(3.18)
$$\begin{aligned}&A {\mathbf {v}}_2^{n+1}={\mathbf {g}}_2^{n}, \end{aligned}$$
(3.19)
$$\begin{aligned}&A {\mathbf {v}}_3^{n+1}={\mathbf {g}}_3^{n}, \end{aligned}$$
(3.20)

where A are defined by (2.22) and

$$\begin{aligned} {\mathbf {v}}_1^{n+1}=\left[ \begin{array}{l}{q_{1}^{n+1}} \\ {p_{1}^{n+1}} \\ {u_{1}^{n+1}} \\ {\phi _{1}^{n+1}}\end{array}\right] , \quad {\mathbf {v}}_2^{n+1}=\left[ \begin{array}{l}{q_{2}^{n+1}} \\ {p_{2}^{n+1}} \\ {u_{2}^{n+1}} \\ {\phi _{2}^{n+1}}\end{array}\right] , \quad {\mathbf {v}}_3^{n+1}=\left[ \begin{array}{l}{q_{3}^{n+1}} \\ {p_{3}^{n+1}} \\ {u_{3}^{n+1}} \\ {\phi _{3}^{n+1}}\end{array}\right] , \end{aligned}$$
(3.21)

and

$$\begin{aligned} \begin{aligned}&{\mathbf {g}}_1^{n}=\left[ \begin{array}{c}{\frac{1}{2 \delta t} q^{n-1}+\frac{1}{2}\Delta p^{n-1}+\frac{\eta ^{n-1}}{2}\phi ^{n}p^{n}+\frac{\lambda ^{n-1}}{2}p^n}\\ { \frac{1}{2 \delta t}p^{n-1}-\frac{1}{2} \Delta q^{n-1}-\frac{\eta ^{n-1}}{2}\phi ^{n}q^{n}-\frac{\lambda ^{n-1}}{2}q^n}\\ {\left( \frac{\varepsilon }{2 \delta t}-\frac{\gamma }{2}\right) u^{n-1}+\left( \frac{1}{2}\Delta -\frac{1}{2}\right) \phi ^{n-1}+\frac{\eta ^{n-1}}{2}((p^{n})^2+(q^{n})^2)}\\ {\frac{\varepsilon }{2 \delta t} \phi ^{n-1}+\frac{1}{2} u^{n-1}}\end{array}\right] , \\&{\mathbf {g}}_2^{n}=\left[ \begin{array}{c}{\frac{\phi ^{n}p^{n}}{2}} \\ {-\frac{\phi ^{n}q^{n}}{2}} \\ {\frac{ \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}}{2}} \\ {0}\end{array}\right] , \quad {\mathbf {g}}_3^{n}=\left[ \begin{array}{c}{\frac{p^{n}}{2}} \\ {-\frac{q^{n}}{2}} \\ {0} \\ {0}\end{array}\right] . \end{aligned} \end{aligned}$$
(3.22)

After finding \({\mathbf {v}}_1^{n+1}\), \({\mathbf {v}}_2^{n+1}\) and \({\mathbf {v}}_3^{n+1}\) from (3.18)–(3.20), we plug (3.17) into (3.12) and (3.13) to obtain a system of two nonlinear algebraic equations for \((\eta ^{n+1}, \lambda ^{n+1})\),

$$\begin{aligned} \left\{ \begin{aligned}&F_1(\eta ^{n+1}, \lambda ^{n+1})=0, \\&F_2(\eta ^{n+1}, \lambda ^{n+1})=0. \end{aligned} \right. \end{aligned}$$
(3.23)

For the readers’ convenience, the exact form of \(F_1,\; F_2\) is provided in the Appendix. We can then find \(\eta ^{n+1}\) and \(\lambda ^{n+1}\) by solving this nonlinear system with a iterative method. Finally, we can obtain \(q^{n+1}, p^{n+1}\), \(u^{n+1}, \phi ^{n+1}\) by (3.17).

To summarize, Scheme LM1 can be implemented as follows:

  1. 1.

    Compute right-hand term \({\mathbf {g}}_1^{n}\), \({\mathbf {g}}_2^{n}\) and \({\mathbf {g}}_3^{n}\) by (3.22);

  2. 2.

    Find \(q_{i}^{n+1}, p_{i}^{n+1}, u_{i}^{n+1}, \phi _{i}^{n+1}, i=1, 2,3\) by solving (3.18)–(3.20);

  3. 3.

    Determine \(\eta ^{n+1}\) and \(\lambda ^{n+1}\) by solving (3.23) using an iterative method, such as the Newton iteration method or the steepest descent method;

  4. 4.

    Update \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) by (3.17).

The first step (3.2)–(3.7) can be implemented similarly.

Scheme LM1 enjoys the following advantages:

  • It is second-order accurate, conserves the wave energy when \(\nu =0\), and conserves (resp. dissipates) the original Hamiltonian when \(\gamma =0\) (resp. \(\gamma >0\) and \(\nu =0\));

  • It only requires solving decoupled, linear systems with constant coefficients at each time step plus a nonlinear algebraic system.

3.2 An Alternative Lagrange Multiplier Scheme

In practice, when the time step is not sufficiently small, the nonlinear algebraic system (3.23) may not have real solutions or the iteration may not converge. Hence, we present an alternative scheme which possesses essentially the same properties of Scheme LM1, but only require solving two decoupled nonlinear quadratic algebraic equations for \(\eta ^{n+1}\) and \(\lambda ^{n+1}\), respectively.

Scheme LM2:

Initialization: Given \(q^{0}, p^{0}, u^{0}, \phi ^{0}\), determine \(q^{1}, p^{1}, u^{1}, \phi ^{1}\) by

$$\begin{aligned}&\frac{q^{1}-q^{0}}{2\delta t}= \frac{\Delta p^{1}+\Delta p^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2} \phi ^{0} p^{0}+\frac{\lambda ^{1}+\lambda ^{0}}{2}p^{0}, \end{aligned}$$
(3.24)
$$\begin{aligned}&\frac{p^{1}-p^{0}}{2\delta t}=-\left( \frac{\Delta q^{1}+\Delta q^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2}\phi ^{0} q^{0}+ \frac{\lambda ^{1}+\lambda ^{0}}{2}q^{0}\right) , \end{aligned}$$
(3.25)
$$\begin{aligned}&\varepsilon \frac{u^{1}-u^{0}}{2\delta t}= \frac{\Delta \phi ^{1}+\Delta \phi ^{0}}{2}-\frac{\phi ^{1}+\phi ^{0}}{2}+\frac{\eta ^{1}+\eta ^{0}}{2}\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}\right) -\gamma \frac{u^{1}+u^{0}}{2}, \end{aligned}$$
(3.26)
$$\begin{aligned}&\varepsilon \frac{\phi ^{1}-\phi ^{0}}{2\delta t}=\frac{u^{1}+u^{0}}{2}, \end{aligned}$$
(3.27)
$$\begin{aligned}&-\frac{\left( \left( {\bar{p}}^{1}\right) ^{2}+\left( {\bar{q}}^{1}\right) ^{2}, \bar{\phi }^{1}\right) -\left( \left( {\bar{p}}^{0}\right) ^{2}+\left( {\bar{q}}^{0}\right) ^{2}, \bar{\phi }^{0}\right) }{2 \delta t} = -\frac{\eta ^{1}+\eta ^{0}}{2}\nonumber \\&\quad \left[ \left( 2p^{0} \frac{p^{1}-p^{0}}{2 \delta t}+ 2q^{0} \frac{q^{1}-q^{0}}{2 \delta t}, \phi ^{0}\right) +\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, \frac{\phi ^{1}-\phi ^{0}}{2 \delta t}\right) \right] , \nonumber \\&\quad -\frac{\lambda ^{1}+\lambda ^{0}}{2} \left[ \left( 2p^{0}, \frac{p^{1}-p^{0}}{2 \delta t}\right) + \left( 2q^{0}, \frac{q^{1}-q^{0}}{2 \delta t} \right) \right] , \end{aligned}$$
(3.28)
$$\begin{aligned}&\left( \left( {\bar{p}}^{1}\right) ^{2}+\left( {\bar{q}}^{1}\right) ^{2}, 1\right) = \left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, 1\right) \end{aligned}$$
(3.29)

Then, for \(n=1,2,\ldots \), we solve \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) as follows: \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) as follows:

$$\begin{aligned}&\frac{q^{n+1}-q^{n-1}}{2\delta t}= \frac{\Delta p^{n+1}+\Delta p^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2} \phi ^{n} p^{n}+\frac{\lambda ^{n+1}+\lambda ^{n-1}}{2}p^{n}, \end{aligned}$$
(3.30)
$$\begin{aligned}&\frac{p^{n+1}-p^{n-1}}{2\delta t}=-\left( \frac{\Delta q^{n+1}+\Delta q^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2}\phi ^{n} q^{n}+ \frac{\lambda ^{n+1}+\lambda ^{n-1}}{2}q^{n}\right) , \end{aligned}$$
(3.31)
$$\begin{aligned}&\varepsilon \frac{u^{n+1}-u^{n-1}}{2\delta t}= \frac{\Delta \phi ^{n+1}+\Delta \phi ^{n-1}}{2}-\frac{\phi ^{n+1}+\phi ^{n-1}}{2}+\frac{\eta ^{n+1}+\eta ^{n-1}}{2}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad -\gamma \frac{u^{n+1}+u^{n-1}}{2}, \end{aligned}$$
(3.32)
$$\begin{aligned}&\varepsilon \frac{\phi ^{n+1}-\phi ^{n-1}}{2\delta t}=\frac{u^{n+1}+u^{n-1}}{2}, \end{aligned}$$
(3.33)
$$\begin{aligned}&-\frac{\left( \left( {\bar{p}}^{n+1}\right) ^{2}+\left( {\bar{q}}^{n+1}\right) ^{2}, \bar{\phi }^{n+1}\right) -\left( \left( {\bar{p}}^{n-1}\right) ^{2}+\left( {\bar{q}}^{n-1}\right) ^{2}, \bar{\phi }^{n-1}\right) }{2 \delta t} = -\frac{\eta ^{n+1}+\eta ^{n-1}}{2}\nonumber \\&\quad \left[ \left( 2p^{n} \frac{p^{n+1}-p^{n-1}}{2 \delta t}+ 2q^{n} \frac{q^{n+1}-q^{n-1}}{2 \delta t}, \phi ^{n}\right) +\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}, \frac{\phi ^{n+1}-\phi ^{n-1}}{2 \delta t}\right) \right] , \nonumber \\&\quad -\frac{\lambda ^{n+1}+\lambda ^{n-1}}{2} \left[ \left( 2p^{n}, \frac{p^{n+1}-p^{n-1}}{2 \delta t}\right) + \left( 2q^{n}, \frac{q^{n+1}-q^{n-1}}{2 \delta t} \right) \right] , \end{aligned}$$
(3.34)
$$\begin{aligned}&\left( \left( {\bar{p}}^{n+1}\right) ^{2}+\left( {\bar{q}}^{n+1}\right) ^{2}, 1\right) = \left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, 1\right) \end{aligned}$$
(3.35)

where \({\bar{p}}^{n+1}=p_{1}^{n+1}+p_{2}^{n+1}+\lambda ^{n+1} p_3^{n+1}\) and \({\bar{q}}^{n+1}=q_{1}^{n+1}+q_{2}^{n+1}+\lambda ^{n+1} q_3^{n+1}\).

By following the same procedure as in the proof of Theorem 3.1, we can prove the following result:

Theorem 3.2

Scheme (3.30)–(3.35) preserves the wave energy

$$\begin{aligned} D_{LM2}^{n}:=\left( \left( {\bar{p}}^{n}\right) ^{2}+\left( {\bar{q}}^{n}\right) ^{2}, 1\right) =\left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, 1\right) , \end{aligned}$$
(3.36)

and satisfies discrete energy law:

$$\begin{aligned} H_{LM2}^{1}- H_{LM2}^{0}=-\delta t \frac{\gamma }{ 2\varepsilon }\left\| u^{1}+u^{0}\right\| , \end{aligned}$$
(3.37)

and

$$\begin{aligned} H_{LM2}^{n+1}- H_{LM2}^{n-1}=-\delta t \frac{\gamma }{ 2\varepsilon }\left\| u^{n+1}+u^{n-1}\right\| ,\quad \forall n\ge 1, \end{aligned}$$
(3.38)

where

$$\begin{aligned} \begin{aligned} H_{LM2}^{n+1}&=\frac{1}{2}\left( \left\| \phi ^{n+1}\right\| ^{2} +\left\| u^{n+1}\right\| ^{2}+\left\| \nabla \phi ^{n+1}\right\| ^{2}\right) \\&\quad +\left( \left\| \nabla p^{n+1}\right\| ^{2}+\left\| \nabla q^{n+1}\right\| ^{2}\right) -\left( \left( {\bar{p}}^{n+1}\right) ^{2}+\left( {\bar{q}}^{n+1}\right) ^{2}, \bar{\phi }^{n+1}\right) ,\quad \forall n\ge 0. \end{aligned} \end{aligned}$$
(3.39)

Scheme LM2 can be efficiently implemented as follows:

Set

$$\begin{aligned} \left\{ \begin{aligned}&p^{n+1}=p_{1}^{n+1}+\eta ^{n+1}p_{2}^{n+1}+\lambda ^{n+1}p_{3}^{n+1}, \\&q^{n+1}=q_{1}^{n+1}+\eta ^{n+1}q_{2}^{n+1}+\lambda ^{n+1}q_{3}^{n+1}, \\&\phi ^{n+1}=\phi _{1}^{n+1}+\eta ^{n+1}\phi _{2}^{n+1}+\lambda ^{n+1}\phi _{3}^{n+1}, \\&u^{n+1}=u_{1}^{n+1}+\eta ^{n+1}u_{2}^{n+1}+\lambda ^{n+1}u_{3}^{n+1}, \end{aligned} \right. \end{aligned}$$
(3.40)

in (3.30)–(3.33), which is similar to the Scheme LM1. After finding \({\mathbf {v}}_1^{n+1}\), \({\mathbf {v}}_2^{n+1}\) and \({\mathbf {v}}_3^{n+1}\) defined in (3.21), we plug

$$\begin{aligned} \left\{ \begin{aligned}&{\bar{p}}^{n+1}=p_{1}^{n+1}+p_{2}^{n+1}+\lambda ^{n+1}p_{3}^{n+1} \\&{\bar{q}}^{n+1}=q_{1}^{n+1}+q_{2}^{n+1}+\lambda ^{n+1}q_{3}^{n+1} \end{aligned} \right. \end{aligned}$$
(3.41)

into (3.35) to find \(\lambda ^{n+1}\) by solving the quadratic equation

$$\begin{aligned} F_1(\lambda ^{n+1}) = 0 \end{aligned}$$
(3.42)

with

$$\begin{aligned} \begin{aligned} F_{1}\left( \lambda ^{n+1}\right)&= \left( \lambda ^{n+1}\right) ^{2}\left( \left( p_{3}^{n+1}\right) ^{2}+\left( q_{3}^{n+1}\right) ^{2}, 1\right) \\&\quad + 2\lambda ^{n+1}\left[ \left( p_{3}^{n+1}, p_{1}^{n+1}+p_{2}^{n+1}\right) +\left( q_{3}^{n+1}, q_{1}^{n+1}+q_{2}^{n+1}\right) \right] \\&\quad + \left( \left( p_{1}^{n+1}\right) ^{2}+\left( p_{2}^{n+1}\right) ^{2}, 1\right) + \left( \left( q_{1}^{n+1}\right) ^{2}+\left( q_{2}^{n+1}, 1\right) ^{2}\right) - \left( \left( p^{0}\right) ^{2}+\left( q^{0}\right) ^{2}, 1\right) . \end{aligned} \end{aligned}$$

Once we obtain \(\lambda ^{n+1}\), we plug (3.40) into (3.34) to find \(\eta ^{n+1}\) by soling another quadratic equation

$$\begin{aligned} F_2(\eta ^{n+1}) = 0 \end{aligned}$$
(3.43)

with

$$\begin{aligned} \begin{aligned} F_{2}\left( \eta ^{n+1}\right)&= \left( \eta ^{n+1}\right) ^{2}\left\{ \left( p^{n}p_{2}^{n+1}+q^{n}q_{2}^{n+1}, \phi ^{n}\right) + \frac{1}{2}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}, \phi _{2}^{n+1}\right) \right\} \\&\quad + \eta ^{n+1}\left\{ \left( p^{n}\phi ^{n}, p_{1}^{n+1}+\lambda ^{n+1}p_{3}^{n+1}-p^{n-1}\right) \right. \\&\quad +\left. \left( q^{n}\phi ^{n}, q_{1}^{n+1}+\lambda ^{n+1}q_{3}^{n+1}-q^{n-1}\right) \right. \\&\quad \left. + \frac{1}{2}\left( \left( p^{n}\right) ^{2} + \left( q^{n}\right) ^{2}, \phi _{1}^{n+1}+\lambda ^{n+1}\phi _{3}^{n+1}-\phi ^{n-1}\right) \right. \\&\quad \left. + \left( \lambda ^{n+1}+\lambda ^{n-1}\right) \left[ \left( p^{n}, p_{2}^{n+1}\right) + \left( q^{n}, q_{2}^{n+1}\right) \right] \right. \\&\quad \left. + \eta ^{n-1}\left( p^{n}p_{2}^{n+1}+q^{n}q_{2}^{n+1}, \phi ^{n}\right) + \frac{1}{2}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}, \phi _{2}^{n+1}\right) \right\} \\&\quad \!+\! \eta ^{n-1} \left( p^{n}\phi ^{n}, p_{1}^{n+1}\!+\!\lambda ^{n+1}p_{3}^{n+1}\!-\!p^{n-1}\right) \!+\! \left( q^{n}\phi ^{n}, q_{1}^{n+1}\!+\!\lambda ^{n+1}q_{3}^{n+1}\!-\!q^{n-1}\right) \\&\quad + \frac{1}{2}\left( \left( p^{n}\right) ^{2}+\left( q^{n}\right) ^{2}, \phi _{1}^{n+1}+\lambda ^{n+1}\phi _{3}^{n+1}-\phi ^{n-1}\right) \\&\quad + \left( \lambda ^{n+1}+\lambda ^{n-1}\right) \left[ \left( p^{n}, p_{1}^{n+1}+\lambda ^{n+1}p_{3}^{n+1}-p^{n-1}\right) \right. \\&\quad \left. + \left( q^{n}, q_{1}^{n+1}+\lambda ^{n+1}q_{3}^{n+1}-q^{n-1}\right) \right] -\left( \left( {\bar{p}}^{n+1}\right) ^{2}+\left( {\bar{q}}^{n+1}\right) ^{2}, \bar{\phi }^{n+1}\right) \\&\quad + \left( \left( {\bar{p}}^{n-1}\right) ^{2}+\left( {\bar{q}}^{n-1}\right) ^{2}, \bar{\phi }^{n-1}\right) . \end{aligned} \end{aligned}$$

Unlike Scheme LM1, here we can find \(\eta ^{n+1}\) and \(\lambda ^{n+1}\) by standard quadratic-root formula instead of iterative method. Finally, we can obtain \(q^{n+1}, p^{n+1}\), \(u^{n+1}, \phi ^{n+1}\) by (3.40).

To summarize, Scheme LM2 can be implemented as follows:

  1. 1.

    Compute right-hand term \({\mathbf {g}}_1^{n}\), \({\mathbf {g}}_2^{n}\) and \({\mathbf {g}}_3^{n}\) by (3.22);

  2. 2.

    Find \(q_{i}^{n+1}, p_{i}^{n+1}, u_{i}^{n+1}, \phi _{i}^{n+1}, i=1, 2,3\) by solving (3.18)–(3.20);

  3. 3.

    Solve (3.42) by quadratic-root formula to determine \(\lambda ^{n+1}\);

  4. 4.

    Solve (3.43) by quadratic-root formula to determine \(\eta ^{n+1}\);

  5. 5.

    Update \(q^{n+1}, p^{n+1}, u^{n+1}, \phi ^{n+1}\) by (3.40).

The first step (3.24)–(3.29) can be implemented similarly.

Scheme LM2 enjoys the following advantages:

  • It is second-order accurate, conserves the wave energy when \(\nu =0\) in the sense of (3.36), and conserves (resp. dissipates) the Hamiltonian when \(\gamma =0\) (resp. \(\gamma >0\) and \(\nu =0\)) in the sense of (3.38);

  • It only requires solving decoupled, linear systems with constant coefficients at each time step and solving two nonlinear quadratic algebraic equations for \(\lambda ^{n+1}\) and \(\eta ^{n+1}\), respectively.

4 Numerical Results

We now present various numerical simulations to demonstrate the efficiency, energy stability and accuracy of the proposed numerical schemes. In all computations, we use the Fourier-spectral method for spatial discretization so that all the linear systems in our time discretization schemes can be solved very efficiently by using the fast Fourier transform. All numerical tests are performed using Matlab on a MacBook Pro with 2.4 GHz Intel Core i5.

Scheme LM1 requires solving a nonlinear algebraic system, which can be solved by, for examples, the Newton iteration method or the steepest descent method. The Newton iteration method has a faster convergence rate, but requires a “good” initial value. The steepest descent method is only linearly convergent, but it can converge with any initial value. For the sake of robustness, we use the steepest descent method.

We define the following numerical errors on the solution, Hamiltonian and wave energy

$$\begin{aligned} \begin{array}{l} e_{q}\left( t_{n}\right) =\left\| \varvec{q}\left( \cdot , t_{n}\right) -\varvec{q}^{n}\right\| _{\ell ^{2}}, \quad e_{p}\left( t_{n}\right) =\left\| \varvec{p}\left( \cdot , t_{n}\right) -\varvec{p}^{n}\right\| _{\ell ^{2}}, \quad e_{\phi }\left( t_{n}\right) =\left\| \varvec{\phi }^{n}-\varvec{\phi }^{0}\right\| _{\ell ^{2}}, \\ e_{H}\left( t_{n}\right) =\left| H(\varvec{q^n, p^n, \phi }^{n})-H(\varvec{q^0, p^0, \phi }^{0})\right| , \quad e_{D}\left( t_{n}\right) =\left| D(\varvec{q^n, p^n})-D(\varvec{q^0, p^0})\right| . \end{array} \end{aligned}$$

4.1 Accuracy Test in 1D

We first examine the temporal convergence rates with an exact solution of KGS equations.

Solitary-wave solution. When \(d=1, \gamma =0\) and \(\nu =0\) in (1.1), the KGS equations admit the solitary-wave solution

$$\begin{aligned}&\psi _{\pm }(x, t)=3 B {\text {sech}}^{2}\left( B x+c_{\pm } t\right) \exp \left[ \mathrm {i}\left( d_{\pm } x+\left( 4 B^{2}-d_{\pm }^{2}\right) t\right) \right] , \end{aligned}$$
(4.1)
$$\begin{aligned}&\phi _{\pm }(x, t)=6 B^{2} {\text {sech}}^{2}\left( B x+c_{\pm } t\right) , \quad x \in {\mathbb {R}} , \quad t \ge 0, \end{aligned}$$
(4.2)

where \(B \ge 0\) and

$$\begin{aligned} c_{\pm }=\pm \frac{\sqrt{4 B^{2}-1}}{2 \varepsilon }=\mathrm {O}\left( \frac{1}{\varepsilon }\right) , \quad d_{\pm }=\mp \frac{\sqrt{4 B^{2}-1}}{4 B \varepsilon }=-\frac{c_{\pm }}{2 B}=\mathrm {O}\left( \frac{1}{\varepsilon }\right) . \end{aligned}$$

The initial data is chosen as

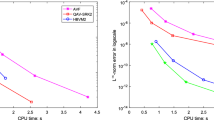
$$\begin{aligned} \psi ^{(0)}(x)=\psi _{+}(x, 0),\quad \phi ^{(0)}(x)=\phi _{+}(x, 0), \quad \phi ^{(1)}(x)=\partial _{t} \phi _{+}(x, 0). \end{aligned}$$
(4.3)

In our computation, we take \(B = 1, \varepsilon =10\) and solve the problem on the interval \([-32, 32]\). We choose 1024 Fourier modes (i.e. spatial step \(h=1/16\)) so that the spatial error is negligible compared with time discretization error. The errors based on discrete \(L^2\)-norm of Scheme SAV, Scheme LM1 and Scheme LM2 are shown in Fig. 1, which indicate that all three schemes are indeed second-order in time.

Fig. 1
figure 1

Errors of Scheme SAV (first), Scheme LM1 (second) and Scheme LM2 (third) at \(T=0.1\) with initial condition (4.3)

Full size image

4.2 Comparison of the Three Schemes

In this subsection, we make a detailed comparison for the three proposed schemes. In Table 1, we list the errors of \(q, p, \phi \), Hamiltonian and wave energy as well as CPU time at different time with initial condition (4.3) and \(\delta t=1e-4, h=1/16\), where \({\tilde{H}}\) represents the modified Hamiltonian \(H_{SAV}\) for Scheme SAV and the modified Hamiltonian \(H_{LM2}\) for Scheme LM2; \({\tilde{D}}\) represents the modified wave energy \(D_{LM2}\) for Scheme LM2. We also plot in Fig. 2 the time evolution of Lagrange multipliers \((\eta , \lambda )\).

We observe from Table 1 that the errors of the three schemes are close for \(T \le 1\); and the errors of Scheme SAV is smaller than that of Scheme LM1 as later times \(T=10, 50\). Scheme LM2 failed to produce correct answer for \(T\ge 10\) due to the appearance of complex roots for the nonlinear algebraic system.

Therefore, Scheme SAV is the most robust while Scheme LM2 is the least robust, but Scheme SAV can only conserve a modified wave energy, while Scheme LM1 preserves the original Hamiltonian and wave energy exactly. On the other hand, we observe that the CPU time for Scheme SAV and Scheme LM2 are essentially the same while Scheme LM1 consumes is a little more expense as an iterative process is needed to solve the nonlinear algebraic system, cf. Fig. 3 for the number of iterations needed by Scheme LM1.

Since Scheme SAV and Scheme LM2 do not conserve the Hamiltonian and wave energy exactly, we plot the errors of the original Hamiltonian H and original wave energy D by Scheme SAV and Scheme LM2 in Fig. 4. We observe that they converge with a third-order rate in time.

We plot in Fig. 2 evolutions of \(|\frac{R^{n+1}+R^{n-1}}{2\sqrt{H_1^n}}-1|\) for Scheme SAV, \(|\eta -1|\) and \(|\lambda |\) for Scheme LM1 and Scheme LM2, and observe that they are all very small as expected.

Table 1 Comparison of three scheme with initial condition (4.3)
Full size table
Fig. 2
figure 2

Comparison of three scheme with initial condition (4.3): evolutions of \(|\frac{R^{n+1}+R^{n-1}}{2\sqrt{H_1^n}}-1|\) for Scheme SAV, \(|\eta ^n-1|, |\lambda ^n|\) for Scheme LM1 and Scheme LM2, respectively

Full size image
Fig. 3
figure 3

Number of iterations needed for Scheme LM1 with initial condition (4.3)

Full size image
Fig. 4
figure 4

Errors of the original Hamiltonian H and original wave energy D of Scheme SAV and Scheme LM2 at \(T=0.1\) with initial condition (4.3)

Full size image

4.3 “Nonrelativistic” Limit (\(0<\varepsilon<< 1\))

We use again the initial condition (4.3) and choose \(h=1/16, \delta t=1e-4\). We show the errors with different \(\varepsilon \) at time \(T=1\) based on Scheme SAV and Scheme LM1 in table 2. We observe that the errors are lager when \(\varepsilon \) is smaller, and that the errors of Scheme SAV and Scheme LM1 are almost the same.

Table 2 Error of different \(\varepsilon \) with \(\delta t=1e-4\) and \(h=1/16\) at time \(T = 1\)
Full size table

Figure 5 shows the orbit of \(\left( Re\left( \psi \right) , Im\left( \psi \right) \right) \) with different \(\varepsilon \). As we can see, there are more knots with smaller \(\varepsilon \).

Fig. 5
figure 5

The orbit of \((Re(\psi ), Im(\psi ))\) with different \(\varepsilon \)

Full size image

4.4 Head-on Collisions of Solitary-Wave Solutions in 1D

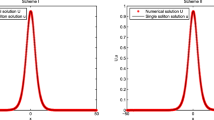
In this and the following subsections, we simulate the interaction between solitary-wave in 1D and dynamic process in 2D [3], which are also the focus of research and have great significance for KGS equations. We first simulate the interaction of solitary-wave solutions in 1D using the standard KGS with \(\varepsilon =1\), \(\nu =0\) and \(\gamma =0\) in (1.1). The initial condition is chosen as

$$\begin{aligned}&\psi (x,0)=\psi _{+}(B,x-p,0)+\psi _{-}(B,x+p,0), \end{aligned}$$
(4.4)
$$\begin{aligned}&\phi (x,0)=\phi _{+}(B,x-p,0)+\phi _{-}(B,x+p,0), \end{aligned}$$
(4.5)
$$\begin{aligned}&\partial _{t}\phi (x,0)=\partial _{t}\phi _{+}(B,x-p,0)+\partial _{t}\phi _{-}(B,x+p,0), \end{aligned}$$
(4.6)

where \(\psi _{\pm }\) and \(\phi _{\pm }\) are defined as in (4.1)–(4.2), and \(x=\pm p\) are initial locations of the two solitons. We set \(p=8\), \(B=1\), and solve the problem in the interval \([-40,40]\) with mesh size \(h=5/128\), time step \(\delta t=1e-3\).

We plot in Fig. 6 evolution of \(|\psi (x,t)|\) at different times using Scheme SAV. We observe that the two solitons are in the same position at time \(t=9.2\), then separate, and waves are emitted during the collision.

Fig. 6
figure 6

Head-on collisions of two symmetric solitary waves without damping: Nucleon density \(\left| \psi (x,t)\right| \)

Full size image

Next, we simulate soliton-soliton collision using KGS with a damping term. We plot in Fig. 7 the time evolution of \(|\psi (x,t)|\) for different values of \(\gamma \), and plot in Fig. 8 the time evolution of the Hamiltonian H(t) and wave energy D(t) for different values of \(\gamma \). We observe that, with \(\gamma =0\), the collision between the two solitons appears to be elastic, although some waves are emitted (cf. Fig. 7, first). With \(\gamma >0\) but very small, the damping effect can be observed in the collision, and the emission of waves is not obvious (Fig. 7, second). When \(\gamma >0\) but not too large, the two solitons no longer separate, and emit some waves after the collision (Fig. 7, third). With \(\gamma >0\) relatively large, the amplitude of the wave is significantly reduced before the collision. In addition, two solitons no longer separates and no wave is emitted after the collision (Fig. 7).

Fig. 7
figure 7

Head-on collisions of two symmetric solitary waves with damping: Nucleon density \(\left| \psi (x,t)\right| \)

Full size image
Fig. 8
figure 8

The temporal evolution of Hamiltonian H with parameter value \(\nu =0, \gamma =0, 0.8, 1, 4\) (left); and wave energy D in semi-logarithmic with parameter values \(\gamma =0, \nu =0, 0.1, 0.5, 1\) (right), the green dotted line is \(e^{-2 \nu t}D(0)\) (Color figure online)

Full size image
Fig. 9
figure 9

Surface plots of nucleon density \(|\psi |^{2}\) (left column) and the meson field \(\phi \left( x, y, t\right) \) (right column) with \(\nu =0, \gamma =0\) at different times

Full size image

We plot in Fig. 8 evolution of the Hamiltonian and wave energy with different parameters \(\nu , \gamma \). We observe that the KGS equations preserve the energy conservation law when \(\nu =0, \gamma =0\) and dissipate the energy when \(\nu =0, \gamma >0\) (cf. Fig. 8, left). We also observe that, when \(\gamma =0\), the wave energy decays to 0 exponentially (cf. Fig. 8, right) which is consistent with (2.9).

4.5 Dynamics of KGS in 2D

As a final example, we simulate a dynamic process of KGS in 2D with \(\nu =0, \gamma =0\) and \(\varepsilon =1\). The initial condition is taken as

$$\begin{aligned}&\psi (x, y, 0) =\frac{2}{e^{x^{2}+2 y^{2}}+e^{-\left( x^{2}+2 y^{2}\right) }} e^{i 5 / \cosh (\sqrt{4 x^{2}+y^{2}})} , \end{aligned}$$
(4.7)
$$\begin{aligned}&\phi (x, y, 0) =e^{-\left( x^{2}+y^{2}\right) }, \quad \phi _{t}(x, y, 0)=\frac{e^{-\left( x^{2}+y^{2}\right) }}{2}. \end{aligned}$$
(4.8)

We solve this problem on the rectangle domain \(\left[ -64, 64\right] ^{2}\) with mesh size \(h=\frac{1}{8}\) and time step \(\delta t=5e-4\) by Scheme SAV. Figure 9 shows the surface plots of \(|\psi |^{2}\) and \(\phi \) at different times. We observe that the nucleon density \(|\psi |^{2}\) gradually split into two waves from one wave in two directions along the x-axis (cf. Fig. 9, left); the meson field \(\phi \) becomes squat, and the wave crest is concave downward (cf. Fig. 9, right).

5 Conclusion

We developed in this paper three efficient and accurate schemes for the KGS equations with/without damping terms based on the SAV approach and the Lagrange multiplier approach. All three schemes are second-order accurate in time and can be combined with any consistent Galerkin type spatial discretization. Scheme SAV is the most efficient as it only requires solving two sets of linear systems with constant coefficients, but it only preserves a modified Hamiltonian and approximates the original Hamiltonian and wave energy to third order. On the other hand, both Scheme LM1 and Scheme LM2 require solving three sets of linear systems with constant coefficients plus a nonlinear algebraic system. Scheme LM1 is theoretically most attractive as it preserves the original Hamiltonian and wave energy exactly, but it requires solving a nonlinear algebraic system for the Lagrange multipliers which may require smaller time steps to have a sensible solution. Scheme LM2 is an alternative as the nonlinear algebraic system is quadratic so it can be solved explicitly for any time step while still preserves the Hamiltonian and wave energy, but it may lead to nonphysical solutions when complex roots appear for the quadratic equation if the time step is not sufficiently small. We presented ample numerical tests using a Fourier-spectral method in space to validate and compare the three schemes.