Abstract
The Klein–Gordon–Schrödinger (KGS) equations are classical models to describe the interaction between conservative scalar nucleons and neutral scalar mesons through Yukawa coupling. In this paper, we propose local discontinuous Galerkin (LDG) methods to solve the KGS equations. The methods involve a Crank–Nicholson time discretization for the Schrödinger equation part, a Crank–Nicholson leap frog method in time for the Klein–Gordon equation part, and local discontinuous Galerkin methods in space. Our designed numerical methods have high-order convergence rate, and energy- and Hamiltonian-preserving properties. We present the proofs of such conservation properties for both semi-discrete and fully-discrete schemes. We also establish optimal error estimates of the semi-discrete methods for the linearized KGS equations and the fully discrete methods for the KGS equations. The analysis can be extended to LDG methods for the nonlinear Klein–Gordon or Schrödinger equation, and the KGS equations in higher spatial dimensions. Several numerical tests are presented to verify some of our theoretical findings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the Klein–Gordon–Schrödinger (KGS) equations given by
with initial conditions \(\psi (x,0) = \psi ^{(0)}(x)\), \(\phi (x,0) = \phi ^{(0)}(x)\) and \(\phi _t(x,0) = \phi ^{(1)}(x)\), and periodic boundary conditions. Here \(\psi (x,t)\) and \(\phi (x,t)\) represent nucleon and meson field, respectively. The KGS equations describe the interaction between conservative scalar nucleons and neutral scalar mesons through Yukawa coupling.
By letting \(\psi (x,t) = p(x,t) + i q(x,t)\), we can rewrite the KGS equations as
where p(x, t) and q(x, t) are the real part and imaginary part of the complex scalar function \(\psi (x,t)\). The KGS Eq. (1.2) have two important invariants: the wave energy
and the Hamiltonian
In this paper, we propose local discontinuous Galerkin methods which not only preserve the energy (1.3) and the Hamiltonian (1.4), but also lead to numerical solutions with high-order accuracy.
There have been a lot of studies about numerical methods for the KGS equations, including finite difference methods [1, 5, 14, 20], spectral methods [2, 3, 9, 13, 15, 16, 18], Sinc collocation methods [28], spline collocation methods [19], generalized moving least squares methods [8] and multi-symplectic schemes [12]. In particular, the authors in [5] proposed second order finite difference methods to preserve the local momentum and Hamiltonian in the fully discrete sense. In [14], a family of high order compact methods with Euler midpoint scheme in time was proposed for the KGS equations, and the fully discrete form of energy and Hamiltonian can be preserved. Similarly, the finite difference methods in [20] also have provable conservation of energy and Hamiltonian in the discrete level. In [2], Fourier pseudospectral methods were proposed for the KGS equations. The conservation of wave energy was proved in the discrete \(l^2\) norm. Also, the discrete form of the conserved quantities were computed numerically. It was shown that the Hamiltonian was preserved up to \(10^{-7}\) during the time interval \(t \in [1, 2]\), with the spatial domain \([-32, 32]\), spatial mesh size 1 / 8 and time step \(10^{-4}\). In [13, 15, 16, 18], various spectral methods were proposed and the conservation of discrete invariant quantities were proved.
In this work, we focus on high-order numerical methods with exactly energy- and Hamiltonian-preserving properties based on the local discontinuous Galerkin (LDG) methods that belong to the family of finite element methods. LDG methods have drawn great attention since the work by Cockburn and Shu in [7]. They were originally proposed to solve a convection-diffusion equation, and then extended to solve partial differential equations with high spatial derivatives [22,23,24] and wave Eq. [6, 21]. The general idea of LDG methods is to introduce auxiliary variables and rewrite a partial differential equation with high spatial derivatives as a first order system, then apply the standard DG method to the resulting system. Since the auxiliary variables can be solved locally, the method was named local discontinuous Galerkin method. One of the most crucial parts in designing LDG methods is to suitably define the numerical fluxes along the element interface. In this paper, we design correct numerical fluxes such that the wave energy and Hamiltonian of the semi-discrete schemes are conserved exactly. For the fully discrete LDG methods, the energy is exactly conserved, but the conservation of Hamiltonian depends on \(\Delta t\) because of the term \((\phi _t)^2\) in (1.4). Due to the nonlinear coupling of Klein–Gordon equation and Schrödinger equation in the KGS system, it is challenging to obtain the error estimates. Thus, we first obtain the optimal error estimates of our semi-discrete methods for the linearized KGS equations. To deal with the difficulty of nonlinearity, we make an assumption about the \(L^{\infty }\) norm of numerical solutions, which is indirectly proved by mathematical induction. Some of the theoretical results above can be verified through our numerical experiments.
The remaining of the paper is organized as follows. In Sect. 2, we present our semi-discrete LDG methods for the Klein–Gordon–Schrödinger equations, and prove the energy- and Hamiltonian-preserving properties of the semi-discrete methods. In Sect. 3, we show the optimal convergence of the semi-discrete LDG methods for the linearized KGS equations, and discuss some estimates for the KGS equations in special cases. In Sect. 4, we define the fully discrete LDG methods, and show the energy- and Hamiltonian-preserving properties of the fully discrete methods. In Sect. 5, we present the optimal error estimates of the fully discrete LDG methods. Since the proofs of some lemmas in Sect. 3 and 5 are very technical, we put some proofs in Sect. 6 to make the primary theorems easy to follow. Finally, in Sect. 7, we perform some numerical experiments to test the optimal convergence of numerical solutions, conservation properties of our methods, and dispersion and dissipation behaviors. We can show that our numerical results in Sect. 7 are consistent with the theoretical findings.
2 Formulation of the semi-discrete LDG methods
2.1 Notations and preliminaries
Throughout this section, we will use the following notations. We use \(H^m\) to denote the \(L^2\)-Sobolev space of order m whose equipped norm is represented by \(\Vert \cdot \Vert _m\). We use \(L^2\) instead of \(H^0\), when \(m = 0\), and its corresponding norm is denoted by \(\Vert \cdot \Vert \). Similarly, we use \(W^{m,\infty }\) to represent the \(L^\infty \)-Sobolev space of order m whose equipped norm is denoted by \(\Vert \cdot \Vert _{m,\infty }\). When \(m = 0\), we simply use \(\Vert \cdot \Vert _{\infty }\) to denote the \(L^\infty \) norm. We consider a one-dimensional domain \(I:=[a,b]\), and partition the computational domain into N elements \(I_{j}= [x_{j-\frac{1}{2}}, x_{j+\frac{1}{2}}]\) for \(j=1, 2, \ldots , N\), with \(a = x_{\frac{1}{2}}< x_{\frac{3}{2}}< \cdots < x_{N + \frac{1}{2}} = b\). The x-coordinate for the midpoint of the element \(I_{j}\) is denoted by \(x_{j}:= (x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}})/2\), and the length of each element is denoted by \(h_j = x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}\). The mesh size of the partition is denoted as \(h = \max _{1\le j \le N} h_j\). In this paper, we assume our mesh is regular. That is, there exists a positive constant \(\lambda \) that is independent of h, such that \(h \le \lambda \cdot \min _{1\le j \le N} h_j\).
We define the piecewise polynomial space as \(V_h^k=\{v : v|_{I_{j}} \in P^k(I_j), \forall I_{j} \}\), where \(P^k(I_j)\) is the space of of one-dimensional polynomials of degree up to k defined on \(I_j\). Note that for any \(q_h \in V_h^k\), there are two values of \(q_h\) defined at each interior element boundary. Therefore, we use \((q_h)_{j+\frac{1}{2}}^-\) and \((q_h)_{j+\frac{1}{2}}^+\) to represent the value of \(q_h\) at \(x_{j+\frac{1}{2}}\) from the left and the right element, respectively. The jump of \(q_h\) across any interior element boundary point \(x_{j+\frac{1}{2}}\) is \([q_h]_{j+\frac{1}{2}} = (q_h)_{j+\frac{1}{2}}^{+} - (q_h)_{j+\frac{1}{2}}^{-}\). For convenience, \(q_{h,t}\) and \(q_{h, tx}\) are used to represent \(\frac{\partial q_h}{\partial t}\) and \(\frac{\partial ^2 q_h}{\partial t \partial x}\), respectively. The following equality involving jumps will be frequently used in our analysis:
For \(v\in H^1(I)\), let \(\Pi v \in V_h^k\) be the standard \(L^2\) projection to the piecewise polynomial space \(V_h^k\), such that \(\int _{I_j} (\Pi v) w \, dx = \int _{I_j} v w \,dx\), \(\forall w \in P^{k}(I_j)\), for \(j=1,2,\ldots , N\). One of the key components in our error estimates is the application of Gauss-Radau projections. We will need two kinds of such projections, i.e., \(\Pi ^{+}\) and \(\Pi ^{-}\). For any \(v\in H^1(I)\), \(\Pi ^{+}v\) and \(\Pi ^{-}v\) are unique in \(V_h^k\), such that
The approximation properties in (2.6) and inverse inequality in (2.7) will be used in our analysis [27]. For sufficiently smooth function v, there exists a positive constant C that is independent of h and v, such that
where \(\mathcal {Q}\) can be \(\Pi ^+\), \(\Pi ^-\) or \(\Pi \). In addition, there exists a positive constant C, such that
2.2 Semi-discrete local discontinuous Galerkin methods
In this subsection, we define the semi-discrete local discontinuous Galerkin (LDG) methods for the KGS Eq. (1.2). In order to define our methods, we first rewrite the KGS equations as the following system
The idea of deriving (2.8) is that we desire to have an equivalent system of PDEs whose highest order of spatial derivative is only one. Our proposed local discontinuous Galerkin methods for the system (2.8) can be formulated as follows: we look for \(q_h\), \(p_h\), \(\phi _h\), \(u_h\), \(s_h\) and \(z_h \in V_h^k\), such that
hold for all test functions \(w_1\), \(w_2, \ldots , w_6 \in V_h^k\), and for all \(j=1,2,\ldots ,N\). The terms \(\widehat{u_h}\), \(\widehat{s_h}\), \(\widehat{z_h}\), \(\widehat{p_h}\), \(\widehat{\phi _h}\) and \(\widehat{q_h}\) in (2.9)–(2.14) are numerical fluxes which will be determined later. We will show that the choice of numerical fluxes will be crucial for energy and Hamiltonian conservation.
2.3 Conservation properties of the semi-discrete LDG methods
In this subsection, we show that the energy and Hamiltonian of the KGS system can be conserved in the semi-discrete case, if appropriate numerical fluxes are used. The proof of energy conservation and Hamiltonian conservation of the Schrödinger part is similar to that in [4].
Theorem 1
(Energy Conservation) The numerical solutions to the scheme (2.9)–(2.14) satisfies:
if the following numerical fluxes are chosen:
Proof
We take \(w_1 = q_h\) and \(w_3 = p_h\) in the Eqs. (2.9) and (2.11), respectively, and sum the two equations over all the intervals \(I_j\) to obtain
Here we have used the periodic condition of the numerical solutions. We then let \(w_4 = z_h\) in (2.12) and \(w_6 = u_h\) in (2.14), and take the difference of the resulting equations to get
which leads to
We add (2.19) to (2.18) to get
Now we consider the numerical flux \(\widehat{u_h} = u_h^-\), \(\widehat{q_h} = q_h^+\), \(\widehat{z_h} = z_h^-\), \(\widehat{p_h} = p_h^+\) in Eq. (2.20), it is easy to show that \(\frac{d}{dt} \int _I\left( q_h^2 + p_h^2 \right) dx = 0\). Here the property of jump in (2.5) has been used. Other choices of numerical fluxes can be proved in the same manner. \(\square \)
Theorem 1 gives the property of energy conservation for our proposed scheme. Note that the key to the energy conservation is that \(\widehat{u_h}\) and \(\widehat{q_h}\), as well as \(\widehat{z_h}\) and \(\widehat{p_h}\), must be taken from opposite directions. If such conditions are not satisfied, the energy is not exactly conserved. In fact, when \(\widehat{u_h} = u_h^+\), \(\widehat{z_h} = z_h^-\), \(\widehat{p_h} = p_h^-\) and \(\widehat{q_h} = q_h^+\) are chosen, there is \(\frac{d}{dt} \int _{I} \left( q_h^2 + p_h^2 \right) dx = - \sum _{j=1}^N [p_h]_{j-\frac{1}{2}} [z_h]_{j-\frac{1}{2}} - \sum _{j=1}^N [q_h]_{j-\frac{1}{2}} [u_h]_{j-\frac{1}{2}} \ne 0\). The next theorem shows the Hamiltonian-preserving property of our semi-discrete methods.
Theorem 2
(Hamiltonian Conservation) The numerical solutions to the scheme (2.9)–(2.14) satisfies:
if the following numerical fluxes are used
Proof
We complete this proof in two steps, given by Eqs. (2.23) and (2.27). The sum of these two equations concludes Theorem 2.
Step 1 We first show
Let \(w_2 = \phi _{h,t}\) in (2.10) and apply the periodic boundary conditions, we have
To simplify the right side of (2.24), we take t derivative on both sides of (2.13), let \(w_5 = s_h\) and sum over all interval \(I_j\), we can get
We then add (2.24) and (2.25) to obtain
We apply the numerical flux \(\widehat{\phi _h} = \phi _h^+\) and \(\widehat{s_h} = s_h^{-}\) in (2.26), take the sum over all \(I_j\) and use the periodic boundary conditions for \(\phi _h\) and \(s_h\), which will eventually lead to Eq. (2.23). Note that the Eq. (2.23) also holds if we take \(\widehat{\phi _h} = \phi _h^-\) and \(\widehat{s_h} = s_h^{+}\) in (2.26), and it is independent of the choices for \(\widehat{u_h}\), \(\widehat{q_h}\), \(\widehat{z_h}\) and \(\widehat{p_h}\).
Step 2 We then show
We take \(w_1 = p_{h,t}\) and \(w_3 = q_{h,t}\) in (2.9) and (2.11), respectively, subtract these two equations and sum over \(I_j\) to obtain
We then take t derivative on both sides of (2.12) and (2.14), let \(w_5 = u_{h}\) and \(w_7 = z_{h}\), and take the sum of these two equations over all \(I_j\) to get
Subtracting (2.28) from (2.29), and applying \(\widehat{u_h} = u_h^{-}\), \(\widehat{q_h} = q_h^{+}\), \(\widehat{z_h} = z_h^{-}\) and \(\widehat{p_h} = p_h^{+}\) leads to the equality (2.27), which concludes this theorem. \(\square \)
Remark 2.1
The choice of numerical fluxes for Hamiltonian conservation is not unique. From step 1 in the proof of Theorem 1, we can see that \(\widehat{\phi _h}\) and \(\widehat{s_h}\) must be from opposite directions. Also note that in our derivation of (2.27), we have to take \(\widehat{u_h}\) and \(\widehat{p_h}\) from opposite directions. Similarly, \(\widehat{z_h}\) and \(\widehat{q_h}\) must be also from opposite directions. Therefore, there are eight different choices of numerical flux for the purpose of energy conservation. However, Theorem 1 indicates that the pair of \(\widehat{u_h}\) and \(\widehat{q_h}\), as well as the pair of \(\widehat{z_h}\) and \(\widehat{p_h}\) must be from opposite directions in order to achieve charge conservation. To obtain energy and Hamiltonian conservation simultaneously, there are only four choices for \(\widehat{u_h}\), \(\widehat{p_h}\), \(\widehat{q_h}\), \(\widehat{z_h}\), \(\widehat{\phi _h}\) and \(\widehat{s_h}\). That is,
3 Error estimates of the semi-discrete LDG methods
In this section, we first present the optimal error estimates of semi-discrete LDG methods for the linearized KGS equations, and then show some estimates for the original KGS Eq. (1.2).
3.1 Error estimates for the linearized Klein–Gordon–Schrödinger equations
Let (\(p_0(x)\), \(q_0(x)\), \(\phi _0(x)\)) be a sufficiently smooth equilibrium solution of the Klein–Gordon–Schrödinger (KGS) Equations. Then the linearization at the equilibrium point is given by
Similar to the schemes for the KGS equations defined in (2.9)–(2.14), the schemes for the linearized KGS equations are as follows: we look for \(q_h\), \(p_h\), \(\phi _h\), \(u_h\), \(s_h\) and \(z_h \in V_h^k\), such that
hold for all test functions \(w_1\), \(w_2, \ldots , w_6 \in V_h^k\). Here we have applied the numerical fluxes
(see Flux 2 in Remark 2.1), and the periodic boundary conditions. The proof of error estimates for other numerical fluxes in Remark 2.1 will follow the same lines, we thus skip it and only focus on the numerical fluxes defined above.
We use p to denote the exact solution of the linearized KGS equations, and denote the error of p by \(e_p = p - p_h = \eta _p - \xi _p\), where \(\eta _p = p - \Pi ^{+}p\) and \(\xi _p = p_h - \Pi ^{+}p\), with \(\Pi ^{+}\) being the Gauss-Radau projection defined in Sect. 2.1. Following the numerical fluxes given by (3.31), we further define \(\eta _u = u - \Pi ^{-}u\), \(\eta _q = q - \Pi ^{+}q\), \(\eta _z = z - \Pi ^{-}z\), \(\eta _{\phi } = \phi - \Pi ^{+} \phi \) and \(\eta _s = s - \Pi ^{-}s\). Similar definitions hold for \(e_u\), \(e_q\), \(e_z\), \(e_{\phi }\), \(e_s\), \(\xi _u\), \(\xi _q\), \(\xi _z\), \(\xi _{\phi }\) and \(\xi _s\). According to the approximation properties in Eq. (2.6), the \(L^2\) norm of \(\eta _{\star }\) (\(\star = p, u, q, z, \phi \) or s) can be estimated directly. Thus, our analysis only focuses on the estimates of terms \(\xi _{\star }\). Next, we derive the error equations for our error estimates. Based on the derivation of the scheme (3.30), we can see that the exact solutions of the linearized KGS equations also satisfy similar equations. That is, if we replace \(q_h\), \(u_h\), \(\phi _h\), \(s_h\), \(p_h\), \(z_h\) in (3.30) with q, u, \(\phi \), s, p and z, respectively, the resulting equations are also satisfied. We then subtract the resulting equations from (3.30), and derive the following error equations:
which hold for all test functions \(w_1\), \(w_2, \ldots , w_6 \in V_h^k\). Here we have used the definition of Gauss-Radau projections, such that \((\eta _u)_{j+\frac{1}{2}}^{-} = (\eta _s)_{j+\frac{1}{2}}^{-} = (\eta _z)_{j+\frac{1}{2}}^{-} = (\eta _p)_{j+\frac{1}{2}}^{+} = (\eta _{\phi })_{j+\frac{1}{2}}^{+} = (\eta _q)_{j+\frac{1}{2}}^{+} = 0\) for all j, and \(\int _{I} \eta _u (w_1)_x dx = \int _{I} \eta _s (w_2)_x dx = \int _{I} \eta _z (w_3)_x dx = \int _{I} \eta _p (w_4)_x dx = \int _{I} \eta _{\phi } (w_5)_x dx = \int _{I} \eta _q (w_6)_x dx = 0\) for any \(w_1\), \(w_2, \ldots , w_6 \in V_h^k\). We now present the error estimates of the scheme (3.30). The following lemmas are the key building blocks of the main results.
Lemma 3.1
The \(L^2\) norm of the function \(\xi _q\) and \(\xi _p\) satisfy the following inequality:
Lemma 3.2
The \(L^2\) norm of the function \(\xi _{\phi }\), \(\xi _{\phi ,t}\) and \(\xi _s\) satisfy the following inequality:
Lemma 3.3
For any \(T>0\), the following estimates about \(\Vert \xi _u\Vert \) and \(\Vert \xi _z\Vert \) are satisfied:
Since the proofs of Lemmas 3.1– 3.3 are very technical, we give these proofs in Sect. 6 so that our error estimates are easy to follow. With these lemmas, we can prove our main theorem.
Theorem 3
Let \((q, p, \phi )\) be a sufficiently smooth exact solution to the linearized Klein–Gordon–Schrödinger equation. For any \(T>0\), let \((q_h, p_h, \phi _h) \in V_h^k \times V_h^k \times V_h^k\) be the solution to the scheme (3.30) at any time \(t \in [0,T]\). Then the following estimates hold:
where C is a constant that depends on T, certain Sobolev norms of the exact solution and the \(L^\infty \) norms of equilibrium solution, and it is independent of the mesh size h.
Proof
Adding inequalities (3.38) and (3.39), we can obtain
where \(\Lambda := \Vert \xi _q\Vert ^2 + \Vert \xi _p\Vert ^2 + \Vert \xi _{\phi }\Vert ^2 + \Vert \xi _{\phi ,t}\Vert ^2 + \Vert \xi _s\Vert ^2\). We then apply Lemma 3.3 to (3.42), and obtain
Here we have used Young’s inequality for \(C h^{k+1} \left( \Vert \xi _q\Vert + \Vert \xi _p\Vert + \Vert \xi _{\phi ,t}\Vert + \Vert \xi _s\Vert \right) \). (3.43) leads to
We take the integral of the inequality (3.44) over [0, t] to obtain the following estimate about \(\Lambda \):
for any \(t \in [0, T]\). Therefore, there is
It is easy to see (3.46) gives rise to \(\Lambda (t) = \Vert \xi _q\Vert ^2 + \Vert \xi _p\Vert ^2 + \Vert \xi _{\phi }\Vert ^2 + \Vert \xi _{\phi ,t}\Vert ^2 + \Vert \xi _s\Vert ^2 \le C h^{2k+2}\). Thus, we have \(\Vert \xi _q\Vert \le C h^{k+1}\). We further apply the approximation properties of \(\Vert \eta _q\Vert \) to get the error estimate of q using triangle inequality. The error estimate of p and \(\phi \) can be obtained similarly. \(\square \)
3.2 Some estimates for the Klein–Gordon–Schrödinger equations
In the previous section, we have presented optimal error estimates of our proposed schemes for the linearized Klein–Gordon–Schördinger equations. The important steps to establish the error estimates are from Lemmas 3.1– 3.3. Now we consider the error estimates for the original KGS equations based on the idea in Sect. 3.1. It is easy to see that if we can obtain similar inequalities as in Lemmas 3.1– 3.3, then the optimal convergence of numerical solutions can be proved. However, as far as the semi-discrete local discontinuous Galerkin methods are concerned, the corresponding lemmas for the original KGS equations can only be proved in special cases where the\(L^{\infty }\)norm of the numerical solutions are bounded.
To establish some error estimates, we first derive the following error equations in the same way as we get (3.32)–(3.37):
Equations (3.47)–(3.52) are held for all test functions \(w_1\), \(w_2, \ldots , w_6 \in V_h^k\). The main challenge of the error estimates are due to the nonlinear terms \(\int _{I} (\phi _h p_h - \phi p) w_1 \, dx\), \(\int _{I} (p_h^2 + q_h^2 - p^2 - q^2) w_2 \, dx\) and \(\int _{I} (\phi _h q_h - \phi q) w_3 \, dx\) in Eqs. (3.47), (3.48) and (3.49), respectively. In order to extend the analysis from Sect. 3.1 to the KGS equations, we need the following inequalities in Lemma 3.4.
Lemma 3.4
For any \(T>0\), let \((q_h, p_h, \phi _h) \in V_h^k \times V_h^k \times V_h^k\) be the numerical solution to the scheme (2.9)–(2.14) at time \(t\in [0, T]\). Then the following inequalities hold:
Here C is a constant that depends on T, certain Sobolev norms of the exact solution \((q, p, \phi )\), and it is independent of the mesh size h.
Lemma 3.4 can be easily proved by applying approximation properties of \(L^2\) projections and Cauchy–Schwartz inequalities to the left side of each inequality. Following similar steps as in the proof of Lemmas 3.1– 3.3, and applying Lemma 3.4, we can prove Lemmas 3.5– 3.7.
Lemma 3.5
The \(L^2\) norm of the function \(\xi _q\) and \(\xi _p\) satisfy the following inequality:
Lemma 3.6
The \(L^2\) norm of the function \(\xi _{\phi }\), \(\xi _{\phi ,t}\) and \(\xi _s\) satisfy the following inequality:
Lemma 3.7
For any \(T>0\), the following estimates about \(\Vert \xi _u\Vert \) and \(\Vert \xi _z\Vert \) are satisfied:
Note that if we further assume the uniform boundedness of \(\Vert \phi _h \Vert _{\infty }\), \(\Vert \phi _{h,t} \Vert _{\infty }\), \(\Vert p_h \Vert _{\infty }\) and \(\Vert q_h \Vert _{\infty }\), Lemmas 3.5– 3.7 will coincide with Lemmas 3.1– 3.3. Here we only consider error estimates for such special cases. With the help of Lemmas 3.5– 3.7, we can obtain the error estimates. For any fixed \(T > 0\) and any \(t \in [0, T]\), we add the two inequalities from Lemmas 3.5 and 3.6, and apply the inequality from Lemma 3.7 to get
where \(\Lambda (t) = \Vert \xi _q \Vert ^2 + \Vert \xi _p \Vert ^2 + \Vert \xi _{\phi } \Vert ^2 + \Vert \xi _{\phi ,t} \Vert ^2 + \Vert \xi _s \Vert ^2\), \(\mu _1 = 1 + \Vert p_h \Vert _{\infty } + \Vert q_h \Vert _{\infty }\) and \(\mu _2 = 1 + \Vert \phi _h \Vert _{\infty } + \Vert \phi _{h,t} \Vert _{\infty }\). Equation (3.53) leads to
Thus, we can show that
Therefore, we take the maximum of the left hand side over all t and get
Finally, the inequality above leads to \(\displaystyle \Lambda (t) \le (2e^{C \mu _1 T} + 4 \mu _2^2 e^{2 C \mu _1 T}) h^{2k+2}\) for any \(t \in [0, T]\). That is, \(\Vert \xi _q \Vert \), \(\Vert \xi _p \Vert \) and \(\Vert \xi _{\phi } \Vert \le C_1 h^{k+1}\), where \(C_1 = \sqrt{2e^{C \mu _1 T} + 4 \mu _2^2 e^{2 C \mu _1 T}}\). If we further apply the approximation properties of \(\Vert \eta _q\Vert \), \(\Vert \eta _p\Vert \) and \(\Vert \eta _{\phi }\Vert \), we can obtain the following error estimates.
Theorem 4
Let \((q, p, \phi )\) be a sufficiently smooth exact solution to the Klein–Gordon–Schrödinger Eq. (1.2). For any \(T>0\), let \((q_h, p_h, \phi _h) \in V_h^k \times V_h^k \times V_h^k\) be the solution to the scheme (2.9)–(2.14) at time \(t \in [0,T]\). Then the following estimates hold:
where C is a constant that depends on T and certain Sobolev norms of the exact solution, and it is independent of the mesh size h. Also, \(C_1 =\sqrt{2e^{C \mu _1 T} + 4 \mu _2^2 e^{2 C \mu _1 T}}\), where \(\mu _1 = 1 + \Vert p_h \Vert _{\infty } + \Vert q_h \Vert _{\infty }\) and \(\mu _2 = 1 + \Vert \phi _h \Vert _{\infty } + \Vert \phi _{h,t} \Vert _{\infty }\).
Remark 3.1
The theorem above indicates the optimal error estimates of our schemes when \(\Vert p_h\Vert _{\infty }\), \(\Vert q_h\Vert _{\infty }\), \(\Vert \phi _h \Vert _{\infty }\) and \(\Vert \phi _{h,t} \Vert _{\infty }\) are bounded. Such conditions cannot be easily proved for our semi-discrete methods. In [11], the authors considered the LDG methods for the nonlinear Schrödinger equation and obtained error estimates of the semi-discrete methods provided that the \(L^{\infty }\) norm of the numerical solution is bounded. Our analysis is consistent with their conclusion. However, we will prove such conditions for fully discrete local discontinuous Galerkin methods in Sect. 5.
4 Formulation of the fully discrete LDG methods
4.1 The fully discrete local discontinuous Galerkin methods
We now define the fully discrete local discontinuous Galerkin schemes based on the semi-discrete formulation (2.9)–(2.14). To be more specific, we apply Crank–Nicholson method to the Schrödinger equation part, i.e., (2.9), (2.11), (2.12) and (2.14), and use the Crank–Nicholson leap-frog scheme for the Klein–Gordon equation part, i.e., (2.10) and (2.13)). We use \(\phi _h^{n}\), \(s_h^{n}\), \(p_h^{n}\), \(q_h^{n}\), \(u_h^{n}\) and \(z_h^{n}\) to represent the numerical solutions at time \(t^n = n \Delta t\), where \(\Delta t\) is the time step size. Even though we assume that the time steps are uniform, our analysis can be easily adapted to the case of non-uniform time step sizes. We denote the exact solution at \(t^n\) as \(\phi ^{n}\), \(s^{n}\), \(p^{n}\), \(q^{n}\), \(u^{n}\), \(z^{n}\).
In our scheme, we first initialize the numerical solution using the following equations
Here \(\Pi ^{+}\) and \(\Pi ^{-}\) are two kinds of Gauss-Radau projections to \(V_h^k\). We then update the numerical solution \((q_h^{n+1}, p_h^{n+1}, \phi _h^{n+2})\) for \(n = 0, 1, 2, \ldots \) in two steps.
Step 1 Update \(q_h^{n+1}\), \(p_h^{n+1}\), \(u_h^{n+1}\) and \(z_h^{n+1}\) by solving the Schrödinger equation part using Crank–Nicholson method:
for any \(w_1\), \(w_2\), \(w_3\) and \(w_4 \in V_h^k\).
Step 2 Update \(\phi _h^{n+2}\) and \(s_h^{n+2}\) by solving the Klein–Gordon equation part using Crank–Nicholson leap-frog method:
for any v and \(w \in V_h^k\).
Note that we have used the numerical fluxes defined in (3.31). Such a choice is not unique. The other choices of numerical fluxes in Remark 2.1 will lead to the same conservation properties and convergence order. Thus we only focus on the analysis with numerical fluxes (3.31). Also, the second strategy in [20] can also be used for the time discretization, which leads to a decoupled LDG scheme.
4.2 Conservation properties of the fully discrete LDG methods
The numerical solutions to (4.55)–(4.56) satisfy the following conservation properties.
Theorem 5
(Energy Conservation) The numerical solutions to the fully discrete LDG methods satisfy:
Proof
Due to the periodic boundary condition, Eq. (4.55) lead to
and
Since Eq. (4.55) hold for all n, it is easy to show that
We take \(w_1 = q_h^{n+1} + q_h^{n}\) in (4.58), \(w_2 = p_h^{n+1} + p_h^{n}\) in (4.59), \(w_3 = -(z_h^{n+1} + z_h^{n})\) in (4.60), \(w_4 = u_h^{n+1} + u_h^{n}\) in (4.61) and add these equations to get
where \(\Lambda _1 = \frac{1}{2} \sum _{j=1}^{N} [(u_h^{n+1} + u_h^{n}) (q_h^{n+1} + q_h^{n})]_{j+\frac{1}{2}} - \frac{1}{2} \sum _{j=1}^{N} (u_h^{n+1} + u_h^{n})_{j+\frac{1}{2}}^{-} [q_h^{n+1} + q_h^{n}]_{j+\frac{1}{2}}\)\(- \frac{1}{2} \sum _{j=1}^{N} (q_h^{n+1} + q_h^{n})_{j+\frac{1}{2}}^{+} [u_h^{n+1} + u_h^{n}]_{j+\frac{1}{2}}\) and \(\Lambda _2 = \frac{1}{2} \sum _{j=1}^{N} [(z_h^{n+1} + z_h^{n}) (p_h^{n+1} + p_h^{n})]_{j+\frac{1}{2}}\)\(- \frac{1}{2} \sum _{j=1}^{N} (z_h^{n+1} + z_h^{n})_{j+\frac{1}{2}}^{-} [p_h^{n+1} + p_h^{n}]_{j+\frac{1}{2}} - \frac{1}{2} \sum _{j=1}^{N} (p_h^{n+1} + p_h^{n})_{j+\frac{1}{2}}^{+} [z_h^{n+1} + z_h^{n}]_{j+\frac{1}{2}}\). Note that \(\Lambda _1 = \Lambda _2 = 0\) from the property of jump (2.5), we can conclude (4.57). \(\square \)
Theorem 5 indicates that the energy is conserved even in the fully discrete sense. The next theorem shows the Hamiltonian-preserving property of the fully discrete LDG methods.
Theorem 6
(Hamiltonian Conservation) The numerical solutions to the fully discrete LDG methods satisfy:
Proof
We prove the theorem in two steps, given by Eqs. (4.63) and (4.67). The sum of these equations multiplied by 1 / 2 leads to (4.62).
Step 1 We first show
We apply the periodic boundary condition of the numerical solutions and rewrite the equation about \(\phi _h^{n+2}\) in (4.56) as
Note that (4.56) is satisfied for all n, we thus have
Let \(v = \phi _h^{n+2} - \phi _h^{n}\) in (4.64), \(w = s_h^{n+2} + s_h^n\) in (4.65), sum them up and obtain the equation
Here we have applied the property of jump in (2.5) to the right side of the equality above. Since \((\phi _h^{n+2} - 2\phi _h^{n+1}+ \phi _h^{n}) (\phi _h^{n+2} - \phi _h^{n}) = ( \phi _h^{n+2} - \phi _h^{n+1} )^2 - (\phi _h^{n+1} - \phi _h^{n})^2\), we can use this equality in (4.66) and rearrange the terms in the resulting equation to get (4.63).
Step 2 We then show
Let \(w_1 = -(p_h^{n+1} - p_h^{n})\) in (4.58), \(w_2 = q_h^{n+1} - q_h^n\) in (4.59), sum up these two equations and obtain
To simplify the right side of the equality above, we further derive the following equations
which can be easily derived in a similar way to (4.60) and (4.61). We now take \(w_3 = u_h^{n+1} + u_h^{n}\) and \(w_4 = z_h^{n+1} + z_h^{n}\) in (4.69) and (4.70), respectively, and add these equations to get
We combine (4.68) and (4.71), and apply the property of jump (2.5) to get (4.67). \(\square \)
Remark 4.1
Note that \(\frac{1}{4} \Vert \phi _h^{n+2} \Vert ^2 - \frac{1}{4} \Vert \phi _h^{n} \Vert ^2 = \frac{1}{2} \int _{I} \frac{\phi _h^{n+2} + \phi _h^n}{2} \phi _h^{n+2} dx - \frac{1}{2} \int _{I} \frac{\phi _h^{n+2} + \phi _h^n}{2} \phi _h^{n} dx\) is an approximation of \(\frac{1}{2} \Vert \phi ^{n+1} \Vert ^2 - \frac{1}{2} \Vert \phi ^{n} \Vert ^2\). Similarly, \(\frac{1}{4} \Vert s_h^{n+2} \Vert ^2 - \frac{1}{4} \Vert s_h^{n} \Vert ^2\) is an approximation of \(\frac{1}{2} \Vert s^{n+1} \Vert ^2 - \frac{1}{2} \Vert s^{n} \Vert ^2\). Therefore, Eq. (4.62) can be rewritten as
which is an approximation of Hamiltonian conservation (1.4) in the fully discrete sense. Unlike in Theorem 5, the fully discrete Hamiltonian is not exactly conserved, and it depends on \(\Delta t\).
5 Error estimates of the fully discrete local discontinuous Galerkin methods
In this section, we present the optimal error estimates of the fully discrete LDG methods (4.55)-(4.56) for the Klein–Gordon–Schrödinger equations, which will be given in Theorem 7.
Without loss of generality, we assume that the time step size and mesh size satisfy \(\Delta t, h \le 1\).
Theorem 7
Let \((q, p, \phi )\) be a sufficiently smooth exact solution to the KGS Eq. (1.2). For any \(T>0\), let \((q_h^n, p_h^n, \phi _h^n) \in V_h^k \times V_h^k \times V_h^k\) be the solution to the scheme (4.55)–(4.56) at time \(t^n \in [0,T]\). Suppose \((\Delta t)^2 \le \gamma h^{1/2}\) for some constant \(\gamma >0\). Then the following estimates hold:
for any \((n+1)\Delta t \le T\). Here C is a constant that depends on T and certain Sobolev norms of the exact solution, and it is independent of the mesh size h.
5.1 Error equations
Let (\(p(x, t^n)\), \(q(x, t^n)\), \(\phi (x, t^n)\)) be the exact solution of the KGS equations at \(t^n = n \Delta t\). For convenience, we use \(p^n\), \(q^n\) and \(\phi ^n\) to denote \(p(x, t^n)\), \(q(x, t^n)\) and \(\phi (x, t^n)\), respectively. We further define \(u^n = p^n_x\), \(z^n = q^n_x\) and \(s^n = \phi ^n_x\). In the next lemma, we give some estimates about truncation errors from time discretization.
Lemma 5.1
Let
where \(T_q^{n+\frac{1}{2}}(x)\), \(T_p^{n+\frac{1}{2}}(x)\) and \(T_{\phi }^{n+1}(x)\) are truncation errors, then
Moreover, there is
Lemma 5.1 can be easily verified using Taylor expansion, thus we omit its proof. In order to derive the error equations for our error estimates, we denote the error of p at time \(t^n\) by \(e_p^n = p^n - p_h^n = \eta _p^n - \xi _p^n\), where \(\eta _p^n = p^n - \Pi ^{+}p^n\) and \(\xi _p^n = p_h^n - \Pi ^{+}p^n\), with \(\Pi ^{+}\) being the Gauss-Radau projection. We use the numerical fluxes in (3.31) and define \(\eta _u^n = u^n - \Pi ^{-}u^n\), \(\eta _q^n = q^n - \Pi ^{+}q^n\), \(\eta _z^n = z^n - \Pi ^{-}z^n\), \(\eta _{\phi }^n = \phi ^n - \Pi ^{+} \phi ^n\) and \(\eta _s^n = s^n - \Pi ^{-}s^n\). We also define \(e_u^n\), \(e_q^n\), \(e_z^n\), \(e_{\phi }^n\), \(e_s^n\), \(\xi _u^n\), \(\xi _q^n\), \(\xi _z^n\), \(\xi _{\phi }^n\) and \(\xi _s^n\) in the similar way. Note that the \(L^2\) norm of \(\eta _{\star }^n\) (\(\star = p, u, q, z, \phi \) or s) can be estimated using the approximation properties in Eq. (2.6).
Next, we multiply arbitrary test functions \(w_1\), \(w_2\) and \(v \in V_h^k\) on both sides of each Equation in (5.74), integrate over the interval I and take integration by parts. We also multiply arbitrary test functions \(w_3\), \(w_4\) and \(w \in V_h^k\) on both sides of \(u^{n+1} = p^{n+1}_x\), \(z^{n+1} = q^{n+1}_x\) and \(s^{n+2} = \phi ^{n+2}_x\), respectively, integrate over the interval I and take integration by parts. We then subtract the six resulting equations from the sum of the fully discrete scheme (4.55)–(4.56) over all intervals \(I_j\), and derive the error equations
and
which hold for all test functions \(w_1\), \(w_2, \ldots , w_6 \in V_h^k\).
Here we have used the definition of Gauss-Radau projections when we derive (5.75), so that \(\sum _{j=1}^{N} (\eta _u^{n+1})_{j+\frac{1}{2}}^{-} [w_1]_{j+\frac{1}{2}} = \sum _{j=1}^N (\eta _u^{n})_{j+\frac{1}{2}}^{-} [w_1]_{j+\frac{1}{2}} = \int _{I} (\eta _u^{n+1} + \eta _u^{n}) (w_1)_x dx = 0\) for any \(v\in V_h^k\). (5.76) and (5.79) can be derived similarly. Equations (5.77), (5.78) and (5.80) are based on the fact that the fully discrete LDG methods (4.55)–(4.56) are satisfied for any n.
The main error estimates for the fully discrete methods will be established based on error Eqs. (5.75)–(5.80). The error estimates for the Schrödinger equation solver and Klein–Gordon equation solver are given in Sect. 5.2 and 5.3, respectively. The proof of the main error estimates in Sect. 5.4 will combine the results from these two subsections. Recall that when we derive the error estimates for the semi-discrete LDG methods, we have used a priori assumption that \(\Vert p_h \Vert _{\infty }\), \(\Vert q_h \Vert _{\infty }\), \(\Vert \phi _h \Vert _{\infty }\) and \(\Vert \phi _{h,t} \Vert _{\infty }\) are bounded. For the fully discrete methods, such an assumption can be indirectly proved by mathematical induction. The next lemma will be used frequently in our analysis, the proof can be referred to part (1) of Lemma 3.3 in [25].
Lemma 5.2
For \(\star = q\), p or \(\phi \), we have
Another important formula in the error estimates for the Schrödinger equation part is the summation-by-parts formula:
5.2 The Schrödinger equation part
We now let \(w_1 = (\xi _q^{n+1} + \xi _q^{n}) (\Delta t)\) in (5.75), \(w_2 = (\xi _p^{n+1} + \xi _p^{n}) (\Delta t)\) in (5.76), \(w_3 = -\frac{1}{2} (\xi _z^{n+1} + \xi _z^{n}) (\Delta t)\) in (5.77), \(w_4 = \frac{1}{2} (\xi _u^{n+1} + \xi _u^{n}) (\Delta t)\) in (5.78), sum up these equations and get the energy equations for p and q:
where
and
Equation (5.82) describes how much the errors of \(p_h\) and \(q_h\) accumulate in one time step. We can further estimate the upper bound of \(\Theta _1\), \(\Theta _2\) and \(\Theta _3\) under some assumptions. The result is summarized in Lemma 5.3. The estimates for \(\xi _u\) and \(\xi _z\) are given in Lemma 5.4 and the detail of its proof will be given in Sect. 6.4.
Lemma 5.3
If \(\Vert \phi _h^{n+1} \Vert _{\infty }\), \(\Vert \phi _h^{n} \Vert _{\infty } \le C\), then the following inequality holds:
Lemma 5.4
If \(\Vert \phi _h^{i}\Vert _{\infty }\), \(\Vert (\phi _h^{i+1} - \phi _h^{i})/\Delta t \Vert _{\infty } \le C\) for any \(i \in [0,n]\), and \(\Vert \phi _h^{n+1}\Vert _{\infty } \le C\), then
5.3 The Klein–Gordon equation part
Lemma 5.5
The following estimate holds if \(\Vert p_h^n\Vert _{\infty }\), \(\Vert q_h^n\Vert _{\infty } \le C\):
Remark 5.1
The error estimates of \(\Vert \xi _{p}^{n}\Vert \) and \(\Vert \xi _{q}^{n}\Vert \) lead to the boundedness of \(\Vert p_h^{n}\Vert _{\infty }\) and \(\Vert q_h^{n}\Vert _{\infty }\), which can be used to get \(\Vert \xi _{\phi }^{n+1}\Vert \) and \(\Vert (\xi _{\phi }^{n+1}-\xi _{\phi }^{n})/\Delta t\Vert \). This implies the boundedness of \(\Vert \phi _h^{i+1}\Vert _{\infty }\) and \(\Vert (\phi _h^{i+1} - \phi _h^{i})/ (\Delta t) \Vert _{\infty }\), which eventually leads to the estimates for \(\Vert \xi _{p}^{n+1}\Vert \) and \(\Vert \xi _{q}^{n+1}\Vert \).
5.4 Proof of Theorem 7
Proof
We first use mathematical induction to prove \(\Vert \xi _p^{n}\Vert ^2 + \Vert \xi _q^{n}\Vert ^2 \le Ch^{2k+2} + C(\Delta t)^4\) for any \((n+1)\Delta t \le T\). For \(n=0\), there is \(\Vert \xi _p^0\Vert ^2 + \Vert \xi _q^0\Vert ^2 = 0\). Thus the inequality is trivially satisfied. Now suppose \(\Vert \xi _p^{n}\Vert ^2 + \Vert \xi _q^{n}\Vert ^2 \le Ch^{2k+2} + C(\Delta t)^4\) for any \(n \le T/\Delta t - 1\). Then there is
Here we have applied the inverse inequality to the second inequality above. The last inequality above is due to \(h<1\) and \((\Delta t)^2 \le \gamma h^{1/2}\). Similarly, there is \(\Vert q_h^{n} \Vert _{\infty } \le C\). Therefore, Lemma 5.5 leads to
where
Here we have used the inequality \(\Vert (\xi _{\phi }^{n+2} - \xi _{\phi }^{n})/(\Delta t) \Vert ^2 \le 2 \Vert (\xi _{\phi }^{n+2} - \xi _{\phi }^{n+1})/(\Delta t) \Vert ^2 + 2 \Vert (\xi _{\phi }^{n+1} - \xi _{\phi }^{n})/(\Delta t) \Vert ^2\). Suppose we choose sufficiently small \(\Delta t\), such that \(C (\Delta t) \le 1/2\), and denote \(\theta := (1 + C \Delta t)/(1 - C \Delta t)\), it is easy to show that \(1/(1 - C \Delta t) \le 2\) and \(\theta > 1\). Thus, we can rewrite (5.86) as \((1 - C \Delta t) E_{s \phi }^{n+1} - (1 + C \Delta t) E_{s \phi }^{n} \le C \Delta t h^{2k + 2} + C (\Delta t)^5\). We divide both sides of the inequality by \((1-C \Delta t) \theta ^{n+1}\), and sum over n to obtain
where the definition of \(\theta \) and the fact that \(\theta > 1\) have been used. Since \(E_{s \phi }^1 \le C (\Delta t)^4 + C h^{2k+2}\) and \(\theta ^{n+1} = (1 + \frac{2C}{1 - C \Delta t} \Delta t)^{n+1} \le (1 + 4 C \Delta t)^{n+1} \le \exp (4CT)\), inequality (5.88) implies that \(E_{s \phi }^{n+1} \le C (h^{2k+2} + (\Delta t)^4)\), where C also depends on T. That is,
for any \(n \le T/\Delta t - 1\). We can apply (5.89) and use the same argument as we prove \(\Vert p_h^n\Vert _{\infty } \le C\) to show that \(\Vert \phi _h^{i}\Vert _{\infty }\), \(\Vert (\phi _h^{i+1} - \phi _h^{i})/\Delta t\Vert _{\infty } \le C\) for \(i \le n\) and \(\Vert \phi _h^{n+1}\Vert _{\infty }\le C\). Therefore, we have proved the conditions of Lemmas 5.3 and 5.4. Thus we apply (5.84) to (5.83), along with the upper bounds of \(\Vert \phi _h^{i}\Vert _{\infty }\), \(\Vert (\phi _h^{i+1} - \phi _h^{i})/\Delta t\Vert _{\infty }\), \(\Vert \xi _{\phi }^{i} \Vert \) and \(\Vert (\xi _{\phi }^{i+1} - \xi _{\phi }^{i})/\Delta t\Vert \) to get
We then divide both sides of (5.90) by \((1-C \Delta t) \theta ^{n+1}\), and sum over n to get
where \(E_{qp}^{i} = \Vert \xi _q^{i}\Vert ^2 + \Vert \xi _p^{i}\Vert ^2\). Following the previous steps, we know that \(E_{qp}^{0} = 0\), \(\theta ^{n+1} \le \exp (4CT)\) and \(\frac{C \Delta t}{1 - C \Delta t} \sum _{i=1}^{n+1} \frac{1}{\theta ^i} \le \frac{1}{2}\). Thus we get
Since (5.92) is satisfied for any \(n \le T/\Delta t - 1\), we get
Here we have used Young’s inequality and sum of square inequality. Therefore, we can draw the conclusion from (5.93) that \(\Vert \xi _p^{n+1}\Vert ^2 + \Vert \xi _q^{n+1}\Vert ^2 \le Ch^{2k+2} + C(\Delta t)^4\), which concludes the mathematical induction.
Moreover, we can see that \(\Vert \xi _{\phi }^n\Vert \le Ch^{2k+2} + C(\Delta t)^4\) based on our previous discussion. Finally, we complete the proof of this theorem using the approximation property and the triangle inequality. \(\square \)
Remark 5.2
The condition \((\Delta t)^2 \le \gamma h^{1/2}\) is needed to prove the boundedness of numerical solutions, and it is due to the application of the inverse inequality. In order to extend this analysis to higher spatial dimension cases, i.e., \(x \in \mathcal {R}^d\) for \(d=1,2\) or 3, we need \(h^{-d/2} (\Delta t)^2 \le \gamma \), which leads to \((\Delta t)^2 \le \gamma h^{d/2}\). Such a condition is easy to be satisfied if \(\Delta t \sim O(h^{d/4})\).
6 Proofs of some Lemmas in Sections 3 and 5
6.1 Proof of Lemma 3.1
Let \(w_1 = \xi _q\) in Eq. (3.32), \(w_3 = \xi _p\) in Eq. (3.34), and add the two resulting equations, we have
where \(\Lambda _1 = \int _{I} \eta _{q,t} \xi _q dx + \int _{I} \eta _{p,t} \xi _p dx - \int _{I} p_0 \eta _{\phi } \xi _q dx - \int _{I} \phi _0 \eta _p \xi _q dx + \int _{I} \phi _0 \eta _q \xi _p dx + \int _{I} q_0 \eta _{\phi } \xi _p dx\), \(\Lambda _2 = -\int _{I} \xi _u (\xi _q)_x dx - \sum _{j=1}^{N} (\xi _u)_{j+\frac{1}{2}}^{-} [\xi _q]_{j+\frac{1}{2}} + \int _{I} \xi _z (\xi _p)_x dx + \sum _{j=1}^{N} (\xi _z)_{j+\frac{1}{2}}^{-} [\xi _p]_{j+\frac{1}{2}}\), and \(\Lambda _3 = \int _{I} p_0 \xi _{\phi } \xi _q dx - \int _{I} q_0 \xi _{\phi } \xi _p dx\). Using Cauchy–Schwartz inequality, the approximation properties of the Gauss-Radau projections and the fact that \(\Vert p_0\Vert _{\infty }\), \(\Vert q_0\Vert _{\infty }\), \(\Vert \phi _0\Vert _{\infty } \le C\), we can show that \(\Lambda _1 \le C h^{k+1} \left( \Vert \xi _q \Vert + \Vert \xi _p \Vert \right) \). Similarly, it is easy to see \(\Lambda _3 \le C \Vert \xi _{\phi }\Vert \left( \Vert \xi _q\Vert + \Vert \xi _p\Vert \right) \). Therefore, the estimates about \(\Lambda _1\) and \(\Lambda _3\) and the inequality (6.94) lead to
To estimate \(\Lambda _2\), we let \(w_4 = \xi _z\) in (3.35) and \(w_6 = \xi _u\) in (3.37) to get
We then add Eq. (6.96) to the formulation of \(\Lambda _2\) and obtain
We can conclude the proof by applying the estimate about \(\Lambda _2\) from (6.97) to the inequality (6.95), and using Young’s inequality.
6.2 Proof of Lemma 3.2
We first take derivative of Eq. (3.36) with respect to t to obtain
We then let \(w_2 = \xi _{\phi , t}\) in Eq. (3.33), \(w_5 = \xi _s\) in Eq. (6.98), and add these two equations, we have
where \(\Lambda _1 = \int _{I} \eta _{\phi ,tt} \xi _{\phi ,t} dx + \int _{I} \eta _{\phi } \xi _{\phi ,t} dx + \int _{I} \eta _{s,t} \xi _s dx - 2 \int _{I} q_0 \eta _q \xi _{\phi ,t} dx - 2\int _{I} p_0 \eta _p \xi _{\phi ,t} dx\),
\(\Lambda _2 = 2 \int _{I} q_0 \xi _q \xi _{\phi ,t} dx + 2\int _{I} p_0 \xi _p \xi _{\phi ,t} dx\), and \(\Lambda _3 = - \int _{I} \xi _s (\xi _{\phi ,t})_x dx - \int _{I} \xi _{\phi ,t} (\xi _{s})_x dx - \sum _{j=1}^N (\xi _s)_{j+\frac{1}{2}}^{-} [\xi _{\phi ,t}]_{j+\frac{1}{2}} - \sum _{j=1}^N (\xi _{\phi ,t})_{j+\frac{1}{2}}^{+} [\xi _s]_{j+\frac{1}{2}}\). Using the approximation properties of Gauss-Radau projections and the fact that \(\Vert p_0\Vert _{\infty }, \Vert q_0\Vert _{\infty } \le C\), we can show that \(\Lambda _1 \le Ch^{k+1} \left( \Vert \xi _{\phi ,t}\Vert + \Vert \xi _s\Vert \right) \). We can also estimate the bound of \(\Lambda _2\) as \(\Lambda _2 \le C \left( \Vert \xi _q\Vert \Vert \xi _{\phi ,t}\Vert + \Vert \xi _p\Vert \Vert \xi _{\phi ,t}\Vert \right) \le C \left( \Vert \xi _q\Vert ^2 \!+\! \Vert \xi _p\Vert ^2 \!+\! \Vert \xi _{\phi ,t}\Vert ^2 \!\right) \). and show that \(\Lambda _3 = \sum _{j=1}^{N} ( [\xi _s \xi _{\phi ,t}] - (\xi _s)_{j+\frac{1}{2}}^{-} [\xi _{\phi ,t}]_{j+\frac{1}{2}} - (\xi _{\phi ,t})_{j+\frac{1}{2}}^{+} [\xi _s]_{j+\frac{1}{2}} ) = 0\). We further apply the estimates about \(\Lambda _1\), \(\Lambda _2\) and \(\Lambda _3\) to the right side of Eq. (6.99) and conclude the lemma.
6.3 Proof of Lemma 3.3
We take derivative of Eqs. (3.35) and (3.37) with respect to t, and take the sum to get
Let \(w_4 = \xi _{u}\) and \(w_6 = \xi _{z}\) in the equation above, we get
where \(\Lambda _1 = \int _{I} \eta _{u,t} \xi _u \, dx + \int _{I} \eta _{z,t} \xi _z \, dx\), and \(\Lambda _2 = -\int _{I} \xi _{p,t} (\xi _u)_x \, dx -\int _{I} \xi _{q,t} (\xi _z)_x dx -\sum _{j=1}^N (\xi _{p,t})_{j+\frac{1}{2}}^{+} [\xi _u]_{j+\frac{1}{2}} -\sum _{j=1}^N (\xi _{q,t})_{j+\frac{1}{2}}^{+} [\xi _z]_{j+\frac{1}{2}}\).
It is easy to show that \(\Lambda _1 \le Ch^{k+1} \left( \Vert \xi _u\Vert + \Vert \xi _z\Vert \right) \). To estimate the term \(\Lambda _2\), we let \(w_1 = \xi _{p,t}\) in Eq. (3.32) and \(w_3 = \xi _{q,t}\) in Eq. (3.34). Thus we can show that
where
We then add the formulation of \(\Lambda _2\) and (6.101). Due to the property of jumps (2.5), we get \(\Lambda _2 = \Lambda _3\). Using this equation and the estimate of \(\Lambda _1\) in (6.100), we can obtain
For any \(\tau \in [0,T]\), we take the time integral of the inequality above from 0 to \(\tau \), and get
where
and
We first estimate the upper bound of \(\Lambda _{31}\). For the term \(\int _{0}^{\tau } dt \int _{I} \eta _{q,t} \xi _{p,t} \, dx\), we can show
In a similar manner, we can get \(- \int _{0}^{\tau } dt \int _{I} \eta _{p,t} \xi _{q,t} \, dx \le C h^{k+1} \displaystyle \max _{t \in [0,T]} \Vert \xi _{q,t}\Vert \). Since the functions \(p_0\), \(q_0\) and \(\phi _0\) only depend on x and \(\Vert p_0\Vert _{\infty }\), \(\Vert q_0\Vert _{\infty }\), \(\Vert \phi _0\Vert _{\infty } \le C\), we can also use the same method to estimate the upper bounds of the terms \(\int _{0}^{\tau } dt \int _{I} p_0 \eta _{\phi } \xi _{p,t} \, dx\), \(\int _{0}^{\tau } dt \int _{I} \phi _0 \eta _p \xi _{p,t} \, dx\), \(\int _{0}^{\tau } dt \int _{I} \phi _0 \eta _q \xi _{q,t} \, dx\) and \(\int _{0}^{\tau } dt \int _{I} q_0 \eta _{\phi } \xi _{q,t} \, dx\). Eventually, one can get the following estimate of \(\Lambda _{31}\):
Here we have used Young’s inequality and the fact that C is a generic constant.
Next, we estimate the upper bound of \(\Lambda _{32}\). For the term \(\int _{0}^{\tau } dt \int _{I} p_0 \xi _{\phi } \xi _{p,t} \, dx\), we apply integration by parts to get
Similarly, there is also the following estimate
To estimate \(\int _{0}^{\tau } dt \int _{I} {\phi }_0 \xi _{p} \xi _{p,t} \, dx\), there is
Similarly, there is
We combine the inequality (6.108)-(6.111), and apply these estimates to (6.105) to get
Note that we have used the fact that C is a generic constant.
Now we combine the estimates from (6.107) and (6.112), thus the inequality (6.103) leads to
Here we have applied Young’s inequality in the last inequality above. Since the inequality above is satisfied for all \(\tau \in [0,T]\), we have
Due to the fact that \(\displaystyle \max _{t\in [0,T]} \left( \Vert \xi _u\Vert ^2 + \Vert \xi _z\Vert ^2\right) \ge \left( \max _{t\in [0,T]} (\Vert \xi _u\Vert + \Vert \xi _z\Vert ) \right) ^2/2\), we get
It is easy to see that the inequality above is equivalent to the conclusion of the lemma.
6.4 Proof of Lemma 5.3
We first apply the jump property (2.5) to the term \(\Theta _1\) in (5.82), and it is easy to see that \(\Theta _1 = 0\).
Next, we consider the term \(\Theta _2\) and obtain
Here we have used Cauchy–Schwartz inequality in the first inequality above, Lemmas 5.1 and 5.2 in the second inequality, and Young’s inequality in the third inequality above.
In order to get an upper bound for \(\Theta _3\), we start by rewriting
Similarly, we can show that
Therefore, we can combine the two equalities above and the definition of \(\Theta _3\) to get
Here we have used Cauchy–Schwartz inequality, and the approximation property in the first and second inequality, respectively. We have also applied Young’s inequality in the last inequality above. Note that the generic constant C in the estimate of \(\Theta _3\) depends on \(\Vert p^{n+1}\Vert _{\infty }\), \(\Vert q^{n+1}\Vert _{\infty }\), \(\Vert p^{n}\Vert _{\infty }\) and \(\Vert q^{n}\Vert _{\infty }\). We conclude this proof by combining (6.114), (6.115) and the fact that \(\Theta _1 = 0\).
6.5 Proof of Lemma 5.4
First we can show the following equation which can be derived similar to (5.77) and (5.78).
Let \(w_3 = \xi _u^{n+1} + \xi _u^n\) and \(w_4 = \xi _z^{n+1} + \xi _z^n\) in (6.116), we have
To estimate the right side of the equality above, we further let \(w_1 = 2(\xi _p^{n+1} - \xi _p^n)\) and \(w_2 = -2(\xi _q^{n+1} - \xi _q^n)\) in (5.75) and (5.76), respectively, and add these equations to get
Adding (6.117) and (6.118) over n, and applying (2.5), one has
where
and
To estimate \(\Lambda _1\), we first denote each line of the right side of \(\Lambda _1\) as \(\Lambda _{11}\) and \(\Lambda _{12}\). \(\Lambda _{11}\) can be estimated by applying Cauchy–Schwartz inequality, Lemma 5.2 and the fact that \((n+1)(\Delta t ) \le T\),
We then apply summation-by-parts formula (5.81) and Lemma 5.2 to \(\Lambda _{12}\) and get
Now we combine the estimates for \(\Lambda _{11}\) and \(\Lambda _{12}\) and can get
For \(\Lambda _2\), using summation-by-parts and Lemma 5.1, we have
For \(\Lambda _3\), we denote each line of the right side of \(\Lambda _3\) as \(\Lambda _{31}\) and \(\Lambda _{32}\). To estimate \(\Lambda _{31}\), we first rewrite
We then apply the equality above to \(\Lambda _{31}\), and have
Using summation-by-parts and Cauchy–Schwartz inequality, we can estimate \(\Lambda _{311}\) as
We then estimate the upper bound of \(\Lambda _{312}\). We define \(f_i := (\phi _h^{i+1} + \phi _h^{i}) (\eta _p^{i+1} + \eta _p^{i})\) and \(g_i := \xi _p^i\) in the summation-by-parts formula (5.81), so that \(\Lambda _{312}\) leads to
Note that \((\phi _h^{i+1} + \phi _h^{i}) (\eta _p^{i+1} + \eta _p^{i}) - (\phi _h^{i} + \phi _h^{i-1}) (\eta _p^{i} + \eta _p^{i-1}) = (\phi _h^{i+1} - \phi _h^{i-1}) (\eta _p^{i+1} + \eta _p^{i}) + (\phi _h^{i} + \phi _h^{i-1}) (\eta _p^{i+1} - \eta _p^{i-1})\), we can estimate the last integral term in \(\Lambda _{312}\) as follows,
The first inequality above is due to Lemma 5.2 and Cauchy–Schwartz inequality, and the second inequality is based on the fact \( n \Delta t \le T\). We combine the estimate above and get
Using the same method as we estimated \(\Lambda _{312}\), we can derive the following inequality for \(\Lambda _{313}\),
The estimate of \(\Lambda _{314}\) is quite similar to that for \(\Lambda _{313}\). It is easy to show that
where we have used the approximation property and Lemma 5.2. Now we combine the estimates for \(\Lambda _{311}\), \(\Lambda _{312}\), \(\Lambda _{313}\) and \(\Lambda _{314}\), and can get the estimate for \(\Lambda _{31}\). That is,
Since the formulation of \(\Lambda _{32}\) is the same as \(\Lambda _{31}\) if q and p are switched, we can estimate \(\Lambda _{3}\) as
With the estimates for \(\Lambda _i\), \(i=1,2,3\), we can finally get the upper bound of \((\Vert \xi _u^{n+1} \Vert + \Vert \xi _z^{n+1} \Vert )^2\),
Since the inequality above is satisfied for all \(n+1 \le T/(\Delta t)\), we can further take the maximum of the left hand side and apply Young’s inequality to the the term \(C h^{k+1} \max _{i} (\Vert \xi _u^i\Vert + \Vert \xi _z^i\Vert )\). The resulting inequality combined with the fact that \(\max _{i} \Vert (\phi _h^{i+1} - \phi _h^{i-1})/(\Delta t) \Vert _{\infty } \le 2 \max _{i} \Vert (\phi _h^{i+1} - \phi _h^{i})/(\Delta t) \Vert _{\infty }\) and \(\max _{i} \Vert (\xi _{\phi }^{i+1} - \xi _{\phi }^{i-1})/(\Delta t) \Vert \le 2 \max _{i} \Vert (\xi _{\phi }^{i+1} - \xi _{\phi }^{i})/(\Delta t) \Vert \) eventually leads to (5.84).
6.6 Proof of Lemma 5.5
We take \(w_5 = \xi _{\phi }^{n+2} - \xi _{\phi }^{n} = (\xi _{\phi }^{n+2} - \xi _{\phi }^{n+1}) + (\xi _{\phi }^{n+1} - \xi _{\phi }^{n})\) in (5.79) and \(w_6 = \frac{1}{2} (\xi _s^{n+2} + \xi _s^n)\) in (5.80), sum them up and obtain the energy equation
where \(\Lambda _1 =- \frac{1}{2} \int _{I} (\xi _s^{n+2} + \xi _s^{n}) (\xi _{\phi }^{n+2} - \xi _{\phi }^{n})_x dx - \frac{1}{2} \sum _{j=1}^{N} \left( \xi _s^{n+2} + \xi _s^{n} \right) _{j+\frac{1}{2}}^{-} [\xi _{\phi }^{n+2} - \xi _{\phi }^{n}]_{j+\frac{1}{2}} - \frac{1}{2} \int _{I} (\xi _{\phi }^{n+2} - \xi _{\phi }^{n}) (\xi _{s}^{n+2} + \xi _{s}^{n})_x dx - \frac{1}{2} \sum _{j=1}^{N} \left( \xi _{\phi }^{n+2} + \xi _{\phi }^{n} \right) _{j+\frac{1}{2}}^{+} [\xi _{s}^{n+2} + \xi _{s}^{n}]_{j+\frac{1}{2}}\), \( \Lambda _2 = \int _{I} \frac{\eta _{\phi }^{n+2} - 2 \eta _{\phi }^{n+1} + \eta _{\phi }^{n}}{(\Delta t)^2} (\xi _{\phi }^{n+2} - \xi _{\phi }^{n}) dx + \frac{1}{2} \int _{I} (\eta _{\phi }^{n+2} + \eta _{\phi }^{n}) (\xi _{\phi }^{n+2} - \xi _{\phi }^{n}) dx - \int _{I} T_{\phi }^{n+1} (\xi _{\phi }^{n+2} - \xi _{\phi }^{n}) dx + \frac{1}{2} \int _{I} (\eta _{s}^{n+2} - \eta _{s}^{n}) (\xi _{s}^{n+2} + \xi _{s}^{n}) dx\), and \( \Lambda _3 = \int _{I} \Big ( (p_h^{n+1})^2 + (q_h^{n+1})^2 - (p^{n+1})^2 - (q^{n+1})^2 \Big ) (\xi _{\phi }^{n+2} - \xi _{\phi }^{n}) dx\).
Applying (2.5) to \(\Lambda _1\), one has \(\Lambda _1 = 0\). For \(\Lambda _2\), using Lemmas 5.1 and 5.2, we have
We then estimate \(\Lambda _3\) as below.
We now combine the estimates for \(\Lambda _1\), \(\Lambda _2\) and \(\Lambda _3\), and conclude this lemma.
7 Numerical experiments
In this section, we demonstrate the performance of our schemes by the solitary wave solutions:
7.1 Accuracy test
We first compute the convergence order of our schemes using the solitary wave solutions at \(T=0.1\). The initial conditions are set to be \(p(x, 0) = 3 {{\,\mathrm{sech}\,}}^2(x) \cos (-\frac{\sqrt{3}}{4} x)\), \(q(x, 0) = 3 {{\,\mathrm{sech}\,}}^2(x) \sin (-\frac{\sqrt{3}}{4} x)\), \(\phi (x,0) = 6 {{\,\mathrm{sech}\,}}^2(x)\) and \(\phi _t(x,0) = -6\sqrt{3} {{\,\mathrm{sech}\,}}^2(x) \tanh (x)\). The computational domain is \(I = [-32, 32]\). The initial mesh is generated by uniformly partitioning the domain I into 64 elements, and then the mesh is further partitioned twice uniformly. Recall that we have proved that each choice of the numerical fluxes in Remark 2.1 can lead to energy and Hamiltonian conservation. Here we choose flux 2 for our accuracy tests. The numerical results using other choices of numerical fluxes are similar, and thus we omit the discussion. In Table 1 and 2, \(L^2\) errors and convergence orders are presented for our proposed methods. The time step size \(\Delta t = 10^{-4}\) is used for the results in Table 1 so that the spatial errors dominate. \(p_h\), \(q_h\) and \(\phi _h \in V_h^k\) for \(k=1, 2, 3\) are used as the approximation spaces. For each k, we start with the simulation when \(N=64\) elements are used, that is, the uniform mesh size is \(h=1\). We then halve the spatial mesh size h for three times and estimate the convergence rates. In particular, for a given k, suppose the \(L^2\) errors of \(p_h\) at mesh size h and h / 2 are \(E_1\) and \(E_2\), respectively, then the convergence order can be estimated by \(\log _2(E_1/E_2)\). The convergence orders for other cases are computed in the same way. From Table 1, we observe the optimal \((k+1)\)th order of convergence for \(k=1, 2, 3\), which is consistent with our results of error estimates. From Table 2, we can see the \(2^{nd}\) order convergence in time.
Note that the \(L^2\) errors of \(p_h\), \(q_h\) and \(\phi _h\) when \(k=2\) and mesh size \(h=1\) are used, are slightly smaller than that when \(k=1\) and mesh size \(h/2 = 1/2\) are used. From our numerical experiments, we also find that the former choice of k and h leads to less computational time than the latter. In fact, when we use our schemes described in Sect. 4.1 to solve the KGS equations, at each time level \(t = t_{n+1}\) (\(n \ge 2\)), we need to update \(\phi _h^{n+1}\) by solving a linear system which has \((k+1)N\) unknowns, and then update \(p_h^{n+1}\) and \(q_h^{n+1}\) by solving another a linear system which has \(2(k+1)N\) unknowns. Here k is the degree of the piecewise polynomial basis and N is the number of elements. In our implementation, we choose the scaled monomial basis, so that the coefficient matrices of the linear systems that we need to solve in order to update \(\phi ^{n+1}\) will be the same for any \(n \ge 2\), if k is fixed and uniform spatial mesh is used. Therefore, one just needs to compute the LU factorization of the coefficient matrix once and store it. However, we cannot follow this idea to compute \(p_h^{n+1}\) and \(q_h^{n+1}\), since their corresponding coefficient matrices also depend on \(\phi _h^{n+1}\), which is a function of t. Thus, the dominant computational cost is from solving the linear systems for \(p_h^{n+1}\) and \(q_h^{n+1}\) at each time level. For a fixed number of time step, such computational cost is around \(O((k+1)^3 N^3)\) flops. When \(k=1\), \(N=N_0\), such number is equal to \(8N_0^3\), whereas when \(k=2\) and \(N=N_0/2\), that number becomes \(27 N_0^3/8\) which is less than a half of \(8N_0^3\). This result indicates that the asymptotic computational time of the schemes when piecewise quadratic polynomial basis with N elements is used, is less than half of the computational time when piecewise linear polynomial basis with 2N elements is used. Numerically, we also see this conclusion for \(N=128\), 256 and 512 when \(k=1\), and for \(N=64\), 128 and 256 when \(k=2\). Moreover, from Table 1, we observe that \(k=2\) with mesh size h always leads to smaller error than the case when \(k=1\) with mesh size h / 2. Therefore, considering all the discussions above, we can draw the conclusion that our proposed numerical schemes with \(p_h\), \(q_h\), \(\phi _h \in V_h^2\) and mesh size h perform better than the methods with \(p_h\), \(q_h\), \(\phi _h \in V_h^1\) and mesh size h / 2, in terms of the \(L^2\) errors and computational time. Similarly, we also see that our schemes with \(k=3\) and mesh size \(h/2^i\) lead to more accurate numerical solutions with less computational time, compared to the schemes with \(k=2\) and mesh size \(h/2^{i+1}\) for \(i=1,2\). Such results demonstrate the advantage of our proposed schemes, i.e., providing accurate solutions with relative coarse mesh.
Time history of the relative error in the total energy and Hamiltonian with \(V_h^2\) basis, \(h=1/8\) and \(\Delta t = 10^{-4}\). Flux 2 (\(\widehat{u_h} = u_h^{-}\), \(\widehat{p_h} = p_h^{+}\), \(\widehat{q_h} = q_h^{+}\), \(\widehat{z_h}=z_h^{-}\), \(\widehat{\phi _h}=\phi _h^{+}\), \(\widehat{s_h}=s_h^{-}\)) is used.
7.2 Energy and Hamiltonian conservation
From the previous section, we have seen the high-order accuracy of our proposed schemes. We now check the conservation properties of the schemes by the simulations of the solitary wave solutions (7.120). As indicated in Theorems 1 and 2, the energy and Hamiltonian are preserved exactly for our semi-discrete schemes. Also note that these theorems are independent of the degree of piecewise polynomial space. Therefore, here we only present the simulations when \(V_h^2\) basis is used. We take the same initial conditions and computational domain as in the accuracy tests. Moreover, we use uniform spatial mesh size \(h = 1/8\) (\(N=512\)) and time step size \(\Delta t = 10^{-4}\) to run the simulation up to \(T=2\), and compute the energy and Hamiltonian at each discrete time \(t^n\) in the following form:
Note that we have applied the second order centered difference to approximate \(\phi _{h,t}\) at \(t^n\) in the semi-discrete form of Hamiltonian. The relative error in the total energy and Hamiltonian is presented in Fig. 1. Here, the relative error in the total energy at each time \(t^n\) is defined with respect to the initial total energy at time \(t=0\). The relative error in the Hamiltonian is defined similarly. The relative error in the energy is at the magnitude of \(10^{-14}\) (see Fig. 1a) over the period of \(2 \times 10^4\) time steps. This implies that the total energy is preserved up to machine epsilon in the relative error, which verifies the result from Theorem 1. Figure 1b shows the relative error in the Hamiltonian. We observe that the relative error in the Hamiltonian is at the magnitude of \(10^{-11}\). According to Theorem 2, the semi-discrete form of the Hamiltonian is conserved exactly. However, our full discrete form of the Hamiltonian leads to an error of \(O(\Delta t)^2\), which causes the Hamiltonian to be conserved only up to around \(O(\Delta t)^2\). Our numerical results in Fig. 1b show that the Hamiltonian is preserved up to \(10^{-10}\), which is less than \((\Delta t)^2\). Thus, our numerical results are consistent with Theorem 2. At \(t=10\), the relative error in the total energy and Hamiltonian is \(2.1714 \times 10^{-12}\) and \(-6.0114 \times 10^{-9}\), respectively.
If we choose non-preserving fluxes, e.g. \(\widehat{u_h} = u_h^{+}\), \(\widehat{p_h} = p_h^{-}\), \(\widehat{q_h} = q_h^{+}\), \(\widehat{z_h}=z_h^{-}\), \(\widehat{\phi _h}=\phi _h^{-}\), \(\widehat{s_h}=s_h^{-}\), we can observe the numerical solutions to blow up. According to Remark 2.1 in Sect. 2, there are other choices of numerical fluxes. Here we present the relative errors for the other three choices in Fig. 2, and the results with central flux are given in Fig. 3. For all five choices of numerical fluxes, the relative errors of total energy are at the magnitude of \(10^{-14}\). If we compare the relative errors of Hamiltonian up to \(T=2\), flux 2 leads to the best results, followed by flux 4, flux 3, central flux and flux 1, in the increasing order of absolute relative errors. The time evolution of \(|\psi |^2 = p^2 + q^2\) and \(\phi \) for solitary wave can be seen in Fig. 4. It is very clear that our numerical solution can capture the behavior of solitary wave.
7.3 Dispersion and dissipation
The dispersion and dissipation properties of numerical methods are crucial for wave simulations. In this section, we discuss the dispersion and dissipation behavior of our proposed methods. The computational domain is still \([-32, 32]\) in space, with the same initial conditions and time step size \(\Delta t = 10^{-4}\). We run the simulations up to \(T = 2\). The numerical solutions with \(h = 1/8\) at T are presented in Fig. 5. Note that the exact solution \(\phi \) is a solitary wave with amplitude 6. When \(T=2\), the maximum of \(\phi \) is achieved at \(x = -\sqrt{3}\). The dissipation error is the absolute value of the difference in the amplitude between \(\phi \) and \(\phi _h\), and the dispersion error is the absolute value of the difference in the phase. To compute these two errors, we need to find the maximum of \(\phi _h\) and the location where it obtains such maximum. When \(N=512\), we find that the maximum is obtained in the 243th element. In Fig. 6a, the zoomed-in numerical solution of \(\phi _h\) at \(T=2\) is presented. The two dashed lines represent two interior element boundaries. Even though the numerical solution \(\phi _h\) has discontinuity at element boundaries, it is not visible at this scale. It is easy to show that \(\phi _h\) obtains its maximum 5.9999891 at \(x = -1.7320543\). Therefore, the dispersion error when \(N=512\) is \(3.4768 \times 10^{-6}\) and the dissipation error is \(1.0855 \times 10^{-5}\). When \(N=256\), we find that the maximum is obtained in the 122th element. Figure 6b shows the zoomed-in \(\phi _h\) for this case. Using the same method, we compute that the dispersion error when \(N=256\) is \(5.4107 \times 10^{-4}\) and the dissipation error is \(1.6452 \times 10^{-4}\).
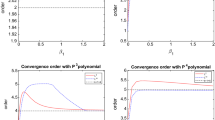
We further compute the dispersion and dissipation errors for various choice of N. To estimate the order of dispersion error, we assume the dispersion error \(E_{disp} = Ch^{r}\) where C is a positive constant. Thus, there is \(\log _{10} E_{disp} = r \log _{10}h + \log _{10}C\). To approximate the order r, we use several points of \((\log _{10}h, \log _{10} E_{disp})\) with different h to fit a straight line whose slope is the approximation of r. The order of dissipation error \(E_{diss}\) can be obtained in the same manner. The least square fitting lines of dispersion and dissipation errors in log-log plot are presented in Fig. 7. Our numerical results show that the orders of dispersion and dissipation errors are about 4.6 and 4.1, respectively. Therefore, we have found that our proposed methods also lead to numerical solutions with high-order accuracy in dispersion and dissipation behavior.
8 Concluding remarks
In this paper, high-order energy and Hamiltonian-preserving local discontinuous Galerkin methods are proposed for the Klein–Gordon–Schrödinger equations. By choosing suitable numerical fluxes, we can prove that the energy and Hamiltonian for the semi-discrete numerical solutions are exactly conserved. Due to the fact that there is \(\phi _{t}\) term in the formulation of Hamiltonian, we apply second-order centered difference to approximate such term numerically. Results of numerical simulations up to \(2\times 10^4\) time steps show that the energy is conserved up to machine epsilon and the Hamiltonian is conserved up to the magnitude of \(10^{-10}\). Moreover, such choices of numerical fluxes lead to optimal convergence order of \((k+1)\) for \(q_h\), \(p_h\) and \(\phi _h\), if \(q_h\), \(p_h\), \(\phi _h \in V_h^{k}\). Since DG methods also have high order accuracy in dispersion and dissipation errors [26], we further compute the convergence order of such errors and verify the high order accuracy of our solitary wave solution.
References
Bao, W., Su, C.: Uniform error estimates of a finite difference method for the Klein-Gordon-Schrödinger system in the nonrelativistic and massless limit regimes. Kinet. Relat. Mod. 11, 1037–1062 (2018)
Bao, W., Yang, L.: Efficient and accurate numerical methods for the Klein–Gordon–Schrödinger equations. J. Comput. Phys. 225, 1863–1893 (2007)
Bao, W., Zhao, X.: A uniformly accurate multiscale time integrator Fourier pseudospectral method for the Klein–Gordon–Schrödinger equations in the nonrelativistic limit regime. Numer. Math. 135, 833–873 (2017)
Cai, W., Sun, Y., Wang, Y., Zhang, H.: Local discontinuous Galerkin methods based on the multisymplectic formulation for two kinds of Hamiltonian PDEs. Int. J. Comput. Math. 95, 114–143 (2018)
Cai, J., Hong, J., Wang, Y.: Local energy and momentum-preserving schemes for Klein–Gordon–Schrödinger equations and convergence analysis. Numer. Methods Partial Differ. Eq. 33, 1329–1351 (2017)
Chou, C.-S., Sun, W., Xing, Y., Yang, H.: Local discontinuous Galerkin methods for the Khokhlov–Zabolotskaya–Kuznetzov equation. J. Sci. Comput. 73, 593–616 (2017)
Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35, 2440–2463 (1998)
Dehghan, M., Mohammadi, V.: Two numerical meshless techniques based on radial basis functions (RBFs) and the method of generalized moving least squares (GMLS) for simulation of coupled Klein-Gordon-Schrödinger (KGS) equations. Comput. Math. Appl. 71, 892–921 (2016)
Dehghan, M., Taleei, A.: Numerical solution of the Yukawa-coupled Klein-Gordon-Schrödinger equations via a Chebyshev pseudospectral multidomain method. Appl. Math. Model. 36, 2340–2349 (2012)
Fukuda, I., Tsutsumi, M.: On coupled Klein–Gordon–Schrödinger equations II. J. Math. Anal. Appl. 66, 358–378 (1978)
Hong, J., Ji, L., Liu, Z.: Optimal error estimate of conservative local discontinuous Galerkin method for nonlinear Schrödinger equation. Appl. Numer. Math. 127, 164–178 (2018)
Hong, J., Jiang, S., Li, C.: Explicit multi-symplectic methods for Klein–Gordon–Schrödinger equations. J. Comput. Phys. 228, 3517–3532 (2009)
Hong, Q., Wang, Y., Wang, J.: Optimal error estimate of a linear Fourier pseudo-spectral scheme for two dimensional Klein–Gordon–Schrödinger equations. J. Math. Anal. Appl. 468, 817–838 (2018)
Kong, L., Chen, M., Yin, X.: A novel kind of efficient symplectic scheme for Klein–Gordon–Schrödinger equation. Appl. Numer. Math. 135, 481–496 (2019)
Kong, L., Zhang, J., Cao, Y., Duan, Y., Huang, H.: Semi-explicit symplectic partitioned Runge-Kutta Fourier pseudo-spectral scheme for Klein–Gordon–Schrödinger equations. Comput. Phys. Comm. 181, 1369–1377 (2010)
Liang, H.: Linearly implicit conservative schemes for long-term numerical simulation of Klein–Gordon–Schrödinger equations. Appl. Math. Comp. 238, 475–484 (2014)
Shimomura, A.: Wave operators for the coupled Klein–Gordon–Schrödinger equations in two space dimensions. Funkc. Ekvac. 47, 63–82 (2004)
Wang, J., Wang, Y., Liang, D.: Analysis of a Fourier pseudo-spectral conservative scheme for the Klein–Gordon–Schrödinger equation. Int. J. Comput. Math. 95, 36–60 (2018)
Wang, S., Zhang, L.: A class of conservative orthogonal spline collocation schemes for solving coupled Klein–Gordon–Schrödinger equations. Appl. Math. Comput. 203, 799–812 (2008)
Wang, T., Zhao, X., Jiang, J.: Unconditional and optimal \(H^2\)-error estimates of two linear and conservative finite difference schemes for the Klein–Gordon–Schrödinger equation in high dimensions. Adv. Comput. Math. 44, 477–503 (2018)
Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for two classes of two-dimensional nonlinear wave equations. Phys. D 208, 21–58 (2005)
Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for high-order time-dependent partial differential equations. Commun. Comput. Phys. 7, 1–46 (2010)
Yan, J., Shu, C.-W.: A local discontinuous Galerkin method for KdV-type equations. SIAM J. Numer. Anal. 40, 769–791 (2002)
Yan, J., Shu, C.-W.: Local discontinuous Galerkin methods for partial differential equations with higher order Derivatives. J. Sci. Comput. 17, 27–47 (2002)
Yang, H., Li, F.: Error estimates of Runge–Kutta discontinuous Galerkin methods for the Vlasov–Maxwell system. ESAIM Math. Model. Numer. Anal. 49, 69–99 (2015)
Yang, H., Li, F., Qiu, J.: Dispersion and dissipation errors of two fully discrete discontinuous Galerkin methods. J. Sci. Comput. 55, 552–574 (2013)
Yang, Y., Shu, C.-W.: Analysis of optimal superconvergence of discontinuous Galerkin methods for linear hyperbolic equations. SIAM J. Numer. Anal. 50, 3110–3133 (2012)
Zhang, J., Kong, L.: New energy-preserving schemes for Klein–Gordon–Schrödinger equations. Appl. Math. Model. 40, 6969–6982 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Yang, H. Error estimates for a class of energy- and Hamiltonian-preserving local discontinuous Galerkin methods for the Klein–Gordon–Schrödinger equations. J. Appl. Math. Comput. 62, 377–424 (2020). https://doi.org/10.1007/s12190-019-01289-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-019-01289-4
Keywords
- Error estimates
- Local discontinuous Galerkin methods
- Energy conservation
- Hamiltonian-preserving
- Klein–Gordon–Schrödinger equations