Mass-, and Energy Preserving Schemes with Arbitrarily High Order for the Klein–Gordon–Schrödinger Equations

Abstract

We present a class of arbitrarily high-order conservative schemes for the Klein–Gordon Schrödinger equations. These schemes combine the symplectic Runge–Kutta method with the quadratic auxiliary variable approach. We first introduce an auxiliary variable that satisfies a quadratic equation to reformulate the original system into an equivalent one. This reformulated system possesses two strong quadratic invariants: energy and mass. Next, we discretize the reformulated system using symplectic Runge–Kutta methods, yielding a class of semi-discrete systems with arbitrarily high-order accuracy in time. The semi-discrete systems naturally preserve the discrete contour part of the strong invariants and the relationship of the quadratic equation. By eliminating the intermediate variable, we obtain the original energy conservation law. Then, the Fourier pseudo-spectral method is employed to obtain the fully discrete scheme that preserves the original energy and mass. We provide a fast solver to implement the proposed methods effectively. Numerical experiments demonstrate the expected accuracy and conservation of proposed schemes.

1 Introduction

In this paper, we consider the following Klein–Gordon–Schrödinger (KGS) equations [2]

$$\begin{aligned} \left\{ \begin{aligned}&\text {i}\partial _{t}\psi ({{x}},t)+\frac{1}{2}\varDelta \psi ({{x}},t)+ u({{x}},t)\psi ({{x}},t)=0,\quad (x,t)\in \varOmega \times (0,T]\\&\partial _{tt}u({{x}},t) -\varDelta u({{x}},t)+u({{x}},t)-|\psi ({{x}},t)|^2=0,\quad (x,t)\in \varOmega \times (0,T] \end{aligned}\right. \end{aligned}$$

(1.1)

equipped with the following initial conditions

$$\begin{aligned} \psi ({{x}},0)=\psi _{0}({{x}}),\ \ u({{x}},0)=u_{0}( {{x}}),\ \ u_{t}({{x}},0)={u}_{1}({{x}}),\quad x\in \varOmega , \end{aligned}$$

where $\text {i}^2=-1$, $\varOmega \subset {\mathbb {R}}^d~(d=1,2)$. The solutions $\psi ({{x}},t)$ and u(x, t) of the KGS equations are complex and real valued functions with periodic boundary conditions, respectively. By introducing $\psi =p+\text {i}q$, $u_t=v$, the KGS Eq. (1.1) can be reformulated as a first-order real valued system as follows:

$$\begin{aligned} \left\{ \begin{aligned}&p_t=-\frac{1}{2}\varDelta q-qu \\&q_t=\frac{1}{2}\varDelta p+pu, \\&u_t=v, \\&v_t=\varDelta u-u+p^2+q^2. \end{aligned}\right. \end{aligned}$$

(1.2)

It is readily to verify that the KGS system (1.2) preserves the mass and energy conservation laws, i.e.,

$$\begin{aligned} \frac{d}{dt}{\mathcal {M}}(t)=0,\quad \text{ with }\quad {\mathcal {M}}(t)=\int _{\varOmega }(p^2+q^2) d{{x}}, \end{aligned}$$

(1.3)

and

$$\begin{aligned} \frac{d}{dt}{\mathcal {H}}(t)=0,\quad \text{ with }\quad {\mathcal {H}}(t)=\int _{\varOmega }\Big ( |\nabla p|^2+|\nabla q|^2+|\nabla u|^2+u^2+v^2-2 u (p^2+q^2)\Big )d{{x}}.\nonumber \\ \end{aligned}$$

(1.4)

In fact, by applying the energy variational principle, we can rewrite (1.2) into a compact infinite-dimensional Hamiltonian system as follows:

$$\begin{aligned} \frac{d z}{d t}={\mathcal {S}} \frac{\delta {\mathcal {H}}}{\delta z},\ \ \ \text {with}\ \ {\mathcal {S}}=\left( \begin{array}{cccc} 0 &{} \frac{1}{4} &{}0&{}0 \\ -\frac{1}{4} &{} 0&{}0&{}0\\ 0 &{} 0 &{}0&{}\frac{1}{2} \\ 0 &{} 0&{}-\frac{1}{2}&{}0 \end{array}\right) , \end{aligned}$$

(1.5)

where $z=(p,q,u,v)^T$ and $\frac{\delta {\mathcal {H}}}{\delta z}$ represents the vector of variational derivatives [10] given by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\delta {\mathcal {H}}}{\delta p}=-2\varDelta p-4pu,\\&\frac{\delta {\mathcal {H}}}{\delta q}=-2\varDelta q-4qu,\\&\frac{\delta {\mathcal {H}}}{\delta u}=-2\varDelta u+2u-2r,\\&\frac{\delta {\mathcal {H}}}{\delta v}=2v. \end{aligned}\right. \end{aligned}$$

(1.6)

To gain deeper insights into the wave propagation and interaction of the KGS equations, it is essential to develop efficient and accurate numerical methods, as analytical solutions of (1.1) are usually unavailable. Theoretical and experimental results consistently highlight the superiority of methods that preserve the invariants of the original system, exhibiting favorable numerical characteristics such as linear error growth, long-term stability, and reduced amplitude. These methods are commonly referred to as structure-preserving algorithms [8, 20, 22, 27]. Over the past few years, significant progress has been made in developing structure-preserving methods. These advancements include the discrete gradient methods [16], the averaged vector field methods [23], and Crank-Nicolson methods [19, 35]. Specifically for the KGS equations, authors have proposed a series of conservative schemes based on the Crank-Nicolson/leap-frog methods [3, 7, 17, 33, 34], and the partitioned averaged vector field methods [6].

However, the above methods are limited to second-order accuracy and fail to meet the precision requirements for long-time simulations. It is well-known that high-order structure-preserving algorithms have higher-accuracy and improved stability for long-time simulations. Therefore, constructing and analyzing high-order structure-preserving algorithms for KGS systems are desirable. Over the past decade, several methods have been used to construct high-order energy-preserving methods for conservative systems, such as the Hamiltonian boundary value (HBVM) methods [4] and the sixth-order average vector field method [23]. These schemes can effectively preserve the original energy, but generally cannot simultaneously preserve the mass and their construction is quite complex. Recently, researchers have proposed invariant quadratization methods (IEQ) [37, 38] and auxiliary variable (SAV) [30, 31] for gradient flows. By combining the symplectic Runge–Kutta (RK) methods [26, 32] with these methods, high-order energy-preserving methods for conservative systems can be obtained [10, 11, 21, 28, 36]. However, the resulting schemes can only preserve the modified energy.

Inspired by the energy quantization method, Gong et al. developed the quadratic auxiliary variable (QAV) technique in [12] for the Korteweg-de Vries equation. Different from the previous IEQ and SAV schemes, the newly proposed schemes inherit the original energy of the system. However, this method has not been utilized to construct high-order conservative schemes for coupled systems or high-dimensional problems. This paper aims to develop a class of high-order schemes for the KGS Eq. (1.1) using the symplectic RK method and the QAV technique. The proposed schemes enjoy the following distinct advantages:

• The first advantage is that when combined with Fourier pseudo-spectral for spatial discretization, these schemes achieve high accuracy in both time and space;

• Another advantage is that these schemes not only preserve the original energy but also conserve the mass of the KGS systems;

• Despite being fully implicit, the proposed schemes are more efficient than the HBVM method in practical numerical simulations.

Additionally, the proposed methods can also be extended to develop high-order structure-preserving algorithms for other conservative systems.

The outline of this paper is as follows. In Sect. 2, an equivalent system with three invariants is obtained by introducing a new auxiliary variable. In Sect. 3, the modified system is discretized using the symplectic Runge–Kutta method, resulting in a semi-discrete system that preserves all the invariants of the reformulated system. The fully discrete system is obtained by employing the Fourier pseudo-spectral method for spatial discretizaion, which are proved to preserve both original energy and mass at a discrete level in Sect. 4. Section 5 presents a fast solver for the proposed methods. Numerical results in Sect. 6 are provided to confirms our theoretical analysis. Finally, in Sect. 6, we summarize our findings and draw conclusions.

2 An Equivalent System via the QAV Approach

In this section, we utilize the QAV approach to derive an equivalent system of the KGS equations. Let us introduce a quadratic auxiliary variable

$$\begin{aligned} r({x},t)=p^2({x},t)+q^2({x},t). \end{aligned}$$

(2.1)

The energy of the KGS equations can then be reformulated into a quadratic one as follows:

$$\begin{aligned} {\mathcal {E}}(t)=\int _{\varOmega }\Big (|\nabla p|^2+|\nabla q|^2+|\nabla u|^2+u^2+v^2-2 u r\Big )d{{x}}. \end{aligned}$$

(2.2)

From the energy variational principle, we take the variational derivatives with respect to p, q, u, v, and also take the time derivative of (2.1). Then according to the Hamiltoninan form (1.5), we can derive the following equivalent KGS system associated with the quadratic energy (2.2) as

$$\begin{aligned} \left\{ \begin{aligned}&p_t=-\frac{1}{2}\varDelta q-qu,\\&q_t=\frac{1}{2}\varDelta p+pu,\\&u_t=v,\\&v_t=\varDelta u-u+r,\\&r_{t}=2pp_t+2qq_t. \end{aligned}\right. \end{aligned}$$

(2.3)

For consistency, the initial condition of r(x, 0) is set to

$$\begin{aligned} r({x},0)=p^2({x},0)+q^2({x},0). \end{aligned}$$

(2.4)

Though an auxiliary variable has been introduced, we will prove that the underlying mass and energy conservation laws are still preserved.

Theorem 1

The equivalent system (2.3), (2.4) preserves the mass and energy conservation laws

$$\begin{aligned} {\mathcal {M}}(t)={\mathcal {M}}(0),\quad {\mathcal {E}}(t)={\mathcal {E}}(0), \end{aligned}$$

(2.5)

and the algebraic relation ${\mathcal {I}}(t)={\mathcal {I}}(0)\equiv 0$, where

$$\begin{aligned} {\mathcal {I}}(t)=r({x},t)-p^2({x},t)-q^2({x},t). \end{aligned}$$

(2.6)

Proof

Integrating the last Eq. (2.3) from 0 to t and utilizing the consistent initial condition (2.4), we can readily establish the conservation of the algebraic relation.

By a direct calculation, we can verify the mass conservation law

$$\begin{aligned} \frac{d}{dt}{\mathcal {M}}(t)=2(p,p_t)+2(q,q_t)=2\left( p,-\frac{1}{2}\varDelta q-qu\right) +2\left( q,\frac{1}{2}\varDelta p+pu\right) =0, \end{aligned}$$

where the integration-by-parts formula and the periodic boundary conditions are employed. The quadratic energy conservation law can then be derived similarly as follows:

$$\begin{aligned} \begin{aligned} \frac{d}{dt}{\mathcal {E}}(t)&=2\Big [(\nabla p,\nabla p_t)+(\nabla q,\nabla q_t)+(\nabla u,\nabla u_t)+(u,u_t)+(v,v_t)-(u_t,r)-(u,r_t)\Big ]\\&=2\Big [-(\varDelta p, p_t)-(\varDelta q, q_t)-(\varDelta u, u_t)+(u,u_t)+(v,v_t)-(u_t,r)-(u,r_t)\Big ]\\&=2\Big [2(pu-q_t, p_t)+2(p_t+qu, q_t)-(v_t+u-r, u_t)+(u,u_t)+(v,v_t)-(u_t,r)-(u,r_t)\Big ]\\&=2\Big [(pu, p_t)+(qu, q_t)-(u,r_t)\Big ]\\&=2\Big [(pu, p_t)+(qu, q_t)-(u,pp_t+qq_t)\Big ]\\&=0.\\ \end{aligned}\nonumber \\ \end{aligned}$$

(2.7)

This completes the proof. $\square$

Since the algebraic relation $r(x,t)=p^2(x,t)+q^2(x,t)$ is exactly preserved, we can deduce that the equivalent system (2.3) equipped with the consistent initial condition (2.4) conserves the original energy of the KGS equations.

Theorem 2

The solution of the equivalent system (2.3) equipped with the initial condition (2.4) preserves the original energy conservation law, i.e.,

$$\begin{aligned} {\mathcal {H}}(t)={\mathcal {H}}(0). \end{aligned}$$

(2.8)

3 Symplectic Runge–Kutta Method for Time Integration

Notice that the equivalent system (2.3) not only inherits the original conservation laws of the KGS equations, but also provides an elegant platform for the development of arbitrarily high order mass and energy preserving schemes. This significant insight stems from the fact that any symplectic Runge–Kutta method preserves quadratic invariants of the original system. In this section, we discretize (2.3) in time by the symplectic Runge-Kutta method and rigorously prove the semi-discrete mass and energy conservation laws.

For a given positive integer N, we set $\tau =T/ N$ as the time step and define $t_n=n \tau$, $n=0,1,\cdots , N$. Let $a_{ij}, b_i$, $c_i$, $i,j=1,\cdots ,s$ be the coefficients of an s-stage Runge-Kutta method, satisfying the following symplectic conditions

$$\begin{aligned} a_{ij}b_i+a_{ji}b_j-b_ib_j=0, \quad \text{ for } \text{ all }~i, j=1, \cdots , s. \end{aligned}$$

(3.1)

We now apply the above symplectic Runge–Kutta method to the reformulated system (2.3) and obtain the equations of the internal stages as

$$\begin{aligned} \left\{ \begin{aligned} P_i&=p^n+\tau \sum _{j=1}^sa_{ij}k_p^j,{} & {} k_p^i=-\frac{1}{2}\varDelta Q_i-Q_iU_i,\\ Q_i&=q^n+\tau \sum _{j=1}^sa_{ij}k_q^j,{} & {} k_q^i=\frac{1}{2}\varDelta P_i+P_iU_i,\\ U_i&=u^n+\tau \sum _{j=1}^sa_{ij}k_u^j,{} & {} k_u^i=V_i,\\ V_i&=v^n+\tau \sum _{j=1}^sa_{ij}k_v^j,{} & {} k_v^i=\varDelta U_i-U_i+R_i,\\ R_i&=r^n+\tau \sum _{j=1}^sa_{ij}k_r^j,{} & {} k_r^i=2(P_ik_p^i+Q_ik_q^i). \end{aligned} \right. \end{aligned}$$

(3.2)

Then $(p^{n+1}, q^{n+1}, u^{n+1},v^{n+1},r^{n+1})$ can be updated by

$$\begin{aligned} \left\{ \begin{aligned}&p^{n+1}=p^n+\tau \sum _{i=1}^sb_{i}k_p^i, \\&q^{n+1}=q^n+\tau \sum _{i=1}^sb_{i}k_q^i, \\&u^{n+1}=u^n+\tau \sum _{i=1}^sb_{i}k_u^i, \\&v^{n+1}=v^n+\tau \sum _{i=1}^sb_{i}k_v^i, \\&r^{n+1}=r^n+\tau \sum _{i=1}^sb_{i}k_r^i, \end{aligned} \right. \end{aligned}$$

(3.3)

where $p^n = p^n(x)$ represents the numerical approximation of $p({x},t_n)$, etc. In the following contexts, we denote the above schemes (3.2), (3.3) satisfying the symplectic condition (3.1) as QAV-SRK methods.

Theorem 3

The QAV-SRK schemes (3.2), (3.3) satisfy the following semi-discrete conservation laws

$$\begin{aligned} {\mathcal {M}}^{n+1}={\mathcal {M}}^{n}, \quad {\mathcal {E}}^{n+1}={\mathcal {E}}^{n},\quad {\mathcal {I}}^{n+1}={\mathcal {I}}^{n}, \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {M}}}^n=(p^n, p^n)+(q^n, q^n), \end{aligned}$$

(3.4)

$$\begin{aligned} {\mathcal {E}}^n=(\nabla p^n, \nabla p^n)+(\nabla q^n, \nabla q^n)+(\nabla u^n, \nabla u^n)+(u^n, u^n)+(v^n, v^n)-2(u^n, r^n), \end{aligned}$$

(3.5)

$$\begin{aligned} {{\mathcal {I}}}^n=r^{n}-(p^n)^2-(q^n)^2. \end{aligned}$$

(3.6)

Proof

Through a direct calculation, we have

$$\begin{aligned} \begin{aligned} {\mathcal {M}}^{n+1}-{\mathcal {M}}^n&= (p^{n+1},p^{n+1})+(q^{n+1},q^{n+1})-( p^n,p^n)-( q^n,q^n)\\&= 2\tau \sum _{i=1}^s b_i(p^n,k^{i}_{p})+\tau ^2\sum _{i,j=1}^sb_ib_j(k_p^i,k_p^j)\\&\quad +2\tau \sum _{i=1}^s b_i(q^n,k^{i}_{q})+\tau ^2\sum _{i,j=1}^sb_ib_j(k_q^i,k_q^j). \end{aligned} \end{aligned}$$

(3.7)

Substituting the identities $P_i=p^n+\tau \sum _{j=1}^sa_{ij}k_p^j$ and $k_p^i=-\frac{1}{2}\varDelta Q_i-Q_iU_i$ into the first two terms yield

$$\begin{aligned} \begin{aligned}&2\tau \sum _{i=1}^s b_i(p^n,k^{i}_{p})+\tau ^2\sum _{i,j=1}^sb_ib_j(k_p^i,k_p^j)=2\tau \sum _{i=1}^s b_i(P_i-\tau \sum _{j=1}^sa_{ij}k_p^j,k^{i}_{p})+\tau ^2\sum _{i,j=1}^sb_ib_j(k_p^i,k_p^j)\\&\quad =2\tau \sum _{i=1}^s b_i(P_i,k^{i}_{p})-2\tau ^2\sum _{i,j=1}^s b_ia_{ij}(k_p^j,k^{i}_{p})+\tau ^2\sum _{i,j=1}^sb_ib_j(k_p^i,k_p^j)\\&\quad =2\tau \sum _{i=1}^s b_i(P_i,k^{i}_{p}),\\&\quad =\tau \sum _{i=1}^s b_i(\nabla P_i,\nabla Q_i)-2\tau \sum _{i=1}^s b_i(P_i,Q_iU_i). \end{aligned} \end{aligned}$$

(3.8)

where the property $\sum \limits _{i,j=1}^s b_ia_{ij}=\sum \limits _{i,j=1}^s b_ja_{ji}$ and the symplectic condition (3.1) are used. Similarly,

$$\begin{aligned} 2\tau \sum _{i=1}^s b_i(q^n,k^{i}_{q})+\tau ^2\sum _{i,j=1}^sb_ib_j(k_q^i,k_q^j)= & {} 2\tau \sum _{i=1}^s b_i(Q_i,k^{i}_{q})\nonumber \\= & {} -\tau \sum _{i=1}^s b_i(\nabla Q_i,\nabla P_i)+2\tau \sum _{i=1}^s b_i(Q_i,P_iU_i).\nonumber \\ \end{aligned}$$

(3.9)

Combining (3.7), (3.8), (3.9), yields ${\mathcal {M}}^{n+1}-{\mathcal {M}}^n=0$.

By performing a direct calculation, we obtain

$$\begin{aligned} \left\{ \begin{aligned}&(\nabla p^{n+1},\nabla p^{n+1})-(\nabla p^n,\nabla p^n)=2\tau \sum _{i=1}^sb_{i}(\nabla P_i,\nabla k_p^i),\\&(\nabla q^{n+1},\nabla q^{n+1})-(\nabla q^n,\nabla q^n)=2\tau \sum _{i=1}^sb_{i}(\nabla Q_i,\nabla k_q^i),\\&(\nabla u^{n+1},\nabla u^{n+1})-(\nabla u^n,\nabla u^n)=2\tau \sum _{i=1}^sb_{i}(\nabla U_i,\nabla k_u^i),\\ \end{aligned}\right. \end{aligned}$$

(3.10)

and

$$\begin{aligned} \left\{ \begin{aligned}&(u^{n+1},u^{n+1})-(u^n,u^n)=2\tau \sum _{i=1}^sb_{i}(U_i,k_u^i),\\&(v^{n+1},v^{n+1})-(v^n,v^n)=2\tau \sum _{i=1}^sb_{i}(V_i,k_v^i),\\&(u^{n+1},r^{n+1})-(u^n,r^n)=\tau \sum _{i=1}^sb_{i}(U_i,k_r^i)+\tau \sum _{i=1}^sb_{i}(R_i,k_u^i). \end{aligned}\right. \end{aligned}$$

(3.11)

The process of calculating ${\mathcal {E}}^{n+1}-{\mathcal {E}}^n$ is analogous to the derivation of the mass conservation law mentioned above.

$$\begin{aligned} \begin{aligned} {\mathcal {E}}^{n+1}-{\mathcal {E}}^n&= 2\tau \sum _{i=1}^sb_i\Big ((\nabla P_i,\nabla k_p^i)\\&\quad +(\nabla Q_i,\nabla k_q^i)+(\nabla U_i,\nabla k_u^i)+(U_i,k_u^i) +(V_i,k_v^i)-(U_i,k_r^i)-(R_i,k_u^i)\Big )\\&= 2\tau \sum _{i=1}^sb_i\Big (-(\varDelta P_i,k_p^i)-(\varDelta Q_i, k_q^i)\\&\quad -(\varDelta U_i,k_u^i)+(U_i,k_u^i) +(V_i,k_v^i)-(U_i,k_r^i)-(R_i,k_u^i)\Big )\\&= 2\tau \sum _{i=1}^sb_i\Big (2(P_iU_i-k_q^i,k_p^i)+2(k_p^i+Q_iU_i, k_q^i)\\&\qquad -(k_v^i+U_i-R_i, k_u^i)+(U_i,k_u^i) +(V_i,k_v^i)-(U_i,k_r^i)-(R_i,k_u^i)\Big )\\&=2\tau \sum _{i=1}^sb_i\Big (2(P_iU_i,k_p^i)+2(Q_iU_i, k_q^i)-(U_i,k_r^i)\Big )\\&= 2\tau \sum _{i=1}^sb_i\Big (2(P_iU_i,k_p^i)+2(Q_iU_i, k_q^i)-2(U_i,P_ik_p^i+Q_ik_q^i)\Big )\\&= 0, \end{aligned} \end{aligned}$$

(3.12)

which leads to the quadratic energy conservation law.

Finally, we confirm the preservation of the algebraic relation. Combining (3.10) and (3.11) provides

$$\begin{aligned} (p^{n+1})^2+(q^{n+1})^2-(p^n)^2-(q^n)^2=2\tau \sum _{i=1}^sb_i(P_ik_p^i+Q_ik_q^i). \end{aligned}$$

(3.13)

Notice that

$$\begin{aligned} r^{n+1}-r^n=\tau \sum _{i=1}^s b_ik_{r}^{i}=2\tau \sum _{i=1}^s b_i(P_ik_{p}^{i}+Q_ik_{q}^{i}). \end{aligned}$$

(3.14)

Comparing (3.13) and (3.14) then yields ${\mathcal {I}}^{n+1}={\mathcal {I}}^n$. The proof is thus completed. $\square$

Theorem 4

The semi-discrete QAV-SRK schemes (3.2)-(3.3) conserve the system energy of the original form, i.e.,

$$\begin{aligned} {\mathcal {H}}^{n+1}={\mathcal {H}}^{n}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {H}}^n&= (\nabla p^n, \nabla p^n)+(\nabla q^n, \nabla q^n)+(\nabla u^n, \nabla u^n)+(u^n, u^n)+(v^n, v^n) \nonumber \\ {}&\quad -2(u^n, (p^n)^2+(q^n)^2). \end{aligned}$$

(3.15)

Proof

According to (3.6) and the consistent initial condition $r^0=(p^0)^2+(q^0)^2$, we have $r^n=(p^n)^2+(q^n)^2$. Inserting it into (3.5) leads to the original energy conservation law. $\square$

4 Fully-Discrete QAV-SRK Schemes

In this section, we develop fully-discrete QAV-SRK schemes by applying the Fourier pseudo-spectral method to the semi-discrete system (3.2)-(3.3).

4.1 Fourier Pseudo-Spectral Method

Without losing generality, we consider the system (1.1) in 2D with $\varOmega =(-L, L)^2$. For a positive even integer M, we partition the domain uniformly with mesh sizes $h=h_x=h_y=2L/M$. Let the spatial grid points

$$\begin{aligned} \begin{aligned} \varOmega _{h}=\{(x_i,y_j) |\ i=j=1, 2, \cdots , M-1\} \end{aligned} \end{aligned}$$

with $x_i=-{L}+ih, y_j=-{L}+jh$. We denote

$$\begin{aligned} \begin{aligned} {\mathcal {U}}_h=\big \{ U| U=(u_{1,1},\cdots ,u_{M-1,1}, u_{0,1},\cdots ,u_{M-1,1},\cdots ,u_{1,M-1}, \cdots , u_{M-1,M-1})^T\big \}, \end{aligned} \end{aligned}$$

For $U, V\in {\mathcal {U}}_h$, defining the corresponding discrete inner product and norms as follows

$$\begin{aligned} \langle U, V\rangle _h=h^2\sum \limits _{i=0}^{{\mathcal {N}}-1}\sum \limits _{j=0}^{{\mathcal {N}}-1} u_{i,j}{{{{v}}}}_{i,j}, \ \ \ \Vert U\Vert =\langle U , U\rangle _h^{\frac{1}{2}}, \ \ \Vert U\Vert _{{\infty }}=\sup \limits _{(x_i,y_j)\in \varOmega _{h}}|u_{i,j}|. \end{aligned}$$

Let $X_{i}(x)$ be the interpolation basis functions given by

$$\begin{aligned} X_{i}(x)=\frac{1}{M}\sum \limits _{m={-M}/{2}}^{{M}/{2}}\frac{1}{c_m}e^{\text {i}m\mu (x-x_i)}, \end{aligned}$$

where $\mu =\pi /L$ and $c_m=\left\{ \begin{array}{lll} 1,\ \ {} &{}|m|< \frac{M}{2}, \\ 2,\ \ {} &{}|m| = \frac{M}{2}. \end{array} \right.$ Then, we can define the two-dimensional interpolation space

$$\begin{aligned} S_{M}=\big \{X_i(x)X_j(y)\big |0\le i, j\le M-1\big \}, \end{aligned}$$

and the interpolation operator $I_{M}:C({\overline{\varOmega }})\rightarrow S_{M}$

$$\begin{aligned} I_{M}u(x,y)=\sum \limits _{i=0}^{M-1}\sum \limits _{j=0}^{M-1}u_{i,j}X_i(x)X_j(y). \end{aligned}$$

The corresponding second-order spectral differential matrices for x- and y-directions are uniformly calculated by

$$\begin{aligned} ({D_2})_{i,l}=\frac{d^2X_l(x_i)}{dx^2}. \end{aligned}$$

Owing to the circulant property of this differential matrices, one can utilize the Fast Fourier Transform (FFT) to accelerate the computation of matrix–vector multiplication with $D_2$. In fact, we have the decomposition that

$$\begin{aligned} {D}_{2}={F}_{M}^H\varLambda {F}_{M}, \end{aligned}$$

(4.1)

where ${F}_{M}$ denotes the matrix of discrete Fourier transform, ${F}_{M}^H$ is the conjugate transpose matrix of ${F}_{M}$ and ${F}_{M}^H={F}_{M}^{-1}$ [13]. The diagonal matrix $\varLambda$ corresponds to the eigenvalues of $D_2$ with the elements given by

$$\begin{aligned} \varLambda =-\mu ^2~\text {diag}\Big [0^2, 1^2, \cdots , \left( \frac{M}{2}\right) ^2, \left( -\frac{M}{2}+1\right) ^2,\cdots , (-2)^2,(-1)^2\Big ]. \end{aligned}$$

(4.2)

Moreover, the approximation of the two-dimensional Laplace operator by the pseudo-spectral method yields the second-order differential matrix $D:=I_M\otimes {D}_{2}+{D}_{2}\otimes {I}_M$, which by (4.1) also admits a diagonal decomposition

$$\begin{aligned} D=(F_M^H\otimes F_M^H)(I_M\otimes {\varLambda }+{\varLambda }\otimes {I_M})(F_M\otimes F_M). \end{aligned}$$

(4.3)

Therefore, the practical computation associated with the differential matrix will be efficiently carried out.

4.2 Conservative Fully-Discrete Schemes

Applying the pseudo-spectral method to discretize the spatial derivative of (3.2), (3.3), The fully discrete QAV-SRK schemes are as follows.

$$\begin{aligned} \left\{ \begin{aligned}&{ P_i}={ P^n}+\tau \sum \limits _{j=1}^sa_{ij}k_{ p}^j, \quad k_{ p}^i=-\frac{1}{2}D { Q_i}-{ Q_i}{ U_i},\\&{ Q_i}={Q^n}+\tau \sum \limits _{j=1}^sa_{ij}k_{ q}^j, \quad k_{ q}^i=\frac{1}{2}D { P_i}+{ P_i}{ U_i},\\&{ U_i}={ {U^n}}+\tau \sum \limits _{j=1}^sa_{ij}k_{ u}^j, \quad k_{ u}^i={ V_i},\\&{ V_i}={ {V^n}}+\tau \sum \limits _{j=1}^sa_{ij}k_{ v}^j, \quad k_{ v}^i=D { U_i}-{ U_i}+{ R_i},\\&{ R_i}={ {R^n}}+\tau \sum \limits _{j=1}^sa_{ij}k_{ r}^j, \quad k_{ r}^i=2({ P_i}k_{ p}^i+{ Q_i}k_{ q}^i). \end{aligned}\right. \end{aligned}$$

(4.4)

for the values of internal stages and

$$\begin{aligned} \left\{ \begin{aligned}&{ P^{n+1}}={ P^n}+\tau \sum \limits _{i=1}^sb_{i}k_{ p}^i, \\&{ Q^{n+1}}={Q^n}+\tau \sum \limits _{i=1}^sb_{i}k_{ q}^i, \\&{ U^{n+1}}={ {U^n}}+\tau \sum \limits _{i=1}^sb_{i}k_{ u}^i, \\&{ V^{n+1}}={ {V^n}}+\tau \sum \limits _{i=1}^sb_{i}k_{ v}^i, \\&{ R^{n+1}}={ {R^n}}+\tau \sum \limits _{i=1}^sb_{i}k_{ r}^i, \end{aligned}\right. \end{aligned}$$

(4.5)

for the numerical solutions at time level $n+1$. For clarity, we use $P_i$ and similar notations to represent the vector-valued functions at the space grid points, and it is a vector in ${\mathbb {R}}^{M^2}$ after vectorizing the original matrix-valued function in the two-dimensional case. The only difference between the semi-discrete schemes (3.2), (3.3) and the fully discrete schemes (4.4), (4.5) is that the continuous Laplace operator is replaced by the discrete spectral differential matrix D. However, in the proof of mass and energy conservation, the symmetry property of the Laplace operator in the continuous inner product is retained by the discrete inner product associated with the symmetric differential matrix D. Therefore, following the same approach as in Theorems 3 and 4, we can similarly prove the fully discrete mass and energy conservation laws for the schemes (4.4), (4.5).

Theorem 5

The fully discrete QAV-SRK schemes (4.4), (4.5) conserve the mass and energy conservation laws and the algebraic relation, that is,

$$\begin{aligned} {M}^n={M}^{0}, \ \ \ {E}^n={E}^{0}, \ \ \ {I}^n={I}^{0}, \end{aligned}$$

where the mass ${{M}}^n$ and quadratic energy are defined by

$$\begin{aligned} {{M}}^n=\langle P^n,P^n\rangle _h+\langle {Q^n},{Q^n}\rangle _h, \end{aligned}$$

(4.6)

$$\begin{aligned} {E}^n=\big \langle D P^n, P^n\big \rangle _h+\big \langle D{Q^n}, {Q^n}\big \rangle _h+\big \langle D{U^n}, {U^n}\big \rangle _h-\big \langle {U^n}, {U^n}\big \rangle _h-\big \langle {V^n}, {V^n}\big \rangle _h+2\big \langle {U^n}, {R^n}\big \rangle _h, \end{aligned}$$

(4.7)

and the algebraic relation reads

$$\begin{aligned} {{I}}^n= r^{n}-\langle P^n,P^n\rangle _h-\langle {Q^n},{Q^n}\rangle _h. \end{aligned}$$

(4.8)

Theorem 6

Under the consistent initial condition $r^0=(u^0)^2+(v^0)^2$, the fully-discrete QAV-SRK schemes (4.4), (4.5) conserve the original energy, i.e.,

$$\begin{aligned} {H}^n={H}^{0}, \end{aligned}$$

where

$$\begin{aligned} {H}^n&=\big \langle D P^n, P^n\big \rangle _h+\big \langle D{Q^n}, {Q^n}\big \rangle _h+\big \langle D{U^n}, {U^n}\big \rangle _h-\big \langle {U^n}, {U^n}\big \rangle _h-\big \langle {V^n},{V^n}\big \rangle _h \nonumber \\ {}&\quad +2\big \langle {U^n}, (P^n)^2+({Q^n})^2\big \rangle _h. \end{aligned}$$

(4.9)

Remark 1

Other recently developed methods, such as the IEQ and SAV approaches, can also be used to construct high-order energy-preserving schemes (see e.g., [21, 25]). However, these schemes only preserve a modified form of energy, rather than the original energy conservation law. In contrast, our proposed QAV-RK schemes can conserve the original energy conservation law.

4.3 Fast Solver for the QAV-SRK Scheme

It is worth noting that the proposed QAV-SRK schemes (4.4)-(4.5) are coupled and fully-implicit, which require a nonlinear iteration to solve the system and can be computationally expensive. However, by diagonalizing the differential D (4.3) and utilizing the FFT algorithm, we can implement the QAV-SRK schemes very efficiently. Specifically, in each iteration, we only need to perform FFTs and inverse FFTs, which can be done in ${\mathcal {O}}(M^2\log M)$ time complexity for two-dimensional problems. This allows us to achieve fast and accurate solutions for the KGS equation.

Substituting $k_u^i$, $k_v^i$, $k_r^i$ in the scheme (4.4) and after some arrangements, we obtain

$$\begin{aligned} \left\{ \begin{aligned}&{ P_i}+\frac{1}{2}\tau \sum \limits _{j=1}^sa_{ij}D { Q_j}=P^n-\tau \sum \limits _{j=1}^sa_{ij}{ Q_j}{ U_j}, \quad k_{ p}^i=-\frac{1}{2}D { Q_i}-{ Q_i}{ U_i},\\&{ Q_i}-\frac{1}{2}\tau \sum \limits _{j=1}^sa_{ij}D { P_j}={Q^n}+\tau \sum \limits _{j=1}^sa_{ij}{ P_j}{ U_j}, \quad k_{ q}^i=\frac{1}{2}D { P_i}+{ P_i}{ U_i},\\&{ U_i}-\tau \sum \limits _{j=1}^sa_{ij}{ V_j}={ U^{n}},\\&{ V_i}-\tau \sum \limits _{j=1}^sa_{ij}(D { U_j}-{ U_j})={ {V^n}}+\tau \sum \limits _{j=1}^sa_{ij}{ R_j}, \quad { R_i}={ {R^n}}+2\tau \sum \limits _{j=1}^sa_{ij}({ P_j}k_{ p}^j+{ Q_j}k_{ q}^j). \end{aligned}\right. \end{aligned}$$

Let $\varvec{P}=(P_1,P_2,\cdots ,P_s)^{\top }\in {\mathbb {R}}^{sM^2}$ and so on. The above system can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{P}+\frac{1}{2}\tau (A\otimes D) \varvec{Q}=I_s\otimes { P^n}-\tau (A\otimes I_{M^2})(\varvec{Q}\odot \varvec{U}), \quad \varvec{k}_{ p}=-\frac{1}{2}(I_{s}\otimes D) \varvec{Q}-\varvec{Q}\odot \varvec{U},\\&\varvec{Q}-\frac{1}{2}\tau (A\otimes D) \varvec{P}=I_s\otimes {{Q^n}}+\tau (A\otimes I_{M^2})(\varvec{P}\odot \varvec{U}), \quad \varvec{k}_{ q}=\frac{1}{2}(I_{s}\otimes D) \varvec{P}+\varvec{P}\odot \varvec{U},\\&\varvec{U}-\tau (A\otimes I_{M^2})\varvec{V}=I_s\otimes { {U^n}},\\ {}&\varvec{V}-\tau \big (A\otimes (D-I_{M^2})\big )\varvec{U}=I_s\otimes { {V^n}}+\tau (A\otimes I_{M^2})\varvec{R}, \\&\varvec{R}=I_s\otimes {R^n}+2\tau (A\otimes I_{M^2})(\varvec{P}\odot \varvec{k}_{p}+\varvec{Q}\odot \varvec{k}_{q}), \end{aligned}\right. \end{aligned}$$

(4.10)

where ${\varvec{Q}}\odot {\varvec{U}}$ represents the pointwise multiplication, etc. Denote ${\varvec{Z}}=({\varvec{P}}, {\varvec{Q}}, {\varvec{U}}, {\varvec{V}})^\top$ and $z^n=(P^n, {Q^n}, {U^n}, {V^n})^\top$. The nonlinear system (4.12) can be further reformulated into a compact form

$$\begin{aligned} {\varvec{A}}{\varvec{Z}}={\varvec{b}}(z^n,{\varvec{Z}}) \end{aligned}$$

(4.11)

where the coefficient matrix reads

$$\begin{aligned} {\varvec{A}}=\left( \begin{array}{cccc} I_{s}\otimes I_{M^2}&{} \frac{1}{2}\tau (A\otimes D) &{} 0 &{} 0\\ -\frac{1}{2}\tau (A\otimes D) &{} I_{s}\otimes I_{M^2} &{}0 &{}0\\ 0&{}0 &{}I_{s}\otimes I_{M^2} &{} -\tau (A\otimes I_{M^2})\\ 0&{}0 &{} -\tau (A\otimes (D-I_{M^2})) &{} I_{s}\otimes I_{M^2} \end{array}\right) , \end{aligned}$$

(4.12)

and ${\varvec{b}}(z^n,{\varvec{Z}})$ is consisted of known terms like $I_s\otimes P^n$ and the unknown nonlinear terms. Since the differential matrix D has the decomposition (4.3), we further denote ${\varvec{\varLambda }}_D=I_M\otimes \varLambda +\varLambda \otimes I_M$, ${\varvec{F}}=I_4\otimes F_M\otimes F_M$ and ${\varvec{F}}^H=I_4\otimes F_M^H\otimes F_M^H$. Then the coefficient matrix ${\varvec{A}}$ can be decomposed by

$$\begin{aligned} \varvec{A}={\varvec{F}}^{H}{\varvec{\varLambda }}_{{\varvec{A}}} {\varvec{F}} \end{aligned}$$

where

$$\begin{aligned} {\varvec{\varLambda }}_{\varvec{A}}= & {} \left( \begin{array}{cccc} I_{s}\otimes I_{M^2}&{} \frac{1}{2}\tau (A\otimes \varLambda _D) &{} 0 &{} 0\\ -\frac{1}{2}\tau (A\otimes \varLambda _D) &{} I_{s}\otimes I_{M^2} &{}0 &{}0\\ 0&{}0 &{}I_{s}\otimes I_{M^2} &{} -\tau (A\otimes I_{M^2})\\ 0&{}0 &{} -\tau (A\otimes (\varLambda _D-I_{M^2})) &{} I_{s}\otimes I_{M^2} \end{array}\right) :\\ {}= & {} \left( \begin{array}{cc} {\varvec{M}}_{11}&{} 0\\ 0 &{} {\varvec{M}}_{22} \end{array}\right) . \end{aligned}$$

Subsequently, the nonlinear system (4.11) is equivalent to

$$\begin{aligned} {\varvec{Z}} = {\varvec{F}}^H{\varvec{\varLambda }}_{{\varvec{A}}}^{-1}{\varvec{F}} {\varvec{b}}(z^n,{\varvec{Z}}), \end{aligned}$$

(4.13)

where ${\varvec{\varLambda }}_{{\varvec{A}}}^{-1}$ is also a sparse and block diagonal matrix and ${\varvec{\varLambda }}_{{\varvec{A}}}^{-1}=\left( \begin{array}{cc} {\varvec{M}}_{11}^{-1}&{} 0\\ 0 &{} {\varvec{M}}_{22}^{-1} \end{array}\right)$. By the formula of the inverse of a $2\times 2$ block matrix we have

$$\begin{aligned}{} & {} {\varvec{M}}_{11}^{-1}=\left( \begin{array}{cc} I_{s}\otimes I_{M^2}&{} -\frac{1}{2}\tau (A\otimes \varLambda _D)\\ \frac{1}{2}\tau (A\otimes \varLambda _D) &{} I_{s}\otimes I_{M^2} \end{array}\right) \left( \begin{array}{cc} {\varvec{B}}_1^{-1}&{} 0\\ 0 &{} {\varvec{B}}_1^{-1} \end{array}\right) , \\{} & {} {\varvec{M}}_{22}^{-1 }=\left( \begin{array}{cc} I_{s}\otimes I_{M^2} &{} \tau (A\otimes I_{M^2})\\ \tau (A\otimes (\varLambda _D-I_{M^2})) &{} I_{s}\otimes I_{M^2} \end{array}\right) \left( \begin{array}{cc} {\varvec{B}}_2^{-1}&{} 0\\ 0 &{} {\varvec{B}}_2^{-1} \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} {\varvec{B}}_1=I_s\otimes I_{M^2}+\frac{\tau ^2}{4}(A^2\otimes \varLambda _D^2)\quad \text{ and }\quad {\varvec{B}}_2=I_s\otimes I_{M^2}-\tau ^2A^2\otimes (\varLambda _D-I_{M^2}) \end{aligned}$$

are two $s\times s$ block diagonal matrices whose inverse can be easily obtained by the following algorithm.

Algorithm Efficient computation of the inverse of ${\varvec{B}}_i$, $i=1,2$
Input: ${\varvec{B}}_i$
Output: ${\varvec{B}}_i^{-1}$
for $k=1,\cdots ,M^2$
$index=k+(0:s-1)M^2$
${\varvec{B}}_i^{-1}(index,index)=\big ({\varvec{B}}_i(index,index)\big )^{-1}$
end

Once the inverse ${\varvec{\varLambda }}_{{\varvec{A}}}^{-1}$ has been obtained, we can apply the fixed-point iteration to the nonlinear system (4.13) where the matrix multiplications can be implemented efficiently by FFT.

5 Numerical Example

In this section, we aim to verify the energy conservation, as well as the accuracy and eff of the proposed QAV-SRK schemes. For clarity, we denote the QAV-SRK schemes with different orders by QAV-SRK i , where $i=2,4,6$ represents the order of the scheme. We also include two other methods for comparison:

• HBVM i ($i=2,4,6$): The ith-order HBVM schemes for the KGS system in Ref. [14];

• AVF: A second-order energy-preserving scheme for the KGS equation based on the AVF method in Ref. [6].

To measure the conservation of mass, energy, and the algebraic relation, we use relative errors defined as

$$\begin{aligned} R\xi ^{n}=|(\xi ^{n}-\xi ^{0})/\xi ^{0}|, \end{aligned}$$

where $\xi ^n=M^n$, $H^n$ or $I^n$, respectively. we compute the numerical errors by using the formula

$$\begin{aligned} \Vert e \Vert _{\infty }=\Vert Z(h,\tau )-z(h,\tau )\Vert _{\infty }, \end{aligned}$$

(5.1)

where $Z(h,\tau )$ and $z(h,\tau )$ represent the numerical and exact solution at $(h,\tau )$. The accuracy of the constructed scheme can be computed by

$$\begin{aligned} \text {Rate} ={\ln \left( \text{ error}_{1} / \text{ error}_{2}\right) }/{\ln \left( \tau _{1} / \tau _{2}\right) }, \end{aligned}$$

(5.2)

where $\tau _{j}$, $\text{ error}_{j}, ({j}=1,2)$ are the time step and the maximum-norm errors with $\tau _{j}$, respectively.

Example 1

We consider the one-dimensional KGS equation with exact solutions given by:

$$\begin{aligned}&\psi (x,t)=\frac{3\sqrt{2}}{4\sqrt{1-l^2}}\text {sech}^{2}\Big (\frac{1}{2\sqrt{1-l^2}}(x-lt-\alpha )\Big )\text {exp}\Big (\text {i}\big (lx+\frac{1-l^2+l^4}{2(1-l^2)}t\big )\Big ),\\&u(x,t)=\frac{3}{4(1-l^2)}\text {sech}^{2}\Big (\frac{1}{2\sqrt{1-l^2}}(x-lt-\alpha )\Big ), \end{aligned}$$

where $\alpha$ represents the initial phase of the system, and $-1<l<1$ is the propagating velocity. In our computations, we take the computational domain as $\varOmega =[-20,20]$, and set $\alpha =0$ and $l=-0.8$.

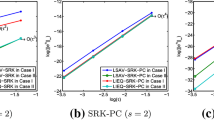
First, we test the time accuracy of different schemes. Table 1 lists the errors in the $L^{\infty }$-norm and the corresponding convergence rates, which shows that all the presented schemes exhibit the expected results. Furthermore, we observe that the numerical errors produced by the QAV-SRK schemes are smaller than those of the other schemes with the same order. We also compare the computational efficiency in Fig. 1. Although all the numerical schemes are fully implicit, the QAV-SRK schemes are the most efficient among them, thanks to the fast solver mentioned earlier.

Table 1 Temporal accuracy of different schemes with $h= 40/256$ at $T=1$

Fig. 1

Numerical errors versus CPU time by different schemes with $T=20, h=40/256$

Figure 2 displays the relative errors of the conservation laws. As shown, the proposed QAV-SRK schemes can conserve both the energy and mass. However, the AVF scheme and HBVM2 schemes can only preserve the energy, but fail to conserve the discrete mass. Interestingly, the HBVM4 and HBVM6 schemes can also conserve mass, due to their high accuracy in time and space directions. As a result, the QAV-SRK method is the optimal choice for constructing high accuracy conservative schemes that conserve both the energy and mass for the KGS equation among the three methods. Figure 3 shows the evolution of the soliton using the QAV-SRK4 scheme. The numerical results demonstrate that the proposed methods can accurately preserve the shape of the solution.

Fig. 2

Relative errors in conservation laws of different schemes at $T=100$ with $\tau =0.01, h=40/256$

Fig. 3

Evolution of numerical solutions of $|\psi ^n|$ and ${U^n}$ by QAV-SRK4

Example 2

This example examines the two-dimensional KGS equation with exact solutions given by:

$$\begin{aligned}&\psi (x,y,t)=\exp (\text {i}(x+y-0.5t)),\ \ u(x,y,t)=|\psi (x,y,t)|,\ \ (x,y) \in [0,2\pi ]^2. \end{aligned}$$

We first set $h=\pi /16$ so that the spatial discretization errors are negligible, and test the time accuracy of the constructed schemes for solving the two-dimensional KGS system. Table 2 lists the $L^{\infty }$-norm errors and convergence rates of the three schemes at $T=1$, which demonstrates that they can also achieve high accuracy in the temporal direction for the two-dimensional KGS equation. We then present the relative errors of the mass, energy, and the algebraic relation in Fig. 4. It is clear that the QAV-SRK schemes can accurately conserve all three discrete conservation laws in two-dimensional cases.

Table 2 Temporal accuracy of different schemes at $T=1$ with $h= \pi /16$

Fig. 4

Relative errors of conservation laws for three schemes at $T=50$ with $\tau =0.01, h=2\pi /16$

Example 3

We further study the two-dimensional KGS equation [15]

$$\begin{aligned} \left\{ \begin{aligned}&\text {i}\partial _{t}\psi ({{x}},t)+\frac{\kappa _1}{2}\varDelta \psi ({{x}},t)+ \gamma u({{x}},t)\psi ({{x}},t)=0,\quad (x,t)\in \varOmega \times (0,T]\\&\partial _{tt}u({{x}},t) -\kappa _2\varDelta u({{x}},t)+\mu ^2 u({{x}},t)-\gamma |\psi ({{x}},t)|^2=0,\quad (x,t)\in \varOmega \times (0,T] \end{aligned}\right. \nonumber \\ \end{aligned}$$

(5.3)

with following initial conditions

$$\begin{aligned}&\psi _0=\sum \limits _{k=0}^1\exp \big (-(x-(-1)^k 2)^2-y^2\big )\exp (\xi \text {i}\big (x-(-1)^k 2)^2+y\big ),\\&u_0 =-\sum \limits _{k=0}^1\sum \limits _{j=0}^1 \exp \big (-(x-(-1)^k 2)^2-(x-(-1)^j 2)^2\big ),\ \ (x,y) \in [-8,8]^2, \end{aligned}$$

the parameters are $\kappa _1=-0.4$, $\kappa _2=0.1$, $\mu =0.1$, $\gamma =0.2$, $\xi =0.1$.

We set $\tau =0.01$, $h=16/64$, and plot the deviation of the invariants for three schemes in Fig. 5. The figure shows that the proposed schemes can preserve original conservation laws in fully-discrete scenes. We also take $t=0, 1, 2$, and show the evolution of the soliton in Figs. 6 and 7. The interactions of circular vector solitons for component $\psi$ are depicted in Fig. 6. At $t=0$, $\psi$ has two peaks which radiate and eventually collide with each other, resulting in the creation of a new peak in the central domain. As time passes, the central peak becomes more pronounced, while the amplitudes of the other two peaks decrease. Figure 7 shows that u has three peaks at $t=0$ and all pointing to the plus direction. With the progression of soliton collisions, the amplitude of the central peak decreases.

Fig. 5

Relative errors of conservation laws for three schemes at $T=20$ with $\tau =0.01, h=16/64$

Fig. 6

Time evolutions of 2D circular vector solitons for component $|\psi |$ of 2D KGS system. The first row: surface plots; the second row: density plots

Fig. 7

Time evolutions of 2D circular vector solitons for component u of 2D KGS system. The first row: surface plots; the second row: density plots

6 Conclusions

In this work, we proposed a family of high-order conservative schemes for solving the Klein-Gordon-Schrödinger equation, which is based on the newly developed quadratic auxiliary variable approach. The proposed schemes conserve the mass and Hamiltonian energy exactly in a fully-discrete sense and arrive at arbitrary high-order accuracy in temporal. Some numerical examples verify our theoretical results. In addition, the approach presented in the paper can be extended to construct conservative schemes for solving other conservative partial differential equations.