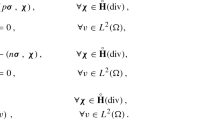Mixed Finite Element Method for Modified Poisson–Nernst–Planck/Navier–Stokes Equations

Abstract

In this paper, a complete mixed finite element method is developed for a modified Poisson–Nernst–Planck/Navier–Stokes (PNP/NS) coupling system, where the original Poisson equation in PNP system is replaced by a fourth-order elliptic equation to more precisely account for electrostatic correlations in a simplified form of the Landau–Ginzburg-type continuum model. A stabilized mixed weak form is defined for each equation of the modified PNP/NS model in terms of primary variables and their corresponding vector-valued gradient variables, based on which a stable Stokes-pair mixed finite element is thus able to be utilized to discretize all solutions to the entire modified PNP/NS model in the framework of Stokes-type mixed finite element approximation. Semi- and fully discrete mixed finite element schemes are developed and are analyzed for the presented modified PNP/NS equations, and optimal convergence rates in energy norms are obtained for both schemes. Numerical experiments are carried out to validate all attained theoretical results.

1 Introduction

The classical theory of the electric double layer and electrokinetic flow near a charged surface is over a century old and still remains extremely powerful in a number of diverse fields such as colloidal science, biophysics, micro- and nanofluidics, and electrochemistry. The classical theory of electrokinetics leads to the popular model of Poisson–Nernst–Planck/Navier–Stokes (PNP/NS) coupling system, which is used to describe the electrohydrodynamic phenomenon, also known as the electro-fluid-dynamics. PNP/NS equations are adopted to study the dynamics of electrically charged fluids, the motions of ionized particles or molecules and their interactions with electric fields and the surrounding fluid. In this model, the convection-diffusion-reaction equations, also particularly called Nernst–Planck equations, are used to model the ionic concentrations, while the Poisson equation is adopted to demonstrate the diffusive behavior of the electrostatic potential, and the fluid flow is generally modeled by Navier–Stokes equations. So, the coupling between PNP equations and Navier–Stokes equations is capable of describing electro-chemical and fluid-mechanical transport throughout the cellular environment. This includes a range of spatial and temporal scales [1]. For extensive applications, we refer to [2,3,4,5].

While the usefulness of the classical electrokinetic theory is not in question, there is a long history of recognizing the limitations and offering new formulations for new applications [6, 7]. In particular, extensions of the classical electrokinetic theory are required for room-temperature ionic liquids (RTILs). RTILs typically have large organic cations and similar organic or smaller inorganic anions and hold promise as solvent-free electrolytes for supercapacitors, batteries, solar cells, and electroactuators [8,9,10]. Recently, Bazant, Storey and Kornyshev (BSK) [11,12,13] derive a Landau–Ginzburg-type continuum model for RTILs to account for the nonlocal dielectric permittivity of ionic liquids resulting from ion-ion correlations, which leads to the following fourth-order modified Poisson equation for a new definition of the electrostatic potential equation:

$$\begin{aligned} \epsilon \left( \ell _c^2\Delta ^2 \phi -\Delta \phi \right) =\rho , \end{aligned}$$

(1.1)

with a fourth-order modified electrostatic boundary condition

$$\begin{aligned} \nabla \left( \Delta \phi \right) \cdot \varvec{n} =0, \end{aligned}$$

(1.2)

where, $\phi$ is the electrostatic potential, $\rho$ is the charge density, $\ell _c$ is an electrostatic correlation length, and $\varepsilon$ is a constant permittivity to describe the polarizability of the ions. The BSK theory and the fourth-order modified Poisson equation (1.1) are first applied to predict double-layer structure and capacitance (RTIL) by using the ion size as the correlation length scale, and a high agreement to experimental results is achieved [12].

Although “The BSK theory provides reasonable agreement to simulation and experimental results for ionic liquids and multivalent electrolytes”, however, Souza and Bazant [13] point out that “the boundary conditions have not yet been proved or validated systematically”. Therefore, our goal in this paper is to mathematically and numerically investigate the rationality of (1.1) and (1.2) while they substitute the original Poisson equation in PNP/NS coupling system, as well as study the numerical performance of the entire PNP/NS model in a more comprehensive way, i.e., not only the primary variables of PNP/NS coupling system, but also their gradient variables which all represent corresponding physical significance, will be analyzed and approximated in an efficient and accurate fashion. Note that the vector-valued gradient of primary variables of PNP equations are crucial for obtaining an accurate electric current field which is remarkable for the validation with experimental data, since the electric current seems the easiest physical quantity to be measured in the experiment. For instance, the electric current across the biological membrane channel can be calculated by the following expression [14]

$$\begin{aligned} I=\sum _{i=1}^{2}q_i\int _{\text {MEM}}D_i\left( \nabla C_i+\frac{q_i}{\kappa _BT}C_i\nabla \phi \right) \cdot {\mathbf {n}} \,\, \mathrm {d}x, \end{aligned}$$

(1.3)

where $C_i\ (i=1,2)$ represent the ionic concentrations. Equation (1.3) clearly shows that the gradients of ionic concentrations and of electrostatic potential are important to produce an accurate electric current everywhere inside the membrane channel. Moreover, another important electrokinetic phenomena existing in ion channels of electrophysiology, the electrical double layer (Debye layer) [15], is formed near the surface of a charged object (membrane) due to the exponential decreases of the electrostatic potential, further, of the ionic concentrations, away from the surface, featuring a distance called Debye length [16]. Such exponential decrease induces a large gradient, so an accurate computation of gradient for the electrostatic potential and ionic concentrations are crucial to determine the location of Debye layer, which has a significant influence on the behavior of surfaces of the charged objects in contact with solutions or solid-state fast ion conductors. Therefore in the PNP system, it is highly necessary to numerically resolve the gradients $\nabla C_1$, $\nabla C_2$ and $\nabla \phi$ in an accurate and efficient fashion.

To achieve the above goal, the mixed finite element method (FEM) shall be the best candidate for stably approximating the fourth-order modified PNP/NS coupling system with the optimal convergence to both primary variables and their gradients, comparing with conventional Lagrange-type finite element methods which need to use certain numerical differentiation for computing the gradient and then lead to a loss in accuracy. In this paper we will employ the Stokes-type mixed FEM by means of a stable Stokes-pair mixed element, e.g., Taylor–Hood element, to tackle each equation in PNP/NS coupling system. To that end, we will need to first reformulate the fourth-order modified Poisson equation and two parabolic-type ionic concentration equations to obtain their $\varvec{H}$(div)-type mixed formulations in terms of both primary variables and their corresponding vector-valued gradient variables, then stabilize them by appropriately introducing stabilization terms in order to apply the Stokes-type mixed FEM to both modified PNP equations and Navier–Stokes equations, simultaneously. Thus, we avoid to introduce different types of mixed finite elements for Stokes-type and $\varvec{H}$(div)-type mixed problem, respectively, which shall be more convenient and more efficient for us to analyze and implement the mixed finite element approximation for the modified PNP/NS coupling in one unified finite element space, simultaneously, bearing with the benefit of optimal convergence rates for all primary variables as well as their gradient variables in respectively proper norms.

Numerical study and analysis for PNP equations [17,18,19] and PNP/NS coupling system [20,21,22,23] have been extensively studied, where the standard FEM is most popularly adopted in recent years. Prohl and Schmuck [19] propose two nonlinear schemes with a linear FEM which preserve electric energy decay and entropy decay properties, respectively. Later, numerical methods for PNP/NS coupling are investigated in [20]. Sun et al. [24] develop a fully nonlinear Crank–Nicolson FEM for PNP equations, where a Picard linearization is used in the inner iteration, an optimal error estimate in $H^1$ norm and a suboptimal error estimate in $L^2$ norm are obtained. Then, Gao and He [25] propose a linearized finite element discretization and establish unconditionally optimal error estimates for all variables in both $L^2$ and $H^1$ norms. To overcome the convergence order reduction and to accurately resolve the electric current that is the gradient of the electrostatic potential as well, He and Sun [26] propose a nonlinear mixed FEM for Poisson equation and still apply the standard FEM to Nernst–Planck equations, which provides optimal error estimates for the electrostatic potential and ionic concentrations in both $H^1$ and $L^2$ norms, moreover, for electric current in $\varvec{H}$(div) norm as well. Later, Gao and Sun [27] develop a linearized mixed finite element discretization for both Poisson equation and Nernst–Planck equations by using Raviart–Thomas element. Considering that the Lagrange-type Taylor–Hood mixed finite element is naturally stable for Stokes equations and easily implementable, it inspires the authors of this paper to employ Taylor–Hood element as a unique mixed finite element to discretize both the mixed Poisson equations and Stokes equations in [28], and obtain optimal convergence rates for all variables of PNP equations and Stokes equations in their energy norms, respectively. In this paper, we will consider to apply the stable Stokes-pair mixed finite element to discretize all solutions to the entire fourth-order modified PNP/NS coupling system, develop its Stokes-type mixed FEM and analyze optimal convergence behaviors of primary variables and of all vector-valued gradient variables of modified PNP equations in both semi- and full discretizations.

This paper is organized as follows. In Sect. 2 we introduce the model of fourth-order modified PNP/NS coupling system. The semi-discrete scheme of the mixed FEM and its error analysis are given in Sect. 3. Section 4 contributes to the definition and analysis of the full discretization. Numerical experiments and validations are illustrated in Sect. 5. Finally, the paper ends with a conclusion in Sect. 6.

In what follows, we adopt the standard notation for Sobolev spaces $W^{l,p}(\Omega )$ and their associated norms and seminorms. For $p=2$, $W^{l,2}(\Omega )=H^l(\Omega )$ and $\varvec{H}^l(\Omega )=H^l(\Omega )^d$. The standard $L^2$ inner product is adopted, as $(\psi , {{\tilde{\psi }}})=\int _\Omega \psi {{\tilde{\psi }}} d\varvec{x}$, $<\psi , {{\tilde{\psi }}}>_{\partial \Omega }=\int _{\partial \Omega }\psi {{\tilde{\psi }}} ds$. Some norm notations are given as $\Vert \cdot \Vert _l=\Vert \cdot \Vert _{H^l(\Omega )}$, $\Vert \cdot \Vert _0=\Vert \cdot \Vert _{L^2(\Omega )}$, and $\Vert \cdot \Vert _{W^{l,m}(W^{p,q})}=\Vert \cdot \Vert _{W^{l,m}(0,T;W^{p,q}(\Omega ))}$. For the sake of simplicity, we sometimes drop the time dependence in variables, such as $\psi =\psi (t)$, drop $i=1,2$ for explaining $C_i$, and use M to denote a generic constant independent of any discretization parameter (h and $\Delta t$) throughout the paper.

2 Model Description and Weak Formulations

In this section, we first present the model of fourth-order modified Poisson–Nernst–Planck/Navier–Stokes coupling system, then reformulate it to a fully mixed form in terms of primary variables and extra vector-valued gradient variables, finally define its stabilized weak formulation in the sense that a stable Stokes-pair mixed finite element defined in a subspace of $\varvec{H}^1(\Omega )\times L^2(\Omega )$ [26, 28], instead of a $\varvec{H}($div)-type mixed finite element space belonging to $\varvec{H}($div;$\Omega )\times L^2(\Omega )$ [27], can be adopted to discretize the fully mixed modified Poisson–Nernst–Planck system.

2.1 The Fourth-Order Modified PNP/NS Coupling System

Let $\Omega \in {\mathbb {R}}^d$ ($d=2,3$) be a bounded Lipschitz domain and $T>0$. We introduce the following governing equations to describe the fourth-order modified PNP/NS coupling system in $\Omega \times [0,T]$ [11,12,13] :

$$\begin{aligned} \left\{ \begin{array}{llllll} \Delta ^2 \phi -\Delta \phi =C_1-C_2, \\ \partial _t C_i-\nabla \cdot \left( \nabla C_i + z_i\nabla \phi C_i -\varvec{u} C_i\right) =0,\quad i=1,2,\\ \partial _t\varvec{u}+(\varvec{u} \cdot \nabla )\varvec{u}-\Delta \varvec{u} +\nabla p =-\left( C_1-C_2\right) \nabla \phi ,\\ \nabla \cdot \varvec{u}=0, \end{array} \right. \end{aligned}$$

(2.1)

where, $\partial _t=\partial /\partial t$, $\phi$ is the electrostatic potential, $C_i$ $(i=1,2)$ are the mass concentration of ions carrying charge $z_i$, (such as $z_{1}=1,~z_{2}=-1$), $\varvec{u}$ and p are the fluid velocity and pressure, respectively. Since in this paper we do not really consider the intrinsic physical feature of the modified PNP/NS coupling system, but put our full efforts on developing numerical discretizations and error analyses of the mixed FEM for the presented model in mathematical and numerical sense, only. So, without loss of generality in this paper, we simply treat all involved physical coefficients as the unit constant “1”, which actually does not really matter in the following error analyses since the value of physical coefficients which are involved in the presented model are all positive constants. In addition, we impose the following boundary conditions and initial conditions for (2.1):

$$\begin{aligned} \left\{ \begin{array}{llllll} \phi =f_1,~ \nabla (\Delta \phi ) \cdot \varvec{n}=f_2 ,&{}\quad \text {on}\quad \partial \Omega , ~t\in (0,T],\\ C_i=g_i,~\varvec{u}=0,&{}\quad \text {on}\quad \partial \Omega , ~t\in (0,T],\\ C_i=C_i^0,~\varvec{u}=\varvec{u}^0, &{}\quad \text {in}\quad \Omega ,~ t=0, \end{array} \right. \end{aligned}$$

(2.2)

where $f_1,\ f_2,\ g_1,\, g_2,\ C_1^0,\ C_2^0$ and $\varvec{u}^0$ are all given functions properly defined on $\partial \Omega$ and in $\Omega$, respectively.

2.2 Reformulation of Mixed Weak Forms

We first reformulate (2.1) in terms of the following three extra vector-valued variables:

$$\begin{aligned} \varvec{q}=-\nabla \phi ,\quad z=\nabla \cdot \varvec{q},\quad \varvec{J}_i=\nabla C_i - z_i \varvec{q} C_i-\varvec{u} C_i. \end{aligned}$$

(2.3)

Here one can see that $\varvec{J}_1$ and $\varvec{J}_2$ are the mass flux of positively and negatively charged particles, respectively, while $\varvec{q}$ denotes the potential flux. With the above variables, we can reformulate the original modified PNP/NS system (2.1) to the following three new systems regarding the fourth-order elliptic equation, Nernst–Planck equations and Navier–Stokes equations, respectively:

$$\begin{aligned} \left. \begin{array}{lllll} \left\{ \begin{array}{lll} \varvec{q}=-\nabla \phi ,\\ z=\nabla \cdot \varvec{q},\\ -\Delta z+z=C_1-C_2,\\ \end{array} \right. \\ \left\{ \begin{array}{ll} \varvec{J}_i=\nabla C_i - z_i \varvec{q} C_i-\varvec{u} C_i,\\ \partial _t C_i-\nabla \cdot \varvec{J}_i=0,\\ \end{array} \right. \\ \left\{ \begin{array}{ll} \partial _t\varvec{u}+(\varvec{u} \cdot \nabla )\varvec{u}-\Delta \varvec{u} +\nabla p =\left( C_1-C_2\right) \varvec{q} ,\\ \nabla \cdot \varvec{u}=0,\\ \end{array} \right. \end{array} \right. \end{aligned}$$

(2.4)

with boundary conditions

$$\begin{aligned} \phi =f_1,~~ \nabla z\cdot \varvec{n}=-f_2,~~ C_i=g_i,~~ \varvec{u}=0,\quad \text {on}~~ \partial \Omega , ~t\in (0,T], \end{aligned}$$

(2.5)

and initial conditions

$$\begin{aligned} C_i=C_i^0,~~\varvec{u}=\varvec{u}^0,\quad \text {in}~~ \Omega . \end{aligned}$$

(2.6)

Define ${\varvec{V}} := \varvec{H}(\text {div};\Omega )=\{\varvec{v} \in \varvec{L}^2(\Omega ), \nabla \cdot \varvec{v} \in L^2(\Omega )\}$, and $\Vert \varvec{v}\Vert _{\varvec{V}}^2=\Vert \varvec{v}\Vert _{0}^2+\Vert \nabla \cdot \varvec{v}\Vert _{0}^2$, where $\Vert \cdot \Vert _0$ is the usual $\varvec{L}^2(\Omega )$-norm for vector-valued variables or $L^2(\Omega )$-norm for scalar-valued variables. Particularly, for the trial functional spaces of $\phi$, $C_i$, $\varvec{u}$ and p, we introduce $L_{f_1}^2(\Omega ):=\{\phi \in L^2(\Omega )|\phi =f_1 \text { on } \partial \Omega \}$, $L_{g_i}^2(\Omega ):=\{C_i\in L^2(\Omega )|C_i=g_i \text { on } \partial \Omega \} \ (i=1,2)$, $\varvec{H}_{0}^1(\Omega ):=\{\varvec{u}\in \varvec{H}^1(\Omega )|\varvec{u}=0 \text { on } \partial \Omega \}$, and $L_0^2(\Omega ):=\{p\in L^2(\Omega )|\int _\Omega p d\varvec{x}=0\}$, respectively.

Then, the mixed weak formulation of (2.4) can be defined as follows: find $(\phi ,\varvec{q}, z)\in L_{f_1}^2(\Omega ) \times {\varvec{V}} \times H^1(\Omega )$, $(C_i,\varvec{J}_i)\in L^2_{g_i}(\Omega )\times {\varvec{V}}$, $(\varvec{u}, p)\in \varvec{H}_{0}^1(\Omega )\times L_0^2(\Omega )$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \partial _t\varvec{u},\tilde{\varvec{u}}\right) +\beta (\varvec{u},\varvec{u},{{\tilde{\varvec{u}}}})+(\nabla \varvec{u},\nabla \tilde{\varvec{u}}) -(p,\nabla \cdot \tilde{\varvec{u}})=((C_1-C_2) \varvec{q},\tilde{\varvec{u}}), &{}\quad \forall \tilde{\varvec{u}}\in \varvec{H}_0^1(\Omega ), \\ (\nabla \cdot \varvec{u}, {{\tilde{p}}})=0, &{}\quad \forall {{\tilde{p}}} \in L^2(\Omega ), \end{array} \right. \end{aligned}$$

(2.9)

where we introduce a trilinear form, $\beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })=\frac{1}{2}((\varvec{\mu } \cdot \nabla )\varvec{\nu }, \varvec{\omega })-\frac{1}{2}((\varvec{\mu } \cdot \nabla )\varvec{\omega }, \varvec{\nu })$, to (2.9) for $\varvec{\mu },\varvec{\nu },\varvec{\omega } \in \varvec{H}_0^1(\Omega )$, and, if $\nabla \cdot \varvec{\mu }=0$, we have $\beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })=((\varvec{\mu } \cdot \nabla )\varvec{\nu },\varvec{\omega })$. The following lemma holds for the trilinear form $\beta (\cdot ,\cdot ,\cdot )$.

Lemma 2.1

[29,30,31]

$$\begin{aligned} \left\{ \begin{array}{lll} \beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })=-\beta (\varvec{\mu },\varvec{\omega },\varvec{\nu }), &{}\quad \forall \varvec{\mu },\varvec{\nu },\varvec{\omega } \in \varvec{H}_0^1(\Omega ),\\ |\beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })|\le C\Vert \nabla \varvec{\mu }\Vert _0\Vert \nabla \varvec{\nu }\Vert _0\Vert \nabla \varvec{\omega }\Vert _0 ,&{}\quad \forall \varvec{\mu },\varvec{\nu },\varvec{\omega } \in \varvec{H}_0^1(\Omega ),\\ |\beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })|\le C \Vert \varvec{\mu }\Vert _0^{\frac{1}{2}}\Vert \nabla \varvec{\mu }\Vert _0^{\frac{1}{2}}\Vert \nabla \varvec{\nu }\Vert _0\Vert \nabla \varvec{\omega }\Vert _0, &{}\quad \forall \varvec{\mu },\varvec{\nu },\varvec{\omega } \in \varvec{H}_0^1(\Omega ),\\ |\beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })|\le C \Vert \nabla \varvec{\mu }\Vert _0\Vert \varvec{\nu }\Vert _2 \Vert \varvec{\omega }\Vert _0, &{}\quad \forall \varvec{\nu }\in \varvec{H}^2(\Omega ), \varvec{\mu },\varvec{\omega } \in \varvec{H}_0^1(\Omega ). \end{array} \right. \end{aligned}$$

Moreover, if $\varvec{\mu }\in \varvec{H}_0^1(\Omega )\cap \varvec{L}^\infty (\Omega ),\varvec{\nu },\varvec{\omega } \in \varvec{H}_0^1(\Omega )$ with $\nabla \cdot \varvec{\mu }=0$, then

$$\begin{aligned} |\beta (\varvec{\mu },\varvec{\nu },\varvec{\omega })|+|\beta (\varvec{\mu },\varvec{\omega },\varvec{\nu })|\le C \Vert \varvec{\mu }\Vert _{{\infty }}\Vert \varvec{\nu }\Vert _0\Vert \nabla \varvec{\omega }\Vert _0. \end{aligned}$$

For the well-posedness property of (2.7a)-(2.9), first of all, we know (2.7c) is well-posed by the Lax–Milgram theorem since its bilinear form $a_z(z,{{\tilde{z}}})=(\nabla z,\nabla \tilde{z})+(z,{{\tilde{z}}})$ satisfies the continuity and the coercivity properties in $H^1(\Omega )$. Secondly, based on Brezzi’s theory [32,33,34], the well-posedness of solutions to the above three mixed weak formulations, (2.7a)–(2.7b), (2.8a)–(2.8b) and (2.9) are assured in $\varvec{V}\times L^2(\Omega )$, $\varvec{V}\times L^2(\Omega )$ and $\varvec{H}_0^1(\Omega )\times L^2(\Omega )$, respectively, if the following two compatibility conditions are held for each mixed weak formulation:

• (1) The coercivity property of bilinear forms $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})=(\varvec{q},{{\tilde{\varvec{q}}}})$ in (2.7a), $a_{\varvec{J}}(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)=(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)$ in (2.8a), and $a_{\varvec{u}}(\varvec{u},{{\tilde{\varvec{u}}}})=(\nabla \varvec{u},\nabla {{\tilde{\varvec{u}}}})$ in (2.9);

• (2) The Ladyzenskaja–Babu$\breve{s}$ka–Brezzi (LBB) or inf-sup condition of bilinear forms $b_{\varvec{q}}({{\tilde{\varvec{q}}}},{{\tilde{\phi }}})=(\nabla \cdot {{\tilde{\varvec{q}}}},{{\tilde{\phi }}})$ in (2.7a)–(2.7b), $b_{\varvec{J}}({{\tilde{\varvec{J}}}}_i,\tilde{C}_i)=(\nabla \cdot {{\tilde{\varvec{J}}}}_i,{{\tilde{C}}}_i)$ in (2.8a)–(2.8b), and $b_{\varvec{u}}({{\tilde{\varvec{u}}}},\tilde{p})=(\nabla \cdot {{\tilde{\varvec{u}}}},{{\tilde{p}}})$ in (2.9).

It is well known that the above two compatibility conditions impose very severe limitations in the choice of a stable mixed finite element for the mixed finite element approximation to the above three mixed weak formulations, in general. For instance, the Stokes-pair mixed finite elements such as Taylor–Hood element is stable for (2.9) in $\varvec{H}_0^1(\Omega )\times L^2(\Omega )$, it is however unstable for (2.7a)–(2.7b) and (2.8a)–(2.8b) in $\varvec{V}\times L^2(\Omega )$ since the coercivity properties of $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})$ and $a_{\varvec{J}}(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)$ are not held in $\varvec{V}$ if both $\varvec{q}$ and $\varvec{J}_i$ are chosen from a Lagrange-type piecewise polynomial space in $\varvec{H}^1(\Omega )\subset \varvec{V}$. Only a locally divergence-free mixed finite element such as Raviart–Thomas (RT) element [35] can fulfill the coercivity of $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})$ and $a_{\varvec{J}}(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)$ in $\varvec{V}$, but RT element cannot discretize the fluid velocity in $\varvec{H}^1(\Omega )$ for the mixed formulation of Navier–Stokes equations in (2.9). In order to apply the Lagrange-type Taylor–Hood mixed finite element to the above three mixed weak formulations, (2.7a)–(2.7b), (2.8a)–(2.8b) and (2.9), simultaneously, we need to add additional stabilization terms to (2.7a)–(2.7b) as well as (2.8a)–(2.8b) to guarantee the coercivity properties of $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})$ and $a_{\varvec{J}}(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)$ in $\varvec{V}$ when both $\varvec{q}$ and $\varvec{J}_i$ are discretized by Taylor–Hood mixed element in $\varvec{H}^1(\Omega )$ [36, 37].

2.3 Stabilized Mixed Weak Formulations

To make $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})$ coercive in $\varvec{V}$ without a divergence-free condition for $\varvec{q}$, we need to change it by taking ${{\tilde{\phi }}} = \nabla \cdot \varvec{q}$ in (2.7b) and then adding to (2.7a), resulting in the following stabilized mixed weak formulation for the electrostatic potential equation [36]

$$\begin{aligned} \left\{ \begin{array}{lll} \left( \varvec{q}, \tilde{\varvec{q}}\right) +(\nabla \cdot \varvec{q}, \nabla \cdot \tilde{\varvec{q}} )-(\phi ,\nabla \cdot \tilde{\varvec{q}})=(z,\nabla \cdot \tilde{\varvec{q}})-<f_1,\tilde{\varvec{q}}\cdot \varvec{n}>_{\partial \Omega }, &{}\quad \forall \tilde{\varvec{q}} \in \varvec{V},\\ (\nabla \cdot \varvec{q}, {{\tilde{\phi }}})=(z,{{\tilde{\phi }}}), &{}\quad \forall {\tilde{\phi }}\in L^2(\Omega ) ,\\ (\nabla z, \nabla {{\tilde{z}}})+(z,{{\tilde{z}}})=(C_1-C_2,\tilde{z})-<f_2,{{\tilde{z}}}>_{\partial \Omega }, &{}\quad \forall {\tilde{z}}\in H^1(\Omega ), \end{array} \right. \end{aligned}$$

(2.10)

where, $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})$ is redefined as $a_{\varvec{q}}(\varvec{q},{{\tilde{\varvec{q}}}})=(\varvec{q}, \tilde{\varvec{q}})+(\nabla \cdot \varvec{q}, \nabla \cdot \tilde{\varvec{q}} )$ that is definitely coercive in $\varvec{V}$.

As to the mixed parabolic form of the concentration equations (2.8a)-(2.8b), we differentiate (2.8a) in time and take ${{\tilde{C}}}_i=\nabla \cdot \varvec{J}_i$ in (2.8b), leading to

Subtract (2.11b) from (2.11a), then add to (2.8a), yield a stabilized mixed weak formulation for the concentration equations [37]

$$\begin{aligned} \left\{ \begin{array}{lll} \left( \partial _t \varvec{J}_i,{{\tilde{\varvec{J}}}}_i\right) +\left( \varvec{J}_i,\tilde{\varvec{J}}_i\right) +\left( \nabla \cdot \varvec{J}_i,\nabla \cdot \tilde{\varvec{J}}_i\right) +\left( C_i, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( z_i\varvec{q} C_i, {{\tilde{\varvec{J}}}}_i\right) +\left( \varvec{u} C_i, {{\tilde{\varvec{J}}}}_i\right) \\ +\left( z_i\partial _t\left( \varvec{q} C_i\right) ,\tilde{\varvec{J}}_i\right) +\left( \partial _t \left( \varvec{u} C_i\right) , \tilde{\varvec{J}}_i\right) =<g_i,{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }+<\partial _t g_i,{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }, &{}\quad \forall {{\tilde{\varvec{J}}}}_i \in {\varvec{V}},\\ \left( \partial _t C_i, {{\tilde{C}}}_i\right) -\left( \nabla \cdot \varvec{J}_i, {{\tilde{C}}}_i\right) =0, &{}\quad \,\,\forall {{\tilde{C}}}_i \in L^2(\Omega ), \end{array} \right. \end{aligned}$$

(2.12)

where, we can rewrite the bilinear form $a_{\varvec{J}}(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)=(\varvec{J}_i,{{\tilde{\varvec{J}}}}_i)+(\nabla \cdot \varvec{J}_i,\nabla \cdot {{\tilde{\varvec{J}}}}_i)$ that is certainly coercive in $\varvec{V}$ as well.

On the other hand, the bilinear form $b_{\varvec{q}}({{\tilde{\varvec{q}}}},{{\tilde{\phi }}})$ in (2.10), $b_{\varvec{J}}({{\tilde{\varvec{J}}}}_i,{{\tilde{C}}}_i)$ in (2.12) and $b_{\varvec{u}}({{\tilde{\varvec{u}}}},{{\tilde{p}}})$ in (2.9) all satisfy the inf-sup condition in their respective spaces [33, 35, 38], so by Brezzi’s theory, the above mixed weak formulations (2.10), (2.12) and (2.9) are all well-posed in their own spaces.

In addition, we assume the following regularity properties hold for the real solutions $\phi$, $\varvec{u}$, p and $C_i$ ($i=1,2$) to (2.1)

$$\begin{aligned}&\phi \in \left( H^1\cap L^{\infty }\right) \left( 0,T;H^{k+3}(\Omega )\cap W^{k+2,\infty }(\Omega )\right) \cap H^2\left( 0,T;H^1(\Omega )\right) , \end{aligned}$$

(2.13)

$$\begin{aligned}&C_i \in \left( H^1\cap L^{\infty }\right) \left( 0,T; H^{k+3}(\Omega )\cap L^{\infty }(\Omega )\right) \cap H^2\left( 0,T;H^1(\Omega )\right) ,\quad i=1,2, \end{aligned}$$

(2.14)

$$\begin{aligned}&\left\{ \begin{array}{l} \varvec{u} \in \left( H^1\cap L^{\infty }\right) \left( 0,T;\varvec{H}^{k+2}(\Omega )\cap \varvec{H}_0^1(\Omega )\cap W^{k+2,\infty }(\Omega )\right) \cap H^2\left( 0,T;L^2(\Omega )\right) ,\\ p \in L^2\left( 0,T;H^{k+1}(\Omega )\cap L_0^2(\Omega )\cap W^{k+1,\infty }(\Omega )\right) . \end{array} \right. \end{aligned}$$

(2.15)

3 Semi-discrete Mixed Finite Element Approximation

Let ${\mathcal {T}}_h$ be a shape-regular simplicial triangulation of $\Omega$ on which we introduce the following finite element spaces for $k\ge 1$:

$$\begin{aligned} {\varvec{V}}_h:= & {} \left\{ \varvec{v}\in \varvec{H}^1(\Omega )\subset \varvec{V}:\varvec{v}|_K \in \left[ P^{k+1}(K)\right] ^d,\forall K \in {\mathcal {T}}_h\right\} , \nonumber \\ W_h:= & {} \left\{ w\in L^2(\Omega ):w|_K\in P^{k}(K),\forall K \in {\mathcal {T}}_h\right\} ,\nonumber \\ W_{h,f_1}:= & {} \left\{ w\in L^2(\Omega ): w|_{\partial \Omega }=f_1,w|_K\in P^{k}(K),\forall K \in {\mathcal {T}}_h\right\} ,\nonumber \\ W_{h,g_i}:= & {} \left\{ w\in L^2(\Omega ): w|_{\partial \Omega }=g_i,w|_K\in P^{k}(K),\forall K \in {\mathcal {T}}_h\right\} ~(i=1,2),\\ Z_h:= & {} \left\{ z\in H^1(\Omega ):z|_K \in P^{k}(K),\forall K \in {\mathcal {T}}_h\right\} , \nonumber \\ \varvec{ U}_{h,0}:= & {} \left\{ \varvec{u}\in \varvec{H}_0^1(\Omega ):\varvec{u}|_K \in \left[ P^{k+1}(K)\right] ^d,\forall K \in {\mathcal {T}}_h\right\} ,\nonumber \end{aligned}$$

(3.1)

where the paris, $\varvec{V}_h \times W_{h,f_1}$, $\varvec{V}_h \times W_{h,g_i}$ and $U_{h,0} \times W_h$, are chosen as Taylor-Hood ($P^{k+1}P^k$) mixed finite element spaces, whereas $Z_h$ is a k-th order standard finite element. In what follows, we will develop and analyze a fully mixed finite element discretization for (2.10), (2.12) and (2.9) in the above finite element spaces.

3.1 Semi-discrete Mixed Finite Element Discretization

According to weak forms (2.10), (2.12) and (2.9), the semi-discrete mixed finite element approximation to the fourth-order modified PNP/NS model (2.1) is then defined as follows: find $(\phi _h,\varvec{q}_h, z_h)\in W_{h,f_1} \times {\varvec{V}}_h \times Z_h$, $(C_{i,h},\varvec{J}_{i,h})\in W_{h,g_i} \times {\varvec{V}}_h$, $(\varvec{u}_h, p_h)\in \varvec{ U}_{h,0}\times W_h$ such that

$$\begin{aligned}&\left\{ \begin{array}{lll} \left( \varvec{q}_h, \tilde{\varvec{q}}\right) +\left( \nabla \cdot \varvec{q}_h, \nabla \cdot \tilde{\varvec{q}} \right) -\left( \phi _h,\nabla \cdot \tilde{\varvec{q}}\right) =(z_h,\nabla \cdot \tilde{\varvec{q}})-<f_1,\tilde{\varvec{q}}\cdot \varvec{n}>_{\partial \Omega },~~~~~~~~~~~~&{} \forall \tilde{\varvec{q}} \in {\varvec{V}}_h,\\ \left( \nabla \cdot \varvec{q}_h, {{\tilde{\phi }}}\right) =\left( z_h,\tilde{\phi }\right) , &{} \forall {\tilde{\phi }}\in W_h,\\ \left( \nabla z_h, \nabla {{\tilde{z}}}\right) +\left( z_h,\tilde{z}\right) =\left( C_{1,h}-C_{2,h},{{\tilde{z}}}\right) -<f_2,\tilde{z}>_{\partial \Omega }, &{}\forall {\tilde{z}}\in Z_h, \end{array} \right. \end{aligned}$$

(3.2)

$$\begin{aligned}&\left\{ \begin{array}{l} \left( \partial _t \varvec{J}_{i,h},\tilde{\varvec{J}}_i\right) +\left( \varvec{J}_{i,h},{{\tilde{\varvec{J}}}}_i\right) +\left( \nabla \cdot \varvec{J}_{i,h},\nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( C_{i,h}, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( z_{i}\varvec{q}_h C_{i,h}, \tilde{\varvec{J}}_i\right) +\left( \varvec{u}_h C_{i,h}, {{\tilde{\varvec{J}}}}_i\right) \\ +\left( z_i\partial _t\left( \varvec{q}_h C_{i,h}\right) , \tilde{\varvec{J}}_i\right) +\left( \partial _t \left( \varvec{u}_h C_{i,h}\right) , \tilde{\varvec{J}}_i\right) =<g_i,{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }+<\partial _t g_i,{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }, \quad \forall {{\tilde{\varvec{J}}}}_i \in {\varvec{V}}_h,\\ \left( \partial _t C_{i,h}, {{\tilde{C}}}_i\right) -\left( \nabla \cdot \varvec{J}_{i,h}, {{\tilde{C}}}_i\right) =0, \forall {{\tilde{C}}}_i \in W_h, \end{array} \right. \nonumber \\ \end{aligned}$$

(3.3)

$$\begin{aligned}&\left\{ \begin{array}{ll} \left( \partial _t\varvec{u}_h,\tilde{\varvec{u}}\right) +\beta \left( \varvec{u}_h,\varvec{u}_h, \tilde{\varvec{u}}\right) +\left( \nabla \varvec{u}_h,\nabla \tilde{\varvec{u}}\right) -\left( p_h,\nabla \cdot \tilde{\varvec{u}}\right) =\left( \left( C_{1,h}-C_{2,h}\right) \varvec{q}_h,\tilde{\varvec{u}}\right) , &{} \forall \tilde{\varvec{u}}\in \varvec{\varvec{ U}}_{h,0},\\ \left( \nabla \cdot \varvec{u}_h, {{\tilde{p}}}\right) =0, &{} \forall {{\tilde{p}}} \in W_h. \end{array} \right. \end{aligned}$$

(3.4)

3.2 Semi-discrete Error Analysis

It is always necessary to decompose the finite element approximation error of the time-dependent and/or nonlinear PDE problems to two parts by introducing a linear and steady state $H^1$-projection of the solution to the original PDE problem, and, such $H^1$-projection shall satisfy the Galerkin orthogonality property. Hence, we introduce the $H^1$-projection of $(\phi , \varvec{q}, z)$ that is defined in (2.10), $(\Pi _h\phi , \Pi _h\varvec{q}, \Pi _hz)\in W_h\times {\varvec{V}}_h\times Z_h$, such that the following system

$$\begin{aligned} \left\{ \begin{array}{lll} \left( \varvec{q}-\Pi _h \varvec{q}, \tilde{\varvec{q}}\right) +\left( \nabla \cdot (\varvec{q}-\Pi _h \varvec{q}), \nabla \cdot \tilde{\varvec{q}} \right) -\left( \phi -\Pi _h \phi ,\nabla \cdot \tilde{\varvec{q}}\right) =0, ~~&{} \forall \tilde{\varvec{q}} \in {\varvec{V}}_h,\\ \left( \nabla \cdot (\varvec{q}-\Pi _h \varvec{q}), {{\tilde{\phi }}}\right) =0, &{} \forall {\tilde{\phi }}\in W_h ,\\ \left( \nabla \left( z-\Pi _hz\right) , \nabla \tilde{z}\right) +\left( z-\Pi _hz,{{\tilde{z}}}\right) =0, &{}\forall {\tilde{z}}\in Z_h. \end{array} \right. \end{aligned}$$

(3.5)

Obviously, (3.5) satisfies all compatibility conditions (continuity, coercivity and inf-sup conditions) of $a_{\varvec{q}}(\cdot ,\cdot )$, $b_{\varvec{q}}(\cdot ,\cdot )$ and $a_{z}(\cdot ,\cdot )$, and is thus well-posed according to Brezzi’s theory. Then we have the following Lemma [36, 38, 39].

Lemma 3.1

Let $(\phi , \varvec{q}, z)$ be the solution to (2.10), and $(\Pi _h\phi , \Pi _h\varvec{q}, \Pi _hz)$ be the solution to (3.5), then for any $t\in [0,T]$, the following error estimates hold

$$\begin{aligned}&\Vert \varvec{q}-\Pi _h \varvec{q}\Vert _{{\varvec{V}}}+\Vert \phi -\Pi _h\phi \Vert _{0} \le M h^{k+1}\left( \Vert \varvec{q}\Vert _{{k+2}} +\Vert \phi \Vert _{{k+1}}\right) \le M h^{k+1}\Vert \phi \Vert _{{k+3}}, \end{aligned}$$

(3.6)

$$\begin{aligned}&\Vert z-\Pi _h z\Vert _0+h\Vert z-\Pi _hz\Vert _1\le M h^{k+1}\Vert z\Vert _{{k+1}}\le M h^{k+1}\Vert \phi \Vert _{{k+3}}, \end{aligned}$$

(3.7)

$$\begin{aligned}&\Vert \partial _t\left( \varvec{q}-\Pi _h \varvec{q}\right) \Vert _{{\varvec{V}}}+\Vert \partial _t\left( \phi -\Pi _h\phi \right) \Vert _{0} \le M h^{k+1}\Vert \partial _t\phi \Vert _{{k+3}}, \end{aligned}$$

(3.8)

$$\begin{aligned}&\Vert \varvec{q}-\Pi _h \varvec{q} \Vert _{\infty }\le M h^{k+1}\Vert \varvec{q}\Vert _{{k+1,\infty }}\le M h^{k+1}\Vert \phi \Vert _{{k+2,\infty }}, \end{aligned}$$

(3.9)

$$\begin{aligned}&\Vert \partial _t\left( \varvec{q}-\Pi _h \varvec{q}\right) \Vert _{\infty }\le M h^{k+1}\Vert \partial _t\varvec{q}\Vert _{{k+1,\infty }}\le M h^{k+1}\Vert \partial _t\phi \Vert _{{k+2,\infty }}. \end{aligned}$$

(3.10)

Remark 3.1

The same $L^\infty$-error estimate as shown in (3.9) is presented in [39] for the mixed FEM using RT element, which relies on the study of a weighted $L^2$-projection, $R_h$, in a divergence-free finite element space. In our case of using Taylor–Hood mixed finite element, to prove the $L^\infty$-error estimate (3.9), we only need to replace the kernel space and the weighted $L^2$-projection which are used in [39] by the following kernel space $\overset{\circ }{{\varvec{V}}_h}=\{\varvec{v}_h\in {\varvec{V}}_h: (\nabla \cdot \varvec{v}_h,q_h)=0,\forall q_h\in W_h\}$, and the following weighted $L^2$-projection, $R_h: \varvec{L}^1(\Omega )\rightarrow \overset{\circ }{{\varvec{V}}_h}$ such that $\forall \varvec{v}\in \varvec{L}^1(\Omega )$, $R_h\varvec{v}\in \overset{\circ }{{\varvec{V}}_h}$, and

$$\begin{aligned} \left( \varvec{v}-R_h\varvec{v}, {{\tilde{\varvec{v}}}}\right) +\left( \nabla \cdot \left( \varvec{v}-R_h\varvec{v}\right) ,\nabla \cdot {{\tilde{\varvec{v}}}}\right) =0, ~~\forall {{\tilde{\varvec{v}}}}\in \overset{\circ }{{\varvec{V}}_h}, \end{aligned}$$

to account for the adoption of a stable Stokes-pair mixed finite element. Thereafter, the rest analyses are the same with [39, Theorem 3.1], then we can still obtain (3.9).

The following theorem is related with error estimates of $\phi -\phi _h$, $\varvec{q}-\varvec{q}_h$ and $z-z_h$ in their corresponding norms.

Theorem 3.1

Let $(\phi _h, \varvec{q}_h, z_h)$ be the solution to (3.2) and $(\phi , \varvec{q}, z)$ be the solution to (2.10), and the regularity property (2.13) is held. Then for any $t\in [0,T]$, the following error estimates hold

$$\begin{aligned}&\Vert \varvec{q}-\varvec{q_h}\Vert _{{L^\infty (\varvec{V})}}+\Vert \phi -\phi _h\Vert _{L^\infty \left( L^2\right) }\le M\left( \sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{L^\infty \left( L^2\right) }+h^{k+1}\right) , \end{aligned}$$

(3.11)

$$\begin{aligned}&\Vert z -z_h\Vert _{L^\infty (L^2)}+h\Vert z -z_h\Vert _{L^\infty \left( H^1\right) }\le M\left( \sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{L^\infty \left( L^2\right) }+ h^{k+1}\right) , \end{aligned}$$

(3.12)

$$\begin{aligned}&\Vert \partial _t(\varvec{q}-\varvec{q_h})\Vert _{{L^2(\varvec{V})}}+\Vert \partial _t\left( \phi -\phi _h\right) \Vert _{L^2\left( L^2\right) } \le M\left( \sum _{i=1}^2\Vert \partial _t\left( C_i-C_{i,h}\right) \Vert _{L^2\left( L^2\right) } + h^{k+1}\right) . \nonumber \\ \end{aligned}$$

(3.13)

Proof

Subtract (3.2) from (2.10), and apply the $H^1$-projection (3.5), yield

$$\begin{aligned}&\left( \Pi _h\varvec{q}-\varvec{q}_h, \tilde{\varvec{q}}\right) +\left( \nabla \cdot \left( \Pi _h\varvec{q}-\varvec{q}_h\right) , \nabla \cdot \tilde{\varvec{q}} \right) -\left( \Pi _h\phi -\phi _h,\nabla \cdot \tilde{\varvec{q}}\right) =\left( z-z_h,\nabla \cdot \tilde{\varvec{q}}\right) ,\quad \forall \tilde{\varvec{q}} \in {\varvec{V}}_h,\qquad \quad \end{aligned}$$

(3.14)

$$\begin{aligned}&\left( \nabla \cdot \left( \Pi _h\varvec{q}-\varvec{q}_h\right) , \tilde{\phi }\right) =\left( z-z_h,{{\tilde{\phi }}}\right) , \quad \forall {\tilde{\phi }}\in W_h, \end{aligned}$$

(3.15)

$$\begin{aligned}&\left( \nabla \left( \Pi _hz - z_h\right) , \nabla {{\tilde{z}}}\right) +\left( \Pi _hz - z_h,\tilde{z}\right) =\left( \left( C_{1}-C_{2}\right) -\left( C_{1,h}-C_{2,h}\right) ,\tilde{z}\right) , \quad \forall {\tilde{z}}\in Z_h. \end{aligned}$$

(3.16)

Let ${{\tilde{z}}}=\Pi _hz - z_h \in Z_h$ in (3.16), utilize the Cauchy–Schwarz inequality, and Young’s inequality with $\epsilon$: $pq\le \epsilon p^2 + \frac{1}{4\epsilon }q^2$, results

$$\begin{aligned} \Vert \nabla \left( \Pi _h z -z_h\right) \Vert _0+\Vert \Pi _h z -z_h\Vert _0\le M\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0. \end{aligned}$$

(3.17)

Further combining with (3.7), we have (3.12).

Because the discrete inf-sup condition holds for $b_{\varvec{q}}({{\tilde{\varvec{q}}}},{{\tilde{\phi }}})$ in Taylor–Hood finite element spaces [34, 38], we attain

$$\begin{aligned} \Vert \Pi _h\phi -\phi _h\Vert _0\le & {} M\sup \limits _{\tilde{\varvec{q}}\in {\varvec{V}}_h}\frac{\left( \Pi _h\phi -\phi _h,\nabla \cdot \tilde{ \varvec{q}}\right) }{\Vert \tilde{\varvec{q}}\Vert _{\varvec{V}}}\nonumber \\ (\text {by}~ (3.14))\le & {} M \sup \limits _{\tilde{\varvec{q}}\in {\varvec{V}}_h}\frac{\Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{\varvec{V}}\Vert \tilde{\varvec{q}}\Vert _{\varvec{V}}+\Vert z-z_h\Vert _0\Vert \tilde{\varvec{q}}\Vert _{\varvec{V}}}{\Vert \tilde{\varvec{q}}\Vert _{\varvec{V}}}\nonumber \\\le & {} M \left( \Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{\varvec{V}}+\Vert z-z_h\Vert _0\right) . \end{aligned}$$

(3.18)

Let $\tilde{\varvec{q}}=\Pi _h\varvec{q}-\varvec{q}_h, {{\tilde{\phi }}}= \Pi _h\phi -\phi _h$ in (3.14) and (3.15), then add them together, leads to

$$\begin{aligned} \Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{\varvec{V}}^2= & {} \left( z-z_h,\nabla \cdot \left( \Pi _h\varvec{q}-\varvec{q}_h\right) \right) +\left( z-z_h,\Pi _h\phi -\phi _h\right) \nonumber \\\le & {} \Vert z-z_h\Vert _0\Vert \nabla \cdot \left( \Pi _h\varvec{q}-\varvec{q}_h\right) \Vert _0+\Vert z-z_h\Vert _0\Vert \Pi _h\phi -\phi _h\Vert _0\nonumber \\ (\text {by}~(3.18))\le & {} M \left( \Vert z-z_h\Vert _0 \Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{\varvec{V}}+ \Vert z-z_h\Vert _0^2\right) \nonumber \\\le & {} M\Vert z-z_h\Vert ^2_0 +\epsilon \Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert ^2_{\varvec{V}}. \end{aligned}$$

(3.19)

Take a sufficiently small $\epsilon$, and apply (3.18), yield

$$\begin{aligned} \Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{\varvec{V}}+\Vert \Pi _h\phi -\phi _h\Vert _0\le M \Vert z-z_h\Vert _0. \end{aligned}$$

(3.20)

Combining with (3.6) and (3.12), then we have (3.11).

Differentiating (3.14)–(3.16) with respect to time, we have

$$\begin{aligned}&\left( \partial _t\left( \Pi _h\varvec{q}-\varvec{q}_h\right) , \tilde{\varvec{q}}\right) +\left( \nabla \cdot \partial _t(\Pi _h\varvec{q}-\varvec{q}_h), \nabla \cdot \tilde{\varvec{q}} \right) -\left( \partial _t\left( \Pi _h\phi -\phi _h\right) ,\nabla \cdot \tilde{\varvec{q}}\right) =\left( \partial _t(z-z_h),\nabla \cdot \tilde{\varvec{q}}\right) ,\nonumber \\&\quad \left( \nabla \cdot \partial _t\left( \left( \Pi _h\varvec{q}-\varvec{q}_h\right) , \tilde{\phi }\right) =\left( \partial _t\left( z-z_h\right) ,{{\tilde{\phi }}}\right) , \right. \nonumber \\&\quad \left( \nabla \partial _t \left( \Pi _hz - z_h\right) , \nabla {{\tilde{z}}}\right) +\left( \partial _t\left( \Pi _hz - z_h\right) ,\tilde{z}\right) =\left( \partial _t\left( \left( C_{1}-C_{2}\right) -\left( C_{1,h}-C_{2,h}\right) ,\tilde{z}\right) \right. . \end{aligned}$$

(3.21)

Taking $\tilde{\varvec{q}}=\partial _t(\Pi _h\varvec{q}-\varvec{q}_h), {{\tilde{\phi }}}= \partial _t(\Pi _h\phi -\phi _h)$, ${{\tilde{z}}}= \partial _t(\Pi _hz - z_h)$ in (3.21), and following the similar error estimate process at above, we can also attain (3.13). $\square$

We further define the $H^1$-projection $(\Pi _h{\varvec{u}},\Pi _h p)\in \varvec{ U}_{h,0}\times W_h$ of $(\varvec{u},p)$ that is the solution to (2.9) such that

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \nabla \Pi _h{\varvec{u}},\nabla \tilde{\varvec{u}}\right) - \left( \Pi _h p,\nabla \cdot \tilde{\varvec{u}}\right) =\left( \nabla \varvec{u},\nabla \tilde{\varvec{u}}\right) -(p,\nabla \cdot \tilde{\varvec{u}}),&{}\quad \forall \tilde{\varvec{u}}\in \varvec{ U}_{h,0},\\ \left( \nabla \cdot \Pi _h{\varvec{u}},{{\tilde{p}}}\right) = \left( \nabla \cdot \varvec{u},{{\tilde{p}}}\right) , &{}\quad \forall {{\tilde{p}}} \in W_h. \end{array} \right. \end{aligned}$$

(3.22)

By [32, Theorems (12.6.7), (12.6.13)], and [29, Theorems 3.1-3.3 ], we have the following lemma.

Lemma 3.2

Let $(\varvec{u}_h, p_h)$ be the finite element solution to (3.4). Suppose $(\Pi _h u, \Pi _h p)\in \varvec{ U}_{h,0}\times W_h$ is defined in (3.22), then we have the following error estimates,

$$\begin{aligned}&\Vert \varvec{u}-\Pi _h{\varvec{u}}\Vert _0 + h\Vert \varvec{u}-\Pi _h{\varvec{u}}\Vert _1 +h\Vert p-\Pi _h p\Vert _0 \le Mh^{k+2}\left( \Vert \varvec{u}\Vert _{{k+2}} + \Vert p\Vert _{{k+1}}\right) ,\\&\quad \Vert \partial _t\left( \varvec{u}-\Pi _h{\varvec{u}}\right) \Vert _0 + h\Vert \partial _t\left( \varvec{u}-\Pi _h{\varvec{u}}\right) \Vert _1\le Mh^{k+2}\left( \Vert \varvec{u}\Vert _{{k+2}}+\Vert \partial _t\varvec{u}\Vert _{{k+2}} + \Vert p\Vert _{{k+1}}\right) ,\\&\quad \Vert \varvec{u}-\Pi _h{\varvec{u}}\Vert _{{\infty }}+h|\ln h|^{\frac{1}{2}}\Vert \varvec{u}-\Pi _h{\varvec{u}}\Vert _{{1,\infty }}\le Mh^{k+2}|\ln h|(\Vert \varvec{u}\Vert _{{k+2,\infty } }+\Vert p\Vert _{{k+1,\infty }}),\\&\quad \Vert \partial _t\left( \varvec{u}-\Pi _h{\varvec{u}}\right) \Vert _{{\infty }} \le Mh^{k+2}|\ln h|\left( \Vert \varvec{u}\Vert _{{k+2,\infty } }+\Vert \partial _t\varvec{u}\Vert _{{k+2,\infty }}+\Vert p\Vert _{{k+1,\infty }}\right) . \end{aligned}$$

Now we carry out error estimates for $\varvec{u}-\varvec{u}_h$ and $p -p_h$, as shown in the following theorem.

Theorem 3.2

Let $(\varvec{u}_h, p_h)$ be the finite element solution to (3.4) and $(\varvec{u}, p)$ is defined in (2.9), and the regularity property (2.15) is held. Then the following error estimates hold

$$\begin{aligned}&\Vert \varvec{u}-\varvec{u}_h\Vert _{L^\infty \left( \varvec{L}^2\right) }+\Vert \varvec{u}-\varvec{u}_h\Vert _{L^2\left( \varvec{H}^1\right) }\nonumber \\&\quad \le M \left[ \sum _{i=1}^2\left( h^{-{\frac{d}{2}}}\Vert C_i-C_{i,h}\Vert _{L^2(L^2)}^2+\Vert C_i-C_{i,h}\Vert _{L^2\left( L^2\right) }\right) + h^{k+1}\right] . \end{aligned}$$

(3.23)

$$\begin{aligned}&\Vert \partial _t\left( \varvec{u}-\varvec{u}_h\right) \Vert _{L^{2}\left( \varvec{L}^2\right) }+\Vert \varvec{u}-\varvec{u}_h\Vert _{L^{\infty }\left( \varvec{H}^1\right) }\nonumber \\&\quad \le M \left[ \sum _{i=1}^2\left( h^{-{\frac{d}{2}}}\Vert C_i-C_{i,h}\Vert _{L^2\left( L^2\right) }^2+\Vert C_i-C_{i,h}\Vert _{L^2\left( L^2\right) }\right) \right. \nonumber \\&\qquad \left. + h^{k+1} +h^{-1}\sum _{i=1}^2 \left( h^{-d}\Vert C_i-C_{i,h}\Vert _{L^2\left( L^2\right) }^4+\Vert C_i-C_{i,h}\Vert _{L^2\left( L^2\right) }^2\right) \right] . \end{aligned}$$

(3.24)

$$\begin{aligned}&\Vert p-p_h\Vert _{L^2\left( L^2\right) }\nonumber \\&\quad \le M \left[ \sum _{i=1}^2\left( h^{-{\frac{d}{2}}}\Vert C_i-C_{i,h}\Vert _{L^{2}\left( L^2\right) }^2+\Vert C_i-C_{i,h}\Vert _{L^{2}\left( L^2\right) }\right) + h^{k+1}\right. \nonumber \\&\qquad \left. +h^{-1}\sum _{i=1}^2 \left( h^{-d}\Vert C_i-C_{i,h}\Vert _{L^{2}\left( L^2\right) }^4+\Vert C_i-C_{i,h}\Vert _{L^{2}\left( L^2\right) }^2\right) \right] . \end{aligned}$$

(3.25)

Proof

Subtract (3.4) from (2.9), and use (3.22), yield

Let $\varvec{u}-\varvec{u}_h=(\varvec{u}-\Pi _h \varvec{u})+(\Pi _h{\varvec{u}}-\varvec{u}_h)=\eta +\xi$, and choose $\tilde{\varvec{u}}=\xi$, ${{\tilde{p}}}=\Pi _h p-p_h$ in (3.26) and (3.27). Then

$$\begin{aligned} \left( \partial _t(\eta +\xi ),\xi \right) + a_{\varvec{u}}\left( \xi ,\xi \right) +\beta (\varvec{u},\varvec{u},\xi )-\beta \left( \varvec{u}_h,\varvec{u}_h,\xi \right) =\sum _{i=1}^2z_i\left( C_i\varvec{q} -C_{i,h}\varvec{q}_h,\xi \right) , \end{aligned}$$

(3.28)

leading to

$$\begin{aligned} \frac{1}{2}\partial _t\Vert \xi \Vert _0^2+ \Vert \nabla \xi \Vert _0^2= & {} -\left( \partial _t\eta ,\xi \right) +\beta \left( \varvec{u}_h,\varvec{u}_h,\xi \right) -\beta \left( \Pi _h\varvec{u},\Pi _h\varvec{u},\xi \right) \nonumber \\&+ \beta \left( \Pi _h\varvec{u},\Pi _h\varvec{u},\xi \right) -\beta (\varvec{u},\varvec{u},\xi )+\sum _{i=1}^2z_i\left( C_i\varvec{q} -C_{i,h}\varvec{q}_h,\xi \right) . \end{aligned}$$

(3.29)

We first estimate terms involving $\beta (\cdot ,\cdot ,\cdot )$ as follows.

$$\begin{aligned} \beta \left( \varvec{u}_h,\varvec{u}_h,\xi \right) -\beta \left( \Pi _h\varvec{u},\Pi _h\varvec{u},\xi \right)= & {} -\beta \left( \varvec{u}_h, \xi ,\xi \right) -\beta \left( \xi ,\Pi _hu,\xi \right) =-\beta \left( \xi ,\Pi _hu,\xi \right) \nonumber \\ (\text {by Lemma}~~ 2.1)\le & {} M \Vert \nabla \Pi _h\varvec{u}\Vert _0\Vert \xi \Vert _0^{\frac{1}{2}}\Vert \nabla \xi \Vert _0^{\frac{3}{2}}\nonumber \\\le & {} M\Vert \xi \Vert _0^2+\epsilon \Vert \nabla \xi \Vert ^2_0, \end{aligned}$$

(3.30)

where we employ the definition of $\beta (\cdot ,\cdot ,\cdot )$, the boundedness of $\Vert \Pi _h\varvec{u}\Vert _1$ due to Lemma 3.2, and Young’s inequality with $\epsilon :\, pq\le Mp^4+\epsilon q^{4/3}$, and

$$\begin{aligned} \beta \left( \Pi _h\varvec{u},\Pi _h\varvec{u},\xi \right) -\beta (\varvec{u},\varvec{u},\xi )= & {} \beta \left( \varvec{u}-\Pi _h\varvec{u},\varvec{u}-\Pi _h\varvec{u},\xi \right) \nonumber \\&-\beta \left( \varvec{u}-\Pi _h\varvec{u},\varvec{u},\xi \right) -\beta (\varvec{u},\varvec{u}-\Pi _h\varvec{u},\xi )\nonumber \\ (\text {by Lemma } 2.1)\le & {} M \left( \Vert \nabla \left( \varvec{u}-\Pi _h\varvec{u}\right) \Vert _0^2+\Vert \varvec{u}-\Pi _h\varvec{u}\Vert _0\right) \Vert \nabla \xi \Vert _0\nonumber \\ (\text {by Lemma } 3.2)\le & {} M\left( h^{4(k+1)}+h^{2(k+2)}\right) +\epsilon \Vert \nabla \xi \Vert ^2_0. \end{aligned}$$

(3.31)

Next, we estimate the last term on the right hand side of (3.29).

$$\begin{aligned}&\sum _{i=1}^2z_i\left( C_i\varvec{q} -C_{i,h}\varvec{q}_h,\xi \right) \nonumber \\&\quad =\sum _{i=1}^2z_i\left( \left( C_i -C_{i,h}\right) \varvec{q},\xi \right) +\sum _{i=1}^2z_i\left( C_{i}(\varvec{q}-\varvec{q}_h),\xi \right) -\sum _{i=1}^2z_i\left( \left( C_{i}-C_{i,h}\right) \left( \varvec{q}-\varvec{q}_h\right) ,\xi \right) \nonumber \\&\quad \le M\sum _{i=1}^2 \left( \Vert \varvec{q} \Vert _{L^{\infty }}\Vert C_i -C_{i,h}\Vert _0\Vert \xi \Vert _0+\Vert C_i\Vert _{L^{\infty }}\Vert \varvec{q}-\varvec{q}_h\Vert _0\Vert \xi \Vert _0\right. \nonumber \\&\qquad \left. +\left( \Vert \varvec{q}-\Pi _h\varvec{q}_h\Vert _{L^\infty }+\Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{L^\infty }\right) \Vert C_{i}-C_{i,h}\Vert _0\Vert \xi \Vert _{0}\right) \nonumber \\&\quad \le M\Vert \xi \Vert _0\sum _{i=1}^2\left( \Vert C_i-C_{i,h}\Vert _{0} +\Vert \varvec{q}-\varvec{q}_h\Vert _0\right. \nonumber \\&\qquad \left. +\left( \Vert \varvec{q}-\Pi _h\varvec{q}\Vert _{L^\infty }+h^{-\frac{d}{2}}\Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _0\right) \Vert C_{i}-C_{i,h}\Vert _0 \right) \nonumber \\&\quad \le M \Vert \xi \Vert _{0}\left( \left( 1+h^{k+1-\frac{d}{2}}\right) \sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{0}+ h^{k+1} + h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2\right) \nonumber \\&\quad \le M \Vert \xi \Vert _{0}\left( \sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{0}+ h^{k+1} + h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2\right) , \end{aligned}$$

(3.32)

where we apply (3.9), (3.11) and the inverse inequality: $\Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _{L^\infty }\le M h^{-\frac{d}{2}}\Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _0$.

Combining the above error estimates together and applying Young’s inequality, we have the following result for (3.29)

$$\begin{aligned} \frac{1}{2}\partial _t\Vert \xi \Vert _0^2+ \Vert \nabla \xi \Vert _0^2\le & {} M \left[ \left( h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2\right) ^2\right. \\&\left. + \sum _{i=1}^2 \Vert C_i-C_{i,h}\Vert _{0}^2+h^{2(k+1)} +\Vert \xi \Vert _0^2\right] +\epsilon \Vert \nabla \xi \Vert _0^2. \end{aligned}$$

Take a sufficiently small $\epsilon$, integrate both sides with respect to time from 0 to t, then apply Grönwall’s inequality with a proper choice on the initial condition $\varvec{u}_h^0=\Pi _h\varvec{u}^0$, leads to

$$\begin{aligned} \Vert \xi \Vert _{L^\infty (\varvec{L}^2)}+\Vert \xi \Vert _{L^2(\varvec{H}^1)} \le M \left( h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{L^2(L^2)}^2+\sum _{i=1}^2 \Vert C_i-C_{i,h}\Vert _{L^2\left( L^2\right) } + h^{k+1}\right) .\,\,\,\,\,\, \end{aligned}$$

(3.33)

Then (3.23) is obtained by combining (3.33) with Lemma 3.2.

On the other hand, choose $\tilde{\varvec{u}}=\partial _t\xi$ in (3.26), differentiate (3.27) in time and then choose ${{\tilde{p}}}=\Pi _h p-p_h$, yield

$$\begin{aligned} \Vert \partial _t\xi \Vert _0^2+\frac{1}{2} \partial _t \Vert \nabla \xi \Vert _0^2= & {} -\left( \partial _{t}\eta ,\partial _t\xi \right) +\beta \left( \varvec{u}-\varvec{u}_h,\varvec{u}-\varvec{u}_h,\partial _t\xi \right) \nonumber \\&-\beta \left( \varvec{u},\varvec{u}-\varvec{u}_h,\partial _t\xi \right) -\beta \left( \varvec{u}-\varvec{u}_h,\varvec{u},\partial _t\xi \right) \nonumber \\&+\sum _{i=1}^2z_i\left( C_i\varvec{q} -C_{i,h}\varvec{q}_h,\partial _t\xi \right) . \end{aligned}$$

(3.34)

By Lemmas 2.1 and 3.2, we have

$$\begin{aligned} |\beta \left( \varvec{u}-\varvec{u}_h,\varvec{u}-\varvec{u}_h,\partial _t\xi \right) |\le & {} M \Vert \nabla \left( \varvec{u}-\varvec{u}_h\right) \Vert _0^2\Vert \nabla \partial _t\xi \Vert _0\le M \Vert \nabla \left( \varvec{u}-\varvec{u}_h\right) \Vert _0^2\ h^{-1}\Vert \partial _t\xi \Vert _0\\\le & {} M h^{-2}\Vert \nabla \left( \varvec{u}-\varvec{u}_h\right) \Vert _0^4+\epsilon \Vert \partial _t\xi \Vert _0^2,\\ \big |-\beta \left( \varvec{u},\varvec{u}-\varvec{u}_h,\partial _t\xi \right)- & {} \beta \left( \varvec{u}-\varvec{u}_h,\varvec{u},\partial _t\xi \right) \big |\\\le & {} M\Vert \varvec{u}\Vert _{\infty } \Vert \nabla \left( \varvec{u}-\varvec{u}_h\right) \Vert _0\Vert \partial _t\xi \Vert _0+ \Vert \nabla \left( \varvec{u}-\varvec{u}_h\right) \Vert _0\Vert \varvec{u}\Vert _2\Vert \partial _t\xi \Vert _0\\\le & {} M \Vert \nabla \left( \varvec{u}-\varvec{u}_h\right) \Vert _0^2+\epsilon \Vert \partial _t\xi \Vert _0^2\\\le & {} M \left( h^{2k+2}+\Vert \nabla \xi \Vert _0^2\right) +\epsilon \Vert \partial _t\xi \Vert _0^2 \end{aligned}$$

Similar to (3.32), the last term on the right hand side of (3.34) can be estimated as

$$\begin{aligned} \begin{aligned} \sum _{i=1}^2z_i\left( C_i\varvec{q} -C_{i,h}\varvec{q}_h,\partial _t\xi \right)\le & {} M \Vert \partial _t\xi \Vert _{0}\left( h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2+\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{0}+ h^{k+1} \right) \\\le & {} M \left( h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2+\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{0}+ h^{k+1} \right) ^2+\epsilon \Vert \partial _t\xi \Vert _{0}^2. \end{aligned} \end{aligned}$$

(3.35)

Then, take a sufficiently small $\epsilon$, (3.34) yields

$$\begin{aligned} \Vert \partial _t\xi \Vert _0+\partial _t \Vert \nabla \xi \Vert _0\le & {} M\left( h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2+\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{0}+ h^{k+1} +\Vert \nabla \xi \Vert _0 \right. \\&\left. + h^{-1}\Vert \varvec{u}-\varvec{u}_h\Vert _1^2\right) . \end{aligned}$$

Integrate both sides in time from 0 to t, and apply Grönwall’s inequality with $\varvec{u}_h(0)=\Pi _h\varvec{u}^0$, results

$$\begin{aligned} \Vert \partial _t\xi \Vert _{L^2\left( \varvec{L}^2\right) }+\Vert \nabla \xi \Vert _{L^{\infty }\left( \varvec{L}^2\right) }\le & {} M\left( h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{L^2\left( \varvec{L}^2\right) }^2+\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _{L^2\left( \varvec{L}^2\right) }\right. \nonumber \\&\left. + h^{k+1}+h^{-1}\Vert \varvec{u}-\varvec{u}_h\Vert _{L^2\left( \varvec{H}^1\right) }^2\right) . \end{aligned}$$

(3.36)

Applying (3.23), we obtain the desired (3.24) with Lemma 3.2.

To prove (3.25), we need to apply the discrete form of inf-sup condition $b_u(\cdot ,\cdot )$, i.e., for any $\Pi _h p\in W_h$, we have [38]

$$\begin{aligned} \Vert \Pi _h p - p_h\Vert _0\le M\sup _{\forall \tilde{\varvec{u}} \in \varvec{ U}_{h,0}\backslash \{0\}}\frac{b_{\varvec{u}}\left( \tilde{\varvec{u}},\Pi _h p - p_h\right) }{\Vert \tilde{\varvec{u}}\Vert _1}. \end{aligned}$$

(3.37)

Then from (3.26) we have

$$\begin{aligned} b_{\varvec{u}}\left( \tilde{\varvec{u}},\Pi _h p - p_h\right)= & {} \left( \partial _t(\varvec{u}-\varvec{u}_h),{\tilde{\varvec{u}}}\right) +a_{\varvec{u}}\left( \Pi _h\varvec{u}-\varvec{u}_h,\tilde{\varvec{u}}\right) +\beta \left( \varvec{u},\varvec{u},\tilde{\varvec{u}}\right) -\beta \left( \varvec{u}_h,\varvec{u}_h,\tilde{\varvec{u}}\right) \\&-\sum _{i=1}^2z_i\left( C_i\varvec{q} -C_{i,h}\varvec{q}_h,\tilde{\varvec{u}}\right) . \end{aligned}$$

By (3.37), the continuity of $a_{\varvec{u}}(\cdot ,\cdot )$ and the same error analyses for (3.30)–(3.32), we can obtain

$$\begin{aligned} \Vert \Pi _h p - p_h\Vert _0\le & {} M\left( \Vert \partial _t\xi \Vert _0+\Vert \xi \Vert _1 +h^{k+1}+\sum _{i=1}^2 \Vert C_i-C_{i,h}\Vert _{0} + h^{-{\frac{d}{2}}}\sum _{i=1}^2\Vert C_i-C_{i,h}\Vert _0^2\right) . \end{aligned}$$

Then integrate both sides in time from 0 to t, by (3.36), (3.23), Lemma 3.2 and the triangular inequality, we obtain (3.25). $\square$

Now we analyze error estimates of (3.3) between $(C_i, \varvec{J}_i)\in L^2(\Omega )\times \varvec{V}$ and $(C_{i,h}, \varvec{J}_{i,h})\in W_h\times \varvec{V}_h$. We first introduce the $H^1$-projection of $(C_i, \varvec{J}_i)$, $(\Pi _h C_i, \Pi _h \varvec{J}_i)\in W_h\times {\varvec{V}}_h$, satisfying

$$\begin{aligned} \left\{ \begin{array}{lll} \left( \varvec{J}_i-\Pi _h \varvec{J}_i, \tilde{\varvec{J}_i}\right) \!+\!\left( \nabla \cdot \left( \varvec{J}_i-\Pi _h \varvec{J}_i\right) , \nabla \cdot \tilde{\varvec{J}_i} \right) +\left( C_i-\Pi _h C_i,\nabla \cdot \tilde{\varvec{J}_i}\right) =0, ~~&{} \forall \tilde{\varvec{J}_i} \!\in \! {\varvec{V}}_h,\\ -\left( \nabla \cdot \left( \varvec{J}_i-\Pi _h \varvec{J}_i\right) , \tilde{C}_i\right) \!=\!0, &{} \forall \tilde{C_i}\!\in \! W_h. \end{array} \right. \end{aligned}$$

(3.38)

Clearly, (3.38) satisfies all compatibility conditions (continuity, coercivity and inf-sup conditions) of $a_{\varvec{J}}(\cdot ,\cdot )$ and $b_{\varvec{J}}(\cdot ,\cdot )$ in $W_h\times \varvec{V}_h$, it is thus well-posed according to Brezzi’s theory, and holds the following Lemma [36, 38].

Lemma 3.3

Let $(C_i, \varvec{J}_i)$ be the solution to (2.12), and $(\Pi _h C_i, \Pi _h \varvec{J}_i)$ be the solution to (3.38). Then for any $t\in [0,T]$, we have the following error estimates

$$\begin{aligned}&\Vert \varvec{J}_i-\Pi _h \varvec{J}_i\Vert _{{\varvec{V}}}+\Vert C_i-\Pi _h C_i\Vert _{0} \le M h^{k+1} \left( \Vert \varvec{J}_i\Vert _{{k+2}}+\Vert C_i\Vert _{{k+1}}\right) ,\end{aligned}$$

(3.39)

$$\begin{aligned}&\Vert \partial _t\left( \varvec{J}_i-\Pi _h \varvec{J}_i\right) \Vert _{{\varvec{V}}}+\Vert \partial _t\left( C_i-\Pi _h C_i\right) \Vert _{0} \le M h^{k+1} \left( \Vert \partial _t\varvec{J}_i\Vert _{{k+2}}+\Vert \partial _tC_i\Vert _{{k+1}}\right) . \end{aligned}$$

(3.40)

The following theorem demonstrates error estimates of (3.3) approximating to (2.12).

Theorem 3.3

Let $(C_i, \varvec{J}_i)$ be the solution to (2.12) and $(C_{i,h}, \varvec{J}_{i,h})$ be the finite element solution to (3.3), the regularity assumption (2.14) is held. Then we have the following error estimates

$$\begin{aligned}&\Vert \varvec{J}_i -\varvec{J}_{i,h} \Vert _{L^{\infty }\left( L^2\right) }+ \Vert \varvec{J}_i -\varvec{J}_{i,h} \Vert _{L^2({\varvec{V}})}+\Vert C_i -C_{i,h} \Vert _{L^{\infty }\left( L^2\right) } \le Mh^{k+1}, \end{aligned}$$

(3.41)

$$\begin{aligned}&\Vert \partial _t\left( \varvec{J}_i -\varvec{J}_{i,h}\right) \Vert _{L^{2}\left( L^2\right) }+ \Vert \varvec{J}_i -\varvec{J}_{i,h} \Vert _{L^\infty ({\varvec{V}})}+\Vert \partial _t\left( C_i -C_{i,h}\right) \Vert _{L^{2}\left( L^2\right) } \le Mh^{k+1}. \end{aligned}$$

(3.42)

Proof

Subtract (3.3) from (2.12), and use (3.38), yield

$$\begin{aligned}&\left( \partial _t\left( \varvec{J}_i -\varvec{J}_{i,h}\right) ,\tilde{\varvec{J}}_i\right) +\left( \Pi _h \varvec{J}_i-\varvec{J}_{i,h},\tilde{\varvec{J}}_i\right) \nonumber \\&\quad +\left( \nabla \cdot \left( \Pi _h \varvec{J}_i - \varvec{J}_{i,h}\right) ,\nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( \Pi _h C_i-C_{i,h}, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) \nonumber \\&\quad +z_{i}\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}, \tilde{\varvec{J}}_i\right) +\left( \varvec{u} C_i-\varvec{u}_h C_{i,h}, {{\tilde{\varvec{J}}}}_i\right) +z_i\left( \partial _t\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}\right) , {{\tilde{\varvec{J}}}}_i\right) \nonumber \\&\quad +\left( \partial _t \left( \varvec{u} C_i-\varvec{u}_h C_{i,h}\right) , {{\tilde{\varvec{J}}}}_i\right) =0,\quad \forall {{\tilde{\varvec{J}}}}_i \in {\varvec{V}}_h, \end{aligned}$$

(3.43)

$$\begin{aligned}&\left( \partial _t \left( C_i-C_{i,h}\right) , \tilde{C}_i\right) -\left( \nabla \cdot \left( \Pi _hJ_i-\varvec{J}_{i,h}\right) , \tilde{C}_i\right) =0, \quad \forall {{\tilde{C}}}_i \in W_h. \end{aligned}$$

(3.44)

Let $\varvec{J}_i -\varvec{J}_{i,h}=(\varvec{J}_i-\Pi _h\varvec{J}_i)+(\Pi _h \varvec{J}_i - \varvec{J}_{i,h})=e_i+\theta _i$, $C_i -C_{i,h}=(C_i-\Pi _hC_i)+(\Pi _h C_i - C_{i,h})=\sigma _i+\delta _i$, choose ${{\tilde{\varvec{J}}}}_i=\theta _i$, $\tilde{C}_i=\delta _i$ in (3.43) and (3.44), and add them together, results

$$\begin{aligned}&\left( \partial _t\left( e_i+\theta _i\right) ,\theta _i\right) +\left( \theta _i,\theta _i\right) \\&\quad +\left( \nabla \cdot \theta _i,\nabla \cdot \theta _i\right) +\left( \partial _t\left( \sigma _i+\delta _i\right) ,\delta _i\right) \\&\quad +z_{i}\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}, \theta _i\right) +\left( \varvec{u} C_i-\varvec{u}_h C_{i,h},\theta _i\right) +z_i\left( \partial _t(\varvec{q} C_i-\varvec{q}_h C_{i,h}), \theta _i\right) \\&\quad +\left( \partial _t \left( \varvec{u} C_i-\varvec{u}_h C_{i,h}\right) ,\theta _i\right) =0. \end{aligned}$$

Then,

$$\begin{aligned}&\frac{1}{2}\partial _t\Vert \theta _i\Vert _0^2+\Vert \theta _i\Vert _{\varvec{V}}^2+\frac{1}{2}\partial _t\Vert \delta _i\Vert _0^2\nonumber \\&\quad =-\left( \partial _t e_i,\theta _i\right) -\left( \partial _t\sigma _i,\delta _i\right) -z_{i}\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}, \theta _i\right) -\left( \varvec{u} C_i-\varvec{u}_h C_{i,h},\theta _i\right) \nonumber \\&\qquad -z_i\left( \partial _t\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}\right) , \theta _i\right) -\left( \partial _t \left( \varvec{u} C_i-\varvec{u}_h C_{i,h}\right) ,\theta _i\right) =\sum _{j=1}^6 G_j. \end{aligned}$$

(3.45)

By Cauchy–Schwarz inequality, Young’s inequality with $\epsilon$ and Lemma (3.3), we have

$$\begin{aligned} G_1\le & {} M \Vert \partial _t e_i\Vert _0^2+\epsilon \Vert \theta _i\Vert _0^2\le M h^{2(k+1)}+\epsilon \Vert \theta _i\Vert _0^2, \end{aligned}$$

(3.46)

$$\begin{aligned} G_2\le & {} M \Vert \partial _t \sigma _i\Vert _0^2+\epsilon \Vert \delta _i\Vert _0^2\le M h^{2(k+1)}+\epsilon \Vert \delta _i\Vert _0^2. \end{aligned}$$

(3.47)

Utilize the same analysis skills for estimating (3.32), and apply Lemmas 3.1 and 3.2, Theorems 3.1 and 3.2 as well as corresponding inverse inequalities, leads to

$$\begin{aligned} G_3= & {} -z_i\left. \left( \left( C_i -C_{i,h}\right) \varvec{q},\theta _i\right) -z_i\left( C_{i}\left( \varvec{q}-\varvec{q}_h\right) ,\theta _i\right) +z_i\left( \left( C_{i}-C_{i,h}\right) \left( \varvec{q}-\varvec{q}_h\right) ,\theta _i\right) \right) \nonumber \\\le & {} M\Vert \theta _i\Vert _0\left( \Vert \varvec{q} \Vert _{L^{\infty }}\Vert C_i -C_{i,h}\Vert _0+\Vert C_i\Vert _{L^{\infty }}\Vert \varvec{q}-\varvec{q}_h\Vert _0 +\Vert \varvec{q}-\varvec{q}_h\Vert _{L^\infty }\Vert C_{i}-C_{i,h}\Vert _0\right) \nonumber \\\le & {} M\Vert \theta _i\Vert _0\left( \Vert C_i-C_{i,h}\Vert _{0} +\Vert \varvec{q}-\varvec{q}_h\Vert _0 +h^{-\frac{d}{2}}\Vert \Pi _h\varvec{q}-\varvec{q}_h\Vert _0 \Vert C_{i}-C_{i,h}\Vert _0 \right) \nonumber \\\le & {} M\left[ \sum _{i=1}^2 \Vert \delta _i\Vert _{0}^2 + h^{2(k+1)}+ \left( h^{-\frac{d}{2}}\Vert \delta _i\Vert _{0}\sum _{j=1}^2 \Vert \delta _j\Vert _{0}\right) ^2+\Vert \theta _i\Vert _0^2\right] , \end{aligned}$$

(3.48)

$$\begin{aligned} G_4= & {} \left( \left( C_i -C_{i,h}\right) \varvec{u},\theta _i\right) +\left( \left( C_{i}\left( \varvec{u}-\varvec{u}_h\right) ,\theta _i\right) -\left( \left( C_{i}-C_{i,h}\right) \left( \varvec{u}-\varvec{u}_h\right) ,\theta _i\right) \right) \nonumber \\\le & {} M\Vert \theta _i\Vert _{0}\left( \Vert \varvec{u} \Vert _{L^{\infty }}\Vert C_i -C_{i,h}\Vert _0 +\Vert C_i\Vert _{L^{\infty }}\Vert \varvec{u}-\varvec{u}_h\Vert _0+\Vert \varvec{u}-\varvec{u}_h\Vert _{L^\infty }\Vert C_{i}-C_{i,h}\Vert _0\right) \nonumber \\\le & {} M\Vert \theta _i\Vert _{0}\left( \Vert C_i-C_{i,h}\Vert _{0}+\Vert \varvec{u}-\varvec{u}_h\Vert _0+ h^{-\frac{d}{2}}\Vert \Pi _h\varvec{u}-\varvec{u}_h\Vert _{0}\Vert C_{i}-C_{i,h}\Vert _0 \right) \nonumber \\\le & {} M\left[ \sum _{i=1}^2 \Vert \delta _i\Vert _{0}^2 +\left( h^{-\frac{d}{2}}\Vert \delta _i\Vert _{0}\sum _{j=1}^2 \Vert \delta _j\Vert _{0} \right) ^2 +\left( h^{-d}\Vert \delta _i\Vert _{0}\sum _{j=1}^2 \Vert \delta _j\Vert _{0}^2 \right) ^2+ h^{2(k+1)}+\Vert \theta _i\Vert _0^2\right] , \nonumber \\ \end{aligned}$$

(3.49)

$$\begin{aligned} G_5= & {} -z_i\left( \partial _t\left( \left( C_i -C_{i,h}\right) \varvec{q}\right) ,\theta _i\right) -z_i\left( \partial _t\left( C_{i}\left( \varvec{q}-\varvec{q}_h\right) \right) ,\theta _i\right) +z_i\left( \partial _t\left( \left( C_{i}-C_{i,h}\right) \left( \varvec{q}-\varvec{q}_h\right) \right) ,\theta _i\right) \nonumber \\\le & {} M\Vert \theta _i\Vert _0\left( \Vert \partial _t\varvec{q} \Vert _{L^{\infty }}\Vert C_i -C_{i,h}\Vert _0+\Vert \varvec{q} \Vert _{L^{\infty }}\Vert \partial _t \left( C_i -C_{i,h}\right) \Vert _0\right. \nonumber \\&+\left. \Vert \partial _tC_i\Vert _{L^{\infty }}\Vert \varvec{q}-\varvec{q}_h\Vert _0+\Vert C_i\Vert _{L^{\infty }}\Vert \partial _t(\varvec{q}-\varvec{q}_h)\Vert _0\right. \nonumber \\&+\left. \Vert \varvec{q}-\varvec{q}_h\Vert _{L^\infty }\Vert \partial _t\left( C_{i}-C_{i,h}\right) \Vert _0+\Vert \partial _t\left( \varvec{q}-\varvec{q}_h\right) \Vert _{L^\infty }\Vert C_{i}-C_{i,h}\Vert _0\right) \nonumber \\\le & {} M\Vert \theta _i\Vert _0\left( \Vert C_i-C_{i,h}\Vert _{0}+\Vert \partial _t\left( C_i-C_{i,h}\right) \Vert _{0}+\Vert \varvec{q}-\varvec{q}_h\Vert _0 +\Vert \partial _t(\varvec{q}-\varvec{q}_h)\Vert _0\right. \nonumber \\&+\left. h^{-\frac{d}{2}}\Vert \Pi _h \varvec{q}-\varvec{q}_h\Vert _{0}\Vert \partial _t(C_{i}-C_{i,h})\Vert _0+ h^{-\frac{d}{2}}\Vert \partial _t(\Pi _h \varvec{q}-\varvec{q}_h)\Vert _{0}\Vert C_{i}-C_{i,h}\Vert _0\right) \nonumber \\\le & {} M \left[ \sum _{i=1}^2\Vert \delta _i\Vert _{0}^2 + h^{2(k+1)}+\Vert \theta _i\Vert _0^2+\left( h^{-\frac{d}{2}}\Vert \theta _i\Vert _0 \sum _{j=1}^2 \Vert \delta _j\Vert _{0}\right) ^2 +\left( h^{-\frac{d}{2}} \Vert \delta _i\Vert _{0}\Vert \theta _i\Vert _0\right) ^2\right] \nonumber \\&+ \epsilon \sum _{i=1}^2\Vert \partial _t\delta _i\Vert _{0}^2. \end{aligned}$$

(3.50)

By conducting the same analysis as for (3.49) and (3.50), we have

$$\begin{aligned} G_6= & {} -\left( \partial _t\left( \left( C_i -C_{i,h}\right) \varvec{u}\right) ,\theta _i\right) -\left( \partial _t\left( C_{i}\left( \varvec{u}-\varvec{u}_h\right) \right) ,\theta _i\right) +z_i\left( \partial _t\left( \left( C_{i}-C_{i,h}\right) \left( \varvec{u}-\varvec{u}_h\right) \right) ,\theta _i\right) \nonumber \\\le & {} M\Vert \theta _i\Vert _0\left( \Vert \partial _t\varvec{u} \Vert _{L^{\infty }}\Vert C_i -C_{i,h}\Vert _0+\Vert \varvec{u} \Vert _{L^{\infty }}\Vert \partial _t \left( C_i -C_{i,h}\right) \Vert _0\right. \nonumber \\&+\Vert \partial _tC_i\Vert _{L^{\infty }}\Vert \varvec{u}-\varvec{u}_h\Vert _0+\Vert C_i\Vert _{L^{\infty }}\Vert \partial _t\left( \varvec{u}-\varvec{u}_h\right) \Vert _0\nonumber \\&\left. +\Vert \varvec{u}-\varvec{u}_h\Vert _{L^\infty }\Vert \partial _t\left( C_{i}-C_{i,h}\right) \Vert _0+\Vert \partial _t\left( \varvec{u}-\varvec{u}_h\right) \Vert _{L^\infty }\Vert C_{i}-C_{i,h}\Vert _0\right) \nonumber \\\le & {} M\Vert \theta _i\Vert _0\left( \Vert C_i-C_{i,h}\Vert _{0}+\Vert \partial _t\left( C_i-C_{i,h}\right) \Vert _{0}+\Vert \varvec{u}-\varvec{u}_h\Vert _0 +\Vert \partial _t\left( \varvec{u}-\varvec{u}_h\right) \Vert _0\right. \nonumber \\&+\left. h^{-\frac{d}{2}}\Vert \Pi _h \varvec{u}-\varvec{u}_h\Vert _{0}\Vert \partial _t\left( C_{i}-C_{i,h}\right) \Vert _0+ h^{-\frac{d}{2}}\Vert \partial _t\left( \Pi _h \varvec{u}-\varvec{u}_h\right) \Vert _{0}\Vert C_{i}-C_{i,h}\Vert _0\right) \nonumber \\\le & {} M \left[ \sum _{i=1}^2\Vert \delta _i\Vert _0^2+\Vert \theta \Vert _0^2+h^{2(k+1)}+\left( h^{-\frac{d}{2}}\sum _{j=1}^2\Vert \delta _j\Vert _0^2 \right) ^2 +\left( h^{-d-1}\sum _{j=1}^2\Vert \delta _j\Vert _0^4\right) ^2\right. \nonumber \\&+\left( h^{-1}\sum _{j=1}^2\Vert \delta _j\Vert _0^2\right) ^2+\left( h^{-d}\Vert \theta _i\Vert _0\sum _{j=1}^2\Vert \delta _j\Vert _0^2\right) ^2+\left( h^{-\frac{d}{2}}\Vert \theta _i\Vert _0\sum _{j=1}^2\Vert \delta _j\Vert _0\right) ^2\nonumber \\&\left. +\left( h^{-\frac{3}{2} d-1}\Vert \theta _i\Vert _0\sum _{j=1}^2\Vert \delta _j\Vert _0^4 \right) ^2+ \left( h^{-\frac{d}{2}-1}\Vert \theta _i\Vert _0\sum _{j=1}^2|\delta _j\Vert _0^2 \right) ^2 \right] + \epsilon \Vert \partial _t\delta _i\Vert _0^2. \end{aligned}$$

(3.51)

Now we conduct a mathematical induction process and propose the following induction hypothesis:

$$\begin{aligned} h^{-\frac{d}{2}}\Vert \delta _i(t)\Vert _{0}\le M,~ \forall t\in [0,T], i=1,2,\, d=2,3. \end{aligned}$$

(3.52)

When $t=0$, by a properly chose initial value $C_{i,h}(0)=\Pi _hC_i^0$, we have $\delta _i(0)=0$, thus (3.52) is satisfied. Assume that (3.52) holds for $G_3, G_4, G_5$ and $G_6$ for $t\in [0,T^*]$, $T^*<T$, then

$$\begin{aligned} G_3+G_4+G_5+G_6\le & {} M\left( \sum _{i=1}^2 \Vert \delta _i\Vert _{0}^2 + h^{2(k+1)}+\Vert \theta _i\Vert _0^2\right) +\epsilon \sum _{i=1}^2\Vert \partial _t\delta _i\Vert _{0}^2.\qquad \end{aligned}$$

(3.53)

On the other hand, let ${{\tilde{C}}}_i= \partial _t \delta _i$ in (3.44), we have

$$\begin{aligned} \left( \partial _t\left( \sigma _i+\delta _i\right) ,\partial _t\delta _i\right) -\left( \nabla \cdot \theta _i,\partial _t\delta _i\right) =0, \end{aligned}$$

(3.54)

thus

$$\begin{aligned} \Vert \partial _t \delta _i\Vert _0\le \Vert \partial _t \sigma _i\Vert _0+\Vert \nabla \cdot \theta _i\Vert _0. \end{aligned}$$

(3.55)

Substitute (3.55) into (3.53), then (3.45) can be estimated as

$$\begin{aligned} \frac{1}{2}\partial _t\Vert \theta _i\Vert _0^2+\Vert \theta _i\Vert _{\varvec{V}}^2+\frac{1}{2}\partial _t \Vert \delta _i\Vert _0^2 \le M\left( \sum _{i=1}^2\Vert \delta _i\Vert _{0}^2+ h^{2(k+1)}+\Vert \theta _i\Vert _0^2\right) + \epsilon \sum _{i=1}^2\Vert \theta _i\Vert _{\varvec{V}}^2. \end{aligned}$$

(3.56)

Sum over i from 1 to 2, take a sufficiently small $\epsilon$, integrate both sides of (3.56) in time from 0 to t, then apply Grönwall’s inequality with $C_{i,h}(0)=\Pi _hC_i^0$ and $\varvec{J}_{i,h}(0)=\Pi _h\varvec{J}_i^0$ (see Remark 3.2), yield

$$\begin{aligned} \sum _{i=1}^2\left( \Vert \theta _i\Vert _{L^\infty (L^2)}+\Vert \theta _i\Vert _{L^2({\varvec{V}})}+\Vert \delta _i\Vert _{L^\infty (L^2)}\right) \le Mh^{k+1}, \end{aligned}$$

(3.57)

which is true for any $t\in [0,T^*]$. (3.57) also shows that for $k \ge 1$ and $d = 2,3$, we always have

$$\begin{aligned} h^{-\frac{d}{2}}\Vert \delta _i(t)\Vert _{0}\le Mh^{k+1-\frac{d}{2}}\le M. \end{aligned}$$

On the other hand, since $h^{-\frac{d}{2}}\Vert \delta _i(t)\Vert _{0}$ is a continuous function with respect to $t\in [0, T]$, thus due to the uniform continuity in time, there exists $\epsilon$ such that for any $t\in [0, T^*+\epsilon ]$, we have $h^{-\frac{d}{2}}\Vert \delta _i(t)\Vert _{0}\le M$. Because [0, T] is a finite interval, so the induction hypothesis (3.52) holds true for all $t\in [0, T]$. Therefore, for any $t\in [0, T]$ we have (3.57).

Combine (3.57) with (3.55), apply Lemma 3.3 and the triangular inequality, (3.41) is then obtained. On the other hand, choose $\tilde{\varvec{J}}_i=\partial _t\theta _i$, ${{\tilde{C}}}_i=\partial _t\delta _i$ in (3.43) and (3.44), yields

$$\begin{aligned}&\Vert \partial _t\theta _i\Vert _0^2+\frac{1}{2}\partial _t\Vert \theta _i\Vert _{0}^2+\frac{1}{2}\partial _t\Vert \nabla \cdot \theta _i\Vert _{0}^2 =-\left( \partial _t e_i,\partial _t\theta _i\right) +\left( \partial _t \left( \sigma _i + \delta _i\right) ,\partial _t\delta _i\right) -\partial _t\left( \delta _i, \nabla \cdot \theta _i\right) \nonumber \\&\quad -z_{i}\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}, \partial _t\theta _i\right) -\left( \varvec{u} C_i-\varvec{u}_h C_{i,h},\partial _t\theta _i\right) -z_i\left( \partial _t\left( \varvec{q} C_i-\varvec{q}_h C_{i,h}\right) ,\partial _t\theta _i\right) \nonumber \\&\quad -\left( \partial _t \left( \varvec{u} C_i-\varvec{u}_h C_{i,h}\right) ,\partial _t\theta _i\right) =\sum _{j=1}^7 R_j. \end{aligned}$$

(3.58)

By Cauchy–Schwarz inequality, Young’s inequality with $\epsilon$, Lemma 3.3 and (3.55), we have

$$\begin{aligned} R_1\le & {} M \Vert \partial _t e_i\Vert _0^2+\epsilon \Vert \partial _t\theta _i\Vert _0^2\le M h^{2(k+1)}+\epsilon \Vert \partial _t\theta _i\Vert _0^2, \end{aligned}$$

(3.59)

$$\begin{aligned} R_2\le & {} M \left( \Vert \partial _t \sigma _i\Vert _0^2+\Vert \partial _t \delta _i\Vert _0^2\right) \le M\left( h^{2(k+1)}+\Vert \nabla \cdot \theta _i\Vert _0^2\right) . \end{aligned}$$

(3.60)

Utilize the same analysis skills as conducted in (3.48), (3.49), (3.50) and (3.51) for Terms $R_4$-$R_7$, results

$$\begin{aligned} R_4+R_5+R_6+R_7\le & {} M\left( \sum _{i=1}^2 \left( \Vert \delta _i\Vert _{0}^2+\Vert \nabla \cdot \theta _i\Vert _{0}^2\right) + h^{2(k+1)}\right) +\epsilon \Vert \partial _t\theta _i\Vert _0^2. \end{aligned}$$

(3.61)

Take a sufficiently small $\epsilon$, and apply (3.57), then (3.58) can be estimated as

$$\begin{aligned} \Vert \partial _t\theta _i\Vert _0^2+\frac{1}{2}\partial _t\Vert \theta _i\Vert _{\varvec{V}}^2 \le M (h^{2(k+1)} +\Vert \nabla \cdot \theta _i\Vert _0^2)-\partial _t(\delta _i, \nabla \cdot \theta _i). \end{aligned}$$

(3.62)

Integrate both sides in time from 0 to t, yields

$$\begin{aligned} \int _0^t\Vert \partial _t\theta _i\Vert _0^2d\tau +\Vert \theta _i\Vert _{\varvec{V}}^2\le & {} M \left( h^{2(k+1)} +\int _0^t\Vert \theta _i\Vert _{\varvec{V}}^2d\tau \right) -\left( \delta _i, \nabla \cdot \theta _i\right) \nonumber \\\le & {} M \left( h^{2(k+1)} +\int _0^t\Vert \theta _i\Vert _{\varvec{V}}^2d\tau \right) +\Vert \delta _i\Vert _0^2+\epsilon \Vert \theta _i\Vert _{\varvec{V}}^2. \end{aligned}$$

(3.63)

Then, further take a sufficiently small $\epsilon$, apply Grönwall’s inequality and (3.57), leads to

$$\begin{aligned} \Vert \partial _t\theta _i\Vert _{L^2(L^2)}+\Vert \theta _i\Vert _{L^\infty ({\varvec{V}})}\le M h^{k+1}. \end{aligned}$$

(3.64)

Combine (3.64) with (3.55), apply Lemma 3.3 and the triangular inequality, (3.42) is then obtained. $\square$

Combining Theorems 3.1, 3.2, 3.3, we finally obtain a complete convergence theorem for the semi-discrete scheme (3.2)–(3.4) as follows.

Theorem 3.4

Let $(\phi , \varvec{q}, z,u,p,C_i,\varvec{J}_i)$ be the solution to (2.7a)–(2.9) satisfying the regularity properties (2.13)–(2.15), and $(\phi _h, \varvec{q}_h, z_h,u_h,p_h,$ $C_{i,h}, \varvec{J}_{i,h})$ be the solution to (3.2)–(3.4). Then the following error estimates hold

$$\begin{aligned}&\Vert \varvec{q}-\varvec{q_h}\Vert _{L^{\infty }({\varvec{V}})}+\Vert \partial _t\left( \varvec{q}-\varvec{q_h}\right) \Vert _{L^{2}({\varvec{V}})} +\Vert \phi -\phi _h\Vert _{L^{\infty }\left( L^2\right) }+\Vert \partial _t\left( \phi -\phi _h\right) \Vert _{L^{2}(L^2)}\nonumber \\&\quad +\Vert z -z_h\Vert _{L^{\infty }\left( L^2\right) }+h\Vert z -z_h\Vert _{L^{\infty }(H^1)}\le M h^{k+1}, \end{aligned}$$

(3.65)

$$\begin{aligned}&\Vert \varvec{u}-\varvec{u}_h\Vert _{L^\infty \left( \varvec{L}^2\right) }+\Vert \varvec{u}-\varvec{u}_h\Vert _{L^\infty \left( \varvec{H}^1\right) }+\Vert \partial _t\left( \varvec{u}-\varvec{u}_h\right) \Vert _{L^{2}\left( \varvec{L}^2\right) }\nonumber \\&\quad +\Vert p-p_h\Vert _{L^{2}\left( L^2\right) } \le Mh^{k+1}, \end{aligned}$$

(3.66)

$$\begin{aligned}&\Vert C_i -C_{i,h} \Vert _{L^{\infty }(L^2)}+\Vert \partial _t\left( C_i -C_{i,h}\right) \Vert _{L^{2}\left( L^2\right) }\nonumber \\&\quad +\Vert \varvec{J}_i -\varvec{J}_{i,h} \Vert _{L^{\infty }(\varvec{V})}+ \Vert \varvec{J}_i -\varvec{J}_{i,h} \Vert _{L^\infty ({L^2})} \le Mh^{k+1}. \end{aligned}$$

(3.67)

Remark 3.2

Given initial values $C_i^0$ and $\varvec{u}^0$, we can obtain $\phi ^0=\phi (0)$ that is determined by the fourth-order elliptic equation in (2.1) at $t=0$ with the boundary condition shown in (2.2). Thereafter, by the definition (2.4), we have $\varvec{J}_{i}^0=\varvec{J}_{i}(0)=\nabla C_{i}^0+z_i \nabla \phi ^0C_{i}^0-\varvec{u}^0C_{i}^0$. Thus, all discrete initial values can be defined as: $C_{i,h}(0)=\Pi _hC_i^0$, $\varvec{J}_{i,h}(0)=\Pi _h\varvec{J}_i^0$ and $\varvec{u}_h(0)=\Pi _h\varvec{u}^0$ by their own $H^1$-projection.

4 Fully Discrete Mixed Finite Element Approximation

In order to develop a full discretization for (2.9), (2.10) and (2.12) , we first define a uniform partition in the time interval [0, T]: $0=t_0<t_1<\cdot \cdot \cdot <t_N=T$ with the time-step size $\Delta t=T/N$, then set $t_n=n\Delta t$ ($0\le n\le N$). Let $\varphi ^n=\varphi (t^n)$, and $d_t\varphi ^{n+1}=\frac{\varphi ^{n+1}-\varphi ^{n}}{\Delta t}$. In what follows, we employ the backward Euler scheme together with Taylor–Hood mixed finite element approximation to define the fully discrete scheme of (2.9), (2.10) and (2.12).

4.1 Fully Discrete Mixed Finite Element Discretization

For $n=0,1,\cdots ,N-1$, suppose $(\phi _h^n,\varvec{q}_h^n, z_h^n, C_{i,h}^n,\varvec{J}_{i,h}^n,\varvec{u}_h^n, p_h^n)$ are given, find $(\phi _h^{n+1},\varvec{q}_h^{n+1}, z_h^{n+1})\in W_{h,f_1} \times {\varvec{V}}_h \times Z_h$, $(C_{i,h}^{n+1},\varvec{J}_{i,h}^{n+1})\in W_{h,g_i} \times {\varvec{V}}_h$, $(\varvec{u}_h^{n+1}, p_h^{n+1})\in \varvec{ U}_{h,0}\times W_h$, $\forall (\tilde{\varvec{q}}, {\tilde{\phi }}, {\tilde{z}}, {{\tilde{\varvec{J}}}}_i, {{\tilde{C}}}_i,\tilde{\varvec{u}},{{\tilde{p}}})\in {\varvec{V}}_h\times W_h \times Z_h\times {\varvec{V}}_h \times W_h\times \varvec{ U}_{h,0}\times W_h$, such that

$$\begin{aligned}&\left\{ \begin{array}{lll} \left( \varvec{q}_h^{n+1}, \tilde{\varvec{q}}\right) +\left( \nabla \cdot \varvec{q}_h^{n+1}, \nabla \cdot \tilde{\varvec{q}} \right) -\left( \phi _h^{n+1},\nabla \cdot \tilde{\varvec{q}}\right) =\left( z_h^{n+1},\nabla \cdot \tilde{\varvec{q}}\right) -<f_1^{n+1},\tilde{\varvec{q}}\cdot \varvec{n}>_{\partial \Omega },\\ \left( \nabla \cdot \varvec{q}_h^{n+1}, {{\tilde{\phi }}}\right) =\left( z_h^{n+1},{{\tilde{\phi }}}\right) ,\\ \left( \nabla z_h^{n+1}, \nabla \tilde{z}\right) +\left( z_h^{n+1},\tilde{z}\right) =\left( C_{1,h}^{n+1}-C_{2,h}^{n+1},\tilde{z}\right) -<f_2^{n+1},{{\tilde{z}}}>_{\partial \Omega }, \end{array} \right. \end{aligned}$$

(4.1)

$$\begin{aligned}&\left\{ \begin{array}{ll} \left( d_t \varvec{J}_{i,h}^{n+1},\tilde{\varvec{J}}_i\right) +\left( \varvec{J}_{i,h}^{n+1},{{\tilde{\varvec{J}}}}_i\right) +(\nabla \cdot \varvec{J}_{i,h}^{n+1},\nabla \cdot {{\tilde{\varvec{J}}}}_i)+\left( C_{i,h}^{n+1}, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +z_{i}\left( \varvec{q}_h^{n+1} C_{i,h}^{n+1},{{\tilde{\varvec{J}}}}_i\right) \\ \qquad +\left( \varvec{u}_h^{n+1} C_{i,h}^{n+1}, \tilde{\varvec{J}}_i\right) +z_i\left( d_t\left( C_{i,h}^{n+1}\varvec{q}_h^{n+1}\right) , \tilde{\varvec{J}}_i\right) +\left( d_t \left( C_{i,h}^{n+1} \varvec{u}_h^{n+1}\right) , {{\tilde{\varvec{J}}}}_i\right) \\ \quad =<g_i^{n+1},\tilde{\varvec{J}}_i\cdot \varvec{n}>_{\partial \Omega }+<\partial _t g_i^{n+1},\tilde{\varvec{J}}_i\cdot \varvec{n}>_{\partial \Omega },\\ \left( d_t C_{i,h}^{n+1}, {{\tilde{C}}}_i\right) -\left( \nabla \cdot {\varvec{J}}_{i,h}^{n+1}, {{\tilde{C}}}_i\right) =0, \end{array} \right. \end{aligned}$$

(4.2)

$$\begin{aligned}&\left\{ \begin{array}{ll} \left( d_t\varvec{u}_h^{n+1},\tilde{\varvec{u}}\right) +\beta \left( \varvec{u}_h^{n+1},\varvec{u}_h^{n+1},\tilde{\varvec{u}}\right) +\left( \nabla \varvec{u}_h^{n+1},\nabla \tilde{\varvec{u}}\right) -\left( p_h^{n+1},\nabla \cdot \tilde{\varvec{u}}\right) \\ \quad =\left( \left( C_{1,h}^{n+1}-C_{2,h}^{n+1}\right) \varvec{q}_h^{n+1},\tilde{\varvec{u}}\right) , \\ \left( \nabla \cdot \varvec{u}_h^{n+1}, {{\tilde{p}}}\right) =0. \end{array} \right. \end{aligned}$$

(4.3)

We use Picard’s method to linearize nonlinear terms in (4.1)–(4.3), and implement the following Algorithm 4.1 to carry out the mixed finite element computation for the presented modified PNP/NS coupling system (2.1).

Algorithm 4.1

• 1. Initialization of time marching: set $n=0$ and adopt the discrete initial values $(C_{i,h}^0,\varvec{J}_{i,h}^0,\varvec{u}_h^0)$ as shown in Remark 3.2.

• 2. Initialization of nonlinear iteration: let $(\phi _h^{n+1,0},\varvec{q}_h^{n+1,0}, z_h^{n+1,0}, C_{i,h}^{n+1,0},\varvec{J}_{i,h}^{n+1,0},\varvec{u}_h^{n+1,0}, p_h^{n+1,0})=(\phi _h^n,\varvec{q}_h^n, z_h^n, C_{i,h}^n,\varvec{J}_{i,h}^n,\varvec{u}_h^n, p_h^n)$ as $n\ge 0$. Set $m=0$.

• 3. Mixed finite element computation at each nonlinear iteration: for $m\ge 0$, find

  $(\phi _h^{n+1,m+1},\varvec{q}_h^{n+1,m+1}, z_h^{n+1,m+1}, C_{i,h}^{n+1,m+1},\varvec{J}_{i,h}^{n+1,m+1},\varvec{u}_h^{n+1,m+1}, p_h^{n+1,m+1}) \in W_{h,f_1} \times {\varvec{V}}_h \times Z_h \times W_{h,g_i} \times {\varvec{V}}_h \times \varvec{ U}_{h,0}\times W_h$, $\forall (\tilde{\varvec{q}}, {\tilde{\phi }}, {\tilde{z}}, {{\tilde{\varvec{J}}}}_i, \tilde{C}_i,\tilde{\varvec{u}},{{\tilde{p}}})\in {\varvec{V}}_h\times W_h \times Z_h\times {\varvec{V}}_h \times W_h\times \varvec{ U}_{h,0}\times W_h$ such that

  $$\begin{aligned}&\left\{ \begin{array}{lll} \left( \varvec{q}_h^{n+1,m+1}, \tilde{\varvec{q}}\right) +\left( \nabla \cdot \varvec{q}_h^{n+1,m+1}, \nabla \cdot \tilde{\varvec{q}} \right) -\left( \phi _h^{n+1,m+1},\nabla \cdot \tilde{\varvec{q}}\right) -\left( z_h^{n+1,m+1},\nabla \cdot \tilde{\varvec{q}}\right) \\ =-<f_1^{n+1},\tilde{\varvec{q}}\cdot \varvec{n}>_{\partial \Omega },\\ \left( \nabla \cdot \varvec{q}_h^{n+1,m+1}, {{\tilde{\phi }}}\right) -\left( z_h^{n+1,m+1},{{\tilde{\phi }}}\right) =0, \\ \left( \nabla z_h^{n+1,m+1}, \nabla \tilde{z}\right) +\left( z_h^{n+1,m+1},\tilde{z}\right) =\left( C_{1,h}^{n+1,m}-C_{2,h}^{n+1,m},\tilde{z}\right) -<f_2^{n+1},{{\tilde{z}}}>_{\partial \Omega }, \end{array} \right. \\&\left\{ \begin{array}{ll} \left( \frac{ \varvec{J}_{i,h}^{n+1,m+1}-\varvec{J}_{i,h}^{n}}{\Delta t},\tilde{\varvec{J}}_i\right) +\left( \varvec{J}_{i,h}^{n+1,m+1},\tilde{\varvec{J}}_i\right) +\left( \nabla \cdot \varvec{J}_{i,h}^{n+1,m+1},\nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( C_{i,h}^{n+1,m+1}, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) \\ \qquad +\left( z_{i}\varvec{q}_h^{n+1,m} C_{i,h}^{n+1,m+1}, \tilde{\varvec{J}}_i\right) +\left( \varvec{u}_h^{n+1,m} C_{i,h}^{n+1,m+1}, \tilde{\varvec{J}}_i\right) +\left( z_i\frac{\varvec{q}_h^{n+1,m}-\varvec{q}_h^{n}}{\Delta t} C_{i,h}^{n+1,m+1}, {{\tilde{\varvec{J}}}}_i\right) \\ \qquad +\left( z_i\varvec{q}_h^{n+1,m}\frac{ C_{i,h}^{n+1,m+1}-C_{i,h}^{n}}{\Delta t},{{\tilde{\varvec{J}}}}_i\right) +\left( \frac{ \varvec{u}_h^{n+1,m}-\varvec{u}_h^{n}}{\Delta t}C_{i,h}^{n+1,m+1}, {{\tilde{\varvec{J}}}}_i\right) +\left( \varvec{u}_h^{n+1,m}\frac{ C_{i,h}^{n+1,m+1}-C_{i,h}^{n}}{\Delta t}, {{\tilde{\varvec{J}}}}_i\right) \\ \quad =<g_i^{n+1},{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }+<\partial _t g_i^{n+1},{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }, \\ \left( \frac{ C_{i,h}^{n+1,m+1}-C_{i,h}^n}{\Delta t}, \tilde{C}_i\right) -\left( \nabla \cdot \varvec{J}_{i,h}^{n+1,m+1}, \tilde{C}_i\right) =0, \\ \end{array} \right. \\&\left\{ \begin{array}{ll} \left( \frac{\varvec{u}_h^{n+1,m+1}-\varvec{u}_h^n}{\Delta t},\tilde{\varvec{u}}\right) +\beta \left( \varvec{u}_h^{n+1,m},\varvec{u}_h^{n+1,m+1},\tilde{\varvec{u}}\right) +\left( \nabla \varvec{u}_h^{n+1,m+1},\nabla \tilde{\varvec{u}}\right) -\left( p_h^{n+1,m+1},\nabla \cdot \tilde{\varvec{u}}\right) \\ \quad =\left( \left( C_{1,h}^{n+1,m}-C_{2,h}^{n+1,m}\right) \varvec{q}_h^{n+1,m},\tilde{\varvec{u}}\right) , \\ \left( \nabla \cdot \varvec{u}_h^{n+1,m+1}, {{\tilde{p}}}\right) =0. \end{array} \right. \end{aligned}$$

• 4. Check stopping criteria for the nonlinear iteration: for a given tolerance $\varepsilon$, stop the iteration if

  $$\begin{aligned}&\Vert \phi _h^{n+1,m+1}-\phi _h^{n+1,m}\Vert _0+\Vert \varvec{q}_{h}^{n+1,m+1}-\varvec{q}_{h}^{n+1,m}\Vert _0+\Vert z_{h}^{n+1,m+1}-z_{h}^{n+1,m}\Vert _0\nonumber \\&\quad +\sum _{i=1}^2\Vert C_{i,h}^{n+1,m+1}-C_{i,h}^{n+1,m}\Vert _0 +\Vert \varvec{u}_{h}^{n+1,m+1}-\varvec{u}_{h}^{n+1,m}\Vert _0+\Vert p_h^{n+1,m+1}-p_h^{n+1,m}\Vert _0\le \varepsilon , \end{aligned}$$

  and set

  $$\begin{aligned}&\left( \phi _h^{n+1},\varvec{q}_h^{n+1}, z_h^{n+1}, C_{i,h}^{n+1},\varvec{J}_{i,h}^{n+1},\varvec{u}_h^{n+1}, p_h^{n+1}\right) \\&\quad =\left( \phi _h^{n+1,m+1},\varvec{q}_h^{n+1,m+1}, z_h^{n+1,m+1}, C_{i,h}^{n+1,m+1},\varvec{J}_{i,h}^{n+1,m+1},\varvec{u}_h^{n+1,m+1}, p_h^{n+1,m+1}\right) . \end{aligned}$$

  Otherwise, set $m\leftarrow m+1$ and go to Step 3 to continue.

• 5. Time marching: stop marching if $n+1=N$, otherwise set $n\leftarrow n+1$ and go to Step 2 to continue.

4.2 Fully Discrete Error Analysis

First, let each term in weak formulations (2.9), (2.10) and (2.12) take the value at $t_{n+1}$, yields

$$\begin{aligned}&\left\{ \begin{array}{lll} \left( \varvec{q}^{n+1}, \tilde{\varvec{q}}\right) +\left( \nabla \cdot \varvec{q}^{n+1}, \nabla \cdot \tilde{\varvec{q}} \right) -\left( \phi ^{n+1},\nabla \cdot \tilde{\varvec{q}}\right) =\left( z^{n+1},\nabla \cdot \tilde{\varvec{q}}\right) -<f_1^{n+1},\tilde{\varvec{q}}\cdot \varvec{n}>_{\partial \Omega },\\ \left( \nabla \cdot \varvec{q}^{n+1}, {{\tilde{\phi }}}\right) =\left( z^{n+1},{{\tilde{\phi }}}\right) ,\\ \left( \nabla z^{n+1}, \nabla {{\tilde{z}}}\right) +\left( z^{n+1},\tilde{z}\right) =\left( C_1^{n+1}-C_2^{n+1},{{\tilde{z}}}\right) -<f_2^{n+1},\tilde{z}>_{\partial \Omega }. \end{array} \right. \end{aligned}$$

(4.4)

$$\begin{aligned}&\left\{ \begin{array}{ll} \left( \partial _t\varvec{u}^{n+1},\tilde{\varvec{u}}\right) +\beta \left( \varvec{u}^{n+1}, \varvec{u}^{n+1},\tilde{\varvec{u}}\right) +\left( \nabla \varvec{u}^{n+1},\nabla \tilde{\varvec{u}}\right) -\left( p^{n+1},\nabla \cdot \tilde{\varvec{u}}\right) =\left( \left( C_1^{n+1}-C_2^{n+1}\right) \varvec{q}^{n+1},\tilde{\varvec{u}}\right) ,\\ \left( \nabla \cdot \varvec{u}^{n+1}, {{\tilde{p}}}\right) =0. \end{array} \right. \nonumber \\ \end{aligned}$$

(4.5)

$$\begin{aligned}&\left\{ \begin{array}{ll} \left( \partial _t \varvec{J}_i^{n+1},\tilde{\varvec{J}}_i\right) +\left( \varvec{J}_i^{n+1},{{\tilde{\varvec{J}}}}_i\right) +\left( \nabla \cdot \varvec{J}_i^{n+1},\nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( C_i^{n+1}, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +\left( z_i\varvec{q}^{n+1} C_i^{n+1}, {{\tilde{\varvec{J}}}}_i\right) \\ \qquad +\left( \varvec{u}^{n+1} C_i^{n+1}, \tilde{\varvec{J}}_i\right) +\left( z_i\partial _t\left( \varvec{q}^{n+1} C_i^{n+1}\right) ,{{\tilde{\varvec{J}}}}_i\right) +\left( \partial _t \left( \varvec{u}^{n+1} C_i^{n+1}\right) , {{\tilde{\varvec{J}}}}_i\right) \\ \quad =<g_i^{n+1},{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega }+<\partial _t g_i^{n+1},{{\tilde{\varvec{J}}}}_i\cdot \varvec{n}>_{\partial \Omega },\\ \left( \partial _t C_i^{n+1}, {{\tilde{C}}}_i\right) -\left( \nabla \cdot \varvec{J}_i^{n+1}, {{\tilde{C}}}_i\right) =0. \end{array} \right. \end{aligned}$$

(4.6)

Subtracting (4.1) from (4.4), and utilizing the $H^1$-projection (3.5) at $t_{n+1}$, we can have the following lemma by doing an analogous proof as for Theorem 3.1 because of its steady state feature.

Lemma 4.1

Let $(\phi _h^{n+1}, \varvec{q}_h^{n+1}, z_h^{n+1})$ be the solution to (4.1), and $(\phi ^{n+1}, \varvec{q}^{n+1}, z^{n+1})$ be the solution to (4.4). Then the following error estimates hold

$$\begin{aligned}&\Vert \varvec{q}^{n+1}-\varvec{q_h}^{n+1}\Vert _{{\varvec{V}}}+\Vert \phi ^{n+1}-\phi _h^{n+1}\Vert _0\le M\left( \sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0+ h^{k+1}\right) , \end{aligned}$$

(4.7)

$$\begin{aligned}&\Vert z ^{n+1}-z_h^{n+1}\Vert _0+h\Vert z^{n+1} -z_h^{n+1}\Vert _1\le M\left( \sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0+ h^{k+1}\right) . \end{aligned}$$

(4.8)

Next, we analysis the fully discrete error estimates for $\varvec{u}^{n+1}-\varvec{u}_h^{n+1}$, $\varvec{J}_i^{n+1}-\varvec{J}_{i,h}^{n+1}$ and $C_i^{n+1}-C_{i,h}^{n+1}$, respectively. Subtract (4.2) from (4.5), and use (3.22) at $t_{n+1}$, reads

$$\begin{aligned}&\left( \partial _t\varvec{u}^{n+1}-d_t\varvec{u}_h^{n+1},\tilde{\varvec{u}}\right) +a_{\varvec{u}}\left( \Pi _h{\varvec{u}^{n+1}}-\varvec{u}_h^{n+1},\tilde{\varvec{u}}\right) - b_{\varvec{u}}\left( \tilde{\varvec{u}},\Pi _h p^{n+1}-p_h^{n+1}\right) \nonumber \\&\qquad +\beta \left( \varvec{u}^{n+1},\varvec{u}^{n+1},\tilde{\varvec{u}}\right) -\beta \left( \varvec{u}_h^{n+1},\varvec{u}_h^{n+1},\tilde{\varvec{u}}\right) =\sum _{i=1}^2z_i\left( C_i^{n+1}\varvec{q}^{n+1} -C_{i,h}^{n+1}\varvec{q}_h^{n+1},\tilde{\varvec{u}}\right) , \end{aligned}$$

(4.9)

$$\begin{aligned}&b_{\varvec{u}}\left( \Pi _h{\varvec{u}^{n+1}}-\varvec{u}_h^{n+1},\tilde{p}\right) =0. \end{aligned}$$

(4.10)

Let $\varvec{u}^{n+1}-\varvec{u}_h^{n+1}=(\varvec{u}^{n+1}-\Pi _h \varvec{u}^{n+1})+(\Pi _h{\varvec{u}^{n+1}}-\varvec{u}_h^{n+1})=\eta ^{n+1}+\xi ^{n+1}$, choose $\tilde{\varvec{u}}=\xi ^{n+1}$, ${{\tilde{p}}}=\Pi _hp^{n+1}-p_h^{n+1}$, and then add (4.9) and (4.10), yield

$$\begin{aligned}&\left( d_t\xi ^{n+1},\xi ^{n+1}\right) +a_{\varvec{u}}\left( \xi ^{n+1},\xi ^{n+1}\right) \nonumber \\&\quad =-\left( \partial _t\varvec{u}^{n+1}-d_t\varvec{u}^{n+1},\xi ^{n+1}\right) +\left( \partial _t\eta ^{n+1}-d_t\eta ^{n+1},\xi ^{n+1}\right) -\left( \partial _t\eta ^{n+1},\xi ^{n+1}\right) \nonumber \\&\qquad \!+\beta \left( \varvec{u}_h^{n+1},\varvec{u}_h^{n+1},\xi ^{n+1}\right) -\beta \left( \varvec{u}^{n+1},\varvec{u}^{n+1},\xi ^{n+1}\right) +\sum _{i=1}^2z_i\left( C_i^{n+1}\varvec{q}^{n+1} -C_{i,h}^{n+1}\varvec{q}_h^{n+1},\xi ^{n+1}\right) . \end{aligned}$$

(4.11)

By Taylor’s expansion, we have

$$\begin{aligned} \partial _t\varphi ^{n+1}-d_t \varphi ^{n+1}=\frac{1}{\Delta t} \int _{t_n}^{t_{n+1}}\left( {\tilde{t}}-t_n\right) \frac{\partial ^2\varphi }{\partial t^2}d {\tilde{t}},\quad \forall \phi \in H^2\left( 0,T;L^2(\Omega )\right) , \end{aligned}$$

(4.12)

then

$$\begin{aligned} \Vert \partial _t\varphi ^{n+1} - d_t \varphi ^{n+1}\Vert _0\le M (\Delta t)\bigg \Vert \frac{\partial ^2\varphi }{\partial t^2}\bigg \Vert _0. \end{aligned}$$

(4.13)

Thus, we have

$$\begin{aligned}&\left( \partial _t\varvec{u}^{n+1}-d_t\varvec{u}^{n+1},\xi ^{n+1}\right) \le M (\Delta t) \Vert \varvec{u}\Vert _{H^{2}\left( L^2\right) }\Vert \xi ^{n+1}\Vert _0\le M \left( (\Delta t)^2+\Vert \xi ^{n+1}\Vert _0^2\right) ,\nonumber \\ \end{aligned}$$

(4.14)

$$\begin{aligned}&(\partial _t\eta ^{n+1}-d_t\eta ^{n+1},\xi ^{n+1})\le M (\Delta t) \Vert \eta \Vert _{H^{2}(L^2)}\Vert \xi ^{n+1}\Vert _0\le M \left( (\Delta t)^2+\Vert \xi ^{n+1}\Vert _0^2\right) ,\nonumber \\ \end{aligned}$$

(4.15)

$$\begin{aligned}&\left( \partial _t\eta ^{n+1},\xi ^{n+1}\right) \le M \Vert \partial _t\eta ^{n+1}\Vert _0\Vert \xi ^{n+1}\Vert _0\le M\left( h^{2(k+2)}+\Vert \xi ^{n+1}\Vert _0^2\right) . \end{aligned}$$

(4.16)

Analyses of the rest terms in (4.11) are similar with (3.30), (3.31) and (3.32) in the proof of Theorem 3.2 and are thus omitted here, then we obtain

$$\begin{aligned} \Vert \xi ^{n+1}\Vert _0^2+\Delta t\Vert \nabla \xi ^{n+1}\Vert _0^2\le & {} \left( \xi ^{n},\xi ^{n+1}\right) +M\Delta t \left( h^{-d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^4 + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^2\right. \\&\left. +\Vert \xi ^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right) +\epsilon \Delta t \Vert \nabla \xi ^{n+1}\Vert _0^2. \end{aligned}$$

Apply Cauchy–Schwarz inequality and Young’s inequality with $\epsilon =\frac{1}{2}$ to the first term on the right hand side, and take a sufficiently small $\epsilon$, yield

$$\begin{aligned} \frac{1}{2}\Vert \xi ^{n+1}\Vert _0^2+\Delta t\Vert \nabla \xi ^{n+1}\Vert _0^2\le & {} M\Delta t \left( h^{-d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^4 + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^2\right. \\&\left. +\Vert \xi ^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right) +\frac{1}{2}\Vert \xi ^{n}\Vert _0^2. \end{aligned}$$

Sum over the time step n from 0 to $L-1$ ($1\le L\le N$), and apply the telescoping technique, results

$$\begin{aligned} \frac{1}{2}\Vert \xi ^{L}\Vert _0^2 +\Delta t\sum _{n=0}^{L-1}\Vert \nabla \xi ^{n+1}\Vert _0^2\le & {} \frac{1}{2}\Vert \xi ^0\Vert _0^2+M \Delta t\sum _{n=0}^{L-1}\left( h^{-d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^4 \right. \\&\left. + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^2+\Vert \xi ^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right) . \end{aligned}$$

Then, by the discrete Grönwall’s inequality, and properly choosing the initial value $\varvec{u}_h^0=\Pi _h\varvec{u}^0$, we have

$$\begin{aligned}&\Vert \xi ^{L}\Vert _0^2 +\Delta t\sum _{n=0}^{L-1}\Vert \nabla \xi ^{n+1}\Vert _0^2\nonumber \\&\quad \le M\left[ \Delta t\sum _{n=0}^{L-1}\left( h^{-d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^4 + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^2\right) +(\Delta t)^2+h^{2(k+1)}\right] . \end{aligned}$$

(4.17)

If choose $\tilde{\varvec{u}}=d_t\xi ^{n+1}$, $\tilde{p}=d_t(\Pi _hp^{n+1}-p_h^{n+1})$ in (4.9) and (4.10), then

$$\begin{aligned}&\left( d_t\xi ^{n+1},d_t\xi ^{n+1}\right) +a_{\varvec{u}}\left( \xi ^{n+1},d_t\xi ^{n+1}\right) \\&\quad =-\left( \partial _t\varvec{u}^{n+1}-d_t\varvec{u}^{n+1},d_t\xi ^{n+1}\right) +\left( \partial _t\eta ^{n+1}-d_t\eta ^{n+1},d_t\xi ^{n+1}\right) -\left( \partial _t\eta ^{n+1},d_t\xi ^{n+1}\right) \\&\qquad +\beta \left( \varvec{u}_h^{n+1},\varvec{u}_h^{n+1},d_t\xi ^{n+1}\right) -\beta \left( \varvec{u}^{n+1},\varvec{u}^{n+1},d_t\xi ^{n+1}\right) \\&\qquad +\sum _{i=1}^2z_i\left( C_i^{n+1}\varvec{q}^{n+1} -C_{i,h}^{n+1}\varvec{q}_h^{n+1},d_t\xi ^{n+1}\right) . \end{aligned}$$

By similar analysis skills as for (4.11) and (3.34), we can have

$$\begin{aligned}&\Delta t\sum _{n=0}^{L-1}\Vert d_t\xi ^{n+1}\Vert _0^2+\Vert \nabla \xi ^{L}\Vert _0^2\nonumber \\&\quad \le M\left[ \Delta t\sum _{n=0}^{L-1}\left( h^{-2}\Vert \nabla (\varvec{u}^{n+1}-\varvec{u}_{h}^{n+1})\Vert _0^4 + \Vert \nabla \left( \varvec{u}^{n+1}-\varvec{u}_{h}^{n+1}\right) \Vert _{0}^2\right. \right. \nonumber \\&\qquad \left. \left. +h^{-d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^4 + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^2\right) +(\Delta t)^2+h^{2(k+1)}\right] .\qquad \qquad \end{aligned}$$

(4.18)

Then by (4.17) we obtain

$$\begin{aligned}&\Delta t\sum _{n=0}^{L-1}\Vert d_t\xi ^{n+1}\Vert _0^2+\Vert \nabla \xi ^{L}\Vert _0^2\nonumber \\&\quad \le M\left[ \Delta t\sum _{n=0}^{L-1}\left( h^{-2}\left( h^{-2d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^8 +\sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^4\right) \right. \right. \nonumber \\&\qquad \left. \left. + h^{-d}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^4 + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}^2\right) +(\Delta t)^2+h^{2(k+1)}\right] .\qquad \qquad \end{aligned}$$

(4.19)

As for the fully discrete error estimates of Nernst-Planck equations, we subtract (4.3) from (4.6), and utilize (3.38) at $t_{n+1}$ to have

$$\begin{aligned}&\left( \partial _t\varvec{J}_i^{n+1}-d_t\varvec{J}_{i,h}^{n+1},{\tilde{\varvec{J}}}_i\right) +\left( \Pi _h \varvec{J}_i^{n+1}-\varvec{J}_{i,h}^{n+1},\tilde{\varvec{J}}_i\right) +\left( \nabla \cdot \left( \Pi _h \varvec{J}_i^{n+1} - \varvec{J}_{i,h}^{n+1}\right) ,\nabla \cdot {{\tilde{\varvec{J}}}}_i\right) \nonumber \\&\quad +\left( \Pi _h C_i^{n+1}-C_{i,h}^{n+1}, \nabla \cdot {{\tilde{\varvec{J}}}}_i\right) +z_{i}\left( \varvec{q}^{n+1} C_i^{n+1}-\varvec{q}_h^{n+1} C_{i,h}^{n+1}, \tilde{\varvec{J}}_i\right) \nonumber \\&\quad +\left( \varvec{u}^{n+1} C_i^{n+1}-\varvec{u}_h^{n+1}C_{i,h}^{n+1}, {{\tilde{\varvec{J}}}}_i\right) +z_i\left( \partial _t\left( \varvec{q}^{n+1} C_i^{n+1}\right) -d_t\left( \varvec{q}_h^{n+1} C_{i,h}^{n+1}\right) , {{\tilde{\varvec{J}}}}_i\right) \nonumber \\&\quad +\left( \partial _t \left( \varvec{u}^{n+1} C_i^{n+1}\right) -d_t\left( \varvec{u}_h^{n+1} C_{i,h}^{n+1}\right) , \tilde{\varvec{J}}_i\right) =0,\quad \forall {{\tilde{\varvec{J}}}}_i \in {\varvec{V}}_h, \end{aligned}$$

(4.20)

$$\begin{aligned}&\left( \partial _t C_i^{n+1}-d_tC_{i,h}^{n+1}, {{\tilde{C}}}_i\right) -\left( \nabla \cdot \left( \Pi _h\varvec{J}_i^{n+1}-\varvec{J}_{i,h}^{n+1}\right) , \tilde{C}_i\right) =0,\quad \forall {{\tilde{C}}}_i \in W_h. \end{aligned}$$

(4.21)

Let $\varvec{J}_i^{n+1} -\varvec{J}_{i,h}^{n+1}=(\varvec{J}_i^{n+1}-\Pi _h\varvec{J}_i^{n+1})+(\Pi _h \varvec{J}_i^{n+1} - \varvec{J}_{i,h}^{n+1})=e_i^{n+1}+\theta _i^{n+1}$, $C_i^{n+1}-C_{i,h}^{n+1}=(C_i^{n+1}-\Pi _hC_i^{n+1})+(\Pi _h C_i^{n+1} - C_{i,h}^{n+1})=\sigma _i^{n+1}+\delta _i^{n+1}$, choose $\tilde{\varvec{J}}_i=\theta _i^{n+1}$, ${{\tilde{C}}}_i=\delta _i^{n+1}$ in (4.20) and (4.21), and add them together, yield

$$\begin{aligned}&\left( d_t\theta _i^{n+1},\theta _i^{n+1}\right) +\left( \theta _i^{n+1},\theta _i^{n+1}\right) +\left( \nabla \cdot \theta _i^{n+1},\nabla \cdot \theta _i^{n+1}\right) +\left( d_t\delta _i^{n+1},\delta _i^{n+1}\right) \nonumber \\&\quad =-\left( \partial _t\varvec{J}_i^{n+1}-d_t\varvec{J}_i^{+1},\theta _i^{n+1}\right) +\left( \partial _te_i^{n+1}-d_te_i^{n+1}, \theta _i^{n+1}\right) -\left( \partial _te_i^{n+1},\theta _i^{n+1}\right) \nonumber \\&\qquad -\left( \partial _tC_i^{n+1}-d_tC_i^{n+1},\delta _i^{n+1}\right) +\left( \partial _t\sigma _i^{n+1}-d_t\sigma _i^{n+1}, \delta _i^{n+1}\right) -\left( \partial _t\sigma _i^{n+1},\delta _i^{n+1}\right) \nonumber \\&\qquad -z_{i}\left( \varvec{q}^{n+1} C_i^{n+1}-\varvec{q}_h^{n+1} C_{i,h}^{n+1}, \theta _i^{n+1}\right) -\left( \varvec{u}^{n+1} C_i^{n+1}-\varvec{u}_h^{n+1}C_{i,h}^{n+1}, \theta _i^{n+1}\right) \nonumber \\&\qquad -z_i\left( \partial _t\left( \varvec{q}^{n+1} C_i^{n+1}\right) -d_t\left( \varvec{q}_h^{n+1} C_{i,h}^{n+1}\right) , \theta _i^{n+1}\right) -\left( \partial _t \left( \varvec{u}^{n+1} C_i^{n+1}\right) -d_t\left( \varvec{u}_h^{n+1} C_{i,h}^{n+1}\right) , \theta _i^{n+1}\right) \nonumber \\&\quad =\sum _{k=1}^{10} T_k. \end{aligned}$$

(4.22)

The analysis of Terms $T_1$–$T_6$ are similar to (4.14), (4.15) and (4.16), leading to

$$\begin{aligned}&T_1+T_2+T_3\le M\left( (\Delta t)^2+ h^{2(k+1)}+\Vert \theta _i^{n+1}\Vert _0^2\right) ,\\&T_4+T_5+T_6\le M\left( (\Delta t)^2+h^{2(k+1)}+\Vert \delta _i^{n+1}\Vert _0^2\right) . \end{aligned}$$

As for $T_7$ and $T_8$, we will do an analogous error estimate with (3.48) and (3.49), i.e., we need to conduct a mathematical induction by assuming the following induction hypothesis for any $n=0,1,\cdots ,N$:

$$\begin{aligned} h^{-\frac{d}{2}}\Vert \delta _i^{n}\Vert _{0}\le M,~~~~i=1,2, \end{aligned}$$

(4.23)

which is obviously true when $n=0$ since $\delta _i^0=0$ by choosing $C_{i,h}(0)=\Pi _hC_i^0$. Now we assume (4.23) holds for any $n=0,1,\cdots ,L-1$, where $1\le L\le N$. Then,

$$\begin{aligned} T_7+T_8\le M\left( \sum _{i=1}^2 \Vert \delta _i^{n+1}\Vert _0^2 +\Vert \theta _i^{n+1}\Vert _0^2+ h^{2(k+1)}\right) . \end{aligned}$$

Next we estimate $T_9$ and $T_{10}$. Let ${{\tilde{C}}}_i= d_t \delta _i^{n+1}$ in (4.21), yields

$$\begin{aligned} \left( \partial _tC_i^{n+1}-d_tC_{i,h}^{n+1},d_t\delta _i^{n+1}\right) -\left( \nabla \cdot \theta _i^{n+1},d_t\delta _i^{n+1}\right) =0, \end{aligned}$$

(4.24)

that is

$$\begin{aligned}&\left( \partial _tC_i^{n+1}-d_tC_{i}^{n+1},d_t\delta _i^{n+1}\right) +\left( d_t\sigma _i^{n+1}-\partial _t\sigma _i^{n+1},d_t\delta _i^{n+1}\right) +\left( \partial _t\sigma _i^{n+1},d_t\delta _i^{n+1}\right) \nonumber \\&\quad +\left( d_t\delta _i^{n+1},d_t\delta _i^{n+1}\right) -\left( \nabla \cdot \theta _i^{n+1},d_t\delta _i^{n+1}\right) =0. \end{aligned}$$

(4.25)

By Cauchy–Schwarz inequality and applying similar estimates as in (4.14), (4.15) and (4.16), we obtain

$$\begin{aligned} \Vert d_t \delta _i^{n+1}\Vert _0\le M\left( \Delta t+ h^{k+1}\right) +\Vert \nabla \cdot \theta _i^{n+1}\Vert _0. \end{aligned}$$

(4.26)

Then,

$$\begin{aligned} \Vert \partial _tC_i^{n+1}-d_tC_{i,h}^{n+1}\Vert _0\le & {} \Vert \partial _tC_i^{n+1}-d_tC_{i}^{n+1}\Vert _0+\Vert d_t\sigma _i^{n+1}\nonumber \\&-\partial _t \sigma _i^{n+1}\Vert _0+\Vert \partial _t \sigma _i^{n+1}\Vert _0+\Vert d_t \delta _i^{n+1}\Vert _0\nonumber \\\le & {} M\left( \Delta t+ h^{k+1}\right) +\Vert \nabla \cdot \theta _i^{n+1}\Vert _0. \end{aligned}$$

(4.27)

On the other hand, differentiate (2.10) in time, and then fully discretize it in both space and time as done for (4.2). The error equation between them can then be obtained by means of the differentiation of (3.5) in time, where, we choose $\tilde{\varvec{q}}=d_t(\Pi _h\varvec{q}^{n+1}-\varvec{q}_h^{n+1})$ and ${{\tilde{\phi }}}=d_t(\Pi _h\phi ^{n+1}-\phi _h^{n+1})$. By Taylor Expansion (4.12) and the same analysis techniques for proving Theorem 3.1, we can obtain

$$\begin{aligned} \Vert d_t(\Pi _h \varvec{q}^{n+1}-\varvec{q}_{h}^{n+1})\Vert _0 \le M\left( \Delta t+ h^{k+1}\right) +\sum _{i=1}^2\Vert \partial _tC_i^{n+1}-d_tC_{i,h}^{n+1}\Vert _0. \end{aligned}$$

(4.28)

Thus by the triangular inequality, (4.13), Lemma 3.1, (4.28) and (4.27), we have

$$\begin{aligned} \Vert \partial _t \varvec{q}^{n+1}-d_t \varvec{q}_{h}^{n+1}\Vert _0\le & {} \Vert \partial _t \varvec{q}^{n+1}-d_t \varvec{q}^{n+1}\Vert _0\nonumber \\&+ \Vert d_t\left( \varvec{q}^{n+1}-\Pi _h \varvec{q}^{n+1}\right) \Vert _0+\Vert d_t\left( \Pi _h \varvec{q}^{n+1}-\varvec{q}_{h}^{n+1}\right) \Vert _0 \nonumber \\\le & {} M\left( (\Delta t)+ h^{k+1}\right) +\Vert \nabla \cdot \theta _i^{n+1}\Vert _0. \end{aligned}$$

(4.29)

Therefore, apply an analogous analysis as for (3.50) and (3.51), and utilize Lemma 4.1, (4.29), (4.27) and the mathematical induction (4.23), yield

$$\begin{aligned} T_9= & {} -z_i\left( \varvec{q}^{n+1} \partial _t C_i^{n+1}-\varvec{q}_h^{n+1}d_t C_{i,h}^{n+1}, \theta _i^{n+1}\right) -z_i\left( C_i^{n+1} \partial _t\varvec{q}^{n+1}-C_{i,h}^{n+1}d_t\varvec{q}_h^{n+1}, \theta _i^{n+1}\right) \\= & {} -z_i\left( \left( \varvec{q}^{n+1}-\varvec{q}_h^{n+1}\right) \partial _t C_i^{n+1},\theta _i^{n+1}\right) -z_i\left( \varvec{q}_h^{n+1}\left( \partial _t C_i^{n+1}- d_t C_{i,h}^{n+1}\right) , \theta _i^{n+1}\right) \\&\left. -z_i\left( \left( C_i^{n+1}-C_{i,h}^{n+1}\right) \right) \partial _t \varvec{q}^{n+1},\theta _i^{n+1}\right) -z_i\left( C_{i,h}^{n+1}\left( \partial _t \varvec{q}^{n+1}- d_t \varvec{q}_{h}^{n+1}\right) ,\theta _i^{n+1}\right) \\\le & {} M\left( \sum _{i=1}^2\Vert \delta _i^{n+1}\Vert _0^2+ \Vert \theta _i^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right) + \epsilon \Vert \nabla \cdot \theta _i^{n+1}\Vert _0^2,\\ T_{10}= & {} -\left( \varvec{u}^{n+1} \partial _t C_i^{n+1}-\varvec{u}_h^{n+1}d_t C_{i,h}^{n+1}, \theta _i^{n+1}\right) -\left( C_i^{n+1} \partial _t\varvec{u}^{n+1}-C_{i,h}^{n+1}d_t\varvec{u}_h^{n+1}, \theta _i^{n+1}\right) \\= & {} -\left( \left( \varvec{u}^{n+1}-\varvec{u}_h^{n+1}\right) \partial _t C_i^{n+1},\theta _i^{n+1}\right) -\left( \varvec{u}_h^{n+1}\left( \partial _t C_i^{n+1}- d_t C_{i,h}^{n+1}\right) , \theta _i^{n+1}\right) \\&\left. -\left( \left( C_i^{n+1}-C_{i,h}^{n+1}\right) \right) \partial _t \varvec{u}^{n+1},\theta _i^{n+1}\right) -\left( C_{i,h}^{n+1}\left( \partial _t \varvec{u}^{n+1}- d_t \varvec{u}_{h}^{n+1}\right) ,\theta _i^{n+1}\right) \\\le & {} M\left( \sum _{i=1}^2\Vert \delta _i^{n+1}\Vert _0^2+ \Vert \theta _i^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}+\Vert \xi ^{n+1}\Vert _0^2+\Vert d_t\xi ^{n+1}\Vert _0^2\right) + \epsilon \Vert \nabla \cdot \theta _i^{n+1}\Vert _0^2. \end{aligned}$$

Then, (4.22) finally yields

$$\begin{aligned}&\left( \frac{\theta _i^{n+1}-\theta _i^{n}}{\Delta t},\theta _i^{n+1}\right) +\Vert \theta _i^{n+1}\Vert _0^2+\Vert \nabla \cdot \theta _i^{n+1}\Vert _0^2+\left( \frac{\delta _i^{n+1}-\delta _i^{n}}{\Delta t}, \delta _i^{n+1}\right) \\&\quad \le M \left( \sum _{i=1}^2\Vert \delta _i^{n+1}\Vert _0^2+ \Vert \theta _i^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}+\Vert \xi ^{n+1}\Vert _0^2+\Vert d_t\xi ^{n+1}\Vert _0^2\right) + \epsilon \Vert \nabla \cdot \theta _i^{n+1}\Vert _0^2. \end{aligned}$$

Take a sufficiently small $\epsilon$, apply Cauchy–Schwarz inequality and Young’s inequality with $\epsilon =\frac{1}{2}$, yield

$$\begin{aligned}&\frac{1}{2}\left( \Vert \theta _i^{n+1}\Vert _0^2+\Vert \delta _i^{n+1}\Vert _0^2\right) +\Delta t\Vert \theta _i^{n+1}\Vert _0^2+\Delta t\Vert \nabla \cdot \theta _i^{n+1}\Vert _0^2\\&\quad \le M\Delta t \left( \sum _{i=1}^2\Vert \delta _i^{n+1}\Vert _0^2+ \Vert \theta _i^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}+\Vert \xi ^{n+1}\Vert _0^2+\Vert d_t\xi ^{n+1}\Vert _0^2\right) \\&\qquad +\frac{1}{2}\left( \Vert \theta _i^{n}\Vert _0^2+\Vert \delta _i^{n}\Vert _0^2\right) . \end{aligned}$$

Sum over the time step n from 0 to $L-1\ (1\le L\le N)$ on both sides, apply the telescoping technique, and properly choose initial values $C_{i,h}^0=\Pi _hC_i^0$ and $\varvec{J}_h^0=\Pi _h\varvec{J}^0$, yield

$$\begin{aligned}&\Vert \theta _i^{L}\Vert _0^2+\Vert \delta _i^{L}\Vert _0^2 +\Delta t\sum _{n=0}^{L-1}\Vert \theta _i^{n+1}\Vert _{\varvec{V}}^2\nonumber \\&\quad \le M\Delta t\sum _{n=0}^{L-1}\left( \sum _{i=1}^2\Vert \delta _i^{n+1}\Vert _0^2+ \Vert \theta _i^{n+1}\Vert _0^2+\Vert \xi ^{n+1}\Vert _0^2+\Vert d_t\xi ^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right) . \end{aligned}$$

(4.30)

Due to the mathematical induction (4.23) and Poincaré inequality, (4.17) leads to

$$\begin{aligned} \Delta t\sum _{n=0}^{L-1}\Vert \xi ^{n+1}\Vert _0^2 \le M \Delta t\sum _{n=0}^{L-1}\Vert \nabla \xi ^{n+1}\Vert _0^2 \le M\left[ \Delta t\sum _{n=0}^{L-1} \sum _{i=0}^2 \Vert \delta _i^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right] , \end{aligned}$$

(4.31)

and so does (4.19), resulting in

$$\begin{aligned} \Delta t\sum _{n=0}^{L-1}\Vert d_t\xi ^{n+1}\Vert _0^2 \le M\left[ \Delta t\sum _{n=0}^{L-1} \sum _{i=0}^2 \Vert \delta _i^{n+1}\Vert _0^2+(\Delta t)^2+h^{2(k+1)}\right] . \end{aligned}$$

(4.32)

Take the sum over i from 1 to 2 in (4.30), then apply the discrete Grönwall’s inequality, results

$$\begin{aligned} \sum _{i=1}^2\left[ \Vert \theta _i^{L}\Vert _0^2 +\Vert \delta _i^{L}\Vert _0^2+\Delta t\sum _{n=0}^{L-1}\Vert \theta _i^{n+1}\Vert _{\varvec{V}}^2 \right] \le M\left( (\Delta t)^2+h^{2(k+1)}\right) . \end{aligned}$$

(4.33)

Because $k+1-\frac{d}{2}>0$ for $k\ge 1$ and $d=2,3$, (4.33) implies that when $\Delta t$ is sufficiently small, we have

$$\begin{aligned} h^{-\frac{d}{2}}\Vert \delta _i^{L}\Vert _{0}\le M, \end{aligned}$$

which proves the mathematical induction hypothesis (4.23) uniformly holds for all $1\le n\le N$.

Combining (4.33) with Lemma 3.3 at $t=t_{L}$ ($1\le L\le N$), by the triangular inequality we obtain

$$\begin{aligned} \Vert \varvec{J}_i^{L}-\varvec{J}_{i,h}^{L}\Vert _{0}+\Vert C_i^{L}-C_{i,h}^{L}\Vert _0\le M\left( \Delta t+ h^{k+1}\right) . \end{aligned}$$

(4.34)

Then Lemma 4.1 results

$$\begin{aligned}&\Vert \varvec{q}^{L}-\varvec{q_h}^{L}\Vert _{{\varvec{V}}}+\Vert \phi ^{L}-\phi _h^{L}\Vert _0\le M\left( \Delta t+ h^{k+1}\right) , \end{aligned}$$

(4.35)

$$\begin{aligned}&\Vert z^{L} -z_h^{L}\Vert _0+h\Vert z^{L}-z_h^{L}\Vert _{1}\le M(\Delta t+ h^{k+1}). \end{aligned}$$

(4.36)

Further combining (4.17)and (4.19) with Lemma 3.2 at $t=t_{L}$ ($1\le L\le N$), we have

$$\begin{aligned} \Vert \varvec{u}^{L}-\varvec{u}_h^{L}\Vert _{0}+\Vert \varvec{u}^{L}-\varvec{u}_h^{L}\Vert _{1}\le M(\Delta t+ h^{k+1}). \end{aligned}$$

(4.37)

On the other hand, taking ${{\tilde{\varvec{J}}}}_i=d_t\theta _i^{n+1}, \tilde{C}_i=d_t\delta _i^{n+1}$ in (4.20) and (4.21) , we have

$$\begin{aligned}&\left( d_t\theta _i^{n+1},d_t\theta _i^{n+1}\right) +\left( \theta _i^{n+1},d_t\theta _i^{n+1}\right) +\left( \nabla \cdot \theta _i^{n+1},d_t\nabla \cdot \theta _i^{n+1}\right) \\&\quad =-\left( \partial _tJ_i^{n+1}-d_tJ_i^{+1},d_t\theta _i^{n+1}\right) +\left( \partial _te_i^{n+1}-d_te_i^{n+1}, d_t\theta _i^{n+1}\right) \\&\qquad -\left( \partial _te_i^{n+1},d_t\theta _i^{n+1}\right) -\left( \delta _i^{n+1},d_t\nabla \cdot \theta _i^{n+1}\right) \\&\qquad -z_{i}\left( \varvec{q}^{n+1} C_i^{n+1}-\varvec{q}_h^{n+1} C_{i,h}^{n+1}, d_t \theta _i^{n+1}\right) -\left( \varvec{u}^{n+1} C_i^{n+1}-\varvec{u}_h^{n+1}C_{i,h}^{n+1}, d_t \theta _i^{n+1}\right) \\&\qquad -z_i\left( \partial _t\left( \varvec{q}^{n+1} C_i^{n+1}\right) -d_t\left( \varvec{q}_h^{n+1} C_{i,h}^{n+1}\right) , d_t\theta _i^{n+1}\right) -\left( \partial _t \left( \varvec{u}^{n+1} C_i^{n+1}\right) \right. \\&\qquad \left. -d_t\left( \varvec{u}_h^{n+1} C_{i,h}^{n+1}\right) , d_t\theta _i^{n+1}\right) . \end{aligned}$$

By using similar analysis techniques as for (4.22), we can obtain the following estimate for any $1\le L\le N$:

$$\begin{aligned}&\Delta t \sum _{i=0}^{L-1}\Vert d_t\theta _i^{n+1}\Vert _0^2 + \Vert \theta _i^{L}\Vert _{\varvec{V}}^2\\&\quad \le \Delta t\sum _{n=0}^{L-1}\left[ M\left( \sum _{i=1}^2\Vert \delta _i^{n+1}\Vert _0^2+ \Vert \theta _i^{n+1}\Vert _{\varvec{V}}^2+(\Delta t)^2+h^{2(k+1)}\right) +\epsilon \Vert d_t\theta _i^{n+1}\Vert _0^2\right] . \end{aligned}$$

Take a sufficiently small $\epsilon$, apply the discrete Grönwall’s inequality and (4.34), yield

$$\begin{aligned} \Vert \theta _i^{L}\Vert _{\varvec{V}} \le M(h^{k+1}+\Delta t). \end{aligned}$$

Further, we have

$$\begin{aligned} \Vert \varvec{J}_i^{L}-\varvec{J}_{i,h}^{L}\Vert _{{\varvec{V}}}\le M(h^{k+1}+\Delta t). \end{aligned}$$

(4.38)

To estimate $p^{n+1}-p^{n+1}_h$, we need the discrete form of inf-sup condition for $b_u(\cdot ,\cdot )$ in (3.37). First, apply (4.9), the continuity of $a_{\varvec{u}}(\cdot ,\cdot )$ and the same error analyses for (4.14) and (3.30)–(3.32), yield

$$\begin{aligned} b_{\varvec{u}}\left( {\tilde{\varvec{u}}},\Pi _h p^{n+1} - p_h^{n+1}\right)= & {} \left( \partial _t\varvec{u}^{n+1}-d_t\varvec{u}_h^{n+1},{{\tilde{\varvec{u}}}}\right) +a_{\varvec{u}}\left( \Pi _h\varvec{u}^{n+1} -\varvec{u}_h^{n+1},{\tilde{\varvec{u}}}\right) \\&+\beta \left( \varvec{u}^{n+1},\varvec{u}^{n+1},{\tilde{\varvec{u}}}\right) \\&-\beta \left( \varvec{u}_h^{n+1},\varvec{u}_h^{n+1},\tilde{\varvec{u}}\right) -\sum _{i=1}^2z_i\left( C_i^{n+1}\varvec{q}^{n+1} -C_{i,h}^{n+1}\varvec{q}_h^{n+1},{\tilde{\varvec{u}}}\right) .\\\le & {} M \left[ \left( \Delta t+h^{k+1}+\Vert d_t\xi ^{n+1}\Vert _0\right) \Vert {\tilde{\varvec{u}}}\Vert _0+\Vert \nabla \xi ^{n+1}\Vert _0\Vert {\tilde{\varvec{u}}}\Vert _1\right. \\&+\left( \Vert \nabla \left( \varvec{u}^{n+1}-\varvec{u}_h^{n+1}\right) \Vert _0^2+\Vert \nabla \varvec{u}^{n+1}\Vert _0\Vert \nabla \left( \varvec{u}^{n+1}-\varvec{u}_h^{n+1}\right) \Vert _0\right) \Vert {\tilde{\varvec{u}}}\Vert _1\\&+\left( h^{-\frac{d}{2}}\sum _{i=1}^2\Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _0^2\right. \\&\left. \left. + \sum _{i=1}^2 \Vert C_i^{n+1}-C_{i,h}^{n+1}\Vert _{0}+h^{k+1}\right) \Vert {\tilde{\varvec{u}}}\Vert _0\right] . \end{aligned}$$

After combining the above inequality with (4.34) and (4.37), we can obtain the following error estimate through (3.37) as:

$$\begin{aligned} \Vert \Pi _h p^{n+1} - p_h^{n+1}\Vert _0\le M \left( \Delta t + h^{k+1}+\Vert d_t\xi ^{n+1}\Vert _0 \right) . \end{aligned}$$

Then apply (4.32) and (4.33), and combine with Lemma 3.2, yield

$$\begin{aligned} \left( \Delta t \sum _{n=0}^{L-1}\Vert p^{n+1} - p_h^{n+1}\Vert ^2_0\right) ^{\frac{1}{2}}\le M \left( \Delta t + h^{k+1}\right) . \end{aligned}$$

Therefore, the following convergence theorem is eventually derived for the fully discrete scheme (4.1)–(4.3).

Theorem 4.1

Let $(\phi ^{n+1}, \varvec{q}^{n+1}, z^{n+1},u^{n+1},p^{n+1},C_i^{n+1},\varvec{J}_i^{n+1})$ be the solution to (2.7a)–(2.9) satisfying the regularity properties (2.13)–(2.15), and $(\phi _h^{n+1}, \varvec{q}_h^{n+1}, z_h^{n+1},u_h^{n+1},p_h^{n+1},C_{i,h}^{n+1}, \varvec{J}_{i,h}^{n+1})$ be the solution to (4.1)–(4.3). Then for $1\le L\le N$, we have the following error estimates,

$$\begin{aligned}&\Vert \varvec{q}^{L}-\varvec{q_h}^{L}\Vert _{{\varvec{V}}}+\Vert \phi ^{L}-\phi _h^{L}\Vert _0+ \Vert z^{L} -z_h^{L}\Vert _0+h\Vert z^{L}-z_h^{L}\Vert _{1}\le M\left( h^{k+1}+\Delta t\right) , \\&\Vert \varvec{u}^{L}-\varvec{u}_h^{L}\Vert _{0}+ \Vert \varvec{u}^{L}-\varvec{u}_h^{L}\Vert _{1}+\left( \Delta t \sum _{n=1}^{L}\Vert p^{n} - p_h^{n}\Vert ^2_0\right) ^{\frac{1}{2}} \le M(h^{k+1}+\Delta t),\\&\Vert C_i^{L}-C_{i,h}^{L}\Vert _0+\Vert \varvec{J}_i^{L}-\varvec{J}_{i,h}^{L}\Vert _{0}+\Vert \varvec{J}_i^{L}-\varvec{J}_{i,h}^{L}\Vert _{{\varvec{V}}}\le M\left( h^{k+1}+\Delta t\right) . \end{aligned}$$

Remark 4.1

The error estimate of pressure in Theorem 4.1 is consistent with its continuous form in Theorem 3.4 which bears $L^2(L^2)$ norm. To obtain the same error estimate for pressure in $L^{\infty }(L^2)$ norm, i.e., $\Vert p-p_h\Vert _{L^{\infty }(L^2)}=O\left( h^{k+1}\right)$, we need to differentiate (3.26) and (3.27) in time, and choose $\tilde{\varvec{u}}=\partial _t(\Pi _h{\varvec{u}}-\varvec{u}_h)$ and $\tilde{p}=\partial _t(\Pi _h p-p_h)$, then conduct similar semi-discrete error estimates by means of analogous analysis skills for proving Theorem 3.2. A similar error analysis process can be carried out for the fully discrete scheme to obtain the error estimate of pressure in the discrete $L^{\infty }(L^2)$ norm, as: $\Vert p^L-p_h^L\Vert _{L^2}=O(h^{k+1}+\Delta t)$ for $1\le L\le N$. We thus omit its proof in this paper to avoid the high similarity, on the other hand, it will be numerically validated in Sect. 5.

5 Numerical Experiments

5.1 Example 1: Convergence Test

In this section we apply the fully discrete mixed FEM and the numerical algorithm developed in Sect. 4 to a numerical example defined below, then validate all theoretical results shown in Theorem 4.1. Let

$$\begin{aligned} \left\{ \begin{array}{llll} \phi &{}=&{}e^{(x+y)}\sin t,\\ C_1&{}=&{}\sin (2\pi x)\sin (2\pi y)\sin t,\\ C_2&{}=&{}\sin (2\pi x)\sin (2\pi y)\sin (2t),\\ \varvec{u}&{}=&{}\left( - \cos (\pi x)\sin (\pi y)\sin (3t),~ \sin (\pi x)\cos (\pi y)\sin (3t)\right) ^\top ,\\ p&{}=&{}\left( \sin x+\sin y\right) (1-e^{-t}) \end{array} \right. \end{aligned}$$

(5.1)

be real solutions to the following fourth-order modified PNP/NS problem defined in $\Omega =[0,1]\times [0,1]$ and the time interval [0, 0.25]:

$$\begin{aligned} \left\{ \begin{array}{llllll} \Delta ^2 \phi -\Delta \phi =C_1-C_2+F_3, \\ \partial _t C_i-\nabla \cdot \left( \nabla C_i + z_i\nabla \phi C_i -\varvec{u} C_i\right) =F_i,\quad i=1,2, \\ \partial _t\varvec{u}+(\varvec{u} \cdot \nabla )\varvec{u}-\Delta \varvec{u} +\nabla p =-\left( C_1-C_2\right) \nabla \phi +F_4,\\ \nabla \cdot \varvec{u}=0, \end{array} \right. \end{aligned}$$

(5.2)

by appropriately choosing right hand side functions $F_i\in L^\infty (0,T;L^2(\Omega ))$ ($1\le i\le 4$), where all $F_i$ are nonzero functions and do not actually affect our error analyses and theoretical results shown in Sects. 3 and 4 at all. And, all boundary and initial conditions are homogeneous, which matches with the adopted real solutions (5.1) on the boundary $\partial \Omega$ or at $t=0$.

In the following, we implement Algorithm 4.1 to find discrete solutions of $(\phi , \varvec{q}, z, C_1, C_2, \varvec{J}_1, \varvec{J}_2$, $\varvec{u}, p)$ to the fully discrete mixed finite element discretization (4.1)–(4.3), and compute convergence errors in corresponding norms for these variables. To that end, we adopt $\Delta t =4h^3$ with the grid doubling, i.e., choose mesh sizes $h=1/4, 1/8, 1/16$ and 1/32 to form a series of nested uniform grids, on which we define corresponding $P^2P^1$ (Taylor–Hood) element to discretize $(\varvec{\phi }, \varvec{q})$, $(\varvec{u}, p)$ and $(\varvec{J}_i,C_i)$ $(i=1,2)$, respectively, and $P^1$ (linear) element to discretize the variable z by choosing $k=1$ in (3.1).

Numerical results are reported in Tables 1, 2, and 3 and Figs. 1, 2, and 3, from which we can see all results are at least in accordance with or even better than the theoretical results of optimal error estimates shown in Theorem 4.1. In particular, optimal (second-order) convergence rates are illustrated for approximation errors of all variables in their corresponding energy norm and $L^2$ norm, except for the velocity’s and the pressure’s errors in $L^2$ norm, i.e., $\Vert \varvec{u}-\varvec{u}_h\Vert _{0}$ and $\Vert p-p_h\Vert _{0}$ that even show a third-order spatial convergence rate in Table 2, which is however one order higher than the result demonstrated in our convergence theorem. Due to the nonlinear source term of the momentum equation that involves ionic concentrations and the gradient of electrostatic potential, our proofs for Theorems 3.4 and 4.1 can only show a second-order convergence rate in space for the velocity’s error in both $H^1$ norm and $L^2$ norm, as well as for the pressure’s error in $L^2$ norm. But, as illustrated by numerical results, it seems that such nonlinear source term does not prevent the mixed FEM for Naiver-Stokes equations from achieving an optimal (third-order) convergence rate for $\Vert \varvec{u}-\varvec{u}_h\Vert _{0}$ with $P^2$ element, moreover, a nearly third-order superconvergence property for $\Vert p-p_h\Vert _{0}$ with $P^1$ element is illustrated as well. Further theoretical studies would be needed in the future to verify both the optimal convergence of velocity and the superconvergence of pressure in $L^2$ norms, for the fourth-order modified PNP/NS coupling system.

Table 1 Convergence results of the electrostatic potential and relevant vector- and scalar-valued variables

Table 2 Convergence results of fluid velocity and pressure

Table 3 Convergence results of ionic concentrations and relevant vector-valued variables

Fig. 1

Linear least squares fitting of convergence trends against mesh size for $\phi$, $\varvec{q}$ and z in respective norms

Fig. 2

Linear least squares fitting of convergence trends against mesh size for $\varvec{u}$ and p in respective norms

Fig. 3

Linear least squares fitting of convergence trends against mesh size for $C_i$ and $\varvec{J}_i$ in respective norms

5.2 Example 2: A Practical Problem to Investigate the Force Between Two Charged Particles

To explain why the modified model with a fourth-order elliptic equation for the electrostatic potential is significant and necessary in contrast to the classical Poisson equation, in this section we use both the classical model and the modified model to study a practical example in two dimension for the electrostatic interaction force between two charged particles, and compare numerically obtained forces with experimental results to show that only the modified model can demonstrate a reasonable result that is consistent with experimental phenomena. Figure 4 depicts two spherical particles (represented by $\Omega _2$) that is submerged into an electrolyte (represented by $\Omega _1$) and is surrounded by a uniformly alternating electric current field. Two spherical particles are uniformly charged dielectrics whose electrostatic potentials are defined through either the modified model—the fourth order elliptic equation (1.1) or the classical model—Poisson equation that is reduced from (1.1) by letting $\ell _c=0$ , while the electrolyte, which is an ionic solvent containing ions (cations and anions), supposes to be modeled by Nernst-Planck equations, as shown in (2.1), for ionic concentrations. But, since in this section we only focus on the comparison between the modified and the classical models of the electrostatic potential, we simply replace Nernst-Planck equations by an empirical function for ionic concentrations that explicitly depends on the electrostatic potential [12]. Such an empirical function is derived based on the Bikerman model [40] for volume constraints only with equal sized cations and anions, as shown below in (5.3).

Fig. 4

The schematics of the submerged particles in an electrolyte

All necessary physical parameters involved in this section are labeled and explained in Table 4. In particular, we let the charge density $\rho =z_1eC_1-z_2eC_2$ in (1.1), where $C_1$ and $C_2$ are concentrations of the ionic species, and, we use $\epsilon _1$ and $\epsilon _2$ to denote the dielectric permittivity in the electrolyte and the particles, respectively, which describes different polarizability of ions. Here we let $\epsilon _1=\epsilon _0\epsilon _s$, $\epsilon _2=\epsilon _0\epsilon _m$. In addition, we assume a binary $z_1:z_2$ electrolyte such that the far field concentrations of cations and anions satisfy $z_1C^+_{\infty }=z_2C^-_{\infty }$. Following the aforementioned reason, in this section we replace ionic concentration (Nernst-Planck) equations by two empirical functions at equilibrium which are explicit functions of the electrostatic potential, defined by [12]

$$\begin{aligned} \left\{ \begin{array}{ll} C_1=C^+_{\infty }e^{-z_1\frac{e}{K_BT}\phi },\\ C_2=\frac{z_1}{z_2}C^+_{\infty }e^{z_2\frac{e}{K_BT}\phi }, \end{array} \right. \end{aligned}$$

(5.3)

where the far field concentration, $C_{\infty }^+$ (in the SI unit of $1/\mathrm{m}^3$), describes the degree of concentration of cations in physical spaces, while $c_0=\frac{C_{\infty }^+}{N_A}$, is often adopted to change the unit of the far field cationic concentration to the most commonly used molar concentration unit: $\mathrm{mol}/\mathrm{m}^3$ [12]. Moreover, to compute the interactional force between two particles, we need to introduce the expression of the Maxwell stress tensor, $\varvec{\tau }$, for a fluid (that is the electrolyte in this example) with a non-local permittivity $\epsilon$, defined as [13],

$$\begin{aligned} \varvec{\tau }=\epsilon \varvec{q} \varvec{q}^T -\frac{1}{2}\epsilon \varvec{q} \cdot \varvec{q} I +\epsilon \ell _c^2\left[ \varvec{q} \cdot \left( \nabla (\nabla \cdot \varvec{q})\right) I-\varvec{q} \left( \nabla (\nabla \cdot \varvec{q})\right) ^T-\left( \nabla (\nabla \cdot \varvec{q})\right) \varvec{q}^T+\frac{1}{2}(\nabla \cdot \varvec{q})^2I\right] , \end{aligned}$$

where $\varvec{q}=-\nabla \phi$ is the electric current field. Then the total electrostatic force, $\varvec{F}$, acting on the surface of the particle, e.g., the surface of the right spherical particle, $\Gamma _3$ (see Fig. 4), can be calculated by $\varvec{F}=\int _{\Gamma _3}\varvec{\tau } \varvec{n} ds$. Since the vertical component of this total force does not contribute to the interaction between two charged particles that lie along a horizontal direction (as shown in Fig. 4), in what follows, we only take the horizontal component of this total force to investigate the interaction effect between them.

Table 4 Notations and physical constants

Specifically in this example, we set two charged particles to carry opposite charges, as shown in Fig. 4. Then due to the Coulomb’s law, their interaction force in between shall be anti-proportional to (the square of) the distance between them. On the other hand, the classical electromagnetism theory tells that two opposite electric charges attract each other, which however no longer holds for the experimental setup in this example when ionic concentrations in the electrolyte increase to a certain extent, i.e., under that circumstance two oppositely charged particles turns out to repel each other instead. It is the most significant phenomenon that only the BSK theory can explain but classical theories cannot. A physically experimental study in [41] fully supports this interesting force reserving phenomenon, and we will essentially validate it in our numerical experiment using the modified fourth-order electrostatic potential model that is derived from the BSK theory, i.e., we still expect from our numerical results that the horizontal force between two oppositely charged particles will decrease along the increase of the distance between them, simultaneously, we will see that their interaction force is gradually reversed from the attractive force to the repulsive force, e.g., the sign of the horizontal force acting on the right particle shown in Fig. 4) will be gradually changed from negative to positive along with the increase of ionic concentrations, which means that its horizontal force is eventually reversed from the left (attractive) direction to the right (repulsive) direction.

Table 5 Horizontal forces (nN) acting on the right particle (see Fig. 4) by two models

After applying the developed mixed finite element method to the fourth-order electrostatic potential equation, which is defined in the domain shown in Fig. 4 and involves with simplified ionic concentration functions defined in (5.3), then numerically computing the Maxwell stress tensor $\varvec{\tau }$ as well as the total electrostatic force $\varvec{F}$, we obtain horizontal forces in the unit of Nanonewton (nN) acting on the surface of the right particle with respect to the distance from the left particle, dL, and with respect to the far field ionic concentration, $c_0$, as shown in Table 5, where Model I represents the modified model with a fourth-order elliptic equation, and Model II represents the classical model with Poisson equation, both are solved for the electrostatic potential. From Table 5 and Fig. 5 we can see that both models show that the magnitude of horizontal forces decreases along with the increase of the distance between two particles, which is consistent with the trend of experimental results shown in [41, Figure 1]. On the other hand, when $c_0$ increases, the direction of horizontal forces computed by Model I are eventually reversed from negative to positive, which is still consistent with the pattern of change of experimental results shown in [41, Figure 2]. Nevertheless, such a phenomenon of reversing the interaction force is not observed in numerical results of Model II due to the lacking of considering the ion-ion electrostatic correlation, which is however fully reflected by the modified Model I.

Thus, we can conclude that the modified model for the electrostatic potential characterized as a fourth-order elliptic equation is superior to the classical Poisson equation in terms of the applicability, the accuracy and the practicality.

6 Conclusion and Future Work

Fig. 5

Horizontal forces (nN) acting on the right particle versus distances and ionic concentrations by two models

In this paper, we analyze error estimates of a fully mixed finite element approximation to a recently founded new electrohydrodynamical (Bazant–Storey–Kornyshev) theory driven model –- a coupled fourth-order modified Poisson–Nernst–Planck/Navier–Stokes equations. Both semi- and fully discrete Stokes-type mixed finite element methods are developed and are analyzed for a stabilized mixed weak formulation of PNP/NS coupling system, and optimal error estimates are obtained for all primary variables and their vector-valued gradient variables in corresponding energy norms, that is, if Taylor–Hood $P^{k+1}P^{k}$ element is employed, then we can obtain optimal error estimates for the electrostatic potential flux $\varvec{q}= \nabla \phi$ and ionic mass fluxes $\varvec{J}_i=\nabla C_i - z_i \varvec{q} C_i-\varvec{u} C_i$ in $L^{\infty }(\varvec{H}(\text {div}))$ norm, for the electrostatic potential $\phi$, ionic concentrations $C_i$ and the fluid pressure p in $L^{\infty }(L^2)$ norm, and for the fluid velocity $\varvec{u}$ in $L^{\infty }(\varvec{H}^1)$ norm. To the authors’ best knowledge, this seems to be the first time to apply a fully mixed FEM with $P^{k+1}P^k$ element to a time-dependent, coupled fourth-order modified PNP/NS equations and obtain optimal convergence rates for all primary variables and their vector-values variables in respective energy norms. In particular, due to the nonlinear coupling effect of PNP/NS system, the fluid velocity’s error in $L^2$ norm reaches a suboptimal (second-order) convergence rate in the convergence theorem, which is however illustrated as an optimal (third-order) convergence behavior in numerical experiments and thus may be considered as a superconvergence property. The same superconvergence behavior is also observed in numerical experiments for the pressure’s convergence rate in $L^2$ norm as well. In addition, we also numerically study a practical example to validate the necessity of introducing the modified electrostatic potential equation characterized as a fourth-order elliptic equation by comparing with the classical Poisson equation. We observe that numerical trends obtained from the modified model are all consistent with experimental results shown in [41], which however cannot be predicted by the classical model.

On the other hand, numerical methodology and analysis tools developed in this paper for the mixed FEM is not limited to the presented fourth-order modified PNP/NS equations with unit constant coefficients, which is the case we study in this paper though, all developed numerical techniques can be easily extended to other kinds of PNP/NS system with more complicated physical coefficients as long as all coefficients are sufficiently differentiable and necessarily bounded. Our future work will be dedicated to applying the newly developed mixed FEM to a physically realistic fourth-order modified PNP/NS problem which could reflect the case of small Debye length and boundary layer effects, etc.