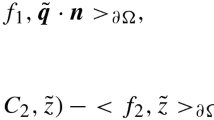A Linearized Local Conservative Mixed Finite Element Method for Poisson–Nernst–Planck Equations

Abstract

In this paper, a linearized local conservative mixed finite element method is proposed and analyzed for Poisson–Nernst–Planck (PNP) equations, where the mass fluxes and the potential flux are introduced as new vector-valued variables to equations of ionic concentrations (Nernst–Planck equations) and equation of the electrostatic potential (Poisson equation), respectively. These flux variables are crucial to PNP equations on determining the Debye layer and computing the electric current in an accurate fashion. The Raviart–Thomas mixed finite element is employed for the spatial discretization, while the backward Euler scheme with linearization is adopted for the temporal discretization and decoupling nonlinear terms, thus three linear equations are separately solved at each time step. The proposed method is more efficient in practice, and locally preserves the mass conservation. By deriving the boundedness of numerical solutions in certain strong norms, an unconditionally optimal error analysis is obtained for all six unknowns: the concentrations p and n, the mass fluxes ${{\varvec{J}}}_p=\nabla p + p {\varvec{\sigma }}$ and ${{\varvec{J}}}_n=\nabla n - n {\varvec{\sigma }}$, the potential $\psi$ and the potential flux ${\varvec{\sigma }}= \nabla \psi$ in $L^{\infty }(L^2)$ norm. Numerical experiments are carried out to demonstrate the efficiency and to validate the convergence theorem of the proposed method.

1 Introduction

In this paper, we consider the following time-dependent Poisson–Nernst–Planck (PNP) equations in regard to the ionic concentrations of the positively and negatively charged particles, $p({{{\varvec{x}}}},t),\,n({{\varvec{x}}},t)$, and the electrostatic potential, $\psi ({{\varvec{x}}},t)$, that is generated by the heterogeneous distribution of the positively and negatively charged particles

$$\begin{aligned}&\frac{\partial p}{\partial t} - \nabla \cdot \big ( \nabla p + p \nabla \psi \big )= 0 \, , \end{aligned}$$

(1.1)

$$\begin{aligned}&\frac{\partial n}{\partial t} - \nabla \cdot \big ( \nabla n - n \nabla \psi \big )= 0 \, , \end{aligned}$$

(1.2)

$$\begin{aligned}&- \Delta \psi = p-n\, , \end{aligned}$$

(1.3)

where, $t \in [0,T]$ and ${{\varvec{x}}} \in \Omega$ which is a bounded, convex polyhedron in $\mathbb {R}^3$ (or polygon in $\mathbb {R}^2$). The boundary and initial conditions are defined as

$$\begin{aligned}&\frac{\partial p}{\partial \mathbf {n}} + p\frac{\partial \psi }{\partial \mathbf {n}} = 0, \quad \frac{\partial n}{\partial \mathbf {n}} - n\frac{\partial \psi }{\partial \mathbf {n}} = 0, \quad \frac{\partial \psi }{\partial \mathbf {n}}=0,&\text {for } {{{\varvec{x}}}} \in \partial \Omega , t \in [0,T], \end{aligned}$$

(1.4)

$$\begin{aligned}&p({{\varvec{x}}},0)=p_0({{\varvec{x}}}), \quad n({{\varvec{x}}},0)=n_0({{\varvec{x}}}),&\text {for } {{{\varvec{x}}}} \in \Omega , \end{aligned}$$

(1.5)

where $\mathbf {n}$ is the unit outward normal vector of the domain boundary $\partial \Omega$. Subject to the homogeneous boundary condition (1.4), the well-posedness of PNP equations requires the following initial electroneutrality condition

$$\begin{aligned} \int _{\Omega }\,\left( p({{\varvec{x}}},0) - n({{\varvec{x}}},0)\right) \,\mathrm {d}{{\varvec{x}}} = 0. \end{aligned}$$

(1.6)

With (1.4), the initial condition (1.6) induces that for all $t \ge 0$

$$\begin{aligned} \int _{\Omega } \, p({{\varvec{x}}},t) \, \mathrm {d}{{\varvec{x}}} \equiv \int _{\Omega } \, p_0({{\varvec{x}}}) \, \mathrm {d}{{\varvec{x}}} = \int _{\Omega } \, n_0({{\varvec{x}}}) \, \mathrm {d}{{\varvec{x}}} \equiv \int _{\Omega } \, n({{\varvec{x}}},t) \, \mathrm {d}{{\varvec{x}}}. \end{aligned}$$

(1.7)

In addition, since $\psi$ is unique up to a constant, here we only consider the zero mean value solution $\psi$ which satisfies $(\psi , 1)=0$, where $(\cdot , \cdot )$ denotes the standard $L^2$ inner product.

The PNP system is served as a popular model in a wide variety of application areas, such as transport of charged particles in biological membrane channels [29, 42, 43], semiconductors [6, 16, 30] and electrokinetic flows [38]. We refer to [2, 3, 16, 33, 38] for theoretical analyses of the PNP equations. Numerical methods and analyses for the PNP system have been extensively studied, see [5, 7, 13,14,15, 19, 25,26,27, 29, 31, 32, 35, 37, 40, 43]. For the regular domain, several finite difference schemes have been investigated, see [13, 19, 26, 32]. For more general geometries and boundary conditions, finite element method (FEM) is much more attractive [4, 41]. We shall review previous studies with finite element method which are closely related to the present work. Prohl and Schmuck [35] propose two nonlinear schemes with a linear finite element method which preserve electric energy decay and entropy decay properties, respectively. The fixed point inner iterations are used at each time step for these schemes and the convergence theorem is also proved in [35]. Later, numerical methods for the PNP system (1.1)–(1.5) coupled with Navier–Stokes equations are investigated in [36]. Sun et al. [40] analyze a fully nonlinear Crank–Nicolson FEM for the PNP equations, where a Picard’s linearization is used in the inner iteration and an optimal error estimate in $H^1$ norm but a sub-optimal error estimate in $L^2$ norm are obtained. To overcome the convergence order reduction and to accurately resolve the electric current that is the gradient of the electrostatic potential, $\nabla \psi$, as well, He and Sun [20] propose a nonlinear mixed finite element method for Poisson equation (1.3) and still use the standard FEM for Nernst–Planck equations (1.1) and (1.2), which provides optimal error estimates for the electrostatic potential and ionic concentrations in both $H^1$ and $L^2$ norms, moreover, for $\nabla \psi$ in $\mathbf {H}(\mathrm {div})$ norm as well. Recently, He and Sun [21] further apply the same type of stable Stokes-pair mixed FEM to the PNP/Navier–Stokes coupling system, and obtain optimal convergence rates for all variables of PNP equations and of Navier–Stokes equations in their own proper norms, respectively.

It should be mentioned that all schemes in [13, 20, 35, 40] are nonlinear. However, it is well known that for nonlinear parabolic problems, linearized schemes are much more efficient, which only need to solve a linear system at each time step, e.g., see [23, 39]. Thereby in this direction, He and Pan [19] propose a linearized finite difference scheme which preserves the mass conservation and electric energy decay, and the optimal convergence rate and electric energy decay properties of the scheme are numerically illustrated. Gao and He [17] extend the scheme to finite element discretization and establish unconditionally optimal error estimates for all variables in both $H^1$ and $L^2$ norms, additionally, they also demonstrate the global energy decay and mass preserving properties for the proposed scheme. We point out that the original PNP system (1.1)–(1.5) satisfies a local mass conservation property. Local conservation in the discrete scheme can be helpful to guarantee the accuracy of numerical methods for the coupled flow and transport system. We refer to [10] for more discussion on the local conservation.

Note that the electric current is crucial for PNP system and its applications. It should be remarked that the obtained numerical solutions need to be validated by comparing with experimental data, where, the electric current seems the easiest physical quantity to be measured in the experiment. For example, the electric current across the biological membrane channel is calculated by the following expression [45]

$$\begin{aligned} I=\sum _{m=1}^{2}q_m\int _{\text {MEM}}D_m\left( \nabla C_m+\frac{q_m}{\kappa _BT}C_m\nabla \psi \right) \cdot \mathbf {n} \,\, \mathrm {d}x, \end{aligned}$$

(1.8)

where, $C_m\ (m=1,2)$ represent the ionic concentrations, i.e., $C_1=p$ and $C_2=n$ in this paper and $\mathbf {n}$ denotes the unit outer normal vector through each cross section inside the membrane channel. Equation (1.8) clearly shows that the gradients of ionic concentrations and of electrostatic potential are important to produce an accurate electric current everywhere inside the membrane channel. Moreover, another important electrokinetic phenomena existing in ion channels of electrophysiology, the electrical double layer (Debye layer) [11], is formed near the surface of a charged object (membrane) due to the exponential decreases of the electrostatic potential, further, of the ionic concentrations, away from the surface, featuring a distance called Debye length [2, 3]. Such exponential decrease induces a large gradient, so an accurate computation of gradient for the electrostatic potential and ionic concentrations are crucial to determine the location of Debye layer, which has a significant influence on the behavior of surfaces of the charged objects in contact with solutions or solid-state fast ion conductors.

Therefore in the PNP system, it is necessary to numerically resolve the gradients $\nabla p$, $\nabla n$ and $\nabla \psi$ in an accurate and efficient fashion. Conventional Lagrange FEMs need a proper postprocessing technique to locally conduct a certain numerical differentiation for the primary variable, then project back to the continuous finite element space for the seek of a continuous gradient variable, which may leads to a loss of accuracy if no advanced recovery technique is adopted [34, 46]. There have been several works on Raviart–Thomas (RT) mixed FEMs for solving the PNP system and related models which couple the PNP equations with Darcy or Stokes flows, see [5, 14, 15]. For a two-dimensional stationary model arose from the discretization of the dynamical PNP equation, Brera et al. in [5] study a conservative mixed method, where the Delaunay type mesh is used which must satisfy certain angle conditions to ensure a discrete maximum principle. For the two-dimensional Stokes–Nernst–Planck–Poisson system, Frank, Ray and Knabner [15] suggest a fully nonlinear backward mixed FEM, where a fixed point inner iteration is used at each time step to solve the nonlinear FEM equation. Numerical experiments are reported to show the effectiveness of the scheme. However, no analysis is available in [15]. Recently, Frank and Knabner [14] proposed a nonlinear BDF2/mixed FEM for the Darcy-Nernst–Planck–Poisson system. A cut-off operator $\mathcal {M}$ is used in their scheme, which needs a cut-off parameter depending on the domain $\Omega$, terminal time T and initial data, see [14, the right-hand side of (2.5)]. Selecting this parameter might be difficult in practice. $L^2$ error estimates of the velocity, pressure, electric potential, electric field, concentrations are derived, which relies on the uniform boundedness of the cut-off parameter. It should be noted that uniqueness and existence of numerical solutions [14, Problem 3.3] are not shown. Moreover, $L^{\infty }(L^2)$ error estimates of the mass fluxes are still missing, which are of great importance in computing electric current and Desbye layer.

Motivated by the above, in this paper we propose and analyze a linearized local conservative mixed finite element method for the PNP system (1.1)–(1.5). We apply the RT mixed FEM for the spatial approximation combined with a linearized (semi-implicit) backward Euler scheme in temporal direction. Our method is linear so that at each time step, one only needs to solve three linear systems. Moreover, RT mixed FEMs have many attractive features over the conventional Lagrange FEMs. For instance, the mass conservation is preserved in each element; the lowest order mixed RT element possesses the smallest number of degree of freedoms as a stable mixed finite element pair; besides the primary variables (ionic concentrations and electrostatic potential), their fluxes can be computed simultaneously in an accurate order, which are desirable in studying the Debye layer and current–voltage curves. The major difficulty in the finite element error analysis lies in the fact that the ionic concentrations p and n are strongly coupled with the electrostatic potential $\psi$ through its gradient. In this paper, we obtain unconditionally optimal error estimates from the proposed mixed finite element approximation for all primary variables and their gradients in appropriate norms, respectively. A key step in our error estimates is to derive the boundedness of numerical solutions in certain strong norms, which is achieved by applying a discrete Sobolev embedding inequality for the RT mixed FEM (see Lemma 2.3).

The rest of this paper is organized as follows. In Sect. 2, we define some notations and introduce several useful lemmas. In Sect. 3, we present a linearized backward Euler RT mixed FEM and the main results on error estimates. In Sect. 4, we prove an optimal $L^2$ error estimate without any restriction on mesh ratio between the time step $\tau$ and the mesh size h. In Sect. 5, we provide several numerical examples to confirm our theoretical analyses and show the efficiency of the proposed methods. Conclusions and discussions are given in Sect. 6.

2 Preliminaries

We first clarify some conventional notations. For integer $k \ge 0$ and $1 \le p \le \infty$, let $W^{k,p}(\Omega )$ be the Sobolev space with the norm

$$\begin{aligned} \Vert u \Vert _{W^{k,p}}=\left\{ \begin{array}{ll} \biggl (\displaystyle \sum _{|\beta |\le k}\int _\Omega |D^\beta u|^p\,\mathrm{d}{{\varvec{x}}}\biggl )^\frac{1}{p}, &{} \text {for } 1 \le p < \infty , \\ \displaystyle \sum _{|\beta | \le k}\mathrm{ess\,sup}_{\Omega }|D^{\beta } u|, &{} \text {for } p=\infty , \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} D^\beta =\frac{\partial ^{|\beta |}}{\partial x_1^{\beta _1}\cdots \partial x_d^{\beta _d}} \, , \end{aligned}$$

for the multi-index $\beta =(\beta _1,\ldots ,\beta _d)$, $\beta _1\ge 0$, $\ldots$, $\beta _d\ge 0$, and $|\beta |=\beta _1+\cdots +\beta _d$. When $p=2$ we also note $H^k(\Omega ) := W^{k,2}(\Omega )$. For vector function space, we denote

$$\begin{aligned} {\mathbf {H}}(\mathrm {div};\Omega ) = \left\{ {{\varvec{u}}} \, \big | \, {{\varvec{u}}} \in \mathbf {L}^{2}(\Omega ), \mathrm {div}\, {{\varvec{u}}} \in L^2(\Omega ) \right\} \, \text {with } \Vert {{\varvec{u}}}\Vert _{{\mathbf {H}}(\mathrm {div})} = \left( \Vert {{\varvec{u}}}\Vert _{{L}^2}^2 + \Vert \mathrm {div}\, {{\varvec{u}}}\Vert _{{L}^2}^2 \right) ^{\frac{1}{2}} \end{aligned}$$

and its subspace with the corresponding dual space with norm

To introduce the linearized mixed finite element method, let ${\left\{ t_{j} \right\} }_{j=0}^{J}$ be a uniform partition in the time direction with step size $\tau = \frac{T}{J}$. For a sequence of functions $\{u^{j}\}_{j=0}^J$ defined in $\Omega$, we denote the backward Euler discretization operator

$$\begin{aligned} {D_{\tau }} u^{j} = \frac{u^{j}-u^{j-1}}{\tau }, \quad \text {for } j=1, \ldots , J. \end{aligned}$$

Let $\mathcal {T}_h = \{K\}$ be a regular mesh partition of $\Omega$ and denote the mesh size $h = \max _{K} \{\mathrm {diam} K \}$. We define the RT mixed finite element space by

$$\begin{aligned}&\mathbf {H}_h^r(\Omega ) := \{{\varvec{q}} \in \mathbf {H}(\mathrm {div};\Omega ) \quad : \quad {\varvec{q}}|_{K} \in [P_r(K)]^d + {{\varvec{x}}} P_r(K), \quad \forall K \in \mathcal {T}_h\} \,, \\&V_h^r(\Omega ) := \{u \in L^{2}(\Omega ) \quad : \quad u|_{K} \in P_r(K), \quad \forall K \in \mathcal {T}_h\} \,, \end{aligned}$$

where $P_r(K)$ is the space of polynomials of degree r or less defined in the element K. It is well-known that $\mathbf {H}_h^r(\Omega ) \times V_h^r(\Omega )$ is a stable finite element pair for solving the second order elliptic problems [44]. Moreover, the following diagram commutes

$$\begin{aligned} \begin{array}{ccc} {\mathbf {H}}(\mathrm {div}) &{} \xrightarrow {\,\, \mathrm {div}\,\,} &{} L^2(\Omega ) \\ \Pi _h \Bigg \downarrow &{} &{} \Bigg \downarrow \Pi _h \\ \mathbf {H}_h^r(\Omega ) &{} \xrightarrow {\,\, \mathrm {div}\,\,} &{} V_h^r(\Omega ) \end{array} \end{aligned}$$

(2.1)

where $\Pi _h$ denotes a general projector. More precisely, $\Pi _h : {\mathbf {H}}(\mathrm {div}) \rightarrow \mathbf {H}_h^r(\Omega )$ is the RT projector [44], and $\Pi _h : L^2(\Omega ) \rightarrow V_h^r(\Omega )$ is the $L^2$ projector, respectively.

In the rest part of this paper, for simplicity of notation we denote by C a generic positive constant and $\epsilon$ a generic small positive constant, which are independent of j, h and $\tau$. We present the Gagliardo–Nirenberg inequality, the discrete Gronwall’s inequality and a discrete inequality for the RT mixed FEM in the following lemmas which will be frequently used in our proofs.

Lemma 2.1

(Gagliardo–Nirenberg inequality [8, Theorem 1.5.2]): Let $\Omega \subset \mathbb {R}^d$ be a bounded domain. Let $m\in \mathbb {N}$, $p,r\in [1,\infty )$, and $u\in L^p(\Omega )\cap L^r(\Omega )$. Assume that $\partial _x^m u\in L^p(\Omega )$. Then for integer $0\le j\le m$ and $\theta \in \left[ \frac{j}{m},1\right]$ (with the exception $\theta \ne 1$ when $m-j-\frac{d}{2}\in \mathbb {N}$), define q by

$$\begin{aligned} \frac{1}{q}=\frac{j}{d}+\theta \left( \frac{1}{p}-\frac{m}{d}\right) +(1-\theta )\frac{1}{r}. \end{aligned}$$

Then, for any $\gamma \in \mathbb {N}^d$ with $|\gamma |=j$, $\partial _x^\gamma u\in L^q(\Omega )$ and we have the Gagliardo–Nirenberg inequality

$$\begin{aligned} ||\partial _x^\gamma u||_{L^q}\le C||\partial _x^m u||_{L^p}^\theta ||u||_{L^r}^{1-\theta } + \widehat{C}||u||_{L^s} \end{aligned}$$

with finite $1\le s\le \max \{p,r\}$, C and ${\widehat{C}}$ independent of u, C independent of $\Omega$.

Lemma 2.2

Discrete Gronwall’s inequality [22] : Let $\tau$, B and $a_{k}$, $b_{k}$, $c_{k}$, $\gamma _{k}$, for integers $k \ge 0$, be non-negative numbers such that

$$\begin{aligned} a_{J} + \tau \sum _{k=0}^{J} b_{k} \le \tau \sum _{k=0}^{J} \gamma _{k} a_{k} + \tau \sum _{k=0}^{J} c_{k} + B \, , \quad \mathrm {for } \quad J \ge 0 \, , \end{aligned}$$

suppose that $\tau \gamma _{k} < 1$, for all k, and set $\sigma _{k}=(1-\tau \gamma _{k})^{-1}$. Then

$$\begin{aligned} a_{J} + \tau \sum _{k=0}^{J} b_{k} \le \exp \left( \tau \sum _{k=0}^{J} \gamma _{k} \sigma _{k}\right) \left( \tau \sum _{k=0}^{J} c_{k} + B\right) \, , \quad \mathrm {for } \quad J \ge 0 \, . \end{aligned}$$

Lemma 2.3

Discrete Sobolev inequalities for the RT mixed FEM [18] : For any given $u_h \in V_h^r(\Omega )$ ($\Omega$ can be a Lipschitz domain), if there exists a function ${\varvec{f}} \in {\varvec{L}}^2(\Omega )$ such that

$$\begin{aligned} ({\varvec{f}},{\varvec{\chi }}_h) + ({u}_h, \mathrm {div}{\varvec{\chi }}_h) =0\, , \qquad \forall {\varvec{\chi }}_h \in \mathbf {H}_h^r(\Omega ) \,, \end{aligned}$$

then the following discrete Sobolev embedding inequalities hold

$$\begin{aligned}&\Vert {u}_h\Vert _{L^p} \le C\Vert {{\varvec{f}}}\Vert _{L^2} \,,&\quad \text {for} {1 \le p < \infty },&\text {in two dimensional space}, \\&\Vert {u}_h\Vert _{L^p} \le C\Vert {{\varvec{f}}}\Vert _{L^2} \,,&\quad \text {for} {1 \le p \le 6},&\text {in three dimensional space}, \end{aligned}$$

where C is a constant only depending upon the domain $\Omega$, r and p.

3 A Linearized Backward Euler RT Mixed FEM and Main Results

In this section, we provide a linearized mixed FEM for solving PNP equations (1.1)–(1.5). We introduce three extra variables below

$$\begin{aligned} {\varvec{\sigma }} = \nabla \psi \,, \quad {\varvec{J}}_p = \nabla p + p {\varvec{\sigma }}, \quad {\varvec{J}}_n = \nabla n - n {\varvec{\sigma }}. \end{aligned}$$

(3.1)

Here one can see that ${\varvec{J}}_p$ and ${\varvec{J}}_n$ are the mass flux of positively and negatively charged particles, respectively, while ${\varvec{\sigma }}$ denotes the potential flux. With the above notations, we can reformulate the original PNP system (1.1)–(1.5) to the following new system

$$\begin{aligned}&\left\{ \begin{array}{l} {\varvec{J}}_p = \nabla p + p {\varvec{\sigma }} \,, \\ \frac{\partial p}{\partial t} - \nabla \cdot {\varvec{J}}_p = 0 \, , \,\,\,\! \\ \end{array}\right. \\&\left\{ \begin{array}{l} {\varvec{J}}_n = \nabla n - n {\varvec{\sigma }} \,, \\ \frac{\partial n}{\partial t} - \nabla \cdot {\varvec{J}}_n = 0\, , \\ \end{array}\right. \\&\left\{ \begin{array}{l} {\varvec{\sigma }} = \nabla \psi \,, \\ - \nabla \cdot {\varvec{\sigma }} = p-n \, , \end{array}\right. \end{aligned}$$

with boundary conditions

$$\begin{aligned} {{\varvec{J}}}_p \cdot \mathbf {n} = {{\varvec{J}}}_n \cdot \mathbf {n} = {\varvec{\sigma }} \cdot \mathbf {n} = 0 \end{aligned}$$

and initial conditions

$$\begin{aligned} p({{\varvec{x}}},0)=p_0({{\varvec{x}}}), \quad n({{\varvec{x}}},0)=n_0({{\varvec{x}}}). \end{aligned}$$

Based on the above mixed PNP system, for $t \in (0,T]$, its weak formulation is to find with $\frac{\partial p}{\partial t}, \frac{\partial n}{\partial t} \in L^2(\Omega )$, and with $(\psi \, ,1) = 0$, such that

Now we are ready to present the linearized backward Euler mixed FEM for the PNP system. For $j=0$, 1, $\ldots$, $J-1$, a linearized mixed FEM is to find $(({\varvec{J}}_p)_h^{j+1},\, P_h^{j+1})$, $(({\varvec{J}}_n)_h^{j+1},\, N_h^{j+1})$ and , with $(\Psi _h^{j+1} \, ,1) = 0$, such that

At the initial step, $P_h^0 = \Pi _h p^0$, $N_h^0 = \Pi _h n^0$ and ${\varvec{\sigma }}_h^0$ is determined by (3.12), (3.13) with $j=-1$. We shall note that the FEM equations (3.12), (3.13) of $({\varvec{\sigma }}_h^{j+1},\Psi _h^{j+1})$ is a pure Neumann problem, which needs special treatments in the programming, we refer to [1] for more discussion.

In the rest part of this paper, if the r-th order finite element is used, we assume that the exact solutions of PNP equations (1.1)–(1.5) exist and satisfy the following regularity results

$$\begin{aligned} \left\{ \begin{array}{l} \Vert p\Vert _{L^\infty (0,T;H^{r+2})} +\Vert p_t\Vert _{L^\infty (0,T;H^{r+2})}+\Vert p_{tt}\Vert _{L^2(0,T;H^{1})} \le C, \\ \Vert n\Vert _{L^\infty (0,T;H^{r+2})} +\Vert n_t\Vert _{L^\infty (0,T;H^{r+2})}+\Vert n_{tt}\Vert _{L^2(0,T;H^{1})} \le C, \\ \Vert \psi \Vert _{L^\infty (0,T;H^{r+2})} +\Vert \psi _t\Vert _{L^\infty (0,T;H^{r+2})}+\Vert \psi _{tt}\Vert _{L^2(0,T;H^{1})} \le C. \end{array}\right. \end{aligned}$$

(3.14)

It should be noted that the above regularity assumptions might be not optimal but necessary for our remaining proofs. In this paper, we only focus on optimal error analyses of the proposed numerical method for the PNP system.

We present our main results on error estimates in the following theorem.

Theorem 3.1

Suppose that the PNP system (1.1)–(1.5) has a unique solution $(p, n, \psi )$ satisfying (3.14). Then the linearized backward Euler RT mixed FEM (3.8)–(3.13) admits a unique solution $(({\varvec{J}}_p)_h^{j},\, P_h^{j})$, $(({\varvec{J}}_n)_h^{j},\, N_h^{j})$ and $({\varvec{\sigma }}_h^{j},\Psi _h^{j})$ for $j=1$, $\ldots$, J, and there exist two positive constants $\tau _0$ and $h_0$ such that when $\tau < \tau _0$ and $h \le h_0$

$$\begin{aligned}&\max _{0 \le j \le J} \left( \Vert P^j_h - p^j\Vert _{L^2} +\Vert N^j_h - n^j\Vert _{L^2} + \Vert \Psi ^{j}_h -\psi ^{j}\Vert _{L^2} \right) \le C_1(\tau + h^{r+1}) , \end{aligned}$$

(3.15)

$$\begin{aligned}&\max _{0 \le j \le J} \left( \Vert ({\varvec{J}}_p)^j_h - {\varvec{J}}_p^j\Vert _{L^2} +\Vert ({\varvec{J}}_n)^j_h - {\varvec{J}}_n^j\Vert _{L^2} +\Vert {\varvec{\sigma }}_h^{j} - {\varvec{\sigma }}^{j}\Vert _{L^2} \right) \le C_2(\tau + h^{r+1}) , \end{aligned}$$

(3.16)

where, $C_1$ and $C_2$ are two positive constants which depend on the domain $\Omega$ and initial and boundary conditions, and are independent of j, h and $\tau$.

It should be noted that the proposed mixed FEM (3.8)–(3.13) uses a linearized backward Euler discretization, which is suitable for PNP equations with moderate smooth coefficients. If the problem is very stiff (i.e., with high surface potentials or very thin double layer in some realistic applications of PNP equations), higher order backward differentiation formula (BDF) type schemes or exponential integrators may help to conquer the stiffness to some extent. In our future work, we will attempt to apply the proposed scheme to a realistic PNP system with practical parameters, in which more comparison studies will be conducted against conventional Lagrange-type FEMs in terms of accuracy and run-time.

4 Proof of the Main Results

We denote the projection errors by

$$\begin{aligned}&\theta _{p} = \Pi _h p - p, \quad \theta _{n} = \Pi _h n - n, \quad \theta _{\psi } = \Pi _h \psi - \psi , \\&{\varvec{\theta }}_{J_p} = \Pi _h {\varvec{J}}_p - {\varvec{J}}_p, \quad {\varvec{\theta }}_{J_n} = \Pi _h {\varvec{J}}_n - {\varvec{J}}_n, \quad {\varvec{\theta }}_{\sigma } = \Pi _h {\varvec{\sigma }} - {\varvec{\sigma }} \,. \end{aligned}$$

Then, by the regularity assumption on the exact solutions (3.14) and classical analyses of the projection $\Pi _h$ [44], we have for $2 \le p < \infty$

$$\begin{aligned} \left\{ \begin{array}{l} \Vert \theta _{p}\Vert _{L^p} \le C h^{r+1} \Vert p \Vert _{W^{r+1,p}} \,,\\ \Vert \theta _{n}\Vert _{L^p} \le C h^{r+1} \Vert n \Vert _{W^{r+1,p}} \,,\\ \Vert \theta _{\psi }\Vert _{L^p} \le C h^{r+1} \Vert \psi \Vert _{W^{r+1,p}} \,, \end{array}\right. \end{aligned}$$

(4.1)

$$\begin{aligned} \left\{ \begin{array}{l}\Vert {\varvec{\theta }}_{J_p}\Vert _{L^p} + \Vert \mathrm {div}\, {\varvec{\theta }}_{J_p}\Vert _{L^p} \le C h^{r+1} \Vert {\varvec{J}}_p\Vert _{W^{r+1,p}} + C h^{r+1} \Vert \mathrm {div}\, {\varvec{J}}_p\Vert _{W^{r+1,p}} \,,\\ \Vert {\varvec{\theta }}_{J_n}\Vert _{L^p} + \Vert \mathrm {div}\, {\varvec{\theta }}_{J_n}\Vert _{L^p} \le C h^{r+1} \Vert {\varvec{J}}_n\Vert _{W^{r+1,p}} + C h^{r+1} \Vert \mathrm {div}\, {\varvec{J}}_n\Vert _{W^{r+1,p}} \,,\\ \Vert {\varvec{\theta }}_{\sigma }\Vert _{L^p} + \Vert \mathrm {div}\, {\varvec{\theta }}_{\sigma }\Vert _{L^p} \le C h^{r+1} \Vert {\varvec{\sigma }}\Vert _{W^{r+1,p}} + C h^{r+1} \Vert \mathrm {div}\, {\varvec{\sigma }}\Vert _{W^{r+1,p}} \,, \end{array}\right. \end{aligned}$$

(4.2)

and

$$\begin{aligned} \left\{ \begin{array}{l} \left\| \frac{\partial \theta _{p}}{\partial t}\right\| _{L^2} \le C h^{r+1} \left\| \frac{\partial p}{\partial t} \right\| _{H^{r+1}} \,, \\ \left\| \frac{\partial \theta _{n}}{\partial t}\right\| _{L^2} \le C h^{r+1} \left\| \frac{\partial n}{\partial t} \right\| _{H^{r+1}} \,, \\ \left\| \frac{\partial \theta _{\psi }}{\partial t}\right\| _{L^2} \le C h^{r+1} \left\| \frac{\partial \psi }{\partial t} \right\| _{H^{r+1}} \,, \end{array}\right. \end{aligned}$$

(4.3)

$$\begin{aligned} \left\{ \begin{array}{l} \left\| \frac{\partial {\varvec{\theta }}_{J_p}}{\partial t}\right\| _{H(\mathrm {div})} \le C h^{r+1} \left( \left\| \frac{\partial {\varvec{J}}_p}{\partial t}\right\| _{H^{r+1}} + \left\| \mathrm {div}\, \frac{\partial {\varvec{J}}_p}{\partial t}\right\| _{H^{r+1}}\right) \,, \\ \left\| \frac{\partial {\varvec{\theta }}_{J_n}}{\partial t}\right\| _{H(\mathrm {div})} \le C h^{r+1} \left( \left\| \frac{\partial {\varvec{J}}_n}{\partial t}\right\| _{H^{r+1}} + \left\| \mathrm {div}\, \frac{\partial {\varvec{J}}_n}{\partial t}\right\| _{H^{r+1}}\right) \,, \\ \left\| \frac{\partial {\varvec{\theta }}_{\sigma }}{\partial t}\right\| _{H(\mathrm {div})} \le C h^{r+1} \left( \left\| \frac{\partial {\varvec{\sigma }}}{\partial t}\right\| _{H^{r+1}} + \left\| \mathrm {div}\, \frac{\partial {\varvec{\sigma }}}{\partial t}\right\| _{H^{r+1}}\right) \,. \end{array}\right. \end{aligned}$$

(4.4)

Clearly, with the projection error (4.1), (4.2), we only need to the analyze the error functions

$$\begin{aligned}&e_{p}^j = P_h^j - \Pi _h p^j , \quad e_{n}^j = N_h^j - \Pi _h n^j, \quad e_{\psi }^j = \Psi _h^j - \Pi _h \psi ^j , \\&{\varvec{e}}_{J_p}^j = ({\varvec{J}}_p)_h^j - \Pi _h {\varvec{J}}_p^j , \quad {\varvec{e}}_{J_n}^j = ({\varvec{J}}_n)_h^j - \Pi _h {\varvec{J}}_n^j , \quad {\varvec{e}}_{\sigma }^j = {\varvec{\sigma }}_h^j - \Pi _h {\varvec{\sigma }}^j\,, \end{aligned}$$

whose estimates will be given in the next two subsections.

4.1 The Proof of (3.15)

Proof

The existence and uniqueness of numerical solutions to the linearized mixed FEM (3.8)–(3.13) follow directly from that at each time step, the coefficient matrices are invertable. Here we prove the following inequality for $j = 0$, $\ldots$, J

$$\begin{aligned}&{\left\| e_{p}^{j}\right\| _{L^2}^2} + {\left\| e_{n}^{j}\right\| _{L^2}^2} + \sum _{m=1}^{j} \tau \left( \left\| {\varvec{e}}_{J_p}^m \right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^m \right\| _{L^2}^2 \right) \le \frac{C_1}{2} \left( \tau ^{2} + h^{2r+2} \right) , \end{aligned}$$

(4.5)

by the mathematical induction. Since

$$\begin{aligned}&{\left\| e_{p}^{0}\right\| _{L^2}^2} + {\left\| e_{n}^{0}\right\| _{L^2}^2} = 0, \end{aligned}$$

(4.5) holds for $j = 0$. We can assume that (4.5) holds for $j \le k-1$ for some $k\ge 1$. We shall find a constant $C_1$, which is independent of j, h, $\tau$, such that (4.5) holds for $j \le k$.

By noting the projection $\Pi _h$ in the diagram (2.1), the weak formulation of the mixed PNP system (3.2)–(3.3) at $t_{j+1}$ satisfies that for any

Then, subtracting (4.6)–(4.9) from the FEM system (3.8)–(3.11), we can derive the following error equations

Taking $({\varvec{\chi }}_h,v_h) =({\varvec{e}}_{J_p}^{j+1},e_p^{j+1})$ into (4.12), (4.13) and $({\varvec{\chi }}_h,v_h) =({\varvec{e}}_{J_n}^{j+1},e_n^{j+1})$ into (4.14), (4.15), respectively, and summing up the results yield

$$\begin{aligned} &\left( D_\tau e_p^{j+1}, e_p^{j+1}\right) + \left( D_\tau e_n^{j+1}, e_n^{j+1}\right) + \left\| {{\varvec{e}}}_{J_p}^{j+1} \right\| _{L^2}^2 + \left\| {{\varvec{e}}}_{J_n}^{j+1} \right\| _{L^2}^2 \nonumber \\&\quad = \left( P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j}, {{\varvec{e}}}_{J_p}^{j+1}\right) -\left( N_h^{j} {\varvec{\sigma }}_h^{j}-n^{j} {\varvec{\sigma }}^{j}, {{\varvec{e}}}_{J_n}^{j+1}\right) \nonumber \\&\qquad -\left( p^{j+1} {\varvec{\sigma }}^{j+1} - p^{j} {\varvec{\sigma }}^{j}, {{\varvec{e}}}_{J_p}^{j+1}\right) +\left( n^{j+1} {\varvec{\sigma }}^{j+1} - n^{j} {\varvec{\sigma }}^{j}, {{\varvec{e}}}_{J_n}^{j+1}\right) \nonumber \\&\qquad -\left( {\varvec{\theta }}_{J_p}^{j+1}, {{\varvec{e}}}_{J_p}^{j+1}\right) -\left( {\varvec{\theta }}_{J_n}^{j+1}, {{\varvec{e}}}_{J_n}^{j+1}\right) -\left( D_\tau p^{j+1}-\frac{\partial p(\cdot ,t_{j+1})}{\partial t}, {e}_p^{j+1} \right) \nonumber \\&\qquad -\left( D_\tau n^{j+1}-\frac{\partial n(\cdot ,t_{j+1})}{\partial t}, {e}_n^{j+1} \right) \nonumber \\&\quad := \sum _{i=1}^8 R_i. \end{aligned}$$

(4.16)

By noting the regularity assumption (3.14) and the projection errors (4.1) and (4.2), we have

$$\begin{aligned} \sum _{i=3}^8 R_i\le & {} \epsilon \left( \Vert {\varvec{e}}_{J_p}^{j+1}\Vert _{L^2}^2 + \Vert {\varvec{e}}_{J_n}^{j+1}\Vert _{L^2}^2) + C(\Vert {e}_p^{j+1}\Vert _{L^2}^2 + \Vert {e}_n^{j+1}\Vert _{L^2}^2 \right) \nonumber \\&+ \epsilon ^{-1} C\left( \tau ^2+ h^{2r+2}\right) \,. \end{aligned}$$

(4.17)

Next, we estimate the two nonlinear terms $R_1$ and $R_2$. It is easy to see that

$$\begin{aligned}&R_1 \le \epsilon \Vert {\varvec{e}}_{J_p}^{j+1}\Vert _{L^2}^2 + \frac{\epsilon ^{-1}}{4} \left\| P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j} \right\| _{L^2}^2, \ \end{aligned}$$

(4.18)

$$\begin{aligned}&R_2 \le \epsilon \Vert {\varvec{e}}_{J_n}^{j+1}\Vert _{L^2}^2 + \frac{\epsilon ^{-1}}{4} \left\| N_h^{j} {\varvec{\sigma }}_h^{j}-n^{j} {\varvec{\sigma }}^{j} \right\| _{L^2}^2. \end{aligned}$$

(4.19)

To analyze the nonlinear terms in the last two inequalities, we shall derive some estimates for $\{{\varvec{e}}_\sigma ^j\}_{j=0}^{k-1}$ and $\{{\varvec{\sigma }}_h^j\}_{j=0}^{k-1}$. Subtracting (4.10), (4.11) from (3.12), (3.13) gives

Taking $({\varvec{\chi }}_h,v_h) =({\varvec{e}}_{\sigma }^{j},e_\psi ^{j})$ into the above error equation (4.20), (4.21) leads to

$$\begin{aligned} \left\| {{\varvec{e}}}_{\sigma }^{j} \right\| _{L^2}^2= & {} -\left( {\varvec{\theta }}_{\sigma }^{j}, {{\varvec{e}}}_{\sigma }^{j} \right) + \left( e_p^{j}-e_n^{j} \, , \, {e}_{\psi }^{j} \right) \\= & {} \frac{1}{4}\Vert {{\varvec{e}}}_{\sigma }^{j}\Vert _{L^2}^2 + \Vert {\varvec{\theta }}_{\sigma }^{j}\Vert _{L^2}^2 + \Vert e_p^{j}-e_n^{j}\Vert _{L^2} \,\Vert {e}_{\psi }^{j} \Vert _{L^2} \\ (\text {by Lemma }2.3)= & {} \frac{1}{4}\Vert {{\varvec{e}}}_{\sigma }^{j}\Vert _{L^2}^2 + C h^{2r+2} + C \Vert e_p^{j}-e_n^{j}\Vert _{L^2} \,\Vert {\varvec{\theta }}_{\sigma }^{j}+ {{\varvec{e}}}_{\sigma }^{j}\Vert _{L^2} \\\le & {} \frac{1}{2}\Vert {{\varvec{e}}}_{\sigma }^{j}\Vert _{L^2}^2 + C \Vert e_p^{j}-e_n^{j}\Vert _{L^2}^2 + C h^{2r+2}\,, \end{aligned}$$

hence,

$$\begin{aligned} \left\| {\varvec{e}}_{\sigma }^{j} \right\| _{L^2}^2 \le C \Vert e_p^{j}\Vert _{L^2}^2 + C\Vert e_n^{j}\Vert _{L^2}^2 + C h^{2r+2} \,. \end{aligned}$$

(4.22)

We also need the boundedness of $\{{\varvec{\sigma }}_h^{j}\}_{j=0}^{k-1}$ in certain strong norms. By using the mathematical assumption that (4.5) holds for $j \le k-1$, we have

$$\begin{aligned} \Vert P_h^{j}-N_h^{j} \Vert _{L^2}\le & {} {\left\| e_{p}^{j}\right\| _{L^2}} + {\Vert \Pi _h{p}^{j}\Vert _{L^2}} + {\left\| e_{n}^{j}\right\| _{L^2}} + {\Vert \Pi _h{n}^{j}\Vert _{L^2}} \nonumber \\\le & {} {\Vert \Pi _h{p}^{j} \Vert _{L^2}} + {\Vert \Pi _h{n}^{j}\Vert _{L^2}} + C_1\left( \tau + h^{r+1} \right) \nonumber \\\le & {} C + 1, \quad \text {for } j \le k-1, \end{aligned}$$

(4.23)

if we require that $C_1\left( \tau + h^{r+1} \right) \le 1$ for appropriately small $\tau$ and h. Furthermore, we can view $({\varvec{\sigma }}_h^{j},\psi _h^j)$ to be the mixed FEM solution of the Poisson equation with homogeneous Neumann boundary condition

$$\begin{aligned} -\Delta \zeta = P_h^{j}-N_h^{j}, \quad \text {for }{{\varvec{x}}}\in \Omega \quad \text {and} \quad \frac{\partial \zeta }{\partial \mathbf {n}} = 0, \quad \text {for }{{\varvec{x}}}\in \partial \Omega . \end{aligned}$$

(4.24)

From the $L^p$ estimate of mixed FEMs developed in [12], we can deduce that

$$\begin{aligned} \Vert {\varvec{\sigma }}_h^{j} \Vert _{L^6}\le & {} \Vert \nabla \zeta \Vert _{L^6} + \Vert {\varvec{\sigma }}_h^{j} - \nabla \zeta \Vert _{L^6} \nonumber \\ {(\text {by Theorem 3.2 of 12}) \quad }\le & {} \Vert \nabla \zeta \Vert _{L^6} + C \Vert \Pi _h {\nabla \zeta } - \nabla \zeta \Vert _{L^6} \nonumber \\ (\text {by Lemma}~2.1)\le & {} C \Vert \zeta \Vert _{H^2} \nonumber \\ {(\text {by the assumption on }\Omega ) \quad }\le & {} C \Vert P_h^{j}-N_h^{j} \Vert _{L^2} \nonumber \\ (\text {by}~(4.23))\le & {} C, \quad \text {for }j \le k-1. \end{aligned}$$

(4.25)

Then, the last term in the right hand side of (4.18) can be bounded by

$$\begin{aligned} \left\| P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j} \right\| _{L^2}\le & {} \left\| (e_p^j+\theta _p^j) {\varvec{\sigma }}_h^{j} \right\| _{L^2} + \left\| p^{j} ({\varvec{e}}_{\sigma }^{j}+ {\varvec{\theta }}_{\sigma }^{j}) \right\| _{L^2} \nonumber \\\le & {} \left\| (e_p^j+\theta _p^j) {\varvec{\sigma }}_h^{j} \right\| _{L^2} + C\left\| {\varvec{e}}_{\sigma }^{j} \right\| _{L^2} + C h^{r+1} \nonumber \\ (\text {by}~(4.22)) \quad\le & {} \left\| (e_p^j+\theta _p^j) \right\| _{L^3} \, \big \Vert {\varvec{\sigma }}_h^{j} \big \Vert _{L^6} + C \Vert e_p^{j}\Vert _{L^2} + C\Vert e_n^{j}\Vert _{L^2} + C h^{r+1} . \nonumber \\ (\text {by}~(4.25)) \quad\le & {} C \left\| (e_p^j+\theta _p^j) \right\| _{L^3} \, + C \Vert e_p^{j}\Vert _{L^2} + C\Vert e_n^{j}\Vert _{L^2} + C h^{r+1} \nonumber \\\le & {} C \left\| e_p^j \right\| _{L^3} \, + C \Vert e_p^{j}\Vert _{L^2} + C\Vert e_n^{j}\Vert _{L^2} + C h^{r+1} \nonumber \\\le & {} C \left\| e_p^j \right\| _{L^2}^{1/2} \left\| e_p^j \right\| _{L^6}^{1/2} \, + C \Vert e_p^{j}\Vert _{L^2} + C\Vert e_n^{j}\Vert _{L^2} + C h^{r+1} . \end{aligned}$$

(4.26)

Applying Lemma 2.3 to (4.12) gives

$$\begin{aligned} \left\| e_p^{j}\right\| _{L^6}\le & {} C \left\| {\varvec{e}}_{J_p}^{j}+{\varvec{\theta }}_{J_p}^{j}\right\| _{L^2} + C \left\| P_h^{j-1} {\varvec{\sigma }}_h^{j-1}-p^{j-1} {\varvec{\sigma }}^{j-1}\right\| _{L^2} + C \left\| p^{j} {\varvec{\sigma }}^{j} - p^{j-1} {\varvec{\sigma }}^{j-1}\right\| _{L^2} \nonumber \\\le & {} C \left\| {\varvec{e}}_{J_p}^{j}\right\| _{L^2} + C \left\| P_h^{j-1} {\varvec{\sigma }}_h^{j-1}-p^{j-1} {\varvec{\sigma }}^{j-1}\right\| _{L^2} +C(\tau + h^{r+1}) \,. \end{aligned}$$

(4.27)

Taking (4.27) into (4.26) leads to

$$\begin{aligned} \left\| P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j} \right\| _{L^2}\le & {} C \left\| e_p^j \right\| _{L^2}^{1/2} \left\| {\varvec{e}}_{J_p}^{j}\right\| _{L^2}^{1/2} \, + C \left\| e_p^j \right\| _{L^2}^{1/2} \left\| P_h^{j-1} {\varvec{\sigma }}_h^{j-1}-p^{j-1} {\varvec{\sigma }}^{j-1}\right\| _{L^2}^{1/2} \\&+ C \Vert e_p^{j}\Vert _{L^2} + C\Vert e_n^{j}\Vert _{L^2} + C ( \tau + h^{r+1} ) \end{aligned}$$

which gives further

$$\begin{aligned} \left\| P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j} \right\| _{L^2}\le & {} \epsilon \left\| P_h^{j-1} {\varvec{\sigma }}_h^{j-1}-p^{j-1} {\varvec{\sigma }}^{j-1}\right\| _{L^2} + \epsilon \left\| {\varvec{e}}_{J_p}^{j}\right\| _{L^2} \nonumber \\&+ \epsilon ^{-1} C \left\| e_p^{j}\right\| _{L^2} + \epsilon ^{-1} C \left\| e_n^{j}\right\| _{L^2} + \epsilon ^{-1} C \left( \tau +h^{r+1}\right) \,, \end{aligned}$$

(4.28)

where the Young’s inequality is used. Similarly, we can derive an estimate for the last term in the right hand side of (4.19)

$$\begin{aligned} \left\| N_h^{j} {\varvec{\sigma }}_h^{j} - n^{j} {\varvec{\sigma }}^{j} \right\| _{L^2}\le & {} \epsilon \left\| N_h^{j-1} {\varvec{\sigma }}_h^{j-1}-n^{j-1} {\varvec{\sigma }}^{j-1}\right\| _{L^2} + \epsilon \left\| {\varvec{e}}_{J_n}^{j}\right\| _{L^2} \nonumber \\&+ \epsilon ^{-1} C \Vert e_p^{j}\Vert _{L^2} + \epsilon ^{-1} C \Vert e_n^{j}\Vert _{L^2} + \epsilon ^{-1} C (\tau + h^{r+1}) \,. \end{aligned}$$

(4.29)

Summing up (4.28), (4.29) with index $j = 1$, $\ldots$, $k-1$, we have

$$\begin{aligned}&\sum _{j=1}^{k-1} \left( \left\| P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j} \right\| _{L^2} + \left\| N_h^{j} {\varvec{\sigma }}_h^{j} - n^{j} {\varvec{\sigma }}^{j} \right\| _{L^2} \right) \\&\le \epsilon \sum _{j=1}^{k-1} \left( \left\| P_h^{j-1} {\varvec{\sigma }}_h^{j-1}-p^{j-1} {\varvec{\sigma }}^{j-1} \right\| _{L^2} + \left\| N_h^{j-1} {\varvec{\sigma }}_h^{j-1} - n^{j-1} {\varvec{\sigma }}^{j-1} \right\| _{L^2} \right) \\&\quad + \sum _{j=1}^{k-1} \left( \epsilon \left\| {\varvec{e}}_{J_p}^{j}\right\| _{L^2} + \epsilon \left\| {\varvec{e}}_{J_n}^{j}\right\| _{L^2} + \epsilon ^{-1} C \Vert e_p^{j}\Vert _{L^2} + \epsilon ^{-1} C \Vert e_n^{j}\Vert _{L^2} + \epsilon ^{-1} C (\tau + h^{r+1}) \right) , \end{aligned}$$

which can be rewritten as

$$\begin{aligned}&(1-\epsilon ) \sum _{j=1}^{k-1} \left( \left\| P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j} \right\| _{L^2} + \left\| N_h^{j} {\varvec{\sigma }}_h^{j} - n^{j} {\varvec{\sigma }}^{j} \right\| _{L^2} \right) \\&\le \sum _{j=1}^{k-1} \left( \epsilon \left\| {\varvec{e}}_{J_p}^{j}\right\| _{L^2} + \epsilon \left\| {\varvec{e}}_{J_n}^{j}\right\| _{L^2} + \epsilon ^{-1} C \Vert e_p^{j}\Vert _{L^2} + \epsilon ^{-1} C \Vert e_n^{j}\Vert _{L^2} + \epsilon ^{-1} C (\tau + h^{r+1}) \right) . \end{aligned}$$

where we have noted that at the initial time step

$$\begin{aligned} \left\| P_h^{0} {\varvec{\sigma }}_h^{0} - p^{0} {\varvec{\sigma }}^{0} \right\| _{L^2} + \left\| N_h^{0} {\varvec{\sigma }}_h^{0} - n^{0} {\varvec{\sigma }}^{0} \right\| _{L^2} \le C h^{r+1}. \end{aligned}$$

Summing up (4.18), (4.19) with index $j=1,\ldots ,k-1$ and noting the above estimate with a small $\epsilon$, we get

$$\begin{aligned} \sum _{j=1}^{k-1} \left( R_1 + R_2 \right)\le & {} \sum _{j=1}^{k} \left( \epsilon \left\| {\varvec{e}}_{J_p}^{j}\right\| _{L^2}^2 + \epsilon \left\| {\varvec{e}}_{J_n}^{j}\right\| _{L^2}^2 \right) \nonumber \\&+ \sum _{j=1}^{k} \big ( \epsilon ^{-3}C \Vert e_p^{j}\Vert _{L^2}^2 + \epsilon ^{-3}C\Vert e_n^{j}\Vert _{L^2}^2 + \epsilon ^{-3}C (\tau + h^{r+1})^2 \big ). \end{aligned}$$

(4.30)

Finally, summing up the index $j=1,\ldots ,k-1$ and substituting estimates (4.17) and (4.30) into the error equation (4.16), we arrive at

$$\begin{aligned}&\left\| e_p^{j+1}\right\| _{L^2}^2 + \left\| e_n^{j+1}\right\| _{L^2}^2 + \tau \sum _{m=0}^j \left( \left\| {\varvec{e}}_{J_p}^{m+1} \right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^{m+1} \right\| _{L^2}^2\right) \\&\le \tau \sum _{m=0}^j \epsilon \left( \left\| {\varvec{e}}_{J_p}^{m+1}\right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^{m+1}\right\| _{L^2}^2 \right) \\&\quad + \tau \sum _{m=0}^{j+1} \epsilon ^{-3} \left( C \left( \left\| e_p^{m}\right\| _{L^2}^2 + \left\| e_n^{m}\right\| _{L^2}^2\right) + C \left( \tau ^2 + h^{2r+2}\right) \right) \end{aligned}$$

Then, we chose a small $\epsilon$ to deduce that

$$\begin{aligned}&\left\| e_p^{j+1}\right\| _{L^2}^2 + \left\| e_n^{j+1}\right\| _{L^2}^2 + \tau \sum _{m=0}^j \left( \left\| {\varvec{e}}_{J_p}^{m+1} \right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^{m+1} \right\| _{L^2}^2\right) \nonumber \\&\le \tau \sum _{m=0}^{j+1} \left( C \left( \left\| e_p^{m}\right\| _{L^2}^2 + \left\| e_n^{m}\right\| _{L^2}^2 \right) + C \left( \tau ^2 + h^{2r+2}\right) \right) \end{aligned}$$

(4.31)

Thanks to the discrete Gronwall’s inequality in Lemma 2.2, when $C \tau \le \frac{1}{2}$, we have

$$\begin{aligned}&\left\| e_p^{j+1}\right\| _{L^2}^2 + \left\| e_n^{j+1}\right\| _{L^2}^2 + \tau \sum _{m=0}^j \left( \left\| {\varvec{e}}_{J_p}^{m+1} \right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^{m+1} \right\| _{L^2}^2\right) \nonumber \\&\le C\exp \left( \frac{TC}{1-C\tau } \right) \left( \tau ^2+h^{2r+2}\right) \nonumber \\&\le C \exp (2TC) \left( \tau ^2+h^{2r+2}\right) \,. \end{aligned}$$

(4.32)

Thus, (4.5) holds for $n=k$ if we take $\frac{C_1}{2} \ge C\exp (2TC)$. We complete the induction.

(3.15) follows immediately from the the projection error estimates and inequalities (4.5) and (4.22).$\square$

Remark 4.1

Combining the projection error estimates (4.2), with (4.22) and (4.5), we conclude at once that

$$\begin{aligned} \left\| {\varvec{\sigma }}_h^{j} - {\varvec{\sigma }}^{j}\right\| _{L^2} \le C_2 \left( \tau + h^{r+1}\right) . \end{aligned}$$

With the help of (4.5), we can prove the following uniform boundedness of the numerical solutions which is the basis in the proof of the error estimates (3.16) in the next subsection.

Corollary 4.1

Under the assumption in Theorem 3.1, there exist two positive constants $\tau _0$ and $h_0$ such that when $\tau \le \tau _0$ and $h \le h_0$, the numerical solutions to the linearized mixed FEM (3.8)–(3.13) possess the following uniform boundedness

$$\begin{aligned}&\max _{0 \le j \le J} \left( \left\| P_h^j \right\| _{L^6} + \left\| N_h^j \right\| _{L^6} \right) \le C, \end{aligned}$$

(4.33)

$$\begin{aligned}&\max _{0 \le j \le J} \left\| {\varvec{\sigma }}_h^j \right\| _{L^{\infty }} \le C \end{aligned}$$

(4.34)

Proof

We shall consider two cases. For $\tau \le h$, by using the inverse inequality, we have

$$\begin{aligned} \left\| P_h^j \right\| _{L^6}\le & {} \left\| \Pi _h p^j \right\| _{L^6} + \left\| e_p^j \right\| _{L^6} \nonumber \\\le & {} C + h^{-1} \left\| e_p^j \right\| _{L^2} \nonumber \\ {(\text {by}~(4.5))}\le & {} C + h^{-1} \sqrt{\frac{C_1}{2} \left( \tau ^{2} + h^{2r+2} \right) } \nonumber \\\le & {} C + h^{-1} \sqrt{\frac{C_1}{2} h^{2}} \nonumber \\\le & {} C. \end{aligned}$$

(4.35)

For $h\le \tau$, (4.5) gives that

$$\begin{aligned}&\sum _{m=1}^{J} \tau \left\| {\varvec{e}}_{J_p}^m \right\| _{L^2}^2 \le \frac{C_1}{2} \left( \tau ^{2} + h^{2r+2} \right) \le \frac{C_1}{2} \left( \tau ^{2} + \tau ^{2r+2} \right) \le C_1 \tau ^{2} \end{aligned}$$

which leads to

$$\begin{aligned}&\left\| {\varvec{e}}_{J_p}^m \right\| _{L^2} \le C_1 {\tau }^{\frac{1}{2}} \,, \quad \text {for }m=1, \ldots , J. \end{aligned}$$

Applying Lemma 2.3 to (3.8), we have

$$\begin{aligned} \left\| P_h^j\right\| _{L^6}\le & {} \left\| ({\varvec{J}}_p)_h^{j+1} \right\| _{L^2} + \left\| P_h^{j} {\varvec{\sigma }}_h^{j}\right\| _{L^2} \\\le & {} \left\| \Pi _h {\varvec{J}}_p^{j+1} \right\| _{L^2} + \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} + \left\| P_h^{j} \right\| _{L^3} \, \left\| {\varvec{\sigma }}_h^{j}\right\| _{L^6} \\ (\text {by}~(4.25)) \quad\le & {} \left\| \Pi _h {\varvec{J}}_p^{j+1} \right\| _{L^2} + \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} + C \left\| P_h^{j} \right\| _{L^3} \\\le & {} C + C_1 {\tau }^{\frac{1}{2}} + C\left\| P_h^{j} \right\| _{L^2}^{1/2} \left\| P_h^{j} \right\| _{L^6}^{1/2} \\\le & {} \frac{1}{2} \left\| P_h^j\right\| _{L^6} + C + C \left\| P_h^{j}\right\| _{L^2} \\\le & {} \frac{1}{2} \left\| P_h^j\right\| _{L^6} + C \,, \end{aligned}$$

which in turn implies $\Vert P_h^j\Vert _{L^6} \le C$.

Thus, for both the cases $\tau \le h$ and $h \le \tau$, we obtain

$$\begin{aligned}&\max _{0 \le j \le J} \Vert P_h^j\Vert _{L^6}\le C, \end{aligned}$$

(4.36)

and similarly, we can show that

$$\begin{aligned}&\max _{0 \le j \le J} \Vert N_h^j\Vert _{L^6}\le C. \end{aligned}$$

(4.37)

Combining the last two estimates, (4.33) is proved. By applying the $L^p$ estimate of mixed FEM [12] to (4.24), we have

$$\begin{aligned} \Vert {\varvec{\sigma }}_h^{j} \Vert _{L^{\infty }}\le & {} \Vert \nabla \zeta \Vert _{L^{\infty }} + \Vert {\varvec{\sigma }}_h^{j} - \nabla \zeta \Vert _{L^{\infty }} \nonumber \\ {(\text {by Theorem 3.2 of}~12) \quad }\le & {} \Vert \nabla \zeta \Vert _{L^{\infty }} + C \Vert \Pi _h {\nabla \zeta } - \nabla \zeta \Vert _{L^{\infty }} \nonumber \\ (\text {by Lemma}~(2.1)) \quad\le & {} C \Vert \zeta \Vert _{W^{2,6}} \nonumber \\ {(\text {by the assumption on }\Omega ) \quad }\le & {} C \Vert P_h^{j}-N_h^{j} \Vert _{L^6} \nonumber \\ (\text {by} (4.33)) \quad\le & {} C \,. \end{aligned}$$

(4.38)

We proved Corollary 4.1.$\square$

4.2 The Proof of Estimate (3.16)

Proof

We take $D_\tau$ to both sides of (4.12) and (4.14) to deduce that

Taking $({\varvec{\chi }}_h,v_h) = ({\varvec{e}}_{J_p}^{j+1},-\nabla \cdot {\varvec{e}}_{J_p}^{j+1})$ into (4.39), (4.40) and $({\varvec{\chi }}_h,v_h) = ({\varvec{e}}_{J_n}^{j+1},-\nabla \cdot {\varvec{e}}_{J_n}^{j+1})$ into (4.41), (4.42), respectively, and summing up the results, we have

$$\begin{aligned} &\left( D_\tau {{\varvec{e}}}_{J_p}^{j+1} \, , \, {{\varvec{e}}}_{J_p}^{j+1} \right) + \left( D_\tau {{\varvec{e}}}_{J_n}^{j+1} \, , \, {{\varvec{e}}}_{J_n}^{j+1} \right) + \left\| \nabla \cdot {{\varvec{e}}}_{J_p}^{j+1}\right\| _{L^2}^2 +\left\| \nabla \cdot {{\varvec{e}}}_{J_n}^{j+1}\right\| _{L^2}^2\nonumber \\&=\left( D_\tau (P_h^{j} {\varvec{\sigma }}_h^{j}-p^{j} {\varvec{\sigma }}^{j}) \, , \, {{\varvec{e}}}_{J_p}^{j+1}\right) + \left( D_\tau (n^{j} {\varvec{\sigma }}^{j}-N_h^{j} {\varvec{\sigma }}_h^{j}) \, , \, {{\varvec{e}}}_{J_n}^{j+1} \right) \nonumber \\&\quad -\left( D_\tau {\varvec{\theta }}_{J_p}^{j+1} \, , \, {{\varvec{e}}}_{J_p}^{j+1} \right) -\left( D_\tau {\varvec{\theta }}_{J_n}^{j+1} \, , \, {{\varvec{e}}}_{J_n}^{j+1} \right) -\left( D_\tau \left( p^{j+1} {\varvec{\sigma }}^{j+1} - p^{j} {\varvec{\sigma }}^{j}\right) , \, {{\varvec{e}}}_{J_p}^{j+1} \right) \nonumber \\&\quad +\left( D_\tau \left( n^{j+1} {\varvec{\sigma }}^{j+1} - n^{j} {\varvec{\sigma }}^{j}\right) , \, {{\varvec{e}}}_{J_n}^{j+1} \right) + \left( D_\tau p^{j+1}-\frac{\partial p(\cdot ,t_{j+1})}{\partial t}, \nabla \cdot {{\varvec{e}}}_{J_p}^{j+1}\right) \nonumber \\&\quad + \left( D_\tau n^{j+1}-\frac{\partial n(\cdot ,t_{j+1})}{\partial t}, \nabla \cdot {{\varvec{e}}}_{J_n}^{j+1}\right) \nonumber \\&:= \sum _{i=1}^8 \widetilde{R}_i. \end{aligned}$$

(4.43)

Again, by noting the regularity assumption (3.14) and the projection errors (4.1) and (4.2), we can derive the following estimate for the linear terms

$$\begin{aligned} \sum _{i=3}^8 {\widetilde{R}}_i\le & {} \epsilon (\Vert \nabla \cdot {\varvec{e}}_{J_p}^{j+1}\Vert _{L^2}^2 + \Vert \nabla \cdot {\varvec{e}}_{J_n}^{j+1}\Vert _{L^2}^2) + C(\Vert {\varvec{e}}_{J_p}^{j+1}\Vert _{L^2}^2 + \Vert {\varvec{e}}_{J_n}^{j+1}\Vert _{L^2}^2) \nonumber \\&+ \epsilon ^{-1} C(\tau ^2+ h^{2r+2}) \,. \end{aligned}$$

(4.44)

Then we turn to the two nonlinear terms ${\widetilde{R}}_1$ and ${\widetilde{R}}_2$. We can rewrite ${\widetilde{R}}_1$ by

$$\begin{aligned} {\widetilde{R}}_1= & {} \left( (D_\tau P_h^{j}) {\varvec{\sigma }}_h^{j} - (D_\tau p^{j}) {\varvec{\sigma }}^{j} \, , \, {\varvec{e}}_{J_p}^{j+1} \right) +\left( P_h^{j-1} (D_\tau {\varvec{\sigma }}_h^{j}) - p^{j-1} (D_\tau {\varvec{\sigma }}^{j}) \, , \, {\varvec{e}}_{J_p}^{j+1}\right) \nonumber \\= & {} \left( (D_\tau e_p^{j}+D_\tau \theta _p^{j}){\varvec{\sigma }}_h^{j} \,,\, {\varvec{e}}_{J_p}^{j+1} \right) + \left( (D_\tau p^{j}) ({\varvec{e}}_{\sigma }^j+{\varvec{\theta }}_{\sigma }^j)\,,\, {\varvec{e}}_{J_p}^{j+1} \right) \nonumber \\&+ \left( P_h^{j-1}(D_\tau {\varvec{e}}_{\sigma }^j+D_\tau {\varvec{\theta }}_{\sigma }^j)\,,\, {\varvec{e}}_{J_p}^{j+1} \right) + \left( ( e_p^{j-1} + \theta _p^{j-1})(D_\tau {\varvec{\sigma }}^j)\,,\, {\varvec{e}}_{J_p}^{j+1} \right) \nonumber \\:= & {} \sum _{i=1}^4 E_i \,. \end{aligned}$$

(4.45)

For the first term, we have

$$\begin{aligned} E_1\le & {} \left\| D_\tau e_p^{j}+D_\tau \theta _p^{j}\right\| _{L^2} \left\| {\varvec{\sigma }}_h^{j}\right\| _{L^{\infty }} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} \nonumber \\ {(\text {by }4.34)\quad }\le & {} \epsilon \left\| D_\tau e_p^{j}+D_\tau \theta _p^{j}\right\| _{L^2}^2 + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 \nonumber \\\le & {} \epsilon \left\| D_\tau e_p^{j}\right\| _{L^2}^2 + Ch^{2r+2} + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2. \end{aligned}$$

(4.46)

By noting the regularity assumption (3.14), the projection error estimates and (4.22), $E_2$ can be bounded by

$$\begin{aligned} E_2\le & {} \left\| D_\tau p^{j} \right\| _{L^{\infty }} \left\| {\varvec{e}}_{\sigma }^j+{\varvec{\theta }}_{\sigma }^j \right\| _{L^{2}} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^{2}} \nonumber \\\le & {} C \left\| {\varvec{e}}_{\sigma }^j+{\varvec{\theta }}_{\sigma }^j \right\| _{L^{2}}^2 + C\left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^{2}}^2 \nonumber \\ {(\text {by }(4.22))\quad }\le & {} C (\tau ^2 + h^{2r+2}) + C\left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^{2}}^2. \end{aligned}$$

(4.47)

Before proceeding to the estimate of $E_3$, we shall take $D_\tau$ to both sides of (4.20) and (4.21) to get

where we have used the fact that

$$\begin{aligned} \left( \nabla \cdot D_\tau {\varvec{\theta }}_{\sigma }^{j} \, , \, v_h \right) =0, \quad \forall v_h \in V_h^r(\Omega ), \end{aligned}$$

It is easy to see that $(D_\tau {\varvec{e}}_{\sigma }^{j}+D_\tau {\varvec{\theta }}_{\sigma }^{j}\,,\,D_\tau e_\psi ^{j})$ can be viewed as the mixed FEM solution to the following Poisson equation

$$\begin{aligned} -\Delta \zeta = D_\tau e_p^{j}- D_\tau e_n^{j}, \quad \text {for }{{\varvec{x}}} \in \Omega \quad \text {and} \quad \frac{\partial \zeta }{\partial \mathbf {n}} = 0, \quad \text {for }{{\varvec{x}}} \in \partial \Omega . \end{aligned}$$

Then, by an $L^p$ estimate of mixed FEM [12], we can derive that

$$\begin{aligned} \left\| D_\tau {\varvec{e}}_{\sigma }^{j}+D_\tau {\varvec{\theta }}_{\sigma }^{j} \right\| _{L^3} \le C \left\| D_\tau e_p^{j}- D_\tau e_n^{j} \right\| _{L^2}. \end{aligned}$$

(4.20)

Consequently, the term $E_3$ can be bounded by

$$\begin{aligned} E_3\le & {} \left\| P_h^{j-1} \right\| _{L^6} \left\| D_\tau {\varvec{e}}_{\sigma }^j+D_\tau {\varvec{\theta }}_{\sigma }^j \right\| _{L^3} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} \nonumber \\ {(\text {by }(4.33))\quad }\le & {} C \left\| D_\tau {\varvec{e}}_{\sigma }^j+D_\tau {\varvec{\theta }}_{\sigma }^j \right\| _{L^3} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} \nonumber \\ {(\text {by }(4.50))\quad }\le & {} C \left\| D_\tau e_p^{j}- D_\tau e_n^{j} \right\| _{L^2} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} \nonumber \\\le & {} \epsilon \left\| D_\tau e_p^{j} \right\| _{L^2}^2 + \epsilon \left\| D_\tau e_n^{j} \right\| _{L^2}^2 + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 \,. \end{aligned}$$

(4.21)

For the last term $E_4$, it is easy to see that

$$\begin{aligned} E_4\le & {} \left\| e_p^{j-1} + \theta _p^{j-1} \right\| _{L^2} \left\| D_\tau {\varvec{\sigma }}^j \right\| _{L^{\infty }} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} \nonumber \\\le & {} C \left\| e_p^{j-1} + \theta _p^{j-1} \right\| _{L^2} \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2} \nonumber \\ {(\text {by }4.5)\quad }\le & {} C (\tau ^2 + h^{2r+2}) + C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2. \end{aligned}$$

(4.22)

Finally, taking all the above estimates of $\{E_i\}_{i=1}^4$ into (4.45) gives

$$\begin{aligned} {\widetilde{R}}_1\le & {} \epsilon \left\| D_\tau e_p^{j}\right\| _{L^2}^2 + \epsilon \left\| D_\tau e_n^{j} \right\| _{L^2}^2 + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \epsilon ^{-1} C (\tau ^2 + h^{2r+2}) \,. \end{aligned}$$

Via a similar analysis, for the term ${\widetilde{R}}_2$, we can derive that

$$\begin{aligned} {\widetilde{R}}_2\le & {} \epsilon \left\| D_\tau e_n^{j}\right\| _{L^2}^2 + \epsilon \left\| D_\tau e_p^{j} \right\| _{L^2}^2 + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \epsilon ^{-1} C (\tau ^2 + h^{2r+2}) \,. \end{aligned}$$

By taking $v_h = D_\tau e_p^{j+1}$ into (4.40) and $v_h = D_\tau e_n^{j+1}$ into (4.42), respectively, we can deduce the following results

$$\begin{aligned}&\left\| D_\tau e_p^{j+1} \right\| _{L^2}^2 \le 2 \left\| \nabla \cdot {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + C \tau ^2 \,, \\&\left\| D_\tau e_n^{j+1} \right\| _{L^2}^2 \le 2 \left\| \nabla \cdot {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + C \tau ^2 \,. \end{aligned}$$

Taking the last two inequalities into the estimates for ${\widetilde{R}}_1$ and ${\widetilde{R}}_2$, we have

$$\begin{aligned} {\widetilde{R}}_1 + {\widetilde{R}}_2\le & {} 2 \epsilon \left( \left\| \nabla \cdot {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_p}^{j} \right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{j} \right\| _{L^2}^2 \right) \nonumber \\&+ \epsilon ^{-1} C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \epsilon ^{-1} C \left( \tau ^2 + h^{2r+1}\right) \,. \end{aligned}$$

(4.23)

At last, taking the estimates (4.44) and (4.23) into (4.43) results in

$$\begin{aligned}&\left( D_\tau {\varvec{e}}_{J_p}^{j+1} \, , \, {\varvec{e}}_{J_p}^{j+1} \right) + \left( D_\tau {\varvec{e}}_{J_n}^{j+1} \, , \, {\varvec{e}}_{J_n}^{j+1} \right) + \left\| \nabla \cdot {\varvec{e}}_{J_p}^{j+1}\right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{j+1}\right\| _{L^2}^2 \nonumber \\&= 2 \epsilon \left( \left\| \nabla \cdot {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_p}^{j} \right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{j} \right\| _{L^2}^2 \right) \nonumber \\&\quad + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \epsilon ^{-1} C \left\| {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \epsilon ^{-1} C \left( \tau ^2 + h^{2r+1}\right) \,. \end{aligned}$$

(4.24)

By fixing the small constant $\epsilon$ and summing up the index j, we arrive at

$$\begin{aligned}&\left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \tau \sum _{m=1}^{j+1} \left( \left\| \nabla \cdot {\varvec{e}}_{J_p}^{m}\right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{m}\right\| _{L^2}^2 \right) \nonumber \\&\le \tau \sum _{m=1}^{j+1} \left( \left\| {\varvec{e}}_{J_p}^{m} \right\| _{L^2}^2 + C \left\| {\varvec{e}}_{J_n}^{m} \right\| _{L^2}^2 \right) + C \left( \tau ^2 + h^{2r+1}\right) \,. \end{aligned}$$

(4.25)

With the help of Gronwall’s inequality, we obtain when $C \tau \le \frac{1}{2}$, we have

$$\begin{aligned}&\left\| {\varvec{e}}_{J_p}^{j+1} \right\| _{L^2}^2 + \left\| {\varvec{e}}_{J_n}^{j+1} \right\| _{L^2}^2 + \tau \sum _{m=1}^{j+1} \left( \left\| \nabla \cdot {\varvec{e}}_{J_p}^{m}\right\| _{L^2}^2 + \left\| \nabla \cdot {\varvec{e}}_{J_n}^{m}\right\| _{L^2}^2 \right) \\&\le C\exp \left( \frac{TC}{1-C\tau } \right) (\tau ^2+h^{2r+2}) \\&\le C_2 (\tau ^2+h^{2r+2}), \quad \text {for }j=0, \ldots , J-1. \end{aligned}$$

Thus, by noting the projection error estimates (4.2) and last inequality, (3.16) is proved. We complete the proof of Theorem 3.1.$\square$

5 Numerical Results

In this section, we provide some numerical examples to confirm our theoretical analyses. The computations are performed with free software FEniCS [28].

Example 5.1

We rewrite the PNP equations (1.1–(1.3) as follow

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial p}{\partial t} - \nabla \cdot ( \nabla p - p \nabla \psi ) = f_1 \, , \\ \frac{\partial n}{\partial t} - \nabla \cdot ( \nabla n + n \nabla \psi ) = f_2 \, , \\ - \Delta \psi = p-n \, . \end{array}\right. \end{aligned}$$

(5.1)

We test the linearized backward Euler FEM (3.8)–(3.13) on the unit square $\Omega = (0,1)^2$. A uniform triangular partition with $M+1$ nodes in each direction is used. An illustration with $M=8$ is shown in Fig. 1. Here we can see that $h=\frac{\sqrt{2}}{M}$.

Fig. 1

A uniform triangulation on the unit square with $M=8$

In our computations, we take

$$\begin{aligned} \left\{ \begin{array}{l} p = 2 \pi ^2 \exp (t) \cos (\pi x) \cos (\pi y) \\ n = 4 \pi ^2 t^3 \cos (2 \pi x) \\ \psi = \exp (t) \cos (\pi x) \cos (\pi y) - t^3 \cos (2 \pi x) \end{array}\right. \end{aligned}$$

to be the exact solution to (5.1). Correspondingly, the right-hand side function $f_1$ and $f_2$ are determined by the above exact solution.

Clearly, $f_1$ and $f_2$ are nonzero source terms which are different from the zero source terms in (1.1) and (1.2). However, we can easily testify that

$$\begin{aligned} \int _0^t\int _\Omega \, f_1({{\varvec{x}}},t)\,\mathrm {d}{{\varvec{x}}}\mathrm {d}t=\int _0^t\int _\Omega \,\, f_2({{\varvec{x}}},t)\,\mathrm {d}{{\varvec{x}}}\mathrm {d}t=0, \end{aligned}$$

which guarantees (1.7) is still true, thus we still have the well-posedness of PNP equations. Furthermore, it is easy to see that nonzero linear source terms do not introduce any difficulty to the analyses of stability and convergence as illustrated in the previous sections. Therefore, Theorem 3.1 holds true for the artificial problem (5.1).

We set the final time $T=1.0$. To confirm our error estimate in Theorem 3.1, for with $r=0$, 1, and 2, we choose $\tau = \left( \frac{1}{M}\right) ^{r+1}$. From Theorem 3.1, we have $(r+1)$-th order convergence for the $L^2$-norm errors. We present the $L^2$-norm errors in Table 1. From Table 1, it is easy to see that the convergence rate for the linearized backward Euler RT mixed FEM (3.8)–(3.13) is optimal.

Table 1 $L^2$-norm errors for the linearized backward Euler RT mixed FEM (3.8)–(3.13) on the unit square. (Example 5.1)

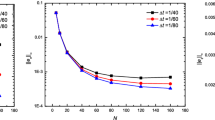
To show the unconditional convergence of the proposed scheme, we use to solve (5.1) with three different time steps $\tau =0.1$, 0.05, 0.01 on gradually refined meshes with $M= 2^{k+2}$, $k=1$, 2, $\ldots$, 5. The $L^2$-norm errors are plot in Fig. 2. We can see from Fig. 2 that for a fixed $\tau$, when refining the mesh gradually, the $L^2$-norm errors asymptotically converge to a small constant, i.e., the temporal error which is $O(\tau )$. Thus, it is clear that the linearized backward Euler FEM is unconditionally convergent (stable) and no mesh ratio restriction is needed in the computation.

Fig. 2

$L^2$-norm errors of the linearized backward Euler RT mixed FEM (3.8)–(3.13) on the unit square. (Example 5.1)

Example 5.2

In this example, we study the dynamics of PNP equations with the following initial values

$$\begin{aligned} p_0= & {} \left\{ \begin{array}{ll} 1, &{} (0,1)^2\backslash \{ (0,0.75)\times (0,1) \cup (0.75,1)\times (0, \frac{11}{20}) \}, \\ 10^{-6}, &{} \text {else}, \end{array} \right. \\ n_0= & {} \left\{ \begin{array}{ll} 1, &{} (0,1)^2\backslash \{ (0,0.75)\times (0,1) \cup (0.75,1)\times (\frac{9}{20},1) \}, \\ 10^{-6}, &{} \text {else}, \end{array} \right. \end{aligned}$$

in the unit square. This example was first used in [35], where a fully nonlinear backward Euler scheme with a linear Lagrange element was analyzed. Later, the authors in [17] applied a conservative decoupled finite element method to investigate this example. For comparison, we test the performance of the linearized backward Euler RT mixed FEM (3.8)–(3.13) with the same settings in [17, 35].

In the computation, we take $\tau = 10^{-3}$ and on a uniform mesh with $M={32}$. We show the snapshots of the numerical solutions $P_h$, $-({\varvec{J}}_p)_h$, $N_h$, $-({\varvec{J}}_n)_h$, $\Psi _h$ and $-{\varvec{\sigma }}_h$ at $T = 0.002$ in Fig. 3, at $T = 0.02$ in Fig. 4 and at $T = 0.1$ in Fig. 5, respectively. All plots in Figs. 3, 4 and 5 agree well with previous results in [17, 35].

Fig. 3

Snapshots of $P_h,-({\varvec{J}}_p)_h,N_h, -({\varvec{J}}_n)_h,\Psi _h$ and $-{\varvec{\sigma }}_h$ at time $T = 0.002$. The results are obtained by the (3.8)–(3.13) with $r=1$ on the mesh with $M={32}$ and $\tau = 10^{-3}$. (Example 5.2)

Fig. 4

Snapshots of $P_h,-({\varvec{J}}_p)_h,N_h, -({\varvec{J}}_n)_h,\Psi _h$ and $-{\varvec{\sigma }}_h$ at time $T = 0.02$. The results are obtained by the (3.8)–(3.13) with $r=1$ on the mesh with $M={32}$ and $\tau = 10^{-3}$. (Example 5.2)

Fig. 5

Snapshots of $P_h$, $-({\varvec{J}}_p)_h$, $N_h$, $-({\varvec{J}}_n)_h$, $\Psi _h$ and $-{\varvec{\sigma }}_h$ at time $T = 0.1$. The results are obtained by the (3.8)–(3.13) with $r=1$ on the mesh with $M={32}$ and $\tau = 10^{-3}$. (Example 5.2)

In addition, we plot in Fig. 6 the global masses $\{(P_h^j,1)\}_{j=0}^J$ and $\{(N_h^j,1)\}_{j=0}^J$ and the electric energy $\frac{1}{2} \Vert {\varvec{\sigma }}_h^j \Vert _{L^2}^2$. From Fig. 6, it is easy to see the mass conservation of $P_h$ and $N_h$ and the decrease of the electric energy $\frac{1}{2} \Vert {\varvec{\sigma }}_h^j \Vert _{L^2}^2$ as time evolves.

Fig. 6

The evolution of global masses and electric energy computed by the linearized backward Euler FEM (3.8)–(3.13) with $r=1$ on the mesh with $M=32$ and $\tau =10^{-3}$. (Example 5.2)

6 Conclusions and Discussion

We have proposed a linearized RT mixed FEM for solving PNP equations. An optimal error estimate in $L^{\infty }(L^2)$ norm for the proposed scheme is established unconditionally (i.e., the analysis does not require mesh ratio restriction $\tau \le C h^{\alpha }$ for a certain $\alpha >0$) for all six unknowns: the concentrations p and n, the mass fluxes ${\varvec{J}}_p=\nabla p + p {\varvec{\sigma }}$ and ${\varvec{J}}_n=\nabla n - n {\varvec{\sigma }}$, the potential $\psi$ and the potential flux ${\varvec{\sigma }}= \nabla \psi$. The method is based on the RT mixed FEM in the spatial discretization and linearization for the coupled terms $p \, \nabla \psi$ and $n \nabla \psi$. Numerical experiments demonstrate that the proposed method is efficient, accurate and stable for simulations of dynamics of ion concentrations, of electrostatic potential and of coupling between two physical processes. As a result of using RT mixed FEMs, the local mass preserving property is also satisfied for all ion concentrations and electrostatic potential. Moreover, the mass fluxes of ion concentrations ${\varvec{J}}_p$ and ${\varvec{J}}_n$ are solved directly and accurately, which is very important in studies of electric current–voltage curves and Debye layer phenomena. We shall make the following remarks.

Remark 6.1

Here we assume the domain $\Omega$ is a convex polygon or polyhedron. The main reason is that we used the $H^2$ estimates of elliptic equations. For more general smooth domains with curved boundary, we refer to [24, 41] for detailed description.

Remark 6.2

In this paper we focus on the RT mixed FEM. It is possible to use the Brezzi–Douglas–Marini (BDM) mixed FEM for the flux approximation. Our error analysis also applies to the BDM mixed FEM. However, we do not recommend to use the BDM element which may suffer from a suboptimal convergence for the PNP model, see [9] for more discussion.