Convergence of the MAC Scheme for the Stokes/Darcy Coupling Problem

Abstract

In this paper, we extend the MAC scheme for Stokes problem to the Stokes/Darcy coupling problem. The interface conditions between two separate regions are discretized and well-incorporated into the MAC grid setting. We first perform the stability analysis of the scheme for the velocity in both Stokes and Darcy regions and establish the stability for the pressure in both regions by considering an analogue of discrete divergence problem. Following the similar analysis on stability, we perform the error estimates for the velocity and the pressure in both regions. The theoretical results show the first-order convergence of the scheme in discrete $L^2$ norms for both velocity and the pressure in both regions. Moreover, in fluid region, the first-order convergence for the x-derivative of velocity component u and the y-derivative of velocity component v is also obtained in discrete $L^2$ norms. However, numerical tests show one order better for the velocity in Stokes region and the pressure in Darcy region.

1 Introduction

The coupling of incompressible fluid flow with porous media flow has been an active research topic in recent years due to various applications of the filtration in biological and environmental engineering. The mathematical modeling of such physical processes consists of Stokes or Navier–Stokes description in the incompressible fluid region and Darcy’s law in the porous media region. These two flow regions are coupled at the fluid–porous interface through some physical interface conditions which we shall describe later. A detailed modeling, analysis and numerical approximation for the problem can be found in a recent review [13]. For past years, numerical methods for Stokes and Darcy coupling problems have been investigated mainly in the framework of finite element method such as in [1, 5,6,7,8,9,10, 12,13,14,15, 19, 20, 23], just to name a few. Among those finite element discretizations, the fully coupled system can be either solved as a whole [5, 9, 10] or be decoupled into two separate subproblems with iteratively updating solution information across the interface [12, 20]. There are other numerical approaches for the Stokes/Darcy coupling problem, such as spectral method (or pseudospectral method) [18, 30], and boundary integral method [2] etc. Recently, an augmented immersed interface method based on finite difference scheme for Stokes/Darcy coupling problem with complex interface has been proposed in [21]. However, unlike most of the finite element methods, there is lack of convergence analysis of the method. This may be due to the absence of the variational formulations. In this paper, we propose a MAC (marker and cell) scheme for the Stokes/Darcy coupling problem and give the convergence proof for the scheme. To the best of our knowledge, this result is new.

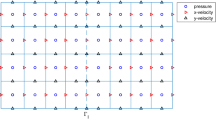
The MAC scheme proposed by Harlow and Welch [16] has been a popular finite difference scheme for Stokes and Navier–Stokes equations. The scheme adopts a nice grid layout in finite difference setting in which the velocity and pressure are located at different locations of a grid cell. More precisely, in 2D, the x component velocity u and the y component velocity v are defined at the middle points of vertical and horizontal edges, respectively; while the pressure p is defined at the cell center as depicted in Fig. 1. Although the MAC scheme has been developed in the 1960s, the first analysis and convergence for Stokes equations were carried out until 1992 by Nicolaides [24] simply because only limited mathematical tools are available for finite difference method. The author showed that the vorticity and the pressure are both first-order accurate. Later Han and Wu [17] proved that the MAC scheme can be obtained from a new mixed finite element method and showed that the first-order convergence for both the velocity (in the $H^1$ norm) and the pressure (in $L^2$ norm). Several similar convergent results using different finite element discretization can be found in the [25]. Until very recently, Li and Sun [22] proved the superconvergence (both velocity and pressure are second-order convergent in $L^2$ norm) for the MAC scheme on non-uniform grids using finite difference approach. Under the assumption of second-order convergence for the pressure, the authors were able to prove the second-order convergence of the velocity. However, the second-order convergence for the pressure is not exactly proved in the MAC framework. Rui and Li [25] established the inf-sup condition and the stability for both velocity and pressure; thus, the superconvergence for the MAC scheme can be obtained on non-uniform grids. For unstructured grids, we refer the interested reader to [3, 4] for more details. For block-centered finite difference methods that is another type of MAC scheme, the second-order convergence of the block-center scheme for incompressible and compressible Darcy-Forchheimer problems has proven in [27, 28] and a two-grid block-centered finite difference scheme is also studied in [26].

In this paper, we first develop a finite difference discretization based on the MAC scheme for the Stokes/Darcy coupling equations. The interface conditions are discretized and can be well-incorporated into the MAC grid setting. Following the similar spirit used in [22, 25] for Stokes equations, we conduct a stability and convergence analysis for the scheme on uniform grids. We would like to emphasize that the extension from Stokes problems to Stokes/Darcy coupling ones is not standard, especially in the proof of stability and convergence of the scheme. The major difficulty comes from the estimates of those relevant terms near the fluid–porous interface where three different interface conditions are imposed. Our analysis shows the first-order convergence in discrete $L^2$ norms for the velocity and the pressure in both incompressible fluid and porous regions. Moreover, in fluid region, the first-order convergence for the x-derivative of velocity component u and the y-derivative of velocity component v is also obtained in discrete $L^2$ norms.

The rest of paper is organized as follows. In Sect. 2, we present the problem with the interface conditions. In Sect. 3, we present the MAC scheme for the Stokes/Darcy coupling equations and the discretization of the interface conditions. The major stability and error analysis are given in Sects. 4 and 5, respectively. Two numerical tests are given in Sect. 6 showing better convergence results than the theory. Concluding remarks are made in Sect. 7.

2 The Stokes/Darcy Coupling Problem

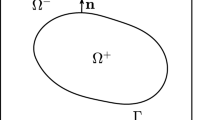
In this paper, the model under consideration consists of Stokes flow in the fluid region $\Omega _f$ and Darcy’s law in the porous media domain $\Omega _p$, where these bounded domains $\Omega _f$ and $\Omega _p \subset {\mathbb {R}}^2$ are assumed to be rectangular and separated by an interface $\Gamma$ as illustrated in Fig. 1. Let the boundary $\Gamma _f (\Gamma _p)$ be $\partial \Omega _f \backslash \Gamma$ ($\partial \Omega _p \backslash \Gamma$) respectively and $n_f$ ($n_p$) be the unit outward normal vector of the domain $\Omega _f$ ($\Omega _p$) respectively.

Let us denote $\varvec{u}=(u,v)$ and p by the fluid velocity and pressure in $\Omega _f$ and $\varvec{u}_p$ and $\phi$ by the fluid velocity and pressure in $\Omega _p$. In the region $\Omega _f$, the Stokes flow $(\varvec{u}, p)$ satisfies the following equations

$$\begin{aligned} -\nu \triangle \varvec{u}+ \nabla p= & {} f_1, \text { in } \Omega _f, \end{aligned}$$

(2.1)

$$\begin{aligned} \nabla \cdot \varvec{u}= & {} 0, \text { in } \Omega _f, \end{aligned}$$

(2.2)

$$\begin{aligned} \varvec{u}= & {} 0, \text { in } \Gamma _f, \end{aligned}$$

(2.3)

where $\nu$ is the viscosity and $f_1=(f^u, f^v)$ is the external force; in the region $\Omega _p$, the Darcy’s flow $(\varvec{u}_p, \phi )$ satisfies the following equations

$$\begin{aligned} \varvec{u}_p= & {} -K \nabla \phi , \text { in } \Omega _p, \end{aligned}$$

(2.4)

$$\begin{aligned} \nabla \cdot \varvec{u}_p= & {} f_2, \text { in } \Omega _p, \end{aligned}$$

(2.5)

$$\begin{aligned} \varvec{u}_p \cdot n_p= & {} 0, \text { in } \Gamma _p, \end{aligned}$$

(2.6)

where K is a symmetric and positive definite tensor representing the rock permeability divided by the fluid viscosity and $f_2$ is the external source. For simplicity, we choose $K=\kappa I_2$ where $\kappa$ is a positive constant and $I_2$ is $2\times 2$ identity matrix. By combining equations (2.4) and (2.5), we obtain

$$\begin{aligned} -\nabla \cdot ( \kappa \nabla \phi ) =f_2, \text { in } \Omega _p. \end{aligned}$$

(2.7)

Here, the source $f_2$ is assumed to satisfy the solvability condition

$$\begin{aligned} \int _{\Omega _p} f_2 \, d \mathbf{x} = 0, \end{aligned}$$

(2.8)

which is due to the no-slip (2.3) and no-flow boundary condition (2.6) on the boundaries $\Gamma _f$ and $\Gamma _p$, respectively; and the mass conservation $\varvec{u}_p \cdot n_p+ \mathbf{u} \cdot n_f = 0$ across the interface $\Gamma$. In the present setting, this mass conservation across the interface results in (2.10). More detailedly, we have

$$\begin{aligned} \int _{\Omega _f} \nabla \cdot \varvec{u}\, d\mathbf{x} + \int _{\Omega _p} \nabla \cdot \varvec{u}_p \, d\mathbf{x}=\int _{\Omega _p} f_2 \, d \mathbf{x}= 0. \end{aligned}$$

The pressures $(p, \phi )$ are assumed to satisfy the condition for the uniqueness of the solutions as follows:

$$\begin{aligned} \int _{\Omega _f} p\, d \mathbf{x} +\int _{\Omega _p} \phi \, d \mathbf{x} = 0. \end{aligned}$$

(2.9)

To complete the problem (2.1)–(2.6), three conditions across the interface $\Gamma$ should be satisfied; namely, the mass conservation, the balance of normal forces, and the Beavers–Joseph–Saffman (BJS) condition, see the detailed physical meanings of those conditions in [13, 20]. Readers who are interested in the well-posedness of the problem with above three interface conditions can refer to the review article [13]. Since the considered interface $\Gamma$ is a straight line in this paper, those three interface conditions can be simplified into

$$\begin{aligned} v= & {} -\kappa \frac{\partial \phi }{\partial y}, \end{aligned}$$

(2.10)

$$\begin{aligned} p-\phi= & {} 2\nu \frac{\partial v}{\partial y}, \end{aligned}$$

(2.11)

$$\begin{aligned} u= & {} \frac{\sqrt{{\tilde{k}}}}{\alpha _1}\left( \frac{\partial u}{\partial y}+ \frac{\partial v}{\partial x}\right) , \end{aligned}$$

(2.12)

where ${\tilde{k}} = \nu \kappa$ and $\alpha _1$ are positive constants. Here, the form of $\sqrt{{\tilde{k}}}/\alpha _1$ has the physical meaning of friction coefficient.

3 Finite Difference Discretization Based on the MAC Scheme

In this section, the finite difference discretization based on the MAC scheme for solving the problem (2.1)–(2.12) is presented. We start with the mesh description. Let $\Omega = \Omega _f \cup \Omega _p$. For simplicity in presentation, the domain $\Omega$ is assumed to be $[0, L_x] \times [-L_y, L_y]$ where $\Omega _f= [0, L_x] \times [0, L_y]$ , $\Omega _p= [0, L_x] \times [-L_y,0]$ and $L_x, L_y$ are positive constants. Given positive integers M and N, the mesh widths $\Delta x$ and $\Delta y$ are equal to $L_x/M$ and $L_y/N$ respectively. Let the nodal points $(x_i, y_j), 0 \le i \le M+1, -N\le j \le N+1$ be defined as follows:

$$\begin{aligned} x_i =\left( i-\frac{1}{2}\right) \Delta x, \, y_j= \left( j-\frac{1}{2}\right) \Delta y. \end{aligned}$$

For possible integers $i, j, \, 0\le i \le M, -N \le j \le N$, we define $x_{i+1/2}=(x_i +x_{i+1})/2$ and $y_{j+1/2}=(y_j +y_{j+1})/2$. Here, the staggered grids are applied. Namely, the pressure is defined on one set of grid points while the velocities are defined on another set of grid points. We let $u_{i+1/2,j}, \, v_{i,j+1/2}$ and $p_{i,j}$ denote discrete approximations of the flow velocity $u(x_{i+1/2}, y_j), \, v(x_{i},y_{j+1/2})$ and the pressure $p(x_{i},y_{j})$ respectively; let $\phi _{i,j}$ denote the discrete approximation of the pressure $\phi (x_{i},y_{j})$ (see Fig. 1).

Fig. 1

a Schematic representation of the finite difference discretization within the staggered grid framework. p and $\phi$ are defined at the cell centres, while u and v are defined at the centre of the cell faces. The interface is defined along $j=1/2$. b Staggered arrangement of the variables

To discretize (2.1), we employ central differences and derive

$$\begin{aligned}&\displaystyle -\nu \Bigg ( \frac{u_{i+3/2, j}-2u_{i+1/2, j}+u_{i-1/2,j}}{(\Delta x)^2} + \frac{u_{i+1/2, j+1}-2u_{i+1/2,j}+u_{i+1/2,j-1}}{(\Delta y)^2} \Bigg )\nonumber \\&\quad \displaystyle + \frac{p_{i+1,j}-p_{i,j}}{\Delta x} =f^u_{i+1/2,j}, 1\le i \le M-1, \, 1\le j \le N, \end{aligned}$$

(3.1)

and

$$\begin{aligned}&\displaystyle -\nu \Bigg ( \frac{v_{i+1,j+1/2}-2v_{i,j+1/2}+v_{i-1,j+1/2}}{(\Delta x)^2} + \frac{v_{i,j+3/2}-2v_{i,j+1/2}+v_{i,j-1/2,}}{(\Delta y)^2} \Bigg ) \nonumber \\&\quad \displaystyle + \frac{p_{i,j+1}-p_{i,j}}{\Delta y} =f^v_{i,j+1/2}, 1\le i \le M, \, 1\le j \le N-1, \end{aligned}$$

(3.2)

where

$$\begin{aligned} f^u_{i+1/2,j}= & {} \frac{1}{\Delta x\Delta y}\iint _{[x_{i},x_{i+1}]\times [y_{j-1/2},y_{j+1/2}]} f^u(x,y) \, dxdy, \\ f^v_{i, j+1/2}= & {} \frac{1}{\Delta x\Delta y}\iint _{[x_{i-1/2},x_{i+1/2}]\times [y_{j},y_{j+1}]} f^v(x,y) \, dxdy. \end{aligned}$$

To discretize (2.2), we derive its discrete approximation at the mesh points $(x_{i}, y_{j})$. That is, we obtain

$$\begin{aligned} \displaystyle \frac{u_{i+1/2,j}-u_{i-1/2,j}}{\Delta x} + \frac{v_{i,j+1/2}-v_{i,j-1/2}}{\Delta y} = 0,\quad 1\le i \le M, \, 1\le j \le N. \end{aligned}$$

(3.3)

As for the finite difference discretization of the equation (2.7), similarly, we have

$$\begin{aligned}&-\kappa \frac{\phi _{i+1,j}-2\phi _{i,j}+ \phi _{i-1,j}}{(\Delta x)^2} -\kappa \frac{\phi _{i,j+1}-2\phi _{i,j}-\phi _{i,j-1}}{(\Delta y)^2} = (f_2)_{i,j}, \nonumber \\&\quad 1\le i \le M, \, -N+1\le j \le 0, \end{aligned}$$

(3.4)

where

$$\begin{aligned} (f_2)_{i,j} =\frac{1}{\Delta x\Delta y}\iint _{[x_{i-1/2},x_{i+1/2}]\times [y_{j-1/2},y_{j+1/2}]} f_2(x,y) \, dxdy. \end{aligned}$$

The discrete approximations (3.1)–(3.4) are employed to determine the pressure and the velocity at the interior points in $\Omega$ except the ones on the interface boundary $\Gamma$. For certain of these equations, the information about the boundary conditions and the ghost points should be provided. For boundary conditions, we have

$$\begin{aligned} u_{1/2,j}= & {} u_{M+1/2,j} = 0, \, j=1, \ldots , N, \end{aligned}$$

(3.5)

$$\begin{aligned} v_{i,N+1/2}= & {} 0, \, i=1, \ldots , M, \end{aligned}$$

(3.6)

$$\begin{aligned} \phi _{0,j}= & {} \phi _{1,j}, \phi _{M+1,j} =\phi _{M,j} \, j=-N+1, \ldots , 0, \end{aligned}$$

(3.7)

$$\begin{aligned} \phi _{i,-N}= & {} \phi _{i,-N+1}, \, i=1, \ldots ,M. \end{aligned}$$

(3.8)

As for the extrapolation of the ghost points on the boundary $\Gamma _f \cup \Gamma _p$, we use linear extrapolation and the boundary condition which lead to

$$\begin{aligned} u_{i+1/2,N+1}= & {} -u_{i+1/2,N} , \, i=0, \ldots , M, \end{aligned}$$

(3.9)

$$\begin{aligned} v_{0,j+1/2}= & {} -v_{1,j+1/2}, \, j=0, \ldots , N, \end{aligned}$$

(3.10)

$$\begin{aligned} v_{M+1,j+1/2}= & {} -v_{M,j+1/2}, \, j=0, \ldots , N. \end{aligned}$$

(3.11)

Regarding the interface conditions on $\Gamma$, we introduce the values of $\phi _{i,1}, 1\le i \le M$ (the pressure on the Darcy region) and $u_{i+1/2,0}, 1\le i \le M-1$ (the velocity on Stokes region) defined on the ghost points $(x_i, y_1)$ and $(x_{i+1/2},y_0)$ respectively. Furthermore, the interface conditions (2.10)–(2.12) can be approximated by choosing the values of $\phi _{i,1}$ and $u_{i+1/2,0}$ such that the following discretizations hold:

$$\begin{aligned} v_{i,1/2}= & {} -\kappa \frac{\phi _{i,1}-\phi _{i,0}}{\Delta y}, \, i=1, \ldots , M, \end{aligned}$$

(3.12)

$$\begin{aligned} p_{i,1}-\phi _{i,0}= & {} 2 \nu \frac{v_{i, 3/2} -v_{i,1/2}}{\Delta y}, \, i=1, \ldots , M, \end{aligned}$$

(3.13)

$$\begin{aligned} \frac{u_{i+1/2,1} +u_{i+1/2,0}}{2}= & {} \frac{\sqrt{{\tilde{k}}}}{\alpha _1} \Bigg ( \frac{u_{i+1/2,1} -u_{i+1/2,0}}{\Delta y} + \frac{v_{i+1,1/2} -v_{i,1/2}}{\Delta x}\Bigg ), \nonumber \\ i= & {} 1, \ldots , M-1. \end{aligned}$$

(3.14)

The idea of the discrete approximations (3.12) and (3.14) is to approximate the differential operators on the interface $\Gamma$ as follows:

$$\begin{aligned} \frac{\partial \phi }{\partial y} \approx \frac{\phi _{i,1} - \phi _{i,0}}{\Delta y}, \frac{\partial u}{\partial y} \approx \frac{u_{i+1/2,1}-u_{i+1/2,0}}{\Delta y}, \frac{\partial v}{\partial x} \approx \frac{v_{i+1, 1/2}-v_{i,1/2}}{\Delta x}, \end{aligned}$$

and apply the linear approximation to obtain the value of u on the interface $\Gamma$ as follows:

$$\begin{aligned} u \approx \frac{u_{i+1/2,1} + u_{i+1/2,0}}{2}. \end{aligned}$$

We remark that the discrete approximation (3.13) of (2.11) is applied by using one-sided first order finite difference methods. The convergence for the unknowns $(\mathbf u, p)$ and $\phi$ in discrete $L^2$ norm is shown to be of first order in Sect. 4. However, the first order approximation on the interface condition does not contaminate the convergence of the second order for the velocity field which is illustrated by numerical experiments in Sect. 5.

To discretize (2.9), we apply direct integration as follows:

$$\begin{aligned} \sum _{i=1}^{M}\sum _{j=1}^{N} p_{i,j} \Delta x \Delta y + \sum _{i=1}^{M}\sum _{j=-N+1}^{0} \phi _{i,j} \Delta x \Delta y= 0. \end{aligned}$$

(3.15)

Remark that the following compatibility condition should be satisfied directly due to the definition of $(f_2)_{i,j}$:

$$\begin{aligned} \sum _{i=1}^{M}\sum _{j=-N+1}^{0} (f_2)_{i,j} \Delta x \Delta y = 0. \end{aligned}$$

(3.16)

Now, we introduce the following standard forward and backward difference operators $D_x^+, D_x^-, D_y^+$ and $D_y^-$ as follows:

$$\begin{aligned} D_x^+ u_{i+1/2,j}= & {} \frac{u_{i+3/2,j}-u_{i+1/2,j}}{\Delta x}, \, D_x^- u_{i+1/2,j} =\frac{u_{i+1/2,j}-u_{i-1/2,j}}{\Delta x}, \\ D_y^+ u_{i+1/2,j}= & {} \frac{u_{i+1/2,j+1}-u_{i+1/2,j}}{\Delta y}, \, D_y^- u_{i+1/2,j} =\frac{u_{i+1/2,j}-u_{i+1/2,j-1}}{\Delta y}. \end{aligned}$$

Similarly, we can define the notations for $D_x^+ v_{i,j+1/2}$, $D_x^- v_{i,j+1/2},$ $D_y^+ v_{i,j+1/2}$, $D_y^- v_{i,j+1/2},$ $D_x^+ p_{i,j},$ $D_x^- p_{i,j},$ $D_y^+ p_{i,j}$ and $D_y^- p_{i,j}$. These notations are also applied for Darcy’s flow.

In summary, we rewrite the finite difference scheme for (3.1) to (3.4) as follows:

$$\begin{aligned}&-\nu D_x^+D_x^-u_{i+1/2,j}-\nu D_y^+D_y^-u_{i+1/2,j} + D_x^- p_{i+1,j} = f^u_{i+1/2,j},\nonumber \\&\quad 1\le i \le M-1, \, 1\le j \le N, \end{aligned}$$

(3.17)

$$\begin{aligned}&-\nu D_x^+D_x^-v_{i,j+1/2}-\nu D_y^+D_y^-v_{i,j+1/2} + D_y^- p_{i,j+1} = f^v_{i,j+1/2}, \nonumber \\&\quad 1\le i \le M, \, 1\le j \le N-1, \end{aligned}$$

(3.18)

$$\begin{aligned}&D_x^- u_{i+1/2,j} + D_y^- v_{i,j+1/2} = 0, 1\le i \le M, 1\le j\le N, \end{aligned}$$

(3.19)

$$\begin{aligned}&-\kappa D_x^+D_x^- \phi _{i,j} -\kappa D_y^+D_y^-\phi _{i,j} = (f_2)_{i,j}, 1\le i \le M, -N+1\le j\le 0. \end{aligned}$$

(3.20)

4 Stability Analysis

In this section, the stability analysis for the scheme (3.17)–(3.20) will be presented. Assume that the discrete solutions $u_{i+1/2,j}, v_{i,j+1/2}$ and $\phi _{i,j}$ satisfy the boundary conditions and interface conditions described in (3.5)–(3.14). We begin with introducing the following discrete norms that will be used later:

$$\begin{aligned} \Vert u\Vert ^2= & {} \sum _{i=1}^{M-1}\sum _{j=1}^{N} |u_{i+1/2,j}|^2 \Delta x\Delta y, \end{aligned}$$

(4.1)

$$\begin{aligned} \Vert v\Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=1}^{N-1} |v_{i,j+1/2}|^2 \Delta x\Delta y + \sum _{i=1}^M |v_{i,1/2}|^2 \frac{\Delta x\Delta y}{2}, \end{aligned}$$

(4.2)

$$\begin{aligned} \Vert p\Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=1}^{N} |p_{i,j}|^2 \Delta x\Delta y, \end{aligned}$$

(4.3)

$$\begin{aligned} \Vert \phi \Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=-N+1}^{0} |\phi _{i,j}|^2 \Delta x\Delta y, \, \Vert f_2\Vert ^2 =\sum _{i=1}^{M}\sum _{j=-N+1}^{0} | (f_2)_{i,j}|^2 \Delta x\Delta y, \end{aligned}$$

(4.4)

$$\begin{aligned} \Vert f^u\Vert ^2= & {} \sum _{i=1}^{M-1}\sum _{j=1}^{N} |f^u_{i+1/2,j}|^2 \Delta x\Delta y, \end{aligned}$$

(4.5)

$$\begin{aligned} \Vert f^v\Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=1}^{N-1} |f^v_{i,j+1/2}|^2 \Delta x\Delta y + \sum _{i=1}^M |f^v_{i,1/2}|^2 \frac{\Delta x\Delta y}{2}, \end{aligned}$$

(4.6)

$$\begin{aligned} \Vert D_x^- u\Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=1}^{N} |D_x^- u_{i+1/2,j}|^2 \Delta x\Delta y, \end{aligned}$$

(4.7)

$$\begin{aligned} \Vert D_y^- u\Vert ^2= & {} \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} |D_y^- u_{i+1/2,j+1}|^2 \Delta x\Delta y \nonumber \\&+ \sum _{i=1}^{M-1} \left( |D_y^- u_{i+1/2,N+1}|^2 + |D_y^- u_{i+1/2,1}|^2\right) \frac{\Delta x\Delta y}{2}, \end{aligned}$$

(4.8)

$$\begin{aligned} \Vert D_x^- v\Vert ^2= & {} \sum _{i=2}^{M}\sum _{j=1}^{N-1} |D_x^- v_{i,j+1/2}|^2 \Delta x\Delta y \nonumber \\&+ \sum _{j=1}^{N-1} \left( |D_x^- v_{M+1,j+1/2}|^2 + |D_x^- v_{1,j+1/2}|^2\right) \frac{\Delta x\Delta y}{2} \nonumber \\&+ \sum _{i=2}^M |D_x^- v_{i,1/2}|^2 \frac{\Delta x\Delta y}{2} + \left( |D_x^- v_{1,1/2}|^2 + |D_x^- v_{M+1,1/2}|^2\right) \frac{\Delta x\Delta y}{4}, \nonumber \\ \end{aligned}$$

(4.9)

$$\begin{aligned} \Vert D_y^- v\Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=1}^{N} |D_y^- v_{i,j+1/2}|^2 \Delta x\Delta y, \end{aligned}$$

(4.10)

$$\begin{aligned} \Vert D_x^- \phi \Vert ^2= & {} \sum _{i=1}^{M-1}\sum _{j=-N+1}^{0} |D_x^- \phi _{i+1,j}|^2 \Delta x \Delta y, \end{aligned}$$

(4.11)

$$\begin{aligned} \Vert D_y^- \phi \Vert ^2= & {} \sum _{i=1}^M\sum _{j=-N+2}^{0} |D_y^- \phi _{i,j}|^2 \Delta x \Delta y + \sum _{i=1}^M |D_y^- \phi _{i,1}|^2 \frac{\Delta x\Delta y}{2}. \end{aligned}$$

(4.12)

Notice that by the definition of $f^u_{i+1/2,j}$ ($f^v_{i,j+1/2}$ and $(f_2)_{i,j}$) respectively, we have the inequality $\Vert f^u\Vert \le \Vert f^u\Vert _{L^2}$ ( $\Vert f^v\Vert \le \Vert f^v\Vert _{L^2}$ and $\Vert f_2\Vert \le \Vert f_2\Vert _{L^2}$) respectively where $\Vert \cdot \Vert _{L^2}$ denotes its corresponding $L^2$ norm. This implies that the discrete $L^2$ norms of the forcing terms are independent of the mesh widths. Before proceeding the stability analysis, we need the following discrete Poincare inequalities:

Lemma 4.1

$$\begin{aligned} \Vert u\Vert ^2\le & {} L_x^2 \Vert D_x^- u\Vert ^2, \end{aligned}$$

(4.13)

$$\begin{aligned} \Vert v\Vert ^2\le & {} \left( L_y + \frac{\Delta y}{2}\right) L_y \Vert D_y^- v\Vert ^2, \end{aligned}$$

(4.14)

$$\begin{aligned} \left| \sum _{i=1}^M \sum _{j=-N+1}^0 (f_2)_{i,j}\phi _{i,j} \Delta x \Delta y\right|\le & {} \sqrt{2\left( L^2_x+L^2_y\right) }\Vert f_2\Vert \Bigg ( \Vert D_x^- \phi \Vert ^2 + \Vert D_y^-\phi \Vert ^2 \Bigg )^{1/2}. \nonumber \\ \end{aligned}$$

(4.15)

Proof

To show (4.13), we have

$$\begin{aligned} \Vert u\Vert ^2= & {} \sum _{i=1}^{M-1}\sum _{j=1}^{N}|\sum _{m=1}^i D_x^- u_{m+1/2,j} \Delta x|^2 \Delta x \Delta y \nonumber \\\le & {} \sum _{i=1}^{M-1}\sum _{j=1}^{N} \Bigg ( \sum _{m=1}^{M-1} | D_x^- u_{m+1/2,j} |^2\Bigg ) M(\Delta x)^3 \Delta y \nonumber \\\le & {} L_x^2 \Vert D_x^- u\Vert ^2. \end{aligned}$$

(4.16)

As for (4.14), by applying similar techniques, we have

$$\begin{aligned} \Vert v\Vert ^2= & {} \sum _{i=1}^{M}\sum _{j=1}^{N-1}\Bigg (\sum _{m=j+1}^{N} D_y^- v_{i,m+1/2} \Delta y \Bigg )^2 \Delta x \Delta y + \sum _{i=1}^M \Bigg (\sum _{m=1}^{N} D_y^-v_{i,m+1/2} \Delta y\Bigg )^2 \frac{\Delta x\Delta y}{2} \nonumber \\\le & {} \sum _{i=1}^M\sum _{j=1}^{N-1} \Bigg ( \sum _{m=2}^{N} | D_y^- v_{i,m+1/2} |^2\Bigg ) N(\Delta y)^3 \Delta x + \frac{L_y \Delta y}{2} \Vert D_y^- v\Vert ^2 \nonumber \\\le & {} \left( L_y + \frac{\Delta y}{2}\right) L_y \Vert D_y^- v\Vert ^2. \end{aligned}$$

(4.17)

As for (4.15), for any $i\ge i'$ and $j\ge j'$ we have

$$\begin{aligned}&(f_2)_{i,j}\phi _{i,j} - (f_2)_{i,j}\phi _{i',j'} \nonumber \\&\quad \le |(f_2)_{i,j}| \Bigg ( \sum _{m=i'+1}^i |D_x^- \phi _{m,j}|\Delta x + \sum _{m=0}^j |D_y^- \phi _{i',m}|\Delta y \Bigg ). \end{aligned}$$

(4.18)

Multiplying (4.18) by $\Delta x\Delta y$ and summing all i and j, applying the condition (3.16) and using Cauchy–Schwarz inequality, (4.15) is obtained.

Then, the proof of Lemma 4.1 is complete. $\square$

Now, in order to make our presentation of the stability analysis clear, we need the following lemmas.

Lemma 4.2

$$\begin{aligned} -\nu D_x^+D_x^-u_{i+1/2,j}-\nu D_x^+D_y^-v_{i,j+1/2}= & {} 0, 1\le i \le M-1, \, 1\le j \le N, \end{aligned}$$

(4.19)

$$\begin{aligned} -\nu D_y^+D_x^-u_{i+1/2,j}-\nu D_y^+D_y^-v_{i,j+1/2}= & {} 0, 1\le i \le M, \, 1\le j \le N-1. \end{aligned}$$

(4.20)

The proof of Lemma 4.2 is established by directly applying (3.19).

Lemma 4.3

$$\begin{aligned}&\sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_x^-p_{i+1,j} \Delta x \Delta y + \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2}D_y^-p_{i,j+1} \Delta x \Delta y\nonumber \\&\quad = -\sum _{i=1}^M v_{i,1/2}p_{i,1}\Delta x, \end{aligned}$$

(4.21)

$$\begin{aligned}&\qquad \displaystyle -\kappa \sum _{i=1}^{M}\sum _{j=-N+1}^{0} \Bigg ( D_x^+D_x^- \phi _{i,j} + D_y^+ D_y^-\phi _{i,j}\Bigg ) \phi _{i,j} \Delta x \Delta y \nonumber \\&\quad \displaystyle =\kappa \Vert D_x^- \phi \Vert ^2 +\kappa \sum _{i=1}^{M}\sum _{j=-N+2}^{0} (D_y^-\phi _{i,j})^2 \Delta x \Delta y - \kappa \sum _{i=1}^M D_y^- \phi _{i,1} \phi _{i,0}\Delta x. \end{aligned}$$

(4.22)

Proof

To show (4.21), we have

$$\begin{aligned} \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_x^-p_{i+1,j} \Delta x \Delta y= & {} \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}(p_{i+1,j} -p_{i,j}) \Delta y \nonumber \\= & {} \sum _{j=1}^{N}\Bigg ( \sum _{i=1}^{M-1} u_{i+1/2,j}p_{i+1,j} - \sum _{i=1}^{M-1} u_{i+1/2,j} p_{i,j} \Bigg ) \Delta y \nonumber \\= & {} \sum _{j=1}^{N}\Bigg ( \sum _{i=2}^{M} u_{i-1/2,j}p_{i,j} - \sum _{i=1}^{M-1} u_{i+1/2,j} p_{i,j} \Bigg ) \Delta y \nonumber \\= & {} - \sum _{j=1}^{N} \sum _{i=1}^{M} D_x^-u_{i+1/2,j}p_{i,j} \Delta x \Delta y, \end{aligned}$$

(4.23)

where the boundary conditions (3.5) are applied. By applying the same technique, we have

$$\begin{aligned} \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2}D_y^-p_{i,j+1} \Delta x \Delta y= & {} - \sum _{i=1}^{M} \sum _{j=1}^{N} D_y^- v_{i,j+1/2}p_{i,j} \Delta x \Delta y -\sum _{i=1}^M v_{i,1/2}p_{i,1} \Delta x,\nonumber \\ \end{aligned}$$

(4.24)

where the boundary conditions (3.6) are applied. (4.21) can be derived by summing (4.23) and (4.24) and applying (3.19). Similar procedures can be applied to obtain (4.22). $\square$

Lemma 4.4

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_x^+ D_x^-u_{i+1/2,j} \Delta x \Delta y = \nu \Vert D_x^- u\Vert ^2, \end{aligned}$$

(4.25)

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_y^+ D_y^-u_{i+1/2,j} \Delta x \Delta y = \nu \Vert D_y^- u \Vert ^2 \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} \frac{u_{i+1/2,1}+ u_{i+1/2,0}}{2}D_y^- u_{i+1/2,1} \Delta x, \end{aligned}$$

(4.26)

$$\begin{aligned}&\qquad -\nu \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2} D_x^+ D_x^-v_{i,j+1/2} \Delta x \Delta y = \nu \sum _{i=1}^{M-1} \sum _{j=1}^{N-1} |D_x^- v_{i,j+1/2}|^2 \Delta x \Delta y \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \Bigg ( |D_x^- v_{M+1,j+1/2}|^2 + |D_x^- v_{1,j+1/2}|^2\Bigg )\Delta x \Delta y, \end{aligned}$$

(4.27)

$$\begin{aligned}&\qquad -\nu \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2}D_y^+ D_y^-v_{i,j+1/2} \Delta x \Delta y = \nu \Vert D_y^- v \Vert ^2 \nonumber \\&\qquad + \nu \sum _{i=1}^M v_{i,1/2} D_y^- v_{i,3/2}\Delta x, \end{aligned}$$

(4.28)

$$\begin{aligned}&\qquad -\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_x^+ D_y^-v_{i,j+1/2} \Delta x \Delta y \nonumber \\&\quad = \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} D_y^- u_{i+1/2,j+1}D_x^- v_{i+1,j+1/2}\Delta x\Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} u_{i+1/2,1}D_x^- v_{i+1,1/2}\Delta x, \end{aligned}$$

(4.29)

$$\begin{aligned}&\qquad -\nu \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2}D_y^+ D_x^-u_{i+1/2,j} \Delta x \Delta y \nonumber \\&\quad = \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} D_y^- u_{i+1/2,j+1}D_x^- v_{i+1,j+1/2}\Delta x\Delta y. \end{aligned}$$

(4.30)

Proof

To show (4.25), we observe that

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_x^+ D_x^-u_{i+1/2,j} \Delta x \Delta y \nonumber \\&\quad = -\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} \Bigg ( u_{i+1/2,j} D_x^+ u_{i+1/2,j}- u_{i+1/2,j}D_x^-u_{i+1/2,j} \Bigg ) \Delta y \nonumber \\&\quad = -\nu \sum _{j=1}^{N} \Bigg ( \sum _{i=1}^{M-1} u_{i+1/2,j} D_x^+ u_{i+1/2,j}- \sum _{i=1}^{M-1} u_{i+1/2,j}D_x^-u_{i+1/2,j} \Bigg ) \Delta y \nonumber \\&\quad = -\nu \sum _{j=1}^{N} \Bigg ( \sum _{i=2}^{M} u_{i-1/2,j} D_x^- u_{i+1/2,j}- \sum _{i=1}^{M-1} u_{i+1/2,j}D_x^-u_{i+1/2,j} \Bigg ) \Delta y \nonumber \\&\quad =-\nu \sum _{j=1}^{N} \Bigg ( \sum _{i=1}^M -|D_x^- u_{i+1/2,j}|^2 \Delta x \Delta y \ + u_{M+1/2,j} D_x^- u_{M+1/2,j} \Delta y \nonumber \\&\qquad - u_{1/2,j}D_x^-u_{3/2,j}\Delta y \Bigg ) \nonumber \\&\quad = \nu \Vert D_x^- u\Vert ^2, \end{aligned}$$

(4.31)

where boundary conditions (3.9) are applied. Then (4.25) is derived. As for (4.26), we have

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_y^+ D_y^-u_{i+1/2,j} \Delta x \Delta y \nonumber \\&\quad = -\nu \sum _{i=1}^{M-1} \Bigg ( \sum _{j=1}^{N} u_{i+1/2,j} D_y^+ u_{i+1/2,j}- \sum _{j=1}^{N}u_{i+1/2,j}D_y^-u_{i+1/2,j} \Bigg ) \Delta x \nonumber \\&\quad = -\nu \sum _{i=1}^{M-1} \Bigg ( \sum _{j=2}^{N+1} u_{i+1/2,j-1} D_y^- u_{i+1/2,j}- \sum _{j=1}^{N} u_{i+1/2,j}D_y^-u_{i+1/2,j} \Bigg ) \Delta x \nonumber \\&\quad =-\nu \sum _{i=1}^{M-1} \Bigg ( \sum _{j=2}^{N} -|D_y^- u_{i+1/2,j}|^2 \Delta x \Delta y + u_{i+1/2,N} D_y^- u_{i+1/2,N+1} \Delta x \nonumber \\&\qquad - u_{i+1/2,1}D_y^-u_{i+1/2,1}\Delta x \Bigg ) \nonumber \\&\quad = \nu \sum _{i=1}^{M-1} \sum _{j=2}^{N} |D_y^- u_{i+1/2,j}|^2 \Delta x \Delta y + \frac{\nu }{2}\sum _{i=1}^{M-1} \Bigg ( |D_y^- u_{i+1/2,N+1}|^2 + |D_y^-u_{i+1/2,1}|^2 \Bigg ) \Delta x \Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} \frac{u_{i+1/2,1}+ u_{i+1/2,0}}{2}D_y^- u_{i+1/2,1} \Delta x \nonumber \\&\quad = \nu \Vert D_y^- u\Vert ^2 + \nu \sum _{i=1}^{M-1} \frac{u_{i+1/2,1}+ u_{i+1/2,0}}{2}D_y^- u_{i+1/2,1} \Delta x, \end{aligned}$$

(4.32)

where the linear extrapolation conditions (3.9) are used. Then (4.26) is obtained. (4.27) and (4.28) can be derived by using similar techniques. The proofs are omitted.

To prove (4.29), we observe

$$\begin{aligned} D_x^+ D_y^-v_{i,j+1/2} = D_y^- D_x^+v_{i,j-1/2}. \end{aligned}$$

(4.33)

Notice that

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}D_y^- D_x^+v_{i,j-1/2} \Delta x \Delta y \nonumber \\&\quad = -\nu \sum _{i=1}^{M-1} \Bigg ( \sum _{j=1}^{N} u_{i+1/2,j} D_x^+ v_{i,j+1/2}- \sum _{j=1}^{N}u_{i+1/2,j}D_x^+v_{i,j-1/2} \Bigg ) \Delta x \nonumber \\&\quad = -\nu \sum _{i=1}^{M-1} \Bigg ( \sum _{j=2}^{N+1} u_{i+1/2,j-1} D_x^+ v_{i,j-1/2}- \sum _{j=1}^{N} u_{i+1/2,j}D_x^+v_{i,j-1/2} \Bigg ) \Delta x \nonumber \\&\quad =-\nu \sum _{i=1}^{M-1} \Bigg ( \sum _{j=2}^{N} -D_y^- u_{i+1/2,j}D_x^+v_{i,j-1/2} \Delta x \Delta y + u_{i+1/2,N} D_x^+ v_{i,N+1/2} \Delta x \nonumber \\&\qquad - u_{i+1/2,1}D_x^+v_{i,1/2}\Delta x \Bigg ) \nonumber \\&\quad = \nu \sum _{i=1}^{M-1}\sum _{j=2}^{N} D_y^- u_{i+1/2,j}D_x^+ v_{i,j-1/2}\Delta x\Delta y + \nu \sum _{i=1}^{M-1} u_{i+1/2,1}D_x^+ v_{i,1/2}\Delta x. \end{aligned}$$

(4.34)

Then, (4.29) is proven.

Again, (4.30) can be done by using the same technique which proof is omitted.

Finally, the proof of Lemma 4.4 is complete. $\square$

Now, we are in a position to state and show the following theorem for the stability analysis of the scheme (3.1)–(3.14) as follows:

Theorem 4.1

Given the mesh widths $\Delta x$ and $\Delta y$ satisfying

$$\begin{aligned} \Delta y \le min\left\{ \frac{\nu \kappa }{2L_y}, \frac{2\alpha ^2_2}{L_y}\right\} , \end{aligned}$$

(4.35)

where $\alpha _2 =\frac{2\sqrt{{\tilde{\kappa }}}}{\alpha _1}$, we have

$$\begin{aligned}&\frac{\nu }{2L_x^2} \Vert u\Vert ^2 + \frac{\nu }{8L_y^2 +2\nu \kappa }\Vert v\Vert ^2 + \frac{\nu }{2}\Vert D_x^-u\Vert ^2 +\frac{\nu }{8}\Vert D_y^- v\Vert ^2 \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \left( D_y^-u_{i+1/2,j+1} +D_x^- v_{i+1,j+1/2}\right) ^2 \, \Delta x\Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} |D_y^- u_{i+1/2,N+1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- v_{1,j+1/2}|^2 + |D_x^- v_{M+1,j+1/2}|^2 \right) \Delta x \Delta y \nonumber \\&\qquad + \frac{\kappa }{2}\Vert D_x^- \phi \Vert ^2 + \frac{\kappa }{2}\Vert D_y^- \phi \Vert ^2 \nonumber \\&\quad \le C_f:=\frac{L_x^2}{2\nu }\Vert f^u\Vert ^2+ \frac{L_y^2+\frac{\nu \kappa }{4}}{2\nu }\Vert f^v\Vert ^2 +\frac{\left( L^2_x+L^2_y\right) }{\kappa }\Vert f_2\Vert ^2. \end{aligned}$$

(4.36)

Proof

By multiplying (3.17), (3.18), (3.20), (4.19) and (4.20) by $u_{i+1/2,j}\Delta x \Delta y$, $v_{i,j+1/2} \Delta x\Delta y$, $\phi _{i,j}\Delta x\Delta y$, $u_{i+1/2,j}\Delta x \Delta y$ and $v_{i,j+1/2} \Delta x\Delta y$ respectively, summing the resulting equations for all i and j, and applying Lemmas (4.3) and (4.4), we obtain

$$\begin{aligned}&2\nu \Vert D_x^- u\Vert ^2 + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \left( D_y^-u_{i+1/2,j+1} +D_x^- v_{i+1,j+1/2}\right) ^2 \, \Delta x\Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} \left( |D_y^- u_{i+1/2,N+1}|^2 + |D_y^- u_{i+1/2,1}|^2\right) \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- v_{1,j+1/2}|^2 + |D_x^- v_{M+1,j+1/2}|^2 \right) \Delta x \Delta y \nonumber \\&\qquad + 2\nu \Vert D_y^- v\Vert ^2 + \kappa \Vert D_x^- \phi \Vert ^2 + \kappa \Vert D_y^- \phi \Vert ^2 \nonumber \\&\quad = \sum _{i=1}^M \Bigg ( v_{i,1/2} p_{i,1} + \kappa D_y^- \phi _{i,1} \phi _{i,0} -2\nu v_{i,1/2}D_y^- v_{i,3/2}\Bigg ) \Delta x \nonumber \\&- \nu \sum _{i=1}^{M-1}\frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}D_y^- u_{i+1/2,1} \Delta x -\nu \sum _{i=1}^{M-1} u_{i+1/2,1}D_x^- v_{i+1,1/2}\Delta x \nonumber \\&\qquad + \kappa \sum _{i=1}^M |D_y^- \phi _{i,1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}f^u_{i+1/2,j} \Delta x \Delta y + \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2}f^v_{i,j+1/2} \Delta x \Delta y \nonumber \\&\qquad + \sum _{i=1}^M \sum _{j=-N+1}^{0}(f_2)_{i,j}\phi _{i, j}\Delta x\Delta y \nonumber \\&\quad :=I_1 + I_2 +I_3 +I_4 + I_5. \end{aligned}$$

(4.37)

Now, we estimate the terms $I_i, i=1, \ldots , 5$. For the term $I_1$, by applying the interface conditions (3.12) and (3.13), we obtain

$$\begin{aligned} I_1= & {} \sum _{i=1}^M \Bigg ( v_{i,1/2} (p_{i,1} -\phi _{i,0} )-2\nu v_{i,1/2}D_y^- v_{i,3/2}\Bigg ) \Delta x=0. \end{aligned}$$

(4.38)

To estimate the term $I_2$, we have

$$\begin{aligned} I_2= & {} - \nu \sum _{i=1}^{M-1}\frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\left( D_y^- u_{i+1/2,1}+D_x^-v_{i+1,1/2}\right) \Delta x \nonumber \\&\quad - \nu \sum _{i=1}^{M-1}\frac{u_{i+1/2,1}-u_{i+1/2,0}}{2} D_x^- v_{i+1,1/2}\Delta x \nonumber \\= & {} -\frac{\nu \alpha _1}{\sqrt{{\tilde{\kappa }}}} \sum _{i=1}^{M-1}\Bigg ( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\Bigg )^2 \Delta x - \nu \sum _{i=1}^{M-1}\frac{u_{i+1/2,1}-u_{i+1/2,0}}{2} D_x^- v_{i+1,1/2}\Delta x, \nonumber \\ \end{aligned}$$

(4.39)

where the interface conditions (3.14) are applied. To estimate the second term on the right-hand side of (4.39), we have

$$\begin{aligned} u_{i+1/2,0}=\frac{-(\Delta y -\alpha _2)}{\Delta y + \alpha _2}u_{i+1/2,1}+ \frac{\alpha _2 \Delta y }{\Delta y + \alpha _2} D_x^- v_{i+1,1/2}, \end{aligned}$$

(4.40)

where the constant $\alpha _2$ is equal to $(2\sqrt{{\tilde{\kappa }}})/(\alpha _1 )$. This leads to

$$\begin{aligned} \frac{u_{i+1/2,1}-u_{i+1/2,0}}{2}=\frac{\Delta y}{\Delta y + \alpha _2}u_{i+1/2,1}- \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} D_x^- v_{i+1,1/2}. \end{aligned}$$

(4.41)

Plugging (4.41) into the second term on the right-hand side of (4.39), we obtain

$$\begin{aligned}&- \nu \sum _{i=1}^{M-1}\frac{u_{i+1/2,1}-u_{i+1/2,0}}{2} D_x^- v_{i+1,1/2}\Delta x \nonumber \\&\quad = - \nu \sum _{i=1}^{M-1} \Bigg ( \frac{\Delta y}{\Delta y + \alpha _2}u_{i+1/2,1}- \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} D_x^- v_{i+1,1/2} \Bigg ) D_x^- v_{i+1,1/2}\Delta x \nonumber \\&\quad = - \nu \sum _{i=1}^{M-1}\frac{\Delta y}{\Delta y + \alpha _2}u_{i+1/2,1}D_x^- v_{i+1,1/2}\Delta x + \nu \sum _{i=1}^{M-1} \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} |D_x^- v_{i+1,1/2}|^2 \Delta x \nonumber \\&\quad =J_1 +J_2. \end{aligned}$$

(4.42)

To estimate the term $J_1$, we have

$$\begin{aligned} J_1= & {} -\nu \frac{\Delta y}{\Delta y + \alpha _2} \sum _{i=1}^{M-1} u_{i+1/2,1} \Bigg ( v_{i+1,1/2} - v_{i,1/2} \Bigg )\nonumber \\= & {} -\nu \frac{\Delta y}{\Delta y + \alpha _2} \Bigg ( \sum _{i=2}^{M} u_{i-1/2,1} v_{i,1/2} - \sum _{i=1}^{M-1} u_{i+1/2,1} v_{i,1/2} \Bigg ) \nonumber \\= & {} \nu \frac{\Delta y}{\Delta y + \alpha _2} \sum _{i=1}^{M} D_x^- u_{i+1/2,1} v_{i,1/2} \Delta x \nonumber \\= & {} \nu \frac{\Delta y}{\Delta y + \alpha _2} \sum _{i=1}^{M} D_x^- u_{i+1/2,1} \Bigg (- \sum _{j=1}^N D_y^- v_{i,j+1/2} \Delta y \Bigg ) \Delta x \nonumber \\= & {} (\text {due to Young's inequality}) \nonumber \\\le & {} \nu \frac{\Delta y}{\Delta y + \alpha _2} \sum _{i=1}^{M} \Bigg (\frac{L_y}{4\alpha _2} |D_x^- u_{i+1/2,1}|^2 + \frac{\alpha _2}{L_y} \Bigg (\sum _{j=1}^N D_y^- v_{i,j+1/2}\Bigg )^2 \Bigg ) \Delta x\Delta y \nonumber \\\le & {} \nu \frac{L_y \Delta y}{4\alpha _2 (\Delta y + \alpha _2)} \sum _{i=1}^M |D_x^- u_{i+1/2,1}|^2 \Delta x\Delta y + \nu \frac{\alpha _2}{\Delta y + \alpha _2} \Vert D_y^- v\Vert ^2 \nonumber \\\le & {} \nu \frac{L_y \Delta y}{4\alpha ^2_2 }\Vert D_x^- u\Vert ^2 + \nu \Vert D_y^- v\Vert ^2. \end{aligned}$$

(4.43)

To estimate the term $J_2$, we have

$$\begin{aligned} J_2= & {} \nu \sum _{i=1}^{M-1} \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} |D_x^- v_{i+1,1/2}|^2\Delta x \nonumber \\= & {} \nu \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} \sum _{i=1}^{M-1}\Bigg (\frac{2}{\alpha _2} \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2} -D_y^-u_{i+1/2,1} \Bigg ) ^2 \Delta x \nonumber \\= & {} \nu \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} \sum _{i=1}^{M-1}\Bigg (\frac{4}{\alpha _2^2} \Big (\frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\Big )^2 +|D_y^-u_{i+1/2,1}|^2 \nonumber \\&- \frac{4}{\alpha _2} \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}D_y^-u_{i+1/2,1} \Bigg ) \Delta x \nonumber \\\le & {} \nu \frac{2 \Delta y }{\left( \Delta y + \alpha _2\right) \alpha _2} \left( 1 + \frac{2}{\epsilon }\right) \sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \Delta x \nonumber \\&+ \nu \frac{\alpha _2 }{\Delta y + \alpha _2} \left( 1+\frac{\epsilon }{2}\right) \sum _{i=1}^{M-1} |D_y^-u_{i+1/2,1}|^2 \frac{\Delta x\Delta y}{2}, \end{aligned}$$

(4.44)

where $\epsilon$ is a positive parameter which will be determined later.

Combining (4.39), (4.43) and (4.44), we obtain

$$\begin{aligned} I_2\le & {} -\frac{2\nu }{\alpha _2\left( \Delta y + \alpha _2\right) }\left( \alpha _2 -\frac{2\Delta y}{\epsilon }\right) \sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \Delta x \nonumber \\&+ \nu \frac{\alpha _2 }{\Delta y + \alpha _2} \left( 1+\frac{\epsilon }{2}\right) \sum _{i=1}^{M-1} |D_y^-u_{i+1/2,1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&+ \nu \frac{L_y \Delta y}{4\alpha ^2_2 }\Vert D_x^- u\Vert ^2 + \nu \Vert D_y^- v\Vert ^2. \end{aligned}$$

(4.45)

Now, set $\epsilon = \frac{2\Delta y}{\alpha _2}$, we can infer from (4.45) that

$$\begin{aligned} I_2\le & {} \nu \sum _{i=1}^{M-1} |D_y^-u_{i+1/2,1}|^2 \frac{\Delta x\Delta y}{2} + \nu \frac{L_y \Delta y}{4\alpha ^2_2}\Vert D_x^- u\Vert ^2 + \nu \Vert D_y^- v\Vert ^2. \end{aligned}$$

(4.46)

To estimate the term $I_3$, we have

$$\begin{aligned} I_3= & {} \frac{1}{\kappa } \sum _{i=1}^M |v_{i,1/2}|^2 \frac{\Delta x\Delta y}{2} \le \frac{1}{\kappa } \sum _{i=1}^M \Bigg (\sum _{j=1}^N |D_y^-v_{i,j+1/2}| \Delta y\Bigg )^2 \frac{\Delta x\Delta y}{2} \nonumber \\\le & {} \frac{L_y \Delta y}{2\kappa } \Vert D_y^- v\Vert ^2. \end{aligned}$$

(4.47)

To estimate the term $I_4$, by applying discrete Poincare inequalities and Young’s inequality, we have

$$\begin{aligned} I_4\le & {} \Vert u\Vert \Vert f^u\Vert + \Vert v\Vert \Vert f^v\Vert \nonumber \\\le & {} L_x\Vert D_x^- u\Vert \Vert f^u\Vert + \sqrt{L_y\left( L_y+\frac{\Delta y}{2}\right) }\Vert D_y^-v\Vert \Vert f^v\Vert \nonumber \\\le & {} \frac{\nu }{2}\Vert D_x^-u\Vert ^2 + \frac{\nu }{2}\Vert D_y^-v\Vert ^2 + \frac{L_x^2}{2\nu }\Vert f^u\Vert ^2 + \frac{L_y\left( L_y + \frac{\Delta y}{2}\right) }{2\nu }\Vert f^v\Vert ^2. \end{aligned}$$

(4.48)

To estimate the term $I_5$, by applying Lemma 4.1, we have

$$\begin{aligned} I_5\le & {} \sqrt{2\left( L^2_x+L^2_y\right) } \Vert f_2\Vert \sqrt{\Vert D_x^- \phi \Vert ^2 +\Vert D_y^- \phi \Vert ^2} \nonumber \\\le & {} \frac{\kappa }{2} \left( \Vert D_x^- \phi \Vert ^2 +\Vert D_y^- \phi \Vert ^2\right) + \frac{\left( L^2_x+L^2_y\right) }{\kappa } \Vert f_2\Vert ^2. \end{aligned}$$

(4.49)

Combining the estimates of $I_i, i=1, \ldots , 5$, we can infer from (4.37) that

$$\begin{aligned}&\Bigg (\frac{3}{2}-\frac{L_y\Delta y}{4\alpha ^2_2} \Bigg ) \nu \Vert D_x^- u\Vert ^2 + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \Big (D_y^-u_{i+1/2,j+1} +D_x^- v_{i+1,j+1/2}\Big )^2 \, \Delta x\Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} |D_y^- u_{i+1/2,N+1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \Big (|D_x^- v_{1,j+1/2}|^2 + |D_x^- v_{M+1,j+1/2}|^2 \Big ) \Delta x \Delta y \nonumber \\&\qquad + \Bigg (\frac{\nu }{2}-\frac{L_y \Delta y}{2\kappa }\Bigg ) \Vert D_y^- v\Vert ^2 + \frac{\kappa }{2}\Vert D_x^- \phi \Vert ^2 + \frac{\kappa }{2} \Vert D_y^- \phi \Vert ^2 \nonumber \\&\quad \le \frac{L_x^2}{2\nu }\Vert f^u\Vert ^2 + \frac{L_y\left( L_y+\frac{\Delta y}{2}\right) }{2\nu }\Vert f^v\Vert ^2 +\frac{\left( L^2_x+L^2_y\right) }{\kappa }\Vert f_2\Vert ^2. \end{aligned}$$

(4.50)

By taking $\Delta y$ to satisfy the following conditions

$$\begin{aligned} \frac{3}{2}-\frac{L_y\Delta y}{4\alpha ^2_2} \ge 1, \text { and } \frac{\nu }{2}-\frac{L_y \Delta y}{2\kappa } \ge \frac{\nu }{4}, \end{aligned}$$

(4.51)

which implies

$$\begin{aligned} \Delta y \le min\left\{ \frac{\nu \kappa }{2L_y}, \frac{2\alpha ^2_2}{L_y}\right\} , \end{aligned}$$

(4.52)

the proof of Theorem 4.1 is complete by using Lemma 4.1. $\square$

To show the boundedness of the pressure p and $\phi$, we need the following lemmas:

Lemma 4.5

Let the mesh widths satisfy (4.35) and $\Delta y = \Delta x$, we have

$$\begin{aligned}&\sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \, \Delta x \le K_1= \frac{\alpha _2}{\nu }C_f + \left( \frac{8\alpha _2L_x^2}{L_y }+ 2\right) \frac{C_f}{\nu }. \end{aligned}$$

Proof

To begin with, we rewrite the summation for $D_x^-v$, apply the triangle inequality and have

$$\begin{aligned} \sum _{i=1}^{M-1}(D_x^- v_{i+1,1/2})^2 \, \Delta x \Delta y= & {} \sum _{i=1}^{M-1} \Bigg ( \sum _{j=1}^N \Bigg ( -D_y^- v_{i+1,j+1/2} + D_y^- v_{i,j+1/2}\Bigg ) \frac{\Delta y}{\Delta x} \Bigg )^2 \Delta x \Delta y \nonumber \\\le & {} \frac{4L_y\Delta y}{(\Delta x)^2}\Vert D_y^- v\Vert ^2. \quad ( N \Delta y = L_y) \end{aligned}$$

(4.53)

Then, we use (4.41) and have

$$\begin{aligned}&\Delta y \sum _{i=1}^{M-1}(D_y^- u_{i+1/2,1})^2 \, \Delta x \Delta y \nonumber \\&\quad \le \frac{8\Delta y}{(\Delta y + \alpha _2)^2}\sum _{i=1}^{M-1} u_{i+1/2,1}^2 \Delta x \Delta y + \frac{2\alpha _2^2\Delta y }{(\Delta y + \alpha _2)^2}\sum _{i=1}^{M-1}(D_x^- v_{i+1,1/2})^2 \, \Delta x\Delta y. \nonumber \\&\quad \le \frac{8\Delta y}{\alpha _2^2}\Vert u\Vert ^2 + 8L_y\Vert D_y^- v\Vert ^2, \end{aligned}$$

(4.54)

where the condition $\Delta y = \Delta x$ and the inequality (4.53) are applied.

To show the desired inequality, we rewrite (4.37) in Theorem 4.1 as follows:

$$\begin{aligned}&2\nu \Vert D_x^- u\Vert ^2 + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \left( D_y^-u_{i+1/2,j+1} +D_x^- v_{i+1,j+1/2}\right) ^2 \, \Delta x\Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} |D_y^- u_{i+1/2,N+1}|^2 \frac{\Delta x\Delta y}{2} + \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- v_{1,j+1/2}|^2 + |D_x^- v_{M+1,j+1/2}|^2 \right) \Delta x \Delta y \nonumber \\&\qquad + 2\nu \Vert D_y^- v\Vert ^2 + \kappa \Vert D_x^- \phi \Vert ^2 + \kappa \Vert D_y^- \phi \Vert ^2 \nonumber \\&\quad = \sum _{i=1}^M \Bigg ( v_{i,1/2} p_{i,1} + \kappa D_y^- \phi _{i,1} \phi _{i,0} -2\nu v_{i,1/2}D_y^- v_{i,3/2}\Bigg ) \Delta x \nonumber \\&\qquad - \nu \sum _{i=1}^{M-1}\frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}D_y^- u_{i+1/2,1} \Delta x -\nu \sum _{i=1}^{M-1} u_{i+1/2,1}D_x^- v_{i+1,1/2}\Delta x \nonumber \\&\qquad -\frac{\nu }{2} \sum _{i=1}^{M-1} |D_y^- u_{i+1/2,1}|^2 \Delta x\Delta y \nonumber \\&\qquad + \kappa \sum _{i=1}^M |D_y^- \phi _{i,1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \sum _{i=1}^{M-1}\sum _{j=1}^{N} u_{i+1/2,j}f^u_{i+1/2,j} \Delta x \Delta y + \sum _{i=1}^{M}\sum _{j=1}^{N-1} v_{i,j+1/2}f^v_{i,j+1/2} \Delta x \Delta y \nonumber \\&\qquad + \sum _{i=1}^M \sum _{j=-N+1}^{0}(f_2)_{i,j}\phi _{i, j}\Delta x\Delta y \nonumber \\&\quad :=I_1 + I'_2 +I_3 +I_4 + I_5. \end{aligned}$$

(4.55)

The estimates for the terms $I_i, \, i=1, 3, 4,5$ remain the same as in (4.38), (4.47), (4.48) and (4.49). To estimate the term $I_2'$, we have

$$\begin{aligned} I'_2= & {} -\frac{2\nu }{\alpha _2}\sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \, \Delta x -\frac{\nu }{2} \sum _{i=1}^{M-1} D_y^- u_{i+1/2,1}D_x^- v_{i+1,1/2} \, \Delta x \Delta y \nonumber \\&-\frac{\nu }{2} \sum _{i=1}^{M-1} |D_y^- u_{i+1/2,1}|^2 \Delta x\Delta y \nonumber \\= & {} -\frac{2\nu }{\alpha _2}\sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \, \Delta x \nonumber \\&- \frac{\nu }{\alpha _2}\sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) D_y^- u_{i+1/2,1} \, \Delta x \Delta y \nonumber \\\le & {} -\frac{\nu }{\alpha _2}\sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \, \Delta x + \frac{\nu \Delta y}{4\alpha _2}\sum _{i=1}^{M-1} \left( D_y^- u_{i+1/2,1}\right) ^2 \, \Delta x \Delta y,\nonumber \\ \end{aligned}$$

(4.56)

where Cauchy–Schwarz and Young’s inequalities are applied from the second line to the third line.

Combining the estimates (4.38), (4.47), (4.48), (4.49) and (4.56) and applying (4.35), we obtain

$$\begin{aligned}&\frac{\nu }{\alpha _2}\sum _{i=1}^{M-1} \left( \frac{u_{i+1/2,1}+u_{i+1/2,0}}{2}\right) ^2 \, \Delta x \le C_f + \frac{\nu \Delta y}{4\alpha _2}\sum _{i=1}^{M-1} \left( D_y^- u_{i+1/2,1}\right) ^2 \, \Delta x \Delta y. \end{aligned}$$

(4.57)

The desired inequality is obtained due to (4.57), (4.54), (4.35) and Theorem 4.1. $\square$

In addition to Lemma 4.5, we need the following lemma extended from the discrete divergence problem for finite difference scheme for Stokes equations to the present Stokes/Darcy coupling equations on a staggered grid.

Lemma 4.6

For any given $p_{i,j}, \, 1\le i \le M, 1\le j \le N$ and $\phi _{i,j}, \, 1\le i \le M, -N+1 \le j \le 0$ satisfying (3.15), there exist two vectors ${{\tilde{u}}}_{i+1/2,j}, 0\le i \le M, 0\le j \le N+1$ and ${{\tilde{v}}}_{i,j+1/2}, 0 \le i \le M+1, 0 \le j \le N$ satisfying the following properties:

$$\begin{aligned} {{\tilde{u}}}_{1/2,j}= & {} {{\tilde{u}}}_{M+1/2,j} = 0, \, 0 \le j \le N+1, \end{aligned}$$

(4.58)

$$\begin{aligned} {{\tilde{u}}}_{i+1/2,N+1}= & {} -{{\tilde{u}}}_{i+1/2,N}, \, 0 \le i \le M, \end{aligned}$$

(4.59)

$$\begin{aligned} {{\tilde{v}}}_{i,N+1/2}= & {} 0, \, 0 \le i \le M+1, \end{aligned}$$

(4.60)

$$\begin{aligned} {{\tilde{v}}}_{0,j+1/2}= & {} -{{\tilde{v}}}_{1,j+1/2}, \, {{\tilde{v}}}_{M+1,j+1/2}= -{{\tilde{v}}}_{M,j+1/2}, \, 0 \le j \le N, \qquad \qquad \end{aligned}$$

(4.61)

$$\begin{aligned} D_x^- {{\tilde{u}}}_{i+1/2,j} + D_y^- {{\tilde{v}}}_{i, j+1/2}= & {} p_{i,j}, \, 1\le i\le M, 1\le j \le N, \end{aligned}$$

(4.62)

and there exists a vector ${{\tilde{\phi }}}_{i,j}, \, 0 \le i \le M+1, \, -N\le j \le 1$ satisfying

$$\begin{aligned} D_x^- {{\tilde{\phi }}}_{1,j}= & {} D_x^- {{\tilde{\phi }}}_{M+1,j}=0 , \, -N+1\le j \le 0, \end{aligned}$$

(4.63)

$$\begin{aligned} D_y^- {{\tilde{\phi }}}_{i,-N+1}= & {} 0, -\kappa D_y^- {{\tilde{\phi }}}_{i,1}={{\tilde{v}}}_{i,1/2} , \, 1\le i \le M, \end{aligned}$$

(4.64)

$$\begin{aligned} -\kappa D_x^+D_x^- {{\tilde{\phi }}}_{i,j} -\kappa D_y^+ D_y^- {{\tilde{\phi }}}_{i,j}= & {} \phi _{i,j}, 1\le i\le M, -N+1\le j \le 0. \end{aligned}$$

(4.65)

Moreover, we have

$$\begin{aligned}&\Vert D_x^- {{\tilde{u}}}\Vert ^2 + \Vert D_y^- {{\tilde{u}}}\Vert ^2+ \Vert D_x^- {{\tilde{v}}}\Vert ^2 + \Vert D_y^- {{\tilde{v}}}\Vert ^2 \nonumber \\&\qquad + \Vert {{\tilde{u}}}\Vert ^2 + \Vert {{\tilde{v}}}\Vert ^2 +\Vert D_x^- {{\tilde{\phi }}}\Vert ^2 + \Vert D_y^- {{\tilde{\phi }}}\Vert ^2 +\sum _{i=1}^{M-1} \left( \frac{{{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2}\right) ^2\Delta x \nonumber \\&\quad \le {{\tilde{C}}}_d \left( \Vert p\Vert ^2 + \Vert \phi \Vert ^2\right) , \end{aligned}$$

(4.66)

where ${{\tilde{C}}}_d=(1+\frac{L_y}{2}+ (1+\frac{1}{\kappa ^2})(L_x^2+L_y^2))C_d$ is a constant independent of the mesh widths $\Delta x$ and $\Delta y$ and $C_d$ is a constant defined in Lemma 4.7.

To prove Lemma 4.6, we need the following lemma related to the finite difference scheme for the Stokes problem on the whole region $\Omega$ with homogenous Dirichlet boundary conditions:

Lemma 4.7

For any given $p_{i,j}, \, 1\le i \le M, 1\le j \le N$ and $\phi _{i,j}, \, 1\le i \le M, -N+1 \le j \le 0$ satisfying (3.15), there exist a positive constant $C_d$ independent of the mesh widths $\Delta x$ and $\Delta y$ and two vectors $U_{i+1/2,j}, \, 0 \le i \le M, -N \le j \le N+1$ and $V_{i,j+1/2}, \, 0 \le i \le M+1, -N+1 \le j \le N$ satisfying

$$\begin{aligned}&U_{1/2,j} = U_{M+1/2,j} = 0, \, -N \le j \le N+1, \end{aligned}$$

(4.67)

$$\begin{aligned}&U_{i+1/2,N+1} = -U_{i+1/2,N}, U_{i+1/2,-N} = -U_{i+1/2,-N+1}, 0 \le i \le M, \end{aligned}$$

(4.68)

$$\begin{aligned}&V_{i,N+1/2}=V_{i, -N+1/2} = 0, \, 0 \le i \le M+1, \end{aligned}$$

(4.69)

$$\begin{aligned}&V_{0, j+1/2}=-V_{1, j+1/2}, V_{M+1, j+1/2}=-V_{M, j+1/2}, -N+1 \le j \le N, \end{aligned}$$

(4.70)

$$\begin{aligned}&D_x^- U_{i+1/2,j} + D_y^- V_{i, j+1/2} = p_{i,j}, \, 1\le i\le M, 1\le j \le N, \end{aligned}$$

(4.71)

$$\begin{aligned}&D_x^- U_{i+1/2,j} + D_y^- V_{i, j+1/2} = \phi _{i,j}, \, 1\le i\le M, -N+1\le j \le 0, \end{aligned}$$

(4.72)

$$\begin{aligned}&\Vert D_x^- U\Vert _{\Omega }^2 + \Vert D_y^- U\Vert _{\Omega }^2 + \Vert D_x^- V\Vert _{\Omega }^2 + \Vert D_y^- V\Vert _{\Omega }^2 \le C_d (\Vert p\Vert ^2 +\Vert \phi \Vert ^2), \end{aligned}$$

(4.73)

where $\Vert \cdot \Vert _{\Omega }$ is the corresponding discrete $L^2$ norm in the region $\Omega$ and $C_d$ depends on the size of the domain $\Omega$.

The proof of Lemma 4.7 can be obtained by following the same processes in [29]. Thus, the proof is omitted.

Now the proof of Lemma 4.6 is presented as follows:

Proof of Lemma 4.6

Assume that two vectors $U_{i+1/2,j}, \, 0 \le i \le M, -N \le j \le N+1$ and $V_{i,j+1/2}, \, 0 \le i \le M+1, -N+1 \le j \le N$ are defined in Lemma 4.7 satisfying (4.67)–(4.73).

For the Stokes region, the velocity field $({\tilde{u}}, {\tilde{v}})$ is defined as follows:

$$\begin{aligned} {{\tilde{u}}}_{i+1/2,j}= & {} U_{i+1/2,j}, \, 0\le i \le M, 0 \le j \le N+1, \\ {{\tilde{v}}}_{i,j+1/2}= & {} V_{i,j+1/2}, \, 0\le i \le M+1, 0 \le j \le N. \end{aligned}$$

It is easy to check that (4.58)–(4.62) are obtained from the definition of $({{\tilde{u}}}, {{\tilde{v}}})$ and Lemma 4.7.

For the Darcy region, thanks to (4.72), the existence of a vector ${\tilde{\phi }}$ satisfying (4.63)–(4.65) is equivalent to show that the vector ${\tilde{\phi }}$ satisfies

$$\begin{aligned} D_x^- {{\tilde{\phi }}}_{1,j}= & {} D_x^- {{\tilde{\phi }}}_{M+1,j}=0 , \, -N+1\le j \le 0, \end{aligned}$$

(4.74)

$$\begin{aligned} D_y^- {{\tilde{\phi }}}_{i,-N+1}= & {} 0, -\kappa D_y^- {{\tilde{\phi }}}_{i,1}={{\tilde{v}}}_{i,1/2} , \, 1\le i \le M, \end{aligned}$$

(4.75)

$$\begin{aligned} U_{i+1/2,j}= & {} -\kappa D_x^- {{\tilde{\phi }}}_{i+1,j}, \, V_{i,j+1/2}=-\kappa D_y^- {{\tilde{\phi }}}_{i,j+1}, \nonumber \\ 1\le & {} i\le M, -N+1\le j \le 0. \end{aligned}$$

(4.76)

From (4.74) and (4.76), ${{\tilde{\phi }}}$ is determined by the choice of ${{\tilde{\phi }}}_{1,j}, j=-N+1, \ldots , 0$. From (4.75) and (4.76), ${{\tilde{\phi }}}$ is determined by the choice of ${{\tilde{\phi }}}_{i,0}, i=1, \ldots , M$. Therefore, this vector ${{\tilde{\phi }}}$ exists up to a constant. Note that, the velocity field in Darcy region are defined by $({U}_{i+1/2,j}, {V}_{i, j+1/2}) = ( - \kappa D_x^- \phi _{i+1,j}, - \kappa D_y^- \phi _{i, j+1})$.

To show (4.66), we use the fact

$$\begin{aligned}&\sum _{i=1}^{M-1} \left( \frac{{{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2}\right) ^2\Delta x \nonumber \\&\quad =\sum _{i=1}^{M-1} \Bigg (-\sum _{j=2}^{N+1} D_y^- {{\tilde{u}}}_{i+1/2,j} + \sum _{j=-N+1}^0 D_y^- U_{i+1/2,j}\Bigg )^2 \frac{(\Delta y)^2 \Delta x}{4} \nonumber \\&\quad \le \frac{L_y}{2} \Vert D_y^- U\Vert _{\Omega }^2. \end{aligned}$$

(4.77)

By applying (4.77)and discrete Poincare inequality, we have

$$\begin{aligned}&\Vert D_x^- {{\tilde{u}}}\Vert ^2 + \Vert D_y^- {{\tilde{u}}}\Vert ^2+ \Vert D_x^- {{\tilde{v}}}\Vert ^2 + \Vert D_y^- {{\tilde{v}}}\Vert ^2 \nonumber \\&\qquad + \Vert {{\tilde{u}}}\Vert ^2 + \Vert {{\tilde{v}}}\Vert ^2 +\Vert D_x^- { {\tilde{\phi }}} \Vert ^2 + \Vert D_y^-{{\tilde{\phi }}}\Vert ^2 +\sum _{i=1}^{M-1} \left( \frac{{{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2}\right) ^2\Delta x \nonumber \\&\quad \le \Vert D_x^- U\Vert _{\Omega }^2 + \left( 1+\frac{L_y}{2}\right) \Vert D_y^- U\Vert _{\Omega }^2 + \Vert D_x^- V\Vert _{\Omega }^2 + \Vert D_y^- V\Vert _{\Omega }^2 \nonumber \\&\qquad + \left( 1+\frac{1}{\kappa ^2}\right) \left( \Vert U\Vert _{\Omega }^2 + \Vert V\Vert _{\Omega }^2\right) \nonumber \\&\quad \le \left( 1+\frac{L_y}{2}+ \left( 1+\frac{1}{\kappa ^2}\right) \left( L_x^2+L_y^2\right) \right) \Bigg ( \Vert D_x^- U\Vert _{\Omega }^2 \nonumber \\&\qquad + \Vert D_y^-U\Vert _{\Omega }^2+ \Vert D_x^- V\Vert _{\Omega }^2 + \Vert D_y^- V\Vert _{\Omega }^2 \Big ). \end{aligned}$$

(4.78)

Then, (4.66) is derived by using Lemma 4.7 and (4.78). $\square$

Now, we are ready to state and show the boundedness of the pressure p and $\phi$ as follows:

Theorem 4.2

Let the mesh widths satisfy (4.35) and $\Delta y = \Delta x$, we have

$$\begin{aligned}&\Vert p\Vert ^2 + \Vert \phi \Vert ^2 \\&\quad \le C_p=\max \left\{ 2\nu , \kappa , 1, \frac{2\nu }{\alpha _2} \right\} {{\tilde{C}}}_d \Bigg ( 16C_f + \frac{2\nu }{\alpha _2}K_1 + \frac{\nu \alpha _2^2}{L_y}K_1+\Vert f^u\Vert ^2 + \Vert f^v\Vert ^2 \Bigg ). \end{aligned}$$

Proof

By multiplying (3.17), (3.18), (4.65), (4.19) and (4.20) by ${{\tilde{u}}}_{i+1/2,j} \Delta x \Delta y$ , ${{\tilde{v}}}_{i,j+1/2}\Delta x \Delta y$, ${ \phi }_{i,j} \Delta x \Delta y$, ${{\tilde{u}}}_{i+1/2,j}\Delta x\Delta y$ and ${{\tilde{v}}}_{i,j+1/2}\Delta x \Delta y$ respectively, summing for all i and j and adding the resulting equations, we obtain

$$\begin{aligned}&\Vert \phi \Vert ^2 + \Vert p\Vert ^2 = 2\nu \sum _{i=1}^M \sum _{j=1}^N D_x^- {{\tilde{u}}}_{i+1/2,j} D_x^- u_{i+1/2,j} \Delta x \Delta y \nonumber \\&\quad + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \Bigg ( D_y^- {{\tilde{u}}}_{i+1/2,j+1} {+} D_x^- {{\tilde{v}}}_{i+1,j+1/2}\Bigg ) \Bigg ( D_y^- u_{i+1/2,j+1} {+} D_x^-v_{i+1,j+1/2}\Bigg ) \Delta x \Delta y \nonumber \\&\quad + \frac{\nu }{2}\sum _{i=1}^{M-1} \Bigg ( D_y^- {{\tilde{u}}}_{i+1/2,N+1} D_y^- u_{i+1/2,N+1}+D_y^- {{\tilde{u}}}_{i+1/2,1} D_y^- u_{i+1/2,1}\Bigg ) \Delta x\Delta y \nonumber \\&\quad + \nu \sum _{i=1}^{M-1} \frac{{{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2} D_y^- u_{i+1/2,1}\Delta x + \nu \sum _{i=1}^{M-1} {{\tilde{u}}}_{i+1/2,1}D_x^- v_{i+1,1/2}\Delta x \nonumber \\&\quad +\frac{\nu }{2} \sum _{j=1}^{N-1} \Bigg ( D_x^- {{\tilde{v}}}_{M+1, j+1/2}D_x^- v_{M+1, j+1/2}+D_x^- {{\tilde{v}}}_{1, j+1/2}D_x^- v_{1, j+1/2} \Bigg ) \Delta x\Delta y \nonumber \\&\quad + 2\nu \sum _{i=1}^M \sum _{j=1}^{N} D_y^- {{\tilde{v}}}_{i,j+1/2} D_y^- v_{i,j+1/2} \Delta x \Delta y + \sum _{i=1}^M {{\tilde{v}}}_{i,1/2}\Bigg ( \phi _{i,0}-p_{i,1}+ 2\nu D_y^- v_{i,3/2}\Bigg ) \Delta x \nonumber \\&\quad + \kappa \sum _{i=2}^{M}\sum _{j=-N+1}^{0} D_x^-\phi _{i,j} D_x^- {{\tilde{\phi }}}_{i,j} \Delta x \Delta y +\kappa \sum _{i=1}^{M}\sum _{j=-N+2}^{0} D_y^-\phi _{i,j} D_y^- {{\tilde{\phi }}}_{i,j} \Delta x \Delta y\nonumber \\&\quad -\sum _{i=1}^{M-1}\sum _{j=1}^N {{\tilde{u}}}_{i+1/2,j} f^u_{i+1/2,j}\Delta x\Delta y - \sum _{i=1}^M\sum _{j=1}^{N-1} {{\tilde{v}}}_{i,j+1/2}f^v_{i,j+1/2}\Delta x \Delta y. \end{aligned}$$

(4.79)

By using the fact

$$\begin{aligned}&\nu \sum _{i=1}^{M-1} \frac{ {{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2} D_y^- u_{i+1/2,1}\Delta x + \nu \sum _{i=1}^{M-1} {{\tilde{u}}}_{i+1/2,1}D_x^- v_{i+1,1/2}\Delta x \nonumber \\&\qquad + \frac{\nu }{2}\sum _{i=1}^{M-1} D_y^- {{\tilde{u}}}_{i+1/2,1} D_y^- u_{i+1/2,1} \, \Delta x\Delta y \nonumber \\&\quad = \frac{2\nu }{\alpha _2} \sum _{i=1}^{M-1} \left( \frac{ {{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2}\right) \left( \frac{u_{i+1/2,1} + u_{i+1/2,0}}{2}\right) \Delta x \nonumber \\&\qquad + \frac{\nu }{2} \sum _{i=1}^{M-1} D_y^- {{\tilde{u}}}_{i+1/2,1}\left( D_x^- v_{i+1,1/2} + D_y^- u_{i+1/2,1}\right) \, \Delta x\Delta y , \end{aligned}$$

and applying Cauchy–Schwarz inequality, Theorem 4.1, Lemmas 4.1 and 4.5, it is inferred from (4.79) that

$$\begin{aligned}&\Vert p\Vert ^2 + \Vert \phi \Vert ^2 \le \frac{\varepsilon _1}{2}\Bigg ( 2\nu \Big ( \Vert D_x^- {{\tilde{u}}}\Vert ^2 + \Vert D_y^- {{\tilde{u}}}\Vert ^2 + \Vert D_x^- {{\tilde{v}}}\Vert ^2 + \Vert D_y^- {{\tilde{v}}}\Vert ^2 \Big ) \nonumber \\&\quad + \Vert {{\tilde{u}}}\Vert ^2 + \Vert {{\tilde{v}}}\Vert ^2 + \kappa \Vert D_x^-{{\tilde{\phi }}}\Vert ^2 + \kappa \Vert D_y^-{{\tilde{\phi }}}\Vert ^2 \nonumber \\&\quad + \frac{2\nu }{\alpha _2} \sum _{i=1}^{M-1} \Big (\frac{{{\tilde{u}}}_{i+1/2,1} + {{\tilde{u}}}_{i+1/2,0}}{2}\Big )^2\Delta x \Bigg ) + \frac{1}{2\varepsilon _1} \Bigg ( 16C_f + \frac{2\nu }{\alpha _2}K_1 + \frac{\nu \alpha _2^2}{L_y}K_1 \nonumber \\&\quad + \Vert f^u\Vert ^2 + \Vert f^v\Vert ^2 \Bigg ), \end{aligned}$$

(4.80)

where $\varepsilon _1$ is a positive parameter which will be determined later.

Then, by applying Lemma 4.6, we can deduce from (4.80) that

$$\begin{aligned}&\Vert p\Vert ^2 + \Vert \phi \Vert ^2 \le \frac{\varepsilon _1}{2}\max \left\{ 2\nu , \kappa , 1, \frac{2\nu }{\alpha _2}\right\} {{\tilde{C}}}_d (\Vert p\Vert ^2 + \Vert \phi \Vert ^2) \nonumber \\&\quad + \frac{1}{2\varepsilon _1} \Bigg ( 16C_f + \frac{2\nu }{\alpha _2}K_1 + \frac{\nu \alpha _2^2}{L_y}K_1+\Vert f^u\Vert ^2 + \Vert f^v\Vert ^2 \Bigg ). \end{aligned}$$

(4.81)

By choosing $\varepsilon _1$ to satisfy

$$\begin{aligned} \varepsilon _1= \frac{1}{\max \left\{ 2\nu , \kappa , 1, \frac{2\nu }{\alpha _2}\right\} {{\tilde{C}}}_d}, \end{aligned}$$

the proof of Theorem 4.2 is complete. $\square$

5 Error Analysis

In this section, the error estimates for the scheme (3.1)–(3.14) will be derived. We begin with introducing the following notations for the errors:

$$\begin{aligned} e^u_{i+1/2,j}= & {} u(x_{i+1/2},y_j) -u_{i+1/2,j}, \\ e^v_{i,j+1/2}= & {} v(x_i, y_{j+1/2}) -v_{i,j+1/2}, \\ e^p_{i,j}= & {} p(x_i,y_j)-p_{i,j}, \quad e^{\phi }_{i,j}=\phi (x_i,y_j)-\phi _{i,j}. \end{aligned}$$

Thus, we can derive the following equations for the errors:

$$\begin{aligned}&-\nu D_x^+ D_x^- e^u_{i+1/2,j}-\nu D_y^+ D_y^- e^u_{i+1/2,j} + D_x^- e^p_{i+1,j} = R^u_{i+1/2,j}, \nonumber \\&\quad 1\le i \le M-1, \, 1\le j \le N, \end{aligned}$$

(5.1)

$$\begin{aligned}&-\nu D_x^+ D_x^- e^v_{i,j+1/2}-\nu D_y^+ D_y^- e^v_{i,j+1/2} + D_y^- e^p_{i,j+1} = R^v_{i,j+1/2}, \nonumber \\&\quad 1\le i \le M, \, 1\le j \le N-1, \end{aligned}$$

(5.2)

$$\begin{aligned}&D_x^- e^u_{i+1/2,j} + D_y^- e^v_{i,j+1/2} = R^d_{i,j}, 1\le i \le M, 1\le j\le N, \end{aligned}$$

(5.3)

$$\begin{aligned}&\quad -\kappa D_x^+D_x^- e^{\phi }_{i,j} -\kappa D_y^+ D_y^- e^{\phi }_{i,j} = R^{\phi }_{i,j}, 1\le i \le M, -N+1\le j\le 0, \end{aligned}$$

(5.4)

where the terms $R^u_{i+1/2,j}$, $R^v_{i,j+1/2}$, $R^d_{i,j}$ and $R^{\phi }_{i,j}$ are defined as

$$\begin{aligned} R^u_{i+1/2,j}= & {} -\nu D_x^+ D_x^- u(x_{i+1/2},y_j) -\nu D_y^+ D_y^- u(x_{i+1/2},y_j) + D_x^- p(x_{i+1},y_j) \nonumber \\&-f^u_{i+1/2,j}, 1\le i \le M-1, \, 1\le j \le N, \end{aligned}$$

(5.5)

$$\begin{aligned} R^v_{i,j+1/2}= & {} -\nu D_x^+ D_x^- v(x_i,y_{j+1/2}) -\nu D_y^+ D_y^- v(x_i,y_{j+1/2}) + D_y^- p(x_i,y_{j+1}) \nonumber \\&-f^v_{i,j+1/2}, 1\le i \le M, \, 1\le j \le N-1, \end{aligned}$$

(5.6)

$$\begin{aligned} R^d_{i,j}= & {} D_x^- u(x_{i+1/2},y_j) + D_y^- v(x_{i},y_{j+1/2}), 1\le i \le M, 1\le j\le N, \end{aligned}$$

(5.7)

$$\begin{aligned} R^{\phi }_{i,j}= & {} -\kappa D_x^+ D_x^- \phi (x_i,y_j) -\kappa D_y^+D_y^- \phi (x_i,y_j) -(f_2)_{i,j}, \nonumber \\ 1\le & {} i \le M, -N+1\le j\le 0. \end{aligned}$$

(5.8)

For boundary conditions, we have

$$\begin{aligned}&e^u_{1/2,j} = e^u_{M+1/2,j} = 0, \, 1\le j\le N; \, e^v_{i,N+1/2} = 0, \, 1\le i \le M. \end{aligned}$$

(5.9)

As for the extrapolation of the ghost points on the boundary $\Gamma _f \cup \Gamma _p$, we define

$$\begin{aligned} u(x_{i+1/2},y_{N+1})= & {} -u(x_{i+1/2},y_N) , \, 0\le i \le M, \\ v(x_0,y_{j+1/2})= & {} -v(x_1,y_{j+1/2}), \, v(x_{M+1},y_{j+1/2}) =-v(x_M,y_{j+1/2}), \, 0 \le j \le N, \\ \phi (x_0,y_j)= & {} \phi (x_1,y_j), \phi (x_{M+1}, y_j) = \phi (x_M, y_j),\, -N+1 \le j \le 0, \\ \phi (x_i, y_{-N})= & {} \phi (x_i, y_{-N+1}), \, \phi (x_i, y_1)= \phi (x_i, y_0)+\Delta y \frac{\partial \phi }{\partial y}(x_i, y_{1/2}), \\ 1\le & {} i \le M, \end{aligned}$$

which imply

$$\begin{aligned} e^u_{i+1/2,N+1}= & {} -e^u_{i+1/2,N} , \, 0 \le i \le M, \end{aligned}$$

(5.10)

$$\begin{aligned} e^v_{0,j+1/2}= & {} -e^v_{1,j+1/2}, \, e^v_{M+1,j1/2} =-e^v_{M,j+1/2}, \, 0 \le j \le N, \end{aligned}$$

(5.11)

$$\begin{aligned} e^{\phi }_{0,j}= & {} e^{\phi }_{1,j}, \, e^{\phi }_{M+1,j}= e^{\phi }_{M,j}, \, -N+1 \le j \le 0, \end{aligned}$$

(5.12)

$$\begin{aligned} e^{\phi }_{i,-N}= & {} e^{\phi }_{i,-N+1}, \, 1 \le i \le M. \end{aligned}$$

(5.13)

Regarding the interface conditions on $\Gamma$, we have

$$\begin{aligned} e^v_{i,1/2}= & {} -\kappa D_y^- e^{\phi }_{i,1}, \, 1 \le i \le M, \end{aligned}$$

(5.14)

$$\begin{aligned} e^p_{i,1}- e^{\phi }_{i,0}= & {} 2 \nu D_y^- e^v_{i, 3/2} +(R^p_{\Gamma })_{i,1/2}, \, 1 \le i \le M, \end{aligned}$$

(5.15)

$$\begin{aligned} \frac{ e^u_{i+1/2,1} + e^u_{i+1/2,0}}{2}= & {} \frac{\sqrt{{\tilde{k}}}}{\alpha _1} \Bigg ( D_y^- e^u_{i+1/2,1} + D_x^- e^v_{i+1,1/2} \Bigg ) + (R^u_{\Gamma })_{i+1/2,1/2}, \nonumber \\ 1\le & {} i \le M-1. \end{aligned}$$

(5.16)

where $(R^p_{\Gamma })_{i,1/2}$ and $(R^u_{\Gamma })_{i+1/2,1/2}$ are defined as

$$\begin{aligned} (R^p_{\Gamma })_{i,1/2}= & {} p(x_i,y_1)-\phi (x_i,y_0)-2 \nu D_y^- v(x_i, y_{3/2}), \, 1 \le i \le M, \end{aligned}$$

(5.17)

$$\begin{aligned} (R^u_{\Gamma })_{i+1/2,1/2}= & {} \frac{u(x_{i+1/2},y_1) +u(x_{i+1/2},y_0)}{2} \nonumber \\&- \frac{\sqrt{{\tilde{k}}}}{\alpha _1} \Bigg ( D_y^- u(x_{i+1/2},y_1) + D_x^- v(x_{i+1},y_{1/2}) \Bigg ), \nonumber \\ 1\le & {} i \le M-1, \end{aligned}$$

(5.18)

and due to that $e^u_{i+1/2,0}$ is evaluated at the ghost point, it is defined as follows

$$\begin{aligned} e^u_{i+1/2,0}= & {} u(x_{i+1/2}, y_0)- u_{i+1/2,0}, \end{aligned}$$

(5.19)

$$\begin{aligned} u(x_{i+1/2}, y_0)= & {} \frac{-(\Delta y -\alpha _2)}{\Delta y + \alpha _2}u(x_{i+1/2}, y_1) + \frac{\alpha _2 \Delta y}{\Delta y + \alpha _2} D_x^- v(x_{i+1},y_{1/2}). \end{aligned}$$

(5.20)

About the condition of the uniqueness, we have

$$\begin{aligned} \sum _{i=1}^M \sum _{j=1}^N e^p_{i,j}\Delta x\Delta y+ \sum _{i=1}^M \sum _{j=-N+1}^0 e^{\phi }_{i,j}\Delta x\Delta y =R^p, \end{aligned}$$

(5.21)

where

$$\begin{aligned} R^p =\sum _{i=1}^M \sum _{j=1}^N p(x_i,y_j)\Delta x\Delta y+\sum _{i=1}^M \sum _{j=-N+1}^0 \phi (x_i,y_j)\Delta x\Delta y. \end{aligned}$$

(5.22)

Notice that the definitions of the discrete norms of the errors $e^u, \, e^v, \, e^p$ and $e^\phi$ are the same as $u, \, v, \, p$ and $\phi$ respectively. Before establishing the error estimates, the following lemmas are needed in the sequel.

Lemma 5.1

$$\begin{aligned} \Vert e^u\Vert ^2\le & {} L_x^2 \Vert D_x^- e^u\Vert ^2, \end{aligned}$$

(5.23)

$$\begin{aligned} \Vert e^v\Vert ^2\le & {} \left( L_y + \frac{\Delta y}{2}\right) L_y \Vert D_y^- e^v\Vert ^2. \end{aligned}$$

(5.24)

The proof of Lemma 5.1 is similar to the proof in Lemma 4.1. Thus, the proof is omitted.

Lemma 5.2

$$\begin{aligned}&-\nu D_x^+ D_x^- e^u_{i+1/2,j} -\nu D_y^+ D_y^- e^v_{i,j+1/2} = -\nu D_x^+ R^d_{i,j}, \nonumber \\&\quad 1\le i \le M-1, \, 1\le j \le N, \end{aligned}$$

(5.25)

$$\begin{aligned}&-\nu D_x^+ D_x^- e^u_{i+1/2,j}-\nu D_y^+ D_y^- e^v_{i,j+1/2} = -\nu D_y^- R^d_{i,j+1}, \nonumber \\&\quad 1\le i \le M, \, 1\le j \le N-1. \end{aligned}$$

(5.26)

The proof of Lemma 5.2 is established by directly applying (5.3).

Lemma 5.3

$$\begin{aligned}&\sum _{i=1}^{M-1}\sum _{j=1}^{N} e^u_{i+1/2,j}D_x^-e^p_{i+1,j} \Delta x \Delta y + \sum _{i=1}^{M}\sum _{j=1}^{N-1} e^v_{i,j+1/2}D_y^- e^p_{i,j+1} \Delta x \Delta y\nonumber \\&\quad = -\sum _{i=1}^M e^v_{i,1/2} e^p_{i,1}\Delta x -\sum _{i=1}^M \sum _{j=1}^N R^d_{i,j} e^p_{i,j}\Delta x \Delta y, \end{aligned}$$

(5.27)

$$\begin{aligned}&\qquad -\kappa \sum _{i=1}^{M}\sum _{j=-N+1}^{0} \Bigg ( D_x^+ D_x^- e^{\phi }_{i,j} + D_y^+ D_y^- e^{\phi }_{i,j} \Bigg ) e^{\phi }_{i,j} \Delta x \Delta y , \nonumber \\&\quad =\kappa \sum _{i=1}^{M-1}\sum _{j=-N+1}^{0} \left( D_x^-e^{\phi }_{i+1,j}\right) ^2 \Delta x \Delta y +\kappa \sum _{i=1}^{M}\sum _{j=-N+2}^{0} \left( D_y^- e^{\phi }_{i,j}\right) ^2 \Delta x \Delta y\nonumber \\&\qquad - \kappa \sum _{i=1}^M \frac{e^{\phi }_{i,1}-e^{\phi }_{i,0}}{\Delta y} e^{\phi }_{i,0}\Delta x. \end{aligned}$$

(5.28)

Lemma 5.4

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} e^u_{i+1/2,j} D_x^+ D_x^- e^u_{i+1/2,j} \Delta x \Delta y = \nu \Vert D_x^- e^u\Vert ^2, \end{aligned}$$

(5.29)

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} e^u_{i+1/2,j} D_y^+ D_y^- e^u_{i+1/2,j} \Delta x \Delta y \nonumber \\&\qquad = \nu \Vert D_y^- e^u \Vert ^2 + \nu \sum _{i=1}^{M-1} \frac{ e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2}D_y^- e^u_{i+1/2,1} \Delta x, \end{aligned}$$

(5.30)

$$\begin{aligned}&-\nu \sum _{i=1}^{M}\sum _{j=1}^{N-1} e^v_{i,j+1/2} D_x^+ D_x^- e^v_{i,j+1/2} \Delta x \Delta y \nonumber \\&\quad = \nu \sum _{i=1}^{M-1} \sum _{j=1}^{N-1} |D_x^- e^v_{i+1,j+1/2}|^2 \Delta x \Delta y \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \Bigg ( |D_x^- e^v_{M+1,j+1/2}|^2 + |D_x^- e^v_{1,j+1/2}|^2\Bigg )\Delta x \Delta y, \end{aligned}$$

(5.31)

$$\begin{aligned}&-\nu \sum _{i=1}^{M}\sum _{j=1}^{N-1} e^v_{i,j+1/2} D_y^+ D_y^- e^v_{i,j+1/2} \Delta x \Delta y = \nu \Vert D_y^- e^v \Vert ^2 + \nu \sum _{i=1}^M e^v_{i,1/2} D_y^- e^v_{i,3/2}\Delta x, \nonumber \\ \end{aligned}$$

(5.32)

$$\begin{aligned}&-\nu \sum _{i=1}^{M-1}\sum _{j=1}^{N} e^u_{i+1/2,j} D_x^+ D_y^- e^v_{i,j+1/2} \Delta x \Delta y \nonumber \\&\quad = \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} D_y^- e^u_{i+1/2,j+1}D_x^- e^v_{i+1,j+1/2}\Delta x\Delta y + \nu \sum _{i=1}^{M-1} e^u_{i+1/2,1}D_x^- e^v_{i+1,1/2}\Delta x, \nonumber \\\end{aligned}$$

(5.33)

$$\begin{aligned}&-\nu \sum _{i=1}^{M}\sum _{j=1}^{N-1} e^v_{i,j+1/2} D_y^+ D_x^-e^u_{i+1/2,j} \Delta x \Delta y \nonumber \\&\quad = \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} D_y^- e^u_{i+1/2,j+1}D_x^- e^v_{i+1,j+1/2}\Delta x\Delta y. \end{aligned}$$

(5.34)

The proofs of Lemma 5.3 and 5.4 are similar to the proofs in Lemma 4.3 and 4.4. Thus, the proofs are omitted, too.

For the convenience of the notation, we denote the maximum norm of the r-th derivatives of any function u as $|D^r u|_{\infty }=|\frac{\partial ^r u}{\partial ^m x \partial ^n y}|_{\infty }$ where $r=m+n$ and m and n are nonnegative integers.

To perform the error estimates of the finite difference scheme, we need the following lemma for the estimates of the terms $R^u_{i+1/2,j}, R^v_{i,j+1/2}$, $R^d_{i,j}, (R^p_{\Gamma })_{i,1/2}, (R_{\Gamma }^u)_{i+1/2,1/2}$ and $R^p$:

Lemma 5.5

$$\begin{aligned}&R^u_{i+1/2,j}=O((\Delta x)^2)( |D^4u|_{\infty }+ |D^3 p|_{\infty } ) + O((\Delta y)^2)|D^4 u|_{\infty } + O(\Delta x\Delta y), j \not = 1, N\\&R^u_{i+1/2,1}=O((\Delta x)^2)( |D^4u|_{\infty }+ |D^3 p|_{\infty } ) + O(\Delta y)|D^3 u|_{\infty } + O(\Delta x\Delta y), \\&R^u_{i+1/2,N}=\frac{\nu }{4}u_{yy}(x_{i+1/2},y_N)+ O((\Delta x)^2)( |D^4u|_{\infty }+ |D^3 p|_{\infty } ) \\&\quad + O(\Delta y)|D^3 u|_{\infty } + O(\Delta x\Delta y), \\&R^v_{i,j+1/2}=O((\Delta x)^2)|D^4v|_{\infty } + O((\Delta y)^2)(|D^4 u|_{\infty }+ |D^3 p|_{\infty } ) + O(\Delta x\Delta y), i \not = 1, M \\&R^v_{i,j+1/2}=\frac{\nu }{4}v_{xx}(x_i, y_{j+1/2})+O(\Delta x)|D^3v|_{\infty } + O((\Delta y)^2)(|D^4 u|_{\infty }+ |D^3 p|_{\infty } ) \\&\quad + O(\Delta x\Delta y), i = 1, M \\&R^d_{i,j}=O((\Delta x)^2)|D^3u|_{\infty } + O((\Delta y)^2)|D^3 v|_{\infty }, \\&D_x^+ R^d_{i,j}=O((\Delta x)^2)|D^4u|_{\infty } + O((\Delta x)^2+(\Delta y)^2)|D^4 v|_{\infty }, \\&D_y^- R^d_{i,j+1}=O((\Delta x)^2+(\Delta y)^2)|D^4u|_{\infty } + O((\Delta y)^2)|D^4 v|_{\infty }, \\&R^{\phi }_{i,j}=(O((\Delta x)^2)+O((\Delta y)^2)) (|D^3\phi |_{\infty }+ |D^2 f_2|_{\infty }), i \not = 1, M \text { and } j \not = 0, -N+1, \\&R^{\phi }_{i,j}=(O( \Delta x)+O((\Delta y)^2)) (|D^3\phi |_{\infty }+ |D^2 f_2|_{\infty }), i = 1, M \text { and } j \not = 0, -N+1, \\&R^{\phi }_{i,j}=(O((\Delta x)^2)+O( \Delta y)) (|D^3\phi |_{\infty }+ |D^2 f_2|_{\infty }), i \not = 1, M \text { and } j = 0, -N+1, \\&R^{\phi }_{i,j}=(O(\Delta x)+O( \Delta y)) (|D^3\phi |_{\infty }+ |D^2 f_2|_{\infty }), i = 1, M \text { and } j = 0, -N+1, \\&(R_{\Gamma }^p)_{i,1/2} = O(\Delta y) (|Dp|_{\infty } + |D\phi |_{\infty } +|D^2 v|_{\infty }), \\&(R_{\Gamma }^u)_{i+1/2, 1/2} = O((\Delta x)^2)|D^3v|_{\infty } + O((\Delta y)^2)|D^3 u|_{\infty }, \\&R^p = (O((\Delta x)^2)+O((\Delta y)^2)) (|D^2\phi |_{\infty }+ |D^2 p|_{\infty }). \end{aligned}$$

The proof of Lemma 5.5 is based on Taylor’s expansion and the assumption on the regularity of the solutions and the forcing. The proof of Lemma 5.5 is skipped. Remark that in the fluid region, the truncation errors inside the domain are of second order but the one near the boundary is some O(1) term plus first-order terms; in the porous region, the truncation errors inside the domain are of second order but the one near the boundary is of the first order. Near the interface, the truncation errors are both of the first order. The following lemma is also needed to control the boundedness of the error estimates of the pressure and related boundary terms:

Lemma 5.6

Let the mesh widths satisfy (4.35) and $\Delta y =\Delta x$, we have

$$\begin{aligned}&\sum _{i=1}^{M-1}\Bigg ( \frac{e^u_{i+1/2,1} + e^u_{i+1/2,0}}{2}\Bigg )^2 \, \Delta x \le K_2= 2 \left( K_1 + L_x |u|^2_{\infty }\right) , \\&\Vert e^p\Vert ^2 + \Vert e^{\phi }\Vert ^2 \le K_3 = 2\left( C_p + L_xL_y |p|^2_{\infty } + L_xL_y|\phi |^2_{\infty }\right) , \end{aligned}$$

where $K_i, i=2,3$ are constants depending only on the size of the domain, the forcing and the solutions.

The proof of Lemma 5.6 can be proven by using the triangle inequality, Lemma 4.5 and Theorem 4.2.

Now, we state and prove our main theorem of the error estimates for the scheme (3.1)–(3.14) as follows:

Theorem 5.1

Let the mesh widths satisfy (4.35) and $\Delta y =\Delta x$, we have

$$\begin{aligned}&\frac{\nu }{2L_x^2} \Vert e^u\Vert ^2 + \frac{\nu }{8L_y^2 +2\nu \kappa }\Vert e^v\Vert ^2 + \frac{\nu }{2}\Vert D_x^-e^u\Vert ^2 +\frac{\nu }{16}\Vert D_y^- e^v\Vert ^2 \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \left( D_y^-e^u_{i+1/2,j+1} +D_x^- e^v_{i+1,j+1/2}\right) ^2 \, \Delta x\Delta y \nonumber \\&\qquad + \frac{\nu }{2} \sum _{i=1}^{M-1} |D_y^- e^u_{i+1/2,N+1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- e^v_{1,j+1/2}|^2 + |D_x^- e^v_{M+1,j+1/2}|^2 \right) \frac{\Delta x \Delta y}{2} \nonumber \\&\qquad + \kappa \Vert D_x^- e^{\phi } \Vert ^2 + \kappa \Vert D_y^- e^{\phi }\Vert ^2 \nonumber \\&\quad =O\left( \left( \Delta x\right) ^2+ \left( \Delta y\right) ^2\right) . \end{aligned}$$

(5.35)

Proof

By multiplying (5.1), (5.2), (5.4), (5.25) and (5.26) by $e^u_{i+1/2,j}\Delta x \Delta y$, $e^v_{i,j+1/2}\Delta x \Delta y$, $e^{\phi }_{i,j}\Delta x \Delta y$, $e^u_{i+1/2,j}\Delta x \Delta y$ and $e^v_{i,j+1/2}\Delta x \Delta y$ respectively, summing for all i and j and adding all the resulting equations, we obtain

$$\begin{aligned}&2\nu \Vert D_x^- e^u\Vert ^2 + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \left( D_y^- e^u_{i+1/2,j+1} +D_x^- e^v_{i+1,j+1/2}\right) ^2 \, \Delta x\Delta y \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} \left( |D_y^- e^u_{i+1/2,N+1}|^2 + |D_y^- e^u_{i+1/2,1}|^2\right) \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- e^v_{1,j+1/2}|^2 + |D_x^- e^v_{M+1,j+1/2}|^2 \right) \Delta x \Delta y \nonumber \\&\qquad + 2\nu \Vert D_y^- e^v\Vert ^2 + \kappa \Vert D_x^- e^{\phi }\Vert ^2 + \kappa \Vert D_y^- e^{\phi }\Vert ^2 \nonumber \\&\quad = \sum _{i=1}^M \Bigg ( e^v_{i,1/2} e^p_{i,1} - e^v_{i,1/2} e^{\phi }_{i,0} -2\nu e^v_{i,1/2}D_y^- e^v_{i,3/2}\Bigg ) \Delta x \nonumber \\&\qquad - \nu \sum _{i=1}^{M-1}\frac{ e^u_{i+1/2,1}+e^u_{i+1/2,0}}{2}D_y^- e^u_{i+1/2,1} \Delta x -\nu \sum _{i=1}^{M-1} e^u_{i+1/2,1}D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\qquad + \kappa \sum _{i=1}^M |D_y^- e^{\phi }_{i,1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \sum _{i=1}^{M-1}\sum _{j=1}^{N} e^u_{i+1/2,j} R^u_{i+1/2,j} \Delta x \Delta y + \sum _{i=1}^{M}\sum _{j=1}^{N-1} e^v_{i,j+1/2} R^v_{i,j+1/2} \Delta x \Delta y \nonumber \\&\qquad + \sum _{i=1}^{M} \sum _{j=-N+1}^{0} R^{\phi }_{i,j} e^{\phi }_{i, j}\Delta x\Delta y + \sum _{i=1}^M\sum _{j=1}^N R^d_{i,j} e^p_{i,j}\Delta x\Delta y \nonumber \\&\qquad -\nu \sum _{i=1}^{M-1}\sum _{j=1}^N D_x^+ R^d_{i,j} e^u_{i+1/2,j}\Delta x\Delta y -\nu \sum _{i=1}^M\sum _{j=1}^{N-1} D_y^- R^d_{i,j+1}e^v_{i,j+1/2}\Delta x\Delta y \nonumber \\&\quad :=I_6 + I_7 +I_8 +I_9 + I_{10}+I_{11}. \end{aligned}$$

(5.36)

Now, we estimate the terms $I_i, i=6, \ldots , 11$. For the term $I_6$, by applying the interface conditions (5.14) and (5.15), we obtain

$$\begin{aligned} I_6= & {} \sum _{i=1}^M \Bigg ( e^v_{i,1/2} \Big (e^p_{i,1} -e^{\phi }_{i,0} \Big )-2\nu e^v_{i,1/2}D_y^- e^v_{i,3/2}\Bigg ) \Delta x \nonumber \\= & {} \sum _{i=1}^M e^v_{i,1/2} (R^p_{\Gamma })_{i,1/2}\Delta x \nonumber \\= & {} \sum _{i=1}^M \sum _{j=1}^N -D_y^- e^v_{i,j+1/2} \Delta y (R^p_{\Gamma })_{i,1/2}\Delta x \nonumber \\\le & {} \Bigg (\sum _{i=1}^M\Bigg ( \sum _{j=1}^N |D_y^- e^v_{i,j+1/2}|\Delta y \Bigg )^2 \Bigg )^{1/2} \Bigg (\sum _{i=1}^M |(R_{\Gamma }^p)_{i,1/2}|^2 \Bigg )^{1/2}\Delta x \nonumber \\\le & {} \varepsilon _2 \nu \Vert D_y^- e^v\Vert ^2 + \frac{L_y}{4\varepsilon _2 \nu }\sum _{i=1}^M |(R_{\Gamma }^p)_{i,1/2}|^2 \Delta x, \end{aligned}$$

(5.37)

where $\varepsilon _2$ is a positive parameter which is determined later. To estimate the term $I_7$, we have

$$\begin{aligned} I_7= & {} - \nu \sum _{i=1}^{M-1}\frac{ e^u_{i+1/2,1}+e^u_{i+1/2,0}}{2}(D_y^- e^u_{i+1/2,1}+D_x^- e^v_{i+1,1/2}) \Delta x \nonumber \\&- \nu \sum _{i=1}^{M-1}\frac{ e^u_{i+1/2,1}- e^u_{i+1/2,0}}{2} D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\= & {} -\frac{2\nu }{\alpha _2} \sum _{i=1}^{M-1}\Bigg ( \frac{e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2}\Bigg )^2 \Delta x \nonumber \\&+\frac{2\nu }{\alpha _2} \sum _{i=1}^{M-1} \frac{ e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2} (R_{\Gamma }^u)_{i+1/2,1/2} \Delta x \nonumber \\&- \nu \sum _{i=1}^{M-1}\frac{ e^u_{i+1/2,1}- e^u_{i+1/2,0}}{2} D_x^- e^v_{i+1,1/2}\Delta x, \end{aligned}$$

(5.38)

where the interface conditions (5.16) are applied. To estimate the second term on the right-hand side of (5.38), by applying Cauchy–Schwarz inequality and Lemma 5.6, we have

$$\begin{aligned}&\frac{2\nu }{\alpha _2} \sum _{i=1}^{M-1} \frac{ e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2} (R_{\Gamma }^u)_{i+1/2,1/2} \Delta x \nonumber \\&\quad \le \frac{2\nu }{\alpha _2}\Bigg ( \sum _{i=1}^{M-1} \Bigg ( \frac{ e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2}\Bigg )^2 \Delta x\Bigg )^{1/2} \Bigg ( \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x \Bigg )^{1/2} \nonumber \\&\quad =\frac{2\nu K^{1/2}_2}{\alpha _2} \Bigg ( \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x \Bigg )^{1/2}. \end{aligned}$$

(5.39)

To estimate the third term on the right-hand side of (5.38), we observe

$$\begin{aligned} e^u_{i+1/2,0}= & {} \frac{-(\Delta y -\alpha _2)}{\Delta y + \alpha _2} e^u_{i+1/2,1}+ \frac{\alpha _2 \Delta y }{\Delta y + \alpha _2} D_x^- e^v_{i+1,1/2} +\frac{2\Delta y}{\Delta y + \alpha _2} (R^u_{\Gamma })_{i+1/2,1/2}.\nonumber \\ \end{aligned}$$

(5.40)

This leads to

$$\begin{aligned} \frac{ e^u_{i+1/2,1}- e^u_{i+1/2,0}}{2}= & {} \frac{\Delta y}{\Delta y + \alpha _2} e^u_{i+1/2,1}- \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} D_x^- e^v_{i+1,1/2} \nonumber \\&-\frac{\Delta y}{\Delta y + \alpha _2} (R^u_{\Gamma })_{i+1/2,1/2}. \end{aligned}$$

(5.41)

Plugging (5.41) into the third term on the right-hand side of (5.38), we obtain

$$\begin{aligned}&- \nu \sum _{i=1}^{M-1}\frac{e^u_{i+1/2,1}- e^u_{i+1/2,0}}{2} D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\quad = - \nu \sum _{i=1}^{M-1} \Bigg ( \frac{\Delta y}{\Delta y + \alpha _2} e^u_{i+1/2,1}- \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} D_x^- e^v_{i+1,1/2}\nonumber \\&\qquad -\frac{\Delta y}{\Delta y + \alpha _2} (R^u_{\Gamma })_{i+1/2,1/2} \Bigg ) D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\quad = - \nu \sum _{i=1}^{M-1}\frac{\Delta y}{\Delta y + \alpha _2}e^u_{i+1/2,1}D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} \frac{\alpha _2 \Delta y }{2(\Delta y + \alpha _2)} D_x^- e^v_{i+1,1/2} D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\qquad + \nu \sum _{i=1}^{M-1} \frac{\Delta y}{\Delta y + \alpha _2} (R^u_{\Gamma })_{i+1/2,1/2} D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\quad = J_3 +J_4+J_5. \end{aligned}$$

(5.42)

To estimate the terms $J_3$ and $J_4$, we apply the similar procedure in estimating $J_1$ and $J_2$ respectively in Theorem 4.1 and have

$$\begin{aligned} J_3\le & {} \nu \frac{L_y \Delta y}{4\alpha ^2_2}\Vert D_x^- e^u\Vert ^2 + \nu \Vert D_y^- e^v\Vert ^2, \end{aligned}$$

(5.43)

$$\begin{aligned} J_4\le & {} \nu \frac{2 \Delta y }{\left( \Delta y + \alpha _2\right) \alpha _2} \left( 1 + \frac{2}{\varepsilon _3}\right) \sum _{i=1}^{M-1} \left( \frac{ e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2}\right) ^2 \Delta x \nonumber \\&\quad + \nu \frac{\alpha _2 }{\Delta y + \alpha _2} \left( 1+\frac{\varepsilon _3}{2}\right) \sum _{i=1}^{M-1} |D_y^- e^u_{i+1/2,1}|^2 \frac{\Delta x\Delta y}{2}, \end{aligned}$$

(5.44)

where $\varepsilon _3$ is a positive parameter which will be determined later. As for the term $J_5$, by applying Cauchy–Schwarz inequality and Lemma 5.6, we have

$$\begin{aligned}&\nu \sum _{i=1}^{M-1} \frac{\Delta y}{\Delta y + \alpha _2} (R^u_{\Gamma })_{i+1/2,1/2} D_x^- e^v_{i+1,1/2}\Delta x \nonumber \\&\quad \le \frac{ \nu }{\alpha _2} \Bigg ( \sum _{i=1}^{M-1} \Big (D_x^- e^v_{i+1,1/2}\Big )^2 \Delta x (\Delta y)^2\Bigg )^{1/2} \Bigg ( \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x \Bigg )^{1/2} \nonumber \\&\quad \le \frac{2\nu L_y^{1/2}}{\alpha _2} \Vert D_y^- e^v\Vert \Bigg ( \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x \Bigg )^{1/2} \nonumber \\&\quad \le \frac{\nu }{16}\Vert D_y^- e^v\Vert ^2 + \frac{128L_y \nu }{\alpha _2^2} \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x, \end{aligned}$$

(5.45)

where the following inequality which is obtained by applying the same idea in (4.53) is used

$$\begin{aligned} \sum _{i=1}^{M-1} \left( D_x^- e^v_{i+1,1/2}\right) ^2 \Delta x (\Delta y)^2 \le 4L_y \Vert D_y^-\Vert ^2. \end{aligned}$$

Combining (5.38), (5.39), (5.43), (5.44) and (5.45), we obtain

$$\begin{aligned} I_7\le & {} -\frac{2\nu }{\alpha _2}\Bigg (1 -\frac{\Delta y}{(\Delta y + \alpha _2)}\Big (1+\frac{2}{\varepsilon _3}\Big )\Bigg ) \sum _{i=1}^{M-1} \left( \frac{ e^u_{i+1/2,1}+ e^u_{i+1/2,0}}{2}\right) ^2 \Delta x \nonumber \\&\quad + \nu \frac{\alpha _2 }{\Delta y + \alpha _2} \left( 1+\frac{\varepsilon _3}{2}\right) \sum _{i=1}^{M-1} |D_y^- e^u_{i+1/2,1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\quad + \nu \frac{L_y \Delta y}{4\alpha ^2_2 }\Vert D_x^- e^u\Vert ^2 + \frac{17\nu }{16} \Vert D_y^- e^v\Vert ^2 \nonumber \\&\quad + \frac{2\nu K_2^{1/2}}{\alpha _2} \Bigg (\sum _{i=1}^{M-1} |(R^u_{\Gamma })_{i+1/2,1/2}|^2\Delta x \Bigg )^{1/2}+ \frac{128L_y \nu }{\alpha _2^2} \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x . \nonumber \\ \end{aligned}$$

(5.46)

Now, by taking $\varepsilon _3 = \frac{2 \Delta y}{\alpha _2}$, we can infer from (5.46) that

$$\begin{aligned} I_7\le & {} \nu \sum _{i=1}^{M-1} |D_y^- e^u_{i+1/2,1}|^2 \frac{\Delta x\Delta y}{2} + \nu \frac{L_y \Delta y}{4\alpha ^2_2 }\Vert D_x^- e^u\Vert ^2 + \frac{17\nu }{16} \Vert D_y^- e^v\Vert ^2 \nonumber \\&+ \frac{2\nu K_2^{1/2}}{\alpha _2} \Bigg (\sum _{i=1}^{M-1} |(R^u_{\Gamma })_{i+1/2,1/2}|^2\Delta x \Bigg )^{1/2}+ \frac{128L_y \nu }{\alpha _2^2} \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x . \nonumber \\ \end{aligned}$$

(5.47)

To estimate the terms $I_8, I_9, I_{10}$ and $I_{11}$, we have

$$\begin{aligned} I_8\le & {} \frac{L_y \Delta y}{2\kappa } \Vert D_y^- e^v\Vert ^2, \end{aligned}$$

(5.48)

$$\begin{aligned} I_9\le & {} \varepsilon _2 \nu \Vert D_x^- e^u\Vert ^2 + \frac{\varepsilon _2 \nu }{2}\Vert D_y^- e^v\Vert ^2 + \frac{L_x^2}{\varepsilon _2 \nu }\Vert {{\tilde{R}}}^u\Vert ^2 + \frac{L_y\left( L_y + \frac{\Delta y}{2}\right) }{2\varepsilon _2 \nu }\Vert {{\tilde{R}}}^v\Vert ^2 \nonumber \\&+ \frac{\nu }{2} \sum _{i=1}^{M-1} |D_y^- e^u_{i+1/2,N+1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&+ \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- e^v_{1,j+1/2}|^2 + |D_x^- e^v_{M+1,j+1/2}|^2 \right) \frac{\Delta x \Delta y}{2} \nonumber \\&+ \frac{\nu \left( \Delta y\right) ^2}{32} \sum _{i=1}^{M-1} \left( u_{yy}\left( x_{i+1/2},y_N\right) \right) ^2 \frac{\Delta x\Delta y}{2} \nonumber \\&+ \frac{\nu \left( \Delta x\right) ^2}{32}\sum _{j=1}^{N-1} \left( \left( v_{xx}\left( x_1,y_{j+1/2}\right) \right) ^2 + \left( v_{xx}\left( x_{M+1},y_{j+1/2}\right) \right) ^2 \right) \frac{\Delta x \Delta y}{2}, \end{aligned}$$

(5.49)

$$\begin{aligned} I_{10}\le & {} K_3^{1/2} \left( \Vert R^{\phi }\Vert + \Vert R^d\Vert \right) , \end{aligned}$$

(5.50)

$$\begin{aligned} I_{11}\le & {} \varepsilon _2 \nu \Vert D_x^- e^u\Vert ^2 + \frac{\varepsilon _2 \nu }{2}\Vert D_y^- e^v\Vert ^2 + \frac{L_x^2}{\varepsilon _2 \nu }\Vert D_x^+R^u\Vert ^2 + \frac{L_y\left( L_y + \frac{\Delta y}{2}\right) }{2\varepsilon _2 \nu }\Vert D_y^- R^v\Vert ^2,\nonumber \\ \end{aligned}$$

(5.51)

where ${{\tilde{R}}}^u$ and ${{\tilde{R}}}^v$ are defined as

$$\begin{aligned} {{\tilde{R}}}^u_{i+1/2, j} = {\left\{ \begin{array}{ll} R^u_{i+1/2,j}, &{}\quad \text { if } j \not = N, \\ R^u_{i+1/2,j}- \frac{\nu }{4}u_{yy}(x_{i+1/2},y_N),&{}\quad \text { if } j = N, \\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {{\tilde{R}}}^v_{i, j+1/2, } = {\left\{ \begin{array}{ll} R^v_{i,j+1/2},&{}\quad \text { if } i \not = 1, M, \\ R^v_{i,j +1/2}- \frac{\nu }{4}v_{xx}(x_i, y_{j+1/2}), &{}\quad \text { if } i = 1, M. \\ \end{array}\right. } \end{aligned}$$

Combining the estimates of $I_i, i=6, \ldots , 11$ and taking $\varepsilon _2=\frac{1}{4}$, we can infer from (5.36) that

$$\begin{aligned}&\Bigg (\frac{3}{2}-\frac{Ly\Delta y}{4\alpha _2} \Bigg ) \nu \Vert D_x^- e^u\Vert ^2 + \nu \sum _{i=1}^{M-1}\sum _{j=1}^{N-1} \left( D_y^- e^u_{i+1/2,j+1} +D_x^- e^v_{i+1,j+1/2}\right) ^2 \, \Delta x\Delta y \nonumber \\&\qquad + \frac{\nu }{2}\sum _{i=1}^{M-1} |D_y^- e^u_{i+1/2,N+1}|^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu }{2}\sum _{j=1}^{N-1} \left( |D_x^- e^v_{1,j+1/2}|^2 + |D_x^- e^v_{M+1,j+1/2}|^2 \right) \frac{\Delta x \Delta y}{2} \nonumber \\&\qquad + \Bigg (\frac{7\nu }{16}-\frac{L_y \Delta y}{2\kappa }\Bigg ) \Vert D_y^- e^v\Vert ^2 + \kappa \Vert D_x^- \phi \Vert ^2 + \kappa \Vert D_y^- \phi \Vert ^2 \nonumber \\&\quad \le \frac{L_y}{ \nu }\sum _{i=1}^M |(R_{\Gamma }^p)_{i,1/2}|^2 \Delta x + \frac{2\nu K_2^{1/2}}{\alpha _2} \Bigg (\sum _{i=1}^{M-1} |(R^u_{\Gamma })_{i+1/2,1/2}|^2\Delta x \Bigg )^{1/2} \nonumber \\&\qquad + \frac{128L_y \nu }{\alpha _2^2} \sum _{i=1}^{M-1} |(R_{\Gamma }^u)_{i+1/2,1/2}|^2 \Delta x + \frac{4L_x^2}{ \nu }\Vert {{\tilde{R}}}^u\Vert ^2 + \frac{2L_y\left( L_y + \frac{\Delta y}{2}\right) }{ \nu }\Vert {{\tilde{R}}}^v\Vert ^2 \nonumber \\&\qquad + \frac{\nu (\Delta y)^2}{32} \sum _{i=1}^{M-1} (u_{yy}(x_{i+1/2},y_N))^2 \frac{\Delta x\Delta y}{2} \nonumber \\&\qquad + \frac{\nu (\Delta x)^2}{32}\sum _{j=1}^{N-1} ((v_{xx}(x_1,y_{j+1/2}))^2 + \left( v_{xx}(x_{M+1},y_{j+1/2}))^2 \right) \frac{\Delta x \Delta y}{2} \nonumber \\&\qquad + K_3^{1/2} (\Vert R^{\phi }\Vert + \Vert R^d\Vert ) + \frac{4L_x^2}{ \nu }\Vert D_x^+R^u\Vert ^2 + \frac{2L_y\left( L_y + \frac{\Delta y}{2}\right) }{ \nu }\Vert D_y^- R_S^v\Vert ^2 . \end{aligned}$$

(5.52)

By taking $\Delta y$ to satisfy the condition (4.35) and applying Lemma 5.5, the proof of Theorem 5.1 is complete. $\square$

To show the error estimates of the pressure p and $\phi$, we need the following lemmas:

Lemma 5.7

Let the mesh widths satisfy (4.35) and $\Delta y = \Delta x$, we have

$$\begin{aligned} \sum _{i=1}^{M-1} \left( \frac{e^u_{i+1/2,1}+e^u_{i+1/2,0}}{2}\right) ^2 \, \Delta x =O((\Delta x)^2+ (\Delta y)^2). \end{aligned}$$

The proof of Lemma 5.7 follows Lemma 4.7 and Theorem 5.1.

Like Lemmas 4.7 and 4.6, we also need the following lemma related to the finite difference method for the divergence problem in the whole domain $\Omega$:

Lemma 5.8

For any given $e^p_{i,j}, \, 1\le i \le M, 1\le j \le N$ and $e^{\phi }_{i,j}, \, 1\le i \le M, -N+1 \le j \le 0$ satisfying (5.21), there exist two vectors $(e^{{\tilde{u}}}, e^{{\tilde{v}}})$ satisfies the following properties:

$$\begin{aligned} e^{{\tilde{u}}}_{1/2,j}= & {} e^{{\tilde{u}}}_{M+1/2,j} = 0, \, 0 \le j \le N+1, \\ e^{{\tilde{u}}}_{i+1/2,N+1}= & {} -e^{{\tilde{u}}}_{i+1/2,N}, \, 0 \le i \le M, \\ e^{{\tilde{v}}}_{0,j+1/2}= & {} -e^{{\tilde{v}}}_{1,j+1/2}, \, e^{{\tilde{v}}}_{M+1,j+1/2}= -e^{{\tilde{v}}}_{M,j+1/2}, \, 0 \le j \le N, \\ D_x^- e^{{\tilde{u}}}_{i+1/2,j} + D_y^- e^{{\tilde{v}}}_{i, j+1/2}= & {} e^p_{i,j}-\frac{R^p}{2L_xL_y}, \, 1\le i\le M, 1\le j \le N, \end{aligned}$$

and there exists a vector $e^{{\tilde{\phi }}}_{i,j}, \, 0 \le i \le M+1, \, -N\le j \le 1$ satisfying

$$\begin{aligned}&D_x^- e^{{\tilde{\phi }}}_{1,j}= D_x^- e^{{\tilde{\phi }}}_{M+1,j}=0 , \, -N+1\le j \le 0, \\&D_y^- e^{{\tilde{\phi }}}_{i,-N+1}=0, -\kappa D_y^- e^{{\tilde{\phi }}}_{i,1}=e^{{\tilde{v}}}_{i,1/2} , \, 1\le i \le M, \\&-\kappa \frac{D_x^- e^{{\tilde{\phi }}}_{i+1,j} -D_x^- e^{{\tilde{\phi }}}_{i,j}}{\Delta x} -\kappa \frac{D_y^- e^{{\tilde{\phi }}}_{i,j+1} -D_y^- e^{{\tilde{\phi }}}_{i,j}}{\Delta y}= e^\phi _{i,j}-\frac{R^p}{2L_xL_y}, \\&1\le i\le M, -N+1\le j \le 0. \end{aligned}$$

Moreover, we have

$$\begin{aligned}&\Vert D_x^- e^{{\tilde{u}}}\Vert ^2 + \Vert D_y^- e^{{\tilde{u}}}\Vert ^2+ \Vert D_x^- e^{{\tilde{v}}}\Vert ^2 + \Vert D_y^- e^{{\tilde{v}}}\Vert ^2 \\&\qquad + \Vert e^{{\tilde{u}}}\Vert ^2 + \Vert e^{{\tilde{v}}}\Vert ^2 +\Vert D_x^- e^{{\tilde{\phi }}}\Vert ^2 + \Vert D_y^- e^{{\tilde{\phi }}}\Vert ^2 +\sum _{i=1}^{M-1} \left( \frac{e^{{\tilde{u}}}_{i+1/2,1} + e^{{\tilde{u}}}_{i+1/2,0}}{2}\right) ^2\Delta x \\&\quad \le {{\tilde{C}}_e}(\Vert e^p\Vert ^2 + \Vert e^{\phi }\Vert ^2+ (R^p)^2), \end{aligned}$$

where ${{\tilde{C}}_e}$ is a constant independent of the mesh widths $\Delta x$ and $\Delta y$.

The proof of Lemma 5.8 can be proven similarly by following the process of showing Lemma 4.6, which needs the following lemma:

Lemma 5.9

For any given $e^p_{i,j}, \, 1\le i \le M, 1\le j \le N$ and $e^{\phi }_{i,j}, \, 1\le i \le M, -N+1 \le j \le 0$ satisfying (5.21), there exist a positive constant $C_e$ independent of the mesh widths $\Delta x$ and $\Delta y$ and two vectors $e^U_{i+1/2,j}, \, 0\le i \le M, -N \le j \le N+1$ and $e^V_{i, j+1/2}, \, 0 \le i \le M+1, \, -N+1 \le l \le N$ satisfying

$$\begin{aligned}&e^U_{1/2,l} = e^U_{M+1/2,l} = 0, \, -N \le l \le N+1, \end{aligned}$$

(5.53)

$$\begin{aligned}&e^U_{i+1/2,N+1} = -e^U_{i+1/2,N}, \, e^U_{k+1/2,-N} = - e^U_{i+1/2,-N+1}, \, 0 \le i \le M, \end{aligned}$$

(5.54)

$$\begin{aligned}&e^V_{i,N+1/2}= e^V_{i, -N+1/2} = 0, \, 0 \le i \le N+1, \end{aligned}$$

(5.55)

$$\begin{aligned}&e^V_{0, j+1/2}=- e^V_{1, j+1/2}, \, e^V_{M+1, j+1/2}=- e^V_{M, j+1/2}, \, -N+1 \le j \le N, \end{aligned}$$

(5.56)

$$\begin{aligned}&D_x^- e^U_{i+1/2,j} + D_y^- e^V_{i, j+1/2} = e^p_{i,j}-\frac{R^\phi }{2L_xL_y}, \, 1\le i\le M, 1\le j \le N, \end{aligned}$$

(5.57)

$$\begin{aligned}&D_x^- e^U_{i+1/2, j} + D_y^- e^V_{i, j+1/2} = e^{\phi }_{i,j}-\frac{R^\phi }{2L_xL_y}, \, 1\le i\le M, -N+1\le j \le 0, \end{aligned}$$

(5.58)

$$\begin{aligned}&\Vert D_x^- e^U\Vert _{\Omega }^2 + \Vert D_y^- e^U\Vert _{\Omega }^2 + \Vert D_x^- e^V\Vert _{\Omega }^2 + \Vert D_y^- e^V\Vert _{\Omega }^2 \le C_e (\Vert e^p\Vert ^2 +\Vert e^{\phi }\Vert ^2 + (R^p)^2).\nonumber \\ \end{aligned}$$

(5.59)

The proof of Lemma 5.9 can be proven similarly in [29]. Thus, the proofs of Lemma 5.8 and 5.9 are omitted.

Now, we are ready to state the error estimates of the pressure p and $\phi$ as follows:

Theorem 5.2

Let the mesh widths satisfy (4.35) and $\Delta y =\Delta x$, we have

$$\begin{aligned}&\Vert e^p\Vert ^2 + \Vert e^\phi \Vert ^2 =O((\Delta x)^2 + (\Delta y)^2). \end{aligned}$$

The proof of Theorem 5.2 can be shown by following the similar procedure in Theorem 4.2 with the aid of Lemmas 5.5, 5.7, 5.9, 5.8 and triangle inequality.

6 Numerical Results

In this section, we carry out some numerical tests for the present MAC scheme of the Stokes/Darcy coupling problem. The computational domain $\Omega _f=[0,1] \times [1,2]$, $\Omega _p=[0,1] \times [0,1]$ and the interface is located at $y=1$ in the domain. For simplicity, all physical constants $\nu , \kappa , {\tilde{k}}, \alpha _1$ are all equal to 1. Throughout the paper, we choose the mesh widths $\Delta x=\Delta y$ so the grid size $M=N$. The discrete $L^2$ error norms for all variables $u, v, p, \phi$ are computed based on the formulas (4.1)–(4.4).

Example 1

The first analytic solution is taken from the initial condition of the test example constructed in [11] written by

$$\begin{aligned} u= & {} -\frac{1}{\pi }e^{y}\sin (\pi x),\\ v= & {} \left( e^{y}-e\right) \cos \left( \pi x\right) ,\\ p= & {} 2e^{y}\cos (\pi x),\\ \phi= & {} \left( e^{y}-ye\right) \cos (\pi x). \end{aligned}$$

One can easily check that this solution satisfies all three interface conditions (2.10)–(2.12). In addition, the solution satisfies zero normal velocity ($v=0$) across the interface $y=1$. Tables 1 and 2 show the grid refinement analysis of $L^{2}$ errors for the velocity u, v and the pressure $p, \phi$, respectively. One can see both velocity components u, v in Stokes region and the pressure $\phi$ in Darcy’s region behave like second-order convergent. However, the pressure p in Stokes region is better than first-order but not exactly second-order convergent. The numerical results show better convergence rates than the ones obtained from the present theoretical analysis.

Table 1 Grid refinement analysis of $L^{2}$ errors for the solutions u and v in Example 1

Table 2 Grid refinement analysis of $L^{2}$ errors for the solutions p and $\phi$ in Example 1

Example 2

The second test example is given by

$$\begin{aligned} u= & {} \left( y-1\right) ^{2}+x(y-1)+3x-1,\\ v= & {} x(x-1)-0.5(y-1)^{2}-3y+1,\\ p= & {} 2x+y-1,\\ \phi= & {} x(1-x)(y-1)+\frac{\left( y-1\right) ^{3}}{3}+2x+2y+4. \end{aligned}$$

Again, the solution satisfies all three interface conditions (2.10)–(2.12) but unlike Example 1, here, the normal velocity v across the interface $y=1$ is nonzero. Tables 3 and 4 show the grid refinement analysis of $L^{2}$ errors for the velocity u, v and the pressure $p, \phi$, respectively. As in Example 1, both velocity components u, v in Stokes region and the pressure $\phi$ in Darcy’s region behave like second-order convergent. However, the pressure p in Stokes region behaves exactly first-order convergent. Again, the numerical results show better convergence rates than the ones obtained from the present theoretical analysis.

Table 3 Grid refinement analysis of $L^{2}$ errors for the solutions u and v in Example 2

Table 4 Grid refinement analysis of $L^{2}$ errors for the solutions p and $\phi$ in Example 2

7 Concluding Remarks

The stability and error estimates for both velocity and pressure have been established for the MAC scheme of stationary Stokes/Darcy coupling problem based on finite difference methods. The stability of the velocity in both Stokes and Darcy regions is derived by performing careful estimates and the stability of the pressure in both regions is established by considering an analogue of discrete divergence problem . We remark that the mesh width $\Delta y$ needs to be below a threshold to make sure the stability. However, there is no limitation on the mesh size $\Delta x$. This is due to the control of the related estimates on the interface. Following the similar analysis on stability, the error estimates for the velocity and the pressure in both regions are performed. The theoretical results show first-order convergence of the scheme in discrete $L^2$ norm for both velocity and the pressure. The main problematic term comes form the estimate of the first order discrete approximation (3.13) of the interface condition (2.11). Moreover, in fluid region, the first-order convergence for the x-derivative of velocity component u and the y-derivative of velocity component v is also obtained in discrete $L^2$ norms. However, numerical tests presented in Sect. 5 show one order better for the velocity in Stokes region and the pressure in Darcy region. This is a gap between theoretical results and numerical evidences which will be studied elsewhere.