1 Introduction

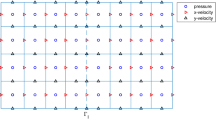
Due to the importance of incompressible flows, many numerical methods (such as finite difference methods, finite element methods, and finite volume methods) have been developed for solving the Stokes and Navier–Stokes equations over the past five decades (e.g., [5, 14] and references therein). However, it is arguably that “Among the many numerical methods that are available for solving the Navier–Stokes equations, one of the best and simplest is the marker-and-cell method.” (Girault and Lopez [4, p. 347]). The same point view has been shared by Han and Wu [6, p. 560]: “It is well known that the marker and cell (MAC) is one of the simplest and most effective numerical schemes for solving Stokes equations and Navier–Stokes equations.” The MAC method was introduced by Lebedev [12] and Daly et al. [3] in 1960s, and has been widely used in engineering applications as evidenced being the basis of many flow packages [17, p. 1579]. The MAC method is a finite difference method on rectangular cells with pressure approximated at the cell center, the \(x\)-component of velocity approximated at the midpoint of vertical edges of the cell, and the \(y\)-component of velocity approximated at the midpoint of horizontal edges of the cell (cf. Fig. 1).

Fig. 1
figure 1

An exemplary staggered grid

Full size image

Though the MAC method has been used successfully since 1965, its theoretical numerical analysis was not carried out until 1992 by Nicolaides and his collaborators [17, 18] by transforming the MAC method into a finite volume method. The difficulty is due to the fact that only a few mathematical tools are available for finite difference or finite volume methods [4, p. 348]. In 1996, Girault and Lopez [4] performed further analysis of the MAC method by interpreting it as a mixed finite element method for the vorticity–velocity–pressure formulation with special numerical quadratures. Then in 1998, Han and Wu [6] showed that the MAC method can be obtained from a new mixed finite element method with the two components of velocity and pressure defined on three staggered rectangular grids. In 2008, Kanschat [11] showed that the MAC scheme is algebraically equivalent to the first-order local discontinuous Galerkin method of Cockburn et al. [2] with a proper quadrature. Their method is based on the \(H(div)\)-conforming Raviart–Thomas \(RT_0\) element. Inspired by the work of Kanschat [11], very soon Minev [15] demonstrated that the MAC scheme can be obtained by using the first-order Nédélec edge element on rectangular cells.

We would like to remark that all these papers [4, 6, 11, 17] proved that the MAC method has first order convergence \(O(h)\) for both the velocity (in \(H^1\) norm) and the pressure (in \(L^2\) norm) on uniform rectangular meshes. But Nicolaides [17, p. 1591] pointed out that numerical results suggest that the velocity is \(O(h^2)\) without any proof. To our best knowledge, there is no any existing paper proving the \(O(h^2)\) convergence for the velocity.

In this paper, inspired by the analysis technique developed by Weiser and Wheeler [24] for elliptic problems, and Süli and Monk [16, 23] for both elliptic and Maxwell’s equations solved by cell-centered non-uniform rectangular grids, we first derive the MAC scheme from a variational form, and then we show that the \(O(h^2)\) superconvergence is indeed true for both the velocity and pressure on non-uniform rectangular grids. Superconvergence for other equations are well studied (cf. [7–9, 19, 25, 26], [13, Ch. 5] and references therein). Finally, we like to mention that (as one anonymous referee pointed out) there are some convergence analysis obtained for the MAC scheme developed for primitive equations (PEs), and planetary geostrophic equation (PGEs). For example, for the PEs the \(O(h^2)\) convergence for the velocity in the \(L^2\) norm is proved on uniform rectangular meshes by Samelson et al. [21], and for PGEs the \(O(h^4)\) convergence in the \(L^2\) norm is proved for the temperature on uniform rectangular meshes by Samelson et al. [22]. It would be interesting to explore in the future if our analysis can be extended to these problems on non-uniform rectangular grids.

The rest of the paper is organized as follows. In Sect. 2, we demonstrate that the MAC scheme can be derived from a variational form, which will be used late in the error analysis. In Sect. 3, we prove a discrete stability, which enjoys the same form in the continuous case. Section 4 is devoted to the \(O(h^2)\) superconvergence analysis for the MAC scheme. Numerical examples are presented in Sect. 5 to support our theoretical analysis. We conclude the paper in Sect. 6.

2 Derivation of the MAC Scheme

Let us consider the Stokes problem in two dimensional space: find the velocity \({\varvec{u}}=(u^x,u^y)^T\) and the pressure \(p\) such that

$$\begin{aligned}&-\mu \Delta {\varvec{u}}+ \nabla p = {\varvec{f}}, \quad \hbox {in}~\Omega :=(0,L_x)\times (0,L_y), \end{aligned}$$
(1)
$$\begin{aligned}&\nabla \cdot {\varvec{u}}= 0, \quad \hbox {in}~\Omega , \end{aligned}$$
(2)
$$\begin{aligned}&{\varvec{u}}=0, \quad \hbox {on}~\partial \Omega , \end{aligned}$$
(3)

where \({\varvec{f}}=(f^x,f^y)^T\) denotes a given force, \(\int _{\Omega }pdxdy=0\), and \(\mu > 0\) is the viscosity. For simplicity, we assume \(\mu =1\) in the rest paper. In the above, \(L_x\) and \(L_y\) denote the length of the rectangular domain \(\Omega \) in the \(x\)- and \(y\)-directions, respectively.

To construct a cell-centered difference scheme for the Stokes problem, we introduce a non-uniform grid of \(\Omega \):

$$\begin{aligned} 0=x_0<x_1<\cdots < x_M=L_x, \quad 0=y_0<y_1<\cdots < y_N=L_y, \end{aligned}$$

and denote the cell center \((x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})\). Furthermore, we approximate the pressure at each cell center \(p(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})\) by \(p_{i+\frac{1}{2},j+\frac{1}{2}}\), the \(x\)-velocity \(u^x\) at each \(x\)-edge center \(u^x(x_i,y_{j+\frac{1}{2}})\) by \(u^x_{i,j+\frac{1}{2}}\), and the \(y\)-velocity \(u^y\) at each \(y\)-edge center \(u^y(x_{i-\frac{1}{2}},y_j)\) by \(u^y_{i-\frac{1}{2},j}\). To measure the convergence rate, we denote \(h_x=\max _{1\le i\le M}(x_i-x_{i-1}),h_y=\max _{1\le j\le N}(y_j-y_{j-1})\), and \(h=\max (h_x,h_y)\).

By integrating the \(x\)-component of Eq. (1) over cell \(\Omega _{i,j+\frac{1}{2}}=(x_{i-\frac{1}{2}},x_{i+\frac{1}{2}})\times (y_j, y_{j+1})\), we have

$$\begin{aligned}&-\left[ \int _{y_j}^{y_{j+1}}\left( \frac{\partial u^x}{\partial x}\left( x_{i+\frac{1}{2}},y\right) -\frac{\partial u^x}{\partial x}\left( x_{i-\frac{1}{2}},y\right) \right) dy \nonumber \right. \\&\quad \left. +\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( \frac{\partial u^x}{\partial y}(x, y_{j+1})-\frac{\partial u^x}{\partial y}(x, y_j)\right) dx\right] \nonumber \\&\quad + \int _{y_j}^{y_{j+1}}\left( p\left( x_{i+\frac{1}{2}},y\right) -p\left( x_{i-\frac{1}{2}},y\right) \right) dy\nonumber \\&\quad = \int _{\Omega _{i,j+\frac{1}{2}}}f^x(x,y)dxdy, ~1\le i \le M-1, 0\le j \le N-1. \end{aligned}$$
(4)

Then approximating those edge integrals by midpoint values, the volume integral by its center value, and dividing both sides by \(|\Omega _{i,j+\frac{1}{2}}|=(x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}})(y_{j+1}-y_j)\), we obtain

$$\begin{aligned}&-\frac{1}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}}\left( \frac{u^x_{i+1,j+\frac{1}{2}}-u^x_{i,j+\frac{1}{2}}}{x_{i+1}-x_i} - \frac{u^x_{i,j+\frac{1}{2}}-u^x_{i-1,j+\frac{1}{2}}}{x_i-x_{i-1}}\right) \nonumber \\&\quad -\frac{1}{y_{j+1}-y_j}\left( \frac{u^x_{i,j+\frac{3}{2}}-u^x_{i,j+\frac{1}{2}}}{y_{j+\frac{3}{2}}-y_{j+\frac{1}{2}}} - \frac{u^x_{i,j+\frac{1}{2}}-u^x_{i,j-\frac{1}{2}}}{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}}\right) \nonumber \\&\quad + \frac{p_{i+\frac{1}{2},j+\frac{1}{2}}-p_{i-\frac{1}{2},j+\frac{1}{2}}}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}}=f^x_{i,j+\frac{1}{2}}, \end{aligned}$$
(5)

which can be rewritten as follows:

$$\begin{aligned} -\frac{\triangle _x^{+}u^x_{i,j+\frac{1}{2}} -\triangle _x^{-}u^x_{i,j+\frac{1}{2}}}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} -\frac{\triangle _y^{+}u^x_{i,j+\frac{1}{2}} -\triangle _y^{-}u^x_{i,j+\frac{1}{2}}}{y_{j+1}-y_j} + \triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}=f^x_{i,j+\frac{1}{2}}, \end{aligned}$$
(6)

where we used the following standard forward and backward difference operators:

$$\begin{aligned} \triangle _x^{+}u^x_{i,j+\frac{1}{2}}=\frac{u^x_{i+1,j+\frac{1}{2}}-u^x_{i,j+\frac{1}{2}}}{x_{i+1}-x_i}, \quad \triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}=\frac{p_{i+\frac{1}{2},j+\frac{1}{2}}-p_{i-\frac{1}{2},j+\frac{1}{2}}}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}}. \end{aligned}$$

Similar notations are used for operations in the \(y\)-direction. Here we denote \(f^x_{i,j+\frac{1}{2}}=f^x(x_i,y_{j+\frac{1}{2}})\).

Similarly, by integrating the \(y\)-component of Eq. (1) over cell \(\Omega _{i-\frac{1}{2},j}=(x_{i-1},x_i)\times (y_{j-\frac{1}{2}},y_{j+\frac{1}{2}})\), we have

$$\begin{aligned}&-\left[ \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( \frac{\partial u^y}{\partial x}(x_i,y)-\frac{\partial u^y}{\partial x}(x_{i-1},y)\right) dy\right. \nonumber \\&\quad \left. +\int _{x_{i-1}}^{x_i}\left( \frac{\partial u^y}{\partial y}\left( x, y_{j+\frac{1}{2}}\right) -\frac{\partial u^y}{\partial y}\left( x,y_{j-\frac{1}{2}}\right) \right) dx\right] \nonumber \\&\quad + \int _{x_{i-1}}^{x_i}\left( p\left( x,y_{j+\frac{1}{2}}\right) -p\left( x,y_{j-\frac{1}{2}}\right) \right) dx\nonumber \\&\quad = \int _{\Omega _{i-\frac{1}{2},j}}f^y(x,y)dxdy,~~1\le i\le M, ~1\le j \le N-1. \end{aligned}$$
(7)

Then approximating those edge integrals by midpoint values, the volume integral by its center value, and using the difference operators introduced above, we can obtain the cell-centered difference scheme for the \(y\)-velocity:

$$\begin{aligned} -\frac{\triangle _x^{+}u^y_{i-\frac{1}{2},j} -\triangle _x^{-}u^y_{i-\frac{1}{2},j}}{x_i-x_{i-1}} -\frac{\triangle _y^{+}u^y_{i-\frac{1}{2},j} -\triangle _y^{-}u^y_{i-\frac{1}{2},j}}{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} + \triangle _y^{-}p_{i-\frac{1}{2},j+\frac{1}{2}}=f^y_{i-\frac{1}{2},j}. \end{aligned}$$
(8)

By integrating Eq. (3) over cell \(\Omega _{i-\frac{1}{2},j+\frac{1}{2}}=(x_i-x_{i-1})\times (y_j,y_{j+1})\), and carring similar techniques as above, we can obtain the cell-centered difference scheme for Eq. (3):

$$\begin{aligned} \triangle _x^{-}u^x_{i,j+\frac{1}{2}} +\triangle _y^{+}u^y_{i-\frac{1}{2},j}=0. \end{aligned}$$
(9)

In summary, we recover the famous MAC scheme for the Stokes problem (1)–(3):

$$\begin{aligned}&-\frac{\triangle _x^{+}u^x_{i,j+\frac{1}{2}} -\triangle _x^{-}u^x_{i,j+\frac{1}{2}}}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} -\frac{\triangle _y^{+}u^x_{i,j+\frac{1}{2}} -\triangle _y^{-}u^x_{i,j+\frac{1}{2}}}{y_{j+1}-y_j} + \triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}=f^x_{i,j+\frac{1}{2}}, \qquad \end{aligned}$$
(10)
$$\begin{aligned}&-\frac{\triangle _x^{+}u^y_{i-\frac{1}{2},j} -\triangle _x^{-}u^y_{i-\frac{1}{2},j}}{x_i-x_{i-1}} -\frac{\triangle _y^{+}u^y_{i-\frac{1}{2},j} -\triangle _y^{-}u^y_{i-\frac{1}{2},j}}{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} + \triangle _y^{-}p_{i-\frac{1}{2},j+\frac{1}{2}}=f^y_{i-\frac{1}{2},j}, \qquad \end{aligned}$$
(11)
$$\begin{aligned}&\triangle _x^{-}u^x_{i,j+\frac{1}{2}}+\triangle _y^{+}u^y_{i-\frac{1}{2},j}=0. \end{aligned}$$
(12)

3 Stability Analysis

In this section, we will carry out the stability analysis for the scheme (10)–(12).

First, let us introduce various discrete norms to be used in the following analysis:

$$\begin{aligned}&||\triangle _x^{-} u^x_{i,j+\frac{1}{2}}||^2=\sum _{i=1}^M\sum _{j=0}^{N-1}(x_i-x_{i-1})(y_{j+1}-y_j)\triangle _x^{-} u^x_{i,j+\frac{1}{2}}\cdot \triangle _x^{-} u^x_{i,j+\frac{1}{2}}, \end{aligned}$$
(13)
$$\begin{aligned}&||\triangle _y^{-} u^x_{i,j+\frac{1}{2}}||^2=\sum _{i=0}^M\sum _{j=0}^{N} \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) \left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) \triangle _y^{-} u^x_{i,j+\frac{1}{2}}\cdot \triangle _y^{-} u^x_{i,j+\frac{1}{2}}, \qquad \end{aligned}$$
(14)
$$\begin{aligned}&||\triangle _x^{-} u^y_{i-\frac{1}{2},j}||^2=\sum _{i=1}^{M+1}\sum _{j=0}^{N} \left( x_{i-\frac{1}{2}}-x_{i-\frac{3}{2}}\right) \left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) \triangle _x^{-} u^y_{i-\frac{1}{2},j}\cdot \triangle _x^{-} u^y_{i-\frac{1}{2},j},\qquad \end{aligned}$$
(15)
$$\begin{aligned}&||\triangle _y^{-} u^y_{i-\frac{1}{2},j}||^2=\sum _{i=1}^{M}\sum _{j=1}^{N}(x_i-x_{i-1})(y_j-y_{j-1})\triangle _y^{-} u^y_{i-\frac{1}{2},j}\cdot \triangle _y^{-} u^y_{i-\frac{1}{2},j},\qquad \end{aligned}$$
(16)

where functions out of the index bounds \((0\le i \le M, 0\le j\le N)\) are treated as zeros, and any coordinates out of the physical domain are treated as their neighboring values. For example, in (14) we treat

$$\begin{aligned} x_{-\frac{1}{2}}=y_{-\frac{1}{2}}=0, ~~ x_{M+\frac{1}{2}}=L_x, ~~y_{N+\frac{1}{2}}=L_y. \end{aligned}$$

Note that to easily distinguish between the various norms, we leave the subindices inside the norms. For functions without operators \(\triangle _x^{\pm }\) or \(\triangle _y^{\pm }\), the discrete norm is defined as the function value at the cell center multiplying the cell area, e.g.,

$$\begin{aligned} ||u^x_{i,j+\frac{1}{2}}||^2=\sum _{i=0}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}} -x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)|u^x_{i,j+\frac{1}{2}}|^2. \end{aligned}$$
(17)

To prove the stability result for our scheme (10)–(12), we need the following lemmas.

Lemma 3.1

$$\begin{aligned}&\sum _{i=0}^M\sum _{j=0}^N\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}} \triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}\nonumber \\&\quad +\sum _{i=1}^M\sum _{j=1}^N(x_i-x_{i-1})\left( y_{j+\frac{1}{2}}- y_{j-\frac{1}{2}}\right) u^y_{i-\frac{1}{2},j} \triangle _y^{-}p_{i-\frac{1}{2},j+\frac{1}{2}}=0. \end{aligned}$$
(18)

Proof

Note that

$$\begin{aligned}&\sum _{i=0}^M\sum _{j=0}^N\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}} \cdot \triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = \sum _i\sum _j (y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}} \cdot \left( p_{i+\frac{1}{2},j+\frac{1}{2}}-p_{i-\frac{1}{2},j+\frac{1}{2}}\right) \nonumber \\&\quad = \sum _j (y_{j+1}-y_j)\left( \sum _i u^x_{i,j+\frac{1}{2}}\cdot p_{i+\frac{1}{2},j+\frac{1}{2}} -\sum _i u^x_{i,j+\frac{1}{2}}\cdot p_{i-\frac{1}{2},j+\frac{1}{2}}\right) \nonumber \\&\quad = -\sum _j (y_{j+1}-y_j)\sum _i \left( u^x_{i,j+\frac{1}{2}}-u^x_{i-1,j+\frac{1}{2}}\right) p_{i-\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = -\sum _i \sum _j (x_i-x_{i-1})(y_{j+1}-y_j)\cdot \left( \triangle _x^{-}u^x_{i,j+\frac{1}{2}}\right) \cdot p_{i-\frac{1}{2},j+\frac{1}{2}}, \end{aligned}$$
(19)

where in the third step we used the identity \( \sum _i u^x_{i,j+\frac{1}{2}}\cdot p_{i+\frac{1}{2},j+\frac{1}{2}} =\sum _i u^x_{i-1,j+\frac{1}{2}}\cdot p_{i-\frac{1}{2},j+\frac{1}{2}}. \) Here and below, without confusion we may not write out the specific bounds of \(i\) and \(j\).

By the same technique, we have

$$\begin{aligned}&\sum _i\sum _j(x_i-x_{i-1})\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) u^y_{i-\frac{1}{2},j} \cdot \triangle _y^{-}p_{i-\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = \sum _i(x_i-x_{i-1})\cdot \left( \sum _j u^y_{i-\frac{1}{2},j} p_{i-\frac{1}{2},j+\frac{1}{2}}-\sum _j u^y_{i-\frac{1}{2},j}p_{i-\frac{1}{2},j-\frac{1}{2}}\right) \nonumber \\&\quad = -\sum _i(x_i-x_{i-1})\sum _j\left( u^y_{i-\frac{1}{2},j+1}-u^y_{i-\frac{1}{2},j}\right) \cdot p_{i-\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = -\sum _i \sum _j (x_i-x_{i-1})(y_{j+1}-y_j)\cdot \left( \triangle _y^{+}u^y_{i-\frac{1}{2},j}\right) \cdot p_{i-\frac{1}{2},j+\frac{1}{2}}. \end{aligned}$$
(20)

The proof is completed by adding (19) and (20), and using (12).\(\square \)

We also need the following discrete Poincaré inequality.

Lemma 3.2

$$\begin{aligned} (i)&||u^x_{i,j+\frac{1}{2}}||^2 \le \frac{L_x^2}{2}||\triangle _x^{-}u^x_{i,j+\frac{1}{2}}||^2 +\frac{L_y^2}{2}||\triangle _y^{-}u^x_{i,j+\frac{1}{2}}||^2, \\ (ii)&||u^y_{i-\frac{1}{2},j}||^2 \le \frac{L_x^2}{2}||\triangle _x^{-}u^y_{i-\frac{1}{2},j}||^2 +\frac{L_y^2}{2}||\triangle _y^{-}u^y_{i-\frac{1}{2},j}||^2. \end{aligned}$$

Proof

(i) By definition of the discrete norm (17), we have

$$\begin{aligned}&||u^x_{i,j+\frac{1}{2}}||^2 = \sum _{i=0}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)\cdot \left( u^x_{i,j+\frac{1}{2}}\right) ^2 \\&\quad = \frac{1}{2}\left\{ \sum _{i=0}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}} -x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)|\sum _{m=1}^i (x_m-x_{m-1})\triangle _x^{-} u^x_{m,j+\frac{1}{2}}|^2 \right. \\&\qquad \left. + \sum _{i=0}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)|\sum _{n=0}^j \left( y_{n+\frac{1}{2}}-y_{n-\frac{1}{2}} \right) \triangle _y^{-} u^x_{i,n+\frac{1}{2}}|^2\right\} \\&\quad \le \frac{1}{2}\left\{ \sum _{i=0}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)\right. \\&\quad \left. \left[ \sum _{m=1}^i (x_m-x_{m-1})\cdot \sum _{m=1}^i(x_m-x_{m-1})|\triangle _x^{-} u^x_{m,j+\frac{1}{2}}|^2\right] \right. \\&\quad \left. + \sum _{i=0}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)\right. \\&\quad \left. \left[ \sum _{n=1}^j \left( y_{n+\frac{1}{2}}-y_{n-\frac{1}{2}}\right) \cdot \sum _{n=1}^j \left( y_{n+\frac{1}{2}}-y_{n-\frac{1}{2}}\right) |\triangle _y^{-} u^x_{i,n+\frac{1}{2}}|^2\right] \right\} \\&\quad \le \frac{1}{2}\left( \sum _{m=1}^M\sum _{j=0}^{N-1}(x_m-x_{m-1}) (y_{j+1}-y_j)|\triangle _x^{-} u^x_{m,j+\frac{1}{2}}|^2\right) \\&\quad \left( \sum _{i=0}^M \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) \cdot \sum _{m=1}^i(x_m-x_{m-1})\right) \\&\qquad + \frac{1}{2}\left( \sum _{i=0}^M\sum _{n=1}^{N-1} \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) \left( y_{n+\frac{1}{2}}-y_{n-\frac{1}{2}}\right) |\triangle _y^{-}u^y_{i,n+\frac{1}{2}}|^2\right) \\&\quad \left( \sum _{j=0}^{N-1}(y_{j+1}-y_j)\cdot \sum _{n=1}^j \left( y_{n+\frac{1}{2}}-y_{n-\frac{1}{2}}\right) \right) \\&\quad \le \frac{L_x^2}{2}||\triangle _x^{-} u^x_{m,j+\frac{1}{2}}||^2 +\frac{L_y^2}{2}||\triangle _y^{-} u^x_{i,n+\frac{1}{2}}||^2, \end{aligned}$$

which completes the proof. (ii) The proof is similar to (i). \(\square \)

Remark 3.1

If a function \(v\) only vanishes on one edge of \(\Omega \), the discrete Poincaré inequality can be modified as:

$$\begin{aligned}&||v_{i,j+\frac{1}{2}}||^2 \le L_x^2||\triangle _x^{-} v_{i,j+\frac{1}{2}}||^2 \quad \forall ~v|_{x=0}=0,\\&||v_{i-\frac{1}{2},j}||^2 \le L_y^2||\triangle _y^{-} v_{i-\frac{1}{2},j}||^2 \quad \forall ~v|_{y=0}=0. \end{aligned}$$

To make the stability analysis clearer, we first prove the following identities.

Lemma 3.3

$$\begin{aligned} (i)&-\sum _{i=1}^{M}\sum _{j=0}^{N-1}(y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}}\cdot \left( \triangle _x^{+} u^x_{i,j+\frac{1}{2}}-\triangle _x^{-} u^x_{i,j+\frac{1}{2}}\right) =||\triangle _x^{-} u^x_{i,j+\frac{1}{2}}||^2, \\ (ii)&-\sum _{i=0}^{M}\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) u^x_{i,j+\frac{1}{2}}\cdot \left( \triangle _y^{+} u^x_{i,j+\frac{1}{2}}-\triangle _y^{-} u^x_{i,j+\frac{1}{2}}\right) =||\triangle _y^{-} u^x_{i,j+\frac{1}{2}}||^2, \\ (iii)&-\sum _{i=1}^{M}\sum _{j=0}^{N}\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) u^y_{i-\frac{1}{2},j}\cdot \left( \triangle _x^{+} u^y_{i-\frac{1}{2},j}-\triangle _x^{-} u^y_{i-\frac{1}{2},j}\right) =||\triangle _x^{-} u^y_{i-\frac{1}{2},j}||^2, \\ (iv)&-\sum _{i=1}^{M}\sum _{j=0}^{N}(x_{i}-x_{i-1})u^y_{i-\frac{1}{2},j}\cdot \left( \triangle _y^{+} u^y_{i-\frac{1}{2},j}-\triangle _y^{-} u^y_{i-\frac{1}{2},j}\right) =||\triangle _y^{-} u^y_{i-\frac{1}{2},j}||^2. \end{aligned}$$

Proof

  1. (i)

    It is easy to see that

    $$\begin{aligned}&-\sum _{i=1}^{M}\sum _{j=0}^{N-1}(y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}}\cdot \left( \triangle _x^{+} u^x_{i,j+\frac{1}{2}}-\triangle _x^{-} u^x_{i,j+\frac{1}{2}}\right) \\&\quad = -\sum _{j=0}^{N-1}(y_{j+1}-y_j)\left[ \sum _{i=1}^{M}u^x_{i,j+\frac{1}{2}}\cdot \triangle _x^{+} u^x_{i,j+\frac{1}{2}} -\sum _{i=1}^{M}u^x_{i,j+\frac{1}{2}}\cdot \triangle _x^{-} u^x_{i,j+\frac{1}{2}}\right] \\&\quad = \sum _{j=0}^{N-1}(y_{j+1}-y_j)\sum _{i=1}^{M}\left( u^x_{i,j+\frac{1}{2}} -u^x_{i-1,j+\frac{1}{2}}\right) \triangle _x^{-} u^x_{i,j+\frac{1}{2}} \\&\quad = \sum _{i=1}^{M}\sum _{j=0}^{N-1}(x_i-x_{i-1})(y_{j+1}-y_j) \triangle _x^{-} u^x_{i,j+\frac{1}{2}}\cdot \triangle _x^{-} u^x_{i,j+\frac{1}{2}} =||\triangle _x^{-} u^x_{i,j+\frac{1}{2}}||^2, \end{aligned}$$

    where we used the definition (13) in the last step.

  2. (ii)

    Similarly, we have

    $$\begin{aligned}&-\sum _{i=0}^{M}\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) u^x_{i,j+\frac{1}{2}}\cdot \left( \triangle _y^{+} u^x_{i,j+\frac{1}{2}}-\triangle _y^{-} u^x_{i,j+\frac{1}{2}}\right) \\&\quad = \sum _{i=0}^{M}(x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}) \left[ \sum _{j=0}^{N-1}u^x_{i,j+\frac{1}{2}}\cdot \triangle _y^{-} u^x_{i,j+\frac{1}{2}} -\sum _{j=0}^{N-1}u^x_{i,j+\frac{1}{2}}\cdot \triangle _y^{+} u^x_{i,j+\frac{1}{2}}\right] \\&\quad = \sum _{i=0}^{M}\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) \left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) \triangle _y^{-} u^x_{i,j+\frac{1}{2}}\cdot \triangle _y^{-} u^x_{i,j+\frac{1}{2}} =||\triangle _y^{-} u^x_{i,j+\frac{1}{2}}||^2, \end{aligned}$$

    where we used the definition (14) in the last step.

The proofs of (iii) and (iv) can be carried out similarly. \(\square \)

With the above preparations, we can obtain the following stability for our scheme.

Theorem 3.1

$$\begin{aligned}&||\triangle _x^{-}u^x_{i,j+\frac{1}{2}}||^2 + ||\triangle _y^{-}u^x_{i,j+\frac{1}{2}}||^2 + ||\triangle _x^{-}u^y_{i-\frac{1}{2},j}||^2 + ||\triangle _y^{-}u^y_{i-\frac{1}{2},j}||^2 \\&\quad \le C\left( ||f^x_{i,j+\frac{1}{2}}||^2+||f^y_{i-\frac{1}{2},j}||^2\right) . \end{aligned}$$

Proof

Multiplying (10) by \((x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}})(y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}}\), and summing up all \(i\) and \(j\), we obtain

$$\begin{aligned}&-\sum _i\sum _j (y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}}\left( \triangle _x^{+}u^x_{i,j+\frac{1}{2}} -\triangle _x^{-}u^x_{i,j+\frac{1}{2}}\right) \nonumber \\&\quad -\sum _i\sum _j \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) u^x_{i,j+\frac{1}{2}}\left( \triangle _y^{+}u^x_{i,j+\frac{1}{2}} -\triangle _y^{-}u^x_{i,j+\frac{1}{2}}\right) \nonumber \\&\quad +\sum _i\sum _j \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}}\triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = \sum _i\sum _j \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)u^x_{i,j+\frac{1}{2}}f^x_{i,j+\frac{1}{2}}, \end{aligned}$$
(21)

where we skipped the detailed lower and upper indices for both \(i\) and \(j\).

Similarly, multiplying (11) by \((x_i-x_{i-1})(y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}})u^y_{i-\frac{1}{2},j}\), we obtain

$$\begin{aligned}&-\sum _i\sum _j \left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) u^y_{i-\frac{1}{2},j} \left( \triangle _x^{+}u^y_{i-\frac{1}{2},j} -\triangle _x^{-}u^y_{i-\frac{1}{2},j}\right) \nonumber \\&\quad -\sum _i\sum _j (x_i-x_{i-1})u^y_{i-\frac{1}{2},j}\left( \triangle _y^{+}u^y_{i-\frac{1}{2},j} -\triangle _y^{-}u^y_{i-\frac{1}{2},j}\right) \nonumber \\&\quad +\sum _i\sum _j (x_i-x_{i-1})\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) u^y_{i-\frac{1}{2},j}\triangle _y^{-}p_{i-\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = \sum _i\sum _j (x_i-x_{i-1})\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) u^y_{i-\frac{1}{2},j}f^y_{i-\frac{1}{2},j}. \end{aligned}$$
(22)

Adding (21) and (22), using the identities given in Lemmas 3.1 and 3.3, then using the Cauchy–Schwarz inequality to those two right-hand side terms and Lemma 3.2, we have

$$\begin{aligned}&||\triangle _x^{-}u^x_{i,j+\frac{1}{2}}||^2 + ||\triangle _y^{-}u^x_{i,j+\frac{1}{2}}||^2 + ||\triangle _x^{-}u^y_{i-\frac{1}{2},j}||^2 + ||\triangle _y^{-}u^y_{i-\frac{1}{2},j}||^2 \\&\quad \le \delta _1\left( \frac{L_x^2}{2}||\triangle _x^{-}u^x_{i,j+\frac{1}{2}}||^2 + \frac{L_y^2}{2}||\triangle _y^{-}u^x_{i,j+\frac{1}{2}}||^2\right) + \frac{1}{4\delta _1}||f^x_{i,j+\frac{1}{2}}||^2 \\&\quad + \delta _2\left( \frac{L_x^2}{2}||\triangle _x^{-}u^y_{i-\frac{1}{2},j}||^2 + \frac{L_y^2}{2}||\triangle _y^{-}u^y_{i-\frac{1}{2},j}||^2\right) + \frac{1}{4\delta _2}||f^y_{i-\frac{1}{2},j}||^2, \end{aligned}$$

which concludes the proof by choosing \(\delta _1\) and \(\delta _2\) sufficiently small. \(\square \)

Remark 3.2

Multiplying (1) by \({\varvec{u}}\), integrating by parts and using (2), we easily have

$$\begin{aligned} ||\nabla {\varvec{u}}||^2_0=({\varvec{f}},{\varvec{u}})\le \frac{1}{4\delta }||{\varvec{f}}||_0^2 + \delta ||{\varvec{u}}||_0^2. \end{aligned}$$

Using the Poincaré inequality [1, p. 135]

$$\begin{aligned} ||{\varvec{u}}||_0^2\le C||\nabla {\varvec{u}}||_0^2, \quad \forall ~{\varvec{u}}\in (H_0^1(\Omega ))^2, \end{aligned}$$

and choosing \(\delta >0\) small enough, we obtain the stability in continuous form

$$\begin{aligned} ||\nabla {\varvec{u}}||^2_0 \le C||{\varvec{f}}||_0^2, \end{aligned}$$
(23)

whose discrete form is given in Theorem 3.1.

4 Error Analysis

In this section, we shall derive the error analysis for our scheme. First, let us denote the errors

$$\begin{aligned} e^x_{i,j+\frac{1}{2}}&= u^x\left( x_i,y_{j+\frac{1}{2}}\right) -u^x_{i,j+\frac{1}{2}},\\ ~e^y_{i-\frac{1}{2},j}&= u^y\left( x_{i-\frac{1}{2}},y_j\right) -u^y_{i-\frac{1}{2},j},\\ ~e^p_{i+\frac{1}{2},j+\frac{1}{2}}&= p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) -p_{i+\frac{1}{2},j+\frac{1}{2}}, \end{aligned}$$

where \(u^x(x_i,y_{j+\frac{1}{2}}), u^y(x_{i-\frac{1}{2}},y_j)\) and \(p(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})\) denote the exact solutions \(u^x, u^y\) and \(p\) of the Stokes problem (1)–(3) at those specific points, respectively.

From our scheme derivation process, we can obtain the following error equations:

$$\begin{aligned}&-\frac{\triangle _x^{+}e^x_{i,j+\frac{1}{2}}-\triangle _x^{-}e^x_{i,j+\frac{1}{2}}}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} -\frac{\triangle _y^{+}e^x_{i,j+\frac{1}{2}}-\triangle _y^{-}e^x_{i,j+\frac{1}{2}}}{y_{j+1}-y_j} + \triangle _x^{-}e^p_{i+\frac{1}{2},j+\frac{1}{2}}=R^x_{i,j+\frac{1}{2}}, \qquad \end{aligned}$$
(24)
$$\begin{aligned}&-\frac{\triangle _x^{+}e^y_{i-\frac{1}{2},j}-\triangle _x^{-}e^y_{i-\frac{1}{2},j}}{x_{i}-x_{i-1}} -\frac{\triangle _y^{+}e^y_{i-\frac{1}{2},j}-\triangle _y^{-}e^y_{i-\frac{1}{2},j}}{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} + \triangle _y^{-}e^p_{i-\frac{1}{2},j+\frac{1}{2}}=R^y_{i-\frac{1}{2},j},\qquad \end{aligned}$$
(25)
$$\begin{aligned}&\triangle _x^{-}e^x_{i,j+\frac{1}{2}}+\triangle _y^{+}e^y_{i-\frac{1}{2},j} =R^d_{i-\frac{1}{2},j+\frac{1}{2}}, \end{aligned}$$
(26)

where detailed expressions for \(R^x, R^y\) and \(R^d\) will be given below.

From (4) and (10), we have

$$\begin{aligned} R^x_{i,j+\frac{1}{2}}&= -\frac{\triangle _x^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right) \!-\!\triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) }{x_{i+\frac{1}{2}}\!-\!x_{i-\frac{1}{2}}} \!-\!\frac{\triangle _y^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right) \!-\!\triangle _y^{-}u^x \left( x_i,y_{j+\frac{1}{2}}\right) }{y_{j+1}-y_j} \nonumber \\&+ \triangle _x^{-}p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) -f^x_{i,j+\frac{1}{2}} \nonumber \\&= \frac{1}{|\Omega _{i,j+\frac{1}{2}}|} \int _{y_j}^{y_{j+1}} \left( \frac{\partial u^x}{\partial x} \left( x_{i+\frac{1}{2}},y\right) -\frac{\partial u^x}{\partial x}\left( x_{i-\frac{1}{2}},y\right) \right) dy\nonumber \\&- \frac{\triangle _x^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right) -\triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) }{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} \nonumber \\&+ \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \left( \frac{\partial u^x}{\partial y}(x, y_{j+1})-\frac{\partial u^x}{\partial y}(x, y_j)\right) dx\nonumber \\&-\frac{\triangle _y^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right) -\triangle _y^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) }{y_{j+1}-y_j} \nonumber \\&- \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{y_j}^{y_{j+1}} \left( p\left( x_{i+\frac{1}{2}},y\right) -p\left( x_{i-\frac{1}{2}},y\right) \right) dy + \triangle _x^{-}p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) \nonumber \\&+ \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{\Omega _{i,j+\frac{1}{2}}}f^x(x,y)dxdy -f^x\left( x_i,y_{j+\frac{1}{2}}\right) \nonumber \\&= R^x_1 + R^x_2 + R^x_3 + R^x_4. \end{aligned}$$
(27)

Similarly, from (7) and (11), we have

$$\begin{aligned} R^y_{i-\frac{1}{2},j}&= -\frac{\triangle _x^{+}u^y\left( x_{i-\frac{1}{2}},y_j\right) \!-\!\triangle _x^{-}u^y(x_{i-\frac{1}{2}},y_j)}{x_i-x_{i-1}} \!-\!\frac{\triangle _y^{+}u^y\left( x_{i-\frac{1}{2}},y_j\right) -\triangle _y^{-}u^y\left( x_{i-\frac{1}{2}},y_j\right) }{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} \nonumber \\&+ \triangle _y^{-}p\left( x_{i-\frac{1}{2}},y_{j+\frac{1}{2}}\right) -f^y_{i-\frac{1}{2},j} \nonumber \\&= \frac{1}{|\Omega _{i-\frac{1}{2},j}|} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( \frac{\partial u^y}{\partial x}(x_i,y)-\frac{\partial u^y}{\partial x}(x_{i-1},y)\right) dy\nonumber \\&- \frac{\triangle _x^{+}u^y \left( x_{i-\frac{1}{2}},y_j\right) - \triangle _x^{-}u^y\left( x_{i-\frac{1}{2}},y_j\right) }{x_i-x_{i-1}} \nonumber \\&+ \frac{1}{|\Omega _{i-\frac{1}{2},j}|}\int _{x_{i-1}}^{x_i} \left( \frac{\partial u^y}{\partial y}\left( x, y_{j+\frac{1}{2}}\right) -\frac{\partial u^y}{\partial y}\left( x, y_{j-\frac{1}{2}}\right) \right) dx\nonumber \\&-\frac{\triangle _y^{+}u^y\left( x_{i-\frac{1}{2}},y_j\right) -\triangle _y^{-}u^y\left( x_{i-\frac{1}{2}}, y_j\right) }{ y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} \nonumber \\&- \frac{1}{|\Omega _{i-\frac{1}{2},j}|}\int _{x_{i-1}}^{x_i} \left( p\left( x,y_{j+\frac{1}{2}}\right) -p\left( x,y_{j-\frac{1}{2}}\right) \right) dx + \triangle _y^{-}p\left( x_{i-\frac{1}{2}},y_{j+\frac{1}{2}}\right) \nonumber \\&+ \frac{1}{|\Omega _{i-\frac{1}{2}, j}|}\int _{\Omega _{i-\frac{1}{2},j}}f^y(x,y)dxdy -f^y\left( x_{i-\frac{1}{2}},y_j\right) \nonumber \\&= R^y_1 + R^y_2 + R^y_3 + R^y_4. \end{aligned}$$
(28)

Finally, from (12), it is easy to see that

$$\begin{aligned} R^d_{i-\frac{1}{2},j+\frac{1}{2}}=\triangle _x^{-}u^x\left( x_i, y_{j+\frac{1}{2}}\right) +\triangle _y^{+}u^y\left( x_{i-\frac{1}{2}},y_j\right) . \end{aligned}$$
(29)

To prove the error analysis of our scheme, below we first estimate \(R^x_1\). Denote the maximum norm for the \(r\)-th derivatives of any function \(w\) as \(|D^rw|_{\infty }=|\frac{\partial ^r w}{\partial x^m\partial y^n}|_{\infty ,\overline{\Omega }}\), where \(m+n=r\), and \(m,n\ge 0\).

Lemma 4.1

$$\begin{aligned} R^x_1&= \frac{1}{|\Omega _{i,j+\frac{1}{2}}|} \int _{y_j}^{y_{j+1}}\left( \frac{\partial u^x}{\partial x}\left( x_{i+\frac{1}{2}},y\right) -\frac{\partial u^x}{\partial x}\left( x_{i-\frac{1}{2}},y\right) \right) dy\nonumber \\&- \frac{\triangle _x^{+}u^x(x_i,y_{j+\frac{1}{2}})-\triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) }{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} \nonumber \\&= -\frac{1}{12}\left( x_{i+1}+x_{i-1}-2x_i\right) \frac{\partial ^3 u^x}{\partial x^3}\left( x_i,y_{j+\frac{1}{2}}\right) +O(h^2)||D^4 u^x||_{\infty }, \end{aligned}$$
(30)

Proof

(i)  Note that \(R_1^x\) can be rewritten as follows

$$\begin{aligned} R^x_1 \!=\! \frac{1}{|\Omega _{i,j+\frac{1}{2}}|} \int _{\Omega _{i,j+\frac{1}{2}}}\!\! \left\{ \frac{\partial ^2 u^x}{\partial x^2}(x,y)dxdy \!-\! \frac{\triangle _x^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right) \!-\!\triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) }{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}}\right\} dxdy. \end{aligned}$$
(31)

By the Taylor expansion, we have

$$\begin{aligned} \triangle _x^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right)&= \frac{\partial u^x_*}{\partial x} +\frac{1}{2}(x_{i+1}-x_i)\frac{\partial ^2 u^x_*}{\partial x^2}\nonumber \\&+\frac{1}{6}(x_{i+1}-x_i)^2\frac{\partial ^3 u^x_*}{\partial x^3} +\frac{1}{24}(x_{i+1}-x_i)^3\frac{\partial ^4 \hat{u}^x}{\partial x^4}, \end{aligned}$$
(32)

where \(\frac{\partial ^k u^x_*}{\partial x^k}, k=1,2,3,\) denote the derivatives evaluated at point \((x_i,y_{j+\frac{1}{2}})\), and \(\frac{\partial ^4 \hat{u}^x}{\partial x^4}\) denotes the derivative at some point between \((x_i,y_{j+\frac{1}{2}})\) and \((x_{i+1},y_{j+\frac{1}{2}})\).

Similarly, by the Taylor expansion, we can obtain

$$\begin{aligned} \triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right)&= \frac{\partial u^x_*}{\partial x} +\frac{1}{2}(x_{i-1}-x_i)\frac{\partial ^2 u^x_*}{\partial x^2}\nonumber \\&+\frac{1}{6}(x_{i-1}-x_i)^2\frac{\partial ^3 u^x_*}{\partial x^3} +\frac{1}{24}(x_{i-1}-x_i)^3\frac{\partial ^4 \check{u}^x}{\partial x^4}, \end{aligned}$$
(33)

where \(\frac{\partial ^4 \check{u}^x}{\partial x^4}\) denotes the derivative at some point between \((x_{i-1},y_{j+\frac{1}{2}})\) and \((x_i,y_{j+\frac{1}{2}})\).

Combining (32) and (33), we have

$$\begin{aligned}&\frac{\triangle _x^{+}u^x\left( x_i,y_{j+\frac{1}{2}}\right) -\triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) }{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} \nonumber \\&\quad = \frac{1}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}}\nonumber \\&\left[ \frac{x_{i+1}-x_{i-1}}{2}\frac{\partial ^2 u^x_*}{\partial x^2} + \frac{x_{i+1}-x_{i-1}}{6}(x_{i+1}+x_{i-1}-2x_i)\frac{\partial ^3 u^x_*}{\partial x^3} +O(h_x^3)||\frac{\partial ^4 u^x}{\partial x^4}||_{\infty }\right] \nonumber \\&\quad = \frac{\partial ^2 u^x_*}{\partial x^2} + \frac{1}{3}(x_{i+1}+x_{i-1}-2x_i)\frac{\partial ^3 u^x_*}{\partial x^3} +O(h_x^2)||\frac{\partial ^4 u^x}{\partial x^4}||_{\infty }, \end{aligned}$$
(34)

where in the last step we used the following property

$$\begin{aligned} x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}=\frac{x_i+x_{i+1}}{2} -\frac{x_{i-1}+x_i}{2}=\frac{x_{i+1}-x_{i-1}}{2}. \end{aligned}$$
(35)

On the other hand, using the Taylor expansion:

$$\begin{aligned} \frac{\partial ^2 u^x}{\partial x^2}=\frac{\partial ^2 u^x_*}{\partial x^2} +(x-x_i)\frac{\partial ^3 u^x_*}{\partial x^3} +\left( y-y_{j+\frac{1}{2}}\right) \frac{\partial ^3 u^x_*}{\partial x^2\partial y} +O(h^2)||D^4 u^x||_{\infty }. \end{aligned}$$

Integrating this expansion over cell \(\Omega _{i,j+\frac{1}{2}}\) and using the property

$$\begin{aligned} \int _{\Omega _{i,j+\frac{1}{2}}}(y-y_{j+\frac{1}{2}})dxdy=0, \end{aligned}$$

we have

$$\begin{aligned} \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{\Omega _{i,j+\frac{1}{2}}}\frac{\partial ^2 u^x}{\partial x^2} = \frac{\partial ^2 u^x_*}{\partial x^2} + \frac{1}{4}(x_{i+1}+x_{i-1}-2x_i)\frac{\partial ^3 u^x_*}{\partial x^3} +O(h^2)||D^4 u^x||_{\infty }.\nonumber \\ \end{aligned}$$
(36)

Subtracting (34) from (36), we have

$$\begin{aligned} R_1^x=-\frac{1}{12}(x_{i+1}+x_{i-1}-2x_i)\frac{\partial ^3 u^x_*}{\partial x^3} +O(h^2)||D^4 u^x||_{\infty }, \end{aligned}$$

which concludes the proof. \(\square \)

Remark 4.1

For simplicity, in Lemma 4.1 we used the maximum norm to bound the error. If we want to bound the error by the Sobolev norm, we have to use the Taylor expansion with error in integral form.

Furthermore, we like to remark that \(R_1^x\) is only \(O(h)\) for a non-uniform grid, since \(x_{i+1}+x_{i-1}-2x_i\ne 0\) unless a uniform mesh is considered. Hence the traditional error analysis technique by using the stability result directly can lead to only \(O(h)\) convergence. Such issue has been noticed before for elliptic problems (e.g., [23, 24]) and Maxwell’s equations [16]. By following similar ideas, we can derive \(O(h^2)\) error estimate by summing up all the contributions of local truncation errors as shown in the next lemma.

Lemma 4.2

$$\begin{aligned} \sum _{i=1}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)R_1^x\cdot e^x_{i,j+\frac{1}{2}} \le Ch_x^2||\triangle _x^{-}e^x_{i,j+\frac{1}{2}}||. \end{aligned}$$

Proof

Denote \(b_{i,j+\frac{1}{2}}=\frac{\partial ^3u^x}{\partial x^3}(x_i,y_{j+\frac{1}{2}})\). For the dominant term \((x_{i+1}+x_{i-1}-2x_i)b_{i,j+\frac{1}{2}}\) of \(R_1^x\), using property (35), we have

$$\begin{aligned}&\sum _{i=1}^M\sum _{j=0}^{N-1}\left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)(x_{i+1}+x_{i-1}-2x_i)\cdot e^x_{i,j+\frac{1}{2}} b_{i,j+\frac{1}{2}} \nonumber \\&\quad = \sum _{j=0}^{N-1}(y_{j+1}-y_j)\sum _{i=1}^M\left( \frac{x_{i+1}-x_{i-1}}{2}\right) (x_{i+1}+x_{i-1}-2x_i)e^x_{i,j+\frac{1}{2}}b_{i,j+\frac{1}{2}} \nonumber \\&\quad = \sum _{j=0}^{N-1}(y_{j+1}-y_j)\sum _{i=1}^M\frac{(x_{i+1}-x_i)+(x_i-x_{i-1})}{2}\nonumber \\&\qquad \cdot [(x_{i+1}-x_i)-(x_i-x_{i-1})]e^x_{i,j+\frac{1}{2}}b_{i,j+\frac{1}{2}} \nonumber \\&\quad = \frac{1}{2}\sum _{j=0}^{N-1}(y_{j+1}-y_j)\sum _{i=1}^M\left[ (x_{i+1}-x_i)^2-(x_i-x_{i-1})^2\right] e^x_{i,j+\frac{1}{2}} b_{i,j+\frac{1}{2}} \nonumber \\&\quad = \frac{1}{2}\sum _{j=0}^{N-1}(y_{j+1}-y_j)\sum _{i=1}^M(x_i-x_{i-1})^2 \left( e^x_{i-1,j+\frac{1}{2}}b_{i-1,j+\frac{1}{2}} -e^x_{i,j+\frac{1}{2}}b_{i,j+\frac{1}{2}}\right) \nonumber \\&\quad = -\frac{1}{2}\sum _{i=1}^M\sum _{j=0}^{N-1}(x_i-x_{i-1})(y_{j+1}-y_j) \cdot (x_i-x_{i-1})^2\nonumber \\&\quad \left[ b_{i,j+\frac{1}{2}}\triangle _x^{-}e^x_{i,j+\frac{1}{2}} + e^x_{i-1,j+\frac{1}{2}} \triangle _x^{-}b_{i,j+\frac{1}{2}}\right] \nonumber \\&\quad \le Ch_x^2||\triangle _x^{-}e^x_{i,j+\frac{1}{2}}||, \end{aligned}$$
(37)

where in the last step we used the Cauchy–Schwarz inequality, the notation of norm (13), and the identity

$$\begin{aligned} \triangle _x^{-}(a_ib_i)=b_i\triangle _x^{-}a_i + a_{i-1}\triangle _x^{-}b_i. \end{aligned}$$

Similar estimates can be obtained for \(R^x_2\). Now we investigate the error caused by \(R^x_3\).

Lemma 4.3

$$\begin{aligned} R_3^x&= \triangle _x^{-}p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) -\frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{y_j}^{y_{j+1}} \left( p\left( x_{i+\frac{1}{2}},y\right) -p\left( x_{i-\frac{1}{2}},y\right) \right) dy\nonumber \\&= O(h^2)||D^3 p||_{\infty }. \end{aligned}$$
(38)

Proof

Note that \(R_3^x\) can be rewritten as

$$\begin{aligned} R_3^x = \triangle _x^{-}p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) -\frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{\Omega _{i,j+\frac{1}{2}}}\frac{\partial p}{\partial x}(x,y)dxdy. \end{aligned}$$
(39)

Using the Taylor expansion at \((x_i,y_{j+\frac{1}{2}})\), we have

$$\begin{aligned} \triangle _x^{-}p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) =\frac{\partial p_*}{\partial x} +\frac{1}{2}\left( x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}}-2x_i\right) \frac{\partial ^2 p_*}{\partial x^2} +O(h_x^2)||\frac{\partial ^3 p}{\partial x^3}||_{\infty }, \end{aligned}$$
(40)

where \(\frac{\partial ^k p_*}{\partial x^k}, k=1,2,\) denote the derivatives evaluated at point \((x_i,y_{j+\frac{1}{2}})\).

Taking the Taylor expansion of \(\frac{\partial p}{\partial x}\) at \((x_i,y_{j+\frac{1}{2}})\), and then integrating over cell \(\Omega _{i,j+\frac{1}{2}}\), we obtain

$$\begin{aligned} \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{\Omega _{i,j+\frac{1}{2}}}\frac{\partial p}{\partial x} = \frac{\partial p_*}{\partial x} + \frac{1}{2}\left( x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}}-2x_i\right) \frac{\partial ^2 p_*}{\partial x^2} +O(h^2)||D^3 p||_{\infty }. \end{aligned}$$
(41)

The proof is completed by substituting (40) and (41) into (39). \(\square \)

Lemma 4.4

$$\begin{aligned} (i)&~ R_4^x = \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{\Omega _{i,j+\frac{1}{2}}}f^x(x,y)dxdy -f^x\left( x_i,y_{j+\frac{1}{2}}\right) \nonumber \\&= \frac{1}{2}(x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}}-2x_i)\frac{\partial f^x}{\partial x} \left( x_i,y_{j+\frac{1}{2}}\right) +O(h^2)||D^2 f^x||_{\infty }, \nonumber \\ (ii)&~ \sum _{i=1}^M\sum _{j=0}^{N-1} \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_j)R_4^x\cdot e^x_{i,j+\frac{1}{2}} \le Ch^2||\triangle _x^{-}e^x_{i,j+\frac{1}{2}}||. \end{aligned}$$
(42)

Proof

  1. (i)

    Using the Taylor expansion of \(f^x\) at \((x_i,y_{j+\frac{1}{2}})\), and then integrating over cell \(\Omega _{i,j+\frac{1}{2}}\), we obtain

    $$\begin{aligned} \frac{1}{|\Omega _{i,j+\frac{1}{2}}|}\int _{\Omega _{i,j+\frac{1}{2}}}f^x = f^x_* + \frac{1}{2}\left( x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}}-2x_i\right) \frac{\partial f^x_*}{\partial x} +O(h^2)||D^2 f^x||_{\infty }, \nonumber \\ \end{aligned}$$
    (43)

    which completes the proof of (i).

  2. (ii)

    The proof of (ii) follows the same idea of Lemma 4.2.

\(\square \)

Lemma 4.5

$$\begin{aligned} R^d_{i-\frac{1}{2},j+\frac{1}{2}}&= \triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) + \triangle _y^{+} u^y\left( x_{i-\frac{1}{2}},y_j\right) \nonumber \\&= O(h^2_x)||\frac{\partial ^3 u^x}{\partial x^3}||_{\infty }+O(h^2_y)||\frac{\partial ^3 u^y}{\partial y^3}||_{\infty }. \end{aligned}$$
(44)

Proof

Taking the Taylor expansion of all functions at \((x_{i-\frac{1}{2}},y_{j+\frac{1}{2}})\), we have

$$\begin{aligned}&\triangle _x^{-}u^x\left( x_i,y_{j+\frac{1}{2}}\right) =\frac{\partial u^x_*}{\partial x}+\frac{1}{2}\left( x_i+x_{i-1}-2x_{i-\frac{1}{2}}\right) \frac{\partial ^2 u^x_*}{\partial x^2}+O(h^2_x)||\frac{\partial ^3 u^x}{\partial x^3}||_{\infty },\\&\triangle _y^{+} u^y\left( x_{i-\frac{1}{2}},y_j\right) =\frac{\partial u^y_*}{\partial y}+\frac{1}{2}\left( y_j+y_{j+1}-2y_{j+\frac{1}{2}}\right) \frac{\partial ^2 u^y_*}{\partial y^2}+O(h^2_y)||\frac{\partial ^3 u^y}{\partial y^3}||_{\infty }. \end{aligned}$$

Summing up the above two estimates, and using (29) and the properties

$$\begin{aligned} x_{i-\frac{1}{2}}=\frac{x_i+x_{i-1}}{2}, \quad y_{j+\frac{1}{2}}=\frac{y_j+y_{j+1}}{2}, \end{aligned}$$

we conclude the proof. \(\square \)

With the above preparations, now we can prove the following convergence result.

Theorem 4.1

Under the assumption that the pressure error is \(O(h^2)\), i.e.,

$$\begin{aligned} ||e^p_{i-\frac{1}{2},j+\frac{1}{2}}||\le Ch^2, \end{aligned}$$
(45)

we have the discrete \(H_1\) error estimate

$$\begin{aligned} ||\triangle _x^{-}e^x_{i,j+\frac{1}{2}}||+||\triangle _y^{-}e^x_{i,j+\frac{1}{2}}|| +||\triangle _x^{-}e^y_{i-\frac{1}{2},j}||+||\triangle _y^{-}e^y_{i-\frac{1}{2},j}||\le Ch^2, \end{aligned}$$
(46)

and the discrete \(L_2\) error estimate

$$\begin{aligned} ||e^x_{i,j+\frac{1}{2}}||+||e^y_{i-\frac{1}{2},j}||\le Ch^2. \end{aligned}$$
(47)

Proof

The proof follows a similar idea to the stability analysis developed in Theorem 3.1. One major difference is that the discrete divergence equation (26) is not zero anymore by comparison to (12).

Multiplying (24) by \(|\Omega _{i, j+\frac{1}{2}}|e^x_{i,j+\frac{1}{2}}\), and (25) by \(|\Omega _{i-\frac{1}{2},j}|e^y_{i-\frac{1}{2},j}\), summing up the results over all \(i\) and \(j\), and using Lemma 3.3 (with \(u\) replaced by \(e\)), we obtain

$$\begin{aligned}&||\triangle _x^{-}e^x_{i,j+\frac{1}{2}}||^2+||\triangle _y^{-}e^x_{i,j+\frac{1}{2}}||^2 +||\triangle _x^{-}e^y_{i-\frac{1}{2},j}||^2+||\triangle _y^{-}e^y_{i-\frac{1}{2},j}||^2 \nonumber \\&\quad = \sum _i\sum _j|\Omega _{i, j+\frac{1}{2}}|e^x_{i,j+\frac{1}{2}}R^x_{i,j+\frac{1}{2}} + \sum _i\sum _j|\Omega _{i-\frac{1}{2},j}|e^y_{i-\frac{1}{2},j}R^y_{i-\frac{1}{2},j} \nonumber \\&\quad - \sum _i\sum _j|\Omega _{i, j+\frac{1}{2}}|e^x_{i,j+\frac{1}{2}}\cdot \triangle _x^{-}e^p_{i+\frac{1}{2},j+\frac{1}{2}} - \sum _i\sum _j|\Omega _{i-\frac{1}{2},j}|e^y_{i-\frac{1}{2},j} \cdot \triangle _y^{-}e^p_{i-\frac{1}{2},j+\frac{1}{2}}. \qquad \quad \end{aligned}$$
(48)

Using Lemmas 4.2-4.4 and the Cauchy–Schwarz inequality, we have

$$\begin{aligned}&\sum _i\sum _j|\Omega _{i, j+\frac{1}{2}}|e^x_{i,j+\frac{1}{2}}R^x_{i,j+\frac{1}{2}} + \sum _i\sum _j|\Omega _{i-\frac{1}{2},j}|e^y_{i-\frac{1}{2},j}R^y_{i-\frac{1}{2},j} \nonumber \\&\quad \le Ch^2\left( ||\triangle _x^{-}e^x_{i,j+\frac{1}{2}}||+||\triangle _y^{-}e^x_{i,j+\frac{1}{2}}|| +||\triangle _x^{-}e^y_{i-\frac{1}{2},j}||+||\triangle _y^{-}e^y_{i-\frac{1}{2},j}||\right) . \end{aligned}$$
(49)

Following the proof of Lemma 3.1, we obtain

$$\begin{aligned}&\sum _i\sum _j|\Omega _{i, j+\frac{1}{2}}|e^x_{i,j+\frac{1}{2}}\cdot \triangle _x^{-}e^p_{i+\frac{1}{2},j+\frac{1}{2}} + \sum _i\sum _j|\Omega _{i-\frac{1}{2},j}|e^y_{i-\frac{1}{2},j} \cdot \triangle _y^{-}e^p_{i-\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = -\sum _i\sum _j(x_i-x_{i-1})(y_{j+1}-y_j)\cdot \left[ \triangle _x^{-}e^x_{i,j+\frac{1}{2}} +\triangle _y^{+}e^y_{i-\frac{1}{2},j}\right] \cdot e^p_{i-\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad \le ||R^d_{i-\frac{1}{2},j+\frac{1}{2}}||\cdot ||e^p_{i-\frac{1}{2},j+\frac{1}{2}}|| \le Ch^2||e^p_{i-\frac{1}{2},j+\frac{1}{2}}||, \end{aligned}$$
(50)

where in the last step we used the Cauchy–Schwarz inequality and Lemma 4.5.

Substituting (49), and (50) with the assumption (45) into (48), we conclude the proof of (46).

Using Lemma 3.2 (with \(u\) replaced by \(e\)) to (46), we have (47). \(\square \)

Remark 4.2

Theorem 4.1 shows that we have the \(O(h^2)\) superconvergence on the non-uniform rectangular grids, which is a much better result than those obtained in earlier works (e.g., [4, 6, 17]). Of course, this result is based on the assumption (45). Actually, from the above proof it is not difficult to see that if we replace the assumption (45) by the normal requirement

$$\begin{aligned} ||e^p_{i-\frac{1}{2},j+\frac{1}{2}}||\le C, \end{aligned}$$
(51)

(i.e., the error of pressure is bounded, which is equivalent to that the numerical pressure is bounded), then we recover the usual \(O(h)\) convergence for the velocity in both discrete \(H_1\) and \(L_2\) norms.

In the rest of this section, we want to show that the assumption (45) actually holds true when the pressure \(p=0\) on just one boundary edge of \(\Omega \). Hence \({\varvec{u}}=0\) is only imposed for either \(u^x\) or \(u^y\) on that edge, and this change of boundary conditions does not affect all previous results (cf. Remark 3.2).

Taking the divergence of (1) and using (2), we have

$$\begin{aligned} \Delta p = \nabla \cdot {\varvec{f}}:= g. \end{aligned}$$
(52)

Integrating (52) over cell \(\Omega _{i+\frac{1}{2},j+\frac{1}{2}}\) and following the same idea used for developing the MAC scheme for the Stokes problem, we can obtain the cell-center difference scheme for the pressure:

$$\begin{aligned} \frac{\triangle _x^{+}p_{i+\frac{1}{2},j+\frac{1}{2}}-\triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}}{x_{i+1}-x_i} +\frac{\triangle _y^{+}p_{i+\frac{1}{2},j+\frac{1}{2}}-\triangle _y^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}}{y_{j+1}-y_j} = g_{i+\frac{1}{2},j+\frac{1}{2}}. \end{aligned}$$
(53)

Multiplying (53) by \(p_{i+\frac{1}{2},j+\frac{1}{2}}|\Omega _{i+\frac{1}{2},j+\frac{1}{2}}|\), and summing up all \(i\) and \(j\), we have

$$\begin{aligned} ||\triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}||^2 +||\triangle _y^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}||^2 \le ||g_{i+\frac{1}{2},j+\frac{1}{2}}||\cdot ||p_{i+\frac{1}{2},j+\frac{1}{2}}||, \end{aligned}$$
(54)

which, along with the discrete Poincaré inequality for \(p\) (cf. Remark 3.2 by assuming \(p=0\) on one edge of \(\Omega \)), we have the stability:

$$\begin{aligned} ||\triangle _x^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}||^2 +||\triangle _y^{-}p_{i+\frac{1}{2},j+\frac{1}{2}}||^2 \le C||g_{i+\frac{1}{2},j+\frac{1}{2}}||^2. \end{aligned}$$
(55)

Following the steps used above for deriving the error estimate for the Stokes problem, we can easily obtain the error estimate:

$$\begin{aligned} ||\triangle _x^{-}\hat{e}^p_{i+\frac{1}{2},j+\frac{1}{2}}|| +||\triangle _y^{-}\hat{e}^p_{i+\frac{1}{2},j+\frac{1}{2}}|| \le Ch^2, \end{aligned}$$
(56)

where the error of \(p\) is denotes by \(\hat{e}^p_{i+\frac{1}{2},j+\frac{1}{2}} =p(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})-p_{i+\frac{1}{2},j+\frac{1}{2}}\).

From (56) and the discrete Poincaré inequality for \(\hat{e}^p_{i+\frac{1}{2},j+\frac{1}{2}}\), we have \(||\hat{e}^p_{i+\frac{1}{2},j+\frac{1}{2}}||\le Ch^2\), which justifies the validity of our assumption (45).

5 Numerical Results

In this section, we present some numerical results to justify our theoretical analysis. For simplicity, we fix our domain \(\Omega =(0,1)^2,\) and \(\mu =1\) in (1). We solve a test problem of [20], which has the exact solution of

$$\begin{aligned} p&= 150(x-0.5)(y-0.5), \\ u^x(x,y)&= -256x^2(x-1)^2y(y-1)(2y-1), \quad u^y(x,y)=-u^x(y,x), \end{aligned}$$

where the corresponding \({\varvec{f}}\) is given by (1). Using the MAC scheme for the problem on uniform and nonuniform meshes, we obtain the errors and the relative errors of pressure and velocity given in Tables  1 and 2, respectively. The non-uniform mesh used here is generated from the corresponding uniform mesh by refining the prime-numbered intervals in both \(x\) and \(y\) directions (cf. Fig. 2).

Table 1 Convergence results obtained with uniform rectangular grids
Full size table
Table 2 Convergence results obtained with nonuniform rectangular grids
Full size table
Fig. 2
figure 2

The non-uniform mesh generated from the \(16\times 16\) uniform mesh

Full size image

To evaluate the convergence rate, we define the following absolute errors for velocity and pressure:

$$\begin{aligned}&||e_{u}^{x}||_{0}^{2}:=\sum _{i=0}^{M}\sum _{j=0}^{N-1}\left[ u_{i,j+\frac{1}{2}}^{x}-u^{x}\left( x_{i},y_{j+\frac{1}{2}}\right) \right] ^2 \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_{j}), \\&||e_{u}^{y}||_{0}^{2}:=\sum _{i=0}^{M-1}\sum _{j=0}^{N}\left[ u_{i+\frac{1}{2},j}^{y}-u^{y}\left( x_{i+\frac{1}{2}},y_{j}\right) \right] ^2 (x_{i+1}-x_{i})\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) , \\&||e_{u}||_{0}^{2}:=||e_{u}^{x}||_{0}^{2}+||e_{u}^{y}||_{0}^{2},\\&||e_{p}||_{0}^{2}:=\sum _{i=0}^{M-1}\sum _{j=0}^{N-1}\left[ p_{i+\frac{1}{2},j+\frac{1}{2}}-p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) \right] ^2(x_{i+1}-x_{i})(y_{j+1}-y_{j}), \end{aligned}$$

and the relative errors for velocity and pressure:

$$\begin{aligned}&\varepsilon _{u}^{x}:=\frac{||e_{u}^{x}||_{0}}{||u^{x}||_{0}}= \frac{\sqrt{\sum _{i:=0}^{M}\sum _{j=0}^{N-1}\left[ u_{i,j+\frac{1}{2}}^{x}-u^{x} \left( x_{i},y_{j+\frac{1}{2}}\right) \right] ^2 \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_{j})}}{\sqrt{\sum _{i=0}^{M}\sum _{j=0}^{N-1}\left[ u^{x}(x_{i},y_{j+\frac{1}{2}})\right] ^{2} \left( x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}\right) (y_{j+1}-y_{j})}}, \\&\varepsilon _{u}^{y}:=\frac{||e_{u}^{y}||_{0}}{||u^{y}||_{0}}\!=\! \frac{\sqrt{\sum _{i=0}^{M-1}\sum _{j=0}^{N} \left[ u_{i+\frac{1}{2},j}^{y}-u^{x}(x_{i+\frac{1}{2}},y_{j})\right] ^2 (x_{i+1}-x_{i-1})\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) }}{\sqrt{\sum _{i=0}^{M-1}\sum _{j=0}^{N}\left[ u^{y}\left( x_{i+\frac{1}{2}},y_{j}\right) \right] ^{2}(x_{i+1} -x_{i})\left( y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}\right) }}, \\&\varepsilon _{u}:=\frac{||e_{u}||_{0}}{||u||_{0}}= \frac{\sqrt{||e_{u}^{x}||_{0}^{2}+||e_{u}^{y}||_{0}^{2}}}{\sqrt{||u^{x}||_{0}^{2}+||u^{y}||_{0}^{2}}}, \\&\varepsilon _{p}:=\frac{||e_{p}||_{0}}{||p||_{0}}= \frac{\sqrt{\sum _{i=0}^{M-1}\sum _{j=0}^{N-1} \left[ p_{i+\frac{1}{2},j+\frac{1}{2}}-p\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) \right] ^2(x_{i+1}-x_{i})(y_{j+1}-y_{j})}}{\sqrt{\sum _{i=0}^{M-1}\sum _{j=0}^{N-1}\left[ p(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})\right] ^{2}(x_{i+1}-x_{i})(y_{j+1}-y_{j})}}. \end{aligned}$$

We also display the ratios of relative errors of adjacently refined meshes (i.e. \(\frac{\varepsilon _{p}(h)}{\varepsilon _{p}(2h)}\) and \(\frac{\varepsilon _{u}(h)}{\varepsilon _{u}(2h)}\)) for uniform meshes and nonuniform meshes in Tables 1 and 2, respectively. It is clear that the ratios of relative errors converges to the expected value of 0.25 with enhanced mesh resolution.

The errors and convergence rates of velocity and pressure obtained on various uniform and non-uniform rectangular grids are displayed in Figs. 3 and 4, where we observe that the convergence rates are of second order in the \(L^{2}\) norm, which confirm our theoretical analysis.

Fig. 3
figure 3

Convergence results with uniform meshes

Full size image
Fig. 4
figure 4

Convergence results with nonuniform meshes

Full size image

6 Conclusions

The MAC method as an effective numerical method for solving 2D Stokes problems has been widely used in practice. However, the second-order (super-)convergence of this method on non-uniform meshes has not been pointed out and theoretically analyzed. In this work, we prove rigorously in the first time that the \(L^2\) errors for both the velocity and pressure converge in the second order in terms of mesh size. Numerical results are provided to verify the theoretical results. We like to mention that similar results hold true for 3D Stokes equations with similar cubic cell-centered grids. Some possible future works are to investigate the convergence analysis for high order MAC scheme for the Stokes problem [10] and for the full Navier–Stokes equation on nonuniform meshes.