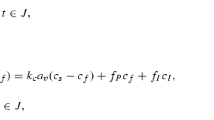A Block-Centered Finite Difference Method for Slightly Compressible Darcy–Forchheimer Flow in Porous Media

Abstract

A block-centered finite difference method is introduced to solve an initial and boundary value problem for a nonlinear parabolic equation to model the slightly compressible flow in porous media, in which the velocity–pressure relation is described by Darcy–Forchheimer’s Law. The method can be thought as the lowest order Raviart–Thomas mixed element method with proper quadrature formulation. By using the method the velocity and pressure can be approximated simultaneously. We established the second-order error estimates for pressure and velocity in proper discrete norms on non-uniform rectangular grid. No time-step restriction is needed for the error estimates. The numerical experiments using the scheme show that the convergence rates of the method are in agreement with the theoretical analysis.

1 Introduction

Darcy’s flow in porous media is of great interest in many fields such as oil recovery and groundwater pollution contamination. Darcy’s law describes the linear relationship between the velocity of creep flow and the gradient of pressure. The relationship is valid by experiment under the condition that the creeping velocity is low and the porosity and permeability is small enough [1]. A theoretical derivation of Darcy’s law can be found in [2, 3].

In some cases, for example when the velocity is higher, a nonlinear relationship between the velocity and the pressure gradient is developed, suggested by Forchheimer [1], by adding a second order term to reach a modified equation. The Darcy–Forchheimer equation (or Forchheimer’s law) is described as follows,

$$\begin{aligned} \mu K^{-1} \mathbf {u} + \beta \rho | \mathbf {u} | \mathbf {u} + \nabla ( p-\rho \mathbf {g}h)=0. \end{aligned}$$

(1)

A theoretical derivation of it can be found in [4].

Forchheimer’s law mainly describes the inertial effects for high speed flow. The most important feature of Forchheimer’s law is that it combines the monotonicity of the nonlinear term and the non-degenerate of the Darcy’s part. There are several papers to analyze the analytical solution for the Forchheimer flow problem, see, for example, [5,6,7].

There are some papers consider the numerical methods for Forchheimer flow in porous media. Mixed element methods for generalized Forchheimer equation were first studied by Douglas et al. [8], then a mixed element method for general nonlinear elliptic problem was studied by Park [9]. A mixed element method with piecewise constant approximation for velocity and nonconforming piecewise linear approximation for pressure, called primal mixed element [10], was considered in [11, 12]. And a mixed element method with Raviart-Thomas element was considered in [13]. Mixed element methods for time-dependent compressible Forchheimer flow was considered by [14]. And a numerical well model with cell-centered finite difference and finite element method for non-Darcy flow was considered in [15]. In [14] only the semi-discrete mixed element method is considered. And since they used the inversive assumption, the lowest-order Raviart–Thomas mixed element is not included in their error estimates.

A series of work about generalized Forchheimer flow can be found in [16,17,18], in which both expanded mixed element form and the nonlinear degenerate parabolic form are used to discrete the model problem. Numerical analysis is based on the monotone properties possessed by Forchheimer operator, [19,20,21].

Block-centered finite difference methods can be thought as the lowest order Raviart-Thomas mixed element method with proper quadrature formulation and has been used widely in reservoir numerical simulation. By using it both the velocity and pressure can be approximated with second-order accuracy for linear elliptic problem with diagonal diffusion coefficient was considered, see [22]. Then in [23, 24] cell-centered finite differences for linear elliptic problem with tensor diffusion coefficients were considered. Another advantage of block-centered, or cell-centered, finite difference method is that it transfers the saddle point system of the mixed element method into symmetric positive definite system, which has been used in many papers, see, for example, [25, 26].

Recently we introduced and analyzed a blocked-centered finite difference method for the incompressible Forchheimer equation with constant coefficients [27] and variable coefficients [28]. We demonstrate that the proposed scheme is second-order accuracy both for velocity and pressure in some discrete norms. A two-grid finite difference method for the the problem is also considered [29].

In this paper we present a blocked-centered finite difference method for the slightly compressible Forchheimer flow problem in porous media. The problem is a kind of nonlinear parabolic problems where the diffusion coefficient depends on the pressure and the absolute value of the vector-valued velocity. It is an extension of our work in [27], where just the nonlinear elliptic Forchheimer problem with constant coefficients was considered. In the scheme, the pressure, the velocity in x-direction and the velocity in y-direction are defined on staggered grids. One key problem to present the scheme is to give a proper approximation to the nonlinear diffusion coefficient, which depend on the pressure and the absolute function of the velocity. The approximation should have the second-order accuracy and reserve the monotonicity of the operator, see Lemma 6 below. We demonstrate that the proposed scheme has these two properties on non-uniform rectangular grid.

Usually for a priori error estimate of numerical solution of nonlinear time-dependent problem, one may employ the inductive assumption and inverse inequality to bound the numerical solution. This may result in a time-step restriction, see, for example, [30,31,32,33,34]. Li and Sun [35, 36] developed a technique to remove the time-step restriction for a priori estimate. In this paper no time-step restriction is needed for the second-order error estimates. Here our technique is different from Li and Sun [35, 36], we used the monotonicity of the nonlinear operator.

Some numerical examples are carried out using the presented scheme. The numerical results show that the convergence rates of our method are in agreement with the theoretical analysis.

The paper is organized as follows. In Sect. 2 we give the problem and some notations. In Sect. 3 we present the block-centered finite difference scheme. In Sect. 4 we give the corresponding numerical analysis. In Sect. 5 some numerical experiments are carried out.

Throughout the paper we use C, with or without subscript, to denote a positive constant, which can have different values in different appearances.

2 The Problem and Some Notations

In this section we present a slightly compressible flow model in porous media, in which the velocity–pressure relation is described by the Darcy–Forchheimer’s law.

Firstly, the equation for mass conservation is as follows

$$\begin{aligned} \frac{\partial ( \phi \rho )}{\partial t} + \nabla \cdot ( \rho \mathbf {u}) = \rho q, \end{aligned}$$

(2)

where $\phi$ is the porosity of the media, q is the source term and $\mathbf {u},\ \rho$ are the velocity and density of the fluid. This model can be simplified under the circumstance that the fluid is slightly compressible [1, 37, 38]. Set $C_F$ be the coefficient of compressibility $C_{_F} = \frac{1}{\rho } \frac{\partial \rho }{\partial p}$, then

$$\begin{aligned} \rho = \rho _0 \exp {(C_{_F} ( p - p_0))}, \end{aligned}$$

(3)

and we have

$$\begin{aligned} \phi \frac{\partial \rho }{\partial p} \frac{\partial p}{\partial t} + \frac{\partial \rho }{\partial p} \nabla p \cdot \mathbf {u} + \rho \nabla \cdot \mathbf {u} = \rho q. \end{aligned}$$

(4)

The term $\frac{\partial \rho }{\partial p} \nabla p \cdot \mathbf {u}$ is effectively quadratic in the velocity, which in almost all of the domain can be neglected [38,39,40]. Thus we arrive the following equation,

$$\begin{aligned} \phi c_{_F} \frac{\partial p}{\partial t} + \nabla \cdot \mathbf {u} = q. \end{aligned}$$

(5)

Combining the mass conservation equation (5) with the velocity–pressure equation (1) we obtain the model describing the slightly compressible flow in porous media, in which the velocity–pressure relation obeys the Forchheimer’s law.

$$\begin{aligned} \left\{ \begin{array}{ll@{\quad }l@{\quad }llll} &{}\displaystyle \text {(a)}&{} \displaystyle \mu K^{-1} \mathbf {u} + \beta \rho (p) | \mathbf {u} | \mathbf {u} + \nabla p =\nabla (\rho (p) \mathbf {g}H), &{} \displaystyle \mathbf {z} &{} \displaystyle \in {\varOmega }\times J, \\ &{}\displaystyle \text {(b)}&{} \displaystyle \phi C_F \frac{\partial p}{\partial t}+ \nabla \cdot \mathbf {u} = f, &{}\displaystyle \mathbf {z} &{} \displaystyle \in {\varOmega }\times J, \\ &{}\displaystyle \text {(c)}&{}\displaystyle \mathbf {u} \cdot \mathbf {n} = f_N, &{} \displaystyle \mathbf {z} &{}\displaystyle \in \partial {\varOmega }\times J. \\ &{}\displaystyle \text {(d)}&{}\displaystyle p|_{t=0} =p_0, &{}\displaystyle \mathbf {z} &{} \displaystyle \in {\varOmega }. \end{array} \right. \end{aligned}$$

(6)

Here p represents the pressure while $\mathbf {u}$ the velocity of the fluid. ${\varOmega }$ is a porous media domain and $J=(0,T)$ is the time interval. For simplicity we consider the problem in two dimensional space. $\mathbf {n}$ represents the unit exterior normal vector to the boundary of ${\varOmega }$, $| \cdot |$ denotes the Euclidean norm, $| \mathbf {u} |^2 = \mathbf {u} \cdot \mathbf {u}$. $\rho$, $\mu$ and $\beta$ are scalar functions which represent the density of the fluid, its viscosity and the Forchheimer number, respectively. For compressible fluid, $\rho$ depends on the pressure p, $\rho =\rho (p)$. $\phi$ represents the porosity. K is the permeability tensor function. For simplicity we suppose that $K=\bar{k}\text{ I }$ where ${\bar{k}}$ is a positive constant and $\text{ I }$ represents the unit matrix. $f \in L^2({\varOmega })$, a scalar function, represents the source and sink of the systems. $\rho (p) \mathbf {g}\nabla H \in (L^2({\varOmega }))^d$, a vector function, is the gradient of the depth function $H \in H^1({\varOmega })$. $f_N \in L^2( \partial {\varOmega })$, a scalar function, represents the Neumann boundary condition, or the flux through the boundary.

A more general compressible Forchheimer flow model was considered in [8] where the dependence of $\rho$ on pressure p does not be described explicitly.

For simplicity of constructing the block-centered finite difference scheme we consider the problem in a two dimensional rectangular domain, ${\varOmega }=(0,L_x)\times (0,L_y)$. We use the notation (x, y) to denote the coordinate of a point in the domain and denote the velocity by $u=(u^x,u^y)$. We suppose that the depth function H is a constant, then $\nabla H=0$. Furthermore we suppose that the problem is with homogeneous boundary condition, $f_N=0$.

With the above assumptions the problem (6) can be re-written as

$$\begin{aligned} \left\{ \begin{array}{ll@{\quad }l@{\quad }lll} &{}\displaystyle \text {(a)}&{} \displaystyle \left( \frac{\mu }{{\bar{k}}} + \beta \rho (p) | \mathbf {u} |\right) \mathbf {u} + \nabla p = 0, &{} \displaystyle \mathbf {z} &{}\displaystyle \in {\varOmega }\times J, \\ &{}\displaystyle \text {(b)}&{} \displaystyle \phi C_F \frac{\partial p}{\partial t}+\nabla \cdot \mathbf {u} = f, &{} \displaystyle \mathbf {z} &{}\displaystyle \in {\varOmega }\times J, \\ &{}\displaystyle \text {(c)}&{} \displaystyle \mathbf {u} \cdot \mathbf {n} = 0, &{} \displaystyle \mathbf {z} &{}\displaystyle \in \partial {\varOmega }\times J. \\ &{}\displaystyle \text {(d)}&{} \displaystyle p|_{t=0} =p_0, &{}\displaystyle \mathbf {z} &{} \displaystyle \in {\varOmega }. \end{array} \right. \end{aligned}$$

(7)

We will derive the block-centered finite difference method for the model problem (7).

Let $N>0$ be a positive integer. Set

$$\begin{aligned} {\varDelta }t=T/N; \quad t^n=n{\varDelta }t \text{ for } n\le T/N. \end{aligned}$$

The domain ${\varOmega }=(0,L_x)\times (0,L_y)$ is partitioned by $\delta _x\times \delta _y$, where

$$\begin{aligned}&\delta _x: 0=x_{\frac{1}{2}}<x_{3/2}<\cdots<x_{N_x-\frac{1}{2}}<x_{N_x+\frac{1}{2}}=L_x,\\&\delta _y: 0=y_{\frac{1}{2}}<y_{3/2}<\cdots<y_{N_y-\frac{1}{2}}<y_{N_y+\frac{1}{2}}=L_y. \end{aligned}$$

For $i=1,\ldots ,N_x$ and $j=1,\ldots ,N_y$, define

$$\begin{aligned}&x_{i}=\frac{x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}}}{2},\\&h_{i}=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}},\qquad h=\max \limits _{i}h_i,\\&h_{i+\frac{1}{2}}=\frac{h_{i+1}+h_{i}}{2}=x_{i+1}-x_{i},\\&y_{j}=\frac{y_{j-\frac{1}{2}}+y_{j+\frac{1}{2}}}{2},\\&k_{j}=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}, \qquad k=\max \limits _{j}k_j,\\&k_{j+\frac{1}{2}}=\frac{k_{j+1}+k_{j}}{2}=y_{j+1}-y_{j},\\&{\varOmega }_{i,j}=(x_{i-\frac{1}{2}},x_{i+\frac{1}{2}})\times (y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}), \\&{\varOmega }_{i+\frac{1}{2},j}=(x_{i},x_{i+1})\times (y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}),\\&{\varOmega }_{i,j+\frac{1}{2}}=(x_{i-\frac{1}{2}},x_{i+\frac{1}{2}})\times (y_{j},y_{j+1}). \end{aligned}$$

We divide each ${\varOmega }_{i,j}$ into 4 parts,

$$\begin{aligned}&{\varOmega }_{i,j}^{L,T}=(x_{i-1/2},x_{i})\times (y_{j},y_{j+1/2}),&{\varOmega }_{i,j}^{R,T}=(x_{i},x_{i+1/2})\times (y_{j},y_{j+1/2}),\\&{\varOmega }_{i,j}^{L,B}=(x_{i-1/2},x_{i})\times (y_{j-1/2},y_{j})&{\varOmega }_{i,j}^{R,B}=(x_{i},x_{i+1/2})\times (y_{j-1/2},y_{j}). \end{aligned}$$

Here the superscript ‘L’, ‘R’, ‘T’ and ‘B’ means ‘Left’, ‘Right’, ‘Top’ and ‘Bottom’, respectively. It is clear that

$$\begin{aligned}&{\varOmega }_{i,j}={\varOmega }_{i,j}^{L,T}\cup {\varOmega }_{i,j}^{L,B}\cup {\varOmega }_{i,j}^{R,T}\cup {\varOmega }_{i,j}^{R,B},\\&{\varOmega }_{i+1/2,j}={\varOmega }_{i,j}^{R,T}\cup {\varOmega }_{i,j}^{R,B}\cup {\varOmega }_{i+1,j}^{L,T}\cup {\varOmega }_{i+1,j}^{L,B},\\&{\varOmega }_{i,j+1/2}={\varOmega }_{i,j}^{L,T}\cup {\varOmega }_{i,j}^{R,T}\cup {\varOmega }_{i,j+1}^{L,B}\cup {\varOmega }_{i,j+1}^{R,B}. \end{aligned}$$

The following Fig. 1 is a description of the dividing.

Fig. 1

A example of mesh partition

For a function $\theta (x,y,t)$, let $\theta _{l,m}^n$ denote $\theta (x_l,y_m,t^n)$ where l may take values $i,\ i+\frac{1}{2}$ for non-negative integers i, and m may take values $j,\ j+\frac{1}{2}$ for non-negative integers j. For discrete functions with values at proper discrete points, define

$$\begin{aligned}&[d_{t}\theta ]_{l,m}^n=\frac{\theta _{l,m}^n-\theta _{l,m}^{n-1}}{{\varDelta }t},\\&[d_{x}\theta ]_{i+\frac{1}{2},j}=\frac{\theta _{i+1,j}-\theta _{i,j}}{h_{i+\frac{1}{2}}},\ \quad [d_{y}\theta ]_{i,j+\frac{1}{2}}=\frac{\theta _{i,j+1}-\theta _{i,j}}{k_{j+\frac{1}{2}}},\\&[D_{x}\theta ]_{i,j}=\frac{\theta _{i+\frac{1}{2},j}-\theta _{i-\frac{1}{2},j}}{h_{i}},\quad [D_{y}\theta ]_{i,j}=\frac{\theta _{i,j+\frac{1}{2}}-\theta _{i,j-\frac{1}{2}}}{k_{j}}, \end{aligned}$$

where for simplicity we omit the subscript n.

Also define the discrete inner products and norms and semi-norms as follows,

$$\begin{aligned}&(\theta ,\tau )_{M}=(\theta ,\tau )_{M_x,M_y}=\sum \limits _{i=1}^{N_x}\sum \limits _{j=1}^{N_y}h_i k_j \theta _{i,j} \tau _{i,j},\\&(\theta ,\tau )_{x}=(\theta ,\tau )_{T_x,M_y}=\sum \limits _{i=2}^{N_x}\sum \limits _{j=1}^{N_y}h_{i-\frac{1}{2}}k_j \theta _{i-\frac{1}{2},j} \tau _{i-\frac{1}{2},j} ,\\&(\theta ,\tau )_{y}=(\theta ,\tau )_{M_x,T_y}=\sum \limits _{i=1}^{N_x}\sum \limits _{j=2}^{N_y}h_{i}k_{j-\frac{1}{2}}\theta _{i,j-\frac{1}{2}} \tau _{i,j-\frac{1}{2}} ,\\&\Vert \theta \Vert _{M}^2=(\theta ,\theta )_{M_x,M_y},\qquad \Vert \theta \Vert _{x}^2=(\theta ,\theta )_{x}, \qquad \Vert \theta \Vert _{y}^2=(\theta ,\theta )_{y} . \end{aligned}$$

3 A Block-Centered Finite Difference Method

In this section we present a block-centered finite difference method for the slightly compressible Forchheimer model.

For simplicity we use the following notation,

$$\begin{aligned} \alpha =\phi C_F, \ \ a_1=\frac{\mu }{{\bar{k}}},\ \ a_2=a_2(p)=\beta \rho (p),\ \ a(p,w)=a_1+a_2(p) w. \end{aligned}$$

(8)

Then the problem (7) can be written as

$$\begin{aligned} \left\{ \begin{array}{ll@{\quad }l@{\quad }ll} &{}\displaystyle \text {~~(i)}&{} \displaystyle (a_1 + a_2(p) | \mathbf {u} |) \mathbf {u} + \nabla p = 0, &{}\displaystyle \text{ in } {\varOmega }\times J, \\ &{}\displaystyle \text {~(ii)}&{} \displaystyle \alpha \frac{\partial p}{\partial t}+\nabla \cdot \mathbf {u} = f, &{}\displaystyle (\mathbf {z},t) \in {\varOmega }\times J, \\ &{}\displaystyle \text {(iii)}&{}\displaystyle \mathbf {u} \cdot \mathbf {n} = 0, \quad &{} \displaystyle (\mathbf {z}, t) \in \partial {\varOmega }\times J. \\ &{}\displaystyle \text {(iv)}&{} \displaystyle p|_{t=0} =p_0,&{}\displaystyle \mathbf {z} \in {\varOmega }. \end{array} \right. \end{aligned}$$

(9)

Here $\partial {\varOmega }$ is the boundary of ${\varOmega }$, and $\mathbf {n}$ denotes the outward unit normal to $\partial {\varOmega }$.

For slightly compressible flow in porous media $\mu ,\ {\bar{k}},\ \phi$ and $C_F$ are positive and bounded up and below, and $\beta$ is non-negative. So $a_1$ and $\alpha$ are positive and bounded up and below, and $a_2$ is non-negative and bounded. For numerical analysis we make the following assumptions on the coefficients and analytical solution.

Assumption 1

$a_1$, $a_2$ and $\alpha$ are continuous functions, and there exist positive constants ${\underline{a}}$ and ${\bar{a}}$ such that,

$$\begin{aligned} 0<{\underline{a}}\le a_1,\ \alpha \le \bar{a},\qquad a_2(p)\ge 0. \end{aligned}$$

Assumption 2

The analytical solution (u, p) has the following regularity.

$$\begin{aligned}&\displaystyle p \in L^{\infty }(0,T;W^{3,\infty }({\varOmega }))\cap W^{1,\infty }(0,T;W^{2,\infty }({\varOmega }))\cap W^{2,\infty }(0,T;L^{\infty }({\varOmega }));\\&u\in \left( W^{1,\infty }(0,T;W^{1,\infty }({\varOmega }))\cap L^{\infty }(0,T;W^{3,\infty }({\varOmega }))\right) ^2; \end{aligned}$$

Assumption 3

$\displaystyle a_2(p) \in L^{\infty }(0,T;W^{2,\infty }({\varOmega }))\cap W^{1,\infty }(0,T;W^{1,\infty }({\varOmega }))$.

The regularity analysis for the solution (u, p) of problem (7), or equivalently (9), can be found in articles and books such as [41,42,43,44,45,46]. For the regularity in Assumption 2 to hold some constraints on the initial value $p_0$, the right-hand term f and the coefficients should be needed, see the references mentioned above.

For the definition of the scheme we define some interpolation operators. For a discrete function $\{q_{i,j}\}$ with value on nodal points $\{(x_{i},y_j)\}$, define a piecewise-constant function ${\varPi }_h q_h$ on ${\varOmega }$ such that,

$$\begin{aligned} {\varPi }_h q(x,y)=q_{i,j},\quad (x,y)\in {\varOmega }_{i,j}, \end{aligned}$$

(10)

and a piecewise constant function $I_h q$ on ${\varOmega }_{i,j}$ such that

$$\begin{aligned} I_h q= \left\{ \begin{array}{ll}\displaystyle {\bar{I}}_h q_{i+\frac{1}{4},j+\frac{1}{4}}, &{} (x,y)\in {\varOmega }_{i,j}^{R,T},\\ \displaystyle {\bar{I}}_h q_{i+\frac{1}{4},j-\frac{1}{4}}, &{} (x,y)\in {\varOmega }_{i,j}^{R,B},\\ \displaystyle {\bar{I}}_h q_{i-\frac{1}{4},j+\frac{1}{4}}, &{} (x,y)\in {\varOmega }_{i,j}^{L,T},\\ \displaystyle {\bar{I}}_h q_{i-\frac{1}{4},j-\frac{1}{4}}, &{} (x,y)\in {\varOmega }_{i,j}^{L,B}. \end{array} \right. \end{aligned}$$

(11)

Here the discrete interpolant function $\{{\bar{I}}_h q\}$ with values at $\displaystyle \{(x_{i}\pm \frac{h_i}{4},y_j\pm \frac{k_j}{4})\}$ is as follows

$$\begin{aligned} \left\{ \begin{array}{l}\displaystyle {\bar{I}}_h q_{i+\frac{1}{4},j\pm \frac{1}{4}}=\frac{1}{4h_{i+\frac{1}{2}}}(h_{i+1}q_{i,j}+h_{i}q_{i+1,j}) +\frac{1}{4k_{j\pm \frac{1}{2}}}(k_{j\pm 1}q_{i,j}+k_{j}q_{i,j\pm 1}),\\ \displaystyle {\bar{I}}_h q_{i-\frac{1}{4},j\pm \frac{1}{4}}=\frac{1}{4h_{i-\frac{1}{2}}}(h_{i-1}q_{i,j}+h_{i}q_{i-1,j}) +\frac{1}{4k_{j\pm \frac{1}{2}}}(k_{j\pm 1}q_{i,j}+k_{j}q_{i,j\pm 1}). \end{array} \right. \end{aligned}$$

For a pair of discrete functions $\{V^x_{i+\frac{1}{2},j}\}$ and $\{V^y_{i,j+\frac{1}{2}}\}$ define the interpolant operator ${\varPi }_2$ as follows.

$$\begin{aligned} {\varPi }_2 V=({\varPi }_x V^x, {\varPi }_y V^y) \end{aligned}$$

(12)

where

$$\begin{aligned} {\varPi }_x V^x(x,y)= & {} V^x_{i+\frac{1}{2},j},\quad (x,y)\in {\varOmega }_{i+\frac{1}{2},j}, \end{aligned}$$

(13)

$$\begin{aligned} {\varPi }_y V^y(x,y)= & {} V^y_{i,j+\frac{1}{2}},\quad (x,y)\in {\varOmega }_{i,j+\frac{1}{2}}. \end{aligned}$$

(14)

Let |(U, V)| be the norm function for a vector (U, V). Direct calculation shows that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle |{\varOmega }_{i,j}^{R,T}|^{-1}\int _{{\varOmega }_{i,j}^{R,T}}|({\varPi }_x V^x,{\varPi }_y V^y)|dxdy &{}=|(V^x_{i+\frac{1}{2},j},V^y_{i,j+\frac{1}{2}})|, \\ \displaystyle |{\varOmega }_{i,j}^{R,B}|^{-1}\int _{{\varOmega }_{i,j}^{R,B}}|({\varPi }_x V^x,{\varPi }_y V^y)|dxdy &{}=|(V^x_{i+\frac{1}{2},j},V^y_{i,j-\frac{1}{2}})|,\\ \displaystyle |{\varOmega }_{i+1,j}^{L,T}|^{-1}\int _{{\varOmega }_{i+1,j}^{L,T}}|({\varPi }_x V^x,{\varPi }_y V^y)|dxdy &{}=|(V^x_{i+\frac{1}{2},j},V^y_{i+1,j+\frac{1}{2}})|, \\ \displaystyle |{\varOmega }_{i+1,j}^{L,B}|^{-1}\int _{{\varOmega }_{i+1,j}^{L,B}}|({\varPi }_x V^x,{\varPi }_y V^y)|dxdy &{}=|(V^x_{i+\frac{1}{2},j},V^y_{i+1,j-\frac{1}{2}})|. \end{array} \right. \end{aligned}$$

(15)

For $w=p,\ I_h p$, define an interpolant ${\bar{Q}}(a_2(w),u)$ on ${\varOmega }_{i,j}$ as follows.

$$\begin{aligned} {\bar{Q}}(a_2(w),u)= \left\{ \begin{array}{ll}\displaystyle a_2(w_{i+\frac{1}{4},j+\frac{1}{4}})|(u^x_{i+\frac{1}{2},j},u^y_{i,j+\frac{1}{2}})|, &{} (x,y)\in {\varOmega }_{i,j}^{R,T},\\ \displaystyle a_2(w_{i+\frac{1}{4},j-\frac{1}{4}})|(u^x_{i+\frac{1}{2},j},u^y_{i,j-\frac{1}{2}})|, &{} (x,y)\in {\varOmega }_{i,j}^{R,B},\\ \displaystyle a_2(w_{i-\frac{1}{4},j+\frac{1}{4}})|(u^x_{i-\frac{1}{2},j},u^y_{i,j+\frac{1}{2}})|, &{} (x,y)\in {\varOmega }_{i,j}^{L,T},\\ \displaystyle a_2(w_{i-\frac{1}{4},j-\frac{1}{4}})|(u^x_{i-\frac{1}{2},j},u^y_{i,j-\frac{1}{2}})|, &{} (x,y)\in {\varOmega }_{i,j}^{L,B}. \end{array} \right. \end{aligned}$$

(16)

Here it is remarkable that $\{I_h p_{i,j}\ne p_{i,j}\}$, then ${\bar{Q}}(a_2(p),u)\ne {\bar{Q}}(a_2(I_h p),u)$. Then define two square root averages as follows.

$$\begin{aligned} \ [Q(a_2(w),u)]_{i+\frac{1}{2},j}= & {} \frac{1}{|{\varOmega }_{i+\frac{1}{2},j}|}\int _{{\varOmega }_{i+\frac{1}{2},j}} {\bar{Q}}(a_2(w),u)dxdy, w=p, I_h p, \end{aligned}$$

(17)

$$\begin{aligned}{}[Q(a_2(w),u)]_{i,j+\frac{1}{2}}= & {} \frac{1}{|{\varOmega }_{i,j+\frac{1}{2}}|}\int _{{\varOmega }_{i,j+\frac{1}{2}}} {\bar{Q}}(a_2(w),u)dxdy, w=p, I_h p. \end{aligned}$$

(18)

Using the above notations the block-centered finite difference approximations $\{U^x_{i+\frac{1}{2},j}\}$, $\{U^y_{i,j+\frac{1}{2}}\}$ and $\{P_{i,j}\}$ to $\{u^x(x_{i+\frac{1}{2},j})\}$, $\{u^y(x_{i,j+\frac{1}{2}})\}$ and $\{p(x_{i,j})\}$, respectively, are chosen so that

$$\begin{aligned}&\alpha [d_t P]_{i,j}^n +[D_x U^x]_{i,j}^n+[D_y U^y]_{i,j}^n=f_{i,j}^n, \end{aligned}$$

(19)

$$\begin{aligned}&\left( a_1 + [Q(a_2(I_h P), U)]_{i+\frac{1}{2},j}^n \right) U^{x,n}_{i+\frac{1}{2},j} =-[d_x P]_{i+\frac{1}{2},j}^n, \end{aligned}$$

(20)

$$\begin{aligned}&\left( a_1 + [Q(a_2(I_h P), U)]_{i,j+\frac{1}{2}}^n \right) U^{y,n}_{i,j+\frac{1}{2}} =-[d_y P]_{i,j+\frac{1}{2}}^n, \end{aligned}$$

(21)

with boundary condition

$$\begin{aligned} U^{x,n}_{\frac{1}{2},j}=0,&\quad U^{x,n}_{N_x+\frac{1}{2},j}=0,&\quad j=0,\ldots ,N_y, \end{aligned}$$

(22)

$$\begin{aligned} U^{y,n}_{i,\frac{1}{2}}=0,&\quad U^{y,n}_{i,N_y+\frac{1}{2}}=0,&\quad i=0,\ldots ,N_x. \end{aligned}$$

(23)

Remark 3.1

One reason to define the interpolation operators $I_h$, ${\varPi }_2$ and Q is to ensure the monotonity of the discrete nonlinear operator, see Lemma  6, which is necessary in convergence analysis. There are other possible definitions which can be used in real computation. Up to now we just proved the convergence with the presented interpolation.

Remark 3.2

The scheme is given suppose that the coefficients are continuous. It is clear that it can be used to solve the problem with piecewise continuous problem, provided that the coefficients are continuous in each cell.

The more complicated problem with tensor permeability are under consideration with the methods of [23, 24].

Remark 3.3

Similar to [28] we know the approximate solution $\{P_{i,j}^n\}$, $\{U^{x,n}_{i+\frac{1}{2},j}\}$ and $\{U^{y,n}_{i,j+\frac{1}{2}}\}$ exist uniquely.

4 Error Estimates

In this section we verify that if the analytical solution u and p are sufficiently smooth, ($U^x$, $U^y$, P) is a second-order approximation to ($u^x$,$u^y$, p).

For this purpose we present some lemmas. Set

$$\begin{aligned} \epsilon _{i+\frac{1}{2},j}^x(p)= & {} \frac{1}{2h_{i+\frac{1}{2}}} \int _{x_{i+\frac{1}{2}}}^{x_{i+1}}\left( \frac{h_{i+1}^2}{4}-(x-x_{i+1})^2\right) \frac{\partial ^3 p}{\partial x^3}(x,y_j,t)dx \nonumber \\&-\,\frac{1}{2h_{i+\frac{1}{2}}}\int _{x_{i+\frac{1}{2}}}^{x_{i}}\left( \frac{h_{i}^2}{4}-(x-x_{i})^2\right) \frac{\partial ^3 p}{\partial x^3}(x,y_j,t)dx . \end{aligned}$$

(24)

$$\begin{aligned} \epsilon _{i,j+\frac{1}{2}}^y(p)= & {} \frac{1}{2k_{j+\frac{1}{2}}}\int _{y_{j+\frac{1}{2}}}^{y_{j+1}}\left( \frac{k_{j+1}^2}{4}-(y-y_{j+1})^2\right) \frac{\partial ^3 p}{\partial x^3}(x_i,y,t)dx \nonumber \\&-\,\frac{1}{2}\int _{y_{j+\frac{1}{2}}}^{y_{j}}\left( \frac{k_{j}^2}{4}-(y-y_{j})^2\right) \frac{\partial ^3 p}{\partial x^3}(x_i,y,t)dx . \end{aligned}$$

(25)

The first lemma can be found in [47].

Lemma 1

If $\displaystyle p \in W^{3,\infty }({\varOmega })$, then there holds

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial p_{i+\frac{1}{2},j}}{\partial x}&{}=&{}\displaystyle [d_x p]_{i+\frac{1}{2},j}-\frac{1}{8}\left[ d_x\left( h^2\frac{\partial ^2 p}{\partial x^2}\right) \right] _{i+\frac{1}{2},j}+\epsilon _{i+\frac{1}{2},j}^x(p),\\ \displaystyle \frac{\partial p_{i,j+\frac{1}{2}}}{\partial y}&{}=&{}\displaystyle [d_y p]_{i,j+\frac{1}{2}}-\frac{1}{8}\left[ d_y\left( k^2\frac{\partial ^2 p}{\partial y^2}\right) \right] _{i,j+\frac{1}{2}}+\epsilon _{i,j+\frac{1}{2}}^y(p), \end{array} \right. \end{aligned}$$

(26)

with the approximation properties $\epsilon _{i+\frac{1}{2},j}^x(p)=O(h^2)$ and $\epsilon _{i,j+\frac{1}{2}}^y(p)=O(k^2)$.

Define

$$\begin{aligned} \delta _{i,j}=\left[ \frac{h^2}{8}\frac{\partial ^2 p}{\partial x^2}+\frac{k^2}{8}\frac{\partial ^2 p}{\partial y^2}\right] _{i,j}=\frac{h_{i}^2}{8}\frac{\partial ^2 p_{i,j}}{\partial x^2}+\frac{k_j^2}{8}\frac{\partial ^2 p_{i,j}}{\partial y^2}, \end{aligned}$$

(27)

and set

$$\begin{aligned} {\tilde{\epsilon }}_{i+\frac{1}{2},j}^x(p)= & {} \epsilon _{i+\frac{1}{2},j}^x(p)+\left[ d_x\left( \frac{k^2}{8}\frac{\partial ^2 p}{\partial y^2}\right) \right] _{i+\frac{1}{2},j}. \end{aligned}$$

(28)

$$\begin{aligned} {\tilde{\epsilon }}_{i,j+\frac{1}{2}}^y(p)= & {} \epsilon _{i,j+\frac{1}{2}}^y(p)+\left[ d_y\left( \frac{h^2}{8}\frac{\partial ^2 p}{\partial x^2}\right) \right] _{i,j+\frac{1}{2}}, \end{aligned}$$

(29)

Similar to Lemma 4.2 of [47] and Lemma 4.1 of [28] we have the following lemma.

Lemma 2

If $\displaystyle p \in W^{3,\infty }({\varOmega })$, then there holds

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle [(a_1+a_2(p) |u|)u^x]_{i+\frac{1}{2},j}&{}=&{}\displaystyle -\left[ d_x (p-\delta )\right] _{i+\frac{1}{2},j}-{\tilde{\epsilon }}_{i+\frac{1}{2},j}^x(p)\\ \displaystyle [(a_1+a_2(p)|u|)u^y]_{i,j+\frac{1}{2}}&{}=&{}\displaystyle -\left[ d_y (p-\delta )\right] _{i,j+\frac{1}{2}}-{\tilde{\epsilon }}_{i,j+\frac{1}{2}}^y(p), \end{array} \right. \end{aligned}$$

(30)

with the following approximate properties

$$\begin{aligned} {\tilde{\epsilon }}_{i+\frac{1}{2},j}^x(p)=O(h^2+k^2),\qquad {\tilde{\epsilon }}_{i,j+\frac{1}{2}}^y(p)=O(h^2+k^2). \end{aligned}$$

(31)

Define

$$\begin{aligned} {\tilde{\delta }}_{i,j}= & {} \frac{a_2(p_{i,j})}{4}\frac{u^x_{i,j}u^y_{i,j}}{|u_{i,j}|}\frac{\partial u^y_{i,j}}{\partial x} h_i^2+\frac{a_2(p_{i,j})}{4}\frac{u^x_{i,j}u^y_{i,j}}{|u_{i,j}|}\frac{\partial u^x_{i,j}}{\partial y} k_j^2 \nonumber \\&+\,\frac{1}{8}\frac{\partial a_2(p)_{i,j}}{\partial x}|u_{i,j}|u^x_{i,j}h_i^2 +\frac{1}{8}\frac{\partial a_2(p)_{i,j}}{\partial y}|u_{i,j}|u^y_{i,j} k_j^2. \end{aligned}$$

(32)

$$\begin{aligned} \eta _{i,j}= & {} \delta _{i,j}+{\tilde{\delta }}_{i,j} . \end{aligned}$$

(33)

Similar to Lemma 4.2 of [27] we can prove the following lemma.

Lemma 3

If $\displaystyle p \in L^{\infty }(0,T;W^{3,\infty }({\varOmega }))$, $u \in \left( L^{\infty }(0,T;L^{\infty }({\varOmega }))\right) ^2$ and $\displaystyle a_2(p) \in L^{\infty }(0,T;W^{2,\infty }({\varOmega }))$, then we have that

$$\begin{aligned} \begin{array}{lll} (a_1+[Q(a_2(p),u)]_{i+\frac{1}{2},j}) u^x_{i+\frac{1}{2},j}= & {} -[d_x (p-\eta )]_{i+\frac{1}{2},j} -\tilde{{\tilde{\epsilon }}}_{i+\frac{1}{2},j}^x(p) , \end{array} \end{aligned}$$

(34)

$$\begin{aligned} \begin{array}{lll} (a_1+[Q(a_2(p),u)]_{i,j+\frac{1}{2}}) u^y_{i,j+\frac{1}{2}}= & {} -[d_y (p-\eta )]_{i,j+\frac{1}{2}} -\tilde{{\tilde{\epsilon }}}_{i,j+\frac{1}{2}}^y(p) , \end{array} \end{aligned}$$

(35)

with the following approximate properties

$$\begin{aligned} \tilde{{\tilde{\epsilon }}}_{i+\frac{1}{2},j}^x(p)=O(h^2+k^2),\qquad \tilde{{\tilde{\epsilon }}}_{i,j+\frac{1}{2}}^y(p)=O(h^2+k^2). \end{aligned}$$

(36)

Lemma 4

Under the condition of Lemma 3, we have that

$$\begin{aligned} \begin{array}{ll} (a_1+[Q( a_2(I_h p),u)]_{i+\frac{1}{2},j}) u^x_{i+\frac{1}{2},j} =&-[d_x (p-\eta )]_{i+\frac{1}{2},j} -\varepsilon _{i+\frac{1}{2},j}^x(p) , \end{array} \end{aligned}$$

(37)

$$\begin{aligned} \begin{array}{lll} (a_1+[Q( a_2(I_h p),u)]_{i,j+\frac{1}{2}}) u^y_{i,j+\frac{1}{2}} =&-[d_y (p-\eta )]_{i,j+\frac{1}{2}} -\varepsilon _{i,j+\frac{1}{2}}^y(p) , \end{array} \end{aligned}$$

(38)

with the following approximate properties

$$\begin{aligned} \varepsilon _{i+\frac{1}{2},j}^x(p)=O(h^2+k^2),\qquad \varepsilon _{i,j+\frac{1}{2}}^y(p)=O(h^2+k^2). \end{aligned}$$

(39)

Proof

Direct calculation shows that

$$\begin{aligned}&\left( a_1+[Q( a_2(I_h p),u)]_{i+\frac{1}{2},j}\right) u^x_{i+\frac{1}{2},j} \nonumber \\&\quad = \left( a_1+[Q( a_2( p),u)]_{i+\frac{1}{2},j}\right) u^x_{i+\frac{1}{2},j}\nonumber \\&\qquad +\left( [Q( a_2(I_h p),u)]_{i+\frac{1}{2},j}-[Q( a_2( p),u)]_{i+\frac{1}{2},j} \right) u^x_{i+\frac{1}{2},j}\nonumber \\&\quad = -\,[d_x (p-\eta )]_{i+\frac{1}{2},j} -\tilde{{\tilde{\epsilon }}}_{i+\frac{1}{2},j}^x(p)\nonumber \\&\qquad +\left( [Q( a_2(I_h p),u)]_{i+\frac{1}{2},j}-[Q( a_2( p),u)]_{i+\frac{1}{2},j} \right) u^x_{i+\frac{1}{2},j} \nonumber \\&\quad \equiv -\,[d_x (p-\eta )]_{i+\frac{1}{2},j} -\varepsilon _{i+\frac{1}{2},j}^x(p) . \end{aligned}$$

(40)

Here the last equivalence is the definition of $\varepsilon _{i+\frac{1}{2},j}^x(p)$. By the definition of $I_h p$ it is clear that

$$\begin{aligned} I_h p_{i\pm \frac{1}{4},j\pm \frac{1}{4}}-p_{i\pm \frac{1}{4},j\pm \frac{1}{4}}=O(h^2+k^2), \end{aligned}$$

Noticing the symmetric structures in the definition (17) we have that

$$\begin{aligned}{}[Q( a_2(I_h p),u)]_{i+\frac{1}{2},j}-[Q( a_2( p),u)]_{i+\frac{1}{2},j}=O(h^2+k^2). \end{aligned}$$

Therefore

$$\begin{aligned} \varepsilon _{i+\frac{1}{2},j}^x(p)= & {} \tilde{{\tilde{\epsilon }}}_{i+\frac{1}{2},j}^x(p)-\left( [Q( a_2(I_h p),u)]-[Q( a_2( p),u)]\right) _{i+\frac{1}{2},j} u^x_{i+\frac{1}{2},j}\nonumber \\= & {} O(h^2+k^2) . \end{aligned}$$

(41)

Similarly we can prove

$$\begin{aligned} \varepsilon _{i,j+\frac{1}{2}}^y(p)= & {} \tilde{{\tilde{\epsilon }}}_{i,j+\frac{1}{2}}^y(p)-\left( [Q( a_2(I_h p),u)]-[Q( a_2( p),u)]\right) _{i,j+\frac{1}{2}} u^y_{i,j+\frac{1}{2}}\nonumber \\= & {} O(h^2+k^2) , \end{aligned}$$

(42)

and

$$\begin{aligned} \left( a_1+[Q( a_2(I_h p),u)]_{i,j+\frac{1}{2}}\right) u^y_{i,j+\frac{1}{2}}= -[d_y (p-\eta )]_{i,j+\frac{1}{2}} -\varepsilon _{i,j+\frac{1}{2}}^y(p) , \end{aligned}$$

which complete the proof. $\square$

The following two lemmas can been found in [5, 6], see Lemma 2.3 of [6] and Proposition III.6 of [5], or in [27].

Lemma 5

Let $\mathbf {z}, \mathbf {h} \in R^d$. The vector-valued function $\mathbf {f} : R^d \rightarrow R^d$ is defined as $\mathbf {f} ( \mathbf {z})= | \mathbf {z} | \mathbf {z}$. Then there exists a positive constant $C_{0}$ such that

$$\begin{aligned} C_{0} ( |\mathbf {z}| + |\mathbf {z} + \mathbf {h}|) |\mathbf {h}|^2 \le ( \mathbf {f}( \mathbf {z} + \mathbf {h}) - \mathbf {f}(\mathbf {z})) \cdot \mathbf {h}. \end{aligned}$$

(43)

Lemma 6

For any vector-valued functions $\mathbf {V}=(V^x,V^y)$ and $\mathbf {W}=(W^x,W^y)$ we have that $( |\mathbf {V}| \mathbf {V} - | \mathbf {W} | \mathbf {W}, \mathbf {V} - \mathbf {W}) \ge 0$, and further

$$\begin{aligned} ( a(|\mathbf {V}|) \mathbf {V} - a(| \mathbf {W} |) \mathbf {W}, \mathbf {V} - \mathbf {W} )\ge a_1 || \mathbf {V} - \mathbf {W}||^2. \end{aligned}$$

(44)

The result of the following lemma is obvious, see [27].

Lemma 7

Let $\{V_{i+\frac{1}{2},j}^x\},\{V_{i,j+\frac{1}{2}}^y\}$, $\{W_{i+\frac{1}{2},j}^x\},\{W_{i,j+\frac{1}{2}}^y\}$ and $\{q^x_{i,j}\},\{q^y_{i,j}\}$ be discrete functions with $W_{\frac{1}{2},j}^x=W_{N_x+\frac{1}{2},j}^x=W_{i,\frac{1}{2}}^y=W_{i,N_y+\frac{1}{2}}^y=0$. Then there hold,

$$\begin{aligned} (-d_x q^x,W^x)_x= ( q^x, D_x W^x)_M,\quad (-d_y q^y,W^y)_y= ( q^y, D_y W^y)_M . \end{aligned}$$

(45)

Now we consider the error estimate.

Theorem 1

Suppose the coefficients $\mu , \alpha , {\bar{k}}$ are continuous functions and are bounded up and below. Suppose also that Assumptions 1–3 are hold. For the solution of the block-centered finite difference scheme when the discretization parameters ${\varDelta }t, h$ and k are sufficiently small there exists a positive constant C independent of ${\varDelta }t$, h and k such that for $m\le \frac{T}{{\varDelta }t}$,

$$\begin{aligned} \Vert (P-p)^m \Vert _{M}\le & {} C({\varDelta }t+h^2+k^2)\\ \sum \limits _{n=1}^m{\varDelta }t\left( \Vert (U- u)^{x,n}\Vert _{x}^2 +\Vert (U- u)^{y,n}\Vert _{y}^2\right) ^{\frac{1}{2}}\le & {} C({\varDelta }t+h^2+k^2). \end{aligned}$$

Proof

From Lemma 4, Eqs. (20), (21) and (9) we have that

$$\begin{aligned}&a_1 [U^{x}-u^{x}]^n_{i+\frac{1}{2},j}+[Q(a_2(I_h P^n), U^{n})]_{i+\frac{1}{2},j}U^{x,n}_{i+\frac{1}{2},j}\nonumber \\&\qquad -\,[Q(a_2(I_h p^n), u^{n})]_{i+\frac{1}{2},j}u^{x,n}_{i+\frac{1}{2},j}\nonumber \\&\quad =\displaystyle -\,\left[ d_x(P-p+\eta )\right] ^n_{i+\frac{1}{2},j}+\varepsilon _{i+\frac{1}{2},j}^{x,n}(p). \end{aligned}$$

(46)

$$\begin{aligned}&a_1 [U^{y}-u^{y}]^n_{i,j+\frac{1}{2}}+[Q(a_2(I_h P^n),U^{n})]_{i,j+\frac{1}{2}}U^{y,n}_{i,j+\frac{1}{2}}\nonumber \\&\qquad -\,Q(a_2(I_h p^n), u^{n})]_{i,j+\frac{1}{2}}u^{y,n}_{i,j+\frac{1}{2}} \nonumber \\&\quad =\displaystyle -\,\left[ d_y(P-p+\eta )\right] ^n_{i,j+\frac{1}{2}}+\varepsilon _{i,j+\frac{1}{2}}^{y,n}(p). \end{aligned}$$

(47)

Define

$$\begin{aligned} \left\{ \begin{array}{l} e_{i,j}^{p,n}=(P-p)_{i,j}^n,\\ e_{i+\frac{1}{2},j}^{x,n}=(U^x-u^x)_{i+\frac{1}{2},j}^n,\quad e_{i,j+\frac{1}{2}}^{y,n}=(U^y-u^y)_{i,j+\frac{1}{2}}^n. \end{array} \right. \end{aligned}$$

(48)

Then

$$\begin{aligned}&a_1 e^{x,n}_{i+\frac{1}{2},j}+[Q(a_2(I_h P),U)]^n_{i+\frac{1}{2},j}U^{x,n}_{i+\frac{1}{2},j}-[Q(a_2(I_h p), u)]^n_{i+\frac{1}{2},j}u^{x,n}_{i+\frac{1}{2},j} \nonumber \\&\quad =\displaystyle -\left[ d_x(e^p+\eta )\right] ^n_{i+\frac{1}{2},j}+\varepsilon _{i+\frac{1}{2},j}^{x,n}(p). \end{aligned}$$

(49)

$$\begin{aligned}&a_1 e^{y,n}_{i,j+\frac{1}{2}}+[Q(a_2(I_h P),U)]^n_{i,j+\frac{1}{2}}U^{y,n}_{i,j+\frac{1}{2}} -[Q(a_2(I_h p), u)]^n_{i,j+\frac{1}{2}}u^{y,n}_{i,j+\frac{1}{2}} \nonumber \\&\quad =\displaystyle -\left[ d_y(e^p+\eta )\right] ^n_{i,j+\frac{1}{2}}+\varepsilon _{i,j+\frac{1}{2}}^{y,n}(p). \end{aligned}$$

(50)

From Eq. (9) we have that

$$\begin{aligned} \alpha d_t p_{i,j}^n+[D_x u^x]_{i,j}^n+[D_y u^y]_{i,j}^n=f_{i,j}^n+\epsilon _{i,j}^{1,n}, \end{aligned}$$

(51)

where

$$\begin{aligned} \epsilon _{i,j}^{1,n}= & {} \alpha d_t p_{i,j}^n-\alpha \frac{\partial p_{i,j}^n}{\partial t}+[D_x u^x]_{i,j}^n-\frac{\partial u_{i,j}^{x,n}}{\partial x}+[D_y u^y]_{i,j}^n-\frac{\partial u_{i,j}^{y,n}}{\partial y} \nonumber \\= & {} O({\varDelta }t+h^2+k^2). \end{aligned}$$

(52)

Here we have used the fact that $x_i$ is the midpoint of $(x_{i-\frac{1}{2}},x_{i+\frac{1}{2}})$ and $y_j$ is the midpoint of $(y_{j-\frac{1}{2}},y_{j+\frac{1}{2}})$.

From (51) and (19) we have that

$$\begin{aligned} \alpha d_t(P-p)_{i,j}^n+[D_x(U^x- u^x)]_{i,j}^n+[D_y(U^y- u^y)]_{i,j}^n=-\epsilon _{i,j}^{1,n}. \end{aligned}$$

(53)

Denote by

$$\begin{aligned} \epsilon _{i,j}^{2,n}= & {} d_t\eta _{i,j}^{n} \nonumber \\= & {} \frac{h_i^2}{8} d_t\left( \frac{\partial ^2 p}{\partial x^2}\right) _{i,j}^{n}+\frac{k_j^2}{8} d_t\left( \frac{\partial ^2 p}{\partial y^2}\right) _{i,j}^{n}\nonumber \\&+\,\frac{h_i^2}{4}d_t\left( a_2(p)\frac{u^x u^y}{|u|}\frac{\partial u^y}{\partial x} \right) _{i,j}^{n} +\frac{k_j^2}{4}\left( a_2(p)\frac{u^x u^y}{|u|}\frac{\partial u^x}{\partial y}\right) _{i,j}^{n}\nonumber \\&+\,\frac{h_i^2}{8}d_t\left( \frac{\partial a_2(p)}{\partial x}|u| u^x\right) _{i,j}^{n} +\frac{k_j^2}{8}d_t\left( \frac{\partial a_2(p)}{\partial y}|u| u^y\right) _{i,j}^{n}. \end{aligned}$$

(54)

When p and u are sufficiently smooth, it is clear that

$$\begin{aligned} \epsilon _{i,j}^{2,n}=O(h^2+k^2). \end{aligned}$$

(55)

From (53) we have that

$$\begin{aligned} d_t(e^p+\eta )_{i,j}^n+[D_x e^x]_{i,j}^n+[D_y e^y]_{i,j}^n =-\epsilon _{i,j}^{1,n}+\epsilon _{i,j}^{2,n}. \end{aligned}$$

(56)

Multiplying (56) by $(e^p+\eta )_{i,j}^n h_i k_j$ and summing for i, j, $1\le i\le N_x,1\le j\le N_y$, we have that

$$\begin{aligned} (d_t(e^p+\eta )^n,(e^p+\eta )^n)_{M}+ & {} (D_x e^{x,n},(e^p+\eta )^n)_{M} \nonumber \\ +\,(D_y e^{y,n},(e^p+\eta )^n)_{M}= & {} (-\epsilon ^{1,n}+\epsilon ^{2,n},(e^p+\eta )^n)_{M}. \end{aligned}$$

(57)

By Lemma 7 we have that

$$\begin{aligned}&(d_t(e^p+\eta )^n,(e^p+\eta )^n)_{M}-(e^{x,n},d_x(e^p+\eta )^n)_{x} -(e^{y,n},d_y(e^p+\eta )^n)_{y} \nonumber \\&\quad = (-\epsilon ^{1,n}+\epsilon ^{2,n},(e^p+\eta )^n)_{M}. \end{aligned}$$

(58)

Using (49) and (50) we have that

$$\begin{aligned}&\frac{1}{2}d_t\Vert (e^p+\eta )^n \Vert _{M}^2+\frac{{\varDelta }t}{2} \Vert d_t(e^p+\eta )^n\Vert _{M}^2 +a_1\left( \Vert e^{x,n}\Vert ^2_{x} +\Vert e^{y,n}\Vert ^2_{y}\right) \nonumber \\&+\left( [Q(a_2(I_h P^n),U^{n})] U^{x,n} -Q(a_2(I_h p^n), u^{n})] u^{x,n} ,e^{x,n}\right) _x \nonumber \\&+\left( [Q(a_2(I_h P^n),U^{n})] U^{y,n} -Q(a_2(I_h p^n), u^{n})] u^{y,n} ,e^{y,n}\right) _y\nonumber \\= & {} (-\epsilon ^{1,n}+\epsilon ^{2,n},(e^p+\eta )^n)_{M} +(e^{x,n},\varepsilon ^{x,n}(p))_{x}+(e^{y,n},\varepsilon ^{y,n}(p))_{y}. \end{aligned}$$

(59)

$$\begin{aligned}&\frac{1}{2}d_t\Vert (e^p+\eta )^n \Vert _{M}^2+\frac{{\varDelta }t}{2} \Vert d_t(e^p+\eta )^n\Vert _{M}^2 +a_1\left( \Vert e^{x,n}\Vert ^2_{x} +\Vert e^{y,n}\Vert ^2_{y}\right) \nonumber \\&+\left( [Q(a_2(I_h P^n),U^{n})] U^{x,n}-[Q(a_2(I_h P^n),u^{n})] u^{x,n},e^{x,n}\right) _x \nonumber \\&+\left( [Q(a_2(I_h P^n),U^{n})] U^{y,n}- [Q(a_2(I_h P^n),u^{n})] u^{y,n},e^{y,n}\right) _y\nonumber \\= & {} (-\epsilon ^{1,n}+\epsilon ^{2,n},(e^p+\eta )^n)_{M} +(e^{x,n},\varepsilon ^{x,n}(p))_{x}+(e^{y,n},\varepsilon ^{y,n}(p))_{y} \nonumber \\&-\left( [Q(a_2(I_h P^n),u^{n})-Q(a_2(I_h p^n),u^{n})] u^{x,n},e^{x,n}\right) _x \nonumber \\&-\left( [Q(a_2(I_h P^n),u^{n})-Q(a_2(I_h p^n),u^{n})] u^{y,n},e^{y,n}\right) _y. \end{aligned}$$

(60)

The third combining with the forth terms on the left hand sides can be estimated as follows.

$$\begin{aligned}&\left( [Q(a_2(I_h P^n),U^{n})] U^{x,n}-[Q(a_2(I_h P^n),u^{n})] u^{x,n},e^{x,n}\right) _x \nonumber \\&\qquad +\left( [Q(a_2(I_h P^n),U^{n})] U^{y,n}- [Q(a_2(I_h P^n),u^{n})] u^{y,n},e^{y,n}\right) _y\nonumber \\&\quad \equiv \sum \limits _{i,j}(I^1_{i,j}+I^2_{i,j}+I^3_{i,j}+I^4_{i,j}), \end{aligned}$$

(61)

where

$$\begin{aligned} I^1_{i,j}= & {} \int _{{\varOmega }^{R,T}_{i,j}}\left\{ {\bar{Q}}(a_2(I_h P^n),U^{n})\left( U^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+U^{y,n}_{i,j+\frac{1}{2}}e^{y,n}_{i,j+\frac{1}{2}}\right) \right. \nonumber \\&\qquad \left. -\,{\bar{Q}}(a_2(I_h P^n),u^{n})\left( u^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+u^{y,n}_{i,j+\frac{1}{2}}e^{y,n}_{i,j+\frac{1}{2}}\right) \right\} dxdy, \end{aligned}$$

(62)

$$\begin{aligned} I^2_{i,j}= & {} \int _{{\varOmega }^{R,B}_{i,j}}\left\{ {\bar{Q}}(a_2(I_h P^n),U^{n})\left( U^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+U^{y,n}_{i,j-\frac{1}{2}}e^{y,n}_{i,j-\frac{1}{2}}\right) \right. \nonumber \\&\quad \left. -\,{\bar{Q}}(a_2(I_h P^n),u^{n})\left( u^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+u^{y,n}_{i,j-\frac{1}{2}}e^{y,n}_{i,j-\frac{1}{2}}\right) \right\} dxdy , \end{aligned}$$

(63)

$$\begin{aligned} I^3_{i,j}= & {} \int _{{\varOmega }^{L,T}_{i+1,j}}\left\{ {\bar{Q}}(a_2(I_h P^n),U^{n})\left( U^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+U^{y,n}_{i+1,j+\frac{1}{2}}e^{y,n}_{i+1,j+\frac{1}{2}}\right) \right. \nonumber \\&\quad \left. -\,{\bar{Q}}(a_2(I_h P^n),u^{n})\left( u^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+u^{y,n}_{i+1,j+\frac{1}{2}}e^{-,n}_{i+1,j+\frac{1}{2}}\right) \right\} dxdy , \end{aligned}$$

(64)

$$\begin{aligned} I^4_{i,j}= & {} \int _{{\varOmega }^{L,B}_{i+1,j}}\left\{ {\bar{Q}}(a_2(I_h P^n),U^{n})\left( U^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+U^{y,n}_{i+1,j-\frac{1}{2}}e^{y,n}_{i+1,j-\frac{1}{2}}\right) \right. \nonumber \\&\quad \left. -\,{\bar{Q}}(a_2(I_h P^n),u^{n})\left( u^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+u^{y,n}_{i+1,j-\frac{1}{2}}e^{y,n}_{i+1,j-\frac{1}{2}}\right) \right\} dxdy . \end{aligned}$$

(65)

From the definition of the interpolant and Lemma 6 we have that

$$\begin{aligned} I^1_{i,j}= & {} \displaystyle a_2\left( I_h P^n_{i+\frac{1}{2},j+\frac{1}{4}}\right) \nonumber \\&\int _{{\varOmega }^{R,T}_{i,j}}\left\{ |\left( U^{x,n}_{i+\frac{1}{2},j},U^{y,n}_{i,j+\frac{1}{2}}\right) |\left( U^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j} +U^{y,n}_{i,j+\frac{1}{2}}e^{y,n}_{i,j+\frac{1}{2}}\right) \right. \nonumber \\&\qquad \left. -|\left( u^{x,n}_{i+\frac{1}{2},j},u^{y,n}_{i,j+\frac{1}{2}}\right) | \left( u^{x,n}_{i+\frac{1}{2},j}e^{x,n}_{i+\frac{1}{2},j}+u^{y,n}_{i,j+\frac{1}{2}}e^{y,n}_{i,j+\frac{1}{2}}\right) \right\} dxdy \nonumber \\\ge & {} 0. \end{aligned}$$

(66)

Similarly we deal with other terms $I^2_{i,j}$ to $I^4_{i,j}$.

Then from (60) and (61) we have that

$$\begin{aligned}&\frac{1}{2}d_t\Vert (e^p+\eta )^n \Vert _{M}^2+\frac{{\varDelta }t}{2} \Vert d_t(e^p+\eta )^n\Vert _{M}^2 +a_1\left( \Vert e^{x,n}\Vert _{x}^2 +\Vert e^{y,n}\Vert _{y}^2\right) \nonumber \\\le & {} (-\epsilon ^{1,n}+\epsilon ^{2,n},(e^p+\eta )^n)_{M} +(e^{x,n},\varepsilon ^{x,n}(p))_{x}+(e^{y,n},\varepsilon ^{y,n}(p))_{y} \nonumber \\&-\left( [Q(a_2(I_h P^n),u^{n})-Q(a_2(I_h p^n),u^{n})] u^{x,n},e^{x,n}\right) _x \nonumber \\&-\left( [Q(a_2(I_h P^n),u^{n})-Q(a_2(I_h p^n),u^{n})] u^{y,n},e^{y,n}\right) _y\nonumber \\\equiv & {} \sum \limits _{l=1}^5 I_l. \end{aligned}$$

(67)

By Schwarz’s inequality it is clear that

$$\begin{aligned} I_1+I_2+I_3\le & {} \Vert (e^p+\eta )^n \Vert _{M}^2+\frac{a_1}{4}(\Vert e^{x,n}\Vert _{x}^2+ \Vert e^{y,n}\Vert _{y}^2)\nonumber \\&+\,C_1(\Vert \epsilon ^{1,n}+\epsilon ^{2,n}\Vert _{M}^2+\Vert \varepsilon ^{x,n}(p)\Vert _{x}^2+\Vert \varepsilon ^{y,n}(p)\Vert _{y}^2). \end{aligned}$$

(68)

Because we use $\{P^n_{i,j}\}$ and $\{p^n_{i,j}\}$ in the definitions of $\{I_h P^n_{i\pm \frac{1}{4},j\pm \frac{1}{4}}\}$ and $\{I_h p^n_{i\pm \frac{1}{4},j\pm \frac{1}{4}}\}$, from some simple calculations we can get

$$\begin{aligned} I_4\le & {} C\Vert P^n-p^n \Vert _{M}\Vert e^{x,n}\Vert _{x} \nonumber \\\le & {} C(\Vert ( e^p+\eta )^n \Vert _{M}+\Vert \eta ^n \Vert _{M})\Vert e^{x,n}\Vert _{x}\nonumber \\\le & {} \frac{a_1}{4}\Vert e^{x,n}\Vert _{x}^2+C_2(\Vert ( e^p+\eta )^n \Vert _{M}^2+\Vert \eta ^n \Vert _{M}^2). \end{aligned}$$

(69)

Similarly

$$\begin{aligned} I_5\le & {} \frac{a_1}{4}\Vert e^{y,n}\Vert _{y}^2+C_3(\Vert ( e^p+\eta )^n \Vert _{M}^2+\Vert \eta ^n \Vert _{M}^2). \end{aligned}$$

(70)

Combining (67) with (68), (69) and (67) we have that

$$\begin{aligned}&\frac{1}{2}d_t\Vert (e^p+\eta )^n \Vert _{M}^2+\frac{{\varDelta }t}{2} \Vert d_t(e^p+\eta )^n\Vert _{M}^2 +\frac{a_1}{2}(\Vert e^{x,n}\Vert _{x}^2 +\Vert e^{y,n}\Vert _{y}^2) \nonumber \\&\quad \le C_4 \Vert (e^p+\eta )^n \Vert _{M}^2 +C_4(\Vert \epsilon ^{1,n}+\epsilon ^{2,n}\Vert _{M}^2+\Vert \eta ^n \Vert _{M}^2 +\Vert \varepsilon ^{x,n}\Vert _{x}^2+\Vert \varepsilon ^{y,n}\Vert _{y}^2). \end{aligned}$$

(71)

Summing (71) for n from 1 to $m,m\le \frac{T}{{\varDelta }t}$, and using the estimates of $\epsilon ^{1,n}$, $\epsilon ^{2,n}$, $\varepsilon ^{x,n}(p)$, $\varepsilon ^{y,n}(p)$ and $\eta ^n$ we have that

$$\begin{aligned}&\Vert (e^p+\eta )^m \Vert _{M}^2+\sum \limits _{n=1}^m{\varDelta }t^2 \Vert (d_t(e^p+\eta )^n\Vert _{M}^2 +a_1(\Vert e^{x,n}\Vert _{x}^2 +\Vert e^{y,n}\Vert _{y}^2) \nonumber \\\le & {} 2C_4 \sum \limits _{n=1}^m {\varDelta }t\Vert (e^p+\eta )^n \Vert _{M}^2+\Vert (e^p+\eta )^0 \Vert _{M}^2\nonumber \\&+\,2C_4\sum \limits _{n=1}^m {\varDelta }t (\Vert \epsilon ^{1,n}+\epsilon ^{2,n}\Vert _{M}^2+\Vert \eta ^n \Vert _{M}^2+\Vert \varepsilon ^{x,n}(p)\Vert _{x}^2+\Vert \varepsilon ^{y,n}(p)\Vert _{y}^2) \nonumber \\\le & {} 2C_4 \sum \limits _{n=1}^m {\varDelta }t\Vert (e^p+\eta )^n \Vert _{M}^2+C({\varDelta }t+h^2+k^2). \end{aligned}$$

(72)

By Gronwall’s inequality when ${\varDelta }t$ is sufficiently small we have that

$$\begin{aligned}&\Vert (P-p+\eta )^m \Vert _{M}^2+\sum \limits _{n=1}^m{\varDelta }t^2 \Vert d_t(P-p+\eta )^n\Vert _{M}^2 \nonumber \\&\quad +\,a_1\sum \limits _{n=1}^m{\varDelta }t (\Vert (U- u)^{x,n}\Vert _{x}^2 +\Vert (U- u)^{y,n}\Vert _{y}^2)\nonumber \\\le & {} C({\varDelta }t^2+h^4+k^4). \end{aligned}$$

(73)

Combining (73) with the estimate for $\eta$ results in

$$\begin{aligned}&\Vert (P-p)^m \Vert _{M}^2 +\sum \limits _{n=1}^m{\varDelta }t(\Vert (U- u)^{x,n}\Vert _{x}^2 +\Vert (U- u)^{y,n}\Vert _{y}^2)\\&\quad \le C({\varDelta }t^2+h^4+k^4), \end{aligned}$$

which completes the proof of the first estimate. It is well-known that

$$\begin{aligned}&\sum \limits _{n=1}^m{\varDelta }t(\Vert (U- u)^{x,n}\Vert _{x}^2 +\Vert (U- u)^{y,n}\Vert _{y}^2)^{\frac{1}{2}} \nonumber \\&\quad \le \left( \sum \limits _{n=1}^m{\varDelta }t\right) ^{\frac{1}{2}}\left( \sum \limits _{n=1}^m{\varDelta }t(\Vert (U- u)^{x,n}\Vert _{x}^2 +\Vert (U- u)^{y,n}\Vert _{y}^2)\right) ^{\frac{1}{2}}\nonumber \\&\quad \le C({\varDelta }t+h^2+k^2), \end{aligned}$$

(74)

which completes the proof of the second one. $\square$

Remark 4.1

In this paper we just considered the homogeneous Neumann boundary condition $\mathbf {u}\cdot \mathbf {n}=0$. For non-homogeneous boundary condition the present interpolant operators does not have second-order accuracy near the boundary. We will improve the result next.

5 Numerical Experiment

In this section we carry out some numerical experiments using the block-centered finite difference scheme in two dimensional region. For simplicity, the region are selected as unit square, i.e. ${\varOmega }= [ 0, 1] \times [ 0, 1]$. The time interval is $(0,T]=(0,1]$. The permeability, the viscosity, density and Forchheimer number $\beta$ are all constants. For simplicity, take $\mu = 2, {\bar{k}} = 4, \rho = 1, \beta = 5$. We use an iterative procedure to solve the nonlinear system obtained from the finite difference discretization.

We test Examples 1 and 2 to verify the convergence rates of the presented scheme. The initial partition is $10 \times 10$ grid. And then the grid is refined 4 times. For each refining we take $\displaystyle \frac{{\varDelta }t}{h^2}$ to be a constant. A grid with degree of freedom is plotted in Fig. 2.

Fig. 2

Grid with degree of freedom of first level

Fig. 3

Convergence rates of Example 1 (The tangent of the triangle is 2)

Fig. 4

Convergence rates of Example 2 (The tangent of the triangle is 2.)

The numerical results are listed in Figs. 3 and 4 and Tables 1 and 2. In the tables $\displaystyle \frac{h_{max}}{h_{min}}$ and $\displaystyle \frac{k_{max}}{k_{min}}$ are listed to show the non-uniformity of the grid, where $h_{max}$ ($h_{min}$) is the maximum (minimum) meshsize in x-direction and $k_{max}$ ($k_{min}$) is the maximum (minimum) meshsize in y-direction. The discrete $l^2$ norms of the errors are defined as follows.

$$\begin{aligned}&E_{u,l^2}&=\max \limits _{m\le T/{\varDelta }t} \left( \Vert (U- u)^{x,m}\Vert _{x}^2 +\Vert (U- u)^{y,m}\Vert _{y}^2\right) ^{\frac{1}{2}},\\&E_{p,l^2}&=\max \limits _{m\le T/{\varDelta }t} \Vert (P-p)^m \Vert _{M}. \end{aligned}$$

Example 1

An example with homogeneous Neumann boundary condition is as below. The flux on the boundary condition, $\mathbf {u} \cdot \mathbf {n}$, is computed according to the analytic solution given as below.

$$\begin{aligned} \left\{ \begin{aligned} p( x, y, t)&= ( x - x^2)( y - y^2), ~~~~\\ \mathbf {u}( x, y, t)&= ( \sin { \pi t} \sin { \pi x} \cos { \pi y}, \sin { \pi t} \cos { \pi x} \sin { \pi y})^T. \end{aligned} \right. \end{aligned}$$

The numerical results are listed in Fig. 3 and Table 1.

Table 1 A priori error and convergence rates for Example 1 at t = 1

Table 2 A priori error and convergence rates for Example 2 at t = 1

Fig. 5

Velocity quiver and pressure distribution for Example 3, t = 0.5

Fig. 6

Velocity quiver and pressure distribution for Example 3, t = 1.0

Example 2

An example with homogeneous Neumann boundary condition is as below. The flux on the boundary condition, $\mathbf {u} \cdot \mathbf {n}$, is computed according to the analytic solution given as below.

$$\begin{aligned} \left\{ \begin{aligned} p( x, y, t)&= \arctan { ( x + y - t - 1)}, ~~~~\\ \mathbf {u}( x, y, t)&= ( e^{ -t} y \sin { \pi x} , e^{ -t} x \sin { \pi y})^T. \end{aligned} \right. \end{aligned}$$

The numerical results are listed in Fig. 4 and Table 2.

Example 3

An example with homogeneous Neumann boundary condition, point-source and point-sink flux is simulated. The right hand side equals zero except at the injection and production wells, where the injection flow rate, $q_{_{_{I}}}$, and production flow rate, $q_{_{_{P}}}$, at wells are,

$$\begin{aligned} \begin{aligned} q_{_{_{I}}}( x, y, t)&= \delta ( 0, 0), \ \ q_{_{_{P}}}( x, y) = - \delta ( 1, 1). \end{aligned} \end{aligned}$$

The numerical results are listed in Figs. 5 and 6.

From Figs. 3 and 4 and Tables 1 and 2, we can see that the block-centered finite difference approximations for pressure and velocity have the second order accuracy in discrete $L^2$-norms. These results are in consistent with the error estimates in Theorem 1. Figures 5 and 6 show that the pressure approximation and velocity approximation are reasonable for the point-source and point-sink problem.