An efficient and long-time accurate third-order algorithm for the Stokes–Darcy system

Abstract

A third-order in time numerical IMEX-type algorithm for the Stokes–Darcy system for flows in fluid saturated karst aquifers is proposed and analyzed. A novel third-order Adams–Moulton scheme is used for the discretization of the dissipative term whereas a third-order explicit Adams–Bashforth scheme is used for the time discretization of the interface term that couples the Stokes and Darcy components. The scheme is efficient in the sense that one needs to solve, at each time step, decoupled Stokes and Darcy problems. Therefore, legacy Stokes and Darcy solvers can be applied in parallel. The scheme is also unconditionally stable and, with a mild time-step restriction, long-time accurate in the sense that the error is bounded uniformly in time. Numerical experiments are used to illustrate the theoretical results. To the authors’ knowledge, the novel algorithm is the first third-order accurate numerical scheme for the Stokes–Darcy system possessing its favorable efficiency, stability, and accuracy properties.

1 Introduction

Certain rocks such as limestone, dolomite and gypsum are susceptible to dissolution due to reaction with carbon-dioxide and water which leads, over long (geological) time, to the formation of voids (vugs) and conduits. This type of landscape is referred to as karst. Due to the existence of vugs and conduits, large amount of water may be stored in karst regions to form karst aquifers that are of great practical importance and are susceptible to pollution [27]. For example, about 90 % of the fresh water used in the State of Florida comes from karst aquifers and contamination is a serious problem [25].

For many important applications such as contaminant transport in karst aquifers, one must couple the fluid motion in the porous media with the fluid motion in the conduit or vugs. For instance, contaminants driven into the porous media during a flood season may be released during a drought season. Moreover, because fluid motion in the porous media (matrix) is much slower compared to fluid motion in conduits, long-time accurate numerical schemes are highly desirable if one is interested in capturing the physically interesting retention and release of contaminants within karst aquifers.

There has been a recent surge in interest in the design and analysis of numerical algorithms for the Stokes–Darcy and related systems that govern the motion of fluids flows in saturated karst aquifers. See, e.g., [4, 7, 9–15, 17–22, 26, 28–35, 37–40]. In particular, first order and second order in time accurate and long-time stable schemes have been proposed and studied in [11, 15, 29, 30, 35].

The purpose of this work is to propose and investigate a novel third-order Adams–Moulton–Bashforth method for the Stokes–Darcy system. The algorithm is a special case of the implicit-explicit (IMEX) class of schemes [1–3, 5]. The coupling term in the interface conditions is treated explicitly in our algorithm so that only two decoupled problems (one Stokes and one Darcy) are solved at each time step. Therefore, the scheme can be implemented very efficiently and, in particular, legacy codes for each of the two components can be utilized. Moreover, we show that our scheme is unconditionally stable and long-time stable in the sense that the solutions remain bounded uniformly in time. The uniform in time bound of the solutions further leads to uniform in time error estimates. This is a highly desirable feature because one would want to have reliable numerical results over the long-time scale of contaminant sequestration and release. We also provide the results of numerical experiments that illustrate our analytical results.

This work can be viewed as an improvement of our earlier work [15] in which a second-order in time Adams–Moulton–Bashforth algorithm was studied. This is the first third-order algorithm that is unconditionally stable, long-time accurate in the sense of the existence of a uniform-in-time error bound, and efficient in the sense that only two decoupled problems (one Stokes, one Darcy) are needed at each time step.

The rest of the paper is organized as follows. In Sect. 2, we introduce the coupled Stokes–Darcy system, the associated weak formulation, and the third-order in time scheme. The unconditional and long-time stability with respect to the $L^2$ norm are presented in Sect. 3. Numerical results that illustrate the accuracy, efficiency, and long-time stability of our algorithms are given in Sect. 4. We close by providing some concluding remarks in Sect. 5.

2 The Stokes–Darcy system and one type of third order IMEX method

In this section we recall the Stokes–Darcy system modeling flows in saturated karst aquifers. A third-order in time numerical scheme based on the Adams–Moulton–Bashforth approach is presented as well.

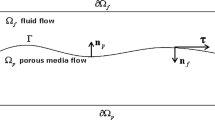
The Stokes–Darcy system. For simplicity, the following conceptual domain is considered for a karst aquifer. It contains a porous media (matrix), denoted by ${\varOmega }_p\in \mathbb {R}^d$, and a conduit, denoted by ${\varOmega }_f\in \mathbb {R}^d$, where $d=2,3$ denotes the spatial dimension. ${\varGamma }$ denotes the interface between the matrix and the conduit. The remaining pieces of the boundaries for the matrix and the conduit are denoted $\partial {\varOmega }_p$ and $\partial {\varOmega }_f$, respectively. We assume $\partial {\varOmega }_p$ and $\partial {\varOmega }_f$ are non-empty for simplicity (Fig. 1).

Fig. 1

The physical domain consisting of a porous media ${\varOmega }_p$ and a free-flow conduit ${\varOmega }_f$

The governing coupled Stokes–Darcy system for karst aquifers is given by

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle S\frac{\partial \phi }{\partial t}-\nabla \cdot ({{\mathbb K}\nabla \phi })=f &{} \quad \text{ in } {\varOmega }_p, \\ \displaystyle \frac{\partial \mathbf {u}_f}{\partial t}- \frac{1}{\rho }\nabla \cdot {\mathbb T}\left( \mathbf {u}_f,p\right) =\mathbf {f}\quad \text{ and }\quad \nabla \cdot {\mathbf {u}_f}=0 &{} \quad \text{ in }\, {\varOmega }_f, \end{array}\right. \end{aligned}$$

(1)

where the unknowns are the hydraulic head $\phi$ in the matrix and the fluid velocity $\mathbf {u}_f$ and the pressure p in the conduit [16]. The Darcy velocity $\mathbf {u}_p$ in the matrix can be recovered by the Darcy equation $\mathbf {u}_p=-{\mathbb K}\nabla \phi$. In (1), f denotes a sink or source in the matrix, $\mathbf {f}$ denotes a body force density in the conduit, $\rho$ the fluid density which is taken to be 1 for simplicity, ${\mathbb T}(\mathbf {u}_f,p)=2\nu {\mathbb D}(\mathbf {u}_f)-p{\mathbb I}$ denotes the stress tensor in the conduit, and ${\mathbb D}(\mathbf {u}_f)=(\nabla \mathbf {u}_f + \nabla \mathbf {u}_f^{T})/2$ is the rate of deformation tensor. The physical parameters involved are the water storage coefficient S, the hydraulic conductivity tensor ${\mathbb K}$, and the kinematic viscosity of the fluid $\nu$. For simplicity, we assume homogeneous Dirichlet boundary conditions for the hydraulic head $\phi$ and the free flow velocity $\mathbf {u}_f$ in the conduit except on the interface ${\varGamma }$. On the interface ${\varGamma }$, we impose the continuity of normal velocity (for conservation of mass), the balance of normal component of the normal stress, and the Beavers–Joseph–Saffman–Jones interface boundary conditions (BJSJ) [6, 23, 24, 36]:

$$\begin{aligned} \left\{ \begin{aligned}&\mathbf {u}_f\cdot \mathbf{n}_f=\mathbf {u}_p\cdot \mathbf{n}_f=-({\mathbb K}\nabla \phi )\cdot \mathbf{n}_f\\&-{{\varvec{\tau }}}_j\cdot ({\mathbb T}(\mathbf {u}_f,p_f)\cdot {\mathbf{n}_f})=\alpha _{BJSJ}{{\varvec{\tau }}}_j\cdot {\mathbf {u}_f},\quad j=1,\ldots ,d-1\\&-\mathbf{n}_f\cdot ({\mathbb T}(\mathbf {u}_f,p_f)\cdot {\mathbf{n}_f})=g\phi . \end{aligned}\right. \end{aligned}$$

(2)

In (2), $\mathbf{n}_f$ denotes the outer normal vector to ${\varOmega }_f$ and $\{{{\varvec{\tau }}}_j\}$, $j=1,2,\ldots ,d-1$, denotes a set of linearly-independent tangential vectors on the interface ${\varGamma }$. The additional physical parameters are the gravitational constant g and the Beavers–Joseph–Saffman–Jones coefficient $\alpha _{BJSJ}=\frac{\widetilde{\alpha }_{BJSJ}\sqrt{d}\nu }{\sqrt{trace({\mathbb K})}}$.

Weak formulation of the Stokes–Darcy system. Let $(\cdot ,\cdot )_D$ and $\Vert \cdot \Vert _D$ denote the standard $L^2(D)$ inner product and norm, respectively, where D can be ${\varOmega }_p$, ${\varOmega }_f$, or ${\varGamma }$. We omit D whenever there is no ambiguity. We define the function spaces

$$\begin{aligned} \mathbf {H}_f= & {} \left\{ \mathbf {v}\in \left( H^1({\varOmega }_f)\right) ^d \mid \mathbf {v}=\mathbf {0}\, \hbox { on }\, \partial {\varOmega }_f{\setminus }{\varGamma } \right\} ,\\ {H}_p= & {} \left\{ \psi \in H^1({\varOmega }_p) \mid \psi =0\, \hbox { on }\, \partial {\varOmega }_p{\setminus } {\varGamma } \right\} ,\\ {Q}= & {} L^2({\varOmega }_f), \qquad \mathbf {W}=\mathbf {H}_f\times {H}_p. \end{aligned}$$

Let $X'$ denote the dual space of X with respect to the duality induced by the $L^2$ inner product. The $X', X$ action is denoted by $\langle \cdot ,\cdot \rangle _{X', X}$ with the subscript omitted if it is clear from the context.

A weak formulation of the Stokes–Darcy system is then derived by the following procedure. First, we multiply the three equations in (1) by three test functions $\mathbf {v}\in \mathbf {H}_f$, $g\psi \in {H}_p$, and $q\in Q$, receptively, and integrate the results over each corresponding domain. Then, integration by parts is applied to the terms involving second order derivatives, a process that produces boundary integrals. Finally, we appropriately substitute the BJSJ interface boundary conditions (2) into the boundary integral terms to arrive at the weak formulation

$$\begin{aligned} \langle \langle \underline{\mathbf {u}}_t,\underline{\mathbf {v}}\rangle \rangle +a(\underline{\mathbf {u}}, \underline{\mathbf {v}})+b(\mathbf {v},p)+a_{\varGamma }(\underline{\mathbf {u}},\underline{\mathbf {v}})= & {} \langle \underline{\mathbf {f}},\underline{\mathbf {v}}\rangle \quad {\forall \,{\underline{\mathbf {v}}}\in {\mathbf {W}}}, \nonumber \\ b(\mathbf {u},q)= & {} 0 \qquad {\forall \,q\in Q}, \end{aligned}$$

(3)

where ${\mathbf {W}}= \mathbf {H}_f\times {H}_p$, $\underline{\mathbf {u}}=[\mathbf {u},\phi ]^T$, $\underline{\mathbf {v}}=[\mathbf {v},\psi ]^T$, $\underline{\mathbf {f}}=[\mathbf {f},gf]^T$, $(\cdot )_t=\partial (\cdot )/\partial t$,

$$\begin{aligned} \begin{aligned} \langle \langle \underline{\mathbf {u}}_t,\underline{\mathbf {v}}\rangle \rangle&=\langle \mathbf {u}_t, \mathbf {v}\rangle _{{\varOmega }_f} + gS\langle \phi _t, \psi \rangle _{{\varOmega }_p},\qquad b(\mathbf {v},q)=-(q, \nabla \cdot \mathbf {v})_{{\varOmega }_f},\\ a(\underline{\mathbf {u}}, \underline{\mathbf {v}})&= a_f(\mathbf {u},\mathbf {v})+a_p(\phi ,\psi )+a_{BJSJ}(\mathbf {u},\mathbf {v}),\\ a_{{\varGamma }}(\underline{\mathbf {u}},\underline{\mathbf {v}})&=g(\phi , \mathbf {v}\cdot \mathbf{n}_f)_{{\varGamma }}-g(\mathbf {u}\cdot \mathbf{n}_f, \psi )_{\varGamma }, \\ \langle \underline{\mathbf {f}},\underline{\mathbf {v}}\rangle&= \langle {\mathbf {f}},{\mathbf {v}}\rangle _{{\varOmega }_f} +\langle gf ,\psi \rangle _{{\varOmega }_p}, \end{aligned} \end{aligned}$$

(4)

with

$$\begin{aligned}&a_f(\mathbf {u},\mathbf {v})=\nu (\nabla \mathbf {u}, \nabla \mathbf {v})_{{\varOmega }_f},\qquad a_p(\phi ,\psi )=g({\mathbb K}\nabla \phi , \nabla \psi )_{{\varOmega }_p} \\&a_{BJSJ}(\mathbf {u},\mathbf {v})=\alpha _{BJSJ}(\mathbf {u}\cdot \mathbf {\tau } ,\mathbf {v}\cdot \mathbf {\tau })_{{\varGamma }}. \end{aligned}$$

The bilinear form $a(\cdot ,\cdot )$ can be shown to be coercive, i.e.,

$$\begin{aligned} a({\underline{\mathbf {u}}},{\underline{\mathbf {u}}}) \ge (\nu \Vert \nabla \mathbf {u}\Vert ^2+gK_{\min }\Vert \nabla \phi \Vert ^2 + \alpha _{BJSJ} \Vert \mathbf {u}\cdot \mathbf {\tau }\Vert ^2_{\varGamma })\ge C_a \Vert \nabla \underline{\mathbf {u}}\Vert ^2, \end{aligned}$$

(5)

where $C_a=\min (\nu ,gK_{\min })>0$ and $K_{\min }$ denotes the smallest eigenvalue of ${\mathbb K}$. Details can be found in, e.g., [8, 15].

For the sake of exposition, we introduce the two norms

$$\begin{aligned} \Vert \underline{\mathbf {u}}\Vert _a= \left( a({\underline{\mathbf {u}}},{\underline{\mathbf {u}}})\right) ^\frac{1}{2}, \quad \Vert \underline{\mathbf {v}}\Vert _S=\langle \langle \underline{\mathbf {v}},\underline{\mathbf {v}}\rangle \rangle ^\frac{1}{2}. \end{aligned}$$

It is easy to see that $\Vert \underline{\mathbf {v}}\Vert _S$ is equivalent to the $L^2$ norm, i.e.,

$$\begin{aligned} C_s\Vert \underline{\mathbf {v}}\Vert _S\le \Vert \underline{\mathbf {v}}\Vert \le C_S \Vert \underline{\mathbf {v}}\Vert _S, \end{aligned}$$

(6)

where $C_s=\min \{1,\sqrt{gS}\}$ and $C_S=\max \{1,\sqrt{gS}\}$.

Third-order Adams–Moulton–Bashforth IMEX method (AMB3). To define our novel third-order scheme that is unconditionally stable and long-time accurate, we first define two Adams-type difference operators. The first is the novel Adams–Moulton difference operator defined on a $2{\varDelta } t$ mesh

$$\begin{aligned} D_{\mathrm {AM}} v^{n+1}=\frac{2}{3}{v}^{n+1}+\frac{5}{12}{v}^{n-1}-\frac{1}{12}{v}^{n-3}, \end{aligned}$$

(7)

and the other is the Adams–Bashforth difference operator

$$\begin{aligned} D_{\mathrm {AB}}v^{n+1}=\frac{23}{12}{v}^{n}-\frac{4}{3}{v}^{n-1}+\frac{5}{12}{v}^{n-2}. \end{aligned}$$

(8)

Note that the Adams–Moulton operator (7) is different from the standard one $\frac{5}{12}v^{n+1}+\frac{2}{3}v^n-\frac{1}{12}v^{n-1}$. The novel form of the Adams–Mouton operator that we adopt here is, due to its dissipativity, crucial to the long-time stability.

The third-order Adams–Moulton–Bashforth method is a combination of the third-order explicit Adams–Bashforth treatment for the coupling term and the novel third-order Adams–Moulton method for the remaining terms. Specifically, we have, for any $\underline{\mathbf {v}}\in {\mathbf {W}}$ and $q\in Q$,

$$\begin{aligned} \left\langle \left\langle \frac{\underline{\mathbf {u}}^{n+1}-\underline{\mathbf {u}}^n}{{\varDelta } t},\underline{\mathbf {v}}\right\rangle \right\rangle+ & {} \widetilde{a}\left( D_{\mathrm {AM}}\underline{\mathbf {u}}^{n+1},\underline{\mathbf {v}}\right) +b\left( \mathbf {v},D_{\mathrm {AM}}{p}^{n+1}\right) \nonumber \\= & {} \left\langle D_{\mathrm {AM}}\underline{\mathbf {f}}^{n+1},{\underline{\mathbf {v}}} \right\rangle -\widetilde{a}_{\varGamma }\left( D_{\mathrm {AB}}{\underline{\mathbf {u}}}^{n+1},\underline{\mathbf {v}}\right) , \nonumber \\ b\left( D_{\mathrm {AM}}{\mathbf {u}}^{n+1},q\right)= & {} 0. \end{aligned}$$

(9)

Here the bilinear form $\widetilde{a}(\underline{\mathbf {u}},\underline{\mathbf {v}})$ is defined as

$$\begin{aligned} \widetilde{a}(\underline{\mathbf {u}},\underline{\mathbf {v}})=a(\underline{\mathbf {u}},\underline{\mathbf {v}})+a_{st}(\underline{\mathbf {u}},\underline{\mathbf {v}}), \end{aligned}$$

where the artificial stabilizing term $a_{st}(\cdot ,\cdot )$ is defined as

$$\begin{aligned} a_{st}(\underline{\mathbf {u}},\underline{\mathbf {v}})=\gamma _f (\mathbf {u}\cdot \mathbf {n}_f, \mathbf {v}\cdot \mathbf {n}_f)_{\varGamma }+\gamma _p(\phi , \psi )_{\varGamma } \end{aligned}$$

(10)

with parameters $\gamma _f,\gamma _p\ge 0$. It is obvious that

$$\begin{aligned} \widetilde{a}(\underline{\mathbf {u}},\underline{\mathbf {u}})\ge {a}(\underline{\mathbf {u}},\underline{\mathbf {u}}) \ge C_a\Vert \nabla \underline{\mathbf {u}}\Vert ^2, \end{aligned}$$

(11)

so that we can define the norm

$$\begin{aligned} \Vert \underline{\mathbf {u}}\Vert ^2_{\widetilde{a}}=\widetilde{a}(\underline{\mathbf {u}},\underline{\mathbf {u}}). \end{aligned}$$

The interface term ${a}_{{\varGamma }}(\underline{\mathbf {u}},\underline{\mathbf {v}})$ is modified by $\widetilde{a}_{{\varGamma }}(\underline{\mathbf {u}},\underline{\mathbf {v}})$ as

$$\begin{aligned} \widetilde{a}_{{\varGamma }}(\underline{\mathbf {u}},\underline{\mathbf {v}}) = a_{\varGamma }(\underline{\mathbf {u}},\underline{\mathbf {v}}) - a_{st}(\underline{\mathbf {u}},\underline{\mathbf {v}}). \end{aligned}$$

Notice that the term $a_{st}$ added to a(u, v) is also subtracted from $a_{{\varGamma }}$, so we are not adding any artificial terms at the continuous in-time level. This treatment leads to a Dupont–Douglas type regularization at time-discrete level. Numerical evidence suggests that this regularization leads to additional stability.

Efficiency of the scheme. Note that the only term that couples the Stokes equation in the conduit with the equation in the matrix is the interface term $\widetilde{a}_{\varGamma }$ through $a_{\varGamma }$. Because this coupling term is treated explicitly in our scheme (9), the scheme is of high efficiency because we only need to solve two decoupled subproblems at each time step, one Stokes and one Darcy:

• 1. At time $t=t_{n+1}$, given $\underline{\mathbf {u}}^{n},\underline{\mathbf {u}}^{n-1},\underline{\mathbf {u}}^{n-2},\underline{\mathbf {u}}^{n-3}$;

• 2. Set $\underline{\mathbf {v}}=[\mathbf {v},0]$ so that all the terms involving $\phi ^{n+1}$ vanish and thus we only need apply a fast Stokes solver to determine $\mathbf {u}^{n+1}$;

• 3. Set $\underline{\mathbf {v}}=[\mathbf {0},g\psi ]$ so that all the terms involving $\mathbf {u}^{n+1}$ vanish and thus we only need apply a fast Darcy solver for $\phi ^{n+1}$;

• 4. Set $n=n+1$ and return to step 1.

The computation of step 2 and 3 can be conducted in a parallel fashion and one can use legacy Stokes and Darcy codes, respectively, for each step, if one so desires.

3 Unconditional and long-time stability

Useful inequalities. We recall a few inequalities to aid readability.

• Trace inequality: if $\underline{\mathbf {v}}\in \mathbf {W}$, then

  $$\begin{aligned} \Vert \underline{\mathbf {v}}\Vert _{{\varGamma }}\le C_{tr} \sqrt{\Vert \underline{\mathbf {v}}\Vert \Vert \nabla \underline{\mathbf {v}}\Vert } , \quad \Vert \underline{\mathbf {v}}\Vert _{{\varGamma }}\le C_{tr} \Vert \nabla \underline{\mathbf {v}}\Vert , \quad \Vert \underline{\mathbf {v}}\Vert _{{\varGamma }}\le C_{tr} \Vert \underline{\mathbf {v}}\Vert _{\widetilde{a}}. \end{aligned}$$

  (12)

• Poincaré inequality:   if $\underline{\mathbf {v}}\in \mathbf {W}$, then

  $$\begin{aligned} \Vert \underline{\mathbf {v}}\Vert \le C_{P} \Vert \nabla \underline{\mathbf {v}}\Vert . \end{aligned}$$

  (13)

• Young inequality:

  $$\begin{aligned} a^{\frac{1}{2}}b^{\frac{1}{2}}c\le \frac{a^2}{64\varepsilon ^{3}}+\varepsilon (b^2+c^2)\quad \forall \, a, b, c, \varepsilon >0. \end{aligned}$$

  (14)

• Triangle inequality: $\Vert a+b\Vert ^{\frac{1}{2}}\le \Vert a\Vert ^{\frac{1}{2}}+\Vert b\Vert ^{\frac{1}{2}}.$

Other variants of Young’s inequality will also be used.

Useful lemmas. Here we introduce a few useful lemmas that are useful in the analysis of our schemes.

The following estimates follow from the basic inequalities.

Lemma 1

Let $a_{\gamma }(\cdot ,\cdot )$ and $a_{st}(\cdot ,\cdot )$ be defined as in (4) and (10), respectively. Then, there exists a constant $C_{ct}$ such that

$$\begin{aligned} |\widetilde{a}_{\varGamma }(\underline{\mathbf {u}},\underline{\mathbf {v}})|\le |a_{st}(\underline{\mathbf {u}},\underline{\mathbf {v}})|+|a_{\varGamma }(\underline{\mathbf {u}},\underline{\mathbf {v}})|\le C_{ct}\Vert \underline{\mathbf {u}}\Vert _{\varGamma }\Vert \underline{\mathbf {v}}\Vert _{\varGamma } \qquad \forall \,\underline{\mathbf {u}}, \underline{\mathbf {v}}\in \mathbf {W}. \end{aligned}$$

Lemma 2

For any $\beta _1>0$, $\underline{\mathbf {v}}, \underline{\mathbf {w}}\in \mathbf {W}$, we have

$$\begin{aligned} |\widetilde{a}_{{\varGamma }}(\underline{\mathbf {v}}, \underline{\mathbf {w}})|\le \beta _1(\Vert \underline{\mathbf {v}}\Vert _{\widetilde{a}}^2+\Vert \underline{\mathbf {w}}\Vert _{\widetilde{a}}^2)+\beta _2\Vert \underline{\mathbf {v}}\Vert _S^2, \end{aligned}$$

(15)

where $\beta _2=\frac{1}{64}\beta _1^{-3}C^{2}_SC^4_{ct}C^8_{tr}C^{-1}_a$.

Proof

By Lemma 1, the equivalence between $\Vert \cdot \Vert _S$ and $\Vert \cdot \Vert$, (6), (11), and the trace theorem, we have, for any $\underline{\mathbf {v}}, \underline{\mathbf {w}}\in \mathbf {W}$,

$$\begin{aligned} \widetilde{a}_{{\varGamma }}(\underline{\mathbf {v}},\underline{\mathbf {w}})\le & {} C_{ct}\Vert \underline{\mathbf {v}}\Vert _{{\varGamma }}\Vert \underline{\mathbf {w}}\Vert _{{\varGamma }}\le C_{ct}C_{tr}^2\Vert \underline{\mathbf {v}}\Vert ^\frac{1}{2}\Vert \nabla \underline{\mathbf {v}}\Vert ^\frac{1}{2}\Vert \underline{\mathbf {w}}\Vert _{\widetilde{a}}\nonumber \\\le & {} C_S^\frac{1}{2}C_{ct}C_{tr}^2C_a^{-\frac{1}{4}}\Vert \underline{\mathbf {v}}\Vert _S^\frac{1}{2}\Vert \underline{\mathbf {v}}\Vert ^\frac{1}{2}_{\widetilde{a}}\Vert \underline{\mathbf {w}}\Vert _{\widetilde{a}}. \end{aligned}$$

(16)

The inequality (15) is then obtained by setting $\varepsilon =\beta _1C_S^{-\frac{1}{2}} C_{ct}^{-1}C_{tr}^{-2}C_a^{\frac{1}{4}}$ in the Young’s inequality.

Lemma 3

The interface term $\widetilde{a}_{\varGamma }(D_{AB}\underline{\mathbf {u}},\underline{\mathbf {u}})$ can be bounded by

$$\begin{aligned}&-2{\varDelta } t\widetilde{a}_{\varGamma }\left( \frac{23}{12}{\underline{\mathbf {u}}}^{n}-\frac{4}{3}{\underline{\mathbf {u}}}^{n-1}+\frac{5}{12}{\underline{\mathbf {u}}}^{n-2},\underline{\mathbf {u}}^{n+1}\right) \\&\quad \le \frac{1}{12}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n+1}\Vert _{\widetilde{a}}^2+\frac{23}{528}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n}\Vert _{\widetilde{a}}^2+\frac{16}{528}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _{\widetilde{a}}^2+ \frac{5}{528}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _{\widetilde{a}}^2\\&\qquad + \frac{23}{6}\beta _2{\varDelta } t \Vert {\underline{\mathbf {u}}}^{n}\Vert _S^2+\frac{8}{3}\beta _2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _S^2+\frac{5}{6}\beta _2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _S^2. \end{aligned}$$

Proof

Set $\beta _1=\frac{1}{88}$ in Lemma 2. Then $\beta _2=10648{{C^{2}_SC^4_{ct}C^8_{tr}C^{-1}_a}}$ and

$$\begin{aligned}&-2{\varDelta } t\widetilde{a}_{\varGamma }\left( \frac{23}{12}{\underline{\mathbf {u}}}^{n}-\frac{4}{3}{\underline{\mathbf {u}}}^{n-1}+\frac{5}{12}{\underline{\mathbf {u}}}^{n-2},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\quad \le \frac{23}{6}{\varDelta } t\left( \beta _2\Vert {\underline{\mathbf {u}}}^{n}\Vert _S^2+\frac{1}{88}\Vert {\underline{\mathbf {u}}}^{n}\Vert _{\widetilde{a}}^2+\frac{1}{88}\Vert \nabla {\underline{\mathbf {u}}}^{n+1}\Vert _{\widetilde{a}}^2\right) \nonumber \\&\qquad +\frac{8}{3}{\varDelta } t\left( \beta _2\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _S^2+\frac{1}{88}\Vert \nabla {\underline{\mathbf {u}}}^{n-1}|_{\widetilde{a}}^2+\frac{1}{88}\Vert \nabla {\underline{\mathbf {u}}}^{n+1}\Vert _{\widetilde{a}}^2\right) \nonumber \\&\qquad +\frac{5}{6}{\varDelta } t\left( \beta _2\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _S^2+\frac{1}{88}\Vert \nabla {\underline{\mathbf {u}}}^{n-2}\Vert _{\widetilde{a}}^2+\frac{1}{88}\Vert \nabla {\underline{\mathbf {u}}}^{n+1}\Vert _{\widetilde{a}}^2\right) \nonumber \\&\quad \le \frac{1}{12}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n+1}\Vert _{\widetilde{a}}^2+\frac{23}{528}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n}\Vert _{\widetilde{a}}^2+\frac{16}{528}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _{\widetilde{a}}^2+ \frac{5}{528}{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _{\widetilde{a}}^2\nonumber \\&\qquad +\frac{23}{6}\beta _2{\varDelta } t \Vert {\underline{\mathbf {u}}}^{n}\Vert _S^2+\frac{8}{3}\beta _2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _S^2+\frac{5}{6}\beta _2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _S^2 \end{aligned}$$

(17)

so that the lemma is proved.

Lemma 4

The interface term $-{a}_{\varGamma }(D_{AB}\underline{\mathbf {u}},\underline{\mathbf {u}})+a_{st}(D_{AB}\underline{\mathbf {u}}-D_{AM}\underline{\mathbf {u}},\underline{\mathbf {u}})$ can be bounded by

$$\begin{aligned}&-2{\varDelta } ta_{\varGamma }\left( \frac{23}{12}{\underline{\mathbf {u}}}^{n}-\frac{4}{3}{\underline{\mathbf {u}}}^{n-1}+\frac{5}{12}{\underline{\mathbf {u}}}^{n-2},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\qquad +2{\varDelta } ta_{st}\left( -\frac{2}{3}{\underline{\mathbf {u}}}^{n+1}+\frac{23}{12}{\underline{\mathbf {u}}}^{n}-\frac{7}{4}{\underline{\mathbf {u}}}^{n-1}+\frac{5}{12}{\underline{\mathbf {u}}}^{n-2}+\frac{1}{12}{\underline{\mathbf {u}}}^{n-3},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\quad \le \frac{58{\varDelta } t}{360}\Vert {\underline{\mathbf {u}}}^{n+1}\Vert _a^2+\frac{27{\varDelta } t}{360}\Vert {\underline{\mathbf {u}}}^{n}\Vert _a^2+\frac{21{\varDelta } t}{360}\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _a^2+\frac{7{\varDelta } t}{360}\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _a^2\nonumber \\&\qquad +\frac{{\varDelta } t}{360 }\Vert {\underline{\mathbf {u}}}^{n-3}\Vert _a^2+(C_2+2C_3){\varDelta } t \Vert {\underline{\mathbf {u}}}^{n+1}-{\underline{\mathbf {u}}}^{n}\Vert _S^2+5C_3{\varDelta } t \Vert {\underline{\mathbf {u}}}^{n}-{\underline{\mathbf {u}}}^{n-1}\Vert _S^2\nonumber \\&\qquad +2C_3{\varDelta } t \Vert {\underline{\mathbf {u}}}^{n-1}-{\underline{\mathbf {u}}}^{n-2}\Vert _S^2+\frac{C_3{\varDelta } t}{3} \Vert {\underline{\mathbf {u}}}^{n-2}-{\underline{\mathbf {u}}}^{n-3}\Vert _S^2, \end{aligned}$$

(18)

where $C_2=4920750{{C^{2}_SC^4_{ct}C^8_{tr}C^{-1}_a}}$ and $C_3=3375{{C^{2}_SC^4_{ct}C^8_{tr}C^{-1}_a}}$.

Proof

Recall $a_{\varGamma }(\underline{\mathbf {u}},\underline{\mathbf {u}})=0$. Therefore, the interface term can be rewritten as

$$\begin{aligned}&-2{\varDelta } ta_{\varGamma }\left( 2\underline{\mathbf {u}}^{n+1}+\frac{23}{12}{\underline{\mathbf {u}}}^{n}-\frac{4}{3}{\underline{\mathbf {u}}}^{n-1}+\frac{5}{12}{\underline{\mathbf {u}}}^{n-2},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\qquad +2{\varDelta } ta_{st}\left( -\frac{2}{3}{\underline{\mathbf {u}}}^{n+1}+\frac{23}{12}{\underline{\mathbf {u}}}^{n}-\frac{7}{4}{\underline{\mathbf {u}}}^{n-1}+\frac{5}{12}{\underline{\mathbf {u}}}^{n-2}+\frac{1}{12}{\underline{\mathbf {u}}}^{n-3},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\quad = 2{\varDelta } ta_{\varGamma }\left( {\underline{\mathbf {u}}}^{n+1}-{\underline{\mathbf {u}}}^{n},\underline{\mathbf {u}}^{n+1}\right) -\frac{11}{6}{\varDelta } t a_{\varGamma }\left( {\underline{\mathbf {u}}}^{n}-{\underline{\mathbf {u}}}^{n-1},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\qquad +\frac{5}{6}{\varDelta } ta_{\varGamma }\left( {\underline{\mathbf {u}}}^{n-1}-{\underline{\mathbf {u}}}^{n-2},\underline{\mathbf {u}}^{n+1}\right) -\frac{4}{3}{\varDelta } ta_{st}\left( {\underline{\mathbf {u}}}^{n+1}-{\underline{\mathbf {u}}}^{n},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\qquad +\frac{5}{2}{\varDelta } ta_{st}\left( {\underline{\mathbf {u}}}^{n}-{\underline{\mathbf {u}}}^{n-1},\underline{\mathbf {u}}^{n+1}\right) -{\varDelta } ta_{st}\left( {\underline{\mathbf {u}}}^{n-1}-{\underline{\mathbf {u}}}^{n-2},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\qquad -\frac{1}{6}{\varDelta } ta_{st}\left( {\underline{\mathbf {u}}}^{n-2}-{\underline{\mathbf {u}}}^{n-3},\underline{\mathbf {u}}^{n+1}\right) . \end{aligned}$$

(19)

Similar as in the proof of Lemma 2, the first term on the right-hand side can be estimated by

$$\begin{aligned} 2{\varDelta } ta_{\varGamma }\left( {\underline{\mathbf {u}}}^{n+1}-{\underline{\mathbf {u}}}^{n},\underline{\mathbf {u}}^{n+1}\right) \le \frac{{\varDelta } t}{180}\Vert {\underline{\mathbf {u}}}^{n+1}\Vert _a^2+C_2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n+1}-{\underline{\mathbf {u}}}^{n}\Vert _S^2 \end{aligned}$$

(20)

and the other terms can be directly estimated by Lemma 2 with $\beta _1=\frac{1}{60}$. The desired result (18) then follows easily.

The following variants of the Grownwall–Bellman inequality will simplify the analysis. They are particularly useful for the stability analysis of multi-step methods.

Lemma 5

Assume that $\{z_n\}$ and $\{y_n\}$ are two non-negative sequences that satisfy

$$\begin{aligned} z_{n+1}+\xi _{-1}y_{n+1}\le z_n +{\varDelta } t\sum _{i=0}^k \zeta _i z_{n-i}+\sum _{i=0}^k\xi _i y_{n-i}+{\varDelta } t \bar{z}, \end{aligned}$$

(21)

where $\bar{z}$, $\xi _i$, and $\zeta _i$ are nonnegative constants and

$$\begin{aligned} \xi _{-1}\ge \sum _{i=0}^k\xi _i. \end{aligned}$$

(22)

Let

$$\begin{aligned} E_{n}=z_{n}+\frac{{\varDelta } t}{1+{\varDelta } t\sum _{i=0}^k\zeta _i}\sum _{i=1}^k\sum _{j=i}^k\zeta _j z_{n-i}+\frac{1}{1+{\varDelta } t\sum _{i=0}^k\zeta _i}\sum _{i=0}^k\sum _{j=i}^k\xi _j y_{n-i}.\nonumber \\ \end{aligned}$$

(23)

Then

$$\begin{aligned} E_{n}\le e^{\sum _{i=0}^k \zeta _i t}\left( E_k+\frac{\bar{z}}{\sum _{i=0}^k \zeta _i}\right) \end{aligned}$$

(24)

for any $n{\varDelta } t\le t$.

Proof

From the definition of $E_n$ and the constraint (22), we have

$$\begin{aligned} E_{n+1}\le \left( 1+{\varDelta } t\sum _{i=0}^k\zeta _i\right) E_n+{\varDelta } t \bar{z} \end{aligned}$$

(25)

so that the bound (24) is easily derived via recursion.

Another variant of Grownwall–Bellman inequality will be useful in the long time stability analysis.

Lemma 6

Assume that $\{z_n\}$ and $\{y_n\}$ are two nonnegative sequences that satisfy

$$\begin{aligned} z_{n+1}+ \zeta _{-1}{\varDelta } t y_{n+1}\le z_n +{\varDelta } t\sum _{i=0}^k \zeta _i y_{n-i} +{\varDelta } t \bar{z}, \end{aligned}$$

(26)

where $\zeta _i$, $i=-1,\ldots ,k$, are nonnegative constants and

$$\begin{aligned} \bar{\zeta }=\frac{1}{k+1}\left( \zeta _{-1}-\sum _{i=0}^k\zeta _i\right) >0. \end{aligned}$$

(27)

Let

$$\begin{aligned} E_{n}=z_{n}+ {\varDelta } t\sum _{i=0}^k\left( (k-i)\bar{\zeta }+\sum _{j=i}^k \zeta _j\right) y_{n-i}. \end{aligned}$$

(28)

Then

$$\begin{aligned} E_{n+1}+\bar{\zeta }{\varDelta } t\sum _{i=0}^{k}y_{n+1-i}\le E_n + {\varDelta } t\bar{z}. \end{aligned}$$

(29)

Moreover, if $z_{n+1}\le C_\zeta y_{n+1}$, then

$$\begin{aligned} E_{n}\le \left( 1+\bar{C}{\varDelta } t\right) ^{-(n-k)}E_k+\frac{\bar{z}}{\bar{C}}, \end{aligned}$$

(30)

where

$$\begin{aligned} \bar{C}=\min \left\{ \frac{\bar{\zeta }}{2C_\zeta }, \frac{\bar{\zeta }}{2(\zeta _{-1}-\bar{\zeta }){\varDelta } t}\right\} . \end{aligned}$$

(31)

Proof

Let $d_i=(k-i)\bar{\zeta }+\sum _{j=i}^k\zeta _j$. Then $E_n=z_n+{\varDelta } t\sum _{i=0}^k d_iy_{n-i}$. It is easily verified that

$$\begin{aligned} d_0+\bar{\zeta }= & {} \zeta _{-1},\end{aligned}$$

(32)

$$\begin{aligned} d_i-d_{i+1}-\bar{\zeta }= & {} \zeta _i,\quad \text{ for }\ i=1,\cdots ,k-1,\end{aligned}$$

(33)

$$\begin{aligned} d_k= & {} \zeta _k, \end{aligned}$$

(34)

so the inequality (26) can be recast as

$$\begin{aligned} z_{n+1}+{\varDelta } t(d_0+\bar{\zeta })y_{n+1}\le z_n+{\varDelta } t\sum _{i=0}^{k-1}(d_i-d_{i+1}-\bar{\zeta })y_{n-i}+{\varDelta } td_k y_{n-k}+{\varDelta } t\bar{z}\nonumber \\ \end{aligned}$$

(35)

or

$$\begin{aligned} z_{n+1}+{\varDelta } t\sum _{i=0}^kd_iy_{n+1-i}+\bar{\zeta }{\varDelta } t\sum _{i=0}^ky_{n+1-i}\le z_n+{\varDelta } t\sum _{i=0}^{k}d_iy_{n-i}+{\varDelta } t\bar{z}, \end{aligned}$$

(36)

which is exactly the inequality (29). Now, if $z_{n+1}\le C_\zeta y_{n+1}$, then

$$\begin{aligned} \sum _{i=0}^ky_{n+1-i}\ge & {} \frac{1}{2C_\zeta }z_{n+1} +\frac{y_{n+1}}{2}+\sum _{i=1}^ky_{n+1-i}\nonumber \\\ge & {} \frac{1}{2C_\zeta }z_{n+1}+ {\varDelta } t\widetilde{C}\sum _{i=0}^kd_iy_{n+1-i}, \end{aligned}$$

(37)

where $\widetilde{C}=\frac{1}{{\varDelta } t}\min \{\frac{1}{2d_0},\min \{d_i^{-1}\}_{i=1}^k\}=\frac{1}{2d_0{\varDelta } t}.$ Note that $d_0=k\bar{\zeta }+\sum _{j=0}^k\zeta _j=\zeta _{-1}-\bar{\zeta }$ so that

$$\begin{aligned} \bar{\zeta }\sum _{i=0}^ky_{n+1-i}\ge \bar{C}\left( z_{n+1}+ {\varDelta } t\sum _{i=0}^kd_iy_{n+1-i}\right) =\bar{C}E_{n+1}, \end{aligned}$$

(38)

where $\bar{C}$ is defined in (31). Then, from (29), we have

$$\begin{aligned} (1+\bar{C}{\varDelta } t)E_{n+1}\le E_n+{\varDelta } t \bar{z}. \end{aligned}$$

(39)

Now by recursion, we have

$$\begin{aligned} E_{n}\le & {} (1+\bar{C}{\varDelta } t)^{-(n-k)}E_k +{\varDelta } t\bar{z}\sum _{i=1}^{n-k}(1+\bar{C}{\varDelta } t)^{-i}\nonumber \\\le & {} (1+\bar{C}{\varDelta } t)^{-(n-k)}E_k +\frac{\bar{z}}{\bar{C}} \end{aligned}$$

(40)

so that the lemma is proved.

Additional sequences are considered in the following lemma.

Lemma 7

Assume that $\{z_n\}$ and $\{y_n^{\ell }\}$, $\ell =1,\ldots ,L$, are nonnegative sequences that satisfy

$$\begin{aligned} z_{n+1}+ {\varDelta } t\sum _{\ell =1}^L\zeta _{-1}^{\ell } y_{n+1}^{\ell }\le z_n +{\varDelta } t\sum _{\ell =1}^{L}\sum _{i=0}^{k_{\ell }} \zeta _i^{\ell } y_{n-i}^\ell +{\varDelta } t \bar{z}, \end{aligned}$$

(41)

where $\zeta _i^{\ell }\ell =1,\ldots , L$ and $i=-1,\ldots ,k_\ell$, are nonnegative constants with $1\le k_\ell \le k$, and

$$\begin{aligned} \bar{\zeta }^{\ell }=\frac{1}{k_{\ell }+1}\left( \zeta _{-1}^{\ell }-\sum _{i=0}^{k_{\ell }}\zeta _i^{\ell }\right) >0. \end{aligned}$$

(42)

Define

$$\begin{aligned} E_{n}=z_{n}+ {\varDelta } t\sum _{\ell =1}^{L}\sum _{i=0}^{k_{\ell }}\left( (k_{\ell }-i)\bar{\zeta }^{\ell }+\sum _{j=i}^{k_{\ell }} \zeta _j^{\ell }\right) y_{n-i}^{\ell }. \end{aligned}$$

(43)

Then

$$\begin{aligned} E_{n+1}+{\varDelta } t \sum _{\ell =1}^L\bar{\zeta }^{\ell }\sum _{i=0}^{k_{\ell }}y_{n+1-i}^{\ell }\le E_n + {\varDelta } t\bar{z}. \end{aligned}$$

(44)

In addition, assume that $z_{n+1}\le C_\zeta y_{n+1}^{\ell _0}$ for some ${\ell _0}$. Then

$$\begin{aligned} E_{n}\le \left( 1+\bar{C}{\varDelta } t\right) ^{-(n-k)}E_k+\frac{\bar{z}}{\bar{C}}, \end{aligned}$$

(45)

where

$$\begin{aligned} \bar{C}=\min \left\{ \frac{\bar{\zeta }^{{\ell _0}}}{2C_\zeta }, \min _{\ell }\frac{\bar{\zeta }^{\ell }}{2(\zeta _{-1}^{\ell }-\bar{\zeta }^{\ell }){\varDelta } t}\right\} . \end{aligned}$$

(46)

The proof is very much the same as that for Lemma 6 and thus is omitted here.

Unconditional stability. Now we can prove that our novel AMB3 scheme is unconditionally stable over any finite time.

Theorem 1

Let $T>0$ be any fixed time. Then, the AMB3 scheme (9) is unconditionally stable in (0, T].

Proof

Set $\underline{\mathbf {v}}=2{\varDelta } t \underline{\mathbf {u}}^{n+1}$ in (9). Using of $\langle 2a,a-b\rangle =|a|^2+|a-b|^2-|b|^2$, we obtain

$$\begin{aligned}&\Vert \underline{\mathbf {u}}^{n+1}\Vert _S^2-\Vert \underline{\mathbf {u}}^{n}\Vert _S^2+\Vert \underline{\mathbf {u}}^{n+1}-\underline{\mathbf {u}}^{n}\Vert _S^2+2{\varDelta } t \widetilde{a}\left( D_{AM}{\underline{\mathbf {u}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\quad = \ 2{\varDelta } t\left\langle D_{AM}{\underline{\mathbf {f}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right\rangle -2{\varDelta } t\widetilde{a}_{\varGamma }\left( D_{AB}{\underline{\mathbf {u}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right) , \end{aligned}$$

(47)

where the pressure term $b(\mathbf {u}^{n+1},\frac{2}{3}{p}^{n+1}+\frac{5}{12}{p}^{n-1}-\frac{1}{12}{p}^{n-3})=0$ because $\mathbf {u}^{n+1}\in \mathbf {H}_f$ and ${p}^{n+1},{p}^{n-1},{p}^{n-3}\in \mathbf {Q}$. A crucial observation is that the last term on the left-hand-side can be bounded below, i.e., according to Young’s inequality, we have

$$\begin{aligned}&2\widetilde{a}\left( \frac{2}{3}\underline{\mathbf {u}}^{n+1}+\frac{5}{12}\underline{\mathbf {u}}^{n-1}-\frac{1}{12}\underline{\mathbf {u}}^{n-3},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\quad \ge 2\left( \frac{2}{3}\Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_{\widetilde{a}}-\frac{5}{24}\left( \Vert \underline{\mathbf {u}}^{n-1}\Vert ^2_{\widetilde{a}}+\Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_{\widetilde{a}}\right) -\frac{1}{24}\left( \Vert \underline{\mathbf {u}}^{n-3}\Vert ^2_{\widetilde{a}}+\Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_{\widetilde{a}}\right) \right) \nonumber \\&\quad \ge \frac{5}{6} \Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_{\widetilde{a}}-\frac{5}{12} t\Vert \underline{\mathbf {u}}^{n-1}\Vert ^2_{\widetilde{a}}-\frac{1}{12} t\Vert \underline{\mathbf {u}}^{n-3}\Vert ^2_{\widetilde{a}}. \end{aligned}$$

(48)

This implies that the special Adams–Moulton operator that we developed is dissipative because the coefficient of the positive term is larger than the sum of the coefficients of the negative terms. This fact will be exploited heavily below to prove the unconditional stability as well as the long-time stability of the scheme.

We also notice that the forcing term on the right-hand-side can be bounded above according to Young’s inequality:

$$\begin{aligned} 2\left\langle D_{AM}{\underline{\mathbf {f}}}^{n+1},\underline{\mathbf {u}}^{n+1} \right\rangle\le & {} \frac{1}{6C^2_P}C_a\left\| \underline{\mathbf {u}}^{n+1}\right\| ^2+6C^2_PC^{-1}_a \left\| D_{AM}{\underline{\mathbf {f}}}^{n+1}\right\| ^2\nonumber \\\le & {} \frac{1}{6}\left\| \underline{\mathbf {u}}^{n+1}\right\| _{\widetilde{a}}^2+\beta _3 \max _{i}\left\| {\underline{\mathbf {f}}}^{i}\right\| ^2, \end{aligned}$$

(49)

where $\beta _3=10C^2_PC^{-1}_a$. Combining the above estimates with Lemma 3 and discarding the term $\Vert \underline{\mathbf {u}}^{n+1}-\underline{\mathbf {u}}^{n}\Vert _S^2$, we have

$$\begin{aligned}&\Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_S+\frac{308}{528}{\varDelta } t\Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_{\widetilde{a}}\\&\quad \le \left( 1+\frac{23}{6}\beta _2{\varDelta } t\right) \Vert {\underline{\mathbf {u}}}^{n}\Vert _S^2+\frac{8}{3}\beta _2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _S^2+\frac{5}{6}\beta _2{\varDelta } t\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _S^2+\frac{23}{528}{\varDelta } t\Vert \underline{\mathbf {u}}^{n}\Vert ^2_{\widetilde{a}}\\&\qquad +\frac{236}{528}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-1}\Vert ^2_{\widetilde{a}}+\frac{5}{528}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-2}\Vert ^2_{\widetilde{a}}+\frac{44}{528}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-3}\Vert ^2_{\widetilde{a}}+\beta _3 {\varDelta } t \max _{i}\left\| {\underline{\mathbf {f}}}^{i}\right\| ^2. \end{aligned}$$

Now, define

$$\begin{aligned} E_n= & {} \Vert {\underline{\mathbf {u}}}^{n}\Vert _S^2+\frac{7\beta _2{\varDelta } t}{2\left( 1+\frac{22}{3}\beta _2{\varDelta } t\right) }\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _S^2+\frac{5\beta _2{\varDelta } t}{6\left( 1+\frac{22}{3}\beta _2{\varDelta } t\right) }\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _S^2\nonumber \\&+ \frac{308{\varDelta } t}{528\left( 1+\frac{22}{3}\beta _2{\varDelta } t\right) }\Vert {\underline{\mathbf {u}}}^{n}\Vert _{\widetilde{a}}^2 +\frac{285{\varDelta } t}{528\left( 1+\frac{22}{3}\beta _2{\varDelta } t\right) }\Vert {\underline{\mathbf {u}}}^{n-1}\Vert _{\widetilde{a}}^2\nonumber \\&+\frac{49{\varDelta } t}{528\left( 1+\frac{22}{3}\beta _2{\varDelta } t\right) }\Vert {\underline{\mathbf {u}}}^{n-2}\Vert _{\widetilde{a}}^2+\frac{44{\varDelta } t}{528\left( 1+\frac{22}{3}\beta _2{\varDelta } t\right) }\Vert {\underline{\mathbf {u}}}^{n-3}\Vert _{\widetilde{a}}^2. \end{aligned}$$

(50)

We then have, by Lemma 5

$$\begin{aligned} \Vert {\underline{\mathbf {u}}}^{n+1}\Vert _S^2\le E_n\le e^{\frac{22}{3}\beta _2 T}\left( E_3+\frac{3\beta _3}{22\beta _2} \max _{i}\left\| {\underline{\mathbf {f}}}^{i}\right\| ^2\right) , \end{aligned}$$

(51)

on any finite time interval [0, T].

Long-time stability. We next show that our scheme is long-time stable in the sense that the solutions will remain bounded uniformly in time as long as a time-step restriction is satisfied. As a direct consequence of this long-time stability, we are able to show that we are able to derive uniform in time bounds on the error.

Theorem 2

Assume that $\underline{\mathbf {f}}\in L^\infty (L^2({\varOmega }))$. For the AMB3 scheme, there exists ${\varDelta } t_0>0$ such that the solution is uniformly bounded in time if ${\varDelta } t\le {\varDelta } t_0$. In particular, there exist $0<\lambda _1<1, 0<\lambda _2<\infty$, and $E_3\ge 0$ such that

$$\begin{aligned} \Vert \underline{\mathbf {u}}^{n+1}\Vert ^2\le \lambda ^{n-2}_1E_3+\lambda _2. \end{aligned}$$

Proof

After rearranging (47) in a slightly different way, we have

$$\begin{aligned}&\Vert \underline{\mathbf {u}}^{n+1}\Vert _S^2-\Vert \underline{\mathbf {u}}^{n}\Vert _S^2+\Vert \underline{\mathbf {u}}^{n+1}-\underline{\mathbf {u}}^{n}\Vert _S^2 + 2{\varDelta } t a\left( D_{AM}{\underline{\mathbf {u}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\quad = \ 2{\varDelta } t\left\langle D_{AM}{\underline{\mathbf {f}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right\rangle -2{\varDelta } ta_{\varGamma }\left( D_{AB}{\underline{\mathbf {u}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right) \nonumber \\&\qquad + 2{\varDelta } ta_{st}\left( D_{AB}{\underline{\mathbf {u}}}^{n+1}-D_{AM}{\underline{\mathbf {u}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right) . \end{aligned}$$

(52)

Similar to the proof of the previous theorem, the bilinear term on the left-hand-side can be bounded from below by

$$\begin{aligned} 2 a\left( D_{AM}\underline{\mathbf {u}}^{n+1},\underline{\mathbf {u}}^{n+1}\right) \ge \frac{5}{6} \Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_a-\frac{5}{12}\Vert \underline{\mathbf {u}}^{n-1}\Vert ^2_a-\frac{1}{12}\Vert \underline{\mathbf {u}}^{n-3}\Vert ^2_a \end{aligned}$$

(53)

and the forcing term can be bounded from above by

$$\begin{aligned} 2 \left\langle D_{AM}{\underline{\mathbf {f}}}^{n+1},\underline{\mathbf {u}}^{n+1}\right\rangle \le \frac{1}{180} \Vert \underline{\mathbf {u}}^{n+1}\Vert _a^2+\beta _4 \max _i\Vert {\underline{\mathbf {f}}}^{i}\Vert ^2, \end{aligned}$$

(54)

where $\beta _4=300C^2_PC^{-1}_a$. The interface term has been estimated in Lemma 4. Combine the above inequalities with Lemma 4, we have

$$\begin{aligned}&\Vert \underline{\mathbf {u}}^{n+1}\Vert _S^2+\frac{240}{360}{\varDelta } t \Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_a+[1-(C_2+2C_3){\varDelta } t]\Vert \underline{\mathbf {u}}^{n+1}-\underline{\mathbf {u}}^{n}\Vert _S^2\nonumber \\&\quad \le \Vert \underline{\mathbf {u}}^{n}\Vert _S^2+\frac{27}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n}\Vert ^2_a+\frac{171}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-1}\Vert ^2_a+\frac{7}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-2}\Vert ^2_a\nonumber \\&\qquad +\frac{31}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-3}\Vert ^2_a+5C_3{\varDelta } t\Vert \underline{\mathbf {u}}^{n}-\underline{\mathbf {u}}^{n-1}\Vert _S^2+2C_3{\varDelta } t\Vert \underline{\mathbf {u}}^{n-1}-\underline{\mathbf {u}}^{n-2}\Vert _S^2\nonumber \\&\qquad +\frac{C_3{\varDelta } t}{3}\Vert \underline{\mathbf {u}}^{n-2}-\underline{\mathbf {u}}^{n-3}\Vert _S^2+\beta _4{\varDelta } t \max _i\Vert {\underline{\mathbf {f}}}^{i}\Vert ^2. \end{aligned}$$

(55)

We require that

$$\begin{aligned} 1-(C_2+2C_3){\varDelta } t>\frac{25C_3}{3}{\varDelta } t. \end{aligned}$$

(56)

A convenient choice is

$$\begin{aligned} {\varDelta } t_0\le \frac{1}{C_2+\frac{31}{3}C_3} \end{aligned}$$

(57)

such that $1-(C_2+2C_3){\varDelta } t\ge \frac{25C_3}{3}{\varDelta } t$ if ${\varDelta } t\le {\varDelta } t_0$. Let

$$\begin{aligned} E_n= & {} \Vert \underline{\mathbf {u}}^{n}\Vert _S^2+\frac{239}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n}\Vert ^2_a+\frac{211}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-1}\Vert ^2_a+\frac{39}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-2}\Vert ^2_a\nonumber \\&+\frac{31}{360}{\varDelta } t\Vert \underline{\mathbf {u}}^{n-3}\Vert ^2_a+\frac{24C_3{\varDelta } t}{3}\Vert \underline{\mathbf {u}}^{n}-\underline{\mathbf {u}}^{n-1}\Vert _S^2\nonumber \\&+\frac{8C_3{\varDelta } t}{3}\Vert \underline{\mathbf {u}}^{n-1}-\underline{\mathbf {u}}^{n-2}\Vert _S^2+\frac{C_3{\varDelta } t}{3}\Vert \underline{\mathbf {u}}^{n-2}-\underline{\mathbf {u}}^{n-3}\Vert _S^2. \end{aligned}$$

(58)

Note that $\Vert \underline{\mathbf {u}}^{n+1}\Vert _S^2\le C_\zeta \Vert \underline{\mathbf {u}}^{n+1}\Vert _a^2$, where $C_\zeta =C_P^2C_a^{-2}C_s^{-2}$. By Lemma 7, we arrive at the conclusion

$$\begin{aligned} \Vert \underline{\mathbf {u}}^{n+1}\Vert ^2_S\le E_{n+1}\le (1+\bar{C}{\varDelta } t)^{n-2}E_3 + \bar{C}^{-1}\beta _4\max _i\Vert \underline{\mathbf {f}}\Vert ^2, \end{aligned}$$

(59)

where $\bar{C}=\min \{\frac{1}{720 C_\zeta },\frac{1}{478}\}$. The theorem is proven if we set $\lambda _1=(1+\bar{C}{\varDelta } t)^{-1}$ and $\lambda _2= \bar{C}^{-1}\beta _4\max _i\Vert \underline{\mathbf {f}}\Vert ^2$.

An immediate consequence of the previous theorem is the following uniform in time error bound. This is a highly desirable property because the retention and release of contaminants in karst aquifers usually occur over very long time scales.

Theorem 3

Suppose that the solutions $\underline{\mathbf {u}}$ and p are smooth and bounded uniformly in time. Let $\underline{\mathbf {e}}^n:=\underline{\mathbf {u}}(n{\varDelta } t) - \underline{\mathbf {u}}^n$ denote the error. Then, provided that the time-step restriction as in the previous theorem is satisfied, we have the estimates

$$\begin{aligned} \Vert \underline{\mathbf {e}}^{n+1}\Vert ^2\le (1+\bar{C}{\varDelta } t)^{-n+2}\epsilon _3^2+C_4 ({\varDelta } t)^6, \end{aligned}$$

where $\bar{C}$ and $C_4$ are appropriate positive constants, and

$$\begin{aligned} \epsilon _3^2= & {} \Vert \underline{\mathbf {e}}^{3}\Vert _S^2+\frac{239}{360}{\varDelta } t\Vert \underline{\mathbf {e}}^{3}\Vert ^2_a+\frac{211}{360}{\varDelta } t\Vert \underline{\mathbf {e}}^2\Vert ^2_a+\frac{39}{360}{\varDelta } t\Vert \underline{\mathbf {e}}^{1}\Vert ^2_a\\&+\frac{24C_3{\varDelta } t}{3}\Vert \underline{\mathbf {e}}^{3}-\underline{\mathbf {e}}^{2}\Vert _S^2 +\frac{8C_3{\varDelta } t}{3}\Vert \underline{\mathbf {e}}^{2}-\underline{\mathbf {e}}^{1}\Vert _S^2+\frac{C_3{\varDelta } t}{3}\Vert \underline{\mathbf {e}}^{1}\Vert _S^2. \end{aligned}$$

Proof

Because $\underline{\mathbf {u}}, p$ are smooth and bounded, and since the scheme 9 is third-order in time, we have that the solution satisfies the scheme in the form of

$$\begin{aligned}&\left\langle \left\langle \frac{\underline{\mathbf {u}}((n+1){\varDelta } t)-\underline{\mathbf {u}}(n{\varDelta } t)}{{\varDelta } t},\underline{\mathbf {v}}\right\rangle \right\rangle +\widetilde{a}\left( D_{\mathrm {AM}}\underline{\mathbf {u}}((n+1){\varDelta } t),\underline{\mathbf {v}}\right) \\&\quad +b\left( \mathbf {v},D_{\mathrm {AM}}{p}((n+1){\varDelta } t)\right) =\left\langle D_{\mathrm {AM}}\underline{\mathbf {f}}^{n+1},{\underline{\mathbf {v}}} \right\rangle -\widetilde{a}_{\varGamma }\left( D_{\mathrm {AB}}{\underline{\mathbf {u}}}((n+1){\varDelta } t),\underline{\mathbf {v}}\right) \\&\quad + \left( R^{n+1}, \underline{\mathbf {v}}\right) ,\, b\left( D_{\mathrm {AM}}{\mathbf {u}}((n+1){\varDelta } t),q\right) =0, \end{aligned}$$

where the remainder term $R^n$ is uniformly bounded by

$$\begin{aligned} \Vert R^n\Vert \le C ({\varDelta } t)^3\quad \forall n=1,2,\ldots . \end{aligned}$$

This implies that the error $\underline{\mathbf {e}}^n$ satisfies

$$\begin{aligned} \left\langle \left\langle \frac{\underline{\mathbf {e}}^{n+1}-\underline{\mathbf {e}}^n}{{\varDelta } t},\underline{\mathbf {v}}\right\rangle \right\rangle+ & {} \widetilde{a}\left( D_{\mathrm {AM}}\underline{\mathbf {e}}^{n+1},\underline{\mathbf {v}}\right) +b\left( \mathbf {v},D_{\mathrm {AM}}e_p^{n+1}\right) \\= & {} -\widetilde{a}_{\varGamma }\left( D_{\mathrm {AB}}{\underline{\mathbf {e}}}^{n+1},\underline{\mathbf {v}}\right) + \left( R^{n+1}, \underline{\mathbf {v}}\right) , \\ b\left( D_{\mathrm {AM}}{\mathbf {e}}^{n+1},q\right)= & {} 0, \end{aligned}$$

where $e_p^{n}=p(n{\varDelta } t)-p^n$. Repeating the same argument as in the previous theorem leads to the desired estimate. Therefore, we have a third-order uniform in time error bound provided that the time-step restriction is satisfied and that the scheme is initiated properly so that $\epsilon _3$ is of third-order. This ends the proof of uniform in time third-order error bound.

Remark 4

If a conforming finite element is used, the scheme is still long-time stable under the constraint ${\varDelta } t\le {\varDelta } t_0$ where ${\varDelta } t_0$ is independent of the finite element mesh size h. Moreover, based on the stability analysis, we can prove that the AMB3 scheme is third-order temporal accurate. Following the analysis in [15], if the Taylor–Hood (P2–P1) finite element pair is used for the discretization of the Stokes system and continuous piecewise quadratic (P2) finite elements are used for discretization of the Darcy system, the error of the fully discretized scheme will be $\Vert \underline{\mathbf {u}}^n(t)-\underline{\mathbf {u}}^n_h\Vert =O({\varDelta } t^3+h^3)$, which is illustrated by the numerical results in next section.

4 Numerical results

We report here on the results of several numerical experiments. The numerical results illustrate the third-order accuracy, unconditional stability, and the long-time stability and uniform in time error bounds.

Suppose that the error behaves like $O(h^{\theta _1}+{\varDelta } t^{\theta _2})$. Then, if we set ${\varDelta } t=h^\theta$, the rate of convergence would be of the order of $r_{h,\theta }=\min (\theta _1,\theta \theta _2)$ with respect to h. The rate of convergence can be numerically estimated by calculating

$$\begin{aligned} r_{h,\theta }\approx \log _2{\frac{\Vert u_{2h,\theta }-u_{exact}\Vert _{l^2}}{\Vert u_{h,\theta }-u_{exact}\Vert _{l^2}}}. \end{aligned}$$

(60)

Here, we use the discrete $l^2$ norm of nodal values to measure errors.

We set ${\varOmega }_f=(0,1)\times (1,2)$, ${\varOmega }_p=(0,1)\times (0,1)$, and the interface ${\varGamma }=(0,1)\times \{1\}$ which separates ${\varOmega }_f$ and ${\varOmega }_p$. Uniform triangular meshes are created by first dividing the rectangular domains ${\varOmega }_p$ and ${\varOmega }_f$ into identical small squares and then dividing each square into two triangles. With respect to such grids, the Taylor–Hood (P2–P1) finite element pair is used to discretize the Stokes system so that the conduit fluid velocity $\mathbf {u}_h$ is approximated by continuous piecewise quadratic functions and the conduit pressure p is approximated by continuous piecewise linear functions. Continuous piecewise quadratic functions are used to approximate the hydraulic head $\phi _h$.

Table 1 Relative error and order of accuracy with respect to the spatial grid size h for Example 4.1 at $t=1$ and with ${\varDelta } t=h$ and $r_{terminal}=r_{1/512,1}$ defined by (60)

Fig. 2

Relative error for the hydraulic head in the matrix $\phi$ (top-left), conduit velocity $\mathbf {u}$ (top-right), and conduit pressure p (bottom) for $0\le t\le 100$ for $h=1/64$

Fig. 3

Long-time behavior of the functionals $E_\phi +E_{\mathbf {u}}$ (left) and $E_p$ (right) for $\nu =1$ and ${\mathbb K}={\mathbb I}$

Fig. 4

Long-time behavior of the functionals $E_\phi +E_{\mathbf {u}}$ (top row) and $E_p$ (bottom row) for $\nu =0.0001$ and ${\mathbb K}={\mathbb I}$

Fig. 5

Long-time behavior of the functionals $E_\phi +E_{\mathbf {u}}$ (top row) and $E_p$ (bottom row) for $\nu =1$ and ${\mathbb K}=0.01{\mathbb I}$

Fig. 6

Long-time behavior of the functionals $E_\phi +E_{\mathbf {u}}$ (top row) and $E_p$ (bottom row) for $\nu =1$, ${\mathbb K}=0.01{\mathbb I}$, and $\gamma _f=\gamma _p=g/2$

4.1 Convergence rates

We choose the manufactured solution of the Stokes–Darcy system (1) given by

$$\begin{aligned} \mathbf{u}_f(\mathbf{x},t)= & {} \left( -\frac{1}{\pi }e^y\sin \pi x\cos 2\pi t,\,\,(e^y-e)\cos \pi x\cos 2\pi t\right) , \\ p_f(\mathbf{x},t)= & {} 2e^y \cos \pi x\cos 2\pi t, \\ \phi (\mathbf{x},t)= & {} (e^y-e y)\cos \pi x\cos 2\pi t. \end{aligned}$$

The right-hand side data in the partial differential equations, initial conditions, and boundary conditions are then chosen correspondingly. Here, we set ${\varDelta } t=h$, $\mathbb {K}=\mathbb {I}$, $\nu =g=S=\gamma _f=\gamma _p=1$, $T=1$, and $\alpha _{BJSJ}=1$.

Table 1 shows that the numerical convergence rate is approximately third order for $\phi$ and $\mathbf {u}$, and of a bit over second order for p. This is all consistent with the third-order temporal scheme and the Taylor–Hood (P2–P1) finite element pair for the Stokes equations and the P2 element for the Darcy equation.

4.2 Long-time error

To illustrate the long-time behavior of our schemes, we use the following manufactured solution that is a slight modification of one used in [9]:

$$\begin{aligned} \mathbf{u}_f(\mathbf{x},t)= & {} \left( [x^2y^2+e^{-y}],[-\frac{2}{3}xy^3+[2-\pi \sin (\pi x)]]\right) [2+\cos (2\pi t)] \\ p_f(\mathbf{x},t)= & {} -[2-\pi \sin (\pi x)]\cos (2\pi y)[2+\cos (2\pi t)] \\ \phi (\mathbf{x},t)= & {} [2-\pi \sin (\pi x)][-y+\cos (\pi (1-y))][2+\cos (2\pi t)]. \end{aligned}$$

The right-hand side data in the partial differential equations, initial conditions, and boundary conditions are then chosen correspondingly. Here, we set $\mathbb {K}=\mathbb {I}$, $\nu =g=S=1$, $T=1$, and $\alpha _{BJSJ}=1$. In this long time numerical experiment, we set the terminal time $T=100$ and $h=1/64$. Figure 2 displays the relative error as a function of t for two different values of ${\varDelta } t$. We see that the long-time error remains bounded, and indeed, seems to not grow.

4.3 Long-time stability analysis

We use the same domain and the same initial conditions as in the Sect. 4.2, i.e., we have

$$\begin{aligned} \mathbf{u}_f(\mathbf{x},0)= & {} \left( -\frac{1}{\pi }e^y\sin \pi x,\,\,(e^y-e)\cos \pi x \right) , \\ p_f(\mathbf{x},0)= & {} 2e^y \cos \pi x, \\ \phi (\mathbf{x},0)= & {} (e^y-e y)\cos \pi x , \end{aligned}$$

but now the forcing terms are set to zero and homogeneous Dirichlet boundary conditions are imposed on the hydraulic head $\phi$ and conduit flow velocity $\mathbf {u}$. To study the long-time stability of the scheme, we define the functionals $E_\phi =\Vert \phi \Vert ^2_{l^2}$, $E_{\mathbf {u}}=\Vert \mathbf {u}\Vert ^2_{l^2}$, and $E_p=\Vert p\Vert ^2_{l^2}$. The the final time is set to $T=100$.

For Fig. 3, we set $h=1/128$, ${\varDelta } t=1/10$, $\mathbb {K}=\mathbb {I}$, $\nu =g=S=1$, and $\gamma _f=\gamma _p=0$. The energy does decay as time evolves, which suggests that the long-time stability time-step size constraint in the analysis is satisfied with the above choices for the parameters.

For Fig. 4, we set $h=1/128$, $\mathbb {K}={\mathbb I}$, $\nu =0.0001$, $g=S=1$, and $\gamma _f=\gamma _p=0$. The figure shows that for this choice of $\nu$, the time-step constraint is between 1/15 and 1/10 which is more restrictive compared to that for Fig. 3 for which $\nu =1$. Thus, we note that the theoretical time step size constraint (57) decreases as $\nu$ becomes smaller so that the long-time numerical results of Figs. 3 and 4 are consistent with our long-time stability analysis.

For Fig. 5, we set $h=1/128$, $\mathbb {K}=0.01{\mathbb I}$, $\nu =g=S=1$, and $\gamma _f=\gamma _p=0$. The figure shows that for this choice of $\mathbb {K}$, the time-step constraint is between 1/50 and 1/45 which is more restrictive compared to that for Fig. 3 for which $\mathbb {K}={\mathbb I}$. Thus, again, the long-time numerical results of Figs. 3 and 5 are consistent with the theoretical time-step size constraint (57), i.e., the time-step constraint becomes smaller as the minimum eigenvalue of $\mathbb {K}$ becomes smaller.

For Fig. 6, we set $h=1/128$, $\mathbb {K}=0.01I$, $\nu =g=S=1$, and $\gamma _f=\gamma _p=g/2$. The figure shows that for this choice of $\gamma _f$ and $\gamma _p$, the time-step constraint is between 1/45 and 1/40 which is less restrictive compared to that for Fig. 5 for which $\gamma _f=\gamma _p=0$. Thus the results show that the stabilizing term does provide better long-time stability.

5 Concluding remarks

We proposed and investigated a long-time, third-order accurate, and efficient numerical method for coupled Stokes–Darcy systems. The algorithm is a combination of a novel third-order Adams–Moulton method and a Adams–Bashforth method. Our algorithm is a special case of the class of implicit-explicit (IMEX) schemes. The interfacial term that requires communications between the porous media and conduit, i.e., between the Stokes and Darcy components of the model, is treated explicitly in our scheme so that, at each time step, only two decoupled problems (one Stokes and one Darcy) are solved. Therefore, our scheme can be implemented very efficiently and, in particular, legacy codes can be used for each component.

We have shown that our scheme is unconditionally stable and, with a mild time-step restriction, long-time stable in the sense that solutions remain bounded uniformly in time. The uniform bound in time of the solution leads to uniform in time error estimates. This is a highly desirable feature because the physically interesting phenomena of contaminant sequestration and release usually occur over a very long time scale and one would like to have faithful numerical results over such time scales. The estimates are illustrated by numerical examples. All these features suggest that the method has strong potential in real applications.

Methods having even higher-order temporal accuracy and the desired unconditional and long-time stability can be derived via suitable combination of a higher-order Adams–Moulton method for the dissipative term and a standard Adams–Bashforth method for the interface term. Details will be reported on elsewhere.