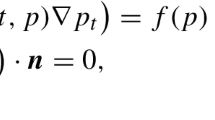A Two-Grid Block-Centered Finite Difference Algorithm for Nonlinear Compressible Darcy–Forchheimer Model in Porous Media

Abstract

In this paper, a block-centered finite difference method is proposed to discretize the compressible Darcy–Forchheimer model which describes the high speed non-Darcy flow in porous media. The discretized nonlinear problem on the fine grid is solved by a two-grid algorithm in two steps: first solving a small nonlinear system on the coarse grid, and then solving a nonlinear problem on the fine grid. On the coarse grid, the coupled term of pressure and velocity is approximated by using the fewest number of node values to construct a nonlinear block-centered finite difference scheme. On the fine grid, the original nonlinear term is modified with a small parameter $\varepsilon$ to construct a linear block-centered finite difference scheme. Optimal order error estimates for pressure and velocity are obtained in discrete $l^\infty (L^2)$ and $l^2(L^2)$ norms, respectively. The two-grid block-centered finite difference scheme is proved to be unconditionally convergent without any time step restriction. Some numerical examples are given to testify the accuracy of the proposed method. The numbers of iterations are reported to illustrate the efficiency of the two-grid algorithm.

1 Introduction

In the study of fluid flow in porous medium, it is well known that Darcy’s law is valid when the fluid velocity is low. When the velocity is high, a second-order term needs to be added, so the equation becomes nonlinear as suggested by Forchheimer [8]. The Darcy–Forchheimer equation takes the following form [1, 2, 8, 24]:

$$\begin{aligned} \dfrac{\mu }{ K}\mathbf {u}+\beta \rho |\mathbf {u}|\mathbf {u}+\nabla p=0. \end{aligned}$$

(1)

Equation (1) describes the nonlinear relationship between the Darcy velocity $\mathbf {u}$ and the gradient of pressure $\nabla p$. Here $\mu$ and $\rho$ denote the viscosity coefficient and the density of the fluid, respectively. The tensor function K represents the permeability tensor. The constant $\beta$ denotes the Forchheimer number. The most important feature of Darcy–Forchheimer equation is that it combines the monotonicity of the nonlinear term and the non-degeneracy of the Darcy part.

In this paper, we consider the compressible Darcy–Forchheimer equation. The continuity equation governing the motion of the fluid is given by

$$\begin{aligned} \dfrac{\partial (\phi \rho )}{\partial t}+\nabla \cdot (\rho \mathbf {u})=\rho f, \end{aligned}$$

(2)

where $\phi$ is the porosity of the porous media and f is the source or sink term. If the fluid is compressible, it holds the following state equation,

$$\begin{aligned} \dfrac{\partial \rho }{\partial p}=C_F\rho , \end{aligned}$$

where $\rho =\rho _0 e^{C_F(p-p_0)}$. Then the governing equation (2) can be rewritten as

$$\begin{aligned} \phi C_F\dfrac{\partial p}{\partial t}+\rho \nabla \cdot \mathbf {u}+\dfrac{\partial \rho }{\partial p}\mathbf {u}\cdot \nabla p=\rho f. \end{aligned}$$

(3)

For the compressible fluid, the coefficient of compressibility $C_F$ is of the order of $10^{-8}$. Therefore, the term $\dfrac{\partial \rho }{\partial p}\mathbf {u}\cdot \nabla p$ can be neglected as shown in [1, 2, 14].

Combining the velocity–pressure relation equation (1) with the governing equation (3), the two-dimensional nonlinear compressible Darcy–Forchheimer model describing high-speed non-Darcy flow in porous media is presented as follows.

$$\begin{aligned} \left\{ \begin{array}{lll} \phi C_F\dfrac{\partial p}{\partial t}+\nabla \cdot \mathbf {u}= f,&{} \mathbf {x}\in \varOmega \times J,\\ \mu K^{-1}\mathbf {u}+\beta \rho (p)|\mathbf {u}|\mathbf {u}+\nabla p=0, &{} \mathbf {x}\in \varOmega \times J,\\ \mathbf {u}\cdot \mathbf {n}=g, &{} \mathbf {x}\in \partial \varOmega \times J,\\ p(\mathbf {x}, 0)=p_0, &{} \mathbf {x}\in \varOmega ,\end{array} \right. \end{aligned}$$

(4)

where $\varOmega$ is a porous media domain and the time interval $J=(0,T]$. The notation $|\cdot |$ represents the Euclidean norm, i.e., $|\mathbf {u}|^2=\mathbf {u}\cdot \mathbf {u}$. For slightly compressible fluid, the density $\rho$ depends on the pressure p, i.e., $\rho =\rho (p)$. For simplicity we assume that the permeability tensor function $K = \bar{k}I$, where $\bar{k}$ is a positive constant and I is the unit matrix. The function $g\in L^2(\partial \varOmega )$ is the flux through the boundary.

Considerable research has been done to study the incompressible Darcy–Forchheimer equation theoretically and numerically, such as [9] by Girault and Wheeler in 2008, [4] by Chaudhary and Cardenas et al. in 2011, [17, 19, 22, 23] by Rui et al. in 2012 and 2015. Recently, slightly compressible Darcy–Forchheimer model starts to receive a great deal of attention. In [1, 2], the authors analyzed the mathematical framework of the well productivity index for fast Forchheimer (non-Darcy) flows in porous media. In [12], the structural stability was established with respect to either the boundary data or the coefficients of the Forchheimer polynomials. In [13], the authors focused on qualitative properties of the solutions of generalized Forchheimer equations for slightly compressible fluids in porous media, subject to the flux condition on the boundary. In [18], the mixed finite element method was used to approximate the solution of the nonlinear system that describes the non-Darcy flow of a single-phase fluid in a porous media, and the optimal order error estimates were established for both pressure and momentum. In [14], the expanded mixed finite element method was used to solve slightly compressible Darcy–Forchheimer model with the initial boundary condition, and priori error estimates were given for the resulting degenerate parabolic equation for the pressure.

In this paper, we study the block-centered finite difference method [25,26,27], which is considered as the lowest order Raviart–Thomas mixed element method with proper quadrature formulation. The application of the finite difference enables us to approximate both the velocity and pressure with second-order accuracy. Moreover, the block-centered finite difference method transfers the saddle point system of the mixed element method into symmetric positive definite system.

The main difficulty of solving model (4) is to treat the strongly nonlinear term including p and $|\mathbf {u}|$. To solve the nonlinear equations resulting from the block-centered finite difference scheme efficiently, we use two-grid method introduced by Xu [28, 29]. The idea is that we first produce a rough approximation of the solution on the coarse grid and then use it to obtain a linearized system on a fine grid. In this approach, solving a nonlinear problem on the fine grid is reduced to solving a linear system on the fine grid and a smaller nonlinear system on the coarse grid. As a result, the two-grid method has attracted many researchers due to its wide applicability, as shown in [3, 5,6,7, 10, 11, 16, 30].

In [19, 22], the method of averaging four subunits was used to construct the discretization scheme for the nonlinear term only involving $\mathbf {u}$. In [20], this idea was adopted to approximate the nonlinear term of the model (4), eleven nodes would be needed on one partition unit, where six nodes are used for approximation of the pressure p and five nodes are used for approximation of the norm function $|\mathbf {u}|$. In this paper, we only use two nodes, which is the fewest as possible, to construct the discretization scheme for the pressure p. To approximate the norm function $|\mathbf {u}|$, we still use five nodes. It is proved that our scheme also preserves the monotonicity of the nonlinear term on the coarse grid. Moreover, our scheme greatly decreases the coupling degree of numerical scheme and hence greatly reduces the computational cost. On the fine grid, a linear system is constructed based on differentiable properties of the nonlinear term. However, one part of the original nonlinear term, namely the norm function $|\mathbf {u}|$, does not have the continuous derivatives. To deal with this difficulty, we add a very small positive parameter $\varepsilon$ to obtain a modified nonlinear term which is twice differentiable with bounded derivatives up to the second order. The modified norm function is only used for the partial derivative term with respect to $\mathbf {u}$. Other parts still use the original nonlinear term to improve the accuracy of approximation scheme. We prove that the block-centered difference scheme preserves the monotonicity of the nonlinear operators on both coarse grid and fine grid. By using the monotonous property of nonlinear operators, we can get the optimal order error estimates for the approximation scheme of slightly compressible Darcy–Forchheimer model (4). The block-centered finite difference scheme is also be proved to be unconditionally convergent. The approach is different from that in [15]. The errors bounds in convergence estimates provide a principle of determining a proper meshsize H for the coarse grid and a proper parameter $\varepsilon$ for the fine grid. Numerical experiments show that two-grid block-centered finite difference method is more efficient than the traditional iterative methods used in [17, 19].

The rest of the paper is organized as follows. In Sect. 2, the two-grid block-centered finite difference formulation is introduced for slightly compressible Darcy–Forchheimer model. The error estimates of two-grid algorithm are presented in Sect. 3. In Sect. 4, several numerical examples are presented to illustrate the algorithm’s accuracy and efficiency. In view of the number of iterations, the two-grid algorithm is more efficient than the traditional iterative method, without loss any accuracy. The conclusions and extensions are given in Sect. 5.

Throughout this paper we use C to denote a generic positive constant independent of the discretization parameters, which may have different values in different appearances.

2 Two-Grid Block-Centered Finite Difference Algorithm

In this section we introduce a two-grid algorithm, based on the block-centered finite difference approximation, for the nonlinear compressible Darcy–Forchheimer model (4).

For simplicity we use the following notations:

$$\begin{aligned} a_1=\mu K^{-1},\quad a_2(p)=\beta \rho (p),\quad \alpha =\phi C_F. \end{aligned}$$

(5)

We assume that $a_1, a_2(p), \alpha$ are continuous functions and

$$\begin{aligned} 0<\underline{a}\le a_1, \alpha , a_2(p)\le \bar{a}, \end{aligned}$$

(6)

for some positive constants $\underline{{a}}$ and $\bar{a}$. Besides, the function $a_2(p)$ is assumed to be twice differentiable with respect to p and have bounded derivatives.

Set $0=t^0<t^1<\cdots <t^{N_t}=T$ and $\varDelta t^k=t^k-t^{k-1}$. We assume the two-dimensional domain $\varOmega$ is rectangular such that $\varOmega =[b^x_1,b^x_2]\times [b^y_1,b^y_2]$.

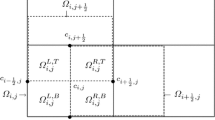
To construct the two-grid algorithm we have to define a regular coarse partition and a regular fine partition of $\varOmega$ simultaneously. First we define the fine partition $\varOmega _h=\varTheta _h^x\times \varTheta _h^y$ as follows:

$$\begin{aligned}&\varTheta _h^x: b^x_1=x_{1/2}< x_{3/2}<\cdots<x_{n_x-1/2}<x_{n_x+1/2}=b^x_2,\\&\varTheta _h^y: b^y_1=y_{1/2}< y_{3/2}<\cdots<y_{n_y-1/2}<y_{n_y+1/2}=b^y_2. \end{aligned}$$

Define

$$\begin{aligned}&x_i=\dfrac{x_{i-1/2}+x_{i+1/2}}{2}, \quad h^x_{i}=x_{i+1/2}-x_{i-1/2},\\&y_j=\dfrac{y_{j-1/2}+y_{j+1/2}}{2},\quad h^y_{j}=y_{j+1/2}-y_{j-1/2},\\&h^x_{i+1/2}=\dfrac{h^x_{i+1}+h^x_{i}}{2}=x_{i+1}-x_{i},\\&h^y_{j+1/2}=\dfrac{h^y_{j+1}+h^y_{j}}{2}=y_{j+1}-y_{j},\\&\varOmega _{i,j}=(x_{i-1/2},x_{i+1/2})\times (y_{j-1/2},y_{j+1/2}),\\&\varOmega _{i+1/2,j}=(x_{i},x_{i+1})\times (y_{j-1/2},y_{j+1/2}),\\&\varOmega _{i,j+1/2}=(x_{i-1/2},x_{i+1/2})\times (y_{j},y_{j+1}), \end{aligned}$$

where $i=1,\ldots ,n_x$ and $j=1,\ldots ,n_y$.

Denote

$$\begin{aligned}&[d_{t}\theta ]^k_{i,j}=\dfrac{\theta ^k_{i,j}-\theta ^{k-1}_{i,j}}{\triangle t^k},\\&[d^x_{h}\theta ]^k_{i+1/2,j}=\dfrac{\theta ^k_{i+1,j}-\theta ^k_{i,j}}{h^x_{i+1/2}},\quad [D^x_{h}\theta ]^k_{i,j}=\dfrac{\theta ^k_{i+1/2,j}-\theta ^k_{i-1/2,j}}{h^x_{i}},\\&[d^y_{h}\theta ]^k_{i,j+1/2}=\dfrac{\theta ^k_{i,j+1}-\theta ^k_{i,j}}{h^y_{j+1/2}},\quad [D^y_{h}\theta ]^k_{i,j}=\dfrac{\theta ^k_{i,j+1/2}-\theta ^k_{i,j-1/2}}{h^y_{j}}, \end{aligned}$$

where $\theta ^k_{s,l}:=\theta (x_s,y_l,t^k)$ for a node-point $(x_s,y_l,t^k)$.

Let the discrete inner products and norms be defined as follows:

$$\begin{aligned}&(\theta ,\omega )_m=\sum _{i=1}^{n_x}\sum _{j=1}^{n_y}h^x_{i}h^y_{j}\theta _{i,j}\omega _{i,j},\\&(\theta ,\omega )_x=\sum _{i=1}^{n_x-1}\sum _{j=1}^{n_y}h^x_{i+1/2}h^y_{j}\theta _{i+1/2,j}\omega _{i+1/2,j},\\&(\theta ,\omega )_y=\sum _{i=1}^{n_x}\sum _{j=1}^{n_y-1}h^x_{i}h^y_{j+1/2}\theta _{i,j+1/2}\omega _{i,j+1/2},\\&\Vert \theta \Vert _m^2=(\theta ,\theta )_m, \qquad \Vert \theta \Vert _x^2=(\theta ,\theta )_x,\qquad \Vert \theta \Vert _y^2=(\theta ,\theta )_y. \end{aligned}$$

Next, we define a piecewise constant function $\bar{q}$ on $(x_{i+1/2},y_j)$ and $(x_i$, $y_{j+1/2})$ such that

$$\begin{aligned} \left\{ \begin{array}{lll} \bar{q}_{i+1/2,j}=\dfrac{1}{2h^x_{i+1/2}}(h^x_{i+1}q_{i,j}+h^x_iq_{i+1,j}),&{}(x,y)\in \varOmega _{i+1/2,j},\\ \bar{q}_{i,j+1/2}=\dfrac{1}{2h^y_{j+1/2}}(h^y_{j+1}q_{i,j}+h^y_jq_{i,j+1}),&{}(x,y)\in \varOmega _{i,j+1/2}. \\ \end{array} \right. \end{aligned}$$

(7)

For a pair of discrete functions $\{V^x_{i+1/2,j}\}$ and $\{V^y_{i,j+1/2}\}$, we give the definition of the interpolation operator $\varvec{\Pi }$ as follows:

$$\begin{aligned} \varvec{\Pi }\mathbf {V}=({\varPi }_xV^x,{\varPi }_yV^y), \end{aligned}$$

with

$$\begin{aligned}&{\varPi }_xV^x(x,y)=V^x_{i+1/2,j},\quad (x,y)\in \varOmega _{i+1/2,j},\\&{\varPi }_yV^y(x,y)=V^y_{i,j+1/2},\quad (x,y)\in \varOmega _{i,j+1/2}. \end{aligned}$$

Let $R(V^x,V^y)$ be the norm function for a vector $(V^x,V^y)$ such that

$$\begin{aligned} R(V^x,V^y)=\sqrt{(V^x)^2+(V^y)^2}. \end{aligned}$$

(8)

Then, define the square-root average operators $Q^x$ and $Q^y$ for $\mathbf {V}=(V^x,V^y)$ as

$$\begin{aligned}{}[Q^x\mathbf {V}]_{i+1/2,j}= & {} \dfrac{1}{\varOmega _{i+1/2,j}}\int _{\varOmega _{i+1/2,j}}R({\varPi }_xV^x,{\varPi }_yV^y)dxdy, \end{aligned}$$

(9)

$$\begin{aligned}{}[Q^y\mathbf {V}]_{i,j+1/2}= & {} \dfrac{1}{\varOmega _{i,j+1/2}}\int _{\varOmega _{i,j+1/2}}R({\varPi }_xV^x,{\varPi }_yV^y)dxdy. \end{aligned}$$

(10)

It follows from direct calculations to (9) and (10) that

$$\begin{aligned}&([Q^x\mathbf {V}]V^x)_{i+1/2,j}\\&\quad = \dfrac{1}{4h^x_{i+1/2}}\bigg (h^x_{i}\Big (R(V^x_{i+1/2,j},V_{i,j+1/2}^y)+ R(V_{i+1/2,j}^x,V_{i,j-1/2}^y)\Big )\\&\qquad +\,h^x_{i+1}\Big (R(V^x_{i+1/2,j},V_{i+1,j-1/2}^y)+R(V^x_{i+1/2,j},V_{i+1,j+1/2}^y)\Big )\bigg )V^x_{i+1/2,j}, \end{aligned}$$

and

$$\begin{aligned}&([Q^y\mathbf {V}]V^y)_{i,j+1/2}\\&\quad = \dfrac{1}{4h^y_{j+1/2}}\bigg (h^y_{j}\Big (R(V^x_{i+1/2,j},V_{i,j+1/2}^y)+ R(V_{i-1/2,j}^x,V_{i,j+1/2}^y)\Big )\nonumber \\&\qquad +\,h^y_{j+1}\Big (R(V^x_{i-1/2,j+1},V_{i,j+1/2}^y)+R(V^x_{i+1/2,j+1},V_{i,j+1/2}^y)\Big )\bigg )V_{i,j+1/2}^y. \end{aligned}$$

Then, we define

$$\begin{aligned}&N^x(\bar{q},\mathbf {V})_{i+1/2,j}=(a_2(\bar{q})[Q^x\mathbf {V}]V^x)_{i+1/2,j}, \end{aligned}$$

(11)

$$\begin{aligned}&N^y(\bar{q},\mathbf {V})_{i,j+1/2}=(a_2(\bar{q})[Q^y\mathbf {V}]V^y)_{i,j+1/2}. \end{aligned}$$

(12)

Let $R_\varepsilon (V^x,V^y)$ be the norm function for a vector $(V^x,V^y)$ with a small positive parameter $\varepsilon$:

$$\begin{aligned} R_\varepsilon (V^x,V^y)=\sqrt{\varepsilon ^2+(V^x)^2+(V^y)^2}. \end{aligned}$$

(13)

We define $N^x_\varepsilon (\bar{q},\mathbf {V})$ on $\varOmega _{i+1/2,j}$ by replacing $R(\cdot , \cdot )$ with $R_\varepsilon (\cdot , \cdot )$ in $N^x(\bar{q},\mathbf {V})$, and define $N^y_\varepsilon (\bar{q},\mathbf {V})$ on $\varOmega _{i,j+1/2}$ by replacing $R(\cdot , \cdot )$ with $R_\varepsilon (\cdot , \cdot )$ in $N^y(\bar{q},\mathbf {V})$ as follows.

$$\begin{aligned}&N_\varepsilon ^x(\bar{q},\mathbf {V})_{i+1/2,j}\nonumber \\&\quad =a_2(\bar{q}_{i+1/2,j})[Q_\varepsilon ^x\mathbf {V}]_{i+1/2,j}V^x_{i+1/2,j}\nonumber \\&\quad = \dfrac{a_2(\bar{q}_{i+1/2,j})}{4h^x_{i+1/2}}\bigg (h^x_{i}\Big (R_\varepsilon (V^x_{i+1/2,j},V_{LT}^y)+ R_\varepsilon (V_{i+1/2,j}^x,V_{LB}^y)\Big )\nonumber \\&\qquad +\,h^x_{i+1}\Big (R_\varepsilon (V^x_{i+1/2,j},V_{RB}^y)+R_\varepsilon (V^x_{i+1/2,j},V_{RT}^y)\Big )\bigg )V^x_{i+1/2,j}, \end{aligned}$$

(14)

and

$$\begin{aligned}&N_\varepsilon ^y(\bar{q},\mathbf {V})_{i,j+1/2}\nonumber \\&\quad =a_2(\bar{q}_{i,j+1/2})[Q_\varepsilon ^y\mathbf {V}]_{i,j+1/2}V_{i,j+1/2}^y\nonumber \\&\quad = \dfrac{a_2(\bar{q}_{i,j+1/2})}{4h^y_{j+1/2}}\bigg (h^y_{j}\Big (R_\varepsilon (V^x_{LT},V_{i,j+1/2}^y)+ R_\varepsilon (V_{LB}^x,V_{i,j+1/2}^y)\Big )\nonumber \\&\qquad +\,h^y_{j+1}\Big (R_\varepsilon (V^x_{RB},V_{i,j+1/2}^y)+R_\varepsilon (V^x_{RT},V_{i,j+1/2}^y)\Big )\bigg )V_{i,j+1/2}^y, \end{aligned}$$

(15)

where

$$\begin{aligned}&v_{LT}^x=v^x_{i-1/2,j+1},\quad v_{LB}^x=v^x_{i-1/2,j},\quad v_{RB}^x=v^x_{i+1/2,j},\quad v_{RT}^x=v^x_{i+1/2,j+1},\\&v_{LT}^y=v^y_{i,j+1/2},\quad v_{LB}^y=v^y_{i,j-1/2},\quad v_{RB}^y=v^y_{i+1,j-1/2},\quad v_{RT}^y=v^y_{i+1,j+1/2}. \end{aligned}$$

When constructing the two-grid algorithm we use a differentiable function $N_\varepsilon ^x(\bar{p},\mathbf {u})$ (resp. $N_\varepsilon ^y(\bar{p},\mathbf {u})$) to replace $N^x(\bar{p},\mathbf {u})$ (resp. $N^y(\bar{p},\mathbf {u})$). The reason is that the partial derivatives of $N^x(\bar{p},\mathbf {u})$ and $N^y(\bar{p},\mathbf {u})$ with respect to $\mathbf {u}$ do not exist, when the velocity $\mathbf {u}=(u^x,u^y)$ is zero. The key is to use $\sqrt{\varepsilon ^2+(u^x)^2+(u^y)^2}$ to replace $\sqrt{(u^x)^2+(u^y)^2}$. When $\varepsilon$ is small enough, $N_\varepsilon ^x(\bar{p},\mathbf {u})$ (resp. $N_\varepsilon ^y(\bar{p},\mathbf {u})$) is close to $N^x(\bar{p},\mathbf {u})$ (resp. $N^y(\bar{p},\mathbf {u})$), and the partial derivative of $N_\varepsilon ^x(\bar{p},\mathbf {u})$ (resp. $N_\varepsilon ^y(\bar{p},\mathbf {u})$) with respect to $\mathbf {u}$ is also very close to that of $N^x(\bar{p},\mathbf {u})$ (resp. $N^y(\bar{p},\mathbf {u})$), see Figs. 1 and 2 for the negligible differences.

Fig. 1

Differences of $\sqrt{\varepsilon ^2+(u^x)^2+(u^y)^2}$ and $\sqrt{(u^x)^2+(u^y)^2}$ for $h=0.1$ and $\varepsilon =h^2$

Fig. 2

Differences of the partial derivative of $\sqrt{\varepsilon ^2+(u^x)^2+(u^y)^2}$ and $\sqrt{(u^x)^2+(u^y)^2}$ with respect to $u^x$ for $h=0.1$ and $\varepsilon =h^2$

Analogous to $\varOmega _h$ we define a coarse grid $\varOmega _H=\varTheta _H^x\times \varTheta _H^y$. We use $H^x,H^y$ to denote the meshsizes in x and y directions of the coarse grid, respectively. Similarly we use $[d_H^{x}\theta ]$, $[D^x_{H}\theta ]$, $[d^y_{H}\theta ]$, $[D^y_{H}\theta ]$, $(\theta ,\omega )_M$, $(\theta ,\omega )_X$, $(\theta ,\omega )_Y$, $\Vert \theta \Vert _M$, $\Vert \theta \Vert _X$, $\Vert \theta \Vert _Y$ to denote the finite difference operators, inner products and norms on the coarse grid, respectively. The norms and semi-norms of a discrete function on the coarse grid can be defined similarly. We also use notations $X_m$ and $Y_n$ such that

$$\begin{aligned} X_m:=b_1^x+\sum \limits _{m=1}^{N_x} H_m^{x},\qquad Y_n:=b_1^y+\sum \limits _{n=1}^{N_y} H_n^{y}. \end{aligned}$$

We define $\hat{p}_H$ and $\hat{\mathbf {u}}_H=(\hat{u}_H^x,\hat{u}_H^y)$ as the bilinear interpolation operator from the coarse grid $\varOmega _H$ to fine grid $\varOmega _h$ . Take $\hat{\mathbf {u}}_H$ for example:

• (i) For each point $(x,y)\in (x_{m+1/2}, x_{m+3/2})\times (y_{n}, y_{n+1})$ with $m=0,\ldots , N_x-1$ and $n=1,\ldots , N_y-1$, we define $\hat{u}_H^x(x,y)$ as the bilinear interpolation by using $u^x_{m+1/2,n+1}$,$u^x_{m+1/2,n}$, $u^x_{m+3/2,n}$ and $u^x_{m+3/2,n+1}$.

• (ii) For each point $(x,y)\in (x_{m+1/2}, x_{m+3/2})\times (y_{1/2}, y_{1})$ with $m=0,\ldots , N_x-1$, we define $\hat{u}_H^x(x,y)$ as the bilinear extrapolation by using $u^x_{m+1/2,2}$, $u^x_{m+1/2,1}$, $u^x_{m+3/2,1}$ and $u^x_{m+3/2,2}$.

• (iii) For each point $(x,y)\in (x_{m+1/2}, x_{m+3/2})\times (y_{Ny}, y_{Ny+1/2})$ with $m=0,\ldots ,$ $N_x-1$, we define $\hat{u}_H^x(x,y)$ as the bilinear extrapolation by using $u^x_{m+1/2,Ny}$, $u^x_{m+1/2,Ny-1}$, $u^x_{m+3/2,Ny-1}$ and $u^x_{m+3/2,Ny}$.

Similarly, we can define $\hat{u}_H^y(x,y)$ based on the values of $u^y_{m,n+1/2}$ for $m=1,\ldots , N_x$ and $n=0,\ldots , N_y$, and define $\hat{p}_H(x,y)$ based on the values of $p_{m,n}$ for $m=1,\ldots , N_x$ and $n=1,\ldots , N_y$.

We are now ready to construct the two-grid block-centered finite difference algorithm in two steps.

Step 1 On the coarse grid $\varOmega _H$ with meshsizes $H^x$ and $H^y$, the nonlinear block-centered finite difference schemes for $(U^x_{H})_{m+1/2,n}^{k}$, $(U^y_{H})_{m,n+1/2}^{k}$ and $(P_H)^k_{m,n}$ are as follows,

$$\begin{aligned}&\alpha [d_tP_H]_{m,n}^k+[D^x_{H}U_H^x]^k_{m,n}+[D^y_{H}U_H^y]^k_{m,n}= f^k_{m,n}, \end{aligned}$$

(16)

$$\begin{aligned}&a_1U^{x,k}_{H,m+1/2,n}+N^x(\bar{P}_H,\mathbf {U}_H)^k_{m+1/2,n}=-[d^x_{H}P_H]^k_{m+1/2,n}, \end{aligned}$$

(17)

$$\begin{aligned}&a_1U^{x,k}_{H,m,n+1/2}+N^y(\bar{P}_H,\mathbf {U}_H)^k_{m,n+1/2}=-[d^y_{H}P_H]^k_{m,n+1/2},\nonumber \\&U_{1/2,n}^{x,k}=-g(b_1^x,Y_n,t^k),\quad U_{N_x+1/2,n}^{x,k}=g(b_2^x,Y_n,t^k),\quad n=1,\ldots ,N_y,\nonumber \\&U_{m,1/2}^{y,k}=-g(X_m,b_1^y,t^k),\quad U_{m,N_y+1/2}^{y,k}=g(X_m,b_2^y,t^k),\quad m=1,\ldots ,N_x,\nonumber \\&P_{m,n}^0=p_0(X_m,Y_n,0), \end{aligned}$$

(18)

for $m=1,\ldots , N_x-1$ , $n=1,\ldots , N_y-1$ and $k=1,\ldots ,N_t$.

Step 2 On the fine grid $\varOmega _h$ with meshsizes $h^x$ and $h^y$, the linear block-centered finite difference approximation for $(U^x_{h})_{i+1/2,j}^{k}$, $(U^y_{h})_{i,j+1/2}^{k}$ and $(P_h)^k_{i,j}$ are as follows,

$$\begin{aligned}&\alpha [d_tP_h]_{i,j}^k+[D^x_{h}U_h^x]^k_{i,j}+[D^y_{h}U_h^y]^k_{i,j}= f^k_{i,j}, \end{aligned}$$

(19)

$$\begin{aligned}&a_1U^{x,k}_{h,i+1/2,j}+L_\varepsilon ^x(\bar{P}_h,\mathbf {U}_h)^k_{i+1/2,j}=-[d^x_{h}P_h]^k_{i+1/2,j}, \end{aligned}$$

(20)

$$\begin{aligned}&a_1U^{x,k}_{h,i,j+1/2}+L_\varepsilon ^y(\bar{P}_h,\mathbf {U}_h)^k_{i,j+1/2}=-[d^y_{h}P_h]^k_{i,j+1/2},\nonumber \\&U_{1/2,j}^{x,k}=-g(b_1^x,y_j,t^k),\quad U_{n_x+1/2,j}^{x,k}=g(b_2^x,y_j,t^k),\quad j=1,\ldots ,n_y,\nonumber \\&U_{i,1/2}^{y,k}=-g(x_i,b_1^y,t^k),\quad U_{i,n_y+1/2}^{y,k}=g(x_i,b_2^y,t^k),\quad i=1,\ldots ,n_x,\nonumber \\&P_{i,j}^0=p_0(x_i,y_j,0), \end{aligned}$$

(21)

for $i=1,\ldots , n_x-1$, $j=1,\ldots , n_y-1$, $k=1,\ldots ,N_t$ and a small positive parameter $\varepsilon$, where

$$\begin{aligned}&L_\varepsilon ^x(\bar{P}_h,\mathbf {U}_h)^k_{i+1/2,j}\nonumber \\&\quad =N^x(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}+\dfrac{\partial N^x}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(\bar{P}_h-\bar{\hat{P}}_H)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(U_h^x-\hat{U}_H^x)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(U_{h}^y-\hat{U}_{H}^y)^k_{i,j+1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(U_{h}^y-\hat{U}_{H}^y)^k_{i,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(U_{h}^y-\hat{U}_{H}^y)^k_{i+1,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(U_{h}^y-\hat{U}_{H}^y)^k_{i+1,j+1/2}, \end{aligned}$$

(22)

and

$$\begin{aligned}&L_\varepsilon ^y(\bar{P}_h,\mathbf {U}_h)^k_{i,j+1/2}\nonumber \\&\quad =N^y(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}+\dfrac{\partial N^y}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(\bar{P}_h-\bar{\hat{P}}_H)^k_{i,j+1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(U_h^y-\hat{U}_H^y)^k_{i,j+1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LT}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(U_{h}^x-\hat{U}_{H}^x)^k_{i-1/2,j+1}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u_{LB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(U_{h}^x-\hat{U}_{H}^x)^k_{i-1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u_{RB}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(U_{h}^x-\hat{U}_{H}^x)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u_{RT}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(U_{h}^x-\hat{U}_{H}^x)^k_{i+1/2,j+1}. \end{aligned}$$

(23)

In the Step 1 on coarse grid, the fewest unknowns are used to construct the block-centered finite difference scheme. We have reduced the degree of coupling of $P_H$ and $\mathbf {U}_H$ as much as possible. Moreover, it brings the convenience to construct the scheme on the fine grid, in which the partial derivatives with respect to the unknowns are the essential parts.

This algorithm first produces a rough approximation of the solution and then uses it as the initial guess on the fine grid. With this method, solving a nonlinear equation on a fine grid is reduced to solving a nonlinear equation on a coarse grid together with solving a linear equation on a fine grid. This means that solving a nonlinear problem is not much more difficult than solving one linear problem, since the cost for solving the nonlinear problem on the coarse grid is relatively negligible.

3 Error Estimates

In this section, we present the optimal error estimates for the two-grid block-centered finite difference method for the slightly compressible Darcy–Forchheimer model (4).

According to Lemma 4.1 in [21], we have the following lemma.

Lemma 1

Suppose p is sufficiently smooth, then

$$\begin{aligned} \begin{array}{lll} &{}\dfrac{\partial p_{i+1/2,j}}{\partial x}=[d^x_hp]_{i+1/2,j}-\dfrac{1}{8}\Big [d^x_h\Big ((h^x)^2\dfrac{\partial ^2 p}{\partial x^2}\Big )\Big ]_{i+1/2,j}+O\Big ((h^x)^2\Big ), \\ &{}\dfrac{\partial p_{i,j+1/2}}{\partial y}=[d^y_hp]_{i,j+1/2}-\dfrac{1}{8}\Big [d^y_h\Big ((h^y)^2\dfrac{\partial ^2 p}{\partial y^2}\Big )\Big ]_{i,j+1/2}+O\Big ((h^y)^2\Big ), \end{array} \end{aligned}$$

where

$$\begin{aligned} h^x=\max _{i}\{h_i^x,h_{i+1/2}^x\},\qquad h^y=\max _{j}\{h_j^y,h_{j+1/2}^y\}. \end{aligned}$$

The following lemma follows directly from Lemma 1.

Lemma 2

Suppose p is sufficiently smooth, then

$$\begin{aligned}&a_1 u^x_{i+1/2,j}+(a_2(p)|\mathbf {u}|u^x)_{i+1/2,j}\\&\quad =-\,[d^x_h(p-\delta )]_{i+1/2,j}+O\Big ((h^x)^2+(h^y)^2\Big ),\\&a_1 u^y_{i,j+1/2}+(a_2(p)|\mathbf {u}|u^y)_{i,j+1/2}\\&\quad =-\,[d^y_h(p-\delta )]_{i,j+1/2}+O\Big ((h^x)^2+(h^y)^2\Big ), \end{aligned}$$

where

$$\begin{aligned} \delta _{i,j}=\dfrac{1}{8}\Big ((h^x)^2\dfrac{\partial ^2 p}{\partial x^2}+(h^y)^2\dfrac{\partial ^2 p}{\partial y^2}\Big )_{i,j}. \end{aligned}$$

(24)

Lemma 3

Suppose p and $\mathbf {u}$ are sufficiently smooth, then

$$\begin{aligned}&a_1 u^x_{i+1/2,j}+(a_2(p)[Q^x\mathbf {u}]u^x)_{i+1/2,j}\\&\quad =-\,[d^x_h(p-\eta )]_{i+1/2,j}+O\Big ((h^x)^2+(h^y)^2\Big ), \\&a_1 u^y_{i,j+1/2}+(a_2(p)[Q^y\mathbf {u}]u^y)_{i,j+1/2}\\&\quad =-\,[d^y_h(p-\eta )]_{i,j+1/2}+O\Big ((h^x)^2+(h^y)^2\Big ), \end{aligned}$$

where

$$\begin{aligned} \eta _{i,j}=\delta _{i,j}+\dfrac{1}{4}\Bigg (a(p)\dfrac{u^xu^y}{|\mathbf {u}|}\Big ((h^x)^2\dfrac{\partial u^y}{\partial x}+(h^y)^2\dfrac{\partial u^x}{\partial y}\Big )\Bigg )_{i,j}. \end{aligned}$$

(25)

Proof

According to Lemma 4.2 in [19] and the Taylor expansion,

$$\begin{aligned}&a_2(p_{i+1/2,j})\bigg (\dfrac{R(u^x_{i+1/2,j},u^y_{i,j+1/2})+R(u^x_{i+1/2,j},u^y_{i,j-1/2})}{2} -|\mathbf {u}_{i+1/2,j}|\bigg )u^x_{i+1/2,j}\\&\quad =a_2(p_{i,j})\dfrac{u_{i,j}^xu_{i,j}^y}{|\mathbf {u}_{i,j}|}\dfrac{\partial u_{i,j}^y}{\partial x}\left( -\dfrac{h_i}{2}\right) +O\Big ((h^x)^2+(h^y)^2\Big ), \end{aligned}$$

and

$$\begin{aligned}&a_2(p_{i+1/2,j})\bigg (\dfrac{R(u^x_{i+1/2,j},u^y_{i+1,j+1/2})+R(u^x_{i+1/2,j},u^y_{i+1,j-1/2})}{2}-|\mathbf {u}_{i+1/2,j}|\bigg )u^x_{i+1/2,j}\\&\quad =a_2(p_{i+1,j})\dfrac{u_{i+1,j}^xu_{i+1,j}^y}{|\mathbf {u}_{i+1,j}|}\dfrac{\partial u_{i+1,j}^y}{\partial x}\left( \dfrac{h_{i+1}}{2}\right) +O\Big ((h^x)^2+(h^y)^2\Big ). \end{aligned}$$

Therefore,

$$\begin{aligned}&(a_2(p)[Q^x\mathbf {u}]u^x)_{i+1/2,j}-(a_2(p)|\mathbf {u}|u^x)_{i+1/2,j}\nonumber \\&\quad =\dfrac{1}{4h_{i+1/2}}\bigg ( (h^x_{i+1})^2 a_2(p_{i+1,j})\dfrac{u_{i+1,j}^xu_{i+1,j}^y}{|\mathbf {u}_{i+1,j}|}\dfrac{\partial u_{i+1,j}^y}{\partial x}\nonumber \\&\qquad -\,(h^x_{i})^2 a_2(p_{i,j})\dfrac{u_{i,j}^xu_{i,j}^y}{|\mathbf {u}_{i,j}|}\dfrac{\partial u_{i,j}^y}{\partial x} \bigg )+O\Big ((h^x)^2+(h^y)^2\Big )\nonumber \\&\quad =\dfrac{1}{4}\Big [d^x_h\Big ((h^x)^2a_2(p)\dfrac{u^xu^y}{|\mathbf {u}|}\dfrac{\partial u^y}{\partial x}\Big )\Big ]_{i+1/2,j}+O\Big ((h^x)^2+(h^y)^2\Big ). \end{aligned}$$

(26)

By Lemma 2, (26) and (25), we have

$$\begin{aligned}&a_1 u^x_{i+1/2,j}+(a_2(p)[Q^x\mathbf {u}]u^x)_{i+1/2,j}\nonumber \\&\quad =(a_2(p)[Q^x\mathbf {u}]u^x)_{i+1/2,j}-(a_2(p)|\mathbf {u}|u^x)_{i+1/2,j}\nonumber \\&\qquad +\,a_1 u^x_{i+1/2,j}+(a_2(p)|\mathbf {u}|u^x)_{i+1/2,j}\nonumber \\&\quad =\dfrac{1}{4}\Big [d_h^x\Big ((h^x)^2a_2(p)\dfrac{u^xu^y}{|\mathbf {u}|}\dfrac{\partial u^y}{\partial x}\Big )\Big ]_{i+1/2,j}-[d_h^x(p-\delta )]_{i+1/2,j}\nonumber \\&\qquad +\,O\Big ((h^x)^2+(h^y)^2\Big )\nonumber \\&\quad =-\,[d^x_h(p-\eta )]_{i+1/2,j}-\dfrac{1}{4}\Big [d_h^x\Big ((h^y)^2a_2(p)\dfrac{u^xu^y}{|\mathbf {u}|}\dfrac{\partial u^x}{\partial y}\Big )\Big ]_{i+1/2,j}\nonumber \\&\qquad +\,O\Big ((h^x)^2+(h^y)^2\Big )\nonumber \\&\quad =-\,[d_h^x(p-\eta )]_{i+1/2,j}+O\Big ((h^x)^2+(h^y)^2\Big ). \end{aligned}$$

(27)

Similarly,

$$\begin{aligned}&a_1 u^y_{i,j+1/2}+(a_2(p)[Q^y\mathbf {u}]u^y)_{i,j+1/2}\nonumber \\&\quad =-\,[d_h^y(p-\eta )]_{i,j+1/2}-\dfrac{1}{4}\Big [d_h^y\Big ((h^x)^2a_2(p)\dfrac{u^xu^y}{|\mathbf {u}|}\dfrac{\partial u^y}{\partial x}\Big )\Big ]_{i,j+1/2}\nonumber \\&\qquad +\,O\Big ((h^x)^2+(h^y)^2\Big )\nonumber \\&\quad =-\,[d_h^y(p-\eta )]_{i,j+1/2}+O\Big ((h^x)^2+(h^y)^2\Big ). \end{aligned}$$

(28)

From the definitions of $\bar{p}_{i+1/2,j}$ and $\bar{p}_{i,j+1/2}$ in (7), we have

$$\begin{aligned}&\bar{p}_{i+1/2,j}-p_{i+1/2,j}=O\Big ((h^x)^2\Big ), \end{aligned}$$

(29)

$$\begin{aligned}&\bar{p}_{i,j+1/2}-p_{i,j+1/2}=O\Big ((h^y)^2\Big ). \end{aligned}$$

(30)

Thus, we get the following lemma by using Lemma 3, the Taylor expansion of $a_2(p)$ and (29) and (30).

Lemma 4

Suppose p and $\mathbf {u}$ are sufficiently smooth, then

$$\begin{aligned} \begin{array}{lll} &{}a_1 u^x_{i+1/2,j}+N^x(\bar{p},\mathbf {u})_{i+1/2,j}=-\,[d_h^x(p-\eta )]_{i+1/2,j}+O\Big ((h^x)^2+(h^y)^2\Big ), \\ &{}a_1 u^y_{i,j+1/2}+N^y(\bar{p},\mathbf {u})_{i,j+1/2}=-\,[d_h^y(p-\eta )]_{i,j+1/2}+O\Big ((h^x)^2+(h^y)^2\Big ). \end{array} \end{aligned}$$

From Lemma 4.4 in [19], Lemma 4.2 in [17] and (6), we can derive the following lemma.

Lemma 5

For any functions $\mathbf {V}=(V^x,V^y)$ and $\mathbf {W}=(W^x,W^y)$ we have

$$\begin{aligned}&( a_2(\bar{q})|\mathbf {V}|V^x-a_2(\bar{q})|\mathbf {W}|W^x, {V}^x - {W}^x )_x\nonumber \\&\qquad +\,(a_2(\bar{q})|\mathbf {V}|V^y-a_2(\bar{q})|\mathbf {W}|W^y, {V}^y - {W}^y )_y\nonumber \\&\quad \quad \quad \ge \underline{a} ( || {V}^x - {W}^x||_x^2+|| {V}^y - {W}^y||_y^2). \end{aligned}$$

(31)

By referring to Lemma 4.6 in [19], Lemma 6 is given as follows.

Lemma 6

Let $\{W^x_{i+1/2,j}\}$, $\{W^y_{i,j+1/2}\}$, $\{V^x_{i+1/2,j}\}$, $\{V^y_{i,j+1/2}\}$, $\varphi _{i,j}^x$, and $\varphi _{i,j}^y$ be discrete functions with $V_{1/2,j}^{x}=V_{i,1/2}^{y}=V_{n_x+1/2,j}^{x}=V_{i,n_y+1/2}^{y}=0$ and satisfy

$$\begin{aligned} \left\{ \begin{array}{lll} &{}[\psi ^xW^x]_{i+1/2,j}=-[d_h^x\varphi ^x]_{i+1/2,j}, \\ &{}[\psi ^yW^y]_{i,j+1/2}=-[d_h^y\varphi ^y]_{i,j+1/2}, \end{array} \right. \end{aligned}$$

where $\psi ^x$ and $\psi ^y$ are generic discrete functions. Then we have

$$\begin{aligned} (\psi ^xW^x,V^x)_x=(\varphi ^x,D_h^xV^x)_m,\qquad (\psi ^yW^y,V^y)_y=(\varphi ^y,D_h^yV^y)_m. \end{aligned}$$

Theorem 1

Let $U_H^{x,k}$, $U_H^{y,k}$, $P_H^k$ be obtained by step 1 of two-grid finite difference algorithm. Suppose the solutions $\mathbf {u}=(u^x,u^y)$ and p are sufficiently smooth, then there exists a positive constant C independent of H and $\varDelta t$ such that

$$\begin{aligned}&\sum _{k=1}^{N_t}\varDelta t^k(\Vert (u^x-U_H^x)^k\Vert ^2_X+\Vert (u^y-U_H^y)^k\Vert ^2_Y)^{1/2}\le C(\varDelta t+H^2),\\&\Vert (p-P_H)^{N_t}\Vert _M\le C(\varDelta t+H^2). \end{aligned}$$

where

$$\begin{aligned} H=\max _{m,n}\{H^x_{m},H^x_{m+1/2}, H^y_{n},H^y_{n+1/2}\},\quad \varDelta t=\max _{k} \{\varDelta t^k\}. \end{aligned}$$

Proof

Denote

$$\begin{aligned}&(E^{p})^k_{m,n}=(P_H-p)^k_{m,n},\\&(E^{x})^k_{m+1/2,n}=(U^x_H-u^x)^k_{m+1/2,n}, \\&(E^{y})^k_{m,n+1/2}=(U^y_H-u^y)^k_{m,n+1/2}. \end{aligned}$$

By (4), the definitions of operators $D_H^x$ and $D_H^y$, we have

$$\begin{aligned}&\alpha [d_tp]^k_{m,n}+[D_H^x(u^x)]^k_{m,n}+[D_H^y(u^y)]^k_{m,n}\nonumber \\&\quad =f_{m,n}^k+\alpha [d_t p]^k_{m,n}-\alpha \dfrac{\partial p^k_{m,n}}{\partial t}+[D_H^x(u^x)]^k_{m,n}-\dfrac{\partial u^{x,k}_{m,n}}{\partial x}\nonumber \\&\qquad +\,[D_H^y(u^y)]^k_{m,n}-\dfrac{\partial u^{y,k}_{m,n}}{\partial y}\nonumber \\&\quad =f_{m,n}^k+O(\varDelta t+H^2). \end{aligned}$$

(32)

From the first equation (16) in step 1 and (32),

$$\begin{aligned}&\alpha [d_t(E^p)]^k_{m,n}+[D_H^x(E^x)]^k_{m,n}+[D_H^y(E^y)]^k_{m,n}\nonumber \\&\quad =\alpha \dfrac{\partial p^k_{m,n}}{\partial t}-\alpha [d_t p]^k_{m,n}+\dfrac{\partial u^{x,k}_{m,n}}{\partial x}-[D_H^x(u^x)]^k_{m,n}\nonumber \\&\qquad +\,\dfrac{\partial u^{y,k}_{m,n}}{\partial y}-[D_H^y(u^y)]^k_{m,n}\nonumber \\&\quad =O(\varDelta t+H^2). \end{aligned}$$

(33)

According to the definition of $\eta$ in (25),

$$\begin{aligned} \alpha [d_t\eta ]^k_{m,n}= & {} \dfrac{\alpha }{8}\Big ((H^x)^2[d_t(\dfrac{\partial ^2 p}{\partial x^2})]^k_{m,n}+(H^y)^2[d_t(\dfrac{\partial ^2 p}{\partial y^2})]_{m,n}^k\Big )\nonumber \\&\qquad +\,\dfrac{\alpha }{4}\Big ((H^x)^2[d_t(a_2(p)\dfrac{u^xu^y}{|\mathbf {u}|}\dfrac{\partial u^y}{\partial x})]^k_{m,n}\nonumber \\&\qquad +\,(H^y)^2[d_t(a_2(p)\dfrac{u^xu^y}{|\mathbf {u}|}\dfrac{\partial u^x}{\partial y})]^k_{m,n}\Big )\nonumber \\&\quad = O\Big ((H^x)^2+(H^y)^2\Big )\nonumber \\&\quad =O(H^2). \end{aligned}$$

(34)

Combing (33) and (34), we get

$$\begin{aligned} \alpha [d_t(E^p+\eta )]^k_{m,n}+[D_H^x(E^x)]^k_{m,n}+[D_H^y(E^y)]^k_{m,n}=O(\varDelta t+H^2). \end{aligned}$$

(35)

By multiplying both sides of (35) by $(E^p+\eta )^k_{m,n}H_m^x H_n^y$ and summing up m and n, we have

$$\begin{aligned}&\alpha ( d_t(E^p+\eta )^k,(E^p+\eta )^k)_M+(D_H^x(E^{x,k}),(E^p+\eta )^k)_M\nonumber \\&+\,(D_H^y(E^{y,k}),(E^p+\eta )^k)_M\nonumber \\&\quad =(O(\varDelta t+H^2),(E^p+\eta )^k)_M. \end{aligned}$$

(36)

It follows from Lemma 6 and (36) that

$$\begin{aligned}&\alpha ( d_t(E^p+\eta )^k,(E^p+\eta )^k)_M-(E^{x,k},d_H^x(E^p+\eta )^k)_X\nonumber \\&-\,(E^{y,k},d_H^y(E^p+\eta )^k)_Y\nonumber \\&\quad =(O(\varDelta t+H^2),(E^p+\eta )^k)_M. \end{aligned}$$

(37)

From (4) and the step 1 of two-grid algorithm (17) and (18), we obtain

$$\begin{aligned}&a_1E^{x,k}_{m+1/2,n}+N^x(\bar{P}_H,\mathbf {U}_H)^k_{m+1/2,n}-(a_2(p)|\mathbf {u}|u^x)^k_{m+1/2,n}\nonumber \\&\quad =\dfrac{\partial p_{m+1/2,n}}{\partial x}-[d_H^xP_H]^k_{m+1/2,n}, \end{aligned}$$

(38)

$$\begin{aligned}&a_1E^{y,k}_{m,n+1/2}+N^y(\bar{P}_H,\mathbf {U}_H)^k_{m,n+1/2}-(a_2(p)|\mathbf {u}|u^y)^k_{m,n+1/2}\nonumber \\&\quad =\dfrac{\partial p_{m,n+1/2}}{\partial y}-[d_H^yP_H]^k_{m,n+1/2}. \end{aligned}$$

(39)

Using Lemmas 2, 3, and 4 to (38) and (39), we get

$$\begin{aligned}&a_1E^{x,k}_{m+1/2,n}+N^x(\bar{P}_H,\mathbf {U}_H)^k_{m+1/2,n}-N^x(\bar{p},\mathbf {u})_{m+1/2,n}^k\nonumber \\&\quad =-\,[d_H^x(E^p+\eta )]^k_{m+1/2,n}+O(H^2), \end{aligned}$$

(40)

$$\begin{aligned}&a_1E^{y,k}_{m,n+1/2}+N^y(\bar{P}_H,\mathbf {U}_H)_{m,n+1/2}^k-N^y(\bar{p},\mathbf {u})_{m,n+1/2}^k\nonumber \\&\quad =-\,[d_H^y(E^p+\eta )]^k_{m,n+1/2}+O(H^2). \end{aligned}$$

(41)

Multiplying (40) and (41) by $E^{x,k}_{m+1/2,n}H^x_{m+1/2} H^y_n$ and $E^{y,k}_{m,n+1/2}H^x_{m} H^y_{n+1/2}$, respectively, and summing up m from 1 to $N_x-1$ and n from 1 to $N_y-1$, we arrive at

$$\begin{aligned}&a_1(E^{x,k},E^{x,k})_X+(N^x(\bar{P}_H,\mathbf {U}_H)^k-N^x(\bar{p},\mathbf {u})^k,E^{x,k})_X\nonumber \\&\quad =-\,(d_H^x(E^p+\eta )^k,E^{x,k})_X+(O(H^2),E^{x,k})_X, \end{aligned}$$

(42)

$$\begin{aligned}&a_1(E^{y,k},E^{y,k})_Y+(N^y(\bar{P}_H,\mathbf {U}_H)^k-N^y(\bar{p},\mathbf {u})^k,E^{y,k})_Y\nonumber \\&\quad =-\,(d_H^y(E^p+\eta )^k,E^{y,k})_Y+(O(H^2),E^{y,k})_Y. \end{aligned}$$

(43)

From (37), (42) and (43),

$$\begin{aligned}&\dfrac{\alpha }{2}d_t\Vert (E^p+\eta )^k\Vert _M^2+\dfrac{\alpha \triangle t^k}{2}\Vert d_t(E^p+\eta )^k\Vert _M^2+a_1(\Vert E^{x,k}\Vert _X^2+\Vert E^{x,k}\Vert _Y^2)\nonumber \\&\qquad +\,(N^x(\bar{P}_H,\mathbf {U}_H)^k-N^x(\bar{P}_H,\mathbf {u})^k,E^{x,k})_X\nonumber \\&\qquad +\,(N^y(\bar{P}_H,\mathbf {U}_H)^k-N^y(\bar{P}_H,\mathbf {u})^k,E^{y,k})_Y\nonumber \\&\quad =(N^x(\bar{p},\mathbf {u})^k-N^x(\bar{P}_H,\mathbf {u})^k,E^{x,k})_X+(N^y(\bar{p},\mathbf {u})^k-N^y(\bar{P}_H,\mathbf {u})^k,E^{y,k})_Y\nonumber \\&\qquad +\,(O(\varDelta t+H^2),(E^p+\eta )^k)_M+(O(H^2),E^{x,k})_X+(O(H^2),E^{y,k})_Y. \end{aligned}$$

(44)

By Lemma 5 and the assumption (6) of $a_2(p)$, we have

$$\begin{aligned}&(N^x(\bar{P}_H,\mathbf {U}_H)^k-N^x(\bar{P}_H,\mathbf {u})^k,E^{x,k})_X\nonumber \\&\qquad +\,(N^y(\bar{P}_H,\mathbf {U}_H)^k-N^y(\bar{P}_H,\mathbf {u})^k,E^{y,k})_Y\nonumber \\&\quad \ge \underline{a} ( || {U}_H^x - {u}^x||_x^2+|| {U}_H^y - {u}^y||_y^2)\nonumber \\&\quad \ge 0. \end{aligned}$$

(45)

Applying the Cauchy–Schwarz inequality and the assumption for $\alpha$, $a_1$ in (6), we have

$$\begin{aligned}&\dfrac{1}{2}d_t\Vert (E^p+\eta )^k\Vert _M^2+\dfrac{\triangle t^k}{2}\Vert d_t(E^p+\eta )^k\Vert _M^2+\Vert E^{x,k}\Vert _X^2+\Vert E^{y,k}\Vert _Y^2\nonumber \\&\quad \le C(\varDelta t^2+H^4+\Vert (E^p+\eta )^k\Vert _M^2+\Vert E^{p,k}\Vert _M^2)\nonumber \\&\qquad +\,\dfrac{1}{2}\Vert E^{x,k}\Vert _X^2+\dfrac{1}{2}\Vert E^{y,k}\Vert _Y^2\nonumber \\&\quad \le C(\varDelta t^2+H^4+\Vert (E^p+\eta )^k\Vert _M^2+\Vert \eta ^k\Vert _M^2)\nonumber \\&\qquad +\,\dfrac{1}{2}\Vert E^{x,k}\Vert _X^2+\dfrac{1}{2}\Vert E^{y,k}\Vert _Y^2. \end{aligned}$$

(46)

Multiplying (46) by $2\triangle t^k$ and summing up k from 1 to $N_t$, we have

$$\begin{aligned}&\Vert (E^p+\eta )^{N_t}\Vert _M^2+\sum _{k=1}^{N_t}(\triangle t^k)^2\Vert d_t(E^p+\eta )^k\Vert _M^2\nonumber \\&\qquad +\,\sum _{k=1}^{N_t}\triangle t^k\Big (\Vert E^{x,k}\Vert _X^2+\Vert E^{x,k}\Vert _Y^2\Big )\nonumber \\&\quad \le C\Bigg (\varDelta t^2+H^4+\sum _{k=1}^{N_t}\triangle t^k\Big (\Vert (E^p+\eta )^k\Vert _M^2+\Vert \eta ^k\Vert _M^2\Big )\nonumber \\&\qquad +\,\Vert (E^p+\eta )^0\Vert _M^2\Bigg )\nonumber \\&\quad \le C\Big (\varDelta t^2+H^4+\sum _{k=1}^{N_t}\triangle t^k\Vert (E^p+\eta )^k\Vert _M^2\Big ). \end{aligned}$$

(47)

Using Gronwall lemma, we get

$$\begin{aligned}&\Vert (P_H-p+\eta )^{N_t}\Vert _M^2+\sum _{k=1}^{N_t}\triangle t^k(\Vert (U_H^x-u^x)^k\Vert _X^2+\Vert (U_H^y-u^y)^k\Vert _Y^2)\nonumber \\&\qquad \le C(\varDelta t^2+H^4). \end{aligned}$$

(48)

Combing the definition of $\eta$ in (25) and triangle inequality, the theorem holds. $\square$

In order to deduce the error estimates for Step 2 of the two-grid algorithm, we give the following useful lemmas.

Lemma 7

Suppose $\{V^x_{i-1/2,j}\}$ and $\{V^y_{i,j-1/2}\}$ are discrete functions with

$$\begin{aligned} V^x_{1/2,j}= & {} V^x_{n_x+1/2,j}=0,\quad j=1,\ldots ,n_y,\\ V^y_{i,1/2}= & {} V^y_{i,n_y+1/2}=0,\quad i=1,\ldots ,n_x. \end{aligned}$$

For the discrete norms $\Vert \cdot \Vert _x$ and $\Vert \cdot \Vert _y$, we have the following inverse estimates.

$$\begin{aligned}&\Vert (V^x)^2\Vert _x^2\le Ch^{-2}\Vert V^x\Vert _x^4,\\&\Vert (V^y)^2\Vert _y^2\le Ch^{-2}\Vert V^y\Vert _y^4, \end{aligned}$$

where

$$\begin{aligned} h=\max _{i,j}\{h^x_{i}, h^x_{i+1/2}, h^y_{j}, h^y_{j+1/2}\}. \end{aligned}$$

We refer to Lemma 3.3 in [22] for the proof of Lemma 7.

Lemma 8

Assume $\mathbf {V}=(V^x,V^y)$ is bounded by a positive constant C which is independent of any mesh grid parameters, we have

$$\begin{aligned}&|N^x(\bar{q},\mathbf {V})_{i+1/2,j}-N^x_\varepsilon (\bar{q},\mathbf {V})_{i+1/2,j}|\le C{\varepsilon }, \\&|N^y(\bar{q},\mathbf {V})_{i,j+1/2}-N^y_\varepsilon (\bar{q},\mathbf {V})_{i,j+1/2}|\le C{\varepsilon }, \end{aligned}$$

with $i=1,\ldots , n_x$ and $j=1,\ldots , n_y$.

Proof

Since

$$\begin{aligned}&|R_\varepsilon (V^x,V^y)-R(V^x,V^y)|\nonumber \\&\quad =\left| \dfrac{\varepsilon ^2}{\sqrt{\varepsilon ^2+(V^x)^2+(V^y)^2}+\sqrt{(V^x)^2+(V^y)^2}}\right| \nonumber \\&\quad \le \varepsilon , \end{aligned}$$

(49)

by combing (6), (49) and the boundedness of $\mathbf {V}$, we deduce

$$\begin{aligned}&|N^x(\bar{q},\mathbf {V})_{i+1/2,j}-N^x_\varepsilon (\bar{q},\mathbf {V})_{i+1/2,j}|\nonumber \\&\quad =|a_2(\bar{q}_{i+1/2,j})V^x_{i+1/2,j}([Q^x\mathbf {V}]_{i+1/2,j}-[Q_\varepsilon ^x\mathbf {V}]_{i+1/2,j})|\nonumber \\&\quad \le C\varepsilon . \end{aligned}$$

(50)

Similarly,

$$\begin{aligned}&|N^y(\bar{q},\mathbf {V})_{i,j+1/2}-N^y_\varepsilon (\bar{q},\mathbf {V})_{i,j+1/2}|\nonumber \\&\quad =|a_2(\bar{q}_{i,j+1/2})V^y_{i,j+1/2}([Q^y\mathbf {V}]_{i,j+1/2}-[Q_\varepsilon ^y\mathbf {V}]_{i,j+1/2})|\nonumber \\&\quad \le C\varepsilon . \end{aligned}$$

(51)

Remark 1

By taking $\varepsilon =O(h^2)$, we obtain

$$\begin{aligned}&|N^x(\bar{q},\mathbf {V})_{i+1/2,j}-N^x_\varepsilon (\bar{q},\mathbf {V})_{i+1/2,j}|\le Ch^2, \end{aligned}$$

(52)

$$\begin{aligned}&|N^y(\bar{q},\mathbf {V})_{i,j+1/2}-N^y_\varepsilon (\bar{q},\mathbf {V})_{i,j+1/2}|\le Ch^2. \end{aligned}$$

(53)

By referring to Lemma 3.8 in [22], we get Lemma 9 as follows.

Lemma 9

Suppose ${\mathbf {v}}$ is bounded, the modified nonlinear terms $N_\varepsilon ^x(\bar{q},\mathbf {v})$ and $N_\varepsilon ^y(\bar{q},\mathbf {v})$ are twice differentiable and have uniformly bounded second-order derivatives with respect to $\mathbf {v}$.

Lemma 10

Suppose $\mathbf {V}=(V^x,V^y)$ and $\mathbf {W}=(W^x,W^y)$ are bounded, $\{V^x_{i+1/2,j}\}$ and $\{V^y_{i,j+1/2}\}$ are discrete functions with

$$\begin{aligned} V^x_{1/2,j}= & {} V^x_{n_x+1/2,j}=0,\quad j=1,\ldots ,n_y,\\ V^y_{i,1/2}= & {} V^y_{i,n_y+1/2}=0,\quad i=1,\ldots ,n_x. \end{aligned}$$

Then, we have

$$\begin{aligned}&\underline{a}(\Vert V^x-W^x\Vert _x^2+\Vert V^y-W^y\Vert _y^2)\nonumber \\&\quad \le (L^x_\varepsilon (\bar{q},\mathbf {V})-L^x_\varepsilon (\bar{q},\mathbf {W}),V^x-W^x)_x\nonumber \\&\qquad +\,(L^y_\varepsilon (\bar{q},\mathbf {V})-L^y_\varepsilon (\bar{q},\mathbf {W}),V^y-W^y)_y. \end{aligned}$$

(54)

Proof

It follows from the definition of $L_\varepsilon ^x(\cdot ,\cdot )$ that

$$\begin{aligned}&L_\varepsilon ^x(\bar{q},\mathbf {V})^k_{i+1/2,j}\nonumber \\&\quad =N^x(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}+\dfrac{\partial N^x}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(\bar{q}-\bar{\hat{P}}_H)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^x-\hat{U}_H^x)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-\hat{U}_{H}^y)^k_{i,j+1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-\hat{U}_{H}^y)^k_{i,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-\hat{U}_{H}^y)^k_{i+1,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-\hat{U}_{H}^y)^k_{i+1,j+1/2}, \end{aligned}$$

(55)

and

$$\begin{aligned}&L_\varepsilon ^x(\bar{q},\mathbf {W})^k_{i+1/2,j}\nonumber \\&\quad =N^x(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}+\dfrac{\partial N^x}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(\bar{q}-\bar{\hat{P}}_H)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(W^x-\hat{U}_H^x)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(W^y-\hat{U}_{H}^y)^k_{i,j+1/2}\nonumber \\&\qquad +\dfrac{\partial N_\varepsilon ^x}{\partial u_{LB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(W^y-\hat{U}_{H}^y)^k_{i,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(W^y-\hat{U}_{H}^y)^k_{i+1,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(W^y-\hat{U}_{H}^y)^k_{i+1,j+1/2}. \end{aligned}$$

(56)

Subtracting (56) from (55), we have

$$\begin{aligned}&L_\varepsilon ^x(\bar{q},\mathbf {V})^k_{i+1/2,j}-L_\varepsilon ^x(\bar{q},\mathbf {W})^k_{i+1/2,j}\nonumber \\&\quad =\dfrac{\partial N_\varepsilon ^x}{\partial u^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^x-W^x)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-W^y)^k_{i,j+1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{LB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-W^y)^k_{i,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RB}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-W^y)^k_{i+1,j-1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RT}^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^y-W^y)^k_{i+1,j+1/2}. \end{aligned}$$

(57)

Similarly,

$$\begin{aligned}&L_\varepsilon ^y(\bar{q},\mathbf {V})^k_{i,j+1/2}-L_\varepsilon ^y(\bar{q},\mathbf {W})^k_{i,j+1/2}\nonumber \\&\quad =\dfrac{\partial N_\varepsilon ^y}{\partial u^y}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(V^y-W^y)^k_{i,j+1/2}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u_{LT}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(V^x-W^x)^k_{i-1/2,j+1}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u_{LB}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i-1/2,j}(V^x-W^x)^k_{i-1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^y}{\partial u_{RB}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i+1/2,j}(V^x-W^x)^k_{i+1/2,j}\nonumber \\&\qquad +\,\dfrac{\partial N_\varepsilon ^x}{\partial u_{RT}^x}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k_{i,j+1/2}(V^x-W^x)^k_{i+1/2,j+1}. \end{aligned}$$

(58)

The estimate (54) can then be obtained by applying Lemma 3.2 in [22] to (57) and (58).

Theorem 2

Let $U_h^{x,k}$, $U_h^{y,k}$, $P_h^k$ be the approximation solutions obtained by step 2 of two-grid finite difference algorithm. Suppose the solutions $\mathbf {u}=(u^x,u^y)$ and p are sufficiently smooth, then there exists a positive constant C independent of h and $\varDelta t$ such that

$$\begin{aligned}&\sum _{k=1}^n\varDelta t^k(\Vert (u^x-U_h^x)^k\Vert ^2_x+\Vert (u^y-U_h^y)^k\Vert ^2_y)^{1/2}\le C(\varDelta t+\varepsilon +h^2+H^3),\\&\Vert (p-P_h)^k\Vert _m\le C (\varDelta t+\varepsilon +h^2+H^3). \end{aligned}$$

Proof

Let

$$\begin{aligned}&(e^{p})^k_{i,j}=(P_h-p)^k_{i,j},\\&(e^{x})^k_{i+1/2,j}=(U^x_h-u^x)^k_{i+1/2,j}, \\&(e^{y})^k_{i,j+1/2}=(U^y_h-u^y)^k_{i,j+1/2}. \end{aligned}$$

From the step 2 of two-grid algorithm (19)–(21), Lemmas 1, 2, 3, and 4,

$$\begin{aligned}&a_1e^{x,k}_{i+1/2,j}+L_\varepsilon ^x(\bar{P}_h,\mathbf {U}_h)^k_{i+1/2,j}-N^x(\bar{p},\mathbf {u})^k_{i+1/2,j}\nonumber \\&\quad =-\,[d^x_h(e^p+\eta )]_{i+1/2,j}^k+O(h^2), \end{aligned}$$

(59)

$$\begin{aligned}&a_1e^{y,k}_{i,j+1/2}+L_\varepsilon ^y(\bar{P}_h,\mathbf {U}_h)^k_{i,j+1/2}-N^y(\bar{p},\mathbf {u})^k_{i,j+1/2}\nonumber \\&\quad =-\,[d^y_h(e^p+\eta )]_{i,j+1/2}^k+O(h^2), \end{aligned}$$

(60)

$$\begin{aligned}&\alpha [d_t(e^p+\eta )]^k_{i,j}+[D_h^x(e^x)]^k_{i,j}+[D_h^y(e^y)]^k_{i,j}\nonumber \\&\quad =O(\varDelta t+h^2). \end{aligned}$$

(61)

Multiplying (59), (60), (61) by $e^{x,k}_{i+1/2,j}h^x_{i+1/2} h^y_j$, $e^{y,k}_{i,j+1/2}h^x_{i} h^y_{j+1/2}$, $(e^p+\eta )^k_{i,j}h_i^x h_j^y$ and summing over i and j, we get

$$\begin{aligned}&\dfrac{\alpha }{2}d_t\Vert (e^p+\eta )^k\Vert _m^2+\dfrac{\alpha \triangle t^k}{2}\Vert d_t(e^p+\eta )^k\Vert _m^2+a_1(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2)\nonumber \\&\qquad +\,(L_\varepsilon ^x(\bar{P}_h,\mathbf {U}_h)^k-L_\varepsilon ^x(\bar{P}_h,\mathbf {u})^k,e^{x,k})_x+ (L_\varepsilon ^y(\bar{P}_h,\mathbf {U}_h)^k-L_\varepsilon ^y(\bar{P}_h,\mathbf {u})^k,e^{y,k})_y\nonumber \\&\quad \le |(L_\varepsilon ^x(\bar{p},\mathbf {u})^k-L_\varepsilon ^x(\bar{P}_h,\mathbf {u})^k,e^{x,k})_x+ (L_\varepsilon ^y(\bar{p},\mathbf {u})^k-L_\varepsilon ^y(\bar{P}_h,\mathbf {u})^k,e^{y,k})_y|\nonumber \\&\qquad +\,|(N_\varepsilon ^x(\bar{p},\mathbf {u})^k-L_\varepsilon ^x(\bar{p},\mathbf {u})^k,e^{x,k})_x+\,(N_\varepsilon ^y(\bar{p},\mathbf {u})^k-L_\varepsilon ^y(\bar{p},\mathbf {u})^k,e^{y,k})_y|\nonumber \\&\qquad +\,|(N^x(\bar{p},\mathbf {u})^k-N_\varepsilon ^x(\bar{p},\mathbf {u})^k,e^{x,k})_x+\,(N^y(\bar{p},\mathbf {u})^k-N_\varepsilon ^y(\bar{p},\mathbf {u})^k,e^{y,k})_y|\nonumber \\&\qquad +\,\dfrac{a_1}{8}(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2)+\Vert (e^p+\eta )^k\Vert _m^2+O(\varDelta t^2+h^4). \end{aligned}$$

(62)

Combining the definitions of $L_\varepsilon ^x(\cdot ,\cdot )$ and $L_\varepsilon ^y(\cdot ,\cdot )$ with Cauchy-Schwarz inequality, we have

$$\begin{aligned}&|(L_\varepsilon ^x(\bar{p},\mathbf {u})^k-L_\varepsilon ^x(\bar{P}_h,\mathbf {u})^k,e^{x,k})_x+ (L_\varepsilon ^y(\bar{p},\mathbf {u})^k-L_\varepsilon ^y(\bar{P}_h,\mathbf {u})^k,e^{y,k})_y|\nonumber \\&\quad \le C(\Vert (e^p+\eta )^k\Vert _m^2+\Vert \eta ^k\Vert _m^2)+\dfrac{a_1}{8}(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2). \end{aligned}$$

(63)

From Theorem 1 and inverse inequality we know that $P_H$, $U_H^x$ and $U_H^y$ are bounded.

Applying Taylor expansion to $N_\varepsilon ^x(\bar{p},\mathbf {u})$ and $N_\varepsilon ^y(\bar{p},\mathbf {u})$ and according to Lemmas 8 and 9, we obtain

$$\begin{aligned}&|(N_\varepsilon ^x(\bar{p},\mathbf {u})^k-L_\varepsilon ^x(\bar{p},\mathbf {u})^k,e^{x,k})_x+(N_\varepsilon ^y(\bar{p},\mathbf {u})^k-L_\varepsilon ^y(\bar{p},\mathbf {u})^k,e^{y,k})_y|\nonumber \\&\quad \le |(N_\varepsilon ^x(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k-N^x(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k,e^{x,k})_x|\nonumber \\&\qquad +\,|(N_\varepsilon ^y(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k-N^y(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k,e^{y,k})_y|\nonumber \\&\qquad +\,|\left( \dfrac{\partial N_\varepsilon ^x}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k(\bar{p}^k-\bar{\hat{P}}_H^k)-\dfrac{\partial N^x}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k(\bar{p}^k-\bar{\hat{P}}_H^k),e^{x,k}\right) _x|\nonumber \\&\qquad +\,|\left( \dfrac{\partial N_\varepsilon ^y}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k(\bar{p}^k-\bar{\hat{P}}_H^k)-\dfrac{\partial N^y}{\partial p}(\bar{\hat{P}}_H,\hat{\mathbf {U}}_H)^k(\bar{p}^k-\bar{\hat{P}}_H^k),e^{y,k}\right) _y|\nonumber \\&\qquad +\,C(|((\bar{p}^k-\bar{\hat{P}}^k_H)^2,e^{x,k})_x|+|((u^{x,k}-{\hat{U}^{x,k}}_H)^2,e^{x,k})_x|\nonumber \\&\qquad +\,|((u^{y,k}-\hat{U}^{y,k}_H)^2,e^{x,k})_x|+|((\bar{p}^k-\bar{\hat{P}}^k_H)^2,e^{y,k})_y|\nonumber \\&\qquad +\,|((u^{y,k}-\hat{U}^{y,k}_H)^2,e^{y,k})_y|+|((u^{x,k}-\hat{U}^{x,k}_H)^2,e^{y,k})_y|)\nonumber \\&\quad \le C(\varepsilon ^2+\Vert (E^{p,k})^2\Vert _M^2+\Vert (E^{x,k})^2\Vert _X^2+\Vert (E^{y,k})^2\Vert _Y^2)\nonumber \\&\qquad +\,\dfrac{a_1}{8}(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2). \end{aligned}$$

(64)

Lemma 9 together with Cauchy–Schwarz inequality yield that

$$\begin{aligned}&|(N^x(\bar{p},\mathbf {u})^k-N_\varepsilon ^x(\bar{p},\mathbf {u})^k,e^{x,k})_x+(N^y(\bar{p},\mathbf {u})^k-N_\varepsilon ^y(\bar{p},\mathbf {u})^k,e^{y,k})_y|\nonumber \\&\quad \le C\varepsilon ^2+\dfrac{a_1}{8}(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2). \end{aligned}$$

(65)

Using Lemma 10 and (6), we get

$$\begin{aligned}&(L_\varepsilon ^x(\bar{P}_h,\mathbf {U}_h)^k-L_\varepsilon ^x(\bar{P}_h,\mathbf {u})^k,e^{x,k})_x\nonumber \\&\qquad +\,(L_\varepsilon ^y(\bar{P}_h,\mathbf {U}_h)^k-L_\varepsilon ^y(\bar{P}_h,\mathbf {u})^k,e^{y,k})_y\nonumber \\&\quad \ge \underline{a} ( || {U}_h^x - {u}^x||_x^2+|| {U}_h^y - {u}^y||_y^2)\nonumber \\&\quad \ge 0. \end{aligned}$$

(66)

Therefore,

$$\begin{aligned}&\dfrac{\alpha }{2}d_t\Vert (e^p+\eta )^k\Vert _m^2+\dfrac{\alpha \triangle t^k}{2}\Vert d_t(e^p+\eta )^k\Vert _m^2+a_1(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2)\nonumber \\&\quad \le C(\varepsilon ^2+\varDelta t^2+h^4+\Vert (e^p+\eta )^k\Vert _m^2+\Vert \eta ^{k}\Vert _m^2+\Vert (E^{p,k})^2\Vert _M^2\nonumber \\&\qquad +\,\Vert (E^{x,k})^2\Vert _X^2+\Vert (E^{y,k})^2\Vert _Y^2)+\dfrac{a_1}{2}\Vert e^{x,k}\Vert _x^2+\dfrac{a_1}{2}\Vert e^{y,k}\Vert _y^2. \end{aligned}$$

(67)

By the assumption of $\alpha$, $a_1$ in (6),

$$\begin{aligned}&\dfrac{1}{2}d_t\Vert (e^p+\eta )^k\Vert _m^2+\dfrac{\triangle t^k}{2}\Vert d_t(e^p+\eta )^k\Vert _m^2+\dfrac{1}{2}(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2)\nonumber \\&\quad \le C(\varepsilon ^2+\varDelta t^2+h^4+\Vert (e^p+\eta )^k\Vert _m^2\nonumber \\&\qquad +\,\Vert (E^{p,k})^2\Vert _M^2+\Vert (E^{x,k})^2\Vert _X^2+\Vert (E^{y,k})^2\Vert _Y^2). \end{aligned}$$

(68)

Multiplying (68) by $2\triangle t^k$ and summing up k from 1 to $N_t$, we have the following result from Lemma 7 and Theorem 1

$$\begin{aligned}&\Vert (e^p+\eta )^{N_t}\Vert _m^2+\sum _{k=1}^{N_t}(\triangle t^k)^2\Vert d_t(e^p+\eta )^k\Vert _m^2\nonumber \\&\qquad +\,\sum _{k=1}^{N_t}\triangle t^k(\Vert e^{x,k}\Vert _x^2+\Vert e^{y,k}\Vert _y^2)\nonumber \\&\quad \le C\Bigg (\varepsilon ^2+\varDelta t^2+h^4+\Vert (e^p+\eta )^{0}\Vert _m^2+\sum _{k=1}^{N_t}\triangle t^k\Vert (e^p+\eta )^k\Vert _m^2\nonumber \\&\qquad +\,\sum _{k=1}^{N_t}\Big (\varDelta t^k\Vert (E^{p,k})^2\Vert _M^2+\varDelta t^k\Vert (E^{x,k})^2\Vert _X^2+\varDelta t^k\Vert (E^{y,k})^2\Vert _Y^2\Big )\Bigg )\nonumber \\&\quad \le C\Big (\varepsilon ^2+\varDelta t^2+h^4+H^6+\sum _{k=1}^{N_t}\triangle t^k\Vert (e^p+\eta )^k\Vert _m^2\Big ). \end{aligned}$$

(69)

Using Gronwall lemma, we have

$$\begin{aligned}&\Vert (P_h-p+\eta )^{N_t}\Vert _m^2+\sum _{k=1}^{N_t}\triangle t^k(\Vert (U_h^x-u^x)^k\Vert _x^2+\Vert (U_h^y-u^y)^k\Vert _y^2)\nonumber \\&\qquad \le C(\varepsilon ^2+\varDelta t^2+h^4+H^6). \end{aligned}$$

(70)

Combing the definition of $\eta$ in (25) and triangle inequality, the theorem establishes. $\square$

In the proofs of Theorems 1 and 2, it can be seen that there is no time step restriction for the optimal error estimates. The key reason is that we employed the monotonicity of the nonlinear operators on the coarse grid and the fine grid as shown in Lemmas 5 and 10, respectively.

4 Numerical Experiments

In this section we present some numerical experiments to illustrate the convergence property and efficiency of two-grid block-centered finite difference (tg-BCFD) method.

We consider the following slightly compressible Darcy–Forchheimer model with time interval $J=(0,1]$.

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{\partial p}{\partial t}+\nabla \cdot \mathbf {u}= f, &{} \quad \mathbf {x}\in \varOmega \times J,\\ \mathbf {u}+p^2|\mathbf {u}|\mathbf {u}+\nabla p=q, &{} \quad \mathbf {x}\in \varOmega \times J,\\ \mathbf {u}\cdot \mathbf {n}=g, &{} \quad \mathbf {x}\in \partial \varOmega \times J. \end{array} \right. \end{aligned}$$

(71)

For simplicity, the domains of Examples 1, 2, 3, and 4 are all chosen to be an unit square, i.e., $\varOmega =[0,1]\times [0,1]$.

We first carry out the following two examples to verify the convergence rate of the tg-BCFD method.

Example 1

The analytical solutions of Darcy–Forchheimer model (71) with homogeneous Neumann boundary condition are given by

$$\begin{aligned} \left\{ \begin{array}{lll} &{}\mathbf {u}(x,y,t)=(-y, x)^{T}, \\ &{}p(x,y,t)=t\mathrm{{sin}}(\pi x)\mathrm{{sin}}(\pi y), \end{array} \right. \end{aligned}$$

(72)

and functions f and q are computed correspondingly.

Example 2

The analytical solutions of Darcy–Forchheimer model (71) with inhomogeneous Neumann boundary condition are given by

$$\begin{aligned} \left\{ \begin{array}{lll} &{}\mathbf {u}(x,y,t)=(e^{1-t}\mathrm{{sin}}(\pi x)\mathrm{{cos}}(\pi y), e^{1-t}\mathrm{{cos}}(\pi x)\mathrm{{sin}}(\pi y))^{T}, \\ &{}p(x,y,t)=arctan(x+y-t+1), \end{array} \right. \end{aligned}$$

(73)

and functions f, q and g are computed correspondingly.

In order to show the efficiency of tg-BCFD algorithm, we compare the numerical results of the algorithm with traditional block-centered finite difference (BCFD) method defined by (19)–(23) in [20] as follows for $P^k_{i,j}$, $U^{x,k}_{i+1/2,j}$, and $U^{y,k}_{i,j+1/2}$.

$$\begin{aligned} \left\{ \begin{array}{lll} &{}\alpha \dfrac{P^{(n),k}_{i,j}-P^{k}_{i,j}}{\varDelta t^k}+[D^x_hU^{x(n)}]^k_{i,j}+[D_h^yU^{y(n)}]^k_{i,j}= f^k_{i,j}, \\ &{}a_{1}(U^{x,(n)})^k_{i+1/2,j}+a_2(I_h{P}^{(n-1)})^k_{i+1/2,j}[Q^x \mathbf {U}^{(n-1)}]^k_{i+1/2,j}(U^{x,(n)})^k_{i+1/2,j} \\ &{}\qquad \qquad =-\,[d_h^xP^{(n)}]^k_{i+1/2,j}, \\ &{}a_{1}(U^{x,(n)})^k_{i,j+1/2}+a_2(I_h{P}^{(n-1)})^k_{i,j+1/2}[Q^y \mathbf {U}^{(n-1)}]^k_{i,j+1/2}(U^{y,(n)})^k_{i,j+1/2} \\ &{}\qquad \qquad =-\,[d_h^yP^{(n)}]^k_{i,j+1/2}. \end{array} \right. \end{aligned}$$

(74)

where the piecewise constant function $I_h q$ on $\varOmega _{i,j}$ such that

$$\begin{aligned} I_h q=\left\{ \begin{array}{ll} \bar{I}_h q_{i+\frac{1}{4},j+\frac{1}{4}}, &{}(x,y)\in (x_i, x_{i+\frac{1}{2}})\times (y_j, y_{j+\frac{1}{2}}),\\ \bar{I}_h q_{i+\frac{1}{4},j-\frac{1}{4}}, &{}(x,y)\in (x_i, x_{i+\frac{1}{2}})\times (y_{j-\frac{1}{2}}, y_{j}),\\ \bar{I}_h q_{i-\frac{1}{4},j+\frac{1}{4}}, &{}(x,y)\in (x_{i-\frac{1}{2}}, x_{i})\times (y_j, y_{j+\frac{1}{2}}),\\ \bar{I}_h q_{i-\frac{1}{4},j-\frac{1}{4}}, &{}(x,y)\in (x_{i-\frac{1}{2}}, x_{i})\times (y_{j-\frac{1}{2}}, y_{j}), \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \left\{ \begin{array}{lll} &{}\bar{I}_h q_{i+\frac{1}{4},j\pm \frac{1}{4}}=\dfrac{1}{4h^x_{i+\frac{1}{2}}}\left( h_{i+1}^x q_{i,j}+h_{i}^x q_{i+1,j}\right) +\dfrac{1}{4h^y_{j\pm \frac{1}{2}}}\left( h^y_{j\pm 1} q_{i,j}+h^y_{j} q_{i,j\pm 1}\right) ,\\ &{}\bar{I}_h q_{i-\frac{1}{4},j\pm \frac{1}{4}}=\dfrac{1}{4h^x_{i-\frac{1}{2}}}\left( h_{i-1}^x q_{i,j}+h_{i}^x q_{i-1,j}\right) +\dfrac{1}{4h^y_{j\pm \frac{1}{2}}}\left( h^y_{j\pm 1} q_{i,j}+h^y_{j} q_{i,j\pm 1}\right) . \end{array} \right. \end{aligned}$$

For the coarse grid $\varOmega _H$, we take uniform grids with mesh size $H=\{\dfrac{1}{4}, \dfrac{1}{9}$, $\dfrac{1}{16}, \dfrac{1}{25}\}$. According to Theorem 2, we use $h=H^{3/2}$ as the mesh size of the fine grid $\varOmega _h$. We take $\varDelta t=O(h^2)$ and $\varepsilon =10^{-4}$. When executing tg-BCFD algorithm and the traditional BCFD method (74), we choose $eps=10^{-9}$ as the criterion of terminating iterations on the fine grid. As for the tg-BCFD method, we choose $eps=10^{-3}$ as the criterion of terminating iterations on the coarse grid $\varOmega _H$, because the correction capability of fine grid space is strong enough. The priori errors of tg-BCFD method in discrete $L^2$ norms and $L^\infty$ norms, convergence rates and the numbers of iterations are listed in Tables 1, 3 and plotted in Fig. 3. Those of BCFD method (74) are shown in Tables 2 and 4.

Table 1 Results of Example 1 by tg-BCFD method when $t=1$ (on the last time level)

Fig. 3

Log–log plots of errors. Left Top errors of p in discrete $L^2$ norm; Left Bottom errors of p in discrete $L^\infty$ norm; Right Top errors of $\mathbf {u}$ in discrete $L^2$ norm; Right Bottom errors of $\mathbf {u}$ in discrete $L^\infty$ norm

It can be observed from Tables 1, 3 and Fig. 3 that the tg-BCFD method have second-order accuracy in discrete $L^2$ norms. These results are consistent with the error estimates in Theorem 2. In the last column of each table, the numbers of iterations on fine grid space are reported when $t=1$. The computational cost on coarse grid of the tg-BCFD method is relatively negligible due to it’s weak iteration terminating condition and small number of node-points. The numbers of iterations for the tg-BCFD method are shown to be significantly less than those produced by the BCFD method (74) only on the last time level. In order to obtain the convergence rate, we choose $\varDelta t=h^2$, which means the numerical experiments need large number of time levels (up to $O(10^6)$ on the finest spatial grids). Seen from Tables 1, 2, 3, and 4, it is obvious that tg-BCFD method needs much less iterations compared with BCFD method.

Moreover, the results by using tg-BCFD method is without loss any accuracy comparing with the errors obtained by BCFD method (74). On the fine grid of tg-BCFD method, the resulting equations are linear and easy to be solved directly, but we still execute the iterative method just for obtaining the same errors as those by the BCFD method (74). It is shown that the resulting solution obtained by the tg-BCFD method still achieves asymptotically optimal accuracy.

In Examples 1 and 2, the errors in $L^\infty$ norms are almost second-order accurate by using tg-BCFD method, though it has not been proved theoretically. Based on the experimental data, we can improve the results of Lemma 7 by using $L^\infty$-norm technique instead of inverse estimate method. Furthermore, the result of Theorem 2 can be rewritten as $O(\varDelta t+\varepsilon +h^2+H^4)$. It will be our future work to obtain the error estimates in $L^\infty$ norms.

Next, we use Example 1 to show the influence of $\varepsilon$ on the errors. The re−esults when $t=1$ are obtained by different values of $\varepsilon$ listed in Tables 5, 6, 7, 8, and 9 and Fig. 4.

Table 2 Results of Example 1 by BCFD method when $t=1$ (on the last time level)

Table 3 Results of Example 2 by tg-BCFD method when $t=1$ (on the last time level)

Table 4 Results of Example 2 by BCFD method when $t=1$ (on the last time level)

Table 5 Errors of Example 1 by tg-BCFD method when $\varepsilon =\dfrac{1}{10}$

Table 6 Errors of Example 1 by tg-BCFD method when $\varepsilon =\dfrac{1}{20}$

Table 7 Errors of Example 1 by tg-BCFD method when $\varepsilon =\dfrac{1}{50}$

Table 8 Errors of Example 1 by tg-BCFD method when $\varepsilon =\dfrac{1}{100}$

Table 9 Errors of Example 1 by tg-BCFD method when $\varepsilon =\dfrac{1}{1000}$

Fig. 4

Log–log plots of errors in different values of $\varepsilon$. Left Top errors of p in discrete $L^2$ norm; Left Bottom errors of p in discrete $L^\infty$ norm; Right Top errors of $\mathbf {u}$ in discrete $L^2$ norm; Right Bottom errors of $\mathbf {u}$ in discrete $L^\infty$ norm

Comparing with Table 1, one can see that the value of $\varepsilon$ have an important influence on the errors of the tg-BCFD method. When $\varepsilon$ is larger than $O(h^2)$, it plays a leading role in errors of $L^2$ norm and $L^\infty$ norm (see Tables 5, 6, 7, and 8). In order to obtain the optimal error order, we should take $\varepsilon =O(h^2)$ as shown in the proof of Theorem 2. In all examples, we choose the same value for parameter $\varepsilon$ in order to obtain the convergence rates easily. Due to the smallest of mesh sizes used in all examples, $\varepsilon$ is chosen as $O(h^2)=10^{-4}$.

Finally, we solve the following two practical problems by using tg-BCFD method. The right-hand side function q, the injection and production flow rates at wells for f and the boundary conditions of slightly compressible Darcy–Forchheimer model (71) are listed as follows.

Example 3

Darcy–Forchheimer model (71) with homogeneous Neumann boundary condition:

$$\begin{aligned} \left\{ \begin{array}{lll} &{}q(x,y,t)=0, \\ &{}f(x,y,t)=\delta (0,0)+\delta (1,0)+\delta (0, 1)+\delta (1, 1)-4\delta (0.5, 0.5), \\ &{}\mathbf {u}\cdot \mathbf {n}=0. \end{array} \right. \end{aligned}$$

(75)

Fig. 5

Numerical pressure distribution and velocity quiver of Example 3 by tg-BCFD method

Example 4

Darcy–Forchheimer model (71) with inhomogeneous Neumann boundary condition:

$$\begin{aligned} \left\{ \begin{array}{lll} &{}q(x,y,t)=0, \\ &{}f(x,y,t)=\delta (0,0)-\delta (1,1), \\ &{}(\mathbf {u}\cdot \mathbf {n})|_{x=0}=y,\\ &{}(\mathbf {u}\cdot \mathbf {n})|_{x=1}=-y,\\ &{}(\mathbf {u}\cdot \mathbf {n})|_{y=0}=-x,\\ &{}(\mathbf {u}\cdot \mathbf {n})|_{y=1}=x. \end{array} \right. \end{aligned}$$

(76)

Fig. 6

Numerical pressure distribution and velocity quiver of Example 4 by tg-BCFD method

As shown in Figs. 5 and 6, the numerical pressure and velocity are reasonable and consistent with the physical phenomenon.

Next, we try to solve the Darcy–Forchheimer model (71) by tg-BCFD method on irregular domain such that $y\in [0,1]$ and $\varGamma \le x\le 0.875$ with $\varGamma =0.56y(y-1)$.

Example 5

Darcy–Forchheimer model (71) with homogeneous Neumann boundary condition:

$$\begin{aligned} \left\{ \begin{array}{lll} &{}q(x,y,t)=0, \\ &{}f(x,y,t)=-e^t\delta (0.4375,0)+5t\delta (0.4375,1), \\ &{}(\mathbf {u}\cdot \mathbf {n})|_\varGamma =0,\\ &{}(\mathbf {u}\cdot \mathbf {n})|_{x=1}=0,\\ &{}(\mathbf {u}\cdot \mathbf {n})|_{y=0}=0,\\ &{}(\mathbf {u}\cdot \mathbf {n})|_{y=1}=0. \end{array} \right. \end{aligned}$$

(77)

In order to use the tg-BCFD method on irregular domain, we replace a boundary point with the grid point inside the computational domain closest to this boundary point. Therefore, an approximation to curve boundary $\varGamma$ with these grid points is obtained as boundary points forming the polygonal boundary. The approximation boundary condition is taken as zero boundary according to the curve boundary condition. Based on the numerical solutions on coarse grids, we use the proper second-order interpolation and extrapolation methods to get the initial iteration values on the fine grids, as in Fig. 7. Thus, a linear system is solved to obtain the numerical solutions of Darcy–Forchheimer model (71) in irregular domain.

Fig. 7

Subdivision of irregular domain for Example 5 by tg-BCFD method. The irregular domain is given in black; the red polylines represent the approximate boundary; the green grids are mesh when $h=1/64$ and the blue ones are mesh when $H=1/16$

The numerical solutions of pressure and velocity are given as in Figs. 8, 9.

Fig. 8

Numerical pressure distribution of Example 5 by tg-BCFD method. Left $\mathrm{t}=0.125$; Right $\mathrm{t=1}$

Fig. 9

Numerical velocity distribution of Example 5 by tg-BCFD method. Left $\mathrm{t}=0.125$; Right $\mathrm{t}=1$

Therefore, tg-BCFD method is useful and efficient for solving the nonlinear Darcy–Forchheimer model on both regular domain and irregular domain with smooth boundary.

5 Conclusions and Extensions

In this paper we apply a two-grid algorithm based on the block-centered finite difference discretization to solve the nonlinear Darcy–Forchheimer equations. The numerical procedure involves two steps: first solving a small nonlinear system on the coarse grid and then solving a linear system on the fine grid. When constructing the nonlinear scheme on coarse grid, we use the fewest possible nodal-points values of p and $\mathbf {u}$ to construct the block-centered finite difference scheme. When constructing the linear scheme on fine grid, a small positive parameter $\varepsilon$ is used to modify the original non-differentiable term in order to make it differentiable. It is proved that the modified nonlinear term still preserves the original property of the nonlinear term. The two-grid block-centered finite difference method is proved to be unconditionally convergent without any time step restriction by using the monotonicity of the discrete nonlinear operators. According to the theoretical analysis and numerical experiments, it is shown that solving such a large class of nonlinear equation will not be much more difficult than solving one single linearized equation, without sacrificing the order of accuracy of the fine grid solution. Moreover, it is clearly shown that $H = O(h^{2/3})$ and $\varepsilon =O(h^2)$ should be chosen to obtain asymptotically optimal approximation results in discrete $L^2$ norms. Numerical experiments show that the errors in $L^\infty$ norms are almost second-order accurate by using the two-grid block-centered finite difference method. If theoretical results in Lemma 7 could be improved by using the experimental results in $L^\infty$ norms, the error bounds in Theorem 2 can be re-derived to be $O(\varDelta t+\varepsilon +h^2+H^4)$, which will be our future work.