Block-Centered Finite Difference Method for Simulating Compressible Wormhole Propagation

Abstract

In this paper, the block-centered finite difference method is introduced and analyzed to solve the compressible wormhole propagation. The coupled analysis approach to deal with the fully coupling relation of multivariables is employed. By this, stability analysis and error estimates for the pressure, velocity, porosity, concentration and its flux in different discrete norms are established rigorously and carefully on non-uniform grids. Finally, some numerical experiments are presented to verify the theoretical analysis and effectiveness of the given scheme.

1 Introduction

A wormhole is a phenomenon in which a worm-like hole is generated and propagated in the subsurface formations due to the injection of acids into a supercritical acid dissolution system. To enhance oil production rate, matrix acidization technique was introduced and applied widely. In this technique, we injected acid into matrix to dissolve the rocks, thus a channel called wormhole [1,2,3,4,5,6] is established. Usually such channel is formed with high porosities. Though this channel, we can easily push oil and gas components in the reservoir to the surface. It is crucial to point out that the advancement of the chemical reaction front does not propagate uniformly along the injection direction. Actually, the heterogeneity of porosity and permeability in the subsurface formations plays an significant role in promoting the non-uniformity of the chemical reaction front. All in all, the chemical reaction front tends to advance in certain directions more that other directions, thus a wormhole pattern is formed.

There are many numerical simulations for wormhole propagation due to its significant role in subsurface reservoir management. Zhao et al. [7] presented the theoretical and numerical analyses of chemical-dissolution front instability in fluid-saturated porous rocks by combining the finite element method and the finite difference method. In 2015, the new Darcy–Brinkman–Forchheimer framework was introduced to simulate the wormhole forming procedure by Wu et al. [3]. Besides, Kou et al. [1] developed a mixed finite element-based fully conservative methods to simulate the wormhole propagation. Recently, Li and Rui [8] have researched the characteristic block-centered finite difference method for simulating incompressible wormhole propagation.

Block-centered finite differences, sometimes called cell-centered finite differences, can be thought as the lowest order Raviart–Thomas mixed element method [9], with proper quadrature formulation. In [10], Wheeler presented the mixed finite elements for elliptic problems with tensor coefficients as cell-centered finite differences. And in 2012, a block-centered finite difference method for the Darcy–Forchheimer model was considered [11]. In [12,13,14,15] block-centered finite difference methods were developed. A parallel CGS block-centered finite difference method for a nonlinear time-fractional parabolic equation has been studied [16]. Recently, Li and Rui [17] applied this method to the nonlinear time-fractional parabolic equation. The applications of the block-centered finite difference methods enable us to approximate pressure, velocity, porosity, concentration and its flux in different discrete norms with second-order accuracy on non-uniform grids, which is the superconvergence. Also the block-centered finite difference methods can guarantee local mass conservation. Besides, the applications of the block-centered finite difference methods enable us to transfer the saddle point problem to symmetric positive definite problem.

As far as we know, there is no block-centered finite difference method for compressible wormhole propagation. Before analyzing the convergence of our block-centred finite difference method, we develop estimates of the mixed finite element method with quadrature applied to linear parabolic equations. Using these estimates, we obtain the superconvergence of the pressure, velocity, porosity, concentration and its flux in different discrete norms. In fact, in our proposed scheme, there are at least three issues in theoretical analysis for the compressible wormhole propagation: the first one is to estimate and bound the porosity which can change during time evolution, the second one is the complication resulted from the introduced auxiliary flux variable and the last one is the fully coupling relation of multi-variables. To resolve these issues, we introduce some usefully lemmas and consider the coupled analysis method. Recently, we have applied this method to the incompressible wormhole propagation in [8]. But for compressible wormhole propagation, due to the appearance of the term $\frac{\partial p}{\partial t}$ in the mass conservation equation, the same technique can not be used. Compared with the error analyses in [8], the error estimates in this paper is more complex which should be taken the time difference of approximate velocity and auxiliary flux into consideration. Moreover, stability results are proven rigorously and carefully which are not given in [8]. The error estimates are deduced rigorously and carefully in this paper, and we carry out some numerical experiments to verify the theoretical analysis and effectiveness of the given scheme.

The paper is organized as follows. In Sect. 2 we give the problem and some preliminaries. In Sect. 3 we present the block-centered finite difference algorithm. In Sect. 4 we demonstrate stability estimates for the discrete scheme. In Sect. 5 we demonstrate error analysis for the discrete scheme. In Sect. 6 some numerical experiments are carried out to verify the theoretical analysis and effectiveness of the given scheme.

Through out the paper we use C, with or without subscript, to denote a positive constant, which could have different values at different appearances.

2 The Problem and Some Preliminaries

In this paper, we consider the usual differential system used to describe compressible wormhole propagation [1]

where $\Omega$ is a rectangular domain in $\mathbb {R}^2$. $J=(0,\hat{T}]$, and $\hat{T}$ denotes the final time. p is the pressure, $\mu$ is the fluid viscosity, $\mathbf u$ is the Darcy velocity of the fluid, $f=f_I+f_P$, $f_P$ and $f_I$ are production and injection rates respectively. $\gamma$ is a pseudo-compressibility parameter that results in slight change of the density of the fluid phase in the dissolution process. $c_f$ is the cup-mixing concentration of the acid in the fluid phase. $c_I$ is the injected concentration. The diffusion coefficient $\mathbf D$ is shown as

$$\begin{aligned} \mathbf D (\mathbf x ,\mathbf u )=d_{m}{} \mathbf I +\alpha _l|\mathbf u | \mathbf E +\alpha _t|\mathbf u |\mathbf E ^{\bot }, \end{aligned}$$

(5)

where $\mathbf E (\mathbf u )=[{u}_i{u}_j/|\mathbf u |^2]$ is a $2\times 2$ matrix representing projection along the velocity vector and $\mathbf E ^{\bot }(\mathbf u )$ its orthogonal complement. $d_m$ is the molecular diffusivity, the diffusion coefficient $\alpha _l$ measures the dispersion in the direction of flow and $\alpha _t$ that transverse to the flow.

$k_c$ is the local mass-transfer coefficient, $a_v$ is the interfacial area available for reaction per unit volume of the medium. The variable $c_s$ is the concentration of the acid at the fluid-solid interface, and the relationship between $c_f$ and $c_s$ can be described as follows.

$$\begin{aligned} c_s=\frac{c_f}{1+k_s/k_c}, \end{aligned}$$

(6)

where $k_s$ is the surface reaction rate constant. The first term in the right hand side of Eq. (3) represents the transfer of acid species from the fluid phase to the fluid-solid interface [2]. $\phi$ and K are the porosity and permeability of the rock respectively, the relationship between the permeability and the porosity is established by the Carman–Kozeny correlation [18]

$$\begin{aligned} \frac{K}{K_0}=\frac{\phi }{\phi _0}\left( \frac{\phi (1-\phi _0)}{\phi _0(1-\phi )}\right) ^2, \end{aligned}$$

(7)

where $\phi _0$ and $K_0$ are the initial porosity and permeability of the rock respectively. In Eq. (4), $\alpha$ is the dissolving power of the acid and $\rho _s$ is the density of the solid phase. Using porosity and permeability, $a_v$ is shown as

$$\begin{aligned} \frac{a_v}{a_0}=\frac{\phi }{\phi _0}\sqrt{\frac{K_0\phi }{K\phi _0}}, \end{aligned}$$

(8)

where $a_0$ is the initial interfacial area.

The boundary and initial conditions are as follows.

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf u \cdot \mathbf n =0,~\phi \mathbf D \nabla c_f\cdot \mathbf n =0,&{}\quad \mathbf x \in \partial \Omega ,~t\in J,\\ p(\mathbf x ,0)=p_0(\mathbf x ),&{}\quad \mathbf x \in \Omega ,\\ c_f(\mathbf x ,0)=c_{f0}(\mathbf x ),&{}\quad \mathbf x \in \Omega ,\\ \phi (\mathbf x ,0)=\phi _0(\mathbf x ),&{}\quad \mathbf x \in \Omega , \end{array} \right. \end{aligned}$$

(9)

where $\mathbf n$ is the unit outward normal vector of the domain $\Omega$. For the physical quantities, we assume that $0\le c_{f0}\le 1$ and $0\le c_{I}\le 1$.

Let $N>0$ be a positive integer. Set

$$\begin{aligned} \triangle t=\hat{T}/N,\quad t_n=n\triangle t, ~~ for~~n\le N. \end{aligned}$$

Let $L^m(\Omega )$ be the standard Banach space with norm

$$\begin{aligned} \Vert v\Vert _{L^m(\Omega )}=\left( \int _{\Omega }| v|^md\Omega \right) ^{1/m}. \end{aligned}$$

For simplicity, let

$$\begin{aligned}(f,g)=(f,g)_{L^2(\Omega )}=\int _{\Omega }fgd\Omega \end{aligned}$$

denote the $L^2(\Omega )$ inner product, $\Vert v\Vert _{\infty }=\Vert v\Vert _{L^{\infty }(\Omega )}.$ And $W_p^k(\Omega )$ be the standard Sobolev space

$$\begin{aligned} W_p^k(\Omega )=\{g:~\Vert g\Vert _{W_p^k(\Omega )}<\infty \}, \end{aligned}$$

where

$$\begin{aligned} \Vert g\Vert _{W_p^k(\Omega )}=\left( \sum \limits _{|\alpha |\le k}\Vert D^\alpha g\Vert _{L^p(\Omega )}^p \right) ^{1/p}. \end{aligned}$$

(10)

Let $S=L^2(\Omega )$ and $\mathbf V =H(\Omega ,div)=\{{{\varvec{v}}}\in (L^2(\Omega ))^2,~\nabla \cdot {{\varvec{v}}}\in L^2(\Omega )\}$. And $\mathbf V ^0$ is denoted as the subspaces of $\mathbf V$ containing functions with normal traces equal to 0.

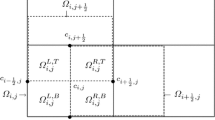
Let $\digamma _h$ be the quasi-uniform partition of $\Omega$ into rectangles in two dimensions with maximal mesh size h. The lowest-order Raviart–Thomas–Nédélec (RTN) space on rectangles [9, 19] is considered. Thus, on an element $D\in \digamma _h$, we have

$$\begin{aligned}&\mathbf V _h(D)=\left\{ (\alpha _1x+\beta _1,~\alpha _2y+\beta _2)^T:~\alpha _i,\beta _i\in \mathbb {R},~i=1,2\right\} ,\\&S_h(D)=\{\alpha :~\alpha \in \mathbb {R}\}, \end{aligned}$$

and $\mathbf V _h^0$ is denoted as the subspaces of $\mathbf V _h$ containing functions with normal traces equal to 0.

Next the standard nodal basis is used, where the nodes are at the centers of the elements for $S_h$, and the nodes are at the midpoints of edges for $\mathbf V _h$. Moreover, the grid points are denoted by

$$\begin{aligned} (x_{i+1/2},y_{j+1/2}),\quad i=0,\dots ,N_x,~~j=0,\dots ,N_y, \end{aligned}$$

and the notations similar to those in [20] are used.

$$\begin{aligned}&x_{i}=\left( x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}}\right) /2,\quad i=1,\dots ,N_x,\\&h_{i}^x=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}},\quad i=1,\dots ,N_x, \\&h_{i+\frac{1}{2}}^x=x_{i+1}-x_{i}=\left( h_{i}^x+h_{i+1}^x\right) /2,\quad i=1,\dots ,N_x-1,\\&y_{j}=\left( y_{j-\frac{1}{2}}+y_{j+\frac{1}{2}}\right) /2,\quad j=1,\dots ,N_y,\\&h_{j}^y=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}},\quad j=1,\dots ,N_y,\\&h_{j+\frac{1}{2}}^y=y_{j+1}-y_{j}=\left( h_{j}^y+h_{j+1}^y\right) /2,\quad j=1,\dots ,N_y,\\&h=\max \limits _{i,j}\left\{ h_{i}^x,h_j^y\right\} . \end{aligned}$$

Let $g_{i,j},~g_{i+\frac{1}{2},j},~g_{i,j+\frac{1}{2}}$ denote $g(x_{i},y_{j}),~g(x_{i+\frac{1}{2}},y_{j}),~g(x_{i},y_{j+\frac{1}{2}}).$ Define the discrete inner products and norms as follows,

$$\begin{aligned}&(f,g)_{M}=\sum \limits _{i=1}^{N_{x}}\sum \limits _{j=1}^{N_{y}}h_{i}^xh_{j}^yf_{i,j}g_{i,j},\\&(f,g)_{x}=\sum \limits _{i=1}^{N_{x}-1}\sum \limits _{j=1}^{N_{y}}h_{i+\frac{1}{2}}^xh_{j}^yf_{i+\frac{1}{2},j}g_{i+\frac{1}{2},j},\\&(f,g)_{y}=\sum \limits _{i=1}^{N_{x}}\sum \limits _{j=1}^{N_{y}-1}h_{i}^xh_{j+\frac{1}{2}}^yf_{i,j+\frac{1}{2}}g_{i,j+\frac{1}{2}},\\&({{\varvec{v}}},{{\varvec{r}}})_{TM}=(v^x,r^x)_{x}+(v^y,r^y)_{y}. \end{aligned}$$

For simplicity from now on we always omit the superscript n if the omission does not cause conflicts. Define

$$\begin{aligned}&[d_{x}g]_{i+\frac{1}{2},j}=\left( g_{i+1,j}-g_{i,j}\right) /h_{i+\frac{1}{2}}^x,\\&[d_{y}g]_{i,j+\frac{1}{2}}=\left( g_{i,j+1}-g_{i,j}\right) /h_{j+\frac{1}{2}}^y,\\&[D_{x}g]_{i,j}=\left( g_{i+\frac{1}{2},j}-g_{i-\frac{1}{2},j}\right) /h_{i}^x,\\&[D_{y}g]_{i,j}=\left( g_{i,j+\frac{1}{2}}-g_{i,j-\frac{1}{2}}\right) /h_{j}^y,\\&[d_{t}g]^n_{i,j}=\left( g_{i,j}^n-g_{i,j}^{n-1}\right) /\Delta t. \end{aligned}$$

Then we present some lemmas used in the following estimates.

Lemma 1

[20] Let $q_{i,j},w_{i+1/2,j}^x~and~ w_{i,j+1/2}^y$ be any values such that $w_{1/2,j}^x=w_{N_x+1/2,j}^x=w_{i,1/2}^y=w_{i,N_y+1/2}^y=0$, then

$$\begin{aligned} (q,D_xw^x)_M= & {} -(d_xq,w^x)_x,\\ (q,D_yw^y)_M= & {} -(d_yq,w^y)_y. \end{aligned}$$

For any ${{\varvec{r}}}\in (H^2(\Omega ))^2$, let ${{\hat{{\varvec{r}}}}}$ denote the projection operator of ${{\varvec{r}}}$ onto $\mathbf{V }_h$, that is

$$\begin{aligned} (\nabla \cdot {\hat{{\varvec{r}}}},w)=(\nabla \cdot {{\varvec{r}}},w),~~\forall w\in S_h, \end{aligned}$$

(11)

with approximation properties [21],

$$\begin{aligned} \Vert {{\varvec{r}}}-{\hat{{\varvec{r}}}}\Vert \le C\Vert {{\varvec{r}}}\Vert _{W^1_2(\Omega )}h, \end{aligned}$$

(12)

$$\begin{aligned} \Vert \nabla \cdot ({{\varvec{r}}}-{\hat{{\varvec{r}}}})\Vert \le C\Vert \nabla \cdot {{\varvec{r}}}\Vert _{W^1_2(\Omega )}h. \end{aligned}$$

(13)

Moreover, by the definition of ${{\hat{{\varvec{r}}}}}$ and the midpoint rule of integration, the $L^\infty$ norm of the projection is obtained by

$$\begin{aligned} \Vert {\hat{{\varvec{r}}}}-{{\varvec{r}}}\Vert _{L^{\infty }(\Omega )}\le Ch\Vert {{\varvec{r}}}\Vert _{W_{\infty }^2(\Omega )}. \end{aligned}$$

(14)

In Eq. (3), define ${{\varvec{q}}}=-\phi \mathbf D (\mathbf x )\nabla c_f,$ we can get the estimates which is necessary for the derivative and analysis of our numerical scheme [22].

$$\begin{aligned} \Vert \hat{{{\varvec{u}}}}^n-{{\varvec{u}}}^n\Vert _{TM}\le Ch^2, \end{aligned}$$

(15)

$$\begin{aligned} \Vert \hat{{{\varvec{q}}}}^n-{{\varvec{q}}}^n\Vert _{TM}\le Ch^2. \end{aligned}$$

(16)

Next we define an interpolant operator which is similar to that in [21]. Define $\Pi _h p$ from the values of $p_{i,j}$ for $i=1,2,\dots ,N_{x}$ and $j=1,2,\dots ,N_{y}$ as follows. For points (x, y), assuming $x\in [x_i,x_{i+1}], y\in [y_j,y_{j+1}]$, then, $\Pi _h p(x,y)$ can be evaluated by

$$\begin{aligned} \Pi _h p(x,y)= & {} \left( p_{i,j}\left( \frac{x_{i+1}-x}{x_{i+1}-x_i}\right) +p_{i+1,j}\left( \frac{x-x_{i}}{x_{i+1}-x_i}\right) \right) \left( \frac{y_{j+1}-y}{y_{j+1}-y_j}\right) \\&+\,\left( p_{i,j+1}\left( \frac{x_{i+1}-x}{x_{i+1}-x_i}\right) +p_{i+1,j+1}\left( \frac{x-x_{i}}{x_{i+1}-x_i}\right) \right) \left( \frac{y-y_{j}}{y_{j+1}-y_j}\right) . \end{aligned}$$

For $j=1,2\dots N_{y}$, we set

$$\begin{aligned} \Pi _h p(x_{1/2},y_{j})=\frac{\left( 2h_1^x+h_2^x\right) p_{1j}-h_1^xp_{2j}}{h_1^x+h_2^x}. \end{aligned}$$

This is a two-point extrapolation, and by Taylor’s expansion, we can obtain that

$$\begin{aligned} |(\Pi _h p-p)(x_{1/2},y_{j})|=O(h^2). \end{aligned}$$

For points (x, y), assuming $x\in [x_{1/2},x_{1}], y\in [y_{j},y_{j+1}]$, then, $\Pi _h p(x,y)$ can be evaluated as the bilinear interpolant between $p_{1,j}$, $p_{1,j+1},~\Pi _h p(x_{1/2},y_{j}),$ and $\Pi _h p(x_{1/2},y_{j+1}).$ And for these points, we can obtain that $|\Pi _h p-p|\le Ch^2$ by interpolation theory. Moreover, for points (x, y), such that $x\in [x_{N_x},x_{N_x+1/2}], y\in [y_{j},y_{j+1}]$ as well as points (x, y), where $x\in [x_i,x_{i+1}], y\in [y_{1/2},y_{1}]$ or $x\in [x_i,x_{i+1}], y\in [y_{N_y},y_{N_y+1/2}],$ we can define $\Pi _h p$ similarly. Lastly, we can define $\Pi _h p(x_{1/2},y_{1/2})$ using three-point extrapolation:

$$\begin{aligned} \Pi _h p(x_{1/2},y_{1/2})= & {} \Pi _h p(x_{1},y_{1/2})+\Pi _h p(x_{1/2},y_{1})-p_{1,1}\\= & {} p_{1,1/2}+p_{1/2,1}-p_{1,1}+Ch^2. \end{aligned}$$

We can easily obtain that $|(\Pi _h p-p)(x_{1/2},y_{1/2})|\le Ch^2$ by Taylor’s theorem. Hence, for points (x, y), assuming $x\in [x_{1/2},x_{1}], y\in [y_{1/2},y_{1}]$, $\Pi _h p(x,y)$ can be evaluated as the bilinear interpolant between $p_{1,1}$, $\Pi _hp_{1/2,1},~\Pi _h p_{1,1/2},$ and $\Pi _h p_{1/2,1/2}.$ We can define $\Pi _hp_{1/2,N_y+1/2}$, $\Pi _hp_{N_x+1/2,1/2}$, $\Pi _hp_{N_x+1/2,N_y+1/2}$ similarly. And in the other three corner regions, the same approximations can be obtained. Thus we can get the following lemma.

Lemma 2

[21] Suppose p is twice differentiable in space, then we have the estimate that

$$\begin{aligned} ||\Pi _hp-p||_{\infty }\le Ch^2. \end{aligned}$$

Lastly, we make the following assumptions which are similar to Kou et al. in [1].

• (H1) $p,~c_f\in W^2_{\infty }(0,T;W^4_{\infty }(\Omega ))$.

• (H2) ${D}_{ll}(\mathbf x )\in W^3_{\infty }(\Omega )$, $\phi \in C^1(0,T;C^2(\Omega ))$.

• (H3) There exist four positive constants $K_{*}$, $K^{*}$, $D_{*}$ and $D^{*}$ such that

  $$\begin{aligned} K_{*}\le K(\mathbf x ,\phi )\le K^{*},~~D_{*}\le D_{ll}(\mathbf x )\le D^{*},~~for ~\mathbf x \in \Omega ,~\phi \in \mathbb {R},~l=1,2. \end{aligned}$$

  (17)

• (H4) $K(\phi )^{-1}$ is uniformly Lipschitz function of $\phi$.

• (H5) $\gamma ,~\alpha ,~\rho _s,~\mu ,~k_c$ and $k_s$ are all given positive constants, and $0< \phi _{0*}\le \phi _0 \le \phi _0^{*}<1,$ $0\le a_{0*}\le a_0 \le a_0^{*}.$

3 A Block-Centered Finite Difference Algorithm

In this section, in order to solve the nonlinear system (1)–(8) efficiently, the block-centered finite difference algorithm is considered.

Using Eqs. (6)–(8), nonlinear system (1)–(4) can be transformed into

where $\displaystyle r_{\phi }=\frac{\alpha a_0k_ck_s}{\rho _s(k_c+k_s)},$ and taking notice of assumption (H5), we obtain $\displaystyle 0\le r_{\phi *}\le r_{\phi }\le r_{\phi }^*.$

To obtain superconvergence, we shall also consider only molecular diffusion [23, 24] in the following. Denoted by $\{\textit{Z}^n,{{\varvec{W}}}^n, \Psi ^n,{{\varvec{Q}}}^n\}_{n=0}^{N}$, the block-centered finite difference approximations to $\{\textit{p}^n,{{\varvec{u}}}^n, \textit{c}_f^n,{{\varvec{q}}}^n\}_{n=0}^{N}$ respectively are as follows, where $\textit{Z}^n,\Psi ^n\in S_h,~{{\varvec{W}}}^n,$ ${{\varvec{Q}}}^n\in \mathbf V _h^0$.

For the calculation of the discrete porosity $\Theta$, we use the following scheme.

$$\begin{aligned}{}[d_t\Theta ]_{i,j}^n=\frac{r_{\phi ,i,j}^n\left( 1-\Theta _{i,j}^n\right) }{1-\phi _{0,i,j}}\overline{\Psi }_{i,j}^{n-1}, \end{aligned}$$

(26)

where $\overline{\Psi }^{n-1}=\max \left\{ 0,\min \{\Psi ^{n-1},1\}\right\} .$

Set the boundary and initial approximations as follows.

$$\begin{aligned} \left\{ \begin{array}{ll} W_{1/2,j}^{x,n}=W_{N_x+1/2,j}^{x,n}=0,&{}\quad 1\le j\le N_y,\\ W_{i,1/2}^{y,n}=W_{i,N_y+1/2}^{y,n}=0,&{}\quad 1\le i\le N_x,\\ Q_{1/2,j}^{x,n}=Q_{N_x+1/2,j}^{x,n}=0,&{}\quad 1\le j\le N_y,\\ Q_{i,1/2}^{y,n}=Q_{i,N_y+1/2}^{y,n}=0,&{}\quad 1\le i\le N_x,\\ Z_{i,j}^0=p_{0,i,j}, 1\le i\le N_x,&{}\quad 1\le j\le N_y,\\ \Psi _{i,j}^0=c_{f0,i,j}, 1\le i\le N_x,&{}\quad 1\le j\le N_y,\\ \Theta _{i,j}^0=\phi _{0,i,j}, 1\le i\le N_x,&{}\quad 1\le j\le N_y.\\ \end{array} \right. \end{aligned}$$

(27)

The difference method will consist of three parts: firstly, if the approximate concentration $\Psi _{i,j}^{n-1}$ and porosity $\Theta _{i,j}^{n-1},~n=1,\dots ,N$ are known, Eq. (26) will be used to obtain a new porosity $\Theta _{i,j}^{n}$; Secondly, by difference scheme (22)–(23), an approximation $Z_{i,j}^{n}$ to the pressure will be calculated using $\Theta _{i,j}^{n}$, and the approximate velocity $W^{x,n}_{i+1/2,j}$ and $W^{y,n}_{i,j+1/2}$ will be evaluated; Finally, a new concentration $\Psi _{i,j}^{n}$ will be calculated using $W^{x,n}_{i+1/2,j}$, $W^{y,n}_{i,j+1/2}$, $d_tZ_{i,j}^{n}$ and $\Theta _{i,j}^{n}$, then we get the approximations $Q^{x,n}_{i+1/2,j}$ and $Q^{y,n}_{i,j+1/2}$. It is easy to see that at each time level, the difference scheme has an explicit solution or is a linear system with strictly diagonally dominant coefficient matrix, thus the approximate solutions exist uniquely.

Remark 1

For the case that $\mathbf D$ is defined by Eq. (5), the block-centered finite difference approximations have a little difference in Eqs. (24) and (25). Here we define $\widetilde{{{\varvec{q}}}}=-\nabla c_f,$ ${{\varvec{q}}}=\phi \mathbf D (\mathbf u )\widetilde{{{\varvec{q}}}},$ then denoted by $\{\Psi ^n,\widetilde{{{\varvec{Q}}}^n},{{\varvec{Q}}}^n\}_{n=0}^{N}$, the block-centered finite difference approximations to $\{\textit{c}_f^n,\widetilde{{{\varvec{q}}}^n},{{\varvec{q}}}^n\}_{n=0}^{N}$ respectively are as follows:

$$\begin{aligned}&\left( \Theta ^nd_t\Psi ^n,w\right) -\left( \gamma \overline{\Psi }^{n-1}d_tZ^n,w\right) -\left( \Pi _h \mathbf W ^n\cdot \Pi _h \widetilde{\mathbf{Q }}^n,w\right) +\left( f_I^n\Psi ^n,w\right) \nonumber \\&\quad +\,(\nabla \cdot {{\varvec{Q}}}^n,w) +\frac{k_ck_s}{k_c+k_s}\left( a_v(\Theta ^n)\Psi ^n,w\right) =\left( f_I^nc_I^n,w\right) ,~~\forall w\in S_h,\end{aligned}$$

(28)

$$\begin{aligned}&\left( \widetilde{{{\varvec{Q}}}}^n,{{\varvec{v}}}\right) _{TM}=\left( \Psi ^n,\nabla \cdot {{\varvec{v}}}\right) ,\quad \forall {{\varvec{v}}}\in \mathbf V _h^0,\end{aligned}$$

(29)

$$\begin{aligned}&\left( {{\varvec{Q}}}^n,{{\varvec{v}}}\right) _{TM}=(\Pi _h \Theta ^n\mathbf D (\Pi _h \mathbf W ^n) \widetilde{\mathbf{Q }}^n,{{\varvec{v}}})_{T},\quad \forall {{\varvec{v}}}\in \mathbf V _h^0, \end{aligned}$$

(30)

where $(\cdot ,\cdot )_T$ is the trapezoidal rule defined by

$$\begin{aligned} (\mathbf f ,\mathbf g )_T= & {} \sum \limits _{i=1}^{N_x-1}\sum \limits _{j=1}^{N_y}h_{i+1/2}^xh_{j}^y\cdot \frac{1}{2}\left( f^x_{i+1/2,j-1/2}g^x_{i+1/2,j-1/2}+f^x_{i+1/2,j+1/2}g^x_{i+1/2,j+1/2}\right) \\&+\,\sum \limits _{i=1}^{N_x}\sum \limits _{j=1}^{N_y-1}h_{i}^xh_{j+1/2}^y\cdot \frac{1}{2}\left( f^y_{i-1/2,j+1/2}g^y_{i-1/2,j+1/2}+f^y_{i+1/2,j+1/2}g^y_{i+1/2,j+1/2}\right) . \end{aligned}$$

Here we use the trapezoidal rule to maintain symmetry in the case that $\mathbf D$ is not diagonal, which is similar to that in [10].

4 Stability Analysis for the Discrete Scheme

In this section, we will give the analysis of stability for the scheme (22)–(26).

For the purpose of theoretical analysis, we first analysis a priori bounds for the discrete solution $\Theta$.

Theorem 3

Assuming that $0<\phi _{0*}\le \phi _0\le \phi _{0}^*<1$, then the discrete porosity $\Theta _{i,j}^n$ is bounded, i.e.,

$$\begin{aligned} \phi _{0*}\le \Theta _{i,j}^n<1,~~1\le i\le N_x,~1\le j\le N_y,~n\le N. \end{aligned}$$

Proof

The proof is given by induction. It is trivial that $\phi _{0*}\le \Theta _{i,j}^0<1$. Suppose that

$$\begin{aligned} \phi _{0*}\le \Theta _{i,j}^{k-1}<1,~k\le N, \end{aligned}$$

next we prove that $\Theta _{i,j}^{k}$ also does.

For simplicity, set $\displaystyle \beta ^{k-1}=\frac{r_{\phi }\overline{\Psi }^{k-1}}{1-\phi _0}\Delta t,$ where $\overline{\Psi }^{n-1}=\max \left\{ 0,\min \{\Psi ^{n-1},1\}\right\} .$ Then Eq. (26) can be transformed into the following.

$$\begin{aligned} \Theta _{i,j}^k=\frac{\beta _{i,j}^{k-1}}{1+\beta _{i,j}^{k-1}}+\frac{\Theta _{i,j}^{k-1}}{1+\beta _{i,j}^{k-1}}. \end{aligned}$$

(31)

By Eq. (31), we can easily obtain that $\Theta _{i,j}^k<1$. Equation (26) can also be calculated as

$$\begin{aligned} \Theta _{i,j}^k-\Theta _{i,j}^{k-1}=\beta _{i,j}^{k-1}(1-\Theta _{i,j}^k), \end{aligned}$$

(32)

thus we have that $\Theta _{i,j}^k>\Theta _{i,j}^{k-1}.$ Then the proof ends.$\square$

Theorem 4

The approximate solutions of (22)–(25) satisfy

$$\begin{aligned}&\Vert Z^m\Vert _M^2+\Vert \frac{\mu }{K(\Pi _h \Theta ^{m})}{{\varvec{W}}}^{m}\Vert _{TM}^2 \nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f^n\Vert ^2_M+C\Vert p_0\Vert _M^2+C\Vert {{\varvec{u}}}_0\Vert _{TM}^2+C{r_{\phi }^*}^2,~~m\le N, \end{aligned}$$

(33)

$$\begin{aligned}&\Vert \Psi ^m\Vert _M^2 +\Vert {{\varvec{Q}}}^m\Vert _{TM}^2+\sum \limits _{n=1}^{m}\Delta t\Vert {{\varvec{Q}}}^n\Vert _{TM}^2 \nonumber \\&\quad \le C\left( \Vert {{\varvec{q}}}_0\Vert _{TM}^2{+}\Vert {{\varvec{u}}}_0\Vert _{TM}^2{+}\Vert c_{f0}\Vert _M^2+{r_{\phi }^*}^2\right) {+}C\sum \limits _{n=1}^{m}\Delta t\left( \Vert f_I^nc_I^n\Vert _M^2+\Vert f^n\Vert ^2_M\right) ,~~m\le N . \end{aligned}$$

(34)

Proof

Taking notice of Eq. (23), we have

$$\begin{aligned} \left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}\right) ,{{\varvec{v}}}\right) _{TM}=\left( d_t\textit{Z}^{n},\nabla \cdot {{\varvec{v}}}\right) ,\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(35)

Setting $w=d_tZ^n$ and ${{\varvec{v}}}={{\varvec{W}}}^{n}$ in Eqs. (22) and (35) respectively, we have

$$\begin{aligned} \gamma \Vert d_tZ^n\Vert _M^2+\left( \nabla \cdot {{\varvec{W}}}^{n},d_tZ^n\right) =\left( f^n,d_tZ^n\right) -\left( d_t\Theta ^n,d_tZ^n\right) , \end{aligned}$$

(36)

and

$$\begin{aligned} \left( d_t\left( \frac{\mu }{K\left( \Pi _h \Theta ^{n}\right) }{{\varvec{W}}}^{n}\right) ,{{\varvec{W}}}^{n}\right) _{TM}=(d_t\textit{Z}^{n},\nabla \cdot {{\varvec{W}}}^{n}). \end{aligned}$$

(37)

Then using Cauchy–Schwarz inequality, we have

$$\begin{aligned}&\gamma \Vert d_tZ^n\Vert _M^2+\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}\right) ,{{\varvec{W}}}^{n}\right) _{TM}\nonumber \\&\quad \le C\Vert f^n\Vert ^2_M+C\Vert d_t\Theta ^n\Vert _M^2+\frac{\gamma }{2}\Vert d_tZ^n\Vert _M^2. \end{aligned}$$

(38)

The second term in the left hand side of Eq. (38) can be estimated by

$$\begin{aligned}&\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}\right) ,{{\varvec{W}}}^{n}\right) _{TM}\nonumber \\&\quad =\frac{1}{2}d_t\Vert \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}\Vert _{TM}^2 +\frac{\Delta t}{2}\frac{\mu }{K(\Pi _h \Theta ^{n-1})}\Vert d_t{{\varvec{W}}}^{n}\Vert _{TM}^2\nonumber \\&\qquad +\,\frac{1}{2}\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}\right) {{\varvec{W}}}^{n},{{\varvec{W}}}^{n}\right) _{TM}. \end{aligned}$$

(39)

Noting Theorem 3, we can easily obtain

$$\begin{aligned} |d_t\Theta ^n_{i,j}|\le \frac{1-\phi _{0*}}{1-\phi _{0}^*}r_{\phi }^*\le Cr_{\phi }^*. \end{aligned}$$

(40)

Combining Eq. (38) with Eqs. (39) and (40), we have

$$\begin{aligned}&\frac{\gamma }{2}\Vert d_tZ^n\Vert _M^2+\frac{1}{2}d_t\Vert \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}\Vert _{TM}^2\nonumber \\&\quad \le C\Vert f^n\Vert ^2_M+C\Vert {{\varvec{W}}}^{n}\Vert _{TM}^2+C{r_{\phi }^*}^2. \end{aligned}$$

(41)

Multiplying Eq. (41) by $2\Delta t$, summing for n from 1 to m, $m\le N$ and applying Gronwall’s inequality, we have

$$\begin{aligned}&\gamma \sum \limits _{n=1}^{m}\Delta t\Vert d_tZ^n\Vert _M^2+\Vert \frac{\mu }{K(\Pi _h \Theta ^{m})}{{\varvec{W}}}^{m}\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f^n\Vert ^2_M+C\Vert {{\varvec{u}}}_0\Vert _{TM}^2+C{r_{\phi }^*}^2. \end{aligned}$$

(42)

Taking notice of that

$$\begin{aligned}Z_{i,j}^n=Z_{i,j}^0+\Delta t\sum \limits _{k=1}^{n}d_tZ_{i,j}^k,~1\le i\le N_x,~1\le j\le N_y,~1\le n\le N, \end{aligned}$$

and using Cauchy–Schwarz inequality, we obtain that

$$\begin{aligned} \left( Z_{i,j}^n\right) ^2\le & {} 2\left( Z_{i,j}^0\right) ^2+2\left( \Delta t\sum \limits _{k=1}^{n}d_tZ_{i,j}^k\right) ^2\nonumber \\\le & {} 2\left( Z_{i,j}^0\right) ^2+2T\Delta t\sum \limits _{k=1}^{n}\left( d_tZ_{i,j}^k\right) ^2,~1\le i\le N_x,~1\le j\le N_y,~1\le n\le N.\nonumber \\ \end{aligned}$$

(43)

Then multiplying both sides of Eq. (43) by $h_ik_j$, and making summation on i, j for $1\le i\le N_x,~1\le j\le N_y$, we have that

$$\begin{aligned} \Vert Z^n\Vert _m^2\le 2\Vert Z^0\Vert _m^2+2T\Delta t\sum \limits _{k=1}^{n}\Vert d_tZ^k\Vert _m^2. \end{aligned}$$

(44)

Thus we have

$$\begin{aligned}&\Vert Z^m\Vert _M^2+\left\| \frac{\mu }{K(\Pi _h \Theta ^{m})}{{\varvec{W}}}^{m}\right\| _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f^n\Vert ^2_M+C\Vert p_0\Vert _M^2+C\Vert {{\varvec{u}}}_0\Vert _{TM}^2+C{r_{\phi }^*}^2. \end{aligned}$$

(45)

We now turn to prove Eq. (34). From Eq. (25), we have

$$\begin{aligned} (d_t((\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n),{{\varvec{v}}})_{TM}=(d_t\Psi ^n,\nabla \cdot {{\varvec{v}}}),\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(46)

Setting $w=d_t\Psi ^n$ and ${{\varvec{v}}}=\mathbf Q ^n$ in Eqs. (24) and (46) leads to

$$\begin{aligned}&(\Theta ^nd_t\Psi ^n,d_t\Psi ^n) +(\nabla \cdot {{\varvec{Q}}}^n,d_t\Psi ^n)\nonumber \\&\quad =(f_I^nc_I^n,d_t\Psi ^n)+(\gamma \overline{\Psi }^{n-1}d_tZ^n,d_t\Psi ^n)+\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n,d_t\Psi ^n\right) \nonumber \\&\qquad -\,(f_I^n\Psi ^n,d_t\Psi ^n)-\frac{k_ck_s}{k_c+k_s}(a_v(\Theta ^n)\Psi ^n,d_t\Psi ^n), \end{aligned}$$

(47)

and

$$\begin{aligned} (d_t((\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n),\mathbf Q ^n)_{TM}=(d_t\Psi ^n,\nabla \cdot \mathbf Q ^n). \end{aligned}$$

(48)

Combining Eq. (47) with Eq. (48) and using Cauchy–Schwarz inequality, we have

$$\begin{aligned}&\phi _{0*}\Vert d_t\Psi ^n\Vert _M^2 +(d_t((\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n),\mathbf Q ^n)_{TM}\nonumber \\&\quad \le C\Vert f_I^nc_I^n\Vert _M^2+C\Vert d_tZ^n\Vert _M^2+C\Vert \Psi ^n\Vert _M^2+\frac{\phi _{0*}}{4}\Vert d_t\Psi ^n\Vert _M^2\nonumber \\&\qquad +\,\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n,d_t\Psi ^n\right) . \end{aligned}$$

(49)

The second term in the left hand side of Eq. (49) can be estimated by

$$\begin{aligned}&\left( d_t((\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n),{{\varvec{Q}}}^n\right) _{TM}\nonumber \\&\quad =\frac{1}{2}d_t\Vert (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n\Vert _{TM}^2+ \frac{\Delta t}{2}(\Pi _h \Theta ^{n-1}{} \mathbf D )^{-1}\Vert d_t{{\varvec{Q}}}^n\Vert _{TM}^2\nonumber \\&\qquad +\,\frac{1}{2}\left( d_t((\Pi _h \Theta ^n\mathbf D )^{-1}){{\varvec{Q}}}^n,{{\varvec{Q}}}^n\right) _{TM}. \end{aligned}$$

(50)

To estimate the last term in the right hand side of Eq. (49), we give the following hypothesis first. Suppose that there exists a positive constant $C^*$ such that

$$\begin{aligned} \Vert \Pi _h\mathbf W ^{n}\Vert _{\infty }\le C^*. \end{aligned}$$

(51)

Then we have

$$\begin{aligned}&\frac{\phi _{0*}}{2}\Vert d_t\Psi ^n\Vert _M^2 +\frac{1}{2}d_t\Vert (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n\Vert _{TM}^2\nonumber \\&\quad \le C\Vert f_I^nc_I^n\Vert _M^2+C\Vert d_tZ^n\Vert _M^2+C\Vert \Psi ^n\Vert _M^2+C\Vert \mathbf Q ^n\Vert _{TM}^2. \end{aligned}$$

(52)

Multiplying Eq. (52) by $2\Delta t$, and summing for n from 1 to m, $m\le N$, we have

$$\begin{aligned}&\phi _{0*}\sum \limits _{n=1}^{m}\Delta t\Vert d_t\Psi ^n\Vert _M^2 +\Vert (\Pi _h \Theta ^m\mathbf D )^{-1}{{\varvec{Q}}}^m\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f_I^nc_I^n\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert d_tZ^n\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert \Psi ^n\Vert _M^2\nonumber \\&\qquad +\,C\sum \limits _{n=1}^{m}\Delta t\Vert \mathbf Q ^n\Vert _{TM}^2+C\Vert (\Pi _h \Theta ^0\mathbf D )^{-1}{{\varvec{q}}}_0\Vert _{TM}^2 \end{aligned}$$

(53)

Next we give the estimates for $\Vert \Psi ^n\Vert _M^2$. Setting $w=\Psi ^n$ and ${{\varvec{v}}}={{\varvec{Q}}}^n$ in Eqs. (24) and (25) respectively, we have

$$\begin{aligned}&\left( \Theta ^nd_t\Psi ^n,\Psi ^n\right) +\left( \nabla \cdot {{\varvec{Q}}}^n,\Psi ^n\right) \nonumber \\&\quad =\left( f_I^nc_I^n,\Psi ^n\right) +\left( \gamma \overline{\Psi }^{n-1}d_tZ^n,\Psi ^n\right) +\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n,\Psi ^n\right) \nonumber \\&\qquad -\,\left( f_I^n\Psi ^n,\Psi ^n\right) -\frac{k_ck_s}{k_c+k_s}\left( a_v(\Theta ^n)\Psi ^n,\Psi ^n\right) , \end{aligned}$$

(54)

and

$$\begin{aligned} ((\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n,{{\varvec{Q}}}^n)_{TM}=(\Psi ^n,\nabla \cdot {{\varvec{Q}}}^n). \end{aligned}$$

(55)

By the similar estimates with the above equations, we can easily obtain

$$\begin{aligned}&\Vert \Psi ^m\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert {{\varvec{Q}}}^n\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f_I^nc_I^n\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert d_tZ^n\Vert _M^2\nonumber \\&\qquad +\,C\sum \limits _{n=1}^{m}\Delta t\Vert \Psi ^n\Vert _M^2+C\Vert c_{f0}\Vert _M^2. \end{aligned}$$

(56)

Combining Eq. (53) with Eq. (56) and using Gronwall’s inequality lead to

$$\begin{aligned}&\sum \limits _{n=1}^{m}\Delta t\Vert d_t\Psi ^n\Vert _M^2+\Vert \Psi ^m\Vert _M^2 +\Vert {{\varvec{Q}}}^m\Vert _{TM}^2+\sum \limits _{n=1}^{m}\Delta t\Vert {{\varvec{Q}}}^n\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f_I^nc_I^n\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert d_tZ^n\Vert _M^2\nonumber \\&\qquad +\,C\Vert {{\varvec{q}}}_0\Vert _{TM}^2+C\Vert c_{f0}\Vert _M^2. \end{aligned}$$

(57)

Taking notice of Eq. (42), we have

$$\begin{aligned}&\sum \limits _{n=1}^{m}\Delta t\Vert d_t\Psi ^n\Vert _M^2+\Vert \Psi ^m\Vert _M^2 +\Vert {{\varvec{Q}}}^m\Vert _{TM}^2+\sum \limits _{n=1}^{m}\Delta t\Vert {{\varvec{Q}}}^n\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\Vert f_I^nc_I^n\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert f^n\Vert ^2_M\nonumber \\&\qquad +\,C\left( \Vert {{\varvec{q}}}_0\Vert _{TM}^2+\Vert {{\varvec{u}}}_0\Vert _{TM}^2+\Vert c_{f0}\Vert _M^2+{r_{\phi }^*}^2\right) . \end{aligned}$$

(58)

Then the proof ends. $\square$

5 Error Analysis for the Discrete Scheme

In this section, to give the error estimates, we consider the following elliptic projections first.

Let $\underline{Z}^n \in S_h$, ${{{\underline{\varvec{{W}}}}}}^n \in \mathbf V _h^0$ be defined by

$$\begin{aligned}&(\nabla \cdot {{{\underline{\varvec{{W}}}}}}^n,w)=(\nabla \cdot \mathbf u ^n,w),\quad \forall w\in S_h,\end{aligned}$$

(59)

$$\begin{aligned}&\left( \frac{\mu }{K(\phi ^n)}{{{\underline{\varvec{{W}}}}}}^n,{{\varvec{v}}}\right) _{TM}=(\underline{Z}^n,\nabla \cdot {{\varvec{v}}}),\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(60)

And $\underline{\Psi }^n \in S_h$, ${{{\underline{\varvec{{Q}}}}}}^n \in \mathbf V _h^0$ be defined by

$$\begin{aligned}&(\nabla \cdot {{{\underline{\varvec{{Q}}}}}}^n,w)=(\nabla \cdot \mathbf q ^n,w),\quad \forall w\in S_h,\end{aligned}$$

(61)

$$\begin{aligned}&((\phi ^n\mathbf D ^n)^{-1}{{{\underline{\varvec{{Q}}}}}}^n,{{\varvec{v}}})_{TM}=(\underline{\Psi }^n,\nabla \cdot {{\varvec{v}}}),\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(62)

Set

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle E_\mathbf{u }^A=\mathbf W -{{{\underline{\varvec{W}}}}},~~E_\mathbf{u }^B={{{\underline{\varvec{W}}}}}-\mathbf u ,\\ \displaystyle E_p^A=Z-\underline{Z},\quad E_p^B=\underline{Z}-p,\\ \displaystyle E_\mathbf{q }^A=\mathbf Q -{{{\underline{\varvec{Q}}}}},\quad E_\mathbf{q }^B={{{\underline{\varvec{Q}}}}}-\mathbf q ,\\ \displaystyle E_{c_f}^A=\Psi -\underline{\Psi },\quad E_{c_f}^B=\underline{\Psi }-c_f,\\ \displaystyle E_{\phi }=\Theta -\phi . \end{array} \right. \end{aligned}$$

(63)

Assume (H1)–(H5) hold, it’s shown by Dawson et al. in [21] that preliminary functions defined by Eqs. (59)–(62) exist and are unique. Besides, the error estimates are illustrated in Lemma 5.

Lemma 5

Assume (H1)–(H5) hold, then there exists a positive constant C independent of h and $\Delta t$ such that

$$\begin{aligned} \Vert d_tE_p^{B,m}\Vert _M+\Vert E_p^{B,m}\Vert _M+\Vert E_\mathbf{u }^{B,m}\Vert _{TM}\le C\left( \Delta t+h^2\right) ,\quad m\le N. \end{aligned}$$

(64)

$$\begin{aligned} \Vert d_tE_{c_f}^{B,m}\Vert _M+\Vert E_{c_f}^{B,m}\Vert _M+\Vert E_\mathbf{q }^{B,m}\Vert _{TM}\le C\left( \Delta t+h^2\right) ,\quad m\le N. \end{aligned}$$

(65)

Lemma 6

The approximate errors of discrete porosity satisfy

$$\begin{aligned} \Vert E_{\phi }^m\Vert ^2_M\le C \sum \limits _{n=1}^m\Delta t\left( \Vert E_{\phi }^n\Vert ^2_M+\Vert E_{c_f}^{A,n-1}\Vert _M^2\right) +C\left( \Delta t^2+h^4\right) , \end{aligned}$$

(66)

$$\begin{aligned} \sum \limits _{n=1}^m\Delta t\Vert d_tE_{\phi }^n\Vert _M^2\le C\sum \limits _{n=1}^m\Delta t\left( \Vert E_{\phi }^n\Vert ^2_M+\Vert E_{c_f}^{A,n-1}\Vert _M^2\right) +C\left( \Delta t^2+h^4\right) ,\quad m\le N, \end{aligned}$$

(67)

where the positive constant C is independent of h and $\triangle t$.

Proof

Subtracting Eq. (21) from Eq. (26), we can obtain

$$\begin{aligned} d_tE_{\phi ,i,j}^n= & {} \frac{r_{\phi ,i,j}^n\left( 1-\Theta _{i,j}^n\right) }{1-\phi _{0,i,j}}\overline{\Psi }_{i,j}^{n-1} -\frac{r_{\phi ,i,j}^n\left( 1-\phi _{i,j}^n\right) }{1-\phi _{0,i,j}}c_{f,i,j}^{n}+\frac{\partial \phi _{i,j}^n}{\partial t}- d_t\phi _{i,j}^n\nonumber \\= & {} \frac{r_{\phi ,i,j}^n\left( 1-\Theta _{i,j}^n\right) }{1-\phi _{0,i,j}}\left( \overline{\Psi }_{i,j}^{n-1}-c_{f,i,j}^{n-1}\right) + \frac{r_{\phi ,i,j}^n\left( 1-\Theta _{i,j}^n\right) }{1-\phi _{0,i,j}}\left( c_{f,i,j}^{n-1}-c_{f,i,j}^{n}\right) \nonumber \\&\quad -\,\frac{r_{\phi ,i,j}^nc_{f,i,j}^{n}}{1-\phi _{0,i,j}}E_{\phi ,i,j}^n+R_1^n, \end{aligned}$$

(68)

where $\displaystyle R_1^n=\frac{\partial \phi _{i,j}^n}{\partial t}- d_t\phi _{i,j}^n.$

Multiplying Eq. (68) by $E_{\phi ,i,j}^nh_i^xh^y_j$ and making summation on i, j for $1\le i\le N_x,~1\le j\le N_y$, we have that

$$\begin{aligned}&(d_tE_{\phi }^n,E_{\phi }^n)_M\nonumber \\&\quad =\left( \frac{r_{\phi }^n(1-\Theta ^n)}{1-\phi _{0}}\left( \overline{\Psi }^{n-1}-c_{f}^{n-1}\right) ,E_{\phi }^n\right) _M +\left( \frac{r_{\phi }^n(1-\Theta ^n)}{1-\phi _{0}}\left( c_{f}^{n-1}-c_{f}^{n}\right) ,E_{\phi }^n\right) _M\nonumber \\&\qquad -\,\left( \frac{r_{\phi }^nc_{f}^{n}}{1-\phi _{0}}E_{\phi }^n,E_{\phi }^n\right) _M+\left( R_1^n,E_{\phi }^n\right) _M. \end{aligned}$$

(69)

The term in the left side of Eq. (69) can be transformed into

$$\begin{aligned} (d_tE_{\phi }^n,E_{\phi }^n)_M=\frac{\Vert E_{\phi }^n\Vert _M^2-\Vert E_{\phi }^{n-1}\Vert _M^2}{2\Delta t}+ \frac{\Delta t}{2}\Vert d_tE_{\phi }^n\Vert _M^2. \end{aligned}$$

(70)

Taking notice of Lemma 5, the first term in the right side of Eq. (69) can be estimated by

$$\begin{aligned}&\left( \frac{r_{\phi }^n(1-\Theta ^n)}{1-\phi _{0}}\left( \overline{\Psi }^{n-1}-c_{f}^{n-1}\right) ,E_{\phi }^n\right) _M \le \frac{r_{\phi }^*}{2}\left( \Vert E_{c_f}^{A,n-1}+E_{c_f}^{B,n-1}\Vert _M^2+\Vert E_{\phi }^n\Vert ^2_M\right) \nonumber \\&\quad \le \frac{r_{\phi }^*}{2}\left( \Vert E_{c_f}^{A,n-1}\Vert _M^2+\Vert E_{\phi }^n\Vert ^2_M\right) +C\left( \Delta t^2+h^4\right) , \end{aligned}$$

(71)

where we used the fact that $|\overline{\Psi }^{n-1}-c_{f}^{n-1}|\le |{\Psi }^{n-1}-c_{f}^{n-1}|.$

Noting the smoothness assumption (H1), the second term in the right side of Eq. (69) can be bounded by

$$\begin{aligned} \left( \frac{r_{\phi }^n(1-\Theta ^n)}{1-\phi _{0}}\left( c_{f}^{n-1}-c_{f}^{n}\right) ,E_{\phi }^n\right) _M \le \frac{r_{\phi }^*}{2}\Vert E_{\phi }^n\Vert ^2_M+C\Delta t^2. \end{aligned}$$

(72)

Combing Eq. (69) with Eqs. (70)–(72), multiplying by $2\Delta t$, and summing for n from 1 to m, $m\le N$, we have

$$\begin{aligned} \Vert E_{\phi }^m\Vert ^2_M\le \Vert E_{\phi }^0\Vert ^2_M+C\Delta t\sum \limits _{n=1}^m\Vert E_{c_f}^{A,n-1}\Vert _M^2+C\Delta t\sum \limits _{n=1}^m\Vert E_{\phi }^n\Vert ^2_M+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(73)

Recalling the initial condition on $T^0$ gives Eq. (66).

On the other hand, multiplying Eq. (68) by $d_tE_{\phi ,i,j}^nh_i^xh^y_j$ and making summation on i, j for $1\le i\le N_x,~1\le j\le N_y$, we have that

$$\begin{aligned} \Vert d_tE_{\phi }^n\Vert _M^2= & {} \left( \frac{r_{\phi }^n(1-\Theta ^n)}{1-\phi _{0}}\left( \overline{\Psi }^{n-1}-c_{f}^{n-1}\right) , d_tE_{\phi }^n\right) _M\nonumber \\&\quad +\,\left( \frac{r_{\phi }^n(1-\Theta ^n)}{1-\phi _{0}}\left( c_{f}^{n-1}-c_{f}^{n}\right) ,d_tE_{\phi }^n\right) _M\nonumber \\&\quad -\,\left( \frac{r_{\phi }^nc_{f}^{n}}{1-\phi _{0}}E_{\phi }^n,d_tE_{\phi }^n\right) _M+\left( R_1^n,d_tE_{\phi }^n\right) _M. \end{aligned}$$

(74)

Similarly we can obtain that

$$\begin{aligned} \sum \limits _{n=1}^m\Delta t\Vert d_tE_{\phi }^n\Vert _M^2\le & {} C\sum \limits _{n=1}^m\Delta t\Vert E_{\phi }^n\Vert ^2_M+C \sum \limits _{n=1}^m\Delta t\Vert E_{c_f}^{A,n-1}\Vert _M^2+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

Then the proof ends. $\square$

Lemma 7

The approximate errors of discrete pressure and velocity satisfy

$$\begin{aligned}&\gamma \sum \limits _{n=1}^{m}\Delta t\Vert d_tE_p^{A,n}\Vert _M^2+\Vert \frac{\mu }{K(\Pi _h\Theta ^m)} E_{\mathbf{u }}^{A,m}\Vert _{TM}^2\\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{\phi }^n\Vert _M^2+\Vert d_tE_{\phi }^n\Vert _M^2\right) + C\sum \limits _{n=1}^{m}\Delta t\Vert E_{\mathbf{u }}^{A,n}\Vert _{TM}^2\\&\quad +\,C\left( \Delta t^2+h^4\right) , ~~m\le N, \end{aligned}$$

where the positive constant C is independent of h and $\triangle t$.

Proof

Subtracting Eq. (59) from Eq. (22), we have that

$$\begin{aligned} \left( \gamma d_tZ^n+d_t\Theta ^n,w\right) +\left( \nabla \cdot E_\mathbf{u }^{A,n},w\right) = \left( \gamma \frac{\partial p^n}{\partial t}+\frac{\partial \phi ^n}{\partial t},w\right) . \end{aligned}$$

(75)

We can get the following equation by subtracting Eq. (60) from Eq. (23).

$$\begin{aligned} \left( \frac{\mu }{K\left( \Pi _h \Theta ^{n}\right) }{{\varvec{W}}}^{n},{{\varvec{v}}}\right) _{TM}- \left( \frac{\mu }{K(\phi ^n)}{{{\underline{\varvec{{W}}}}}}^n,{{\varvec{v}}}\right) _{TM} =\left( E_p^{A,n},\nabla \cdot \mathbf v \right) ,\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(76)

By Eq. (76), we have that

$$\begin{aligned} \left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}- \frac{\mu }{K(\phi ^n)}{{{\underline{\varvec{{W}}}}}}^n\right) ,{{\varvec{v}}}\right) _{TM}=\left( d_tE_p^{A,n},\nabla \cdot {{\varvec{v}}}\right) ,\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(77)

Setting $w=d_tE_p^{A,n}$ and ${{\varvec{v}}}=E_{\mathbf{u }}^{A,n}$ in Eqs. (75) and (77) respectively, we have

$$\begin{aligned}&\gamma \Vert d_tE_p^{A,n}\Vert _M^2+\left( \nabla \cdot E_\mathbf{u }^{A,n},d_tE_p^{A,n}\right) =\gamma \left( \frac{\partial p^n}{\partial t}-d_tp^n,d_tE_p^{A,n}\right) -\gamma \left( d_tE_p^{B,n},d_tE_p^{A,n}\right) \nonumber \\&\quad -\,\left( d_tE_{\phi }^n,d_tE_p^{A,n}\right) +\left( \frac{\partial \phi ^n}{\partial t}-d_t\phi ^n,d_tE_p^{A,n}\right) , \end{aligned}$$

(78)

and

$$\begin{aligned} \left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}- \frac{\mu }{K(\phi ^n)}{{{\underline{\varvec{{W}}}}}}^n\right) ,E_{\mathbf{u }}^{A,n}\right) _{TM}=\left( d_tE_p^{A,n},\nabla \cdot E_{\mathbf{u }}^{A,n}\right) . \end{aligned}$$

(79)

By Cauchy–Schwarz inequality, the first term in the right hand side of Eq. (78) can be estimated by

$$\begin{aligned} \gamma \left( \frac{\partial p^n}{\partial t}-d_tp^n,d_tE_p^{A,n}\right) \le C\Vert p\Vert ^2_{W^{\infty }_2\left( t^{n-1},t^n;L^{\infty }(\Omega )\right) }\Delta t^2+\frac{\gamma }{8}\Vert d_tE_p^{A,n}\Vert _M^2. \end{aligned}$$

(80)

The second term in the right hand side of Eq. (78) can be estimated by

$$\begin{aligned} \gamma \left( d_tE_p^{B,n},d_tE_p^{A,n}\right) \le C\Vert d_tE_p^{B,n}\Vert _M^2+\frac{\gamma }{8}\Vert d_tE_p^{A,n}\Vert _M^2. \end{aligned}$$

(81)

Easily we have

$$\begin{aligned} \left( d_tE_{\phi }^{n},d_tE_p^{A,n}\right) \le C\Vert d_tE_{\phi }^{n}\Vert _M^2+\frac{\gamma }{8}\Vert d_tE_p^{A,n}\Vert _M^2, \end{aligned}$$

(82)

and

$$\begin{aligned} \left( \frac{\partial \phi ^n}{\partial t}-d_t\phi ^n,d_tE_p^{A,n}\right) \le C\Vert \phi \Vert ^2_{W^{\infty }_2(t^{n-1},t^n;L^{\infty }(\Omega ))}\Delta t^2+\frac{\gamma }{8}\Vert d_tE_p^{A,n}\Vert _M^2. \end{aligned}$$

(83)

The term in the left hand side of Eq. (79) can be transformed into

$$\begin{aligned}&\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}{{\varvec{W}}}^{n}- \frac{\mu }{K(\phi ^n)}{{{\underline{\varvec{{W}}}}}}^n\right) ,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\quad =\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}E_{\mathbf{u }}^{A,n}\right) ,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\qquad +\,\left( d_t\left( \left( \frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\phi ^n)}\right) {{{\underline{\varvec{{W}}}}}}^n\right) ,E_{\mathbf{u }}^{A,n}\right) _{TM}. \end{aligned}$$

(84)

The first term in the right hand side of Eq. (84) can be estimated by

$$\begin{aligned}&\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}E_{\mathbf{u }}^{A,n}\right) ,E_{\mathbf{u }}^{A,n}\right) _{TM}= \frac{1}{2}d_t\Vert \frac{\mu }{K(\Pi _h \Theta ^{n})}E_{\mathbf{u }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad +\, \frac{\Delta t}{2}\frac{\mu }{K(\Pi _h \Theta ^{n-1})}\Vert d_tE_{\mathbf{u }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad +\,\frac{1}{2}\left( d_t(\frac{\mu }{K(\Pi _h \Theta ^{n})})E_{\mathbf{u }}^{A,n},E_{\mathbf{u }}^{A,n}\right) _{TM}. \end{aligned}$$

(85)

The second term in the right hand side of Eq. (84) can be bounded by

$$\begin{aligned}&\left( d_t\left( (\frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\phi ^n)}){{{\underline{\varvec{{W}}}}}}^n\right) ,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\quad =\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\phi ^n)}\right) {{{\underline{\varvec{{W}}}}}}^n,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\qquad +\,\left( (\frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\phi ^n)})d_t{{{\underline{\varvec{{W}}}}}}^n,E_{\mathbf{u }}^{A,n}\right) _{TM} \end{aligned}$$

(86)

Then, we prove the boundedness of $\Vert {{{\underline{\varvec{{W}}}}}}^n\Vert _{\infty }$, which is necessary in the following estimates. By the triangle inequality,

$$\begin{aligned} \Vert {{{\underline{\varvec{{W}}}}}}^n\Vert _{\infty }\le \Vert {{{\underline{\varvec{{W}}}}}}^n-\hat{{{\varvec{u}}}}^n\Vert _{\infty } +\Vert \hat{{{\varvec{u}}}}^n-{{\varvec{u}}}^n\Vert _{\infty }+ \Vert {{\varvec{u}}}^n\Vert _{\infty }.\\ \end{aligned}$$

Taking notice of the inverse assumption and the triangle inequality, we have

$$\begin{aligned} \Vert {{{\underline{\varvec{{W}}}}}^n}-\hat{{{\varvec{u}}}}^n\Vert _{\infty }\le & {} Ch^{-1}\Vert {{{\underline{\varvec{{W}}}}}^n}-\hat{{{\varvec{u}}}}^n\Vert _{TM}\\\le & {} Ch^{-1}\left( \Vert {{{\underline{\varvec{{W}}}}}^n} -{{\varvec{u}}}^n\Vert _{TM}+\Vert {{\varvec{u}}}^n -\hat{{{\varvec{u}}}}^n\Vert _{TM}\right) . \end{aligned}$$

Then using Eqs. (14), (15) and Lemma 5, we obtain

$$\begin{aligned} \Vert {{{\underline{\varvec{{W}}}}}^n}\Vert _{\infty }\le & {} Ch^{-1}\left( \Vert {{{\underline{\varvec{{W}}}}}^n} -{{\varvec{u}}}^n\Vert _{TM}+\Vert {{\varvec{u}}}^n -\hat{{{\varvec{u}}}}^n\Vert _{TM}\right) +\Vert \hat{{{\varvec{u}}}}^n-{{\varvec{u}}}^n\Vert _{\infty }+ \Vert {{\varvec{u}}}^n\Vert _{\infty }\nonumber \\\le & {} Ch^{-1}(h^2+\Delta t)+\Vert {{\varvec{u}}}^n\Vert _{\infty } \le C_1, \end{aligned}$$

(87)

where $h,~\triangle t$ are selected such that $h^{-1}\triangle t$ is sufficiently small and similar to the derivation of Eq. (87), we can obtain that

$$\begin{aligned} \Vert d_t{{{\underline{\varvec{{W}}}}}^n}\Vert _{\infty }\le C_2. \end{aligned}$$

(88)

Noting the definition of $\Pi _h$, the first term in the right hand side of Eq. (86) can be bounded by

$$\begin{aligned}&\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\phi ^n)}\right) {{{\underline{\varvec{{W}}}}}}^n,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\quad =\left( d_t\left( \frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\Pi _h\phi ^n)}\right) {{{\underline{\varvec{{W}}}}}}^n, E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\qquad +\,\left( d_t\left( \frac{\mu }{K(\Pi _h \phi ^{n})}-\frac{\mu }{K(\phi ^n)}\right) {{{\underline{\varvec{{W}}}}}}^n,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\quad \le C\left\| \frac{\partial ^3(\mu K^{-1})}{\partial \phi \partial t^2}\right\| _{L^{\infty }(t^{n-1},t^n;L^{\infty }(\mathbb {R}))}\left( \Vert E_{\phi }^n\Vert _M^2+\Vert \Pi _h\phi ^n-\phi ^n\Vert _M^2\right) +C\Vert E_{\mathbf{u }}^{A,n}\Vert _{TM}^2\nonumber \\&\qquad +\,C\left\| \frac{\partial (\mu K^{-1})}{\partial \phi }\right\| _{L^{\infty }(\mathbb {R})}\left( \Vert d_tE_{\phi }^n\Vert _M^2+\Vert d_t(\Pi _h\phi ^n-\phi ^n)\Vert _M^2\right) . \end{aligned}$$

(89)

By the boundedness of $\Vert d_t{{{\underline{\varvec{{W}}}}}}^n\Vert _{\infty }$, the second term in the right hand side of Eq. (86) can be bounded by

$$\begin{aligned}&\left( \left( \frac{\mu }{K(\Pi _h \Theta ^{n})}-\frac{\mu }{K(\phi ^n)}\right) d_t{{{\underline{\varvec{{W}}}}}}^n,E_{\mathbf{u }}^{A,n}\right) _{TM}\nonumber \\&\quad \le C\left\| \frac{\partial (\mu K^{-1})}{\partial \phi }\right\| _{L^{\infty }(\mathbb {R})}\left( \Vert E_{\phi }^n\Vert _M^2+\Vert \Pi _h\phi ^n-\phi ^n\Vert _M^2\right) +C\Vert E_{\mathbf{u }}^{A,n}\Vert _{TM}^2. \end{aligned}$$

(90)

Combining the above equations and noting Lemma 5, we obtain

$$\begin{aligned}&\frac{\gamma }{2}\Vert d_tE_p^{A,n}\Vert _M^2+\frac{1}{2}d_t\Vert \frac{\mu }{K(\Pi _h\Theta ^n)} E_{\mathbf{u }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad \le C\left( \Vert E_{\phi }^n\Vert _M^2+\Vert d_tE_{\phi }^n\Vert _M^2\right) + C\Vert E_{\mathbf{u }}^{A,n}\Vert _{TM}^2+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(91)

Multiplying by $2\Delta t$, and summing for n from 1 to m, $m\le N$, we have

$$\begin{aligned}&\gamma \sum \limits _{n=1}^{m}\Delta t\Vert d_tE_p^{A,n}\Vert _M^2+\left\| \frac{\mu }{K(\Pi _h\Theta ^m)} E_{\mathbf{u }}^{A,m}\right\| _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{\phi }^n\Vert _M^2+\Vert d_tE_{\phi }^n\Vert _M^2\right) + C\sum \limits _{n=1}^{m}\Delta t\Vert E_{\mathbf{u }}^{A,n}\Vert _{TM}^2\nonumber \\&\qquad +\,C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(92)

Then the proof ends. $\square$

Lemma 8

The approximate errors of discrete concentration and flux variable satisfy

$$\begin{aligned}&\phi _{0*}\sum \limits _{n=1}^{m}\Delta t\Vert d_tE_{c_f}^{A,n}\Vert _M^2+\Vert E_{c_f}^{A,m}\Vert _M^2+\Vert (\Pi _h \Theta ^m\mathbf D )^{-1}E_{\mathbf{q }}^{A,m}\Vert _{TM}^2 +C\sum \limits _{n=1}^{m}\Delta t\Vert E_{\mathbf{q }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{\phi }^n\Vert _{M}^2+\Vert d_tE_{\phi }^n\Vert _{M}^2\right) +C\sum \limits _{n=1}^{m}\Delta t\Vert d_tE_{p}^{A,n}\Vert _{M}^2\nonumber \\&\qquad +\,C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_\mathbf{q }^{A,n}\Vert _{TM}^2+\Vert E_\mathbf{u }^{A,n}\Vert _{TM}^2\right) \nonumber \\&\qquad +\,C\left( \Delta t^2+h^4\right) , \end{aligned}$$

(93)

where the positive constant C is independent of h and $\triangle t$.

Proof

Subtracting Eq. (61) from Eq. (24), we have that

$$\begin{aligned}&(\Theta ^nd_t\Psi ^n,w)-(\gamma \overline{\Psi }^{n-1}d_tZ^n,w)-\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n,w\right) \nonumber \\&\qquad +\,\left( \nabla \cdot E_\mathbf{q }^{A,n},w\right) +\left( f_I^n\Psi ^n,w\right) +\frac{k_ck_s}{k_c+k_s}\left( a_v(\Theta ^n)\Psi ^n,w\right) \nonumber \\&\quad =\phi ^n\frac{\partial c_f^n}{\partial t}-\gamma c_f^n\frac{\partial p^n}{\partial t} -\left( (\phi ^n \mathbf D )^{-1}{} \mathbf u ^n\cdot \mathbf q ^n+f_I^nc_f^n,w\right) \nonumber \\&\qquad +\,\frac{k_ck_s}{k_c+k_s}\left( a_v(\phi ^n)c_f^n,w\right) ,\quad \forall w\in S_h. \end{aligned}$$

(94)

And subtracting Eq. (62) from Eq. (25), we can obtain

$$\begin{aligned} \left( (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n,{{\varvec{v}}}\right) _{TM}- \left( (\phi ^n\mathbf D )^{-1}{{{\underline{\varvec{{Q}}}}}}^n,{{\varvec{v}}}\right) _{TM} =\left( E_{c_f}^{A,n},\nabla \cdot {{\varvec{v}}}\right) ,\quad \forall {{\varvec{v}}}\in \mathbf V _h^0. \end{aligned}$$

(95)

By Eq. (95), we have that

$$\begin{aligned} \left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n- (\phi ^n\mathbf D )^{-1}{{{\underline{\varvec{{Q}}}}}}^n\right) ,{{\varvec{v}}}\right) _{TM}=\left( d_tE_{c_f}^{A,n},\nabla \cdot {{\varvec{v}}}\right) ,\quad \forall {{\varvec{v}}}\in \mathbf V _h^0, \end{aligned}$$

(96)

Set $w=d_tE_{c_f}^{A,n}$ and ${{\varvec{v}}}=E_{\mathbf{q }}^{A,n}$ in Eqs. (94) and (96) respectively, we have

$$\begin{aligned}&\left( \Theta ^nd_tE_{c_f}^{A,n},d_tE_{c_f}^{A,n}\right) +\left( \nabla \cdot E_\mathbf{q }^{A,n},d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad =\left( \phi ^n\frac{\partial c_f^n}{\partial t}-\Theta ^nd_t\underline{\Psi }^n,d_tE_{c_f}^{A,n}\right) -\left( \gamma c_f^n\frac{\partial p^n}{\partial t}-\gamma \overline{\Psi }^{n-1}d_tZ^{n},d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad +\,\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n-(\phi ^n \mathbf D )^{-1}{} \mathbf u ^n\cdot \mathbf q ^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad -\,\frac{k_ck_s}{k_c+k_s}\left( a_v(\Theta ^n)\Psi ^n-a_v(\phi ^n)c_f^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad -\,\left( f_I^n(\Psi ^n-c_f^n),d_tE_{c_f}^{A,n}\right) , \end{aligned}$$

(97)

and

$$\begin{aligned} \left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n- (\phi ^n\mathbf D )^{-1}{{{\underline{\varvec{{Q}}}}}}^n\right) ,E_{\mathbf{q }}^{A,n}\right) _{TM}=\left( d_tE_{c_f}^{A,n},\nabla \cdot E_{\mathbf{q }}^{A,n}\right) . \end{aligned}$$

(98)

By Cauchy–Schwarz inequality, the first term in the right hand side of Eq. (97) can be estimated by

$$\begin{aligned}&\left( \phi ^n\frac{\partial c_f^n}{\partial t}-\Theta ^nd_t\underline{\Psi }^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad = \left( (\phi ^n-\Theta ^n)\frac{\partial c_f^n}{\partial t},d_tE_{c_f}^{A,n}\right) + \left( \Theta ^n\left( \frac{\partial c_f^n}{\partial t}-d_tc_f^n\right) ,d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad -\,\left( \Theta ^nd_tE_{c_f}^{B,n},d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad \le C\Vert c_f\Vert ^2_{W^{\infty }_1(J;L^{\infty (\Omega )})}\Vert E_{\phi }^n\Vert _M^2 +C\Vert \Theta \Vert ^2_{L^{\infty }(J;L^{\infty }(\Omega ))}\Vert c_f\Vert ^2_{W^{\infty }_2(J;L^{\infty (\Omega )})}\Delta t^2\nonumber \\&\qquad +\,C\Vert \Theta \Vert ^2_{L^{\infty }(J;L^{\infty }(\Omega ))}\Vert d_tE_{c_f}^{B,n}\Vert _M^2 +\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2. \end{aligned}$$

(99)

The second term in the right hand side of Eq. (97) can be estimated by

$$\begin{aligned}&\gamma \left( c_f^n\frac{\partial p^n}{\partial t}-\overline{\Psi }^{n-1}d_tZ^{n},d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad = \gamma \left( \left( c_f^n-\overline{\Psi }^{n-1}\right) \frac{\partial p^n}{\partial t},d_tE_{c_f}^{A,n}\right) + \gamma \left( \overline{\Psi }^{n-1}\left( \frac{\partial p^n}{\partial t}-d_tp^n\right) ,d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad -\,\gamma \left( \overline{\Psi }^{n-1}\left( d_tE_{p}^{A,n}+d_tE_{p}^{B,n}\right) ,d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad \le C\Vert p\Vert ^2_{W^{\infty }_1(J;L^{\infty (\Omega )})}\left( \Vert E_{c_f}^{A,n}\Vert _M^2+\Vert E_{c_f}^{B,n}\Vert _M^2 +\Vert c_f\Vert ^2_{W^{\infty }_1(J;L^{\infty (\Omega )})}\Delta t^2\right) \nonumber \\&\qquad +\,C\Vert \overline{\Psi } \Vert ^2_{L^{\infty }(J;L^{\infty }(\Omega ))}\Vert p\Vert ^2_{W^{\infty }_2(J;L^{\infty (\Omega )})}\Delta t^2 +\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2\nonumber \\&\qquad +\,C\Vert \overline{\Psi }\Vert ^2_{L^{\infty }(J;L^{\infty }(\Omega ))}\left( \Vert d_tE_{p}^{A,n}\Vert _M^2+ \Vert d_tE_{p}^{B,n}\Vert _M^2\right) . \end{aligned}$$

(100)

The third term in the right hand side of Eq. (97) can be estimated by

$$\begin{aligned}&\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n-(\phi ^n \mathbf D )^{-1}{} \mathbf u ^n\cdot \mathbf q ^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad =\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot (\Pi _h \mathbf Q ^n-\mathbf q ^n),d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad +\,\left( (\Theta ^n\mathbf D )^{-1}(\Pi _h \mathbf W ^n-\mathbf u ^n)\cdot \mathbf q ^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\qquad +\,\left( (\Theta ^{-n}-\phi ^{-n})\mathbf D ^{-1}{} \mathbf u ^n\cdot \mathbf q ^n,d_tE_{c_f}^{A,n}\right) \end{aligned}$$

(101)

The first term in the right hand side of Eq. (101) can be estimated by

$$\begin{aligned}&\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot (\Pi _h \mathbf Q ^n-\mathbf q ^n),d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad \le C\Vert (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\Vert ^2_{L^{\infty }(\Omega )} \left( \Vert \Pi _h\mathbf Q ^n{-}\Pi _h\mathbf q ^n\Vert _{M}^2{+}\Vert \Pi _h\mathbf q ^n-\mathbf q ^n\Vert _{M}^2\right) {+}\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2\nonumber \\&\quad \le C\left( \Vert E_\mathbf{q }^{A,n}\Vert _{TM}^2+\Vert E_\mathbf{q }^{B,n}\Vert _{TM}^2\right) +\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2+Ch^4. \end{aligned}$$

(102)

The second term in the right hand side of Eq. (101) can be estimated by

$$\begin{aligned}&\left( (\Theta ^n\mathbf D )^{-1}(\Pi _h \mathbf W ^n-\mathbf u ^n)\cdot \mathbf q ^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad \le C\Vert (\Theta ^n\mathbf D )^{-1}{} \mathbf q ^n\Vert ^2_{L^{\infty }(\Omega )} \left( \Vert \Pi _h\mathbf W ^n-\Pi _h\mathbf u ^n\Vert _{M}^2+\Vert \Pi _h\mathbf u ^n-\mathbf u ^n\Vert _{M}^2\right) +\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2\nonumber \\&\quad \le C(\Vert E_\mathbf{u }^{A,n}\Vert _{TM}^2+\Vert E_\mathbf{u }^{B,n}\Vert _{TM}^2)+\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2+Ch^4. \end{aligned}$$

(103)

The last term in the right hand side of Eq. (101) can be estimated by

$$\begin{aligned} \left( (\Theta ^{-n}-\phi ^{-n})\mathbf{D }^{-1}\mathbf{u }^n\cdot \mathbf{q }^n,d_tE_{c_f}^{A,n}\right) \le C\left\| \frac{\mathbf{u }^n\cdot \mathbf{q }^n}{\Theta ^n\phi ^n}\right\| _{L^{\infty }(\Omega )}\Vert E_{\phi }^n\Vert _M^2 +\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2.\nonumber \\ \end{aligned}$$

(104)

Recalling that $0\le a_v(\Theta ^n)\le a_0$ and $|a_v(\phi ^n)-a_v(\Theta ^n)|\le \frac{a_0}{1-\phi _0}|E_{\phi }|$, we can estimate the second to last term in the right hand side of Eq. (97) by

$$\begin{aligned}&\frac{k_ck_s}{k_c+k_s}\left( a_v(\phi ^n)c_f^n-a_v(\Theta ^n)\Psi ^n,d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad \le \frac{k_ck_s}{k_c+k_s}\left( (a_v(\phi ^n)-a_v(\Theta ^n))c_f^n,d_tE_{c_f}^{A,n}\right) + \frac{k_ck_s}{k_c+k_s}\left( a_v(\Theta ^n)(c_f^n-\Psi ^n),d_tE_{c_f}^{A,n}\right) \nonumber \\&\quad \le C\Vert c_f^n\Vert _{L^{\infty }}^2\Vert E_{\phi }^n\Vert _M^2+\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(105)

The last term in the right hand side of Eq. (97) can be estimated by

$$\begin{aligned} f_I^n(c_f^n-\Psi ^n,d_tE_{c_f}^{A,n})\le C\Vert E_{c_f}^{A,n}\Vert _M^2+\frac{\phi _{0*}}{14}\Vert d_tE_{c_f}^{A,n}\Vert _M^2+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(106)

The term in the left hand side of Eq. (98) can be transformed into

$$\begin{aligned}&\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n- (\phi ^n\mathbf D )^{-1}{{{\underline{\varvec{{Q}}}}}}^n\right) ,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\quad =\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}E_{\mathbf{q }}^{A,n}\right) ,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\qquad +\,\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}-(\phi ^n\mathbf D )^{-1}){{{\underline{\varvec{{Q}}}}}}^n\right) ,E_{\mathbf{q }}^{A,n}\right) _{TM}. \end{aligned}$$

(107)

The first term in the right hand side of Eq. (107) can be estimated by

$$\begin{aligned}&\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}E_{\mathbf{q }}^{A,n}\right) ,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\quad = \frac{1}{2}d_t\Vert (\Pi _h \Theta ^n\mathbf D )^{-1}E_{\mathbf{q }}^{A,n}\Vert _{TM}^2+ \frac{\Delta t}{2}(\Pi _h \Theta ^{n-1}{} \mathbf D )^{-1}\Vert d_tE_{\mathbf{q }}^{A,n}\Vert _{TM}^2\nonumber \\&\qquad +\,\frac{1}{2}\left( d_t((\Pi _h \Theta ^n\mathbf D )^{-1})E_{\mathbf{q }}^{A,n},E_{\mathbf{q }}^{A,n}\right) _{TM}. \end{aligned}$$

(108)

The second term in the right hand side of Eq. (107) can be bounded by

$$\begin{aligned}&\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}-(\phi ^n\mathbf D )^{-1}){{{\underline{\varvec{{Q}}}}}}^n\right) ,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\quad =\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}-(\phi ^n\mathbf D )^{-1}\right) {{{\underline{\varvec{{Q}}}}}}^n,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\qquad +\,\left( ((\Pi _h \Theta ^n\mathbf D )^{-1}-(\phi ^n\mathbf D )^{-1})d_t{{{\underline{\varvec{{Q}}}}}}^n,E_{\mathbf{q }}^{A,n}\right) _{TM}. \end{aligned}$$

(109)

Similar to the derivations of Eqs. (87) and (89), the first term in the right hand side of Eq. (109) can be bounded by

$$\begin{aligned}&\left( d_t\left( (\Pi _h \Theta ^n\mathbf D )^{-1}-(\phi ^n\mathbf D )^{-1}\right) {{{\underline{\varvec{{Q}}}}}}^n,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\quad \le C\Vert d_t(\Pi _h \Theta \mathbf D \phi )^{-1}\Vert _{L^{\infty }(t^{n-1},t^n;L^{\infty }(\mathbb {R}))}\left( \Vert E_{\phi }^n\Vert _M^2+\Vert \Pi _h\phi ^n-\phi ^n\Vert _M^2\right) +C\Vert E_{\mathbf{q }}^{A,n}\Vert _{TM}^2\nonumber \\&\qquad +\,C\Vert (\Pi _h \Theta \mathbf D \phi )^{-1}\Vert _{L^{\infty }(t^{n-1},t^n;L^{\infty }(\mathbb {R}))}\left( \Vert d_tE_{\phi }^n\Vert _M^2+\Vert d_t(\Pi _h\phi ^n-\phi ^n)\Vert _M^2\right) . \end{aligned}$$

(110)

Similar to the derivations of Eqs. (88) and (90), the second term in the right hand side of Eq. (109) can be bounded by

$$\begin{aligned}&\left( ((\Pi _h \Theta ^n\mathbf D )^{-1}-(\phi ^n\mathbf D )^{-1})d_t{{{\underline{\varvec{{Q}}}}}}^n,E_{\mathbf{q }}^{A,n}\right) _{TM}\nonumber \\&\quad \le C\Vert (\Pi _h \Theta \mathbf D \phi )^{-1}\Vert _{L^{\infty }(t^{n-1},t^n;L^{\infty }(\mathbb {R})}\left( \Vert E_{\phi }^n\Vert _M^2+\Vert \Pi _h\phi ^n-\phi ^n\Vert _M^2\right) +C\Vert E_{\mathbf{q }}^{A,n}\Vert _{TM}^2.\nonumber \\ \end{aligned}$$

(111)

Combining Eq. (97) with Eqs. (98)–(111), we can obtain

$$\begin{aligned}&\frac{\phi _{0*}}{2}\Vert d_tE_{c_f}^{A,n}\Vert _M^2+\frac{1}{2}d_t\Vert (\Pi _h \Theta ^n\mathbf D )^{-1}E_{\mathbf{q }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad \le C\left( \Vert E_{\phi }^n\Vert _{M}^2+\Vert d_tE_{\phi }^n\Vert _{M}^2\right) +C\left( \Vert E_{c_f}^{A,n}\Vert _{M}^2+\Vert d_tE_{p}^{A,n}\Vert _{M}^2\right) \nonumber \\&\qquad +\,C\left( \Vert E_\mathbf{q }^{A,n}\Vert _{TM}^2+\Vert E_\mathbf{u }^{A,n}\Vert _{TM}^2\right) \nonumber \\&\qquad +\,C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(112)

Multiplying by $2\Delta t$, and summing for n from 1 to m, $m\le N$, we have

$$\begin{aligned}&\phi _{0*}\sum \limits _{n=1}^{m}\Delta t\Vert d_tE_{c_f}^{A,n}\Vert _M^2+\Vert (\Pi _h \Theta ^m\mathbf D )^{-1}E_{\mathbf{q }}^{A,m}\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{\phi }^n\Vert _{M}^2+\Vert d_tE_{\phi }^n\Vert _{M}^2\right) +C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{c_f}^{A,n}\Vert _{M}^2+\Vert d_tE_{p}^{A,n}\Vert _{M}^2\right) \nonumber \\&\qquad +\,C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_\mathbf{q }^{A,n}\Vert _{TM}^2+\Vert E_\mathbf{u }^{A,n}\Vert _{TM}^2\right) \nonumber \\&\qquad +\,C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(113)

Next we give the estimates for $\Vert E_{c_f}^{A,n}\Vert _M^2$. Taking $w=E_{c_f}^{A,n}$ and ${{\varvec{v}}}=E_{\mathbf{q }}^{A,n}$ in Eqs. (94) and (95) respectively, we have

$$\begin{aligned}&\left( \Theta ^nd_tE_{c_f}^{A,n},E_{c_f}^{A,n}\right) +\left( \nabla \cdot E_\mathbf{q }^{A,n},E_{c_f}^{A,n}\right) \nonumber \\&\quad =\left( \phi ^n\frac{\partial c_f^n}{\partial t}-\Theta ^nd_t\underline{\Psi }^n,E_{c_f}^{A,n}\right) -\left( \gamma c_f^n\frac{\partial p^n}{\partial t}-\gamma \overline{\Psi }^{n-1}d_tZ^{n},E_{c_f}^{A,n}\right) \nonumber \\&\qquad +\,\left( (\Theta ^n\mathbf D )^{-1}\Pi _h \mathbf W ^n\cdot \Pi _h \mathbf Q ^n-(\phi ^n \mathbf D )^{-1}{} \mathbf u ^n\cdot \mathbf q ^n,E_{c_f}^{A,n}\right) \nonumber \\&\qquad -\,\frac{k_ck_s}{k_c+k_s}\left( a_v(\Theta ^n)\Psi ^n-a_v(\phi ^n)c_f^n,E_{c_f}^{A,n}\right) \nonumber \\&\qquad -\,\left( f_I^n\left( \Psi ^n-c_f^n\right) ,E_{c_f}^{A,n}\right) , \end{aligned}$$

(114)

and

$$\begin{aligned} \left( (\Pi _h \Theta ^n\mathbf D )^{-1}{{\varvec{Q}}}^n,E_{\mathbf{q }}^{A,n}\right) _{TM}- \left( (\phi ^n\mathbf D )^{-1}{{{\underline{\varvec{{Q}}}}}}^n,E_{\mathbf{q }}^{A,n}\right) _{TM} =\left( E_{c_f}^{A,n},\nabla \cdot E_{\mathbf{q }}^{A,n}\right) . \end{aligned}$$

(115)

By the similar estimates with the above equations, we can easily obtain

$$\begin{aligned}&\Vert E_{c_f}^{A,m}\Vert _M^2+C\sum \limits _{n=1}^{m}\Delta t\Vert (\Pi _h \Theta ^n\mathbf D )^{-1}E_{\mathbf{q }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{c_f}^{A,n}\Vert _M^2 +\Vert d_tE_p^{A,n}\Vert _M^2+\Vert E_{\phi }^{n}\Vert _{M}^2\right) \nonumber \\&\qquad +\,C\sum \limits _{n=1}^{m}\Delta t\Vert E_{\mathbf{u }}^{A,n}\Vert _{TM}^2+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(116)

Combining Eq. (113) with (116) and using Gronwall’s inequality, we have

$$\begin{aligned}&\phi _{0*}\sum \limits _{n=1}^{m}\Delta t\Vert d_tE_{c_f}^{A,n}\Vert _M^2+\Vert E_{c_f}^{A,m}\Vert _M^2+\Vert (\Pi _h \Theta ^m\mathbf D )^{-1}E_{\mathbf{q }}^{A,m}\Vert _{TM}^2 +C\sum \limits _{n=1}^{m}\Delta t\Vert E_{\mathbf{q }}^{A,n}\Vert _{TM}^2\nonumber \\&\quad \le C\sum \limits _{n=1}^{m}\Delta t\left( \Vert E_{\phi }^n\Vert _{M}^2+\Vert d_tE_{\phi }^n\Vert _{M}^2\right) +C\sum \limits _{n=1}^{m}\Delta t\Vert d_tE_{p}^{A,n}\Vert _{M}^2\nonumber \\&\qquad +\,C\sum \limits _{n=1}^{m}\Delta t\Vert E_\mathbf{u }^{A,n}\Vert _{TM}^2+C\left( \Delta t^2+h^4\right) . \end{aligned}$$

(117)

Then the proof ends. $\square$

It remains to testify induction hypothesis (51). This proof is given through two steps.

Steps 1 (Definition of $C^*$ ): Using scheme (22)–(23) for $n=0$ and Eq. (87), we can get the approximation ${{\varvec{W}}}^1$ and the following property.

$$\begin{aligned} \Vert {{\varvec{W}}}^1\Vert _{\infty }\le & {} \Vert E_\mathbf{u }^{A,1}\Vert _{\infty }+\Vert {{\varvec{\underline{W}}}}^1\Vert _{\infty } \le Ch^{-1}\Vert E_\mathbf{u }^{A,1}\Vert _{TM}+\Vert {{\varvec{\underline{W}}}}^1\Vert _{\infty }\\\le & {} C(h+h^{-1}\Delta t)+\Vert {{\varvec{\underline{W}}}}^1\Vert _{\infty }\le C. \end{aligned}$$

Thus define the positive constant $C_*$ independent of h and $\Delta t$ such that

$$\begin{aligned} C^*\ge \max \{\Vert \mathbf W ^{1}\Vert _{\infty }, 2\Vert {{{\underline{\varvec{W}}}}}^{n}\Vert _{\infty }\}. \end{aligned}$$

Steps 2 (Induction): By the definition of $C^*$, it is trivial that hypothesis (51) holds true for $l=1$. Supposing that $\Vert \Pi _h\mathbf W ^{l-1}\Vert _{\infty }\le C^*$ holds true for an integer $l=1,\dots ,N-1$, by Lemmas 6–8 with $m=l$, we have that

$$\begin{aligned} \Vert E_\mathbf{u }^{A,l}\Vert _{TM}\le C(h^2+\Delta t). \end{aligned}$$

Next we prove that $\Vert \Pi _h\mathbf W ^{l}\Vert _{\infty }\le C^*$ holds true. Since

$$\begin{aligned} \Vert \mathbf W ^l\Vert _{\infty }\le & {} \Vert E_\mathbf{u }^{A,l}\Vert _{\infty }+\Vert {\underline{W}}^l\Vert _{\infty } \le Ch^{-1}\Vert E_\mathbf{u }^{A,l}\Vert _{TM}+\Vert {{\varvec{\underline{W}}}}^l\Vert _{\infty }\nonumber \\\le & {} C_3(h+h^{-1}\Delta t)+\Vert {{\varvec{\underline{W}}}}^l\Vert _{\infty }. \end{aligned}$$

(118)

Let $\Delta t\le C_4h^2$ and a positive constant $h_1$ be small enough to satisfy

$$\begin{aligned} C_3(1+C_4)h_1\le \frac{C^*}{2}. \end{aligned}$$

Then for $h\in (0,h_1],$ Eq. (118) can be estimated by

$$\begin{aligned} \Vert \mathbf W ^l\Vert _{\infty }\le & {} C_3(h+h^{-1}\Delta t)+\Vert {{\varvec{\underline{W}}}}^l\Vert _{\infty }\\\le & {} C_3(h_1+C_4h_1)+\frac{C^*}{2}\\\le & {} C^*. \end{aligned}$$

It is obvious that

$$\begin{aligned} \Vert \Pi _h \mathbf W ^l\Vert _{\infty }\le \Vert \mathbf W ^l\Vert _{\infty }\le C^*, \end{aligned}$$

then the proof ends.

Based on the above lemmas and using Gronwall’s inequality, we have the main error estimates below.

Theorem 9

Suppose (H1)–(H5) hold then there exists a positive constant C independent of h and $\triangle t$ such that

$$\begin{aligned}&\Vert (Z-p)^{m}\Vert _M+\Vert (\mathbf W -\mathbf u )^{m}\Vert _{TM} + \Vert (\Psi -c_f)^{m}\Vert _M+\Vert (\mathbf Q -\mathbf q )^{m}\Vert _{TM}\\&\qquad +\,\left( C\sum \limits _{n=1}^{m}\Delta t\Vert (\mathbf Q -\mathbf q )^{n}\Vert _{TM}^2\right) ^{1/2} +\Vert (\Theta -\phi )^m\Vert _M^2\\&\quad \le C(\Delta t+h^2),~~m\le N. \end{aligned}$$

Remark 2

In our future work, we will consider the case that $\mathbf D$ is defined in Eq. (5). By using the similar technique in [10], it is supposed that the superconvergence rate $O(h^2+\Delta t)$ is obtained for concentration of the acid and rate $O(h^{3/2}+\Delta t)$ for its flux in certain discrete norms. Besides, Examples 5 and 6 in the next section are presented to verify that the block-centered finite difference method is still effective for the case that $\mathbf D$ is not diagonal.

6 Numerical Examples

In this section, some numerical experiments using the block-centered finite difference method have been carried out.

We test Examples 1 and 2 to verify the convergence rates. The time step is refined as $\displaystyle \Delta t=1/{N_x^2}=1/{N_y^2}$ to show the convergence and

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mathbf D =10^{-2}~\mathbf I ,~K_0=1,~\hat{T}=0.5,\\ \displaystyle \alpha =k_c=k_s=\mu =f_I=1,\\ \displaystyle a_0=0.5,~~\rho _s=10,~~\gamma =0.1, \end{array} \right. \end{aligned}$$

where $\mathbf I$ is an identity matrix. In Example 1, the domain $\Omega =(0,1)\times (0,1)$ is uniformly divided by the rectangles decomposition. The numerical results are listed in Tables 1 and 2. Moreover, as to report the features of the block-centered finite difference method vividly, Figs. 1, 2, 3 and 4 are given with $\displaystyle N=20,~t=0.5$ for Example 1. And in Example 2, set $\Omega =(-1,1)\times (-1,1)$. The initial spatial partition is a $5\times 5$ grid. Then the grid is refined by dividing each edge into two equal parts and the nonuniform meshes are used which are generated from the corresponding uniform mesh by adding a random in both x and y directions (cf. Fig. 5). The numerical results are listed in Tables 3 and 4.

Table 1 Error and convergence rates of Example 1 on uniform grids

Table 2 Error and convergence rates of Example 1 on uniform grids

Fig. 1

The pressure figures for Example 1. Left the exact solution p. Right the numerical solution Z

Fig. 2

The velocity figures for Example 1. Left the exact solution $\mathbf{u }$. Right the numerical solution $\mathbf{W }$

Fig. 3

The concentration figures for Example 1. Left the exact solution $c_f$. Right the numerical solution $\Psi$

Fig. 4

The porosity figures for Example 1. Left the exact solution $\phi$. Right the numerical solution $\Theta$

Fig. 5

The non-uniform mesh generated from the $20\times 20$ uniform mesh for Example 2

Table 3 Error and convergence rates of Example 2 on nonuniform grids

Table 4 Error and convergence rates of Example 2 on nonuniform grids

Fig. 6

The distributions of porosity for Example 3. a $\hbox {time} =5\times 10^5$ s, b $\hbox {time} =1\times 10^6$ s, c $\hbox {time} =1.5\times 10^6$ s, d $\hbox {time} =2\times 10^6$ s

Fig. 7

The distributions of porosity for Example 4. a $\hbox {time} =5\times 10^5$ s, b $\hbox {time} =1\times 10^6$ s, c $\hbox {time} =1.5\times 10^6$ s, d $\hbox {time} =2\times 10^6$ s

Fig. 8

The distributions of porosity for Example 5. a $\hbox {time} =5\times 10^5$ s, b $\hbox {time} =1\times 10^6$ s, c $\hbox {time} =1.5\times 10^6$ s, d $\hbox {time} =2\times 10^6$ s

Fig. 9

The distributions of porosity for Example 6. a $\hbox {time} =5\times 10^5$ s, b $\hbox {time} =1\times 10^6$ s, c $\hbox {time} =1.5\times 10^6$ s, d $\hbox {time} =2\times 10^6$ s

Example 1

Here the initial condition and the right hand side of the equation are computed according to the analytic solution given as below.

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle p(\mathbf x ,t)=tcos(\pi x)cos(\pi y),\\ \displaystyle c_f(\mathbf x ,t)=tx^2(1-x)^2y^2(1-y)^2,\\ \displaystyle \phi (\mathbf x ,t)=1-\displaystyle e^{ -\frac{1}{80}t^2x^2(1-x)^2y^2(1-y)^2e^{x+y+1}-(x+y+1)}. \end{array} \right. \end{aligned}$$

Example 2

Here the initial condition and the right hand side of the equation are computed according to the analytic solution given as below.

$$\begin{aligned} \left\{ \begin{array}{l} p(\mathbf x ,t)=t(x+1)^2(x-1)^2(y+1)^2(y-1)^2,\\ c_f(\mathbf x ,t)=t\left( sin(\frac{\pi x}{2})sin(\frac{\pi y}{2})+1\right) ,\\ \phi (\mathbf x ,t)=1-\displaystyle e^{-\frac{1}{80}t^2(sin(\frac{\pi x}{2})sin(\frac{\pi y}{2})+1)e^{x+y+3}-(x+y+3)}. \end{array} \right. \end{aligned}$$

In the following examples, $\Omega =(0,1)\times (0,1),~J=[0,2\times 10^6],~\Delta t=2\times 10^4.$ the physical parameter is more realistic which is taken from the data in [1, 3]. The the initial concentration of acid flow is zero. The initial pressure is $10^5$ Pa. The parameter $\gamma$ is set to 0.01. Besides, some properties of acid flow in porous media, the injection and production flow rates are listed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mu =10^{-2},~~\rho _s=2500,~~a_0=0.5,\\ \displaystyle \alpha =k_c=0.1,~~c_I=10,~~k_s=1. \end{array} \right. \end{aligned}$$

$$\begin{aligned} f_I=\left\{ \begin{array}{ll} 1,&{}\quad x=1/160,\\ 0,&{}\quad otherwise.\\ \end{array} \right. f_P=\left\{ \begin{array}{ll} -1,&{}\quad x=159/160,\\ 0,&{}\quad otherwise.\\ \end{array} \right. \end{aligned}$$

Example 3

In this example, $\mathbf D =10^{-9}~\mathbf I$. The distributions of initial porosity and permeability are listed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \phi _0=0.4,~~K_0=10^{-6},\quad (x,y)=(1/160,41/160),\\ \phi _0=0.6,~~K_0=10^{-5},\quad (x,y)=(1/160,121/160),\\ \phi _0=0.2,~~K_0=10^{-7},\quad otherwise.\\ \end{array} \right. \end{aligned}$$

Example 4

In this example, $\mathbf D =10^{-9}~\mathbf I$. The initial porosity in the porous medium also obeys the uniform distribution and the range is from 0.05 to 0.35. The initial permeability of the porous media comply with the uniform distribution and the range is from $10^{-5}$ to $10^{-4}$.

Example 5

In this example, $d_m=10^{-9},~\alpha _l=10^{-3},~\alpha _t=10^{-4}$. The distributions of initial porosity and permeability are listed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \phi _0=0.4,~~K_0=10^{-6},\quad (x,y)=(1/160,41/160),\\ \phi _0=0.6,~~K_0=10^{-5},\quad (x,y)=(1/160,121/160),\\ \phi _0=0.2,~~K_0=10^{-7},\quad otherwise.\\ \end{array} \right. \end{aligned}$$

Example 6

In this example, $d_m=10^{-9},~\alpha _l=10^{-3},~\alpha _t=10^{-4}$. The initial porosity in the porous medium also obeys the uniform distribution and the range is from 0.05 to 0.35. The initial permeability of the porous media comply with the uniform distribution and the range is from $10^{-5}$ to $10^{-4}$.

The distributions of porosity for Examples 3–6 are calculated at the end of 25th time step, 50th time step, 75th time step and 100th time step respectively. We show the distributions of porosity in Figs. 6, 7, 8 and 9. These results are computed on the grid of $80\times 80$ cells.

From Figs. 6, 7, 8 and 9, we can see that the average porosities in all frameworks are increasing, which reveal that the matrix is eaten by the acid. Moreover, it can be observed that at the beginning of the development, all frameworks demonstrate the formation of some small fingers. As time elapses, some major fingers appear. However, compared Figs. 6 and 7 with 8 and 9, we can see that the framework curves are thinner when the effective dispersion tensor $D_e$ is diagonal.

From Tables 1, 2, 3 and 4 and Figs. 1, 2, 3, 4, 5, 6, 7, 8 and 9, we can see that the block-centered finite difference approximations for the pressure, velocity, porosity, concentration and its flux have the $(h^2+\Delta t)$ accuracy in discrete norms. These results are in consistent with the error estimates in Theorem 9. As shown in Figs. 6, 7, 8 and 9, the heterogeneity of porosity and permeability in wormhole formations also has great effect on the field, which promotes the non-uniformity of the chemical reaction. Those examples vividly show that the block-centered finite difference method is capable of effectively simulating wormhole propagation.

7 Conclusion

In this paper, we have developed a block-centered finite difference method for compressible wormhole propagation during reactive dissolution of carbonate, which is effectively applied to enhance oil and gas production rate. The coupled analysis approach to deal with the fully coupling relation of multivariables is employed. Based on this method, stability analysis are established rigorously and carefully. Using estimates of the mixed finite element method with quadrature applied to linear parabolic equations, we obtain superconvergence of the pressure, velocity, porosity, concentration and its flux in different discrete norms on non-uniform grids. Finally, some numerical experiments are presented to verify the theoretical analysis and effectiveness of the given scheme.