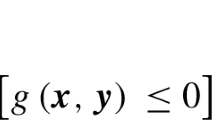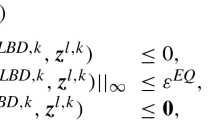1 Introduction

Semi-infinite programs (SIPs) are mathematical programs with a finite number of variables and an infinite number of constraints. This is commonly expressed by a parameterized constraint that has to hold for all possible realizations of its parameter(s). Here we consider SIPs of the form

figure a

where the restriction to \(|\mathcal {Y}| = \infty \) is made only for convenience. Furthermore, additional constraints (semi-infinite or otherwise) do not pose a problem for the methods presented here. The generalizations to arbitrarily many constraints and mixed-integer problems are discussed in Sect. 5. No convexity or concavity assumptions are made on the participating functions. The properties of the sets and functions participating in (SIP) are discussed in detail in Sect. 2.2 along with other assumptions.

SIPs emerge in many problems from science and engineering including robust design [7], model reduction [3], and design centering [19]. For a review of SIP theory, methods, and applications, the reader is referred to [6, 8, 15, 16]. The difficulty in solving (SIP) lies in the definition of the feasible set by infinitely many constraints. In order for a point \(\bar{\varvec{x}}\in \mathcal {X}\) to be feasible in (SIP), the globally optimal objective of the lower-level program

$$\begin{aligned} \underset{\varvec{y} \in \mathcal {Y}}{\text {max}}\, g(\bar{\varvec{x}},\varvec{y}) \end{aligned}$$

must be non-positive. For constraint functions \(g(\bar{\varvec{x}},\cdot )\) that are concave on \(\mathcal {Y}\) and satisfy constraint qualification, the lower-level program can be replaced equivalently by its Karush–Kuhn–Tucker (KKT) conditions and the SIP can be reduced to a finite problem. However, in the nonconcave case considered here, this approach is not applicable.

There exist approaches that approximate (SIP) by a finite problem, e.g., through replacing \(\mathcal {Y}\) with a discretization [4]. Such discretization approaches represent outer approximations and generally do not provide feasible points finitely. Bhattacharjee et al. [1] proposed a method that guarantees the generation of feasible points in finite time under appropriate assumptions. This is achieved through the replacement of the semi-infinite constraint by an overestimation based on interval extensions. Convergence of the overestimation is achieved through a subdivision of the parameter set. Subsequently, Bhattacharjee et al. [2] used the above approach in conjunction with a discretization-based lower bounding procedure to solve (SIP) approximately to global optimality in finite time. Therein, the central assumption is that there exists a sequence of SIP-Slater points, i.e., points satisfying the Slater condition for the semi-infinite constraints. Alternatively, convex overestimation approaches were proposed by Floudas and Stein [5] and then by Mitsos et al. [13]. The former was later extended to arbitrary index sets by Stein and Steuermann [20]. While providing tighter overestimations than interval extensions, these approaches are typically more expensive [13]. Mitsos [11] proposed an approach that employs a discretization-based outer approximation and an approximation that is based on discretization and restriction of the right-hand side of the discretized constraints. The algorithm is guaranteed to solve (SIP) approximately to global optimality in finite time under mild assumptions. Indeed this approach only requires the existence of a single \(\varepsilon \)-optimal SIP-Slater point. This approach has subsequently been extended to generalized SIPs (GSIPs) by Mitsos and Tsoukalas [14]. Tsoukalas and Rustem [24] proposed an approach that is centered around an oracle problem that decides whether a given objective value is attainable by (SIP) or not. Through a binary search of the objective space, the algorithm solves (SIP) approximately to global optimality under slightly stronger assumptions than the approach by Mitsos [11]. The oracle approach was originally proposed for GSIPs, bilevel, and continuous coupled min-max programs by Tsoukalas et al. [25]. As SIPs and GSIPs are closely related to bilevel programs [21], it bears mentioning that discretization-based approaches to the solution of bilevel programs have been proposed by Mitsos for the nonconvex case [12] and by Mitsos et al. for the mixed-integer case [10]. Furthermore, a method with feasible iterates for GSIPs with convex lower-level problems has been proposed by Stein and Winterfeld [22].

Here, we present a hybrid of the algorithm by Mitsos [11] and the algorithm by Tsoukalas and Rustem [24]. As its predecessors, the algorithm employs existing NLP-solvers to solve the finite subproblems and thus appropriate assumptions on the solution provided by these solvers are necessary. We propose a strategy to determine the required optimality tolerance for the NLP-solvers, which allows weakening of the assumptions. Under these relaxed assumptions, the hybrid algorithm is guaranteed to solve (SIP) approximately to global optimality in finite time. Furthermore, the hybridization addresses the issue of choosing appropriate values for the tuning parameters for the algorithm by Mitsos [11] and the hybrid algorithm shows superior overall performance over its predecessors.

The remainder of the present manuscript is organized as follows. In Sect. 2, definitions and assumptions used throughout the manuscript are introduced. In Sect. 3, the algorithm by Mitsos [11] is presented along the proposed strategy for the determination of NLP-solver tolerances and a proof of finite termination. In Sect. 4, the properties of the oracle problem and its adaptation to the hybrid algorithm are discussed, followed by the statement of the hybrid algorithm and a proof of finite convergence. In Sect. 5, generalizations of (SIP) to mixed-integer problems and multiple constraints are discussed. In Sect. 6, numerical experiments performed on established SIP benchmark problems and a newly developed problem are presented, while Sect. 7 gives conclusions and potential future work.

2 Definitions and assumptions

In this section, definitions and assumptions are introduced that are used throughout the remainder of the manuscript.

2.1 Definitions

Definition 1

(Approximate solution) Given an optimality tolerance \(\varepsilon ^{NLP}\), the approximate solution of a feasible nonlinear program

$$\begin{aligned} \varphi ^* = \underset{\varvec{z} \in \mathcal {Z}}{\text {min}}\, \varphi (\varvec{z}), \quad \mathcal {Z} \subseteq {\mathbb {R}}^{n_z} \end{aligned}$$

provides a feasible solution point \(\bar{\varvec{z}}\) and a lower bound \(\varphi ^-\) on the exact globally optimal objective value \(\varphi ^*\) with

$$\begin{aligned} \varphi (\bar{\varvec{z}}) \ge \varphi ^* \ge \varphi ^- \ge \varphi (\bar{\varvec{z}}) - \varepsilon ^{NLP}. \end{aligned}$$

In compact notation we write

$$\begin{aligned} \left[ \varphi ^-,\varphi (\bar{\varvec{z}})\right] \ni \varphi ^* = \underset{\varvec{z} \in \mathcal {Z}}{\text {min}}\, \varphi (\varvec{z}), \quad \mathcal {Z} \subseteq {\mathbb {R}}^{n_z}. \end{aligned}$$

Similarly, for a maximization problem, with approximate solution \(\bar{\varvec{z}}\), upper bound \(\psi ^+\), and exact globally optimal objective value \(\psi ^*\) we write

$$\begin{aligned} \left[ \psi (\bar{\varvec{z}}),\psi ^+\right] \ni \psi ^* = \underset{\varvec{z} \in \mathcal {Z}}{\text {max}}\, \psi (\varvec{z}), \quad \mathcal {Z} \subseteq {\mathbb {R}}^{n_z}. \end{aligned}$$

Definition 2

(Lower level program) For a given point \(\bar{\varvec{x}} \in \mathcal {X}\), the lower level program is denoted along with its optimal objective value and approximate solution according to Definition 1

$$\begin{aligned} \left[ g(\bar{\varvec{x}},\bar{\varvec{y}}),g^+(\bar{\varvec{x}}) \right] \ni g^*(\bar{\varvec{x}}) = \underset{\varvec{y} \in \mathcal {Y}}{\text {max}}\, g(\bar{\varvec{x}}, \varvec{y}). \end{aligned}$$
(LLP)

Definition 3

(SIP-feasibility) A given point \(\bar{\varvec{x}} \in \mathcal {X}\) is called SIP-feasible if and only if

$$\begin{aligned} g(\bar{\varvec{x}},\varvec{y}) \le 0, \quad \forall \varvec{y} \in \mathcal {Y}, \end{aligned}$$

or equivalently

$$\begin{aligned} g^*(\bar{\varvec{x}}) \le 0. \end{aligned}$$

Definition 4

(\(\varepsilon \) -optimality) A point \(\bar{\varvec{x}} \in {\mathbb {R}}^{n_x}\) is \(\varepsilon \)-optimal if and only if it is SIP-feasible and its objective value is not more than \(\varepsilon \) worse than the optimal solution \(f^*\) of (SIP), i.e.,

Definition 5

(SIP-Slater point) A point \(\bar{\varvec{x}} \in \mathcal {X}\) is called SIP-Slater point if and only if it satisfies the semi-infinite constraint strictly, i.e.,

$$\begin{aligned} g(\bar{\varvec{x}},\varvec{y}) < 0, \quad \forall \varvec{y} \in \mathcal {Y}. \end{aligned}$$

Remark 1

Note that \(\bar{\varvec{x}}\) is not restricted to the interior of \(\mathcal {X}\). Therefore, finite constraints are not required to be satisfied strictly at an SIP-Slater point.

2.2 Assumptions

Assumption 1

(Host sets) The host sets \(\mathcal {X} \subsetneq {\mathbb {R}}^{n_x}\) and \(\mathcal {Y} \subsetneq {\mathbb {R}}^{n_y}\) are compact.

Assumption 2

(Basic properties of functions) The functions \(f : \mathcal {X} \rightarrow {\mathbb {R}}\) and \(g : \mathcal {X} \times \mathcal {Y} \rightarrow {\mathbb {R}}\) are continuous on \(\mathcal {X}\) and \(\mathcal {X} \times \mathcal {Y}\) respectively.

Remark 2

Assumptions 1 and 2 are standard in deterministic global optimization.

Assumption 3

(\({\tilde{\varepsilon }}^f\) -optimal SIP-Slater point) There exists some \({\tilde{\varepsilon }}^f > 0\) such that there exists an SIP-Slater point \(\varvec{x}^S \in \mathcal {X}\) that is \({\tilde{\varepsilon }}^f\)-optimal, i.e.,

Assumption 3 was first used in [11]. As discussed in [14], it is slightly weaker than the assumption in [24], which is equivalent to Assumption 3 holding for arbitrarily small \({\tilde{\varepsilon }}^f\).

Assumption 4

(Approximate solution of NLPs) If a nonlinear program (NLP) is infeasible, it is found to be infeasible without any infeasibility tolerance (\(\varepsilon ^{INF} = 0\)). Otherwise, it can be solved globally to within an arbitrary optimality tolerance \(\varepsilon ^{NLP}>0\).

Assumption 4 is a relaxation of similar assumptions in [11] and [24]. In [11], it is assumed that the approximate solution of (LLP) provides either \(g^+(\bar{\varvec{x}}) \le 0\) or \(g(\bar{\varvec{x}},\bar{\varvec{y}}) > 0\), which may not be given, especially for \(g^*(\bar{\varvec{x}}) = 0\). In [24], it is assumed implicitly that all NLP subproblems are solved exactly. Obviously this is the strongest of the mentioned assumptions and can in general not be provided by numerical solution methods.

3 Restriction of the right-hand-side

The algorithm proposed by Mitsos [11] solves (SIP) by employing three finite subproblems. Through the solution of these problems by existing NLP-solvers, bounds on the solution of (SIP) are obtained. Under mild assumptions discussed later on, the algorithm terminates finitely with an \(\varepsilon ^f\)-optimal point, where \(\varepsilon ^f > 0\) is a user-defined optimality tolerance. In Sect. 3.1, the subproblems used in the original algorithm are reviewed, followed by the statement of the algorithm with revisions in Sect. 3.2. In Sect. 3.3, a proof of finite convergence is given for the revised algorithm under weaker assumptions than in [11]. While the overall structure of the proof remains unchanged from [11], the weaker assumptions, specifically Assumption 4, require the explicit consideration of NLP-tolerances. This approach is inspired by the proofs provided in [12] and [10]. Finally, in Sect. 3.4, the choice of values for the tuning parameters of the algorithm is discussed on the basis of a newly developed benchmark case.

3.1 Review of subproblems in [11]

The first problem is the lower bounding problem (LBD) originally proposed by Blankenship and Falk [4]. A finite relaxation of (SIP) is obtained by replacing the parameter set \(\mathcal {Y}\) with a finite discretization \(\mathcal {Y}^{LBD} \subsetneq \mathcal {Y}\).

figure b

Due to the fact that the discretization \(\mathcal {Y}^{LBD}\) is a subset of the parameter set \(\mathcal {Y}\), (LBD) is a valid relaxation of (SIP). Consequently, any lower bound \(f^{LBD,-}\) on its exact globally optimal objective value is a lower bound on the exact globally optimal objective value of (SIP).

The second problem is the upper bounding problem (UBD). It is obtained by first replacing the parameter set \(\mathcal {Y}\) with a finite discretization \(\mathcal {Y}^{UBD}\) and subsequently restricting the right-hand-side of the semi-infinite constraint by a restriction parameter \(\varepsilon ^g > 0\).

figure c

In general, this problem is neither a relaxation nor a restriction of (SIP). Therefore, it is possible that a solution \(\bar{\varvec{x}}^{UBD}\) of (UBD) is SIP-infeasible. Consequently, an upper bound \(f(\bar{\varvec{x}}^{UBD})\) to (UBD) is not necessarily an upper bound to (SIP). Also, due to the restriction of the right-hand-side, a lower bound \(f^{UBD,-}\) to (UBD) is not necessarily a lower bound to (SIP). SIP-feasible points and therefore upper bounds to (SIP) are obtained by successively reducing the restriction parameter \(\varepsilon ^g\) and populating the discretization \(\mathcal {Y}^{UBD}\). Three cases can be distinguished in order to determine the required modification of (UBD):

  1. 1.

    (UBD) is infeasible. In this case, the restriction parameter \(\varepsilon ^g\) is reduced in order to relax (UBD) and obtain a feasible instance of (UBD) in a following iteration.

  2. 2.

    (UBD) is feasible and its solution \(\bar{\varvec{x}}^{UBD}\) is SIP-infeasible. In this case, \(\mathcal {Y}^{UBD}\) is populated with a new discretization point in order to make \(\bar{\varvec{x}}\) infeasible in the following iteration of (UBD).

  3. 3.

    (UBD) is feasible and its solution \(\bar{\varvec{x}}^{UBD}\) is SIP-feasible. In this case, \(f(\bar{\varvec{x}}^{UBD})\) is an upper bound to (SIP). The restriction parameter \(\varepsilon ^g\) is reduced in order to obtain tighter upper bounds in following iterations.

Consequently, in all three cases, (UBD) is refined to better approximate (SIP).

The final problem is the lower-level program (LLP) from Definition 2.

$$\begin{aligned} \left[ g(\bar{\varvec{x}},\bar{\varvec{y}}),g^+(\bar{\varvec{x}})\right] \ni g^*(\bar{\varvec{x}}) = \underset{\varvec{y} \in \mathcal {Y}}{\text {max}}\, g(\bar{\varvec{x}}, \varvec{y}) \end{aligned}$$
(LLP)

For a given point \(\bar{\varvec{x}}\), \(g^*(\bar{\varvec{x}})\) is positive if \(\bar{\varvec{x}}\) is SIP-infeasible and non-positive if \(\bar{\varvec{x}}\) is SIP-feasible. Within the algorithm, (LLP) is solved for the solution points of (LBD) and (UBD) to either determine their SIP-feasibility or populate the respective discretization sets \(\mathcal {Y}^{LBD}\) and \(\mathcal {Y}^{UBD}\) with the solution point \(\bar{\varvec{y}}\) of (LLP). To guarantee convergence, Mitsos [11] assumes that an approximate solution of (LLP) either provides \(g^+(\bar{\varvec{x}}) \le 0\) or \(g(\bar{\varvec{x}},\bar{\varvec{y}}) > 0\). Thereby, either \(\bar{\varvec{x}}\) is found to be SIP-feasible, or a solution \(\bar{\varvec{y}} \in \mathcal {Y}\) is found that when added to the respective discretization makes \(\bar{\varvec{x}}\) infeasible in the following iteration of (LBD) or (UBD). In the following section, the algorithm is formally stated with revisions that allow the relaxation of this assumption. This is of interest since the previous assumptions cannot be guaranteed by state-of-the-art NLP-solvers. While the case \(g^+(\bar{\varvec{x}}) > 0 \ge g(\bar{\varvec{x}},\bar{\varvec{y}})\) becomes increasingly unlikely for decreasing NLP-tolerances, it cannot be excluded a priori.

3.2 Algorithm statement with revisions

Here, the revised algorithm by Mitsos [11] is stated formally based on the subproblems (LBD), (UBD), and (LLP). These problems are solved approximately according to Definition 1 with their respective tolerances \(\varepsilon ^{LBD}, \varepsilon ^{UBD}, \varepsilon ^{LBD,LLP}, \varepsilon ^{UBD,LLP} > 0\). In the original statement of the algorithm, the tolerances \(\varepsilon ^{LBD,LLP}\) and \(\varepsilon ^{UBD,LLP}\) are fixed by the user, while in the revised version below they are adjusted to guarantee finite termination under the relaxed assumptions. This refinement is contained in Lines 10 and 14 of Algorithm 1.

figure d

In the upper bounding procedure, (LLP) is always solved with \(\varepsilon ^{UBD,LLP} < \varepsilon ^g\) due to \(\varepsilon ^{UBD,LLP} = \varepsilon ^g/r^{UBD,LLP}\) (Line 14) and \(r^{UBD,LLP} > 1\). Consequently, if \(\bar{\varvec{x}}^{UBD}\) is not found to be SIP-feasible it is guaranteed to be infeasible in the next instance of (UBD). This is shown in detail in Lemma 3. Note that \(\bar{\varvec{x}}^{UBD}\) may become feasible in a subsequent instance of (UBD) due to the reduction of \(\varepsilon ^g\) and the fact that \(g(\bar{\varvec{x}}^{UBD},\bar{\varvec{y}}) > 0\) does not necessarily hold. Indeed, the case \(g^+(\bar{\varvec{x}}^{UBD}) > 0 \ge g(\bar{\varvec{x}}^{UBD},\bar{\varvec{y}})\) may occur since the contrary is not assumed as it is in [11]. This however, does not impede the finite termination of the algorithm since only a finite number of reductions of \(\varepsilon ^g\) can occur before the algorithm terminates (see Lemma 4). In the lower bounding procedure, a value for \(\varepsilon ^{LBD,LLP}\) cannot be given a priori such that \(\bar{\varvec{x}}^{LBD}\) becomes infeasible in the following instance of (LBD). However, in Lemma 1 it is shown that the proposed reduction strategy is sufficient to make \(\bar{\varvec{x}}^{LBD}\) infeasible in (LBD) with a finite number of reductions. With these properties, the proposed refinement strategy replaces the assumption in [11] that either \(g^+(\bar{\varvec{x}}) \le 0\) or \(g(\bar{\varvec{x}},\bar{\varvec{y}}) > 0\).

By Assumption 3, there exists an \({\tilde{\varepsilon }}^f\)-optimal SIP-Slater point and consequently (SIP) is feasible. Theorem 1 of the following section states that for appropriately chosen \(\varepsilon ^f\), \(\varepsilon ^{LBD}\), and \(\varepsilon ^{UBD}\), Algorithm 1 terminates finitely with an \(\varepsilon ^f\)-optimal point \(\varvec{x}^*\).

Remark 3

Note that the algorithm could be changed to check for convergence after each update of the bounds, which would potentially save the last iteration of the upper bounding procedure.

3.3 Finite termination

The proof follows the structure of the proof provided in [11] but considers explicitly the NLP-tolerances and the revisions to the algorithm. In order to prove finite termination of Algorithm 1, it is first proven in Lemma 1 that the successive refinement of the optimality tolerance \(\varepsilon ^{LBD,LLP}\) guarantees that a point \(\bar{\varvec{x}}^{LBD}\) can only be visited a finite number of times by (LBD), unless it is SIP-feasible. Note that due to approximate solution of (LLP), an SIP-Slater point \(\bar{\varvec{x}}^{LBD}\) can indeed be visited by (LBD) without the algorithm terminating immediately. This however, is not a problem since at this point, the lower bound LBD is sufficiently accurate for the algorithm to terminate finitely. Indeed, given Lemma 1, Lemma 2 shows that the lower bounding procedure provides an \(\varepsilon ^{LBD}\)-underestimate of \(f^*\) finitely or in the limit. Next, it is proven in Lemma 3 that the discretization point added in the upper bounding procedure is guaranteed to make the associated point \(\bar{\varvec{x}}^{UBD}\) infeasible in the following iteration of (UBD). Based on this, Lemma 4 shows that the upper bounding procedure furnishes an \(({\tilde{\varepsilon }}^f + \varepsilon ^{UBD})\)-optimal point finitely. Finally, Theorem 1 proves that, given appropriate choices of the optimality tolerances \(\varepsilon ^f\), \(\varepsilon ^{LBD}\), and \(\varepsilon ^{UBD}\), Algorithm 1 terminates finitely with an \(\varepsilon ^f\)-optimal point.

In the following, \(\{\bar{\varvec{x}}^{LBD,k}\}_{k \ge 1}\) is the sequence of points produced by approximate solutions of (LBD). For each \(\bar{\varvec{x}}^{LBD,k}\), \(\{\bar{\varvec{y}}^{LBD,j}\}_{j \in \mathcal {J}^k}\) is the sequence of points produced by approximate solutions of (LLP) for \(\bar{\varvec{x}} = \bar{\varvec{x}}^{LBD,k}\).

Lemma 1

For some \(k \ge 1\), let \(\bar{\varvec{x}}^{LBD,k}\) be SIP-infeasible (\(g^*(\bar{\varvec{x}}^{LBD,k}) > 0\)). Assume that the optimality tolerance \(\varepsilon ^{LBD,LLP}\) is tightened successively according to Algorithm 1. Then, under Assumption 4, \(\bar{\varvec{x}}^{LBD,k}\) can only be visited a finite number of times by (LBD) before one of the discretization points generated by the solution of (LLP) makes \(\bar{\varvec{x}}^{LBD,k}\) infeasible in (LBD).

Proof

It is to show that the index set \(\mathcal {J}^k\) has finite cardinality and that there exists an index \(j^k \in \mathcal {J}^k\) with \(g(\bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}) > 0\).

It holds \(g^*(\bar{\varvec{x}}^{LBD,k}) > 0\). Therefore and by approximate solution of (LLP) (Assumption 4), if at any iteration of Algorithm 1, \(\bar{\varvec{x}}^{LBD,k}\) is evaluated and it holds \(\varepsilon ^{LBD,LLP} < g^*(\bar{\varvec{x}}^{LBD,k})\), it also holds

$$\begin{aligned} g\left( \bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}\right) \ge g^+ \left( \bar{\varvec{x}}^{LBD,k}\right) - \varepsilon ^{LBD,LLP} \ge g^*\left( \bar{\varvec{x}}^{LBD,k}\right) - \varepsilon ^{LBD,LLP} > 0\nonumber \\ \end{aligned}$$
(1)

and \(\varepsilon ^{LBD,LLP}\) remains unchanged. The consequently generated discretization point \(\bar{\varvec{y}}^{LBD,j^k}\) renders \(\bar{\varvec{x}}^{LBD,k}\) infeasible in (LBD) for all following iterations. If conversely \(\bar{\varvec{x}}^{LBD,k}\) is evaluated and (1) does not hold, \(\varepsilon ^{LBD,LLP}\) is reduced. Therefore, it follows \(|\mathcal {J}^k|=1\) in the case that \(\varepsilon ^{LBD,LLP} < g^*(\bar{\varvec{x}}^{LBD,k})\) holds the first time \(\bar{\varvec{x}}^{LBD,k}\) is evaluated. Otherwise, according to Algorithm 1, \(\bar{\varvec{x}}^{LBD,k}\) is rendered infeasible in (LBD) after at most \(\lceil \log _{r^{LBD,LLP}}(\varepsilon ^{LBD,LLP}/g^*(\bar{\varvec{x}}^{LBD,k}))\rceil + 1\) reductions of \(\varepsilon ^{LBD,LLP}\). With \(r^{LBD,LLP} > 1\) and \(\varepsilon ^{LBD,LLP} \ge g^*(\bar{\varvec{x}}^{LBD,k}) > 0\) it holds \(|\mathcal {J}^k| < \infty \). \(\square \)

Remark 4

Given a finite sequence of SIP-infeasible points \(\bar{\varvec{x}}^{LBD,k}\), Lemma 1 implies that there exists a value \(\varepsilon ^{LBD,LLP} > 0\) such that each point \(\bar{\varvec{x}}^{LBD,k}\) can only be visited once by (LBD). However, the sequence of points generated by (LBD) depends on the particular instance of (SIP) and the NLP-solver used to solve the subproblems. Furthermore, it is not obvious how the existence of points \(\varvec{x} \in \mathcal {X}\) with \(g^*(\varvec{x})\) positive but arbitrarily small could be excluded for nontrivial and feasible instances of (SIP) obeying Assumption 2. Consequently, it is not obvious how to determine said value for \(\varepsilon ^{LBD,LLP}\) a priori. Similarly, given an initial value \(\varepsilon ^{LBD,LLP,0}\), it is not obvious how to determine a priori whether or not a refinement of \(\varepsilon ^{LBD,LLP}\) will become necessary.

Lemma 2

Let \(\mathcal {Y}^{LBD,0} \subsetneq \mathcal {Y}\). Then, under Assumptions 1, 2, and 4, the lower bound \(f^{LBD,-}\) produced by the lower bounding procedure of Algorithm 1 converges to an \(\varepsilon ^{LBD}\)-underestimate of the globally optimal objective value \(f^*\) of (SIP) either finitely or in the limit.

Proof

It will be shown that the lower bounding procedure furnishes an SIP-feasible point either finitely or in the limit. In both cases, it will be shown that the corresponding lower bound is an \(\varepsilon ^{LBD}\)-underestimate of \(f^*\).

If for any k, (LBD) furnishes a point \(\bar{\varvec{x}}^{LBD,k}\) with \(g^*(\bar{\varvec{x}}^{LBD,k}) \le 0\), then the lower bounding procedure has finitely furnished an SIP-feasible point. By definition of \(f^*\) and by SIP-feasibility of \(\bar{\varvec{x}}^{LBD,k}\), it holds \(f(\bar{\varvec{x}}^{LBD,k}) \ge f^*\). Furthermore, since (LBD) is a valid relaxation of (SIP) and is solved to \(\varepsilon ^{LBD}\)-optimality, it holds \(f^* \ge f^{LBD,-}\) and \(f^{LBD,-} \ge f(\bar{\varvec{x}}^{LBD,k}) - \varepsilon ^{LBD}\). Consequently,

$$\begin{aligned} f^* \ge f^{LBD,-} \ge f\left( \bar{\varvec{x}}^{LBD,k}\right) - \varepsilon ^{LBD} \ge f^* - \varepsilon ^{LBD} \end{aligned}$$

is achieved finitely.

Otherwise, it will be shown that an SIP-feasible point is generated in the limit. Consider an infinite sequence of solutions to (LBD). By compactness of \(\mathcal {X}\) and Lemma 1, an infinite subsequence can be selected with the limit point \(\hat{\varvec{x}}^{LBD} \in \mathcal {X}\), i.e., \(\bar{\varvec{x}}^{LBD,k} \xrightarrow {k \rightarrow \infty } \hat{\varvec{x}}^{LBD}\). By Lemma 1 the sequences \(\{\bar{\varvec{y}}^{LBD,j}\}_{j \in \mathcal {J}^k}\) are finite and furthermore, it holds \(g(\bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}) > 0, \; \forall k \ge 1\). By construction of (LBD), it holds

$$\begin{aligned} g\left( \bar{\varvec{x}}^{LBD,l},\bar{\varvec{y}}^{LBD,j^k}\right) \le 0, \quad \forall l,k : l > k \ge 1. \end{aligned}$$

By continuity of \(g(\cdot ,\cdot )\) on \(\mathcal {X} \times \mathcal {Y}\) and compactness of \(\mathcal {X} \times \mathcal {Y}\), \(g(\cdot ,\cdot )\) is uniformly continuous. Therefore, for any \(\varepsilon > 0\) there exists \(\delta > 0\) such that

$$\begin{aligned} g\left( \varvec{x},\bar{\varvec{y}}^{LBD,j^k}\right)< \varepsilon , \quad \forall \varvec{x} \in \mathcal {X} : ||\varvec{x} - \bar{\varvec{x}}^{LBD,l}|| < \delta , \quad \forall l,k : l > k \ge 1. \end{aligned}$$
(2)

Since \(\bar{\varvec{x}}^{LBD,k} \xrightarrow {k \rightarrow \infty } \hat{\varvec{x}}^{LBD}\), for any \(\delta > 0\) there exists K such that

$$\begin{aligned} ||\bar{\varvec{x}}^{LBD,l} - \bar{\varvec{x}}^{LBD,k}|| < \delta , \quad \forall l,k : l > k \ge K \ge 1. \end{aligned}$$
(3)

Combining (2) and (3), we obtain that for any \(\varepsilon > 0\), there exists K such that

$$\begin{aligned} g\left( \bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}\right) < \varepsilon , \quad \forall k \ge K \ge 1. \end{aligned}$$

With \(g(\bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}) > 0\) it follows that \(g(\bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}) \xrightarrow {k \rightarrow \infty } 0\). Consequently, the limit point \(\hat{\varvec{x}}^{LBD}\) is SIP-feasible, i.e.,

$$\begin{aligned} g^*\left( \hat{\varvec{x}}^{LBD}\right) = \lim _{k \rightarrow \infty } g\left( \bar{\varvec{x}}^{LBD,k},\bar{\varvec{y}}^{LBD,j^k}\right) = 0. \end{aligned}$$

By definition of \(f^*\) and by SIP-feasibility of \(\hat{\varvec{x}}^{LBD}\), it holds \(f(\hat{\varvec{x}}^{LBD}) \ge f^*\). Due to \(\bar{\varvec{x}}^{LBD,k} \rightarrow \hat{\varvec{x}}^{LBD}\) it follows by continuity of \(f(\cdot )\) that \(f(\bar{\varvec{x}}^{LBD,k}) \rightarrow f(\hat{\varvec{x}}^{LBD})\). Since (LBD) is a valid relaxation of (SIP) and by solution of (LBD) to \(\varepsilon ^{LBD}\)-optimality, the lower bounds to (LBD) converge to a value in the set

$$\begin{aligned} \left[ f \left( \hat{\varvec{x}}^{LBD}\right) - \varepsilon ^{LBD}, f^*\right] \subseteq \left[ f^* - \varepsilon ^{LBD}, f^*\right] , \end{aligned}$$

which gives the desired property. \(\square \)

In the following, \(\{\bar{\varvec{x}}^{UBD,k}\}_{k \ge 1}\) is the sequence of points produced by approximate solutions of (UBD). Furthermore, \(\{\bar{\varvec{y}}^{UBD,k}\}_{k \ge 1}\) is the sequence of points produced by approximate solutions of (LLP).

Lemma 3

For any \(k \ge 1\), under Assumption 4, either \(\bar{\varvec{x}}^{UBD,k}\) is found to be SIP-feasible, or the addition of the solution \(\bar{\varvec{y}}^{UBD,k}\) to \(\mathcal {Y}^{UBD}\) renders \(\bar{\varvec{x}}^{UBD,k}\) infeasible in the following iteration of (UBD).

Proof

Consider the first case that \(g^+(\bar{\varvec{x}}^{UBD,k}) \le 0\). With \(g^*(\bar{\varvec{x}}^{UBD,k}) \le g^+(\bar{\varvec{x}}^{UBD,k})\), it follows immediately that \(\bar{\varvec{x}}^{UBD,k}\) is found to be SIP-feasible. Otherwise it holds \(g^+(\bar{\varvec{x}}^{UBD,k}) > 0\) and by solution of (LLP) to \(\varepsilon ^{UBD,LLP}\)-optimality

$$\begin{aligned} g\left( \bar{\varvec{x}}^{UBD,k},\bar{\varvec{y}}^{UBD,k}\right) \ge g^ + \left( \bar{\varvec{x}}^{UBD,k} \right) -\varepsilon ^{UBD,LLP} > -\varepsilon ^{UBD,LLP}. \end{aligned}$$

The constraint resulting from the addition of \(\bar{\varvec{y}}^{UBD,k}\) to \(\mathcal {Y}^{UBD}\) is

$$\begin{aligned} g\left( \varvec{x},\bar{\varvec{y}}^{UBD,k}\right) \le -\varepsilon ^g. \end{aligned}$$

Due to \(\varepsilon ^{UBD,LLP} < \varepsilon ^g\), \(\bar{\varvec{x}}^{UBD,k}\) is infeasible in the following iteration of (UBD). \(\square \)

Lemma 4

Let \(\mathcal {Y}^{UBD,0} \subsetneq \mathcal {Y}\), \(\varepsilon ^{g,0} > 0\), and \(r^g > 1\). Then, under Assumptions 1, 2, 3, and 4, the upper bounding procedure furnishes an \(({\tilde{\varepsilon }}^f + \varepsilon ^{UBD})\)-optimal point \(\hat{\varvec{x}}^{UBD}\) finitely.

Proof

At each iteration of the upper bounding procedure there are three possible outcomes:

  1. 1.

    (UBD) is infeasible.

  2. 2.

    (UBD) is feasible and furnishes a point that is confirmed to be SIP-feasible by (LLP).

  3. 3.

    (UBD) is feasible and furnishes a point that is not confirmed to be SIP-feasible by (LLP).

In the former two cases, the restriction parameter \(\varepsilon ^g\) and the lower-level tolerance \(\varepsilon ^{UBD,LLP}\) are reduced. In the latter case, \(\mathcal {Y}^{UBD}\) is populated. Any point \(\varvec{x} \in \mathcal {X}\) can be characterized either as SIP-feasible or SIP-infeasible. Moreover, any point has either an objective value \(f(\varvec{x}) \le f^* + {\tilde{\varepsilon }}^f + \varepsilon ^{UBD}\) or not. It will first be shown that an infinite sequence of infeasible problems (UBD) or points \(\bar{\varvec{x}}^{UBD,k}\) with \(f(\bar{\varvec{x}}^{UBD,k}) > f^* + {\tilde{\varepsilon }}^f + \varepsilon ^{UBD}\) cannot occur. Subsequently, it will be shown that the case of an infinite sequence of SIP-infeasible points or points with undetermined SIP-feasibility cannot occur.

At all iterations it holds \(\mathcal {Y}^{UBD} \subsetneq \mathcal {Y}\). By assumption, there exists an \({\tilde{\varepsilon }}^f\)-optimal SIP-Slater point with

$$\begin{aligned} f\left( \varvec{x}^S\right) \le f^* + {\tilde{\varepsilon }}^f, \quad g\left( \varvec{x}^S,\varvec{y}\right) \le - \varepsilon ^S, \quad \forall \varvec{y} \in \mathcal {Y}. \end{aligned}$$

This point is feasible in (UBD) for \(\varepsilon ^g \le \varepsilon ^S\) irrespective of \(\mathcal {Y}^{UBD}\). Therefore, (UBD) is feasible for \(\varepsilon ^g \le \varepsilon ^S\) irrespective of \(\mathcal {Y}^{UBD}\). Moreover, the approximate global solution of (UBD) guarantees that for \(\varepsilon ^g \le \varepsilon ^S\), the upper bounding procedure produces points \(\bar{\varvec{x}}^{UBD,k}\) with

$$\begin{aligned} f\left( \bar{\varvec{x}}^{UBD,k}\right) \le f\left( \varvec{x}^S\right) + \varepsilon ^{UBD} \le f^* + {\tilde{\varepsilon }}^f + \varepsilon ^{UBD}. \end{aligned}$$

The restriction parameter \(\varepsilon ^g\) is updated if and only if (UBD) is infeasible, or it furnishes an SIP-feasible point \(\bar{\varvec{x}}^{UBD,k}\). As a consequence, after \(\lceil \log _{r^g}(\varepsilon ^{g,0}/\varepsilon ^S)\rceil \) updates of \(\varepsilon ^g\) the upper bounding problem generates points \(\bar{\varvec{x}}^{UBD,k}\) with \(f(\bar{\varvec{x}}^{UBD,k}) \le f^* + {\tilde{\varepsilon }}^f + \varepsilon ^{UBD}\). If one of these points is found to be SIP-feasible, the algorithm terminates. Otherwise, the restriction parameter is not updated beyond a final value \(\varepsilon ^{g,\text {min}} \ge \varepsilon ^S/r^g\).

It remains to be shown that it is impossible for (UBD) to furnish an infinite sequence of SIP-infeasible points or points with undetermined SIP-feasibility. Since \(\varepsilon ^g \ge \varepsilon ^{g,\text {min}} > 0\) holds for all iterations, this can be proven similarly to Lemma 2. Consider an infinite sequence of solutions to instances of (UBD). By compactness of \(\mathcal {X}\) and Lemma 3, we can select a convergent subsequence \(\bar{\varvec{x}}^{UBD,k} \xrightarrow {k \rightarrow \infty } \hat{\varvec{x}}^{UBD}\), \(\hat{\varvec{x}}^{UBD} \in \mathcal {X}\). Consider the corresponding solutions to (LLP) \(\bar{\varvec{y}}^{UBD,k}\). By construction of (UBD) we have

$$\begin{aligned} g\left( \bar{\varvec{x}}^{UBD,l},\bar{\varvec{y}}^{UBD,k}\right) \le -\varepsilon ^{g,\text {min}}, \quad \forall l,k : l > k \ge 1. \end{aligned}$$

By continuity of \(g(\cdot ,\bar{\varvec{y}}^{UBD,k})\) and compactness of \(\mathcal {X}\), \(g(\cdot ,\bar{\varvec{y}}^{UBD,k})\) is uniformly continuous on \(\mathcal {X}\). Therefore, for any \(0< \gamma < 1\), there exists \(\delta > 0\) such that

$$\begin{aligned} g\left( \varvec{x},\bar{\varvec{y}}^{UBD,k}\right)< -\gamma \varepsilon ^{g,\text {min}}< 0, \quad \forall \varvec{x} \in \mathcal {X} : ||\varvec{x} - \bar{\varvec{x}}^{UBD,l}|| < \delta , \quad \forall l,k : l > k \ge 1.\quad \end{aligned}$$
(4)

Since \(\bar{\varvec{x}}^{UBD,k} \xrightarrow {k \rightarrow \infty } \hat{\varvec{x}}^{UBD}\), for any \(\delta > 0\), there exists K such that

$$\begin{aligned} ||\bar{\varvec{x}}^{UBD,l} - \bar{\varvec{x}}^{UBD,k}|| < \delta , \quad \forall l,k : l > k \ge K \ge 1. \end{aligned}$$
(5)

Combining (4) and (5) yields that for any \(0< \gamma < 1\) there exists K such that

$$\begin{aligned} g\left( \bar{\varvec{x}}^{UBD,k},\bar{\varvec{y}}^{UBD,k}\right)< -\gamma \varepsilon ^{g,\text {min}} < 0, \quad \forall k : k \ge K \ge 1. \end{aligned}$$

Therefore, after a finite number K of iterations, the points furnished by the upper bounding procedure are SIP-feasible. Moreover, since \(\varepsilon ^{UBD,LLP} < \varepsilon ^{g,\text {min}}\), these points are found by (LLP) to be SIP-feasible. \(\square \)

Remark 5

In Lemma 4, it is used that \(\varepsilon ^g\) is not updated beyond a final value \(\varepsilon ^{g,\text {min}} \ge \varepsilon ^S/r^g\). It follows by Algorithm 1 that the tolerance \(\varepsilon ^{UBD,LLP}\) is not updated beyond \(\varepsilon ^{g,\text {min}}/r^{UBD,LLP}\). By extension, setting \(\varepsilon ^{UBD,LLP,0} < \varepsilon ^S/r^g\) would render the tolerance update obsolete. However, determining \(\varepsilon ^S\) usually requires the solution of (SIP). Consequently, finding a value for \(\varepsilon ^{UBD,LLP,0}\) a priori that guarantees that no tolerance updates are required is usually not possible.

Theorem 1

Let \(\varepsilon ^f\), \(\varepsilon ^{LBD}\), and \(\varepsilon ^{UBD}\) be chosen such that

$$\begin{aligned} \varepsilon ^f > {\tilde{\varepsilon }}^f + \varepsilon ^{LBD} + \varepsilon ^{UBD}. \end{aligned}$$

Then, under Assumptions 1, 2, 3, and 4, Algorithm 1 terminates finitely with an \(\varepsilon ^f\)-optimal point \(\varvec{x}^*\).

Proof

By Lemma 2, the lower bound \(f^{LBD,-}\) converges to an \(\varepsilon ^{LBD}\)-underestimate of \(f^*\), i.e.,

$$\begin{aligned} \lim _{k \rightarrow \infty } f^{LBD,-,k} \in \left[ f^* - \varepsilon ^{LBD}, f^*\right] , \end{aligned}$$

with the lower bound \(f^{LBD,-,k}\) produced by instance k of (LBD). Therefore, for any \(\delta > 0\) there exists \(K^{LBD}\) such that

$$\begin{aligned} f^{LBD,-,k} \ge f^* - \varepsilon ^{LBD} - \delta , \quad \forall k > K^{LBD} \ge 0. \end{aligned}$$
(6)

By Lemma 4, after a finite number \(K^{UBD}\) of instances of (UBD), the upper bounding procedure furnishes an \(({\tilde{\varepsilon }}^f + \varepsilon ^{UBD})\)-optimal point \(\hat{\varvec{x}}^{UBD}\). It holds

$$\begin{aligned} f\left( \bar{\varvec{x}}^{UBD,k}\right) \le f^* + {\tilde{\varepsilon }}^f + \varepsilon ^{UBD}, \quad \forall k > K^{UBD} \ge 0. \end{aligned}$$
(7)

Combining (6) and (7) and choosing \(\delta = \varepsilon ^f - {\tilde{\varepsilon }}^f - \varepsilon ^{LBD} - \varepsilon ^{UBD} > 0\), we obtain that there exists a finite number \(K = \max \{K^{LBD}, K^{UBD}\}\) of iterations of Algorithm 1 such that

$$\begin{aligned} f\left( \bar{\varvec{x}}^{UBD,K}\right) - f^{LBD,K} \le \varepsilon ^f, \end{aligned}$$

at which point the algorithm terminates with an \(\varepsilon ^f\)-optimal point. \(\square \)

Recall that \(\varepsilon ^f\), \(\varepsilon ^{UBD}\), and \(\varepsilon ^{LBD}\) are tolerances set as inputs to Algorithm 1. \({\tilde{\varepsilon }}^f\) on the other hand is assumed to be nonzero and is, in general, unknown a priori. In case \({\tilde{\varepsilon }}^f\) is known, \(\varepsilon ^{LBD}\) and \(\varepsilon ^{UBD}\) should be chosen such that the desired \(\varepsilon ^f\) can be guaranteed. Absent such information, it may be assumed that \({\tilde{\varepsilon }}^f\) is of similar magnitude as the chosen \(\varepsilon ^{LBD}\) and \(\varepsilon ^{UBD}\). In any case, \(\varepsilon ^{LBD}\) and \(\varepsilon ^{UBD}\) should be substantially smaller, e.g., by one order of magnitude, than \(\varepsilon ^f\).

3.4 Choice of parameter values and benchmark problem

Although the algorithm is guaranteed to converge finitely under Assumptions 1, 2, 3, and 4, its computational performance is subject to the choice of the parameters \(\varepsilon ^{g,0}\) and \(r^g\). In the following, small values for \(\varepsilon ^{g,0}\) and large values for \(r^g\) are termed aggressive since such a choice is aimed at achieving the termination criterion in few updates of the restriction parameter. Accordingly, large values for \(\varepsilon ^{g,0}\) and small values for \(r^g\) are termed conservative. In general, for aggressive parameter choices, the worst case number of reductions of \(\varepsilon ^g\) that is required to obtain feasibility in (UBD) of a point \(\varvec{x}\) with \(f(\varvec{x}) \le f^* + \varepsilon ^f\) is lower than for conservative choices. However, if a small value for \(\varepsilon ^g\) is reached before \(\mathcal {Y}^{UBD}\) is sufficiently populated, the subsequent solutions of (UBD) may furnish many SIP-infeasible points before \(\mathcal {Y}^{UBD}\) contains the discretization points that entail an SIP-feasible iterate. This phenomenon manifests in a dense population of \(\mathcal {Y}^{UBD}\) and slow convergence of the upper bound.

For the initial restriction \(\varepsilon ^{g,0}\), the above discussion suggests that a conservative choice is appropriate. Starting with an aggressive value for \(\varepsilon ^g\) would defeat the purpose of Algorithm 1, which is to find a small discretization that appropriately represents (SIP). While there are problems that are not particularly prone to a dense population of \(\mathcal {Y}^{UBD}\), choosing a small value \(\varepsilon ^{g,0}\) for an unknown problem seems to be undesirable.

The reduction parameter \(r^g\) has already been discussed as pivotal by Mitsos [11]. Therein, it was shown for certain test problems that a wide range of values (approximately \(r^g \in [2,20]\)) yields acceptable results for overall performance of the algorithm. Here we expand on that analysis by considering the impact on the upper bounding procedure specifically. If overall algorithm performance is considered, a slowly converging lower bounding procedure may mask the impact of the choice of parameters on the upper bounding procedure. In order to explore the possible adverse impact of an aggressive choice of \(r^g\), consider the dense population problem (DP) described by

figure e

Figure 1 depicts the objective function \(f(\cdot ) \), multiple instances \(g(\cdot ,y^i)\) of the semi-infinite constraint, as well as the parametric optimal objective value \(g^*(\cdot )\) of (LLP). While the problem is equivalently represented by a single instance of the semi-infinite constraint (\(y = 2\)), it is expected that this instance is not found immediately by Algorithm 1 because it is the solution to (LLP) for values \({\bar{x}} \in \mathcal {X}\) with relatively large objective value \(f({\bar{x}})\). Rather, it is expected that the upper bounding procedure furnishes \({\bar{x}}^{UBD}\) of large value. The corresponding solutions of (LLP) in turn yield large values \({\bar{y}}\). For these parameter values, \(g(x,{\bar{y}}) \le 0\) holds for values x that are only slightly lower than \({\bar{x}}^{UBD}\). Therefore, if \(\varepsilon ^g\) is very small, many iterations are required, until an SIP-feasible point is found. Furthermore, since (LBD) is equivalent to (UBD) for \(\varepsilon ^g = 0\), it is also expected to converge slowly on this problem.

Fig. 1
figure 1

Benchmark problem (DP): Objective function \(f(\cdot )\), constraint function instances \(g(\cdot ,y^i)\) for \(y^i \in \{2,3,4,5\}\), and parametric optimal objective value of (LLP) \(g^*(\cdot )\). Optimal solution: \(x^{*} = 2\) with \(f(x^{*}) = 8\)

Full size image
Table 1 Benchmark results for (UBD) on problem (DP)
Full size table

Table 1 contains the benchmark results for the upper bounding procedure in problem (DP). It can be observed that the number discretization points that are added to \(\mathcal {Y}^{UBD}\) depends on the reduction parameter \(r^g\). The more aggressive the choice, the more points are added due to SIP-infeasible iterates of the upper bounding procedure. Furthermore, the computational times required for the upper bound to converge are adversely impacted by aggressive choices for \(r^g\). In the following section, a strategy is presented that aims at providing an adaptive restriction update that remains conservative on problems like (DP) and provides aggressive parameter updates when possible.

4 Hybrid algorithm

In this section, a hybrid algorithm is derived by employing subproblems from Algorithm 1 and an oracle problem adapted from Tsoukalas and Rustem [24]. The hybridization provides an adaptive update to the restriction parameter \(\varepsilon ^g\) in order to circumvent the problem of a dense discretization \(\mathcal {Y}^{UBD}\). The aim is for the update to reduce the restriction parameter quickly when possible while avoiding a dense population of \(\mathcal {Y}^{UBD}\) in problems similar to (DP). The original oracle problem is reviewed in Sect. 4.1 and adapted for hybridization in Sect. 4.2. In Sect. 4.3, the hybrid algorithm is formally stated and a proof of finite convergence is given in Sect. 4.4.

4.1 An oracle problem

Similarly to Algorithm 1, the algorithm proposed by Tsoukalas and Rustem [24] solves (SIP) by solving multiple finite subproblems which are obtained through discretization of the parameter set \(\mathcal {Y}\). A so-called oracle problem is solved to determine whether or not a certain target objective function value is attainable by (SIP). Based on this problem, a binary search of the objective function space is performed, which under slightly stronger assumptions than previously, yields an \(\varepsilon ^f\)-optimal point finitely. In a previous publication [25], the authors use a stochastic global optimization algorithm to solve the subproblems of a similar algorithm for generalized semi-infinite programs and related problems.

The central subproblem of the algorithm is the oracle problem (ORA). For given lower and upper bounds LBD and UBD on \(f^*\), a target objective value is set to \(f^{ORA} = \tfrac{1}{2}(LBD + UBD)\). With a finite discretization \(\mathcal {Y}^{ORA} \subsetneq \mathcal {Y}\) the oracle problem is the program

$$\begin{aligned} \underset{\varvec{x} \in \mathcal {X}}{\text {min}}\,\max \left\{ f(\varvec{x})-f^{ORA}, \max _{\varvec{y} \in \mathcal {Y}^{ORA}} g(\varvec{x},\varvec{y})\right\} . \end{aligned}$$

To facilitate comparability with the subproblems (LBD) and (UBD), the oracle problem is here rewritten equivalently as

figure f

The oracle problem can be understood as a decision problem that determines whether or not the target objective value \(f^{ORA}\) is attainable by (LBD) with the discretization \(\mathcal {Y}^{LBD} = \mathcal {Y}^{ORA}\). If \(\zeta ^*\) is negative, then there exists no point \(\bar{\varvec{x}}^{ORA} \in \mathcal {X}\) that is feasible with respect to the discretized semi-infinite constraint and has an objective value \(f(\bar{\varvec{x}}^{ORA}) \le f^{ORA}\). Consequently, \(f^{ORA}\) is a lower bound to (LBD) with \(\mathcal {Y}^{LBD} = \mathcal {Y}^{ORA}\) and by the properties of (LBD) also a lower bound to (SIP). If, in contrast, \(\zeta ^*\) is non-negative and the solution point \(\bar{\varvec{x}}^{ORA}\) of (ORA) is SIP-feasible, \(f(\bar{\varvec{x}}^{ORA})\) is an upper bound to (SIP). Considering that \(f^{ORA}\) is always chosen below the current upper bound on (SIP), \(f(\bar{\varvec{x}}^{ORA})\) is an update to the upper bound. The third possible outcome (\(\zeta ^* \ge 0\) and \(\bar{\varvec{x}}^{ORA}\) SIP-infeasible) does not yield information about bounds on the globally optimal objective value of (SIP). In this case, \(\mathcal {Y}^{ORA}\) is refined to yield a conclusive instance of (ORA) in a following iteration.

Remark 6

Due to the possibility of an instance of (ORA) being non-conclusive, the number of iterations needed to obtain a certain optimality tolerance is not known a priori.

Due to the choice \(f^{ORA} = \tfrac{1}{2}(LBD + UBD)\), the bound update resulting from the solution of (ORA) will always be the update that closes the gap between lower and upper bound the furthest. Indeed, consider the case \(f^{ORA} \ge f^*\). Obviously, \(f^{ORA}\) is an upper bound and when an SIP-feasible point \(\bar{\varvec{x}}^{ORA}\) is found, it holds

$$\begin{aligned} UBD - f\left( \bar{\varvec{x}}^{ORA}\right) \ge UBD - f^{ORA} = f^{ORA} - LBD \ge f^* - LBD, \end{aligned}$$

where \(UBD - f(\bar{\varvec{x}}^{ORA})\) is the reduction in the gap due to the new upper bound \(f(\bar{\varvec{x}}^{ORA})\) and \(f^* - LBD\) is the maximum possible reduction in the gap due to an exact lower bound. Similarly, if \(f^{ORA} < f^*\), it holds

$$\begin{aligned} f^{ORA} - LBD = UBD - f^{ORA} > UBD - f^*, \end{aligned}$$

where \(UBD - f^*\) is the maximum possible reduction in the gap due to an exact upper bound.

The second subproblem is the lower-level program (LLP). It is solved to determine SIP-feasibility of a point \(\bar{\varvec{x}}^{ORA}\) or populate the discretization \(\mathcal {Y}^{ORA}\).

The algorithm must be initialized with lower and upper bounds on \(f^*\) based on which the binary search on the objective function space is performed. Finite termination of the algorithm is contingent on Assumptions 1, 2, as well as the exact solution of all subproblems. Obviously, the latter assumption is stronger than both Assumption 4 and the original assumption by Mitsos [11] on the approximate solution of subproblems. Furthermore, it is required that the case \(f^{ORA} = f^*\) does not occur and that \(g^*(\cdot )\) does not have a local minimum with value 0 at the exact global solution of (SIP). This last assumption can be compared to Assumption 3. Given the structure of (SIP), the assumption by Tsoukalas and Rustem [24] gives \({\tilde{\varepsilon }}^f\)-optimal SIP-Slater points for arbitrarily small \({\tilde{\varepsilon }}^f\) and is therefore stronger than Assumption 3. This relation has previously been observed by Mitsos and Tsoukalas [14] for similar assumptions used in the context of generalized semi-infinite programs in [25] and [14]. A formal statement of the oracle algorithm is given in “Appendix 1”.

4.2 Adapted oracle problem

With respect to Algorithm 1 and especially with respect to a dense population of \(\mathcal {Y}^{UBD}\), an alternative interpretation of (ORA) is useful. In (ORA), the dummy variable \(-\zeta \) is bounded from below by \(f(\varvec{x})\,-\,f^{ORA}\) and also by \(g(\varvec{x},\varvec{y})\) for all \(\varvec{y} \in \mathcal {Y}^{ORA}\). Therefore, the objective of (RES) is a compromise between minimizing \(f(\varvec{x})\) and maximizing the restriction of the discretized semi-infinite constraint such that the solution point remains feasible with respect to the restricted constraints. In particular, if (ORA) returns \(\zeta ^* \ge 0\), a point \(\bar{\varvec{x}}^{ORA}\) is guaranteed to exist with objective value \(f(\bar{\varvec{x}}^{ORA}) \le f^{ORA}\) that is feasible in (UBD) with \(\mathcal {Y}^{UBD} = \mathcal {Y}^{ORA}\) and \(\varepsilon ^g = \zeta ^*\). If beyond that, \(\bar{\varvec{x}}^{ORA}\) is SIP-feasible, \(f(\bar{\varvec{x}}^{ORA})\) is an upper bound to (SIP), and \(\varepsilon ^g = \zeta ^*\) is a value for the restriction parameter under which the current upper bound is attainable by (UBD) with \(\mathcal {Y}^{UBD} = \mathcal {Y}^{ORA}\). Since the objective of a subsequent solution of (UBD) is to improve on the upper bound, \(\varepsilon ^g = \zeta ^*\) may be considered a sensible choice for (UBD). However, due to the involvement of term \(f(\varvec{x}) - f^{ORA}\), \(\zeta ^*\) may still be an aggressive choice, which would not solve the problem of a dense population of \(\mathcal {Y}^{UBD}\) described in Sect. 3.4.

For this reason, we propose the adapted problem (RES) to provide lower and upper bounds as well as a truly conservative choice of the restriction parameter.

figure g

Note that (RES) has the same bounding and decision properties as (ORA). If \(\eta ^*\) is negative, \(f^{RES}\) is a lower bound to (SIP). If \(\eta ^*\) is non-negative and the solution point \(\bar{\varvec{x}}^{RES}\) is SIP-feasible, \(f(\bar{\varvec{x}}^{RES})\) is an upper bound to (SIP) and provided \(f^{RES} < UBD\) an update to the upper bound. Beyond that, in the case of an SIP-feasible solution \(\bar{\varvec{x}}^{RES}\), \(\varepsilon ^g = \eta ^*\) is the largest possible restriction under which \(f(\bar{\varvec{x}}^{RES})\) is attainable by (UBD) for \(\mathcal {Y}^{UBD} = \mathcal {Y}^{RES}\). Therefore, provided that (UBD) and (RES) utilize the same discretization, any choice \(\varepsilon ^g > \eta ^*\) will not decrease the upper bound further. Since (RES) considers the objective function only in form of a constraint, it is possible that (UBD) can improve on the upper bound for \(\varepsilon ^g = \eta ^*\). However, it is expected that this will only yield small improvements and that a choice \(\varepsilon ^g = \eta ^*/r^g\) with a small value for \(r^g\) will yield better results.

While these properties are desirable in the context of an adaptive update of \(\varepsilon ^g\), (RES) cannot be guaranteed to be conclusive regardless of the discretization \(\mathcal {Y}^{RES}\) under Assumptions 1, 2, 3, and 4. While very unlikely, the following proposition illustrates the point.

Proposition 1

Let \(f^{RES} = f^*\). Then, under Assumptions 1, 2, 3, and 4, (RES) cannot be guaranteed to be conclusive.

Proof

Since \(f^{RES}\) is the exact global solution to (SIP), it is both an exact lower and upper bound. We will show that based on approximate solution of (RES) and (LLP), it cannot be guaranteed to be confirmed to be either.

Due to \(f^{RES}=f^*\), it holds \(\eta ^+ \ge 0\) irrespective of \(\mathcal {Y}^{RES}\). Therefore, the condition for the detection of a lower bound (\(\eta ^+ < 0\)) cannot be reached.

Furthermore, consider the following example, for which \(f^{RES}\) cannot be found to be an upper bound. Suppose that the exact globally optimal solution \(\varvec{x}^*\) of (SIP) is unique and that it holds \(g^*(\varvec{x}^*) = 0\), which does not conflict with any of the assumptions. Then, \(\varvec{x}^*\) is the only SIP-feasible point that is also feasible in (RES). Therefore, in order to decide \(f^{RES}\) to be an upper bound to (SIP), (LLP) must be solved for \(\varvec{x}^*\) such that \(g^+(\varvec{x}^*) = 0\). This, in turn, can only be guaranteed under the assumption of exact solution of (LLP). \(\square \)

As mentioned, this scenario is very unlikely and numerical experiments confirm that this property has little impact on algorithm performance. However, to guarantee convergence under the given assumptions, it must be ensured that (RES) cannot lead to an infinite loop in which discretization points are added to \(\mathcal {Y}^{RES}\). This is done by deferring to (LBD) whenever (RES) fails to be conclusive.

4.3 Algorithm statement

Here, the hybrid algorithm is stated formally based on the subproblems (LBD), (UBD), (RES), and (LLP). All subproblems are assumed to be solved approximately according to Definition 1 with their respective tolerances \(\varepsilon ^{LBD}, \varepsilon ^{UBD}, \varepsilon ^{RES}, \varepsilon ^{LLP} > 0\). The subproblems (LBD), (UBD), and (RES) operate on a single discretization set \(\mathcal {Y}^{LBD} = \mathcal {Y}^{UBD} = \mathcal {Y}^{RES} = \mathcal {Y}^D\) to leverage the properties discussed in Sect. 4.1. Due to the shared discretization, there is also a shared tolerance \(\varepsilon ^{LLP}\) used for all problems to ensure the appropriate accuracy of the entries in the discretization.

figure h

Remark 7

Similar to Algorithm 1, the algorithm could be changed to check for convergence after each update of the bounds, which would potentially save the solution of one subproblem instance.

In Algorithm 2, the lower bounding problem (LBD) serves mainly the purpose of initializing the lower bound on (SIP). Due to the decision properties discussed in Sect. 4.1, (RES) is preferred for lower bounding. (LBD) is only used in the main loop of the algorithm if (RES) fails to be conclusive. Note that (RES) can only loop onto itself a finite number of times before it either provides a bound update or defers to one of the subproblems from Algorithm 1. Therefore, Algorithm 2 inherits the convergence guarantees from Algorithm 1. Nevertheless, for the sake of completeness, a formal proof of convergence is given in the following section.

4.4 Finite termination

The proof of finite termination for Algorithm 2 relies on Lemmata 1, 2, 3, and 4.

Theorem 2

Let \(\varepsilon ^f\), \(\varepsilon ^{LBD}\), and \(\varepsilon ^{UBD}\) be chosen such that

$$\begin{aligned} \varepsilon ^f > {\tilde{\varepsilon }}^f + \varepsilon ^{LBD} + \varepsilon ^{UBD}. \end{aligned}$$

Then, under Assumptions 1, 2, 3, and 4, Algorithm 2 terminates finitely with an \({\tilde{\varepsilon }}^f\)-optimal point \(\varvec{x}^*\).

Proof

By Lemma 2, the lower bounds \(f^{LBD,-,k}\) to (LBD) converge to an \(\varepsilon ^{LBD}\)-underestimate of \(f^*\), i.e.,

$$\begin{aligned} \lim _{k \rightarrow \infty } f^{LBD,-,k} \in \left[ f^* - \varepsilon ^{LBD}, f^*\right] . \end{aligned}$$

Therefore, for any \(\delta > 0\) there exists a \(K^{LBD}\) such that

$$\begin{aligned} f^{LBD,-,k}> f^* - \varepsilon ^{LBD} - \delta , \quad \forall k > K^{LBD}. \end{aligned}$$
(8)

By Lemma 4, after a finite number \(K^{UBD}\) of instances of (UBD), the upper bounding procedure furnishes an \(({\tilde{\varepsilon }}^f + \varepsilon ^{UBD})\)-optimal point \(\hat{\varvec{x}}^{UBD}\). It holds

$$\begin{aligned} f\left( \bar{\varvec{x}}^{UBD,l}\right) \le f^* + {\tilde{\varepsilon }}^f + \varepsilon ^{UBD}, \quad \forall l > K^{UBD}. \end{aligned}$$
(9)

Combining (9) and (10), we obtain

$$\begin{aligned} f\left( \bar{\varvec{x}}^{UBD,l}\right) - f^{LBD,-,k}< {\tilde{\varepsilon }}^f + \varepsilon ^{UBD} + \varepsilon ^{LBD} < \varepsilon ^f, \quad \forall k> K^{LBD}, l > K^{UBD} \end{aligned}$$

The first solution of (LBD) is guaranteed to provide a finite value for the lower bound \(LBD > -\infty \). Similarly, after a finite number of instances of (UBD), a finite value for the upper bound \(UBD < \infty \) is found. Therefore, the gap \(\Delta f = UBD - LBD\) is finite when (RES) is solved for the first time.

For any \(f^{RES} = \tfrac{1}{2}(LBD + UBD)\), (RES) is only solved a finite number of times. At this point, if a lower bound \(LBD = f^{RES}\) is obtained, (RES) is solved for the updated \(f^{RES}\). If an upper bound \(UBD = f(\bar{\varvec{x}}^{RES}) \le f^{RES}\) is obtained, (UBD) is solved. Otherwise, (LBD) and (UBD) are solved. After at most

$$\begin{aligned} K^{RES} = \log _{2}\left( \Delta f/\varepsilon ^f\right) \end{aligned}$$
(10)

bound updates by (RES), the optimality tolerance \(\varepsilon ^f\) is reached.

(RES) either provides \(K^{RES}\) bound updates or refers \(K^{LBD}\) times to (LBD). Either way, the optimality tolerance \(\varepsilon ^f\) is achieved finitely. \(\square \)

Note that the tolerance \(\varepsilon ^{RES}\) is not required to fulfill any condition. This is due to the fact, that the convergence guarantee is inherited from Algorithm 1. The same is true for the solutions of (LLP) at the solution points of (RES).

5 Generalizations

In this section, the generalizations to multiply constrained SIPs and mixed-integer SIPs are discussed. For the latter case, the discussion provided by Mitsos [11] is fully applicable to Algorithm 2 and consequently, these problems pose no additional challenge as long as an MINLP-solver is available that satisfies Assumption 4.

Consider the generalization of (SIP) to multiple semi-infinite constraints according to

Algorithm 2 is applicable with minor alterations. In particular, multiple lower-level problems must be solved to determine SIP-feasibility of a given point \(\bar{\varvec{x}}\). Furthermore, two questions emerge concerning the number of discretizations and restriction parameters to use. With respect to the number of discretizations, there is no reason to expect the use of one shared discretization is justified in the general case. This was observed previously by Mitsos [11]. With respect to the number of restriction parameters, the introduction of the restriction update changes prior observations. There are two possibilities to preserve the bounding and decision properties of (RES) when considering multiple constraints:

  1. 1.

    One instance of (RES) is used, in which \(\eta \) is bounded by all constraints. This results in a single update to a shared restriction parameter.

  2. 2.

    An instance of (RES) is introduced for each constraint, such that \(\eta \) is bounded by only one constraint, while all other constraints are considered in their original form. This results in a dedicated restriction parameter for each constraint.

While the latter option is preferable in terms of the conservatism of the updates to the restriction, it has disadvantageous solution properties. Indeed, such a problem is similar to (LBD) with respect to the constraints not bounding \(\eta \). As a consequence, the finite generation of an SIP-feasible point cannot be guaranteed even under strong assumptions. Therefore, the former option seems more promising.

6 Numerical results

Algorithms 1, 2, and 3 are implemented in the general algebraic modeling system (GAMS) 24.3.1 [17] with the GAMS-F preprocessor. Note that in the implementation of Algorithm 3 in “Appendix 1”, a single instance of (LBD) is solved to initialize the lower bound with a finite value. This initialization is not part of the original algorithm by Tsoukalas and Rustem [24] and is added to remove the requirement for an initial lower bound. Furthermore, while the authors require a finite initial value for the upper bound, this is not necessary since the first instance of (ORA) with \(f^{ORA} = \infty \) is guaranteed to provide a finite upper bound. The NLP subproblems are solved with BARON 14.0.2 [18, 23]. The implementation of the algorithms is available in the supplementary material. All numerical experiments were run on a 64-bit Intel Core i3-2100 CPU with 3.1 GHz running Windows 7.

The test set consists of small-scale SIPs with up to six variables, two parameters, and four semi-infinite constraints, most of which were proposed by Watson in [26] and in some cases corrected by Mitsos et al. in [13]. The problems 2, 5, 6, 7, 8, and 9 were selected from the Watson test set, taking the corrections by [13] into account. Problems 1, 3, and 4 were excluded due to the involvement of trigonometric functions, which cannot be handled by BARON. Beyond that, the problems H, N, S, and the design centering problems D1_0_1 through D2_1_2 by Mitsos were added alongside the newly proposed dense population problem (DP). All benchmark problems are available in [9] and in the supplementary material. The labels of the problems are kept in line with the labels in the original publications while the dense population problem is labeled as DP.

All algorithms are initialized with empty initial discretizations \(\mathcal {Y}^{LBD,0} = \mathcal {Y}^{UBD,0} = \mathcal {Y}^{ORA,0} = \mathcal {Y}^{D,0} = \emptyset \). The initial restriction parameter \(\varepsilon ^{g,0}\) is set to 1 in all cases but the problem DP, where a value of 8 is used. For all cases, the optimality tolerances are set to \(\varepsilon ^f = 10^{-3}\) and \(\varepsilon ^{LBD} = \varepsilon ^{UBD} = \varepsilon ^{ORA} = \varepsilon ^{RES} = \varepsilon ^{LLP,0} = \varepsilon ^{LBD,LLP,0} = \varepsilon ^{UBD,LLP,0} = \varepsilon ^{ORA,LLP,0} = \varepsilon ^{RES,LLP,0} = 10^{-4}\). \(\varepsilon ^f\), \(\varepsilon ^{LBD}\), \(\varepsilon ^{UBD}\), \(\varepsilon ^{ORA}\), and \(\varepsilon ^{RES}\) are used as both absolute and relative tolerances. Further NLP-solver options are \(\text {lpsol} = 3\), \(\text {nlpsol} = 4\), \(\text {contol} = 10^{-12}\), \(\text {boxtol} = 10^{-3}\), and \(\text {inttol} = 10^{-9}\). The complete results are given in Tables 2, 3, 4 and 5 in “Appendix 2”.

In general terms, it can be observed that all algorithms show promise with respect to their scaling properties, which has previously been observed for Algorithm 1 in [11]. Indeed, while problems 7, 8, and 9 exhibit two-dimensional parameter sets \(\mathcal {Y}\), they only require moderately more or similarly many NLP solutions as the problems with one-dimensional parameter sets. Note that the design centering problems D1_0_1 through D2_1_2 exhibit up to four semi-infinite constraints, each generating a lower-level problem that is solved to establish SIP-feasibility. Therefore, the relatively large number of NLPs solved is expected. Furthermore, the majority of the relatively large CPU requirement on these problems is due the relatively expensive problems (LBD), (UBD), (RES), and (ORA) with up to six dimensions in \(\mathcal {X}\). This indicates that for the tested algorithms, the difficulty of an SIP is mainly determined by the difficulty of the NLP subproblems. Note however that this inference is drawn from the numerical results on a limited test set and does not derive from a theoretical analysis of the scaling properties of the algorithms.

Fig. 2
figure 2

Performance plot for the algorithm by Mitsos [11], Algorithm 1 (\(r^g = 1.2, 2.0\)), the algorithm by Tsoukalas and Rustem [24], Algorithm 3, and the hybrid algorithm, Algorithm 2 (\(r^g = 1.2\))

Full size image

Figure 2 depicts the performance plot comparing the tested algorithms on all problems in the test set. It can be observed that only the algorithm by Mitsos (Algorithm 1) and the hybrid algorithm (Algorithm 2) solve all problems. This is expected because of the stronger assumptions required for convergence of Algorithm 3. Indeed, in every case the failure of Algorithm 3 is due to either (ORA) or (LLP) failing to be conclusive. Recall that this is due to the use of Algorithm 3 with the approximate solution of subproblems, which violates the assumptions in [24]. Therefore, finite convergence is not guaranteed and the large number of failed problem instances can be explained.

Beyond the number of solved problems, the hybrid algorithm offers the best overall performance, both in terms of the number of quickest solutions and in terms of the time factor in adverse cases. Particularly the superior performance compared to Algorithm 1 with aggressive parameter choice \(r^g = 2\), which in turn is superior to Algorithm 1 with \(r^g = 1.2\) indicates that the adaptive restriction allows the hybrid algorithm to produce competitive results despite employing a conservative reduction parameter.

7 Conclusions

A hybrid of two existing discretization algorithms for the global solution of SIPs is proposed. The algorithm employs a lower and an upper bounding problem of a bounding algorithm [11] and an adapted problem from an oracle algorithm [24]. The upper bounding problem is based on discretization and the restriction of the right-hand-side of semi-infinite constraints. Adaptive updates to the restriction parameter are introduced through the hybridization with the oracle algorithm. By virtue of the adaptive restriction, the algorithm hedges against a dense population the discretization of the parameter set and the associated poor performance. Employing a loosened assumption on the solution of the NLP subproblems, the algorithm is guaranteed to terminate finitely with an \(\varepsilon ^f\)-optimal point finitely under weaker assumptions than its predecessors. The superiority of the hybrid approach is demonstrated through theoretical discussion and numerical experiments.

One possible variant of the hybrid algorithm is the solution of the added oracle problem by stochastic solvers as was done by the authors of the original oracle algorithm [25]. Possibly improving overall performance through the quicker solution of the oracle problem, this would leave the convergence guarantees intact since the solutions of the oracle problem do not need to fulfill any conditions for the algorithm to converge. Another possible task for future work is the initialization of the discretization sets to nonempty sets. While empty sets are used here to investigate the core functionality of the algorithms, nonempty sets promise performance gains, which may allow the application of the proposed methods to larger problems.