A general method for analog test point selection using multi-frequency analysis

Abstract

An important problem that arises in analog testing for fault dictionary approach is the test point selection. It consists of selecting a minimum set of test points to achieve the highest percentage of isolation. By using the concepts of ambiguity set and integer-coded dictionary, it can be formulated as a combinatorial optimization problem. On the basis of the formulation, this paper develops a general and accurate method for test point selection. This is achieved by presenting a new ambiguity set partition method based on hierarchical clustering and an improved entropy index method. Besides, multi-frequency analysis is also incorporated in the described method. The proposed method is tested and compared with exhaustive search through its application to two benchmark circuits. The results indicate that, compared with the extant methods, our method search for a test point set that not only includes a minimum number of test points but also has a good performance in terms of diagnostic accuracy and fault isolation rate. Meanwhile, the proposed method can be extended to deal with the problem of test point selection for some specific fault model.

1 Introduction

Analog testing has gained widespread attention recently due to the rapid growth in the development of analog VLSI chips, mixed-signal systems, and system on chip (SoC) products. Although large electronic systems are usually implemented by digital circuits, quite often they interface with the external world through analog devices. At present, there are many well-consolidated testing techniques for digital circuits and devices, such as automatic test pattern generator, boundary scan and built-in self-test (BIST); while in the analog filed, it is still at a rather embryonal level. The main reasons for this gap can be found in the intrinsic differences between digital and analog fields. To be specific, in digital circuits, a large class of defects can be modeled by stuck-at fault, but for analog circuits, it is difficult to model an analog component with a clearly defined boundary between “well working” and “fault state”, being concerned not only with the catastrophic faults (open and short faults), but also with the parametric faults. This is further complicated by the presence of nonlinearity and tolerance effect in analog circuits [1]. As a consequence, analog testing continues to remain as a challenging problem.

It is well known that specification-driven test and fault-driven test are alternative techniques followed for analog testing. For the latter technique, according to the time of simulations, it can be sorted into simulation-after-test (SAT) and simulation-before-test (SBT). The SAT approaches are carried out by estimating the circuit parameters, given a sufficiently large set of independent measurements and knowledge of circuit topology, so they are often time consuming when applied to large-scale circuits. Conversely, the SBT approaches simulate the circuit-under-test (CUT) for each anticipated faults before any test activity is considered and require a very short time at the testing stage even if complex circuits are envisaged. In a way, the time efficiency of a SBT approach is mainly dominated by the computational effort consumed before testing; nevertheless, this computational effort is required only once [2, 3].

Among various SBT approaches, fault dictionary is a poplar choice. Conceptually, a fault dictionary is a set of signatures associated with different faults and organized before the test via simulations. The signatures could be obtained at different physical test nodes with all test variables being fixed, or at specific values of the test variable such as frequency for selected test nodes. In this paper, all of them are defined as the test points. In practical testing, the range of candidate test points is much larger than the number of test points at which they are either necessary or economically feasible to get fault signatures. Therefore, optimum selection of test points is required to reduce the test cost and computation effort by reducing the dimensionality of the fault dictionary. Test point selection is also a critical issue in the domain of testability analysis. By analyzing the testability of a CUT, we can determine which test points to make accessible for testing and know how many such test points are needed so as to satisfy the given testability requirements.

The objective of test point selection for dictionary approach, in view of fault diagnosis, is to isolate the maximum number of faults (fault isolation rate is not always 100 %) by a minimum set of test points. Up to now, many efforts have been made to develop efficient methods by researchers. Varghese et al. [4] proposed a heuristic method to find an optimum set of measurement nodes, using a performance index called “confidence level”. Hochwald and Bastian [5] introduced the concept of ambiguity set and developed logical rules to select test nodes. However, no formal procedure for selection of test nodes was highlighted by them. Lin and Elcherif [6] improved the logical rules presented in [5] and proposed an integer-coded dictionary technique for fault isolation phase. By employing this technique, test point selection can be formulated as a combinatorial optimization problem. To provide a good solution to the problem, many different methods have been proposed. They can be classified into greedy algorithm and evolutionary algorithm. The former category includes inclusive and exclusive method [7], entropy-based approach [8], and heuristic graph search [9], while the latter category includes genetic algorithm [10], particle swarm optimization [11], quantum-inspired evolutionary algorithm [12], and greedy randomized adaptive search procedure [13]. However, in these papers test points are selected without considering the accuracy of fault diagnosis. Recently, two improved methods [14, 15] on this subject based on Monte Carlo simulations have been reported. But they need a huge number of Monte Carlo simulations if an accurate result is desired and hence are only applicable to small-size analog circuits. More recent study by Yang et al. [16] developed a slope fault model and proposed a fault-pair Boolean table technique for test point selection.

From the above discussion, it can be seen that test point selection has been researched extensively. However, we still believe that more works need to be done. The reasons are: (1) most of the methods mentioned before use the concept of ambiguity set defined by Hochwald and Bastian [5]. But there is a lack of a general method to partition ambiguity sets; (2) test point selection is carried out in published methods with the objective of finding a minimum set of test points, but neglecting the performance of fault diagnosis in terms of diagnostic accuracy and fault isolation rate.

In an attempt to resolve the previously mentioned problems, we are motivated to develop a new method for test point selection, which addresses several critical issues that are limiting the application scope and the accuracy of the extant methods: ambiguity set partition, optimization problem solution and multi-frequency analysis. The structure of the paper is organized as follows. Section 2 formulates the problem of test point selection. Section 3 elaborates on the proposed method. Section 4 presents some application examples. The comparison results with other methods are also given in this section. Finally, the conclusion follows in Sect. 5.

2 Problem formulation

2.1 Ambiguity set and integer-coded dictionary

In analog testing, there is an important phenomenon which is commonly encountered and difficult to solve: measurement ambiguity. Distinct faults may result in signatures at the test point of interest whose values are close to each other. Hence, it is impossible to distinguish among them with considering tolerance effect. Such faults are said to be in the same ambiguity set. Presently, most of the methods for test point selection use node voltages to construct fault dictionary, and an ambiguity set is defined as a list of faults if the gap between the voltage values produced by them is less than 0.7-V (a diode drop) [5, 6]. To illustrate how ambiguity sets are partitioned, let us consider a simple example.

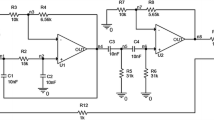
Figure 1 shows a low-pass filter. A sinusoidal wave with amplitude of 3-V and frequency of 1-kHz is used as test stimulus. For demonstration, 13 potential catastrophic faults f ₀ ∼ f ₁₂ (f ₀ represents fault-free case, which is treated as a special fault condition) are defined and three test nodes n ₁ ∼ n ₃ marked in Fig. 1 are assumed to be accessible. The signatures (voltages) under different fault conditions are tabulated in Table 1, where each test point actually corresponds to a physical test node because test variables such as amplitude and frequency are the same for all nodes. The characters -O and -S represent open- and short-circuit failure conditions, respectively.

Fig. 1

Low-pass filter

Table 1 Fault dictionary (Unit: V)

For each test point, we can determine its ambiguity sets. Take test point n ₁ for example. The voltage gap produced by f ₀ and f ₁ is 1.08-V (>0.7-V), so they are classified into two different ambiguity sets {f ₀} and {f ₁}. Similarly, f ₂ is also classified into a new ambiguity set {f ₂} since the voltage gap produced by f ₂ and any one of the fault from the existing ambiguity sets ({f ₀} and {f ₁}) is larger than 0.7-V. Successive faults are checked in the same way. Finally, three ambiguity sets, as shown in Table 2, are obtained for test point n ₁.

Table 2 Ambiguity sets of Table 1

Through computation of the ambiguity set intersections, we can determine which faults can be isolated, and then choose a subset of test points that can isolate those faults, but it is very time-consuming. To facilitate fault isolation, Lin and Elcherif [6] proposed an integer-coded dictionary, which is generated by encoding ambiguity sets using integer numbers. As an illustration, consider test point n ₁ in Table 2. The ambiguity set {f ₁, f ₈} is coded as “0”. Accordingly, in integer-coded dictionary faults f ₁ and f ₈ are also coded as “0”. This indicates that they belong to the same ambiguity set. Similarly, other ambiguity sets can be dealt with. Table 3 shows the integer-coded dictionary derived from Table 2.

Table 3 Integer-coded dictionary derived from Table 2

The integer-coded dictionary can be looked upon as an array of “m” elements. If all the elements of this array are different, it means that each fault has a unique integer number. Hence, all faults can be diagnosed. If an entry of this array repeats, it indicates that these faults can not be separated with the set of test points used for making this array. See [6, 7] for details.

2.2 Mathematical optimization model

Let F = {f ₀, f ₁, …, f _m−1} be the set of all potential faults, N = {n ₁, n ₂, …, n _q } be the set of available test points (nodes), and ${\boldsymbol{A}} = \left( {a_{ij} } \right)_{m \times q}$ be the relevant integer-coded dictionary of the CUT.

Let ${{N}}_{s} = \left\{ {n_{{s_{1} }} ,n_{{s_{2} }} , \ldots ,n_{{s_{k} }} } \right\} \subseteq {{N}}$ be a subset of N and ${{A}}_{is} = \left( {a_{{is_{1} }} ,a_{{is_{2} }} , \ldots ,a_{{is_{k} }} } \right)$ be the integer number of fault f _i determined by N _s , where $s_{j} \in \left\{ {1,2, \ldots ,q} \right\}\left( {j = 1,2, \ldots ,k} \right)$.

If fault f _i and any other one fault f _j , we always have ${{A}}_{is} \oplus {{A}}_{js} = 1$, then the fault f _i can be isolated by N _s . Where notation ⊕ is “logical exclusive OR” calculation and employed to compare the difference between A _is and A _js ; if they are identical, the result is 0, otherwise 1.

Denote by F _s the set of faults isolated by N _s , that is

$$F_{s} = \left\{ {f_{i} \left| {f_{i} \in F,\sum\limits_{{f_{j} \in F}} {{{A}}_{is} \oplus {{A}}_{js} = m} - 1} \right.} \right\}$$

(1)

Then, the following optimization model is derived.

$$\left\{ \begin{array}{l} \hbox{min} \left| {{{N}}_{s} } \right| \hfill \\ s.t. \, \mathop { \hbox{max} }\limits_{{N_{s} \subseteq N}} |{{F}}_{s} | \hfill \\ \end{array} \right.$$

(2)

where $| \cdot |$ is the cardinality of the set. From (2), we note that, in view of integer-coded dictionary, test point selection is equivalent to select a minimum set of columns to distinguish the maximum number of rows. For the previous example, from Table 3, we can easily find that the optimum test point sets are {n ₁, n ₂} and {n ₁, n ₃}. By using any one of them, the faults are classified into five ambiguity sets $\left\{ {f_{0} ,f_{4} ,f_{6} ,f_{9} ,f_{11} } \right\}$, {f ₁, f ₈}, $\left\{ {f_{3} ,f_{5} ,f_{10} ,f_{12} } \right\}$, {f ₂} and {f ₇}. Obviously, only faults f ₂ and f ₇ can be isolated, and thus the fault isolation rate is 15.39 %.

3 Test point selection method

3.1 Ambiguity set partition

In Sect. 2.1, we describe the concept of ambiguity set and a method (as used in references [5, 6]) to partition ambiguity sets. This method has been widely applied because it can be easily implemented. A number of improved versions of this method have also been reported. In [14], the authors verified that taking 0.7-V as a unified threshold to partition ambiguity sets is not reasonable and accurate. In [17], the authors suggested that the threshold of 0.2-V is enough to distinguish two faults. However, these methods are not applicable for general case because the signatures stored in the dictionary are not always voltages and are depended on the fault model adopted.

At a specific test point, several faults are said to be in the same ambiguity set since their associated signatures are similar. Graphically, they are located close to each other in the signature space and formed a cluster. For illustration, we present the information in Table 1 in the form of plots as shown in Fig. 2. It is clear that each ambiguity set in Table 2 corresponds to a cluster in Fig. 2. Inspired by this phenomenon, we develop a new method for partition ambiguity sets that is based on hierarchical clustering. It is given as follows:

Fig. 2

Formation of ambiguity sets

Step 1:

Assign each fault f _i (i = 0, 1, …, m − 1) to an individual cluster C _i and denote by C the set of clusters formed initially, i.e. C = {C ₁, C ₂, …, C _m−1}.

Step 2:

Calculate the similarity matrix D = (d(C _i , C _j )) _m×m , where d(C _i , C _j ) is the Euclidean distance between clusters C _i and C _j , and used to measure the similarity of these two clusters. It is defined by the following formula.

$$d\left( {C_{i} ,C_{j} } \right) = \left\{ \begin{array}{lll} \left| {\left( {\overline{Center} } \right)_{{C_{i} }} - \left( {\overline{Center} } \right)_{{C_{j} }} } \right|_{2} \,& i \ne j \hfill \\ 0 \,& i = j \hfill \\ \end{array} \right.$$

(3)

in which $\left| {\overline{x} } \right|_{2}$ represents the 2-norm of the vector $\overline{x}$. The vectors $\left( {\overline{Center} } \right)_{{C_{i} }}$ and $\left( {\overline{Center} } \right)_{{C_{j} }}$ denote the centers of the clusters C _i and C _j , respectively and are defined as

$$\left( {\overline{{Center}} } \right)_{{C_{i} }} = \frac{1}{{Num_{i} }}\sum\limits_{{f_{k} \in C_{i} }} {\overline{{p_{k} }} } ;\quad\left( {\overline{{Center}} } \right)_{{C_{j} }} = \frac{1}{{Num_{j} }}\sum\limits_{{f_{k} \in C_{j} }} {\overline{{p_{k} }} }$$

(4)

where $\overline{{p_{k} }} = \left( {p_{k1} ,p_{k2} , \ldots ,p_{kt} } \right)$ represents the signature of fault f _k , Num _i and Num _j are the number of fault conditions included in clusters C _i and C _j , respectively. Obviously, at first Num _i and Num _j are all equal to 1.

Step 3:

Find the most similar pair of clusters over all clusters in $C$, say C _r and C _l , according to

$$d\left( {C_{r} ,C_{l} } \right) = \mathop {\hbox{min} }\limits_{\begin{subarray}{l} C_{i} ,C_{j} \subseteq C \\ \, i \ne j \end{subarray} } d\left( {C_{i} ,C_{j} } \right)$$

(5)

Step 4:

Check whether $d\left( {C_{r} ,C_{l} } \right)$ is smaller than a predefined threshold β. If so, then stop. All clusters contained in C are just the ambiguity sets that we are desired.

Step 5:

Merge clusters C _r and C _l into a new cluster C _new and add it to C. Simultaneously, eliminate C _r and C _l from C.

Step 6:

Update the distance matrix D, by deleting the rows and columns corresponding to clusters C _r and C _l , and adding a row and column corresponding to the newly formed cluster C _new . The distance d(C _new , C _k ) between the new cluster C _new and each of the old clusters C _k in C is calculated by using Eq. (3). Go to Step 3.

In Step 2, the signature $\overline{{p_{k} }}$ consists of one or more parameters and each of them can be of any type. This will make our method have a wider scope of application. In Step 4, a threshold β, similar to 0.7-V (or 0.2-V), is used to check whether two faults belong to the same ambiguity set, but the way is different from that of the traditional methods (see Eq. 3).

3.2 An improved entropy index method

Once the integer-coded dictionary is constructed, test point selection is transformed into a combinatorial optimization problem, as shown in (2). It has been proven to be NP-hard. The global minimum set of test points can only be guaranteed by exhaustive search (ES) which needs a huge amount of calculations [8, 10]. To efficiently achieve the desired degree of fault diagnosis, an alternative solution is to search for a local minimum set of test points. In [8], Starzyk et al. proposed a promising entropy index method, which is found to be more efficient than other greedy methods from our computational experience [13]. In order to increase the accuracy and robustness of the method, some improvements are made.

For the sake of completeness and comparison, we start first by outlining Starzyk’s method. It is given as follows.

Step 1:

Initialize the desired optimum set of test points N _opt as a null set.

Step 2:

Calculate the entropy index E(n _j ) for each test point n _j ($j = 1,2, \ldots ,\left| N \right|$) and search for an optimum test point n _k that corresponds to the minimum value of entropy index. Where the entropy index E(n _j ) is defined as

$$E(n_{j} ) = \sum\limits_{i = 1}^{k} {F_{ij} } \log F_{ij}$$

(6)

In Eq. (6), k is the number of ambiguity sets for test point n _j , and F _ij is the number of faults included in ith ambiguity set.

Step 3:

Add test point n _k to N _opt and update N by eliminating n _k and the test points that have no more isolation effect from N. If N is empty, stop.

Step 4:

Partition the rows of the integer-coded dictionary according to the ambiguity sets of N _opt and rearrange the dictionary by removing the rows whose size is unit in their partitions. If all rows are removed, stop. Else, go to Step 2.

It is obvious that the above method belongs to greedy algorithm. At every turn, an optimum test point with respect to entropy index (selection criterion) is selected. However, this way is not always effective. For illustration, we return to the example given in Sect. 2.1. From Table 3, the entropy indices for all test points are calculated by (6) and the results are $E\left( {n_{1} } \right) = 10.60$ and $E\left( {n_{2} } \right) = E\left( {n_{3} } \right) = 8.16$. According to the Step 2, test points n ₂ and n ₃ all are optimum. But in regard to which one to be selected, the method is a lack of a clear criterion. On the other hand, it is also important to note that test points n ₂ and n ₃ have no distinction from point view of integer-coded dictionary since they have identical integer codes (or ambiguity sets). Therefore, other available selection criteria, as discussed in [13], are also useless because they are all derived from integer-coded dictionary.

To overcome the dilemma, we develop a new selection criterion by considering fault isolation optimization. Refer to Fig. 2, it can be seen that, if two ambiguity sets associated with test point n _j (j = 1, 2, 3) have a large distance between them then their corresponding fault signatures are significantly distinct as well. This implies that these two ambiguity sets are highly distinguishable and hence can be separated from each other by n _j with a higher accuracy even if their fault signatures are perturbed by component tolerances and measurement errors. By considering all ambiguity sets $\left\{ {C_{1} ,C_{2} , \ldots ,C_{k} } \right\}$ of test point n _j , a new selection criterion, referred to distance index DI(n _j ), is defined as

$$DI\left( {n_{j} } \right) = \sum\limits_{i,r = 1,i \ne r}^{k} {d\left( {C_{i} ,C_{r} } \right)} \, \cdot \, \mathop {\hbox{min} }\limits_{{i,r \in \left\{ {1,2, \ldots k} \right\},i \ne r}} d\left( {C_{i} ,C_{r} } \right)$$

(7)

where d(C _i , C _r ) is defined by Eq. (3). Reconsider the above example. The distance indices for test points n ₂ and n ₃ are $DI\left( {n_{2} } \right) = 33.23$ and $DI\left( {n_{3} } \right) = 34.75$. Hence, n ₃ should be selected first.

Based on above analysis, an improved entropy index method can be obtained by making a small change to the Step 2 of Starzyk’s method (other steps are the same). The counterpart is given below.

Step 2′: Calculate the entropy index E(n _j ) for each test point n _j ($j = 1,2, \ldots ,\left| N \right|$) and search for an optimum test point n _k that corresponds to the minimum value of entropy index. In case of tie, the one with the maximum value of distance index is selected as the test point n _k .

Starzyk’s method uses entropy index to evaluate fault isolation capability of each test point and the one with maximum isolation capability is selected firstly at every turn. When several test points have the same isolation capabilities, the improved method uses distance index to select the one with highest isolation accuracy among them. Therefore, compared with Starzyk’s method, the improved method search for a test point set, focusing not only on number of test points but also on fault diagnostic accuracy. It is necessary to point out that in Starzyk’s method only integer-coded dictionary A is required. While in the improved method, other than integer-coded dictionary A, the corresponding fault dictionary FD is also needed.

3.3 Multi-frequency analysis

Multi-frequency analysis has been introduced into test generation and testability evaluation [18, 19], but it has not been considered in the domain of test point selection to the best of our knowledge. Most published methods for test point selection use a sinusoidal signal with fixed test variables to excite the CUT and the signatures are sampled at various test nodes. As such, test point selection amounts to select a minimum set of test nodes (see Sect. 2.1). However, this may result in poor fault isolation. In some circuits, the accessible test nodes are very limited.

What happens if all test nodes have been used, and still less than designated fault isolation rate is achieved? One effective way is to use multi-frequency analysis, i.e. sample the signatures under different frequencies. In such situation, the process of test point selection will have to be modified slightly. In our case, it consists of two phases, which will be illustrated through the circuit given in Fig. 1. As before, a sinusoidal stimulus with amplitude of 3-V is applied.

(1) Selection of an optimum set of test points (test frequencies) for each node. Using AC sweep analysis of any circuit design software (such as PSPICE), the signatures associated with different fault conditions are obtained at nodes n ₁ ∼ n ₃. Now, for each node, there is one fault dictionary. Following the procedure in Sect. 2.1, its corresponding integer-coded dictionary can be created. Tables 4 and 5 show the fault dictionary $FD_{{n_{1} }}$ and the integer-coded dictionary $A_{{n_{1} }}$ of node n ₁. Note that in Tables 4 and 5 each column corresponds to a test frequency. According to the definition of the test point, it can also be defined as the test point. For uniformity, here we use the concept of test point rather than test frequency. Then, the improved entropy index method can be applied. In the following, we will briefly illustrate how it is implemented with given $FD_{{n_{1} }}$ and $A_{{n_{1} }}$.

Table 4 Fault dictionary $FD_{{n_{1} }}$ of node n ₁ (Unit: V)

Table 5 Integer-coded dictionary $A_{{n_{1} }}$ of node n ₁

At first, $N_{opt}$ is initialized as a null set. According to $A_{{n_{1} }}$, the entropy index for each test point is calculated and listed in Table 6. Obviously, F ₅ has a minimum value of entropy index 9.19. Hence, F ₅ is selected and added to N _opt and now N _opt  = {F ₅}. Since the condition to stop is not satisfied, dictionary $A_{{n_{1} }}$ is partitioned into four sub-dictionaries by the ambiguity sets of N _opt . The result of partition is shown in Table 7. It can be seen that faults {f ₂, f ₇} are concluded as uniquely isolated by F ₅, and the corresponding rows should be removed from Table 7. After first partition, there are only three test points {F ₂, F ₃, F ₄} that still have isolation effect. Therefore, other test points will not consider in future.

Table 6 Results of entropy indices for the first iteration

Table 7 Partitioned integer-coded dictionary for the first iteration

Repeat computation of the entropy indices based on the update dictionary (i.e. Table 7). The results show that these three test points {F ₂, F ₃, F ₄} have equal values of entropy index 6.70. Then, their distance indices are calculated and the results are: DI(F ₂) = 6.29, DI(F ₃) = 6.40 and DI(F ₄) = 5.61. From the results, F ₃ has a maximum value of distance index. So, F ₃ is added to N _opt . Now, N _opt  = {F ₅, F ₃}. Based on the updated N _opt , the dictionary is further partitioned as shown in Table 8. At this point, the algorithm stops because there are no test points available.

Table 8 Partitioned integer-coded dictionary for the second iteration

After two iterations, two test points {F ₃, F ₅} are selected for node n ₁. We record the result as $F_{{n_{1} }} = \left\{ {F_{5} ,F_{3} } \right\}$. Similarly, an optimum set of test points is selected for nodes n ₂ and n ₃, respectively. The results are $F_{{n_{2} }} = \left\{ {F_{2} , { }F_{5} } \right\}$ and $F_{{n_{3} }} = \left\{ {F_{6} } \right\}$.

(2) Selection of an optimum set of test points for the CUT. Starting from the results in phase (1), the fault dictionary FD and the integer-coded dictionary A for the CUT are formed by the columns that correspond to the selected test points in the above fault dictionaries and integer-coded dictionaries, respectively. They are shown in Tables 9 and 10. Reuse the improved entropy index method on them. An optimum set of test points $T_{opt} = \left\{ {n_{1} \left( {F_{3} } \right),n_{2} \left( {F_{2} } \right),n_{2} \left( {F_{5} } \right)} \right\}$ for the CUT is selected. Using it, we can clearly distinguish faults $\left\{ {f_{0} ,f_{2} ,f_{3} ,f_{5} ,f_{7} ,f_{10} ,f_{12} } \right\}$, whereas in Sect. 2.2, only two faults {f ₂, f ₇} can be isolated. As a result, the fault isolation rate has increased to 53.85 %.

Table 9 Fault dictionary FD of the CUT

Table 10 Integer-coded dictionary A of the CUT

As can be seen from the above description, our strategy is to consider each node separately. A set of test points for each node under different test frequencies is selected first. The desired set of test points for the CUT is then selected among those sets of test points. In this way, each selected test point no longer corresponds to a test node, but a combination of test node and frequency. In this sense, our strategy provides a solution to jointly optimize test nodes and frequencies in fault diagnosis and testability evaluation. Presently, most researches consider them separately. Our work just fills the blank. Following the framework of our method, a joint optimization of test node selection and test generation can be developed without much effort.

3.4 Procedure of the proposed method

4 Case studies

The methodology presented in Fig. 3 has been tested for efficiency on three circuits, which are chosen among those considered as benchmarks in the related literatures. In the first two circuits, node voltages are used to construct fault dictionary, and catastrophic faults are mainly concerned because of other similar methods consider such faults. This allows a direct comparison of the obtained results. In the third circuit, we extend our method to select test points for slope fault model.

Fig. 3

Procedure of the proposed method

4.1 Example 1: Active filter

The circuit is shown in Fig. 4. A sinusoidal stimulus with amplitude of 4-V is applied. The sweep frequencies, as shown in Table 11, are selected among 11 feasible logarithmic spaced frequency values belonging to the [100 Hz, 10 kHz] interval. For simplification, 23 potential catastrophic faults f ₀ ∼ f ₂₂ are defined, and 6 test nodes n ₁ ∼ n ₆ marked in Fig. 4 are assumed to be accessible.

Fig. 4

Active filter

Table 11 Sweep frequencies for each node (unit: Hz)

4.2 Test point selection

After AC sweep analysis, there are 6 fault dictionaries. Their corresponding integer-coded dictionaries can be created. For each node, an optimum set of test points is selected first. The results are tabulated in Table 12. According to the Table 12, the fault dictionary FD and the integer-coded dictionary A can be constructed, as shown in Tables 13 and 14. Applying the improved entropy index method on FD and A, the resulting optimum set of test points is $T_{opt} = \left\{ {n_{1} \left( {F_{6} } \right),n_{1} \left( {F_{7} } \right),n_{3} \left( {F_{6} } \right),n_{4} \left( {F_{6} } \right),n_{6} \left( {F_{4} } \right)} \right\}$ which can fully isolate all given faults f ₀ ∼ f ₂₂. Table 15 shows the optimum fault dictionary.

Table 12 Selected test points for each node

Table 13 Fault dictionary $FD$ of active filter (unit: V)

Table 14 Integer-coded dictionary $A$ of active filter

Table 15 Optimum fault dictionary

4.3 Performance evaluation

It is well known that test point selection aims to reduce the dimensionality of the fault dictionary. Once an optimum set of test points is selected, its corresponding optimum fault dictionary can be obtained (see Table 15). Generally, such dictionary must be as small as possible to reduce the test cost and large enough to provide satisfactory fault isolation and diagnostic accuracy. Based on these requirements, we propose three kinds of metrics to evaluate the merits of T _opt .

• Number of optimum test points $\left| {T_{opt} } \right|$: refers to the number of test points included in T _opt .

• Fault isolation rate (FIR): refers to the fraction of isolated faults relative to all potential faults, i.e.

  $$FIR = \frac{IsoN}{m}$$

  (8)

  where IsoN is the number of faults that can be isolated by T _opt .

• Fault diagnostic accuracy (FDA): used to assess the diagnostic accuracy that can be achieved by T _opt . To calculate FDA, There are four steps involved.

Step 1:

Generate the optimum fault dictionary FD _opt . According to T _opt , the optimum fault dictionary FD _opt can be generated easily and expressed as

$$FD_{opt} = \left( \begin{aligned} \, \overline{{s_{0} }} \hfill \\ \, \overline{{s_{1} }} \hfill \\ \, \vdots \hfill \\ \overline{{s_{m - 1} }} \hfill \\ \end{aligned} \right)$$

where the vector $\overline{{s_{i} }}$ (i = 0, 1, …, m - 1) represent the optimum signature of fault f _i .

Step 2:

Monte Carlo simulation. For fault f _i (i = 0, 1, …, m − 1), 100 times of Monte Carlo simulation with regard to 5 % tolerances of passive components are carried out. During each simulation, the signature of f _i at the selected test points are saved in vector $\overline{{u_{i,j} }}$ (j = 1, 2, …, 100). All simulation results are saved in

$$U_{f} = \left( \begin{aligned} \overline{{u_{0,1} }} \, \overline{{ \, u_{0,2} }} \, \cdots \, \overline{{u_{0,100} }} \hfill \\ \overline{{u_{1,1} }} \, \overline{{u_{1,2} }} \, \cdots \, \overline{{u_{1,100} }} \hfill \\ \, \vdots \, \vdots \, \vdots \, \vdots \hfill \\ \overline{{u_{m - 1,1} }} \, \overline{{u_{m - 1,2} }} \, \cdots \, \overline{{u_{m - 1,100} }} \hfill \\ \end{aligned} \right)$$

Step 3:

Fault diagnosis. A variable ω is initialized to 0. For any vector $\overline{{u_{i,j} }}$ in U _f , find

$$k = \arg \mathop {\hbox{min} }\limits_{0 \le h \le m - 1} \left( {\left| {\overline{{u_{i,j} }} - \overline{{s_{h} }} } \right|_{2} } \right)$$

If k = i, the fault diagnosis result is right and ω = ω + 1.

Step 4:

When all vectors in U _f are examined, the fault diagnostic accuracy of T _opt is calculated by (9).

$$FDA = \frac{\omega }{100 \times m} \times 100\,\%$$

(9)

As an example, three metrics for the above test point set are calculated and the results are: $\left| {T_{opt} } \right| = 5$, $FIR = 100\,\%$ and $FDA = 96.83\,\%$.

4.4 Comparison with exhaustive search (ES)

This circuit has been studied in many literatures [7–12, 14], where a sinusoidal voltage source with amplitude of 4-V and frequency of 1-KHz is used as test stimulus. The voltages sampled at nodes n ₁ ∼ n ₆ are used to construct fault dictionary. By employing the procedures described in Sect. 2.1, an integer-coded dictionary can be created. Then, many different methods [7–12] can be applied. However, these methods can not guarantee to find the optimum test point set except ES. That is to say, the test point sets produced by these methods are not better than those obtained from ES. For this reason, ES is selected as a reference method here.

Meanwhile, we note that whether our method or ES is influenced by the threshold. In the above, the threshold of 0.7 is used to illustrate how our method works. To sufficiently validate the efficiency of our method, two additional thresholds are considered. The comparison results are given in Table 16.

Table 16 Comparison of our method with exhaustive search for active filter

From Table 16, it can be observed that our method and ES all are sensitive to the value of threshold. For the first two thresholds (i.e. 0.2 and 0.4), two methods find the same number of test points, but the test point sets found by ES exhibit poor performances in terms of FIR and FDA compared with that of our method. For the third threshold, ES concludes that all test points are necessary for the CUT. Even so, the achieved FIR is only 52.17 %. While our method asserts that five test points are enough to achieve 100 % fault isolation.

4.5 Example 2: Leapfrog filter

This CUT is used to further demonstrate the efficiency of our method. The circuit is shown in Fig. 5. A sinusoidal stimulus with amplitude of 5-V is applied. In AC sweep analysis, we consider a grid of 21 logarithmic spaced feasible frequencies sampling the [100 Hz, 10 kHz] interval. They are listed in Table 17. In total, there are 30 potential faults f ₀ ∼ f ₂₉ and 6 test nodes n ₁ ∼ n ₆. All fault conditions are tabulated in Table 18, where 8 specific parametric faults are included. Then, the proposed method can be applied. To avoid verbosity, the steps involving test point selection are omitted. Table 19 shows the results of test point selection.

Fig. 5

Leapfrog filter

Table 17 Sweep frequencies for each node (unit: Hz)

Table 18 Fault conditions of Leapfrog filter

Table 19 Comparison of our method with exhaustive search for Leapfrog filter

4.6 Comparison with exhaustive search

As in the previous example, a 5-V 1-KHz sinusoidal wave is used to excite the CUT. The voltages measured at nodes n ₁ ∼ n ₆ are used to constitute the fault dictionary. Similarly, several integer-coded dictionaries can be created according to given thresholds. Then, apply ES on these integer-coded dictionaries. The corresponding results are also listed in Table 19.

As indicated in Table 19, the test point sets found by our method include four test points. Using any one of them, all faults can be isolated with accuracy of no less than 92.43 %. While for ES, it finds the same number of test points only at threshold of 0.2, but fault diagnostic accuracy of the resulting test point set is only 84.30 %. For other two thresholds 0.4 and 0.7, ES concludes that more than four test points are necessary.

In summary, the results of the two analyzed circuits suggest that, our method search for an optimum test point set that not only includes the minimum number of test points but also has a good performance in terms of FIR and FDA, while the test point set found by ES together with other test point selection methods can not achieve satisfactory results for three metrics simultaneously. Therefore, we conclude that our method outperforms other reported methods for test point selection.

4.7 Example 3: Continuous-time state-variable filter

This CUT is used to illustrate how the proposed method is applied to select test points for slope fault model. The circuit is shown in Fig. 6. Due to a lack of a generic fault model, fault dictionary approach is traditionally used in catastrophic fault diagnosis and not fit for parametric fault diagnosis. Recently, it has been extended to both catastrophic and parametric fault diagnosis [16, 20]. In [16], the authors propose a new fault dictionary approach for linear analog circuits based on the slope fault model. For a CUT with q accessible test nodes, the fault dictionary has such form as shown in Table 20.

Fig. 6

Continuous-time state-variable filter

Table 20 Fault dictionary for slope fault model

In Table 20, x _l (l = 1, 2, …, p) represents any one potential fault component, p is the number of components, (n _i , n _j ) ($i,j = 1,2, \ldots ,q,i \ne j$) represents any one pair of test nodes, and k _l,k is the slope of x _l determined by node-pair (n _i , n _j ). According to [16], the slope k _l,k is not related with component x _l , but determined by other components in circuit and topology of the circuit. When the component x _l is faulty, including parametric deviation and catastrophic fault, k _l,k is invariable and thus can be used as fault signature to test any fault that occurs to component x _l .

Assume that V _i,0 and V _j,0 are fault-free voltages measured on the test nodes n _i and n _j when the CUT is in the nominal state, and fault voltages V _i,l and V _j,l are measured on the test nodes n _i and n _j when the component x _l is faulty. Then, the slope k _l,k is calculated by using the following formula [16]:

$$k_{l,k} = \frac{{V_{j,l} - V_{j,0} }}{{V_{i,l} - V_{i,0} }} \,$$

(10)

where V _i,0, V _j,0, V _i,l and V _j,l take complex numbers under an AC stimulus. Hence, the slope k _l,k is also a complex number. Thus, it can be written as: k _l,k  = κ _l,k  + j · γ _l,k , where κ _l,k and γ _l,k are real and imaginary parts of k _l,k . It can be seen that fault signature k _l,k is no longer voltage, but a new type of derived quantity. Hence, the extant methods for test point selection are no longer applicable because they are lack of an effective method to partition ambiguity sets.

Rewrite k _l,k as $k_{l,k} = \left( {\kappa_{l,k} ,\gamma_{l,k} } \right)$. In such situation, the signature of each component consists of two parameters. Then, our method can be applied. After AC sweep analysis, by using Eq. (10), 6 fault dictionaries are obtained. The sweep frequencies are the same as shown in Table 17. For each node-pair, a set of test points is selected first. The resulting optimum test point set for the CUT is $T_{opt} = \left\{ {\left( {n_{1} ,n_{3} } \right)\left( {F_{1} } \right),\left( {n_{3} ,n_{4} } \right)\left( {F_{21} } \right)} \right\}$. Table 21 shows the optimum fault dictionary. Using the same procedures shown before, FDA is calculated and the result is $FDA = 100\,\%$.

Table 21 Optimum fault dictionary

5 Conclusion

Today’s analog systems have posed problems for fault diagnosis with in-circuit testers because only limited access to the CUT is allowed. An efficient method to select a minimum set of test points is, therefore, badly needed. In this paper, we develop a general and accurate method for test point selection by addressing three critical issues as follows:

• Propose a new ambiguity set partition method based on hierarchical cluster analysis.

• Propose an improved entropy index method by considering fault isolation optimization.

• Introduce multi-frequency analysis into test point selection.

The results show that the proposed method obtains a better set of test points compared with other recently reported methods. Therefore, it is a good candidate for analog test point selection. Additionally, our method also provides a solution to jointly optimize test nodes and frequencies.