Quantum Image Compression-Encryption Scheme Based on Quantum Discrete Cosine Transform

Abstract

To obtain higher encryption efficiency and to realize the compression of quantum image, a quantum gray image encryption-compression scheme is designed based on quantum cosine transform and 5-dimensional hyperchaotic system. The original image is compressed by the quantum cosine transform and Zigzag scan coding, and then the compressed image is encrypted by the 5-dimensional hyperchaotic system. The proposed quantum image encryption-compression algorithm has larger key space and higher security, since the employed 5-dimensional hyperchaotic system has more complex dynamic behavior, better randomness and unpredictability than the low-dimensional hyper-chaotic system. Simulation and theoretical analyses show that the proposed quantum image encryption-compression scheme is superior to the corresponding classical image encryption scheme in term of efficiency and security.

1 Introduction

Image compression can be divided into lossy compression and lossless compression. Similarly, quantum image compression can be classified into lossy compression and lossless compression. In 2002, Lewis et al. proposed the compression of digital images by 2-D orthogonal wavelet transform, where the 2-D orthogonal wavelet transform decomposes images into both spatial and spectrally local coefficients [1]. An effective bit plane coding method for quantifying DCT coefficients was proposed to provide better quality of decoding images than that of JPEG2000 [2]. Kouda et al. proposed an image compression scheme based on hierarchical quantum neural network, where the performance of the quantum neural network of large size in image compression problems was considered [3]. The encoding time of traditional fractal image coding method is too long. To solve this problem, Yang R put forward an image compression algorithm based on quantum BP network to obtain a better reconstructed image [4]. In 2016, Yuen et al. proposed an image compression and encryption algorithm based on discrete cosine transform (DCT) and safe Hashing algorithm (SHA-1) [5]. An image compression-encryption scheme based on hyper-chaotic system and 2D compressive sensing was also presented [6]. There are many good encryption schemes for classical images [7,8,9]. With the rapid development of quantum computing and quantum information, many classical time-frequency transform tools have been extended into the quantum field, such as quantum discrete cosine transform [10, 11], quantum Fourier transform [12, 13], quantum fractional Walsh transform [14], quantum wavelet transform [15], and etc.

Many other applications with quantum algorithms were provided [16,17,18,19,20]. In 2013, a quantum image watermarking scheme by quantum wavelet transform was designed [16]. Yang et al. proposed a gray level image encryption and decryption scheme based on quantum Fourier transform and double random phase encoding technique [17]. To overcome the problem of excessive storage of quantum images, Pang et al. designed an image compression scheme with quantum discrete cosine transform [18]. Jiang et al. proposed a quantum image compression scheme based on JPGE and the generalized quantum image representation [19]. In addition, quantum image compression algorithm [21] and quantum image encryption algorithms [22, 23] were proposed. Most quantum image compression algorithms did not consider image security while most quantum image encryption algorithms did not consider compression. Therefore, it is necessary to design a quantum image encryption and compression scheme.

2 Related Theoretical Foundation

2.1 Novel Enhanced Quantum Representation for Digital Image

The most popular quantum grayscale image representation method is the new enhanced quantum representation (NEQR) for digital image [24].

$$ \left|I \right\rangle =\frac{1}{2^{n}}\sum\limits_{y = 0}^{2^{n}-1} \sum\limits_{x = 0}^{2^{n}-1} \underset{i = 0}{\overset{7}{\otimes}} \left|C_{yx}^{i} \right\rangle \left|yx\right.\rangle $$

(1)

where $C_{yx}^{i} \in \left \{ {0,1} \right \}$, |yx〉 = |y〉 |x〉. |yx〉 encodes the location information of the quantum gray image, $\left |C_{yx}^{0}C_{yx}^{1}{\ldots } C_{yx}^{7} \right \rangle$ encodes the gray-level information of the quantum gray image, |y〉 = |y_n− 1y_n− 2…y₀〉 and |x〉 = |x_n− 1x_n− 2 … x₀〉 encode vertical location information and horizontal location information, respectively. In the new enhanced quantum representation, a grayscale quantum image requires 2n + q quantum bits.

2.2 Quantum Discrete Cosine Transform

Since the discrete Fourier transform is realized in a quantum form, quantum discrete cosine transform can be realized by quantum Fourier transform and sparse matrix of length 2N [18].

$$ U_{N}^{\dag} \cdot F_{2N} \cdot V_{N} =C_{N} \oplus \left( {-i} \right)S_{N} $$

(2)

where

(3)

and

(4)

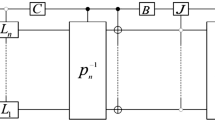
and w = exp (2πi /4N), i² = 1. Figure 1 is the quantum circuit for the quantum discrete cosine transform.

Fig. 1

Circuit of the quantum discrete cosine transform

2.3 Hyper-Chaotic System

5D hyper-chaotic system is defined as [25]:

$$ \left\{ {\begin{array}{l} \dot{{x}}_{1} =a\left( {x_{2} -x_{1}} \right)+x_{4} +x_{5} \\ \dot{{x}}_{2} =cx_{1} -x_{1} x_{3} -x_{2} \\ \dot{{x}}_{3} =x_{1} x_{2} -bx_{3} \\ \dot{{x}}_{4} =-x_{1} x_{3} +px_{4} \\ \dot{{x}}_{5} =qx_{1} \end{array}} \right. $$

(5)

where T (x₁, x₂, x₃, x₄, x₅) ∈R⁵, a, b, c, p, q ∈ R. If a = 10, b = 8/3, c = 28, p = 1.3 and q = 2.5, then the Layapunov exponents of the 5D hyper-chaotic system will be 0.4195, 0.2430, 0.0145, 0 and − 13.0405.

2.4 Zigzag Transform

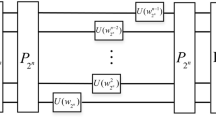
Zigzag transform is a scrambling tool, which is popularly applied into the image encryption and compression field [26]. Suppose the original image is of size N × N, then the two-dimensional quantum image can be transformed into a one-dimensional sequence Q (i), i = 1, 2, … , N × N. Finally, the size of the scrambled image can be changed adaptively according to the actual requirement. Figure 2 is the process of Zigzag transform.

Fig. 2

Zigzag transform

3 Quantum Image Compression-Encryption Scheme Based on Quantum Discrete Cosine Transform

3.1 Quantum Image Compression-Encryption Scheme

The compression-encryption procedure is shown in Fig. 3, and the detailed compression-encryption process is as follows.

• (1) Quantum gray image is represented with the NEQR model.

  $$ \left|I \right\rangle =\frac{1}{2^{n}}\sum\limits_{y = 0}^{2^{n}-1} {\sum\limits_{x = 0}^{2^{n}-1} \underset{i = 0}{\overset{7}{\otimes}}} \left|C_{yx}^{i} \right\rangle \left|yx\right.\rangle $$

  (6)

• (2) Quantum discrete cosine transform is performed on quantum gray image |I〉. The low-frequency part of the main components in the image is concentrated in the upper left corner, and the high frequency part is along the diagonal to the lower right corner.

  $$\begin{array}{@{}rcl@{}} \left|M \right\rangle &=&\text{QDCT}\left|I \right\rangle\\ {\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}&=&\text{QDCT}\left( I_{0} \otimes \frac{1}{2^{n}}\sum\limits_{y = 0}^{2^{n}-1} {\sum\limits_{x = 0}^{2^{n}-1} \underset{i = 0}{\overset{7}{\otimes}}} \left|C_{yx}^{i} \right\rangle \left|yx \right.\rangle \right)\\ &=& \text{QDCT}\left( \frac{1}{2^{n}}{\sum}_{y = 0}^{2^{n}-1}{\sum}_{y = 0}^{2^{n}-1}\underset{i = 0}{\overset{7}{\otimes}} \left|Q_{yx}^{i} \right\rangle \left|yx \right.\rangle \right)\\ &=& \frac{1}{2^{n}}{\sum}_{y = 0}^{2^{n}-1}{\sum}_{y = 0}^{2^{n}-1}\left( \text{QDCT}\left|Q_{yx}^{i} \right\rangle \left|yx \right.\rangle \right)\\ \end{array} $$

  (7)

• (3) The quantum image |M〉 is transformed by the Zigzag transform, and the transformed quantum image |M〉 was scanned by Zigzag scanning sequence to form a one-dimensional vector |M₁〉.

• (4) The quantum state of a one-dimensional quantum vector is compressed and a two-dimensional quantum image of size m × m is reconstructed.

  $$ q=\frac{m^{2}}{n^{2}} $$

  (8)

• (5) The five initial parameters x_i (0) (i ∈ {1, 2, 3, 4, 5}) of the 5D hyper-chaotic system should be selected.

• (6) Hyper-chaotic sequence {x_i (j)} is transformed into inter sequence {X_i (j)}.

  $$ X_{i} (j )=\text{floor}\left( {\bmod x_{i} \left( j \right)\ast 10^{15}\bmod 256} \right) $$

  (9)

• (7) A hyper-chaos sequence $L=\left \{ {L_{1} ,L_{2} {\cdots } ,L_{2^{2n}}} \right \}$ is constructed by using $X_{5}^{\prime }$ to control the execution of quantum exclusive OR operation. If $X_{5}^{\prime } = 0$, then L_j = X₁ (j); if $X_{5}^{\prime } = 1$, then L_j = X₂ (j); if $X_{5}^{\prime } = 2$, then L_j = X₃ (j); if $X_{5}^{\prime } = 3$, then L_j = X₄ (j); and if $X_{5}^{\prime } = 4$, then L_j = X₅ (j). $X_{5}^{\prime }$ is given by

  $$ X_{5}^{\prime} =X_{5} (j)\bmod 5 $$

  (10)

• (8) A two dimensional quantum compression-encryption image |G〉 is constructed by the one-dimensional sequence $L=\left \{ {L_{1} ,L_{2} {\cdots } ,L_{2^{2m}}} \right \}$.

Fig. 3

Quantum image compression-encryption

3.2 Quantum Image Decryption Scheme

The decryption process is depicted in Fig. 3, which is the inverse operation of quantum image compression-encryption process. The detailed decryption process is described as follows:

• (1) Integer sequence {X_i (j)} is obtained with initial parameter x_i (0).

• (2) The one-dimensional vector |M₁〉 is transformed by the inverse Zigzag transform to generate |M〉.

• (3) The inverse quantum discrete cosine transform is performed on |M〉 to obtain |I〉.

  $$\begin{array}{@{}rcl@{}} \left|I \right\rangle &=&\text{IQDCT}\left|M \right\rangle\\ &=&\text{IQDCT}\left( I_{0} \otimes \frac{1}{2^{n}}\sum\limits_{y = 0}^{2^{n}-1} {\sum\limits_{x = 0}^{2^{n}-1} \underset{i = 0}{\overset{7}{\otimes}}} \left|Q_{yx}^{i} \right\rangle \left|yx\right.\rangle \right)\\ &=&\text{IQDCT}\left( \frac{1}{2^{n}}\sum\limits_{y = 0}^{2^{n}-1} {\sum\limits_{x = 0}^{2^{n}-1} \underset{i = 0}{\overset{7}{\otimes}}} \left|C_{yx}^{i} \right\rangle \left|yx\right.\rangle \right)\\ &=&\frac{1}{2^{n}}\sum\limits_{y = 0}^{2^{n}-1} {\sum\limits_{x = 0}^{2^{n}-1}}\left( \left|C_{yx}^{i} \right\rangle \left|yx\right.\rangle\right) \end{array} $$

  (11)

4 Numerical Simulation and Discussion

Three test images “Plane”, “Bridge” and “Baboon” with 512 × 512 pixels are shown in Fig. 4a, d and g. In the compression-encryption process, the parameters x_i(0) (i ∈ {1, 2, 3, 4, 5}) of the used 5D hyper-chaotic system are set as 0.798, 0.465, 0.628, 5.126 and 1.6, respectively. The resulting images obtained with the presented gray image compression-encryption scheme are shown in Fig. 4b, e and h. The corresponding correct decryption images are shown in Fig. 4c, f and i.

Fig. 4

Results of test images: a “Plane”, b encryption “Plane”, c decryption “Plane”; d “Bridge”, e encryption “Bridge”, f decryption “Bridge”; g “Baboon”, h encryption “Baboon”, I decryption “Baboon”

4.1 Information Entropy

Information entropy H (s) of an image is the most important feature of randomness.

$$ H\left( s \right)=-\sum\nolimits_{i = 0}^{2^{n}-1} {P\left( {s_{i}} \right)} \log_{2} P\left( {s_{i}} \right) $$

(12)

where P (s_i) denotes the probability of symbol s_i, 2ⁿ is the total states of the image. Table 1 shows the information entropy of six different original images and corresponding encryption ones. The information entropies of the encryption images are enhanced and more close to the theoretical value 8 bits. It means that information leakage during the compression-encryption process is negligible and the proposed image compression and encryption scheme is secure upon information entropy attack.

Table 1 Information entropy

4.2 Histogram Analysis

The histogram of grayscale image can directly reflect the distribution state of pixels. The histogram of the plain-images “Plane”, “Bridge” and “Baboon” are shown in Fig. 5a, c and e, and those of the encryption images are shown in Fig. 5b, d and f. It can be seen that the histograms of the encryption images are more evenly distributed. Therefore, the image compression-encryption algorithm can effectively resist histogram attack.

Fig. 5

Histograms: a “Plane”, b encryption “Plane”, c “Bridge”, d encryption “Bridge”, e “Baboon”, f encryption “Baboon”

4.3 Correlation of Adjacent Pixels

The correlation between two adjacent pixels in original images and encryption images is given in Fig. 6 and Table 2. It is shown that the correlation of the cipher-text image is much lower than that of the original image.

Fig. 6

Correlation distributions between two adjacent pixels: a and b are horizontal direction of “Baboon” and encryption “Baboon”, c and d are vertical direction of “Baboon” and encryption “Baboon”, e and f are diagonal direction of “Baboon” and encryption “Baboon”

Table 2 Correlation coefficient of adjacent pixels

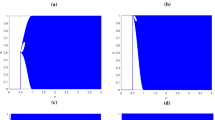
4.4 Key Sensitivity and Key Space

The proposed image compression-encryption algorithm has five keys, i.e., x_i (0) (i ∈ {1, 2, 3, 4, 5}). Figure 7a–e shows the MSE curve for x_i (0) (i ∈ {1, 2, 3, 4, 5}). The sensitivity of the five keys is high enough since the curves change very violently. Therefore, the proposed image compression and encryption algorithm is sensitive enough to the keys. Figure 8 shows the decryption images with only one incorrect key and other correct keys. Figure 8a–e are the decryption images with incorrect key x₁ (0) = 0.798 + 10^− 15, x₂ (0) = 0.465 + 10^− 15, x₃ (0) = 0.628 + 10^− 14, x₄ (0) = 5.126 + 10^− 14, x₅ (0) = 1.6 + 10^− 14, respectively. It can be concluded that a tiny change in any key could influence the encryption image greatly.

Fig. 7

MSE curves of key: a x₁(0), b x₂(0), c x₃(0), d x₄(0), e x₅(0)

Fig. 8

Decryption images with the incorrect keys: ax₁(0) + 10^− 15, b x₂(0) + 10^− 15, c x₃(0) + 10^− 14, d x₄(0) + 10^− 14, e x₅(0) + 10^− 14

In the proposed image compression and encryption scheme, let s_i represent the subkey space of chaotic key x_i(0). The key total space is $S=\prod \limits _{i = 0}^{5} s_{i} = 10^{72}$, so the proposed image compression-encryption scheme can resist the brute-force attack.

4.5 Noise Attack

Suppose the noise is added into the encryption image as C^′ = C + kG, where C^′ and C are the noisy and the standard encryption images, respectively, k is the Gaussian random noise intensity. G is the Gaussian noise with mean 0 and variance 1. Figure 9a gives the MSE curve versus noise intensity. Figure 9b–g shows the decryption images with the noise intensity coefficients 1, 5, 10, 15, 20 and 25, respectively. Although the quality of the decryption image will decrease, the major information of the images can still be distinguished under certain noise intensity. Therefore, the proposed quantum image compression and encryption algorithm can resist noise attack to some degree.

Fig. 9

Results of noise attack: a MSE curve, bk = 1, c k = 5, d k = 10, e k = 15, f k = 20, g k = 25

4.6 Computational Complexity

The original quantum grayscale image contains 2²ⁿ pixels. In this proposed quantum image compression-encryption scheme, the computational complexity is mainly derived from quantum cosine transform and quantum XOR operation. The computational complexity of quantum discrete cosine transform is $O\left ({\sqrt n} \right )$. In addition, the quantum XOR operation can be realized with 8n − 16 Toffoli gates [27], and the Toffoli gate can be realized by six basic gates, thus the quantum XOR operation involves 6 × (8n − 16) × 8 = 384n − 768 basic logic gates. Consequently, the computational complexity of the quantum image compression-encryption algorithm is O (n). While in the similar classical image encryption scheme, the computational complexity of the XOR operation is O (2²ⁿ) and that of the discrete cosine transform is O (n) [28]. The computational complexity of the similar classical image encryption algorithm is O (2²ⁿ). Therefore, the computational complexity of the proposed quantum image compression and encryption algorithm is much lower.

4.7 Compression Performance

Figure 10 shows the original image and decryption images with different compression ratios. From Fig. 10, the quality of the decryption image under different compression ratios remains acceptable to some degree. Therefore, the quantum image compression and encryption algorithm has acceptable compression performance.

Fig. 10

Results of images with different compression ratios: a original image, b compression ratio 0.75, c compression ratio 0.5, d compression ratio 0.25

4.8 Three Images Encryption

The proposed quantum image compression-encryption algorithm can compress and encrypt three images or multiple quantum grayscale images simultaneously. First of all, the three quantum grayscale images are compressed by combining quantum cosine transform with Zigzag transform, and then the compressed images are encrypted by the 5-dimensional hyper chaotic system. The encryption image is shown in Fig. 11d. The decryption “Baboon”, “Bridge” and “Peppers” are shown in Fig. 11e, f and g. Therefore, the proposed quantum image compression and encryption algorithm can compress and encrypt three quantum images flexibly and simultaneously.

Fig. 11

Results of three image encryption: a “Baboon”, b “Bridge”, c “Peppers”; d encryption image; e decryption “Baboon”, f decryption “Bridge”, g decryption “Peppers”

5 Conclusion

The quantum image compression-encryption algorithm based on quantum cosine transform is proposed. The original quantum image is transformed into spectrum by the quantum discrete cosine transform, and then the resulting spectrum is compressed by Zigzag operation. To ensure the security of the compressed image, the 5D hyper-chaotic system is adopted to encrypt the compressed image further. Compared with quantum image compression algorithm or quantum image encryption algorithm, the proposed quantum image compression and encryption algorithm can simultaneously compress and encrypt single image or three-quantum-grayscale-image. Simulation results indicate that the proposed quantum image compression–encryption scheme is effective, robust and secure with good compression and security performances.