Abstract
We provide the spectral-domain solutions for the gravity forward modelling of a 2D body with constant, polynomial and exponential density distributions, including the gravitational attraction and its arbitrary-order derivatives. The gravity effects may be directly obtained from the derivatives of a constructed scalar quantity and the surface integral of the density function over the 2D body. Then, the surface integrals of the spectral expansion coefficients of the scalar and the density function are converted to the line integrals along the boundary of the mass body using the Gauss divergence theorem and thus can be evaluated by numerical integration. The surface integrals for the exponential density model are expressed as the infinite expansions of line integrals and converge fast. Approximating the mass body to a 2D polygon, the surface integrals can be evaluated by simple analytic formulas for the constant density model and by linear recursive relations for the polynomial density model. The numerical implementation shows that the spectral-domain algorithm of this paper can produce high accurate forward results, e.g. 13–16 digits achievable precision for the gravity vector. Although the spectral-domain method is only suitable for forward computation of the external gravity effects of the 2D body, it is numerically stable for arbitrary observation point outside the smallest enclosed circle. The closed-form solutions for the 2D body with constant or polynomial density distribution are high precision to evaluate the gravity anomaly at the point near or inside the body, but may be lower precision when the computation point moves away from the body. The spectral-domain algorithm can handle the polynomial and exponential density model in both horizontal and vertical directions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Forward modelling computation for the gravity effects of a mass body, including gravitational potential, gravity vector, gravity gradient tensor and higher-order derivatives, is an important issue in physical geodesy. The gravity effects also reveal the geophysical and geological informations. The gravitational field of the 3D body can be expressed by the Newton integrals of the contributions exerted by the volume elements of the source body on an unit mass located at an observation point. For the 3D body with a general shape, the volume integrals can be evaluated by numerical integration and differentiation (Fukushima 2016, 2017). On the other hand, the volume integrals of the whole 3D body can be decomposed into the summation of volume integrals of elementary homogeneous mass elements, e.g. tesseroids (Heck and Seitz 2007; Grombein et al. 2013; Uieda et al. 2016; Fukushima 2018a), prisms (Nagy et al. 2000; Tsoulis 2000; D’Urso 2012; D’Urso and Trotta 2015) and general polyhedra (Werner and Scheeres 1997; Tsoulis and Petrović 2001; D’Urso 2013, 2014a; Zhang and Chen 2018). The non-constant density model is a more accurate description for the density distribution of the mass body (García-Abdeslem 1992, 2005; Artemjev et al. 1994; Pohánka 1998; Zhou 2009a). Inverting the volume integrals of the gravity effects into surface integrals and further into line integrals, the closed expressions of the gravity field of prisms and general 3D polyhedral bodies with polynomial density in space domain have been proposed in the literature (Pohánka 1998; Hansen 1999; Holstein 2003; Hamayun Prutkin and Tenzer 2009; D’Urso 2014b; D’Urso and Trotta 2017; Zhang and Jiang 2017; Jiang et al. 2017, 2018; Ren et al. 2017a, b, 2018; Fukushima 2018b). Fourier-domain method can also be applied to the gravity forward computation of 3D bodies with a polyhedral or general shape (Wu and Chen 2016; Wu 2018a, b, 2019). For the polyhedral bodies, the achievable precision of the Fourier-domain method is 2–7 digits.
In gravity prospecting, the vertical component of the earth’s gravity field is measured to infer changes in the density of the geological structures. The gravity forward modelling of the geological structures plays an important role in gravity data interpretation. Many common geological structures are approximated by the configurations parallel to a given horizontal direction, and their density distributions vary as the same function of position on each of a family of parallel planes which are perpendicular to that direction, e.g. the sedimentary basins (Netteton 1940; Hubbert 1948; Bott 1960). When the actual dimension in the horizontal direction is far larger than the distance from the cross section to the observation point, the issue of the gravity effects of these geological structures can be degenerated into the gravity computation of 2D mass bodies (namely the cross sections of the geological structures) within rather small error (Netteton 1940; Zhou 2008). The 2D mass body model has been applied to the computation of the vertical component of actual structures in the literature, e.g. for the New Red Sandstone basins near Dumfries in the south of Scotland, Mendocino submarine fracture zone and San Jacinto Graben, California (Talwani et al. 1959; Bott 1960; Murthy and Rao 1979). Geometrically, the 2D body can be approximated by a polygonal body whose boundary is made up of a number of line segments for the convenience of calculation. In practical survey works, a finite number of measurement points for the 2D body also lead to an approximated 2D polygon. The geologic evaluation of the structures is complex, and then, the density model is diversiform. The numerical solutions for the gravity effects of the 2D body with constant density have been investigated by several authors (Talwani et al. 1959; Bott 1960). For accurate calculation, the non-constant density model has been used to the gravity forward computation of the 2D body, e.g. exponential function (Cordell 1973; Chai and Hinze 1988; Litinsky 1989; Rao et al. 1993; Chappell and Kusznir 2008), hyperbolic function (Litinsky 1989; Rao et al. 1995; Silva et al. 2006), parabolic function (Rao et al. 1994; Chakravarthi and Sundararajan 2004) and polynomial function including the linear, quadratic and higher-degree polynomial (Murthy and Rao 1979; Rao 1985, 1986a, b, 1990; García-Abdeslem 1992, 2005; Ruotoistenmäki 1992; Martín-Atíenza and Garcia-Abdeslem 1999). For the 2D body with general polynomial density contrast in both horizontal and vertical directions which is approximated by a polygon, the analytical solutions of the gravity effects can be obtained by using the Stokes theorem (Zhang et al. 2001; Zhou 2010) or the Gauss divergence theorem (D’Urso 2015). As general density models, the depth-dependent (vertical) density distribution and the horizontally and vertically dependent density distribution have been considered by Zhou (2008, 2009b), where the line integrals for the gravity effects are evaluated by numerical integration. Zhou’s (2009b) algorithm requires the integrals for the horizontal or vertical density components should be integrable. Different from the space-domain methods above, the Fourier-domain method for evaluating gravity effects of 2D mass bodies first constructs the Fourier spectrum of the gravity effects and then transforms the spectrum back to the spatial domain using fast Fourier transform techniques (Wu 2018b, 2019). The Fourier transform expressions of the gravity effects of the 2D polygonal body with constant or exponential density distribution can be directly obtained from the coordinates of the vertices (Pedersen 1978; Chai and Hinze 1988; Hansen and Wang 1988; Rao et al. 1993; Wu 2019).
For 3D bodies, the gravitational potential may satisfy the 3D Laplace’s equation, and then, the spherical harmonic spectral techniques can be applied to the gravity forward modelling. Because the boundary condition is unknown, the volume integral expressions of the spherical harmonic coefficients of the gravitational potential should be given instead of the surface integrals, which are derived by using the expansion of the reciprocal distance (Heiskanen and Moritz 1967; Hofmann-Wellenhof and Moritz 2006). The spherical harmonic expansion of the potential for the Phobos with assumption of constant density has been considered by Chao and Rubincam (1989) and Martinec et al. (1989). Balmino (1994) derived the analytical solutions for the potential harmonic coefficients of the homogeneous body which shape is also given as a series of spherical harmonics. Werner (1997) constructed the forward modelling for the potential harmonic coefficients of the uniform polyhedral body. The spherical harmonic coefficients are evaluated by the trinomial integrals over the divided tetrahedron. By applying the Gauss divergence theorem and the Stokes theorem, the potential harmonic coefficients of the polyhedral body with constant or polynomial density can be evaluated by the linear recursive algorithms using line integrals along the edge of the polyhedron (Jamet and Thomas 2004; Tsoulis et al. 2009; Chen et al. 2019a, b). The recursive algorithms require the polyhedral body to be divided into a number of tetrahedra or polygonal pyramids. To guarantee numerical stability of the recursive algorithm, the initial 3D reference frame must be rotated to a new 3D reference frame to make the vertical axis coincident with the normal vector of the polygonal faces. According to the spherical harmonic expansions of the derivatives of the gravitational potential and the conversions of the arbitrary- order derivatives of the potential between the initial and rotated reference frames, the arbitrary-order derivatives can be obtained with no need for evaluation of the rotation of spherical harmonic coefficients of each tetrahedron or polygonal pyramid (Cunningham 1970; Petrovskaya and Vershkov 2010; Chen et al. 2019b). The dot products of the final analytical expressions of the gravity effects of the polyhedral body in space domain containing the position vector of the observation point lead to the numerical instabilities for the remote observation point (D’Urso 2013, 2014a, b; D’Urso and Trotta 2017; Ren et al. 2018). Although the spherical harmonic spectral method is only suitable for evaluating the external field of the 3D body, it may be numerically stable for arbitrary observation point outside the smallest enclosed sphere (Chen et al. 2019b). The spectral-domain method based on the 2D Laplace’s equation can also be used to the forward modelling for the gravity field of 2D bodies which may be numerically stable for the external point, and it has not be seen in the literature.
The present work provides a spectral-domain approach for gravity forward modelling of the 2D mass body with constant, polynomial and exponential density distributions. We construct a scalar quantity related to the gravity effects of the 2D body which meets the 2D Laplace’s equation, and then get the spectral expansions of the scalar and its derivatives (Sect. 2). The gravitational attraction of the 2D body and its arbitrary-order derivatives can be obtained from the derivatives of the scalar and the surface integral of the density function over the 2D body. Usually, the spectral expansion coefficients can be obtained from the boundary values of the scalar on a closed curve. In this case, the coefficients can be written as the line integrals of the boundary values along that curve. However, for the gravity forward computation of the 2D body the boundary values are unknown. Therefore, in this paper the surface integral expressions of the spectral expansion coefficients over the 2D body are derived and then converted to the line integrals along the boundary of the body using the Gauss divergence theorem, which can be evaluated by numerical integration (Sect. 3). The surface integral of the density function can also be expressed as line integrals. When the 2D body is approximated by a polygon, the spectral expansion coefficients can be evaluated by simple analytic formulas for the constant density model and by linear recursive relations for the polynomial density model. Computation of the surface integral of the density function is analogous. In Sect. 4, three polygonal models including a rectangular cylinder with quadratic density contrast varying with depth, a 26-sided polygon body with quadratic density contrast varying in both horizontal and vertical directions and a 2D rectangular cylinder with exponential density contrast varying with depth were used to test numerical accuracies and stabilities of this work’s algorithms. Finally, we draw some conclusions in Sect. 5.
2 Spectral expansions for the gravity effects of 2D bodies
2.1 Construction of the 2D Laplace’s equation
For a 3D body \({\widehat{\varOmega }}\), its gravitational attraction exerted at a point \({\widehat{P}}(x,y,z)\) is given by (Kellogg 1929)
where x and y are the horizontal axes, z is the vertical axis, G represents the gravitational constant, \(\widehat{{\mathbf {r}}}\) represents the 3D position vector from the observation point \({\widehat{P}}\) to the internal point \({\widehat{Q}}(x',y',z')\), \(\rho (\widehat{{\mathbf {r}}})\) is the density function varying with the point \({\widehat{Q}}\) and \(\mathrm{d}{\widehat{\varOmega }}\) is the volume element. Denoting \(\widehat{{\mathbf {u}}}_x\), \(\widehat{{\mathbf {u}}}_y\), \(\widehat{{\mathbf {u}}}_z\) as the 3D unit vector along the three axes, the horizontal and vertical components of the gravitation are \(g_x({\widehat{P}})={\mathbf {g}}({\widehat{P}})\cdot \widehat{{\mathbf {u}}}_x\), \(g_y({\widehat{P}})={\mathbf {g}}({\widehat{P}})\cdot \widehat{{\mathbf {u}}}_y\), \(g_z({\widehat{P}})={\mathbf {g}}({\widehat{P}})\cdot \widehat{{\mathbf {u}}}_z\). When the configuration of the 3D body \({\widehat{\varOmega }}\) is parallel to the horizontal axis y and the density distribution \(\rho (\widehat{{\mathbf {r}}})\) is independent of the variable \(y'\), the three gravitation components can be expressed as
where \(\varOmega \) represents the 2D integration domain of the cross section of the 3D body, \(\mathrm{d}\varOmega \) is the area element in the \(z'x'\)-plane, \(d_{y_1}\), \(d_{y_2}\) are the y-coordinates of the two sides of the 3D bodies, \({\mathbf {r}}\) is the 2D position vector from the projections of the points \({\widehat{P}}\) to \({\widehat{Q}}\) on the zx-plane and \({\mathbf {u}}_x\), \({\mathbf {u}}_z\) are the 2D unit vectors along the x-, z-axes, respectively.
Assuming \(d_{y_1}\rightarrow - \infty \), \(d_{y_2}\rightarrow + \infty \) (Zhou 2008; D’Urso 2015), Eq. (2) yields
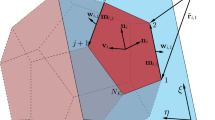
where we denote \(\rho (z',x')\) as \(\rho ({\mathbf {r}})\) because \(\rho ({\mathbf {r}})\) depends only on x, z and likewise can use the symbols \(g_x(z,x)\), \(g_z(z,x)\) to represent \(g_x({\widehat{P}})\), \(g_z({\widehat{P}})\). Thus, the gravitational components \(g_x(z,x)\), \(g_z(z,x)\) independent of y can be handled as the gravity effects of a 2D body \(\varOmega \) (namely the cross section of the 3D body \({\widehat{\varOmega }}\), in Fig. 1). The 2D mass body model is a common approach to evaluate approximately the gravity effects of many geological structures in the literature, and the vertical component is often considered in practical application. This paper illustrates the 2D mass body model more clearly.
We now define a quantity
Differentiating the scalar V with respect to z and x, we have
where the symbol \(D_{\rho }\) represents the surface integral of the density function as
Further, the second-order derivatives of the quantity V can be expressed as
where the symbols \(g_{zz}(z,x)\), \(g_{zx}(z,x)\) and \(g_{xx}(z,x)\) are the derivatives of \(g_{z}(z,x)\) and \(g_{x}(z,x)\), i.e. the gravity gradients. To evaluate the vertical and horizontal components of the gravitational attraction and their derivatives of the 2D body, we may need to evaluate the derivatives of V and the double integral \(D_{\rho }\).
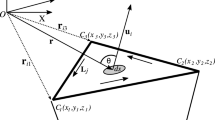
The 2D Cartesian coordinates can be written as \(z=r\cos \theta \), \(x=r\sin \theta \) where the radius r and the angle \(\theta \) are the polar coordinates. We denote \((r',\theta ')\) as the polar coordinates of the point Q, l as the distance between the points P and Q, \(\psi \) as the running angle between the radial directions of the points P and Q, as shown in Fig. 1. Since
the quantity V in Eq. (4) can be expressed as
where \(t=r'/r\). From Eqs. (2), (8) and (10), for the external observation point, we have
Therefore, the quantity V satisfies the 2D Laplace’s equation at the external point. We choose a circle that completely encloses the 2D body, where the centre of the enclosed circle is the origin O. Then, from Eqs. (13) and (14), the quantity V at the point P outside the enclosed circle can be expressed as the spectral expansion (Riley et al. 2006)
where a is the radius of the enclosed circle, i.e. the reference distance and \(C_n\) and \(S_n\) are the coefficients of the spectral expansion. Because the logarithmic expression in Eq. (13) can be expanded into power series of t in which the power of each term is greater than zero, the constant and logarithmic terms in the expansion (15) are vanished.
Analogous to computation of the spherical harmonic coefficients in gravity forward modelling of 3D case in which the coefficients are expressed as the volume integrals over the 3D body (Heiskanen and Moritz 1967; Hofmann-Wellenhof and Moritz 2006), we may derive the surface integral expressions of the coefficients \(C_n\) and \(S_n\) over the 2D body. From Gradshteyn and Ryzhik (2007), the logarithm expression in Eq. (13) can be expressed as the expansion
which can be derived from the expansion of \(\ln (1-2t\cos \psi +t^2)\) into the Taylor series of \(-2t\cos \psi +t^2\), binomial expansion of \((t-2\cos \psi )^k\) and cosine expression \(\cos (n\psi )\) expanded to the power polynomial of \(\cos \psi \). Since \(\psi =\theta -\theta '\), we have
Hence, the spectral expansion coefficients can be expressed as
i.e.
where the vector
van Gelderen (1992) used another form of the series expansion of \(\ln \left( \frac{l}{r}\right) \) to get the expansion of the potential \(G\iint _{\varOmega } \ln \left( \frac{1}{l}\right) \rho (z',x')\mathrm{d}\varOmega +\mathrm{constant}\), which is connected with Eq. (17). Through some simple derivations, van Gelderen’s [1992, Formulas (2.7) and (2.8)] results are actually the same as Eqs. (17)–(19) of this paper.
2.2 Spectral expansions of the derivatives of the quantity V
Cunningham (1970) and Petrovskaya and Vershkov (2010) gave the spherical harmonic expansions of the derivatives of the gravitational potential of the 3D body, where the potential meets the 3D Laplace’s equation. For the 2D body, we can also derive the spectral expressions of the derivatives of the quantity V, where V meets the 2D Laplace’s equation.
Similar to Cunningham (1970), we define
where \(\mathbb {i}\) is the imaginary unit; then, the quantity V can be written as
where the symbol \(\mathrm{Re}\) denotes the real part operator. Since \(\cos \theta =\frac{z}{r}\), \(\sin \theta =\frac{x}{r}\), the quantity \(V_n\) can be expressed as
and then, its derivative with respect to z is
Likewise, the derivative with respect to x is
Hence,
Now we can write the spectral expansions of the first-order derivatives as
where the spectral expansion coefficients \(C_n^z\), \(S_n^z\), \(C_n^x\) and \(S_n^x\) can be obtained from the coefficients \(C_n\) and \(S_n\) by
We can also use the formulas of the Cartesian partial derivatives in polar coordinates
to get the spectral expansions (29) and (30).
We can infer that the two recursive relations (31) and (32) are actually suitable for evaluating the coefficients of the spectral expansions of higher-order derivatives. Hence, the spectral expansions of the second-order derivatives are
where the coefficients are
In general, the spectral expansion of the arbitrary-order derivative of V can be written as
where \(j_1,j_2,\ldots ,j_k=1,2\), \(k=1,2,\ldots \), \(z_1=z\), \(z_2=x\) and the coefficients \(C_n^{z_{j_1}z_{j_2}\ldots z_{j_k}}\) and \(S_n^{z_{j_1}z_{j_2}\ldots z_{j_k}}\) can be obtained from the spectral expansion coefficients of the lower-order derivatives by
The degree of the finite expression for the kth-order derivative \(V_{z_{j_1}z_{j_2}\ldots z_{j_k}}\) is \(N+k\) corresponding to the degree N for the quantity V. From Eqs. (3) and (4), we can get the expression of the gravitational attraction and its arbitrary-order derivatives
3 Computation of the gravity effects caused by 2D bodies
3.1 Gravity effects of a 2D body with constant density
To evaluate the gravity effects of a 2D body with certain density distribution \(\rho (z',x')\), we need to evaluate the spectral expansions of V and its derivatives and the double integral \(D_{\rho }\). We denote the symbols \(\partial \varOmega \) as the boundary curve of the 2D body, \(H_{n}\) as corresponding integral of product of the density function \(\rho \) and the either component \(h_{n}\) of the vector \(\varvec{\mathrm{h}}_{n}\). The parametric equation of the boundary \(\partial \varOmega \) can be expressed as: \(\varvec{\mathrm{r}}=\varvec{\mathrm{r}}(s)\), where \(\varvec{\mathrm{r}}\) represents the position vector. Then, the unit direction vector \(\varvec{\mathrm{v}}\) along \(\partial \varOmega \) is
and the unit normal vector \(\varvec{\mathrm{n}}\) pointing outward can be written as
According to the divergence formula in polar coordinate reference frame
and the product rule of divergence for a scalar-valued function and a vector field, and from Eqs. (20) and (21), for the uniform 2D body with constant density \(\rho \) we have
where the linear closed integral is counted counterclockwise. To avoid numerical problems for large n, the integrals \(H_n\) ought to be normalized. The coefficients \(C_n\) and \(S_n\) can be rewritten as
where the normalized terms are
Hence, the vector \(\overline{\varvec{\mathrm{H}}}_{n}\) can be given by
For the uniform body, since \(\mathrm{div} \left( \varvec{\mathrm{r}} \right) =2\), the integral \(D_{\rho }\) can be expressed as
also counted counterclockwise along the boundary. For numerical experiments, we can evaluate the vector \(\overline{\varvec{\mathrm{H}}}_{n}\) and the integral \(D_{\rho }\) using numerical integration, e.g. the Gauss–Kronrod quadrature formula (Laurie 1997). The vector \(\overline{\varvec{\mathrm{h}}}_{n}(s)\) in the line integral can be obtained from the polar coordinates of the moving point. The polar coordinates of a point can be evaluated from its Cartesian coordinates. The expression of the radius r is given in Eq. (11). According to Vermeille (2011) and Chen et al. (2019b), we take the arctan expression
for the point in the region: \(z+\sqrt{z^2+x^2}<\varepsilon \sqrt{z^2+x^2}\), and the expression
for the point in other region to evaluate the angle \(\theta \), where the threshold can be taken as \(\varepsilon =10^{-3}\).
The 2D body can be approximated by a polygonal body for the convenience of calculation and the agreement with the constituted shape of the measured points, as shown in Fig. 2. We denote \(N_E\) as the total number vertices of the polygon, \((\xi _i,\eta _i)\) as the Cartesian coordinates of the ith vertex of the polygon and \(\varvec{\mathrm{p}}_{i}\) as the position vector of the ith vertex counted counterclockwise. Then, the unit direction vector \(\varvec{\mathrm{v}}_{i}\) and the position vector \(\varvec{\mathrm{r}}_{i}\) along the ith edge of the polygon can be expressed as
where \(\varvec{\mathrm{p}}_{i+1}\) becomes \(\varvec{\mathrm{p}}_{1}\) when \(i=N_E\), \(l_i\) represents the length of the ith edge, being \(l_i=|\varvec{\mathrm{p}}_{i+1}-\varvec{\mathrm{p}}_{i} |\), and \(s_i\) is the length parameter, meeting \(0 \leqslant s_{i} \leqslant l_{i}\). It is obvious that \(v_{i,1}^2+v_{i,2}^2=1\). Since \(d_i=\varvec{\mathrm{r}}_i \cdot \varvec{\mathrm{n}}_i\) is a constant on the ith edge where \(\varvec{\mathrm{n}}_i\) is the unit normal vector, the vector \(\varvec{\mathrm{H}}_{n}\) can be written as
where the symbol \(\varvec{\mathrm{I}}_{n,i}\) represents
Since
for the point on the ith edge we have
Integrating along the ith edge with respect to the parameter \(s_i\), we can get
By assuming the normalized term
Eq. (63) can be rewritten as
where \(\overline{\varvec{\mathrm{h}}}_{n}\) for \(s_i=0\) and \(s_i=l\) can be obtained from the polar coordinates of the starting point and the ending point of the ith edge. We can also get the vector \(\overline{\varvec{\mathrm{I}}}_{n,i}\) using recursive algorithm, see Sect. 3.2. Now we can evaluate the vector \(\overline{\varvec{\mathrm{H}}}_{n}\) by
The integral \(D_{\rho }\) can be expressed as
3.2 Gravity effects of a 2D body with polynomial density
The density function \(\rho (z',x')\) of a 2D body with polynomial density distribution can be expressed as (Rao 1985; Zhang et al. 2001; Zhou 2010; D’Urso 2015)
where the positive integer \(N_{\rho }\) is the degree of the polynomial, \(\rho _{j,k}\) are the constant polynomial factors which are independent of \(Q(z',x')\) and the natural numbers j, k are the exponents, meeting \(0\leqslant j,k\leqslant N_{\rho }\) and \(j+k\leqslant N_{\rho }\). From Eq. (20), the vector \(\varvec{\mathrm{H}}_{n}\) is
We denote \(H_{n,j,k}\) as the either component of the vector \(\varvec{\mathrm{H}}_{n,j,k}\).
From Eq. (47), we have
Hence,
We can further get the spectral coefficients
where
Since
the double integral \(D_{\rho }\) is
For the point inside the 2D area \(\varOmega \), it may be \(|\frac{z'}{a}|,|\frac{x'}{a}|,\frac{r'}{a}<1\), and then, the line integrals in Eqs. (73) and (75) are convergent. For the 2D body with polynomial density, the vector \(\overline{\varvec{\mathrm{H}}}_{n}\) and the integral \(D_{\rho }\) can also be obtained by using numerical integration.
When the 2D body is approximated by a polygonal body, the integral \(H_{n,j,k}\) can be rewritten as
Since
for the point on the ith edge, where the symbol
the line integral in Eq. (76) is
Now we denote the symbol \(\varvec{\mathrm{I}}_{n,m,i}\) as the corresponding \(2\times 1\) vector of \(I_{n,m,i} \) and then have
From Eq. (62), we can get
Integrating along the ith edge with respect to \(s_i\), we have
Due to the trigonometric identity
we get another recursive relation for the vector \(\varvec{\mathrm{I}}_{n,m,i}\)
Then from Eqs. (82) and (84), we can have
and
i.e.
where the initial values \(\varvec{\mathrm{I}}_{n,0,i}\) and \(\varvec{\mathrm{I}}_{0,m,i}\) are
Both Eqs. (85) and (87) can be applied for evaluating the vector \(\varvec{\mathrm{I}}_{n,m,i}\). In this work, we choose the latter algorithm.
We assume the normalized term
and then get the vector \(\overline{\varvec{\mathrm{H}}}_{n,j,k}\)
From Eq. (87), the recursive computation for the vector \(\overline{\varvec{\mathrm{I}}}_{n,m,i}\) is
where the initial value \(\varvec{\mathrm{I}}_{0,m,i}\) is
It is obvious that \(0<\frac{l_{i}}{a}<2\). When \(\frac{l_{i}}{a}>1\) and m is large (\(0\leqslant m \leqslant N_{\rho }\)), the vector \(\left( \frac{s_i}{a}\right) ^{m}s_i\overline{\varvec{\mathrm{h}}}_{n} \big |_0^{l_i}\) and the integral \(\overline{\varvec{\mathrm {I}}}_{0,m,i}\) may be divergent. However, for these segments (\(\frac{l_{i}}{a}>1\)) we can divide them into two small ones with equal length whose lengths meet \(\frac{l_{i}}{a} < 1\). In practice, the degree \(N_{\rho }\) is often small. The spectral radius of the propagator matrix meets
and then, the recursive relation Eq. (92) is stable. Moreover, Eq. (85) with normalized is also numerically stable for evaluating the vector \(\overline{\varvec{\mathrm{I}}}_{n,m,i}\). If \(m=0\), Eq. (92) becomes
where \(\overline{\varvec{\mathrm{I}}}_{n,i}=\overline{\varvec{\mathrm{I}}}_{n,0,i}\). The recursion (95) can also be used for evaluating the vector \(\overline{\varvec{\mathrm{I}}}_{n,i}\) in Sect. 3.1.
For the integral \(D_{\rho }\), we can also get
where the line integral is
3.3 Gravity effects of a 2D body with exponential density
We now consider a 2D body with exponential density distribution (Cordell 1973; Zhou 2008; Wu 2019):
where \(\varvec{{\lambda }}=(\lambda _z,\lambda _x)\) is a constant vector indicating the direction and magnitude of the exponential decay. For the 2D body, the vector \(\varvec{\mathrm{H}}_{n}\) can be expressed as
Since
we have
The right-hand side of Eq. (101) still contains the double integral term. Applying the divergence formula
we further have
In general, we have the divergence relation
and finally get
where
Because \((n+2)(n+3)\ldots (n+k+2)\) increases faster than \(|(\varvec{{\lambda }}\cdot \varvec{\mathrm{r}})^{k+1}|\) when \(n+k+2>|\varvec{{\lambda }}\cdot \varvec{\mathrm{r}}|\), the double integral \(\varvec{\mathrm{D}}_{n,N_k}\) converges to zero when \(N_k\rightarrow +\,\infty \), i.e. \(\lim _{N_k\rightarrow +\,\infty }\varvec{\mathrm{D}}_{n,N_k}=\varvec{0}\). Hence, the vectors \(\varvec{\mathrm{H}}_{n}\) and \(\overline{\varvec{\mathrm{H}}}_{n}\) can be expressed as the infinite expansions
where
For numerical experiments, we can use
to evaluate the spectral expansion coefficients, where the vector \(\overline{\varvec{\mathrm{K}}}_{n,k}\) (\(n=1,2,3,\ldots ,k=0,1,2,\ldots \)) is evaluated by numerical integration. Since \((\varvec{{\lambda }}\cdot \varvec{\mathrm{r}})^k/((n+2)(n+3)\ldots (n+k+2))\) converges fast to zero, we can evaluate the expression with the required accuracy up to a certain degree. For larger n, the required degree \(N_k\) may be smaller. Analogously, the double integral \(D_{\rho }\) for the 2D body with exponential density can be written as
where
We can also evaluate the integral \(D_{\rho }\) with the required accuracy up to a certain degree \(N_k\) by
where the line integral \(K_{0,k}\) is evaluated by numerical integration.
When the 2D body is approximated by a polygonal body, we can get the vector \(\varvec{\mathrm{H}}_{n}\) and the normalized term \(\overline{\varvec{\mathrm{H}}}_{n}\)
where
and the dot product \(\varvec{{\lambda }}\cdot \varvec{\mathrm{r}}_{i}\) can be expressed as \(\varvec{{\lambda }}\cdot \varvec{\mathrm{r}}_{i} =\varvec{{\lambda }}\cdot \varvec{\mathrm{p}}_{i}+(\varvec{{\lambda }}\cdot \varvec{\mathrm{v}}_{i})s_{i}\). For numerical experiments, we can use
to get the spectral expansion coefficients. For the double integral \(D_{\rho }\), we can get
where
and also evaluate the integral \(D_{\rho }\) for numerical implementation by
The line integrals \(\overline{\varvec{\mathrm{K}}}_{n,k,i}\) and \(K_{0,k,i}\) are obtained by numerical integration.
4 Numerical experiments
Three polygonal models were used to test the formulas of this paper. These models include a rectangular cylinder with quadratic density contrast varying with depth, a 26-sided polygon body with quadratic density contrast varying in both horizontal and vertical directions and a rectangular cylinder with exponential density contrast varying with depth. The methods for evaluating the gravity effects of the 2D source body in the literature are based on the surface integrals of the contributions exerted by the surface elements of the body on an unit mass located at the observation point. Then, we can compare the results of the spectral-domain algorithm in this work with the space-domain algorithm including the semi-numerical method (Zhou 2008, 2009b) and the analytical method (D’Urso 2015). Because the vertical component of the gravity anomaly of the 2D body is often considered, e.g. Rao (1985, 1990), Zhang et al. (2001), Zhou (2008, 2009b) and D’Urso (2015), we focus on the evaluation of the gravity anomaly \(g_z\) in numerical implementation. According to Sect. 2, for numerical experiments the gravity anomaly \(g_z\) of the 2D body can be evaluated by
where the value of the gravitational constant is \(G=6.67259\times 10^{-11}~\mathrm{m}^3~\mathrm{kg}^{-1}\,\mathrm{s}^{-2}\). The Gauss–Kronrod quadrature formula was used to the numerical integrations for Zhou (2008, 2009b) and this work (only for the quantities \(\overline{\varvec{\mathrm{H}}}_{n}\) and \(D_{\rho }\) of the 2D rectangular cylinder body with exponential density contrast). We can first evaluate the spectral expansion coefficients and the double integral \(D_{\rho }\) and store these data on the hard drive of the computer. When evaluating the gravity effects of a 2D polygonal body at an external point by spectral-domain method, we read the coefficients and integral data from the hard drive.
The program codes using double precision were written in Fortran 90. The codes compiled by the Intel Visual Fortran Composer XE 2013 SP1 Update 1 executed at a PC with an Intel Core i5-7300HQ CPU and 16 GB main memory under the 64 bit Windows 10. The processor base frequency and max turbo frequency of the Intel Core i5-7300HQ CPU are 2.50 GHz and 3.50 GHz, respectively. For the logarithm \(\log _{10}|\mathrm{Value}|\) of the plottings, we evaluate \(\log _{10}|\mathrm{Value}|\) using the machine epsilon of the double-precision arithmetic to avoid the singularity when \(\mathrm{Value}=0\), saying at this point \(\mathrm{Value}=2.220446049250313\hbox {E}{-}16\) (\(2^{-52}\)).
4.1 A 2D rectangular cylinder with quadratic density contrast varying with depth
The first experiment refers to a 2D rectangular cylinder body with 6 km wide and 1 km high at a depth of 1 km (in Fig. 3), which has been investigated by Rao (1986b), Zhang et al. (2001), D’Urso (2015) and Wu (2018b). We denote \((z_0,x_0)\) as the Cartesian coordinates of the initial 2D reference frame and choose a circle centred at the new origin O: \(z_0=1.5\) km, \(x_0=6\) km. The radius of the circle is \(a=\sqrt{0.5^2+3^2}\approx 3.0414\) km to make the circle enclose the 2D rectangular cylinder. Then, the range of the calculable observation point along the line \(z_0=0\) km is \(x_0=-\,\infty \sim 3.3542\) km, \(x_0=8.6458\sim +\,\infty \) km. Due to the symmetry of the rectangular cylinder, the gravity anomalies at the symmetrical points of the two ranges are equal. Since the converted relation of the coordinates between the initial and new 2D Cartesian reference frames (in Fig. 3) is: \(z=z_0-1.5,x=x_0-6\), the density contrast of the 2D body in the new frame can be expressed as \(\rho (z,x)=1.54+0.24z_0-0.035z_0^2=1.82125 + 0.135 z - 0.035 z^2\), where the coordinates \(z,z_0\) are in km and the density is in \(\mathrm{g}~\mathrm{cm}^{-3}\), i.e. \(10^3\)\(\mathrm{kg}~\mathrm{m}^{-3}\). Equation (25) of Zhou’s (2008) paper using algebraic kernel is used to evaluate the gravity anomaly of the 2D rectangular cylinder, which leads to higher-precision results than Eq. (15) of Zhou’s (2008) paper using arctangent kernel.
The executed time for evaluating the spectral expansion coefficients \(C_n^z\), \(S_n^z\) up to degree 360 and the double integral \(D_{\rho }\) is 0.00241 s (average cost for 1000 times executions). The diagrams of the coefficients of degree \(n=2{-}361\) (\(N=360\)) are illustrated in Fig. 4. The coefficient \(C_n^z\) displays a periodically damped oscillation which may be caused by the factor \(\left( \frac{r'}{a}\right) ^n\cos (n\theta ')\) of the integral expression (18) of the spectral expansion coefficient. Due to the symmetries of the 2D rectangular cylinder and the density contrast about the vertical axis \(z_0\), for the two symmetric points \((r',\theta ')\) and \((r',2\pi -\theta ')\) inside the body the integrands of Eq. (19) are opposite, and then, \(S_n^z=S_n=0\). In Fig. 4, the evaluated values of \(S_n^z\) are very close to the true values zero. Because the time costs for D’Urso (2015), Zhou (2008) and this work are very short where the costs for the computation of \(C_n^z\), \(S_n^z\) and \(D_{\rho }\) and the data reading are not counted, we take 100,000 times repetitive executions for timing the computation of the gravity anomalies at the distances \(x_0=8.6458\), 10, 20, 30, 40, 50 km. Then, the computational costs for D’Urso (2015), Zhou (2008) and this work are 2.391 s, 8.703 s and 19.580 s, respectively. To verify the results by using the spectral-domain method, we make the numerical experiments with the degree N of the spectral expansion and the distance \(x_0\) of the test point. The diagrams of the gravity anomalies evaluated by spectral-domain method and their relative errors compared with D’Urso (2015) and Zhou (2008) varying with the degree N at the points \(x_0=8.6458\), 10, 20, 30, 40, 50 km are illustrated in Fig. 5, and their values at the degree \(N=360\) are given in Table 1. For the point on the enclosed circle (\(x_0=8.6458\) km), the results of the spectral expansions of the gravity anomalies at the degrees \(N=36,360,3600,36{,}000,360{,}000,3{,}600{,}000\) are listed in Table 2. Then, the gravity anomaly and its relative error varying with the distance \(x_0=8.6458{-}50\) km of the test point are shown in Fig. 6. The accuracy of the spectral expansion depends on the expanded degree and the position of the observation point. We plot the needed degrees of the spectral expansions of the gravity anomalies with accuracy less than the levels \(|\delta g_z/g_{z}^0|=10^{-4},10^{-6},10^{-8},10^{-10},10^{-12},10^{-14}\) for the rectangular cylinder in Fig. 7, where \(g_{z}^0\) represents the result evaluated by Zhou (2008) and \(\delta g_z\) denotes the difference between Zhou (2008) and this work.
Gravity anomaly of the 2D rectangular cylinder body with quadratic density contrast evaluated by this work and the relative errors compared with D’Urso (2015) and Zhou (2008) varying with the distance \(x_0=8.6458{-}50\) km of the test point. The spectral expansions have been evaluated up to degree 360
Figure 5 demonstrates the result of the spectral expansion of the gravity anomaly converges with the degree N. When the point moves away from the 2D rectangular cylinder body, the expansion converges faster. For the point near the 2D body, we may need to expand the expansion at ultra-high degree to obtain the high-precision result, which is also shown in Table 2. For the computation of the coefficients \(C_n^z\), \(S_n^z\) up to degree \(N=3{,}600{,}000\), the cost is 31.095 s. From Fig. 6, the gravity anomaly evaluated by spectral-domain method decreases with the distance of the test point and has good accuracy compared with the analytical solutions of D’Urso (2015) and Zhou (2008). Figure 7 shows the needed degree \(N_d\) (\(N_d=N+1\)) of the spectral expansion of the gravity anomaly with accuracy less than a level reduces with the distance and reaches a steady value when the distance of the test point exceeds a certain range (except for \(10^{-14}\)). The steady degrees with the levels \(|\delta g_z/g_{z}^0|=10^{-4},10^{-6},10^{-8},10^{-10},10^{-12}\) for the 2D rectangular cylinder are 3, 5, 7, 9, 11, respectively. From Table 2 and Figs. 5, 6, we can see the relative error \(|\delta g_z/g_{z}^0|\) (absolute value) compared with Zhou (2008) is in \(10^{-16}{-}10^{-13}\) and with D’Urso (2015) becomes larger when the test observation point relatively keeps away from the body, which may be caused by the inaccuracy of the analytical method for the observation point outside the body although the analytical method is more accurate for the point near and inside the body, see Sect. 4.4.
Gravity anomaly of the 2D rectangular cylinder body with quadratic density contrast evaluated by this work where the body is divided into three parts, and the relative errors compared with D’Urso (2015) and Zhou (2008) varying with the distance \(x_0=0{-}50\) km of the test point. The spectral expansions have been evaluated up to degree 90
For the region between the boundary of the 2D polygonal body and the smallest enclosed circle, the spectral expansion may be divergent. Then, for the point in the range \(x_0=3.3542{-}8.6458\) km, the spectral expansion may be divergent. To evaluate the gravity anomaly at that point by using spectral-domain method, we can split the body into three same 2D rectangular cylinders (in Fig. 8). Then, we set up three new local reference frames with the origins at the geometrical centres of the three small cylinders and with the vertical and horizontal axes coincident with the directions of the \(z_0\)-, \(x_0\)-axes. Thus, the origins of the three new local reference frames are \(O_1\): \(z_0=1.5\) km, \(x_0=4\) km, \(O_2\): \(z_0=1.5\) km, \(x_0=6\) km and \(O_3\): \(z_0=1.5\) km, \(x_0=8\) km, and the radii of the three circles enclosed these small cylinders are \(a_1=a_2=a_3=\sqrt{0.5^2+1^2}\approx 1.1181\) km. The Cartesian coordinates of the three new reference frames are: \(z_1=z_0-1.5,x_1=x_0-4\), \(z_2=z_0-1.5,x_2=x_0-6\), \(z_3=z_0-1.5,x_3=x_0-8\). For the small cylinders, its internal density contrast can be written as \(\rho (z_1,x_1)=\rho (z_2,x_2)=\rho (z_3,x_3)=1.82125 + 0.135 z - 0.035 z^2\), where \(z_1=z_2=z_3=z\).
For the nearest point \(x_0=6\) km, when the spectral expansion is evaluated up to degree 90, the result of the gravity anomaly of this paper reaches the accuracy \(10^{-15}\). Therefore, the degree of the spectral expansion can be taken as 90 to obtain the high-precision gravity anomaly along the line \(z_0=0\) km. The executed time for evaluating the coefficients \(C_n^z\), \(S_n^z\) up to degree 90 and the integral \(D_{\rho }\) is 0.00181 s (average cost for 1000 times executions). The time costs of D’Urso (2015), Zhou (2008) and this work for the computation of the gravity anomalies at the distances \(x_0=6, 10, 20, 30, 40, 50\) km with 100,000 times executions are 2.423 s, 9.860 s and 11.032 s, respectively. Figure 9 shows these modelling results and their relative errors compared with D’Urso (2015) and Zhou (2008) varying with the degree N. Figure 10 shows the gravity anomaly of the 2D rectangular cylinder which is divided into three parts and its relative error varying with the distance \(x_0=0{-}50\) km of the test point.
4.2 A 26-sided polygon body with quadratic density contrast varying in both horizontal and vertical directions
As shown in Fig. 11, the 2D source body is bounded by the four curves: \(z_0=0\), \(x_0=f_1(z_0)=-\,4-0.07z_0+0.3z_0^2+0.01z_0^3\), \(z_0=3\) and \(x_0=f_2(z_0)=4.5+0.5z_0-0.2z_0^2\), which has been studied by Martín-Atíenza and Garcia-Abdeslem (1999), Zhou (2009b), D’Urso (2015) and Wu (2018b). D’Urso (2015) approximated the boundary of the body by a 26-sided polygon which is also tested in this paper. The 26-sided polygon is produced by taking the segments every 0.25 km in vertical direction along the curves \(x_0=f_1(z_0)\) and \(x_0=f_2(z_0)\). The centre and radius of the circle enclosed the 26-sided polygon body can be chosen as O: (1.5 km, 0.25 km) and \(a=4.5774\) km, respectively, and then, the calculable range along the line \(z_0=0\) km is \(x_0=-\,\infty \sim -\,4.0747\) km, \(x_0=4.5747\sim +\,\infty \) km. The Cartesian coordinates in the new reference frame (in Fig. 11) can be written as \(z=z_0-1.5,x=x_0-0.25\). Hence, the density function of the 26-sided polygon body can be expressed as \(\rho (z,x)=-\,0.7-0.05x_0 z_0+0.04x_0^2+0.06z_0^2=-\,0.58125-0.055x+0.1675 z-0.05xz+0.04 x^2+0.06 z^2\), where the coordinates \(z,x,z_0,x_0\) are in km and the density is in \(\mathrm{g}~\mathrm{cm}^{-3}\). In order to guarantee the numerical stability of Zhou’s (2009b) algorithm when the observation point moves away from the body, the gravity anomaly caused by the horizontal density contrast should be calculated by Eq. (11) using algebraic kernel instead of Eqs. (6) and (19) using logarithmic kernel, where in Eq. (19) of Zhou’s (2009b) paper we take the function \(Z_1(x,z)=z-(x-x_i)\arctan (\frac{z}{x-x_i})\).
The time cost for evaluating the spectral expansion coefficients \(C_n^z\), \(S_n^z\) up to degree 360 and the double integral \(D_{\rho }\) for the 26-sided polygon body is 0.0174 s (average cost for 1000 times executions). The coefficients of degree \(n=2{-}361\) are plotted in Fig. 12. The coefficients \(C_n^z\) and \(S_n^z\) of the 26-sided polygon body are periodically damped and oscillated because of the factors \(\left( \frac{r'}{a}\right) ^n\cos (n\theta ')\) and \(\left( \frac{r'}{a}\right) ^n\sin (n\theta ')\) of the integral expressions of the spectral expansion coefficients. The gravity anomalies of the 26-sided polygon body evaluated by spectral-domain method and their relative errors compared with D’Urso (2015), Zhou (2009b) varying with the degree N at the distances \(x_0=4.5747\), 10, 20, 30, 40, 50 km are plotted in Fig. 13, and their values with the degree \(N=360\) at these points are listed in Table 3. The time costs of D’Urso (2015), Zhou (2009b) and this work for 100,000 times executions are 14.298 s, 103.585 s and 20.924 s, respectively. We also plot the gravity anomaly of the 26-sided polygon body the relative error varying with the distance \(x_0\) in Fig. 14. Figure 14 also demonstrates the relative errors between D’Urso (2015) and this work and Zhou (2009b) increase when the test point moves away from the body.
4.3 A 2D rectangular cylinder with exponential density contrast varying with depth
The final tested body refers to a 2D rectangular cylinder body with exponential density contrast which has same geometry as the one in Sect. 4.1. Its density function varying with depth is chosen as (Cordell 1973; Wu 2019): \(\rho (z,x)= 2.67 \hbox {e}^{-0.64z_0}= 1.022324005553549 \hbox {e}^{-0.64z}\), where the coordinates \(z,z_0\) are in km and the density is in \(\mathrm{g}~\mathrm{cm}^{-3}\).
Results of the gravity anomalies of the 2D rectangular cylinder body with exponential density contrast evaluated by this work and the relative errors compared with Zhou (2008) varying with the degree N at the distances \(x_0=8.6458\), 10, 20, 30, 40, 50 km
Results of the gravity anomaly of the 2D rectangular cylinder body with exponential density contrast evaluated by this work and its relative error compared with Zhou (2008) varying with the distance \(x_0=8.6458{-}50\) km of the test point. The spectral expansions have been evaluated up to degree 360
Assuming \({\overline{H}}_{n,N_k}\) as the either component of the vector \(\overline{\varvec{\mathrm{H}}}_{n}\) (namely the coefficient \(C_n\) or \(S_n\)) evaluated up to degree \(N_k\), we can take the true component \({\overline{H}}_{n}\approx {\overline{H}}_{n,N_k}\) when \({\overline{H}}_{n,N_k+1}={\overline{H}}_{n,N_k}\) in double-precision arithmetic, where the accuracy (relative error) of \({\overline{H}}_{n}\) is in \(10^{-16}\). Figure 15 shows results of the first component of the vector \(\overline{\varvec{\mathrm{H}}}_{n}\) (\(C_n\)) and the relative error \(\delta _{n,N_k}=|({\overline{H}}_{n,N_k+1} -{\overline{H}}_{n,N_k})/{\overline{H}}_{n,N_k}|\) varying with the index \(N_k\) at the degrees \(n=1,2+1,2^2+1,2^3+1,2^4+1,2^5+1\). The diagrams of the second component (\(S_n\)) are similar although the evaluated value of \(S_n\) is very close to the true values zero for the 2D rectangular cylinder body. The executed time for evaluating the spectral expansion coefficients \(C_n^z\), \(S_n^z\) up to degree 360 and the double integral \(D_{\rho }\) is 0.578 s. The computational costs for evaluating the gravity anomalies at the distances \(x_0=8.6458\), 10, 20, 30, 40, 50 km by Zhou (2008) and this work with 100,000 times are 9.552 s and 20.393 s, respectively. Figure 16 shows the coefficients \(C_n^z\), \(S_n^z\) of degree \(n=2{-}361\), where \(C_n^z\) is also periodically damped and oscillated and the evaluated values of \(S_n^z\) are also close to the true value zero (\(S_n^z=S_n=0\)). Results of the gravity anomaly of the 2D rectangular cylinder body with exponential density contrast varying with the degree \(N=1{-} 360\) and the distance \(x_0=8.6458{-}50\) km of the test point are presented in Figs. 17 and 18, respectively.
4.4 Numerical stabilities at remote observation point
D’Urso (2015) indicated the result of the closed solution for evaluating the gravity anomaly of a 2D body with polynomial density contrast at a remote point is inaccurate and this may be caused by which the 2D body is approximately a point source, analogous to the 3D case (Holstein and Ketteridge 1996; Holstein et al. 2007; Ren et al. 2018; Chen et al. 2019b). In this section, the numerical experiments for the gravity anomalies of the two 2D bodies in Sects. 4.1 and 4.2 (the 2D rectangular cylinder body and the 26-sided polygon body with quadratic density contrast) evaluated by D’Urso (2015) and this work varying with the distance \(x_0=50{-}5000\) km of the test point are implemented in Fig. 19, where the values of the gravity anomalies of the two 2D bodies are limited in \([0,3\times 10^{-5}]\) mGal and \([-1 \times 10^{-4},2\times 10^{-5}]\) mGal, respectively. The relative errors for the three bodies in Sects. 4.1, 4.2 and 4.3 between Zhou (2008, 2009b) and this work varying with the distance \(x_0=50{-}500{,}000\) km are illustrated in Fig. 20.
Results of the gravity anomalies of the 2D rectangular cylinder body and 26-sided polygon body with quadratic density contrast by D’Urso (2015) and this work and the relative errors varying with the distance \(x_0=50{-}5000\) km of the test point. The spectral expansions have been evaluated up to degree 360
Figure 19 demonstrates the results of the gravity anomalies of the 2D bodies evaluated by D’Urso (2015) have the problem of oscillation at the point \(x_0=50{-}5000\) km. However, the spectral-domain method of this paper is numerically stable at these points. The spectral expansion of the gravity effects of a 2D body is determined by the radius r and the angle \(\theta \) of the observation point and is convergent with needing to expand at fewer degree for the point of larger distance. Therefore, the result of the gravity anomaly of this work remains accurate in theory when the observation point moves away from the 2D body. Figure 20 also illustrates the space-domain algorithm evaluating the line integral using numerical integration (Zhou 2008, 2009b) is high accurate for the remote observation point and highly coincident with the spectral-domain algorithm. The differences increasing with the distance in Fig. 20 may be caused by the machine error of double-precision arithmetic (about 2.22E\(-\)16), and quadruple precision arithmetic can be used to get higher-precision results whose machine error is about 1.93E\(-\)34, i.e. having about 34 significant digit. The arctan kernel \(Z_1(x,z)\) in Zhou’s (2009b) paper may lead to the slightly larger growth for the 26-sided polygon body with quadratic density contrast (in Fig. 20). The reasons for the numerical stabilities may be that both the integrands of the numerical integrations in Eq. (25) of Zhou’s (2008) paper and Eqs. (11) and (19) (excluding the logarithmic kernel) of Zhou’s (2009b) paper and the factor \(\left( \frac{a}{r}\right) ^n\) in the spectral expansion of this paper converge with the distance of the observation point increasing. However, each dot product containing the position vector of the observation point in Eq. (86) of D’Urso’s (2015) paper diverges with the distance increasing, and then, the algorithm may be numerical ill-conditioning for large distance. Due to the same reason, Zhang’s et al. (2001) and Zhou’s (2010) algorithms are also numerically instable at the remote observation point.
5 Conclusions
The spectral-domain approach based on the 2D Laplace’s equation for evaluating the gravity effects of a 2D body with constant, polynomial and exponential density models has been proposed and extended to the normalized case for numerical stabilities. We also presented the spectral-domain algorithm for the mass body approximated by a 2D polygon. For the applicability of the spectral-domain method to gravity forward computation, the surface integral expressions of the spectral expansion coefficients are given. Once the spectral expansion coefficients and the double integral of the density function are obtained, the gravitational attraction, gravity gradient tensor and higher-order derivatives can be immediately evaluated. The numerical experiments show the spectral-domain algorithm is high accurate for the external observation point, e.g. 13–16 digits achievable precision for the gravitational attraction.
Although the closed solution in space domain for the gravity anomaly of the 2D body with polynomial density model (Zhang et al. 2001; Zhou 2010; D’Urso 2015) is fastest, it is numerically instable for the remote observation point. The space-domain method using numerical integration (Zhou 2008, 2009b) and the spectral-domain method are stable for arbitrary external observation point. Zhou’s (2008; 2009b) algorithms are suitable for evaluating the gravity anomaly of the 2D body with exponential density model varying in a single dimension z or x. However, for the exponential density model varying in both horizontal and vertical directions, the integrals in Eqs. (18) and (19) of Zhou (2009b)’s paper are hard to be obtained. Then, the Zhou (2008, 2009b)’s algorithms may do not work for this case. The spectral-domain method in this paper can handle the constant, polynomial and exponential density models in both horizontal and vertical directions, and the gravitational attraction and its arbitrary-order derivatives. For the region between the boundary of the 2D body and the smallest enclosed circle, the spectral-domain method may be divergent. In order to reduce the possible non-convergence region, we can split the body into small ones, as shown in the numerical experiments of this paper, and we can also apply the elliptical harmonic method (van Gelderen 1992) which will be considered in future works. Compared to the closed-form solutions having declined accuracies when the point moves away from the body (D’Urso and Trotta 2017; Ren et al. 2018; Chen et al. 2019b), the space-domain approach using numerical integration and the spectral-domain approach based on the 2D/3D Laplace’s equation are more suitable for accurate forward computation of the external gravity effects of the 2D/3D body. The Fourier-domain approach evaluating the Fourier spectrum using numerical method can also be applied to obtain the forward modelling results and is high accurate for the observation point near the 2D body (Wu 2018b). Although there was no numerical test for the remote point in Wu’s (2018b) paper, the Fourier-domain method may be numerically stable at this point including the 2D and 3D case because of the numerical computation of the Fourier spectrum. For the 3D body, the Fourier-domain method can produce the forward results with a few significant digits (Wu 2018b, 2019). Moreover, it should be noted that the observation point is usually not too far from the cross section for common actual applications due to the approximation of the 3D parallel body by the 2D body model, and then, the numerical and analytical methods can be both applied to the 2D gravity forward problems.
References
Artemjev M, Kaban M, Kucherinenko V, Demyanov G, Taranov V (1994) Subcrustal density inhomogeneities of Northern Eurasia as derived from the gravity data and isostatic models of the lithosphere. Tectonophysics 240:249–280
Balmino G (1994) Gravitational potential harmonics from the shape of an homogeneous body. Celest Mech Dyn Astron 60:331–364
Bott M (1960) The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins. Geophys J Int 3:63–67
Chai Y, Hinze WJ (1988) Gravity inversion of an interface above which the density contrast varies exponentially with depth. Geophysics 53:837–845
Chakravarthi V, Sundararajan N (2004) Ridge-regression algorithm for gravity inversion of fault structures with variable density. Geophysics 69:1394–1404
Chao BF, Rubincam DP (1989) The gravitational field of phobos. Geophys Res Lett 16:859–862
Chappell A, Kusznir N (2008) An algorithm to calculate the gravity anomaly of sedimentary basins with exponential density-depth relationships. Geophys Prospect 56:249–258
Chen C, Chen Y, Bian S (2019a) Evaluation of the spherical harmonic coefficients for the external potential of a polyhedral body with linearly varying density. Celest Mech Dyn Astron 131:1–28
Chen C, Ouyang Y, Bian S (2019b) Spherical harmonic expansions for the gravitational field of a polyhedral body with polynomial density contrast. Surv Geophys 40:197–246
Cordell L (1973) Gravity analysis using an exponential density-depth function; San Jacinto Graben, California. Geophysics 38:684–690
Cunningham LE (1970) On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite. Celest Mech 2:207–216
D’Urso MG (2012) New expressions of the gravitational potential and its derivatives for the prism. In: VII Hotine-Marussi symposium on mathematical geodesy. Springer, Berlin, pp 251–256
D’Urso MG (2013) On the evaluation of the gravity effects of polyhedral bodies and a consistent treatment of related singularities. J Geod 87:239–252
D’Urso MG (2014a) Analytical computation of gravity effects for polyhedral bodies. J Geod 88:13–29
D’Urso MG (2014b) Gravity effects of polyhedral bodies with linearly varying density. Celest Mech Dyn Astron 120:349–372
D’Urso MG (2015) The gravity anomaly of a 2D polygonal body having density contrast given by polynomial functions. Surv Geophys 36:391–425
D’Urso MG, Trotta S (2015) Comparative assessment of linear and bilinear prism-based strategies for terrain correction computations. J Geod 89:199–215
D’Urso MG, Trotta S (2017) Gravity anomaly of polyhedral bodies having a polynomial density contrast. Surv Geophys 38:781–832
Fukushima T (2016) Numerical integration of gravitational field for general three-dimensional objects and its application to gravitational study of grand design spiral arm structure. Mon Not R Astron Soc 463:1500–1517
Fukushima T (2017) Precise and fast computation of the gravitational field of a general finite body and its application to the gravitational study of asteroid eros. Astron J 154:145
Fukushima T (2018a) Accurate computation of gravitational field of a tesseroid. J Geod 92:1371–1386
Fukushima T (2018b) Recursive computation of gravitational field of a right rectangular parallelepiped with density varying vertically by following an arbitrary degree polynomial. Geophys J Int 215:864–879
García-Abdeslem J (1992) Gravitational attraction of a rectangular prism with depth-dependent density. Geophysics 57:470–473
García-Abdeslem J (2005) The gravitational attraction of a right rectangular prism with density varying with depth following a cubic polynomial. Geophysics 70:J39–J42
Gradshteyn IS, Ryzhik IM (2007) Table of integrals, series, and products, 7th edn. Academic Press, London
Grombein T, Seitz K, Heck B (2013) Optimized formulas for the gravitational field of a tesseroid. J Geod 87:645–660
Hamayun Prutkin I, Tenzer R (2009) The optimum expression for the gravitational potential of polyhedral bodies having a linearly varying density distribution. J Geod 83:1163–1170
Hansen R (1999) An analytical expression for the gravity field of a polyhedral body with linearly varying density. Geophysics 64:75–77
Hansen R, Wang X (1988) Simplified frequency-domain expressions for potential fields of arbitrary three-dimensional bodies. Geophysics 53:365–374
Heck B, Seitz K (2007) A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J Geod 81:121–136
Heiskanen WA, Moritz H (1967) Physical geodesy. Freeman, San Francisco
Hofmann-Wellenhof B, Moritz H (2006) Physical geodesy, 2nd edn. Springer, Berlin
Holstein H (2003) Gravimagnetic anomaly formulas for polyhedra of spatially linear media. Geophysics 68(1):157–167
Holstein H, Ketteridge B (1996) Gravimetric analysis of uniform polyhedra. Geophysics 61(2):357–364
Holstein H, Sherratt E, Anastasiades C (2007) Gravimagnetic anomaly formulae for triangulated homogeneous polyhedra. In: 69th EAGE conference and exhibition incorporating SPE EUROPEC 2007
Hubbert MK (1948) A line-integral method of computing the gravimetric effects of two-dimensional masses. Geophysics 13:215–225
Jamet O, Thomas E (2004) A linear algorithm for computing the spherical harmonic coefficients of the gravitational potential from a constant density polyhedron. In: Proceedings of the 2nd international GOCE user workshop, GOCE. The Geoid and Oceanography, ESA-ESRIN, Frascati, Italy, Citeseer, pp 8–10
Jiang L, Zhang J, Feng Z (2017) A versatile solution for the gravity anomaly of 3D prism-meshed bodies with depth-dependent density contrast. Geophysics 82:G77–G86
Jiang L, Liu J, Zhang J, Feng Z (2018) Analytic expressions for the gravity gradient tensor of 3D prisms with depth-dependent density. Surv Geophys 39:337–363
Kellogg OD (1929) Foundations of potential theory. Springer, Berlin
Laurie DP (1997) Calculation of Gauss–Kronrod quadrature rules. Math Comput 66:1133–1145
Litinsky VA (1989) Concept of effective density: key to gravity depth determinations for sedimentary basins. Geophysics 54:1474–1482
Martín-Atíenza B, Garcia-Abdeslem J (1999) 2-D gravity modeling with analytically defined geometry and quadratic polynomial density functions. Geophysics 64:1730–1734
Martinec Z, Pěč K, Burša M (1989) The phobos gravitational field modeled on the basis of its topography. Earth Moon Planets 45(3):219–235
Murthy IR, Rao DB (1979) Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth. Geophysics 44:1525–1530
Nagy D, Papp G, Benedek J (2000) The gravitational potential and its derivatives for the prism. J Geod 74:552–560
Netteton LL (1940) Geophysical prospecting for oil. McGraw-Hill Book Company Inc., New York
Pedersen LB (1978) Wavenumber domain expressions for potential fields from arbitrary 2-, 21/2-, and 3-dimensional bodies. Geophysics 43:626–630
Petrovskaya M, Vershkov A (2010) Construction of spherical harmonic series for the potential derivatives of arbitrary orders in the geocentric earth-fixed reference frame. J Geod 84:165–178
Pohánka V (1998) Optimum expression for computation of the gravity field of a polyhedral body with linearly increasing density. Geophys Prospect 46:391–404
Rao DB (1985) Analysis of gravity anomalies over an inclined fault with quadratic density function. Pure Appl Geophys 123:250–260
Rao DB (1986a) Gravity anomalies of a trapezoidal model with quadratic density function. Proc Indian Acad Sci Earth Planet Sci 95:275–284
Rao DB (1986b) Modelling of sedimentary basins from gravity anomalies with variable density contrast. Geophys J R Astron Soc 84:207–212
Rao DB (1990) Analysis of gravity anomalies of sedimentary basins by an asymmetrical trapezoidal model with quadratic density function. Geophysics 55:226–231
Rao DB, Prakash M, Babu NR (1993) Gravity interpretation using Fourier transforms and simple geometrical models with exponential density contrast. Geophysics 58:1074–1083
Rao CV, Chakravarthi V, Raju M (1994) Forward modeling: gravity anomalies of two-dimensional bodies of arbitrary shape with hyperbolic and parabolic density functions. Comput Geosci 20:873–880
Rao CV, Raju M, Chakravarthi V (1995) Gravity modelling of an interface above which the density contrast decreases hyperbolically with depth. J Appl Geophys 34:63–67
Ren Z, Chen C, Pan K, Kalscheuer T, Maurer H, Tang J (2017a) Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surv Geophys 38:479–502
Ren Z, Zhong Y, Chen C, Tang J, Pan K (2017b) Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics 83:G1–G13
Ren Z, Zhong Y, Chen C, Tang J, Kalscheuer T, Maurer H, Li Y (2018) Gravity gradient tensor of arbitrary 3D polyhedral bodies with up to third-order polynomial horizontal and vertical mass contrasts. Surv Geophys 39:901–935
Riley KF, Hobson MP, Bence SJ (2006) Mathematical methods for physics and engineering: a comprehensive guide. Cambridge University Press, Cambridge
Ruotoistenmäki T (1992) The gravity anomaly of two-dimensional sources with continuous density distribution and bounded by continuous surfaces. Geophysics 57:623–628
Silva JB, Costa DC, Barbosa VC (2006) Gravity inversion of basement relief and estimation of density contrast variation with depth. Geophysics 71:J51–J58
Talwani M, Worzel JL, Landisman M (1959) Rapid gravity computations for two-dimensional bodies with application to the Mendocino submarine fracture zone. J Geophys Res 64:49–59
Tsoulis D (2000) A note on the gravitational field of the right rectangular prism. Boll Geod Sci Affin 59:21–35
Tsoulis D, Petrović S (2001) On the singularities of the gravity field of a homogeneous polyhedral body. Geophysics 66:535–539
Tsoulis D, Jamet O, Verdun J, Gonindard N (2009) Recursive algorithms for the computation of the potential harmonic coefficients of a constant density polyhedron. J Geod 83:925–942
Uieda L, Barbosa VC, Braitenberg C (2016) Tesseroids: forward-modeling gravitational fields in spherical coordinate. Geophysics 81:F41–F48
van Gelderen M (1992) The geodetic boundary value problem in two dimensions and its iterative solution. PhD thesis, Faculty of Civil Engineering and Geosciences, Technische Universiteit Delft, Delft
Vermeille H (2011) An analytical method to transform geocentric into geodetic coordinates. J Geod 85:105–117
Werner RA (1997) Spherical harmonic coefficients for the potential of a constant-density polyhedron. Comput Geosci 23:1071–1077
Werner RA, Scheeres DJ (1997) Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 castalia. Celest Mech Dyn Astron 65:313–344
Wu L (2018a) Comparison of 3-D Fourier forward algorithms for gravity modelling of prismatic bodies with polynomial density distribution. Geophys J Int 215:1865–1886
Wu L (2018b) Efficient modeling of gravity fields caused by sources with arbitrary geometry and arbitrary density distribution. Surv Geophys 39:401–434
Wu L (2019) Fourier-domain modeling of gravity effects caused by polyhedral bodies. J Geod 93:635–653
Wu L, Chen L (2016) Fourier forward modeling of vector and tensor gravity fields due to prismatic bodies with variable density contrast variable density contrast. Geophysics 81:G13–G26
Zhang Y, Chen C (2018) Forward calculation of gravity and its gradient using polyhedral representation of density interfaces: an application of spherical or ellipsoidal topographic gravity effect. J Geod 92:205–218
Zhang J, Jiang L (2017) Analytical expressions for the gravitational vector field of a 3-D rectangular prism with density varying as an arbitrary-order polynomial function. Geophys J Int 210:1176–1190
Zhang J, Zhong B, Zhou X, Dai Y (2001) Gravity anomalies of 2-D bodies with variable density contrast. Geophysics 66:809–813
Zhou X (2008) 2D vector gravity potential and line integrals for the gravity anomaly caused by a 2D mass of depth-dependent density contrast. Geophysics 73:I43–I50
Zhou X (2009a) 3D vector gravity potential and line integrals for the gravity anomaly of a rectangular prism with 3D variable density contrast. Geophysics 74:I43–I53
Zhou X (2009b) General line integrals for gravity anomalies of irregular 2D masses with horizontally and vertically dependent density contrast. Geophysics 74:I1–I7
Zhou X (2010) Analytic solution of the gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function. Geophysics 75:I11–I19
Acknowledgements
We are grateful to the editors and two anonymous reviewers for their valuable comments and suggestions that improved the manuscript. This work is supported by National Natural Science Foundation of China under Grant Nos. 41631072, 41774021 and 41771487.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chen, C., Bian, S. & Li, H. A spectral-domain approach for gravity forward modelling of 2D bodies. J Geod 93, 2123–2144 (2019). https://doi.org/10.1007/s00190-019-01308-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00190-019-01308-z