1 Introduction

Footings are sometimes built on geosynthetic reinforced soil structures, such as walls and artificial slopes. Such structures are used quite extensively to support bridge loads and to form approach roads. In fact, the bearing capacity of a footing on a sloped fill structure can be considerably improved by incorporating geosynthetic reinforcements down to an appropriate depth. To design a footing on a reinforced sloped fill it is important to understand fully the effect of the load on the structure performance.

Several studies, especially experimental, on the use of reinforcements to improve the bearing capacity behaviour of footings on soil structures have been reported in the literature. They mainly include: studies of full-scale structures (Thamm et al. 1990; Bathurst et al. 2003; Yoo and Kim 2008), reduced-scale models, where the investigations were performed with soil structures with slope angle ranging essentially between 20° and 35° (Selvadurai and Gnanendran 1989; Huang et al. 1994; Shin and Das 1998; Lee and Manjunath 2000; Yoo 2001; El Sawwaf 2007; Alamshahi and Hataf 2009; Choudhary et al. 2010) and centrifuge model tests (Sommers and Viswanadham 2009). Some Authors have also shown a comparison of these laboratory model test results with those obtained by analytical and numerical approaches.

Bathurst et al. (2003) reported the results of an experimental investigation on two large-scale geosynthetic reinforced soil embankments and one unreinforced soil embankment 3.4 m high. The results show that the ultimate footing load capacity of the reinforced soil embankments is 1.6–2.0 times that of the nominal identical control embankment without reinforcement.

Selvadurai and Gnanendran (1989), Lee and Manjunath (2000) and Huang et al. (1994) reporting the results obtained by small-scale tests show that the load–settlement behaviour and ultimate bearing capacity of the footing can be significantly improved using reinforcing layer at the appropriate location in the fill slope. Lee and Manjunath (2000) also show that for both reinforced and unreinforced slopes, the bearing capacity decreases with an increase in slope angle and a decrease in edge distance and that at an edge distance of five times the width of the footing, the bearing capacity becomes independent of the slope angle. The study of Huang et al. (1994) focused on the failure mechanism of the reinforced slope and the strain distributions in geogrid layers. Yoo (2001) drew the conclusion that the failure zone for the reinforced slope loaded with a footing tends to become wider and deeper than that for the unreinforced slope and this affects the required anchorage length of reinforcements. The results obtained by Alamshahi and Hataf (2009) on a sand slope also show that the presence of reinforcement increases the bearing capacity behaviour and this increase depends greatly on the geogrid distribution. Moreover, the effect of the ordinary geogrid in improving the soil bearing capacity is less than that of the grid-anchor reinforcement.

El Sawwaf (2007) investigated the bearing capacity of a strip footing resting on a replaced sand layer constructed on a soft clay slope also in the presence of geogrid reinforcement. The study focused on the influence between the footing response and the replaced sand depth, the distance of footing from the edge slope and the geosynthetic configurations.

Choudhary et al. (2010) conducted a series of model footing tests on bearing capacity behaviour of a strip footing on reinforced slope covering a wide range of boundary conditions. These experimental results are highly consistent with the results reported previously in the literature although the fill material used in the study is flyash, an industrial waste.

Sommers and Viswanadham (2009), on the basis of their centrifuge model tests, reported that the vertical spacing between reinforcement layers has a significant impact on the stability of a reinforced slope when subjected to vertical loading and less vertical distance between reinforcement layers allows the slope to tolerate much greater loads than layers spaced further apart.

In addition, analytical models have been developed. They are most used by practitioners to analyze the bearing capacity of footings resting on reinforced soil structures.

Zhao (1996a) used the slip-line method to calculate the limit loads on geosynthetic-reinforced soil slopes, and he also presented the stress characteristic fields to better understand the plastic failure regions of reinforced structures. These results were compared with those obtained using the limit analysis method (Zhao 1996b).

To analyze the bearing capacity of footing placed on reinforced soil structures under seismic condition Jahanandish and Keshavarz (2005) presented a new approach to the slip-line method. They considered uniform or non-uniform distribution of the reinforcement and showed the results in the form of non-dimensional design charts.

Basha and Basudhar (2010) used the limit equilibrium method with a logarithmic spiral failure surface to analyze reinforced soil structures under the seismic condition also in the presence of surcharge load placed on the backfill.

Ausilio (2012) presented the results obtained with the kinematic theorem to show the effects of both soil and structure inertia and of seismic vertical acceleration on the reduction of the seismic bearing.

The above studies considered a uniformly distributed load while surprisingly, analytical studies on the bearing capacity behaviour of a strip footing with loading width placed close to the crest of a reinforced slope are limited.

Blatz and Bathurst (2003) used a conventional two-part wedge limit equilibrium method to predict the ultimate capacity of a footing placed close to the crest of the earth structure constructed with multiple layers of geogrid reinforcement.

Haza et al. (2000) used the overall approach of the double wedge method based on the limit equilibrium principle to evaluate the stability of a reinforced structure with a local surcharge load. The studies of Blatz and Bathurst (2003) and of Haza et al. (2000) considered the static case.

The seismic performance of a geo-reinforced structure is usually analyzed with the pseudo-static approach. The pseudo-static approach generally leads to a conservative design and for large values of the seismic coefficient the design could prove very expensive, and in some cases even impracticable. In such circumstances it is reasonable to accept that the reinforced slope is affected by tolerable permanent displacement and so it is necessary to use an alternative approach based on the assessment of displacement.

Several methods have been proposed for predicting the seismic induced permanent displacement of earth structures. Most of these methods are based on the rigid-block analysis procedure originally proposed by Newmark (1965) and they refer to geosynthetic reinforced soil retaining walls or slopes (Cai and Bathurst 1996; Ling et al. 1997; Ling and Leshchinsky 1998; Ausilio et al. 2000; Kramer and Paulsen 2004; Huang and Wang 2005).

This paper uses the kinematic approach of limit analysis as a theoretical framework to derive upper bound solutions for the seismic bearing capacity of shallow strip foundation on geo-reinforced soil structures. The analysis is based on the pseudo-static method and the dynamic effects of earthquake shaking on the pore pressures and the change of soil strength are disregarded. A parametric study is carried out to investigate the influence of various parameters on the bearing capacity including the geosynthetic configuration, edge distance between the footing and the crest of the slope, slope angle, backfill soil friction angle, horizontal seismic coefficients. The results of the analysis are presented in the form of non-dimensional graphs to facilitate preliminary design with static and pseudo-static conditions.

Finally, a simple and rational procedure based on the assessment of earthquake-induced permanent displacements is proposed for the design of a strip footing placed close to the crest of the geo-reinforced soil structures subjected to earthquake loading. Examples illustrating the application of the preliminary design procedures are presented.

2 Method of Analysis

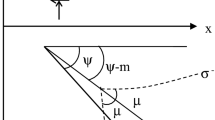
The kinematic theorem of the plasticity theory is applied here for evaluating the seismic bearing capacity of a strip footing of width B on a geosynthetic reinforced soil slope at a distance D from the edge (Fig. 1). Application of this theorem states that the rate of internal work is not smaller than the rate of work of external forces in any kinematically admissible collapse mechanism and that the soil deforms plastically according to the normality rule associated with the Coulomb yield condition.

Fig. 1
figure 1

The geometry of the reinforced soil structure with the log-spiral failure surface

Full size image

According to the pseudo-static approach, the earthquake effect is considered in an approximate manner as equivalent horizontal and vertical forces acting both on the foundation and on the soil below the foundation. The horizontal and vertical inertial forces in the soil are calculated as the product of the seismic intensity coefficients (k h and k v ) and the weight of the potential sliding mass, whereas those applied to the foundation are calculated as the product of seismic intensity coefficients (k h1 and k v1) and a uniform distributed load, q, which is assumed to be applied to the foundation soil. The seismic coefficients for the foundation, k h1 and k v1, and the inertia forces of the soil mass, k h and k v , can be different, to make the solution as general as possible (Askari and Farzaneh 2003; Castelli and Motta 2010; Sawada et al. 1994). This also allows the ductility classes of the structures in elevation to be taken into account (Eurocode 8—Part 1 and 5 2003). Positive values of k v and k v1 are assumed to act upwards, whereas positive k h and k h1 indicate inertial forces acting in direction away from the slope.

The kinematically admissible mechanism considered in this work is illustrated in Fig. 1. This mechanism is characterized by a log-spiral failure surface, which is assumed to pass through the right-edge of strip footing on the surface of the reinforced slope and it is consistent with the observed failure mechanisms shown in the tests both full-scale structures and reduced small models (Thamm et al. 1990; Bathurst et al. 2003; Selvadurai and Gnanendran 1989; Huang et al. 1994; Yoo 2001; Sommers and Viswanadham 2009). The reinforced soil mass rotates as a rigid body with velocity of rotation \( \dot{\omega } \) about the log-spiral center O. The geometry of the failure surface is described by the log spiral equation:

$$ r = r_{o} e^{{(\theta - \theta_{0} )tg\varphi }} $$
(1)

where r o is the radius at initial angle θ o , as shown in Fig. 1, and φ is the angle of soil shearing resistance.

The rate of external work is due to rate work done by soil weight and inertial forces and it can be written as:

$$ \dot{W} = (1 - k_{v} )\gamma r_{o}^{3} \dot{\omega }(f_{1} - f_{2} - f_{3} ) + k_{h} \gamma r_{o}^{3} \dot{\omega }(f_{4} - f_{5} - f_{6} ) $$
(2)

where γ is the soil unit weight.

The functions f 1–f 6 are dependent on the slope angle (β), the angles defining the position of the failure surface, (θ o , θ h ) and the angle of soil shearing resistance (φ). They can be found in several works (Chang et al. 1984; Saada et al. 2011).

The rate of internal dissipation derived by Chen (1975) is:

$$ \dot{D}_{c} = \frac{{c\dot{\omega }r_{0}^{2} }}{2\tan \varphi }\left[ {e^{{2(\theta_{h} - \theta_{0} )tg\varphi }} - 1} \right] $$
(3)

where c is the soil cohesion.

The rate of work done by the surcharge boundary load q and inertial forces is:

$$ \dot{Q} = (1 - k_{v1} )qB\dot{\omega }\left[ {r_{0} \cos \theta_{0} - \frac{B}{2}} \right] + k_{h1} qB\dot{\omega }r_{0} \sin \theta_{0} $$
(4)

where B is width of the strip footing.

For uniformly placed geosynthetic reinforcement, the energy dissipation rate during rotational failure due to reinforcement is calculated by integrating the unit energy dissipation and it can be written as:

$$ \dot{D} = \frac{1}{2}k_{t} \dot{\omega }r_{0}^{2} \left[ {\sin^{2} \theta_{h} e^{{2(\theta_{h} - \theta_{0} )tg\varphi }} - \sin^{2} \theta_{0} } \right] $$
(5)

where k t is an average tensile strength per unit cross-section and it is defined as:

$$ k_{t} = \frac{T}{d} $$
(6)

where T is the tensile strength of a single the reinforcement layer per unit width, and d is the vertical distance between the layers of the reinforcement layers. In this paper the geosynthetic layers are only characterised by their tensile strength, but not by their stiffness modulus.

By equating the rate of external work to the rate of energy of dissipation and substituting the relationships one obtains the following expression:

$$ q = \frac{{\frac{1}{2}k_{t} r_{0} \left[ {\sin^{2} \theta_{h} e^{{2(\theta_{h} - \theta_{0} )tg\varphi }} - \sin^{2} \theta_{0} } \right] + \frac{{cr_{0} }}{2\tan \varphi }\left[ {e^{{2(\theta_{h} - \theta_{0} )tg\varphi }} - 1} \right] - (1 - k_{v} )\gamma r_{0}^{2} (f_{1} - f_{2} - f_{3} ) - k_{h} \gamma r_{0}^{2} (f_{4} - f_{5} - f_{6} )}}{{B\left[ {(1 - k_{v1} )\left( {\cos \theta_{0} - \frac{B}{{2r_{0} }}} \right) + k_{h1} \sin \theta_{0} } \right]}} $$
(7)

Equation (7) provides a lower-bound solution for the bearing capacity of a footing placed at the crest of a reinforced slope considering a log-spiral failure mechanism. In order to find the best estimation of q, Eq. (7) needs to be minimized with respect to angles θ o e θ h . Once these angles are found, substituting these values into Eq. (7) the limit load is calculated. Furthermore, the geometry of the log-spiral failure surface is fully defined by the two angles θ o and θ h , the initial and final log-spiral angles.

In the case of general distribution of the reinforcements the energy dissipation rate during failure due to reinforcements can be rewritten and the expression (5) becomes:

$$ \dot{D} = \dot{\omega }r_{0} \sum\limits_{i = 1}^{n} {T_{i} } \left( {\sin \theta_{0} + \frac{{z_{i} }}{{r_{0} }}} \right) $$
(8)

where z i is the depth of layer ith measured downwards from the top of the slope, n is the number of the reinforcement layers, T i is the force of the ith layer per unit width.

Consequently the expression to calculate the q becomes:

$$ q = \frac{{r_{0} \sum\limits_{i = 1}^{n} {T_{i} } \left( {\sin \theta_{0} + \frac{{z_{i} }}{{r_{0} }}} \right) + \frac{{cr_{0} }}{2\tan \varphi }\left[ {e^{{2(\theta_{h} - \theta_{0} )tg\varphi }} - 1} \right] - (1 - k_{v} )\gamma r_{0}^{2} (f_{1} - f_{2} - f_{3} ) - k_{h} \gamma r_{0}^{2} (f_{4} - f_{5} - f_{6} )}}{{B\left[ {(1 - k_{v1} )\left( {\cos \theta_{0} - \frac{B}{{2r_{0} }}} \right) + k_{h1} \sin \theta_{0} } \right]}} $$
(9)

Again, Eq. (9) must be minimized with respect to angles θ o e θ h to obtain the limit load.

It should be noted that the above expressions are derived under the assumption that the geosynthetic layers are anchored beyond the critical failure surface into the stable soil with an adequate anchorage length.

In this study only the results of the parametric analyses for a uniformly placed geosynthetic reinforcement are shown, while Eq. (9) is used to make the comparisons with the experimental and theoretical data.

3 Comparison

A method to evaluate the accuracy of the approach used here requires the comparison between the numerical calculated results with those obtained in others investigations and above all with experimental data.

At first, the comparison is shown for a footing on an unreinforced slope, for the pseudo-static case, in Table 1 where the failure load obtained in this study is compared with those obtained using the upper-bound technique of limit analysis by Sawada et al. (1994) and Askari and Farzaneh (2003). Sawada et al. (1994) used a logarithmic spiral failure mechanism while Askari and Farzaneh (2003) considered a failure mechanism composed of an active wedge, a passive wedge, and a shear transition zone between the two wedges. The case presented in Table 1 is characterized by β = 20°, φ = 30°, c’ = 9.8 kPa, B = 10 m and D = 20 m for different γ and kh/kh1.

Table 1 Comparison of variation of bearing capacity (kPa) with kh1/kh and γ (kN/m3) for the case of β = 20°, φ = 30°, c = 9.8 kPa, B = 10 m and D = 20 m (adapted from Askari and Farzaneh 2003)
Full size table

The results of the present analysis are lower than those obtained by Sawada et al. (1994) but higher than those of Askari and Farzaneh (2003).

For the static case the comparison can also be made with experimental studies. Figure 2 shows the displacement vectors for the test ARS4 of the centrifuge model tests conducted by Sommers and Viswanadham (2009) to study the performance of geotextile-reinforced slopes when subjected to loading applied to a strip footing positioned close to the slope crest. The failure mechanism for the same case carried out in the present study is also shown in Fig. 2 with an unbroken line. As regards the footing pressure at failure, the experimental value obtained with the centrifuge test is 154 kPa while that calculated with Eq. (9) is 140 kPa.

Fig. 2
figure 2

The displacement vectors for the test ARS4 of the centrifuge model tests conducted by Sommers and Viswanadham (2009) and the failure mechanism obtained in this study (adapted from Sommers and Viswanadham 2009)

Full size image

The latter comparison regards a large-scale geosynthetic reinforced soil structure with height of 2.68 m and composed of five layers of gravelly sand separated by geosynthetic sheets (Thamm et al. 1990). The profile of the embankment after failure is shown in Fig. 3, which also reports the failure mechanism derived in this study with a dashed line. The maximal failure load obtained in this study using the Eq. (9) of 241 kN/m is slightly lower than that measured during the experiment, which is 296 kN/m.

Fig. 3
figure 3

The profile of the embankment after failure with the failure mechanism derived in this study (adapted from Thamm et al. 1990)

Full size image

The three comparisons above show a reasonable agreement in terms of bearing capacity and failure mechanism, between the results obtained in this study and those of other investigations available in the literature. The agreement can be considered reasonable because the comparisons have been made with both analytical methods and experimental tests that have considered both full-scale structures and small-scale models in centrifuge.

4 Results

Since the principal objective of this study is to investigate the influence of some parameters on the bearing capacity of strip footings resting on geo-reinforced soil structures to facilitate preliminary design, it is convenient to present the results obtained from the present investigation in non-dimensional form.

Since there are many factors that influence the bearing capacity the results of the static condition are shown in the first part of this section. After that, the dynamic condition is performed.

In the calculations it is assumed that the soil is cohesionless with γ = 17 kN/m3 and the angle of shearing resistance φ ranging from 20° to 45°.

To evaluate the efficiency of reinforcement in improving the bearing capacity of the fill slopes, it is convenient to present the results of the reinforced system with respect to the corresponding results derived for the footing on an unreinforced slope.

The benefits of using reinforcements are then shown in terms of a non-dimensional factor called bearing capacity ratio BCR. This factor is defined as the ratio of the bearing capacity of a footing on the reinforced slope to the bearing capacity of a footing on the corresponding unreinforced slope.

Figure 4a shows variation of BCR with the non-dimensional factor γB/k t for different values of edge-distance for the case with β = 30° and φ = 40°. The results clearly indicate that the inclusion of geosynthetic reinforcements improves the performance of the footing by increasing the bearing capacity. The maximum benefit of reinforcement is obtained when the footing is placed closer to the slope crest and for low values of γB/k t . It can be observed that when the edge distance increases, the bearing capacity ratio decreases (Fig. 4b). For example, for a value of γB/k t  = 0.4 the improvement in the bearing capacity for D/B = 0.25 is about 2.5 while it is about 1.2 when the foundation is positioned at D/B = 5. These trends are consistent with the experimental and numerical results obtained by El Sawwaf (2007) with model tests and finite element analyses and with those shown by Choudhary et al. (2010).

Fig. 4
figure 4

Variation of BCR with γB/kt ratio (a) at different D/B and with D/B ratio (b) at different γB/kt for β = 30° and φ = 40°

Full size image

Figure 5a presents the normalized ultimate bearing capacity (expressed as non-dimensional ratio, q/γB, where q is the ultimate bearing capacity) on reinforced slopes as functions of the factor γB/k t for different slope angles (β = 35°, 45°, 60° and 75°) for a footing placed at an edge distance of 0.25 times the width of the footing D/B = 0.25 and φ = 35° with unbroken lines. In general this figure indicates that the non-dimensional bearing capacity decreases with increase in slope angle β and in the factor γB/k t . Similar trends are also observed in Fig. 5b, c, which are obtained for D/B = 1 and D/B = 3, respectively.

Fig. 5
figure 5

The normalized limit load versus γB/kt ratio at different slope angles for a D/B = 0.25, b D/B = 1 and c D/B = 3 for φ = 35°

Full size image

The influence of the edge distance between the footing and the crest of the slope on the limit load can be observed in Fig. 6 where the normalized ultimate bearing capacity is plotted against the factor γB/k t at different D/B for a reinforced slope with β = 45° and φ = 35°. The result clearly indicates that the ultimate bearing capacity increases with increasing edge distance. The importance of the edge distance on limit load is also shown in Fig. 7 where the limit load is plotted against D/B for different slope angles and for γB/k t  = 0.4 with unbroken lines.

Fig. 6
figure 6

The normalized limit load versus γB/kt ratio at different edge distances D/B for φ = 35° and β = 45°

Full size image
Fig. 7
figure 7

The normalized limit load versus edge distances D/B at different slope angles for φ = 35° and γB/kt = 0.4

Full size image

The effect of slope is minimized when the footing is placed at an edge distance beyond four or five times the width of the footing for the case with φ = 35° and γB/k t  = 0.4. In Fig. 8a–c the failure mechanism height H, as defined in Fig. 1, is plotted against the factor γB/k t at different slope angles for the cases examined in Fig. 5a–c. The mechanism height is presented in non-dimensional form as ratio (H/B) with respect to the width B. This height is very important in the design of footing on reinforced slopes, because it represents the depth to which the reinforcement is needed, namely that the reinforcement must be at least extended to the maximum depth of the failure mechanism.

Fig. 8
figure 8

The normalized mechanism height versus γB/kt ratio at different slope angles for a D/B = 0.25, b D/B = 1 and c D/B = 3 for φ = 35°

Full size image

Figure 9 shows the normalized limit load against the shearing resistance angle φ for γB/k t  = 0.4 and 2.2, D/B = 0.25 and 3 and for β = 45°. As can be expected, q/γB increases with increasing φ and as noted also in Figs. 5 and 6 with decreasing with γB/k t and with increasing distance from the edge slope. The increase in q/γB is greater in the case of the greater φ.

Fig. 9
figure 9

The normalized limit load versus φ for D/B = 0.25 and 3 and for γB/K t  = 0.4 and 2.2 (β = 45°)

Full size image

As regards the seismic condition, for the purposes of this study, only the horizontal component of earthquake shaking is considered (k v  = k v1 = 0).

The influence of the seismic coefficient is illustrated in Fig. 10 where the limit load is plotted against the shearing resistance angle for different values of the horizontal seismic coefficient (k h  = k h1 = 0 up to 0.6) for the case with slope angle β = 45°, distance edge D/B = 2 and γB/k t  = 2.0. As can be noted q/γB decreases with increasing k h , and the influence of k h is similar for all the shearing resistance angles.

Fig. 10
figure 10

The normalized limit load versus φ for D/B = 2, γB/K t  = 2 and β = 45°

Full size image

Figure 11a shows the normalized limit load against the ratio γB/k t at different horizontal seismic coefficients for the case with slope angle β = 60°, distance edge D/B = 3 and φ = 35°. These results are also presented in Fig. 11b, which reports the values of the seismic coefficient k h on the horizontal axis. Both Fig. 11a, b show that the bearing capacity is significantly influenced by the loading seismic, especially for low values of the ratio γB/k t .

Fig. 11
figure 11

The normalized limit load (a) versus γB/k t at different horizontal seismic coefficients, (b) versus kh at different γB/k t for D/B = 3, β = 60° and φ = 35°

Full size image

Similar observations can also be made from the results presented in Fig. 5a–c where the curves obtained for k h  = k h1 = 0.2 are shown, with dashed lines, beside those for the static condition (k h  = k h1 = 0) with unbroken lines.

As regards the mechanism height in the seismic condition it is smaller than that obtained considering the absence of seismic loading. This can be noted in Fig. 8a–c where the ratios H/B are reported also for the case with k h  = k h1 = 0.2 with dashed lines whereas those calculated with k h  = k h1 = 0 are marked by unbroken lines. The height decreases with increase in k h . For example, the mechanism height is halved from the case with k h  = k h1 = 0 to that with k h  = k h1 = 0.2. Taking into account that the seismic condition is a transient one, it should be recommended using the higher depths obtained from static condition for design purposes, and in any case the reinforcements must be positioned along the height of the structure, if it is necessary for the stability of the structure.

In order to understand better the effects of the seismic coefficient on the other design parameters of the footing bearing capacity, Figs. 12 and 13 are shown. In these figures the normalized limit load is reported versus the seismic coefficient to vary γB/k t , D/B and β.

Fig. 12
figure 12

The normalized limit load versus horizontal seismic coefficient for D/B = 0.25 and 4 and for β = 45°, 60° and 75°, γB/K t  = 2.2 and φ = 35°

Full size image
Fig. 13
figure 13

The normalized limit load versus horizontal seismic coefficient for γB/K t  = 0.4 and 2.2 and for β = 45°, 60° and 75°, D/B = 0.25 and φ = 35°

Full size image

The graphs given in Figs. 12 and 13 can also be used to determine the critical horizontal coefficient or yield seismic coefficient k y , in order to compute the possible displacement of the footing during large earthquakes. For any given load on the footing the graphs define the critical horizontal acceleration that the footing can withstand without failure. If during an earthquake the acceleration is greater than critical, permanent displacements of the footing will take place. It can be noted that the critical seismic coefficient increases with decreasing β and γB/k t and the increase of φ and of the edge distance.

Figure 14 shows the reduction in the bearing capacity owing to the soil inertia and the structure inertia for the case with γB/k t  = 0.4, D/B = 1 and φ = 35°. Figure 14 reports the results for the static case, for the conditions in which the soil inertia (k h  ≠ 0 and k h1 = 0) and the structure inertia (k h1 ≠ 0 and k h  = 0) are separately accounted for and when both the inertias are considered simultaneously. It can be noted that the effects of soil inertia are less important than those owing to the structure inertia especially for low values of the slope angle.

Fig. 14
figure 14

The normalized limit load versus slope angle for γB/K t  = 0.4, D/B = 1 and φ = 35°

Full size image

The charts shown above can be used for practical applications. Given the width (B) of the footing and its position respect to the edge slope (D), the soil (γ, φ) and reinforcement (T and d) parameters, the ultimate bearing capacity can be obtained from Figs. 5 (for static condition) and 11 (for seismic condition) and the depth to which the reinforcement is needed from Fig. 8. If the required bearing capacity and soil and geometrical parameters are known, the necessary reinforcement configuration can be obtained from Figs. 5 and 11 for static and dynamic condition respectively. The necessary reinforcement or tensile strength can then be calculated from Eq. (6) and again the depth of failure and then the least depth for the reinforcement is determined from Fig. 8.

Two examples are selected here to illustrate the use of the charts to evaluate the bearing capacity of a strip footing resting on reinforced earth structure.

Example 1

Assume a strip foundation with 2 m width and placed at 6 m from the edge slope. In addition, it is assumed: slope angle β = 45°, angle of shearing resistance of the fill φ = 35°, unit weight γ = 17 kN/m3. The reinforcement used is a strip reinforcement with a tensile limit force of 17 kN/m (for single strip) and vertical distance of 0.5 m. The ultimate bearing capacity can be calculated as follows:

  • k t  = T/d = 17/0.5 = 34 kPa then γB/k t  = 1, from Fig. 5c q/γB = 32 and q = 1,088 kPa and from Fig. 8c H/B = 1.98 thus H = 3.96 m. Therefore, considering H = 4 m, 8 layers of reinforcement are required.

Example 2

For a strip footing with 2 m width and placed at 2 m from the edge slope and with slope angle β = 60° on a cohesionless soil of φ = 35° and γ = 17 kN/m3, the required ultimate bearing capacity is 550 kPa. The reinforcement configuration can be calculated as follows:

  • from Fig. 5b having q/γB = 16.1 the value of γB/k t is 0.63. The required k t is 53.96 kPa and selecting a strip reinforcement with a tensile limit force T = 20 kN/m the vertical spacing of the reinforcement can be evaluated from Eq. (6): d = 0.37 m. These reinforcements must be placed at least at a depth of H = 5 m, which is obtained using Fig. 8b. The number of reinforcement layers is calculated as H/d and is equal to 14.

The use of the above procedure in the pseudo-static analyses requires the appropriate choice of horizontal seismic coefficient, k h , which is related to a specified horizontal peak ground acceleration for the site, a max .

The relationship between a max and a representative value of k h is nevertheless complex and there does not appear to be a general consensus in the literature on how to relate these parameters.

Recently, based on observations of uni-axial shaking table tests performed on geosynthetic-reinforced slope, Huang et al. (2011) have demonstrated that the relationships suggested by Segrestin and Bastick (1988) and Idriss (1990) are adequate.

5 Displacement-Based Analysis

The results obtained with the pseudo-static analysis indicate that the reinforcement force required to ensure an adequate bearing capacity could be excessively great or even impracticable for elevated seismic coefficients. In such circumstances it is reasonable to accept that the structure is affected by tolerable permanent displacement.

The conventional rigid-block analysis procedure originally proposed by Newmark (1965) is usually used to calculate the permanent displacement. In this procedure the calculation of displacement is based on the assumption that the failure soil mass displaces together with the foundation (Sarma and Iossifelis 1990; Richards et al. 1993) as a rigid-plastic block whenever ground acceleration exceeds yield acceleration of the slope.

Given a design accelerogram the earthquake-induced displacement can be obtained by integrating twice the equation of motion, which in the case of rotational failure-mechanism it is more appropriate to express in terms of the angular rotation of the failure mass relative to the stable soil. The angular acceleration \( \ddot{\omega } \) of the failure soil mass is obtained as (Ling and Leshchinsky 1995):

$$ \ddot{\omega } = [k_{h} (t) - k_{y} ]g\frac{{\cos \beta_{cg} }}{{r_{cg} }} $$
(10)

where rcg is the distance of the centre of gravity of the sliding mass from the centre of rotation, βcg is its inclination measured from the vertical, kh(t)g is the ground acceleration time-history and kyg is the yield acceleration. The change of the yield acceleration due to the change in geometry is usually neglected. The rotation ω of the soil mass is obtained by double integrating Eq. (10), from which the horizontal and vertical permanent displacements may be calculated at any point along the log-spiral surface and then the displacements of the foundation by simple geometrical considerations.

To evaluate the seismic induced permanent displacement, the Newmark double-integration method requires the ground motion time history to be known.

Accurate prediction of such a record is not yet feasible since it is highly random. In the absence of the earthquake motion record, several empirical relationships have been developed to predict the seismic induced permanent displacement of earth structures using the Newmark rigid-block theory by integrating existing acceleration records. These relationships between the permanent displacement and the input ground motion parameters are very suitable to be used in design practice. Among these relations the one proposed by Jibson (2007) gives an adequate estimate of permanent displacement. It was obtained using 2,270 ground motion recordings from 30 different earthquake events with moment magnitudes (M w ) ranging between 5.3 and 7.6 and it assumes the following form:

$$ \log \delta = - 2.71 + \log \left[ {\left( {1 - \frac{{k_{y} }}{{k_{\hbox{max} } }}} \right)^{2.335} \left( {\frac{{k_{y} }}{{k_{\hbox{max} } }}} \right)^{ - 1.478} } \right] + 0.424M_{w} + S\sigma_{\log \delta } $$
(11)

where, k y is the seismic yield coefficient (in g, acceleration due to gravity), k max is the peak acceleration of the rock outcrop motion (in g), δ is the permanent displacement (in cm), σlogδ is the standard deviation of the logarithm (base 10) of displacement prediction, and S is the standardized normal variate (with μ = 0 and σ = 1). Jibson (2007) reports a value of 0.454 for σlogδ.

The displacement δ calculated with Eq. (11) is the final cumulative displacement of a rigid block on a horizontally-vibrating surface. The final cumulative displacement s of a generic point P along the slip surface has modulus equal to the product of the final cumulative rotation and the corresponding radius r and has direction orthogonal to the radius r (Fig. 1). It can be evaluated with the expression (Crespellani et al. 1998):

$$ s = \delta F\frac{r}{{r_{o} }} $$
(12)

where r o is the radius at initial angle θ o of the log-spiral failure surface. Parameter F is a function of the geometry of the moving mass, defined by the angles θ o , θ h , β and the angle of soil shearing resistance (φ), whose expression can be found in Crespellani et al. (1998). Also in this case, the horizontal and vertical displacements of the foundation can be obtained by knowledge of the displacements of the points along the failure surface.

An alternative and simplified approach is to consider the displacement evaluated by Eq. (11) as the displacement of the midpoint of the failure surface (based on the values that can take parameter F), and, as rough first approximation, as the displacement of the unstable soil mass.

The calculated seismic displacement δ must be viewed appropriately as order-of-magnitude estimate rather than accurate prediction and therefore as an index of seismic performance. However, when viewed as an index of potential seismic performance, the predicted displacement can and has been used effectively in preliminary design purposes.

The subsequent step in the design is to decide whether the calculated displacement is acceptable. The amount of displacement that is tolerable depends on the characteristics of the geo-reinforced soil structure and what it supports and accordingly, allowable displacement levels must be established from engineering judgment.

The charts shown above and Eq. (11) can be used for practical applications in the seismic design where the performance expectations are established in terms of acceptable amount of displacement. Given the width (B) of the footing and its position with respect to edge slope (D), the soil (φ, γ) and reinforcement (T and d) parameters and the ultimate bearing capacity, the critical acceleration factor k y can be obtained from Fig. 11b. The parameters of seismic design event (M w , k max ) required to calculate the displacements are determined by using seismic hazard maps. The permanent displacements can be calculated using Eq. (11) for given confidence levels.

If the evaluated displacements are considered tolerable for the specific application, the scheduled reinforcements must be placed to a depth that can be drawn from Fig. 8, but if the displacements are not acceptable then one has to repeat the process by considering a different reinforcement configuration.

To show how the proposed procedure, incorporating a tolerable displacement, may be used for designing footing placed on reinforced soil structures, an example is considered.

Example 3

Assume a strip foundation with 4 m width and placed at 12 m from the edge slope. In addition, it is assumed: slope angle β = 60°, angle of shearing resistance of the fill φ = 35°, unit weight γ = 17 kN/m3. The reinforcements used are a strip reinforcements with a tensile limit force of 15 kN/m (for single strip) and are installed at equal vertical spacing of 0.5 m. The design event is characterized by M w  = 6.7 and k max  = 0.57 (in g) which are obtained from seismic hazards maps. If the bearing capacity of the footing must be of 950 kPa then q/γB = 14 and γB/k t  = 2.26. For these values a critical acceleration factor k y  = 0.1 is obtained from Fig. 11b. Equation (11) provides the permanent displacements of 11 and 62 cm for confidence levels of 50 and 95 % respectively.

If the calculated displacements can be considered allowable, the depth of reinforcements can be obtained from Fig. 8. If the displacements are not allowable then the process has to be repeated changing the tensile limit force or the vertical distance or both and such to have a greater value of k t . Assuming a strip reinforcement with a tensile force of 24 kN/m and a vertical distance of 0.3 m again from Fig. 11b for q/γB = 14 and γB/k t  = 0.85 the critical acceleration factor k y  = 0.27 is obtained. As can be noted k y increases with an increase in k t .

The values of the permanent displacements of 0.9 cm. and 5 cm for confidence levels of 50 and 95 % respectively, are obtained from Eq. (11). As expected these values are lower than those of the previous calculation.

Obviously this procedure can be applied by calculating k y as a function of allowable displacement, earthquake magnitude and peak acceleration from Eq. (11) and using Fig. 11b to derive the value of the bearing capacity for assigned geometrical characteristics, soil properties and reinforcement configuration parameters.

6 Conclusions

The kinematic theorem of the limit analysis set up within the framework of the pseudo-static method is used to assess the seismic bearing capacity of shallow strip foundations placed close to the crest of the geo-reinforced soil structures. The study primarily aims at determining the effects of the various design parameters on the bearing capacity of such footings.

The ultimate bearing capacity of the footing on both unreinforced and reinforced slopes increases with an increase in edge distance and decreases with an increase in slope angle. The provision of geosynthetic reinforcements considerably improves the performance of the footing situated on the crest of sloping ground. The degree of bearing capacity increase depends not only on the geosynthetic configuration but also on the location of the footing from the slope face. In terms of BCR, the reinforcement is most effective when the footing is placed at closer slope crest and for low values of the ratio γB/k t .

However, the ultimate bearing capacity seems to be affected by the presence of the slope with an edge distance smaller than four or five times the width of the footing.

The results obtained from the analyses show the influence of the several factors and they are presented in the form of non-dimensional charts that can be used for preliminary seismic design based on a pseudo-static approach. Design procedures allow one to obtain the bearing capacity of a footing, the required strength of geosynthetic layers, the vertical distance between the layers of reinforcement and the depth to which the reinforcement is needed. Effects of seismic coefficients are also investigated. Examples are included to illustrate the use of the charts. The charts can also be used to evaluate the yield seismic coefficient. It is increases as the ratio γB/k t and the slope angle decrease and with an increase in the edge distance.

The pseudo-static approach generally leads to a conservative design often rendering seismic design uneconomical. In such circumstances it is reasonable to accept that the reinforced slope is affected by an induced permanent displacement that does not exceed a threshold limit and therefore an alternative approach based on a tolerable displacement is used.

An example is considered to show how the proposed procedure, incorporating a tolerable displacement, can be used for designing a footing placed on reinforced soil structures.