1 Introduction

Stability analysis of reinforced earth walls under earthquake loading is one of the most important topics in Geotechnical engineering and drawn the attention of researchers. Conventional earth structures are prone to catastrophic failure during earthquakes. One of the reasons of collapse is the softening behavior of the soil which results in accumulation of the strain energy in the shear bands during the earthquakes that ultimately causes large displacements. In contrast to the conventional retaining structures, reinforced soil structures (RSS) are well known for their improved performance during earthquakes. As such, design procedures are being evolved for such structures considering their stability under earthquake loading and still there exists scope for further development of a simple but improved method to analyze and design such mechanically stabilized walls with inclusions under seismic condition. In the following sections an overview of the performance of RSS during earthquakes, review of the currently developed analyses procedures and the objective and scope of the present paper are presented.

1.1 Performance of Reinforced Soil Structures (RSS) During Earthquake Loading

Frankenberger et al. (1997) studied the performances of 23 reinforced earth structures located with in the affected area of the Northridge earthquake. Of these, over 65% were higher than 5 m and over 25% are higher than 10 m. The distance of the reinforced earth structures from the earthquake epicenter ranged from 13 to 83 km. The only damage that appeared was minor spalling of concrete in some of the panels of the walls. It is interesting to note that adjacent structures to the reinforced earth structures, such as buildings, suffered much more severe damage and in some instances were posted as unsafe. Of the 120 reinforced earth structures inspected after the Kobe earthquake, 70% were over 5 m high and 15% were over 10 m high. The structures were designed using estimated ground accelerations of 0.15 to 0.2 g. The actual ground acceleration was 0.27 g. Ground movement was evident above or next to 22 of the structures, with 10 walls showing minor cracking of isolated concrete panels and 3 walls exhibiting significant lateral movement (Tatsuoka et al. 1995; Kobayashi et al. 1997). Deformations recorded in walls at Awaji Island and Hosiga-oka Park varied between 4 mm to 113 mm (displacement relative to bottom of the panel at mid-height and top of walls). All of the walls remained functional after the earthquake.

The Hyogoken-Nambu Earthquake caused serious damage to conventional masonry retaining walls, un-reinforced concrete gravity-type retaining walls and cantilever type steel reinforced concrete retaining walls, while geogrid reinforced soil retaining walls, having a full-height concrete facing, performed very well during the earthquake (Tatsuoka et al. 1995). A review of the Reinforced Soil Structures (RSS) near the epicenters of the Northridge, Kobe and Hyogoken-Nambu earthquakes indicated that very little damage occurred to any of the structures. Therefore even though RSS has not undergone any serious damage during earthquakes, for the past several years, research is being conducted to find out better, more rational and substantiated solutions for protection of reinforced earth structures from severe earthquake attack controlling their damage within an acceptable limit.

1.2 Pseudo-Static Method

The most common approach to seismic stability evaluation of reinforced earth structures is the pseudo-static analysis, which is based on limit equilibrium methods. In the 1920s, Mononobe and Okabe developed a method to estimate the lateral earth pressures acting on retaining structures during earthquakes (Kramer 2003). This approach is one of the earliest and most common methods used in engineering practice today. In a pseudo-static analysis, static horizontal and vertical forces are used to represent the effects of an earthquake assuming these inertial forces to act through the centre of gravity of the failure mass. It is an extension to the conventional Coulomb sliding wedge theory incorporating the effects of lateral inertia forces on the retained soil mass and is applicable to circular and noncircular failure surfaces as well. Hence in this paper, pseudo-static method is adopted for the stability analysis of reinforced soil retaining structures.

2 Overview of Literature

Leshchinsky and Boedeker (1989) presented an approach for stability analysis of geosynthetic reinforced earth structures based on variational limiting equilibrium method (LEM). Using LEM and assuming a planar failure surface, Saran et al. (1992) developed non-dimensional design charts for computing the resultant active earth pressure for a reinforced soil retaining wall carrying a uniform surcharge load. To assess the stability of simple slopes, Leshchinsky and San (1994) reported the work of variational limiting equilibrium approach using pseudo-static method in the design of reinforced soil slope. Many studies are reported in the literature regarding the seismic stability analysis of geosynthetics-reinforced soil structures based on a pseudo-static limit equilibrium analysis (Bathurst and Cai 1995; Ling et al. 1997; Ling and Leshchinsky 1998; Ismeik and Guler 1998; Basha and Basudhar 2005).

Ausilio et al. (2000) conducted a pseudo static seismic stability analysis of geosynthetic reinforced slopes applying the kinematic theory of limit analysis assuming different failure modes like rotation, translation and direct sliding and linear slip surface considering only horizontal seismic acceleration coefficients. Caltabiano et al. (2000) conducted pseudo-static methods for the computation of soil thrust acting on the retaining walls under seismic condition by employing planar failure mechanism. The analysis takes into account the effect of the presence of the wall and it was applied to soil-wall systems with surcharged backfills. Nouri et al. (2008) presented an approach for the design of reinforced soil structures for the internal stability based on limit equilibrium and pseudo-static methods of analysis, by employing a log-spiral failure mechanism and horizontal slices. This study did not address the external seismic stability of reinforced soil structures as it is very important in view of overall stability of RSS. Choudhury et al. (2007) investigated the external seismic stability of reinforced soil walls against base sliding and overturning modes of failure using a pseudo-dynamic method of analysis and computed the length of geosynthetic required to the stabilize the wall. This study did not address the stability of RSS against tensile failure and pullout failure of reinforcement for internal stability, eccentricity of the resultant force and bearing capacity of the foundation soil for external stability. In this paper an attempt is made to address all these issues with regard to the stability analysis of RSS.

3 Objectives of the Present Study

The focus of the paper is to examine the internal and external stability analysis of RSS when subjected to horizontal and vertical earthquake loading ensuring adequate safety factor against various types of possible failure modes viz. tension and pullout failure of all layers along the depth of wall, sliding failure, overturning failure, eccentricity failure and bearing failure. The calculation of the tensile strength of reinforcement and the corresponding length required to ensure the internal stability is important in practical terms in the seismic design of reinforced soil retaining structures. The efforts have been made to derive an analytical solution for the internal seismic stability of RSS considering log-spiral failure surface (as shown in Fig. 1) and external seismic stability of RSS considering sliding wedge failure mechanism. Uniformly distributed surcharge load placed on the backfill soil is also considered in the analysis. In addition to the inertial forces due to backfill soil, the inertial force due to surcharge load is also calculated using the equivalent surcharge height method.

Fig. 1
figure 1

The geometry of RSS and logarithmic spiral failure mechanism

Full size image

4 Formulation for Internal Seismic Stability Analysis of RSS

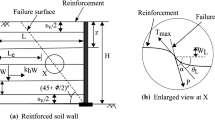
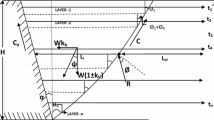
Let us consider a RSS of height, H supporting horizontal cohesionless backfill and the developing failure surface can be represented by a logarithmic spiral as shown in Fig. 1. Logarithmic spiral portion of the failure surface (GH 1) is governed by height of the reinforced soil slope (EG) and the location of centre of the logarithmic spiral arc (A). AH 1 and AG are respectively the initial and final radius of the logarithmic spiral passing through the centre ‘A‘. Thus the location of the center of the log-spiral (A) can be accurately defined by the subtended angle ‘θ 1‘and ‘H 1 NJ‘as shown in Fig. 1 where in the various terms are defined as follows: r 0 = initial radius of the log-spiral wedge (AH 1 G), r 1 = final radius of the log-spiral wedge (AH 1 G), θ 1 = subtended angle of log-spiral wedge (AH 1 G), H 1 NJ = the angle of the initial radius of the log-spiral wedge (AH 1) with the horizontal, IGJ = unit weight of the backfill soil and H 1 IJ = friction angle of the backfill soil. More information can be obtained from Appendix.

4.1 Justification of the Assumption of Log-Spiral Failure Mechanism

The studies of shaking table and centrifugal tests in the laboratory on scaled models of reinforced walls and slopes show that the most frequently observed failure surface occurring during a seismic event is a rotational failure mechanism following a log-spiral slip surface. (Sawada et al. 1993; Leshchinsky and Perry 1987; Leshchinsky and Boedeker 1989). Hence in this study, log-spiral failure mechanism is adopted in the analysis of seismic stability of RSS in conformity with the earlier studies.

4.2 Reinforcement Force Required to Stabilize the Wall (T r )

The horizontal and vertical inertial forces due to earthquake loading and surcharge load (q) acting on the wedge SH 1 G are shown in Fig. 2. The weight of the log-spiral wedge SH 1 G which can be estimated as:

Fig. 2
figure 2

Log-spiral failure mechanism and forces considered in the limit equilibrium method under seismic conditions

Full size image
$$ W_{{SH_{1} G}} = {\text{weight of wedge}}\,\,\,AH_{1} G\,\,\, - \left[ \begin{gathered} {\text{weight of wedge}}\,\,ESG\,{ + }\,{\text{weight of wedge}}\,\,AH_{1} EK \hfill \\ + {\text{weight of wedge}}\,\,KEGC - \,\,{\text{weight of wedge}}\,\,ACG \hfill \\ \end{gathered} \right] $$
(1)
$$ W_{{SH_{1} G}} = W_{{AH_{1} G}} - \left( {W_{ESG} + W_{{AH_{1} EK}} + W_{KEGC} - W_{ACG} } \right) $$
(2)

The reinforcement force (T r ) under seismic conditions can be obtained by resolving the forces acting on the wedge, SH 1 G horizontally and vertically (Fig. 2). By considering the horizontal equilibrium condition (∑ H = 0) for the wedge SH 1 G, we get

$$ T_{r} = k_{h} \left[ {W_{{SH_{1} G}} + q\left( {br_{o} - H\cot \alpha } \right)} \right] + F_{H} $$
(3)

where, q = intensity of uniformly distributed surcharge load placed on the backfill soil and F H is the horizontal component of reaction force acting along the radial line of the logarithmic spiral. Rearranging the above equation, we get

$$ F_{H} = T_{r} - k_{h} \left[ {W_{{SH_{1} G}} + q\left( {br_{o} - H\cot \alpha } \right)} \right] $$
(4)

where F H can be estimated as

$$ F_{H} = \int\limits_{0}^{{\theta_{1} }} {F\cos \left( {\theta_{1} + \theta_{2} - \theta } \right)} d\theta = F\left[ {\sin (\theta_{1} + \theta_{2} ) - \sin \theta_{2} } \right] $$
(5)

F = resultant force acting along the radial line of the logarithmic spiral. By considering the vertical equilibrium condition (∑ V = 0) for the wedge SH 1 G, vertical component of reaction force acting along the radial line of the logarithmic spiral can be written as

$$ F_{V} = \left[ {W_{{SH_{1} G}} + q\left( {br_{o} - H\cot \alpha } \right)} \right]\left( {1 - k_{v} } \right) $$
(6)

where br o  − H cot α = L g is the length of the failure zone of reinforced backfill at the top of structure and F V can be estimated as

$$ F_{V} = \int\limits_{0}^{{\theta_{1} }} {F\sin \left( {\theta_{1} + \theta_{2} - \theta } \right)} d\theta = F\left[ {\cos \theta_{2} - \cos (\theta_{1} + \theta_{2} )} \right] $$
(7)

Using Eqs. (4) and (6), an expression for reinforcement force (T r ) under seismic conditions can be obtained as follows:

$$ T_{r} = k_{h} \left[ {W_{{SH_{1} G}} + q\left( {br_{o} - H\cot \alpha } \right)} \right] + \cot \left( {\theta_{1} /2 + \theta_{2} } \right)\left[ {\left( {W_{{SH_{1} G}} + q\left[ {br_{0} - H\cot \alpha } \right]} \right)\left( {1 - k_{v} } \right)} \right] $$
(8)

The above equation can further be rearranged and be expressed as,

$$ T_{r} = \left[ {k_{h} + \left( {1 - k_{v} } \right)\cot \left( {\theta_{1} /2 + \theta_{2} } \right)} \right]\left( {W_{{SH_{1} G}} + q\left( {br_{0} - H\cot \alpha } \right)} \right) $$
(9)

4.3 Optimum Force of the Reinforcement Required To Ensure Equilibrium (T or )

The objective of optimization is to locate the critical log-spiral failure surface to detect the maximum of force of the reinforcement required to ensure equilibrium (T or ). “Improved Nelder-Mead simplex method” is adopted in the study for the numerical optimization of reinforcement force (T r ) (Basha and Babu 2009). It is a direct search algorithm in the optimization of nonlinear functions and also accounts for variable bounds. Based on this algorithm, ‘fminsearch’ function in Matlab optimization toolbox (The MathWorks Inc 2007), the minimum of a scalar function of several variables are obtained. The present maximization problem of T r is subjected to bound constraints such as 0° < θ1 < 90° and 0° < θ2 < 90° can be stated as follows:

$$ {\text{Find}}\;\theta_{ 1} \;{\text{and}}\;\theta_{ 2} \;{\text{which}}\left\{ {\begin{array}{*{20}c} {\text{maximizes}} & {T_{r} } \\ {{\text{subjected}}\;{\text{to}}} & {\left\{ \begin{gathered} 0^{o} < \theta_{ 1} < 90^{o} \hfill \\ 0^{o} < \theta_{ 2} < 90^{o} \hfill \\ \end{gathered} \right.} \\ \end{array} } \right. $$
(10)

In the following sections, the optimum reinforcement force (T or ) obtained in this section is utilized for computing the factors of safety against tension and pullout modes of failure as shown in Fig. 3.

Fig. 3
figure 3

Pullout length of reinforcement (L ei ) calculation for the layer under consideration

Full size image

4.4 Estimation of Factors of Safety

The design for internal and external seismic stability should be carried out such that there is an adequate margin of safety against the internal and external failure modes of RSS during the design life of the structure. Consideration should be given to local instability relating to rupture and pullout of the individual layers of reinforcement. In addition, due consideration must be paid to external stability relating to sliding along the base of wall, overturning about the toe point, eccentricity of the resultant force and bearing capacity of foundation. The expressions of factors of safety against six modes of failure viz. tension failure, pullout failure, sliding failure, overturning failure, eccentricity failure and bearing failure of RSS are derived as given in the following sections.

4.5 Factor of Safety Against Tension Failure of Reinforcement

In the present study, FHWA (2001) guidelines in the design of RSS have been adopted, which specifies that the available tension (i.e. the tensile resistance provided by the reinforcement layers) must exceed or equal to the design tension to guard against the rupture failure of the reinforcement layers. When the stability against tension failure the reinforcement layer under consideration is assigned as the factor of safety, the ultimate tensile strength of the reinforcement layer under consideration (T u ) should be more than the maximum load in the soil reinforcement under consideration (T imax). The factor of safety against tension failure is given by,

$$ FS_{t} = {\frac{{{\text{ T}}_{\text{u}} \, }}{{{\text{T}}_{\text{imax}} }}} $$
(11)

where T imax based on vertical spacing (S v ) and horizontal spacing (S h ) can be calculated as

$$ T_{i\max } = \left( {z\gamma + q} \right)K\left( {S_{v} \times S_{h} } \right) $$
(12)

where, K = reinforcement force coefficient which can be computed by dividing the optimum force of the reinforcement (T or ) with 0.5γH 2 as shown below:

$$ K = {\frac{{T_{or} }}{{0.5\gamma H^{2} }}} $$
(13)

where S v  = H/n, S h  = 1 m (is considered in the present study), n = number of layers of the reinforcement and z is the depth of reinforcement layer under consideration from the top of slope. The factor of safety against tension failure can be written as,

$$ FS_{t} = {\frac{{{\text{ T}}_{\text{u}} \, }}{{{\text{T}}_{\text{imax}} }}} = {\frac{{{\text{ T}}_{\text{u}} \, }}{{\left( {z\gamma + q} \right)K\left( {S_{v} \times 1} \right)}}} $$
(14)

4.6 Factor of Safety Against Pullout Failure of Reinforcement

The reinforcement pullout failure analysis has to be performed to verify that the length of the reinforcement is appropriate to carry the design loads. When the length of the reinforcement within the resisting zone is unable to mobilize sufficient shear resistance, the reinforcing elements tend to pull out, producing gross distortions in the structure, or even triggering a collapse. The available design pullout resistance of individual reinforcing elements must be equal to or exceed the design tension in the reinforcement to guard against failure due to pullout of the reinforcements. Pullout resistance of reinforcing elements is computed using the overburden pressure and surcharge load acting on the length of the reinforcement embedded in the resisting zone. When the stability against pullout failure of the reinforcement is assigned as the factor of safety, the available resisting force (P ri ) on the embedded reinforcement length of layer under consideration should be more than the maximum load in the soil reinforcement under consideration (T imax).

The factor of safety against pullout failure is given by,

$$ FS_{po} = {\frac{{P_{ri} }}{{T_{i\max } }}} $$
(15)

The available resisting force (P ri ) on the embedded reinforcement length of each layer (L ei ) beyond the failure surface is given by the following equation

$$ P_{ri} = 2\sigma_{vi} L_{ei} \tan \delta_{i} \,({\text{Fig}}.\,3) $$
(16)

where σ vi  = zγ = effective vertical stress acting on the embedded reinforcement length of layer under consideration (L ei ) and δ i  = soil-reinforcement interface friction angle. The factor of safety against pullout failure can be written as,

$$ FS_{po} = {\frac{{{\text{ P}}_{\text{ri}} \, }}{{{\text{T}}_{\text{imax}} }}} = {\frac{{ \, 2\sigma_{vi} L_{ei} \tan \delta_{i} \, }}{{\left[ {z\gamma + q} \right]K\left( {S_{v} \times 1} \right)}}} $$
(17)

4.7 Estimation of Total Length of the Reinforcement

The log-spiral failure surface passing through the wall toe divides the total reinforcement length in two portions, one near the slope face in the active wedge (L a ), the other embedded behind in the resisting area (L ei ) as shown in Fig. 4.

Fig. 4
figure 4

Active length of reinforcement (L a ) calculation with in the failure zone

Full size image

Total length of the reinforcement (L) required to stabilize the wall can be written as

$$ L = {\text{active reinforcement length (}}L_{a} ) {\text{ + pullout lengh of reinforcement (}}L_{ei} ) $$
(18)

The active reinforcement length (L a ) at a depth, z below the top of structure can be written as

$$ L_{a} = br_{o} - L_{s} - L_{b} $$
(19)

where

$$ L_{b} = r_{0} \cos \theta_{2} - r\cos \left( {\theta_{2} + \theta } \right)\;{\text{and}}\;L_{s} = \left( {H - z} \right)\cot \alpha $$
(20)

The active reinforcement length (L a ) then can be written as

$$ L_{a} = br_{o} - \left( {H - z} \right)\cot \alpha - \left[ {r_{0} \cos \theta_{2} - r\cos \left( {\theta_{2} + \theta } \right)} \right] $$
(21)

after simplification (See Appendix), Eq. (21) reduces to

$$ {\frac{{L_{a} }}{H}} = \frac{1}{a}\left[ {e^{\theta \tan \phi } \cos \left( {\theta_{2} + \theta } \right) - e^{{\theta_{1} \tan \phi }} \cos \left( {\theta_{1} + \theta_{2} } \right)} \right] - \left( {1 - z/H} \right)\cot \alpha $$
(22)

where z = depth of reinforcement layer under consideration and is given by

$$ \frac{z}{H} = \frac{1}{a}\left[ {e^{\theta \tan \phi } \sin \left( {\theta + \theta_{2} } \right) - \sin \theta_{2} } \right],\,{\text{where}}\,\theta = i\,\,\left( {\theta_{1} /n} \right),\,i\,{\text{varies}}\,{\text{from}}\, 1\,{\text{to}}\,n - 1 $$
(23)

5 Formulation for External Seismic Stability Analysis of RSS

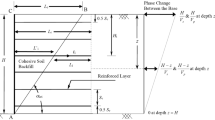
The volume of retained soil that is reinforced by horizontal layers of geo-synthetics can be imagined to act as a monolithic block of material. Sliding wedge failure mechanism as suggested by Ling et al. (1997) and Ling and Leshchinsky (1998) is considered for the external stability analysis (Fig. 5). The composite mass must be stable against sliding failure along the base of the structure at the foundation/backfill interface, overturning failure about the toe, eccentricity failure of resultant force and bearing-capacity failure of the supporting foundation soils (Fig. 5). Bearing capacity calculations assume that the base of the reinforced zone acts as an eccentrically loaded footing with an equivalent footing width (i.e., the conventional Meyerhof approach). The measure of relative stability against the external modes of failure shown in Fig. 5 is defined by the ratio of resisting forces to restraining forces (or moments in the case of overturning) as in the design of conventional gravity wall structures. A free body diagram of the wall showing different forces coming onto it from soil, and due to seismic loading along with their respective points of applications is shown in Fig. 5. k h and k v are the design acceleration coefficients in the horizontal and vertical directions respectively that are used to estimate the inertial forces acting at the centre of gravity of the failure mass and surcharge load under consideration.

Fig. 5
figure 5

External stability analysis and forces acting on reinforced soil block under seismic conditions

Full size image

5.1 Seismic Active Earth Pressure

The seismic active earth pressure on the wall is calculated using the pseudo-static Mononobe–Okabe’s approach (Kramer 2003). The basic expression for the calculation of the total seismic active earth thrust (P ae ) including the effect of surcharge (q) can be written as,

$$ P_{aet} = \frac{1}{2}\gamma_{eq} H^{2} K_{ae} \left( {1 - k_{v} } \right) $$
(24)

where, \( \gamma_{eq} = \left( {\gamma + \frac{2q}{H}} \right) \) is the sum of unit weight of reinforced backfill and equivalent surcharge height of backfill and K ae is the seismic active earth pressure coefficient is given by the following expression:

$$ K_{ae} = {\frac{{\cos^{2} \left( {\phi - \theta_{w} - \psi } \right)}}{{\cos \psi \cos^{2} \theta_{w} \cos \left( {\delta + \theta_{w} + \psi } \right)\left[ {1 + \sqrt {{\frac{{\sin \left( {\delta + \phi } \right)\sin \left( {\phi - \beta - \psi } \right)}}{{\cos \left( {\delta + \theta_{w} + \psi } \right)\cos \left( {\beta - \theta_{w} } \right)}}}} } \right]^{2} }}} $$
(25)

where, \( \psi = \tan^{ - 1} \left( {{\frac{{k_{h} }}{{1 - k_{v}}}}} \right),\,\theta_{w} = 90^{\circ} - \alpha \) is the angle of slope with vertical (= 0°), β is the angle of backfill with horizontal (= 0°). The point of application of total later thrust (due to backfill, seismic acceleration and surcharge load) acting on the reinforced block ‘ABFE‘as reported in Kramer (2003) is given by

$$ h = {\frac{{P_{a} \left( {H/3} \right) + \Updelta P_{ae} \left( {0.6H} \right) + P_{qe} \left( {0.5H} \right)}}{{P_{aet} }}} $$
(26)

where P a  = active earth pressure due to backfill soil can be written as 0.5γH 2 K a , ΔP ae  = seismic component of active earth pressure (P ae  − P a ), P ae  = P a  + ΔP ae  = Sum of static and seismic active earth pressure can be written as 0.5γH 2 K ae , P qe  = seismic active earth pressure due to surcharge load (P aet  − P ae ). Adopting the limit equilibrium method, the external stability of the wall is checked for overturning failure, sliding failure, eccentricity failure and bearing failure. The expressions of factor of safety for each of these four modes of failure of the wall are derived as given below.

5.2 Factor of Safety Against Sliding Failure Mode

For the stability against sliding failure along the base of RSS, sum of the horizontal resisting forces (∑Fr) should be more than sum of the horizontal driving forces (∑Fd). The factor of safety against sliding failure is given by,

$$ FS_{sli} = {\frac{{\sum {{\text{F}}_{\text{r}} } }}{{\sum {{\text{F}}_{\text{d}} } }}} = {\frac{{N_{b} \tan \delta_{b} }}{{P_{aet} \cos \delta + k_{h} \left[ {W_{ABFE} + qL} \right]}}} $$
(27)

where, N b  = [W ABFE  + qL](1 − k v ) + P aet  sin δ is the normal force at the base (can be found from the vertical force equilibrium of reinforced soil block ‘ABFE‘as shown in Fig. 5), δ b  = interface friction angle between wall base and foundation soil (= 2/3ϕ b ), ϕ b  = friction angle of the soil below the base slab of the retaining wall, δ = interface friction angle between backfill soil and reinforced backfill soil (= 0° considered in Mononobe–Okabe equation), W ABFE  = weight of the reinforced soil block ‘ABFE‘(= γHL), q = surcharge load acting on the backfill soil as shown in Fig. 5 and L = length of the reinforced soil block, ‘ABFE’. Substituting δ = 0 in Eq. (27), it reduces to

$$ FS_{sli} = {\frac{{\left[ {2\left( {L/H} \right)\left( {1 - k_{v} } \right) + Q\left( {L/H} \right)\left( {1 - k_{v} } \right)} \right]\tan \delta_{b} }}{{K_{aet} + 2k_{h} \left( {L/H} \right) + Qk_{h} \left( {L/H} \right)}}} $$
(28)

where, Q = 2q/(γH) is the surcharge coefficient and K aet  = P aet /0.5γH 2 is the total active earth pressure coefficient.

5.3 Factor of Safety Against Overturning Failure Mode

For stability against overturning failure about the toe point, the resisting moment about the toe point of wall should be more than the overturning moment about the toe point. The factor of safety against overturning failure of a RSS can be estimated as the ratio of sum of the moments resisting the overturning (∑ M R ) and moments causing the overturning (∑ M O ) as shown below:

$$ FS_{ot} = {\frac{{\sum M_{R} }}{{\sum M_{O} }}} = {\frac{{\left[ {\left( {W_{ABFE} + qL} \right)\left( {1 - k_{v} } \right)} \right]\left( {L/2} \right) + \left( {P_{aet} \sin \delta } \right)L}}{{\left( {P_{aet} \cos \delta } \right)h + \left[ {W_{ABFE} + qL} \right]k_{h} \left( {H/2} \right)}}} $$
(29)

substituting δ = 0 and after simplification, Eq. (29) reduces to

$$ FS_{ot} = {\frac{{\left( {2\frac{L}{H} + Q\frac{L}{H}} \right)\left( {1 - k_{v} } \right)\left( {\frac{1}{2}\frac{L}{H}} \right)}}{{K_{aet} \frac{h}{H} + \left( {2\frac{L}{H}k_{h} + Q\frac{L}{H}k_{h} } \right)\left( {\frac{1}{2}} \right)}}} $$
(30)

5.4 Factor of Safety Against Eccentricity Failure Mode

For the stability of RSS in terms of eccentricity (of resultant force), resultant of all the forces should fall within the middle third of the base. The factor of safety against eccentricity failure can be estimated as the ratio of one-sixth of base width of the wall (i.e. L/2 − L/3 = L/6) and the distance of sum of the vertical forces striking the base from middle point of the base (e) is given by

$$ FS_{e} = {\frac{{\left( {L/6} \right)}}{e}} $$
(31)

where, eccentricity (e) of the resulting force on the base can be calculated by summing the moments of resisting forces and disturbing forces about the center line of the wall base as shown in the following equation.

$$ e = {\frac{{\left( {P_{aet} \cos \delta } \right)h + \left[ {W_{ABFE} + qL} \right]k_{h} \left( {H/2} \right) - \left( {P_{aet} \sin \delta } \right)L/2}}{{\left[ {W_{ABFE} + qL} \right]\left( {1 - k_{v} } \right) + P_{aet} \sin \delta }}}\,\left( {{\text{FHWA\, 2}}00 1} \right) \, $$
(32)

Substituting δ = 0.0 in the above Eq. (32), we get

$$ e = {\frac{{P_{aet} h + \left[ {\gamma HL + qL} \right]k_{h} \left( {H/2} \right)}}{{\left[ {\gamma HL + qL} \right]\left( {1 - k_{v} } \right)}}} $$
(33)

5.5 Factor of Safety Against Bearing Failure Mode

Bearing capacity refers to the ability of the foundation soil to support the weight of the RSS placed upon it. Meyerhof distribution assumes that eccentric loading results in a uniform redistribution of pressure over a reduced area at the base of the wall (Fig. 5). This area is defined by a width equal to the wall width less twice the eccentricity (L − 2e). The factor of safety against bearing capacity failure can be estimated as the ratio of ultimate bearing capacity of a foundation below the base slab of RSS (q u ) and vertical stress at the base (σ v ) calculated with the Meyerhof type distribution as shown below:

$$ FS_{b} = {\frac{{q_{u} }}{{\sigma_{v} }}} $$
(34)

where,

$$ q_{u} = cN_{c} F_{cd} F_{ci} + q_{e} N_{q} F_{qd} F_{qi} + 0.5\gamma_{b} \left( {L - 2e} \right)N_{\gamma } F_{\gamma d} F_{\gamma i} $$

q e  = effective stress at the level of the bottom of the foundation (it is zero in the present case as height of soil at the toe side of the wall = 0.0), F cd , F qd , F γd are depth factors, F ci , F qi , F γi are load inclination factors and N c , N q , N γ are bearing capacity factors (see Appendix for the expressions). The vertical stress at the base (σ v ) can be written as

$$ \sigma_{v} = {\frac{\sum V }{L - 2e}} $$
(35)

6 Results and Discussion

The stability of RSS can be predicted by substituting the practically acceptable values of the different parameters involved in the factors of safety expressions derived in the above sections. Vertical seismic acceleration (k v ) acting in the downward direction is considered as positive in the present study. The values and ranges of these parameters for the present study are shown in Table 1. Effects of these parameters on the tension, pullout, sliding, overturning, eccentricity and bearing stability are presented in Figs. 6, 7, 8, 9, 10, 11, 12, 13. For the purpose of verifying the present methodology for design, the results obtained are compared with existing works as presented in the following section.

Table 1 Range of parameters considered in the analysis
Full size table
Fig. 6
figure 6

a Effect of ϕ on factor of safety against tension failure (FS t ). b Effect of k h on factor of safety against tension failure (FS t ). c Effect of Q = 2q/γH on factor of safety against tension failure (FS t )

Full size image
Fig. 7
figure 7

a Influence of ϕ on factor of safety against pullout failure (FS po ) along the depth of wall, computed for L/H = 1.0. b Influence of ϕ on pullout length of geo-synthetic layer (L ei /H) along the depth of wall for L/H = 1.0

Full size image
Fig. 8
figure 8

a Influence of k h on factor of safety against pullout failure (FS po ) along the depth of wall, computed for L/H = 1.0. b Influence of k h on pullout length of geo-synthetic layer (L ei /H) along the depth of wall for L/H = 1.0

Full size image
Fig. 9
figure 9

a Influence of Q = 2q/(γH) on factor of safety against pullout failure (FS po ) along the depth of wall, computed for L/H = 1.0. b Influence of Q = 2q/(γH) on pullout length of geo-synthetic layer (L ei /H) along the depth of wall for L/H = 1.0

Full size image
Fig. 10
figure 10

a Influence of friction angle of the backfill soil (ϕ) and length of the geosynthetic layer on factors of safety against sliding (FS sli ) and overturning failure (FS ot ) for k h  = 0.1 and k v /k h  = 0.5. b Influence of friction angle of the backfill soil (ϕ) and length of the geosynthetic layer on factors of safety against eccentricity (FS e ) and bearing failure (FS b ) for k h  = 0.1 and k v /k h  = 0.5

Full size image
Fig. 11
figure 11

a Influence of horizontal seismic acceleration coefficient (k h ) and length of the geosynthetic layer on factors of safety against sliding (FS sli ) and overturning failure (FS ot ) for k v /k h  = 0.5. b Influence of horizontal seismic acceleration coefficient (k h ) and length of the geosynthetic layer on factors of safety against eccentricity (FS e ) and bearing failure (FS b ) for k v /k h  = 0.5

Full size image
Fig. 12
figure 12

a Influence of vertical seismic acceleration coefficient (k h ) and length of the geosynthetic layer on factors of safety against sliding (FS sli ) and overturning failure (FS ot ) for k h  = 0.2. b Influence of vertical seismic acceleration coefficient (k h ) and length of the geosynthetic layer on factors of safety against eccentricity (FS e ) and bearing failure (FS b ) for k h  = 0.2

Full size image
Fig. 13
figure 13

a Influence of surcharge coefficient (Q) and length of the geosynthetic layer on factors of safety against sliding (FS sli ) and overturning failure (FS ot ) for k h  = 0.2. b Influence of surcharge coefficient (Q) and length of the geosynthetic layer on factors of safety against eccentricity (FS e ) and bearing failure (FS b ) for k h  = 0.2

Full size image

6.1 Validity of the Present Formulation for Internal Stability

To verify the accuracy of the present solution, the calculated values of reinforcement force coefficient (K) as defined in Eq. (13) and length of the failure zone at the crest of the wall (L g /H) for internal stability by means of the expressions derived in the present paper to those obtained from other solutions published in the literature are compared. Several plots have been published by Ling and Leshchinsky (1998) to illustrate the effect of seismic forces on the internal stability of reinforced slopes. Specifically, Ling and Leshchinsky (1998) conducted a parametric study for pseudo-static case and results in terms of reinforcement force and length necessary to ensure internal stability were presented. A comparative study of the results obtained by using the developed method presented in this paper with that of Ling and Leshchinsky (1998) is given in Tables 2 and 3. Table 1 presents the values of seismic reinforcement force coefficients (K) obtained by the present method and the values reported in Ling and Leshchinsky (1998) for the case of k h  = 0.2, ϕ = 20°, 30° and 40° and k v /k h  = 1, 0. 5, 0.0, −0.5 −1.0, slope angle (α) = 90°. As can be seen from Table 1, the equations derived in this work provide values for reinforcement force coefficients (K) that are in close agreement with those read from the graphs by Ling and Leshchinsky (1998). Table 2 presents the values of normalized length of the failure zone at the crest of the wall (L g /H) obtained from the present method and the values reported in Ling and Leshchinsky (1998) and for k h  = 0.1, 0.2 and 0.25, k v  = 0.0, slope angle (α) = 90° and ϕ = 20°, 30° and 40°. It can be seen from Table 2 that the two approaches are in very good agreement and sometimes with relatively minor differences. Hence, it confirms the validity of the present formulation.

Table 2 A comparison of length of the failure zone at the top of wall (L g /H) for k h  = 0.1, 0.2 and 0.25, k v  = 0.0 and ϕ = 20°, 30° and 40°
Full size table
Table 3 A comparison of reinforcement force coefficients (K) for k h  = 0.2, ϕ = 20°, 30° and 40° and k v /k h  = 1, 0. 5, 0, −0.5 −1.0
Full size table

6.2 Influence of ϕ and k h on Factor of Safety against Tension Failure (FS t )

Figure 6a and b show the variation of factor of safety against tension failure (FS t ) of all the layers of reinforcement along the depth of wall for ϕ = 30°, 35° and 40° and k h  = 0.0, 0.1, 0.2 and 0.3 respectively for typical values δ i /ϕ = 1.0, T u  = 45 kN/m, Q = 0.0, k v /k h  = 0.5 and total length of the reinforcement (L/H) = 1.0. For the top layers where axial tensile force in the geosynthetic layer is significantly less, a very high value (more than 18) of factor of safety is observed. It can be seen from the figure that the bottom layers of reinforcement from the top of wall are more critical to the tension mode of failure due to overburden pressure and generally have lower factor of safety values. For this purpose, the number of reinforcement layers (n) required to maintain the factor of safety against tension failure (FS t ) ≥1.0 for all layers of reinforcement is computed and presented in Fig. 6a and b. As an illustration from Fig. 6b, for k h  = 0.0, 12 layers of geosynthetic reinforcement should be provided in the 9 m height of wall with a vertical spacing (S v ) of 0.75 m (i.e. H/n = 9/12) to obtain FS t  ≥  1.0 for all layers.

It can also be seen from Fig. 6a and b that number of reinforcement layers (n) required to maintain desired stability (FS t  ≥  1.0) should be increased significantly with reduction in ϕ value from 40° to 30° and increase in k h value from 0.0 to 0.30. For example, for ϕ = 40°, 12 layers of reinforcement should be provided in the 9 m height of wall with a vertical spacing (S v ) of 0.75 m (= 9/12) to obtain FS t  ≥ 1.0 for all layers. Similarly n = 14 layers for ϕ = 35°, n = 18 layers for ϕ = 30° should be accommodated in the 9 m height of wall to avoid the tension failure of all layers of reinforcement. This behavior is attributed to decreasing shear resistance in the reinforced backfill soil. It can also be observed that for a constant values of ϕ and k h , the factor of safety (FS t ) significantly reduces as the depth of the layer increases. For letting a constant value of k h  = 0.2, factor of safety (FS t ) decreases significantly from 20 to 1.2 when depth increases from the topmost to bottommost layer. Similar observations can also be made for the influence of friction angle. This important observation helps in judicious selection of the number of reinforcement layers as the increase in horizontal seismic accelerations adversely affects the wall stability.

6.3 Influence of Surcharge Load (q) on Factor of Safety against Tension Failure (FS t )

If a structure is expected to support a surcharge load, a designer should consider the influence of surcharge load in the wall design calculations. An additional number of layers should be provided in the wall design in order to maintain the desired safety level in relation to tension failure mode when surcharge load is placed on the wall. For this purpose, Fig. 6c is presented to show the influence of uniformly distributed surcharge intensity (defined in terms of surcharge coefficient, Q = 2q/(γH)) on the variation of factor of safety against tension failure (FS t ) along the depth of wall for typical values adopted in the earlier sections. As an illustration, to avoid tension failure of all layers, number of layers (n) to be accommodated in the 9 m height of wall are 15, 20 and 26 for Q = 0.0, 0.2 and 0.4 respectively.

6.4 Influence of ϕ, k h and Surcharge Load (q) on Factor of Safety against Pullout Failure (FS po ) and Pullout Length (L ei /H)

The pullout length of the reinforcement (L ei ) gives rise to the stability against pullout failure of RSS. Figures 7 and 8 show the variation of factor of safety against pullout failure (FS po ) and corresponding pullout length (L ei /H) of all the layers of reinforcement along the depth of wall for ϕ = 30°, 35° and 40° and k h  = 0.0 – 0.3 respectively for typical value of total length of reinforcement (L/H) = 1.0 (uniform for all layers). It can be seen from Figs. 7a and 8a that the upper layers of reinforcement from the top of wall are more critical to the pullout mode of failure and wall should have adequate pullout length to maintain the factor of safety against pullout failure (FS po ). From Figs. 7b and 8b, it can be obtained that the contribution of pullout length for all the layers required to be provided which are already established in Fig. 6a and b.

Results presented in Figs. 7a and 8a demonstrate that for a constant value of k h and total length of the reinforcement (L/H) = 1.0, i.e. L = 9 m, the factor of safety against pullout failure (FS po ) significantly increases as the depth of the layer increases. For letting a constant value of k h  = 0.1 (Fig. 8a), the factor of safety (FS po ) increases significantly from 1.5 to 15.5 when depth increases from the topmost layer (1st layer) to bottommost layer (13th layer). This is because, the available pullout length (L ei /H = L/H − L a /H) for k h  = 0.1 in Fig. 8b, increases from 0.3 to 0.8 as depth increases from the uppermost layer (1st layer) to the bottommost layer (13th layer). An observation that can also be made from Figs. 7b and 8b is that the available pullout length (L ei /H) reduces as the magnitude of friction angle (ϕ) decreases from 40° to 30° and k h value increases from 0.0 to 0.3. Similar observations can also be made from the results presented in Fig. 9a and b for the influence of surcharge load (q).

6.5 Effect of Angle of Shearing Resistance (ϕ) on External Stability of RSS

Figure 10 a and b show the variation of factors of safety against sliding, overturning, eccentricity and bearing modes of failure with length of the geosynthetic reinforcement (L) for different values of soil friction angles (ϕ) for interface friction angle between backfill and reinforced backfill soil (δ) = 0.0. With the increase in values of ϕ from 30° to 40°, there is a significant increment in factors of safety against sliding, overturning, eccentricity and bearing modes of failure for typical values of ϕ b  = 30°, δ b /ϕ = 2/3, c = 10 kN/m2, Q = 0.2, k h  = 0.2 and k v /k h  = 0.5. This is due to the fact that there is a significant reduction in the seismic active earth pressure when the backfill soil is dense and it increases the shear resistance. It is also observed from Fig. 10a and b that the length of geosynthetic reinforcement (L) have a substantial influence on the stability against overturning and eccentricity modes of failure, whereas it has comparatively less influence on the stability against sliding and bearing modes of failure.

6.6 Effect of the Horizontal Seismic Acceleration (k h g) on External Stability of RSS

From Fig. 11a and b it is observed that for a particular value of ratio of length of the geosynthetic reinforcement to height of wall ratio (L/H), the factors of safety in sliding, overturning, eccentricity and bearing modes decreases drastically with an increase in the value of horizontal seismic acceleration coefficient (k h ). It shows that a stable reinforced soil structure can fail with the increase in horizontal seismic acceleration. As an illustration, for chosen value of L/H = 0.8, factors of safety against sliding, overturning, eccentricity and bearing failure modes respectively are 2.7, 7.3, 3.6 and 7.8 when there is no earthquake (k h  = 0.0); while the same reduces to 0.3, 1.8, 0.5 and 0.5 when the value of k h is increased to 0.3 (values can be obtained from Fig. 11a and b). Hence, a decrease in factors of safety against sliding, overturning, eccentricity and bearing failure modes respectively are 88.88, 75.34, 88.57 and 93.58% for an increase in k h value from 0 to 0.3. Another important observation which can be made from Fig. 11a and b is that the effect of L/H ratio on the factors of safety against four failure modes for lower k h values is significant as can be observed from figures that a large difference in values of factor of safety for a particular k h value, say 0 or 0.2. But the effect of L/H ratio on factors of safety in all four modes of failure is marginal at higher values of k h , say beyond 0.2.

6.7 Effect of Vertical Seismic Acceleration (k v g) on External Stability of RSS

This section illustrates the influence of vertical seismic acceleration on the external stability of RSS. The effect of vertical component of seismic acceleration (expressed in terms of k h as 0, 0.50 k h and k h ) on factors of safety against sliding (FS sli ), overturning (FS ot ), eccentricity (FS e ) and bearing (FS b ) modes of failure is presented in Fig. 12a and b for typical values shown in the above sections. It is observed from Fig. 12a and b that the effect of k v on factors of safety against sliding (FS sli ), overturning (FS ot ), eccentricity (FS e ) and bearing (FS b ) modes is insignificant for values of L/H ≤  1.0. But the effect of ‘k v ‘on factors of safety in all four modes of failure is significant at higher values of L/H (>1.0).

6.8 Effect of Uniformly Distributed Surcharge Intensity (q) on External Stability of RSS

Figure 13a and b show the effect of surcharge coefficient (Q) on the stability against sliding, overturning, eccentricity and bearing modes of failure. It can be seen from Fig. 13a and b that the design length of the reinforcement (L) is marginally affected by the magnitude of surcharge coefficient (Q). It is also depicts from these figures that as the ‘Q‘value vary from 0.2 to 1.4, the length of the reinforcement (L) should be increased marginally for maintaining the stability against sliding, overturning, eccentricity and bearing modes of failure of RSS.

7 Conclusions

The present study gives a simple design methodology for analyzing the reinforced soil structures subjected to earthquake forces for the internal stability and external stability. A closed-form solution is obtained to estimate seismic active earth pressure acting on reinforced earth structures and the factor of safety against different modes of stability.

From the present investigations, the following conclusions can be made:

  1. 1.

    The newly developed method provides a closed form solution for the active earth pressure acting on reinforced soil structures under earthquake loading ensuring both internal and external stability. The obtained results using the developed method are in very close proximity with other approximate solutions reported in literature. Thus the solutions obtained by using the developed method can be used as a bench mark for the other approximate solutions developed for the purpose.

  2. 2.

    The design parameters such as the horizontal and vertical seismic accelerations and number of reinforcement layers (n), total length of the reinforcement (L), angle of shearing resistance (ϕ), uniformly distributed surcharge load (q) have significant influence on the internal and external seismic stability of the wall.

  3. 3.

    It is noted that the bottom layers of reinforcement from the top of wall are more critical to the tension mode of failure due to axial tensile force in the geosynthetic layer is significantly high and have lower factor of safety values.

  4. 4.

    It is observed that the upper layers of reinforcement from the top of wall are more critical to the pullout mode of failure and wall should have adequate pullout length of the reinforcement to maintain the targeted value of factor of safety in pullout mode.

  5. 5.

    As the value of k h increases from 0 to 0.3, factors of safety against sliding, overturning, eccentricity and bearing failure modes are drastically reduced by 88.88, 75.34, 88.57 and 93.58%, respectively.

  6. 6.

    The effect of L/H ratio on the factors of safety against external modes of failure is significant for k h values less than 0.2 and it is marginal at higher values of k h , i.e. beyond 0.2.

  7. 7.

    The effect of vertical component of seismic acceleration (k v ) on factors of safety against sliding (FS sli ), overturning (FS ot ), eccentricity (FS e ) and bearing (FS b ) modes is insignificant for values of L ≤ H and it is significant at higher values of L/H, i.e. beyond 1.0.