1 Introduction

One of the main issues in geotechnical engineering is to calculate the bearing capacity of shallow foundations. Conventional methods for calculating the bearing capacity include limit equilibrium method (LEM), limit analysis and numerical methods such as finite difference and finite elements analysis.

Many studies have been conducted on the seismic behavior of unreinforced soil. Budhu and Al-Karni (1993), Richards et al. (1993), Johari et al. (2017), Conti (2018) and Alzabeebee (2020) evaluated the seismic bearing capacity or settlement of shallow foundations resting on unreinforced soils. Furthermore, Mansour et al. (2016), Dimitriadi et al. (2017, 2018) and Chaloulos et al. (2020) studied the effect of liquefaction on the seismic performance of the footings.

In recent decades, natural or polymeric materials have been extensively used for soil reinforcement. In this case, the soil bears more stress because of high tensile strength of reinforcements. There are different types of reinforcements. Some of them such as geogrids or geotextiles are plate-like materials. Fibers are one of the other types of reinforcements. The fibers can be very short or long fibrous materials. Some of the advantages of the fiber reinforcement include: (1) the bearing capacity of the soil increases, (2) the construction procedure may be similar to that of the conventional soil stabilization methods, (3) the strength and stiffness of the soil can be significantly improved, (4) fibers improves the permeability and compressibility characteristics of soil, and (5) the soil liquefaction potential decreases (Kumar Shukla 2017).

One of the challenges for geotechnical engineers is to investigate the stability of reinforced earth structures and calculate the bearing capacity of reinforced soils. Stress characteristics method (SCM) is one of the efficient methods for analyzing soil problems. SCM was first proposed by Sokolovski (1960). SCM has been frequently used by researchers in various fields of geotechnical engineering such as bearing capacity, lateral earth pressure, etc. As an advantage, SCM does not need a failure surface unlike LEM and it is achieved by solving the problem. As other numerical methods, the seismic effects can be applied as the horizontal and vertical pseudo-static coefficients.

Many studies have been carried out on unreinforced soils using SCM. Kumar and Mohan Rao (2002, 2003) used SCM to calculate the seismic bearing capacity of strip footings and slopes, respectively. SCM has also been used to analyze lateral pressures in unreinforced soils (Peng and Chen 2013; Keshavarz and Ebrahimi 2017). SCM has also been applied for stability analysis of reinforced earth structures. Jahanandish and Keshavarz (2005) used SCM to calculate the bearing capacity of strip footings on reinforced soil slopes. Keshavarz et al. (2011) used SCM to calculate the seismic bearing capacity of strip footings on reinforced soils.

For geotechnical analysis by SCM, a reliable failure criterion compatible with existing conditions should be used. Michalowski and Zhao (1996), Michalowski and Cermák (2003) and Michalowski (2008) conducted extensive research and found a suitable failure criterion for fiber-reinforced soils.

The use of fiber-reinforced soils in various geotechnical problems is increasing. However, there are limited analytical or numerical methods for fiber-reinforced soils. In many cases, an equivalent soil is used for analyzing fiber-reinforced soils. In other words, the fiber-reinforced soil mass is considered as an equivalent unreinforced soil with enhanced mechanical properties.

In this study, the SCM is used to calculate the static and seismic bearing capacity of strip footings on fiber reinforced soils. The failure criterion of Michalowski (2008) is used. Keshavarz and Nemati (2017) also applied SCM to compute the bearing capacity of fiber-reinforced soils but the isotropic distribution of fiber orientation has been used. In the isotropic case, the equivalent soil friction angle proposed by Michalowski (2008) can be used, considering the soil as an unreinforced soil having the equivalent friction angle and the solution procedure is very simpler. Due to the in situ mixing and compacting, the distributions of fibers in engineering applications are anisotropic (Michalowski 2008; Kumar Shukla 2017). Therefore, in the present study, the distribution of fiber orientation in the soil mass is assumed anisotropic. The pseudo-static method is used to evaluate the seismic effects on the bearing capacity factors and the failure pattern.

2 Methodology

2.1 Stress Equilibrium Equations

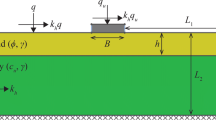
Stress equilibrium equations for anisotropic soils under plane strain condition have been obtained by Booker and Davis (1972). If the soil mass is considered under the plane strain condition, unknown stresses in the soil mass include σx, σz and τxz as shown in Fig. 1. The stress equilibrium equations at any point in the soil can be expressed as follows

$$\begin{array}{*{20}l} {\frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xz} }}{\partial z} = X} \hfill \\ {\frac{{\partial \sigma_{z} }}{\partial z} + \frac{{\partial \tau_{xz} }}{\partial x} = Z} \hfill \\ \end{array}$$
(1)

X and Z are body or inertial forces defined as X = γkh and Z = γ(1 − kv), where kh and kv are the horizontal and vertical pseudo-static seismic coefficients, respectively, and γ represents the unit weight of the soil. If reinforced soil is assumed to be homogeneous and anisotropic, the failure condition of the soil mass can be written as follows

$$f\left( {\sigma_{x} ,\sigma_{z} ,\tau_{xz} } \right) = R - F\left( {p,\psi } \right) = 0$$
(2)
Fig. 1
figure 1

Unknown stresses and orientations of the stress characteristics

Full size image

According to the Mohr stress circle for the soil element

$$\begin{aligned} \sigma_{x} & = p + R\cos 2\psi \\ \sigma_{z} & = p - R\cos 2\psi \\ \tau_{xz} & = R\sin 2\psi \\ \end{aligned}$$
(3)

where p and R are the mean stress and radius of the Mohr circle, respectively, and ψ represents the angle between the horizontal axis and the direction of the major principal stress, σ1 (Fig. 1). Using Eqs. (1) and (3) and after various algebraic operations, two characteristics can be found in the soil (Fig. 1). Stress equilibrium equations on these characteristics can be expressed as follows (Jahanandish and Keshavarz 2005; Keshavarz et al. 2011)

Along the σ+characteristics,

$$\begin{array}{*{20}l} {\frac{{{\text{d}}z}}{{{\text{d}}x}} = \tan \left( {\psi - m + \mu } \right)} \hfill \\ {\frac{{\sin 2\left( {m + \mu } \right)}}{\cos 2m}{\text{d}}p + \frac{2F}{\cos 2m}{\text{d}}\psi = \left( {\sin 2\mu {\text{d}}x - \cos 2\mu {\text{d}}z} \right)X + \left( {\cos 2\mu {\text{d}}x + \sin 2\mu {\text{d}}z} \right)Z} \hfill \\ \end{array}$$
(4)

and along the σ− characteristics

$$\begin{array}{*{20}l} {\frac{{{\text{d}}z}}{{{\text{d}}x}} = \tan \left( {\psi - m - \mu } \right)} \hfill \\ {\frac{{\sin 2\left( {m - \mu } \right)}}{\cos 2m}{\text{d}}p + \frac{2F}{\cos 2m}{\text{d}}\psi = - \left( {\sin 2\mu {\text{d}}x + \cos 2\mu {\text{d}}z} \right)X + \left( {\cos 2\mu {\text{d}}x - \sin 2\mu {\text{d}}z} \right)Z} \hfill \\ \end{array}$$
(5)

where

$$\begin{aligned} \tan 2m & = \frac{1}{2F}\frac{\partial F}{\partial \psi } \\ \cos 2\mu & = \cos 2m\frac{\partial F}{\partial p} \\ \end{aligned}$$
(6)

If the parameters x, z, p and ψ are known at points A and B and AC and BC are respectively the minus and plus characteristics lines, these parameters at point C can be achieved from the finite difference form of Eqs. (4) and (5) (Fig. 2). The trial and error method is used to obtain the properties of point C. In the first step, unknowns on the plus and minus characteristics at point C are assumed to be equal with corresponding values at the points B and A, respectively. Using the obtained values, new values are calculated and this process will continue until the difference between the calculated parameters in two consecutive steps becomes small enough.

Fig. 2
figure 2

The geometry of the problem and a typical stress characteristics network

Full size image

2.2 Failure Criterion

The failure criterion proposed by Michalowski (2008) properly considers the role of fiber reinforcements in the soil mass. In addition to the reinforcement density in the soil, fiber orientation distribution in the soil mass is also considered. The criterion provided by Michalowski (2008) assumes isotropic or anisotropic orientation of the fibers. In this study, fiber orientation is assumed anisotropic.

Anisotropic distribution of fiber orientation means that the distribution function of the fiber density versus orientation angle is non-circular. The ellipsoidal function is expressed as (Michalowski 2008):

$$\rho \left( \theta \right) = \frac{ab}{{\sqrt {a^{2} \sin^{2} \theta + b^{2} \cos^{2} \theta } }}$$
(7)

where a and b are the half-axes of the elliptical cross section and θ represents the inclination angle of fibers with the preferred bedding plane. The aspect ratio of the distribution is:

$$\zeta = \frac{b}{a}$$
(8)

For the isotropic distribution, ρ(θ) becomes spherical (a = b; ζ = 1) and fibers are uniformly distributed along all fiber orientations.

There are two main mechanisms for fiber failure in the soil, including (1) fiber rupture due to high stresses and (2) fiber slippage. Experimental results show that fiber rupture during loading can be neglected in geotechnical engineering applications and only fiber slippage can be evaluated in the failure criterion (Maher and Gray 1990; Michalowski and Zhao 1996; Michalowski 2008). Therefore, the criterion used in this study ignores fiber rupture.

Failure criterion is obtained using the energy method by equaling the work done by external and internal plastic forces during fiber slippage in the soil mass. The following equation is used as a failure criterion for fiber reinforced granular soils (Michalowski 2008)

$$R = - \left( {\frac{{D_{f} }}{{\dot{\bar{\varepsilon }}_{1} }}\frac{1 - \sin \phi }{2} + p\sin \phi } \right)\frac{1}{{\cos 2\left( {\psi + \omega } \right)}}$$
(9)

where \(\dot{\bar{\varepsilon }}_{1}\) represents the major principal strain rate and \(D_{f} /\dot{\bar{\varepsilon }}_{1}\) is calculated as follows

$$\frac{{D_{f} }}{{\dot{\bar{\varepsilon }}_{1} }} = C_{1} p$$
(10)

where

$$C_{1} = \frac{1}{\uppi}\eta \tan \phi_{w} \mathop \int \limits_{0}^{{\frac{\uppi}{2}}} \mathop \int \limits_{{ - \theta^{ *} }}^{{\theta^{ *} }} \rho \left( \theta \right)\left| {\sin^{2} \theta - K_{p} \cos^{2} \alpha \cos^{2} \theta } \right|\cos \theta {\text{d}}\theta {\text{d}}\alpha$$
(11)

and \(K_{p} = { \tan }^{2} \left( {\uppi/4 + \phi /2} \right)\). Fibers are assumed to be cylindrical and are characterized by their aspect ratio as η = l/2r, where l and r are the length and radius of fibers, respectively. ϕ is the internal friction angle of the soil and ϕw represents the friction angle between the fiber and soil. Integration is taken in the range of (− θ*, θ*) where \(\theta^{*} = \tan^{ - 1} \left( {\cos \alpha \tan \theta_{0} } \right)\) and \(\theta_{0} = \pm \left( {\uppi/4 + \phi /2} \right)\). In this study, a function is written in MATLAB to numerically calculate the integration of Eq. (11) and compute the minimum value of R in Eq. (9) with the angle ω being variable.

The average fiber concentration \(\bar{\rho }\) is defined as

$$\bar{\rho } = \frac{{V_{r} }}{V} = 0.5\mathop \int \limits_{{ -\uppi/2}}^{{\uppi/2}} \rho \left( \theta \right)\cos \theta {\text{d}}\theta$$
(12)

where Vr is the volume of the fibers in an element of volume V.A simple closed-form solution for R can be obtained for the isotropic case (ζ = 1) as (Michalowski 2008):

$$R = p\lambda$$
(13)

where

$$\begin{aligned} \lambda & = \sin \phi + \frac{{N\bar{\rho }\eta \tan \phi_{w} }}{3} \\ N & = \frac{\cos \phi }{\uppi} + \left( {\frac{1}{2} + \frac{\phi }{\uppi}} \right)\sin \phi \\ \end{aligned}$$
(14)

2.3 Boundary Conditions

Figure 2 shows the geometry of the problem and an example of the solved stress characteristics network. The failure zone of the problem is shown by ODEFG. OD and OG, respectively, show the boundary under the footing and on the earth’s surface. A surcharge q is applied on the boundary OG.

Boundary conditions are defined to set the parameters x, z, p and ψ on OG and OD boundaries. Stress condition on the boundary OG is known so that the normal stress, σ0 and shear stress, τ0 are applied to this boundary

$$\sigma_{0} = q\left( {1 - k_{v} } \right), \tau_{0} = qk_{h}$$
(15)

For any point on OG boundary, Eqs. (3) and (15) and Mohr stress circle are used to determine p0 and ψ0 as:

$$\begin{array}{*{20}l} {{\text{if}} \; q = 0: \psi_{0} = 0, p_{0} = 0 } \hfill \\ {\text{else}} \hfill \\ {\psi_{0} = 0.5\left( {\sin^{ - 1} \left( {p_{0} \sin \delta /R_{0} } \right) - \delta } \right);\; p_{0} = \left( {\sigma_{0} + \sqrt {\sigma_{0}^{2} - C_{2} \left( {\sigma_{0}^{2} + \tau_{0}^{2} } \right)} } \right)/C_{2} } \hfill \\ \end{array}$$
(16)

where

$$\begin{aligned} C_{2} & = 1 - \left( {\frac{{0.5C_{1} \left( {1 - \sin \phi } \right) + \sin \phi }}{{\cos 2\left( {\psi_{0} + \omega_{0} } \right)}}} \right)^{2} \\ \delta & = \tan^{ - 1} \left( {\frac{{k_{h} }}{{1 - k_{v} }}} \right) \\ \end{aligned}$$
(17)

As seen in Eq. (16), p0 depends on ψ0, and vice versa. Therefore, an iterative procedure is used to compute the values of p0 and ψ0.

On the boundary under the footing (boundary OD), ψf and the normal stress, qu can be achieved as follows

$$\begin{aligned} \psi_{f} & = 0.5\left( {\uppi - \delta - \sin^{ - 1} \left( {\frac{{p_{f} \sin \delta }}{{R_{f} }}} \right)} \right) \\ q_{u} & = \frac{{p_{f} \left( {1 - k_{v} } \right) + \sqrt {R_{f}^{2} \left( {1 - k_{v} } \right)^{2} + \left( {R_{f}^{2} - p_{f}^{2} } \right)k_{h}^{2} } }}{{\left( {1 - k_{v} } \right)^{2} + k_{h}^{2} }} \\ \end{aligned}$$
(18)

where Rf is the radius of Mohr circle on the boundary OD.

2.4 Solution Procedure

The solution procedure in this study is similar to the conventional SCM. The stress characteristics network can be divided into three zones (Fig. 2) including: OGF, OFE and OED. The solution starts from the boundary with a known stress, i.e. OG. In this boundary, stress characteristic values (x, z, p and ψ) are known and thus the network can be solved. O is a singular point because the stress states on the left and right sides of point O are not the same. At this point, x = z = 0. Therefore, at point O, according to Eq. (5):

$$\begin{array}{*{20}c} {\sin 2\left( {m - \mu } \right){\text{d}}p + 2F{\text{d}}\psi = 0} \\ \end{array}$$
(19)

To solve the OFE zone, the point O must be resolved first. Dividing this zone near point O into certain sections and having ψ0 and ψf, p is obtained from the finite difference form of Eq. (19) using the trial and error method. In fact, Eq. (19) is integrated from the left to the right side of point O in division points with known ψ values. This will provide the conditions for solving the OFE zone.

Having the values at point O and on the line OF, OFE zone can be solved. ODE zone can then be solved using the properties of the line OE. z in known on the line OD and there is a relationship between p and ψ [Eq. (18)]. There are two equations [Eq. (5)] for the characteristics lines crossing the line OD. Therefore, the unknowns x, p and ψ can be calculated by writing the Eq. (5) in the finite difference form. Accordingly, the stress distribution under the footing can be determined. The length of OD is dependent on the initial assumption on OG length. If a footing with a certain width is considered, the problem should be solved with a iterative method.

3 Results and Discussion

According to the described methodology in the previous section, a computer program was developed to solve the problem. With the inputs of the geometry and characteristics of the soil and reinforcements, the program is able to solve the stress characteristics network to obtain the bearing capacity, which is the average stress distribution under the footing.

While geotechnical designing of foundations, the bearing capacity as well as the settlement should be considered. However, all results of the present study are based on failure criterion and displacement is not considered.

Similar to the unreinforced soils, the bearing capacity of strip footings on granular fiber-reinforced soils is written as follows

$$q_{u} = qN_{q} + 0.5\gamma BN_{\gamma }$$
(20)

where B is the width of footing (Fig. 2), Nγ and Nq are respectively the bearing capacity factors from the unit weight of the soil and surcharge. To calculate these coefficients, the principle of superposition is used. The superposition approach is commonly used in engineering practice for bearing capacity of footings. Many research works have been done using this method to compute the bearing capacity of shallow foundations (Budhu and Al-Karni 1993; Choudhury and Subba Rao 2005; Chavda and Dodagoudar 2018; Conti 2018). According to Bolton and Lau (1993) and Zhu et al. (2003), the error of superposition assumption is less than, respectively, 20% and 10% on the safe side. Note that in the present study, the ultimate bearing capacity can be obtained from the written computer code without using the superposition assumption. Also, in the absence of surcharge, there is no error in the bearing capacity computation by applying the superposition method.

To calculate Nq, the unit weight of the soil is assumed zero. To calculate Nγ, the surcharge q cannot be assumed zero, because the singular point cannot be solved. Therefore, to calculate Nγ, a very small value is considered for q and the following equation is used to reduce the contribution of the surcharge

$$N_{\gamma } = N_{\gamma }^{\prime } - \frac{{2qN_{q} }}{\gamma B}$$
(21)

where N′γ is the bearing capacity factor obtained assuming a small value for q.

Using the criterion used in this study but by the kinematic approach of the limit analysis, Michalowski (2008) calculated the static bearing capacity factor, Nγ. As far as the authors are aware, there are no experimental or field results in the literature, which can be used to compare with the results of the present study. Therefore, the comparison is made with the theoretical results of Michalowski (2008) in Table 1. As seen, Nγ coefficients obtained in this study are smaller than those of Michalowski (2008) with a maximum and average difference of 27.2% and 22.6%, respectively. As the friction angle of the soil increases, the difference between the two methods decreases. Obviously, SCM gives lower bearing capacity factors as compared with the upper bound method. For each friction angle, the maximum difference between two methods is in the unreinforced case (\(\bar{\rho }\eta \tan \phi_{w} = 0\)).

Table 1 Comparison of the bearing capacity factors, Nγ with those obtained by Michalowski (2008)
Full size table

Figures 3, 4 and 5 show the bearing capacity factor Nq for different values of \(\bar{\rho }\eta \tan \phi_{w}\), namely, 0.2, 0.4 and 0.6, for ζ = 1, 0.5 and 0.2, respectively. Note that ζ = 1 describes the isotropic distribution of fiber orientation but other values indicate anisotropic distribution. As seen, the bearing capacity factor Nq increases with increasing reinforcement properties including concentration, aspect ratio and the friction angle between the soil and reinforcement. For the case of isotropic distribution (ζ = 1), an exact closed-form solution can be obtained for Nq as

$$N_{q} = \left( {1 - \lambda \cos 2\psi_{f} } \right)\frac{{1 + \sqrt {\lambda^{2} \left( {1 + \tan^{2} \delta } \right) - \tan^{2} \delta } }}{{1 - \lambda^{2} }}\exp \left( {\frac{{2\lambda \left( {\psi_{f} - \psi_{0} } \right)}}{{\sqrt {1 - \lambda^{2} } }}} \right)$$
(22)

where λ is defined in Eq. (14).

Fig. 3
figure 3

For ζ = 1, the bearing capacity factor Nq for different values of \(\bar{\rho }\eta \tan \phi_{w}\)

Full size image
Fig. 4
figure 4

For ζ = 0.5, the bearing capacity factor Nq for different values of \(\bar{\rho }\eta \tan \phi_{w}\)

Full size image
Fig. 5
figure 5

For ζ = 0.2, the bearing capacity factor Nq for different values of \(\bar{\rho }\eta \tan \phi_{w}\)

Full size image

Similarly, Figs. 6, 7 and 8 show Nγ values at different conditions. The changes and the effect of different parameters on the Nγ are similar to those found for Nq. The Bearing capacity for unreinforced soil (\(\bar{\rho }\eta \tan \phi_{w} = 0\)) are shown in Fig. 9. The seismic bearing capacity factor Nq for unreinforced soil can be obtained from simplifying Eq. (22) as

$$N_{q} = \frac{{\cos^{2} \delta + \sin \left( {\phi + \delta } \right)\sin \left( {\phi - \delta } \right) + 2\cos \delta \sqrt {\sin \left( {\phi + \delta } \right)\sin \left( {\phi - \delta } \right)} }}{{\cos^{2} \phi }} \times \exp \left( {\left( {\uppi - 2\sin^{ - 1} \left( {\frac{\sin \delta }{\sin \phi }} \right)} \right)\tan \phi } \right)$$
(23)
Fig. 6
figure 6

For ζ = 1, the bearing capacity factor Nγ for different values of \(\bar{\rho }\eta \tan \phi_{w}\)

Full size image
Fig. 7
figure 7

For ζ = 0.5, the bearing capacity factor Nγ for different values of \(\bar{\rho }\eta \tan \phi_{w}\)

Full size image
Fig. 8
figure 8

For ζ = 0.2, the bearing capacity factor Nγ for different values of \(\bar{\rho }\eta \tan \phi_{w}\)

Full size image
Fig. 9
figure 9

The bearing capacity factors Nq and Nγ for unreinforced soil (\(\bar{\rho }\eta \tan \phi_{w} = 0\))

Full size image

Figure 10 is prepared to demonstrate the effect of reinforcement on the bearing capacity factors Nq and Nγ. The larger the values of \(\bar{\rho }\eta \tan \phi_{w}\), the greater the values of the bearing capacity factors. This effect increases with increasing the soil friction angle. Furthermore, the bearing capacity factors decrease with an increase in the value of ζ. This means that the bearing capacity for anisotropic distribution of fiber orientation is more than the isotropic distribution.

Fig. 10
figure 10

For kh= kv= 0, the bearing capacity factors Nq and Nγ versus \(\bar{\rho }\eta \tan \phi_{w}\): (a) Nq, ζ = 0.2, (b) Nq, ζ = 0.5, (c) Nγ, ζζ = 0.2 and (d) Nγ, ζ = 0.5

Full size image

For \(\bar{\rho }\eta \tan \phi_{w} = 0.3\) and ζ = 0.5, the impact of the vertical seismic coefficient kv on the bearing capacity factors is presented in Fig. 11 for two values of ϕ, namely, 25 and 35 degrees. Graphs are plotted for different values of kv/kh. It is obvious that increasing the values of kv leads to decrease the values of Nq and Nγ. Figure 12 shows the maximum depth of the failure zone (Dp, see Fig. 2). As discussed next, Dp increases with increasing \(\bar{\rho }\eta \tan \phi_{w}\) or decreasing ζ and kh. Therefore, relatively large value of \(\bar{\rho }\eta \tan \phi_{w}\) and small value of ζ are selected to prepare Fig. 12. Having the characteristics of the soil and the reinforcement, the maximum depth of the failure zone is achieved from this chart for different friction angles of the soil. The depth Dp is higher for larger soil friction angles and increases with increased surcharge. Note that the present study considers all of the soil below the foundation as fiber-reinforced soil. Therefore, to use the results of this study, the depth of the reinforced soil should be greater than Dp.

Fig. 11
figure 11

For \(\bar{\rho }\eta \tan \phi_{w} = 0.3\) and ζ = 0.5, the bearing capacity factors (a) Nq and (b) Nγ with different values of kv/kh

Full size image
Fig. 12
figure 12

Maximum depth of the failure zone versus internal friction angle of the soil

Full size image

As stated, SCM does not need an initial assumption on the failure surface, and the failure zone is obtained after solving the problem. In the following, in Figs. 13, 14, 15 and 16, 20 examples are selected to illustrate the effect of the values of kh, \(\bar{\rho }\eta \tan \phi_{w}\), q/(γB) and ζ on the failure zone. For each case, the values of the normalized ultimate bearing capacity qu/(γB) are also indicated on the figures. Figure 13 shows the changes of the failure zone with horizontal seismic coefficient kh. As clearly seen in Fig. 13, as kh increases, the failure zone becomes smaller and shallower. This behavior has been observed for bearing capacity of geogrid reinforced soils (Keshavarz et al. 2011), strip footings on unreinforced soils (Soubra 1999; Choudhury and Subba Rao 2005; Yang and Sui 2008) and rock mass (Yang 2009).

Fig. 13
figure 13

For \(\bar{\rho }\eta \tan \phi_{w} = 0.3\), ζ = 0.5, ϕ = 30° and q/(γB) = 1, the impact of the horizontal seismic coefficient on the stress characteristics network

Full size image
Fig. 14
figure 14

For kh= kv= 0, ζ = 0.5, ϕ = 30° and q/(γB) = 1, the impact of \(\bar{\rho }\eta \tan \phi_{w}\) on the stress characteristics network

Full size image
Fig. 15
figure 15

For kh= kv= 0, ζ = 0.5, ϕ = 30° and \(\bar{\rho }\eta \tan \phi_{w} = 0.3\), the impact of q/γB on the stress characteristics network

Full size image
Fig. 16
figure 16

For kh= kv= 0, ϕ = 30°, q/(γB) = 1 and \(\bar{\rho }\eta \tan \phi_{w} = 0.35\), the impact of ζ on the stress characteristics network

Full size image

Figure 14 shows the impact of \(\bar{\rho }\eta \tan \phi_{w}\) on the failure zone. As seen, increasing \(\bar{\rho }\eta \tan \phi_{w}\) leads to a non-linear increase in the depth and surface length of the failure zone.

Figure 15 shows the impact of the surcharge on the shape of the failure zone. As can be seen, the depth of the failure zone increases with increased surcharge. Figure 16 demonstrates the impact of ζ on the failure zone. As ζ decreases, the depth of the failure zone increases. However, the values of ζ does not have a great effect on the failure zone.

4 Conclusions

The bearing capacity of strip footings on granular fiber-reinforced soils was evaluated using the Stress Characteristics Method (SCM). The failure criterion of Michalowski (2008) was used for anisotropic distribution of fiber orientation. The stress equilibrium equations along the stress characteristics were solved by the finite difference method. Vertical and horizontal pseudo-static coefficients were used to include seismic effects. A computer program was developed in MATLAB. Entering inputs, the characteristics network is solved and the failure zone is plotted. The program is also able to obtain the stress distribution under the footing and the average bearing capacity.

The bearing capacity of strip footings on fiber-reinforced sandy soil was expressed by the bearing capacity factors of the soil unit weight, Nγ, and surcharge, Nq. A chart was prepared to determine the depth of the failure zone. Bearing capacity factors were plotted in different conditions. The larger the values of the soil friction angle and reinforcement characteristics including density, aspect ratio and friction between the soil and the reinforcement, the greater the bearing capacity factors. The effect of the vertical seismic coefficient on the bearing capacity factors was also studied.

The failure zones were studied in different conditions. As the horizontal seismic coefficient increases, the depth of the failure zone decreases. The depth of the failure zone increases with increased reinforcement (\(\bar{\rho }\eta \tan \phi_{w}\)), surcharge and ζ. However, the value of ζ does not have great impact on the stress characteristics network.