1 Introduction

A disclination is a rotational defect, which may be wedge or twist in character. A wedge disclination has its line parallel to the Frank vector of rotation, whereas a twist disclination has its line perpendicular to the vector, in analogy to screw and edge dislocations, respectively. Conceptually, a positive wedge disclination can be created by removing a wedge of material from a circular cylinder, mending the cut faces and allowing the cylinder to relax (Romanov and Vladimirov 1992). Similarly, a negative wedge disclination can be visualized in terms of inserting a wedge into a cylinder. On its own, a disclination has a logarithmic stress singularity at the defect line and at long range. For this reason, disclinations usually exist in dipole or quadrupole configurations containing both positive and negative defects, with a screened stress at long range. Single disclinations may also exist in objects with boundaries that screen their stress field, such as a nanowire. Moreover, disclinations can be represented by dislocation walls. A negative wedge disclination can be created by the insertion of a wedge as mentioned above, or equivalently by a succession of edge dislocations with small Burgers vectors.

Disclination dipoles have been used to describe and model rotational plastic deformation and microstructures, and as basic building units of grain boundaries, in polycrystalline materials. Romanov and Vladimirov (1992) and subsequently Seefeldt (2001) reviewed the connection between disclination dipoles and rotational microstructures such as misorientation bands and fragmentation. Li (1972) and Nazarov et al. (2000) developed the concept of disclination dipoles as building blocks of high angle grain boundaries. More recently, Suhanov et al. (2015) analysed disclination dipoles and quadrupoles in nanocrystalline metals. Direct experimental evidence of disclination dipoles at the atomic level has been reported by Murayama et al. (2002) in nanocrystalline iron which has undergone severe plastic deformation by mechanical milling. In a recent paper, Cordier et al. (2014) reported the presence of disclination dipoles in deformed olivine aggregates by electron backscattering diffraction, and interpreted the dipoles as the carriers of grain boundary migration.

Disclinations carry stress singularities at their lines. They may relax by mechanisms such as the emission of dislocations, crack nucleation, and amorphization of their cores. Rybin and Zhukovskii (1978) analyzed crack nucleation from a wedge disclination with the strength of \(\sim \,1.72^{\circ }\) at a triple junction of grains, and calculated the nucleated crack length to be \(\sim ~0.07~\upmu \)m, for grain size of the order of 100 \(\upmu \)m. Gutkin and Ovid’ko (1994) compared crack nucleation from a triple junction containing a single disclination to one containing several split disclinations lying on the periphery of an amorphized core. They found that increasing the size of the amorphization reduces the probability of crack nucleation from the triple junction. Wu and Zhou (1996) studied the characteristics of cracks nucleated from a negative wedge disclination in a cylinder. They found that two types of cracks are possible: unstable submicron-size cracks and stable, longer micron-size cracks. Subsequently, Wu et al. (2007) and Zhou et al. (2007) investigated the nucleation problem by atomistic simulations. They determined the disclination strength at the triple junction of three tilt boundaries of various misorientations, and found that the disclination can relax by the emission of dislocations and the formation of branched microcracks with branches on the grain boundaries. A number of other works related to disclinations include the interaction of a wedge disclination dipole with a circular inclusion (Liu et al. 2006), disclinated Zener crack with cohesive end zones (Wu 2001), and nucleation of a Zener crack from a wedge disclination dipole in the presence of a circular inhomogeneity (Wang et al. 2009).

Fig. 1
figure 1

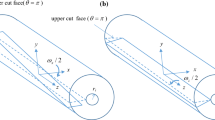
a A wedge disclination dipole subjected to a remote stress \(\sigma \), where the shifted axes of the negative and positive disclinations are located in the dipole arm interior (\(t_1 >0\), \(t_2 <0)\). b A crack of length 2l nucleated from the positive disclination, with the coordinate system \(x-y\) attached to the crack center. The added edge dislocations result from the shift of the rotation axes of the disclinations. Also, \(\omega \) denotes each disclination strength, 2a the dipole arm length, \(r_{0}\) the disclination core radius, and \(b_{1}\), \(b_{2}\) the Burgers vector magnitudes

Full size image

The early work of Wu and Zhou (1996), however, does not investigate crack nucleation in the strict sense. Specifically, the “nucleated” crack lengths are predicted from the intersections of the curve of the mode I stress intensity factor \(K_{\mathrm{I}}\), calculated as a function of the crack length l, with a horizontal line representing the constant critical value. If the derivative \(\hbox {d}{K}_{\mathrm{I}}/\hbox {d}l > 0\) at the critical length, the crack is unstable, whereas if it is less than zero the crack is stable. The previous work assumes that the crack can be nucleated from the disclination. However, nucleation of a crack is not always energetically favorable, even though it has an equilibrium length. This is demonstrated by the results in this paper.

Secondly, the crack nucleation kinetics of disclinations has not been previously studied in detail, mainly because of the immense computational effort associated with the continuous dislocation modeling of the crack. Each stress intensity factor calculation requires the solution of an integral equation to determine the dislocation density distribution of the crack. There is a lack of a single, and simple, expression to determine the crack length that can vary over six orders of magnitude. It is also computationally demanding to calculate the energy of the cracked solid repetitively (as a function of crack length), if an energy method of analysis is to be pursued.

Thirdly, a wedge disclination dipole has important characteristics which have not been investigated in relation to crack nucleation. Besides the dipole strength \(\omega \) and its arm length 2a (distance between the positive and negative disclinations), the rotation axis of each disclination of the dipole in general does not coincide with the defect line (de Wit 1973; Romanov and Vladimirov 1992). The separation distance between the disclination line and its rotation axis is denoted by t, or \(t_{1}\) (first disclination) and \(t_{2}\) (second disclination). Algebraically, t is positive (negative) if the rotation axis lies to the right (left) of the defect line. As explained in these references, the separation between defect axis and line results in an edge dislocation with Burgers vector \({\varvec{\omega }} \times {\varvec{t}}\) at the defect line, where \({\varvec{\omega }}\) and t represent the disclination strength and displacement of the defect line from the rotation axis, respectively. Figure 1 illustrates such a dipole with the shifts \(t_{1}\) and \(t_{2}\). It is a biaxial dipole if the disclinations have different rotation axes. If they share a common axis, such that \(t_{1}-t_{2} = 2a\), the dipole is uniaxial. Hence, a wedge disclination dipole with shifted rotation axes is represented by the two wedge disclinations with coincident edge dislocations.

Disclination dipoles with shifted rotation axes can practically represent dislocation walls with complex configurations. In the case of a two-axis dipole with no rotation axis shift, the negative disclination is represented by a semi-infinite wall terminating at the disclination position, while the positive disclination by dislocations of opposite sign terminating at its location. The annihilation of dislocations of opposite signs outside the dipole arm leaves a wall of dislocations in the dipole arm region. Thus, the two-axis dipole with no rotation axis shift represents a finite wall of dislocations. On the other hand, a disclination dipole with shifted axes of rotation can be represented by finite dislocation walls, each capped by a dislocation with sign opposite to those in the corresponding wall. A uniaxial dipole is formed when the two shifted axes coincide. Complicated dislocation wall configurations can thus be modeled by disclination dipoles with variously shifted rotation axes. In essence, a disclination dipole with shifted rotation axes can be viewed as a disclination-dislocation defect. Pertsev et al. (1981) described the structure and motion of kink bands in oriented polymers and fiber composites by means of disclination-dislocation defects. Basically, two biaxial dipoles (a quadrupole) transform into two uniaxial dipoles by shifting their rotation axes. This introduces edge dislocations at the defect locations. The disclinations model the macromolecular bending while the dislocations describe the intermolecular slip. Romanov and Vladimirov (1992) also explained the generation of a misorientation band by the transformation of a uniaxial dipole into a biaxial dipole and the separation and escape of the associated edge dislocations. Furthermore, a terminated twist boundary with a misorientation has been modeled by a chain of twist disclinations with shifted rotation axes, as reviewed in Romanov and Vladimirov (1992). Screened disclinations in general can be used to describe processes of plastic deformation through the motion of wedge disclination dipoles (Romanov 1993).

In the previous works on crack nucleation, it is assumed that there are no shifts of the rotation axes, \(t_{1}=t_{2} = 0\). A recent example is Wu (2018), who showed that short stable cracks and long unstable cracks are characteristic of such biaxial dipoles with no axis shift, and that a significant number of these crack length solutions are energetically unfavorable. Shift of the rotation axes has been shown by Krasavin (2007) to affect the residual resistivity of metals, which varies with the dipole arm length raised to the power of \(-\,3\) for biaxial dipoles and a different power of \(-\,2\) for uniaxial dipoles. It is conjectured that the axial shifts will also influence crack nucleation.

This paper addresses the issue of crack nucleation from uniaxial and biaxial wedge disclination dipoles by means of an energy analysis, generalizing the earlier work (Wu 2018). A remotely applied stress is also considered. Interaction energies are accounted for. The nucleated crack is assumed to be a composite Zener–Griffith crack, which has been investigated by Weertman (1996). A Zener crack is characterized by a crack head opening \(b_{\mathrm{T}}\) and length 2l, while a Griffith crack by the remote stress \(\sigma \) and its length 2l. This crack profile is a physical approximation which reduces the computational effort required if the continuous dislocation modeling approach is used. As shown in the next section, a single algebraic expression representing the derivative of the energy of the cracked solid can be solved numerically to determine the equilibrium lengths \(b_{\mathrm{T}}\) and 2l, and the corresponding energy equation can be used to compare the energy state before crack nucleation to the energy of the cracked solid.

The physical modelling and the mathematical formulation are laid out in Sect. 2. The parametric investigation, which focuses on the disclination axis shifts, is presented in Sect. 3. The results are further discussed in Sect. 4. Conclusions are given in Sect. 5.

2 Zener–Griffith crack and energy approach

2.1 Physical modeling and formulation

Figure 1 illustrates the physical problem of a wedge disclination dipole consisting of a positive disclination and a negative disclination, each of strength or power \(\omega \) and separated by a dipole arm of length 2a. It is also subjected to the remotely applied stress \(\sigma \). In Fig. 1a, the negative and positive disclinations are on the left and right sides of the dipole, and their shifted axes are located at \(t_1 \) and \(t_2 \) respectively. If the shifted axes are located within the dipole arm, then \(t_{1} > 0\) and \(t_{2} < 0\). This is a biaxial dipole if the shifted axes do not coincide. If \(t_{1 }-t_{2 }= 2a\), the axes coincide and the dipole is uniaxial. If \(t_{1} < 0\) and \(t_{2} > 0\) both axes are outside the dipole arm. Figure 1b is a redrawn version of Fig. 1a, showing the \(x-y\) coordinate system centered at the Zener–Griffith crack, with the crack head and tip located at –l and l, respectively. In addition, it is assumed that each disclination, with a coincident edge dislocation, has a core of radius \(r_0\). The positive and negative disclinations are located at \(x=-l-r_0\) and \(x=-l-2a-r_0\), respectively.

The energy of the uncracked disclinated solid under an applied stress is the sum of \(E_\omega \) and \(E_\sigma \), where \(E_\omega \) is the energy of the disclination dipole and \(E_\sigma \) the elastic strain energy due to the applied stress. The energy E of the cracked disclinated solid consists of the crack surface energy \(E_\mathrm{s}\), the energy respectively of the disclination \(E_\omega \), the Zener crack \(E_{\mathrm{Z}}\), the Griffith crack \(E_{\mathrm{G}} \), as well as the interaction energy \(E_{\mathrm{int}} \). The energy terms \(E_\mathrm{s} \), \(E_{\mathrm{Z}}\) and \(E_{\mathrm{G}} \) can be written as:

$$\begin{aligned} E_\mathrm{s}= & {} 4\gamma l, \quad E_Z =\frac{D}{2}b_\mathrm{T}^\mathrm{2} \ln \frac{2R}{l}, \quad \nonumber \\ E_\mathrm{G}= & {} E_\sigma -\frac{\sigma ^{2}l^{2}}{4D}, \end{aligned}$$
(1)

where \(\gamma \) is the surface energy per unit area, \(D=\mu /2\pi (1-\nu )\), R the structural size, and the parameters \(\mu \), \(\nu \) in D denote the usual shear modulus and Poisson’s ratio. The elementary stress, energy and displacement formulas can be obtained in Weertman (1996) for the Zener and Griffith cracks and in Romanov and Vladimirov (1992) for the disclination dipoles. The explicit forms for \(E_\omega \) and \(E_\sigma \) are not needed since it is the derivative of the energy expression and the change in energy state that are relevant for determining the equilibrium lengths and whether the crack nucleation is favourable. The energy of the cracked solid can be written as:

$$\begin{aligned} E=4\gamma l+E_\omega +\frac{D}{2}b_\mathrm{T}^2 \ln \frac{2R}{l}+E_\sigma -\frac{\sigma ^{2}l^{2}}{4D}+E_{\mathrm{int}}. \end{aligned}$$
(2)

The energy difference is then given by \(E-E_\omega -E_\sigma \):

$$\begin{aligned} \Delta E=4\gamma l+\frac{D}{2}b_\mathrm{T}^2 \ln \frac{2R}{l}-\frac{\sigma ^{2}l^{2}}{4D}+E_{\mathrm{int}} . \end{aligned}$$
(3)

To derive an expression for the interaction energy, imagine that the Zener crack is created first, in the presence of the disclination dipole and the remote stress. This yields the interaction energy \(E_{\mathrm{int1}} \):

$$\begin{aligned} E_{\mathrm{int1}} =-\int _{-R}^{+l} {(\sigma _\omega +\sigma )\Delta u_Z } dx. \end{aligned}$$
(4)

In Eq. (4), the normal stress on the line \(y = 0\) due to the disclination dipole is given by:

$$\begin{aligned} \sigma _\omega= & {} D\omega \left[ \left( {\frac{t_1 }{x+l+2a+r_0 }-\frac{t_2 }{x+l+r_0}} \right) \right. \nonumber \\&\left. \quad -\frac{1}{2}\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) ^{2}\right] , \end{aligned}$$
(5)

where \(t_1 >0\) and \(t_2 <0\) if the rotation axes are in the dipole arm interior. The denominators \(x+l+2a+r_0 \) and \(x+l+r_0 \) simply reflect the locations of the disclinations/dislocations with respect to the Zener crack. The crack opening displacement of the Zener crack is given by:

$$\begin{aligned} \Delta u_\mathrm{Z} =\left\{ {{\begin{array}{ll} b_\mathrm{T}, &{}\quad x<-l \\ \frac{b_\mathrm{T}}{\pi }\left( {\frac{\pi }{2}-\sin ^{-1}\frac{x}{l}} \right) ,&{}\quad -l<x<l \\ 0, &{}\quad x>l \\ \end{array} }} \right. . \end{aligned}$$
(6)

Substituting Eqs. (5) and (6) into Eq. (4) and, because of the three regions in Eq. (6), splitting the integral over these regions and neglecting the integration over the small core regions yields:

$$\begin{aligned} E_{\mathrm{{int}}1}= & {} -\int _{-R}^{-l-2r_0 -2a} {-\int _{-l-2a}^{-l-2r_0 } {-\int _{-l}^{+l} {\sigma _\omega \Delta u_Z } } } dx\nonumber \\&-\,\int _{-R}^{-l-2r_0 -2a} {-\int _{-l-2a}^{-l-2r_0 } {-\int _{-l}^{+l} {\sigma \Delta u_Z } } } dx,\nonumber \\ \end{aligned}$$
(7)

where the first three integrals can be written as \(-\,D\omega b_\mathrm{T} I\), and:

$$\begin{aligned} I= & {} \int _{-R}^{-l-2r_0 -2a} \left[ -\frac{1}{2}\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) ^{2}\right. \nonumber \\&\left. +\left( {\frac{t_1 }{x+l+2a+r_0}-\frac{t_2 }{x+l+r_0 }} \right) \right] \cdot \hbox { 1}dx \nonumber \\&+\,\int _{-l-2a}^{-l-2r_0 } \left[ -\frac{1}{2}\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) ^{2}\right. \nonumber \\&\left. +\left( {\frac{t_1 }{x+l+2a+r_0}-\frac{t_2 }{x+l+r_0 }} \right) \right] \cdot \hbox { 1}dx\nonumber \\&+\,\int _{-l}^{+l} \left[ -\frac{1}{2}\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) ^{2}\right. \nonumber \\&\left. +\,\left( {\frac{t_1 }{x+l+2a+r_0}-\frac{t_2 }{x+l+r_0 }} \right) \right] \nonumber \\&\quad \cdot \left( {\frac{1}{2}-\frac{1}{\pi }\sin ^{-1}\frac{x}{l}} \right) dx. \end{aligned}$$
(8)

These integrals can be worked out exactly, except for the last one with the arcsine function in the integrand. Specifically:

$$\begin{aligned} I=I_1 +I_2 +I_3 +I_4 +I_5 +I_6 , \end{aligned}$$
(9)

where

$$\begin{aligned} I_1= & {} -2a\ln \frac{2a+r_0 }{R-l-2a-r_0 }\nonumber \\&-\,(R-l-r_0 )\ln \frac{R-2a-l-r_0 }{R-l-r_0 }\nonumber \\&+\,r_0 \ln \frac{r_0 }{2a+r_0 }, \end{aligned}$$
(10)
$$\begin{aligned} I_2= & {} -\,a\ln \left( {1+\frac{2l}{2a+r_0 }} \right) \nonumber \\&-\,l\ln \left( {1+\frac{2a}{2a+r_0 }} \right) \nonumber \\&-\,\frac{r_0 }{2}\ln \left[ {\frac{r_0 }{2l+r_0 }\left( {1+\frac{2l}{2a+r_0 }} \right) } \right] , \end{aligned}$$
(11)
$$\begin{aligned} I_3= & {} \frac{1}{2\pi }\int _{-l}^{+l} {\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) } ^{2}\sin ^{-1}\left( {\frac{x}{l}} \right) dx, \end{aligned}$$
(12)
$$\begin{aligned} I_4= & {} t_1 \ln \frac{2a-r_0 }{R-l-2a-r_0 }\nonumber \\&+\,t_2 \ln \left( {\frac{2a-r_0 }{2a+r_0 }\frac{R-l-r_0 }{r_0 }} \right) , \end{aligned}$$
(13)
$$\begin{aligned} I_5= & {} \frac{t_1 }{2}\ln \left( {1+\frac{2l}{2a+r_0 }} \right) -\frac{t_2 }{2}\ln \left( {1+\frac{2l}{r_0 }} \right) , \end{aligned}$$
(14)
$$\begin{aligned} I_6= & {} -\frac{1}{\pi }\int _{-l}^{+l} \left( \frac{t_1 }{x+l+2a+r_0 }-\frac{t_2 }{x+l+r_0 } \right) \nonumber \\&\times \sin ^{-1}\frac{x}{l}dx. \end{aligned}$$
(15)

The integrals \(I_{3}\) and \(I_{6}\) are evaluated numerically. The exact forms of the other integrals have been verified by numerical integration. It can also be seen that I has the dimension of length. Furthermore, the last three integrals in Eq. (7) can be reduced to a simple exact form:

$$\begin{aligned}&\displaystyle -\,\int _{-R}^{-l-2r_0 -2a} {-\int _{-l-2a}^{-l-2r_0 } {-\int _{-l}^{+l} {\sigma \Delta u_Z } } } dx\nonumber \\&\quad =-\sigma b_\mathrm{T} (R-4r_0 ). \end{aligned}$$
(16)

In summary, the interaction energy of Eq. (7) can be written as:

$$\begin{aligned} E_{\mathrm{int1}} =-D\omega b_\mathrm{T} I-\sigma b_\mathrm{T} (R-4r_0 ), \end{aligned}$$
(17)

where I is given by Eqs. (9)–(15).

After the Zener crack has been created, the Griffith crack is now created in the presence of the disclination dipole stress and the stress of the Zener crack. The corresponding interaction energy is:

$$\begin{aligned} E_{\mathrm{{int}}2} =-\int _{-R}^{+l} {(\sigma _\omega +\sigma _\mathrm{Z} )\Delta u_\mathrm{G} } dx, \end{aligned}$$
(18)

where the Zener stress on the line of the crack is

$$\begin{aligned} \sigma _\mathrm{Z} =\left\{ {{\begin{array}{ll} -\frac{Db_\mathrm{T} }{\sqrt{x^{2}-l^{2}}}, &{} x<-l \\ 0, &{} |x|<l \\ \frac{Db_\mathrm{T} }{\sqrt{x^{2}-l^{2}}}, &{} x>l \\ \end{array} }} \right. , \end{aligned}$$
(19)

and the Griffith crack opening displacement is

$$\begin{aligned} \Delta u_\mathrm{G} =\left\{ {{\begin{array}{ll} \frac{2(1-\nu )}{\mu }\sigma \sqrt{l^{2}-x^{2}}, &{} |x|<l \\ 0, &{} |x|>l \\ \end{array} }} \right. . \end{aligned}$$
(20)

Since \(\Delta u_\mathrm{G} \) is non-zero only where \(\sigma _\mathrm{Z} \) is zero, the product of the Zener stress and the Griffith crack opening displacement is zero over the entire region. The integral of Eq. (18) then reduces to:

$$\begin{aligned} E_{\mathrm{{int}}2} =-\int _{-R}^{+l} {\sigma _\omega \Delta u_\mathrm{G} } dx=-\int _{-l}^{+l} {\sigma _\omega \Delta u_\mathrm{G} } dx, \end{aligned}$$
(21)

where the integration range has also been reduced to \((-l,l)\) because \(\Delta u_\mathrm{G} \) is zero outside this range. Upon substitution from Eqs. (5) and (20), Eq. (21) becomes:

$$\begin{aligned} E_{\mathrm{int2}}= & {} -\int _{-l}^{+l} D\omega \left[ \left( {\frac{t_1 }{x+l+2a+r_0 }-\frac{t_2 }{x+l+r_0 }} \right) \right. \nonumber \\&\left. -\frac{1}{2}\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) ^{2} \right] \nonumber \\&\cdot \frac{2(1-\nu )}{\mu }\sigma \sqrt{l^{2}-x^{2}}dx. \end{aligned}$$
(22)

Factoring out \(\omega \sigma \) yields the following result:

$$\begin{aligned} E_{\mathrm{int2}} =-\,\omega \sigma J, \end{aligned}$$
(23)

where J has the dimension of the square of length:

$$\begin{aligned} J=J_1 +J_2 , \end{aligned}$$
(24)

with

$$\begin{aligned} J_1= & {} t_1 \left( {l+2a+r_0 -\sqrt{(2l+2a+r_0 )(2a+r_0 )}} \right) \nonumber \\&-\,t_2 \left( {l+r_0 -\sqrt{(2l+r_0 )r_0 }} \right) , \end{aligned}$$
(25)

and

$$\begin{aligned} J_2 =-\frac{1}{2\pi }\int _{-l}^l {\ln \left( {1+\frac{2a}{x+l+r_0 }} \right) } ^{2}\sqrt{l^{2}-x^{2}}dx. \end{aligned}$$
(26)

The interaction energy is the sum of Eqs. (17) and (23):

$$\begin{aligned} E_{\mathrm{int}}= & {} E_{\mathrm{int1}} +E_{\mathrm{int2}}\nonumber \\= & {} -D\omega b_\mathrm{T} I-\sigma b_\mathrm{T} (R-4r_0 )-\omega \sigma J, \end{aligned}$$
(27)

where the products \(\omega b_\mathrm{T} \), \(\sigma b_\mathrm{T}\) and \(\omega \sigma \) indicate the interaction terms.

The energy of the cracked solid in Eq. (2) can be rewritten as:

$$\begin{aligned} E= & {} 4\gamma l+E_\omega +\frac{D}{2}b_\mathrm{T}^2 \ln \frac{2R}{l}+E_\sigma -\frac{\sigma ^{2}l^{2}}{4D}\nonumber \\&-\,D\omega b_\mathrm{T} I-\sigma b_\mathrm{T} (R-4r_0 )-\omega \sigma J, \end{aligned}$$
(28)

and the energy difference between the cracked and uncracked states is then, by Eq. (3):

$$\begin{aligned} \Delta E= & {} 4\gamma l+\frac{D}{2}b_\mathrm{T}^2 \ln \frac{2R}{l}-\frac{\sigma ^{2}l^{2}}{4D}\nonumber \\&-\,D\omega b_\mathrm{T} I-\sigma b_\mathrm{T} (R-4r_0 )-\omega \sigma J. \end{aligned}$$
(29)

Differentiating Eq. (28) with respect to \(b_\mathrm{T} \) and setting it to zero yields an expression for determining the equilibrium crack head opening. This results in:

$$\begin{aligned} b_\mathrm{T} =\frac{D\omega I+\sigma (R-4r_0 )}{D\ln (2R/l)}. \end{aligned}$$
(30)

Similarly, differentiating Eq. (28) with respect to l yields an expression for determining the equilibrium crack length:

$$\begin{aligned} {E}'= & {} \partial E/\partial l=4\gamma -\frac{D}{2}\frac{b_\mathrm{T}^2 }{l}+\frac{D}{2}\frac{b_\mathrm{T}^2 }{R}-\frac{\sigma ^{2}l}{2D}\nonumber \\&-\,D\omega b_\mathrm{T} {I}'-\sigma b_\mathrm{T} -\omega \sigma {J}', \end{aligned}$$
(31)

where, as noted by Weertman (1996), \(\partial R/\partial l=1\) since the crack advances only at the right tip, and the crack center, from which R is defined, moves in step with the crack increment. The symbols \({I}'=\partial I/\partial l\) and \({J}'=\partial J/\partial l\). Equation (30) is substituted into Eq. (31), which then contains just one unknown l.

2.2 Solution of energy derivative equation in normalized form

It is convenient to represent the energy derivative equation and the energy difference equation in non-dimensional form. This is achieved by normalizing all length variables by R, stresses by D, the energy derivative by DR, and the energy by \(DR^{2}\). The normalized variables are denoted by an overhead bar. Specifically:

$$\begin{aligned}&\bar{{a}}=a/R,\; \bar{{r}}_0 =r_0 /R, \;\bar{{b}}_\mathrm{T} =b_\mathrm{T} /R, \nonumber \\&\bar{{I}}=I/R, \; \bar{{J}}=J/R^{2}\; {\bar{{I}}}'=\partial \bar{{I}}/\partial \bar{{l}}\nonumber \\&\quad =\partial (I/R)/\partial (l/R)={I}' \nonumber \\&{\bar{{J}}}'=\partial \bar{{J}}/\partial \bar{{l}}=\partial (J/R^{2})/\partial (l/R)=1/R\nonumber \\&\qquad \cdot \partial J/\partial l={J}'/R\nonumber \\&\bar{{\gamma }}=\gamma /DR, \bar{{E}}=E/DR^{2} \nonumber \\&{\bar{{E}}}'=\partial \bar{{E}}/\partial \bar{{l}}=\partial (E/DR^{2})/\partial (l/R)={E}'/DR. \end{aligned}$$
(32)

Equations (30), (31) and (29) then reduce to:

$$\begin{aligned} \bar{{b}}_\mathrm{T}= & {} \frac{\omega \bar{{I}}+\bar{{\sigma }}(1-4\bar{{r}}_0 )}{\ln (2/\bar{{l}})}, \end{aligned}$$
(33)
$$\begin{aligned} \bar{{{E}'}}= & {} 4\bar{{\gamma }}-\frac{1}{2}\frac{\bar{{b}}_\mathrm{T}^2 }{\bar{{l}}}+\frac{1}{2}\bar{{b}}_\mathrm{T}^2 -\frac{\bar{{\sigma }}^{2}\bar{{l}}}{2}\nonumber \\&-\,\omega \bar{{b}}_\mathrm{T} \bar{{{I}'}}-\bar{{\sigma }}\bar{{b}}_\mathrm{T} -\omega \bar{{\sigma }}\bar{{{J}'}}, \end{aligned}$$
(34)
$$\begin{aligned} \Delta \bar{{E}}= & {} 4\bar{{\gamma }}\bar{{l}}+\frac{1}{2}\bar{{b}}_\mathrm{T}^2 \ln \frac{2}{\bar{{l}}}-\frac{\bar{{\sigma }}^{2}\bar{{l}}^{2}}{4}\nonumber \\&-\,\omega \bar{{b}}_\mathrm{T} \bar{{I}}-\bar{{\sigma }}\bar{{b}}_\mathrm{T} (1-4\bar{{r}}_0 )-\omega \bar{{\sigma }}\bar{{J}}. \end{aligned}$$
(35)

Substituting Eq. (33) into Eq. (34) yields a single nonlinear algebraic equation for the energy derivative. Setting \(\bar{{{E}'}}\) to zero allows the determination of \(\bar{{l}}\):

$$\begin{aligned}&\bar{{{E}'}}=4\bar{{\gamma }}-\frac{1}{2}\left( {\frac{1}{\bar{{l}}}-1} \right) \left( {\frac{\omega \bar{{I}}+\bar{{\sigma }}(1-4\bar{{r}}_0 )}{\ln (2/\bar{{l}})}} \right) ^{2}\nonumber \\&\quad -\,\frac{\bar{{\sigma }}^{2}\bar{{l}}}{2}-\left( {\omega \bar{{{I}'}}+\bar{{\sigma }}} \right) \frac{\omega \bar{{I}}+\bar{{\sigma }}(1-4\bar{{r}}_0 )}{\ln (2/\bar{{l}})}-\omega \bar{{\sigma }}\bar{{{J}'}}=0.\nonumber \\ \end{aligned}$$
(36)

The crack head opening is then determined from Eq. (33). With the equilibrium \(\bar{{l}}\) and \(\bar{{b}}_\mathrm{T} \) determined, the energy difference between the cracked and uncracked states is calculated using Eq. (35). If \(\Delta \bar{{E}}<0\), the crack nucleation is favorable because the cracked state has a lower energy state. If \(\Delta \bar{{E}}>0\), it is unfavorable.

3 Numerical results

To investigate the dependence of crack nucleation on the axis shifts, the following values for the loading, geometrical and material parameters are used. The disclination strength is typically of the order of a few degrees (Romanov and Vladimirov 1992) and strengths of up to \(\sim \,10^{\circ }\) are considered in this paper. The remotely applied stress range is kept small, up to \(\sim \) 10 MPa, in order to study the effect of adding a small stress to the disclinated solid. For the geometrical parameters, \(2a = 20\,\upmu \hbox {m}\), \(R = 1000\,\upmu \hbox {m}\), and \(r_{\mathrm{o}} = 2\) Å. The dipole arm length in general scales with the structural size, and the core radius \(r_{\mathrm{o}}\) is assumed to be of the order of the Burgers vector magnitude. The material parameters selected are those of aluminium, with the surface energy \(\gamma = 1\,\hbox {J/m}^{2}\), \(\mu = 26\,\hbox {GPa}\), \(\nu = 0.347\), yielding \(D = 6.337\,\hbox {GPa}\). The dependence of crack nucleation on the geometrical and material parameters has been investigated in the previous paper (Wu 2018) for a biaxial dipole with no axis shift, i.e., \(t_{1}=t_{2} = 0\). Attention is focused on axis shifts within the interior of the dipole arm in this paper, i.e., \(t_1 >0\), \(t_2 <0\), and the geometrical and material parameters are kept at the stated values.

3.1 Stress field of uniaxial and biaxial dipoles

A study of the stress field around a dipole is first conducted, as it contributes to the understanding of crack nucleation. In Figs. 2 and 3, let the origin of the \(x-y\) coordinate system be attached to the center of the dipole; in all other figures, the origin is at the center of the crack as shown in Fig. 1b.

Fig. 2
figure 2

Contour plots of the stress \(\bar{{\sigma }}=\sigma _{yy} /D\omega \) in a square region \(-100<x/a<100\) and \(-100<y/a<100\) due to a biaxial dipole with no axis shifts \(t_1 =t_2 =0\), and b a uniaxial dipole with \(t_1 =a,t_2 =-\,a\). The positive and negative disclination lines are located at (a, 0) and (\(-\,a\), 0), respectively. Note the four orders of magnitude difference between the stresses in a, b

Full size image
Fig. 3
figure 3

Variation of the normal stress \(\bar{{\sigma }}=\sigma _{yy} /D\omega \) at \(x/a=\pm 1.2\) with \(t_2 /a\) for a \(t_1 /a= 1\), b \(t_1 /a= -1\). A crack will likely nucleate from the positive disclination when the shifted axes are within the dipole interior, whereas the nucleation is more likely from the negative disclination when the axes are outside the dipole

Full size image

Figure 2 plots the contours of the normal stress \(\bar{{\sigma }}=\sigma _{yy} /D\omega \) in a square region of size \(-\,100<x/a<100\) containing a wedge disclination dipole of strength \(\omega \), where the positive and negative disclinations are located at (a, 0) and \((-\,a,0)\), respectively. The upper figure shows the stress contours around a biaxial dipole with no axis shifts, i.e., \(t_1 =t_2 =0\), whereas the lower figure shows the contours for a symmetrical uniaxial dipole with \(t_1 =-t_2 =a\). One can immediately observe that the symmetrical uniaxial dipole is strongly screened, with stress magnitude four orders smaller than that of a biaxial dipole. It is conjectured that a symmetrical uniaxial dipole will less likely nucleate a crack compared to a biaxial dipole. Based on the location of the tensile stress region, Fig. 2a also suggests that crack nucleation tends to occur from the negative disclination of the biaxial dipole with no axis shift, while it tends to occur from the positive disclination of the symmetrical uniaxial dipole shown in Fig. 2b.

Figure 3 plots the stress \(\bar{{\sigma }}\) at the positions \((x/a=\pm 1.2, y = 0)\) versus \(t_2 /a\). Specifically, Fig. 3a shows the results for the case of \(t_1 /a=1\), i.e., the axis of the negative disclination is shifted to the center of the dipole arm. It can be seen that the stress is mostly tensile at \(x/a=1.2,y\hbox { = }0\), i.e., just right of the positive disclination when \(t_2 /a < 0\), whereas it is completely negative at \(x/a=-1.2,y\hbox { = }0\), i.e., just left of the negative disclination. This suggests that a crack will more likely initiate from the positive disclination when \(t_1 /a>0,t_2 /a<0\), i.e., the shifted axes are within the interior of the dipole. In contrast, Fig. 3b plots \(\bar{{\sigma }}\) versus \(t_2 /a\) for \(t_1 /a=-1\), i.e., the axis of the negative disclination is outside the dipole arm. In this case, the stress is tensile at \(x/a=-1.2,y\hbox { = }0\) for all values of \(t_2 /a\), suggesting that a crack will more likely nucleate from the negative disclination when both axes are outside the dipole arm region. In this paper, the focus is on the case where the shifted axes are within the dipole arm \(t_1 /a>0,t_2 /a<0\), so that crack nucleation from the positive disclination is investigated.

3.2 Curves of the energy derivative

Two examples of the derivative \({\bar{{E}}}'=\partial \bar{{E}}/\partial \bar{{l}}\) used to determine the equilibrium crack lengths are illustrated in Fig. 4. In Fig. 4a, \({\bar{{E}}}'\) is plotted against \(\bar{{l}}\) for \(\bar{{t}}_1 =\bar{{a}}\), \(\bar{{\sigma }}=0\), and \(\bar{{t}}_2 =-\,0.65\bar{{a}},-\,0.6958\bar{{a}},-\,0.72\bar{{a}}\). At \(\bar{{t}}_2 =-\,0.65\bar{{a}}\), the \({\bar{{E}}}'\) curve crosses the \(\bar{{l}}\) axis twice over the range \(0<\bar{{l}}<0.01\), thus predicting a shorter unstable crack \(({\bar{{E}}}''< 0)\) and a longer stable crack \(({\bar{{E}}}''>0)\). As \(\bar{{t}}_2 \) increases negatively to \(-\,0.6958\bar{{a}}\), the curve touches the \(\bar{{l}}\) axis at one point. This is a stable solution (\({\bar{{E}}}''=0,{\bar{{E}}}'''>0)\). If \(\bar{{t}}_2 \) increases further to \(-\,0.72\bar{{a}}\), no equilibrium solutions can be found within this range of \(\bar{{l}}\). Hence, a larger negative value of \(\bar{{t}}_2 \) results in a dipole more resistant to crack nucleation. The value \(\bar{{t}}_2 =-\,0.6958\bar{{a}}\) may be interpreted as a critical axis shift above which the disclination dipole is stable or resistant against crack nucleation.

Fig. 4
figure 4

Plot of the energy derivative versus crack length for \(\omega =1^{\circ }\). a \(\bar{{t}}_1 =\bar{{a}}\), \(\bar{{\sigma }}=0\) and \(\bar{{t}}_2 \) is varied, b \(\bar{{t}}_1 =\bar{{a}}\), \(\bar{{t}}_2 =-\,0.65\bar{{a}}\) and \(\bar{{\sigma }}\) is varied. In a, there are two solutions for \(\bar{{t}}_2 =-\,0.65\bar{{a}}\) (a shorter unstable solution and a longer stable solution), a single stable solution for \(\bar{{t}}_2 =-\,0.6958\bar{{a}}\) and no solution for \(\bar{{t}}_2 <-\,0.6958\bar{{a}}\). In b, there are two solutions at \(\bar{{\sigma }}=4.8\times 10^{-3}\) (a shorter stable solution and a longer unstable solution), a single unstable solution at \(\bar{{\sigma }}=5.38\times 10^{-3}\) and no solution for \(\bar{{\sigma }}>5.38\times 10^{-3}\)

Full size image

The lower figure illustrates another possible profile of the \({\bar{{E}}}'\) versus \(\bar{{l}}\) curve. In Fig. 4b, the curves are plotted for \(\bar{{t}}_1 =\bar{{a}}\), \(\bar{{t}}_2 =-\,0.65\bar{{a}}\) and three values of the remote stress \(\bar{{\sigma }}=4.8,5.38,5.8 \times 10^{-3}\) over the range \(0.02<\bar{{l}}<0.5\). The curves are the upside-down version of the curves of Fig. 4a. At the stress of 4.8, there are two solutions: a shorter stable crack and a longer unstable crack. At \(\bar{{\sigma }}=5.38\times 10^{-3}\), the curve touches the \(\bar{{l}}\) axis at one point, which is also an unstable solution (\({\bar{{E}}}^{{\prime }{\prime }}=0,{\bar{{E}}}^{{\prime }{\prime }{\prime }}<0)\). At \(\bar{{\sigma }}=5.8\times 10^{-3}\), no equilibrium solutions can be found over the range.

Having presented the various possible characteristics of the \({\bar{{E}}}'\) curve, the parametric study of the dependence of crack nucleation on the axis shifts is presented below. In addition, the energy change \(\Delta \bar{{E}}\) between the equilibrium state (with crack) and the initial state (no crack) is also calculated to determine if the crack nucleation is favourable or otherwise. Exceptions are made in Figs. 8 and 10, where this calculation is omitted in order to avoid excessive computations.

3.3 Parametric investigation

In Sects. 3.3.1–3.3.3 below, no remote stress is applied and the crack is purely Zener. Composite Zener–Griffith cracks are considered in Sects. 3.3.4–3.3.5, when both the disclination loading and the remote stress are present in the solid. The primary objective of these sections is to investigate the dependence of crack nucleation on the axis shifts of the disclinations within the dipole arm region.

3.3.1 Equilibrium length of cracks nucleated from a uniaxial dipole

As shown in Fig. 2, a symmetrical uniaxial dipole has a strongly screened stress field, with stress magnitude four orders of magnitude smaller than that of a biaxial dipole. Considering \(\omega =1^{\circ }\) and \(5^{\circ }\) for a uniaxial dipole with \(\bar{{\sigma }}=0\), the stable and unstable crack lengths \(\bar{{l}}_\mathrm{s} \) and \(\bar{{l}}_\mathrm{u} \) are plotted against the axis shift \(\bar{{t}}_2 /\bar{{a}}\) in Fig. 5a. Note that the relation \(\bar{{t}}_1 -\bar{{t}}_2 =2\bar{{a}}\) holds for a uniaxial dipole. Three possible solutions are predicted: stable and energetically favorable cracks (full line), stable and energetically unfavorable cracks (dotted line), and unstable and energetically unfavorable cracks (dashed line). In addition, Fig. 5b plots the corresponding crack head opening \(\bar{{b}}_\mathrm{T} \) against \(\bar{{t}}_2 /\bar{{a}}\) for \(\omega =1^{\circ }\) and \(5^{\circ }\). The crack length curves resemble upward-pointing loops, while the crack head opening curves resemble downward-pointing loops.

Fig. 5
figure 5

Variation of a the stable and unstable crack lengths \(\bar{{l}}_{\mathrm{s}}, \bar{{l}}_\mathrm{u} \) , b the crack head opening \(\bar{{b}}_\mathrm{T} \) with the axis shift \(\bar{{t}}_2 /\bar{{a}}\) of the positive disclination for a uniaxial dipole with \(\bar{{t}}_1 -\bar{{t}}_2 =2\bar{{a}},\bar{{\sigma }}=0\). The two values of the disclination strength are \(\omega =1^{\circ },\hbox { 5}^{\circ }\)

Full size image

An observation of Fig. 5 is that the equilibrium solutions only exist for a limited range of \(\bar{{t}}_2 /\bar{{a}}\). For \(\omega =1^{\circ }\) and \(5^{\circ }\), solutions exist for \(-\,0.35<\bar{{t}}_2 /\bar{{a}}<0\) and \(-\,0.5<\bar{{t}}_2 /\bar{{a}}<0\), respectively. Unstable cracks are shorter than the stable ones. Both stable and unstable crack lengths generally increase as \(\bar{{t}}_2 /\bar{{a}}\) becomes more negative. Note, however, that the stable lengths decrease abruptly just before they merge with the unstable ones. This descending branch of the stable solutions consists of both energetically favorable and unfavorable solutions. The stable/unfavorable solutions merge with the unstable/unfavourable solutions. The merging point corresponds to the touching of the valley of the \({\bar{{E}}}'\) curve with the \(\bar{{l}}\) axis shown in Fig. 4a. This critical point itself represents a stable solution, as explained previously. Moreover, if in Fig. 5a \(\bar{{t}}_2 /\bar{{a}}\) increases negatively beyond \(-\,0.35\) for the \(\omega =1^{\circ }\) curve, or beyond \(-\,0.5\) for the \(\omega =5^{\circ }\) curve, the valley would be lifted out of the length axis in the corresponding \({\bar{{E}}}'\) versus \(\bar{{l}}\) curve and no solutions can be found. Hence, for the range of \(\bar{{t}}_2 /\bar{{a}}\) with no solutions, the disclination dipole with shifted axes are stable against crack nucleation, including the symmetrical uniaxial dipole where \(\bar{{t}}_1 /\bar{{a}}=1,\bar{{t}}_2 /\bar{{a}}=-1\).

Comparing the results for the two disclination strengths, the stronger dipole nucleates longer stable cracks (and shorter unstable cracks) over a wider range of axis shifts. The loops are larger for the stronger dipole. Stable crack lengths about 0.0003–0.0005 and 0.0005–0.0045 are found for the \(\omega =1^{\circ }\) and \(5^{\circ }\) disclination dipoles, respectively. In summary, if the unfavorable solutions are omitted, a uniaxial wedge disclination dipole with the strength of a few degrees generally nucleates a stable crack when the axis shift of the positive disclination in the dipole arm region is smaller than \(\sim \) 0.5a, and is resistant against crack nucleation when the axis shift is larger than \(\sim \) 0.5a.

The corresponding crack head openings \(\bar{{b}}_\mathrm{T} \) shown in Fig. 5b are roughly one to two orders of magnitude smaller than the crack lengths. The nucleated crack is thus very long compared to the opening at its head. Interestingly, \(\bar{{b}}_\mathrm{T} \) for the stable cracks decreases in magnitude as \(\bar{{t}}_2 /\bar{{a}}\) becomes more negative, unlike \(\bar{{l}}_\mathrm{s} \) for the most part. This implies that the aspect ratio \(\bar{{b}}_\mathrm{T} /\bar{{l}}_\mathrm{s} \) of the stable cracks decreases further as the axis shift of the positive disclination increases. The stronger dipole also nucleates a stable crack with a larger \(\bar{{b}}_\mathrm{T} \), although the opposite holds for the unstable/unfavorable crack.

3.3.2 Equilibrium length of cracks nucleated from a biaxial dipole

A natural question to ask is whether the results of Fig. 5 would change marginally or significantly if the dipole is biaxial. Figure 6 plots the equilibrium \(\bar{{l}}_\mathrm{s} \), \(\bar{{l}}_\mathrm{u} \) and \(\bar{{b}}_\mathrm{T} \) against \(\bar{{t}}_2 /\bar{{a}}\) for \(\bar{{t}}_1 /\bar{{a}}= 0.25\), \(\omega =1^{\circ }\), \(5^{\circ }\) and \(\bar{{\sigma }}= 0\). Noting the different vertical scales of Figs. 5 and 6, the cracks nucleated from biaxial dipoles are about one order of magnitude longer than those nucleated from uniaxial dipoles. The crack head openings associated with the biaxial dipoles are about half an order of magnitude larger than those associated with the uniaxial dipoles. In addition, the range of \(\bar{{t}}_2 /\bar{{a}}\) where crack nucleation can occur increases significantly when the dipole is biaxial. For \(\omega =1^{\circ }\) and \(5^{\circ }\), the range is \(-\,1.15< \bar{{t}}_2 /\bar{{a}}< 0\) and \(-\,1.38<\bar{{t}}_2 /\bar{{a}}< 0\), respectively. As in Fig. 5, the existence of stable/favorable, stable/unfavorable and unstable/unfavorable solutions also exist for the biaxial dipole. The variation of these equilibrium lengths with \(\bar{{t}}_2 /\bar{{a}}\) is similar for both uniaxial and biaxial dipoles.

Fig. 6
figure 6

Variation of a the stable and unstable crack lengths \(\bar{{l}}_{\mathrm{s},} \bar{{l}}_\mathrm{u}\), b the crack head opening \(\bar{{b}}_\mathrm{T} \) with the axis shift \(\bar{{t}}_2 /\bar{{a}}\)of the positive disclination for \(\bar{{t}}_1 /\bar{{a}}=0.25,\bar{{\sigma }}=0\). The two values of the disclination strength are \(\omega =1^{\circ },\hbox {5}^{\circ }\)

Full size image

In Fig. 6, \(\bar{{t}}_1 /\bar{{a}}= 0.25\), while \(\bar{{t}}_2 /\bar{{a}}\) is varied. If \(\bar{{t}}_1 /\bar{{a}}= 1\) instead, and \(\bar{{t}}_2 /\bar{{a}}\) is varied as before, the solution loops shrink in size, as shown in Fig. 7, where \(\omega =1^{\circ }\) and \(\bar{{\sigma }}= 0\). Hence, \(\bar{{l}}_\mathrm{s} \) and \(\bar{{b}}_\mathrm{T} \) both decrease as \(\bar{{t}}_1 /\bar{{a}}\) increases, although \(\bar{{l}}_\mathrm{u} \) behaves in the opposite manner. This result is not intuitively obvious. Also, for the larger loop \(\bar{{t}}_1 /\bar{{a}}= 0.25\) in Fig. 7, no solutions exist for \(\bar{{t}}_2 /\bar{{a}}< -\,1.15\). For the smaller loop \(\bar{{t}}_1 /\bar{{a}}= 1\), the range is \(\bar{{t}}_2 /\bar{{a}}< -\,0.7\). This again shows that uniaxial dipoles with \(\bar{{t}}_1 /\bar{{a}}= 0.25\), \(\bar{{t}}_2 /\bar{{a}}= -\,1.75\) or \(\bar{{t}}_1 /\bar{{a}}= 1\), \(\bar{{t}}_2 /\bar{{a}}=-\,1\) are resistant against crack nucleation. In fact, a general conclusion can be reached: disclination dipoles are stable against crack nucleation if the axis shifts within the dipole arm are large. In other words, the axis of each disclination lies closer to the defect line of the other disclination.

Fig. 7
figure 7

Variation of a the stable and unstable crack lengths \(\bar{{l}}_{\mathrm{s}}\), \(\bar{{l}}_\mathrm{u}\), b the crack head opening \(\bar{{b}}_\mathrm{T}\) with the axis shift \(\bar{{t}}_2 /\bar{{a}}\) of the positive disclination for \(\omega =1^{\circ },\bar{{\sigma }}=0\). The two values for the negative disclination axis shift are \(\bar{{t}}_1 /\bar{{a}}= 0.25\), 1.

Full size image

3.3.3 Critical disclination strength

Figures 5, 6 and 7 show that disclination dipoles with different combinations of \(\omega \), \(\bar{{t}}_1 /\bar{{a}}\) and \(\bar{{t}}_2 /\bar{{a}}\) may or may not nucleate a crack. A fundamental question is: for crack nucleation what is the minimum disclination strength of a dipole with axis shifts? For given axis shifts \(\bar{{t}}_1 /\bar{{a}}= 0, 0.5\) and 1, and \(-\,2< \bar{{t}}_2 /\bar{{a}} < 0\), the minimum or critical disclination strength \(\omega _{\mathrm{cr}}\) to nucleate a crack (whether favorable or unfavorable) is plotted in Fig. 8. To explain the meaning of \(\omega _{\mathrm{cr}} \), consider Fig. 6a, where it can seen that \(\bar{{t}}_1 /\bar{{a}}= 0.25\) and \(\bar{{t}}_2 /\bar{{a}}= -1.15\) correspond to the tip of the \(\omega =1^{\circ }\) loop. A weaker dipole strength \(\omega <1^{\circ }\)would result in a smaller loop, thus implying that a dipole with the stated axis shifts would not nucleate a crack if \(\omega <1^{\circ }\). The critical dipole strength for \(\bar{{t}}_1 /\bar{{a}}= 0.25\) and \(\bar{{t}}_2 /\bar{{a}}= -\,1.15\) is thus \(1^{\circ }\). Strictly speaking, the tip of the loop corresponds to an unfavorable solution, but it is not too far from the stable, favorable solution. To avoid excessive computations, this small difference is neglected in constructing Fig. 8.

Fig. 8
figure 8

a Variation of the critical disclination power \(\omega _{cr}\) to nucleate a crack with the dipole axis shifts \(\bar{{t}}_1 /\bar{{a}}\) and \(\bar{{t}}_2 /\bar{{a}}\). b Linear relation between the axis shifts for a critical disclination strength \(\omega _{\mathrm{cr}} = 10^{\circ }\), as compared to the relation for the shifts of a uniaxial dipole

Full size image

The three curves of critical dipole strength shown in Fig. 8 are cut off at the value of \(\omega _{\mathrm{cr}} = 10^{\circ }\). Fig. 8a shows that at any value of \(\bar{{t}}_1 /\bar{{a}}\), a smaller negative value of \(\bar{{t}}_2 /\bar{{a}}\) would lead to a lower \(\omega _{\mathrm{cr}} \). At the same time, for any given value of \(\bar{{t}}_2 /\bar{{a}}\), \(\omega _{\mathrm{cr}} \) would be lower the smaller the value of \(\bar{{t}}_1 /\bar{{a}}\). Together, this means that the disclination dipole would tend to nucleate a crack for small absolute values of \(\bar{{t}}_1 /\bar{{a}}> 0\) and \(\bar{{t}}_2 /\bar{{a}} < 0\). The biaxial dipole with \(\bar{{t}}_1 /\bar{{a}}=\bar{{t}}_2 /\bar{{a}}= 0\) has very small critical strength, and crack nucleation is essentially spontaneous.

Conversely, a disclination dipole would be strongly resistant against crack nucleation for large absolute values of the axis shifts. If one considers a high critical strength such as \(\omega _{\mathrm{cr}} = 10^{\circ }\), a question can be asked: what would be the values of \(\bar{{t}}_1 /\bar{{a}}\) and \(\bar{{t}}_2 /\bar{{a}}\) that would result in this strength? This can be answered by drawing a horizontal line at \(\omega _{\mathrm{cr}} = 10^{\circ }\) in Fig. 8a and determining its intersection with the various \(\bar{{t}}_1 /\bar{{a}}\) curves to yield the corresponding \(\bar{{t}}_2 /\bar{{a}}\) values. Figure 8b plots the resulting linear relation \(\bar{{t}}_1 /\bar{{a}}-1.304\bar{{t}}_2 /\bar{{a}}=2.136\). The result that a linear relation holds between the axis shifts leading to the same critical disclination strength is somewhat surprising. This relation is close to the relation \(\bar{{t}}_1 -\bar{{t}}_2 =2\bar{{a}}\) for a uniaxial dipole. The relation can be interpreted in the following way: for a given value of \(\bar{{t}}_1 /\bar{{a}}>0\) it gives the minimum absolute value of \(\bar{{t}}_2 /\bar{{a}}<0\) that would yield a critical disclination strength of at least \(10^{\circ }\). For instance, if \(\bar{{t}}_1 /\bar{{a}}=0.5\) the relation yields \(\bar{{t}}_2 /\bar{{a}}\approx -\,1.255\), and if \(\bar{{t}}_2 /\bar{{a}}\) actually equals − 1.3 the critical disclination strength will be larger than \(10^{\circ }\). Below (above) the line \(\bar{{t}}_1 /\bar{{a}}-1.304\,, \bar{{t}}_2 /\bar{{a}}=2.136\), the disclination dipole has a critical strength of more (less) than \(10^{\circ }\).

3.3.4 Dependence of crack nucleation on stress

In this subsection, the dependence of \(\bar{{l}}_\mathrm{s} \), \(\bar{{l}}_\mathrm{u} \) and the corresponding \(\bar{{b}}_\mathrm{T} \) on the remote stress \(\bar{{\sigma }}\) is investigated for a disclination dipole of strength \(1^{\circ }\), as shown in Fig. 9a ,b. Comparison of the results is made between a biaxial dipole \((\bar{{t}}_1 /\bar{{a}}=\bar{{t}}_2 /\bar{{a}}= 0)\) and a uniaxial dipole \((\bar{{t}}_1 /\bar{{a}}= 1.75,\,\bar{{t}}_2 /\bar{{a}}= -0.25)\). All four types of solutions are predicted: stable/favorable (solid line), stable/unfavorable (dotted line), unstable/favorable (dot-dashed line), and unstable /unfavorable (dashed). If one disregards the unfavorable solutions in Fig. 9a, it can be seen that short, stable/favorable solutions dominate the nucleation from \(\bar{{\sigma }} = 0\) up to \(\sim 0.85 \times 10^{-3}\) and \(\sim 1.1 \times 10^{-3}\) for the uniaxial and biaxial dipoles, respectively. Longer, unstable/favorable solutions appear at higher stresses and merge with the stable/favorable solutions at the tip of the loops. The stable/favorable cracks increase in length with \(\bar{{\sigma }}\), while the unstable/favorable cracks decrease in length with it. The unstable/favorable cracks appear to reflect their Griffith character. In Fig. 9b, the stable/favorable cracks also show an increase in \(\bar{{b}}_\mathrm{T} \) with \(\bar{{\sigma }}\), and their increase in length with \(\bar{{\sigma }}\) or \(\bar{{b}}_\mathrm{T} \) reflects more of their Zener character.

Fig. 9
figure 9

Dependence of a the stable and unstable crack lengths \(\bar{{l}}_{\mathrm{s},} \bar{{l}}_\mathrm{u} \), b the crack head opening \(\bar{{b}}_\mathrm{T}\) on the applied stress \(\bar{{\sigma }}\) for a biaxial dipole \((\bar{{t}}_1 /\bar{{a}}=\bar{{t}}_2 /\bar{{a}}=0)\) and a uniaxial dipole \((\bar{{t}}_1 /\bar{{a}}=1.75,\,\bar{{t}}_2 /\bar{{a}}=-\,0.25)\). Four different kinds of solutions exist. The solid line and the dot-dashed line indicate the stable favorable and unstable favorable solutions, respectively

Full size image

Unfavorable solutions, both stable and unstable, are also predicted. At any applied stress, one, two, or even three solutions may exist simultaneously. For instance, at \(\bar{{\sigma }}= 0.9\times 10^{-13}\) only a stable/favorable solution is predicted for the biaxial dipole, while at \(\bar{{\sigma }}= 1.05\times 10^{-3}\) three solutions are predicted: stable/favorable, unstable/favorable and stable/unfavorable. Discarding the unfavorable solution in the last case, two solutions are still possible. Of the two, the shorter, stable/favorable solution may occur preferentially over the longer, unstable/favorable solution as there is an energy barrier between them. Overall, the nucleation kinetics is complex. The uniaxial dipole also has very small unstable/unfavorable solutions at low stress \(\bar{{\sigma }}< 0.15\times 10^{-3}\), beyond which there is a jump to long unstable/favorable solutions. In contrast, the biaxial dipole does not have such behaviour at low stress.

Fig. 10
figure 10

Plot of the nucleation stress against the axis shift of the positive disclination for a wedge disclination dipole of strength \(1^{\circ }\). The results for a uniaxial dipole and a biaxial dipole are shown. The two curves intersect at \(\bar{{t}}_2 /\bar{{a}} = -\,1\), smaller than which the crack nucleation stress of the biaxial dipole is higher

Full size image

Figure 9b also shows that the biaxial dipole has a larger crack head opening than the uniaxial dipole. For both dipoles, the crack length/crack head opening ratio is about \(10^{2}\)–\(10^{3}\). For comparison, Fig. 5b shows that in the absence of a remote stress, the ratio is only about \(10^{1}\)–\(10^{2}\).

3.3.5 Critical nucleation stress

It has been shown in Figs. 5, 6 and 7 that crack nucleation in the absence of remote loading does not occur when the negative value of \(\bar{{t}}_2 /\bar{{a}}\) is large. For \(\omega =1^{\circ }\) in Fig. 5a, crack nucleation from a uniaxial dipole does not occur when \(\bar{{t}}_2 /\bar{{a}} < -0.35\). In Fig. 6a, nucleation from a biaxial dipole does not occur when \(\bar{{t}}_2 /\bar{{a}} < -\,1.15\) (for \(\bar{{t}}_1 /\bar{{a}} = 0.25\)). For such stable dipoles, Fig. 10 plots the minimum or critical remote stress to enable crack nucleation. Two cases are considered: a uniaxial dipole and a biaxial dipole with \(\bar{{t}}_1 /\bar{{a}}= 1\). The results show that the critical stress increases with increase in the negative value of \(\bar{{t}}_2 /\bar{{a}}\) in both cases, i.e., the rotation axis of the positive disclination approaches the location of the negative disclination line. At \(\bar{{t}}_2 /\bar{{a}} = -\,2\), the critical stress reaches its maximum of \(\sim 0.56 \times 10^{-3}\) for the uniaxial dipole. However, no equilibrium solutions are found for the biaxial dipole at \(\bar{{t}}_2 /\bar{{a}}=-\,2\). Spontaneous crack nucleation (i.e., no applied stress needed) occurs when \(\bar{{t}}_2 /\bar{{a}} > -\,0.35\) for the uniaxial dipole and \(\bar{{t}}_2 /\bar{{a}} > -\,0.7\) for the biaxial dipole, as also shown in Figs. 5a and 7a, respectively.

The two curves for the uniaxial and biaxial dipoles cross at \(\bar{{t}}_2 /\bar{{a}}= -\,1\). Left of this value, the critical stress for the biaxial dipole is higher than that of the uniaxial dipole, while the opposite is true right of this value. In general, comparing a uniaxial dipole to a biaxial dipole with the same \(\bar{{t}}_1 /\bar{{a}}\) value, the biaxial dipole with an absolute \(\bar{{t}}_2 /\bar{{a}}\) value larger (or smaller) than the absolute \(\bar{{t}}_2 /\bar{{a}}\) value (which equals \({\vert }\bar{{t}}_1 /\bar{{a}}-2{\vert })\) of the uniaxial dipole, the critical nucleation stress of the biaxial dipole is larger (smaller).

4 Discussion

The results in this paper reveal the complexity of the kinetics of crack nucleation from a wedge disclination dipole with axis shifts. In the following, some general results and trends are highlighted. Modeling and computational issues are also discussed.

Crack nucleation is not merely a function of the dipole strength and the dipole arm as shown by Wu (2018), but also a strong function of the shifts of the rotation axes of the positive and negative disclinations. Generally speaking, a clear distinction in nucleation kinetics can be made between uniaxial and biaxial dipoles. In the absence of an applied stress, the uniaxial dipoles are resistant against crack nucleation, except when there is a large positive shift of the negative disclination axis (and a corresponding small negative shift of the positive disclination).

For the biaxial dipoles, crack nucleation also depends on the specific shifts of the axes of rotation. For small or no shifts, a biaxial dipole may spontaneously nucleate a stable crack provided the disclination strength is sufficiently large. Generally speaking, it is resistant against crack nucleation if both axis shifts are large. A linear relation exists between the axis shifts which represents a critical disclination strength for crack nucleation. Above the line represented by this linear relation, biaxial dipoles with strength above that critical value will nucleate a crack, whereas below the line biaxial dipoles with strength below the critical value are resistant against crack nucleation.

An applied stress assists and enables crack nucleation from disclination dipoles. In the case of uniaxial dipoles, the critical applied stress to nucleate a crack increases if the common rotation axis lies closer to the negative disclination. For biaxial dipoles, the critical stress increases as the rotation axis of each disclination lies closer to the other disclination.

Multiple equilibrium solutions are possible for the crack length and crack head opening. These include stable and unstable solutions, either of which may be energetically favorable or unfavorable. Ignoring the unfavorable solutions, wedge disclination dipoles generally nucleate stable cracks with large crack length/crack head opening ratios. In the presence of a remote stress, longer unstable cracks compete with the shorter stable cracks for nucleation.

Experimentally, cracks nucleated in triple junctions of plastically deformed polycrystalline metals are of the order of 0.05–0.1 \(\upmu \)m (Lyles and Wilsdorf 1975), and early calculations based on the disclination model suggest crack length to grain size ratio of 0.1–0.001 (Rybin and Zhukovskii 1978; Gutkin and Ovid’ko 1994). The predictions of the current work are in overall agreement with these data. Atomistic calculations by Wu et al. (2007) for a crack nucleated from a nanowire containing a disclination of large strength of the order of \(20^{\circ }\) suggest ratios of the order of 0.1–0.8. These longer crack lengths are closer to the predictions of Wu and Zhou (1996) for long stable cracks in a small cylinder. The rather wide range of crack length to grains size ratios may originate from the fact that several disclination parameters play a significant role in crack nucleation, including the strength, multipole configuration, and as demonstrated in this paper, the shifts in the rotation axes of the disclinations. Direct measurements of the crack head openings have apparently not been attempted, possibly due to the difficulty of resolving submicron or nanometer sizes.

Although care has been taken in the current work to determine the likely nucleation site, i.e., at the positive disclination if the axes are within the dipole arm region, the general situation is more complicated. As has already been pointed out, nucleation from the negative disclination is more likely if both rotation axes are outside the dipole arm interior. Moreover, nucleation may occur from either disclination into the dipole arm interior. There is thus the possibility of a more complex crack configuration. Wu et al. (2007) have studied disclination relaxation by the embedded atom method. The results show that branched cracks can nucleate from a triple junction disclination in a nanowire, with the branches extending on the three grain boundaries meeting at the triple junction. Also, other mechanisms of relaxation of the disclination dipole may also be viable, for example dislocation emissions and disclination core amorphization, as reviewed earlier (Gutkin and Ovid’ko 1994).

Finally, the results here are made computationally possible by the physical assumption of a Zener–Griffith crack, neglecting the specific crack profile that can be estimated via a continuous dislocation modeling of the crack. Hence, instead of solving an integral equation to determine the dislocation density function, a single algebraic energy derivative equation containing the crack length can be solved directly. This is not a trivial issue because the crack length may vary over six orders of magnitude from the nanometer to the millimeter scale. Solutions over these many orders of magnitude can be easily missed. In the actual execution, the range of solutions is divided into six or more intervals, i.e, \(10^{-6}\)–\(10^{-5}\), \(10^{-5}\)–\(10^{-4}\), etc., and solutions are sought in each of them. This is supplemented by directly observing the zeroes of the energy derivative curve. For example, two zeroes are found in the same subdivided interval when the stable and unstable solutions are about to merge. One of these solutions, due to their close proximity, may be missed.

5 Conclusions

Crack nucleation kinetics of a wedge disclination dipole is investigated in this paper, focusing on the effect of the shifts of the rotation axes of the positive and negative disclinations of the dipole. The nucleated crack is modeled as a composite Zener–Griffith crack, and the energy method is used to predict the crack head opening and the crack length. The formulation leads to a nonlinear algebraic equation for determining the equilibrium lengths, and the nucleation is considered energetically favourable if the difference between the final and original energy states is negative. For rotation axes within the dipole arm interior, the following results have been obtained.

Both stable and unstable cracks can nucleate from the positive disclination, but some of them are energetically unfavorable. For favourable nucleation, stable crack length to structural size ratio is typically of the order of 0.001–0.01, and can be as high as 0.1 in the presence of a remote stress. The crack head opening is one to two orders of magnitude smaller than the crack length, and can be even smaller if an applied stress is present.

Typically, uniaxial dipoles are stable and resistant against crack nucleation if the positive axis shift of the negative disclination is more than 1.5 times the half dipole arm length. Biaxial dipoles are stable if the axis shifts are both large, i.e., a large positive shift of the negative disclination and a large negative shift of the positive disclination. A linear relation connecting the axis shifts associated with a critical disclination strength is found, such that biaxial dipoles with strength smaller than the critical value and with axis shifts below the line representing the linear relation are stable against crack nucleation. Furthermore, an applied stress can enable crack nucleation from a dipole. For a uniaxial dipole, the nucleation stress increases with the negative value of the shift of the positive disclination. For a biaxial dipole, it increases with the value of either of the two axis shifts. For a uniaxial and a biaxial dipole with the same negative disclination shift, the critical nucleation stress of the biaxial dipole is larger if its positive disclination shift is larger than that of the uniaxial dipole.