On the Effect of External Stress on the Stability of a Crack Located near a Wedge Disclination Dipole

Abstract

Conditions for the existence of equilibrium stable cracks in the combined elastic field of the biaxial wedge disclination dipole and external stress are analyzed. In the configuration space of the parameters of the system under consideration (the strength and length of the disclinations dipole and the magnitude of the external stress), the ranges of parameters are determined at which such cracks can appear. It is shown that an increase in the external stress leads to a significant localization of the existence domain of stable microcracks, originating in the vicinity of a disclination dipole, and its displacement towards smaller dipole lengths. The ranges of the lengths of stable cracks are determined. It is shown that an increase in the external stress leads to a contraction of the intervals of realization of stable crack lengths at each fixed value of the dipole arm and a shift of the upper and lower boundaries of this interval towards smaller crack lengths.

INTRODUCTION

Experimental and theoretical studies show that many regularities of the mechanical behavior of polycrystalline solids at large plastic strains can be explained on the basis of the concept of linear rotational mesodefects: strain-induced junction disclinations [1–4]. They arise at triple junctions of grain boundaries due to the difference in plastic strain in the grains of the polycrystal, as well as at the vertices of strain-induced facets arising at the grain boundaries during their interaction with localized lattice shears [2, 4, 5]. Junction disclinations induce powerful nonuniform fields of internal stresses. As a result, at true strain ε > 0.2, in their vicinity, specific accommodation structures arise in the form of broken dislocation walls, propagating from the triple junctions and vertices of strain-induced facets into the body of grain [1]. This process underlies fragmentation of polycrystals, i.e., splitting grains into mutually misoriented domains (fragments). Theoretical studies of the nucleation and evolution of broken dislocation boundaries in elastic fields of junction disclinations using analytical and computer simulation methods were carried out in [2–4].

Along with the plastic deforming, in a fragmented structure, local regions appear that have exhausted the resources of further accommodative adjustment of the structure [4]. In this case, the only channel for relaxation of elastic stresses induced by junction disclinations is the nucleation of microcracks. The rise and accumulation of microcracks in such “critical” regions of the fragmented structure triggers the appearance of regions of ductile fracture, which precedes the macroscopic destruction of the material.

As follows from the aforesaid, an important stage in the construction of the physical theory of ductile fracture of polycrystalline solids is the development of adequate models for the nucleation, growth, and accumulation of microcracks in elastic fields of systems of rotational mesodefects.

The development of such a theory is still at an early stage. Currently available theoretical studies in this direction are limited to the consideration of the simplest configurations of mesodefects. In particular, the conditions for the appearance of microcracks in the elastic field of a single wedge disclination were considered in [6–9]. Later, similar studies were carried out for the case of a wedge disclination dipole and a disclination the stress field of which is screened by a distributed dislocation ensemble [6]. In [10], the conditions for the Zener–Griffith crack nucleation near a disclination dipole were analyzed. In [11], an analysis was made of the conditions for the existence of cracks in the field of internal stresses from a rotational-shear mesodefect, which is a superposition of a wedge disclination dipole and a planar mesodefect. In [12, 13], the conditions of propagation of cracks originating on rotational mesodefects in heterogeneous materials were analyzed.

In this paper, we consider the conditions for the equilibrium of a microcrack in the combined field of external and internal stresses from a biaxial wedge disclination dipole and determine the existence domain of stable cracks in the configuration space of the parameters of the system under consideration.

1 DESCRIPTION OF THE MODEL

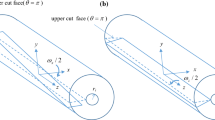
Consider a biaxial wedge disclination dipole of strength ${{w}_{{{\text{dp}}}}}$ with an arm $2a,$ containing in the vicinity of its negative disclination a crack of length $l~$ (Fig. 1).

Fig. 1.

Schematic representation of a disclination dipole with a crack located near the negative disclination dipole.

We choose a right-handed Cartesian coordinate system such that its origin coincides with the position of the negative disclination of the dipole and the$x$-axis is directed along the dipole arm. The energetically most favorable orientation of a crack generally depends on the stressed state. Further on, for simplicity, we will consider the case of uniaxial tension along the axis ${\text{O}}y,$ in which the orientation of the crack coincides with the direction of the dipole arm. We will analyze the equilibrium conditions for such a crack in the combined field of external stresses and internal stresses (the latter) from a disclination dipole. For this, we will use the configurational force approach [14]. For planar deformation of an isotropic material, the expression for the configurational force $F,$ defined as the value of the elastic energy released during the propagation of a crack over a unit length, has the form

$$F\left( l \right) = \frac{l}{{8D}}\left( {\bar {\sigma }_{{yy}}^{2} + \bar {\sigma }_{{xy}}^{2}} \right),$$

(1)

where $D = {G \mathord{\left/ {\vphantom {G {\left[ {2\pi \left( {1 - \nu } \right)} \right]}}} \right. \kern-0em} {\left[ {2\pi \left( {1 - \nu } \right)} \right]}},$ $G$ is the shear modulus, $\nu$ is Poisson’s ratio, ${{\bar {\sigma }}_{{yy}}}$ and ${{\bar {\sigma }}_{{xy}}}$ are the weighted average combined stresses from the disclination dipole, $~{{\sigma }^{{{\text{dp}}}}}$, and external stress ${{\sigma }^{{{\text{ext}}}}}{\text{:}}$

$${{\bar {\sigma }}_{{yy}}} = \frac{2}{{\pi l}}\int\limits_0^l {\left[ {\sigma _{{yy}}^{{{\text{dp}}}}\left( {x,0} \right) + \sigma _{{yy}}^{{{\text{ext}}}}} \right]} \sqrt {\frac{x}{{x - l}}} dx;$$

(2)

$${{\bar {\sigma }}_{{xy}}} = \frac{2}{{\pi l}}\int\limits_0^l {\left[ {\sigma _{{xy}}^{{{\text{dp}}}}\left( {x,0} \right) + \sigma _{{xy}}^{{{\text{ext}}}}} \right]} \sqrt {\frac{x}{{x - l}}} dx.$$

(3)

The components $\sigma _{{yy}}^{{{\text{dp}}}}$ and $\sigma _{{xy}}^{{{\text{dp}}}}$ of the stress tensor of the disclination dipole [15] in the chosen coordinate system have the form

$$\sigma _{{yy}}^{{{\text{dp}}}}\left( {x,0} \right) = D{{w}_{{{\text{dp}}}}}{\text{l}}n\left| {1 + \frac{{2a}}{x}} \right|,\,\,\,\sigma _{{xy}}^{{{\text{dp}}}}\left( {x,0} \right) = 0.$$

(4)

Analysis of the dependence of the configurational force $F$ on the crack length $l$ makes it possible to find all points of unstable and stable equilibrium of the crack, which satisfy the following relations:

— for the case of unstable equilibrium,

$$\left\{ {\begin{array}{*{20}{c}} {F\left( {l = l{\text{*}}} \right) = 2\gamma ,} \\ {F_{l}^{'}\left( {l = l{\text{*}}} \right) \geqslant 0,} \end{array}} \right.$$

(5)

— for the case of stable equilibrium,

$$\left\{ {\begin{array}{*{20}{c}} {F\left( {l = l{\text{*}}} \right) = 2\gamma ,} \\ {F_{l}^{'}\left( {l = l{\text{*}}} \right) < 0,} \end{array}} \right.$$

(6)

where $\gamma$ is the specific energy of the free surface.

2 CALCULATION RESULTS AND DISCUSSION

Numerical calculations were performed for the following parameter values: $b = 3 \times {{10}^{{ - 4}}}$ µm, G = $45\,000\,\,{\text{MPa,}}$ $\nu = 0.3,$ $\gamma = {{Gb} \mathord{\left/ {\vphantom {{Gb} 8}} \right. \kern-0em} 8},$ $2a = 0.1{\text{--}}1.4\,\,\mu {\text{m}},$ and ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = \left( {0 - 4} \right) \times {{10}^{{ - 3}}}.$

The dependences $F\left( l \right)$ calculated for $2a = 0.7\,\,\mu {\text{m}}$ and ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 2.2 \times {{10}^{{ - 3}}}$ for different strengths of the disclination dipole ${{w}_{{{\text{dp}}}}}$ are shown in Fig. 2.

Fig. 2.

Configurational force $F$ vs. the crack length $l$ at given values $2a = 0.7\,\,\mu {\text{m}}$ and ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 2.2 \times {{10}^{{ - 3}}},$ calculated for different values of ${{w}_{{{\text{dp}}}}}{\text{:}}$ (a) (1) ${{w}_{{{\text{dp}}}}} = 0.050,$ (2) ${{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{d}}} \approx 0.054,$ (3) ${{w}_{{{\text{dp}}}}} = 0.058,$ (4) ${{w}_{{{\text{dp}}}}} = 0.062,$ (5) ${{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{u}}} \approx 0.064;$ (b) (1) ${{w}_{{{\text{dp}}}}} = 0.056$ and (2) ${{w}_{{{\text{dp}}}}} = 0.060.$

Analysis of these dependences shows that, at fixed values of the external stress and dipole length, the existence of stable equilibrium cracks (henceforward, such cracks will be called stable) is feasible only in a certain range of ${{w}_{{{\text{dp}}}}}$.

The lower bound of this interval, $w_{{{\text{dp}}}}^{{\text{d}}}$, satisfies the relations:

$$\left\{ {\begin{array}{*{20}{c}} {{{{\left. {F\left( {l = {{l}^{{\text{d}}}},\,\,\,\,{{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{d}}}} \right)} \right|}}_{{2a,{{{{\sigma }}}^{{{\text{ext}}}}}}}} = 2\gamma ;} \\ {{{{\left. {F_{l}^{'}\left( {l = {{l}^{{\text{d}}}},\,\,\,\,{{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{d}}}} \right)} \right|}}_{{2a,{{{{\sigma }}}^{{{\text{ext}}}}}}}} = 0;} \\ {{{{\left. {F_{l}^{''}\left( {l = {{l}^{{\text{d}}}},\,\,\,\,{{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{d}}}} \right)} \right|}}_{{2a,{{{{\sigma }}}^{{{\text{ext}}}}}}}} < 0.} \end{array}} \right.$$

(7)

The dependence $F\left( l \right)$ for ${{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{d}}}$ is shown in Fig. 2a by curve 2.

The upper bound of this interval, $w_{{{\text{dp}}}}^{{\text{u}}},$ satisfies the relations

$$\left\{ {\begin{array}{*{20}{c}} {{{{\left. {F\left( {l = {{l}^{{\text{u}}}},\,\,\,\,{{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{u}}}} \right)} \right|}}_{{2a,{{{{\sigma }}}^{{{\text{ext}}}}}}}} = 2\gamma ;} \\ {{{{\left. {F_{l}^{'}\left( {l = {{l}^{{\text{u}}}},\,\,\,\,{{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{u}}}} \right)} \right|}}_{{2a,{{{{\sigma }}}^{{{\text{ext}}}}}}}} = 0;} \\ {{{{\left. {F_{l}^{''}\left( {l = {{l}^{{\text{u}}}},\,\,\,\,{{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{u}}}} \right)} \right|}}_{{2a,{{{{\sigma }}}^{{{\text{ext}}}}}}}} > 0.} \end{array}} \right.$$

(8)

Figure 2a shows the dependence $F\left( l \right)$ for ${{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{u}}}~$ (curve 4).

The dependence $F\left( l \right)$ for an intermediate value of ${{w}_{{{\text{dp}}}}}$ from the interval $\left( {w_{{{\text{dp}}}}^{{\text{d}}},w_{{{\text{dp}}}}^{{\text{u}}}} \right)$ is shown in Fig. 2a, curve 3. In this case, with an increase in the crack length, after reaching a certain value $l = {{l}_{0}}$, the crack reaches a state of unstable equilibrium. When $l > {{l}_{0}}$, the crack opens spontaneously and reaches a position of stable equilibrium, $l = {{l}_{{{\text{eq}}}}}$ (stable crack). Below, following the terminology proposed in [6, 11], the crack with length $l = {{l}_{0}}$ will be called a crack nucleus.

With an increase in the strength of the disclination dipole ${{w}_{{{\text{dp}}}}}$ within the interval under consideration, $\left( {w_{{{\text{dp}}}}^{{\text{d}}},w_{{{\text{dp}}}}^{{\text{u}}}} \right)$, the length of the crack nucleus decreases and the length of the stable crack increases (Fig. 2b). Carrying out similar calculations for different values of the dipole arm $2a$ (at a fixed value of the external stress), the dependences of $w_{{{\text{dp}}}}^{{\text{d}}}$ and $w_{{{\text{dp}}}}^{{\text{u}}}$ on the dipole length can be found.

The results are shown in Fig. 3. The upper and lower curves in Figs. 3b and 3c represent the dependences $w_{{{\text{dp}}}}^{{\text{u}}}\left( {2a} \right)$ and $w_{{{\text{dp}}}}^{{\text{d}}}\left( {2a} \right)$, respectively. In the configuration space $\left( {{{w}_{{{\text{dp}}}}},2a} \right)$, the curves $w_{{{\text{dp}}}}^{{\text{d}}}\left( {2a} \right)$ and $w_{{{\text{dp}}}}^{{\text{u}}}\left( {2a} \right)$ cut off the domains (fields) of existence of stable cracks (Fig. 3, highlighted in gray).

Fig. 3.

Domains of existence of a stable crack in the configuration parameter space $\left( {{{w}_{{{\text{dp}}}}},2a} \right)$ at (a) ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 0,$ (b) ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 2.2 \times {{10}^{{ - 3}}},$ and (c) ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 3.3 \times {{10}^{{ - 3}}}.$

As can be seen from the analysis performed, with an increase in the dipole length, the interval $\left( {w_{{{\text{dp}}}}^{{\text{d}}},w_{{{\text{dp}}}}^{{\text{u}}}} \right)$ gradually narrows and shrinks to a point at $w_{{{\text{dp}}}}^{*} = w_{{{\text{dp}}}}^{{\text{d}}} = w_{{{\text{dp}}}}^{{\text{u}}}$ at a certain value of the disclination dipole length $2a{\text{*}}.$ To illustrate the aforesaid, Fig. 4 shows the evolution of the dependences $F\left( l \right)$ with an increase in the dipole length $2a$, calculated at the values of the dipole strength ${{w}_{{{\text{dp}}}}} = {{\left( {w_{{{\text{dp}}}}^{{\text{d}}} + w_{{{\text{dp}}}}^{{\text{u}}}} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{{\text{dp}}}}^{{\text{d}}} + w_{{{\text{dp}}}}^{{\text{u}}}} \right)} 2}} \right. \kern-0em} 2}.$ It can be seen that, with an increase in the dipole arm, the difference between the values of the local maximum F_max and the local minimum ${{F}_{{{\text{min}}}}}$ on the curves $F\left( l \right)$ decreases and, at $2a = 2a{\text{*}}$, the curve with the local maximum and minimum degenerates into a curve with an inflection (in this case, ${{F}_{{{\text{max}}}}} = {{F}_{{{\text{min}}}}} = 2\gamma$). With a further increase in the disclination dipole length, the existence of stable cracks becomes impossible.

Fig. 4.

Dependences of the configurational force $F\left( l \right),$ calculated for different values of the strength ${{w}_{{{\text{dp}}}}}$ and arm $2a$ of the disclination dipole at ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 3.3 \times {{10}^{{ - 3}}}{\text{:}}$ (1) ${{w}_{{{\text{dp}}}}} = 0.12,$ $2a = 0.2\,\,\mu {\text{m}};$ (2) ${{w}_{{{\text{dp}}}}} = 0.09,$ $2a = 0.3\,\,\mu {\text{m}};$ (3) ${{w}_{{{\text{dp}}}}} = 0.07,$ $2a = 0.4\,\,\mu {\text{m}};$ (4) ${{w}_{{{\text{dp}}}}} = 0.06,$ $2a = 0.5\,\,\mu {\text{m}};$ and (5) ${{w}_{{{\text{dp}}}}} = 0.06,$ $2a = 0.59\,\,\mu {\text{m}}.$

Comparison of Figs. 3a, 3b, and 3c shows that a successive increase in the external stress ${{\sigma }^{{{\text{ext}}}}}$ leads to an increasingly pronounced localization of the field of existence of stable microcracks originating in the vicinity of a disclination dipole and its shift towards smaller values of the dipole length.

Since stable equilibrium of cracks is possible only at values of ${{w}_{{{\text{dp}}}}}$ inside the interval $\left( {w_{{{\text{dp}}}}^{{\text{d}}},w_{{{\text{dp}}}}^{{\text{u}}}} \right)$ and their length at fixed ${{\sigma }^{{{\text{ext}}}}}$ and 2а increases monotonically with increasing ${{w}_{{{\text{dp}}}}},$ the crack length also turns out to be enclosed in a certain interval $\left( {{{l}^{{\text{d}}}},{{l}^{{\text{u}}}}} \right).$ Its lower bound ${{l}^{{\text{d}}}}$ corresponds to the strength of the disclination dipole ${{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{d}}},$ and the upper bound ${{l}^{{\text{u}}}}$ corresponds to ${{w}_{{{\text{dp}}}}} = w_{{{\text{dp}}}}^{{\text{u}}}.$ The region of possible lengths of stable cracks calculated at ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 0,$ ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 2.2 \times {{10}^{{ - 3}}},$ and ${{~{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{~{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 3.3 \times {{10}^{{ - 3}}}$ are shown in Fig. 5. As expected, an increase in the external stress leads to a contraction of the intervals of (the existence of) stable crack lengths at each fixed value of the dipole arm and a shift of the upper and lower bounds of this interval towards smaller $l.$

Fig. 5.

Ranges of the lengths of stable cracks, calculated at different values of external stress: (a) ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 0;$ (b) ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 2.2 \times {{10}^{{ - 3}}};$ and (c) ${{{{\sigma }^{{{\text{ext}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{{\text{ext}}}}}} G}} \right. \kern-0em} G} = 3.3 \times {{10}^{{ - 3}}}.$

CONCLUSIONS

The analysis performed in this work shows that the emergence of equilibrium stable microcracks in the vicinity of a disclination dipole at a given value of the external stress is possible only in a certain region of the configuration space of the parameters of the mesodefect under consideration.

Despite the relative simplicity of the presented model, some conclusions can be drawn about the character of the accumulation of cracks in the fragmented structure. In the first approximation, rotational mesodefects in such a structure can be represented as a set of dipoles of junction disclinations of different strength, distributed along the boundaries of fragments. In this case, the emergence of stable cracks is possible near those disclination dipoles whose strengths fall within the critical interval $\left( {w_{{{\text{dp}}}}^{{\text{d}}},w_{{{\text{dp}}}}^{{\text{u}}}} \right)$ considered above. The rise of such critical structural sections during plastic deformation will lead to the accumulation of microcracks in them and the formation of ductile fracture centers.