1 Introduction

Using elasticity theory, Eshelby [1] predicted that a screw dislocation in a finite cylindrical rod can twist the crystalline lattice into a chiral pattern. This ‘Eshelby twist’ has been observed in chiral branched nanowires [2, 3] and in nanotubes [4]. The Eshelby twist was recently applied to synthesize helical multilayered van der Waals crystals [5,6,7,8,9].

This paper is concerned with two defect problems in nanowires. In the first part of our study, we consider the problem of an arbitrary number of identical parallel screw dislocations evenly distributed along a concentric circle in an isotropic elastic rod of radius R. An equilibrium configuration for all of these screw dislocations is possible only in such a distribution (our extensive calculations suggest that no equilibrium configuration can be found for other distributions of the screw dislocations). The incorporation of the Eshelby twist resulting from these screw dislocations implies the co-existence of both a stable and an unstable equilibrium position for each dislocation. As the number of screw dislocations approaches infinity, these stable and unstable equilibrium positions become extremely close to each other (although the two cannot merge) and are at a distance of 0.7071R from the centerline. When each screw dislocation is at its stable equilibrium position, the ratio of the induced twist to that caused by a super-dislocation at the center of the rod is a decreasing function of the dislocation number N ranging from unity for \(N = 1\) to 0.5 as \(N \to \infty\). In the second part of this paper, we consider the problem of a mode III Zener–Stroh central crack in an isotropic elastic rod of circular cross-section. According to Zener [10] and Stroh [11], dislocations piled up along a slip plane stopped by an obstacle or a bi-material interface could coalesce into a micro crack to release the high level energy accumulated in the dislocation pileup. On the other hand, the mode III Zener–Stroh central crack will induce the Eshelby twist, which suppresses the stress level near the crack tips, and meanwhile keeps the boundary value problem as simple as possible. The Zener–Stroh central crack is simulated by a continuous distribution of screw dislocations. Consequently, a Cauchy-type singular integral equation is derived and is solved numerically using the Gauss–Chebyshev integration formula [12] leading to the mode III stress intensity factor at the crack tip and the Eshelby twist induced by the imaginary screw dislocations comprising the Zener–Stroh crack. Our numerical result indicates that the Eshelby twist will significantly reduce the magnitude of the stress intensity factor. In our discussions, we neglect the surface effects on the lateral surface of the rod (for the two problems) and on the crack surfaces (for the second crack problem).

2 Multiple screw dislocations in a nanowire

As shown in Fig. 1, we first consider an arbitrary number N of screw dislocations each with a common Burgers vector b that lie parallel to the \(x_{3}\)-axis of a rod of radius R with its center at the origin of the coordinate system. These screw dislocations are evenly distributed at \(z = x_{1} + {\text{i}}x_{2} = \delta \exp \left( {{\text{i}}\frac{2\pi (n - 1)}{N}} \right), \, n = 1, \, 2, \cdots , \, N, \, 0 \le \delta < R\) along the circle \(\left| z \right| = \delta\). The rod is isotropic elastic with shear modulus μ and its surface \(\left| z \right| = R\) is traction-free. Using the Peach–Koehler formula [13], the image force F acting on each screw dislocation is along the radial direction of the rod and is given explicitly by

$$ \frac{2\pi RF}{{\mu b^{2} }} = \sum\limits_{n = 2}^{N} {\frac{1}{{t - t\exp \left( {{\text{i}}\frac{2\pi (n - 1)}{N}} \right)}}} - \sum\limits_{n = 1}^{N} {\frac{1}{{t - \frac{1}{t}\exp \left( {{\text{i}}\frac{2\pi (n - 1)}{N}} \right)}}} - 2Nt(1 - t^{2} ), $$
(1)

where

$$ t = \frac{\delta }{R}. $$
(2)
Fig. 1
figure 1

An arbitrary number N of like-signed identical parallel screw dislocations evenly distributed along the concentric circle \(\left| z \right| = \delta\) in an isotropic elastic rod of radius R. The dots represent the N screw dislocations

Full size image

The last term on the right-hand side of Eq. (1) is the contribution of the Eshelby twist caused by the N screw dislocations. When \(N = 1\), the first sum on the right-hand side of Eq. (1) becomes zero. Thus, the image force expression in Eq. (1) is valid for an arbitrary positive integer N. Our numerical results indicate that there always exist two equilibrium positions \(t = t_{1} , \, t_{2} \, (0 \le t_{1} < t_{2} < 1)\) for each screw dislocation. Specifically, as shown in Fig. 2, the force is positive when \(0 \le t < t_{1}\), indicating that the N like-signed dislocations repel each other; the force is negative when \(t_{1} < t < t_{2}\), indicating that each dislocation is repelled from the outer equilibrium position at \(t = t_{2}\) and is attracted toward the inner equilibrium position at \(t = t_{1}\); the force is positive again when \(t > t_{2}\), indicating that each dislocation is repelled from the outer equilibrium position at \(t = t_{2}\). Thus \(t = t_{1}\) is a stable equilibrium position and \(t = t_{2}\) is an unstable equilibrium position for each screw dislocation. We illustrate in Fig. 3 the two equilibrium positions \(t_{1}\) and \(t_{2}\) for different values of N. It is seen from Fig. 3 that: (i) \(t_{1} = 0, \, t_{2} = 0.54\) when \(N = 1\), which is in agreement with that by Eshelby [1]; (ii) \(t_{1} = 0.4, \, t_{2} = 0.67\) when \(N = 2\), which is in agreement with that by Zhu et al. [2]; (iii) \(t_{1}\) increases monotonically from zero to 0.7071 as N increases from 1 to infinity; (iv) \(t_{2}\) first increases and then decreases to 0.7071 as N increases from 1 to infinity, and attains its maximum value of 0.8 when \(N = 10\); (v) \(t_{1} \approx t_{2} \cong 0.7071\) as \(N \to \infty\) (the stable and unstable equilibrium positions cannot merge as \(N \to \infty\)).

Fig. 2
figure 2

Variations of the image force on each screw dislocation as a function of t for different values of \(N = 10, \, 10^{2} , \, 10^{3} , \, 10^{4}\)

Full size image
Fig. 3
figure 3

Variations of the equilibrium positions \(t_{1}\) and \(t_{2}\) as functions of N

Full size image

The Eshelby twist of the rod induced by the N screw dislocations each located at the stable equilibrium position \(t = t_{1}\) is

$$ \alpha = - \frac{{bN(1 - t_{1}^{2} )}}{{\pi R^{2} }}, $$
(3)

which is illustrated in Fig. 4. In Eq. (3), α is the twist in radians per unit length. It is seen from Fig. 4 that \(- {{\pi R^{2} \alpha } \mathord{\left/ {\vphantom {{\pi R^{2} \alpha } {(bN)}}} \right. \kern-0pt} {(bN)}}\), which is the ratio of the induced twist to that caused by a super-dislocation with Burgers vector \(Nb\) at the center of the rod, is a decreasing function of N ranging from unity for \(N = 1\) to 0.5 as \(N \to \infty\).

Fig. 4
figure 4

Variation of the Eshelby twist as a function of N

Full size image

The problem becomes more involved if the membrane-type Gurtin–Murdoch surface elasticity [14,15,−16] is taken into account at the boundary \(\left| z \right| = R\). No closed-form solution is available in this case. However, we can roughly sketch this rather complex scenario. Since a membrane-type stiff surface at \(\left| z \right| = R\) will always repel the nearby screw dislocations, there may exist three equilibrium positions for each screw dislocation: two stable and one unstable in between. This case is worthy of further investigation.

3 A mode III Zener–Stroh central crack in a nanowire

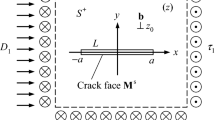
As shown in Fig. 5, we next consider an isotropic elastic rod of radius R weakened by a mode III Zener–Stroh crack \(L: \, \left\{ {x_{2} = 0^{ \pm } , \, - a < x_{1} < a} \right\}\) with its net Burgers vector \(b_{T}\). The surface \(\left| z \right| = R\) is traction-free. The Zener–Stroh crack can be simulated by a continuous distribution of screw dislocations. By enforcing the traction-free condition on the crack surfaces, we arrive at the following Cauchy-type singular integral equation:

$$ \frac{1}{\pi }\int_{ - a}^{a} {\left[ {\frac{1}{{x_{1} - \delta }} - \frac{\delta }{{x_{1} \delta - R^{2} }} - \frac{2}{{R^{4} }}x_{1} (R^{2} - \delta^{2} )} \right]g(\delta ){\text{d}}\delta } = 0, \, - a < x_{1} < a, $$
(4)

where \(g(\delta )\) is the unknown dislocation density function which satisfies the condition that

$$ \int_{ - a}^{a} {g(\delta ){\text{d}}\delta } = b_{T} $$
(5)

for a Zener–Stroh crack. The last term in the square brackets on the left-hand side of Eq. (4) is the contribution of the Eshelby twist induced by the imaginary screw dislocations comprising the Zener–Stroh crack. Using the following change of variables:

$$ x_{1} = ax, \, \delta = at, $$
(6)
Fig. 5
figure 5

An isotropic elastic rod of radius R weakened by a mode III Zener–Stroh central crack of half-length a

Full size image

Equations (4) and (5) can be written in the following normalized form

$$ \begin{gathered} \frac{1}{\pi }\int_{ - 1}^{1} {\left[ {\frac{1}{x - t} + \frac{{\beta^{2} t}}{{1 - \beta^{2} xt}} - 2\beta^{2} x(1 - \beta^{2} t^{2} )} \right]\tilde{g}(t){\text{d}}t} = 0, \, - 1 < x < 1; \hfill \\ \frac{1}{\pi }\int_{ - 1}^{1} {\tilde{g}(t){\text{d}}t} = 1, \hfill \\ \end{gathered} $$
(7)

where

$$ \beta = \frac{a}{R}, \, \tilde{g}(t) = \frac{\pi ag(t)}{{b_{T} }} = \frac{\pi ag(\delta )}{{b_{T} }}. $$
(8)

The dimensionless function \(\tilde{g}(t)\) can be written as

$$ \tilde{g}(t) = \frac{Y(t)}{{\sqrt {1 - t^{2} } }}, \, - 1 \le t \le 1, $$
(9)

where \(Y(t)\) is an unknown regular function.

By substituting Eq. (9) into Eq. (7) and applying the Gauss–Chebyshev integration formula [12], we arrive at the following set of n linear algebraic equations for the n unknowns \(Y(t_{1} ), \, Y(t_{2} ), \cdots , \, Y(t_{n} )\)

$$ \begin{gathered} \sum\limits_{k = 1}^{n} {\frac{1}{n}Y(t_{k} )\left[ {\frac{1}{{x_{r} - t_{k} }} + \frac{{\beta^{2} t_{k} }}{{1 - \beta^{2} x_{r} t_{k} }} - 2\beta^{2} x_{r} (1 - \beta^{2} t_{k}^{2} )} \right]} = 0, \hfill \\ \sum\limits_{k = 1}^{n} {\frac{1}{n}Y(t_{k} )} = 1, \, t_{k} = \cos \frac{\pi }{2n}(2k - 1), \, x_{r} = \cos \frac{\pi r}{n}, \, r = 1, \, 2, \cdots , \, n - 1. \hfill \\ \end{gathered} $$
(10)

Once \(Y(t_{1} ), \, Y(t_{2} ), \cdots , \, Y(t_{n} )\) have been uniquely determined by solving the set of n simultaneous linear algebraic equations in Eq. (10), the mode III stress intensity factor at the right crack tip, denoted as K, is given by

$$ \frac{K}{{K^{\infty } }} = Y(1), $$
(11)

where

$$ K^{\infty } = \frac{{\mu b_{T} }}{{2\sqrt {\pi a} }} $$
(12)

is the mode III stress intensity factor for a Zener–Stroh crack of half-length a in an infinite homogeneous material [17]. In addition, the Eshelby twist of the rod induced by the imaginary screw dislocations comprising the Zener–Stroh crack is determined by

$$ \frac{\alpha }{{\alpha_{0} }} = \frac{1}{\pi }\int_{ - 1}^{1} {(1 - \beta^{2} t^{2} )\tilde{g}(t){\text{d}}t} = \sum\limits_{k = 1}^{n} {\frac{1}{n}Y(t_{k} )(1 - \beta^{2} t_{k}^{2} )} , $$
(13)

where

$$ \alpha_{0} = - \frac{{b_{T} }}{{\pi R^{2} }}, $$
(14)

which is the twist induced by a screw dislocation with Burgers vector \(b_{T}\) at the center of the rod.

We illustrate in Fig. 6 the determined dislocation density function \(\tilde{g}(t)\) with \(\beta = 0.8\). For ease of comparison, we also present in Fig. 6 the result when the rod is under anti-plane strain deformation without twist. It is seen from Fig. 6 that: (i) \(\tilde{g}(t)\) is an even function of t, i.e., \(\tilde{g}( - t) = \tilde{g}(t)\); (ii) \(\tilde{g}(t)\) attains its local maximum at \(t = 0\) in the presence of Eshelby twist and can only attains its global minimum at \(t = 0\) in the absence of Eshelby twist; (iii) the majority of the imaginary screw dislocations (around 70%) forming the Zener–Stroh crack are almost constantly distributed in the central portion \(- 0.8 \le t \le 0.8\) due to the Eshelby twist.

Fig. 6
figure 6

Variation of the function \(\tilde{g}(t) = {{Y(t)} \mathord{\left/ {\vphantom {{Y(t)} {\sqrt {1 - t^{2} } }}} \right. \kern-0pt} {\sqrt {1 - t^{2} } }}\) as a function of t with \(\beta = 0.8\)

Full size image

We illustrate in Fig. 7 the variation of \({K \mathord{\left/ {\vphantom {K {K^{\infty } }}} \right. \kern-0pt} {K^{\infty } }}\) as a function of β. In Fig. 7, we also present the result when the rod is under anti-plane strain deformation without twist. It is seen from Fig. 7 that: (i) \({K \mathord{\left/ {\vphantom {K {K^{\infty } }}} \right. \kern-0pt} {K^{\infty } }} < 1\) when \(\beta < 0.97\) and \({K \mathord{\left/ {\vphantom {K {K^{\infty } }}} \right. \kern-0pt} {K^{\infty } }} > 1\) when \(0.97 < \beta < 1\); (ii) \(\min \left\{ {{K \mathord{\left/ {\vphantom {K {K^{\infty } }}} \right. \kern-0pt} {K^{\infty } }}} \right\} = 0.63\) at \(\beta = 0.812\); (iii) the magnitude of the stress intensity factor is significantly reduced when the Eshelby twist of the rod is taken into account (e.g., \({K \mathord{\left/ {\vphantom {K {K^{\infty } }}} \right. \kern-0pt} {K^{\infty } }}\) is always larger than unity when there is no twist).

Fig. 7
figure 7

Variation of \({K \mathord{\left/ {\vphantom {K {K^{\infty } }}} \right. \kern-0pt} {K^{\infty } }}\) as a function of β

Full size image

We illustrate in Fig. 8 the variation of \({\alpha \mathord{\left/ {\vphantom {\alpha {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }}\) as a function of β. It is seen from Fig. 8 that \({\alpha \mathord{\left/ {\vphantom {\alpha {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }}\) is a decreasing function of β ranging from \({\alpha \mathord{\left/ {\vphantom {\alpha {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }} = 1\) at \(\beta = 0\) to \({\alpha \mathord{\left/ {\vphantom {\alpha {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }} = 0.1323\) as \(\beta \to 1\).

Fig. 8
figure 8

Variation of \({\alpha \mathord{\left/ {\vphantom {\alpha {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }}\) as a function of β

Full size image

4 Conclusions

We have solved two defect problems associated with (i) multiple screw dislocations and (ii) a Zener–Stroh central crack in an elastic rod of circular cross-section. In the first problem, all of the N real screw dislocations are evenly distributed along the concentric circle \(\left| z \right| = \delta\) (see Fig. 1); in the second problem, the imaginary screw dislocations are continuously and unevenly distributed along the segment \([ - a, \, a]\) (see Fig. 6). Due to the stabilizing force provided by the Eshelby twist, an arbitrary number N of identical screw dislocations can find a stable equilibrium configuration at \(t = t_{1}\). Due to the effect of the Eshelby twist, the magnitude of the mode III stress intensity factor at the crack tip is significantly reduced. Although multiple dislocation lines were not observed in PbSe chiral branched nanowires [2], additional suitably designed experiments are expected to validate our theoretical predictions (e.g., for central cracked nanowires).