Uncertain interest rate model for Shanghai interbank offered rate and pricing of American swaption

Abstract

In the framework of uncertainty theory, this paper investigates the pricing problem of American swaption. By assuming that the floating interest rate obeys an uncertain differential equation, the pricing formula of American swaption is derived. Furthermore, parameter estimation of the uncertain interest rate model is given, and the uncertain hypothesis test shows that the uncertain interest rate model fits the Shanghai interbank offered rate well. Finally, as a byproduct, this paper also indicates that stochastic differential equations cannot model real-world interest rates.

1 Introduction

An interest rate swap is a contract between two players who consent to exchange cash flows over an expiration time. The buyer of a payer (receiver) swaption has a right to pay fixed (floating) interest rate cash flow and receive floating (fixed) interest rate cash flow. As a vital type of derivative, swaption gives its owner the right but not the obligation to enter into an underlying interest rate swap, which allows to price and hedge interest rate risk. According to the exercise timing right, swaption can be divided into two classes. One is European swaption, which can be exercised only at the expiration date. The other one is American swaption, which can be exercised at any time prior to and including its maturity date.

The traditional pricing models of swaption are mainly based on probability theory, which assumes that the floating interest rate follows a stochastic differential equation. For example, Jagannathan et al. (2003) discussed European swaption based on the Cox-Ingersoll-Ross model; Choi and Shin (2016) proposed European swaption in the multifactor Gaussian term structure model; Filipović and Kitapbayev (2018) studied American swaption in the linear-rational term structure model.

However, Liu (2013) pointed out that stochastic differential equations may be unsuitable for modeling financial markets and suggested uncertain differential equations (UDEs) based on uncertainty theory to model finance. Here uncertainty theory (Liu, 2007) is a branch of mathematics established on normality, duality, subadditivity, and product axioms. Later, Liu and Liu (2022b) offered a UDE to model Alibaba stock price; Ye and Liu (2022a) suggested a UDE to model the USD-CNY exchange rate rather than a stochastic differential equation with the help of the uncertain hypothesis test. Nowadays, UDE theory has become a potential mathematical tool to model financial markets. For more details on the UDE, please refer to Yao (2016).

In the field of UDE’s parameter estimation, Yao and Liu (2020) presented the method of moments from a difference scheme, which needs to be observed for short enough time intervals. On the other hand, for the big time intervals between observations, Liu and Liu (2022b) revised the method of moments based on the concept of UDE’s residuals. Besides, Lio and Liu (2021) considered the initial value estimation, and Liu and Liu (2022a) proposed the uncertain maximum likelihood estimation method. Finally, Ye and Liu (2022a) used an uncertain hypothesis test to determine whether or not a UDE fits the observed data. For more details on the uncertain hypothesis test, please refer to Ye and Liu (2022b).

In the uncertain financial market, Xiao et al. (2016) first proposed the interest rate swap problem; Liu and Yang (2022) considered the European swaption pricing problem; Liu and Yang (2021) studied the barrier swaption pricing problem; Lu et al. (2022) further investigated the barrier swaption in an uncertain mean-reverting model; Yu et al. (2022) put forward the equity swaps problem.

This paper analytically prices American swaption in the framework of uncertainty theory, which increases the option’s value to the holder relative to the European one. The rest of the paper is structured as follows. Section 2 reviews some preliminaries in uncertainty theory and proves a lemma to prepare for the main result. Section 3 proposes the American swaption assuming that the floating interest rate follows a UDE and derives the pricing formula. Section 4 estimates the parameters of the uncertain interest rate model according to the Shanghai interbank offered rate (SHIBOR) and gives a numerical example to calculate the American swaption. Finally, Section 5 offers the conclusion.

2 Preliminaries

This section will introduce some basic definitions and theorems in uncertainty theory and then prove a lemma.

Definition 1

(Liu, 2009) An uncertain process $C_t$ is called Liu process if the following three conditions are satisfied,

(i) $C_0$ = 0 and almost all sample paths are Lipschitz continuous,

(ii) $C_t$ has stationary and independent increments,

(iii) the increment $C_{s+t}-C_s$ is a normal uncertain variable with an uncertainty distribution

$$\begin{aligned} F_t\left( x\right) = \left( 1+\exp \left( \frac{-\pi x}{\sqrt{3} t}\right) \right) ^{-1}. \end{aligned}$$

Definition 2

(Liu, 2008) Let $C_t$ be a Liu process and $g(\cdot )$ and $h(\cdot )$ be two real functions. Then

$$\begin{aligned} \mathrm{d}r_t = g\left( t, r_t \right) \mathrm{d}t + h\left( t, r_t\right) \mathrm{d}C_t \end{aligned}$$

(1)

is called a UDE. The uncertain process $r_t$ satisfying the above equation at time t is the solution.

Definition 3

(Yao & Chen, 2013) Let $\alpha$ be a number with $0<\alpha <1$. A UDE (1) is said to have an $\alpha$-path $r_t^\alpha$ if it solves the corresponding ordinary differential equation

$$\begin{aligned} \mathrm{d}r_t^\alpha = g\left( t,r_t^\alpha \right) \mathrm{d}t + |h\left( t,r_t^\alpha \right) |F^{-1}\left( \alpha \right) \mathrm{d}t \end{aligned}$$

(2)

where $F^{-1}\left( \alpha \right)$ is the inverse standard normal uncertainty distribution, i.e.,

$$\begin{aligned} F^{-1}\left( \alpha \right) =\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }. \end{aligned}$$

Theorem 1

(Yao & Chen, 2013) Let $r_t$ and $r_t^\alpha$ be the solution and $\alpha$-path of the UDE (1), respectively. Then

$$\begin{aligned} {{\mathcal {M}}}\left\{ r_t \le r_t^\alpha ,\forall t\right\} = \alpha ,\quad {{\mathcal {M}}}\left\{ r_t > r_t^\alpha ,\forall t\right\} = 1-\alpha . \end{aligned}$$

Lemma 1

Let $r_t$ and $r_t^\alpha$ be the solution and $\alpha$-path of the UDE (1), respectively, and r be a positive number. Then for any time $T>0$, the supremum

$$\begin{aligned} \sup _{0\le s\le T}\left( -\int _0^sr_t\mathrm{d}t+rs\right) \end{aligned}$$

has an inverse uncertainty distribution

$$\begin{aligned} {\bar{F}}_T^{-1}(\alpha )=\sup _{0\le s\le T}\left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) , \end{aligned}$$

and the infimum

$$\begin{aligned} \inf _{0\le s\le T}\left( -\int _0^sr_t\mathrm{d}t+rs\right) \end{aligned}$$

has an inverse uncertainty distribution

$$\begin{aligned} {\underline{F}}_T^{-1}(\alpha )=\inf _{0\le s\le T}\left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) . \end{aligned}$$

Proof

For any give time T, it is always true that

$$\begin{aligned} \begin{aligned}&\left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) \le \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} \\&\quad \supset \left\{ -\int _0^s r_{t}\mathrm{d}t+rs\le -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs, \forall \ s\in [0,T]\right\} \\&\quad \supset \{r_{t}\ge r_{t}^{1-\alpha },\forall t\}. \end{aligned} \end{aligned}$$

By monotonicity theorem of the uncertain measure and Theorem 1, we get

$$\begin{aligned} \begin{aligned}&{{\mathcal {M}}}\left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) \le \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} \\&\quad \ge {{\mathcal {M}}}\left\{ r_{t}\ge r_{t}^{1-\alpha },\forall t\right\} =\alpha . \end{aligned} \end{aligned}$$

(3)

Timilarly, we also obtain

$$\begin{aligned} \begin{aligned}&{{\mathcal {M}}}\left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) > \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} \\&\quad \ge {{\mathcal {M}}}\left\{ r_{t}< r_{t}^{1-\alpha },\forall t\right\} =1-\alpha . \end{aligned} \end{aligned}$$

(4)

In addition, since

$$\begin{aligned} \left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) \le \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} \end{aligned}$$

and

$$\begin{aligned} \left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) > \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} \end{aligned}$$

are opposite events, the duality axiom makes

$$\begin{aligned} \begin{aligned}&{{\mathcal {M}}}\left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) \le \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} \\&\quad +{{\mathcal {M}}}\left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) >\sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} =1. \end{aligned} \end{aligned}$$

(5)

It follows from equations (3)-(5) that

$$\begin{aligned} {{\mathcal {M}}}\left\{ \sup _{0\le s\le T}\left( -\int _0^s r_{t}\mathrm{d}t+rs\right) \le \sup _{0\le s\le T}\left( -\int _0^s r_{t}^{1-\alpha }\mathrm{d}t+rs\right) \right\} =\alpha . \end{aligned}$$

Hence,

$$\begin{aligned} \sup _{0\le s\le T}\left( -\int _0^sr_t\mathrm{d}t+rs\right) \end{aligned}$$

has an inverse uncertainty distribution

$$\begin{aligned} {\bar{F}}_T^{-1}(\alpha )=\sup _{0\le s\le T}\left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) . \end{aligned}$$

Similarly, we can prove that the infimum

$$\begin{aligned} \inf _{0\le s\le T}\left( -\int _0^sr_t\mathrm{d}t+rs\right) \end{aligned}$$

has an inverse uncertainty distribution

$$\begin{aligned} {\underline{F}}_T^{-1}(\alpha )=\inf _{0\le s\le T}\left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) . \end{aligned}$$

The theorem is thus verified. $\square$

3 American swaption

In the framework of uncertainty theory, this section proposes the American swaption, which can be exercised at any time prior to and including its maturity date.

3.1 Payer swaption

The buyer of a payer swaption has the right to pay fixed interest rate cash flow and receive floating interest rate cash flow at any time prior to and including its maturity date T.

Let r be the fixed interest rate, and $r_t$ be the floating interest rate at time t. Assume that $r_t$ follows a UDE (1) with an initial value $r_0$, $A_0$ represents the notional principal amount, and $f_p$ represents the price of payer swaption. Then the holder of payer swaption pays $f_p$ for buying this contract at time 0, and has the following cash flow

$$\begin{aligned} \begin{aligned}&A_0\sup _{0\le s\le T}\left[ \exp \left( -\int _0^{s}r_\tau \mathrm{d}\tau \right) \left( \exp \left( \int _0^{s}r_\tau \mathrm{d}\tau \right) -\exp \left( r s\right) \right) \right] ^+\\&\quad =A_0\sup _{0\le s\le T}\left[ 1-\exp \left( -\int _0^{s}r_t\mathrm{d}t+rs\right) \right] ^+\\&\quad =A_0\left[ 1-\inf _{0\le s\le T}\exp \left( -\int _0^{s}r_t\mathrm{d}t+rs\right) \right] ^+. \end{aligned} \end{aligned}$$

Thus the net return of the holder at time 0 is

$$\begin{aligned} -f_p+A_0\left[ 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right] ^+ \end{aligned}$$

Similarly, the net return of the seller at time 0 is

$$\begin{aligned} f_p-A_0\left[ 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right] ^+ \end{aligned}$$

Then, the fair price of this payer swaption should make the holder and the seller have an identical expected return, that is,

$$\begin{aligned} \begin{aligned}&-f_p+A_0\left[ 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right] ^+\\&\quad =f_p-A_0\left[ 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right] ^+. \end{aligned} \end{aligned}$$

Therefore, the payer swaption price is

$$\begin{aligned} f_p=\mathrm{E}\left[ A_0\left( 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right) ^+\right] , \end{aligned}$$

and we have the following definition.

Definition 4

Let r be the fixed interest rate, T be the maturity date, and $A_0$ be the notional principal amount. The floating interest rate $r_t$ follows an uncertain differential Eq. (1) with an initial value $r_0$. For the payer swaption, its price is defined as

$$\begin{aligned} \displaystyle f_p=\mathrm{E}\left[ A_0\left( 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right) ^+\right] . \end{aligned}$$

(6)

Theorem 2

For the payer swaption, its price can be calculated as

$$\begin{aligned} \displaystyle f_p=\int _0^1\left[ A_0\left( 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t^{\alpha }\mathrm{d}t+rs\right) \right) ^+\right] \mathrm{d}\alpha \end{aligned}$$

(7)

where $r_t^\alpha$ is the solution of (2).

Proof

From Lemma 1, we obtain the inverse uncertainty distribution of

$$\begin{aligned} \inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \end{aligned}$$

is

$$\begin{aligned} {\underline{F}}_T^{-1}(\alpha )=\inf _{0\le s\le T}\exp \left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) . \end{aligned}$$

Since the function

$$\begin{aligned} A_0\left( 1-x\right) ^+ \end{aligned}$$

is decreasing with respect to x, we have the inverse uncertainty distribution of

$$\begin{aligned} A_0\left( 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \right) ^+ \end{aligned}$$

is

$$\begin{aligned} A_0\left( 1-{\underline{F}}_T^{-1}(1-\alpha )\right) ^+=:F_T^{-1}(\alpha ) \end{aligned}$$

from the operational law of uncertain variables. Then, we get

$$\begin{aligned} F_T^{-1}(\alpha )=A_0\left( 1-\inf _{0\le s\le T}\exp \left( -\int _0^sr_t^\alpha \mathrm{d}t+rs\right) \right) ^+. \end{aligned}$$

Based on the expected value of the uncertain variable, we have

$$\begin{aligned} f_p=\int _0^1F_T^{-1}(\alpha )\mathrm{d}\alpha . \end{aligned}$$

The theorem is thus verified. $\square$

3.2 Receiver swaption

The buyer of a receiver swaption has the right to pay floating interest rate cash flow and receive fixed interest rate cash flow at any time prior to and including its maturity date T.

Let $f_r$ represent the price of receiver swaption. Then the holder of reveiver swaption pays $f_r$ for buying this contract at time 0, and has the following cash flow

$$\begin{aligned} \begin{aligned}&A_0\sup _{0\le s\le T}\left[ \exp \left( -\int _0^sr_\tau \mathrm{d}\tau \right) \left( \exp \left( r s\right) -\exp \left( \int _0^sr_\tau \mathrm{d}\tau \right) \right) \right] ^+\\&\quad =A_0\sup _{0\le s\le T}\left[ \exp \left( -\int _0^sr_\tau \mathrm{d}\tau +rs\right) -1\right] ^+\\&\quad =A_0\left[ \sup _{0\le s\le T}\exp \left( -\int _0^sr_\tau \mathrm{d}\tau +rs\right) -1\right] ^+. \end{aligned} \end{aligned}$$

Thus the net return of the holder at time 0 is

$$\begin{aligned} -f_r+A_0\left[ \sup _{0\le s\le T}\exp \left( -\int _0^sr_\tau \mathrm{d}\tau +rs\right) -1\right] ^+ \end{aligned}$$

Similarly, the net return of the seller at time 0 is

$$\begin{aligned} f_r-A_0\left[ \sup _{0\le s\le T}\exp \left( -\int _0^sr_\tau \mathrm{d}\tau +rs\right) -1\right] ^+. \end{aligned}$$

Then, the fair price of this receiver swaption should make the holder and the seller have an identical expected return, that is,

$$\begin{aligned} \begin{aligned}&-f_r+\mathrm{E}\left[ A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_\tau \mathrm{d}\tau +rs\right) -1\right) ^+\right] \\&\quad =f_r-\mathrm{E}\left[ A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_\tau \mathrm{d}\tau +rs\right) -1\right) ^+\right] . \end{aligned} \end{aligned}$$

Therefore, the receiver swaption price is

$$\begin{aligned} f_r=\mathrm{E}\left[ A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) -1\right) ^+\right] , \end{aligned}$$

and we have the following definition.

Definition 5

Let r be the fixed interest rate, T be the maturity date, and $A_0$ be the notional principal amount. The floating interest rate $r_t$ follows an uncertain differential equation (1) with an initial value $r_0$. For the receiver swaption, its price is defined as

$$\begin{aligned} \displaystyle f_r=\mathrm{E}\left[ A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) -1\right) ^+\right] . \end{aligned}$$

(8)

Theorem 3

For the receiver swaption, its price can be calculated as

$$\begin{aligned} \displaystyle f_r=\int _0^1\left[ A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_t^{\alpha }\mathrm{d}t+rs\right) -1\right) ^+\right] \mathrm{d}\alpha \end{aligned}$$

(9)

where $r_t^\alpha$ is the solution of (2).

Proof

From Lemma 1, we obtain the inverse uncertainty distribution of

$$\begin{aligned} \sup _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) \end{aligned}$$

is

$$\begin{aligned} {\bar{F}}_T^{-1}(\alpha )=\sup _{0\le s\le T}\exp \left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) . \end{aligned}$$

Since the function

$$\begin{aligned} A_0\left( x-1\right) ^+ \end{aligned}$$

is increasing with respect to x, we have the inverse uncertainty distribution of

$$\begin{aligned} A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_t\mathrm{d}t+rs\right) -1\right) ^+ \end{aligned}$$

is

$$\begin{aligned} A_0\left( {\bar{F}}_T^{-1}(\alpha )-1\right) ^+=:F_T^{-1}(\alpha ) \end{aligned}$$

from the operational law of uncertain variables. Then, we get

$$\begin{aligned} F_T^{-1}(\alpha )=A_0\left( \sup _{0\le s\le T}\exp \left( -\int _0^sr_t^{1-\alpha }\mathrm{d}t+rs\right) -1\right) ^+. \end{aligned}$$

Based on the expected value of the uncertain variable, we have

$$\begin{aligned} f_r=\int _0^1F_T^{-1}(\alpha )\mathrm{d}\alpha =\int _0^1F_T^{-1}(1-\alpha )\mathrm{d}\alpha . \end{aligned}$$

The theorem is thus verified. $\square$

4 Uncertain interest rate model

This section will first give the parameter estimation of the uncertain interest rate model based on the SHIBOR and then show an example to calculate American swaption.

4.1 Parameter estimation of the uncertain interest rate model

Consider the overnight SHIBOR from April 1, 2021 to March 15, 2022 (see Table 1 and Fig. 1).

Table 1 Overnight SHIBOR from April 1, 2021 to March 15, 2022 (%)

Fig. 1

Overnight SHIBOR from April 1, 2021 to March 15, 2022

Let $r_1,r_2,\ldots ,r_{238}$ represent the interest rates. Assume the interest rate $r_t$ follows the UDE

$$\begin{aligned} \mathrm{d}r_t=(m-ar_t)\mathrm{d}t+\sigma \mathrm{d}C_t \end{aligned}$$

where m, a and $\sigma$ are unknown parameters. From the revised method of moments proposed by Liu and Liu (2022b), for any fixed parameters $m,\ a,\ \sigma$ and $i\ (2\le i\le 238)$, we solve the updated UDE with an initial value $r_{i-1}$

$$\begin{aligned} \mathrm{d}r_t=(m-ar_t)\mathrm{d}t+\sigma \mathrm{d}C_t, \end{aligned}$$

and get the uncertainty distribution of $r_{t}$

$$\begin{aligned} F_i(x)=\left( 1+\exp \left( \frac{\pi ((ar_{i-1}-m)\exp (-a)+m-ax)}{\sqrt{3}\sigma (1-\exp (-a))}\right) \right) ^{-1}. \end{aligned}$$

Based on the definition of ith residual (Liu & Liu, 2022b), we have

$$\begin{aligned} \varepsilon _i(m,a,\sigma )=F_i(r_i)=\left( 1+\exp \left( \frac{\pi ((ar_{i-1}-m)\exp (-a)+m-ar_i)}{\sqrt{3}\sigma (1-\exp (-a))}\right) \right) ^{-1}. \end{aligned}$$

Then, $\varepsilon _i(m,a,\sigma )\in (0,1)$ can be regarded as a sample of linear uncertainty distribution ${{\mathcal {L}}}(0,1)$.

Since the number of unknown parameters is three and the first three moments of the linear uncertainty distribution ${{\mathcal {L}}}(0,1)$ are 1/2, 1/3, and 1/4, we have the following equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{237}\sum _{i=2}^{238}\varepsilon _i(m,a,\sigma )=\frac{1}{2}\\ \displaystyle \frac{1}{237}\sum _{i=2}^{238}\varepsilon _i^2(m,a,\sigma )=\frac{1}{3}\\ \displaystyle \frac{1}{237}\sum _{i=2}^{238}\varepsilon _i^3(m,a,\sigma )=\frac{1}{4}, \end{array}\right. } \end{aligned}$$

(10)

whose root is

$$\begin{aligned} m=0.0229,\quad a=1.1591,\quad \sigma =0.0032. \end{aligned}$$

Thus we obtain an uncertain interest rate model,

$$\begin{aligned} \mathrm{d}r_t=(0.0229-1.1591r_t)\mathrm{d}t+0.0032\mathrm{d}C_t \end{aligned}$$

(11)

where $r_t$ represents the interest rate. Finally, let us test whether the uncertain interest rate model (11) fits SHIBOR. That is, we should test whether the linear uncertainty distribution ${{\mathcal {L}}}(0,1)$ fits the 237 residuals

$$\begin{aligned} \varepsilon _i(0.0229,1.1591,0.0032),\ i=2,3,\ldots ,238. \end{aligned}$$

See Fig. 2. Given a significance level $\alpha =0.05$, it follows from $\alpha \times 237=11.85$ and the test is

$$\begin{aligned} \begin{aligned} W=&\left\{ (z_2,z_3,\ldots ,z_{238}): \text{ there } \text{ are } \text{ at } \text{ least } \text{12 } \text{ of } \text{ indexes } \text{ i }'\text{ s } \text{ with } \right. \\&\qquad \qquad \qquad \qquad \left. 2\le i\le 238 \text{ such } \text{ that } z_i<0.025 \text{ or } z_i>0.975\right\} . \end{aligned} \end{aligned}$$

(12)

Since only $\varepsilon _{25},\varepsilon _{59},\varepsilon _{127},\varepsilon _{128},\varepsilon _{188},\varepsilon _{189},\varepsilon _{209},\varepsilon _{210},\varepsilon _{211}\notin [0.025,0.975]$, we have $\varepsilon _{2},\varepsilon _{3},\cdots ,\varepsilon _{238}\notin W$. Thus the uncertain interest rate model (11) is a good fit to the interest rates.

Fig. 2

Residual plot of uncertain interest rate model (11)

4.2 Numerical results of American swaption

Consider a payer swaption with notional principal $A_0=10000$, fixed interest rate $r=2.20\%$, floating interest rate $r_t$ follows the uncertain interest rate model (11) with initial value $r_0=2.063\%$, and maturity date $T=1$. First, we obtain the $\alpha$-path of uncertain interest rate model (11) as

$$\begin{aligned} r_t^{\alpha }=r_0\exp {(-at)}+\frac{1}{a}(1-\exp {(-at)})\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) . \end{aligned}$$

Then, from Theorem 2, the price of the payer swaption is

$$\begin{aligned} f_p=0.3883 \end{aligned}$$

and the price of the receive swaption is

$$\begin{aligned} f_r=15.4942. \end{aligned}$$

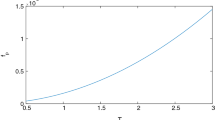
Figure 3a shows $f_p$ with the change of the maturity date T; Fig. 3b shows $f_p$ with the change of the fixed interest rate r, and when $r\ge 2.34\%$, $f_p=0$; Fig. 4a shows $f_r$ with the change of the maturity date T; Fig. 4b shows $f_r$ with the change of the fixed interest rate r, and when $r\le 1.76\%$, $f_r=0$.

Fig. 3

The price $f_p$ with different parameters

Fig. 4

The price $f_r$ with different parameters

5 Conclusion

This paper considered the pricing problem of American swaption in the framework of uncertainty theory. First, assuming that the floating interest rate follows a UDE, the explicit formula of American swaption was derived. In addition, the parameter estimation of the uncertain interest rate model was given based on the data from SHIBOR. Finally, a numerical example was given to show American swaption.

Appendix A Stochastic interest rate model

Let us reconsider overnight SHIBOR from April 1, 2021 to March 15, 2022 (see Table 1). Assume the interest rate obeys a stochastic differential equation

$$\begin{aligned} \mathrm{d}r_t=(m-ar_t)\mathrm{d}t+\sigma \mathrm{d}W_t \end{aligned}$$

where m, a and $\sigma$ are unknown parameters, and $W_t$ is a Wiener process. For any fixed parameters $m,\ a,\ \sigma$ and $i\ (2\le i\le 238)$, we solve the updated stochastic differential equation with an initial value $r_{i-1}$

$$\begin{aligned} \mathrm{d}r_t=(m-ar_t)\mathrm{d}t+\sigma \mathrm{d}W_t, \end{aligned}$$

and get the probability distribution of normal random variable $r_{i}$

$$\begin{aligned} F_i(x)=\frac{1}{\nu \sqrt{2\pi }}\int _{-\infty }^x\exp \left( -\frac{(y-\mu _i)^2}{2\nu ^2}\right) \mathrm{d}y \end{aligned}$$

where $\mu _i$ is the expected value, i.e.,

$$\begin{aligned} \mu _i=\frac{m}{a}+\exp (-a)\left( x_{i-1}-\frac{m}{a}\right) , \end{aligned}$$

and $\nu ^2$ is the variance, i.e.,

$$\begin{aligned} \nu ^2=\frac{\sigma ^2}{2a}+(1-\exp (-2a)). \end{aligned}$$

Define the i-th residual

$$\begin{aligned} \varepsilon _i(m,a,\sigma ):=F_i(r_i). \end{aligned}$$

Then, $\varepsilon _i(m,a,\sigma )\in (0,1)$ can be regarded as a sample of uniform probability distribution ${{\mathcal {U}}}(0,1)$.

Since the number of unknown parameters is three and the first three moments of the uniform probability distribution ${{\mathcal {U}}}(0,1)$ are 1/2, 1/3, and 1/4, we have the following equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{237}\sum _{i=2}^{238}\varepsilon _i(m,a,\sigma )=\frac{1}{2}\\ \displaystyle \frac{1}{237}\sum _{i=2}^{238}\varepsilon _i^2(m,a,\sigma )=\frac{1}{3}\\ \displaystyle \frac{1}{237}\sum _{i=2}^{238}\varepsilon _i^3(m,a,\sigma )=\frac{1}{4}, \end{array}\right. } \end{aligned}$$

(13)

whose root is

$$\begin{aligned} m=0.0303,\quad a=1.5261,\quad \sigma =0.0031. \end{aligned}$$

Thus we obtain a stochastic interest rate model,

$$\begin{aligned} \mathrm{d}r_t=(0.0303-1.5261r_t)\mathrm{d}t+0.0031\mathrm{d}W_t \end{aligned}$$

(14)

Let us test whether the stochastic interest rate model (14) fits SHIBOR interest rates. That is, we should test whether the uniform probability distribution ${{\mathcal {U}}}(0,1)$ fits the 237 residuals

$$\begin{aligned} \varepsilon _i(0.0229,1.1591,0.0032),\ i=2,3,\cdots ,238. \end{aligned}$$

See Fig. 5. To check if the residuals are from the same population ${{\mathcal {U}}}(0,1)$, we apply the “Chi-square goodness-of-fit test” (Snedecor & Cochran, 1989) with a significance level 0.05. Then using the function ‘chi2gof’ in Matlab, we obtain the p-value as 0.0011, indicating that the residuals do not come from the same population ${{\mathcal {U}}}(0,1)$. Therefore, the stochastic interest rate model (14) does not fit overnight SHIBOR.

Fig. 5

Residual plot of stochastic interest rate model (14)