Residual analysis and parameter estimation of uncertain differential equations

Abstract

All existing methods to estimate unknown parameters in uncertain differential equations are based on difference scheme, and do not work when the time intervals between observations are not short enough. In order to overcome this shortage, this paper presents a concept of residual. Afterwards, an algorithm is designed for calculating residuals of uncertain differential equation corresponding to observed data. In addition, this paper presents a method of moments based on residuals to estimate the unknown parameters in uncertain differential equations. Finally, some examples (including Alibaba stock price) are provided to illustrate the parameter estimation method.

1 Introduction

For the purpose of rationally handling the belief degree that something will happen, uncertainty theory was founded by Liu (2007) and perfected by Liu (2009). To this day, uncertainty theory has spawned many theoretical branches and has been successfully applied in various fields of science and engineering.

Among the theoretical branches of uncertainty theory, uncertain differential equation was first proposed by Liu (2008) to model time-varying system. For the purpose of investigating the solution of an uncertain differential equation, Chen and Liu (2010) verified the existence and uniqueness theorem of the solution under linear growth condition and Lipschitz condition. Besides, the stability of uncertain differential equation was first investigated by Liu (2009) to study the dependence of the solution on the initial value. Following that, some theorems were verified by Yao et al. (2013) to perfect the stability analysis of uncertain differential equations, which has been developed by many scholars such as stability in p-th moment (Sheng and Wang 2014), almost sure stability (Liu et al. 2014) and stability in mean (Yao et al. 2015), etc. Another vital problem in uncertain differential equations is how to solve it. For the sake of dealing with this problem, Yao-Chen formula, as one of the most important contributions to uncertain differential equations, was proved by Yao and Chen (2013) to associate uncertain differential equation with ordinary differential equations. On the basis of Yao-Chen formula, some numerical solution methods for uncertain differential equations were studied by scholars such as Euler method (Yao and Chen 2013), Runge-Kutta method (Yang and Shen 2015), Adams method (Yang and Ralescu 2015) and Milne method (Gao 2016), among others. Up to now, the theory of uncertain differential equations has been well developed.

Assume an uncertain process follows an uncertain differential equation and some realizations of this process are observed. A critical problem in the practical application of uncertain differential equations is how to estimate the unknown parameters based on the observed data. For the purpose of dealing with this problem, several methods have been proposed. For instance, Yao and Liu (2020) presented the method of moments, Sheng et al. (2020) investigated least squares estimation, Yang et al. (2020) discussed minimum cover estimation, Liu and Liu (2020) proposed maximum likelihood estimation, Liu (2021) studied generalized moment estimation, and Lio and Liu (2021) presented initial value estimation. Based on those methods, uncertain differential equations have been applied to handling the real-life problems such as pharmacokinetics (Liu and Yang 2021), chemical reaction (Tang and Yang 2021) and epidemic spread (Lio and Liu 2021; Jia and Chen 2021; Chen et al. 2021).

However, the above parameter estimation methods are all based on difference scheme and do not work when the time intervals between observations are not short enough. In order to overcome this shortage, this paper proposes a concept of residual, and investigates a method of moments based on residuals to estimate unknown parameters in uncertain differential equations. The structure of this paper adopts the form of six parts, including this Introduction section. Sect. 2 begins by introducing the concept of residual, and Sect. 3 begins by designing an algorithm to calculate residuals of uncertain differential equation corresponding to observed data. Afterwards, the method of moments based on residuals is presented to estimate unknown parameters of uncertain differential equations in Sect. 4. As an application, the method of moments based on residuals is used to model Alibaba stock price in Sect. 5. Finally, a concise conclusion is given in Sect. 6.

2 Residual

In order to make a connection between uncertain differential equation and observed data of some uncertain process, this section will introduce a concept of residual. Let us consider an uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}C_t \end{aligned}$$

(1)

where f and g are known continuous functions and $C_t$ is a Liu process. Assume

$$\begin{aligned} x_{t_1},x_{t_2},\ldots ,x_{t_n} \end{aligned}$$

(2)

are n observations of some uncertain process $X_t$ at the times $t_{1},t_{2},\ldots ,t_{n}$ with $t_{1}<t_{2}<\cdots <t_{n}$, respectively.

For any given index i with $2\le i\le n$, let us first solve the updated uncertain differential equation,

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}X_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}C_t&{} \\ X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

(3)

where $x_{t_{i-1}}$ is the new initial value at the new initial time $t_{i-1}$. The uncertainty distribution of $X_{t_{i}}$ is thus obtained and represented by $\Phi _{t_{i}}$. Then for any x with $0< x<1$, we have

$$\begin{aligned} \begin{aligned} \text{ M }\{\Phi _{t_i}(X_{t_{i}})\le x\}=\text{ M }\{X_{t_{i}}\le \Phi _{t_i}^{-1}(x)\}=\Phi _{t_i}(\Phi ^{-1} _{t_i}(x)) =x. \end{aligned} \end{aligned}$$

Thus $\Phi _{t_i}(X_{t_{i}})$ is always a linear uncertain variable whose uncertainty distribution is

$$\begin{aligned} F(x)= {\left\{ \begin{array}{ll} 0,&{}\text{ if }~x\le 0\\ x,&{}\text{ if }~0<x\le 1\\ 1,&{}\text{ if }~x>1\\ \end{array}\right. } \end{aligned}$$

denoted by $\text{ L }(0,1)$. Substitute $X_{t_{i}}$ with the observed value $x_{t_{i}}$, and write

$$\begin{aligned} \varepsilon _i=\Phi _{t_i}(x_{t_{i}}). \end{aligned}$$

(4)

Then $\varepsilon _i$ can be regarded as a sample of the linear uncertain variable $\Phi _{t_i}(X_{t_{i}})$. In other words, $\varepsilon _i$ is a sample of linear uncertainty distribution $\text{ L }(0,1)$.

Definition 1

For each index i with $2\le i\le n$, the term $\varepsilon _i$ defined by (4) is called the ith residual of uncertain differential Eq. (1) corresponding to the observed data (2).

Example 1

Assume $x_{t_{1}},x_{t_{2}},\ldots ,x_{t_{n}}$ are observed values of some uncertain process $X_t$ that follows the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu \mathrm{d}t+\sigma \mathrm{d}C_t \end{aligned}$$

(5)

where $\mu$ and $\sigma$ are constants. For each index i with $2\le i\le n$, we solve the updated uncertain differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}X_t=\mu \mathrm{d}t+\sigma \mathrm{d}C_t&{} \\ X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the uncertainty distribution of $X_{t_{i}}$ as follows,

$$\begin{aligned} \Phi _{t_{i}}(x)=\left( 1+\exp \left( \frac{\pi (x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-x)}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-1}. \end{aligned}$$

It follows from Definition 1 that the ith residual is

$$\begin{aligned} \begin{aligned} \varepsilon _i&=\left( 1+\exp \left( \frac{\pi (x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-x_{t_{i}})}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-1}. \end{aligned} \end{aligned}$$

Example 2

Assume $x_{t_{1}},x_{t_{2}},\ldots ,x_{t_{n}}$ are observed values of some uncertain process $X_t$ that follows the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu X_t\mathrm{d}t+\sigma X_t \mathrm{d}C_t \end{aligned}$$

(6)

where $\mu$ and $\sigma$ are constants. For each index i with $2\le i\le n$, we solve the updated uncertain differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}X_t=\mu X_t\mathrm{d}t+\sigma X_t \mathrm{d}C_t&{} \\ X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the uncertainty distribution of $X_{t_{i}}$ as follows,

$$\begin{aligned} \Phi _{t_{i}}(x)=\left( 1+\exp \left( \frac{\pi (\ln x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-\ln x)}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-1}. \end{aligned}$$

It follows from Definition 1 that the ith residual is

$$\begin{aligned} \begin{aligned} \varepsilon _i&=\left( 1+\exp \left( \frac{\pi (\ln x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-\ln x_{t_{i}})}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-1}. \end{aligned} \end{aligned}$$

Example 3

Assume $x_{t_{1}},x_{t_{2}},\ldots ,x_{t_{n}}$ are observed values of some uncertain process $X_t$ that follows the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu tX_t\mathrm{d}t+\sigma tX_t \mathrm{d}C_t \end{aligned}$$

(7)

where $\mu$ and $\sigma$ are constants. For each index i with $2\le i\le n$, we solve the updated uncertain differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}X_t=\mu tX_t\mathrm{d}t+\sigma tX_t \mathrm{d}C_t&{} \\ X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the uncertainty distribution of $X_{t_{i}}$ as follows,

$$\begin{aligned} \Phi _{t_{i}}(x)=\left( 1+\exp \left( \frac{\pi (2\ln x_{t_{i-1}}+\mu (t_{i}^2-t_{i-1}^2)-2\ln x)}{\sqrt{3}\sigma (t_{i}^2-t_{i-1}^2)}\right) \right) ^{-1}. \end{aligned}$$

It follows from Definition 1 that the ith residual is

$$\begin{aligned} \begin{aligned} \varepsilon _i&=\left( 1+\exp \left( \frac{\pi (2\ln x_{t_{i-1}}+\mu (t_{i}^2-t_{i-1}^2)-2\ln x_{t_{i}})}{\sqrt{3}\sigma (t_{i}^2-t_{i-1}^2)}\right) \right) ^{-1}. \end{aligned} \end{aligned}$$

Example 4

Assume $x_{t_{1}},x_{t_{2}},\ldots ,x_{t_{n}}$ are observed values of some uncertain process $X_t$ that follows the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=(m-aX_t)\mathrm{d}t+\sigma \mathrm{d}C_t \end{aligned}$$

(8)

where m, a and $\sigma$ are constants. For each index i with $2\le i\le n$, we solve the updated uncertain differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}X_t=(m-aX_t)\mathrm{d}t+\sigma \mathrm{d}C_t&{} \\ X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the uncertainty distribution of $X_{t_{i}}$ as follows,

$$\begin{aligned} \Phi _{t_{i}}(x)=\left( 1+\exp \left( \frac{\pi \left( (ax_{t_{i-1}}-m)\exp \left( a(t_{i-1}-t_{i})\right) +m-ax\right) }{\sqrt{3}\sigma \left( 1-\exp \left( a(t_{i-1}-t_{i})\right) \right) } \right) \right) ^{-1}. \end{aligned}$$

It follows from Definition 1 that the ith residual is

$$\begin{aligned} \begin{aligned} \varepsilon _i&=\left( 1+\exp \left( \frac{\pi \left( (ax_{t_{i-1}}-m)\exp \left( a(t_{i-1}-t_{i})\right) +m-ax_{t_{i}}\right) }{\sqrt{3}\sigma \left( 1-\exp \left( a(t_{i-1}-t_{i})\right) \right) } \right) \right) ^{-1}. \end{aligned} \end{aligned}$$

3 Numerical method for calculating residuals

For general uncertain differential equations, the following algorithm is able to calculate the ith residual $\varepsilon _i$.

• Algorithm 1

• Step 0: Set $l=0$, $r=1$ and a precision $\delta =0.0001$.

• Step 1: Set $\displaystyle \alpha = (l+r)/2$.

• Step 2: Compute $X_{t_i}^{\alpha }$ of the uncertain differential Eq. (3) by Euler method.

• Step 3: If $X_{t_{i}}^{\alpha }<x_{t_i}$, then $l= \alpha$. Otherwise, $r= \alpha$.

• Step 4: If $|l-r|>\delta$, then go to Step 1.

• Step 5: Output $\varepsilon _i= (l+r)/2$.

Next we provide some examples to illustrate the above algorithm.

Table 1 Observed data in Example 5

Table 2 Residuals in Example 5

Example 5

Table 1 shows 30 observed data of some uncertain process $X_t$ that follows the uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=\left( \frac{2}{t^2}+\frac{1}{X_t}\right) \mathrm{d}t+\frac{X_t}{t}\mathrm{d}C_t. \end{aligned} \end{aligned}$$

(9)

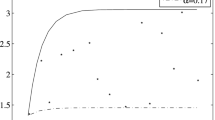
According to Algorithm 1, the 29 residuals of uncertain differential Eq. (9) corresponding to the observed data can be obtained and are shown in Table 2 and Fig. 1.

Fig. 1

Residual plot in Example 5

Example 6

Table 3 shows 30 observed data of some uncertain process $X_t$ that follows the uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=\exp \left( \frac{2}{X_t}\right) \mathrm{d}t+\ln X_t\mathrm{d}C_t. \end{aligned} \end{aligned}$$

(10)

According to Algorithm 1, the 29 residuals of uncertain differential Eq. (10) corresponding to the observed data can be obtained and are shown in Table 4 and Fig. 2.

Table 3 Observed data in Example 6

Table 4 Residuals in Example 6

Fig. 2

Residual plot in Example 6

4 Parameter estimation

Next we will provide a parameter estimation method based on residuals to estimate the unknown parameters in uncertain differential equations. Let us consider the following uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t;\varvec{\theta })\mathrm{d}t+g(t,X_t;\varvec{\theta })\mathrm{d}C_t \end{aligned}$$

(11)

where f and g are known continuous functions but $\varvec{\theta }$ is an unknown vector of parameters. Assume

$$\begin{aligned} x_{t_1},x_{t_2},\ldots ,x_{t_n} \end{aligned}$$

(12)

are observed values of some uncertain process $X_{t}$ at the times $t_{1},t_{2},\ldots ,t_{n}$ with $t_{1}<t_{2}<\cdots <t_{n}$, respectively.

For each given $\varvec{\theta }$, we can produce $n-1$ residuals $\varepsilon _2(\varvec{\theta }),\varepsilon _3(\varvec{\theta }),\ldots ,\varepsilon _n(\varvec{\theta })$ of the uncertain differential Eq. (11) corresponding to the observed data (12). Note that the $n-1$ residuals $\varepsilon _2(\varvec{\theta }),\varepsilon _3(\varvec{\theta }),\ldots ,\varepsilon _n(\varvec{\theta })$ can be regarded as samples of the linear uncertainty distribution $\text{ L }(0,1)$, i.e.,

$$\begin{aligned} \varepsilon _2(\varvec{\theta }),\varepsilon _3(\varvec{\theta }),\ldots ,\varepsilon _n(\varvec{\theta })\sim \text{ L }(0,1). \end{aligned}$$

For each positive integer k, the kth sample moment of the $n-1$ residuals is

$$\begin{aligned} \frac{1}{n-1}\sum _{i=2}^{n}\varepsilon _i^k(\varvec{\theta }), \end{aligned}$$

and the kth population moment of the linear uncertainty distribution $\text{ L }(0,1)$ is

$$\begin{aligned} \frac{1}{k+1}. \end{aligned}$$

The moment estimate $\varvec{\theta }$ is then obtained by equating the first p sample moments to the corresponding first p population moments, where p is the number of unknown parameters. In other words, the moment estimate $\varvec{\theta }$ should solve the system of equations,

$$\begin{aligned} \frac{1}{n-1}\sum _{i=2}^{n}\varepsilon _i^k(\varvec{\theta })=\frac{1}{k+1},\ k=1,2,\ldots ,p. \end{aligned}$$

(13)

The above method to estimate the unknown parameters in uncertain differential equations is called the method of moments based on residuals, and we can solve the system of Eqs. (13) by using MATLAB¹.

Remark 1

Sometimes the system of Eq. (13) has no solution. In this case, we suggest the generalized moment estimation that solves the following minimization problem,

$$\begin{aligned} \min _{\varvec{\theta }}\sum _{k=1}^{p}\left( \frac{1}{n-1}\sum _{i=2}^{n}\varepsilon _i^k(\varvec{\theta })-\frac{1}{k+1}\right) ^2 \end{aligned}$$

(14)

where $\varepsilon _2(\varvec{\theta }),\varepsilon _3(\varvec{\theta }),\ldots ,\varepsilon _n(\varvec{\theta })$ are the residuals and p is the number of unknown parameters. In particular, we can solve the minimization problem (14) by MATLAB².

Table 5 Observed data in Example 7

Example 7

Consider the uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=\mu X_t\mathrm{d}t+\sigma X_t\mathrm{d}C_t \end{aligned} \end{aligned}$$

where $\mu$ and $\sigma >0$ are two unknown parameters to be estimated. Suppose that we have 30 observed data as shown in Table 5, and denote the observed data of $X_t$ at the times $t_1,t_2,\ldots ,t_{30}$ by $x_{t_1},x_{t_2},\ldots ,x_{t_{30}}$, respectively. For any given parameters $\mu$ and $\sigma$, we can obtain the 29 residuals

$$\begin{aligned} \varepsilon _i(\mu ,\sigma )=\left( 1+\exp \left( \frac{\pi (x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-x_{t_{i}})}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-1},\ i=2,3,\ldots ,30 \end{aligned}$$

according to Example 2. Since the number of unknown parameters is 2 and the first two moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2 and 1/3, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{29}\sum _{i=2}^{30}\left( 1+\exp \left( \frac{\pi (x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-x_{t_{i}})}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-1}=\frac{1}{2} &{} \\ \displaystyle \frac{1}{29}\sum _{i=2}^{30}\left( 1+\exp \left( \frac{\pi (x_{t_{i-1}}+\mu (t_{i}-t_{i-1})-x_{t_{i}})}{\sqrt{3}\sigma (t_{i}-t_{i-1})}\right) \right) ^{-2}=\frac{1}{3}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} \mu ^*=1.1201,\ \sigma ^*=0.5417. \end{aligned}$$

Thus we obtain an uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=1.1201X_t\mathrm{d}t+0.5417 X_t\mathrm{d}C_t. \end{aligned} \end{aligned}$$

(15)

Table 6 Observed data in Example 8

Example 8

Consider the uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=\mu \sqrt{X_t}\mathrm{d}t+\sigma \sqrt{X_t}\mathrm{d}C_t \end{aligned} \end{aligned}$$

where $\mu$ and $\sigma >0$ are two unknown parameters to be estimated. Suppose that we have 12 observed data as shown in Table 6. For any given parameters $\mu$ and $\sigma$, we can produce 11 residuals

$$\begin{aligned} \varepsilon _2(\mu ,\sigma ),\varepsilon _3(\mu ,\sigma ),\ldots ,\varepsilon _{12}(\mu ,\sigma ) \end{aligned}$$

by Algorithm 1. Since the number of unknown parameters is 2 and the first two moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2 and 1/3, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{11}\sum _{i=2}^{12}\varepsilon _i(\mu ,\sigma )=\frac{1}{2} &{} \\ \displaystyle \frac{1}{11}\sum _{i=2}^{12}\varepsilon ^{2}_i(\mu ,\sigma )=\frac{1}{3}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} \mu ^*=2.2759,\ \sigma ^*=0.5166. \end{aligned}$$

Thus we obtain an uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=2.2759\sqrt{X_t}\mathrm{d}t+0.5166 \sqrt{X_t}\mathrm{d}C_t. \end{aligned} \end{aligned}$$

(16)

Table 7 Observed data in Example 9

Example 9

Consider the uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=\sin (\mu t)X_t\mathrm{d}t+\cos (\sigma t)X_t\mathrm{d}C_t \end{aligned} \end{aligned}$$

where $\mu$ and $\sigma >0$ are two unknown parameters to be estimated. Suppose that we have 30 observed data as shown in Table 7. For any given parameters $\mu$ and $\sigma$, we can produce 29 residuals

$$\begin{aligned} \varepsilon _2(\mu ,\sigma ),\varepsilon _3(\mu ,\sigma ),\ldots ,\varepsilon _{30}(\mu ,\sigma ) \end{aligned}$$

by Algorithm 1. Since the number of unknown parameters is 2 and the first two moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2 and 1/3, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{29}\sum _{i=2}^{30}\varepsilon _i(\mu ,\sigma )=\frac{1}{2} &{} \\ \displaystyle \frac{1}{29}\sum _{i=2}^{30}\varepsilon ^{2}_i(\mu ,\sigma )=\frac{1}{3}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} \mu ^*=4.9662,\ \sigma ^*=1.0786. \end{aligned}$$

Thus we obtain an uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=\sin (4.9662 t)X_t\mathrm{d}t+\cos (1.0786 t)X_t\mathrm{d}C_t. \end{aligned} \end{aligned}$$

(17)

Table 8 Plasma cimetidine concentration-time data during the constant-rate intravenous infusion in a beagle dog ( Yu and Cao (2017))

Example 10

Pharmacokinetics is the study of the dynamic movement of drug concentrations in the blood of a body. Consider plasma cimetidine concentration in beagle blood during and subsequent to a constant-rate intravenous infusion. Yu and Cao (2017) has provided a collection of data as shown in Table 8. For this experiment of plasma cimetidine concentration, Liu and Yang (2021) derived that the blood plasma cimetidine concentration $X_t$ follows the uncertain pharmacokinetic equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_{t}=\left( k_0-k_1X_t\right) \mathrm{d}t+\sigma \mathrm{d}C_{t} \end{aligned} \end{aligned}$$

where $k_0$, $k_1$ and $\sigma$ are unknown parameters to be estimated. Based on the observed data, the uncertain pharmacokinetic equation was inferred as

$$\begin{aligned} \begin{aligned} \mathrm{d}X_{t}=\left( 5.581-1.473X_t\right) \mathrm{d}t+1.304\mathrm{d}C_{t} \end{aligned} \end{aligned}$$

(18)

by using the method of moments based on difference scheme.

Let us re-estimate the parameters by using the method of moments based on residuals. Denote the observed data of $X_t$ at the times $t_1,t_2,\ldots ,t_{12}$ by $x_{t_1},x_{t_2},\ldots ,$ $x_{t_{12}}$, respectively. For any fixed parameters $k_0$, $k_1$, $\sigma$ and each index i with $2\le i\le 12$, we solve the updated uncertain pharmacokinetic equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \mathrm{d}X_{t}=\left( k_0-k_1X_t\right) \mathrm{d}t+\sigma \mathrm{d}C_{t}&{} \\ \displaystyle X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the ith residual as follows,

$$\begin{aligned} \begin{aligned} \varepsilon _i(k_0,k_1,\sigma )&=\!\!\left( \!1+\exp \!\left( \!\! \frac{\pi \left( (k_1x_{t_{i-1}}-k_0)\exp \left( k_1(t_{i-1}-t_{i})\right) +k_0-k_1x_{t_{i}}\right) }{\sqrt{3}\sigma \left( 1-\exp \left( k_1(t_{i-1}-t_{i})\right) \right) } \!\right) \!\!\right) ^{-1}. \end{aligned} \end{aligned}$$

Since the number of unknown parameters is 3 and the first three moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2, 1/3 and 1/4, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{11}\sum _{i=2}^{12}\varepsilon _i(k_0,k_1,\sigma )=\frac{1}{2} &{} \\ \displaystyle \frac{1}{11}\sum _{i=2}^{12}\varepsilon ^{2}_i(k_0,k_1,\sigma )=\frac{1}{3} &{} \\ \displaystyle \frac{1}{11}\sum _{i=2}^{12}\varepsilon ^{3}_i(k_0,k_1,\sigma )=\frac{1}{4}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} k_0^*=1.7429,\ k_1^*=0.3820,\ \sigma ^*=0.4026. \end{aligned}$$

Thus we obtain an uncertain pharmacokinetic equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_{t}=\left( 1.7429-0.3820X_t\right) \mathrm{d}t+0.4026\mathrm{d}C_{t}. \end{aligned} \end{aligned}$$

(19)

Table 9 ${\mathrm{N}}_2O_5$ concentration data of the decomposition reaction $\mathrm 2N_2O_5 \longrightarrow 4NO_2 + O_2$ ( Henold and Walmsley (1984))

Example 11

Chemical reaction rate is an important research object in chemical kinetics and is a measure of how fast a chemical reaction goes. Consider the decomposition reaction of $\mathrm N_2O_5$ in gas phase. Henold and Walmsley (1984) has provided a collection of experimental data for the concentration of $\mathrm N_2O_5$ as shown in Table 9. For this decomposition reaction, Tang and Yang (2021) derived that the $\mathrm N_2O_5$ concentration $X_t$ obeys the following uncertain chemical reaction equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=-2\mu X_t^2\mathrm{d}t-2\sigma X_t^2\mathrm{d}C_t \end{aligned} \end{aligned}$$

according to the law of mass action, where $\mu$ and $\sigma$ are unknown parameters to be estimated. Based on the observed data, the uncertain chemical reaction equation was obtained as

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=-0.0022 X_t^2\mathrm{d}t-0.0010 X_t^2\mathrm{d}C_t \end{aligned} \end{aligned}$$

(20)

by using the method of moments based on difference scheme.

Let us employ the method of moments based on residuals to re-estimate the parameters. Denote the observed data of $X_t$ at the times $t_1,t_2,\ldots ,t_{10}$ by $x_{t_1},x_{t_2},\ldots ,$ $x_{t_{10}}$, respectively. For any fixed parameters $\mu$, $\sigma$ and each index i with $2\le i\le 10$, we solve the updated uncertain chemical reaction equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}X_t=-2\mu X_t^2\mathrm{d}t-2\sigma X_t^2\mathrm{d}C_t&{} \\ X_{t_{i-1}}=x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the ith residual as follows,

$$\begin{aligned} \begin{aligned} \varepsilon _i(\mu ,\sigma )&=\left( 1+\exp \left( \frac{\pi }{\sqrt{3}\sigma } \left( \frac{x_{t_{i-1}}-x_{t_{i}}}{2(t_{i}-t_{i-1})x_{t_{i-1}}x_{t_{i}}}-\mu \right) \right) \right) ^{-1}. \end{aligned} \end{aligned}$$

Since the number of unknown parameters is 2 and the first two moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2 and 1/3, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{9}\sum _{i=2}^{10}\varepsilon _i(\mu ,\sigma )=\frac{1}{2} &{} \\ \displaystyle \frac{1}{9}\sum _{i=2}^{10}\varepsilon ^{2}_i(\mu ,\sigma )=\frac{1}{3}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} \mu ^*=0.001345,\ \sigma ^*=0.000835. \end{aligned}$$

Thus we obtain an uncertain chemical reaction equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_t=-0.00269 X_t^2\mathrm{d}t-0.00167X_t^2\mathrm{d}C_t. \end{aligned} \end{aligned}$$

(21)

Example 12

RC circuit is a circuit system composed of resistor and capacitor, and is driven by a voltage source. Consider the simple series RC circuit with a constant potential source (5V). Liu (2021) provided a collection of data for the charge stored on the capacitor as shown in Table 10. For this simple series RC circuit, the charge $Q_{t}$ stored on the capacitor was derived to follow the uncertain circuit equation

$$\begin{aligned} \begin{aligned} \mathrm{d}Q_{t}=\left( \frac{5}{r}-\frac{Q_{t}}{rc}\right) \mathrm{d}t+\frac{\sigma }{r}\mathrm{d}C_{t} \end{aligned} \end{aligned}$$

based on the fundamental laws of electrical circuits, where r, c and $\sigma$ are unknown parameters to be estimated. Based on the observed data, the uncertain circuit equation was inferred as

$$\begin{aligned} \begin{aligned} \mathrm{d}Q_{t}=\left( 0.4614-0.0921Q_{t}\right) \mathrm{d}t+0.0133\mathrm{d}C_{t} \end{aligned} \end{aligned}$$

(22)

by using the method of moments based on difference scheme.

Let us re-estimate the parameters by using the method of moments based on residuals. Denote the observed data of $Q_t$ at the times $t_1,t_2,\ldots ,t_{30}$ by $q_{t_1},q_{t_2},\ldots ,$ $q_{t_{30}}$, respectively. For any fixed parameters r, c, $\sigma$ and each index i with $2\le i\le 30$, we solve the updated uncertain circuit equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \mathrm{d}Q_{t}=\left( \frac{5}{r}-\frac{Q_{t}}{rc}\right) \mathrm{d}t+\frac{\sigma }{r}\mathrm{d}C_{t}&{} \\ \displaystyle Q_{t_{i-1}}=q_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and obtain the ith residual as follows,

$$\begin{aligned} \begin{aligned} \varepsilon _i(r,c,\sigma )&=\left( 1+\exp \left( \frac{\pi \left( (q_{t_{i-1}}-5c)\exp \left( \displaystyle \frac{t_{i-1}-t_{i}}{rc}\right) +5c-q_{t_{i}}\right) }{\sqrt{3}\sigma c\left( 1-\exp \left( \displaystyle \frac{t_{i-1}-t_{i}}{rc}\right) \right) } \right) \right) ^{-1}. \end{aligned} \end{aligned}$$

Table 10 Charge data stored on the capacitor of series RC circuit ( Liu (2021))

Since the number of unknown parameters is 3 and the first three moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2, 1/3 and 1/4, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{29}\sum _{i=2}^{30}\varepsilon _i(r,c,\sigma )=\frac{1}{2} &{} \\ \displaystyle \frac{1}{29}\sum _{i=2}^{30}\varepsilon ^{2}_i(r,c,\sigma )=\frac{1}{3} &{} \\ \displaystyle \frac{1}{29}\sum _{i=2}^{30}\varepsilon ^{3}_i(r,c,\sigma )=\frac{1}{4}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} r^*=9.7957,\ c^*=0.9976,\ \sigma ^*=0.1400. \end{aligned}$$

Thus we obtain an uncertain circuit equation

$$\begin{aligned} \begin{aligned} \mathrm{d}Q_{t}=\left( 0.5104-0.1023Q_{t}\right) \mathrm{d}t+0.0143\mathrm{d}C_{t}. \end{aligned} \end{aligned}$$

(23)

5 Alibaba stock price

As a famous internet company, Alibaba is closely related to our daily life. The following data

$$\begin{aligned} \begin{aligned}&136.03\ \ 148.96\ \ 153.60\ \ 154.81\ \ 163.82\ \ 168.87\ \ 168.02\ \ 172.37\ \ 183.66\ \ 181.75 \\&180.61\ \ 180.60\ \ 178.81\ \ 181.47\ \ 186.75\ \ 185.84\ \ 186.66\ \ 189.48\ \ 181.26\ \ 173.52 \\&158.78\ \ 151.91\ \ 152.29\ \ 160.19\ \ 165.34\ \ 168.65\ \ 174.62\ \ 167.96\ \ 173.66\ \ 177.36 \\&170.18\ \ 158.32\ \ 165.39\ \ 173.44\ \ 169.48\ \ 175.59\ \ 177.25\ \ 179.81\ \ 173.23\ \ 167.59 \\&166.89\ \ 173.91\ \ 172.04\ \ 177.25\ \ 183.93\ \ 184.89\ \ 184.77\ \ 196.49\ \ 198.28\ \ 202.65 \\&209.51\ \ 215.24\ \ 215.45\ \ 219.58\ \ 226.68\ \ 219.38\ \ 208.58\ \ 218.73\ \ 219.46\ \ 218.32 \\&206.71\ \ 209.29\ \ 196.41\ \ 181.17\ \ 186.91\ \ 189.86\ \ 196.70\ \ 206.91\ \ 207.81\ \ 201.74 \\&195.80\ \ 202.03\ \ 212.23\ \ 202.45\ \ 215.42\ \ 219.26\ \ 221.62\ \ 222.85 \\ \end{aligned} \end{aligned}$$

show Alibaba stock prices (weekly average) in US$\$$ from January 1, 2019 to June 30, 2020 reported by Nasdaq. See Fig. 3.

Fig. 3

Alibaba stock prices (weekly average) from January 1, 2019 to June 30, 2020

Let $i=1,2,\ldots ,78$ represent the weeks from January 1, 2019 to June 30, 2020, and denote the stock prices by

$$\begin{aligned} \begin{aligned} x_{1},x_{2},\ldots ,x_{78}. \end{aligned} \end{aligned}$$

(24)

In order to fit them, we employ the uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_{t}=\left( m-aX_t\right) \mathrm{d}t+\sigma \mathrm{d}C_{t} \end{aligned} \end{aligned}$$

where m, a and $\sigma$ are unknown parameters to be estimated. For any fixed parameters m, a, $\sigma$ and each index i with $2\le i\le 78$, we solve the updated uncertain differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \mathrm{d}X_{t}=\left( m-aX_t\right) \mathrm{d}t+\sigma \mathrm{d}C_{t}&{} \\ \displaystyle X_{i-1}=x_{i-1} \end{array}\right. } \end{aligned}$$

and obtain the ith residual as follows,

$$\begin{aligned} \begin{aligned} \varepsilon _i(m,a,\sigma )&=\left( 1+\exp \left( \frac{\pi \left( (ax_{i-1}-m)\exp \left( -a\right) +m-ax_{i}\right) }{\sqrt{3}\sigma \left( 1-\exp \left( -a\right) \right) } \right) \right) ^{-1}. \end{aligned} \end{aligned}$$

Since the number of unknown parameters is 3 and the first three moments of the linear uncertainty distribution $\text{ L }(0,1)$ are 1/2, 1/3 and 1/4, the system of Eq. (13) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{77}\sum _{i=2}^{78}\varepsilon _i(m,a,\sigma )=\frac{1}{2} &{} \\ \displaystyle \frac{1}{77}\sum _{i=2}^{78}\varepsilon ^{2}_i(m,a,\sigma )=\frac{1}{3} &{} \\ \displaystyle \frac{1}{77}\sum _{i=2}^{78}\varepsilon ^{3}_i(m,a,\sigma )=\frac{1}{4}. \end{array}\right. } \end{aligned}$$

Solving the above system of equations by MATLAB, we can get

$$\begin{aligned} m^*=45.9292,\ a^*=0.2404,\ \sigma ^*=8.6308. \end{aligned}$$

Thus we obtain an uncertain differential equation

$$\begin{aligned} \begin{aligned} \mathrm{d}X_{t}=\left( 45.9292-0.2404X_t\right) \mathrm{d}t+8.6308\mathrm{d}C_{t} \end{aligned} \end{aligned}$$

(25)

where $X_t$ is Alibaba stock price.

6 Conclusion

In order to make a connection between uncertain differential equation and observed data of some uncertain process, this paper first introduced the concept of residual, and designed an algorithm to calculate residuals of uncertain differential equation corresponding to observed data. Following that, a method of moments based on residuals was presented to estimate the unknown parameters in uncertain differential equations. Finally, some examples (including Alibaba stock price) were provided to illustrate the method of moments.