Abstract
As an important macroeconomic variable and monetary policy tool, interest rate has been included in the core of the economic analysis for a long time. Reasonable interest rate is significant in the aspects of improving the social credit level and playing the economic leverage role, so the modeling approach of interest rate is our concern. This paper proposes a new interest rate model on the basis of exponential Ornstein–Uhlenbeck equation under the uncertain environment. Based on the model, the pricing formulas of the zero-coupon bond, interest rate ceiling and interest rate floor are derived through the Yao–Chen formula. In addition, some numerical algorithms are designed to calculate the prices of derivations according to the pricing formulas above.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The root of Brownian motion to model the asset prices which change over time may be dated back to 1900. The Brownian motion made enormous contribution in the field of finance, while it may take negative value which is impossible in the reality. For this reason, geometric Brownian motion was introduced into the financial market after stochastic calculus was founded by Itô in 1944 and was widely applied to financial market. In 1973, Black and Scholes (1973) as well as Merton (1973) used the geometric Brownian motion to construct an option pricing theory. From then on, the Black–Scholes pricing formula broke through the limits in financial engineering.
Later on, in order to study the price of the zero-coupon bond in stochastic environment, stochastic process was employed to price the interest rate. In 1973, Merton (1973) firstly introduced an interest rate model, and then, Ho and Lee (1986) proposed a no-arbitrage model which is an extension of Merton’s model. In addition, many other economists have built plenty of equilibrium models, such as Hull and White (1990), Vasicek (1977). The valuations of interest rate ceiling and interest rate floor have been studied by many scholars. For example, the pricing and hedging interest rate options from ceiling–floor markets were discussed by Gupta and Subrahmanyam (2005). Marcozzi (2009) considered the valuation of interest rate products with effected cash flow under a multifactor Heath–Jarrow–Morton model of the term structure of interest rates by hierarchical approximation. Suarez-Taboada and Vazquez (2012) presented a numerical method to investigate the ratchet caplets pricing problems. The currency option was also studied in detail by early researchers based on the stochastic processes.
As we can see, when we use probability or statistics to build models, we need a large amount of historical data. In most case, however, the sample size is not large enough for us to estimate a probability distribution, which may lead to counterintuitive results if we insist on considering the problem by using the probability theory. As the result, we have to invite some domain experts to evaluate the chance that each event will occur through their belief degree. This provided a motivation for Liu (2007) to found an uncertainty theory. Based on normality, duality, subadditivity and product axioms, it has become a branch of axiomatic mathematics to model human uncertain behavior. In order to describe the uncertain variable, Liu (2007) employed the definitions of uncertainty distribution, inverse uncertainty distribution, expected value and variance. For the purpose of describing dynamic uncertain systems, Liu (2008) introduced uncertain process in 2008. Moreover, Liu (2009) presented canonical process which could be considered as a counterpart of Brownian motion. On the basis of canonical process, Liu introduced uncertain calculus Liu (2009) and uncertain differential equations Liu (2008). In 2012, Ge and Zhu (2012) presented a method to solve an uncertain delay differential equation which is a type of functional differential equations driven by canonical process. In 2015, Ji and Zhou (2015) studied the multi-dimensional uncertain differential equation and proved it has a unique solution provided that its coefficients satisfy the Lipschitz condition and the linear growth condition.
In a complicated market, the changes which arise from political policies, social events and many other unknown factors will more or less affect the variation trend of interest rate in the near future, and it is almost impossible to give an exact estimation of consequence led by the parameters and the probabilities. In this case, under the assumption that stock price follows a geometric canonical process, uncertain differential equations were first applied to finance to monitor the market behavior by Liu (2009) in 2009. Furthermore, Liu (2008) proposed an uncertain stock model and derived a European option pricing formula. Chen (2011) studied American option pricing formula for uncertain stock market subsequently. In addition, Peng and Yao (2010) proposed an uncertain mean-reverting stock model to describe the fluctuation of the stock price in the long term. Considering the sudden drifts on the stock price, Ji and Zhou (2015) proposed an uncertain stock model with both positive jumps and negative jumps in the form of uncertain differential equation with jumps. Recently, Liu et al. (2015) proposed an uncertain currency model and explored its mathematical properties. In 2013, Chen and Gao (2013) proposed three different uncertain term structure models of interest rate which are the counterparts of the Ho and Lee (1986) model, Vasicek (1977) model and Cox–Ingersoll–Ross Cox et al. (1985) model, respectively, and they priced zero-coupon bond by using one of the three models. In the year of 2015, Zhu (2015) presented an uncertain interest rate model based on the concept of uncertain fractional differential equation and obtained the price of a zero-coupon bond. For exploring the recent developments of uncertain finance, readers may consult Liu (2010).
The exponential Ornstein–Uhlenbeck equation can provide a consistent stationary distribution for the volatility with data Masoliver and Perello (2006) Cisana et al. (2007) Eisler et al. (2007). It fairly reproduces the realized volatility which has some degree of predictability in future return changes Eisler et al. (2007). For these reasons, we propose a new type of interest rate model in this paper based on the exponential Ornstein–Uhlenbeck equation and discuss the pricing problem of zero-coupon bond, interest rate ceiling and interest rate floor within the framework of uncertainty theory. The rest of the paper is organized as follows. In the next section, we introduce some significant concepts as well as theorems in uncertainty theory. In Sections 3, we introduce the new interest rate model for the purpose of improving Chen and Gao’s (2013) model. In Sects. 4–6, we derive the pricing formulas of zero-coupon bond, interest rate ceiling and interest rate floor for uncertain interest rate model and design some numerical algorithms to calculate the prices of these derivations according to the pricing formulas above, respectively. Finally, a brief conclusion is given in the last section.
2 Preliminary
In this section, we introduce some basic definitions and theorems about uncertainty variables and uncertain differential equations.
2.1 Uncertain variable
Definition 1
(Liu 2007, Liu 2009) Let  be a \(\sigma \)-algebra on a non-empty set \(\Gamma \). A set function
be a \(\sigma \)-algebra on a non-empty set \(\Gamma \). A set function  :
:  is called an uncertain measure if it satisfies the following axioms:
is called an uncertain measure if it satisfies the following axioms:
-
Axiom 1: (Normality Axiom)
 for the universal set \(\Gamma \).
for the universal set \(\Gamma \). -
Axiom 2: (Duality Axiom)
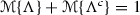 for any event \(\Lambda \).
for any event \(\Lambda \). -
Axiom 3: (Subadditivity Axiom) For every countable sequence of events \(\Lambda _1, \Lambda _2,\ldots \), we have

-
Axiom 4: (Product Axiom) Let
 be uncertainty spaces for \(k=1,2,\ldots \). The product uncertain measure
be uncertainty spaces for \(k=1,2,\ldots \). The product uncertain measure  is an uncertain measure satisfying
is an uncertain measure satisfying 
where \(\Lambda _k\) are arbitrarily chosen events from
 for \(k=1,2,\ldots \), respectively.
for \(k=1,2,\ldots \), respectively.
Definition 2
(Liu 2007) An uncertain variable is a measurable function \(\xi \) from an uncertainty space  to the set of real numbers. Therefore, for any Borel set B of real numbers, the set
to the set of real numbers. Therefore, for any Borel set B of real numbers, the set
is an event.
The uncertainty distribution \(\Phi (x)\) of an uncertain variable \(\xi \) is defined by  for any real number x. An uncertainty distribution \(\Phi (x)\) is called regular if it is a continuous and strictly increasing function with respect to x at which \(0<\Phi (x)<1\), and
for any real number x. An uncertainty distribution \(\Phi (x)\) is called regular if it is a continuous and strictly increasing function with respect to x at which \(0<\Phi (x)<1\), and
The inverse function \(\Phi ^{-1}(\alpha )\) of the regular uncertainty distribution \(\Phi (x)\) is called the inverse uncertainty distribution of the uncertain variable \(\xi \). For example, the linear uncertain variable \(\mathcal{L}(a,b)\) has an uncertainty distribution
and an inverse uncertainty distribution
where a and b are real numbers with \(a<b\).
Definition 3
(Liu 2009) The uncertain variables \(\xi _1, \xi _2,\ldots , \xi _n\) are said to be independent if

for any Borel sets \(B_1, B_2,\ldots , B_n\) of real numbers.
Theorem 1
(Liu 2010) Let \(\xi _1, \xi _2,\ldots , \xi _n\) be independent uncertain variables with regular uncertainty distributions \(\Phi _1, \Phi _2,\ldots , \Phi _n\), respectively. If the function \(f(x_1,x_2,\ldots ,x_n)\) is strictly increasing with respect to \(x_1, x_2,\ldots , x_m\) and strictly decreasing with respect to \(x_{m+1}, x_{m+2},\ldots , x_n\), then
is an uncertain variable with an inverse uncertainty distribution
For example, let \(\xi _1\) and \(\xi _2\) be two independent uncertain variables with regular uncertainty distributions \(\Phi _1\) and \(\Phi _2\), respectively. Take \(f(x_1, x_2)=\exp (x_1)+\exp (-x_2)\), then \(f(\xi _1, \xi _2)\) has an inverse uncertainty distribution
Definition 4
(Liu 2007) The expected value of an uncertain variable \(\xi \) is defined by

provided that at least one of the two integrals exists.
Liu (2007) showed, for an uncertain variable \(\xi \) with an uncertainty distribution \(\Phi \), if its expected value exists, then
Theorem 2
(Liu 2010) Assume the uncertain variable \(\xi \) has a regular uncertainty distribution \(\Phi .\) Then,
2.2 Uncertain differential equation
In order to model the evolution of uncertain phenomena, Liu (2008) put up the concept of uncertain process which is a sequence of uncertain variables indexed by the time and gave the concept of time integral which is an integral of uncertain process with respect to the time.
Definition 5
(Liu 2008) Let \(X_t\) be an uncertain process. For any partition of closed interval [a,b] with \(a=t_1<t_2<\ldots <t_{k+1}=b\), the mesh is written as
Then, the time integral of \(X_t\) with respect to t is
provided that the limit exists almost surely and is finite. In this case, the uncertain process \(X_t\) is said to be time integrable.
Definition 6
(Liu 2009) An uncertain process \(C_t\) is called a canonical Liu process if
-
(i)
\(C_0=0\) and almost all sample paths are Lipschitz continuous,
-
(ii)
\(C_t\) has stationary and independent increments,
-
(iii)
every increment \(C_{s+t}-C_s\) is a normal uncertain variable with an uncertainty distribution
$$\begin{aligned} \Phi _t(x)=\left( 1+\exp \left( \frac{-\pi x}{\sqrt{3}t}\right) \right) ^{-1}. \end{aligned}$$
Definition 7
(Liu 2009) Let \(X_t\) be an uncertain process and \(C_t\) be a canonical Liu process. For any partition of closed interval [a, b] with \(a=t_1<t_2<\ldots <t_{k+1}=b,\) the mesh is written as
Then, Liu integral of \(X_t\) with respect to \(C_t\) is defined by
provided that the limit exists almost surely and is finite.
Definition 8
(Liu 2008) Suppose that \(C_t\) is a canonical Liu process, and f and g are continuous functions. Then,
is called an uncertain differential equation.
Theorem 3
(Chen and Liu 2010) Let \(u_{1t}, u_{2t}, v_{1t}, v_{2t}\) be integrable uncertain processes. Then, the linear uncertain differential equation
has a solution
where
Definition 9
(Yao and Chen 2013) The \(\alpha \)-path \((0< \alpha < 1)\) of an uncertain differential equation
with an initial value \(X_0\) is a deterministic function \(X_{t}^{\alpha }\) with respect to t that solves the corresponding equation
where \(\Phi ^{-1}(\alpha )\) is the inverse uncertainty distribution of standard normal uncertain variable, i.e.,
Theorem 4
Yao–Chen Formula (Yao and Chen 2013) Assume that \(X_t\) and \(X_t^\alpha \) are the solution and \(\alpha \)-path of the uncertain differential equation
Then,

Theorem 5
(Yao and Chen 2013) Let \(X_t\) and \(X_t^{\alpha }\) be the solution and \(\alpha \)-path of the uncertain differential equation
Then, the solution \(X_t\) has an inverse uncertainty distribution
Theorem 6
(Yao 2013) Let \(X_t\) and \(X_t^{\alpha }\) be the solution and \(\alpha \)-path of the uncertain differential equation
Then, for any time \(t > 0\) and strictly increasing function J(x), the time integral
has an \(\alpha \)-path
Conversely, for any time \(t > 0\) and strictly decreasing function H(x), the time integral
has an \(\alpha \)-path
Theorem 7
(Yao 2015) Let \(X_{1t}, X_{2t}, \ldots , X_{nt}\) be independent uncertain processes with \(\alpha \)-paths \(X_{1t}^\alpha \), \(X_{2t}^\alpha \), \(\ldots \), \(X_{nt}^\alpha \), respectively. If the function \(f(x_1, x_2, \ldots , x_n)\) is strictly increasing with respect to \(x_1, x_2,\ldots , x_m\) and strictly decreasing with respect to \(x_{m+1}, x_{m+2}, \ldots , x_n\), then the uncertain process
has an \(\alpha \)-path
3 Uncertain interest rate model
The uncertain differential equations play a significant role in the financial market. In 2013, Chen and Gao (2013) assumed that the interest rate \(r_t\) follows uncertain differential equations and proposed an uncertain term structure model of interest rate as below,
which is the counterpart of the Ho and Lee (1986) model. However, this model has a flaw: The interest rate \(r_t\) may take negative value.
In this section, we make some improvements referring to Chen and Gao’s model (2) based on the exponential Ornstein–Uhlenbeck equation which describes the velocity of a massive Brownian particle under the influence of friction. Considering that the exponential Ornstein–Uhlenbeck equation can ensure the volatility of data which follows a consistent stationary distribution and can predict the future return changes in some degree, we propose a new uncertain interest rate model in the form of exponential Ornstein–Uhlenbeck equation as below,
where \(r_t\) denotes interest rate, \(\mu , c, \sigma \) are some positive constants and \(C_t\) is a canonical Liu process.
Theorem 8
Let \(\mu , c, \sigma \) be some positive constants and \(C_t\) be a canonical Liu process. Then, the uncertain differential equation
has a solution
Proof
Divide both sides of the equation by \(r_t\) simultaneously, then we have
Replacing \(\ln r_t\) with \(X_t\), we could get
By Theorem 3, since
we have
Since \(X_t=\ln r_t\), \(X_0=\ln r_0\), we have
which is equivalent to
The proof is complete.
According to Yao–Chen Formula (Theorem 4), the \(\alpha \)-path of \(X_t\) in Equation (5) solves the ordinary differential equation
where
so we have
As mentioned, \(X_t^\alpha =\ln r_t^\alpha \) and \(X_0=\ln r_0\), we have
So the \(\alpha \)-path of \(r_t\) is
4 Zero-coupon bond pricing formulas
A zero-coupon bond is a bond bought at a price lower than its face value but repaid at the face value on the maturity date. For simplicity, we assume the face value is always 1 dollar. According to Chen and Gao (2013), the price of a zero-coupon bond with a maturity date t is
Theorem 9
Assume the uncertain interest rate \(r_t\) follows the exponential Ornstein–Uhlenbeck equation
where \(\mu , c, \sigma \) are some positive numbers, and \(C_t\) is a canonical Liu process. Then, the price of a zero-coupon bond with a maturity date t is
where
Proof
Let \(\Phi _t^{-1}(\alpha )\) denote the inverse uncertainty distribution of \(r_t\) and \(r_t^\alpha \) denote the \(\alpha \)-path of \(r_t\). Then, it follows from Theorem 6 that the time integral
has an inverse uncertainty distribution
Since \(\exp (-x)\) is a strictly decreasing function, the uncertain variable
has an inverse uncertainty distribution
Thus, the price for the zero-coupon bond with a maturity date t is
according to Theorem 2. \(\square \)
Zero-coupon bond price \(f_z\) with respect to maturity date t in Example 1
Based on Theorem 9, the algorithm to calculate the price of the zero-coupon bond based on the interest rate model (3) is designed as below:
- Step 0: :
-
Choose two large numbers N and M according to the desired precision degree. Set \(\alpha _i=i/N\) and \(t_j=j \cdot t/M\), \(i=1,2,\ldots ,N,\) \(j=1,2,\ldots ,M.\)
- Step 1: :
-
Set \(i=0.\)
- Step 2: :
-
Set \(i\leftarrow i+1.\)
- Step 3: :
-
Set \(j=0.\)
- Step 4: :
-
Set \(j\leftarrow j+1.\)
- Step 5: :
-
Calculate the interest rate

If \(j<M\), return to Step 4.
- Step 6: :
-
Calculate the discount rate
$$\begin{aligned} \exp \left( -\int _0^t r_s^{\alpha _i}\mathrm{d}s\right) \leftarrow \exp \left( -\frac{t}{M}\sum _{j=1}^Mr_{t_j}^{\alpha _i}\right) . \end{aligned}$$If \(i<N-1\), return to Step 2.
- Step 7: :
-
Calculate the price of zero-coupon bond price
$$\begin{aligned} f_z\leftarrow \frac{1}{N-1}\sum _{i=1}^{N-1}\exp \left( -\frac{t}{M}\sum _{j=1}^Mr_{t_j}^{\alpha _i}\right) . \end{aligned}$$
Example 1
Assume the initial value of the interest rate is \(r_0=0.03\), and other parameters of the interest rate are \(c=0.1, \mu =0.05\) and \(\sigma =0.04\). Then, the price of a zero-coupon bond with a maturity date \(t=5\) is \(f_z=0.8359.\) Figure 1 shows that the price \(f_z\) is a decreasing function with respect to the maturity date t when the other parameters remain unchanged.
5 Interest rate ceiling pricing formula
An interest rate ceiling is a derivative contract which is an agreement reached by the bank and the customer. Buying the contract means the borrower will not need to pay any more than a predetermined level of interest on his loan. For simplicity, we assume the amount of loan is always 1 dollar. According to Zhang et al. (2016), the price of the interest rate ceiling with a maturity date t and a striking price K is
Theorem 10
Assume the uncertain interest rate \(r_t\) follows the exponential Ornstein–Uhlenbeck equation
where \(\mu , c, \sigma \) are some positive numbers, and \(C_t\) is a canonical Liu process. Then, the price of the interest rate ceiling with a maximum interest rate K and a maturity date t is
where
Proof
Let \(\Phi _t^{-1}(\alpha )\) denote the inverse uncertainty distribution of \(r_t\) and \(r_t^\alpha \) denote the \(\alpha \)-path of \(r_t\). Since \((r_s-K)^+\) is a strictly increasing function, it follows from Theorem 6 that the time integral
has an inverse uncertainty distribution
Since \(\exp (-x)\) is a strictly decreasing function with respect to x, the uncertain variable
has an inverse uncertainty distribution
Thus, the price for the interest rate ceiling with a maturity date t and a striking price K is
according to Theorem 2.\(\square \)
Based on Theorem 10, the algorithm to calculate the price of the interest rate ceiling based on the interest rate model (3) is designed as below:
- Step 0: :
-
Choose two large numbers N and M according to the desired precision degree. Set \(\alpha _i=i/N\) and \(t_j=j \cdot t/M\), \(i=1,2,\ldots ,N,\) \(j=1,2,\ldots ,M.\)
- Step 1: :
-
Set \(i=0.\)
- Step 2: :
-
Set \(i\leftarrow i+1.\)
- Step 3: :
-
Set \(j=0.\)
- Step 4: :
-
Set \(j\leftarrow j+1.\)
- Step 5: :
-
Calculate the interest rate
$$\begin{aligned}&r_{t_j}^{\alpha _i}=\exp \left( \ln r_0\cdot \exp (-c\mu t_j)+(1-\exp (-c\mu t_j))\right. \nonumber \\&\qquad \left. \times \,\left( \frac{1}{c}+\frac{\sqrt{3}\sigma }{\pi \mu c}\ln \frac{\alpha _i}{1-\alpha _i}\right) \right) . \end{aligned}$$ - Step 6: :
-
Calculate the the positive deviation between the interest rate at time \(t_j\) and the maximum interest rate K
$$\begin{aligned} \left( r_{t_j}^{\alpha _i}-K\right) ^+=\max \left( 0,r_{t_j}^{\alpha _i}-K\right) . \end{aligned}$$If \(j<M\), return to Step 4.
- Step 7: :
-
Calculate
$$\begin{aligned}&\exp \left( -\int _0^t \left( r_s^{\alpha _i}-K\right) ^+\mathrm{d}s\right) \\&\quad \leftarrow \exp \left( -\frac{t}{M}\sum _{j=1}^M\left( r_{t_j}^{\alpha _i}-K\right) ^+\right) . \end{aligned}$$If \(i<N-1\), return to Step 2.
- Step 8: :
-
Calculate the price of interest rate ceiling
$$\begin{aligned} f_c\leftarrow 1-\frac{1}{N-1}\sum _{i=1}^{N-1}\exp \left( -\frac{t}{M}\sum _{j=1}^M\left( r_{t_j}^{\alpha _i}-K\right) ^+\right) . \end{aligned}$$
Example 2
Assume the initial value of the interest rate is \(r_0=0.03\), and other parameters of the interest rate are \(c=0.1, \mu =0.05\) and \(\sigma =0.04\). Then, the price of an interest rate ceiling with a striking price \(K=0.02\) and a maturity date \(t=5\) is \(f_c=0.0762.\) Figure 2 shows that the price \(f_c\) is an increasing function with respect to the maturity date t when the other parameters remain unchanged.
Interest rate ceiling price \(f_c\) with respect to maturity date t in Example 2
Example 3
Assume the initial value of the interest rate is \(r_0=0.03\), and other parameters of the interest rate are \(c=0.1, \mu =0.05\) and \(\sigma =0.04\). Then, the price of an interest rate ceiling with a striking price \(K=0.02\) and a maturity date \(t=2\) is \(f_c=0.0240.\) Figure 3 shows that the price \(f_c\) is a decreasing function with respect to the striking price K when the other parameters remain unchanged.
Interest rate ceiling price \(f_c\) with respect to striking price K in Example 3
6 Interest rate floor pricing formula
An interest rate floor is a derivative contract which is an agreement reached by the bank and the customer. Buying the contract means the investor will not receive any less than a predetermined level of interest on his investment. For simplicity, we assume the amount of loan is always 1 dollar. According to Zhang et al. (2016), the price of the interest rate floor with a maturity date t and a striking price K is
Theorem 11
Assume the uncertain interest rate \(r_t\) follows the exponential Ornstein–Uhlenbeck equation
where \(\mu , c, \sigma \) are some positive numbers, and \(C_t\) is a canonical Liu process. Then, the price of the interest rate floor with a minimum interest rate K and a maturity date t is
where
Proof
Let \(\Phi _t^{-1}(\alpha )\) denote the inverse uncertainty distribution of \(r_t\) and \(r_t^\alpha \) denote the \(\alpha \)-path of \(r_t\). Since \((K-x)^+\) is a strictly decreasing function, it follows from Theorem 6 that the time integral
has an inverse uncertainty distribution
Since \(\exp (x)\) is a strictly increasing function with respect to x, the uncertain variable
has an inverse uncertainty distribution
Thus, the price for the interest rate floor with a maturity date t and a striking price K is
according to Theorem 2.
Interest rate floor price \(f_l\) with respect to maturity date t in Example 4
Interest rate floor price \(f_l\) with respect to striking price K in Example 5
Regarding interest rate floor of the interest rate model (3) based on Theorem 10, the first five steps are the same as interest rate ceiling, and the rest steps are as follows.
- Step 6: :
-
Calculate the the positive deviation between the interest rate at time \(t_j\) and the minimum interest rate K
$$\begin{aligned} \left( K-r_{t_j}^{\alpha _i}\right) ^+=\max \left( 0,K-r_{t_j}^{\alpha _i}\right) . \end{aligned}$$If \(j<M\), return to Step 4.
- Step 7: :
-
Calculate
$$\begin{aligned} \exp \left( \int _0^t \left( K-r_s^{\alpha _i}\right) ^+\mathrm{d}s\right) \leftarrow \exp \left( \frac{t}{M}\sum _{j=1}^M\left( K-r_{t_j}^{\alpha _i}\right) ^+\right) . \end{aligned}$$If \(i<N-1\), return to Step 2.
- Step 8: :
-
Calculate the price of interest rate floor
$$\begin{aligned} f_l\leftarrow \frac{1}{N-1}\sum _{i=1}^{N-1}\exp \left( \frac{t}{M}\sum _{j=1}^M\left( K-r_{t_j}^{\alpha _i}\right) ^+\right) -1. \end{aligned}$$
Example 4
Assume the initial value of the interest rate is \(r_0=0.03\), and other parameters of the interest rate are \(c=0.1, \mu =0.05\) and \(\sigma =0.04\). Then, the price of an interest rate floor with a striking price \(K=0.04\) and a maturity date \(t=5\) is \(f_l=0.0260.\) Figure 4 shows that the price \(f_l\) is an increasing function with respect to the maturity date t when the other parameters remain unchanged.
Example 5
Assume the initial value of the interest rate is \(r_0=0.03\), and other parameters of the interest rate are \(c=0.1, \mu =0.05\) and \(\sigma =0.04\). Then, the price of an interest rate floor with a striking price \(K=0.04\) and an maturity date \(t=2\) is \(f_l=0.0158.\) Figure 5 shows that the price \(f_l\) is an increasing function with respect to the striking price K when the other parameters remain unchanged.
7 Conclusions
In this paper, we proposed an interest rate model referring the exponential Ornstein–Uhlenbeck equation and employed it to price the zero-coupon bond, interest rate ceiling and interest rate floor under the uncertain environment. Subsequently, some numerical methods were designed to calculate the price of the zero-coupon bond as well as the interest rate ceiling and interest rate floor, and some numerical experiments were performed. Future research could consider the currency pricing problems using the interest rate model proposed in this paper.
References
Black F, Scholes M (1973) The pricing of options and corporate liabilities. J Polit Econ 81:637–654
Chen X, Liu B (2010) Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optim Dec Mak 9(1):69–81
Chen X (2011) American option pricing formula for uncertain financial market. Int J Op Res 8(2):32–37
Chen X, Gao J (2013) Uncertain term structure model for interest rate. Soft Comput 17(4):597–604
Cisana E, Fermi L, Montagna G, Nicrosini O (2007) A comparative study of stochastic volatility models, arXiv:0709.0810v1
Cox J, Ingersoll J, Ross S (1985) An intertemporal general equilibrium model of asset prices. Econometrica 53:363–382
Eisler Z, Perello J, Masoliver J (2007) Volatility: a hidden Markov process in financial time series. Phys Rev 76:056105
Ge XT, Zhu YG (2012) Existence and uniqueness theorem for uncertain delay differential equations. J Comput Inf Syst 8(20):8341–8347
Gupta A, Subrahmanyam MG (2005) Pricing and hedging interest rate options: evidence from cap-floor markets. J Bank Financ 29(2):701–733
Ho T, Lee S (1986) Term structure movements and pricing interest rate contingent claims. J Financ 5:1011–1029
Hull J, White A (1990) Pricing interest rate derivative securities. Rev Fin Stud 3:573–592
Ji XY, Zhou J (2015) Multi-dimensional uncertain differential equation: existence and uniqueness of solution. Fuzzy Optim Dec Mak 14(4):477–491
Ji XY, Zhou J (2015) Option pricing for an uncertain stock model with jumps. Soft Comput 19(11):3323–3329
Liu B (2007) Uncertainty theory, 2nd edn. Springer-Verlag, Berlin
Liu B (2008) Fuzzy process, hybrid process and uncertain process. J Uncertain Syst 2(1):3–16
Liu B (2009) Some research problems in uncertainty theory. J Uncertain Syst 3(1):3–10
Liu B (2010) Uncertainty theory: a branch of mathematics for modeling human uncertainty. Springer-Verlag, Berlin
Liu Y, Chen X, Ralescu DA (2015) Uncertain currency model and currency option pricing. Int J Intell Syst 30(1):40–51
Marcozzi MD (2009) On the valuation of interest rate products under multifactor HJM term structures. Appl Numer Math 59(2):2873–2890
Masoliver J, Perello J (2006) Multiple time scales and the exponential Ornstein-Uhlenbeck stochastic volatility model. Quant Financ 6(2):423–433
Merton R (1973) Theory of rational option pricing. Bell J Econ Manag Sci 4(1):141–183
Peng J, Yao K (2010) A new option pricing model for stocks in uncertainty markets. Int J Oper Res 7(4):213–224
Suarez-Taboada M, Vazquez C (2012) Numerical solution of a PDE model for a ratchet-cap pricing with BGM interest rate dynamics. Appl Math Comput 218(2):5217–5230
Vasicek O (1977) An equilibrium characterization of the term structure. J Fin 5:177–188
Yao K, Chen X (2013) A numerical method for solving uncertain differential equations. J Intell Fuzzy Syst 25(3):825–832
Yao K (2013) Extreme values and integral of solution of uncertain differential equations. J Uncertain Anal Appl 1(2):1
Yao K (2015) Uncertain contour process and its application in stock model with floating interest rate. Fuzzy Optim Dec Mak 14(4):399–424
Zhang ZQ, Ralescu DA, Liu WQ (2016) Valuation of interest rate ceiling and floor in uncertain financial market. Fuzzy Optim Dec Mak 15(2):139–154
Zhu YG (2015) Uncertain fractional differential equations and an interest rate model. Math Methods Appl Sci 38(15):3359–3368
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos. 61403360 and 61374082) and the Special Funds for Science and Education Fusion of University of Chinese Academy of Sciences.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Sun, Y., Yao, K. & Fu, Z. Interest rate model in uncertain environment based on exponential Ornstein–Uhlenbeck equation. Soft Comput 22, 465–475 (2018). https://doi.org/10.1007/s00500-016-2337-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2337-1




 for the universal set
for the universal set 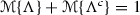 for any event
for any event 
 be uncertainty spaces for
be uncertainty spaces for  is an uncertain measure satisfying
is an uncertain measure satisfying 
 for
for 




