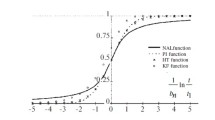
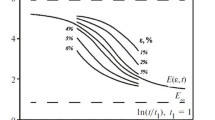
The method for calculating the relaxation properties of polymer textile materials developed using mathematical models allows assessing qualitatively the performance properties of these materials.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
When carrying out a qualitative assessment of the relaxation properties of polymer textile materials, it is possible to use the criteria developed for this purpose separately or combining them into one complex criterion. It is possible because the relaxation properties as parameters of mathematical models of relaxation processes of these materials obey the Cauchy law possessing the additivity property [1].
For a qualitative assessment of the relaxation properties of polymer textile materials, the following criteria were developed:
- the intensity of material recovery after operation;
- the degree of material recoverability after operation;
- the possibility of the material repeated recovery during the operation process;
- the recovery time of the material functional properties after operation;
- material resistance to repeated recovery of functional properties during the operation process.
In addition to these five local criteria, two complex criteria for the qualitative assessment of the relaxation properties of polymer textile materials have been developed [2].
Assessment of the operational parameters of polymer textile materials, taking into account the criteria for relaxation properties formulated above, should be carried out in dimensionless units.
To develop criteria for qualitative assessment of the relaxation properties of polymer textile materials, let us use a mathematical model of relaxation written in the form [3]
where t is the time; σt is the stress arising in the material under the action of the applied deformation ε; bε is the parameter of relaxation intensity; E0 and E” are the asymptotic values of the relaxation modulus Eεt = (σt/ε); t1 is the value of the datum time; φεt is the relaxation function in the form of the normalized arctangent of logarithm (NAL).
Local Criteria for Assessing Relaxation Properties
Let us consider the first criterion for the qualitative assessment of the relaxation properties of polymer textile materials – the intensity of material recovery after operation [4].
Let us denote α1 = bnε – a dimensionless quantity characterizing the degree of intensity of a polymer textile material recovery after operation. The quantity α1 is numerically equal to the relaxation intensity parameter, which is responsible for the recovery of the material functional properties.
One can note that the quantity α1 takes only non-negative values: α1 > 0. The smaller the value of α1, the faster the material recovers after operation. And vice versa, the higher its value, the slower the material recovers after operation.
If for two different materials the inequality α1k > α1n is fulfilled, it means that the material with the number n recovers after operation faster than the material with the number k.
The considered criterion should be applied when it is required to assess how quickly the functional properties of polymer textile materials recover after operation. Sometimes it is important that the material quickly recovers its functional properties after operation and is ready for subsequent operation [5].
Let us consider the second criterion for the qualitative assessment of the relaxation properties of polymer textile materials – the degree of material recoverability after operation [6].
Let us denote α2 = [E”/(E0 + E”)] – a dimensionless quantity characterizing the degree of polymer textile material recoverability after operation.
One can note that the introduced quantity α2 can take only non-negative values: α2 > 0. The smaller the value of α2, the more complete the recoverability of the polymer textile material after operation.
And vice versa, the higher the value of α2, the less complete the recoverability of the polymer textile material after operation.
It means that if for two different materials the inequality α2k > α2n is fulfilled, the material with the number n recovers more completely after operation than the material with the number k.
According to the denotation of α2, the material completely recovers at a zero value of the viscoelastic modulus E” = 0. In this case, obviously, α2 = 0.
The introduced criterion is of particular value when it is required to assess how long the material under study can retain its functional properties [7].
When considering the third criterion for the qualitative assessment of the relaxation properties of polymer textile materials – the possibility of the material repeated recovery during operation [8], let us denote α3 = ε0/εr – a dimensionless quantity characterizing the possibility of such recovery.
Here, εr is the experimentally obtained value of the rupture deformation (in %); ε0 is a certain normalizing value of deformation; for example, ε0 = 10%.
The quantity α3 can take only non-negative values: α3 > 0. The smaller the value of α3, the greater the ability of the material to repeatedly recover the functional properties during operation. And vice versa, the higher the value of α3, the less the ability of the polymer textile material to repeatedly recover its functional properties during operation.
The introduced criterion is of particular importance when it is necessary to assess how many times polymer textile materials can recover their operational properties during operation [9].
Let us consider the fourth criterion for the qualitative assessment of the relaxation properties of polymer textile materials – the recovery time of the material functional properties after operation [10].
Let us denote α4 = \( \overline{\uptau} \)ε/t1 – a dimensionless quantity characterizing the recovery time of the functional properties of the polymeric textile material after operation.
Here, t1 is a certain value of normalizing datum time; for example, t1 = 600 s; \( \overline{\uptau} \)ε is the average relaxation time, which can be calculated using the formula
where ε1 is the lower limit of the studied deformation range; ε2 is the upper limit of this range.
It means that the studied deformation can vary within the limits ε ∈ [ε1, ε2].
The quantity α4 can take only non-negative values: α4 > 0. The smaller the value of α4, the faster the material recovers after operation. And vice versa, the higher the value of α4, the slower the material recovers after operation.
The introduced criterion is of particular importance when it is necessary to assess how quickly or slowly a certain material recovers after operation [11].
Considering the fifth criterion for the qualitative assessment of the relaxation properties of polymer textile materials – the material resistance to repeated recovery of functional properties during operation [12], let us denote α5 = E”/(E0 – E”) – a dimensionless quantity characterizing the material resistance to repeated recovery of functional properties during operation.
The quantity α5 can take only non-negative values: α5 > 0. The smaller the value of α5, the more resistant the polymer textile material to repeated recovery of its functional properties during operation. And vice versa, the higher the value of α5, the less resistant the material to repeated recovery of its functional properties during operation.
The higher the resistance of a polymeric textile material to repeated recovery of functional properties during operation, the less dependent the properties on the influence of external factors (temperature, humidity, radiation, etc.).
A zero value of quantity α5 = 0 means that the material is absolutely resistant to repeated recovery of its functional properties during operation [13].
Complex Criteria for Assessing Relaxation Properties
An important role in the qualitative assessment of the relaxation properties of polymer textile materials is played by the NAL normalized relaxation function– the basis of the mathematical model of these properties, which is an integral function for the Cauchy distribution, which possesses the additivity property [14].
Due to this, the numerical values of the parameters of the mathematical model of relaxation of the studied polymer textile materials, namely E0, E”, bnε, τε, should also obey the Cauchy probability law. Hence it follows that the proposed values α1, α2, α3, α4, α5 are also subject to Cauchy law.
It is known that the Cauchy probability distribution is close to the normal distribution and differs from it by the delayed convergence of the NAL integral function to its asymptotes, which is not true for the integral function of normal distribution – the probability integral [15].
The described feature of the NAL integral function of the Cauchy distribution substantiates the adequacy of processing statistical samples – relaxation properties and parameters determined experimentally.
Let us note that the rupture characteristic εr, although it is not a relaxation parameter of a polymer textile material, is subject to the Cauchy law, since it is close enough to normal [16]. Let us also note that with respect to the introduced probabilistic quantities α1, α2, α3, α4, α5, one can assume that they are distributed according to the Cauchy law.
Therefore, it is advisable to consider a new complex relaxation quantity Ar = α1 + α2 + α3 + α4 + α5, which includes all the mentioned quantities α1, α2, α3, α4, α5 and is also distributed according to the Cauchy probability law due to its additivity [17].
Taking into account the properties of the quantities α1, α2, α3, α4, α5, one can argue that their sum, the quantity Ar, is non-negative: Ar > 0.
Analysing the local criteria for the qualitative assessment of the relaxation properties of polymer textile materials considered above, one can note that for all the introduced quantities α1, α2, α3, α4, α5, the functional properties of these materials are the better, the smaller the values of the indicated quantities, i.e. the smaller the complex relaxation quantity Ar [18].
Hence, for example, it follows that such a material for which the complex relaxation quantity has a zero value (Ar = 0) possesses the best functionality [19]. However, such materials do not exist in nature.
Analysing the above, let us obtain an analytical form of writing the first complex criterion for optimizing the relaxation properties of polymer textile materials [20]:
where k is the number of the material sample; Ark is the value of the relaxation quantity of the k-th sample of the material; N is the material sample size (the number of samples taken); \( \overline{A} \)r is the average value for relaxation quantities Ark.
In the case when in the qualitative assessment of the relaxation properties of polymer textile materials, it is necessary to reveal the dominant role of one or several quantities from the set A = {α1, α2, α3, α4, α5}, or, on the contrary, the role of one or several quantities from this set is insignificant, the most appropriate criterion for optimizing the relaxation properties of polymer textile materials is the second complex criterion. It includes the quantities α1, α2, α3, α4, α5 with the corresponding weights λ1, λ2, λ3, λ4, λ5 [21].
The set of these weights can be written as Λ = {λ1, λ2, λ3, λ4, λ5}.
The analytical form of writing the second complex criterion for optimizing the relaxation properties of polymer textile materials has the form [22]:
where k is the number of the material sample; \( {\overline{A}}_{\mathrm{p}k}^{\uplambda} \) is the value of the relaxation quantity of the k-th sample of the material; N is the material sample size (the number of samples taken); \( {\overline{A}}_{\mathrm{p}k}^{\uplambda} \) is the average value for relaxation quantities \( {A}_{\mathrm{p}k}^{\uplambda} \); λ is the superscript of the relaxation quantities Ar, showing that the quantities α1, α2, α3, α4, α5 are included in the assessment criterion of Eq. (5) with their weights λ1, λ2, λ3, λ4, λ5.
Along with the analytical form of writing the second complex criterion for optimizing the relaxation properties of polymer textile materials of Eq. (5), it is also convenient to write it in a vector form [23].
Thus, assuming that A and Λ are five-dimensional vectors, the vector form of writing the second complex criterion for optimizing the relaxation properties of polymer textile materials is obtained [24]:
where k is the number of the material sample.
Thus, the first and second complex criteria for optimizing the relaxation properties of polymer textile materials have been developed. These criteria include the local criteria for qualitative assessment of the specified properties of the materials under study as components: the intensity of material recovery after operation; the degree of material recoverability after operation; the possibility of the material repeated recovery during operation; the recovery time of the material functional properties after operation; material resistance to repeated recovery of functional properties during operation.
The developed criteria for qualitative assessment of the relaxation properties of polymer textile materials allow assessing their functionality and giving recommendations for optimizing the relaxation properties of these materials in order to increase their functionality.
References
N. V. Pereborova, A. G. Makarov, et al., “Methods of simulation and comparative analysis of shadow and deformation-reducing properties of aramide textile materials,” Izv. VUZ, Tekhnol. Tekst. Promysh., 375, No. 3, 253-257 (2018).
A. S. Gorshkov, A. G. Makarov, et al., “Modelling of directed polymers deformation processes based on the description of the kinetics of supramolecular structures separated by energy barriers,” Mag. Civil Eng., 44, No. 9, 76-83 + 103-104 (2013).
A. G. Makarov, N. V. Pereborova, et al., “Quality analysis of deformation-relaxation properties of aramid cords mountain rescue appointments,” Izv. VUZ, Tekhnol. Tekst. Promysh., 368, No. 2, 309-313 (2017).
P. P. Rymkevich, A. A. Romanova, et al., “The energy barriers model for the physical description of the viscoelasticity of synthetic polymers: application to the uniaxial orientational drawing of polyamide films,” J. Macromol. Sci. B, 52, No. 12, 1829-1847 (2013).
N. V. Pereborova, A. G. Makarov, et al., “Methods of increasing the competitiveness of domestic aramid textile materials based on complex analysis of their functional properties,” Izv. VUZ, Tekhnol. Tekst. Promysh., 378, No. 6, 267-272 (2018).
N. V. Pereborova, A. V. Demidov, et al., “Methods of mathematical modeling and qualitative analysis of relaxation-deformation processes of aramide textile materials,” Izv. VUZ, Tekhnol. Tekst. Promysh., 374, No. 2, 251-255 (2018).
A. V. Demidov, A. G. Makarov, et al., “Forecasting of deformation-relaxation properties of poly amide fabric used to make the canopy,” Izv. VUZ, Tekhnol. Tekst. Promysh., 367, No. 1, 250-258 (2017).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “System analysis of viscoelasticity of textile stuffs,” Izv. VUZ, Tekhnol. Tekst. Promysh., 298, No. 3, 11-14 (2007).
A. G. Makarov, N. V. Pereborova, et al., “Mathematical modelling of deformation-relaxation processes polymeric materials in conditions of variable temperatures,” Izv. VUZ, Tekhnol. Tekst. Promysh., 370, No. 4, 287-292 (2017).
A. G. Makarov, N. V. Pereborova, et al., “Modelling and forecasting viscoelastic properties of textile materials with a complex structure,” Izv. VUZ, Tekhnol. Tekst. Promysh., 354, No. 6, 120-124 (2014).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “The criteria of optimal selection of mathematical model of textile materials viscoelasticity,” Izv. VUZ, Tekhnol. Tekst. Promysh., 293, No. 5, 21-25 (2006).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “A version of modeling of nonlinear-hereditary viscoelasticity of polymer materials,” Mech. Sol., 44, No. 1, 122-130 (2009).
A. G. Makarov, N. V. Pereborova, et al., “Ways of modelling deformation and relaxation properties of textile materials with a complex structure,” Izv. VUZ, Tekhnol. Tekst. Promysh., 351, No. 3, 110-115 (2014).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “Definition of the computer forecasting trends of deformation properties of textile stuffs,” Izv. VUZ, Tekhnol. Tekst. Promysh., 297, No. 2, 14-17 (2007).
A. G. Makarov, A. V. Demidov, et al., “Modelling and prediction of estimated relaxation and deformation properties of the polymer parachute line,” Izv. VUZ, Tekhnol. Tekst. Promysh., 360, No. 6, 194-205 (2015).
A. M. Stalevich and A. G. Makarov, “Determining the inherent viscoelastic relaxation spectrum for synthetic filaments,” Izv. VUZ, Tekhnol. Tekst. Promysh., 255, No. 3, 8-12 (2000).
A. V. Demidov, A. G. Makarov, et al., “Research of changes of deformation properties of polyester threads depending on twist amount,” Izv. VUZ, Tekhnol. Tekst. Promysh., 292, No. 4, 9-13 (2006).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “Definition of the mechanical characteristics of textile stuffs at variable temperature,” Izv. VUZ, Tekhnol. Tekst. Promysh., 291, No. 3, 13-17 (2006).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “Definition of the mechanical characteristics of textile stuffs at variable temperature,” Izv. VUZ, Tekhnol. Tekst. Promysh., 294, No. 6, 15-18 (2006).
A. V. Demidov, A. G. Makarov, and A. M. Stalevich, “Predicting the nonlinear hereditary viscoelasticity of polymers,” J. Appl. Mech. Tech. Phy., 48, No. 6, 897-904 (2007).
A. M. Stalevich, A. G. Makarov, and E. D. Saidov, “Relaxation spectrometry of synthetic yarns,” Izv. VUZ, Tekhnol. Tekst. Promysh., 270, No. 1, 16-22 (2003).
A. G. Makarov, “Determining the analytical correlation between the standardized nuclei of relax-ation and creep in textile materials,” Izv. VUZ, Tekhnol. Tekst. Promysh., 266, No. 2, 13-17 (2002).
A. M. Stalevich and A. G. Makarov, “Forecasting the deformation recovery process and the reverse relaxation in polymer materials,” Izv. VUZ, Tekhnol. Tekst. Promysh., 267, No. 3, 10-13 (2002).
A. M. Stalevich and A. G. Makarov, “Forecasting the deformation recovery process and the reverse relaxation in polymer materials,” Izv. VUZ, Tekhnol. Tekst. Promysh., 268, No. 4-5, 15-18 (2002).
The research was financed within the framework of fulfilling the state assignment of the Ministry of Science and Higher Education of the Russian Federation. Project No. FSEZ-2020-0005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Khimicheskie Volokna, No. 2, pp. 74-78, March-April, 2021.
Rights and permissions
About this article
Cite this article
Pereborova, N.V. Criteria for Qualitative Assessment of Relaxation Properties of Polymer Textile Materials. Fibre Chem 53, 132–136 (2021). https://doi.org/10.1007/s10692-021-10253-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10692-021-10253-7