Functional-use and performance properties of textile industry materials are based primarily on determination of the physicomechanical properties of these materials, to the study of which paramount attention must be paid.

For a comprehensive study and prediction of the functional-use and performance properties of textile industry materials to improve the quality of goods therefrom, it is proposed to conduct investigations of the basic relaxationrecovery and deformation-performance processes, i.e., relaxation and creep, which characterize the key physicomechanical properties of the materials [1,2,3].

It is expedient to conduct such study making use of mathematical modeling, followed by computer-aided prediction of relaxation and creep.

Although relaxation and creep processes are different in physical nature, they are, in fact, reciprocal processes harmoniously complementing each other. Because of this, the study of relaxation and deformation properties of textile industry materials relating primarily to the class of viscoelastic solids is an essential and, in some cases, an urgent task [4,5,6].

Relaxation process implies a change in the stress σt (or force Ft) applied to a material over a time t under the action of deformative ε:

$$ \upsigma =\upsigma (t)=\frac{F(t)}{s}. $$
(1)

A key property of relaxation process is relaxation modulus Eεt = σt/ε, which has two asymptotic values:modulus of viscoelasticity

$$ {E}_{\infty }=\underset{t\to \infty }{\lim }{E}_{\varepsilon t} $$
(2)

and modulus of elasticity [7,8,9]

$$ {E}_0=\underset{t\to 0}{\lim }{E}_{\varepsilon t}. $$
(3)

The relaxation modulus Eεt can be modeled mathematically using increasing normalized relaxation function φεt that acquires significance in the segment [0.1]:

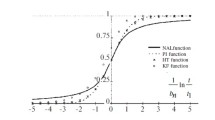
$$ {E}_{\varepsilon t}={E}_0-\left({E}_0-{E}_{\infty}\right){\varphi}_{\varepsilon t}. $$
(4)

Let us take the normalized arc tangent of logarithm (NAL) that characterizes the Cauchy integral distribution as the relaxation function φεt [10, 14]:

$$ {\varphi}_{\varepsilon t}=\frac{1}{2}+\frac{1}{2\pi}\mathrm{arctg}\left(\frac{1}{b_{n\varepsilon}}\mathrm{In}\frac{t}{\tau_{\varepsilon }}\right), $$
(5)

where τε − a characteristic of mean relaxation time and bnε − a characteristic of relaxation intensity.

For ease of modeling, logarithmic scale of reduced dimensionless time is used.

Instead of the mean relaxation time parameter τε, which is defined by the deformation-time function of shears in logarithmic time scale, it is proposed to consider the mean relaxation time \( {\overline{\tau}}_{\varepsilon } \) determined by the equation

$$ {\overline{\tau}}_{\varepsilon }=\frac{1}{\varepsilon_2-{\varepsilon}_1}\underset{\varepsilon_1}{\overset{\varepsilon_1}{\int }}{\tau}_{\varepsilon } d\varepsilon, $$
(6)

where ε1, ε2 – minimum and maximum values from the studied deformation range [15,16,17,18].

When determination only of qualitative properties of the materials is needed, switch from functional relationship to a constant is justified for mathematical modeling of relaxation-recovery properties. Such switch greatly simplifies the mathematical model, which is of considerable importance for investigating qualitative viscoelastic properties. Note that in more detailed studies of viscoelastic-relaxation processes, for example, from the spectral analysis premises, such switch to a simplified mathematical model is unjustified [19,20,21].

Thus, equation (4) is a mathematical model of polymer material relaxation process.

The choice of the function NAL as the foundation of the mathematical model of relaxation is not accidental because the Cauchy probability distribution, the integral function of distribution of which it is, possesses a unique property, i.e., the sum of the characteristics distributed in accordance with the Cauchy probability law also has by its distribution the Cauchy probability distribution. For textile industry materials obeyance to this law is extremely important because any complex textile object is an aggregate of simpler textile objects (yarns consist of fibers, fabrics consist of yarns, etc.). So, if the parameters of simpler textile materials obey the Cauchy probability distribution law, the parameters of more complex textile materials will also obey this distribution law [22,23,24,25].

The method of determination of functional-use relaxation-recovery properties of textile and light industry materials is based on numerical treatment of experimental “family” of relaxation curves for values of deformation constant ε = const obtained on a stress relaxometer.

An example of the graph of “family” of relaxation curves for Nitron polymer yarn with a linear density of 33.3 tex at constant values of deformation ε is given in Fig. 1.

Fig. 1
figure 1

Graph depicting experimental “family” of relaxation curves of 33.3 tex Nitron yarn at constant deformation values.

Full size image

Introducing the formula for the studied normalized relaxation function (5)

$$ {\varphi}_{\varepsilon t}=\frac{1}{2}+\frac{1}{\pi}\mathrm{arctg}\left({W}_{\varepsilon t}\right)=\varphi \left({W}_{\varepsilon t}\right) $$
(7)

with the argument

$$ {W}_{\varepsilon t}=\frac{1}{b_{n\varepsilon}}\mathrm{In}\frac{1}{\tau_{\varepsilon }}=\frac{1}{b_{n\varepsilon}}\left[\mathrm{In}\left(\frac{t}{t_1}\right)+\mathrm{In}\left(\frac{t}{\tau_{\varepsilon }}\right)\right] $$
(8)

and differentiating (4) further we get the expression for the derivative from the relaxation modulus:

$$ {E}_{\varepsilon t}^{\prime }=\frac{{\partial E}_{\varepsilon t}}{\partial \mathrm{In}\frac{\mathrm{t}}{t_1}}=-\left({E}_0-{E}_{\infty}\right){\overline{r}}_{\varepsilon t}=-\frac{1}{b_{n\varepsilon}}\bullet \frac{1}{\pi}\bullet \left({E}_0-{E}_{\infty}\right)\frac{1}{1+{W}_{\varepsilon t}}, $$
(9)

which contains the relaxation core \( {\overline{r}}_{\varepsilon t} \):

$$ {\overline{r}}_{\varepsilon t}=\frac{{\partial \varphi}_{\varepsilon t}}{\partial \mathrm{In}t}=\frac{1}{b_{n\varepsilon}}\bullet \frac{1}{\pi}\bullet \frac{1}{1+{W}_{\varepsilon t}^2}. $$
(10)

The quantity t1 means the value of the “base” time, which we will assume for convenience as t1 = 60 sec. The base time value is needed so that a dimensionless quantity lay under the sign of the logarithm.

Considering that the extreme value of the derivative from the relaxation modulus \( {E}_{\varepsilon \tau}^{\prime } \) is attained at Wεt = Wτ = 0, let us determine its corresponding characteristic value of relaxation modulus Eτ:

$$ {E}_{\tau }={E}_0-\left({E}_0-{E}_{\infty}\right)\bullet 0.5=\frac{\left({E}_0+{E}_{\infty}\right)}{2}, $$
(11)

which enables determination of the width of the band of relaxation modulus values:

$$ 2\Delta {E}_{\tau }=2\bullet \left({E}_0-{E}_{\infty}\right)={E}_0-{E}_{\infty }=2\bullet \left({E}_{\tau }-{E}_{\infty}\right), $$
(12)

whence we get the elasticity modulus value

$$ {E}_0={E}_{\tau }+{\Delta E}_{\tau } $$
(13)

and the viscoelasticity modulus value

$$ {E}_{\infty }={E}_{\tau }-\Delta {E}_{\tau }. $$
(14)

Hence, under the condition of attainability of the extremum at the midpoint of the band at Wτ = 0 we can determine using expression (9) the characteristic value for the derivative from the relaxation modulus:

$$ {E}_{\tau}^{\prime }=-\frac{1}{b_{n\varepsilon}}\bullet \frac{1}{\pi}\bullet \left({E}_0-{E}_{\infty}\right)=-\frac{1}{b_{n\varepsilon}}\bullet \frac{2}{\pi}\bullet \Delta {E}_{\tau }. $$
(15)

Further, from expressions (9) and (15) we get

$$ {E}_{\varepsilon \tau}^{\prime }={E}_{\tau}^{\prime}\bullet \frac{1}{1+{W}_{\varepsilon t}^2}, $$
(16)
$$ {W}_{\varepsilon \tau}=\sqrt[\pm ]{\frac{E_{\tau}^{\prime }}{E_{\varepsilon \tau}^{\prime }}}-1. $$
(17)

Subtracting equation (4) from equation (11) and taking account of (12) we get:

$$ {E}_{\varepsilon t}-{E}_{\tau }=\left({E}_0-{E}_{\infty}\right)\bullet \left(0.5-{\varphi}_{\varepsilon t}\right)=2\Delta {E}_{\tau}\left(0.5-{\varphi}_{\varepsilon t}\right), $$
(18)

or

$$ {\Delta E}_{\tau }=-0.5\frac{\left({E}_{\varepsilon \tau}-{E}_{\tau}\right)}{\varphi \left({W}_{\varepsilon \tau}\right)-0.5}, $$
(19)

whence we get the characteristic value of the relaxation intensity 1/bnε:

$$ \frac{1}{b_{\varepsilon t}}=-\frac{\pi }{2}\bullet \frac{E_{\tau}^{\prime }}{{\Delta E}_{\tau }}. $$
(20)

The characteristic of the mean relaxation time τε is obtained as a parameter of time shift of the relaxation curve obtained for the deformation ε value until coincidence with the generalized relaxation curve obtained by equation (4) [26,27,28].

The relaxation characteristics E0, E∞, τε, and bnε of textile industry materials obtained by the method of modeling of the functional-use relaxation-recovery properties of these materials are proposed to be used further for evaluation of their quality. Note as well that the relaxation properties obtained by mathematical modeling using NAL function obey Cauchy probability distribution, which is particularly important for materials that have a complex (composite) macroscopic structure.

The method of determination of functional-use relaxation-recovery properties of textile industry materials is applicable for a variety of textile materials, such as textile yarns (technical characteristics listed in Table 1), Capron tapes (Table 2), and technical fabrics (Table 3).

Table 1 Technical Characteristics of Studied Textile Yarns.
Full size table
Table 2 Technical Characteristics of Studied Capron Tapes.
Full size table
Table 3 Technical Characteristics of Studied Technical Fabrics.
Full size table

The calculated relaxation-recovery properties of textile yarns are listed in Table 4, of Capron tapes, in Table 5, and of technical fabrics, in Table 6.

Table 4 Calculated Relaxation-Recovery Properties of Textile Yarns.
Full size table
Table 5. Calculated Relaxation-Recovery Properties of Studied Capron Tapes.
Full size table
Table 6 Calculated relaxation-recovery properties of studied technical fabrics.
Full size table

A preliminary evaluation of the functional-use relaxation-recovery properties of the studied materials can be made from the calculation parameters of the functional-use relaxation-recovery properties of textile industry materials, namely, elasticity modulus E0, viscoelasticity modulus E∞, relaxation process intensity 1/bnε, and mean relaxation time \( {\overline{\tau}}_{\varepsilon } \) [29,30,31,32].

For example, among the textile yarns, Nitron yarn having a linear density of 33.3 tex is the one whose elastic properties are restored most fully after deformation because its viscoelasticity modulus is the lowest (E = 0.8 GPa). The elastic properties of Lavsan yarn having a linear density of 15.6 tex are least restored because its viscoelasticity modulus is the highest (E∞ = 6.5 GPa).

At the same time, the restoration is most intense for Capron yarn having a linear density of 91 tex because its intensity parameter value is the highest (1/bnε = 0.43). The restoration process is least intense for Lavsan yarn because its intensity parameter has the lowest value (1/bnε = 0.09).

If the textile yarns are compared in terms of mean relaxation time, it can be stated here that among the textile yarns the elastic properties of Capron yarn having a linear density of 149 tex are restored fastest because its mean relaxation time is the least (\( {\overline{\tau}}_{\varepsilon } \) = 98 sec) and the elastic properties of Capron yarn with a linear density of 410 tex are restored the slowest because its mean relaxation time is the longest (\( {\overline{\tau}}_{\varepsilon } \) = 207 sec).

Thus, application of the mathematical model and the method of determination of functional-use relaxationrecovery properties of textile industry materials is tested on a representative group of textile materials, for which predictable relaxation-recovery parameters and properties, which have a decisive importance for comparative analysis and qualitative sapling of materials possessing specific properties, were obtained.